Dynamic heterogeneity as a strategy of stem cell self-renewal

Significance

In many tissues, such as intestine and skin, cells are constantly turned over throughout life. To replenish cells that are lost, new cells are generated by stem cells, which divide and differentiate to maintain tissue in a steady state. The mechanisms that allow stem cells to achieve perfect self-renewal promise fundamental insights into processes leading to diseased states. Efforts to define strategies of stem cell self-renewal have placed emphasis on models in which stem cells progress one way through a differentiation hierarchy. Here, we show that a different paradigm, in which stem cells transfer reversibly between states primed for renewal or poised for differentiation, offers a viable and robust mechanism of tissue self-renewal.

Abstract

To maintain cycling adult tissue in homeostasis the balance between proliferation and differentiation of stem cells needs to be precisely regulated. To investigate how stem cells achieve perfect self-renewal, emphasis has been placed on models in which stem cells progress sequentially through a one-way proliferative hierarchy. However, investigations of tissue regeneration have revealed a surprising degree of flexibility, with cells normally committed to differentiation able to recover stem cell competence following injury. Here, we investigate whether the reversible transfer of cells between states poised for proliferation or differentiation may provide a viable mechanism for a heterogeneous stem cell population to maintain homeostasis even under normal physiological conditions. By addressing the clonal dynamics, we show that such models of “dynamic heterogeneity” may be equally capable of describing the results of recent lineage tracing assays involving epithelial tissues. Moreover, together with competition for limited niche access, such models may provide a mechanism to render tissue homeostasis robust. In particular, in 2D epithelial layers, we show that the mechanism of dynamic heterogeneity avoids some pathological dependencies that undermine models based on a hierarchical stem/progenitor organization.

Stem cells are defined by their capacity to self-renew long-term while giving rise to more differentiated cell types. To achieve homeostasis, the choice between proliferation and differentiation—stem cell fate—needs to be perfectly balanced (1–4). In recent years, experimental techniques for tracing cell lineages in vivo have enabled quantitative information to be gathered on the proliferative potential of stem cells. In particular, inducible genetic labeling methods have allowed the fate behavior of individual cells and their progeny—clones—to be traced over time (5–7). Using these approaches, quantitative analyses have shown that the cell lineage data in many mammalian tissues conform to a pattern by which stem cell fate is chosen stochastically in a balanced way, such that the average number of stem cells in a tissue is conserved (8–11).

In defining the quantitative fate behavior of stem cells and their differentiating progeny, most studies begin with a model in which stem and progenitor cells are organized in a one-way proliferative hierarchy. In this paradigm, the loss of stem cell competence and entry into a differentiation pathway is an irreversible process. However, in recent years it has been shown that, under conditions of stress or injury, cells normally committed to differentiation may reacquire stem cell competence and contribute to the long-term maintenance of tissue (12–18). Moreover, intravital imaging studies of mouse testis and intestine suggest that, even under normal physiological conditions, adult stem cells are not homogeneous but may transfer reversibly between states primed for proliferation and differentiation (19–21). Finally, evidence for stem cell flexibility has also been observed in the context of cell competition, induced through the activation of oncogenic mutation, with potential implications for the initiation of cancer (11, 22, 23).

Taken together, these observations suggest that transition through a differentiation pathway may not involve the sequential one-way progression through a hierarchy of functionally equivalent states but may instead be dynamic and heterogeneous, allowing cells to move reversibly between states primed for duplication or differentiation (24–26). The genetic basis of such behavior, which we term “dynamic heterogeneity,” has been considered in a variety of contexts (21, 27, 28).

In this study, we address theoretically the question of whether tissue maintenance can be sustained by a process of dynamic stem cell heterogeneity, whether it can be discriminated from hierarchical self-renewal strategies by cell lineage tracing assays, and whether such a mechanism offers advantages in promoting robustness. Specifically, we consider a paradigm in which a (stem) cell may switch stochastically between internal “states” that may differ in their potential to enter into a differentiation pathway or to proliferate. As well as investigating the clonal fate behavior of the model system we also explore how the spatial distribution of cell types is affected by dynamic heterogeneity.

Results

Dynamic Heterogeneity as a Model of Tissue Maintenance.

As a starting point, we consider a model of a cycling adult tissue that comprises a heterogeneous population of self-renewing progenitor cells that give rise to more differentiated progeny. However, the fate potential of individual progenitors is not invariant but conforms to a process of dynamic heterogeneity in which progenitors transit reversibly between states primed for proliferation or biased toward differentiation and loss. Whether these states represent defined cell types marked by signature expression of molecular markers, or whether they are simply primed by location within a niche environment, we do not distinguish. Both scenarios will lead to the same long-term clonal dynamics, the focus of the present study. For simplicity, and to illustrate the paradigmatic features of the model, we consider only two progenitor cell states, termed A and B type. State B is primed but not yet committed to terminal differentiation and loss, and is nonproliferative, whereas an A-type cell remains in cycle. However, this bias is temporary, and cells can switch reversibly and stochastically between the two states; an A-type cell can transit into a B-type cell, and a primed B-type cell can also return to the proliferative state A. From a biological perspective, the B-type cell may represent some transition state, poised in G₀, and deciding stochastically between reentry into cell cycle or commitment to terminal differentiation. Furthermore, for convenience, we assume that cell division leads to asymmetric fate outcome, $A\mathrm{\to }A+B$, noting that other “channels” of division—cell duplication or terminal division—can be captured through a combination of division and “reversion” $B\mathrm{\leftrightarrow }A$.

Within this framework, the model dynamics is specified by the “zero-dimensional” nonequilibrium process:

$$A\stackrel{\lambda }{\to }A\mathrm{+}B,\hspace{1em}A\underset{\underset{{\mathit{\omega }}_A}{\leftarrow }}{\overset{{\mathit{\omega }}_B}{\to }}B,\hspace{1em}B\stackrel{\mathit{\gamma }}{\to }\mathrm{Ø}$$ [1]

where λ denotes the cell division rate and ${\mathit{\omega }}_{B,A}$ represent the transition rates from $A\to B$, respectively $B\to A$. The last process denotes the rate, γ, at which B-type cells commit to terminal differentiation and loss. In the following we refer to this dynamics as the dynamic heterogeneity (DH) model. Finally, for simplicity, we suppose that all processes are stochastic and Markovian, with the defined average rates. Although periodicity in the timing of cell division and differentiation would affect the short-term dynamics, the long-term behavior would be unaffected.

In the following, we will compare the kinetics of the DH model with that of a more orthodox hierarchical scheme (termed the H model) in which progenitor cell fate is assigned irreversibly following cell division, with only A-type cells retaining stem-like renewal potential (cf. refs. 8 and 11):

$$A\stackrel{\lambda }{\to }\{\begin{array}{ll}A+A\hfill & \text{Pr}.r+\mathrm{\Delta }/2\hfill \\ A+B\hfill & \text{Pr}.1-2r\hfill \\ B+B\hfill & \text{Pr}.r-\mathrm{\Delta }/2\hfill \end{array},\hspace{1em}B\stackrel{\mathit{\gamma }}{\to }\mathrm{Ø}\mathrm{.}$$ [2]

Here $0\le r\le 1/2$ determines the relative frequency of symmetric ($A\to A+A,\hspace{0.17em}B+B$) vs. asymmetric cell division ($A\to A+B$), and $\mathrm{\Delta }$ parameterizes the potential bias in cell fate toward cell proliferation or differentiation. The parameters r and Δ may be constant and set intrinsically, or be moderated by extrinsic cues from their niche environment (9, 10, 29). Moreover, one can conceive of further adaptations of the model in which the B-type cell population has a limited renewal potential (viz. transit amplification) or represents just one cell type in a longer hierarchy (30). Crucially, however, the H model, as defined by Eq. 2, is paradigmatic of all models that involve a one-way proliferative hierarchy in which the differentiating progeny of A-type cells are irreversibly committed to differentiation.

In recent years, lineage tracing studies of stratified epithelial tissues (including interfollicular epidermis, esophagus, and trachea), have found that the dynamics of epithelial cell populations are consistent with models based on the hierarchical scheme (8, 9, 11). In the following, we will investigate whether a model of dynamic heterogeneity can also provide a basis for long-term tissue maintenance, and whether its dynamics can be discriminated from that of a hierarchical model through clone size statistics alone.

Robustness of Homeostasis.

If the rates of cell division and cell fate ratios of the H and DH model are fixed, for a given arbitrary choice of parameters, the average size of the cell population is not stationary and the system is not homeostatic. Instead, the average number of A- and B-type cells would expand or contract over time. To achieve homeostasis in the H model, the net rate of progenitor cell duplication must perfectly balance differentiation and loss, requiring that the degree of imbalance, $\mathrm{\Delta }$, must be tuned to zero. In ref. 31 it was suggested that the dynamics of the H model can be rendered stable by imposing a feedback mechanism in which $\mathrm{\Delta }$ depends on the total size of the A-cell pool. Indeed, it is known that the cell division rate can be correlated with local cell density (32) (contact inhibition) as well as the cell loss rate (33, 34), a phenomenon that we call crowding feedback (for a discussion of potential feedback mechanisms, see refs. 35–39). For the H model, such crowding feedback in the cell division rate or loss rate is not sufficient to confer stability. Without spatial regulation, only by controlling the cell fate bias $\mathrm{\Delta }$ may stability be imposed (Supporting Information).

In the DH model, the time evolution of the average densities of cell type A, $n_A$, and of cell type B, $n_B$—where $n_{B,A}$ are cell numbers normalized by volume—is given by (Supporting Information)

$$\begin{array}{l}{\partial }_t{n}_A={\omega }_A\hspace{0.17em}{n}_B-{\omega }_B\hspace{0.17em}{n}_A\\ {\partial }_t{n}_B=\left(\lambda +{\omega }_B\right)\hspace{0.17em}{n}_A-\left(\gamma +{\omega }_A\right)\hspace{0.17em}{n}_B.\end{array}$$ [3]

Therefore, to achieve homeostasis, viz. ${\partial }_t{n}_{A,B}=0$, the corresponding rates must also be fine-tuned such that

$$\frac{\gamma }{\mathit{\lambda }}=\frac{{\omega }_A}{{\omega }_B}\hspace{0.17em}.$$ [4]

Under these conditions, with constant rates (i.e., no feedback), the average density of A- and B-type cells remains constant with $n_B=\left(\lambda /\gamma \right)n_A$. When seeded away from these values, $n_A$ and $n_B$ will converge back to their steady-state values, as depicted in the flow diagram (Fig. 1A). If, however, the balance condition is not met, the populations of A- and B-type cells either decay to zero ($n_{A,B}=0$) or grow indefinitely (cf. Fig. 1B).

Fig. 1.

Flow diagrams of the time evolution of the system, Eq. 3, as a function of $n_A,n_B$ measured in units ${\lambda }_0/k$, where $k=-{\partial }_n\lambda$ is the strength of the crowding feedback. We chose $\gamma ,{\omega }_B=0.5{\lambda }_0$. The arrows show the direction of the time evolution $\left({\partial }_t{n}_A,{\partial }_t{n}_B\right)$. (A) Without crowding feedback, $\lambda ={\lambda }_0$, but balanced parameters ${\omega }_A=\gamma {\omega }_B/\lambda$. There is a line of fixed points $n_B=\left(\lambda /\gamma \right)\hspace{0.17em}{n}_A$, but along this line cell densities undergo neutral drift. (B) Without crowding feedback, $\lambda ={\lambda }_0$, no fate balance, ${\omega }_A=2.1{\omega }_B>\gamma \hspace{0.17em}{\omega }_B/\lambda$. The cell population diverges. (C) For crowding feedback with $\lambda \left(n\right)={\lambda }_0-k\hspace{0.17em}n$ a stable fixed point emerges (black dot).

Even when the systems are fine-tuned to conditions of homeostasis, without further regulation, both models are unstable toward fluctuations. In particular, in a closed system in which the size of the cell population is only finite, statistical fluctuations due to stochastic dynamics will inevitably lead to the chance extinction of the population.

The mechanism of crowding feedback can be incorporated in the models by imposing a dependence of the parameters on the average total density of cells $n=n_A+n_B$. To illustrate this, we consider the case where the cell division rate depends on n, viz. $\lambda =\lambda \left(n\right)$, and decreases monotonically with n, ${\partial }_n\lambda <0$, as would be the case for contact inhibition (32). With this implementation, the DH model, Eq. 3, acquire a single stable fixed point with

$$n^{\mathrm{\ast }}={\lambda }^{-1}\left(\frac{{\omega }_B\gamma }{{\omega }_A}\right),\hspace{1em}{n}_A^{\mathrm{\ast }}=\rho \hspace{0.17em}{n}^{\mathrm{\ast }},$$ [5]

where ${\lambda }^{-1}\left(\mathrm{\cdots }\right)$ denotes the inverse of the function $\lambda \left(n\right)$ and $\rho ≔{\omega }_A/\left({\omega }_A+{\omega }_B\right)$ is an effective parameter, equivalent to the steady-state fraction of A-type cells (Supporting Information). In particular, for a linear response $\lambda \left(n\right)={\lambda }_0-k\hspace{0.17em}n$, where ${\lambda }_0$ is the unconstrained cell division rate without crowding and $k=-{\partial }_n\lambda >0$ parameterizes the strength of the feedback, the stationary point is $n^{\mathrm{\ast }}=\left({\lambda }_0-{\omega }_B\gamma /{\omega }_A\right)/k$. Inspection of the flow diagram (Fig. 1C) shows that in this case the stationary point is indeed globally stable. In Supporting Information we show that, in fact, the system achieves a stable homeostatic state for any monotonically decreasing function, $\lambda \left(n\right)$, that achieves the point $\lambda ={\omega }_B\gamma /{\omega }_A$ at some given value of n. Since there is only one stable point, the system will eventually attain this homeostatic steady state.

Importantly, referring to Supporting Information for details, a stable homeostatic state is also attained when any of the other parameters, γ, ${\omega }_A$, or ${\omega }_B$, are subject to negative feedback from the total cell density n. In each case, the parameters self-adjust to attain the balance condition 4. It therefore follows that, in the case of dynamic heterogeneity, the system is robust, meaning that the failure of one feedback pathway can be compensated by another to maintain homeostasis. By contrast, for the H model, a stable homeostatic state is only attained if the cell fate bias $\mathrm{\Delta }$ is a function of cell density n (Supporting Information). Crowding feedback in the parameters λ, γ, and r is not sufficient to confer stability.

Clonal Dynamics.

So far we have discussed the average behavior of the DH model and its stability, but we have not addressed the dynamics of clones. Because the dynamics of the model is stochastic, the time evolution and survival of individual clones is variable and unpredictable. However, the dynamics of the statistical ensemble of clones can be determined. In the following we will consider the time-evolution of the clone size distribution in the balanced case (fulfilling Eq. 4), defined as the probability $P_{N_A,N_B}\left(t\right)$ to find a clone with $N_A$ A cells and $N_B$ B cells at time t when starting with a single labeled cell at $t=0$ (clonal induction).

Assuming a representative labeling of cell types, starting with a single cell means that we have initially a cell of type A with probability $\rho ={\omega }_A/\left({\omega }_A+{\omega }_B\right)$ and of type B with probability $\left(1-\rho \right)$. For the H model, Eq. 2, it was shown that, over time, the distribution of total clone sizes N converges onto the form (8, 29) (for $N\gg 1$)

$$P_N^H\left(t\right)=\frac{1}{{\left(\mathrm{\Omega }t\right)}^2}\hspace{0.17em}\exp \left(-\frac{N}{\mathrm{\Omega }t}\right),$$ [6]

where $\mathrm{\Omega }=\lambda \hspace{0.17em}r/\rho$ defines the growth rate of the average size of surviving clones, that is, clones that retain at least one cell, ${\langle N\rangle }_s={\left(1-P_0^H\left(t\right)\right)}^{-1}{\displaystyle {\sum }_{N>0}N{P}_N^H\left(t\right)=\mathrm{\Omega }\hspace{0.17em}t}$, and $P_0^H\left(t\right)=\mathrm{\Omega }t/(1+\mathrm{\Omega }t)$ is the extinction probability (40). In turn, the survival probability (norm of $P_N^H$ in Eq. 6) diminishes as $1/\left(\mathrm{\Omega }t\right)$ at large times, so that the total cell number remains on average constant, consistent with homeostasis.

Formally, the dynamics of the clone size distribution for the DH model can be obtained from the master equation for the probability $P_{N_A,N_B}^{DH}\left(t\right)$, as given in Eq. S2 of the Supporting Information. In general, a full analytic solution to the master equation is unavailable. However, to address the long-time dependence of the probability distribution in the balanced case (fullfilling Eq. 4), we proceed by a van Kampen system size expansion (41) to transform the master equation into the Fokker–Planck equation (FPE) involving a continuous function $P\left(N_A,N_B\right)$ that interpolates $P_{N_A,N_B}^{DH}$ (Supporting Information). The latter can be solved by an adequate variable substitution, and for large times the solution can be expressed as a function of $N=N_A+N_B$ only (Supporting Information),

$$P\left(N,t\right)=\frac{1}{{\left(\mathrm{\Omega }t\right)}^2}\hspace{0.17em}\text{exp}\left(-\frac{N}{\mathrm{\Omega }t}\right),$$ [7]

with

$$\mathrm{\Omega }=\frac{{\omega }_B}{\rho }\frac{1+\frac{{\omega }_B}{\lambda }}{{\left(1+\frac{{\omega }_B}{\lambda \mathit{\rho }}\right)}^2}\hspace{0.17em},$$ [8]

where we chose to eliminate the parameter γ through Eq. 4. From these results it follows that the long-term clone size distribution of the DH model is identical to that of the hierarchical model. It also follows that for a slow rate of cell type conversion, ${\omega }_{A,B}\ll \lambda$, the clonal growth rate $\mathrm{\Omega }\approx {\omega }_B/\rho$ is proportional to the switching rate, whereas for fast conversion, ${\omega }_{A,B}\gg \lambda$, we have $\mathrm{\Omega }\approx \lambda \rho$, proportional to the cell division rate. In the latter case, each cell loses memory about its priming quickly and the two cell types behave just like a single proliferating cell population with both cell division rate and terminal differentiation rate $\lambda \rho$. This means that, between two divisions, the probability of each cell to differentiate is 1/2, which corresponds to the cell fate model suggested by Marques-Pereira and Leblond (42) in their study of esophageal maintenance.

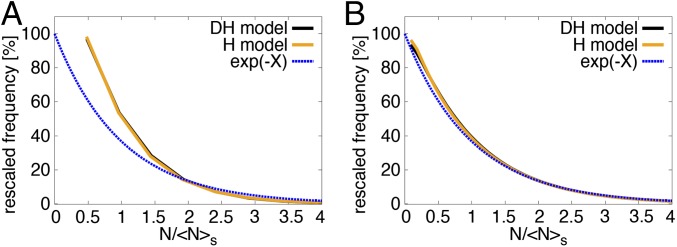
To assess how rapidly the system converges onto the limiting size dependences defined above, the full solution of the master equation can be determined at arbitrary times from numerical integration (Materials and Methods). In Fig. 2 and Fig. S1, the numerical solutions for the distribution of clone sizes for the DH and H model are shown as a function of the clone size, scaled by the average clone size. This comparison shows that H and DH models are not distinguishable, both at short times ($t=1/\mathrm{\Omega }$) and at longer times ($t=10/\mathrm{\Omega }$). Moreover, at $t=10/\mathrm{\Omega }$, the distributions have already converged onto the predicted long-term scaling form, Eq. 7. In the Supporting Information and Fig. S2 it is also confirmed that Eq. 8 for $\mathrm{\Omega }$ agrees well with the numerical solution of the master equation.

Fig. 2.

Rescaled clone size distribution, showing normalized clonal frequencies as a function of rescaled clone size $X=N/{\langle N\rangle }_s$, where ${\langle N\rangle }_s=\mathrm{\Omega }t$ is the average size of surviving clones (i.e., with $N>0$). Here we choose ${\omega }_{A,B}=\gamma =\lambda$ in the DH model, so that $\mathrm{\Omega }=\left(4/9\right)\hspace{0.17em}\lambda$, and we choose $r=2/9$ for the H model to mimic this. Black lines are numerical results from the DH model (Eq. 1), orange lines are numerical results from the H model (Eq. 2), and dashed blue lines are the analytical result for long times, $\text{exp}\left(-X\right)$. (A) At short times postinduction, $\mathrm{\Omega }t=1.0$, the clone statistics of the DH and H model are indistinguishable but are distinct from the long-time exponential asymptotic dependence. (B) At long times, $\mathrm{\Omega }t=10.0$, both models coincide with each other and the predicted long-term dependence.

Fig. S1.

Rescaled clone size distribution. Clonal frequencies as a function of rescaled clone size $X=N/{\langle N\rangle }_s$, where ${\langle N\rangle }_s={\left(1-P_0\right)}^{-1}{\displaystyle {\sum }_{N>0}N{P}_N}$ is the average size of surviving clones. Chosen parameters are $\gamma ={\omega }_A={\omega }_B/3$, ${\omega }_B=\lambda$ in the DH model, so that $\mathrm{\Omega }=\left(8/\mathrm{25}\right)\hspace{0.17em}\lambda$, and we choose $r=2/25$ for the H model to mimic this (note that in contrast to the main text, here ${\omega }_B\ne {\omega }_A$). Black lines are numerical results from the DH model, orange lines are numerical results from the H model (see main text), and dashed blue lines are the analytical result for long times, $\text{exp}\left(-X\right)$. (A) At short times postinduction, $\mathrm{\Omega }t=\mathrm{1.0}$. (B) At long times, $\mathrm{\Omega }t=10.0$.

Fig. S2.

Theoretical prediction for the scaling parameter $\mathrm{\Omega }$ as defined in Clonal Evolution Without Spatial Regulation, according to Eq. S33 (blue line), together with results for $\mathrm{\Omega }$ from numerical solution of the original master equation, Eq. S2 (points, see Materials and Methods) for $K=\mathrm{1}$.

Thus, when expressed in terms of the dimensionless rescaled variable $X=N/{\langle N\rangle }_s$, the clone size distribution of the DH model and of the H model cannot be discriminated, based only on static clonal data.

Spatial Regulation.

Although both the H model and DH model can be rendered stable in the zero-dimensional system through feedback mechanisms, the advantage of the latter theory, in terms of homeostatic control, becomes apparent when the system is embedded into a defined stem cell niche geometry (see refs. 43 and 44 for niche-based regulation mechanisms). To illustrate this point, in the following we consider two concrete examples: (i) one-dimensional layers of progenitor cells, where the lowest layer is stem-like (A cells) and higher layers are prone to differentiation (B cells) and (ii) a 2D epithelial sheet, as originally conceived for the H model in its application to basal interfollicular epidermis (45).

One-dimensional layers.

As a starting point, we consider a quasi one-dimensional organization of cells in which a chain of B-type cells is maintained by an adjacent population of A-type cells, as illustrated in Fig. 3A. In the course of turnover, following the rules of the DH model (Eq. 1) we suppose that A-type cells divide asymmetrically so that the daughter B-type cell replaces another B-type cell in the upper layer, which is presumed to be lost. Alternatively, an A-type cell (respectively B-type cell) can “switch” into a B-type cell (respectively A-type cell). However, to maintain the architecture of the tissue, this change of identity is accompanied by a switch of a neighboring B-type cell (respectively A-type cell) and an exchange of their positions.

Fig. 3.

Results of the DH model with spatial regulation in one dimension. (A) Illustration of the model dynamics, as defined by Eqs. 10 and 11. Cells in the lowest layer are stem cell-like (A cells) and divide asymmetrically. Cells in the upper layer (B cells) are prone to differentiation but can also switch back into an A-type cell. The different colors of the cell boundaries represent the affiliation to different clones. (B) Clone size distribution as a function of $X=N/{\langle N\rangle }_s$, resulting from stochastic simulations. Parameters: $\omega =0.1\lambda$, runtime = $100/\lambda$, system size = 10,000 lattice sites. Points are simulation results and the curve is the function $P\left(X\right)=\left(\pi /2\right)\hspace{0.17em}X\exp \left(-\pi X^2/4\right)$, which is the theoretical prediction for the hierarchical cell fate model in one dimension, Eqs. 10 and 11, and is consistent with experimental data (10).

Such dynamics mimics the process of niche-based regulation in which stem cell competence relies only on the proximity of progenitors to a localized niche environment. A similar dynamics has been conjectured to define the maintenance of the intestinal epithelium, where stem cell competence is linked to the proximity of cells to Paneth cells, which are restricted to the crypt base (19).

Effectively, the model can be reorganized as a single one-dimensional chain of alternating cell types, with each cell initially belonging to a different clone:

$$A_i\hspace{0.17em}{B}_j\hspace{0.17em}{A}_k\hspace{0.17em}{B}_l\hspace{0.17em}{A}_m\mathrm{\cdots }\text{,}$$ [9]

where the indices denote the clone affiliation. The model dynamics then read

$$A_i\hspace{0.17em}{B}_j\stackrel{\lambda }{\to }{A}_i\hspace{0.17em}{B}_i$$ [10]

$$A_i\hspace{0.17em}{B}_j\stackrel{\mathit{\omega }}{\to }{A}_j\hspace{0.17em}{B}_i.$$ [11]

Eq. 10 represents asymmetric division wherein a neighboring B-type cell of clone j is replaced by one of clone i, and Eq. 11 represents a reversion of cell type followed by an exchange of position, with rate $\omega ={\omega }_A={\omega }_B$, according to the DH model. (Note that such exchanges can occur in both directions.) With these rules, the configuration of A- and B-type cells remains by definition unchanged, ensuring homeostasis.

To explore the clonal dynamics implied by this model, we made use of a Monte Carlo simulation (Materials and Methods). The resulting clone size distribution is shown in Fig. 3B together with the theoretical prediction for the analogous one-dimensional hierarchical model, a one-dimensional voter model in which stem cell loss through differentiation is compensated by the replacement of a neighbor through duplication (29). At long times, both models converge onto the same distribution. Thus, we conclude that the process of dynamic heterogeneity can provide a viable means to ensure long-term homeostasis and cannot be discriminated from a hierarchical model by static clonal fate data alone.

Two-dimensional cell sheet.

In the following we now turn to address the implementation of cell fate models in a 2D geometry, like the arrangement of cells in an epithelial basal layer. More precisely, we consider a 2D lattice of cells illustrated in Fig. 4, in which all sites play host to either an A- or B-type cell. Keeping the total number of cells on the lattice fixed (viz. uniform cell density), cell division of an A-type cell only occurs when a neighboring B-type cell commits to terminal differentiation and leaves the cell sheet (stratification). Effectively, the constraint of fixed cell number implements (local) crowding feedback, because cell division becomes licensed only when another cell leaves the cell layer, or vice versa. For the hierarchical scheme this dynamics is captured by the following process:

$$AB\stackrel{\lambda }{\to }\{\begin{array}{ll}AA\hfill & \text{Pr}.r+\mathrm{\Delta }/2\hfill \\ BA\hfill & \text{Pr}.\left(1-2r\right)/2\hfill \\ AB\hfill & \text{Pr}.\left(1-2r\right)/2\hfill \\ BB\hfill & \text{Pr}.r-\mathrm{\Delta }/2\hfill \end{array},$$ [12]

where only neighboring lattice sites are depicted (lattice H model). Formally, as the differentiating cell B leaves the cell layer, the neighboring proliferative A-type cell may divide to replenish the vacated site, with each progeny occupying either of the two sites with equal probability. However, this process is licensed to occur only on the condition that there is an A-type progenitor bordering the differentiated B type cell. In cases where A cells border A cells, or B cells border B cells, the system is “blocked” from cell division or stratification.

Fig. 4.

Illustration of the dynamic heterogeneity model dynamics on a 2D lattice (lattice DH model), defined by the rules of Eq. 13. When an A cell (blue) divides, with rate λ, a neighboring B-type cell (white) commits to terminal differentiation and is lost (dashed boundary) and replaced by the offspring of the A-type cell. At any time an A-type cell can turn into a B-type cell, and vice versa, according to the rules of the DH model.

The process defined by Eq. 12 has been studied for the balanced case $\mathrm{\Delta }=0$ in ref. 45. There it was shown that the system coarsens over time and becomes increasingly inhomogeneous: The layer phase separates into A- and B-cell-rich domains that grow over time (see also Fig. 5, top row). This process of coarsening is accompanied by the gradual cessation of tissue turnover because only cells on the boundary of clusters can divide. Thus, the system remains in a nonhomeostatic state until the lattice consists of A cells or B cells only (fixation). Therefore, to achieve steady-state turnover, further steps must be taken to regulate proliferative activity and/or fate behavior to ensure tissue maintenance in the hierarchical model. This lack of a homeostatic state also renders the definition of a clone size distribution problematic, because it depends on the specific initial condition of the configuration of cell types.

Fig. 5.

Spatial distribution of cell states in the 2D lattice models, at different times $\lambda t=5,50,500$, and 5,000, obtained by Monte Carlo simulations of the lattice H model, Eq. 12, and lattice DH model, Eq. 13. Each pixel represents a cell in the lattice; blue pixels are A cells and white pixels are B cells. Top row: H model, r = 0.1, $\mathrm{\Delta }=0$. Bottom row: DH model, ${\omega }_{A,B}=0.1\lambda$.

By contrast, in the paradigm of dynamic heterogeneity, steady-state behavior of the 2D system is ensured when the dynamics are implemented through the following process (Fig. 4):

$$AB\stackrel{\lambda }{\to }\{\begin{array}{cc}AB& \text{Pr}.1/2\\ BA& \text{Pr}.1/2\end{array},\hspace{1em}A\underset{\underset{{\mathit{\omega }}_A}{\leftarrow }}{\overset{{\mathit{\omega }}_B}{\to }}B$$ [13]

(lattice DH model). Formally, although the chance development of A- or B-cell-rich clusters would, respectively, inhibit cell division and differentiation, the reversible transition of A- and B-type cells will always serve to release the deadlock, allowing the system to achieve long-term steady-state behavior.

To illustrate the process by which the system evolves spatially, we implemented the model by Monte Carlo simulation (Materials and Methods) to determine the lattice configurations and clonal distributions. Fig. 5 shows the time course of spatial configurations of cell types. For the lattice DH model (bottom row) the system remains homeostatic and homogeneous on large length scales. In contrast, the lattice H model (Fig. 5, top row) shows a persistent, nonhomeostatic coarsening over time. Furthermore, the constraint of fixed cell number leads to a stable ratio of cell types in the lattice DH model, for any choice of parameters, while in the lattice H model any choice of Δ ≠ 0 leads to an imbalanced growth of one cell type population (see Supporting Information and Fig. S3).

Fig. S3.

Spatial distribution of cell states in the lattice H model, with a symmetric division ratio $r=0.1$ and a nonzero cell fate imbalance $\mathrm{\Delta }=0.01$, obtained by Monte Carlo simulations (see Materials and Methods) at different times t (time unit is $1/\lambda$). Each pixel represents a cell in the lattice; blue pixels are A cells and white pixels are B cells.

Superficially, the “pathological” coarsening behavior of the lattice H model emerged through the rigid constraint on local cell density, which appeared in the model through the tight correlation of cell division with differentiation of a neighboring cell. This constraint may be relaxed by accommodating a degree of compressibility in the model. Formally, this can be achieved by accommodating vacancies or holes allowing for stratification of B-type cells uncompensated by the division of neighboring A-type cells. However, even under these conditions (considered in ref. 45), the dynamics of the lattice H model are qualitatively the same and phase-separated domains of cell types grow (see Supporting Information and Fig. S4).

Fig. S4.

Spatial distribution of cell states in the 2D lattice model with vacancies (Eq. S38, at different times t = 5, 50, 500, and 5,000 in units $\mathrm{1}/\lambda$. Results are obtained by Monte Carlo simulations for the lattice H model, Eq. S39, and for the lattice DH model, Eq. S40. Each pixel represents a cell in the lattice; blue pixels are A cells and white pixels are B cells. Top row: lattice H model, $r=0.1$; bottom row: lattice DH model, ${\omega }_{A,B}=0.1\hspace{0.17em}\lambda$.

Further insight into the steady-state properties of the system can be obtained by mapping these lattice models onto a corresponding “kinetic spin model,” as encountered in statistical physics. By interpreting an A-type cell as a spin $\uparrow$ degree of freedom and a B-type cell as spin $\mathrm{\downarrow }$, the lattice DH model translates to a kinetic Ising model at infinite temperature, featuring a combination of Glauber dynamics (random spin flips) and Kawasaki dynamics (spin exchange) (46) (Supporting Information). Starting from any initial condition, the system flows to a homogeneous equilibrium distribution of spins, with the ratio of $\uparrow$, $\rho ={\omega }_A/\left({\omega }_B+{\omega }_A\right)$, corresponding to a homeostatic state. By contrast, the lattice H model translates to a voter model, in which cells are stochastically and irreversible replaced by neighboring cells, following the transitions $\uparrow \hspace{0.17em}\downarrow \hspace{0.17em}\to \hspace{0.17em}\uparrow \hspace{0.17em}\uparrow$ or $\uparrow \hspace{0.17em}\downarrow \hspace{0.17em}\to \hspace{0.17em}\downarrow \hspace{0.17em}\downarrow$, respectively, with equal probability (47). The latter model is nonergodic, exhibiting coarsening and phase separation into large irregular domains of cell states that grow over time (45, 47). This dynamics does not support a homeostatic state.

Tracing the clonal dynamics in the lattice DH model, we also compared the clone size distribution with results of a voter model, shown in Fig. 6 as the result of Monte Carlo simulations (Materials and Methods). According to Fig. 6 the rescaled clone size distributions of the lattice DH model cannot be distinguished from the voter model. Because it has been rigorously shown that the voter model clone size distribution converges onto an exponential distribution, we expect this also to be the case for the 2D lattice DH model (47).

Fig. 6.

Rescaled clone size distributions for 2D lattice model, as a function of $X=N/{\langle N\rangle }_s$, where N is clone size and ${\langle N\rangle }_s$ the average size of surviving clones. The black lines are Monte Carlo simulation results from the lattice DH model (Eq. 13) and orange are results from the voter model (47). In the simulations we used as initial condition a randomly mixed distribution of cells, with a fraction ρ of A-type cells, and each cell representing an initial clone. The blue dashed line is an exponential distribution that is known to be the long-term clone size distribution of the voter model. Parameters: lattice length $L=\mathrm{1,000}$, ${\omega }_{A,B}=\lambda$, simulation time $t=20/\mathrm{\Omega }$, with $\mathrm{\Omega }$ according to Eq. 8.

Discussion

Our study shows that dynamic heterogeneity in stem cell populations of cells reversibly switching between states that differ in their proliferative potential and their propensity toward differentiation yields a viable mechanism to maintain homeostatic tissues. Moreover, considering the long-term clone size dependences, a model based on dynamic heterogeneity cannot be discriminated from a hierarchical model. Because hierarchical schemes involving intrinsic or extrinsic (niche-based) regulation have been used to infer self-renewal strategies in epithelial tissues such as mouse epidermis, esophagus, germline, and intestine (8–11), it follows that both dynamic heterogeneity and hierarchical fate may be equally capable of describing the results of recent lineage tracing assays. It is important to find further short-term characteristics that can help to discriminate these models. This remains true when the model is embedded in specific spatial niche architectures that resemble tissues. Nonetheless, both dynamic heterogeneity and hierarchical balanced fate belong to the class of population asymmetry (4), in which stem cells are lost and replaced, with equal probability.

Through sensing of the cellular environment, cells may respond to variations in cell density and adjust cell division (contact inhibition) (32) and loss rate (33). We show that with this crowding feedback a dynamically heterogeneous system adjusts to attain a stable homeostatic state. The biological background of crowding feedback, by which the cells can measure local cell density, may find a basis in the mechanisms of mechanosensing (48), the limited exposure to diffusible molecules released by the niche environment (20), or biochemical communication between cells (44). Importantly, for dynamic heterogeneity, homeostasis is robust toward disruption of some crowding feedback pathways. In contrast, for hierarchical models, involving intrinsic or cell-autonomous regulation of fate, it is essential that cell fate outcomes are specified at cell division, whereas the control of cell division or loss rates are not sufficient to maintain homeostasis.

In a 2D epithelium, however, the spatial dynamics of cell types show fundamental differences between dynamic heterogeneity and hierarchical cell fate, if left unchecked. The dynamics of the hierarchical model lead to a nonhomeostatic coarsening of the tissue structure, in that regions enriched with one cell type emerge so that the cell types phase-separate over time. In contrast, for dynamic heterogeneity, reversible switching between states homogenizes the tissue structure, leading to a macroscopically homogeneous, homeostatic cell population. The constraint of fixed total cell number in the lattice is sufficient to confer cell fate balance in the case of dynamic heterogeneity, whereas for the hierarchical model the ratios of symmetric cell divisions need to be fine-tuned to assure balance.

To summarize, dynamic heterogeneity provides an alternative paradigm for cell fate dynamics in homeostatic tissues, in accordance with cell lineage data. It provides a simple mechanism to balance tissue homeostasis and to homogenize the distribution of cell types in epithelial sheets. The two cell types in our model may be considered as a caricature of a single progenitor cell population carrying some memory over cell generations that renders cells primed toward proliferation or differentiation. In the case of fast cell type conversion, this priming would be lost. In this limit the system can be considered as a homogeneous cell population following the random differentiation dynamics of the model introduced by Marques-Pereira and Leblond (42). To determine whether cell fate behavior in epithelial tissues may involve dynamic heterogeneity, further detailed studies will be required that track cell lineages and distinguish cell states over time.

Materials and Methods

Numerical Solution of Master Equation.

The master equation, Eq. S2, is solved by numerical integration of the constituent ordinary differential equations, when a cutoff in $N_A$ and $N_B$ is applied. Specifically, we considered only terms with $N_{A,B}\le 50$ and used an adaptive Runge–Kutta method via Mathematica to solve the resulting $50\times 50$ ordinary differential equations to obtain $P_{N_A,N_B}$. We then determined the rescaled clone size distribution $P\left(X\mathrm{=}N/{\langle N\rangle }_s\right)$, where ${\langle N\rangle }_s$ denotes the average size of surviving clones ($N>0$).

Monte Carlo Simulations of Lattice Models.

Time is subdivided in discrete time steps $\mathrm{\Delta }t=1/{\mathit{\varphi }}_{\text{max}}$, where ${\mathit{\varphi }}_{\text{max}}$ is the largest transition rate out of any system configuration. At each time step $\mathrm{\Delta }t$, a lattice site and one of its neighbors are N times randomly chosen (N is the number of lattice sites). Then a random variable is generated and any possible transition, as defined by the models 10, 12, and 13, with given rate ϕ, is chosen to be updated with probability $\varphi \mathrm{\Delta }t$, according to the Gillespie algorithm (49).

Here we outline in detail the stability analysis of the discussed cell fate models, the analytical derivation of the clone size distribution, and support our findings for the 2D lattice models.

In the simple model for dynamical heterogeneity, without spatial regulation (DH model), A-type cells divide asymmetrically, with rate λ, to produce one A-type and one B-type cell as daughters. A- and B-type cells can interconvert between each other with rates ${\omega }_{A,B}$, respectively, and B-type cells may terminally differentiate and leave the niche, with rate γ. These rules, also given as Eq. 1 in the main text, read as

$$A\stackrel{\lambda }{\to }A+B,\hspace{1em}A\underset{\underset{{\mathit{\omega }}_A}{\leftarrow }}{\overset{{\mathit{\omega }}_B}{\to }}B,\hspace{1em}B\stackrel{\mathit{\gamma }}{\to }\mathrm{Ø,}$$ [S1]

where cell division, loss, and fate choice are assumed to occur stochastically with constant rates given above the arrows. The model thus represents a Markov process with the given stochastic transition rates. Formally, this dynamics is described by the master equation, the time evolution for the probability of having $N_A$ A cells and $N_B$ B cells at time t, $P_{N_A,N_B}\left(t\right)$,

$$\begin{array}{c}{\partial }_t{P}_{N_A,N_B}=\lambda \left[N_A\hspace{0.17em}{P}_{N_A,N_B-1}-N_A\hspace{0.17em}{P}_{N_A,N_B}\right]\\ +{\omega }_B\left[\left(N_A+1\right)\hspace{0.17em}{P}_{N_A+1,N_B-1}-N_A\hspace{0.17em}{P}_{N_A,N_B}\right]\\ +{\omega }_A\left[\left(N_B+1\right)\hspace{0.17em}{P}_{N_A-1,N_B+1}-N_B\hspace{0.17em}{P}_{N_A,N_B}\right]\\ +\gamma \left[\left(N_B+1\right)\hspace{0.17em}{P}_{N_A,N_B+1}-N_B\hspace{0.17em}{P}_{N_A,N_B}\right].\end{array}$$ [S2]

To keep a compact notation we do not explicitly write the time dependence of the probabilities $P_{N_A,N_B}$ here, and we do not write out the superscript “DH” as in the notation in Clonal Dynamics of the main text. This equation forms the basis for determining the time evolution of average cell densities and of the clone size distribution (i.e., the statistical distribution of the progeny of single cells).

Stability of the Cell Population

Assuming a fixed unit volume, cell densities are proportional to cell numbers, and we define the average cell densities by $n_{A,B}={\displaystyle {\sum }_{N_A,N_B=0}{N}_{A,B}{P}_{N_A,N_B}}$ (note that $N_{A,B}$ stands here and in the following for “$N_A$ and $N_B$, respectively”; the same is valid for $n_{A,B}$). Furthermore, we assume—considering a whole tissue and not just individual clones—that cell numbers are large so that the probability of extinction can be neglected, $P_{0,N_B}=P_{N_A,0}=0$. With that, we get by using master equation, Eq. S2, the time evolution of $n_A$,

$$\begin{array}{c}{\partial }_t{n}_A={\displaystyle \sum _{N_A,N_B=0}^{\infty }{N}_A{\partial }_t{P}_{N_A,N_B}}\\ =\lambda \left[{\displaystyle \sum _{N_A^{\prime },N_{\mathit{B}}^{\prime }=0}^{\infty }{N}_A^{\prime 2}\hspace{0.17em}{P}_{N_A^{\prime },N_B^{\prime }}-{\displaystyle \sum _{N_A^{\prime },N_{\mathit{B}}^{\prime }=0}^{\infty }{N}_A^{\prime 2}\hspace{0.17em}{P}_{N_A^{\prime },N_B^{\prime }}}}\right]\\ +{\omega }_B\left[{\displaystyle \sum _{N_A^{\prime },N_{\mathit{B}}^{\prime }=0}^{\infty }\left(N_A^{\prime }-1\right)N_A^{\prime }\hspace{0.17em}{P}_{N_A^{\prime },N_{\mathit{B}}^{\prime }}-{\displaystyle \sum _{N_A^{\prime },N_{\mathit{B}}^{\prime }=0}^{\infty }{N}_A^{\prime 2}\hspace{0.17em}{P}_{N_A^{\prime },N_{\mathit{B}}^{\prime }}}}\right]\\ +{\omega }_A\left[{\displaystyle \sum _{N_A^{\prime },N_{\mathit{B}}^{\prime }=0}^{\infty }\left(N_A^{\prime }+1\right)N_{\mathit{B}}^{\prime }\hspace{0.17em}{P}_{N_A^{\prime },N_{\mathit{B}}^{\prime }}-{\displaystyle \sum _{N_A^{\prime },N_{\mathit{B}}^{\prime }=0}^{\infty }{N}_A^{\prime }{N}_B^{\prime }\hspace{0.17em}{P}_{N_A^{\prime },N_{\mathit{B}}^{\prime }}}}\right]\\ +\gamma \left[{\displaystyle \sum _{N_A^{\prime },N_{\mathit{B}}^{\prime }=0}^{\infty }{N}_A^{\prime }{N}_B^{\prime }\hspace{0.17em}{P}_{N_A^{\prime },N_{\mathit{B}}^{\prime }+1}-{\displaystyle \sum _{N_A^{\prime },N_{\mathit{B}}^{\prime }=0}^{\infty }{N}_A^{\prime }{N}_B^{\prime }\hspace{0.17em}{P}_{N_A^{\prime },N_{\mathit{B}}^{\prime }}}}\right],\end{array}$$ [S3]

where in each sum we redefined the indices by $N_{A,B}^{\prime }=N_{A,B}\pm 1$ or $N_{A,B}^{\prime }=N_{A,B}$, respectively, such that in each occurrence of P the indices are identical, giving $P_{N_A^{\prime },N_{\mathit{B}}^{\prime }}$. Proceeding analogously for ${\partial }_t{n}_B$, and resubstituting the definition for $n_{A,B}$ above, we obtain the time evolution for the average cell densities (cell numbers),

$$\begin{array}{c}{\partial }_t{n}_A={\omega }_A\hspace{0.17em}{n}_B-{\omega }_B\hspace{0.17em}{n}_A\\ {\partial }_t{n}_B=\left(\lambda +{\omega }_B\right)n_A-\left(\gamma +{\omega }_A\right)n_B,\end{array}$$ [S4]

which corresponds to Eq. 3 in the main text. When we substitute $n_B=n-n_A$, where $n≔n_A+n_B$ is the total average cell density, Eq. S4 becomes

$${\partial }_t{n}_A\left(t\right)=f\left(n_A,n\right),\hspace{1em}{\partial }_{t}n\left(t\right)=g\left(n_A,n\right),$$ [S5]

where we introduced the functions

$$\begin{array}{c}f\left(n_A,n\right)≔{\omega }_A\hspace{0.17em}\left(n-n_A\right)-{\omega }_B\hspace{0.17em}{n}_A\\ g\left(n_A,n\right)≔\lambda \hspace{0.17em}{n}_A-\gamma \left(n-n_A\right).\end{array}$$ [S6]

The steady-state condition ${\partial }_t{n}_A={\partial }_{t}n=0$, that is, $f\left(n_A,n\right)=g\left(n_A,n\right)=0$, is fulfilled for

$$\frac{\lambda }{\gamma }=\frac{{\omega }_B}{{\omega }_A}$$ [S7]

and

$$n_A^{\mathrm{\ast }}=\rho \hspace{0.17em}n$$ [S8]

with

$$\rho ≔\frac{{\omega }_A}{{\omega }_A\mathrm{+}{\omega }_B}.$$ [S9]

Thus, for any n, there exists $n_A^{\mathrm{\ast }}\left(n\right)$ that renders Eq. S5 stationary. Without any further feedback in the parameters, that is, when all parameters are independent of cell densities $n_A,n$, there is not a single fixed point but a line of fixed points defined by Eq. S8. To check whether fixed points are stable, we perform a linear stability analysis. For that purpose we compute the Jacobian matrix of Eq. S5,

$$J\left(n_A,n\right)≔\left(\begin{array}{cc}{\partial }_{n_A}f\left(n_A,n\right)& {\partial }_{n}f\left(n_A,n\right)\\ {\partial }_{n_A}g\left(n_A,n\right)& {\partial }_{n}g\left(n_A,n\right)\end{array}\right).$$ [S10]

A fixed point $\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)$ is stable if both eigenvalues of J at the fixed point are negative (see ref. 50). This is the case if

$$\text{det}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)>0\hspace{1em}\text{tr}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)<0.$$ [S11]

For the system defined by Eqs. S5 and S6, the Jacobian reads

$$J\left(n_A,n\right)=\left(\begin{array}{cc}-{\omega }_A-{\omega }_B& {\omega }_A\\ \gamma +\lambda & -\gamma \end{array}\right)$$ [S12]

having the trace and determinant

$$\text{det}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)=0\hspace{1em}\text{tr}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)=-\gamma -{\omega }_A-{\omega }_B.$$ [S13]

Because $\text{det}\left(J\right)=0$, the stability condition, Eq. S11, is never fulfilled. The fixed point is not stable without further assumptions on the dependence of parameters.

In the main text we discuss the situation where certain parameters depend on the total cell density (crowding feedback). Note that for simplicity we assumed that those parameters do only depend on the average cell density n, not considering fluctuations in the cell density. With this approximation, the derivation of the dynamics of average cell densities from the master equation follows the same procedure as above (see Eq. S3), and Eqs. S5 and S6 remain valid, yet with the parameters being functions of n.

First we consider the case where only λ depends on n [contact inhibition (32)]; below we show that the same arguments remain valid for other parameters being subject to crowding feedback. Let us assume that λ strictly decreases with n, that is, $\lambda \prime \left(n\right)<0$. As long as ${\lambda }^{\mathrm{\ast }}≔\gamma \hspace{0.17em}{\omega }_B/{\omega }_A$ (matching the balance condition, Eq. S7) is within the range of the function $\lambda \left(n\right)$, we get a unique fixed point $n_A^{\mathrm{\ast }}=\rho \hspace{0.17em}{n}^{\mathrm{\ast }}$ with $n^{\mathrm{\ast }}={\lambda }^{-1}\left({\lambda }^{\mathrm{\ast }}\right)$. In that case $\lambda \left(n^{\mathrm{\ast }}\right)={\lambda }^{\mathrm{\ast }}$ and cell fate is balanced. The stability of the fixed point can again be assessed by the trace and determinant of the Jacobian matrix J, Eq. S10, of the dynamic system, Eq. S5. Note that although we use formally the same functions f and g as in Eq. S6, the fact that $\lambda =\lambda \left(n\right)$ leads to different forms of the derivatives ${\partial }_{n}f,{\partial }_{n}g$. The trace and determinant read, evaluated at the fixed point $\left(n_A^{\mathrm{\ast }},n\right)$,

$$\begin{array}{c}\text{det}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)=-n^{\mathrm{\ast }}\lambda \prime \left(n^{\mathrm{\ast }}\right){\omega }_A\\ \text{tr}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)=-\gamma -{\omega }_B-{\omega }_A+\lambda \prime \left(n^{\mathrm{\ast }}\right)\rho \hspace{0.17em}{n}^{\mathrm{\ast }}.\end{array}$$ [S14]

Because $n^{\mathrm{\ast }}={\lambda }^{-1}\left({\lambda }^{\mathrm{\ast }}\right)>0$ and $\rho >0$, conditions S11 are always fulfilled for $\lambda \prime \left(n\right)<0$. Thus, the system is always stable for λ subject to crowding feedback with $\lambda \prime \left(n\right)<0$.

Also the other model parameters may be subject to crowding feedback through a dependence on n. If $\gamma =\gamma \left(n\right)$ for example, we get

$$\begin{array}{c}\text{det}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)=n^{\mathrm{\ast }}\gamma \prime \left(n^{\mathrm{\ast }}\right){\omega }_B\\ \text{tr}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)=-{\omega }_A-\frac{\lambda \hspace{0.17em}{\omega }_A}{{\omega }_B}-\left(1-\rho \right)\left(n^{\mathrm{\ast }}\gamma \prime \left(n^{\mathrm{\ast }}\right)+{\omega }_A+{\omega }_B\right).\end{array}$$ [S15]

Therefore, conditions S11 are always fulfilled for $\gamma \prime \left(n\right)>0$. For ${\omega }_B={\omega }_B\left(n\right)$, we get

$$\begin{array}{c}\text{det}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)=n^{\mathrm{\ast }}\gamma \hspace{0.17em}{\omega \prime }_B\left(n^{\mathrm{\ast }}\right)\\ \text{tr}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)=-\gamma -{\omega }_A-\frac{\lambda \hspace{0.17em}{\omega }_A}{\gamma }\end{array}$$ [S16]

and conditions S11 are fulfilled for ${\omega \prime }_B\left(n\right)>0$. Finally, for ${\omega }_A={\omega }_A\left(n\right)$, we get

$$\begin{array}{c}\text{det}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)=-n^{\mathrm{\ast }}\lambda \hspace{0.17em}{\omega \prime }_A\left(n^{\mathrm{\ast }}\right)\\ \text{tr}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)=-\gamma -{\omega }_B-\frac{\gamma \hspace{0.17em}{\omega }_B}{\lambda },\end{array}$$ [S17]

which again fulfills condition S11 for ${\omega }_A^{\prime }\left(n\right)<0$.

Thus, if any of the parameters $\lambda ,\gamma ,{\omega }_A,{\omega }_B$ are subject to crowding feedback, with the correct trend in the parameters’ dependency on n, the stability of homeostasis is maintained.

It is important to note that the stability does not depend on the explicit form of the crowding feedback, in terms of the functions $\lambda \left(n\right),\gamma \left(n\right),{\omega }_{A,B}\left(n\right)$; just the correct sign of the feedback is required. Fine-tuning of parameters and of the crowding feedback mechanism is not required for stability of homeostasis. If more than one parameter exhibits crowding feedback, the homeostatic state is robust toward disruptions (e.g., by mutations that disrupt feedback in one of the parameters). It is sufficient if one out of four parameters retains the feedback dependence.

For the H model (Eq. 2, main text), the dynamics are more sensitive to disruptions, even in case of crowding feedback. The time evolution of that model is given by Eq. S5, but now with the functions

$$\begin{array}{c}f\left(n_A,n\right)=\lambda \hspace{0.17em}{n}_A\mathrm{\Delta }\\ g\left(n_A,n\right)=\lambda \hspace{0.17em}{n}_A-\gamma \left(n-n_A\right).\end{array}$$ [S18]

A stationary state is only attained for

$$\mathrm{\Delta }=0,$$ [S19]

giving the fixed point(s)

$$n_A^{\mathrm{\ast }}=\rho \hspace{0.17em}n.$$ [S20]

From condition S19 it becomes immediately clear that stability of the system necessarily requires that $\mathrm{\Delta }$ is controlled through crowding feedback. A response of $\lambda ,\gamma ,$ or r on the cell density n is not sufficient to keep the system in homeostasis. To check the stability under crowding feedback of $\mathrm{\Delta }$, we follow the same steps as above, with $\mathrm{\Delta }=\mathrm{\Delta }\left(n\right)$. With this we get the Jacobian J:

$$J\left(n_A,n\right)=\left(\begin{array}{cc}\lambda \hspace{0.17em}\mathrm{\Delta }& \lambda \hspace{0.17em}{n}_A\hspace{0.17em}\mathrm{\Delta }\prime \left(n\right)\\ \lambda +\gamma & -\gamma \end{array}\right)$$ [S21]

with determinant and trace

$$\begin{array}{c}\text{det}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)=-n^{\mathrm{\ast }}\hspace{0.17em}\gamma \hspace{0.17em}\lambda \hspace{0.17em}\mathrm{\Delta }\prime \left(n\right)\\ \text{tr}\left(J\left(n_A^{\mathrm{\ast }},n^{\mathrm{\ast }}\right)\right)=-\gamma ,\end{array}$$ [S22]

which fulfills condition S11 for $\mathrm{\Delta }\prime \left(n\right)<0$. Thus, crowding response of $\mathrm{\Delta }$ can in fact render the H model stable; however, this stability only prevails for that specific parameter responding to crowding. If regulation of this single cell fate parameter fails, crowding response of the other parameters on its own is not sufficient to maintain homeostasis.

Clonal Evolution Without Spatial Regulation

Here we outline how the solution of the master equation, Eq. S2, is obtained for large $N_{A,B}\gg 1$. In that case, the probability distribution P is broad and varies only slowly between subsequent numbers $N_{A,B}$. Therefore, $N_A$ and $N_B$ are treated as continuous variables and $P_{N_A,N_B}$ is approximated by a continuous function $P\left(N_A,N_B\right)$. Then, differences of the probability in neighboring values of $N_A,N_B$ can be approximated by a second-order Taylor expansion [corresponding to a van Kampen expansion (41)]:

$$P_{N_A+{\delta }_A,N_B+{\delta }_B}\approx P\left(N_A,N_B\right)+{\partial }_{N_A}P\left(N_A,N_B\right)\cdot {\delta }_A+{\partial }_{N_B}P\left(N_A,N_B\right)\cdot {\delta }_B+1/2\hspace{0.17em}{\partial }_{N_A}^{2}P\left(N_A,N_B\right)\cdot {\delta }_A^2+{\partial }_{N_A,N_B}P\left(N_A,N_B\right)\cdot {\delta }_A{\delta }_B+1/2\hspace{0.17em}{\partial }_{N_B}^{2}P\left(N_A,N_B\right)\cdot {\delta }_B^2.$$ [S23]

In the following, we only consider the balanced case for which ${\omega }_A/{\omega }_B=\gamma /\lambda$ (see Eq. S7). Substituting the Taylor approximation, Eq. S23, in Eq. S2, gives the FPE:

$$\begin{array}{l}{\partial }_{t}P\left(N_A,N_B\right)=\left[K\lambda +\left(1+K\right)\omega \right]\hspace{0.17em}P\left(N_A,N_B\right)\\ +[\omega \left(N_A-N_B\hspace{0.17em}K-K+1\right){\partial }_{N_A}\hspace{0.17em}P\left(N_A,N_B\right)\\ +\left[K\lambda +\left(K-1\right)\omega +\left(\lambda +\omega \right)\left(N_{B}K-N_A\right)\right]{\partial }_{N_B}P\left(N_A,N_B\right)\\ +1/2\hspace{0.17em}\left[\omega \left(1+K\right)+\omega \hspace{0.17em}{N}_A+\omega K\hspace{0.17em}{N}_B\right]{\partial }_{N_A}^{2}P\left(N_A,N_B\right)\\ +1/2\hspace{0.17em}\left[K\lambda +\omega \left(1+K\right)+\left(\lambda +\omega \right)\left(N_A+N_B\hspace{0.17em}K\right)\right]\hspace{0.17em}{\partial }_{N_B}^{2}P\left(N_A,N_B\right)\\ -\left[\omega \left(1+K+N_A+N_{B}K\right)\right]{\partial }_{N_A,N_B}P\left(N_A,N_B\right),\end{array}$$ [S24]

where for convenience we introduced the effective parameters $K≔{\omega }_A/{\omega }_B=\gamma /\lambda$ to eliminate γ and used $\omega ≔{\omega }_B$. In the following we want to obtain analytical solutions for the FPE when the “fast” degrees of freedom are integrated out. For that purpose, we introduce auxiliary variables $Z≔N_A+\frac{\omega }{\lambda +\omega }{N}_B$ and $W≔N_B-N_A/K$. When substituting these variables, and rearranging derivatives by partial integration, the FPE reads, expressed in the new variables $\left(Z,W\right)$,

$${\partial }_{t}P\left(Z,W\right)={\partial }_W\left[W\left(\omega +K\left(\lambda +\omega \right)\right)\hspace{0.17em}P\left(Z,W\right)\right]+{\partial }_W^2[(W\hspace{0.17em}\frac{K\left(\lambda -\omega \right)\omega -{\omega }^2+K^2\omega \left(\lambda +\omega \right)+K^3{\left(\lambda +\omega \right)}^2}{2K\omega +2K^2\left(\lambda +\omega \right)}+Z\hspace{0.17em}\frac{\left(\lambda +\omega \right)\left(\omega +2K\omega +K^2\left(\lambda +\omega \right)\right)}{K\omega +K^2\left(\lambda +\omega \right)}+\frac{\omega +3\hspace{0.17em}K\omega +3\hspace{0.17em}{K}^2\omega +K^3\left(\lambda +\omega \right)}{2\hspace{0.17em}{K}^2})P\left(Z,W\right)]+{\partial }_W{\partial }_Z[(W\hspace{0.17em}\frac{\lambda \omega \left(\omega -K\left(\lambda +\omega \right)\right)}{\left(\lambda +\omega \right)\left(\omega +K\left(\lambda +\omega \right)\right)}-Z\frac{2\lambda \omega }{\omega +K\left(\lambda +\omega \right)}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{\left(1+2K\right)\lambda \omega }{K\left(\lambda +\omega \right)})P\left(Z,W\right)]+{\partial }_Z^2[(W\frac{K\lambda \omega \left(K\left(\lambda +\omega \right)-\omega \right)}{2\left(\lambda +\omega \right)\left(\omega +K\left(\lambda +\omega \right)\right)}+\frac{\lambda \omega \left(\lambda +K\lambda +K\omega \right)}{2{\left(\lambda +\omega \right)}^2}+Z\frac{K\lambda \omega }{\omega +K\left(\lambda +\omega \right)})P\left(Z,W\right)].$$ [S25]

Now we make the Gaussian ansatz

$$P\left(Z,W\right)=P\left(Z\right)\cdot \text{exp}\left(-W^2/\left(2\hspace{0.17em}Z\right)\right)/\sqrt{2\pi Z}$$ [S26]

and integrate out the fast variable W. For this ansatz, boundary terms of the integration vanish because ${\text{lim}}_{W\to \pm \infty }{W}^{\alpha }P\left(Z,W\right)=0$ for any α. Thus, all terms starting with the differential operator ${\partial }_W$ vanish by intergration over W, and we arrive at

$${\partial }_{t}P\left(Z\right)={\partial }_Z^2\left[\left(\mathrm{\Lambda }+\overline{\mathrm{\Omega }}\hspace{0.17em}Z\right)P\left(Z\right)\right]$$ [S27]

with

$$\begin{array}{c}\mathrm{\Lambda }=\frac{\lambda \omega \left(\lambda +K\lambda +K\omega \right)}{2{\left(\lambda +\omega \right)}^2}\\ \overline{\mathrm{\Omega }}=\frac{K\lambda \omega }{\omega +K\left(\lambda +\omega \right)}.\end{array}$$ [S28]

Here we have used that ${\displaystyle {\int }_{-\infty }^{\infty }dW\hspace{0.17em}W\hspace{0.17em}P\left(Z,W\right)=0}$ and ${\displaystyle {\int }_{-\infty }^{\infty }dW\hspace{0.17em}P\left(Z,W\right)=P\left(Z\right)}$ for the Gaussian ansatz. The partial differential Eq. S27 is solved by

$$P\left(Z,t\right)=\frac{1}{{\left(\overline{\mathrm{\Omega }}t\right)}^2}\text{exp}\left(-\frac{Z+\mathrm{\Lambda }/\overline{\mathrm{\Omega }}}{\overline{\mathrm{\Omega }}t}\right).$$ [S29]

After all, we want to find the clone size distribution as a function of the total cell number N, $P\left(N\right)$, where $N=N_A+N_B$. From the solution, Eq. S29, it follows that $\langle Z\rangle =\overline{\mathrm{\Omega }}t-\mathrm{\Lambda }/\overline{\mathrm{\Omega }}$; thus, for large times $t\gg \mathrm{\Lambda }/{\overline{\mathrm{\Omega }}}^2$, the term $\mathrm{\Lambda }/\overline{\mathrm{\Omega }}$ can be neglected for $Z\sim \langle Z\rangle$. Because the distribution of W is Gaussian with variance Z, and $Z\sim t$, fluctuations in W are of order $O\left({\left(\overline{\mathrm{\Omega }}t\right)}^{1/2}\right)$, so that $N_B=N_A/K+O\left({\left(\overline{\mathrm{\Omega }}t\right)}^{1/2}\right)$, and we can approximate

$$\frac{Z}{\overline{\mathrm{\Omega }}t}=\frac{N_A+\frac{\mathit{\omega }}{\omega +\lambda }{N}_B}{\overline{\mathrm{\Omega }}t}=\frac{{\left(\omega +K\omega +K\lambda \right)}^2}{K\left(1+K\right)\omega \lambda \left(\omega +\lambda \right)}\frac{N}{t}+O\left({\left(\overline{\mathrm{\Omega }}t\right)}^{-1/2}\right).$$ [S30]

Neglecting $O\left({\left(\overline{\mathrm{\Omega }}t\right)}^{-1/2}\right)$ for large times and substituting Eq. S30 into Eq. S29, we find the clone size distribution as a function of N

$$P\left(N,t\right)=\frac{1}{{\left(\mathrm{\Omega }t\right)}^2}\text{exp}\left(-\frac{N}{\mathrm{\Omega }t}\right),$$ [S31]

with

$$\mathrm{\Omega }=\frac{\lambda \hspace{0.17em}\omega \hspace{0.17em}K\left(1+K\right)\left(\lambda +\omega \right)}{{\left(\omega +K\hspace{0.17em}\omega +K\hspace{0.17em}\lambda \right)}^2}.$$ [S32]

Using the effective parameter $\rho ={\omega }_A/\left({\omega }_B+{\omega }_A\right)$, which corresponds to the steady-state fraction of A-type cells, we can substitute $K=\rho /\left(1-\rho \right)$ and $\omega ={\omega }_B$, and arrive at the form used in the main text:

$$\mathrm{\Omega }=\frac{{\omega }_B}{\rho }\frac{1+\frac{{\omega }_B}{\lambda }}{{\left(1+\frac{{\omega }_B}{\lambda \mathit{\rho }}\right)}^2}.$$ [S33]

By comparing with the numerical solution of the original master equation, Eq. S2, we show in Fig. 2 in the main text that Eq. S31 approximates well the clone size distribution of the DH model. In Fig. 2 in the main text, we used the parameters ${\omega }_A={\omega }_B$, which led to almost identical solutions for both the H and DH model. However, it turns out that this perfect match is due to the special case ${\omega }_A={\omega }_B$; in the case ${\omega }_A\ne {\omega }_B$ a discrepancy between the models becomes apparent at short times, $t=1/\mathrm{\Omega }$, as shown in Fig. S1. At late times, $t=10/\mathrm{\Omega }$, nonetheless, both solutions coincide again and resemble the analytical result, Eq. S31.

In Fig. S2 it is also shown that Eq. S33 matches well the numerical results for $\mathrm{\Omega }$ as obtained from solving the master equation numerically.

Spatial Regulation in the Lattice Model

Imbalance in the Hierarchical Lattice Model.

For the DH model implemented on a lattice geometry (lattice DH model), no fine-tuning of the parameters is required to achieve homeostasis. In that case, the constraint of fixed cell number acts in a same way as crowding feedback in the nonspatial model to confer a stable state. Here we check whether this is also the case for the lattice H model. For that purpose, we implemented the lattice H model, Eq. 12 in the main text, with $\mathrm{\Delta }\ne 0$. In Fig. S3 the time course of the cell-type configuration is shown for a slight cell fate bias $\mathrm{\Delta }=0.01$. Even for such a small imbalance A-type cells take over the whole lattice, and no homeostatic state is attained.

Coarsening.

In this section we argue by general analytical considerations that for the lattice H model the system always coarsens, characterized by a diverging correlation length and the absence of a homeostatic state, in contrast to the lattice DH model, which attains a homeostatic (equilibrium) state with a finite correlation length.

The lattice models as defined in the main text can be simplified as follows, when the clonal identity of cells is neglected. We denote X as a randomly chosen cell in the lattice, Y is one of its four neighboring cells, and $\overline{X}$ is the opposite cell type of X ($\overline{X}=B$ if $X=A$, and vice versa). In this terminology the lattice H model reads

$$\begin{array}{c}X+Y\to X+X\hspace{1em}\text{with}\hspace{0.17em}\text{rate}\hspace{0.17em}\lambda r\\ \text{symmetric}\hspace{0.17em}\text{divisions}\end{array}$$ [S34]

$$X+Y\to Y+X\hspace{1em}\text{with}\hspace{0.17em}\text{rate}\hspace{0.17em}\lambda \left(1-2r\right)/4\hspace{1em}\hspace{0.17em}\text{asymmetric}\hspace{0.17em}\text{division}+\text{swap}\hspace{0.17em}\text{sites}$$ [S35]

and the DH model can be expressed as

$$\begin{array}{c}X+Y\to Y+X\hspace{1em}\text{with}\hspace{0.17em}\text{rate}\hspace{0.17em}\lambda /4\\ \text{asymmetric}\hspace{0.17em}\text{division}+\text{swap}\hspace{0.17em}\text{sites}\end{array}$$ [S36]

$$X\leftrightarrow \overline{X}\hspace{1em}\text{with}\hspace{0.17em}\text{rates}\hspace{0.17em}{\omega }_B,{\omega }_A\hspace{0.17em}\hspace{1em}\text{state}\hspace{0.17em}\text{switching}.$$ [S37]

To clarify, the correspondences to the lattice models introduced in the main text are the following:

• •Event S34 describes symmetric divisions: cell divisions may only occur at an $AB$ pair site, viz. when the B-type cell is lost. Without loss of generality we allow that cell division may happen both when the A cell is selected and when the B cell of this pair is selected. This means that cell division is executed only at half the normal rate, $\lambda /2$, to compensate for the doubled probability to choose a pair of cells to update. Either of the two sites is selected with equal probability, thus redefining the rules such that symmetric renewal occurs when the A site is selected, $AB\to AA$, and symmetric differentiation occurs when the B site is selected, $BA\to BB$.
• •Asymmetric division allows two configurations of daughter cells, $AB\to AB$ or $AB\to BA$. Events S35 and S36 correspond to the second option, whereas in the first case the system configuration does not change.
• •Event S37 comprises the two switch events $A\to B$ and $B\to A$, with rates ${\omega }_B$ and ${\omega }_A$, respectively.

Note that when $X=Y$, execution of processes S34–S36 lead to no change of configurations, which is consistent with the lattice update rule that cell division only occurs when an A cell is next to a B cell. This simplification is only possible because clonal identity is not considered, otherwise the chosen update rule does explicitly depend on the values of X and Y.

The dynamics S34–S37 are equivalent to paradigmatic models of statistical physics. To see this, let us interpret the state of a cell at a given site as a spin where A denotes $\uparrow$ and B denotes $\downarrow$.

• •Event S34 is equivalent to the dynamics of a voter model (47). This stochastic process exhibits coarsening with domain sizes growing on average over time t as $\sim t^{1/2}$ in one dimension and $\sim t/\text{ln}\left(t\right)$ in a 2D lattice.
• •Events S35 and S36 correspond to the spin exchange dynamics under Kawasaki spin update rules of an Ising model without interactions.
• •Event S37 corresponds to the spin-flip dynamics in a Glauber update scheme of the Ising model without interactions, but with an external field $h=\text{ln}({\omega }_A/{\omega }_B)$ at unit temperature T = 1.

Hence, in this picture, the lattice H model corresponds to a voter model with Kawasaki spin-exchange dynamics. For that model, it was shown that any domain front between $\uparrow ‐$ and $\downarrow$-domains is stable (i.e., ergodic) if there is no bias in the spin exchange dynamics (51). This means that domain walls evolve on large scales as in the voter model, so that domain sizes grow over time. This is also consistent with studies on the combination of voter and Kawasaki dynamics in two dimensions (45) that have shown that the correlation length diverges and the system performs coarsening, even for large ratios of Kawasaki dynamics. Thus, for the H model on a lattice, nonhomeostatic coarsening and divergence of the correlation length prevails.

The DH model corresponds to the combination of Glauber (spin-flip) and Kawasaki (spin-exchange) dynamics without interactions. This is an implementation of a kinetic, noninteracting Ising model and leads to a stationary (equilibrium) state, characterized by a finite correlation length and a density of up-spins $\rho ={\omega }_A/\left({\omega }_A+{\omega }_B\right)$. Thus, no coarsening emerges and a homeostatic state is reached for the lattice DH model.

Mobile Vacancies in the Lattice.

Here we want to consider the model alternative where B-type cells may be lost even if there is no adjacent dividing A-type cells. In that case the B-type cell leaves a vacancy $\mathrm{Ø}$ ($B\to \mathrm{Ø}$) when lost. We assume that this vacancy may move in the lattice by exchanging sites with neighbors randomly, until it is adjacent to an A-type cell that then divides to fill the vacancy. This is defined by the following rules:

$$A\mathrm{Ø,}\stackrel{\lambda }{\to }XX,B\mathrm{Ø,}\stackrel{\sigma }{\to }\mathrm{Ø,}B,\hspace{1em}B\stackrel{\mathit{\gamma }}{\to }\mathrm{Ø,}$$ [S38]

where the identity of daughter cells after division, $A\mathrm{Ø,}\to XX$, depends on the model implementation. For the lattice H model, we have

$$XX=\{\begin{array}{ll}AA\hfill & \text{Pr}.r\hfill \\ BA\hfill & \text{Pr}.\left(1-2r\right)/2\hfill \\ AB\hfill & \text{Pr}.\left(1-2r\right)/2\hfill \\ BB\hfill & \text{Pr}.r\hfill \end{array}$$ [S39]

and for the lattice DH model

$$XX=\{\begin{array}{cc}BA& \text{Pr}.1/2\\ AB& \text{Pr}.1/2\end{array},$$ [S40]

and furthermore the cell fates switch reversibly:

$$A\stackrel{{\omega }_B}{\to }B,B\stackrel{{\omega }_A}{\to }A.$$ [S41]

Here we consider the limit $\sigma ,\lambda \to \infty$, that is, whenever a vacancy emerges it immediately explores the lattice until finding an A-type cell that divides and fills the vacancy with its progeny. With this choice of parameters, cell loss and division are still coupled, but this coupling may be between A- and B-type cells that are far from each other.

For this model we show the time course of cell configuration in Fig. S4, both for the lattice H model and the lattice DH model. We can see that the same phenomenology as without holes prevails: In the lattice H model the system coarsens without reaching a homeostatic state (as was also shown for the same model in ref. 45), whereas for the DH model the system is well-mixed and assumes quickly a homeostatic state.