Knotting and unknotting of a protein in single molecule experiments

Significance

Knots and entanglements are common in biology, but little is known about their formation or function. Here, we use state-of-the-art single-molecule force spectroscopy to mechanically unfold a protein, ubiquitin C-terminal hydrolase isoenzyme L1, which has a 5₂ knot in its structure. The exquisite control inherent in this technique enables us to specifically unfold the protein to different knotted and unknotted denatured states, from which we can then watch the protein refold. These experiments establish the effect of knots on folding pathways. Many intermediate structures are detected, suggesting both on- and off-pathway intermediates are populated. Our results also highlight the potential difficulties in degrading a 5₂-knotted protein and therefore may have implications for some diseases.

Abstract

Spontaneous folding of a polypeptide chain into a knotted structure remains one of the most puzzling and fascinating features of protein folding. The folding of knotted proteins is on the timescale of minutes and thus hard to reproduce with atomistic simulations that have been able to reproduce features of ultrafast folding in great detail. Furthermore, it is generally not possible to control the topology of the unfolded state. Single-molecule force spectroscopy is an ideal tool for overcoming this problem: by variation of pulling directions, we controlled the knotting topology of the unfolded state of the 5₂-knotted protein ubiquitin C-terminal hydrolase isoenzyme L1 (UCH-L1) and have therefore been able to quantify the influence of knotting on its folding rate. Here, we provide direct evidence that a threading event associated with formation of either a 3₁ or 5₂ knot, or a step closely associated with it, significantly slows down the folding of UCH-L1. The results of the optical tweezers experiments highlight the complex nature of the folding pathway, many additional intermediate structures being detected that cannot be resolved by intrinsic fluorescence. Mechanical stretching of knotted proteins is also of importance for understanding the possible implications of knots in proteins for cellular degradation. Compared with a simple 3₁ knot, we measure a significantly larger size for the 5₂ knot in the unfolded state that can be further tightened with higher forces. Our results highlight the potential difficulties in degrading a 5₂ knot compared with a 3₁ knot.

Over the last few decades, protein folding studies have focused largely on relatively small, monomeric model systems that possess simple topologies. Extensive experimental and computational studies have provided significant mechanistic insight into folding pathways (1–5). These proteins, which fold rapidly, have been shown to possess relatively smooth energy landscapes (6, 7). However, the emergence of classes of topologically complex knotted protein structures in recent years (8–11) challenges some long-standing views in the field as such proteins have to avoid kinetic traps and also overcome significant topological barriers during folding. To date, more than 750 knotted proteins have been discovered within the Protein Data Bank (PDB), each containing either a trefoil (3₁), figure-of-eight (4₁), Gordian (5₂), or stevedore (6₁) knot in its structure (10–12). The conservation of these knotted topologies across different families has suggested that the knot may, in some way, be advantageous and important to the stability and/or function of the protein (12). As yet, not much is known about the advantages, if any, of knotted structures over their unknotted counterparts. It has been proposed that the knot may play a part in enhancing a protein’s thermodynamic, kinetic, mechanical, or cellular stability (13–15).

To date, relatively few experimental studies on the knotting and folding of topologically knotted proteins have been published (14). Most of these investigations have been focused on the trefoil-knotted bacterial methyltransferases YibK and YbeA (16–24). Extensive in silico studies have provided insights into how these 3₁-knotted conformations may be formed (13, 14). Some simulations report formation of intermediate “slipknot” configurations, partial unfolding (backtracking) events, or specific, nonnative interactions that promote threading, during the folding of 3₁-knotted proteins (25, 26). Other experimental studies have also examined the folding of designed and naturally occurring trefoil-knotted proteins (27–29). In contrast with the trefoil-knotted proteins, much less is known about the folding of proteins with more complex knots.

Ubiquitin C-terminal hydrolase isoenzyme L1 (UCH-L1) is a monomeric cysteine protease that belongs to the UCH family, a subgroup of deubiquitinating enzymes. The overall structure of UCH-L1 consists of six β-strands forming a central β-sheet that is flanked on either side by seven α-helices. The polypeptide chain threads through itself to create a 5₂ knot in the native state (Fig. 1). UCH-L1 is highly expressed in neurons and accounts for 1–2% of the brain proteome (30) and has been linked to neurodegenerative diseases such as Parkinson’s disease (PD) and Alzheimer’s disease (AD) (31, 32).

Fig. 1.

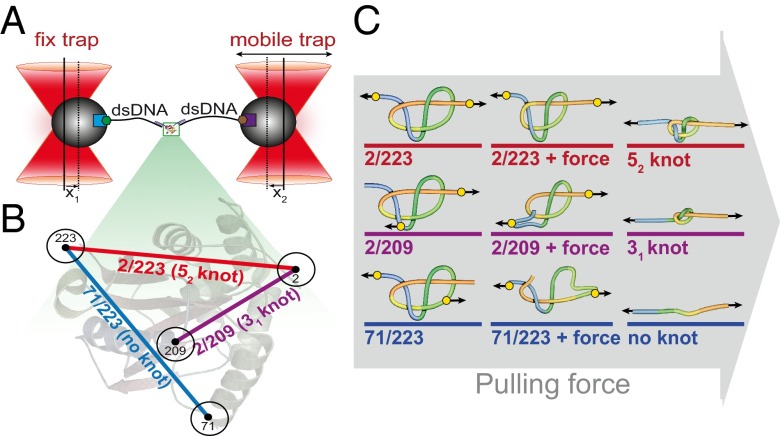
Design of optical tweezers assay and knotted structure of the variants of UCH-L1 used. (A) Schematic experimental setup of the dual-beam optical tweezers assay. Forces are measured through the deflections of the beads (x₁, x₂) out of the trap centers. (B) Structure of UCH-L1 with the different attachment points: Pulling at positions 2 and 223 (N and C termini) leads to an unfolded structure with a 5₂-knotted topology (red); pulling at positions 2 and 209 leads to an unfolded structure with a 3₁-knotted topology (violet); and pulling at positions 71 and 223 leads to an unfolded structure without a knot (blue). (C) Schematic representation of the tightening of the mutant protein structures on application of force, colored as in B.

Previously, we probed the folding mechanism of UCH-L1 and showed that it reversibly unfolds in vitro on addition of chemical denaturant to a state with no detectable secondary or tertiary structure (33). The same study established that chemical denaturant-induced unfolding is three-state and an intermediate populated under equilibrium conditions (33). Using NMR hydrogen-deuterium exchange (HDX) experiments, the intermediate state was characterized indirectly, and it was found that the central β-sheet core of the protein remains structured, whereas many of the surrounding α-helices have unfolded (33). Recently, a detailed kinetic analysis undertaken by Luo et al. has also established that UCH-L1 exhibits multiphasic kinetics indicative of parallel pathways and the population of at least two, metastable intermediate states (34).

Single-molecule force spectroscopy offers unique control over the conformation of proteins (35–39). In this study, we use high-precision optical tweezers to unfold and refold UCH-L1 in three distinct pulling geometries (Fig. 1 A and B). By varying the pulling geometry using cysteine engineering (40), we are able to specifically, mechanically unfold the protein chain to a state containing either a 5₂ or 3₁ knot or completely untie the chain such that the denatured state is the unknot (0). These experiments allow us to (i) characterize not only a 5₂ knot in an unfolded polypeptide chain, but also a 3₁ knot created in the same chain, (ii) quantify the mechanical stability of 5₂-knotted proteins, (iii) directly detect unfolding and refolding intermediates, and most importantly, (iv) directly measure the influence of knot formation on the rate of folding of a knotted protein.

Results

Design and Ensemble Characterization of the UCH-L1 Variants.

For the optical tweezers experiments, cysteines for oligo-DNA handle attachment were introduced at exposed positions in the native structure. As indicated in Fig. 1C, the locations of these residues were chosen in such a way that the conformation of the knotted chain could be manipulated (i.e., converted into a tightened 5₂ or 3₁ knot or untied) when pulling forces are applied. In this study, three double-cysteine variants of UCH-L1 were chosen: Q2C-A223C (2/223), Q2C-Q209C (2/209), and K71C-A223C (71/223) (Fig. 1C). For the 2/223 construct, the protein is attached to the DNA handles and pulled from its N and C termini, which should lead to the formation of a tightened 5₂ knot after mechanical unfolding. In the 2/209 construct, pulling should lead to an unfolded state with a 3₁ knot, whereas pulling from the cysteine residues at positions 71 and 223 should result in an unknotted linear polypeptide chain.

Before performing the optical tweezers experiments, the double-cysteine variants were characterized using ensemble techniques to assess the impact of the amino acid substitutions on the structure, stability, and unfolding and refolding kinetics of the protein. The secondary structure of the variants was probed by far-UV circular dichroism (SI Appendix, Fig. S1), the effect of the amino acid substitutions on the thermodynamic stability of the native and intermediate states was assessed using urea-induced unfolding under equilibrium conditions (SI Appendix, Fig. S2), and the unfolding and refolding kinetics were investigated using single (denaturant)-jump stopped flow experiments (SI Appendix, Fig. S3). In the latter two cases, intrinsic fluorescence was used to probe the unfolding/folding of the protein. Collectively, these experiments established that the amino acid substitutions do not significantly affect the structure of the native state, the stability of the intermediate state, or the folding pathway. In all cases, the amino acid substitutions destabilized the native state of UCH-L1 to a similar degree, but the protein still formed a highly stable native state relative to the intermediate state. More importantly, the folding rate constants in water calculated for the three variants used in the optical tweezers experiments do not differ significantly; see SI Appendix, Section 3.3 and Table S2 for further details.

Mechanical Unfolding of UCH-L1 with Different Pulling Directions Shows Different Unfolding Patterns.

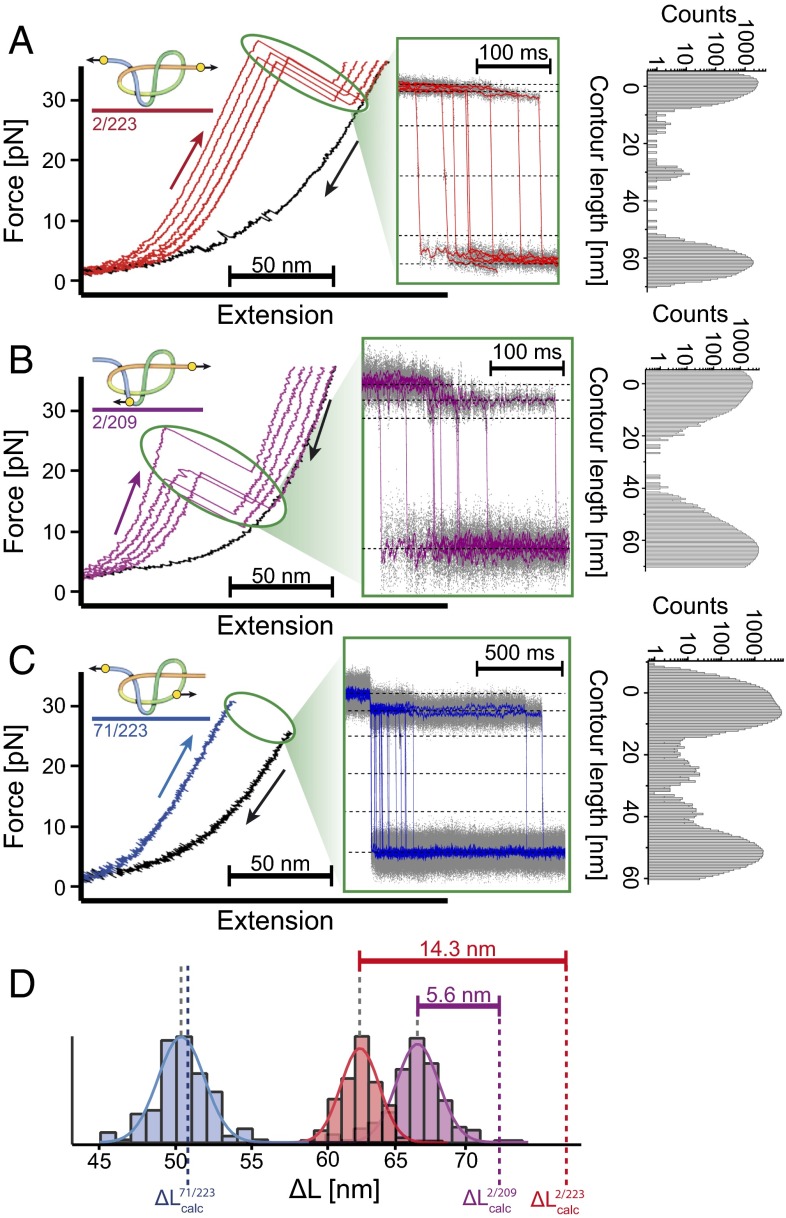
Fig. 2A shows a force-extension curve for unfolding of UCH-L1 in the N- and C-terminal direction (2/223). We observe unfolding forces of about 37 pN at a pulling velocity of 200 nm⋅s⁻¹ and four very short-lived unfolding intermediates. The first two can be shown to be due to rupturing of the N-terminal α-helix, followed by the N-terminal β-strand (Fig. 2A and SI Appendix, Fig. S9A). The folded distance between residues 2 and 223 calculated from the crystal structure is 3.7 nm (PDB ID code 2ETL) (41). Together with the length of 0.365 nm for a single peptide bond in an unfolded polypeptide chain (42), this allows us to estimate the contour length gain one would expect for full unfolding of UCH-L1 from residues 2–223

$$\mathrm{\Delta }{L}_p=\left(223-2\right)\times 0.365\hspace{0.17em}\text{nm}-3.7\hspace{0.17em}\text{nm}=77.0\hspace{0.17em}\text{nm}.$$

Experimentally, a contour length gain of 62.4 nm is observed. The “missing contour length,” i.e., the difference between calculated and measured values of 14.6 nm, corresponds to a chain ∼40 residues long. This difference can be explained by either (i) 40 residues forming a tightened knotted structure after unfolding or (ii) the unfolding of a 40-residue segment of protein structure at forces below the detection threshold of our setup (<0.5 pN). The second possibility can be excluded as such a flexible segment is not observed for either of the two other constructs 71/223 and 2/209. Because 71/223 contains the full C-terminal region and 2/209 the full N-terminal region, if present in the structure, a flexible segment would be detectable in at least one of these other two constructs.

Fig. 2.

Sample force-extension traces of experiments with the three UCH-L1 variants. UCH-L1 2/223 (A), UCH-L1 2/209 (B), and UCH-L1 71/223 (C). (Left) Force-extension curves. (Center) Zoom into the unfolding phase of force extension curves transformed into a contour length vs. time representation (SI Appendix, Section 2.7). Unfolding intermediates are marked by dotted lines. (Right) Position histogram of the unfolding phase of those traces. Note that that for UCH-L1 71/223 (C), waiting times of seconds to minutes at forces of ∼35 pN were required. Therefore, Inset shows an overlay of unfolding events in constant distance mode, exhibiting the characteristic unfolding pattern (SI Appendix, Fig. S6). (D) Contour length increases associated with the unfolding of all three UCH-L1 variants: 2/223 (red), 2/209 (violet), and 71/223 (blue). The calculated values (see Results) are indicated as colored dotted lines. Difference between calculated and observed distances leads to an estimation for the size of the tightened 5₂ (red) and 3₁ (violet) knot.

Fig. 2B shows the unfolding of native UCH-L1 in the 2/209 direction. The major unfolding force peak is in the range of 18 pN at a pulling velocity of 200 nm⋅s⁻¹. Unfolding also proceeds through several intermediates (Fig. 2B and SI Appendix, Fig. S9C). In contrast to the results for the 2/223 construct, the major unfolding peak is preceded by a transition where the protein rapidly samples both native and intermediate states (see zoom in SI Appendix, Fig. S9C). This transition shows a contour length increase of 6.3 nm that is likely caused by unfolding of the first N-terminal α-helix (SI Appendix, Fig. S9D and Section 3.5). Note that the direction of force application to this α-helix is different from in 2/223 explaining the different forces and kinetics for α-helix detachment in the two variants (SI Appendix, Fig. S9). The total contour-length increase for full unfolding is 66.7 nm, shorter by a missing contour length of 5.7 nm than the contour length gain for an extended, unknotted polypeptide chain as calculated using

$$\mathrm{\Delta }{L}_p=\left(209-2\right)\times 0.365\hspace{0.17em}\text{nm}-3.2\hspace{0.17em}\text{nm}=72.4\hspace{0.17em}\text{nm}.$$

This result establishes that the 3₁ knot, comprising of ∼16 residues, remains in the mechanically unfolded state of 2/209 as predicted.

The 71/223 construct, designed for complete unknotting of UCH-L1 on unfolding, requires a significantly higher unfolding force. At the pulling velocities used (200 nm⋅s⁻¹) unfolding of the native structure in most cases did not occur at forces below 35 pN (Fig. 2C). The structure then could only be unfolded by waiting for seconds to minutes at forces between 35 and 40 pN. Because our optical tweezers setup does not allow application of higher forces, it was not possible to obtain a distribution of unfolding forces as for the other two variants. However, the rare unfolding events that occur while pulling the 71/223 construct with constant velocity (SI Appendix, Fig. S5C, Right) show exactly the same fingerprint as additional unfolding experiments performed at a constant distance: all unfolding events exhibit a characteristic first unfolding step to an intermediate associated with a contour length increase of 6.2 nm (Fig. 2C, Center and Right), sometimes followed by up to three, very short-lived, additional unfolding intermediates consistent with a kinetic partitioning mechanism for unfolding (43, 44).

A contour length increase of 50.4 nm was obtained for the 71/223 construct, consistent with the calculated contour length gain for an extended, unknotted polypeptide chain

$$\mathrm{\Delta }{L}_p=\left(223-71\right)\times 0.365\hspace{0.17em}\text{nm}-4.1\hspace{0.17em}\text{nm}=51.4\hspace{0.17em}\text{nm}.$$

Distinct from the results obtained for the 2/223 and 2/209 constructs, in 71/223 we find no evidence for a remaining knotted structure in the unfolded chain.

Tightening of the 5₂ Knot.

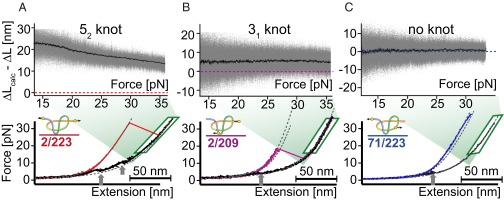
As shown above, the presence of a knot in the taut unfolded chains of the 2/223 and 2/209 constructs manifests itself indirectly in the difference between contour length observed and that calculated for an unknotted chain of the same length. Because a 5₂ knot contains five crossings of the chain, one might expect to observe more contributions from steric clashes of side chains during the compaction of the knot on tightening it at high loads compared with a 3₁ knot. If tightening of the knot proceeds through discrete transitions, we expect to measure a growing contour length of the unfolded chain owing to the stepwise compaction of the knot toward high forces. In other words, the missing contour length should shrink with force. Indeed, plotting the missing contour length of unfolded polypeptide chain vs. the applied force (Fig. 3, Upper) reveals a clear difference between the 2/223 construct and both the other constructs: The measured contour lengths of 71/223 and 2/209 do not depend on force and can thus be well described by the typical elasticity of an entropic polymer chain (see SI Appendix, Section 2.5 for a detailed description). Note that the occurrence of the 3₁ knot in 2/209 leads to a missing contour length of 5.7 nm (Fig. 3B, Upper); however, this value does not change with force. In contrast, the missing contour length decreases with force in the unfolded 2/223 chain, indicating further tightening of the 5₂ knot at high forces. Between 20 and 36 pN, the missing contour length reduces by ∼6 nm (Fig. 3A, Upper). A close inspection of the data (SI Appendix, Fig. S8B) reveals a series of discrete transitions, likely intermediate states with different degrees of compactness populated during the tightening of the 5₂ knot. Because the tightening transitions occur close to equilibrium, integrating the force vs. extension traces in this transition regime allows estimation of the free energy required for compaction of the knot between 20 and 36 pN to ∼23.1 kT (SI Appendix, Section 2.8).

Fig. 3.

Effect of force on the size of the 5₂ and 3₁ knots in the unfolded state of UCH-L1. Plotting the difference between calculated and measured contour length (ΔL_calc − ΔL) against force shows a significantly different behavior of (A) the construct with a 5₂ knot in the unfolded state compared with (B) the construct with the smaller and more compact 3₁ knot and (C) the construct without a knot in the unfolded state. (Upper) Black curves are an average of 15–20 different measurements in the same experiment and gray dots are overlay of all of the original traces. (Lower) Sample unfolding (colored) and relaxation curves (black) for all three constructs. The gray arrows indicate the region where fast equilibrium transitions between preformed structures occur. These show different behavior than the knot tightening at higher forces.

Folding Intermediates.

Relaxation traces in force spectroscopy experiments allow observation of rapidly forming intermediate states. Even though overall folding to the native state was slow (see next paragraph), all three constructs exhibit rapid fluctuations between extended and collapsed structures when relaxing the force after unfolding (black curves in Fig. 3). These close-to-equilibrium transitions (see arrows in Fig. 3) appear in a force range between 3 and 12 pN indicating the rapid and early population of intermediate states; 2/223 shows two regions at 12 and 6 pN, respectively, whereas 2/209 shows only one such region at around 4 pN, and 71/223 shows one region at 5 pN (see SI Appendix, Fig. S8 for more details). Those rapidly forming intermediates involve large regions of the protein that, judged by the large change in contour lengths, are of almost the same compactness as the native state.

We can estimate the ΔG of the rapidly forming equilibrium structures by integrating the area enclosed by the relaxation force curve and the worm-like chain (WLC) curve of the fully unfolded state. We find a ΔG of 8 kT for the low-force intermediates and 11 kT for the high-force intermediates in the 2/223 construct and a ΔG of 6–7 and 8 kT for the (2/209) and (71/223) constructs, respectively (SI Appendix, Section 2.8). It is important to note that those intermediates are heterogeneous in both contour length and kinetics, indicating that there is an ensemble of intermediate states: analysis of a sample trace for the low-force region of the force-relaxation curves of the 2/223 construct (SI Appendix, Fig. S10) using a hidden Markov model (45) shows the heterogeneity of this ensemble. We find that even direct transitions between the intermediate states are possible without visiting the unfolded state reminiscent of the folding network model proposed in ref. 46. Apparently, this ensemble also contains longer-lived intermediate states that are stable for many seconds even under load (see long dwell time in the trace of SI Appendix, Fig. S8D). A similar heterogeneous population can be observed in traces where we relax the chain to zero load and, after a certain waiting time, rapidly pull and unfold the chain (sample traces in SI Appendix, Fig. S7). Longer-lived intermediate states then lead to pronounced force peaks at nonnative contour lengths, whereas more dynamic intermediates lead to low force peaks (SI Appendix, Fig. S7D).

Refolding Kinetics.

In the next set of experiments, the effect of the three different knotted unfolded states on the refolding kinetics of the protein was investigated. To this end, we first unfolded the various constructs and subsequently relaxed the tension to zero force and allowed the protein a certain time to refold. The folding state of the molecule was then probed in another force-ramp experiment (for details of the experimental protocol, see SI Appendix, SI Methods). A summary of the time-dependent refolding probability for all three constructs is shown in Fig. 4. The refolding kinetics strongly differ with pulling direction. Using a simplified two-state model of folding, the following global folding rate constants were calculated from the data: $k_{2/223}=0.118\hspace{0.17em}\pm \hspace{0.17em}0.016\hspace{0.17em}{\text{s}}^{-1}$, $k_{2/209}=0.035\hspace{0.17em}\pm \hspace{0.17em}0.005\hspace{0.17em}{\text{s}}^{-1}$, and $k_{71/223}=0.011\hspace{0.17em}\pm \hspace{0.17em}0.002\hspace{0.17em}{\text{s}}^{-1}$. Thus, a preformed 5₂ knot accelerates folding to the native state by one order of magnitude compared with refolding from a fully unfolded and unknotted chain. A preformed trefoil knot also leads to an increase in folding rate compared with the unknotted denatured state; however, the effect is smaller than for the 5₂ knot. It is important to note that, in all constructs, a broad range of different metastable folding intermediates is observed. These intermediates account for the deviations of the data in Fig. 4 from a single-exponential fit. Typical sequences of unfolding/refolding cycles with varying waiting times are shown in SI Appendix, Fig. S4.

Fig. 4.

Probability P_F folding to the native state plotted against waiting time at zero force for all three constructs (colored as in Fig. 2). Refolding rate constants of each construct were obtained from a single-exponential fit of the optical tweezers data.

Discussion

Size of Knots in the Stretched Polypeptide Chain.

Although the contour length increase on unfolding the 71/223 construct is in good agreement with the calculated length of the fully unfolded polypeptide chain, the contour length increase for the 2/223 and 2/209 constructs are shorter than expected for unknotted, unfolded chains containing the same number of residues. Pulling in the 2/209 direction provides a size estimate for the 3₁ knot of 5.7 nm, which corresponds to ∼16 amino acid residues. This value is in good agreement with atomic force microscopy (AFM) measurements on AFV3-109 (47) and phytochrome C (48), as well as values from simulations of tight knots in polypeptide chains under force (49).

In contrast to the results for the 2/209 and 71/223 constructs, the missing length measured for the residual 5₂ knot in the 2/223 construct has a surprisingly large size of 14.6 nm, which corresponds to roughly 40 residues, significantly larger than simple estimates on knotted ropes (which for a 5₂ knot vary from 6.4 to 9.2 nm) (50). A dense network of crossing strands in the 5₂ knot may make it more difficult to tighten the knot leaving its size larger than expected under certain loads.

Tightening the 5₂ Knot.

Consistent with the putative “bulkiness” of the 5₂ knot compared with the simpler 3₁ knot, additional transitions are observed that relate to compaction of this knot at high forces (Fig. 3). It is important to note that knot compaction occurs at much higher forces (>20 pN) than those at which the early refolding intermediates fold/unfold (<12 pN; see arrows in Fig. 3), enabling us to clearly distinguish between the processes. Despite the small contour length change of roughly 6 nm on compaction of the 5₂ knot between 20- and 36-pN pulling force, the associated equilibrium free energy changes are large (∼23.1 kT or 13.7 kcal⋅mol⁻¹), a value far too high to be explained by folding/unfolding of a small element of protein structure such as an α-helix or a small β-sheet (51). The increasing contour length for the 2/223 construct toward high forces shows the knot is not yet compact and offers an explanation for the apparently overly large size of the 5₂ knot at low forces. This compaction is only observed for the 5₂ knot indicating that the simpler 3₁ knot has no significant free energy barriers opposing compaction and thus easily assumes a tight, compact structure at forces of 5 pN and above. It is possible to speculate on the potential biological consequences of this large difference in knot size between the 5₂ and the 3₁ knot. Our results suggest that 3₁-knotted proteins may be degradable by either the bacterial or eukaryotic degradation machinery as the tightened knot is approximately the same size as the channel in which a polypeptide chain has to be translocated through to reach the central proteolytic site (52–54). In contrast, degradation may be challenging for a 5₂-knotted protein, where a large 5₂ knot might block the entry pore of the degradation machine thus preventing or slowing degradation and also potentially thereby hindering the degradation of other cellular proteins. In this context, it may be interesting that UCH-L1 is an abundant protein in human neurons and has been associated with a number of neurodegenerative diseases (31, 32). Additionally, an isoform of UCH-L1 is bound to the proteasome and had better protection against accidental degradation (55).

Influence of Knotting on the Folding Kinetics of UCH-L1.

The single-molecule mechanical assay used here provides a unique direct method to measure the effect of knot formation on folding rates. For UCH-L1, we observe significant effects of both 3₁ and 5₂ knots in the unfolded states on the folding rates. Folding from an unknotted denatured state is one order of magnitude slower than from knotted unfolded states (Fig. 4). These results establish that knotting, or a step associated with knotting, is rate limiting for the folding of this family of knotted proteins. Recent in vitro translation and folding studies on trefoil-knotted methyltransferases are consistent with this result (16). Note that the conclusion of knotting as the rate limiting step only holds if the back-reactions (unknotting and unfolding) are assumed to be slow compared with the overall timescale of folding. The overall timescale for folding observed here using single-molecule force spectroscopy (between 10 and 100 s) agrees well with previous measurements of folding rates in solution from a chemically denatured state (34). Our results can also be compared with values from computational studies where it is facile to create an unknotted variant of a knotted protein with the same secondary structural elements packed against each other in the same manner but with a different connectivity, essentially “rewiring” the polypeptide chain. Coarse-grained lattice-based approaches have been used to estimate the effect knots on the folding and unfolding rates of a model system (56). A 5₂ knot had an effect on both the folding rate ($k_f^{\mathrm{knot}}$ = 0.61 $k_f^{\mathrm{unknot}}$) and unfolding rate ($k_u^{\mathrm{knot}}$ = 0.59 $k_u^{\mathrm{unknot}}$). Remarkably, the folding rate was only decreased by a factor of two, compared with the factor of ten observed in this experimental study of a naturally occurring 5₂ knotted protein.

Folding Pathways.

Both the mechanical unfolding and refolding studies conducted here establish that there are a large number of intermediate states populated during force unfolding measurements and during refolding at low force. These intermediates vary in contour length, therefore structure, and mechanical stability. Ideally, the data from the optical tweezers experiments could be used to reconstruct the energy landscape for folding/unfolding of UCH-L1 as was achieved for calmodulin (57). Unfortunately, the number and heterogeneity of intermediates observed, together with the fact that timescales of unfolding/folding events do not allow us to monitor equilibrium transitions that include folding to the native state, means it is currently not possible to do this for UCH-L1. However, important information on the folding pathway can still be extracted (see also discussion in SI Appendix, Section 3.7).

The results of the optical tweezers experiments presented here are consistent with our unfolding and refolding kinetic studies on UCH-L1 (34). The overall timeframes for formation of the native state are similar and intermediate states are observed during unfolding and refolding in both cases. The results of the optical tweezers experiments focused on the refolding of mechanically unfolded UCH-L1 show that there are long-lived intermediate states, stable for quite some time even under load. It is highly likely that these are the same as the metastable states observed in both equilibrium and kinetic measurements on UCH-L1 folding using chemical denaturants and intrinsic fluorescence as a probe of structure. Thus, despite the fact that the two studies used different methods to unfold the protein, the results suggest that both report on the same key features of the folding energy landscape for this knotted protein. However, the single-molecule optical tweezers results provide considerably more detail on this landscape. Our results support the view that the folding of knotted proteins is a complex process with a large number of intermediate structures that may include nonnative contacts (58, 59) and consists very likely of on-pathway states as well as off-pathway, kinetically trapped, states.

Conclusions

The exquisite control inherent in single-molecule force spectroscopy experiments has enabled us to control the knotted topology of an unfolded state of a protein providing the unique ability to study the folding of a knotted protein from three different knotted states thereby establishing the effect of different knot types on folding rates and pathways. Here, we provide direct evidence that a threading event associated with formation of either a 3₁ or 5₂ knot, or a step closely associated with it, significantly slows down folding of UCH-L1. The results of the optical tweezers experiments highlight the complex nature of the folding of a knotted protein, and detect many additional intermediate structures that cannot be resolved by intrinsic fluorescence. Given the number of intermediates observed, it is likely that some of these are off pathway and we can speculate that these species may have a significant number of nonnative contacts (58, 59). Mechanical stretching of knotted proteins is also of importance for understanding the possible implications of knots in proteins for cellular degradation. Our results highlight the potential difficulties in degrading a 5₂ knot compared with a 3₁ knot and therefore have possibly important implications for knotted proteins in proteostasis and associated disease states (14, 15, 32).

Methods

The engineering, expression and purification of the double-cysteine variants of UCH-L1 were performed as described in SI Appendix, SI Methods. Protein characterization using far-UV CD, thermodynamic, and kinetic folding experiments was carried out as described in SI Appendix, SI Methods. For the single-molecule mechanical measurements, a dumbbell configuration was generated by attaching the biotin/digoxigenin functionalized end of the DNA handles to micrometer-sized streptavidin/anti-digoxigenin silica beads (Fig. 1A). The beads were trapped in the foci of a custom-built dual beam optical-tweezer setup and subjected to stretch-and-relax cycles at a constant velocity or at a constant force bias with fixed trap positions. All measurements were conducted in PBS at pH 7.4. A complete description of the methods used is given in SI Appendix, SI Methods.