Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jul 11;6:29009. doi: 10.1038/srep29009

Electronic and magnetic properties of H-terminated graphene nanoribbons deposited on the topological insulator Sb2Te3

Wei Zhang 1,2,*, Farideh Hajiheidari 2,*, Yan Li 2,3, Riccardo Mazzarello 2,4,a
PMCID: PMC4941537  PMID: 27405058

Abstract

Magnetism in zigzag graphene nanoribbons (GNRs) has received enormous attention recently, due to the one-dimensional nature of this phenomenon, as well as its potential applications in the field of spintronics. In this work, we present a density functional theory (DFT) investigation of H-passivated GNRs on the (111) surface of the topological insulator Sb2Te3. We show that the chemical interaction between the GNR and the substrate is weak. As a result, the GNR-surface distance is large, of the order of 3.4 Angstrom, doping effects are almost negligible, and the mean-field magnetic properties of the GNR are preserved. Nevertheless, the presence of the substrate affects significantly the magnitude of the exchange coupling constants between the edges. Although our DFT calculations do not properly describe quantum fluctuations that destabilize the edge magnetism in free-standing GNRs, they provide important information about the stabilizing mechanisms which originate from the substrate-induced spin orbit coupling and the decoherence effects due to the surface states of Sb2Te3. We argue that, owing to these mechanisms, Sb2Te3 may be a suitable substrate to investigate experimentally the transition from “quantum” to “classical” magnetism in GNRs.

Two-dimensional graphene1 has been the focus of intensive investigation since its discovery in 2004, due to its peculiar electronic and transport properties2. In an effort to induce a sizable energy gap in the band structure of graphene, which could lead to ground-breaking applications in information technology, quasi one-dimensional graphene nanoribbons (GNRs) have been thoroughly investigated recently3,4,5,6,7. Remarkably, zigzag-terminated GNRs have been predicted to possess magnetic electronic states localized at the edge, with antiferromagnetic (AFM) coupling between the two edges8,9. Experimental evidence, albeit indirect, for the presence of edge magnetism in GNRs has been recently provided10. However, edge magnetism in isolated GNRs is generally not stable, in principle. There are two intrinsic sources of instability due to the one-dimensional nature of this phenomenon: quantum fluctuations brought about by the AFM inter-edge coupling, which lead to an entangled singlet ground state11, and thermal fluctuations12. The two effects can be suppressed by increasing the width of the GNR and by reducing temperature, respectively.

A generic mechanism capable of stabilizing edge magnetism is the anisotropy due to spin-orbit coupling (SOC), i.e., the dependence of the energy of electrons on the absolute orientation of their spins. A sufficiently strong magnetic anisotropy would a) damp out spin waves, leaving only domain-wall-like excitations at finite temperature, as well as b) suppress quantum fluctuations. Although the intrinsic SOC in GNRs is extremely weak, anisotropy effects can be greatly enhanced by depositing graphene on a substrate with strong SOC.

A more subtle stabilizing mechanism could occur in the presence of a substrate which possesses surface states near the Fermi energy. Such states could lead to decoherence effects and to the emergence of “classical” edge magnetism from the highly entangled singlet ground state11.

The last two mechanisms may be prominent in the recently discovered class of band insulators called three-dimensional topological insulators (TIs)13,14,15,16,17. TIs have several remarkable properties, which stem from time-reversal symmetry and strong SOC. They possess robust, conducting surface states in the bulk band gap, which exhibit spin-momentum locking and are symmetry protected against non-magnetic disorder.

Besides the stabilizing effects of the TI substrate, another interesting phenomenon is the possible back action of edge magnetism (if stable) on the TI surface state. The proximity of a TI to a magnetic system breaking time-reversal symmetry can lead to fascinating phenomena, such as an anomalous quantum Hall effect and the formation of one-dimensional chiral states induced by domain walls in the magnet18. Recent efforts to break time-reversal symmetry in TIs have focused on (a) depositing magnetic impurities19,20,21 or magnetic insulators22,23 on the surface of TIs or (b) doping TIs with magnetic impurities24,25. These proximity effects could be exploited in spintronics devices integrating TIs with magnetic materials. Since the magnetic edge states have AFM ordering across the GNR, their effect on a TI could bear some similarities with that of a domain wall.

In this work, we present a DFT study of the structural, electronic and magnetic properties of mono-hydrogenated zigzag GNRs deposited on the (111) surface of the TI Sb2Te326. In principle, standard spin-polarized DFT calculations are not suitable to investigate quantum fluctuations in GNRs, because they break spin-rotational invariance from the outset. Nevertheless, they provide valuable information about the “mean-field” ground-state properties of the system, from which one can extract the substrate-induced effects on the SOC parameters and the exchange coupling constants in GNRs. Furthermore, they enable one to determine the strength of the interaction between the GNR and the TI electronic states.

Graphene-TI heterostructures have recently become an active field of research, see e.g. Refs 27, 28, 29, 30, 31. The main focus of these works was the enhancement of the spin-orbit gap in graphene due to the TI, which could open the way to experimental observation of the quantum spin Hall effect in graphene32. In this work, we instead investigate the effect of the TI on the edge magnetism of GNRs.

It is of great interest to study the interaction between GNRs and a substrate like Sb2Te3, which has surface states with p character. Recently, we have shown that H-terminated GNRs interact very strongly with metal surfaces like Ir(111), which possess d-like surface states near the K point of the surface Brillouin zone33,34. On the other hand, the chemical interaction with Au(111) is weak, such that the magnetic properties of the GNR are preserved35. The Cu(111) surface exhibits intermediate behaviour35,36. However, metal substrates are less suitable to investigate theoretically decoherence effects, in that they possess bulk bands crossing the Fermi energy, which makes the derivation of effective model Hamiltonians very cumbersome.

Results

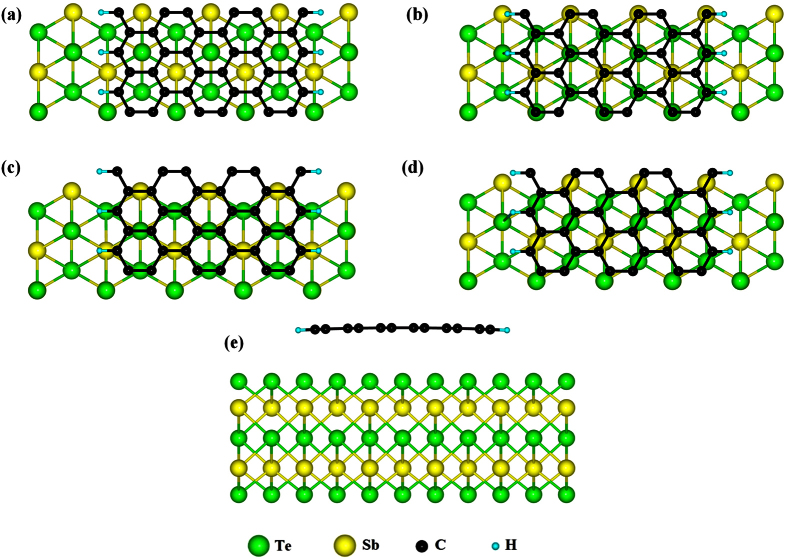
We focus on the (111) surface of Sb2Te3 and we assume that the GNR is parallel to the (Inline graphic) direction of the substrate. We consider Sb2Te3 as TI substrate for two reasons. First, it possesses a simple Dirac cone surface spectrum; second, the lattice constant of its (111) surface is exactly 3 times as large as that of graphene (4.26 Å versus 1.42 Å). The second property allows us to use a small supercell lattice vector along the direction parallel to the GNR (in spite of this, our models are very large and demanding from the computational point of view, as further discussed in the Methods section). We study several adsorption configurations. Top views of these configurations are shown in Fig. 1(a–d). Upon structural optimization, the most stable configuration is the one where the surface Te atoms are at the center of graphene hexagon rings (Fig. 1(a)). Notice that this is the stable structure for perfect graphene on Sb2Te3 as well27. The bending of the GNR is small and the distance between the GNR and the substrate is around 3.4 Å, which is also compatible with the previous study on perfect graphene27. The side view of the most stable configuration is shown in Fig. 1(e) and geometrical data about the relaxed GNR are shown in Table 1.

Figure 1.

Figure 1

Open in a new tab

(a–d) Top view of the four adsorption configurations considered in this work. The supercell contains 3 GNR units, and the GNR has a width of 6 graphene units. (e) Side view of the energetically most stable adsorption configuration (shown in (a)). Upon relaxation, the GNR is slightly bent. Sb, Te, C, and H atoms are rendered with yellow, green, black and blue spheres.

Table 1. Minimum and maximum distance between the H-terminated GNR and the Sb2Te3 (111) surface.

  H-terminated GNR
Min (Å) Max (Å)
hollow (a) 3.37 3.49
on-top (b) 3.40 3.58
bridge-1 (c) 3.44 3.56
bridge-2 (d) 3.43 3.57
Open in a new tab

Distances are in Angstrom. The letters refer to the structures shown in Fig. 1.

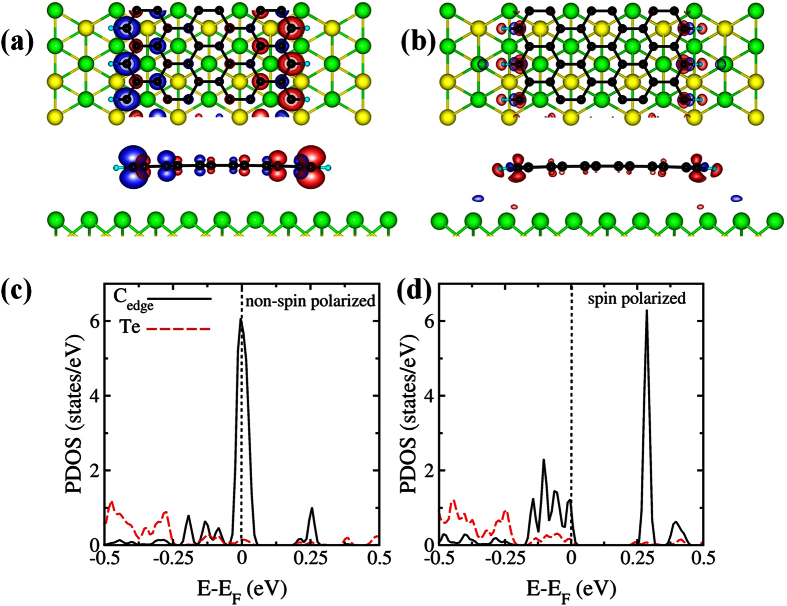
It turns out that the magnetic properties of the GNR are not strongly affected by the presence of the surface (see Fig. 2(a)). The GNR displays edge magnetism with AFM coupling between the two edges. The magnetization per edge C atom is 0.30 μB/cell, which is similar to the one displayed by a free-standing GNR (using an equivalent k-point mesh). Nevertheless, the energy difference between the inter-edge ferromagnetic (FM) and AFM configuration, EFM-EAFM, is reduced significantly with respect to the free-standing case (3.9 meV versus 6.5 meV per edge C atom), due to screening effects by the surface states. This decrease in the inter-edge AFM coupling constant is beneficial for the stabilization of edge magnetism (see Discussion section).

Figure 2.

Figure 2

Open in a new tab

(a) Top and side view of an isovalue surface of the edge state spin density of the deposited GNR. The system exhibits AFM coupling between the two edges. The red (blue) surface indicates spin up (down) density. (b) Top and side view of two isovalue surfaces (corresponding to the values ± 5 · 10−4 a.u.) of the difference between the total charge of the GNR plus substrate system and the charge of the isolated GNR and Sb2Te3. The red (blue) color indicates accumulation (depletion) of charge. (c,d) Non-spin-polarized and spin-polarized projected density of states (PDOS) for the 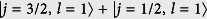Inline graphic spin-angle functions of an edge C atom and a nearest neighbour Te atom. The peak at the Fermi energy in (c) corresponds to the edge state. The PDOS in (d) were calculated for spin-polarization along x but the direction of the polarization has negligible effect on the PDOS.

We calculate the interaction energy between the GNR and the substrate by computing the difference between the energy of the full system and those of the isolated GNR and the clean substrate. This energy is equal to 41 meV per edge C atom, indicating weak chemical interaction between the two systems. Figure 2(b) shows that the charge redistribution upon deposition of the GNR, obtained by subtracting the total charge of the isolated GNR and substrate from the charge of the GNR plus Sb2Te3 system, is small as well. In the following, we assume that the surface is perpendicular to the z axis and the GNR is parallel to the y axis. Our calculations indicate that the easy axis of magnetization is in-plane and perpendicular to the GNR (x-axis). However, the magnetic anisotropy energies (MAEs) are quite small: the energy difference between the x-axis and the y-axis (respectively z-axis) configuration is of the order of 0.2 meV (resp. 0.1 meV). It is important to stress that these numbers should be considered as order-of-magnitude estimates of the MAEs, rather than exact values. Due to the large size of the models, it is not possible to fully assess the convergence of the MAEs with respect to the number of relaxed Sb2Te3 layers and the k-point mesh (this point is further discussed in the Methods section). Nevertheless, this estimate is sufficient for our goal of determining the relative magnitude between the MAE and the AFM coupling strength. It is worth mentioning that the electronic structure of the GNR and the substrate is hardly affected by the direction of magnetization.

The non-spin-polarized and spin-polarized projected density of states (PDOS) for the valence p orbitals (more precisely, for the 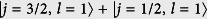Inline graphic spin-angle functions) of an edge C atom and the nearest neighbour Te atom are shown in Fig. 2(c,d). The interaction-induced splitting of the 2p PDOS peaks of the C atom, which reflects the ferromagnetic ordering along the edge, is about 0.3 eV. This value is smaller than the splitting obtained for an unsupported GNR with the same width (0.7 eV). This reduction stems from the non-negligible (albeit small) hybridization between C and the neighbour Te atoms, as shown in the figure. The broadening of the lower peak at the Fermi energy is also due to said hybridization.

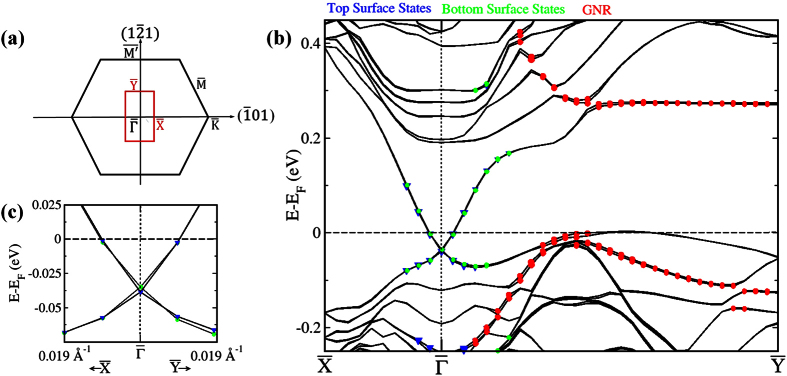
The band structure of the system along the 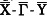Inline graphic lines of the first Brillouin zone (BZ) of the supercell (with orthorhombic symmetry) is shown in Fig. 3(a) for the case of magnetization along x (easy axis). The line 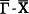Inline graphic (resp. 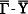Inline graphic) corresponds to the 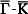Inline graphic (resp. 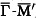Inline graphic) line of the first BZ of the Sb2Te3(111) surface. Since our supercell contains 3 GNR units along y, the portion (2/3π/a-π/a) of the one-dimensional BZ of the GNR (where a is the lattice parameter of graphene) is exactly folded onto the 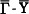Inline graphic portion of the supercell, see inset of Fig. 3(a). Hence, 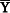Inline graphic coincides with the boundary of the BZ of the GNR. The bands of the surface states of the top and bottom surface are coloured in green and blue, respectively. There is a tiny shift of the Dirac point of the top surface state to lower energies by about 4 meV. Therefore, doping effects are practically negligible. Notice that a perfect graphene sheet on Sb2Te3 at the equilibrium distance of 3.4 Å is slightly n-doped. However, the type of doping (n or p) depends on the distance between graphene and the Sb2Te3. Similarly to what occurs for some metallic substrates37, graphene is n-doped for small distances and becomes p-doped for distances exceeding 3.5 Å, see Fig. 4 (the figure shows data about the doping of the Sb2Te3 surface, which, obviously, displays the opposite trend). The equilibrium distance turns out to be close to the transition point. In the case of GNRs, the absence of doping can be ascribed to small differences in the chemical interaction with Sb2Te3, as compared to perfect graphene, which stem from the presence of the edge states.

Figure 3.

Figure 3

Open in a new tab

(a) The surface Brillouin zone (BZ) of Sb2Te3(111) (black) and of the orthorhombic supercell employed in our simulations (red). The directions indicated in the figure refer to the rhombohedral lattice. (b) Band structure for the H-terminated GNR on Sb2Te3 along the 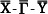Inline graphic lines of the surface BZ of the supercell for magnetization along x (easy axis). 1) Top and 2) bottom surface state bands and 3) GNR edge state bands are identified by requiring that the sum of the squares of the projections of the states on the orbitals of the atoms of the 1) 5 topmost Sb2Te3 layers, 2) 5 bottommost layers and 3) edge C row be larger than 0.3. (c) Zoomed-in view of the band structure around the 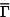Inline graphic point, which shows more clearly that the top and bottom surface state bands almost coincide.

Figure 4. Doping effects in perfect graphene deposited on Sb2Te3(111).

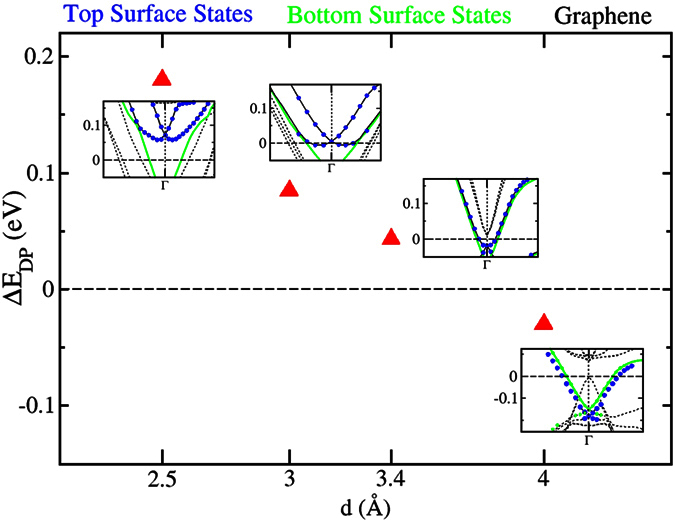
Figure 4

Open in a new tab

The plot shows the energy difference ΔEDP between the Dirac point of the top surface state of Sb2Te3 (which interacts with graphene) and the bottom surface state, as a function of the graphene-Sb2Te3 distance d. Positive (resp. negative) ΔEDP indicate p-doping (resp. n-doping) of the top surface and, thus, n-doping (resp. p-doping) of graphene. 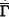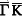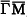The insets show the corresponding band structures around Inline graphic the point (along the directions Inline graphic and Inline graphic). In the insets, energies are in eV and EF is set at 0 eV. Notice that graphene displays a sizable energy gap even at large d, which is induced by the substrate29.

In principle, the effects of a magnetic perturbation on the surface states of a TI depend on the direction of magnetization. For idealized, rotationally invariant surfaces, a magnetization axis perpendicular to the surface induces a gap in the band structure, whereas an in-plane magnetization does not16. However, for surfaces with C3 v symmetry like Sb2Te3(111), in-plane magnetic fields can also open a gap due to hexagonal warping effects38 (interestingly, warping terms in hexagonal surfaces had previously been investigated by Henk et al.39, in the context of the SOC-induced Rashba-splitting of the L-surface state of Au(111)40,41). In our model, no gap is observed, irrespective of the direction of magnetization of the GNR edge states. This behaviour originates from the fact that the exchange interaction between the edge-state electrons and the surface state electrons is weak, owing to the large GNR-substrate distance. Moreover, no evidence for the formation of quasi one-dimensional chiral states at the surface (induced by the AFM configuration of the GNR) is found.

Discussion and conclusions

We have shown that the chemical interaction between the GNR and the substrate does not upset the mean-field magnetic properties of the GNRs. However, quantum fluctuations (not included in our DFT simulations) will destroy edge magnetism, unless spin-orbit coupling and/or decoherence effects are sufficiently strong. Our simulations indicate that there is an easy axis, which is in-plane and perpendicular to the GNR, and the MAEs are of the order of 0.1-0.2 meV. This energy scale has to be compared with the magnitude of the AFM coupling across the GNR. For this purpose, it is useful to consider a different edge geometry, consisting of zigzag segments separated by steps (chiral GNR), which possesses well localized edge states. This geometry allows for an essentially exact mapping onto a Heisenberg spin ladder with AFM rung coupling JAFM and FM leg coupling JFM, as discussed in ref.11. Since a) the AFM coupling in free-standing GNRs does not depend strongly on the edge geometry (for fixed GNR width) and b) our results indicate that, for H-terminated GNRs, the reduction in this coupling upon deposition on the Sb2Te3 substrate is not dramatic (it is a factor of 2 reduction), we can safely conclude that the AFM coupling in deposited GNRs with zigzag and chiral geometry is of the same order of magnitude. We also expect that the strength of the MAE does not depend strongly on the edge geometry, since it is mainly determined by the effective SOC induced by the substrate. We can thus estimate the parameters of the ladder Hamiltonian from our simulations. Since a zigzag segment of length equal to 3 GNR units (corresponding to our supercell) can host a localized state and, thus, an unpaired spin, the anisotropy strength for each edge spin in the effective ladder model is of order 0.1 meV, whereas the AFM exchange rung coupling, proportional to EFM-EAFM, is of the order of 10 meV. The relatively large value of JAFM is due to the small width W of the GNR (W = 1.14 nm). According to ref. 42, the spin ladder exhibits a phase transition from a “rung singlet” (corresponding to the entangled singlet state in the GNR) to a “stripe ferromagnetic phase” (corresponding to edge magnetism) as a function of the anisotropy strength. Although the critical anisotropy for a given JAFM also depends on JFM (which is more difficult to determine from DFT simulations, because twice as large supercells along the GNR direction must be employed), it is clear from the phase diagram shown in ref. 42 that, for such small ratio between the anisotropy and JAFM, the system is in a singlet state. Since, however, the MAE is expected to be largely width-independent while the JAFM decreases strongly with ribbon width W, this material system provides means to study the rung singlet - stripe FM phase transition, which should happen as W is increased. Notice that very recent work has shown that effective spin theories are applicable to the zigzag geometry as well43. Nonetheless, the long-range nature of the exchange couplings along the leg in the corresponding spin ladder model could lead to differences in the phase diagram with respect to the chiral GNR.

The second important stabilizing mechanism is decoherence, which stems from the coupling of the GNR edge states (the “system”, in the language of open systems) to the surface states of Sb2Te3, which correspond to the environment. The basic principle of this stabilization can be understood best if decoherence is viewed as the dynamical leakage of quantum information into the environment, so that the environment continuously measures the system. The macroscopic ground state of an isolated GNR is a highly entangled singlet state11. The individual electron spins at each edge are aligned with each other and thus give rise to large “superspins”, one at each edge. However, this macroscopic spin points in all directions simultaneously. As soon as such a superposition state is allowed to interact with the environment, information about the alignment of the superspin is acquired by the environment. In the extreme case where the system-environment interaction (which leads to a continuous measurement of the system) dominates over the intrinsic dynamics (which tends to restore the entangled singlet state), this mechanism should lead to a complete collapse of the wave function toward the classical magnetic state, i.e. to edge magnetism. Hence, although this classical state is not intrinsically stable in an isolated GNR, the continuous monitoring by the environment gives rise to an extrinsic stabilization11. This is known as the Quantum-Zeno effect44: strong decoherence implies that the environment projects the system into the same unstable state over and over again by measuring it45,46.

We argue that these effects should lead to a quantum-to-classical transition as the ribbon width is increased. Quantitative investigation of these fascinating phenomena requires the derivation of effective low-energy theories (based on our DFT simulations) for the interaction between topological surface states and GNR edge states. The first step of this derivation would be a model of interacting fermions restricted to only the essential degrees of freedom, namely the TI surface states and the graphene π-band. The TI bulk states and the σ band in graphene, which are next-closest to the Fermi level, are both gapped and therefore not a priori important for the low-energy domain. In a second step, this fermionic model should be further reduced to a model of localized spins and their interaction with the TI surface state electrons. Such simplified model should be amenable to many body methods beyond the mean-field approximation. This will be the subject of future work.

In conclusion, our DFT simulations indicate that the chemical interaction between H-terminated GNRs and the Sb2Te3(111) is weak: as a consequence, there is small structural relaxation of the GNRs. Furthermore, the mean-field magnetic properties of the GNRs are not strongly affected by the presence of the substrate. Exact results about spin ladder Hamiltonians42 suggest that the estimated magnetic anisotropy energies (of the order of 0.1 meV) are not sufficiently strong to stabilize edge magnetism against quantum fluctuations, except for very wide GNRs. Nevertheless, decoherence phenomena due to the interaction with the surface states of Sb2Te3(111) may be effective in restoring classical behaviour and, thus, deserve further investigation.

Methods

Computational details

We use the DFT plane-wave package Quantum-Espresso47. We employ scalar-relativistic and fully-relativistic norm-conserving pseudopotentials48 and local-density-approximation and gradient-corrected Perdew-Burke-Ernzerhof functionals49. For the latter, we include the semi-empirical van der Waals corrections by Grimme50. The plane-wave cut-off energy is 816 eV (60 Ry). We carry out the geometry optimization without SOC and converge the total energy to 2 × 10−6 eV. Subsequently, we include SOC to determine the electronic and magnetic properties of the relaxed structures. Upon inclusion of SOC, all the components of the forces acting on the atoms change by less than 5 × 10−3 eV Å−1. The MAEs are calculated by computing the total energy for different orientations of the magnetization. We employ an orthorhombic supercell of the surface that corresponds to 5 x sqrt(3) of the hexagonal Sb2Te3(111) unit cell, which has a lattice parameter of 4.26 Å. We consider thick slabs containing 30 layers to model the substrate, separated by a vacuum layer of 17 Å. Thick Sb2Te3 slabs are required to decouple the surface states on opposite surfaces of the slab51. Thinner slabs lead to a spurious gap due to the hybridization between said states. The GNR has a width of 6 graphene units, corresponding to 1.14 nm. The supercell contains 3 GNR units along the y direction parallel to the GNR. The GNRs is on the top surface of the slab. In total, the model contains 342 atoms. 1 × 8 × 1 Monkhorst-Pack (MP) meshes52 are used to perform the integration over the Brillouin zone. We have also considered a 1 × 4 × 1 MP mesh and found that the two meshes yield the same easy axis. Due to the large size of the models, it is computationally unfeasible to employ denser MP meshes to assess the convergence of the MAEs. All of the atoms of the GNRs and of the four topmost layers of the surface are allowed to relax during structural optimization.

Additional Information

How to cite this article: Zhang, W. et al. Electronic and magnetic properties of H-terminated graphene nanoribbons deposited on the topological insulator Sb2Te3. Sci. Rep. 6, 29009; doi: 10.1038/srep29009 (2016).

Acknowledgments

We acknowledge enlightening discussions with M. Schmidt and S. Wessel. W. Z. gratefully thanks the Young Talent Support Plan of Xi’an Jiaotong University. We also gratefully acknowledge the computational resources provided by JARA-HPC from RWTH Aachen University under project JARA0107, and the support by the HPCC Platform, Xi’an Jiaotong University.

Footnotes

The authors declare no competing financial interests.

Author Contributions Simulations were performed by W. Z. and F. H, with help from Y. L. Analysis of the data was carried by W.Z., F. H. and R.M. The paper was written by R. M., with help from all the co-authors. R. M. conceptualized the project.

References

  1. Novoselov K. S. et al. Electric Field Effect in Atomically Thin Carbon Films. Science 306, 666–669 (2004). [DOI] [PubMed] [Google Scholar]
  2. Castro Neto A. H., Guinea F., Peres N. M. R., Novoselov K. S. & Geim A. K. The electronic properties of graphene. Rev Mod Phys 81, 109–162 (2009). [Google Scholar]
  3. Son Y. W., Cohen M. L. & Louie S. G. Half-metallic graphene nanoribbons. Nature 444, 347–349 (2006). [DOI] [PubMed] [Google Scholar]
  4. Jiao L., Zhang L., Wang X., Diankov G. & Dai H. Narrow graphene nanoribbons from carbon nanotubes. Nature 458, 877–880 (2009). [DOI] [PubMed] [Google Scholar]
  5. Cai J. et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 466, 470–473 (2010). [DOI] [PubMed] [Google Scholar]
  6. Li X., Wang X., Zhang L., Lee S. & Dai X. Chemically Derived, Ultrasmooth Graphene Nanoribbon Semiconductors. Science 319, 1229–1232 (2008). [DOI] [PubMed] [Google Scholar]
  7. Ritter K. A. & Lyding J. W. The influence of edge structure on the electronic properties of graphene quantum dots and nanoribbons. Nat Mater 8, 235–242 (2009). [DOI] [PubMed] [Google Scholar]
  8. Fujita M., Wakabayashi K., Nakada K. & Kusakabe K. Peculiar localized state at zigzag graphite edge. J Phys Soc Jpn 65, 1920–1923 (1996). [Google Scholar]
  9. Nakada K., Fujita M., Dresselhaus G. & Dresselhaus M. S. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Phys Rev B 54, 17954–17961 (1996). [DOI] [PubMed] [Google Scholar]
  10. Magda G. Z. et al. Room-temperature magnetic order on zigzag edges of narrow graphene nanoribbons. Nature 514, 608–611 (2014). [DOI] [PubMed] [Google Scholar]
  11. Golor M., Wessel S. & Schmidt M. J. Quantum Nature of Edge Magnetism in Graphene. Phys Rev Lett 112, 046601 (2014). [DOI] [PubMed] [Google Scholar]
  12. Yazyev O. V. & Katsnelson M. I. Magnetic Correlations at Graphene Edges: Basis for Novel Spintronics Devices. Phys Rev Lett 100, 047209 (2008). [DOI] [PubMed] [Google Scholar]
  13. Fu L., Kane C. L. & Mele E. J. Topological Insulators in Three Dimensions. Phys Rev Lett 98, 106803 (2007). [DOI] [PubMed] [Google Scholar]
  14. Moore J. E. & Balents L. Topological invariants of time-reversal-invariant band structures. Phys Rev B 75, 121306(R) (2007). [Google Scholar]
  15. Roy R. Topological phases and the quantum spin Hall effect in three dimensions. Phys Rev B 79, 195322 (2009). [Google Scholar]
  16. Hasan M. Z. & Kane C. L. Colloquium: Topological insulators. Rev Mod Phys 82, 3045–3067 (2010). [Google Scholar]
  17. Qi X.-L. & Zhang S.-C. Topological insulators and superconductors. Rev Mod Phys 83, 1057–1110 (2011). [Google Scholar]
  18. Pankratov O. A. Supersymmetric inhomogeneous semiconductor structures and the nature of a parity anomaly in (2 + 1) electrodynamics. Phys Lett A 121, 360–366 (1987). [Google Scholar]
  19. Wray L. A. et al. A topological insulator surface under strong Coulomb, magnetic and disorder perturbations. Nat Phys 7, 32–37 (2010). [Google Scholar]
  20. Scholz M. R. et al. Tolerance of Topological Surface States towards Magnetic Moments: Fe on Bi2Se3. Phys Rev Lett 108, 256810 (2012). [DOI] [PubMed] [Google Scholar]
  21. Honolka J. et al. In-Plane Magnetic Anisotropy of Fe Atoms on Bi2Se3(111). Phys Rev Lett 108, 256811 (2012). [DOI] [PubMed] [Google Scholar]
  22. Fu L. & Kane C. L. Probing Neutral Majorana Fermion Edge Modes with Charge Transport. Phys Rev Lett 102, 216403 (2009). [DOI] [PubMed] [Google Scholar]
  23. Akhmerov A. R., Nilsson J. & Beenakker C. W. J. Electrically Detected Interferometry of Majorana Fermions in a Topological Insulator. Phys Rev Lett 102, 216404 (2009). [DOI] [PubMed] [Google Scholar]
  24. Chen Y. L. et al. Massive Dirac Fermion on the Surface of a Magnetically Doped Topological Insulator. Science 329, 659–662 (2010). [DOI] [PubMed] [Google Scholar]
  25. Checkelsky J. G., Ye J., Onose Y., Iwasa Y. & Tokura Y. Dirac-fermion-mediated ferromagnetism in a topological insulator. Nat Phys 8, 729–733 (2012). [Google Scholar]
  26. Hsieh D. et al. Observation of Time-Reversal-Protected Single-Dirac-Cone Topological-Insulator States in Bi2Te3 and Sb2Te3. Phys Rev Lett 103, 146401 (2009). [DOI] [PubMed] [Google Scholar]
  27. Jin K.-H. & Jhi S.-H. Proximity-induced giant spin-orbit interaction in epitaxial graphene on a topological insulator. Phys Rev B 87, 075442 (2013). [Google Scholar]
  28. Zhang J., Triola C. & Rossi E. Proximity Effect in Graphene–Topological-Insulator Heterostructures. Phys Rev Lett 112, 096802 (2014). [DOI] [PubMed] [Google Scholar]
  29. Sa B. & Sun Z. Electron interactions and Dirac fermions in graphene-Ge2Sb2Te5 superlattices. J. Appl. Phys. 115, 233714 (2014). [Google Scholar]
  30. Kou L. et al. Proximity enhanced quantum spin Hall state in graphene. Carbon 87, 418–423 (2015). [Google Scholar]
  31. Lee P. et al. Proximity Effect Induced Electronic Properties of Graphene on Bi2Te2Se. ACS Nano 9, 10861–10866 (2015). [DOI] [PubMed] [Google Scholar]
  32. Kane C. L. & Mele E. J. Quantum spin Hall effect in graphene. Phys Rev Lett 95, 226801 (2005). [DOI] [PubMed] [Google Scholar]
  33. Subramaniam D. et al. Wave-Function Mapping of Graphene Quantum Dots with Soft Confinement. Phys Rev Lett 108, 046801 (2012). [DOI] [PubMed] [Google Scholar]
  34. Li Y. et al. Absence of edge states in covalently bonded zigzag edges of graphene on Ir(111). Adv Mater 25, 1967–1972 (2013). [DOI] [PubMed] [Google Scholar]
  35. Li Y., Zhang W., Morgenstern M. & Mazzarello R. Electronic and Magnetic Properties of Zigzag Graphene Nanoribbons on the (111) Surface of Cu, Ag, and Au. Phys Rev Lett 110, 216804 (2013). [DOI] [PubMed] [Google Scholar]
  36. Li Y. & Mazzarello R. Structural and electronic properties of hybrid graphene and boron nitride nanostructures on Cu. Phys Rev B 88, 045317 (2013). [Google Scholar]
  37. Giovannetti G. et al. Doping Graphene with Metal Contacts. Phys Rev Lett 101, 026803 (2008). [DOI] [PubMed] [Google Scholar]
  38. Fu L. Hexagonal Warping Effects in the Surface States of the Topological Insulator Bi2Te3. Phys Rev Lett 103, 266801 (2009). [DOI] [PubMed] [Google Scholar]
  39. Henk J., Ernst A. & Bruno P. Spin polarization of the L-gap surface states on Au(111). Phys Rev B 68, 165416 (2003). [Google Scholar]
  40. LaShell S., McDougall B. A. & Jensen E. Spin Splitting of an Au(111) Surface State Band Observed with Angle Resolved Photoelectron Spectroscopy. Phys Rev Lett 77, 3419–3422 (1996). [DOI] [PubMed] [Google Scholar]
  41. Mazzarello R., Dal Corso A. & Tosatti E. Spin-orbit modifications and splittings of deep surface states on clean Au(111). Surf Sci 602, 893–905 (2008). [Google Scholar]
  42. Hijii K., Kitazawa A. & Nomura K. Phase diagram of S = 1/2 two-leg XXZ spin-ladder systems. Phys Rev B 72, 014449 (2005). [Google Scholar]
  43. Koop C. & Schmidt M. J. Effective spin theories for edge magnetism in graphene zigzag ribbons. Phys Rev B 92, 125416 (2015). [Google Scholar]
  44. Sudarshan E. C. G. & Misra B. The Zeno’s paradox in quantum theory. J Math Phys 18, 756–763 (1977). [Google Scholar]
  45. Zurek W. H. Decoherence, einselection, and the quantum origins of the classical. Rev Mod Phys 75, 715–775 (2003). [Google Scholar]
  46. Zurek W. H. Quantum Darwinism. Nat Phys 5, 181–188 (2009). [Google Scholar]
  47. Giannozzi P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J Phys Cond Matt 21, 395502 (2009). [DOI] [PubMed] [Google Scholar]
  48. Troullier N. & Martins J. L. Efficient pseudopotentials for plane-wave calculations. Phys Rev B 43, 1993–2006 (1991). [DOI] [PubMed] [Google Scholar]
  49. Perdew J. P., Burke K. & Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
  50. Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J Comput Chem 27, 1787–1799 (2006). [DOI] [PubMed] [Google Scholar]
  51. Jiang Y. et al. Landau Quantization and the Thickness Limit of Topological Insulator Thin Films of Sb2Te3. Phys Rev Lett 108, 016401 (2012). [DOI] [PubMed] [Google Scholar]
  52. Monkhorst H. J. & Pack J. D. Special points for Brillouin-zone integrations. Phys Rev B 13, 5188–5192 (1976). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES