Methanethiol Binding Strengths and Deprotonation Energies in Zn(II)–Imidazole Complexes from M05-2X and MP2 Theories: Coordination Number and Geometry Influences Relevant to Zinc Enzymes

Abstract

Zn(II) is used in nature as a biocatalyst in hundreds of enzymes and the structure and dynamics of its catalytic activity is the subject of considerable interest. Many of the Zn(II)-based enzymes are classified as hydrolytic enzymes, in which the Lewis acidic Zn(II) center facilitates proton transfer(s) to a Lewis base, from proton donors such as water or thiol. This report presents the results of a quantum computational study quantifying the dynamic relationship between the zinc coordination number (CN), its coordination geometry, and the thermodynamic driving force behind these proton transfers originating from a charge-neutral methylthiol ligand. Specifically, density functional theory (DFT) and second-order perturbation theory (MP2) calculations have been performed on a series of [(Imidazole)_nZn–S(H)CH₃]²⁺ and [(Imidazole)_nZn–SCH₃]⁺ complexes with the CN varied from one to six, n=0–5. As the number of imidazole ligands coordinated to zinc increases, the S–H proton dissociation energy also increases, (i.e. −S(H)CH₃ becomes less acidic), and the Zn–S bond energy decreases. Furthermore, at a constant CN, the S–H proton dissociation energy decreases as the S–Zn–(ImH)_n angles increase about their equilibrium position. The zinc-coordinated thiol can become more or less acidic depending upon the position of the coordinated imidazole ligands. The bonding and thermodynamic relationships discussed may apply to larger systems that utilize the [(His)₃Zn(II)–L] complex as the catalytic site, including carbonic anhydrase, carboxypeptidase, β-lactamase, the tumor necrosis factor-α-converting enzyme, and the matrix metalloproteinases.

TOC Graphic

Introduction

Zinc is one of the most abundant and important metals in living systems, serving as an essential cofactor in thousands of proteins.^1,2 Found in all six classes of enzymes, hydrolases being the most common, zinc is also involved in signaling and plays both structural and regulatory roles.^3,4 The coordinating environment of zinc in proteins is dominated by ligation to nitrogen atoms of imidazole (ImH) from histidine (His, or H) side chains and sulfur atoms of thiol and thiolate from cysteine (Cys, or C) side chain amino acid residues, as revealed by numerous X-ray crystal and solution NMR structures.^5–7 Of particular interest is the three-His coordination to zinc, [(His)₃Zn(II)–L], with the L site occupied by a ligand or ligands that may (H₂O, Cys, Glu,.) or may not (inhibitor) be native to the enzyme. The [(His)₃Zn(II)–L] center acts as the catalytic “active” site in numerous enzymes, including carbonic anhydrase, β-lactamase, cytosine deaminase, matrix metalloproteinases, and the tumor necrosis factor-α-converting enzyme (TACE). As the center of catalysis, it seems important to understand the physical and chemical properties governing the stability of the first coordination sphere in the [(His)₃Zn(II)–L] system. This report constitutes a step in that direction. Herein we present a detailed investigation of the interplay among coordination number (CN), molecular geometry, and both the bond strength and proton dissociation energy of the Zn–S(H)CH₃ moiety for a series of [(Imidazole)_nZn(II)–S(H)CH₃] complexes. These systems are models for the [(His)₃Zn(II)–Cys] coordination environment, which, among other things, is an important entity in the activation and inhibition processes of the matrix metalloproteinase (MMP) family of endopeptidases, as outlined below.

The MMPs comprise a family of 26 Zn(II)-dependent hydrolytic enzymes, which are involved in degrading and remodeling the macromolecular components of the extra-cellular matrix.^8–10 With such breadth in their physiological roles, the MMPs have been implicated in a host of ailments, including cardiovascular disease, arthritis, cancer, and play a role in the development of neuropathic pain.^11–17 In this regard, a widespread effort has been made over the last three decades to control and regulate the activities of these enzymes through selective, competitive inhibition. While little clinical success has been realized, selective MMP inhibition may still be attainable^18,19 by, in part, exploiting structural relationships of the type reported herein.

The MMPs are members of the metzincin family of enzymes, which are distinguished by two highly conserved motifs, one containing three histidine residues that bind zinc at the catalytic site, and the second being the conserved methionine turn that sits beneath the active site zinc forming a hydrophobic floor.^8,20,21 The signature zinc-binding motif of all MMPs reads HExGHxxGxxH in the catalytic domain, wherein the resting catalytic site consists of an approximately tetrahedral zinc center that is bonded to the protein through nitrogen atoms provided by the imidazole side chains of the three conserved histidines. In the inactive proMMP (Scheme 1A), the thiolate group of a cysteine residue within the propeptide coordinates Zn(II) and blocks substrate access, thereby causing latency.

Scheme 1.

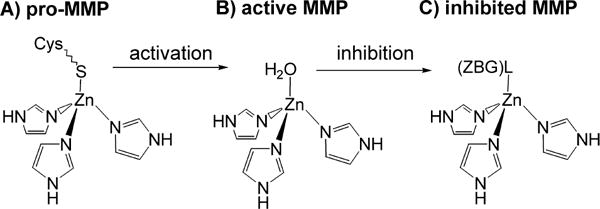
Depiction of the first coordination sphere of the catalytic zinc center of A) inactive proMMP, B) activated MMP, and C) inhibited MMP.

Upon activation, the cysteine-thiolate ligand is replaced by a water molecule, producing the proteolytically active [(His)₃Zn(OH₂)]²⁺ complex, as shown in Scheme 1B. Several lines of evidence suggest that the extent of ligand protonation is crucial. For example, in the proposed MMP mechanism the Zn–OH₂ moiety plays a central role, losing both hydrogen atoms, as protons, to the hydrolysis products.^22,23 Reports also argue for a critical protonation step of the Zn–S moiety, and possibly a change in CN, as a prerequisite for activation of proMMPs.^24,25 When the activated enzyme is rendered inactive by competitive inhibition, whether through binding of a tissue inhibitor of metalloproteinase (TIMP) or an exogenous inhibitor, the H₂O ligand is replaced by the inhibitor’s zinc binding group (ZBG), the functional group that directly coordinates to the catalytic Zn(II) ion, as illustrated in Scheme 1C. Proton transfer events may also occur to varying extents upon inhibitor binding; protic site(s) on the ZBG can remain protonated, serve as a hydrogen bond donor to a nearby amino acid, or donate a proton essentially completely to a stronger base/weaker acid in the active site cleft.

These putative steps involving proton transfer reactions between the Zn–L moiety and the protein environment are likely crucial to the processes of MMP activation, catalysis, and inhibition. Examination of the many MMPs in the RCSB protein data bank reveals an array of experimentally determined active site geometries. For instance, X-ray crystal and NMR solution structures of MMPs have shown a variety of 4- and 5-coordinate [(His)₃Zn(II)–L] geometries that include tetrahedral, trigonal-bipyramidal, and square-pyramidal, demonstrating that the zinc active site of the MMPs is both coordinatively and geometrically flexible. To illustrate, Figure 1 shows the first coordination shell of Zn(II) centers that are from three X-ray crystal structures of MMPs, with selected bonding parameters listed in Table 1. Figure 1 (TBP) shows a complex of MMP-3 with a synthetic inhibitor (PDB code: 1BIW), wherein the inhibitor is coordinated through a bidentate hydroxamic acid ZBG, yielding a pentacoordinate Zn(II) center.²⁶ The zinc geometry in Figure 1(TBP) is best described as trigonal-bipyramidal with the N_ImH–Zn–N_ImH angles slightly distorted from the idealized 90.0° and 120.0° (see Table 1). Figure 1 (SQP) shows a complex of MMP-1 with a synthetic inhibitor (PDB code: 1HFC), also having a bidentate hydroxamic acid ZBG.²⁷ However, in this case the geometry about the pentacoordinate zinc is best described as a square-based pyramid. Last, Figure 1 (Tet.) shows the active site of proMMP-3 (PDB code: 1SLM), in which zinc is 4-coordinate and tetrahedral with N_ImH–Zn–N_ImH angles only slightly less than the idealized 109.5°.²⁸ The variability in these experimentally determined [(ImH)₃Zn(II)–L] geometries, despite the high degree of sequence and structure homologies of the MMP catalytic domain, clearly show that the active sites of the MMPs are not rigid.

Figure 1.

First coordination spheres of the catalytic zinc centers of three MMPs. Coordinates taken from published X-ray crystal structures; color scheme is CPK. TBP: trigonal bipyramidal, MMP-3, chelated by synthetic hydroxamic acid based inhibitor (PDB code: 1BIW.) SQP: square pyramidal, MMP-1, chelated by synthetic hydroxamic acid based inhibitor (PDB code: 1HFC.) Tet.: tetrahedral, cysteine thiolate from the pro domain of proMMP-3 (PDB code: 1SLM.)

Table 1.

Selected bonding parameters from first coordination shells of catalytic Zn(II) centers taken from MMP X-ray crystal structures shown in Figure 1. Bond lengths in Angstroms and angles in degrees.

MMP (PDB code)	MMP-3 (1BIW)	MMP-1 (1HFC)	MMP-3 (1SLM)
Coord. Geometry	TBP	SQP	Tet.
Zn–NImH (Å)	2.20	2.08	1.93
	2.12	2.02	1.87
	2.11	1.88	1.80
mean Zn–NImH (Å)	2.14	1.99	1.87
∠NImHZnNImH(°)	107.1	104.0	105.6
	101.4	100.4	105.1
	92.2	96.6	104.0
mean ∠NImHZnNImH(°)	100.2	100.3	104.9

The extent to which changes in the [(His)₃Zn(II)–L] coordination environment are a factor in Zn–L bond cleavage or proton transfer events that occur upon activation, catalysis, and inhibition is unknown. Experimentally, the various protic Zn–L species and their interactions are difficult to examine in the enzyme, since electron density maps from crystal structures are, in general, not sufficiently defined to locate hydrogen atoms.^29,30 However, small-molecule model complexes of the active sites, their structures, and relative energies, are tractable by computational methods. Thus, we herein report the results of a series of quantum chemical calculations carried out to investigate the driving forces for both Zn–S bond dissociation and S–H deprotonation of Zn(II)-coordinated methylthiol, S(H)CH₃. Using density function theory and second-order perturbation theory, calculations are carried out on a series of [(ImH)_nZn(II)–S(H)CH₃] and [(ImH)_nZn(II)–SCH₃], n=0–5, complexes. Particular attention is given to the geometry and geometry changes within the four-coordinate [(ImH)₃Zn–S(H)CH₃]²⁺, and its conjugate base, as models for the pro- or thiol inhibited-MMPs. The results of the calculations reveal that the coordination environment about the zinc center has a significant impact on the driving force for both bond dissociation and proton transfer processes involving the Zn(II)–S(H)CH₃ moiety.

Computational Methods

All quantum mechanical calculations were performed using Gaussian 09 software (RevA.02),³¹ with most input files having been built using GaussView 5.0.8,³² all running on in-house MacPro and iMac computers. Density functional theory (DFT) calculations were performed using the M05-2X hybrid meta functional,³³ incorporating an ultrafine integration grid. Full geometry optimizations and vibrational frequency calculations were performed to ensure true minima and obtain the zero-point vibrational energy and thermodynamic parameters, unless stated otherwise. Single-point ab initio calculations were performed using the frozen-core second order Møller-Plesset perturbation theory (MP2) method with a small number of calculations obtained using the frozen-core coupled-cluster theory with single and double excitations and a quasiperturbative treatment of connected triple excitations, CCSD(T), both at the M05-2X geometries. Calculations were performed in the gas-phase, and the all electron cc-pVDZ or cc-pVTZ basis sets were used on all atoms including zinc.^34–36 The closed shell singlet electronic state was used in all calculations.

The reaction(s) to determine the Zn–S bond dissociation energy (BDE, or binding energy) and the S–H proton dissociation energy (PDE) are shown in equations (1) through (3) below. In these reactions the imidazole (ImH) variable n is set at 0 through 5.

$${\left[{\left(\text{ImH}\right)}_{\mathrm{n}}\text{Zn–S}\left(\mathrm{H}\right){\text{CH}}_3\right]}^{2+}\to {\left[{\left(\text{ImH}\right)}_{\mathrm{n}}\text{Zn}\right]}^{2+}+\mathrm{S}\left(\mathrm{H}\right){\text{CH}}_3\left(\text{methylthiol BDE}\right)$$ (1)

$${\left[{\left(\text{ImH}\right)}_{\mathrm{n}}{\text{Zn–SCH}}_3\right]}^{+}\to {\left[{\left(\text{ImH}\right)}_{\mathrm{n}}\text{Zn}\right]}^{2+}+{\text{CH}}_3{\mathrm{S}}^{-}\left(\text{methylthiolate BDE}\right)$$ (2)

$${\left[{(\text{ImH})}_{\mathrm{n}}\text{Zn–S}(\mathrm{H}){\text{CH}}_3\right]}^{2+}\to {\left[{(\text{ImH})}_{\mathrm{n}}{\text{Zn–SCH}}_3\right]}^{+}+{\mathrm{H}}^{+}(\text{PDE})$$ (3)

Reaction (1) is used to calculate the Zn–S BDE for the binding of the charge neutral S(H)CH₃ to the Zn(II)–ImH complexes, while (2) depicts anionic CH₃S⁻ binding. With the release of the proton in (3), it is sometimes referred to as the gas-phase acidity reaction. In all cases the BDE and PDE were determined by calculating the difference in energy of the products minus the reactants. The reported BDE and PDE values are at 0 K and include zero-point vibrational energies, therefore they are D_o values (= ΔH_o = ΔG_o). Inclusion of thermal and entropic effects at 298K (ΔG₂₉₈) are also reported at the M05-2X/cc-pVTZ level, under the particle-in-a-box, rigid rotor, and harmonic oscillator approximations.

As a test of our methods used, M05-2X/cc-pVTZ calculations yield a 298 K gas-phase Gibbs’ deprotonation energy, ΔG₂₉₈, of 1480 kJ/mol (353.6 kcal/mol) for HSCH₃, while single-point MP2/cc-pVTZ//M05-2X/cc-pVTZ results yield 1488 kJ/mol (355.6 kcal/mol), respectively. Both these values compare satisfactorily with the experimental value of 1476±9 kJ/mol (352.7±2.1 kcal/mol) for HSCH₃.³⁷ Single-point CCSD(T)/cc-pVTZ//M05-2X/cc-pVTZ results yield a value that is roughly 1.5% higher than experiment for ΔG₂₉₈ at 1498 kJ/mol. Experimental bond lengths, binding energies, and deprotonation energies are not available for Zn(II) complexes like the ones investigated in this study. However, two recent reports by Amin, Truhlar, and co-workers, assessing the performance of theoretical methods on energies and geometric properties of Zn(II) complexes found that the M05-2X method performs very well.^38,39 In fact, the M05-2X performed best, on average, for calculations of bond lengths, dipole moments, and Zn-ligand bond dissociation energies among 39 DFT methods studied, and they recommend the M05-2X functional for the accurate calculation of geometries, dipole moments, and energetics of Zn compounds. While a recent report by Weaver et. al., has evaluated numerous DFT methods for their accuracy in calculating heats of formation of small Zn(II) complexes, the M05-2X functional was not included in their study.⁴⁰

Results and Discussion

1) Coordination Number Influence on Zn–S(H)CH₃ Bond Energies

Foremost, both HSCH₃ and CH₃S⁻ coordinate to Zn(II) through their sulfur atoms to yield stable gas-phase complexes for all six of the CNs studied. Figure 2 shows the optimized structures for [(ImH)_1–5Zn(II)–S(H)CH₃] and [(ImH)_1–5Zn(II)–SCH₃] at the M05-2X/cc-pVTZ level of theory. Selected parameters are also listed in Table 2, with complete coordinates included in the supplementary material. For comparison, Table 2 also includes parameters at the M05-2X/cc-pVDZ level, which differ only slightly from those using the larger basis set.

Figure 2.

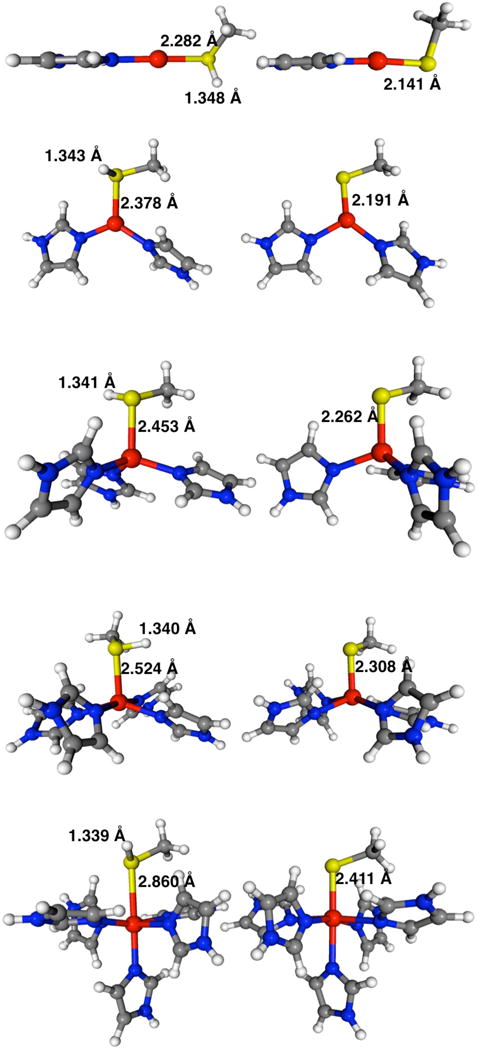
Geometry optimized structures for the [(ImH)_nZn–S(H)CH₃]²⁺ complexes on the left and their deprotonated [(ImH)_nZn–SCH₃]⁺ counterparts on the right, n = 1 through 5 from top to bottom. Selected parameters (in Angstroms) listed at the M05-2X/cc-pVTZ level of theory.

Table 2.

Selected bond lengths (Å) and partial atomic charges (a.u., atomic units) for [(ImH)_nZn(II)–S(H)CH₃] and [(ImH)_nZn(II)–SCH₃] systems at the M05-2X/cc-pVTZ level of theory. Last three columns contain M05-2X/cc-pVDZ values.

Molecule/Ion	Bond Lengths (Å)			Mulliken Atomic Charges			cc-pVDZ Bond Lengths (Å)
Thiols	Zn–S	Zn–N(avg)	S–H	H	S	Zn	Zn–S	Zn–N(avg)	S–H
[S(H)CH3]			1.3368	0.111	−0.173				1.3503
[Zn–S(H)CH3]2+	2.308		1.3547	0.231	0.213	1.207	2.322		1.3670
[(ImH)1Zn–S(H)CH3]2+	2.282	1.892	1.3477	0.213	0.092	0.983	2.289	1.895	1.3598
[(ImH)2Zn–S(H)CH3]2+	2.378	1.958	1.3434	0.201	−0.020	0.945	2.385	1.960	1.3557
[(ImH)3Zn–S(H)CH3]2+	2.453	2.017	1.3406	0.178	−0.046	0.882	2.454	2.020	1.3528
[(ImH)4Zn–S(H)CH3]2+	2.524	2.133	1.3403	0.175	−0.071	0.942	2.520	2.136	1.3525
[(ImH)5Zn–S(H)CH3]2+	2.860	2.168	1.3387	0.169	−0.147	0.996	2.837	2.171	1.3508
Δ[(n=5)–(n=1)]*	0.578	0.276	−0.0090	−0.044	−0.239		0.548	0.276	−0.0090
Thiolates
[SCH3]1−					−0.851
[Zn–SCH3]+	2.179				−0.068	0.879	2.190
[(ImH)1Zn–SCH3]+	2.141	1.935			−0.224	0.776	2.145	1.938
[(ImH)2Zn–SCH3]+	2.191	2.009			−0.346	0.807	2.192	2.014
[(ImH)3Zn–SCH3]+	2.262	2.070			−0.411	0.775	2.269	2.070
[(ImH)4Zn–SCH3]+	2.308	2.186			−0.429	0.830	2.295	2.196
[(ImH)5Zn–SCH3]+	2.411	2.246			−0.474	0.890	2.403	2.251
Δ[(n=5)–(n=1)]*	0.270	0.311			−0.250		0.258	0.313

^*Differences between (ImH)₅ & (ImH)₁ systems.

The calculated Zn(II)–S BDEs of [(ImH)_n Zn–S(H)CH₃]²⁺ and [(ImH)_nZn–SCH₃]⁺, n=0–5, are listed in Table 3 at the M05-2X/cc-pVTZ level of theory, with MP2/cc-pVTZ//M05-2X/cc-pVTZ values listed for comparison. Both methylthiol and methylthiolate are bound very strongly to the bare Zn(II) ion with BDEs of 576 and 1785 kJ/mol, respectively. In fact, the Zn(II)–S_thiolate bond is much stronger than its Zn(II)–S_thiol counterpart, for all CNs. The binding energy of both methylthiolate and methylthiol decrease significantly with the addition of ImH ligands to the Zn(II) center. The Zn–S_thiolate BDEs decrease step-wise first to 1401 kJ/mol in [(ImH)Zn–SCH₃]⁺ down to their minimum of 699 kJ/mol in the 6-coordinate, octahedral [(ImH)₅Zn–SCH₃]⁺ complex. The Zn–S_thiol BDEs drop to 385 kJ/mol in [(ImH)Zn–S(H)CH₃]²⁺ down to their minimum of a very weak 14 kJ/mol in the 5-coordinate square-pyramidal [(ImH)₄ Zn–S(H)CH₃]²⁺ complex, in which HSCH₃ occupies the apex position, see Figure 2. The Addison parameter (τ) can be used to quantify square-pyramidal/trigonal-bipyramidal geometries for five-coordinate complexes, with a value of 0.0 indicating a true square-pyramid and a value of 1.0 indicating a trigonal-bipyramid.⁴¹ In the case of [(ImH)₄Zn–S(H)CH₃]²⁺, τ = 0.45 indicating a structure closer to square-pyramid. A meager 3 kJ/mol higher in energy is a structure described as trigonal-bipyramidal, τ = 0.63, in which HSCH₃ occupies an equatorial position (2 kJ/mol higher at MP2/cc-pVTZ//M05-2X/cc-pVTZ level). The Zn–S BDE of the 6-coordinate [(ImH)₅Zn–S(H)CH₃]²⁺, 38 kJ/mol, is low but noticeably greater than that of its 5-coordinate counterpart. The stable 5-coordinate [(ImH)₄Zn–S(H)CH₃]²⁺ complexes were difficult to locate computationally. Starting with an initial trigonal-bipyramidal geometry having HSCH₃ in an axial position resulted in dissociation of the thiol ligand from zinc to form the unbound tetrahedral [(ImH)₄Zn]²⁺ 4 and S(H)CH₃ systems using multiple levels of theory: M05-2X/cc-pVDZ, M05-2X/cc-pVTZ, M05-2X/aug-cc-pVDZ, B3LYP/cc-pVDZ, BLYP/cc-pVDZ, or MP2/cc-pVDZ. Both square-pyramidal (τ = 0.30) and trigonal-bipyramidal (τ = 1.04) geometries were also located for the 5-coordinate thiolate complex, [(ImH)₄Zn–SCH₃]⁺, of which the square-pyramidal is again lower in energy, by 2 kJ/mol, with a considerable BDE of 740 kJ/mol. The low stability of the protonated [(ImH)₄Zn–S(H)CH₃]²⁺ to Zn–S dissociation may have implications regarding the activation process of the MMPs wherein the Zn–SCH₃ bond must break. It has been reported that a CN change from four to five accompanies protonation of the coordinated sulfur atom of Cys upon Zn–S bond cleavage.²⁵ In that study it is the carboxylate oxygen of the conserved Glutamic acid that binds to zinc. Our results are consistent with that finding; the calculations reveal a CN change from 4 to 5 would indeed result in a significantly weakened Zn–S bond. Surprisingly, while [(ImH)₄Zn–S(H)CH₃]²⁺ is stable at 0 K, inclusion of thermal and entropic effects show that it would undergo spontaneous thiol dissociation at 298 K, with ΔG₂₉₈ = −37 kJ/mol (Table 3, values in parentheses). Thiol dissociation from the 6-coordinate [(ImH)₅Zn–S(H)CH₃]²⁺ complex would also be spontaneous with ΔG₂₉₈ = −10 kJ/mol. Lastly, the Zn–S BDEs obtained using the MP2/cc-pVTZ//M05-2X/cc-pVTZ method are in good agreement with the M05-2X/cc-pVTZ values. The energy differences between the two methods are much less than their overall magnitudes, and the two methods yield identical trends.

Table 3.

Zn–S Bond Dissociation Energies (BDEs) and S–H Proton Dissociation Energies (PDEs), both D_o values (=ΔH_o), for [(ImH)_nZn(II)–S(H)CH₃] and [(ImH)_nZn(II)–SCH₃] systems at various levels of theory. All numbers in kJ/mol. (ΔG₂₉₈ values listed in parentheses)

	Zn–S Bond Dissociation Energies (kJ/mol)		S–H Proton Dissociation Energies (kJ/mol)
	cc-pVTZ		cc-pVTZ			cc-pVDZ
	M05-2X	MP2//M05-2X	M05-2X	MP2//M05-2X	CCSD(T)//M05-2X	M05-2X
Thiols
[S(H)CH3]			1504 (1480)	1512	1522	1533
[Zn–S(H)CH3]2+	576 (547)	545	296 (270)	294	303	287
[(ImH)1Zn–S(H)CH3]2+	385 (341)	374	488 (461)	487	499	482
[(ImH)2Zn–S(H)CH3]2+	175 (133)	165	618 (592)	618		616
[(ImH)3Zn–S(H)CH3]2+	117 (73)	113	721 (692)	723		715
[(ImH)4Zn–S(H)CH3]2+	14 (−37)	11	778 (749)	779		784
[(ImH)5Zn–S(H)CH3]2+	38 (−10.)	42	843 (820)	846		848
Δ[(n=5)−(n=1)]*			355 (359)	359		366
Thiolates
[Zn–SCH3]+	1785 (1756)	1764
[(ImH)1Zn–SCH3]+	1401 (1360)	1400
[(ImH)2Zn–SCH3]+	1061 (1021)	1059
[(ImH)3Zn–SCH3]+	901 (861)	902
[(ImH)4Zn–SCH3]+	740 (693)	745
[(ImH)5Zn–SCH3]+	699 (649)	708
Δ[(n=5)−(n=1)]*	−702 (−711)	−692

^*Difference in energy between (ImH)₅ & (ImH)₁ systems.

Structurally, two trends stand out in the first coordination sphere bond length parameters starting with the [(ImH)₁Zn(II)–L] complex. First, with the addition of 1 to 4 imidazole ligands, the Zn–S bond length (R_Zn–S) increases, as listed in Table 2 and illustrated in Figure 2. In the thiolate complexes R_Zn–S increases from 2.141 to 2.411 Å, a lengthening of +0.270Å, an even larger increase occurs in the thiol complexes (+0.578 Å) with R_Zn–S values extending from 2.282 to 2.860 Å. Second, accompanying the increase in R_Zn–S, a corresponding increase in the average Zn–N bond lengths (R_Zn–N(avg)) occurs with the progression in coordination number. R_Zn–N(avg) increases 0.310Å and 0.276Å for the thiolate and thiol complexes, respectively. Even the very weakly bound [(ImH)₄Zn–S(H)CH₃]²⁺ follows the step-wise pattern. In other words, for all [(ImH)_1–5Zn(II)–L] complexes, as the CN increases, all bonds to zinc increase in length. This parallels the step-wise reduction in the methylthiolate binding strength and the almost step-wise reduction (excluding [(ImH)₄Zn–S(H)CH₃]²⁺ in the methylthiol binding strength.

2) Coordination Number Influence on H–SCH₃ Deprotonation Energies

Accompanying the increase in zinc’s coordination number, changes in bonds not directly adjacent to the zinc atom are also observed. The primary example is the methylthiol S–H bond lengths and corresponding proton dissociation energies. The S–H proton dissociation energy (PDE) of the [(ImH)_nZn–S(H)CH₃]²⁺ complexes are listed in Table 3 at the M05-2X, MP2 and selective CCSD(T) levels of theory. The calculated PDE’s of methylthiol are significantly diminished from its native value when its sulfur atom is bonded to the zinc atom in any of the [(ImH)_nZn–S(H)CH₃]²⁺ complexes. Thus, predictably, methylthiol becomes more acidic by virtue of its association with the Lewis acidic Zn(II) ion. Furthermore, the fewer the ligands coordinated to zinc, the lower the PDE becomes. Hence, the lowest PDE occurs when methylthiol is bound to the bare Zn(II) ion at 296 kJ/mol, a striking reduction of 1208 kJ/mol from the unbound HSCH₃ value of 1504 kJ/mol. MP2 and CCSD(T) methods calculate similar PDE reductions of 1218 and 1219 kJ/mol, respectively. The thiol PDE increases monotonically with CN. As the number of ImH ligands is increased from 1 to 5, the PDE trends upward to 488 kJ/mol for the linear [(ImH)Zn–S(H)CH₃]²⁺, finishing at 843 kJ/mol in the 6-coordinate [(ImH)₅Zn–S(H)CH₃]²⁺. This upper value is still 661 kJ/mol (44%) less than the PDE of the unbound HSCH₃. Even the very weakly bound [(ImH)₄Zn–S(H)CH₃]²⁺ follows the step-wise progression of proton dissociation energies. Although the Zn–S BDE is only 14 kJ/mol in [(ImH)₄Zn–S(H)CH₃]²⁺, the reduction in the S–H PDE is over 726 kJ/mol, or almost one-half the unbound value.

These absolute PDEs and their changes are similar (≤ 3% difference) to those calculated using the smaller cc-pVDZ basis set, the ab initio MP2/cc-pVTZ//M05-2X/cc-pVTZ, and high-level CCSD(T)/cc-pVTZ//M05-2X/cc-pVTZ methods. Furthermore, among the ligand protons in these complexes, removal of the S–H proton is the least endergonic. For example, in [(ImH)₃Zn–S(H)CH₃]²⁺ the imidazole N–H PDE is significantly higher,^42,43 at 826 kJ/mol, than the S–H PDE of 715 kJ/mol (M05-2X/cc-pVDZ values for D_o).

The most noticeable structural change in methylthiol upon binding to Zn²⁺ is its S–H bond length (R_S–H), as seen in Table 2 and Figure 2. When HSCH₃ binds to the bare Zn(II) ion R_S–H increases in length from its initial value of 1.337 Å to 1.355 Å (+0.018 Å). With the addition of imidazole ligands, R_S–H decreases, first to 1.348 Å in [(ImH)Zn–S(H)CH₃]²⁺, reaching 1.339 Å in the 6-coordinate [(ImH)₅Zn–S(H)CH₃]²⁺. This decrease in R_S–H of 0.9 pm with increasing numbers of ImH ligands is accompanied by the increase in methanethiol’s proton dissociation energy of +355 kJ/mol.

Atomic (Mulliken) charges were used to track shifts in electron density on the Zn, S and H atoms as a function of the number of Lewis basic ImH ligands coordinated to Zn²⁺. Although the charge on zinc does not follow a simple pattern, the charges on S and H do (Table 2). As the CN increases, an accumulation of negative charge density on S is observed for both the thiol and thiolate complexes. Likewise, in the protonated [(ImH)_nZn–S(H)CH₃]²⁺ complexes the positive charge on H also decreases as n increases. Hence, although the –S(H) unit becomes more negatively charged as zinc’s CN increases, the partial charge differences between S and H indicate that the ionic character in the S–H bond increases with n. Although the PDE involves energies of both the protonated and deprotonated complexes, the results show a clear correlation between positive charge on H and the ease with which it is removed as a proton. This result has implications regarding the strength of intermolecular forces (i.e. H-bonding) required to modulate the Zn–S bond strength for coordinated −S(H)R ligands, since the amount of positive electrostatic charge collection would modulate the proton interactions with negative charges/bases in the vicinity.

3) Molecular Geometry Influence on H–SCH₃ Deprotonation Energies

Significant deprotonation energy differences have been established for the series of [(ImH)_nZn–S(H)CH₃]²⁺ complexes, with the PDE increasing as zinc’s coordination number increases. However, as the CN changes, so does its coordination geometry; linear for n=0&1, trigonal planar for n=2, tetrahedral for n=3, square-pyramidal for n=4, and octahedral at CN=6 (n=5). This begs the question of whether the change in PDE derives from (a) the change in CN, (b) the change in geometry, or (c) both CN and geometry changes? To test (b), the influence of geometry on the PDE, we need a systematic way to change the geometry while leaving the CN constant. Inspection of Figure 2 reveals that it is the angles about zinc that change the most with CN. Specifically, the S–Zn–N_n angles, ∠SZnN_n, ranges from a minimum of 83° in the hexacoordinate [(ImH)₅Zn–S(H)CH₃]²⁺ structure to a maximum of 132° in the three-coordinate [(ImH)₂Zn–SCH₃]⁺ structure (omitting all angles near 180°). Therefore, to measure the influence of geometry on the PDE, we systematically modified the coordination geometry by incrementally adjusting the S–Zn–N_n angles and calculating the resulting PDE at constant CNs. This approach was applied to the 3 and 4-coordinate systems, [(ImH)₂Zn–S(H)CH₃]²⁺ and [(ImH)₃Zn–S(H)CH₃]²⁺, primarily because their symmetry-equivalent bond angles make it straight forward to systematically modify their geometries. Additionally, the 4-coordinate [(ImH)₃Zn(II)–S(H)CH₃] is structurally similar to [(His)₃Zn(II)–L], which is an important catalytic center in many enzymes.

In the series of constrained geometry calculations, the two/three symmetry-related S–Zn–(ImH)_n angles in [(ImH)_2,3Zn–S(H)CH₃]²⁺ were incrementally varied approximately ±20° about the idealized trigonal planar (120.0°) and tetrahedral (109.5°) angles; all other internal coordinates (bond lengths & angles) were allowed to vary during the geometry optimization process. Energies were obtained for both the thiol and thiolate complexes with the PDE calculated from the difference in energy between the optimized structures. The results of these constrained optimizations are used to systematically gauge the impact that geometry alone has on the PDEs/acidities. These constrained angle calculations were carried out with the cc-pVDZ basis set, which we have demonstrated performs on par with the larger cc-pVTZ basis set for PDE calculations in this study. As no vibrational frequency calculations were performed, no zero-point energies are included in these results. Therefore these PDE values are D_es.

Results of the constrained angle calculations are arranged in Table 4, while Figure 3 shows 8 of these structures, 4 for each of the protonated and deprotonated complexes at the constrained ∠SZnN_2,3 of 95° and 125°. The trend in PDEs is clearly apparent in Figure 4, which reveals the cause and effect relationship between the ∠SZnN_n and PDE. This plot unambiguously demonstrates that as ∠SZnN_n increases the PDE decreases for both [(ImH)₂Zn–S(H)CH₃]²⁺ and [(ImH)₃Zn–S(H)CH₃]²⁺; in other words, the complexes become more acidic. These results imply an intrinsic relationship between coordination geometry and deprotonation energy.

Table 4.

Selected bond lengths, partial charges, proton dissociation energies (D_e), and relative energies for [(ImH)₂Zn–S(H)CH₃]²⁺ (top set) and [(ImH)₃Zn–S(H)CH₃]²⁺ (bottom set) as a function of S–Zn–N_n angles. Values from M05-2X/cc-pVDZ calculations.

Bond angles	Bond lengths (Å)			Partial charges (a.u.)				Energies (kJ/mol)
								(S–H) PDE	Relativec
	Zn–S	S–H	Zn–(N)na	Zn	H	S	(ImH)nb		Thiol (Thiolate)
∠SZn(ImH)2			Zn–(ImH)2				(ImH)2
95°	2.565	1.3536	1.943	0.760	0.168	−0.062	0.921	680	36.7 (75.5)
105°	2.460	1.3545	1.948	0.727	0.175	−0.009	0.882	662	10.0 (30.7)
115°	2.398	1.3554	1.957	0.697	0.182	0.034	0.856	651	0.6 (10.1)
120°	2.377	1.3556	1.963	0.689	0.185	0.050	0.840	647	0.5 (6.1)
125°	2.358	1.3560	1.972	0.685	0.188	0.060	0.829	642	3.5 (4.2)
135°	2.327	1.3563	2.009	0.671	0.193	0.080	0.804	627	28.8 (14.5)
Δ(135°−95°)	−0.238	0.0027	0.066	−0.089	0.025	0.142	−0.117	−53
fully optd	2.385	1.3557	1.960	0.699	0.186	0.035	0.842	641	0.0 (0.0)
∠SZn(ImH)3			Zn–(ImH)3				(ImH)3
85°	2.857	1.3513	1.997	0.699	0.129	−0.097	1.125	813	57.8 (129.4)
95°	2.592	1.3522	2.006	0.626	0.143	−0.041	1.106	770	18.9 (47.3)
105°	2.473	1.3527	2.016	0.570	0.155	0.004	1.085	750	1.6 (9.9)
110°	2.436	1.3533	2.024	0.548	0.161	0.021	1.074	741	1.4 (0.9)
115°	2.409	1.3536	2.036	0.543	0.167	0.030	1.062	737	7.0 (3.2)
125°	2.361	1.3546	2.084	0.548	0.179	0.055	0.997	722	49.2 (30.4)
Δ(125°−85°)	−0.496	0.0033	0.087	−0.151	0.050	0.152	−0.128	−91
fully optd	2.454	1.3528	2.020	0.567	0.163	−0.005	1.079	741	0.0 (0.0)

^aaverage Zn–N_n distance,

^btotal charge on the zinc coordinated imidazole ligands,

^cEnergy of the constrained thiol and (thiolate) relative to their fully optimized (ImH)₂ and (ImH)₃ complexes.

^dFully opt numbers are from optimizations with no constraints, in which the average ∠SZn(ImH)₂ = 117.6° and the average ∠SZn(ImH)₃ = 108.0°, for the thiol complexes

Figure 3.

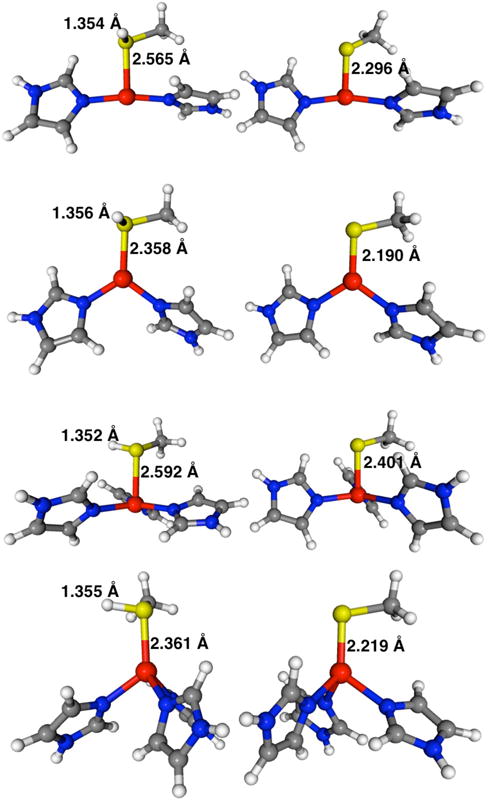
Constrained geometry optimized structures for [(ImH)₂Zn–S(H)CH₃]²⁺ and [(ImH)₃Zn–S(H)CH₃]²⁺ on the left and the deprotonated [(ImH)₂Zn–SCH₃]⁺ and [(ImH)₃Zn–SCH₃]⁺ complexes on the right, at S–Zn–(ImH)_n angles of 95° (1^st and 3^rd set) and 125° (2^nd and 4^th set). Selected bonding parameters (in Angstroms) at the M05-2X/cc-pVDZ level of theory.

Figure 4.

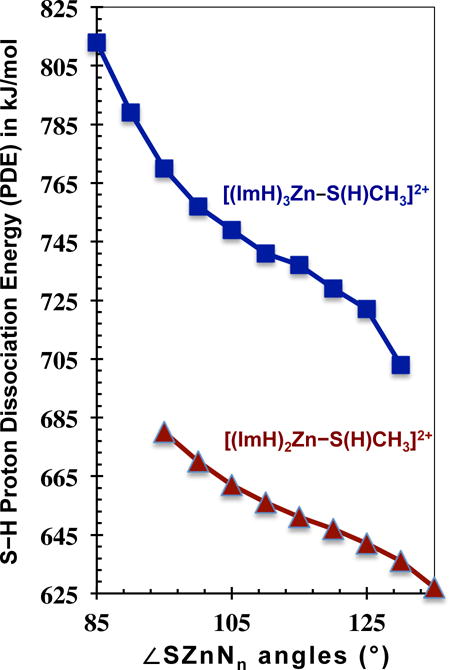
Proton dissociation energy (kJ/mol) plotted versus the S–Zn–(ImH)_n angle for [(ImH)₃Zn–S(H)CH₃]²⁺, top square data, and [(ImH)₂Zn–S(H)CH₃]²⁺, bottom triangle data. Proton dissociation energies calculated at the M05-2X/cc-pVDZ level of theory. This figure represents the energy difference between the geometry-optimized deprotonated and geometry-optimized protonated complexes, with the only constraint being ∠SZn(ImH)_2,3.

A close analysis of the PDE variations in Table 4 shows that the PDE decreases by 91 kJ/mol across the 40° increase in ∠SZn(ImH)₃, and by 53 kJ/mol across the 40° increase in ∠SZn(ImH)₂. The magnitudes of these PDE changes are considerable and, for [(ImH)₃Zn–S(H)CH₃]²⁺, equivalent to the strength of a weak covalent bond. The 91 kJ/mol is also of the same order as the PDE change from CN three to four, and is greater than the four to five or five to six changes (Table 3). While a 40° change in S–Zn–N_2,3 angle is a large geometry change for a given CN, changes of a few degrees to either side of the lowest energy structure requires little energy. The last columns of Table 4 lists the relative energies upon ∠SZn(ImH)_2,3 change. These relative energies are with respect to the fully optimized M05-2X/cc-pVDZ structures, in which the average ∠SZn(ImH)_n are 117.6° for the trigonal planar [(ImH)₂Zn–S(H)CH₃]²⁺ and 108.0° for the tetrahedral [(ImH)₃Zn–S(H)CH₃]²⁺ (Figure S1). Over the 40° range in constrained angles the energy of the [(ImH)_2,3Zn(II)–S(H)CH₃] systems increases by up to 58 kJ/mol, while a ±10° change about the equilibrium positions requires significantly less energy, <15 kJ/mol. Thus the part of the potential energy well encompassing this physiologically relevant angular motion is shallow. Consistent with this result, variability in coordination angles observed in the many X-ray crystal and NMR structures of pro- and inhibited MMPs reveals that protein conformational forces are sufficient to distort the active-sites from their intrinsically optimum geometries (Table 1, Figure 1).^25,44–47

The plots of relative [(ImH)₃Zn–S(H)CH₃]²⁺ and [(ImH)₃Zn–SCH₃]⁺ energies versus change in S–Zn–N₃ angle (Figure 5) reveals an interesting relationship between these systems. First, note that the thiolate plot is shifted to larger angles relative to the thiol plot, owing to the stronger and shorter Zn–S bond forcing ∠SZn(ImH)₃ to greater values in the fully optimized thiolate complex (average ∠SZn(ImH)₃ =113.2° thiolate vs. 108.0° thiol) (see Figure S1). Also apparent in the rightmost columns of Table 4 and in Figure 5 is the approximately harmonic nature of the molecular distortions along the S–Zn–(ImH)_2,3 bending coordinates. The bottom of each well falls near the average S–Zn–(ImH)₃ angles of the respective fully optimized structures for both the protonated and deprotonated complexes. For any molecule, there is a thermodynamic driving force to obtain its equilibrium ground state geometry. So a structure, either protonated or deprotonated, that is located anywhere above the potential energy minimum will undergo a spontaneous change to the lowest energy structure, thereby releasing energy in proportion to the height of the structure on the potential well. It appears that the factors indicating whether the PDE of a compound will change with geometry are: 1) the extent of separation between the protonated and deprotonated geometries along the S–Zn–(ImH)_2,3 bending coordinate (i.e. how far the bottom of the wells are from each other) and, 2) how high in energy the structure is above that of its conjugate acid or base (magenta triangles = blue squares – red diamonds), which, for a given separation of minima, scales with the steepness of the potential wells. In other words, if the coordination geometries of the protonated and deprotonated structures are very similar, and the structures are energetically the same height from the minimum of their acid/base conjugate, any change in geometry will affect both structures equally and the PDE/acidity will not be a steep function of geometry.

Figure 5.

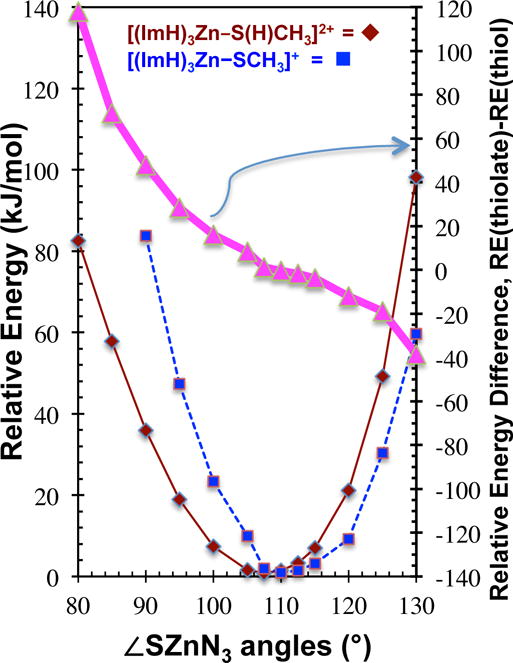
Relative energy versus S–Zn–N₃ angle for [(ImH)₃Zn–S(H)CH₃]²⁺, (red solid diamonds) and [(ImH)₃Zn–SCH₃]⁺, (blue square dashes) systems. Energies are with respect to the fully optimized geometries at the M05-2X/cc-pVDZ level of theory. Also shown is the difference in relative energies (magenta triangles = blue squares – red diamonds), RE([(ImH)₃Zn–SCH₃]⁺) – RE([(ImH)₃Zn–S(H)CH₃]²⁺). Points are connected by straight lines for ease of viewing. For clarity, 80° and 85° points missing from thiolate plot.

The above relationships are illustrated by the relative energy difference plot in Figure 5 (magenta, triangles). The difference plot in Figure 5 was constructed by subtracting the thiol points from the thiolate points. Note the strong resemblance to the PDE curve in Figure 4. The slope of the difference curve provides a quantitative measure of the extent to which the PDE will change as a function of ∠SZn(ImH)₃. The following three examples serve to further clarify this relationship. Example 1: Consider a [(ImH)₃Zn–S(H)CH₃]²⁺ like-complex with a geometry that is energetically and structurally similar to the geometry minima of the thiol, that is to the left of 108.0° in Figure 5. The resulting PDE is predicted to be higher than that of the fully optimized structure. Example 2: Consider an experimentally determined [(ImH)₃Zn–S(H)CH₃]²⁺ complex with a geometry near the bottom of the potential wells, between that of the protonated and deprotonated complexes, between 108.0° and 113.2°. The resulting PDE of the structure will be relatively unchanged, and near its value for the optimized structure. Example 3: Consider a [(ImH)₃Zn–S(H)CH₃]²⁺ complex having S–Zn–N₃ angles greater than 113.0°, a structure more thiolate like. The resulting PDE is predicted to be lower than that of the optimized geometry. Moreover, the further to the left or right on the plot, the greater will be the change in PDE. Therefore, intentionally restricting the L–Zn–N_n angles to be large or small, as can be done in synthetic model complexes such as the tris(pyrazolyl)borate or cycen/cyclam tetraazamacrocycle structures, could lead to constrained zinc geometries affecting the protonation state, acidity, and chemistry of the models.^45,48–51

Three important interatomic distance changes that accompany changes in ∠SZn(ImH)_2,3 are listed in Table 4, and include the Zn–S, S–H, and average Zn–N_ImH bond lengths. Overall, R_Zn–S decreases significantly, while both R_S–H and R_Zn–N(avg) are less sensitive to ∠SZn(ImH)_2,3 for both CNs. Figure 6 illustrates the downward trend in R_Zn–S and the upward trend in R_S–H with increasing ∠SZn(ImH)_n. The increase in R_S–H is consistent with the lower PDE upon increasing the S–Zn–(ImH)_n angles. Importantly, these bond length trends mimic those that occur with the decrease in CN (see Table 2). Although Zn–S BDEs as a function of angle were not calculated here, the results from the CN changes taught us that, in general, the shorter R_Zn–S is the stronger the Zn–S bond is. Therefore, it is reasonable to suggest that increasing ∠SZn(ImH)_2,3 increases the Zn–S bond strength.

Figure 6.

Plots of Zn–S, (triangles) and S–H, (squares) bond lengths as a function of the S–Zn–(ImH)_n angles, ∠SZnN_2,3 for [(ImH)₂Zn–S(H)CH₃]²⁺, open points, and [(ImH)₃Zn–S(H)CH₃]²⁺, solid points.

The partial atomic charges on the Zn atom, the imidazole ligands, and the S and H atoms of HSCH₃, are also listed in Table 4. The numbers suggest a transfer of negative charge density (electrons) from H and S and into the Zn(II)–(ImH)_n moiety with increasing ∠SZn(ImH)_n. This charge redistribution is clearly revealed in Figure 7 where H and S partial charges are plotted versus ∠SZn(ImH)_n. Although the –S(H) unit becomes more positively charged as ∠SZn(ImH)_2,3 increases, the partial charge differences between S and H indicate that the ionic character in the S–H bond decreases, the covalent character increases, with increasing ∠SZn(ImH)_2,3 (Table 4 and Figure 7). The end result is that as ∠SZn(ImH)_2,3 increases there is an buildup of positive charge on H and, accompanying the accumulation of positive charge on H, there is an increase in R_S–H and a concomitant decrease in the S–H proton dissociation energy.

Figure 7.

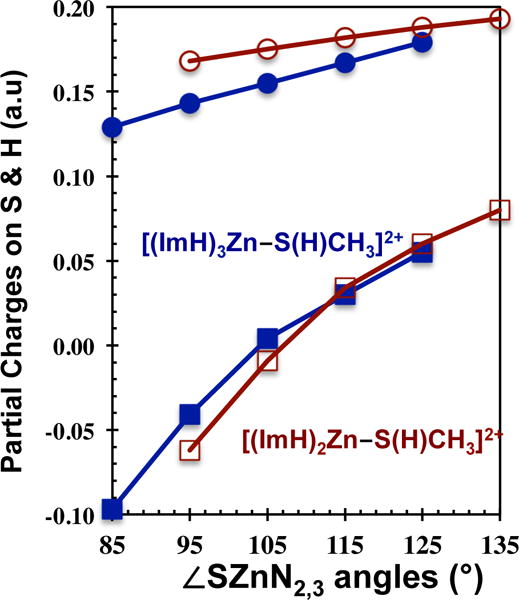
Plots of Partial Charges (atomic units) on S (squares) and H (circles) as a function of the S–Zn–(ImH)_2,3 angles, ∠SZnN_2,3, for [(ImH)₂Zn–S(H)CH₃]²⁺, open red data points, and [(ImH)₃Zn–S(H)CH₃]²⁺, solid blue data points.

4) Conclusions and Further Implications

Through high-quality density functional theory and MP2 calculations performed on a series of [(ImH)_0-5Zn(II)–S(H)CH₃] complexes, we have demonstrated that both the coordination number and the coordination geometry have major impacts on the Zn–S(H)CH₃ bond strength and the S–H proton dissociation energy. Predictably, when a ligand, in this case –S(H)CH₃, is coordinated to a transition metal ion, the coordinated ligand becomes “activated” toward greater acidity, (i.e. a lower pK_a), and a reduced proton dissociation energy. Our calculations reveal that as the Zn(II) CN increases, the influence on the PDE becomes considerably and quantifiably less, albeit still substantial, even for CN=6, wherein the S–H PDE in [(ImH)₅Zn(II)–S(H)CH₃] is almost one-half the intrinsic value as that for the uncoordinated S(H)CH₃. Accompanying the increase in PDE, the Zn–S bond becomes longer and weaker as CN increases. Perhaps less obvious is that at a constant CN, the geometry about the Zn(II) center also changes the thiol’s PDE to a significant extent. In both [(ImH)₂Zn(II)–S(H)CH₃] and [(ImH)₃Zn(II)–S(H)CH₃], as the S–Zn–(ImH)_2,3 angles increase the S–H PDE significantly decreases, making them more acidic as ∠SZn(ImH)_n increases. Accompanying the reduction in proton dissociation energy, either through CN or geometry, the S–H bond becomes less ionic, the bond lengthens, and the atomic charge on H becomes more positive.

When considering Zn–S(H)R ligation in proteins, the coupling of ligand acidity to conformational changes may play a role the aforementioned activation of proMMPs wherein proton transfer to the coordinated cysteine thiolate appears to be crucial. Additionally, in the quest to develop new drugs/inhibitors for the zinc enzymes, sulfur coordination by zinc-binding-groups contributes strongly to the energetic stability of the inhibitor complex and, as shown in the present study, their protonation state is vital.⁵² To date, the potential role of active site conformational reorganization in regulating its protonation state via modulation of its pK_a and, therefore, its catalytic mechanism has not been discussed for the MMPs. Based on the analysis presented herein, the experimental [(His)₃Zn–L] active sites shown in Figure 1 should have different PDEs when L=thiol. Since the mean ∠NZnN is the greatest in the 1SLM structure (the ∠SZnN₃ would be the smallest), we predict that it would have the highest PDE (left side of Figure 4 and Figure 5 plots). Likewise, the 1BIW structure would have the lowest PDE (right side of Figure 4 and Figure 5 plots), since the mean ∠NZnN are the smallest and the imidazoles closest together. When a methylthiol is bound to the Zn(II) in the three structures of Figure 1, after removing the inhibitors and performing a constrained optimization at the experimental geometries, we find that the results are completely consistent with the above predictions. The 1BIW structure has a S–H PDE of 722 kJ/mol while 1SLM has a PDE = 765 kJ/mol (M05-2X/cc-pVDZ values for D_e). Although the experimental structures of MMPs indicate both 4- and 5-coordinate Zn(II) centers having different geometries, our results point toward changes in both the Zn(II) CN and coordination geometry conspiring to modulate the acidity and, therefore, the active-site hydrolytic chemistries.

A recent study has suggested the dynamic nature of the active site zinc geometry may be linked to the activation of homocystein in methionine synthases, an enzyme with a catalytic zinc center comprising His and Cys ligation,⁵³ as well as other enzymes.^54,55 If experimental pK_a differences within the different zinc enzymes derive from variability in the CN or as a result of the flexibility in the coordination spheres of their catalytic zinc centers, it should be possible to exploit active site pK_a differences to gain specificity in their inhibition through judicious choice of ZBGs with the appropriate acidity, as has been suggested.⁵⁶ Additionally, it may be possible to design inhibition strategies that involve ternary complexes, including co-inhibitors, that modulate the coordination geometry at the catalytic zinc center.

ABBREVIATIONS

DFT

density functional theory

MP2

second-order perturbation theory

MMP

matrix metalloproteinase

ImH

imidazole

CN

coordination number