Automated Lung Segmentation from HRCT Scans with Diffuse Parenchymal Lung Diseases

Abstract

Performing accurate and fully automated lung segmentation of high-resolution computed tomography (HRCT) images affected by dense abnormalities is a challenging problem. This paper presents a novel algorithm for automated segmentation of lungs based on modified convex hull algorithm and mathematical morphology techniques. Sixty randomly selected lung HRCT scans with different abnormalities are used to test the proposed algorithm, and experimental results show that the proposed approach can accurately segment the lungs even in the presence of disease patterns, with some limitations in the apices and bases of lungs. The algorithm demonstrates a high segmentation accuracy (dice similarity coefficient = 98.62 and shape differentiation metrics d_mean = 1.39 mm, and d_rms = 2.76 mm). Therefore, the developed automated lung segmentation algorithm is a good candidate for the first stage of a computer-aided diagnosis system for diffuse lung diseases.

Introduction

In the estimate of the World Health Organization, 600 million people have chronic obstructive pulmonary disease (COPD) worldwide [1]. Lung cancer is one of the most serious cancers in the world. In fact, the number of deaths caused by lung cancer is greater than the sum of the deaths due to breast, prostate, and colorectal cancers. It is expected that the number of annual cancer cases will rise from its 14 million in 2012 to 22 million within the next two decades [2]. However, early detection and treatment of lung cancer can improve the survival rates and prognosis of the patient [3]. As high-resolution computed tomography (HRCT) is the key protocol for the evaluation characterization of diffuse parenchyma lung diseases, often characterized by non-uniform distribution in the lung volume. But, it also leads to high unpredictability in interobserver and intraobserver interpretations, mainly due to the lack of standardized criteria and the burden of reviewing a large amount of data [4–6]. Computer-aided detection/diagnosis (CAD) is considered to be the promising tool to aid the radiologist in automatically detecting and analyzing the disease patterns. In order to realize such a CAD system, it is prerequisite to segment the principal human organ regions and human structures from computed tomography (CT) images. In chest CT scans, the principal region is the lung and its structure built by bronchus, lung vessels, and fissures is very important for the diagnosis of diseases related to lungs. In a lung CAD system, prior to the detection of lung lesions, the segmentation of lung parenchyma from thoracic images [7–9] has to be conducted in order to reduce the amount of computation to minimize the computation time. Good lung segmentation can improve the efficiency of the entire CAD system and reduce misdiagnosis. Hence, the lung parenchyma segmentation is a key procedure of a CAD system for lung diseases and pulmonary function assessment [10], which will affect the accuracy of the whole lung CAD system.

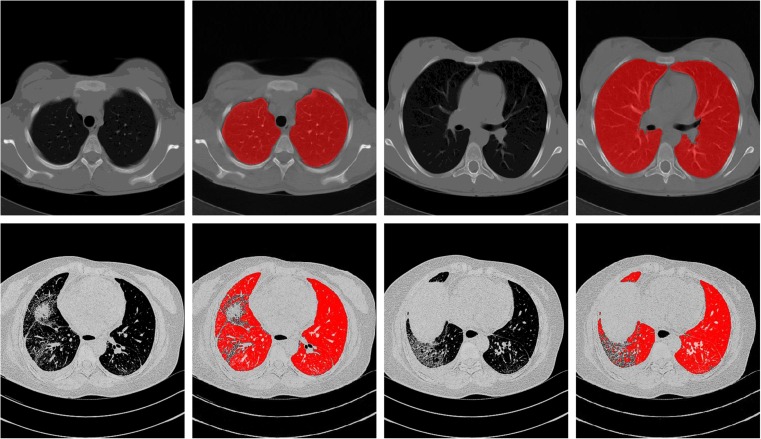
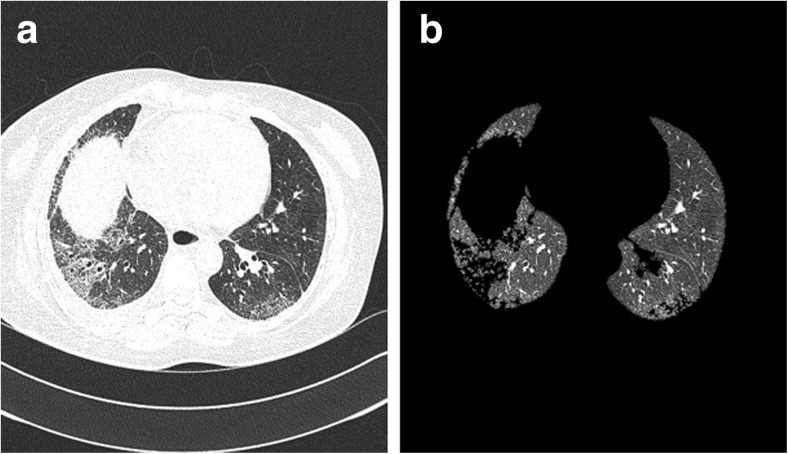
A large amount of research has been devoted to the topic of lung segmentation in 3D CT scans. Most of the methods are based on the observation that, for normal lung parenchyma, there is a large difference in attenuation between the lung parenchyma and the surrounding tissue. These conventional methods perform well on scans that do not contain dense abnormalities. However, dense pulmonary or subpleural abnormality areas are not included in the lung segmentation of these algorithms which is shown in Fig. 1. Other methods are specifically designed to handle such abnormalities but are too slow or too specialized to be used in clinical practice.

Fig. 1.

The performance of a traditional lung segmentation method based on gray-value thresholding. The top row shows two slices from normal lungs; the first original slice is followed by the lung segmentation result overlaid. The bottom row shows two slices containing pathologic abnormalities. The traditional method fails on this type of scan because of the higher densities of the abnormalities compared to the density of normal lung parenchyma

In practice, there is a trade-off between required computation time and quality of the segmentation results; the results should be as precise as possible and available in as short time as possible. As a result, most available automatic chest CT analysis systems rely on conventional, threshold-based segmentation since this is much less time consuming than, for example, a registration-based approach (several minutes vs. several hours) and produces effective results in a large number of scans. However, this method may not prove well and omitted segmentation errors when scans contain (substantial) pathologic abnormalities and they would require clinicians to compute the result manually.

Considering the above problems in lung segmentation, an attempt is made in this paper to present a fully automatic lung segmentation algorithm that can even tackle CT scans affected by diffuse parenchymal lung diseases. The proposed algorithm has four main steps viz., (1) initial region segmentation of chest CT images, (2) elimination of airways in each CT slice, (3) extraction of the lung regions, and (4) repairing the boundary based on modified convexity algorithm and mathematical morphology techniques. The algorithm can effectively segment lungs with severe interstitial lung disease (ILD) in thoracic HRCT scans. The algorithm is evaluated on a set of CT cases spanning over a range of diffused parenchymal lung diseases including honeycombing, reticular pattern, ground glass opacity, pleural plaques, and emphysema. The accuracy of the algorithm is assessed by comparing with ground truth images provided by an expert radiologist. Furthermore, the improvement brought about by using the combination of modified convex algorithm and morphology techniques is analyzed and compared with the results of conventional methods.

Previous Work

In recent years, scholars from various strata of the globe have put forward a series of lung segmentation methods. These methods can be generally divided into the following four major categories: threshold method [11–18], deformable boundary models [19–24], edge-based methods [25–28], and registration-based method [29, 30]. Lungs appear as dark regions in CT scans, since they are essentially bags full of air inside the body. In addition, image intensities of the lung and surrounding tissues are clearly contrasted. This fact has encouraged many scholars to search for an optimum threshold which separates the lungs from all other tissues. They computed a threshold to get an initial lung region. The initial segmentation was then refined by gray-level thresholding [11], histogram thresholding [12], multiple 2D thresholding [13], and iterative 3D thresholding [14, 15]. In case of lung-edge affecting pathologies, all these methods are found to be ineffective. This is because of the change of image intensities in pathological regions as well as gray levels coming closer to muscle, fat, or bone [16]. To solve these problems, thresholding methods are combined with other techniques based on mathematical morphology [12] or rolling ball operation [16], region growing, and anatomical knowledge [17, 18]. The accuracy of threshold-based segmentation is the major problem which is affected by many factors, such as image acquisition protocol, scanner type, etc. Moreover, densities (in Hounsfield Units (HU)) of some pulmonary structures, such as vessels, bronchi, and bronchioles, are very close to densities of the chest tissues. Because of this, the threshold-based segmentation may not be accurate for the whole lung region. It needs further intensive postprocessing steps to overcome the non-homogeneity of densities in the lung region.

An active contour or the deformable boundary model starts from some initial position and shape. It functions under specific internal and external guiding forces to fit into the shape of one or more desired objects. A region of interest (ROI) or locate an object boundary can be extracted by active contours. Extract the lung region with a 2D parametric deformable model using the lung borders as an external force. The deformable model starts from an initial segmentation which was obtained by a threshold estimated from CT data. The segmentation results were used as an initial step to classify abnormal areas within each lung field [19]. A 2D geometric active contour was initialized along the boundary of the chest region, which was then automatically split into two regions representing the left and right lungs in [20]. The critical drawbacks of the deformable model-based segmentation include the excessive sensitivity to initialization and the inability of traditional external forces to capture natural in-homogeneity in the lung regions. Consequently, it is hard to provide an adequate guidance to the deformable model to achieve the accurate segmentation. The shape-based techniques add prior information about the lung shape to image signals, for improving the segmentation accuracy. Integrating a prior shape term [21], with a term describing edge feature points and a term representing region-based data statistics in a variation energy framework for lung segmentation, is calculated as described in [22]. In order to segment the lung fields from posterior-anterior (PA) chest X-ray images, the formulated energy was used to guide a level set deformable model. The segmentation of the lung fields was iteratively refined by the iterative conditional mode (ICM) relaxation that maximizes a Markov-Gibbs random field (MGRF) energy which accounts for the first-order visual appearance model and the spatial interactions between the image voxels. Further, they enlarged their work by applying their iterative MGRF-based segmentation framework on different scale spaces [23, 24].

The edge-based lung segmentation is performed using spatial edge detector filters or wavelet transforms. A preprocessing outline of lung borders was identified by using the first derivative of Gaussian filters taken at various orientations. Then, an edge tracking procedure using the Laplacian of Gaussian (LoG) operator at different scales was used to find a continuous external lung contour that was further integrated with the initial outline to produce the final lung segmentation from PA chest radiographs [25]. The ROIs from PA chest radiographs are rectangular areas which surround each lung field as closely as possible through an iterative procedure. Edge points, such as the mediastinal, costal, top, and bottom edge points, were detected using spatial edge-detector filters (SED) and combined to define a closed contour for the lung borders [26]. To highlight lung borders in a stack of 2D images, a 2D wavelet transform is used [27]. An optimal threshold, selected by the minimum error criterion [28], was applied to the wavelet-processed 3D stacks to segment lung volumes.

For the automated segmentation of the pathological lung in CT, the segmentation-by-registration scheme (SRS) was proposed by [29] where a scan with normal lungs is registered to a scan containing pathology. When the resulting transformation is applied to a mask of the normal lungs, segmentation is found for the pathological lungs [30]. Refined registration-based segmentation approaches, which yield significant accuracy improvements compared to a standard SRS approach, however, fail in speed efficiency due to the registration and classification processes. Similarly, 3D morphological processing was further performed to refine the final segmentation.

Proposed Method

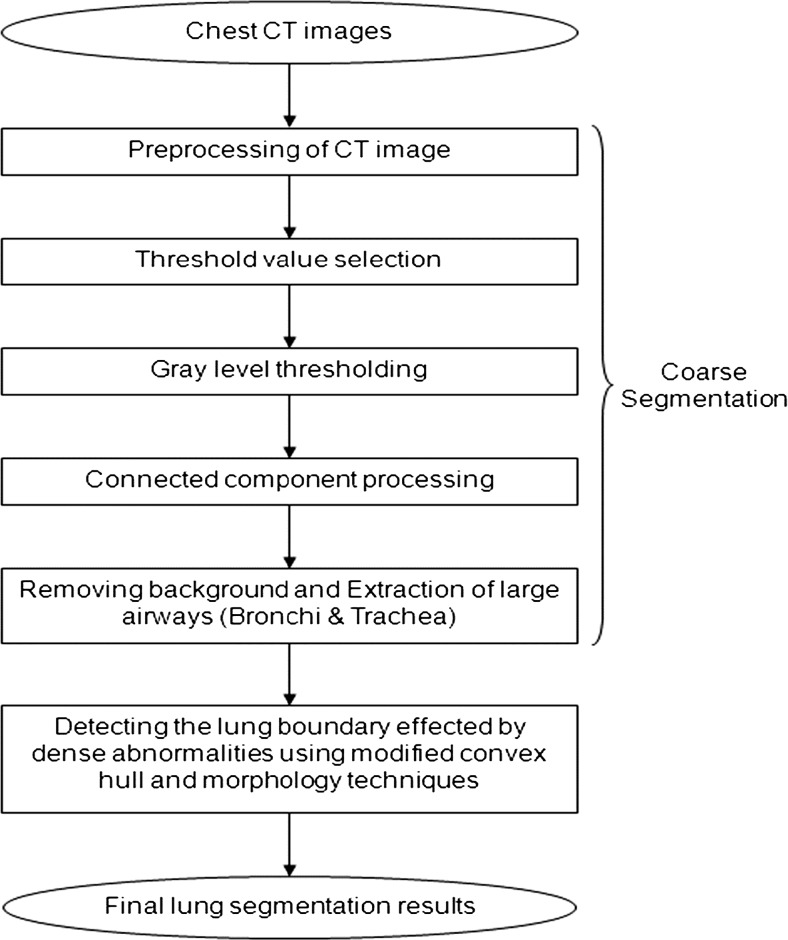
The schematic of the different stages of the proposed algorithm is given in Fig. 2.

Fig. 2.

Flow chart of the proposed method

Coarse Segmentation of Lungs

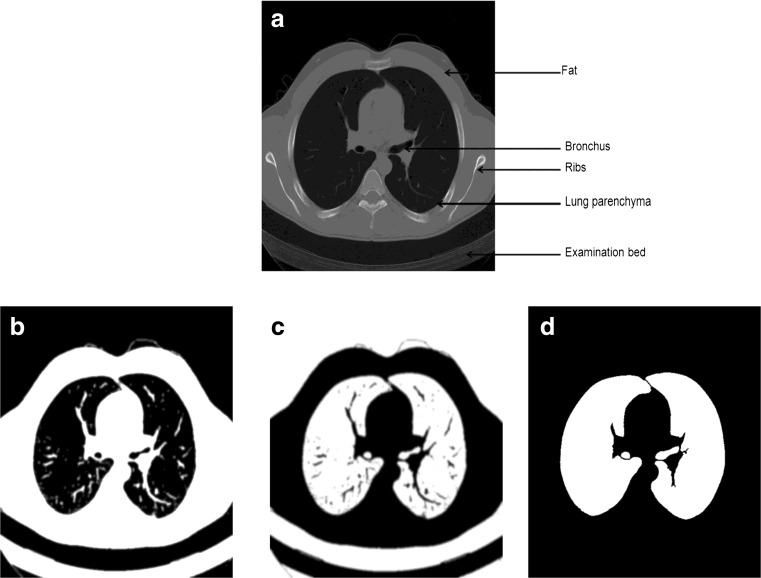
The original CT scan includes the examination bed, fat, ribs, lung parenchyma, main trachea, etc. As the air noise in the scans may lead to many small contours, Gaussian smoothing is used to eliminate the air noise. Otherwise, these small contours may be incorrectly segmented as lung border. In our implementation, the CT images are convolved with a 3D Gaussian kernel that has a standard deviation of 1.0 mm.

In CT images, the intensities of ribs, examination bed, and fat is generally above −100 HU and the tissue of the lung is in the range of −400 to −600 HU. We have used iterative thresholding to segment the lung regions. The process of obtaining the threshold is as follows:

1. Set the initial background gray scale F_b, object grayscale F_o, and the initial threshold value is

$$T_{\mathit{0}}\mathit{=}\frac{F_b\mathit{+}{F}_o}{\mathit{2}}$$

• 2.Calculate the average gray level of the background region and object region G_b and G_o.
• 3.Set $T_{\mathit{1}}\mathit{=}\frac{G_b\mathit{+}{G}_o}{\mathit{2}}$, and the new threshold is T₁.
• 4.Iteration termination condition is T₁ ≈ T₀, that is, the difference between T₁ and T₀ is less
• 5.Otherwise, assign T₁ values to T₀ and go back to step (2).

Figure 3b presents the results of iterative thresholding. To remove the non-lung regions left after iterative thresholding, we have applied 2D flooding. This operation is applied slice by slice using the pixels along the image borders as flooding seeds.

Fig. 3.

a The original thoracic CT image. b Segmented image by iterative threshold. c Inverted image. d Initial mask after removing background

Elimination of Trachea and Bronchi

As shown in Fig. 3d, the trachea and bronchi will be preserved even after the coarse segmentation. We have used 3D-connected component labeling and 3D region growing to eliminate the trachea and bronchi. As trachea and bronchi are filled with air, they have very low CT values, approximately −1000 HU. A threshold of −900 HU is employed to segment trachea and bronchi such that the pixels having CT values less than −900 HU are taken as air component pixels.

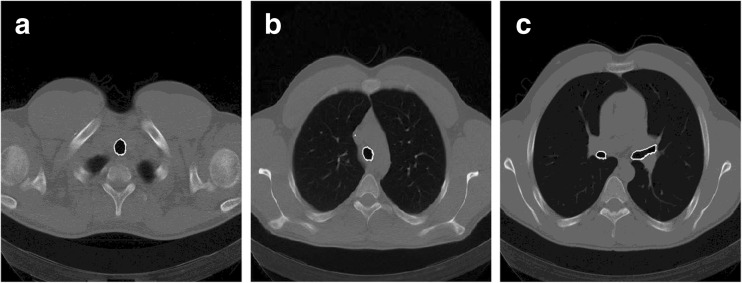
3D-connected component labeling is applied to the first 30 slices with a view to identify and retain the largest volume of air component pixels. Now, these pixels represent the upper part of the trachea. The remaining small connected components are dismissed as noise. Later on, the identified trachea is used as a seed for the region growing technique, which resulted in tracing the entire airways from an upper slice to a lower one through the CT scan. Provided an air-component pixel is adjacent to an airway pixel in the previous slice, it will be added as the air component pixel to the airway. A morphological opening and 3D-connected component labeling are used to isolate the airways from unwanted regions. The segmented airways are eliminated from the CT images to prevent interference in lung segmentation, the white curves in Fig. 4 represent the airways in the upper slice, the middle slice, and the lower slice of a CT scan.

Fig. 4.

The segmentation of airways in upper, middle, and lower slices in a CT scan respectively

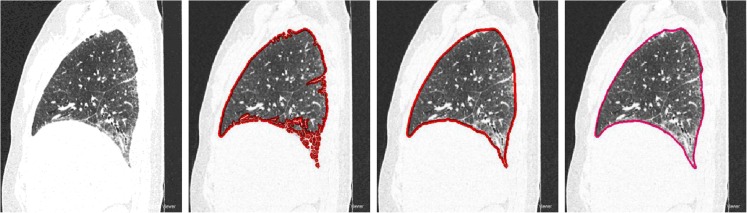
From Fig. 4, it can be concluded that the coarse segmentation methods perform well on healthy scans. However, Fig. 5 reveals that if the scans are having abnormalities, then coarse segmentation methods fail to include the areas of abnormalities. As the gray level characteristics of these abnormalities are similar to that of the surrounding lung tissue, they will be wiped off during coarse segmentation that results to a concave region on the corresponding lung border. This will lead to misdiagnosis as they are important for lung disease CAD system. Other methods [29, 30] which are specifically designed to handle such abnormalities in lung segmentation framework are too slow or too specialized to be used in clinical practice. In this work, we address this challenge using a lung parenchyma repairing method based on modified convexity algorithm and mathematical morphology.

Fig. 5.

a The CT of a patient with severe interstitial lung disease (ILD) and severe interstitial lung disease. It is proved that the thresholding fails to identify the severe ILD pattern since it suffers from poor segmentation of the initial lung (b)

Modified Convexity Algorithm

Convexity of a planar point set S is the intersection of the entire half-planes containing S [31]. The shape of convexity is a convex polygon whose vertices belong to S. For an edge pq, all convexity points lie on one side of the line running through p and q. Generally, in convex algorithms, the given image is scanned and a non-self-intersecting polygon is extracted, or a convex hull is extracted from the polygon by checking the convexity of the polygon [32]. These algorithms have high complexities of time and space. To meet this issue, we have used monotonicity characteristic to design convex hull algorithm for binary image.

The proposed modified convexity algorithm first extracts eight extreme points on the boundary of the binary image and then partitions the image into four regions by using these extreme points. While computing the vertex, only these extreme points in the four regions are processed. By orderly scanning, the ad hoc convexity is extracted. The entire convexity is finally obtained by continuously updating the ad hoc convexity. Since the scanned areas are few and only the vertices of ad hoc convexity require storage, the proposed algorithm has low complexities of time and space.

Finding the Extreme Points

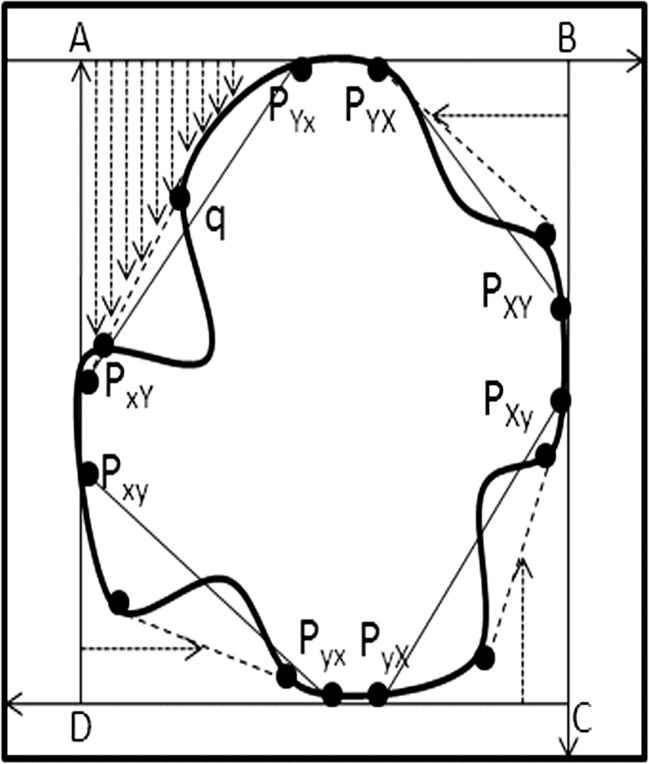
Let P = {p₁, p₂, …, p_M} be a planar point set. In the subset whose points x-coordinate are maximal among P, P_XY, and P_Xy denote the points with maximal and minimal y-coordinate, respectively. In the subset whose points x-coordinate are minimal among P, P_xY, and P_xy represent the points with maximal and minimal y-coordinate, respectively. Similarly, in the subset whose points y-coordinate are maximal among P, P_YX, and P_Yx denote the points with maximal and minimal x-coordinate, respectively. In the subset whose points y-coordinate are minimal among P, P_yX, and P_yx represent the points with maximal and minimal x-coordinate, respectively. In the subscript of variables, the first denotes the extremum of coordinate and the second subscript denotes the extremum of the other coordinate under the first coordinate. Subscripts of capitalization and minuscule mean maximum and minimum, respectively. These extreme points in the planar point set P are the convex hull vertices. The process scanning from outside to inner is applied to extract the extreme points as shown in Fig. 6. The detailed steps are as follows.

1. Starting at the top left corner, scan the image from top to bottom until the image boundary is encountered. Each row scan starts from left to right. Let the leftmost and rightmost boundary points be P_Yx and P_YX, respectively. Thus, two top extreme points on the image boundary P_Yx and P_YX are obtained.

2. In the second step, starting at the top row running through P_YX and P_Yx, scan the image from right to left in every column, from top to bottom, until the topmost and bottommost boundary points of the image are encountered. Thus, two right extreme points on the image boundary P_XY and P_Xy are obtained.

3. In the third step, at the rightmost column running through rightmost extreme points, scan the image from bottom to top until the image boundary is encountered. Each row scan starts from right to left. Let the rightmost and leftmost boundary points be P_yX and P_yx, respectively. Thus, two bottom extreme points on the image boundary P_yX and P_yx are obtained.

4. In the final step, scan the image from left to right from bottom to top in between bottom row running through P_yX and P_yx, and top row running through P_Yx and P_YX until the topmost and bottommost boundary pixels, respectively, are encountered. Thus two left extreme points on the image boundary P_yX and P_yx are obtained.

Fig. 6.

Extreme points of image convex hull and scanned regions of image

Monotone Segment

Since the extreme points are convex hull vertices, the convex hull can be obtained by determining the vertices on the monotone segments between each pair of extreme points.

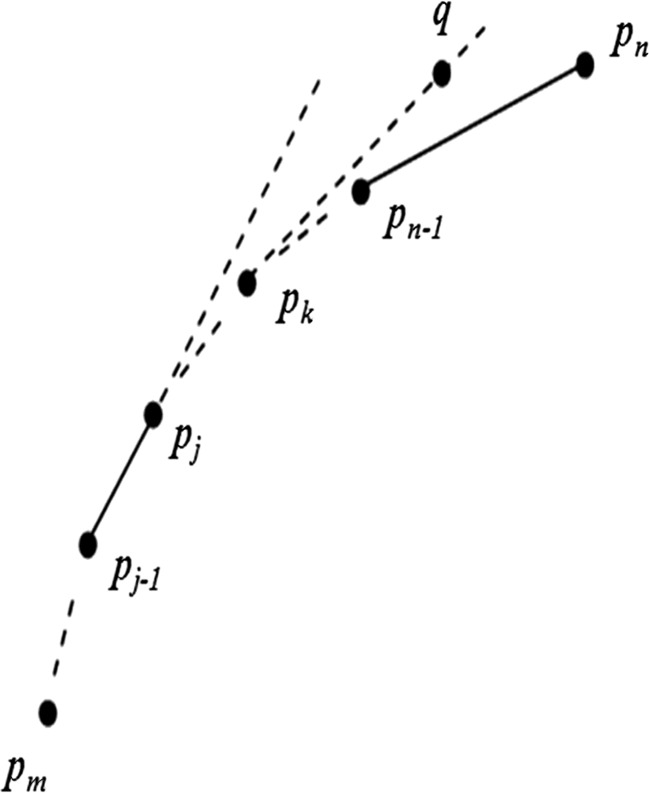
Let P = {p_m, p_m+1, …, p_n} (n > m) be the vertices of a monotone segment of a specific convex hull, and the coordinate of p_i and q be (x_i, y_i) and (x, y), respectively, P′ = {q}∪P and min{y_n−1,y_n} < y < max{y_n−1, y_n}. If q and p_k (k < n) are both the points in a specific monotone segment of P′, then p_m, p_m + 1… p_k, q, p_n are all vertices on the monotone segment as shown in Fig. 7.

Fig. 7.

Monotone segment

Finding the Scanned Regions and Convex Hull

By the above steps, we obtain eight extreme points. From the lines connecting adjacent extreme points, we obtain four regions that are AP_yXP_Yx, BP_YXP_XY, CP_XyP_yx, and DP_yxP_xy. Beginning from the AP_yXP_Yx region, scan the region horizontally from left to right (Fig. 6). Each column in the region is scanned vertically from top to bottom. If there is no boundary pixel on the scanned line, then scan the next column until a boundary point “q” is encountered on the scanned line. Then, q is a vertex of temporary convex hull in the scanned image. Compute the monotone increasing top segment of the temporary convex hull. These processes continue in the remaining regions to obtain the convex hulls of the image.

Then, the convex hull for an image can be obtained as follows:

1. Scan the image and compute the eight extreme points, P_xy, P_xY, P_Xy, P_XY, P_yx, P_yX, P_Yx, and P_YX.

2. Use these eight extreme points to determine the four regions (AP_yXP_Yx, BP_YXP_XY, CP_XyP_yx, and DP_yxP_xy) where the convex hull vertices may exist.

3. Scan the four regions dynamically and obtain convex hull vertices on each monotone segment, respectively.

4. Extract convex hull vertices on each monotone segment according to the following order: P_xY → P_Yx, P_YX → P_XY, P_Xy → P_yX, P_yx → P_xy. Each extreme point is extracted only once.

Then, the convex hull is obtained.

Morphological Image Analysis

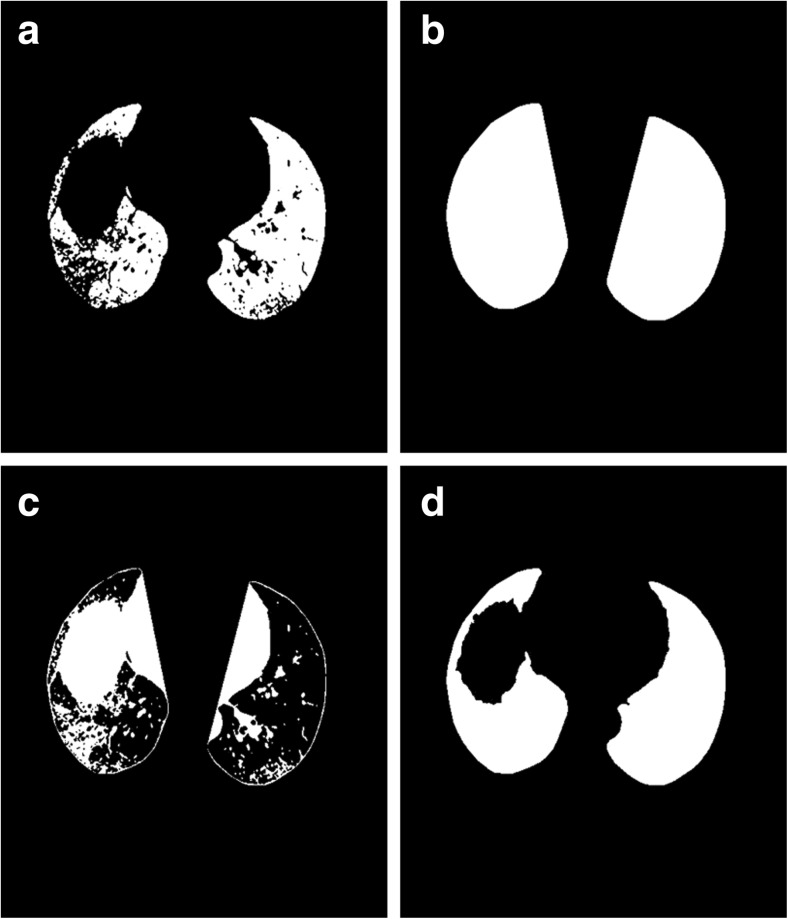
After applying modified convex hull algorithm, finally, the following postprocessing techniques based on mathematical morphology are used to obtain the final lung segmentation. Firstly, the coarse segmented lung image is subtracted from the result of modified convex hull algorithm. The resultant image is as shown in Fig. 8c. As the resultant image contains some small responses and objects at the border, morphological erosion with a spherical kernel of size 7 and 18-connected label filtering are then applied to remove these responses. The areas left in the resultant image after the erosion and connected component labeling specify the errors in the segmentation. Finally, the eroded image is subtracted from the result of the modified convex hull algorithm to extract the final lung region.

Fig. 8.

a Image of binary result for Fig. 5b. b Filling result of convex areas of the proposed algorithm. c Difference of coarse and modified convex hull. d Final lung segmentation of our method

Experimental Results and Discussion

Sixty chest HRCT scans are tested by the proposed lung segmentation method. Forty scans are provided by local hospitals, the other 20 scans are randomly selected from publicly available databases. Image data are stored in DICOM format and reconstructed to 512 × 512 with 1 mm slice thickness, 15 mm slice increment, and 12-bit gray level resolution. Pixel spacing lay in the range of 0.51–0.79 mm, with an average value of 0.63 mm. To qualitatively evaluate the proposed algorithm, all the images have been traced by an experienced chest radiologist on all slices from the top to bottom parts of the lungs. The proposed algorithm is implemented in MATLAB 2014b on Core i7 3.33 GHz PC with 16 GB memory. The comparison of implementation time between our algorithm and the other methods is given in Table 1, from which we can see that the implementation time of the proposed algorithm is less compared to other methods.

Table 1.

Comparison of average implementation time per frame between our algorithm and the other methods

	Region growing method	Texture-feature method	The rolling-ball method	Our method
Average implementation time per frame (in seconds per frame)	12	5	1.13	0.66

Performance Metrics

To quantify the performance of our algorithm, three metrics are used.

First is the dice similarity coefficient (DSC) which is defined as,

$$DSC=\frac{2*\left|M\cap A\right|}{\left|M\right|+\left|A\right|}$$ 1

M is the manual lung area segmentation, while A is the segmented area of the proposed lung segmentation method. The DSC value is bound between zero (no correspondence) and one (exact match).

As the lung is a large object, small local errors at the boundary are not captured in the overlap measure. For this reason, the contour shape is assessed by two distance metrics:

1. Mean distance.

2. Root mean square distance

The mean distance (d_mean) is defined as

$$d_{\mathit{mean}}=\frac{{\displaystyle {\sum }_{q=1}^{p^M}d\left(q,M\right)+{\displaystyle {\sum }_{q=1}^{p^A}d\left(q,A\right)}}}{p^M+p^A}$$ 2

where p^A and p^M are pixel numbers defining the contours obtained by the proposed method and the ground truth, respectively.

d(q, M) and d(q, A) are defined as

$$d\left(q,M\right)={}_r{}^{min}\left\{\sqrt{{\left(x_q^A-x_r^M\right)}^2-{\left(y_q^A-y_r^M\right)}^2}\right\}$$ 3

$$d\left(q,A\right)={}_r{}^{min}\left\{\sqrt{{\left(x_r^A-x_q^M\right)}^2-{\left(y_r^A-y_q^M\right)}^2}\right\}$$ 4

where (x^M, y^M) is the ground truth contour pixel location and (x^A, y^A) is the contour pixel location of the proposed method.

The root mean square distance (d_rms), between the proposed method border (A) and the border obtained by the ground truth (M), is calculated by

$$d_{rms}=\sqrt{\frac{{\displaystyle {\sum }_{q=1}^{p^M}d{\left(q,M\right)}^2+{\displaystyle {\sum }_{q=1}^{p^A}d{\left(q,A\right)}^2}}}{p^M+p^A}}$$ 5

Evaluation of Methodology

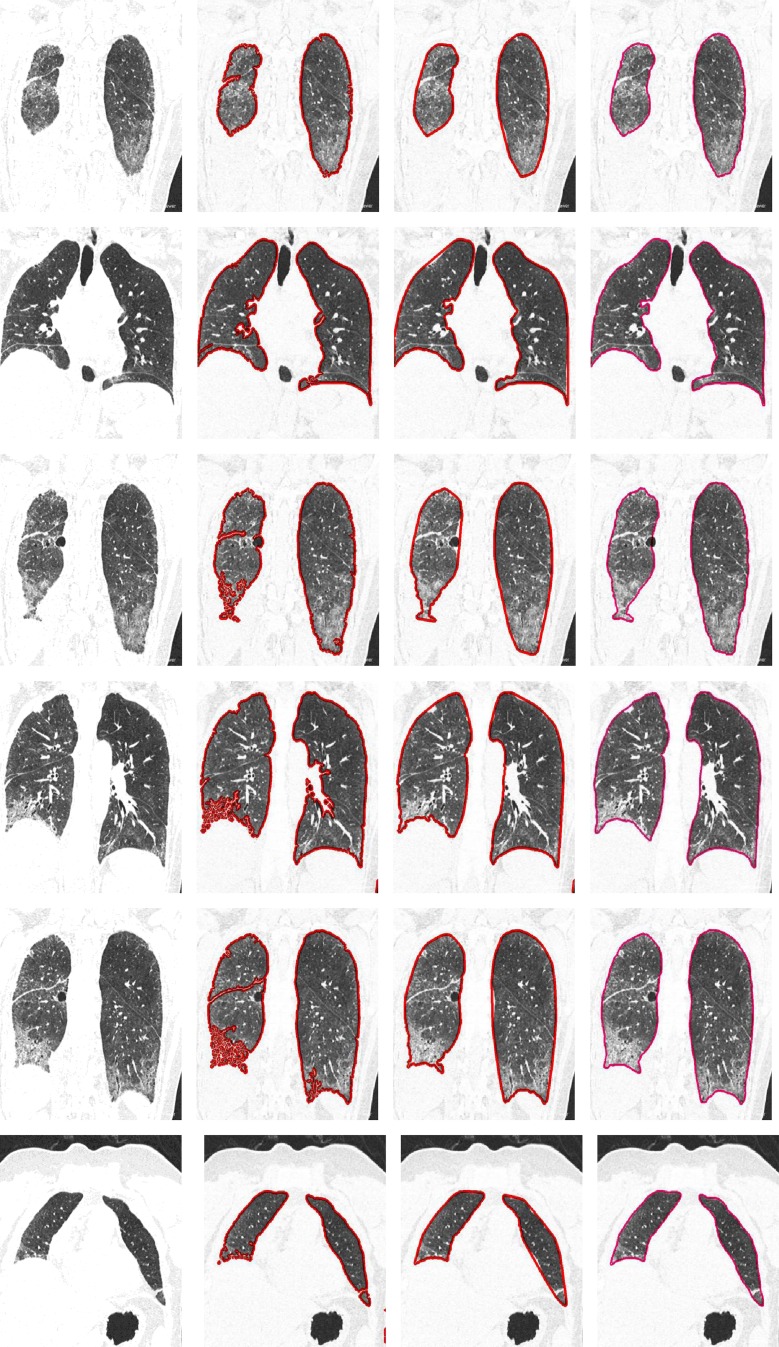
In order to evaluate the proposed method, the results are compared with the results of the rolling ball method and the manual segmentations made by the expert. From Fig. 9, it can be observed that the proposed method provides accurate lung segmentation results (Fig. 9 (1–5) and (8–10)) for all kinds of diffuse parenchyma lung diseases. Both the rolling ball method and the proposed method perform precisely for scans corresponding to normal lung parenchyma. The result of the scan having honeycomb disease is shown in Fig. 9 (1–5). The proposed method extracts the lung region accurately compared to the rolling ball method as it uses modified convex algorithm and mathematical morphology. Even when the coarse segmentation step produces poor quality in diseased areas, the use of modified convex algorithm and mathematical morphology permits refinement of a good final segmentation in more standard cases. When one of the lungs is not found, due to the segmentation (Fig. 9 (8)) which is used as a starting point for the lung segmentation, the automatic initialization of the threshold segmentation fails. However, it can be seen that the developed method and ground truth contours disagree in the mediastinum area for some specific cases.

Fig. 9.

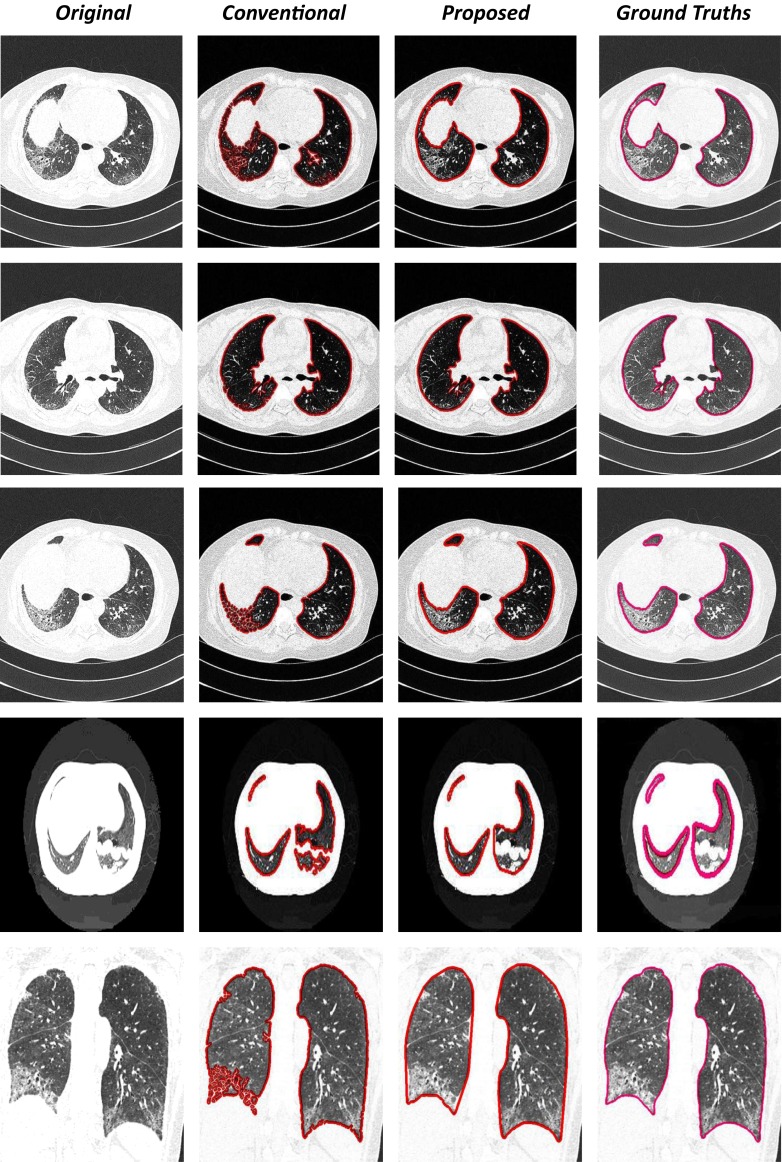
Examples of automated lung region detection results in an axial (1, 2), sagittal (3, 4), and coronal (5) view of the modified convexity algorithm and mathematical morphology technique segmentation for the 12 scans in which an error was detected after the conventional lung segmentation method. The first column shows the original slice, the second column shows the conventional lung segmentation (red contour), the third column shows the modified convexity algorithm and mathematical morphology techniques method (red contour), and the last column shows the result of the manual segmentation (pink contour)

Table 2 presents the performance metrics viz. dice similarity coefficient (DSC), mean distance (d_mean), and root mean square distance (d_rms) for both the rolling ball method and the proposed method with respect to the ground truth. Statistical (mean and standard deviation) and ranking values (minimum, maximum, and median) are computed on a total of 60 scans and 612 images and also for each specific disease pattern. The proposed method achieves a good overlap area with a mean DSC of 98.62 % together with a small error distance (d_mean = 1.39 mm). The initial estimate of lung segmentation provided by the anatomy-driven framework is also of good quality but still significantly lower, with an average DSC of 95.06 %. However, the error distance is higher (d_mean = 4.61 mm) with a maximum value of 55.24 mm. A direct comparison is achieved between the segmentations of the rolling ball method and the proposed method by calculating the difference of each measure on each CT image. The proposed method provides an average improvement of 4.61 % in DSC and 4.49 mm in terms of mean distance error. However, in some cases, this improvement reaches impressive maximum values of 58 % and 78 mm. At the disease pattern level, it appears that the proposed method is more robust, since the same performance is reached independently on all the disease patterns considered. Compared to this fact, the rolling ball method segmentation results are much more desperate, with more difficulties in achieving good results for ground glass, honeycombing, and emphysema patterns. The comparison slice by slice between coarse and final segmentations also comes to the similar conclusion (Table 2).

Table 2.

Segmentation accuracy of the developed method for the final segmentation (after modified convexity and mathematical morphology), for the coarse segmentation (anatomy-driven) and difference in the segmentation accuracy of the two methods

		Final segmentation			Coarse segmentation			Difference
		DSC	dmean	drms	DSC	dmean	drms	∆DSC	∆dmean	∆drms
CT scans having abnormalities	Mean	98.05	1.57	3.26	91.19	6.06	10.34	6.86	−4.49	−7.08
	SD	5.37	2.55	5.47	10.4	5.18	7.64	−5.03	−2.63	−2.17
	Min	63.29	0.3	0.42	48.85	0.63	1.09	14.44	−0.33	−0.67
	Max	99.65	18.04	37	98.56	29.29	52.88	1.09	−11.25	−15.88
	Median	98.43	0.74	1.35	93.42	5.2	8.45	5.01	−4.46	−7.1
Normal	Mean	99.18	1.21	2.26	98.93	3.15	7.78	0.25	−1.94	−5.52
	SD	5.16	4.62	5.26	9.76	5.87	9.11	−4.6	−1.25	−3.85
	Min	60.02	0.19	0.34	47.14	0.39	0.37	12.88	−0.2	−0.03
	Max	99.59	21.66	43.07	99.47	81.18	110	0.12	−59.52	−66.93
	Median	99.47	0.52	0.97	96.36	3.53	6.09	3.11	−3.01	−5.12
Overall	Mean	98.62	1.39	2.76	95.06	4.61	9.06	3.56	−3.22	−6.3
	SD	5.27	3.59	5.37	10.08	5.53	8.38	−4.82	−1.94	−3.01
	Min	61.66	0.25	0.38	48	0.51	0.73	13.66	−0.27	−0.35
	Max	99.62	19.85	40.04	99.02	55.24	81.44	0.61	−35.39	−41.41
	Median	98.95	0.63	1.16	94.89	4.37	7.27	4.06	−3.74	−6.11

Results are given for disease pattern, normal lungs, and overall slices (DSC is given in % and shape metrics in mm)

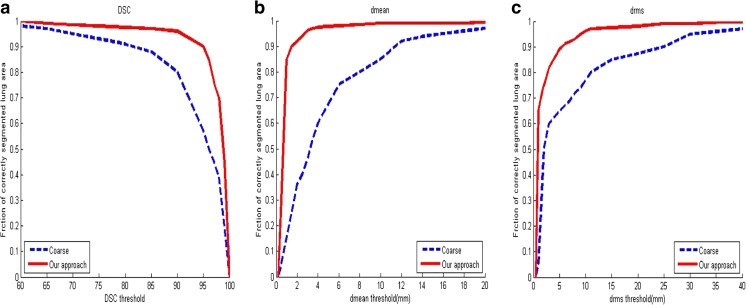
In Fig. 10, cumulative curves of the fractions of correctly segmented lung area are shown as functions of (a) DSC, (b) d_mean, and (c) d_rms thresholds for the segmentations of the proposed and rolling ball methods. The fraction of correctly segmented lung area is defined as the percentage (in absolute value) of lung area with a DSC value greater than the threshold and as the percentage of lung area with a distance metric value lower than the threshold. As observed (Fig. 10a), at a DSC value of 98 %, the fraction of correctly segmented lung area is 0.70 for the final segmentation, while it is 0.39 for the anatomy-driven segmentation. This difference persists even for the distance metrics. At a d_mean value of 2 mm (Fig. 10b), the fraction of correctly segmented lung area is 0.92 for the final segmentation, while it is only 0.36 for the anatomy-driven segmentation. At a d_rms value of 4 mm (Fig. 10c), the fraction of correctly segmented lung area is 0.975 for the final segmentation, while it is only 0.6 for the anatomy-driven segmentation.

Fig. 10.

Three sets of curves show the cumulative of the fraction of correctly segmented lung area

Discussion and Conclusion

Segmentation of structures in medical images is a challenging task, including among other things, anatomical differences, abnormalities, image noise, and differences in acquisition parameters. A fully automatic framework for segmentation of the lungs in thoracic CT scans is a crucial prerequisite for automatic analysis of chest CT scans. Each available chest CT analysis system incorporates automatic lung segmentation. However, the lung segmentation methods incorporated in most automatic analysis systems are highly conventional methods which are based on thresholding and region growing since these techniques are generally fast. The lung segmentations produced by such systems are often erroneous for clinical scans, which may lead to incorrect analysis of the data. The discrepancy between the results reported in the literature and the actual results in a clinical setting are partly caused by the reason that many algorithms have been tested only on very few selected patient populations which may not necessarily represent actual clinical practice.

Lung segmentation is a primary requisite for automated analysis of chest CT scans; ignoring the fact that the conventional methods of lung segmentation depend on large attenuation differences between lung parenchyma and surrounding tissue. These methods were not successful in scans where dense abnormalities are present, which holds for a large percentage of clinical scans. This work successfully segments the lung region even when the scans have dense abnormalities. The key feature of the proposed algorithm is that it uses the monotonicity property in modified convex hull algorithm to extract the convex hull of an object such that the accuracy in segmentation and the computing speed increases. The proposed algorithm has a very less computational cost in the following ways: (1) it divides the binary image into several regions by using the extreme points such that only those boundary pixels in few regions require computation. (2) The boundary pixels obtained by scanning are computed dynamically and only these vertices of temporary convex hull require storage. Performance evaluation of the proposed method shows that the method can accurately segment lungs even in the presence of all kinds of diffuse parenchyma lung diseases, with some limitations in the apices and bases of the lungs. We compare the implementation time of the proposed algorithm with the other methods. Hence, the proposed automatic lung segmentation method is an absolute fit for the first stage of a CAD system for diffuse lung diseases.