Q-Space Truncation and Sampling in Diffusion Spectrum Imaging

Abstract

Purpose

To characterize the q-space truncation and sampling on the spin-displacement probability density function (PDF) in diffusion spectrum imaging (DSI).

Methods

DSI data were acquired using the MGH-USC connectome scanner (G_max=300mT/m) with b_max=30,000s/mm², 17×17×17, 15×15×15 and 11×11×11 grids in ex vivo human brains and b_max=10,000s/mm², 11×11×11 grid in vivo. An additional in vivo scan using b_max=7,000s/mm², 11×11×11 grid was performed with a derated gradient strength of 40mT/m. PDFs and orientation distribution functions (ODFs) were reconstructed with different q-space filtering and PDF integration lengths, and from down-sampled data by factors of two and three.

Results

Both ex vivo and in vivo data showed Gibbs ringing in PDFs, which becomes the main source of artifact in the subsequently reconstructed ODFs. For down-sampled data, PDFs interfere with the first replicas or their ringing, leading to obscured orientations in ODFs.

Conclusion

The minimum required q-space sampling density corresponds to a field-of-view approximately equal to twice the mean displacement distance (MDD) of the tissue. The 11×11×11 grid is suitable for both ex vivo and in vivo DSI experiments. To minimize the effects of Gibbs ringing, ODFs should be reconstructed from unfiltered q-space data with the integration length over the PDF constrained to around the MDD.

INTRODUCTION

The advent and widespread adoption of diffusion tensor imaging (DTI) (1, 2) in the 1990's was concurrent with improvements in magnetic resonance imaging (MRI) gradient specifications that enabled single-shot read-outs that allow whole-brain measurements in reasonable scan-times, and confer robustness against motion artifacts. Recently, dramatic improvements in gradient technology for human scanners (3-8) have enabled further increases in gradient amplitudes that once again provide new opportunities to exploit the diffusion MRI signal. Namely, the increased maximum gradient amplitudes are making high b-value methods such as diffusion spectrum imaging (DSI) (9) more feasible in the in vivo human brain. Here, we aim to characterize the q-space truncation and sampling in DSI using unique in vivo and ex vivo human brain DSI data acquired on the 3T MGH-USC connectome scanner.

DSI is one approach proposed to resolve intra-voxel crossing fibers, which have been observed throughout the human brainstem (10) and cerebral hemispheres (11, 12). Although DTI can accurately estimate a single fiber orientation, it fails to delineate multiple intra-voxel orientations, thus limiting its utility in studying complex fiber configurations and accurately tracing fiber pathways. DSI is based on the Fourier relationship between the attenuated echo signal in q-space and the spin-displacement probability density function (PDF) (13, 14). In DSI, q-space is most commonly sampled on a Cartesian grid extending to a sphere with a radius equal to the maximum q-value (q_max). By analogy to normal k-space imaging (15), q-space coverage determines the PDF resolution (1/2q_max), i.e. the ability to differentiate between different spin-displacement lengths, while q-space sampling density determines the field-of-view (FOV) in the PDF domain (1/Δq). An insufficient q-space coverage and sampling density can create Gibbs ringing artifacts and aliasing artifacts respectively in the reconstructed PDF (16).

The PDF represents the density of the average spin displacement in a voxel, is therefore also called ensemble average propagator or diffusion propagator (17). In order to simplify its angular structure, a radial projection of the PDF is taken to generate the orientation distribution function (ODF). ODFs are then used to reconstruct white matter pathways in the brain (i.e. fiber tractography) (18-20). DSI in conjunction with tractography has been used extensively and was recently used to propose a new theory regarding the fundamental geometric structure of hemispheric fiber pathways (21).

DSI has been studied previously in terms of the optimal maximum b-value (22), q-space sampling density (23, 24) and pattern (25-28), q-space truncation (29-32) and reconstruction methods (33-36). These prior studies have focused predominantly on the ODF and tractography results when developing and evaluating methods. In contrast, our study characterizes the q-space sampling density and ODF reconstruction by analyzing the spin-displacement PDF.

The PDF is the direct result of the Fourier transform of the acquired q-space data. Therefore, the PDF displays the immediate effects of different q-space signal acquisition schemes. ODF and tractography results are computed using various algorithms and therefore are one step removed from the q-space acquisition. Namely, the ODF is reconstructed via a radial projection of the PDF. Studying the PDF provides more direct assessment of the source of artifacts and informs ODF reconstruction methods. Further, the PDF itself provides rich information about the microstructural properties of the tissue and many NMR and MRI works have studied the optimal methods to obtain accurate PDF and related measures (30, 32, 37-41).

Using the MGH-USC connectome scanner for data acquisition provides several advantages. The high gradient strength (up to 300 mT/m) achieves a higher maximum b-value in shorter gradient durations, which brings our experiments closer to the narrow pulse approximation and improves signal-to-noise ratio (SNR). The MGH-USC connectome scanner also enables acquisition of ex vivo DSI data on a whole, fixed human brain. Previously, ex vivo DSI experiments have been performed predominantly in animal brains (21, 42, 43) since a whole, fixed human brain does not fit in a small-bore animal MRI unit that has conventionally been the only system with sufficiently strong gradients. Ex vivo imaging in itself is of great interest to many research groups because it provides gold-standard data at ultra-high resolution and enables comparison with histology in the same specimen (44-48). Ex vivo DSI can provide very high quality data because it is devoid of motion and enables long scan time such that many samples may be acquired to increase SNR and q-space sampling density.

In this study, we focus on characterizing the effects of q-space truncation and sampling on the PDF for a DSI acquisition. For q-space truncation, we demonstrate the presence of Gibbs ringing in the PDF and investigate different methods to mitigate the ringing. We approximate the PDF extent using the mean displacement distance (MDD) of the tissue and constrain the integration length over the PDF to the MDD to avoid ringing in the PDF from translating into the ODF. For q-space sampling density, we explore how the determined FOV compares to the PDF extent. Using down-sampled data, we demonstrate how the PDF is affected by aliasing and when the aliasing artifacts obscure information in the ODF.

METHODS

Data Acquisition

Ex vivo and in vivo data were acquired with Institutional Review Board (IRB) approval. Written informed consent was provided by healthy control subjects for in vivo imaging and by next-of-kin for ex vivo imaging. All data were acquired using the MGH-USC connectome scanner (3T MAGNETOM CONNECTOM, Siemens Healthcare). The scanner consists of a novel AS302 gradient system capable of producing gradients of up to 300 mT/m at a slew rate of up to 200 T/m/s. A custom-built 64-channel RF receive coil was used for signal acquisition (49). A 2D single-refocused diffusion-weighted SE-EPI sequence was used to acquire three ex vivo datasets in a single whole, human brain specimen and two in vivo datasets from healthy human subjects. The data acquisition parameters are shown in Table 1 and example diffusion-weighted images (DWIs) are shown in Fig. 1.

Table 1.

Data acquisition parameters.

Acquisition	In Vivo		Ex Vivo
Parameters	DSI-11-Gmax225	DSI-11-Gmax40	DSI-11	DSI-15	DSI-17
Δ/δ*(ms)	20.9/12.9	49.2/42.3	29.4/16.7
Gmax(mT/m)	225	40	252
bmax(s/mm2)	10,000	7,000	30,000
qmax/Δq(mm−1)	123.5/24.7	71.1/14.2	178.5/35.7	178.5/25.5	178.5/22.3
q-sample #	515	515	515	1419	2109
TE/TR(ms)	47/5900	106/6900	65/13300
Resolution(mm3)	2 × 2 × 2	2.5 × 2.5 × 2.5	1.5 × 1.5 × 1.5
FOV(mm2)	220 × 220	220 × 200	180 × 138
Slice #	80	52	112
Partial Fourier	6/8	6/8	6/8
GRAPPA R	3	3	2
BW(Hz/pixel)	2526	2470	1985
Echo spacing(ms)	0.53	0.51	0.53
Scan time(min)	55	55	120	330	490

^*Note that δ includes the time from the start of the ramp up to the strongest gradient strength used for the diffusion encoding pulse until the start of the ramp down.

Fig. 1.

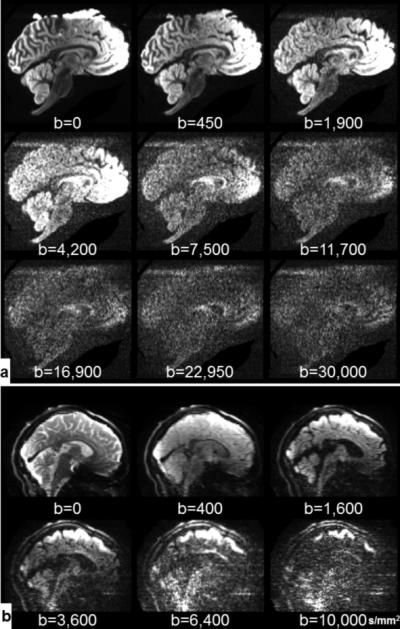
Example diffusion-weighted images at various b-values with left-right diffusion-encoding direction for ex vivo DSI-17 data (a) and in vivo DSI-11-Gmax225 data (b). The images have been individually windowed and leveled for improved visualization.

Ex vivo data was required on one whole, fixed human brain (14-hour post-mortem interval, 7 months fixation) from a 58-year-old woman who died of non-neurological causes. For imaging, the brain specimen was immersed in a non-protonated solution called fomblin (perfluoropolyether, Ausiomont USA Inc., Thorofare, NJ). Three ex vivo datasets were acquired with the same q_max =178.6 mm⁻¹ (equivalent to b_max=30,000 s/mm² given the diffusion time (Δ) and gradient pulse duration (δ) used in the experiments) but different q-space grid sizes (17×17×17, 15×15×15 and 11×11×11). These Cartesian grids in q-space will be referred to herein as DSI-17, DSI-15 and DSI-11. A larger b_max was used for the ex vivo acquisitions to compensate for the slower diffusion rates in ex vivo tissue. The larger ex vivo b_max results in longer TE, TR and Δ values because the diffusion encoding gradients must be longer in duration to achieve the higher b_max. Non-diffusion-weighted (b=0 s/mm²) images were interleaved between every 17 DWIs for the DSI-17 dataset and between every 16 DWIs for DSI-15 and DSI-11 datasets. There were 124, 102, 37 non-diffusion-weighted images in total for DSI-17, DSI-15 and DSI-11, respectively. Positive and negative gradient pairs from the q-space lattice were acquired sequentially.

Two in vivo datasets were acquired in a healthy 23-year-old male volunteer and a 24-year-old female volunteer using the DSI-11 sampling protocol. A high gradient strength of 225 mT/m was used to acquire the dataset DSI-11-Gmax225 with q_max=123.5 mm⁻¹ (equivalent to b_max=10,000 s/mm²). A commonly used gradient strength of 40 mT/m was used to acquire the dataset DSI-11-Gmax40 with q_max=71.1 mm⁻¹ (equivalent to b_max=7,000 s/mm²). Non-diffusion-weighted images were interspersed every 16 DWIs. There were 33 non-diffusion-weighted images in total. For DSI-11-Gmax225, positive and negative gradient pairs from the q-space lattice were acquired sequentially.

Data Processing

For the three ex vivo datasets and DSI-11-Gmax225 in vivo data, DWI opposite polarity pairs were registered one to the other, constraining for the expected translations, dilations and shears and then the “half-way” transform was calculated to correct eddy current distortions (50). Linear transformations calculated from the interspersed non-diffusion-weighted images were used to correct for effects of magnetic field drift and (for the in vivo data) bulk motion between image volumes that was not as easily detected in the DWIs with lower signal-to-noise ratio (SNR). The three ex vivo datasets were co-registered. All transformations were applied in a single step to prevent unnecessary blurring using the linear registration tool provided by the FMRIB Software Library (FSL, www.fmrib.ox.ac.uk/fsl) called “FLIRT” (51). For the DSI-11-Gmax40 in vivo data, an FSL function called “EDDY_CORRECT” was used to correct eddy current distortions, field drift and bulk motion.

Two ROIs in the ex vivo and in vivo datasets were selected. One is a 2×4 voxel region located in the center of the corpus callosum (CC) with known left-right principal diffusion orientation. The other is a 5×9 voxel region located in the centrum semiovale that contains the intersection of three white matter bundles: the CC, the corona radiata (CR) and the superior longitudinal fasciculus (SLF).

DSI reconstruction followed the procedures described in (9) and was modified based on the object “DiffusionSpectrumModel” of the Diffusion Imaging in Python (DIPY, http://nipy.org/dipy/) software (52). Specifically, the q-space data were first placed in a cubic grid. A window function was applied to the q-space data to ensure a smooth attenuation of the signal at the edge of q-space to mitigate Gibbs ringing artifacts. The q-space grid was zero-padded such that the calculated PDF is represented by a sufficiently dense grid. The PDF is computed by performing a 3D Fast Fourier Transform of the zero-padded q-space data and taking the real and non-negative parts of the resulting transform, as the diffusion signal is real, non-negative and symmetric (9, 39, 53). Finally, the ODF is computed as the radial summation of the weighted PDF by the square or higher powers of the displacement distance (9, 54).

The analysis in the following sections was conducted using Python in the IPython interactive computing environment (55) and DIPY software. The raw data for the selected ROIs and the implementation of the analysis that led to each of the figures are available on Github (see https://github.com/mcnablab/DSIQspace).

Extent of the Probability Density Function

To investigate whether the FOV, determined by the q-space sampling density, is sufficiently large, we studied the extent of the PDF. Unlike a physical object with bounded size, a spin-displacement PDF measures the probability of a spin being displaced a specific distance along a specific orientation. Thus, its “extent” is not well defined. We used the mean displacement distance (MDD) given the apparent diffusion coefficient (ADC) measured parallel to the CC as an upper bound of the PDF extent. Assuming Gaussian diffusion, the MDD is equal to the standard deviation of the Gaussian distribution and can be calculated following Einstein's equation (56, 57) as:

$$MDD=\sqrt{6D(\Delta -\frac{\delta }{3})}$$ (1)

where D is the ADC parallel to the CC, Δ is the experimental diffusion time and δ is the duration of one of the diffusion gradient pulses. D was estimated by fitting data from the CC to the diffusion tensor model using the “DTIFIT” function in FSL (51) and taking the mean of the principal eigenvalues (i.e. the ADC along the principal orientation). In order to have a sufficient number of diffusion weighting directions for tensor model fitting, DWIs with b-values up to 3,000 s/mm², 2,000 s/mm² and 1,680 s/mm² were used for this estimation for the ex vivo DSI-17, in vivo DSI-11-Gmax225 and DSI-11-Gmax40 data respectively. For the ex vivo data, ex vivo DSI-17 was used for the estimation of the ADC parallel to the CC since it has more DWIs with b-values under 3,000 s/mm² compared to the other two.

Improving ODF Reconstruction

To investigate how Gibbs ringing in a PDF translates to the subsequently reconstructed ODF and to determine how to mitigate these effects, ODFs were calculated on example voxels from the CC ROI and crossing-fiber ROI of the ex vivo and in vivo DSI-11 data using three different reconstruction pipelines. The pipelines were:

• (1)Unfiltered q-space and integration of the PDF to the full FOV;
• (2)Filtered q-space and integration of the PDF to the full FOV;
• (3)Unfiltered q-space and integration of the PDF to the estimated MDD.

For pipeline (2), three different filters were tested:

• Hanning window: h(n) = 0.5 + 0.5· cos(2πn /W)

• Hamming window: h(n) = 0.54 + 0.46 · cos(2πn /W)

• Blackman window: h(n) = 0.42 + 0.5· cos(2πn /W) + 0.08· cos(4πn /W)

where n is the discrete distance of a q-space point to the origin in the q-space grid and W is the window width. For DSI-11 data, n equals to 0, 1, 2, 3, 4, 5 and W is selected as 10. The roll-off weights equal to 0, 0.08 and 0 at q_max for the Hanning, Hamming and Blackman windows respectively.

We also displayed the weighted PDF by the square of displacement distance, and further examined the effect of weighting the PDF using even higher powers of displacement distance to enhance the contributions of faster diffusing components on the reconstructed ODFs. The orientations determined by the local maximas (peaks) of ODFs were visualized to demonstrate the how the ODF influences tractography. The ODF peaks were detected using the DIPY object “peaks_from_model”. The deterministic tractography was performed using the DIPY object “LocalTracking” with default parameters and the centrum semiovale ROI as a seed mask. The generated streamlines were visualized in TrackVis software (http://trackvis.org). Exclusion masks were drawn to exclude the cingulum and contralateral tracts for ease of interpretation.

Q-space Sampling Density Requirement

To explore the q-space sampling density requirement, we down-sampled the data to simulate various sampling densities and examined the potential aliasing artifacts in the PDF and their effects on the subsequently reconstructed ODF. Specifically, we down-sampled all three ex vivo data and DSI-11-Gmax225 in vivo data by a factor of 2 and 3 in the CC ROI. Down-sampling was performed by preserving every other 2 or 3 q-space points from the center of q-space while replacing the signal in other positions with zeros. Using this down-sampling scheme, the spatial extent over which the PDF is plotted is kept constant and PDF replicas can be therefore visualized. The data at the maximum b-value were preserved in all cases to maintain a constant q_max. The ODF reconstruction was performed on the unfiltered q-space with integration of the weighted PDF by the square of displacement distance to the estimated MDD. When the FOV of the down-sampled data is smaller than the MDD, the integration over the PDF only extends to the FOV.

RESULTS

Extent of the Probability Density Function

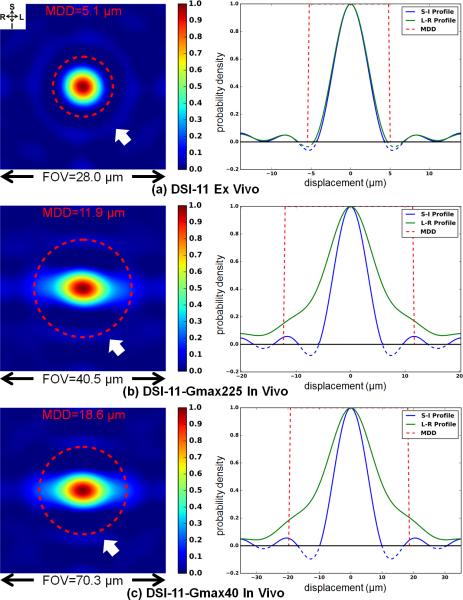
Fig. 2 depicts coronal cross-sections through the center of the 3D spin-displacement PDF of voxels from the CC ROI (left) and the superior-inferior (S-I) and left-right (L-R) profiles through the center of the cross-sections (right). The PDF was computed from raw q-space data without windowing. One typical voxel from DSI-11 ex vivo and in vivo data are depicted. The red dashed circles over the PDF cross-sections (left) and the red dashed rectangles over the PDF profiles (right) represent the approximated extent of PDFs, with their radii being the estimated MDDs. The MDDs are 5.1 μm, 11.9 μm and 18.6 μm for the DSI-11 ex vivo, DSI-11-Gmax225 and DSI-11-Gmax40 in vivo data, respectively, calculated using the estimated ADCs parallel to the CC of 1.8×10⁻⁴ mm²/s, 1.4×10⁻³ mm²/s and 1.6×10⁻³ mm²/s. As a reference, assuming a free water diffusion rate of 2.51×10⁻³ mm²/s (58), the MDDs are 18.9 μm, 15.8 μm and 23.0 μm with the diffusion times and gradient durations employed in the ex vivo and in vivo experiments. These approximated extents of the PDF are visually consistent with the spin displacements observed in the depicted PDF computed by Fourier transform. For the ex vivo data (Fig. 2a), the MDD includes all of the spin displacements along both the principal orientation (L-R) and its perpendicular orientation (S-I). For the in vivo data (Fig. 2b and c), the estimated MDD includes most of the spin displacements along the principal orientation (L-R). Since the diffusion rates and the displacement distances are much smaller in the orientation perpendicular to the principal orientation (S-I), the estimated MDD is larger than the PDF extents and even includes the ringing.

Fig. 2.

Coronal cross-sections through the center of the 3D spin-displacement PDF (left) and the superior-inferior (S-I) and left-right (L-R) profiles through the center of the cross-section (right) for one voxel from the center corpus callosum that has left-right principal orientation for the ex vivo DSI-11 (a), in vivo DSI-11-Gmax225 (b) and in vivo DSI-11-Gmax40 (c) data. Ringing is observed in the PDFs (left, white arrows; right, blue and green curves). The different q-space sampling densities correspond to different PDF field-of-views (FOV). The red dashed circles represent the mean displacement distance (MDD) based on Einstein's equation.

Fig. 2 depicts that the FOVs are all sufficiently large to hold the entire PDFs. For DSI-11 ex vivo, DSI-11-Gmax225 and DSI-11-Gmax40 in vivo data, the q-space sampling densities correspond to FOVs (=1/Δq) of 28.0 μm, 40.5 μm and 70.3μm respectively, which are 2.7, 1.7 and 1.9 times of the approximated PDF extent (2×MDD). The FOVs for the ex vivo data are relatively large compared to the short displacement distances in ex vivo tissue. Therefore, the majority of the area within the FOV contains Gibbs ringing with only a small fraction of the FOV containing PDF signals.

Improving ODF Reconstruction

In Fig. 2, although negative values in the PDFs were clipped to 0 in an attempt to remove Gibbs ringing, the positive values of the ringing still remain for both ex vivo and in vivo data (Fig. 2 white arrows). The S-I profiles (blue curves) and L-R profiles (green curves) through the center of the cross-sections demonstrate the ringing more clearly (Fig. 2 right column). The ringing extends throughout the entire FOV. The magnitude of the ringing is relatively small compared to the PDF peak. The amplitude of the first and second side lobe of S-I profiles is about 5% of the peak.

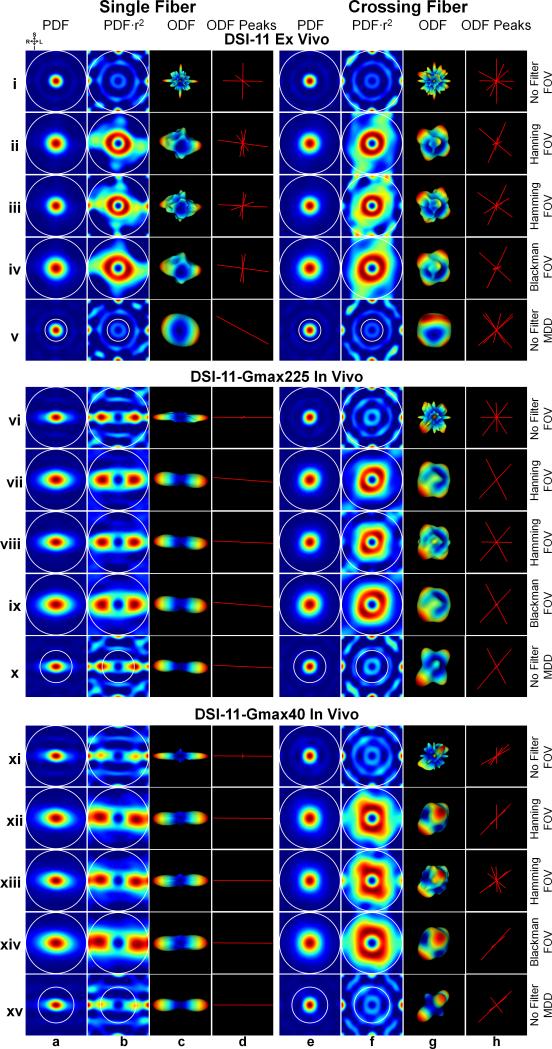
Fig. 3 demonstrates the effects of applying a filter to q-space data and modifying the distance over which the PDF is integrated (white circles in Fig. 3) on the ODF.

Fig. 3.

Three different ODF reconstruction pipelines for DSI-11 ex vivo (rows i to v), DSI-11-Gmax225 in vivo (rows vi to x) and DSI-11-Gmax40 in vivo data (rows xi to xv). The three pipelines are (1) Unfiltered q-space and integration of the PDF to the full the field-of-view (FOV) (rows i, vi and xi); (2) Filtered q-space and integration of the PDF to the full FOV (rows ii to iv, vii to ix and xii to xiv); (3) Unfiltered q-space and integration of the PDF to the estimated mean displacement distance (MDD) (rows v, x and xv). The single-fiber voxel is from the center corpus callosum. The crossing-fiber voxel is from centrum semiovale (as shown in Fig. 5e, f and g dashed white boxes). Coronal cross-sections through the center of the 3D spin-displacement PDFs are shown in columns a and e. These same PDFs weighted by the square of the displacement distance are shown in columns b and f. The ODFs that correspond to the PDFs in columns b and f are shown in columns c and g. The local maximas (peaks) detected from the ODFs are shown in columns d and h. The white circles represent the integration distance. The color map for both the PDFs and ODFs represents low to high values as blue to red.

(1) Unfiltered q-space and integration of the PDF to the full FOV

In Fig. 3 rows i, vi and xi, PDFs that were computed from the raw (unfiltered) q-space signal suffer from Gibbs ringing for all ex vivo and in vivo data. The common practice of weighting the PDF by the square of diffusion distance (9) further enhances ringing and noise at the edges of the PDF (Fig. 3, rows i, vi and xi, columns b and f). The enhanced ringing and noise in the PDFs translates into artifacts in the reconstructed ODF, if these parts of the PDF are included in the PDF integration (i.e. if the integration is performed across the full FOV). The resultant ODFs are noisy (Fig. 3, rows i, vi and xi, columns c and g) and could erroneously indicate crossing fibers for the single fiber (Fig. 3, rows i, vi and xi, column d) and orientation information is lost for the crossing fiber (Fig. 3, rows i, vi and xi, column h).

(2) Filtered q-space and integration of the PDF to the full FOV

In Fig. 3, rows ii to iv, vii to ix and xii to xiv, the common practice of applying a window to the q-space signal substantially suppresses the ringing and the resultant PDFs are smoother for all the ex vivo and in vivo data. However, if the PDFs are weighted by the displacement distance, the remaining Gibbs ringing that has not been completely suppressed by the window are again enhanced (Fig. 3, rows ii to iv, vii to ix and xii to xiv, columns b and f). Integrating the PDF from filtered q-space to the full FOV still includes these enhanced ringing artifacts and therefore the resultant ODFs become slightly smoother but still obscure the orientation information, with the exception for the single fiber in the two in vivo data (Fig. 3, rows vii to ix and xii to xiv, column d).

(3) Unfiltered q-space and integration of the PDF to the estimated MDD

In Fig. 3, rows v, x and xv, constraining the integration length over the PDF to the estimated MDD avoids most of the ringing and noise at the edge of the PDF while covering the majority of the spin displacements. Therefore, the resultant ODFs clearly indicate the left-right principal diffusion orientation for the single fiber (Fig. 3, rows v, x and xv, column d) and the expected orientations for the intra-voxel crossing fibers (Fig. 3, rows v, x, and xv, column h). For the in vivo data, the ODF anisotropy is the highest since the q-space signal is not low-pass filtered using a window function (Fig. 3, rows x and xv, columns g and d). For the ex vivo data, the ODF is much cleaner without erroneous peaks (Fig. 3, row v, columns g and h).

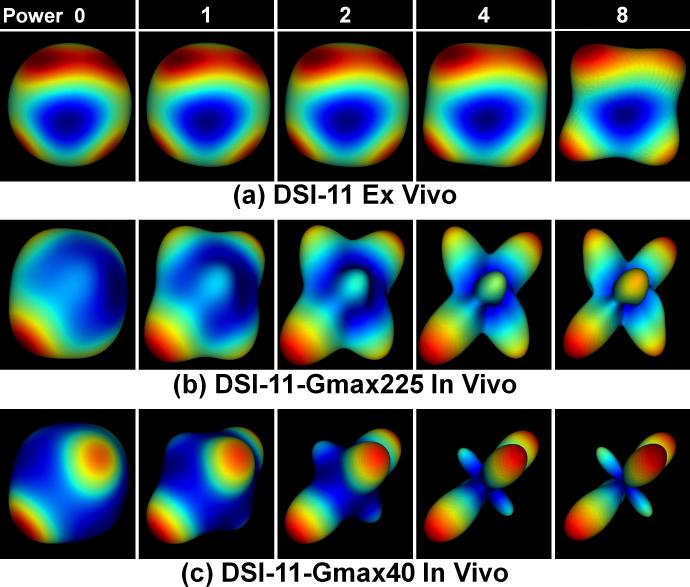
Fig. 4 demonstrates the effects of weighting the PDF by different powers, i.e. 0, 1, 2, 4 and 8, of the displacement distance. Using higher powers of the displacement distance enhances the contributions of faster diffusing components and thereby sharpens the ODFs. This sharpening is only possible after limiting the integration length to the estimated MDD, which excludes the ringing artifacts and noise at the edges of the PDF. Otherwise, the ringing artifacts and noise would be significantly enhanced. Since the in vivo data has higher anisotropy, the commonly used power of 2 of displacement distance is sufficient for the ODF reconstruction. For the ex vivo data, a higher power than 2 is preferred.

Fig. 4.

An example of the effects of weighting the PDF by different powers, i.e. 0, 1, 2, 4 and 8, of displacement distance on the reconstructed ODF. The crossing-fiber voxel is from centrum semiovale (as shown in Fig. 5e, f and g dashed white boxes). The color map represents low values (blue) to high values (red) in the ODF.

ODF results from the centrum semiovale using unfiltered q-space signal and a weighted PDF integration to the MDD are shown in Fig. 5e, f and g. The PDF is weighted by the displacement distance to the power of 8 for the ex vivo data and to the power of 2 for the two in vivo data. The reconstructed ODFs depict sufficient anisotropy to resolve the expected intra-voxel crossing fibers in the centrum semiovale, i.e. the CC, CR and SLF.

Fig. 5.

Reconstructed tensors and ODFs from centrum semiovale ROI (a) containing the corpus callosum (CC), the corona radiata (CR) and the superior longitudinal fasciculus (SLF) for the ex vivo DSI-11 (b and e), in vivo DSI-11-Gmax225 (c and f) and in vivo DSI-11-Gmax40 data (d and g). The primary eigenvectors of tensors were plotted over the fraction anisotropy maps (b to d). The PDFs were weighted by the displacement distance to the power of 8 for the ex vivo data (e) and to the power of 2 for the in vivo data (f and g) for the ODF reconstruction, which integrates the weighted PDFs to the estimated mean diffusion distance. The white dashed boxes in (d and e) indicate the crossing-fiber voxels presented in Fig. 3 and 4. The ODF color map represents low values as blue to high values as red in ODF.

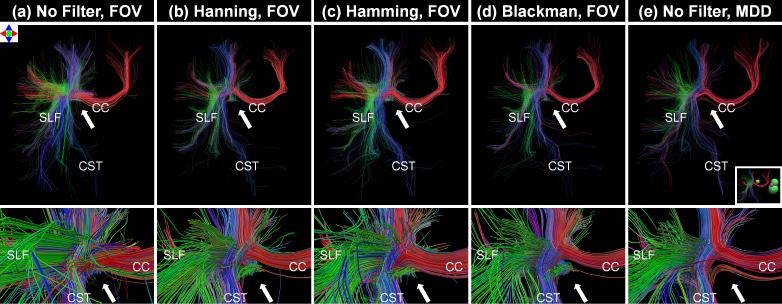
Fig. 6. compares tractography results from ODFs created using the three reconstruction pipelines. Visual analysis of the tractography results demonstrates that the filters greatly decrease the number of false positive tracts. The method of constraining the PDF integration to the MDD produces streamlines that appear to have fewer false positive streamline trajectories than the alternative methods. Additionally, multiple “dead-end” truncated fiber tracts are observed at the site where the CC, SLF and corticospinal tract (CST) cross (white arrows) in all of the techniques except the technique of constraining the PDF integration distance to the MDD.

Fig. 6.

Deterministic tractography results shown from an anterior view (top row) and anterior zoomed view (bottom row) for the three ODF processing pipelines from the DSI-11-Gmax40 in vivo data. The three pipelines are (1) Unfiltered q-space and integration of the PDF to the full the field-of-view (FOV) (column a); (2) Filtered q-space and integration of the PDF to the full FOV (columns b to d); (3) Unfiltered q-space and integration of the PDF to the estimated mean displacement distance (MDD) (column e). The tractography results were generated using the centrum semiovale ROIs shown in Fig. 5 as a seed mask. The inset figure shows four spherical exclusion masks placed to eliminate cingulum and contralateral tracts for ease of interpretation. Streamlines are color-coded according to the direction of their middle segment (red: medial-lateral; green: anterior-posterior; blue: superior-inferior).

Q-Space Sampling Density Requirement

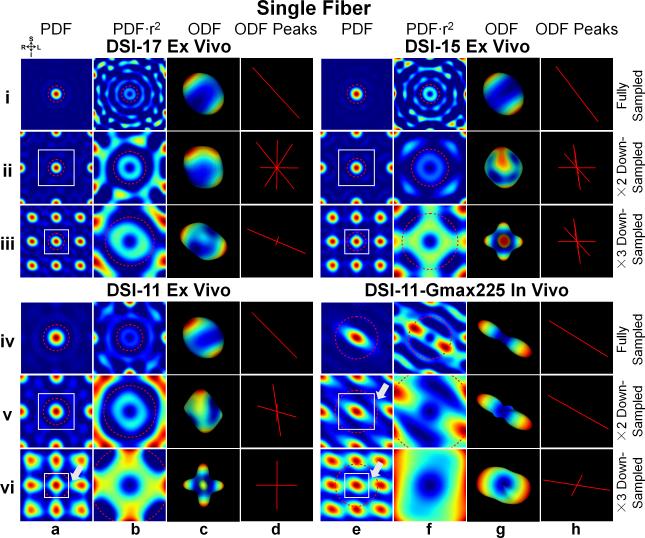
Fig. 7 demonstrates the effects of different q-space sampling densities on the PDF, ODF and ODF peaks. The down-sampling operation decreases the FOV in the PDF domain (Fig. 7, columns a and e, white boxes). For DSI-17 and DSI-15 ex vivo data, even with the highest down-sampling rate of 3, the reduced FOVs of size 14.9 μm and 13.1 μm respectively, are still larger than twice the MDD 10.2 μm (comparing white boxes and red dashed circles in Fig. 7, row iii, columns a and e). For DSI-11 ex vivo data, the FOV for 2× down-sampling is also larger than twice the MDD (14.0 μm versus 10.4 μm). In these cases, the PDF (set by the approximated extent of MDD) and its replicas do not overlap. Unfortunately, the orientation information in the ODF is still obscured because the ringing from the first PDF replicas overlaps with the desired PDF. When the FOV is larger, the artifacts are less severe since the portion of ringing that enters the desired PDF has lower magnitude (comparing DSI-17 to DSI-15 and DSI-11 ex vivo). In the most severe cases, the artifacts create a false representation of fibers along the three orthogonal q-space axes in the resulting ODF (Fig. 7, row iii, columns g and h).

Fig. 7.

The PDF, weighted PDF, ODF and ODF peak for the fully sampled (rows i and iv) and down-sampled (rows ii and v by a factor of 2, rows iii and vi by a factor of 3) q-space signal from a voxel in the corpus callosum of the three ex vivo (DSI-11, DSI-15 and DSI-17) and one in vivo (DSI-11-Gmax225) datasets. Coronal cross-sections through the center of the 3D spin-displacement PDFs are shown in columns a and e. The spatial extent over which the PDF was plotted is kept constant across different down-sampling schemes. The portion of these same PDFs in the field-of-view (FOV, represented by white boxes) is weighted by the square of the displacement distance and shown in columns b and f. All ODFs were reconstructed using unfiltered q-space signal and integrating the PDF to either the estimated mean displacement distance (MDD, red dashed circles) or the new FOV after down-sampling if it is smaller than MDD (i.e. row vi, column b; rows v and vi, column f). The ODFs that correspond to the PDFs in columns b and f are shown in columns c and g. White arrows indicate the regions of aliasing artifacts in the PDF. The color map represents low values (blue) to high values (red) in both the PDF and ODF.

DSI-11-Gmax225 in vivo data has a higher diffusion rate and larger displacement, therefore even for the lowest down-sampling rate of 2, the FOV becomes smaller than the PDF extent (20.3 μm versus 23.8μm). The 3× down-sampled DSI-11 ex vivo data also has a smaller FOV than the PDF extent (9.3 μm versus 10.2 μm). In these cases, aliasing artifacts can be observed in the PDF (highlighted by the white arrows in Fig. 7). The aliasing artifacts in the PDF obscure the orientation in the ODFs (Fig. 7, rows v and vi, columns g and h) and create three artifactual orthogonal orientations in the worst case (Fig. 7, row vi, columns c and d).

DISCUSSION

Extent of the Probability Density Function

A good approximation of the PDF extent is critical for determining the q-space sampling rate and guiding the ODF reconstruction. The Fourier relationship between the attenuated echo signal in q-space and the spin-displacement PDF is strictly valid only when the narrow pulse assumption (δ<<Δ) is met. In practice, it is difficult to generate δ<<Δ on a clinical scanner with 40-60 mT/m gradient strength. As a consequence, the diffusion distance is usually slightly underestimated (9, 59, 60). It is for this reason that the effective diffusion time used to estimate the MDD takes the reduced value of Δ-δ/3 (13). The ADC parallel to the CC is a useful upper bound MDD estimate for all voxels. This estimated MDD includes about 70% of the spin displacements (34) parallel to the fiber orientation and all of the spin displacements perpendicular to the fiber orientation. It is more accurate to use a voxel-specific and direction-dependent estimate of the ADC to constrain the PDF integration length. In practice, this could be incorporated into a DSI reconstruction software package. One practical issue for estimating the ADC using DSI data is that the DSI data often includes very few DWIs to be in the Gaussian regime and among these DWIs an even more limited number of unique diffusion encoding directions. Ideally, only DWIs in the Gaussian regime should be included in a tensor fit. If only DSI data is available then the DWIs used for the MDD estimate should include measurements made with b-values under a threshold to ensure a sufficient number of unique diffusion encoding directions and sufficient SNR. We fit tensors using subsets of the two in vivo DSI-11 data with different b-value thresholds and found that a cut-off around 1500-2000 s/mm² provided estimates of the principal eigenvalue along a white matter tract that were consistent with literature (1.2-1.7×10⁻³ mm²/s (61)). The optimal cut-off point is not clear but this approach appears to provide reasonable compromise between unique diffusion encoding directions, SNR and limiting non-Gaussian effects.

Improving ODF Reconstruction

Truncating q-space at a non-zero signal intensity contaminates the PDF by convolving the true PDF with a point spread function (PSF) after the Fourier transform. The main lobe of the PSF blurs the PDF, determining the PDF resolution (1/2q_max) and rendering the ODF less sharp. Canales-Rodríguez et al. deblurred the measured PDF using a model free deconvolution method to sharpen the PDF and ODF (35). The side lobes of the PSF cause the Gibbs ringing in the PDF, which translates into severe artifacts in the ODF that hamper the accurate identification of orientational information in a voxel and lead to tractography errors. We have demonstrated that the Gibbs ringing in the PDF is the major source of ODF artifacts.

The most straightforward method to resolve Gibbs ringing is to acquire a larger q-space coverage such that the diffusion signal decays nearly to zero at the q-space edge, which is a common k-space practice. For our DSI-17 ex vivo, DSI-11-Gmax225 and DSI-11-Gmax40 in vivo data, the average signals at the b_max of voxels from the center CC are about 32%, 5% and 11% of the non-diffusion-weighted signals parallel to the CC and 42%, 32% and 40% of the non-diffusion-weighted signals perpendicular to the CC. One major consideration for increasing q-space coverage is the increase in scan time of the already lengthy DSI scan and the impact of noise from the very low SNR measurements at even higher q-values. Additional high q-value measurements are not effective if the signals at the q-space edge reflect only the rectified noise floor (65).

Another approach to minimize Gibbs ringing is to multiply the q-space signal by a window function (apodization function). This method is also commonly used on k-space data (15, 66, 67) although for three- and higher-dimensional NMR experiments, alternatives to the Fourier transform such as the filter diagonalization and maximum entropy methods are used to generate spectra without ringing (68). However, as shown in Fig. 3, the ringing is not fully suppressed after windowing, despite the fact that the adopted Hanning and Blackman filters attenuate the q-space signal to zero at q_max. The ODFs reconstructed after q-space apodization reflect this and are still noisy because the common practice of weighting the PDF by the square of the displacement distance for ODF sharpening re-amplifies any remaining ringing. Another drawback of the q-space apodization approach is the loss of high frequency information that contributes details to the PDF and ODF and the effectively wasted scan time spent acquiring these high q-value data.

Extrapolating the q-space data to higher q-values is another approach to bring the signal smoothly down to zero at the q-space edge (31, 32, 37, 38). This method is more computationally intensive than a normal DSI reconstruction. Further, the extrapolation requires fitting the data to a model, while the model-free nature of DSI is often considered to be favorable.

In this study, we demonstrated that limiting the integration length over the PDF to the estimated MDD of the tissue is a useful way to avoid Gibbs ringing from translating into artifacts in the ODF. Specifically, assuming an N×N×N (N is an odd integer) q-space grid zero-padded to N₀×N₀×N₀ (N₀ is an odd integer) grid, the end point on the discrete grid for the PDF integration is calculated as:

$$r_{end}=\frac{MDD}{FOV}\cdot (N_0-1)$$ (2)

Using Eq. 1 and the relationship between b-value and q-value, this equation can be simplified to:

$$r_{end}=\frac{\sqrt{6D{b}_{\max }}}{\pi }\cdot \frac{N_0-1}{N-1}$$ (3)

where D is the ADC parallel to the CC. Integrating the PDF only to the MDD includes the majority of the PDF signal while excluding the ringing and noise at the edge within the FOV. As a consequence, as shown in Fig. 5, it is possible to weight the PDF by the square (or even higher powers) of the displacement distance to enhance the displacements of the fastest diffusing components, from which the orientation contrast is derived, without amplifying the ringing at the edge of the FOV. The reconstructed ODFs are sharper and cleaner. Enhancing the features of the fast diffusing components and avoiding q-space filtering that blurs the PDF and ODF is particularly important in ex vivo tissue that has lower diffusion rates and lower anisotropy. This is normally achieved by starting the PDF integration at a distance from the PDF center (by default a discrete distance of 2.1 in a 17×17×17 q-space grid for DSI-11).

Our study provides clear evidence regarding the optimal selection of the integration length in the DSI reconstruction to mitigate the effects of Gibbs ringing. We highlight the importance of adapting the integration length accordingly for ex vivo and in vivo tissues and for different tissue types to ensure accurate DSI reconstruction. For ex vivo data, the optimal integration length is ~30% of the integration length used for in vivo tissues. We have also demonstrated, for the first time, why the default practice of integrating the PDF to a discrete distance of 6.1 (0.75×FOV) for a standard in vivo human DSI acquisition (i.e., DSI-11 zero-padded to a 17×17×17 q-space grid with a b-value of 6000-8000 s/mm²) is effective. This default practice is adopted in software packages such as DIPY and DSI Studio (http://dsi-studio.labsolver.org). Previously, Yeh et al. recommended an integration length of 1 to 1.3 times of the MDD of free water (computed with diffusion rate of 2.51×10⁻³ mm²/s) (34, 36). This recommendation is approximately in agreement with our in vivo results but is invalid for ex vivo brain data. Paquette et al. recommended PDF integration starting at 0.4×FOV and ending between 0.7×FOV and the full FOV depending on the SNR. Paquette's results are based on synthetic data and evaluated based on tractography accuracy (33). Our study builds on this prior work by providing empirical data and demonstrating the specific ways in which artifacts propagate through q-space to the PDF and ODF.

Q-Space Sampling Density Requirement

Discrete sampling in q-space leads to replicas of the spin-displacement PDF. The minimum q-space sampling density required to prevent overlapping PDFs can be determined by taking into account the MDD. Specifically, the Shannon-Nyquist sampling theorem requires the FOV to be at least as large as twice the MDD given in Eq. 1:

$$\frac{1}{\Delta q}\ge 2\cdot MDD$$ (4)

This equation can be also described in terms of b-value using the relationship between q-value and b-value as:

$$\frac{N-1}{2}\ge \frac{\sqrt{6D{b}_{\max }}}{\pi }$$ (5)

This equation prescribes a requirement in terms of the q-space grid size N (N is an odd integer) and the maximum b-value that needs to be considered in DSI acquisition and analysis. For hybrid diffusion imaging (32, 69) in which diffusion data acquired on multi-shell q-space can be gridded to a Cartesian lattice for DSI analysis, and generalized q-sampling imaging (34), a variant of DSI that mathematically combines the Fourier transform and PDF integration, the q-space sampling density of the data has to meet the requirement specified by Eq. 4 and Eq. 5.

Given the maximum b-values in our experiments (30,000 s/mm² for ex vivo data, 10,000 s/mm² for DSI-11-Gmax225 in vivo and 7,000 s/mm² for DSI-11-Gmax40 in vivo data) and the estimated mean diffusivity in the center of the corpus callosum, the required q-space grid sizes are at least 5×5×5 for ex vivo and 9×9×9 for in vivo. Considering the side lobes of the potential Gibbs ringing that may extend beyond the MDD, a slightly larger q-space grid is preferred. Therefore, the commonly used DSI-11 q-space grid (11×11×11) is appropriate for a b_max under 10,000 s/mm² in an in vivo DSI experiment. Due to SNR constraints, in vivo DSI is rarely used with a b-value greater than 10,000 s/mm² and therefore insufficient sampling density is unlikely to be the cause of aliasing artifacts for in vivo DSI experiments. These q-grid size requirements are in agreement with prior studies that looked at the optimal b_max for a fixed 11×11×11 grid size (22).

For ex vivo tissue that has a slower diffusion rate and a shorter mean displacement, the q-space sampling density requirement is much lower theoretically. However, a decrease in q-space grid size also results in a decrease in angular resolution which is a critical issue. For Cartesian q-space grid constrained in a sphere of sizes from 1×1×1 to 17×17×17, there are 1, 6, 26, 90, 134, 258, 410, 494 and 690 q-space samples on the outer shell. Acquiring less data also results in lower SNR of the combined DSI dataset and therefore potentially influences the quality of DSI results even when the sampling density requirements are satisfied. Therefore, the DSI-11 q-space grid is a suitable trade-off of q-space sampling density, SNR and angular resolution in both in vivo and ex vivo DSI experiments.

In summary, this study analyzes DSI data with a higher q_max and q-space grid size than has previously been presented in whole, human brains. We used the unique ex vivo and in vivo DSI data to study the effects of q-space truncation and sampling on the PDF and ODF, in an attempt to provide guidelines for the optimal integration length over the PDF that minimizes Gibbs ringing artifacts (Eq. 2 and Eq. 3) and the required q-space sampling density to avoid aliasing in the PDF (Eq. 4 and Eq. 5). Equation 3 provides a formalism for calculating a suitable integration length given a q-space grid size, zero-padded q-space grid size and the maximum b-value. Equation 5 provides a formalism for calculating an upper bound for the maximum b-value for a given q-space grid size or a lower bound for the q-space grid size given a maximum b-value. For in vivo acquisitions acquired with the most commonly used 11×11×11 grid size, Equations 2-5 indicate that a maximum b-value under 10,000 s/mm² should provide a PDF that is free of aliasing artifacts and an integration length of around 5 should avoid most Gibbs ringing if the unfiltered q-space data is zero-padded to a 17×17×17 grid. The effects of different amounts of q-space truncation on the PDF and ODF is another important consideration that was not explored in the current study. Further, a full optimization of DSI requires a more comprehensive comparison and evaluation of q_max, q-space grid size and q-space filtering parameters. Testing the efficacy of voxel-specific and direction-dependent estimates of MDD to limit the integration length of the PDF would also offer potential further improvements to ODF reconstruction.

CONCLUSION

Gibbs ringing was observed in the PDF of both ex vivo and in vivo data, resulting in obscured orientations in the ODFs. Using unfiltered q-space data but constraining the integration length over the PDF to around the MDD of the experimental tissue was demonstrated to be a preferred way to reconstruct more accurate and sharper ODFs. For in vivo DSI, aliasing of the PDF is unlikely to occur for the commonly used DSI-11 acquisition with a maximum b-value under 10,000 s/mm². For ex vivo DSI, the sampling density requirement is significantly lower since ex vivo tissue has a lower diffusion rate and shorter MDD. However, when taking into account angular resolution and SNR considerations, the DSI-11 acquisition is well-suited to both ex vivo and in vivo DSI experiments. In conclusion, the data and analysis presented here clarify guidelines for acquiring and reconstructing DSI data such that Gibbs ringing is minimized and subsequent fiber tracking is as accurate as possible.