Abstract
Cells accomplish the process of fate decisions and form terminal lineages through a series of binary choices in which cells switch stable states from one branch to another as the interacting strengths of regulatory factors continuously vary. Various combinatorial effects may occur because almost all regulatory processes are managed in a combinatorial fashion. Combinatorial regulation is crucial for cell fate decisions because it may effectively integrate many different signaling pathways to meet the higher regulation demand during cell development. However, whether the contribution of combinatorial regulation to the state transition is better than that of a single one and if so, what the optimal combination strategy is, seem to be significant issue from the point of view of both biology and mathematics. Using the approaches of combinatorial perturbations and bifurcation analysis, we provide a general framework for the quantitative analysis of synergism in molecular networks. Different from the known methods, the bifurcation-based approach depends only on stable state responses to stimuli because the state transition induced by combinatorial perturbations occurs between stable states. More importantly, an optimal combinatorial perturbation strategy can be determined by investigating the relationship between the bifurcation curve of a synergistic perturbation pair and the level set of a specific objective function. The approach is applied to two models, i.e., a theoretical multistable decision model and a biologically realistic CREB model, to show its validity, although the approach holds for a general class of biological systems.
Keywords: Cell fate decisions, Combinatorial perturbations, Bifurcation
Introduction
Cell fate decisions are binary choices typically depicted by bistable systems in which the state transition may occur due to various perturbations. Binary choices play significant roles in almost all processes of cell development, especially in the progression of stem and progenitor cells towards various specialized cells in multicellular organisms [1–3]. State transition such as the transitions between disease and disease-free states also occur in the context of health care [4, 5]. In mathematical models, critical thresholds for such transitions correspond to bifurcations [6]. Typical bifurcations are those that mark the transition from one stable equilibrium to another one through a saddle-node or a pitchfork bifurcation [7] or the transition from an oscillatory attractor to a stable equilibrium through a Hopf bifurcation [8].
When bifurcations are considered, some parameters that can be varied or perturbed easily bear the potential to act as bifurcation parameters. If a chosen parameter in a mathematical model is perturbed and all other parameters are kept unchanged, the model becomes a single parameter perturbation system. Increasing the perturbation from zero to a critical value at which a bifurcation occurs induces a transition between two discrete, alternative stable states [9]. The critical value can be regarded as the perturbation threshold corresponding to the bifurcation parameter. Similarly, combinatorial perturbations of two or more parameters can also lead to such transitions [10, 11]. For instance, in the p42 MAPK/Cdc2 system in oocytes, the active signaling protein can switch its stable expression from a low to a high state as a response to concurrent regulations of an external stimulus and feedback strength [11]. From the point of view both mathematics and biology, it is crucial to quantitatively detect synergism, i.e., the effect of two or more perturbations given in combination is greater than what is expected from their individual perturbations.
That determination of synergism and its application to the quantitative evaluation of combinatorial perturbations is the aim of this paper. Some experiments have shown that synergism is not merely a property of combinatorial perturbations. It also depends on the quantities of each perturbation in synergistic combinations. The determination of synergism is crucial to understand combinatorial control in molecular networks, e.g., how cells respond optimally to two or more mixed signals [12–14], how to optimize the combinatorial therapies in pharmaceutical development [15–17], and how to control the processes of fate decisions [18]. Prior works on synergism have mainly focused on combination drug therapies. For example, Nelander et al. presented a method called combinatorial perturbation-based interaction analysis, and constructed a perturbed cellular network model by which a dual drug perturbation experiment involving six inhibitors in MCF7 breast cancer cells was designed [19]. The model prediction of system responses and experimental observations have a good correlation. A mathematical model of apoptosis has been built to provide insight into synergistic drug pairs in prostate cancer [20].
Synergism has been quantified by using the Chou-Talalay method [21–23], Loewe combination index [24, 25], Bliss independence [26, 27], and the degrees of non-linear blending and additive synergism [28]. All these methods depend heavily on transient state responses to stimuli, and therefore also depend absolutely on the initial conditions. However, from the perspective of state transitions, combinatorial effects can be quantified by the effects of perturbations in combination on transitions between stable expression states [10]. For instance, the state transition in pancreatic cancer with combination drug treatment. Both simulations based on mathematical models and experimental data show that the combination of TGF β silencing and immune activation treatment, or combinations of EGFR silencing and TGF β sequestration treatments are more conducive for promoting state transition of cancer cells [4]. Because such transitions are associated with the occurrence of different kinds of bifurcation, we propose a bifurcation-based approach to detect synergism induced by combinatorial perturbations imposed on molecular components. The approach is more computationally efficient because all transient dynamics can be neglected.
To address the issue of synergism and optimal combinatorial perturbation strategies in molecular networks, we provide a new framework by integrating combinatorial perturbations and bifurcation analysis. Different from the known methods, the approach does not involve any transient state responses to stimuli. More importantly, optimal combinatorial perturbation strategies can be easily obtained. The main ideas are illustrated by analyzing two models, i.e., a theoretical multistable decision model and a biologically realistic CREB (cAMP-response element binding) model, although the approach holds for a general class of biological systems. The approach may provide insight into both the rational design of combination drug therapies and the identification of combinatorial control strategies in cell fate decisions.
Methods
Quantification of synergism by integrating combinatorial perturbations and bifurcation analysis
Let the dynamical system of n elements with interactions take the form:
| 1 |
where , and the state variable xj(t) denotes the concentration of a molecular component at time t. The parameter vector represents the intensity of interactions existing among the components that may involve positive or negative regulations, activation or deactivation rates, dissociation constants, degeneration rates, and basal production rates, etc. The vector function f(x,p) determined by the logical relationships among the components is smooth with respect to both x and p.
The main ideas are illustrated by supposing that system (1) stays at a stable state, e.g., a stable equilibrium or oscillation, when the parameters are at their basal values, i.e., p = pb. Without loss of generality, we assume that only two parameters are concurrently perturbed, i.e., m=2 and system (1) stays at a stable equilibrium when (p1,p2)T=(p1b,p2b)T although the approach holds for other cases, e.g., oscillations. Keep p2 = p2b fixed and continuously change p1 from p1b until a bifurcation occurs. When the bifurcation point is crossed, system (1) jumps suddenly from a lower branch xl to a higher one xh (Fig. 1a), with two branches corresponding to two different cell fates. Mathematically, such a process is equivalent to transforming system (1) into the following perturbed one by introducing a perturbation Δp1 to p1,
| 2 |
where Δp1 can be positive or negative, depending on the sign of with the bifurcation value .
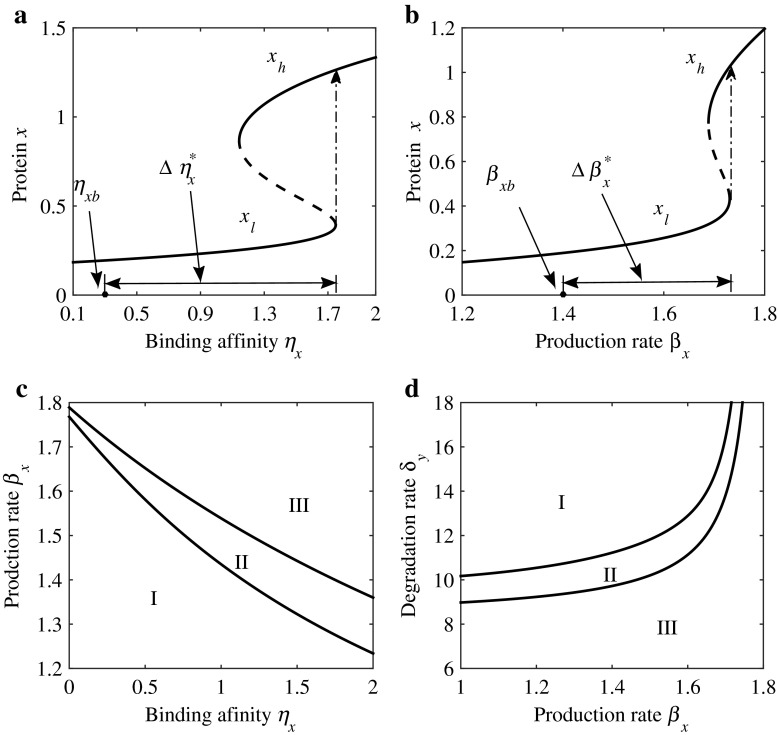
Fig. 1.
Bistable switch decision network composed of two interacting proteins denoted by x and y, respectively. a The system undergoes saddle-node bifurcation by increasing the ratio of binding affinities η x, where Δη x∗ is the required critical perturbation from the basal value η xb to the saddle-node bifurcation point η xb+Δη x to achieve state transition from the low steady stable states x l to the high steady stable states x h. Solid and dashed curves denote stable and unstable states of protein x, respectively. b A similar state transition occurs by increasing the basal production rate β x from the basal value β xb to the saddle-node bifurcation point β xb+Δβ x. c The two-parameter bifurcation in the parameter space (η x, β x) shows the underlying relationship between η x and β x for inducing the state transition through a saddle-node bifurcation (the black solid curves). The system has only one steady stable state x l or x h when parameters η x, β x are located in the region I or I I I. Whereas, the system has two steady stable states x l and x h when parameters η x, β x are located in the region I I. d The state transition can also be induced by combinatorially perturbing the basal production rate β x and the basal degradation rate δ y
For the parameter p2, a similar argument is made, which brings system (1) to the following form:
| 3 |
The coordination of multiple perturbations can be written in a system with combinatorial perturbation as:
| 4 |
or in its normalized form:
| 5 |
where μi≥0 and , whose values are determined by (2) and (3), respectively.
Set and . It is obvious that p1C and p2C denote the fractional contributions simultaneously made by the parameters p1 and p2 to the occurrence of the bifurcation in system (5). Note that due to the same perturbation direction. By the definitions of the Chou-Talalay combination index and the Loewe combination index, the detection of synergism with the parameters p1 and p2 depends on the value of
| 6 |
Parameters p1 and p2 are regarded as synergistic, antagonistic, or additive when CI<1, CI>1, or CI=1, respectively. The value 1/μi denotes the dose-reduction index of parameter pi(i=1,2) [21, 23].
Now, the combinatorial control of cell fate decisions is finally transformed into a problem of a two-parameter bifurcation of system (5). In addition, detection of synergism depends on the location of the two-parameter bifurcation curve with and (or equivalently μ1 and μ2) as control parameters, which can be obtained by using standard bifurcation algorithms. If the bifurcation curve lies below the isobole representing additive combinatorial effects, i.e., μ1 + μ2=1, then the perturbation pairs in any point locating on the bifurcation curve act synergistically (Fig. 1a). Therefore, the bifurcation-based approach provides a graphical method for deducing synergism.
Generality of the perturbation transformation
In fact, the perturbation form of system (2), i.e., pi↦ pib+Δpi, is generally used and can be easily realized. For instance, in combination drug therapies, adding an activator denoted by to a protein may affect ηx by the form
| 7 |
where is the concentration of the activator and is the Michaelis-Menten constant. The quantity denotes the intensity of influence by the activator on [20, 29, 30]. Note that (7) can be rewritten as
| 8 |
so that it can be simplified into the form in (2) if we set .
On the other hand, when an inhibitor I is introduced to weaken a certain regulatory mechanism pi, we can use
| 9 |
to describe its influence [20, 29]. Similarly, (9) can be rewritten as
| 10 |
with
| 11 |
Optimal combinatorial perturbation strategies
After detecting synergism by combinatorial perturbation of specific parameter pairs, we know that any perturbation pair located on the two-parameter bifurcation curve act synergistically. In addition, an optimal combinatorial control strategy in all synergistic pairs needs to be determined. In fact, besides location on the bifurcation curve, the optimal combinatorial strategy depends also on the objective function denoted by g(μ1,μ2,c1,c2), which may have different forms based on the choices of objective, involving the least cost, the least side-effects, dose and toxicity reduction, drug resistance minimization and so on.
Take a linear objective function g(μ1,μ2,c1,c2) = c1μ1 + c2μ2 as an example. The lines satisfying Tc = c1μ1 + c2μ2 are the level sets of an objective function that move up and down, depending on the choice of Tc values. If we choose the least cost as the objective, the optimal combinatorial strategy will be the intersection point of the two-parameter bifurcation curve and the line Tc = c1μ1 + c2μ2 with the minimum Tc. Of course, the objective function is not necessarily linear. The non-linear situation can be similarly discussed.
Results
Synergism and antagonism in a multistable decision model
We apply our approach to a multistable decision network composed of two interacting proteins. It involves several regulatory mechanisms including auto-regulation, cross-regulation, binding and unbinding of transcription factors to the promoters, transcriptions, translations, and degradations [7] and takes the form
| 12 |
| 13 |
where x and y are state variables that present the concentrations of two proteins, respectively. The parameters βi and δi (i = x,y) are the basal production rates and degradation rates of the two proteins. The parameters ηx, ηy, ηxy, and ηyx are the ratios of binding affinities in the case of transcriptional interactions. The parameters ρi (i = x,y) are the auto-activation coefficients and vi (i = x,y) quantify the cross-activation or cross-inhibition strengths, depending on their values, i.e., mutual inhibition when 0<vi<1 and mutual activation when vi>1. The model and its simplified form are often used to describe the coexistence of multiple stable states in cell fate decisions [31–33]. As shown in [7], strong auto-activation (ρx≫1, ρy≫1) in the model (12)–(13) is necessary for the existence of multiple stable states. The existence of bistable states also needs strong cross-activation (vx≫1, vy≫1) under which coexistence of more than two stable states is not possible. To illustrate the ideal of the approach, strong auto-activation and cross-activation strengths of the two proteins are chosen so as to obtain bistability. The standard values of all parameters are shown in Table 1.
Table 1.
| Parameters | Definitions | Values | Reference |
|---|---|---|---|
| v x, v y | Cross-activation strengths of proteins x and y | 18, 16 | [7] |
| ρ x, ρ y | Auto-activation strengths of proteins x and y | 10, 15 | [7] |
| β x, β y | Basal production rates of proteins x and y | 1.4, 1.2 | [7] |
| η x, η y | Ratios of binding affinities in the case of transcriptional interactions | 0.3, 0.25 | [7] |
| δ x, δ y | Basal degradation rates of proteins x and y | 10, 14 | [7] |
| μ x, μ y | Joint regulatory strengths | 0.1, 0.1 | [7] |
| η xy, η yx | Joint binding constants | 0, 0 | [7] |
The occurrence of state a transition depends on the change of regulatory mechanisms that can be embodied by introducing a perturbation to a specific parameter. For instance, we can rewrite the ratio of binding affinity ηx into the form:
| 14 |
where ηxb is the basal value of ηx and Δηx is the perturbation. Transformation (14) is generally used in biological systems and can be easily realized by some control mechanisms. For instance, the intake of drugs in drug therapies may promote or suppress the intensity of interactions between molecular components, as shown by (7) and (9), respectively.
A saddle-node bifurcation occurs at when the perturbation Δηx is increased from zero to a critical value with the relationship . If the perturbation is further increased, the system (12)–(13) achieves a state transition from a lower branch, xl, to a higher one, xh, as shown in Fig. 1a. The critical value is the minimal perturbation required to induce the bifurcation by solely perturbing ηx. Similar cases also occur when parameters βx and δy are solely perturbed, as shown in Fig. 1b, c and d. In addition, the state transitions induced by the saddle-node bifurcation can be achieved by jointly perturbing βx and ηx, or jointly perturbing βx and δy (see Fig. 1c and d). The difference between jointly perturbing the two pairs of the parameters (ηx, βx) and (βx, δy) when inducing the state transition is their efficiency. Undoubtedly, it is an interesting topic from the point of view of understanding the regulatory mechanism of normal cellular functions and pathological conditions.
We now identify if concurrent variations in a pair of the parameters ηx and βx can act synergistically. In other words, we detect if synergism occurs by combinatorially perturbing ηx and βx. Similar to (5), the combinatorial perturbations is in its normalized form:
| 15 |
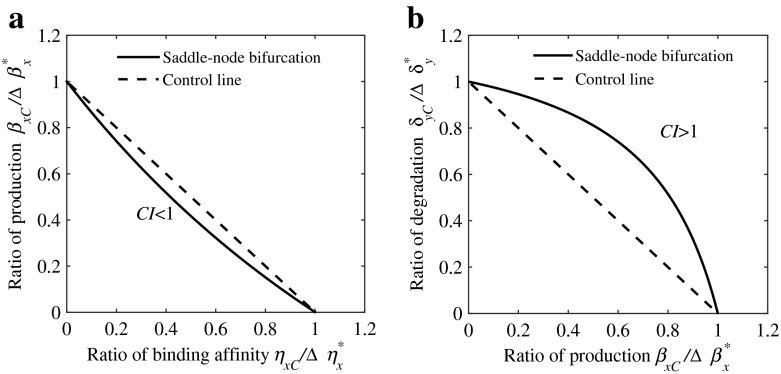
Actually, transformation (15) is general and even includes the case of single parameter perturbation if we set (μ1,μ2)=(1,0) or (μ1,μ2)=(0,1). Therefore, the normalized isobole plotted in the plane of (, ) passes through two boundary points (1,0) and (0,1) (see the dashed lines in Fig. 2a and b). The two-parameter bifurcation curve is located fully below the isobole, which means that ηx and βx are a synergistic pair. In other words, a perturbation pair in any point located on the bifurcation curve (except two boundary points) satisfies the condition and therefore acts synergistically, as shown by the solid curve in Fig. 2a.
Fig. 2.
Synergistic and antagonistic combinatorial perturbations, where β xC/Δβ x∗, η xC/Δη x∗ and δ yC/Δδ y∗ are ratios of required values when combinatorially and solely perturbed to induce the state transition. a The state transition from the low expression x l to the high expression x h through saddle-node bifurcation can also be achieved by combinatorially perturbing basal production rate β x and the binding affinity strength η x. The bifurcation curve located below the control line, which means the concurrent perturbations of β xC and η xC are synergistic, i.e., C I = η xC/Δη x∗ + β xC/β x∗<1. b The state transition induced by combinatorially perturbing the basal production rate β x and the basal degradation rate δ y. The concurrent perturbations of β xC and δ yC are antagonistic because C I = δ yC/Δδ y∗ + β xC/β x∗>1
The case of antagonism is shown in Fig. 2b in which concurrent perturbations of βx and another parameter δy have a lower efficiency than perturbing each of them solely. Following the approach introduced above, we can identify the efficiency of combinatorial perturbations of all pairs of parameters.
Classification of combinatorial perturbations
After performing concurrent perturbations of all pairs of parameters, we find that there are two other cases of combinatorial effects besides the cases of synergism and antagonism, i.e., the combinatorial effects can be also additive or hybrid. More exactly, the combinatorial effects of concurrently perturbing all pairs of parameters can be classified into the following fours cases.
Synergistic if CI = μ1 + μ2<1 for all (μ1,μ2) except the two boundary points. Synergistic perturbation combinations allow lower quantities of each constituent perturbation and consequently lower side effects.
Antagonistic if CI = μ1 + μ2>1 for all (μ1,μ2) except the two boundary points.
Additive if CI = μ1 + μ2=1 for all (μ1,μ2), i.e., the effect of combinatorial perturbations is consistent with the individual perturbation potencies. The term additivity provides the basis for assessing synergism and antagonism.
Hybrid if there exist some such that and some other such that . In other words, concurrent combinations are found to be synergistic over some combinations and antagonistic over other combinations.
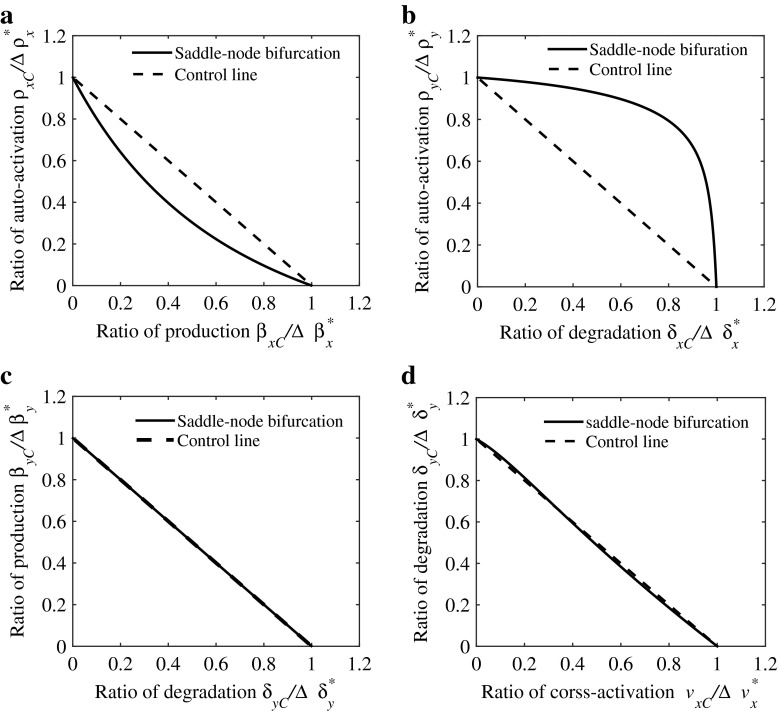
Different combinatorial effects of concurrent perturbing pairs of parameters are shown in Fig. 3. For instance, synergism is present when the pair of parameters, the activation rate ρx and the basal production rate βx, are perturbed. In other words, the response to the combinatorial perturbation of parameters ρx and βx is greater than the sum of the response to perturbing individual parameters, therefore allowing for lower perturbation quantities, as shown in Fig. 3a, in which the two-parameter saddle-node bifurcation curve in the (, ) plane falls above the isobole satisfying (dashed line). On the contrary, concurrent variations in the activation rate ρy and the degeneration rate δx act antagonistically, as shown in Fig. 3b.
Fig. 3.
The classification of bifurcation-based combinatorial perturbations. a Combinatorial regulation of auto-activation strength ρ x and basal production rate η x presents synergism, i.e., ρ xC/Δρ x∗ + β xC/Δβ x∗<1. b Combinatorial regulation of auto-activation strength ρ x and basal degradation rate δ x presents antagonism, i.e., ρ yC/Δρ y∗ + δ xC/Δδ x∗>1. c The additivity of combinatorial regulation is shown by changing basal production and degradation rates δ y and β y, i.e., β yC/Δβ y∗ + δ yC/Δδ y∗=1. d The hybrid case including synergistic, antagonistic, and additive effects can be obtained by jointly perturbing the basal degradation rate δ y and cross-activation strength v x
Of course, not concurrent variations in all pairs of parameters act either synergistically or antagonistically. The two-parameter saddle-node bifurcation curve (solid line) in the (δy, βy) plane falls fully on the isobole, as shown in Fig. 3c. Therefore, the combinatorial effects of concurrent perturbing the parameters βy and δy are additive, which implies that the combinatorial perturbations of βy and δy have the same contribution to perturbing each of them solely. One also notes that combinatorial effects of concurrently perturbing the pair of parameters δy and vx are hybrid, as shown in Fig. 3d. In other words, the combinatorial effects can be synergistic or antagonistic, depending on the perturbation quantities.
Robustness of synergism and antagonism
It is not difficult to detect synergism or antagonism by integrating combinatorial perturbations and the bifurcation-based approach. However, besides detection of synergism and antagonism, if sensitive dependence of combinatorial effects on the choices of perturbation quantities, i.e., their robustness, is also crucial. This will determine whether the synergism observed at the basal parameter values can be kept when the basal values are changed.
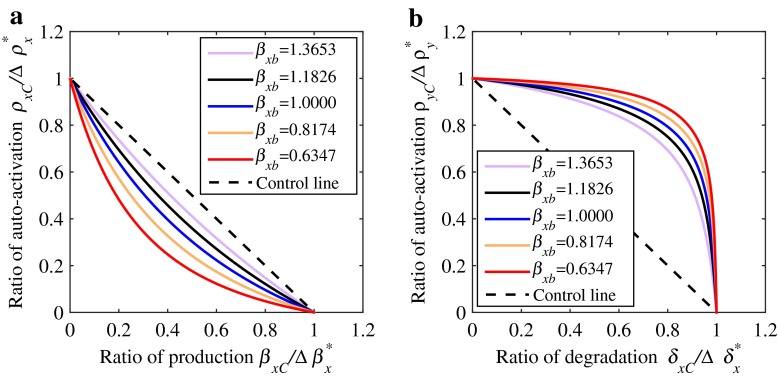
The perturbations of parameter pairs (ρx, βx) and (ρy, δx) show synergism and antagonism, as shown in Fig. 3a and b, respectively. To study their robustness, we choose five distinct basal values of βx, i.e., , , βxb, , and , where is the perturbation required corresponding to the basal value βxb. Five two-parameter saddle-node bifurcation curves corresponding to the five βx values can be obtained, as shown in Fig. 4a. One can see that the synergism observed at the basal value βxb can be retained when the basal value is changed, showing good robustness. Similar results can be obtained for the antagonistic case, as shown in Fig. 4b.
Fig. 4.
Robustness of synergism and antagonism when basal production rate β xb takes different values. a Synergism of basal production rate β x and auto-activation strength ρ x. b Antagonism of basal degradation rate δ x and auto-activation ρ x
Different from good robustness of synergism and antagonism, the additive and hybrid cases may show poor robustness. The reason for poor robustness in the additive case is due to its strong linearity. When the linearity is broken, the additive property can not be retained, therefore showing poor robustness. In contrast, for the hybrid case, it is easy to verify that its robustness is also poor because the combinatorial effects in the hybrid case can be synergistic or antagonistic, depending on the choices of parameter values or perturbation quantities. In addition, the transition between synergism and antagonism or vice versa in the hybrid case may also occur. In applications, we usually need to avoid the occurrence of the hybrid case due to its sensitivity and nondeterminacy.
Optimal combinatorial strategies in the decision model
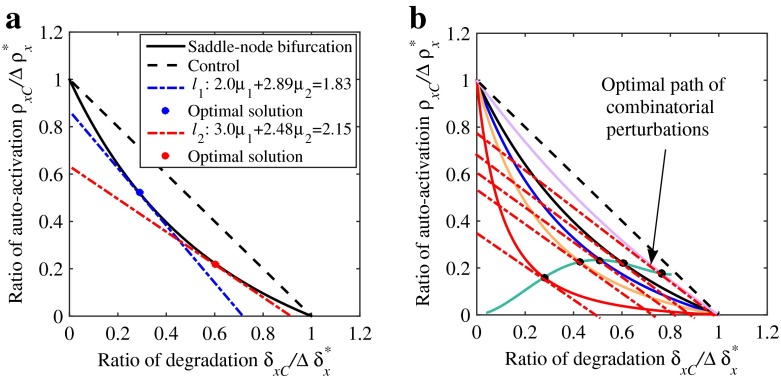
Assuming that the pair of parameters (ρx, δx) are combinatorially perturbed, we have and . The lines satisfying Tc = c1μ1 + c2μ2 are the level sets of objective functions that move up and down, depending on the choice of Tp values. If we choose the least cost as the objective, the optimal combinatorial strategy will be the intersection point of the two-parameter bifurcation curve and the line Tc = c1μ1 + c2μ2 with the minimum Tc. For instance, choosing a price pair (2.0,2.89), we can get an optimal perturbation pair (0.6039,0.2153) and a minimum total cost Tc=1.83, i.e., the optimal perturbation pair (0.6039,0.2153) is the intersection point of the bifurcation curve and the line 2.0μ1+2.89μ2=1.83, as shown by the red dot in Fig. 5a. A different price pair (3.0,2.48) gives another optimal pair (0.2903,0.5158) with a minimum cost Tc=2.15, as shown by the blue dot in Fig. 5a. If multiple intersection points are found, other objectives, e.g., the least side-effects, need to be further chosen to determine which optimal combinatorial strategy is much better.
Fig. 5.
Optimal perturbation strategies and path of combinatorial perturbations. a Optimal strategies of combinatorial perturbation of basal degradation rate δ x and auto-activation strength ρ x corresponding to two different linear objective functions l 1:2.0μ 1+2.89μ 2=1.83 and l 2:3.0μ 1+2.48μ 2=2.15. The points of tangency of objective functions l 1 and l 2 and the bifurcation curves are optimal solutions (the blue and red points). b An example that shows how to find an optimal path (the green solid curve) of combinatorial perturbations
Note that the normal direction of the lines Tc = c1μ1 + c2μ2 is (c1,c2)T. Therefore, the value of function c1μ1 + c2μ2 decreases with its movement toward the lower-left region. Following the approach to determine the optimal combinatorial strategy, it is not difficult to identify the optimal path of combinatorial perturbations because the system dynamics may change when combinatorial perturbations are adopted, resulting in new optimal combinatorial strategies that need to be further determined. For instance, when the value of parameter βx is varied, the optimal path of combinatorial perturbations with βx=0.8, 0.6, 0.45, 0.3, 0.1 (from top to bottom) and price pair (c1,c2)=(2.0,2.89) is shown by the green curve in Fig. 5b.
Synergism in the CREB model
The bifurcation-based approach is applied to a biologically realistic model describing interlocked positive and negative feedback loops governing the interaction of two proteins, CREB 1 and CREB 2. Via CRE elements near the promoters of both creb1 and creb2 genes, these loops can be generated by auto- and cross-regulation of CREB proteins. Two proteins are assumed to bind competitively to the same cAMP-response elements. One, as the activator, activates expression of creb1 and creb2 genes, and enhances its own synthesis through the positive auto-regulation loop. The other, as the repressor, represses transcription of both genes, and represses its own synthesis. In addition, CREB 2 also represses the synthesis of CREB 1 through the negative feedback loop. The cAMP-response element binding (CREB) proteins are involved in many cellular processes and have been investigated widely [28, 34, 35]. A minimal model has also been developed to describe the interactions of CREB proteins by omitting some regulations [35]. The dynamics of the model are governed by the following equations:
| 16 |
| 17 |
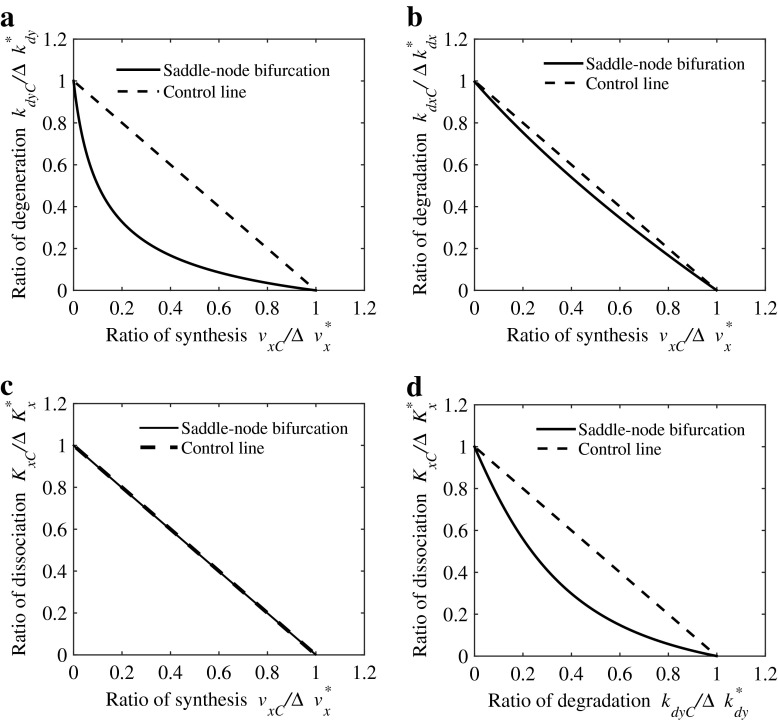
The parameters involved in the model are their synthesis rates vx, vy, their dissociation constants, Kx, Ky, their degeneration rates kdx, kdy, and their basal production rates rbas,x, rbas,y. Standard values of these parameters are the same as those used in [28, 35], and given in Table 2. Non-linear dynamics including bistability and oscillation are involved in the CREB model. There are eight parameters in the model (16)–(17) and in total 28 possible distinct two-parameter combinations. For the bistable case, when the [CREB1]/[CREB2] ratio in the absence of parameter changes is chosen as the control, the percentage increase of the ratio over the control to perturbations of the 28 parameter pairs has been investigated and it has been shown that the parameter pair (vx, kdy) exhibits a strong degree of synergism [28].
Table 2.
| Parameters | Definitions | Values | References |
|---|---|---|---|
| v x, v y (min −1) | Synthesis rates of CREB 1 and CREB 2 | 0.4, 0.01 | [35] |
| K x, K y (nM) | Dissociation constants of CREB 1 and CREB 2 | 25, 10 | [28, 35] |
| r bas,x, r bas,y (min −1) | Basal production rates of CREB 1 and CREB 2 | 0.03, 0.02 | [28, 35] |
| k dx, k dy (min −1) | Degeneration rates of CREB 1 and CREB 2 | 0.04, 0.005 | [28, 35] |
To apply our method to the CREB model, we define the degree of bifurcation-based synergistic combinatorial perturbation, following the definition of the degree of non-linear blending synergism in [28]. Here, the maximum distance between the two-parameter bifurcation curve and the control line is defined as the degree of synergism, i.e., the larger the distance is, the better the combinatorial effects become. With the standard parameter values in Table 2, protein CREB 1 is at a low stable state. An increase in synthesis rate vx of CREB 1 enhances the strength of the positive auto-regulatory loop of CREB 1, thus promoting the state transition from a low stable state to a high stable one via saddle-node bifurcation. In addition, an acceleration in the degradation rate kdy of CREB 2 suppresses not only the negative auto-regulatory loop of CREB 2, but also the negative feedback between two CREB proteins, thus inducing a similar state transition to the case of increasing vx. Furthermore, it is found that concurrent increases of parameters vx and kdy exhibit a good synergism when inducing a state transition. We also detect the synergism of all 28 parameter pairs by using the bifurcation-based approach and find that concurrent perturbations of vx and kdy have a stronger synergism than other parameter pairs, as shown in Fig. 6, which is consistent with the results in [28] and further supports the validity of our approach.
Fig. 6.
Different combinatorial effects in the CREB model. a Concurrent perturbations of synthesis rate v x of CREB 1 and degradation rate k dy of CREB 2 show a stronger synergism; b Synergism induced by combinatorially perturbing synthesis rate v x of CREB 1 and degradation rate k dx of CREB 1; c Additive effects induced by combinatorial perturbations of synthesis rate v x and dissociation constant K x; d Synergism induced by combinatorially perturbing dissociation constant K x of CREB 1 and degradation rate k dy of CREB 2
Discussion
Recent developments in genetic engineering have made the design and the implementation of tunable synthetic biomolecular circuits realistic from both theoretical and experimental viewpoints [36], which makes efficiently modulating and even rewiring endogenous networks for therapeutic applications realistic. The bifurcation-based technique provides a simple procedure to combinatorially perturb endogenous networks if their mathematical models have been developed. This is particularly relevant since combination drug therapies have been applied in the treatment of diseases such as cancer, AIDS, neurological disorders, diabetes, mycobacterial diseases and many other chronic infectious diseases [21, 37, 38]. The potential benefits of synergistic therapy are drug dose and toxicity reduction, minimizing undesirable effects and drug resistance. Therefore, many experimental and theoretical works have been performed to understand the molecular mechanisms underlying the synergism determined by combinatorial drugs [21, 22, 37–39].
In this paper, we develop a new methodology based on combinatorial perturbations and bifurcation analysis to detect synergism induced by concurrent perturbations of parameter pairs or different regulation combinations. The approach depends only on stable states, therefore; the effects of transient states of molecular components can be fully neglected. In addition, the bifurcation-based approach is computationally efficient because two-parameter bifurcation curves can be easily obtained. These results have implications for the rational design of combination drugs and other combinatorial control strategies, e.g., combinatorial control of gene expression.
The synergism of combinatorial perturbation was investigated by using the bifurcation-based method. In fact, the method holds for a general class of biological systems although it is just presented by studying the state transitions of bistable systems in which only saddle-node bifurcation is involved. As mentioned in Section 1, the method is associated with state transitions via occurrence of different kinds of bifurcations. Thus, the bifurcation-based method, besides being applied to the case of bistability, is also feasible when used to check synergism of combinatorial perturbation relating to state transitions via other bifurcations, e.g., pitchfork, transcritical, and Hopf bifurcations.
It is worth noting that many approaches address only the efficiency of combinatorial perturbations and ignore other correlated factors. For instance, in the studies of combination drug therapies, suppression of resistance, reduced toxicity and other aims that often lie outside the purview should be amenable to quantitative study. In addition, most combination therapies focus mainly on fixed-dose combinations of drugs, which may be a barrier to the development of combinatorial drug therapies because the synergism may depend on the initial setting of individual parameters. Indeed, quantitative analysis of combinatorial perturbations should include the process of both detecting synergism and determining optimal perturbation quantities in synergistic pairs, which are the main desirable properties of the bifurcation-based approach.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable comments and suggestions. This research is supported by the National Natural Science Foundation of China (No. 11171206).
References
- 1.Graham TGW, Tabei SMA, Dinner AR, Ilaria R. Modeling bistable cell-fate choices in the Drosophila eye: Qualitative and quantitative perspectives. Development. 2010;137:2265–2278. doi: 10.1242/dev.044826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kimble J. Molecular regulation of the mitosis/meiosis decision in multicellular organisms. Cold Spring Harb. Perspect. Biol. 2011;3:a002683. doi: 10.1101/cshperspect.a002683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.LaBarge MA, Nelson CM, Villadsen R, Fridriksdottir A, Ruth JR, Stampfer MR, Petersen OW, Bissell MJ. Human mammary progenitor cell fate decisions are products of interactions with combinatorial microenvironments. Integr. Biol. (Camb.) 2009;1:70–79. doi: 10.1039/B816472J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Louzoun Y, Xue C, Lesinski GB, Friedman A. A mathematical model for pancreatic cancer growth and treatments. J. Theor. Biol. 2014;351:74–82. doi: 10.1016/j.jtbi.2014.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhao G, Dharmadhikari G, Maedler K, Meyer-Hermann M. Possible role of interleukin-1 in type 2 diabetes onset and implications for anti-inflammatory therapy strategies. PLoS Comput. Biol. 2014;10:e1003798. doi: 10.1371/journal.pcbi.1003798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kuznetsov YA. Elements of Applied Bifurcation Theory. New York: Springer; 1998. [Google Scholar]
- 7.Guantes R, Poyatos JF. Multistable decision switches for flexible control of epigenetic differentiatioin. PLoS Comput. Biol. 2008;4:e1000235. doi: 10.1371/journal.pcbi.1000235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang RQ, Liu K, Chen L, Aihara K. Neural fate decisions mediated by trans-activation and cis-inhibition in notch signaling. Bioinformatics. 2011;27:3158–3165. doi: 10.1093/bioinformatics/btr551. [DOI] [PubMed] [Google Scholar]
- 9.Angeli D, Ferrell JE, Sontag ED. Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. Proc. Natl. Acad. Sci. U.S.A. 2004;101:1822–1827. doi: 10.1073/pnas.0308265100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wang GY. Singularity analysis of the AKT signaling pathway reveals connections between cancer and metabolic diseases. Phys. Biol. 2010;7:046015. doi: 10.1088/1478-3975/7/4/046015. [DOI] [PubMed] [Google Scholar]
- 11.Xiong W, Ferrell JE. A positive-feedback-based bistable “memory module” that governs a cell fate decision. Nature. 2013;426:460–465. doi: 10.1038/nature02089. [DOI] [PubMed] [Google Scholar]
- 12.Benedito R, Roca C, Srensen I, Adams S, Gossler A, Fruttiger M, Adams RH. The notch ligands Dll4 and Jagged1 have opposing effects on angiogenesis. Cell. 2009;137:1124–1135. doi: 10.1016/j.cell.2009.03.025. [DOI] [PubMed] [Google Scholar]
- 13.Bollenbach T, Kishony R. Resolution of gene regulatory conflicts caused by combinations of antibiotics. Mol. Cell. 2011;42:413–425. doi: 10.1016/j.molcel.2011.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hayward P, Brennan K, Sanders P, Balayo T, DasGupta R, Perrimon N, Arias AM. Notch modulates wnt signalling by associating with Armadillo/beta-catennin and regulating its transcriptional activity. Development. 2005;132:1819–1830. doi: 10.1242/dev.01724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Keith CT, Borisy AA, Stockwell BR. Mulicomponent therapeutics for networked systems. Nat. Rev. Drug Discov. 2005;4:71–78. doi: 10.1038/nrd1609. [DOI] [PubMed] [Google Scholar]
- 16.Lehar J, Krueger AS, Avery W, Heilbut AM, Johansen LM, Price ER, Rickles RJ, Short GFIII, Staunton JE, Jin X, Lee MS, Zimmermann GR, Borisy AA. Synergistic drug combinations tend to improve therapeutically relevant selectivity. Nat. Biotechnol. 2009;27:659–666. doi: 10.1038/nbt.1549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lehar J, Zimmermann GR, Krueger AS, Molnar RA, Ledell JT, Heilbut AM, Short GFIII, Gusti LC, Nolan GP, Magid OA, Lee MS, Borisy AA, Stockwell BR, Keith CT. Chemical combination effects predict connectivity in biological systems. Mol. Syst. Biol. 2007;3:80. doi: 10.1038/msb4100116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dixon JE, Shah DA, Rogers C, Hall S, Weston N, Parmenter CDJ, McNally D, Denning C, Shakesheff KM. Combined hydrogels that switch human pluripotent stem cells from self-renewal to differentiation. Proc. Natl. Acad. Sci. U.S.A. 2014;111:5580–5585. doi: 10.1073/pnas.1319685111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nelander S, Wang W, Nilsson B, She QB, Pratilas C, Rosen N, Gennemark P, Sander C. Models from experiments: Combinatorial drug perturbations of cancer cells. Mol. Syst. Biol. 2008;4:216. doi: 10.1038/msb.2008.53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sun X, Bao J, Nelson KC, Li KC, Kulik G, Zhou X. Systems modeling of anti-apoptotic pathways in prostate cancer: Psychological stress triggers a synergism pattern switch in drug combination therapy. PLoS Comput. Biol. 2013;9:e1003358. doi: 10.1371/journal.pcbi.1003358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chou TC. Theoretical basis, experimental design, and computerized simulation of synergism and antagonism in drug combination studies. Pharmacol. Rev. 2006;58:621–681. doi: 10.1124/pr.58.3.10. [DOI] [PubMed] [Google Scholar]
- 22.Chou TC. Preclinical versus clinical drug combination studies. Leukemia Lymphoma. 2008;49:2059–2080. doi: 10.1080/10428190802353591. [DOI] [PubMed] [Google Scholar]
- 23.Chou TC. Drug combination studies and their synergy quantification using the Chou-Talalay method. Cancer Res. 2010;70:440–446. doi: 10.1158/0008-5472.CAN-09-1947. [DOI] [PubMed] [Google Scholar]
- 24.Fitzgerald JB, Schoeberl B, Nielsen UB, Sorger PK. Systems biology and combination therapy in the quest for clinical efficacy. Nat. Chem. Biol. 2006;2:458–466. doi: 10.1038/nchembio817. [DOI] [PubMed] [Google Scholar]
- 25.Loewe S. The problem of synergism and antagonism of combined drugs. Arzneimittelforschung. 1953;3:285–290. [PubMed] [Google Scholar]
- 26.Bliss CI. The calculation of microbial assays. Bacteriol. Rev. 1956;20:243–258. doi: 10.1128/br.20.4.243-258.1956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Greco WR, Bravo G, Parsons JC. The search for synergy: A critical review from a response surface perspective. Pharmacol. Rev. 1995;47:331–385. [PubMed] [Google Scholar]
- 28.Zhang Y, Smolen P, Baxter DA, Byrne JH. Computational analyses of synergism in small molecular network motifs. PloS Comput. Biol. 2014;10:e1003524. doi: 10.1371/journal.pcbi.1003524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yang K, Bai H, Ouyang Q, Lai L, Tang C. Finding multiple target optimal intervention in disease related molecular network. Mol. Syst. Biol. 2008;4:228. doi: 10.1038/msb.2008.60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yin N, Ma W, Pei J, Ouyang Q, Tang C, Lai L. Synergistic and antagonistic drug combinations depend on network topology. PLoS ONE. 2014;9:e93960. doi: 10.1371/journal.pone.0093960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chickarmane V, Troein C, Nuber UA, Sauro HM, Peterson C. Transcriptional dynamics of the embryonic stem cell switch. PLoS Comput. Biol. 2006;2:e123. doi: 10.1371/journal.pcbi.0020123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Huang S, Guo YP, May G, Enver T. Bifurcation dynamics in lineage-commitment in bipotent progenitor cells. Dev. Biol. 2007;305:695–713. doi: 10.1016/j.ydbio.2007.02.036. [DOI] [PubMed] [Google Scholar]
- 33.Roeder I, Glauche I. Towards an understanding of lineage specification in hematopoietic stem cells: a mathematical model for the interaction of transcription fators GATA-1 and PU-1. J. Theor. Biol. 2006;241:852–865. doi: 10.1016/j.jtbi.2006.01.021. [DOI] [PubMed] [Google Scholar]
- 34.Lonze BE, Ginty DD. Function and regulation of CREB family transcription factors in the nervous system. Neuron. 2002;35:605–623. doi: 10.1016/S0896-6273(02)00828-0. [DOI] [PubMed] [Google Scholar]
- 35.Song H, Smolen P, Av-Ron E, Baxter DA, Byrne JH. Dynamics of a minimal model of interlocked positive and negative feedback loops of transcriptional regulation by cAMP-response element binding proteins. Biophys. J. 2007;92:3407–3424. doi: 10.1529/biophysj.106.096891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nissim L, Perli SD, Fridkin A, Perez-Pinera P, Lu TK. Multiplexed and programmable regulation of gene networks with an integrated RNA and CRISPR/Cas toolkit in human cells. Molecular Cell. 2014;54:698–710. doi: 10.1016/j.molcel.2014.04.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bijnsdorp IV, Giovannetti E, Peters GJ. Analysis of drug interactions. Methods Mol. Biol. 2011;731:421–434. doi: 10.1007/978-1-61779-080-5_34. [DOI] [PubMed] [Google Scholar]
- 38.Marchetti C, Tafi E, Middei S, Rubinacci MA, Restivo L, Ammassari-Teule M, Marie H. Synaptic adaptations of CAI pyramidal neurons induced by highly effective combination antidepressant therapy. Biol. Psychiatry. 2009;67:146–154. doi: 10.1016/j.biopsych.2009.09.017. [DOI] [PubMed] [Google Scholar]
- 39.Axelrod M, Gordon VL, Conaway M, Tarcsafalvi A, Neitzke DJ, Gioeli D, Weber MJ. Combinatorial drug screening identifies compensatory pathway interactions and adaptive resistance mechanisms. Oncotarget. 2013;4:622–635. doi: 10.18632/oncotarget.938. [DOI] [PMC free article] [PubMed] [Google Scholar]