Net Fluorescein Flux Across Corneal Endothelium Strongly Suggests Fluid Transport is due to Electro-osmosis

Abstract

We have presented prior evidence suggesting that fluid transport results from electro-osmosis at the intercellular junctions of the corneal endothelium. Such phenomenon ought to drag other extracellular solutes. We have investigated this using fluorescein-Na₂ as an extracellular marker. We measured unidirectional fluxes across layers of cultured human corneal endothelial (HCE) cells. SV-40-transformed HCE layers were grown to confluence on permeable membrane inserts. The medium was DMEM with high glucose and no phenol red. Fluorescein-labeled medium was placed either on the basolateral or the apical side of the inserts; the other side carried unlabeled medium. The inserts were held in a CO₂ incubator for 1 h (at 37 °C), after which the entire volume of the unlabeled side was collected. After that, label was placed on the opposite side, and the corresponding paired sample was collected after another hour. Fluorescein counts were determined with a (Photon Technology) DeltaScan fluorometer (excitation 380 nm; emission 550 nm; 2 nm bwth). Samples were read for 60 s. The cells utilized are known to transport fluid from the basolateral to the apical side, just as they do in vivo in several species. We used 4 inserts for influx and efflux (total: 20 1-h periods). We found a net flux of fluorescein from the basolateral to the apical side. The flux ratio was 1.104 ± 0.056. That difference was statistically significant (p = 0.00006, t test, paired samples). The endothelium has a definite restriction at the junctions. Hence, an asymmetry in unidirectional fluxes cannot arise from osmosis, and can only point instead to paracellular solvent drag. We suggest, once more, that such drag is due to electro-osmotic coupling at the paracellular junctions.

Electronic supplementary material

The online version of this article (doi:10.1007/s00232-016-9887-0) contains supplementary material, which is available to authorized users.

Introduction

For any fluid transporting epithelium, the mechanism by which electrolyte and fluid movements are coupled, and the routes traversed by the transported fluid, remains contested (Hill et al. 2004) (Mathias and Wang 2005). Local osmosis through membrane water channels has been invoked as a cause, but the fact that fluid transport can proceed in the absence of membrane water channels (Oshio et al. 2005) (Kuang et al. 2004) or in the absence of ion transport (Diecke et al. 2007) (Fischbarg 2010) casts doubts on such explanation. We have proposed that electro-osmotic coupling at the paracellular (extracellular) junctions can explain corneal endothelial fluid transport. In those papers (Sanchez et al. 2002; Fischbarg 2003; Rubashkin et al. 2005; Fischbarg and Diecke 2005; Fischbarg et al. 2006; Fischbarg, 2010; Montalbetti and Fischbarg 2009; Cacace et al. 2011), we presented evidence that fluid movement appears to be driven across the paracellular pathways by an intense electrical current. This current traverses the lateral cell border, then goes towards the posterior side extracellularly across the tight junctions, then crosses the cell at the posterior side, and then returns through the cells to the lateral cell border. It generates electro-osmotic coupling with fluid at the level of the tight junctions.

In the current work, we have tested whether there is solvent drag of an extracellular solute through the paracellular route (Sofia Hernandez et al. 1995) (Larsen 2002). We chose to use cultured human corneal endothelial (HCE) cells (Bednarz et al. 2000), which transport fluid in vitro, as other corneal endothelia do (Maurice 1972; Narula et al. 1992). We utilized fluorescein-Na₂ (Sigma Chem. Co., St Louis, MO.), which is known as an extracellular marker (Cvenkel et al. 2015), and it is used to determine paracellular permeability (Chang and Karasov 2004).

Methods

SV-40-transformed Human Corneal Endothelial (HCE) layers (J. Bednarz’s line) were grown to confluence in an incubator (4–6 days) on permeable membrane inserts (Transwell Costar #3450). The culture solution was Dulbecco’s Modified Eagle’s Medium (DMEM, Gibco BRL) with high glucose (4.5 g/l) plus 6 % FBS, penicillin (100 U/ml) and streptomycin (100 ng/ml), and no phenol red. Confluence was verified visually with a phase-contrast inverted microscope (Nikon TMS, 200X), and by measuring the transendothelial resistance (≈25 Ωcm² at confluence) using an Endohm-24 tissue resistance measurement chamber in conjunction with an EVOM epithelial voltohmmeter (both from WPI, Sarasota, FL) .

For the experiments, the inserts were placed on top of matching small beakers, both with culture medium. The incubator CO₂ level was 5 %, temperature was 37 °C, and relative humidity was 90 %.

Na₂-fluorescein (Sigma Chem. Co., St Louis, MO.) was dissolved directly into the medium (0.15 mg/ml). An aliquot of the fluorescein-labeled medium (300 µl) was added either to the basolateral or to the apical side of the inserts, while the other sides carried unlabeled medium. Chamber volumes were 1.5 ml in the upper (basal) compartment and 2.6 ml in the lower (apical) one. After the media were added, the inserts were held in the incubator for 1 h. At that point, the entire volumes were collected. A sample (50 μl) of each chamber mixed with saline (3 ml) was placed in a quartz vial, and the amount of fluorescein was determined with a Photon Technology International DeltaScan fluorometer (excitation 380 nm; emission 550 nm; 2 nm bwth) in photon counting mode, using Felix^® software. Samples were read for 60 s. Calculations were done using the package Mathcad^® 8 (Mathsoft, USA) for numerical manipulations, and using the package FlexPDE 3.11^® (PDE Solutions Inc., USA), for the solution of simulated diffusion of fluorescein across a layer of endothelium. The respective programs utilized are available as Supplementary Materials.

Results and Discussion

In four inserts, we were able to determine successfully 20 flux periods of 1 h each, 10 in one direction and 10 in the opposite one (Table 1). For each given insert, one period was paired with the following one. We alternated randomly the direction of the flux measured. We determined that the fluorescein unidirectional flux, going from the basolateral towards the apical side (the same direction as fluid transport), was modestly larger than the opposite one (ratio: 1.104 ± 0.056, Table 1), and that such difference was statistically significant (p = 0.00006). To avoid a difference in hydrostatic pressure, the size of the compartments was unequal (basolateral: 2.6 ml; apical: 1.5 ml).

Table 1.

Fluorescein fluxes across the endothelial layer

n		col C flux from apex to base (leak) 50-µl sample	col D flux from base to apex (pump + leak) 50-µl sample	col D/col C paired data
1	Insert 1	57,712	61,902	1.0726
2		57,460	65,300	1.1365
3	Insert 2	84,798	88,669	1.0457
4		84,486	86,708	1.0263
5		74,114	90,762	1.2246
6	Insert 3	111,107	123,098	1.1079
7		117,202	132,691	1.1322
8	Insert 4	63,365	67,714	1.0686
9		63,003	69,410	1.1017
10		60,214	67,923	1.1280
	AVGs	77,346	85,418	1.1044
	STDEV	21,911	24,785	0.0564
	STD err			0.0188
	z dev			0.0170
	Ratio paired unidirs	1.1044
	p, paired t test 2 tails	0.000667	cols d and c, paired row-wise
	Size apex	1.5	ml
	Size base	2.6	ml
	Factor base	52
	Factor apex	30

All other factors outside of the compartment counts cancel out of the calculations. In detail

$$\begin{array}{cc}\text{Basal specific activity}:\text{Sab}=\text{A cts}/\left(2.6\text{ml}+300\mathrm{\mu }\text{l}\right)& \left(\text{A are the counts in 3}00\mathrm{\mu }\text{l of the}\text{``}\text{hot}\text{''}\text{solution}\right)\end{array}$$

$$\begin{array}{cc}\text{Apical specific activity}:\text{SAa}=\text{A cts}/\left(1.5\text{ml}+300\mathrm{\mu }\text{l}\right)& \left(\text{A is the same as above}\right)\end{array}$$

$$\text{ml transferred from base to apex}=\text{tot}.\text{cts}.\text{in Ap}/\text{Sab}=\text{cts Ap}\times 30\times 2.6+300\mathrm{\mu }\text{l}/\text{A}=\mathit{\alpha }$$

$$\text{ml transferred from apex to base}=\text{tot}.\text{cts}.\text{In Base}/\text{SAa}=\text{cts}.\text{Bse}.\times 52\times 1.5+300\mathrm{\mu }\text{l}/\text{A}=\mathit{\beta }$$

$$\%\text{net}=\mathit{\alpha }/\mathit{\beta }=\text{cts}.\text{In apex}/\text{cts in base}.$$

Observing the data in Table 1, it can be gathered that (1) the diffusional data are widely dispersed from a given insert to the next one; (2) for the paired flux data, the spread is much tighter. There is an inherent lack of order in how the cells grow, what is their size, and which size is the leak through the layer. However, if we compare the fluxes for a given layer, all those variability factors cancel out, and we are left with the tight grouping of the paired data in the last column of Table 1, which is the basis of our analysis.

The calculated active component (fluid transport) was hence some 10 % of the magnitude of the passive leak. This makes sense, as the junctional restriction (4 nm wide) will still allow a sizable active (forward) flux, and hence it would also allow passive (backwards) unidirectional fluxes of a similar order.

The intercellular spaces (≈20 nm wide) are comparatively open and communicate freely with the basal space, at which end a “pleated skirt” effect increases the cross-sectional area (Hirsch et al. 1977). However, they are restricted at the apical end (4 nm wide). Hence, any hypothetical hydrostatic pressure buildup in the intercellular spaces (say, of osmotic origin) would drive the fluid freely through the open basal end. That direction is however exactly opposite to the one for endothelial fluid transport universally observed (basal to apical). Therefore, one is driven to admit that any combination of cellular water channels (aquaporins) and/or classical osmosis fails to explain fluid transport through the paracellular space in the direction observed, and that instead those experimental findings strongly suggest the presence of an electro-osmotic impelling force along the paracellular space and the junctional restriction, from basolateral towards apical. A similar reasoning applies to the direction of the paracellular Na⁺ flux; such Na⁺ ions are secreted by the lateral cell membrane. If left free to diffuse, they would find an easy way out through the open basal end. However, it was seen experimentally that the net radioactive Na⁺ flux goes in the opposite direction, from basal to apical (Hodson, 1974). This old finding, which has not been emphasized in the present manner until today, is in itself consistent with paracellular electro-osmosis.

The fact that no data are presented for the label concentration in the “hot” compartments limits somewhat the impact for the current findings. However, that limitation can be remedied in future work; in the meantime, calculations can be done to approximate such data. Using reasonable numbers for the volume of the illumination path in the DeltaScan sample vial, plus using a detection efficiency of 15 %, one can extrapolate the “hot” label activities. With those, we calculate a present fluid transport rate of 1.83 µl h⁻¹ cm⁻². This rate, if somewhat lower, is of a similar order as that found across layers of cultured bovine cells (Narula et al. 1992), which was 3.96 µl h cm⁻². In addition, the percent of the (apical) “hot” compartment that diffused to the other side (base) during 1 h (passive diffusion, or leak, (apex to base) was 2.59 × 10⁻³. Further support for this line of reasoning came from simulations of trans-epithelial diffusion of fluorescein done with the FlexPDE software, with which the matching percent of back-diffusion was 3.75 × 10⁻⁴ (to be compared with the figure of 2.59 × 10⁻³ cited above). There are limitations in trying to assume dimensions for the cells in culture, which tend to be smaller and therefore higher in density, more irregular in shape and therefore with more extracellular space than animal samples. Therefore, the tenfold difference between both methods of calculation does not appear excessive, and the conclusions stated above appear to hold. These calculations are given in the Supplementary Material.

If one lastly resorts to “desesperado” reasoning, there would be a very far possibility of fluid transport by osmosis across the cell apical membrane. However, as we have mentioned before, such transfer would violate the diffusion equation by a very uncomfortable factor of ×118. A sample calculation follows. For the hypothetical osmotic gradient that would have to exist across the apical cell membrane, we will use values from control and AQP1 knockout mice (Kuang et al. 2004). In both cases, one has ΔC = Jv/Pf. The steady-state osmotic gradient ΔC required is already unusually large (if not altogether impossible): 4.5 mM salt for control mice and 6 mM for AQP1 knockout mice.

For control mice, the concentration of salt just outside the cell would be 4.5 mM of salt higher than that in the bulk solution. But such ΔC would in turn generate a diffusional flux of absurd magnitude. Estimating in 50 µm the unstirred layer, the flux would be some ×70 larger than the bicarbonate flux that does exist through the endothelium (Hodson and Miller 1976) (Diecke et al. 2004). For knockout mice, that discrepancy is of course larger, of the order of ×118. An analysis of this incongruence has been published (Fischbarg et al. 2006) and reiterated (Fischbarg, 2010).

The accompanying diagrams (Figs. 1, 2, 3) summarize the mechanism proposed.

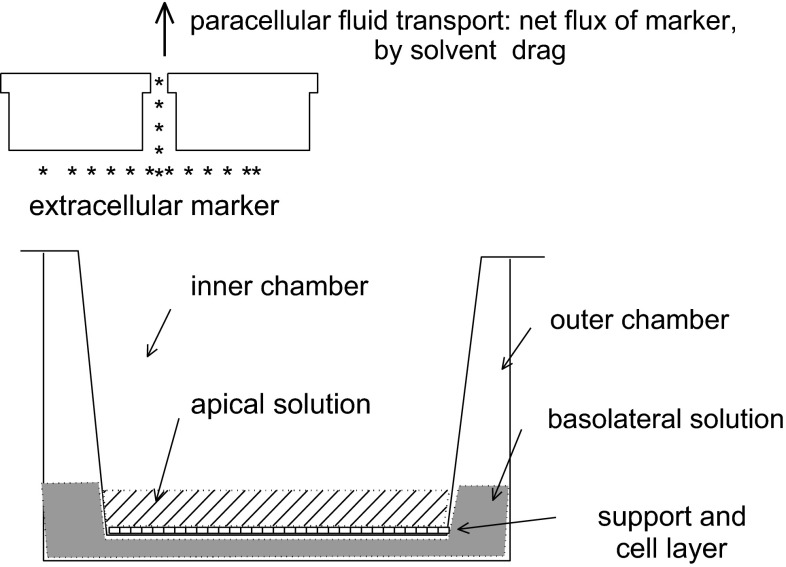
Fig. 1.

Top fluorescein marker permeates the paracellular, but not the cell membrane. Bottom Costar insert placed inside its well, with the endothelial layer grown on top. Graph depicts the outer and inner compartments filled with DMEM solution

Fig. 2.

Schematic view of two endothelial cells and the intercellular (paracellular) route, depicting fluid transport across such route

Fig. 3.

Electro-osmosis: a schematic description of the transendothelial routes for ionic fluxes, electrical currents, and fluid movements. Note the intense paracellular electro-osmotic current carried by Na⁺ ions. From J. Fischbarg, Physiol. Revs., 2011

The suggestion of epithelial fluid transport by epithelial electro-osmotic coupling (rather than by local osmosis) is not altogether novel. Although there never was an avalanche of publications, a few precedents exist for other epithelia (Hill 1975; Lyslo et al. 1985; Hemlin 1995), and even for this corneal endothelium (Lyslo et al. 1985; Sanchez et al. 2002) (see also our other references in the present Introduction). There was even a reference pointing at the insufficiency of electro-osmosis to account for fluid transport along the paracellular spaces of kidney tubule (McLaughlin & Mathias, 1985). One novelty here is that osmosis, regularly mentioned as a possible alternative for fluid transport, can at this point be discarded by the present arguments for the present preparation.

In recent years, reviewers for ocular epithelia (Candia and Alvarez 2008; Bonanno 2012) have begun cautiously mentioning electro-osmosis as a contender for the explanation of epithelial fluid transport. One wishes technical progress would allow this possibility to be tested in other tissues as well.

Electronic supplementary material

Below is the link to the electronic supplementary material.