Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jul 13;6:28906. doi: 10.1038/srep28906

Dual band metamaterial perfect absorber based on artificial dielectric “molecules”

Xiaoming Liu 1, Chuwen Lan 1, Bo Li 1, Qian Zhao 2, Ji Zhou 1,a
PMCID: PMC4942773  PMID: 27406699

Abstract

Dual band metamaterial perfect absorbers with two absorption bands are highly desirable because of their potential application areas such as detectors, transceiver system, and spectroscopic imagers. However, most of these dual band metamaterial absorbers proposed were based on resonances of metal patterns. Here, we numerically and experimentally demonstrate a dual band metamaterial perfect absorber composed of artificial dielectric “molecules” with high symmetry. The artificial dielectric “molecule” consists of four “atoms” of two different sizes corresponding to two absorption bands with near unity absorptivity. Numerical and experimental absorptivity verify that the dual-band metamaterial absorber is polarization insensitive and can operate in wide-angle incidence.

Crystal is formed by periodically arranged atoms, ions or molecules bonding together by attractive and repulsive forces. Similar to this natural material, metamaterial is composed of periodically arranged artificial “atoms” or “molecules” with predesigned dimensions. However, the exotic electromagnetic effects such as negative index of refraction1,2,3,4,5,6,7,8, superlens9,10,11,12,13, cloak14,15,16,17,18 and perfect absorption19,20,21,22,23,24,25,26,27,28,29,30,31,32 make metamaterials more attractive than natural materials. Metamaterial perfect absorbers composed of structured subwavelength artificial “atoms” can be considered as homogeneous materials whose effective electric permittivity ε(ω) and magnetic permeability μ(ω) can be changed separately at resonant frequency by altering the size or shape of artificial “atoms”. According to the relationship among absorptivity A, reflectivity R, and transmissivity T, A = 1-R-T, near unity absorptivity can be obtained at predesigned frequency when both reflectivity R and transmissivity T are minimized. T is zero across the entire frequency range when we add a metallic ground plane thicker than the penetration depth. Therefore, the critical issue to achieve near unity absorptivity is to make reflectivity R = 0. When the incident electromagnetic wave is normal to the metamaterial absorber, the reflectivity R is as follows:

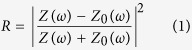graphic file with name srep28906-m1.jpg

where 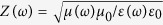Inline graphic is the impedance of the metamaterial absorber and 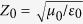Inline graphic is the impedance of free space. If we want reflectivity R = 0, the impedance match condition must be met: 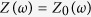Inline graphic, leading to ε(ω) = μ(ω). Metamaterials make it possible to tune the effective electric permittivity ε(ω) and magnetic permeability μ(ω) simultaneously. Therefore, metamaterial absorbers can be designed to perform near unity absorption at certain frequency by impedance-matched to free space ε(ω) = μ(ω). Due to the interesting absorption mechanism, metamaterial perfect absorbers with single and broad absorption peak were widely studied from radio frequency range to the optical realm19,20,21,22,23,24,25,26,27,28,29,30,31,32. Dual-band metamaterial perfect absorbers with two absorption bands were proposed subsequently because of their potential application areas such as detectors, transceiver system, and spectroscopic imagers33,34,35,36,37,38. However, all these dual-band metamaterial absorbers are based on metal “atoms” with different patterns. The anisotropy of metal “atoms” makes those absorbers sensitive to polarization and incident angles. Actually, dielectric “atoms” with high symmetry can also be used to construct metamaterial absorbers. When a plane wave is incident to a single isolated dielectric sphere with radius r and relative refractive index n, the scattered field can be decomposed into a multipole series39, with the 2m-pole term of the scattered electric field proportional to

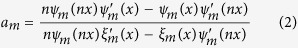graphic file with name srep28906-m5.jpg

and the 2m-pole term of the scattered magnetic field proportional to

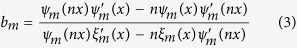graphic file with name srep28906-m6.jpg

where x = k0r, k0 is the free-space wavenumber, ψm and ξm are the Riccati-Bessel functions. The scattering coefficient am and bm are respectively related to the electric and magnetic responses of the sphere. Therefore, dielectric “atoms” can support a series of electric and magnetic resonance modes owing to multiple Mie resonances. Plenty of exotic electromagnetic properties have been demonstrated based on the Mie resonances of dielectric spheres40,41,42, cubes43,44 and rods45,46,47. In this work, we numerically and experimentally proposed a dual-band metamaterial perfect absorber with near unity absorptivity based on dielectric cubic “molecules” composed of four “atoms” of two different sizes.

Results

Design and numerical simulations

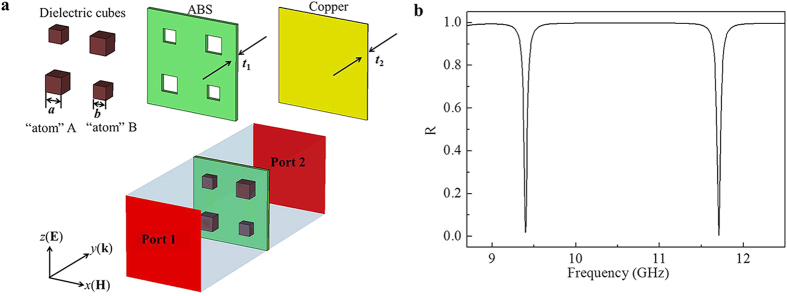
The unit cell of the dielectric “molecules” based dual-band metamaterial absorber is demonstrated in Fig. 1a. It consists of dielectric “atoms” with two different sizes (“atoms” A and “atoms” B) periodically embedded into a background matrix (acrylonitrile butadiene styrene: ABS) on the metallic ground plane. The unit cell of the metamaterial absorber has the dimensions, in millimeters, of: a = 1.8, b = 1.45, p = 10, t1 = 0.4, t2 = 0.1. The background matrix ABS with permittivity ε1 = 2.67 and loss tangent tanδ1 = 0.006 is used to fix the position of the dielectric “atoms”. The permittivity and loss tangent of the dielectric cubes are ε2 = 341, tanδ2 = 0.002, respectively. The metallic ground plane is made of copper with conductivity σ = 5.8 × 107 s/m. Numerical simulations were performed using the finite-difference time domain (FDTD) method. The electromagnetic plane wave with incident angle θ, polarization angle φ was launched from Port 1 to the absorber sample along y direction. Periodic boundary conditions were set along the x and z axis. The simulated reflection spectrum (θ = 0, φ = 0) shown in Fig. 1b indicated that we achieved two reflection minimum with R = 2% at 9.4 GHz and R = 1% at 11.7 GHz. The transmission T is zero across the entire frequency range due to the metallic ground plane. Therefore, two absorption peaks with A = 98% at 9.4 GHz and A = 99% at 11.7 GHz were achieved according to A = 1-R-T.

Figure 1. Unit cell characterization.

Figure 1

Open in a new tab

(a) Schematic diagram of the unit cell of the dielectric “molecules” based dual-band metamaterial absorber. (b) The simulated reflection spectrum.

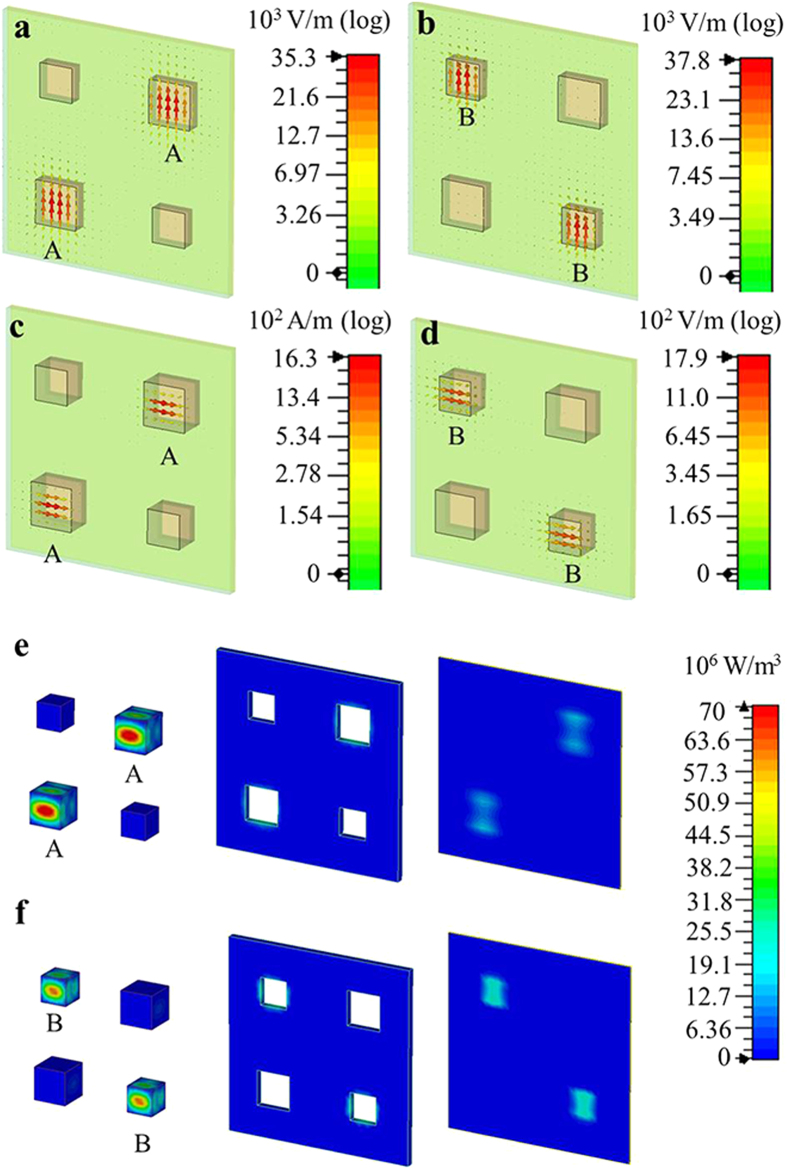
To explore how the two absorption bands were generated, we then simulated the electric and magnetic field distributions in the dielectric “atoms” at 9.4 and 11.7 GHz. As shown in Fig. 2a, there was a strong electric field distribution in “atoms” A with bigger size at lower frequency 9.4 GHz, which coupled strongly to the incident electric field leading to an intense electric resonance. At the same time, it is shown in Fig. 2c that there was also a strong magnetic field distributions in “atoms” A which generate a magnetic resonance at the same frequency. The similar electric and magnetic resonances were also found in “atoms” B with smaller size at 11.7 GHz, as demonstrated in Fig. 2b,d. The simultaneous resonances of electric permittivity ε(ω) and magnetic permeability μ(ω) made our metamaterial absorber impedance-matched to free space ε(ω) = μ(ω) at two absorption frequencies. The incident electromagnetic wave was trapped in the dielectric “atoms” without reflection R. The transmissivity T is zero across the entire frequency range due to the metallic ground plane. Therefore, two absorption peaks with near unity absorptivity A were achieved. The power loss density of this metamaterial absorber at 9.4 and 11.7 GHz in Fig. 2e,f indicated that the main loss was produced by the dielectric loss of the resonant dielectric “atoms”.

Figure 2. Numerical results of electromagnetic properties of the absorber.

Figure 2

Open in a new tab

The electric field distributions in dielectric “atoms” at (a) 9.4 and (b) 11.7 GHz. The magnetic field distributions in dielectric “atoms” at (c) 9.4 and (d) 11.7 GHz. The power loss density in dielectric “atoms”, ABS, and copper at (e) 9.4 and (f) 11.7 GHz.

Experimental results

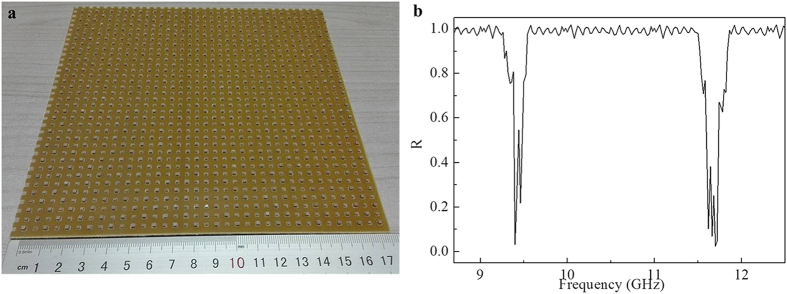
We built a dielectric “molecules” based dual-band metamaterial absorber sample according to the predesigned structure. The dielectric “atoms” was made by strontium titanate ceramic SrTiO3 (ε2 = 341, tanδ2 = 0.002), the absorber sample was composed of 289 artificial “molecules” (1156 artificial “atoms”) inserted into an ABS matrix on a metallic ground plane shown in Fig. 3a. The absorption performance was experimentally measured in free space by two linearly polarized antennas moving along the arc line. These two antennas were connected to a vector network analyzer (Agilent HP8720ES) to launch and receive electromagnetic waves. The experimental reflection spectrum shown in Fig. 3b demonstrated two reflection minimums with R = 3% at 9.4 GHz and R = 2.5% at 11.7 GHz. Therefore, two absorption peaks with A = 97% at 9.4 GHz and A = 97.5% at 11.7 GHz were experimentally achieved, which was in reasonable agreement with the simulation though the absorption peaks were lower than expected and there were some small split peaks due to fabrication imperfections.

Figure 3. Experimental sample and characterization.

Figure 3

Open in a new tab

(a) Dielectric “molecules” based dual-band metamaterial absorber sample. (b) The experimental reflection spectrum.

Discussion

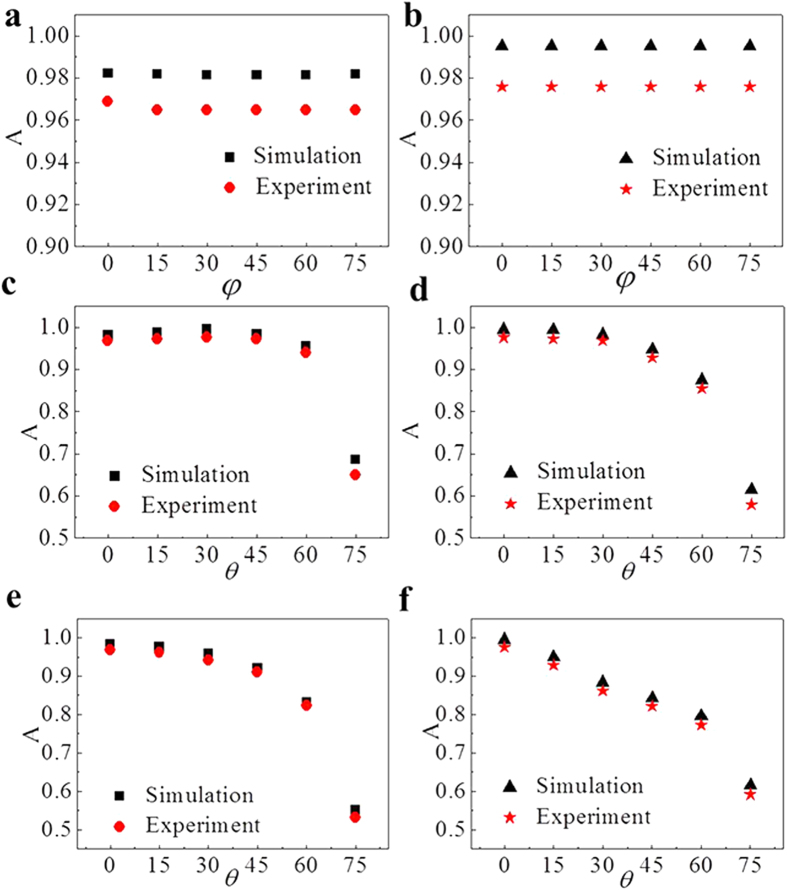
Absorptivity with different polarization angle φ, and incident angle θ in transverse electric (TE) and transverse magnetic (TM) modes were further considered to evaluate the absorption properties. Figure 4a,b demonstrated the simulated and experimental absorptivity with different polarization angle φ at 9.4 and 11.7 GHz, respectively. It indicated that the two absorption peaks were independent on the polarization angle φ changing from 0 to 75 degrees. With TE incident wave, the absorptivity at 9.4 GHz was above 94% when the incident angle θ changed from 0 to 60 degrees. Then the absorptivity decreased dramatically from 94% to 65% as θ varied from 60 to 75 degrees shown in Fig. 4c. Figure 4d indicated that the absorptivity at 11.7 GHz was above 85% when the incident angle θ changed from 0 to 60 degrees. Then decreased from 85% to 60% as θ varied from 60 to 75 degrees. With TM incident wave, the absorptivity at 9.4 GHz decreased from 98% to 55% and the absorptivity at 11.7 GHz decreased from 99% to 60% when the incident angle θ changed from 0 to 75 degrees as shown in Fig. 4e,f. Simulated and experimental absorptivity was always above 78% when the incident angle below 60 degree in both TE and TM modes showing efficient function in wide-angle incidence.

Figure 4. Absorptivity with polarization angle φ, and incident angle θ in TE and TM modes.

Figure 4

Open in a new tab

Absorptivity with different polarization angle φ at (a) 9.4 and (b) 11.7 GHz, with different incident angle θ of the transverse electric (TE) wave at (c) 9.4 and (d) 11.7 GHz, with different incident angle θ of the transverse magnetic (TM) wave at (e) 9.4 and (f) 11.7 GHz.

In conclusion, a dual-band metamaterial perfect absorber based on artificial dielectric “molecules” was experimentally and numerically demonstrated. The metamaterial absorber consisted of a metallic ground plane and 289 dielectric cubic “molecules” (1156 dielectric “atoms”) embedded in ABS matrix. The dielectric “atoms” of different sizes coupled strongly to the incident electric and magnetic field at different frequencies leading to two absorption bands with simulated absorptivity of 98% and 99%, experimental absorptivity of 97% and 97.5% at 9.4 and 11.7 GHz. Numerical and experimental absorption spectra verified that the dule-band metamaterial absorber was polarization insensitive and could operate in wide-angle incidence.

Methods

Sample fabrication

High temperature solid-state reaction method was used to synthesize the ceramic material strontium titanate SrTiO3. We added 5% polyvinyl alcohol (PVA) to SrTiO3 powders with the mass ratio of 1:10 and mixed them homogeneously. The mixture was then uniaxially pressed into cylinders at 20 MPa, cold isostatically pressed at 200 MPa, and pressurelessly sintered at 873K for 2h and 1673 K for 4 h in air. Then we cut the ceramic cylinders into cubes with geometric parameters obtained from numerical simulations. We inserted dielectric cubes into the background matrix ABS and added a copper plate at the back to achieve the due-band dielectric metamaterial absorber.

Additional Information

How to cite this article: Liu, X. et al. Dual band metamaterial perfect absorber based on artificial dielectric “molecules”. Sci. Rep. 6, 28906; doi: 10.1038/srep28906 (2016).

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant Nos 11274198 and 51532004.

Footnotes

Author Contributions J.Z. proposed the ideas for the research. X.L. performed the experiments. C.L. and X.L. performed the numerical simulations. X.L., Q.Z. and B.L. wrote the manuscript. All authors contributed to scientific discussion and critical revision of the article.

References

  1. Dolling G., Wegener M., Soukoulis C. M. & Linden S. Negative-Index Metamaterial at 780 Nm Wavelength. Opt. Lett. 32, 53–55 (2007). [DOI] [PubMed] [Google Scholar]
  2. Paniagua-Domínguez R., Abujetas D. R. & Sánchez-Gil J. A. Ultra Low-Loss, Isotropic Optical Negative-Index Metamaterial Based On Hybrid Metal-Semiconductor Nanowires. Sci. Rep.-UK . 3 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Shelby R. A., Smith D. R. & Schultz S. Experimental Verification of a Negative Index of Refraction. Science. 292, 77–79 (2001). [DOI] [PubMed] [Google Scholar]
  4. Smith D. R., Padilla W. J., Vier D. C., Nemat-Nasser S. C. & Schultz S. Composite Medium with Simultaneously Negative Permeability and Permittivity. Phys. Rev. Lett. 84, 4184–4187 (2000). [DOI] [PubMed] [Google Scholar]
  5. Smith D. R., Pendry J. B. & Wiltshire M. C. K. Metamaterials and Negative Refractive Index. Science. 305, 788–792 (2004). [DOI] [PubMed] [Google Scholar]
  6. Valentine J. et al. Three-Dimensional Optical Metamaterial with a Negative Refractive Index. Nature. 455, 376–379 (2008). [DOI] [PubMed] [Google Scholar]
  7. Veselago V. G. The Electrodynamics of Substances with Simultaneously Negative Values of E and M. Sov. Phys. Usp . 10, 509–514 (1968). [Google Scholar]
  8. Ziolkowski R. W. & Heyman E. Wave Propagation in Media Having Negative Permittivity and Permeability. Phys Rev E Stat Nonlin Soft Matter Phys. 64, 056625 (2001). [DOI] [PubMed] [Google Scholar]
  9. Fang N. & Zhang X. Imaging Properties of a Metamaterial Superlens. Appl. Phys. Lett. 82, 161–163 (2003). [Google Scholar]
  10. Fang N., Lee H., Sun C. & Zhang X. Sub-Diffraction-Limited Optical Imaging with a Silver Superlens. Science. 308, 534–537 (2005). [DOI] [PubMed] [Google Scholar]
  11. Jacob Z., Alekseyev L. V. & Narimanov E. Optical Hyperlens: Far-Field Imaging Beyond the Diffraction Limit. Opt. Express. 14, 8247–8256 (2006). [DOI] [PubMed] [Google Scholar]
  12. Pendry J. B. Negative Refraction Makes a Perfect Lens. Phys. Rev. Lett. 85, 3966–3969 (2000). [DOI] [PubMed] [Google Scholar]
  13. Smolyaninov I. I., Hung Y. J. & Davis C. C. Magnifying Superlens in the Visible Frequency Range. Science. 315, 1699–1701 (2007). [DOI] [PubMed] [Google Scholar]
  14. Chen H., Wu B., Zhang B. & Kong J. A. Electromagnetic Wave Interactions with a Metamaterial Cloak (Vol 99, Art No 063903, 2007). Phys. Rev. Lett. 99, 063903 (2007). [DOI] [PubMed] [Google Scholar]
  15. Li J. & Pendry J. B. Hiding Under the Carpet: A New Strategy for Cloaking. Phys. Rev. Lett. 101, 203901 (2008). [DOI] [PubMed] [Google Scholar]
  16. Liu R. et al. Broadband Ground-Plane Cloak. Science. 323, 366–369 (2009). [DOI] [PubMed] [Google Scholar]
  17. Tsakmakidis K. L., Boardman A. D. & Hess O. ‘Trapped Rainbow’ Storage of Light in Metamaterials. Nature. 450, 397–401 (2007). [DOI] [PubMed] [Google Scholar]
  18. Zhang G. et al. Selective Etching of Metallic Carbon Nanotubes by Gas-Phase Reaction. Science. 314, 974–977 (2006). [DOI] [PubMed] [Google Scholar]
  19. Landy N. I., Sajuyigbe S., Mock J. J., Smith D. R. & Padilla W. J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 100, 207402 (2008). [DOI] [PubMed] [Google Scholar]
  20. Tao H. et al. A Metamaterial Absorber for the Terahertz Regime: Design, Fabrication and Characterization. Opt. Express. 16, 7181–7188 (2008). [DOI] [PubMed] [Google Scholar]
  21. Aydin K., Ferry V. E., Briggs R. M. & Atwater H. A. Broadband Polarization-Independent Resonant Light Absorption Using Ultrathin Plasmonic Super Absorbers. Nat. Commun. 2, 517 (2011). [DOI] [PubMed] [Google Scholar]
  22. Cao T., Wei C., Simpson R. E., Zhang L. & Cryan M. J. Broadband Polarization-Independent Perfect Absorber Using a Phase-Change Metamaterial at Visible Frequencies. Sci. Rep.-UK . 4 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Cheng Q., Cui T. J., Jiang W. X. & Cai B. G. An Omnidirectional Electromagnetic Absorber Made of Metamaterials. New J. Phys. 12 (2010). [Google Scholar]
  24. Cui Y. et al. Ultrabroadband Light Absorption by a Sawtooth Anisotropic Metamaterial Slab. Nano Lett. 12, 1443–1447 (2012). [DOI] [PubMed] [Google Scholar]
  25. Hao J. et al. High Performance Optical Absorber Based On a Plasmonic Metamaterial. Appl. Phys. Lett. 96, 251104 (2010). [Google Scholar]
  26. He X. J., Wang Y., Wang J. M., Gui T. L. & Wu Q. Dual-Band Terahertz Metamaterial Absorber with Polarization Insensitivity and Wide Incident Angle. Progress in Electromagnetics Research-Pier. 115, 381–397 (2011). [Google Scholar]
  27. Ji D. et al. Broadband Absorption Engineering of Hyperbolic Metafilm Patterns. Sci. Rep.-UK . 4 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Liu X., Starr T., Starr A. F. & Padilla W. J. Infrared Spatial and Frequency Selective Metamaterial with Near-Unity Absorbance. Phys. Rev. Lett. 104, 207403 (2010). [DOI] [PubMed] [Google Scholar]
  29. Narimanov E. E. & Kildishev A. V. Optical Black Hole: Broadband Omnidirectional Light Absorber. Appl. Phys. Lett. 95, 41106 (2009). [Google Scholar]
  30. Sun J., Liu L., Dong G. & Zhou J. An Extremely Broad Band Metamaterial Absorber Based On Destructive Interference. Opt. Express. 19, 21155–21162 (2011). [DOI] [PubMed] [Google Scholar]
  31. Watts C. M., Liu X. & Padilla W. J. Metamaterial Electromagnetic Wave Absorbers. Adv. Mater. 24, P98–P120 (2012). [DOI] [PubMed] [Google Scholar]
  32. Zhong S. & He S. Ultrathin and Lightweight Microwave Absorbers Made of Mu-Near-Zero Metamaterials. Sci. Rep.-UK . 3 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Chen K., Adato R. & Altug H. Dual-Band Perfect Absorber for Multispectral Plasmon-Enhanced Infrared Spectroscopy. ACS Nano. 6, 7998–8006 (2012). [DOI] [PubMed] [Google Scholar]
  34. Jiang Z. H., Yun S., Toor F., Werner D. H. & Mayer T. S. Conformal Dual-Band Near-Perfectly Absorbing Mid-Infrared Metamaterial Coating. ACS Nano. 5, 4641–4647 (2011). [DOI] [PubMed] [Google Scholar]
  35. Li M. H., Yang H. L., Hou X. W., Tian Y. & Hou D. Y. Perfect Metamaterial Absorber with Dual Bands. Progress in Electromagnetics Research-Pier. 108, 37–49 (2010). [Google Scholar]
  36. Ma Y. et al. A Terahertz Polarization Insensitive Dual Band Metamaterial Absorber. Opt. Lett. 36, 945–947 (2011). [DOI] [PubMed] [Google Scholar]
  37. Tao H. et al. A Dual Band Terahertz Metamaterial Absorber. J. Phys. D Appl. Phys. 43 (2010). [Google Scholar]
  38. Wen Q., Zhang H., Xie Y., Yang Q. & Liu Y. Dual Band Terahertz Metamaterial Absorber: Design, Fabrication, and Characterization. Appl. Phys. Lett. 95, 241111 (2009). [Google Scholar]
  39. Bohren C. F. & Huffman D. R. Absorption and Scattering of Light by Small Particles . Wiley-Interscience, New York (1983). [Google Scholar]
  40. Kuznetsov A. I., Miroshnichenko A. E., Fu Y. H., Zhang J. & Luk Yanchuk B. Magnetic Light. Sci. Rep.-UK . 2 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Paniagua-Dominguez R., Lopez-Tejeira F., Marques R. & Sanchez-Gil J. A. Metallo-Dielectric Core-Shell Nanospheres as Building Blocks for Optical Three-Dimensional Isotropic Negative-Index Metamaterials. New J. Phys. 13 (2011). [Google Scholar]
  42. Shi L., Tuzer T. U., Fenollosa R. & Meseguer F. A New Dielectric Metamaterial Building Block with a Strong Magnetic Response in the Sub-1.5-Micrometer Region: Silicon Colloid Nanocavities. Adv. Mater. 24, 5934–5938 (2012). [DOI] [PubMed] [Google Scholar]
  43. Zhao Q., Zhou J., Zhang F. & Lippens D. Mie Resonance-Based Dielectric Metamaterials. Mater. Today. 12, 60–69 (2009). [Google Scholar]
  44. Liu X., Zhao Q., Lan C. & Zhou J. Isotropic Mie Resonance-Based Metamaterial Perfect Absorber. Appl. Phys. Lett. 103, 31910 (2013). [Google Scholar]
  45. Peng L. et al. Experimental Observation of Left-Handed Behavior in an Array of Standard Dielectric Resonators. Phys. Rev. Lett. 98, 157403 (2007). [DOI] [PubMed] [Google Scholar]
  46. Schuller J. A., Zia R., Taubner T. & Brongersma M. L. Dielectric Metamaterials Based On Electric and Magnetic Resonances of Silicon Carbide Particles. Phys. Rev. Lett. 99, 107401 (2007). [DOI] [PubMed] [Google Scholar]
  47. Vynck K. et al. All-Dielectric Rod-Type Metamaterials at Optical Frequencies. Phys. Rev. Lett. 102, 133901 (2009). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES