Standardized evaluation of algorithms for computer-aided diagnosis of dementia based on structural MRI: the CADDementia challenge

Abstract

Algorithms for computer-aided diagnosis of dementia based on structural MRI have demonstrated high performance in the literature, but are difficult to compare as different data sets and methodology were used for evaluation. In addition, it is unclear how the algorithms would perform on previously unseen data, and thus, how they would perform in clinical practice when there is no real opportunity to adapt the algorithm to the data at hand. To address these comparability, generalizability and clinical applicability issues, we organized a grand challenge that aimed to objectively compare algorithms based on a clinically representative multi-center data set. Using clinical practice as starting point, the goal was to reproduce the clinical diagnosis. Therefore, we evaluated algorithms for multi-class classification of three diagnostic groups: patients with probable Alzheimer’s disease, patients with mild cognitive impairment and healthy controls. The diagnosis based on clinical criteria was used as reference standard, as it was the best available reference despite its known limitations. For evaluation, a previously unseen test set was used consisting of 354 T1-weighted MRI scans with the diagnoses blinded. Fifteen research teams participated with in total 29 algorithms. The algorithms were trained on a small training set (n=30) and optionally on data from other sources (e.g., the Alzheimer’s Disease Neuroimaging Initiative, the Australian Imaging Biomarkers and Lifestyle flagship study of aging). The best performing algorithm yielded an accuracy of 63.0% and an area under the receiver-operating-characteristic curve (AUC) of 78.8%. In general, the best performances were achieved using feature extraction based on voxel-based morphometry or a combination of features that included volume, cortical thickness, shape and intensity. The challenge is open for new submissions via the web-based framework: http://caddementia.grand-challenge.org.

Graphical abstract

1. Introduction

In 2010, the number of people over 60 years of age living with dementia was estimated at 35.6 million worldwide. This number is expected to almost double every twenty years (Prince et al., 2013). Accordingly, the cost of care for patients with Alzheimer’s disease (AD) and other dementias is expected to increase dramatically, making AD one of the costliest chronic diseases to society (Alzheimer’s Association, 2014). Early and accurate diagnosis has great potential to reduce the costs related to care and living arrangements as it gives patients access to supportive therapies that can help them maintain their independence for longer and delay institutionalization (Paquerault, 2012; Prince et al., 2011). In addition, early diagnosis supports new research into understanding the disease process and developing new treatments (Paquerault, 2012; Prince et al., 2011).

While early and accurate diagnosis of dementia is challenging, it can be aided by assessment of quantitative biomarkers. The five most commonly investigated biomarkers were recently included in the revised diagnostic criteria for AD (McKhann et al., 2011; Jack et al., 2011) and in the revised diagnostic criteria for mild cognitive impairment (MCI) due to AD (Albert et al., 2011). These five biomarkers can be divided into two categories: 1) measures of brain amyloid, which include cerebrospinal fluid (CSF) measures of Aβ42 and amyloid positron emission tomography (PET) imaging, and 2) measures of neuronal injury and degeneration, which include CSF tau measurement, fluoro deoxyglucose (FDG) PET and structural MRI (Jack et al., 2012). Of these biomarkers, structural MRI is very important as it is widely available and non-invasive. Also, it is a good indicator of progression to AD in an individual subject, because it becomes abnormal in close temporal proximity to the onset of the cognitive impairment (Jack et al., 2010, 2013).

Structural MRI data can be used to train computer-aided diagnosis methods. These methods make use of machine-learning and other multivariate data-analysis techniques that train a model (classifier) to categorize groups (e.g., patients and controls). Computer-aided diagnosis techniques use features derived from neuroimaging or related data, and may therefore benefit from the large amounts of neuroimaging data that have become available over the last years. The techniques may improve diagnosis as they can potentially make use of group differences that are not noted during qualitative visual inspection of brain imaging data, potentially leading towards an earlier and more objective diagnosis than when using clinical criteria (Klöppel et al., 2012). In addition, computer-aided diagnosis algorithms can be used to 1) improve diagnosis in hospitals with limited neurological and neuroradiological expertise, 2) increase the speed of diagnosis, and 3) aid the recruitment of specific, homogeneous patient populations for clinical trials in pharmacological research (Klöppel et al., 2012).

Structural-MRI-based computer-aided diagnosis methods for dementia, mainly for AD and MCI, have previously shown promising results in the literature. A few years ago, Cuingnet et al. (2011) compared the performance of various feature extraction methods (e.g., voxel-based features, cortical thickness, hippocampal shape and volume) for dementia classification using a support vector machine (SVM) based on structural MRI. Using data from 509 subjects from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) cohort, three classification experiments were performed: 1) AD versus healthy controls (CN), 2) patients with MCI versus CN, and 3) MCI who had converted to AD within 18 months (MCI converters, MCIc) versus MCI who had not converted to AD within 18 months (MCI non-converters, MCInc). For the AD/CN classification, the best results were obtained with whole-brain methods (voxel-based and cortical thickness) achieving 81% sensitivity and 95% specificity for the best method. The performances of the MCI/CN classifications were much lower than those of AD/CN, and the MCIc/MCInc classifications yielded no performances better than chance. A recent review paper by Falahati et al. (2014) discussed the literature on AD classification and MCI prediction. The research field of computer-aided diagnosis of dementia based on structural MRI is rather extensive, as evidenced by this paper reviewing 50 papers with at least 50 subjects per diagnostic group. The reviewed papers mainly trained a classification model on the AD/CN groups and subsequently tested this model on both AD/CN and MCIc/MCInc classifications. The paper concluded that classification methods are difficult to compare, because the outcome is influenced by many factors, such as feature extraction, feature selection, robustness of the validation approach, image quality, number of training subjects, demographics, and clinical diagnosis criteria. In general, the accuracy obtained for AD/CN classification was 80–90%, and the accuracy for prediction of MCI conversion is somewhat lower. To promote comparison of algorithms, Sabuncu and Konukoglu (2014) published results based on six large publicly available data sets for AD and other diseases (e.g., schizophrenia, autism). A comparison was performed using four feature extraction strategies, including volumetric and cortical thickness features computed with FreeSurfer (Fischl, 2012), and three types of machine learning techniques (SVM, neighborhood approximation forest (Konukoglu et al., 2013), and relevance voxel machine (Sabuncu and Van Leemput, 2012)). Using the ADNI database, the accuracies ranged from 80–87% for AD/CN classification and 58–66% for MCI/CN classification. The authors made all processed data and computational tools available to promote extension of their benchmark results.

Taken together, these publications show very promising results of algorithms for computer-aided diagnosis of AD and MCI. However, they are difficult to compare as different data sets and methodology were used for evaluation. In addition, it is unclear how the algorithms would perform on previously unseen data, and thus, how they would perform in clinical practice when there is no opportunity to adapt the algorithm to the data at hand. Adaptation of an algorithm would be necessary if the algorithm had been trained or optimized on data that are not representative for the data used in a clinical setting. This seriously hampers clinical implementation of algorithms for computer-aided diagnosis. In medical image analysis research, issues related to comparability and clinical applicability have been addressed in grand challenges¹. Such grand challenges have the goal of comparing algorithms for a specific task on the same clinically representative data using the same evaluation protocol. In such challenges, the organizers supply reference data and evaluation measures on which researchers can evaluate their algorithms. For this work, we initiated a grand challenge on Computer-Aided Diagnosis of Dementia (CAD-Dementia). The CADDementia challenge aims to objectively compare algorithms for classification of AD and MCI based on a clinically representative multi-center data set. We recently organized a workshop at the 17th International Conference on Medical Image Computing and Computer-Assisted Interventions (MICCAI). At this workshop, the methods and results of the algorithms were presented by the 15 teams that originally participated in the challenge.

In the CADDementia challenge, we evaluated algorithms that made a multi-class classification of three diagnostic groups: patients with AD, patients with MCI and CN. The algorithms covered the complete image-processing and classification pipeline starting from structural MRI images. The current clinical diagnosis criteria for AD and MCI (McKhann et al., 2011; Petersen, 2004) were used as the reference standard. Although MCI is known to be heterogeneous, as some of the patients will convert to AD and others will not, it is considered to be one diagnostic entity according to these clinical diagnosis criteria. Hence, in this challenge we did not address prediction of MCI progression, but focused on diagnosis as a crucial first step. Regarding diagnostic classification, binary AD/CN classification overestimates true clinical performance as the most difficult to diagnose patients are left out. Therefore we chose to stay close to the clinical problem and address the three-class classification problem.

An evaluation framework was developed consisting of evaluation measures and a reference data set. All methodological choices for the evaluation framework are based on considerations related to our aim to take a step towards clinical implementation of algorithms for computer-aided diagnosis of dementia. This can be summarized in three key points: comparability, generalizability, and clinical applicability. First, by evaluating all algorithms using the same data set and evaluation methods, the results of the algorithms were better comparable. Second, by providing a previously unseen multi-center data set with blinded ground truth diagnoses, overtraining was avoided and generalizability of the algorithms is promoted. Third, according to the current clinical standards, a multi-class diagnosis of AD, MCI and CN was evaluated. The data for the evaluation framework consisted of clinically-representative T1-weighted MRI scans acquired at three centers. For testing the algorithms, we used scans of 354 subjects with the diagnoses blinded to the participants. Because the aim of this challenge was to evaluate the performance in a clinical situation, when not much data are available, we decided to make only a small training set available. This training set consisted of 30 scans equally representing the three data-supplying centers and the diagnostic groups. The diagnostic labels for the training set were made available. For both training and test data, age and sex were provided. In addition to the provided training data, teams were encouraged to use training data from other sources. For this purpose, most algorithms used data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI)² or from the Australian Imaging Biomarker and Lifestyle flagship study of aging (AIBL)³.

In this article, we present the CADDementia challenge for objective comparison of computer-aided diagnosis algorithms for AD and MCI based on structural MRI. The article describes the standardized evaluation framework consisting of evaluation measures and a multi-center structural MRI data set with clinical diagnoses as reference standard. In addition, this paper presents the results of 29 algorithms for classification of dementia developed by 15 international research teams that participated in the challenge.

2. Evaluation framework

In this section, we describe our evaluation framework including the data set, the reference standard, the evaluation measures and the algorithm ranking methods.

2.1. Web-based evaluation framework

The evaluation framework as proposed in this work is made publicly available through a web-based interface⁴. From this protected web site, the data and the evaluation software are available for download. The data available for download are, for the training set: a total of 30 structural MRI scans from the probable AD, MCI and CN groups including diagnostic label, age, sex and scanner information; and for the test set: 354 structural MRI scans from the probable AD, MCI and CN groups including age, sex and scanner information. The data set and the evaluation measures are detailed in the following sections. Everyone who wishes to validate their algorithm for classification of AD, MCI and CN can use the data set for validation. To be allowed to download the data, participants are required to sign a data usage agreement and to send a brief description of their proposed algorithm. The predictions and a short article describing the algorithm are submitted via the web site⁴. The algorithms are validated with the software described in the following sections. The web site remains open for new submissions to be included in the ranking.

2.2. Data

A multi-center data set was composed consisting of imaging data of 384 subjects from three medical centers: VU University Medical Center (VUMC), Amsterdam, the Netherlands; Erasmus MC (EMC), Rotterdam, the Netherlands; University of Porto / Hospital de São João (UP), Porto, Portugal. The data set contained structural T1-weighted MRI (T1w) scans of patients with the diagnosis of probable AD, patients with the diagnosis of MCI, and CN without a dementia syndrome. In addition to the MR scans, the data set included demographic information (age, sex) and information on which institute the data came from. Within the three centers, the data sets of the three classes had a similar age and sex distribution.

The data characteristics are listed in Table 1 and the sizes of the complete data set, training set and test set are listed in Table 2. Most of the data were used for evaluation of performance: the test set. Only after the workshop, we released the class sizes of the test set, marked with a * in Table 2. Therefore only the prior for each class (~1/3) was known to the authors of the algorithms in this paper. A small training data set with diagnostic labels was made available, which consisted of 30 randomly chosen scans distributed over the diagnostic groups. Suitable data from other sources could be used for training (see Sec. 3.1).

Table 1.

Data characteristics. ASSET: array spatial sensitivity encoding technique, FSPGR: fast spoiled gradient-recalled echo, IR: inversion recovery, MPRAGE: magnetization prepared rapid acquisition gradient echo, TE: echo time, TI: inversion time, TR: repetition time

	VUMC	EMC	UP
Scanner		3T, GE Healthcare
	3T, GE Healthcare	Protocol 1: Discovery MR750	3T, Siemens
	Signa HDxt	Protocol 2: Discovery MR750	Trio A Tim
		Protocol 3: HD platform
Sequence	3D IR FSPGR	3D IR FSPGR	3D MPRAGE
Scan parameters (TI/TR/TE)	450ms / 7.8ms / 3.0ms	Protocol 1: 450ms / 7.9ms / 3.1ms	900ms / 2300ms / 3.0ms
		Protocol 2: 450ms / 6.1ms / 2.1ms
		Protocol 3: 300ms / 10.4ms / 2.1ms
Parallel imaging	Yes (ASSET factor=2)	Protocol 1: Yes (ASSET factor=2)	No
		Protocol 2: Parallel imaging: No
		Protocol 3: Parallel imaging: No
Resolution	0.9x0.9x1 mm (sagittal)	Protocol 1: 0.9x0.9x1.0 mm (sagittal)	1x1x1.2 mm (sagittal)
		Protocol 2: 0.9x0.9x0.8 mm (axial)
		Protocol 3: 0.5x0.5x0.8 mm (axial)
Number of scans	180	174	30
Age Mean (Std)
Overall	62.2 (5.9) years	68.6 (7.8) years	67.8 (9.1) years
CN	62.1 (6.0) years	65.5 (7.3) years	64.1 (8.8) years
MCI	62.5 (5.5) years	73.1 (5.5) years	70.0 (8.5) years
AD	62.0 (6.0) years	67.2 (8.4) years	64.6 (7.8) years
Percentage of males
Overall	59 %	63 %	50 %
CN	62 %	61 %	40 %
MCI	68 %	69 %	60 %
AD	47 %	57 %	50 %

Table 2.

Sizes of the complete data set, training set and test set, distributed over the three data-supplying centers and the three classes. The numbers in the columns marked by a * were unknown to the authors of the algorithms discussed in this paper.

Complete data set					Training data					Test data
	nAD*	nMCI *	nCN *	n		nAD	nMCI	nCN	n		nAD*	nMCI *	nCN *	n
VUMC	60	60	60	180	VUMC	5	4	5	14	VUMC	55	56	55	166
EMC	42	61	71	174	EMC	3	4	6	13	EMC	39	57	65	161
UP	10	10	10	30	UP	1	1	1	3	UP	9	9	9	27
Total	112	131	141	384	Total	9	9	12	30	Total	103	122	129	354

2.3. Reference standard

The clinical diagnosis was used as the reference standard in this evaluation framework. The data were acquired either as part of clinical routine or as part of a research study at the three centers. All patients underwent neurological and neuropsychological examination as part of their routine diagnostic work up. The clinical diagnosis was established by consensus of a multidisciplinary team. Patients with AD met the clinical criteria for probable AD (McKhann et al., 1984, 2011). MCI patients fulfilled the criteria specified by Petersen (2004): i.e. memory complaints, cognitive impairment in one or multiple domains confirmed by neuropsychological testing, not demented, intact global cognitive function, clinical dementia rating score=0.5. No hard threshold values were used, but all mentioned criteria were considered. Subjects with psychiatric disorder or other underlying neurological disease were excluded. Center-specific procedures are specified in the following sections.

2.3.1. VU University Medical Center (VUMC), Amsterdam, the Netherlands

Patients with AD, patients with MCI and controls with subjective complaints were included from the memory-clinic based Amsterdam Dementia Cohort (van der Flier et al., 2014). The protocol for selection of patients and controls was the same as used by Binnewijzend et al. (2013). Controls were selected based on subjective complaints and had at least 1 year of follow-up with stable diagnosis. For the controls, the findings from all investigations were normal; they did not meet the criteria for MCI. The patients’ T1w-scans showed no stroke or other abnormalities. All patients gave permission for the use of the data for research.

2.3.2. Erasmus MC (EMC), Rotterdam, the Netherlands

From the Erasmus MC, the data were acquired either as part of clinical routine or as part of a research study. All patients were included from the outpatient memory clinic. Diagnostic criteria for AD and MCI (Papma et al., 2014) were as mentioned above. Healthy control subjects were volunteers recruited in research studies and did not have any memory complaints. All subjects signed informed consent and the study was approved by the local medical ethical committee.

2.3.3. University of Porto / Hospital de São João (UP), Porto, Portugal

The majority of the included patients were included from the outpatient dementia clinic of Hospital de São João (Porto, Portugal). Two patients with AD were referred from external institutions for a second opinion. In addition, healthy control subjects were volunteers recruited in research studies. All subjects provided consent to be included in this study.

2.4. Data preprocessing

The T1w MRI data was anonymized and facial features were masked (Leung et al., 2014). All anonymized scans were visually inspected to check if no brain tissue was accidentally removed by the facial masking. Skull stripping was performed by the participants themselves, if needed for their algorithm. Next to the original anonymized T1w scans, we provided these scans after non-uniformity correction with N4ITK (Tustison et al., 2010) using the following settings: shrink factor = 4, number of iterations = 150, convergence threshold = 0.00001, initial b-spline mesh resolution = 50 mm. Images were stored in NIfTI-1 file format⁵.

2.5. Evaluation measures

The performance of the algorithms was quantified by the classification accuracy, area under the receiver-operating-characteristic (ROC) curve (AUC) and the true positive fraction for the three classes. The performance was evaluated on all 354 test subjects (ALL) and in addition per data-providing center (VUMC, EMC, UP).

2.5.1. Accuracy for multi-class classification

Classification accuracy is in case of a binary design defined as the number of correctly classified samples divided by the total number of samples. For extending the accuracy measure to three-class classification, there are two main options (Hand and Till, 2001). The difference between these is whether or not the difference between the two other classes is taken into account when the performance for one class is assessed.

To determine a simple measure of accuracy, all diagonal elements of the confusion matrix (Table 3), the true positives (tp) and true negatives (tn), are divided by the total number of samples (n):

$$\mathit{accuracy}=\frac{tp+tn}{n}=\frac{n_{0,0}+n_{1,1}+n_{2,2}}{n_0+n_1+n_2}.$$ (1)

Table 3.

Confusion matrix for a three-class classification problem

		True class
		c0	c1	c2
Hypothesized class	C0	n0,0	n0,1	n0,2
	C1	n1,0	n1,1	n1,2
	C2	n2,0	n2,1	n2,2
Column totals:		n0	n1	n2

The alternative, the average accuracy,

$$\begin{array}{l}{\mathit{accuracy}}_{\mathit{average}}=\frac{1}{L}\sum _{i=0}^{L-1}\frac{{tp}_i+{tn}_i}{n}\\ =\frac{1}{L}\sum _{i=0}^{L-1}\frac{n_{i,i}+{\sum }_{j=0,j\ne i}^{L-1}{\sum }_{k=0,k\ne i}^{L-1}{n}_{j,k}}{n},\end{array}$$ (2)

assesses the accuracy separately for each class without distinguishing between the two other classes. For calculation of the accuracy for i = 0, the true positive samples (tp_i) are n_0,0. The true negative samples in this case (tn_i) are n_1,1, n_1,2, n_2,1 and n_2,2. The separate per-class accuracies are averaged to yield the final accuracy. L denotes the number of classes.

Eq. 2 is mainly applicable when the class sizes are very different. In this evaluation framework, we use the accuracy in Eq. 1 as it provides a better measure for the overall classification accuracy (Hand and Till, 2001).

2.5.2. AUC for multi-class classification

The performance of a binary classifier can be visualized as an ROC curve by applying a range of thresholds on the probabilistic output of the classifier and calculating the sensitivity and specificity. The AUC is a performance measure which is equivalent to the probability that a randomly chosen positive sample will have a higher probability of being positively classified than a randomly chosen negative sample (Fawcett, 2006). The advantage of ROC analysis - and accordingly the AUC measure - is that the performance of a classifier is measured independently of the chosen threshold. When more than two dimensions are used the ROC-curve becomes more complex. With L classes, the confusion matrix consists of L² elements: L diagonal elements denoting the correct classifications, and L² - L off-diagonal elements denoting the incorrect classifications. For ROC analysis, the trade-off between these off-diagonal elements is varied. For three-class classification, there are 3² − 3 = 6 off-diagonal elements, resulting in a 6-dimensional ROC-curve. Therefore, for simplicity, multi-class ROC analysis is often generalized to multiple per-class or pairwise ROC curves (Fawcett, 2006).

Similarly to accuracy in the previous section, the multi-class AUC measure can be defined in two ways. The difference between the two definitions is whether or not the third class is taken into account when the difference between a pair of classes is assessed.

First, Provost and Domingos (2001) calculate the multi-class AUC by generating an ROC curve for every class and measuring the AUCs. These per-class AUCs are averaged using the class priors p(c_i) as weights:

$${\mathit{AUC}}_1=\sum _{i=0}^{L-1}\mathit{AUC}(c_i)·p(c_i).$$ (3)

This method has the advantage that the separate ROC curve can be easily generated and visualized. The method calculates an AUC for every class separately, which is sensitive for the class distributions. Even though the class priors are used in averaging, the total AUC still depends on the class sizes.

Second, Hand and Till (2001) proposed a different method for multi-class AUC which is based on calculating an AUC for every pair of classes, without using information from the third class. The method is based on the principle that the AUC is equivalent to the probability that a randomly chosen member of class c_i will have a larger estimated probability of belonging to class C_i than a randomly chosen member of class c_j. Using this principle, the AUC can also be calculated directly from the ranks of test samples instead of first calculating the ROC curves. To achieve this, the class c_i and c_j test samples are ranked in increasing order of the output probability for class C_i. Let S_i be the sum of the ranks of the class c_i test samples. The AUC for a class c_i given another class, Â(c_i|c _j), is then given by

$$\widehat{A}(c_i\mid c_j)=\frac{S_i-n_i(n_i+1)/2}{n_i{n}_j},$$ (4)

see Hand and Till (2001) for the complete derivation.

For situations with three or more classes, Â(c_i|c_j), Â(c _j|c_i). Therefore, the average of both is used:

$$\widehat{A}(c_i,c_j)=\frac{\widehat{A}(c_i\mid c_j)+\widehat{A}(c_j\mid c_i)}{2}.$$ (5)

The overall AUC is obtained by averaging this over all pairs of classes:

$${\mathit{AUC}}_2=\frac{2}{L(L-1)}\sum _{i=0}^{L-1}\sum _{j=0}^i\widehat{A}(c_i,c_j),$$ (6)

in which the number of pairs of classes is $\frac{L(L-1)}{2}$.

In contrast to the accuracy, AUC measurement does not require a threshold on the classifier’s output probabilities and therefore the AUC generally does not rely on the class priors (Hand and Till, 2001). However, the first multi-class approach is dependent on the class priors as these are used for averaging the per-class AUCs. Therefore for this challenge, the second approach for AUC was adopted (Fawcett, 2006).

2.5.3. True positive fraction

For binary classifications in computer-aided diagnosis, often the sensitivity and the specificity are reported in addition to the accuracy. For this multi-class application, the true positive fractions (TPF) for the three classes provide the same information:

$${\mathit{TPF}}_i=\frac{n_{i,i}}{n_i},i\in 0,1,2.$$ (7)

The TPF for the diseased class (TPF_AD; TPF_MCI) can be interpreted as the two-class sensitivity, and the TPF for the control group equals the two-class specificity.

2.6. Submission guidelines

In this challenge, the participating teams were allowed to submit up to five algorithms. Submitting the diagnostic label for each sample of the test set was obligatory. Additionally, the output probabilities for each label were requested but this was optional to not rule out approaches that do not produce probabilistic outcomes. Every team had to write one full workshop paper describing their algorithms in the style of Lecture Notes in Computer Science.

2.7. Final results and ranking

For every algorithm, a confusion matrix was made based on the test data. Accuracy (Eq. 1) and the TPF_i (Eq. 7) for the three classes were calculated from the diagnostic labels. For every class, an ROC curve and per-class AUCs were calculated from the output probabilities reduced to a binary solution, e.g. AD versus non-AD, showing the ability of the classifier to separate that class from the other two classes. An overall AUC was calculated using Eqs. 4–6. Confidence intervals on the accuracy, AUC and TPF were determined with bootstrapping on the test set (1000 resamples). To assess whether the difference in performance between two algorithms was significant, the McNemar test (Dietterich, 1996) was used. Evaluation measures were implemented in Python scripting language (version 2.7.6) using the libraries Scikit-learn⁶ (version 14.1) and Scipy⁷ (version 14.0).

If an algorithm failed to produce an output for certain subjects, these subjects were considered misclassified as a fourth class. This fourth class was considered in the calculation of all performance measures. For calculation of the per-class ROC curves, sensitivity and specificity were determined on the subjects that were classified by the algorithm and subsequently scaled to the total data set to take missing samples into account.

The participating algorithms were ranked based on accuracy of diagnosing the cases in the test set. Algorithms for which output probabilities were available were also ranked based on the AUC of diagnosing the cases in the test set. The algorithm with the best accuracy (rank=1) on the test set, was considered the winning algorithm. In case two or more algorithms had equal accuracies, the average rank was assigned to these algorithms.

3. MICCAI 2014 workshop

The evaluation framework was launched in March 2014 and the deadline for the first submissions was in June 2014. The evaluation framework and the results of the first participating algorithms were presented at the Challenge on Computer-Aided Diagnosis of Dementia Based on Structural MRI Data workshop that was organized on September 18th 2014 in conjunction with the 17th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI) conference in Boston (USA).

We invited around 100 groups from academia and industry by email to participate in the challenge. The challenges were advertised by the MICCAI organizers as well. Eighty-one teams made an account on the web site, of which 47 sent a data usage agreement and a brief description of the proposed algorithm, which was required for downloading the data. Finally, 16 teams submitted results, of which 15 were accepted for participation in the workshop. One team was excluded from participation because their workshop submission did not meet the requirements and because they only submitted results for AD/CN classification. The 15 participating teams submitted a total of 29 algorithms. These algorithms are described in Section 3.2. More details can be found in the short articles that all authors submitted for the workshop (Bron et al., 2014).

3.1. Training data from other sources

In addition to the provided training data set of 30 scans, other sources of training data could be used by the participants. All algorithms except for two were trained on data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database⁸. The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. For up-to-date information, see www.adni-info.org. Acquisition of these data had been performed according to the ADNI acquisition protocol (Jack et al., 2008).

Two teams additionally trained on data from the Australian Imaging Biomarkers and Lifestyle (AIBL) flagship study of ageing⁹ funded by the Commonwealth Scientific and Industrial Research Organisation (CSIRO). These data were collected by the AIBL study group. AIBL study methodology has been reported previously (Ellis et al., 2009).

3.2. Algorithms

In this section, the 29 algorithms submitted by 15 teams are summarized. In Table 4, an overview of the algorithms is presented including a listing of the size of the used training set and the performance on the provided 30 training scans.

Table 4.

Overview of the participating algorithms. The training accuracy was computed on the 30 training subjects by training on the data from different sources only. As indicated below, three algorithms instead trained on all data using 5-fold or 10-fold cross-validation.

	Algorithm	Features	Classifier	Size training data	Training accuracy [%]
1	Abdulkadir	VBM	SVM	1492	60
2	Amoroso	Volume and intensity relations	Neural network	288	67 5-fold
3	Cárdenas-Peña	Raw intensities	SVM	451	83
4	Dolph	Volumes	SVM	30	80 10-fold
5	Eskildsen-ADNI1	Volume and intensity relations	Regression	794	77
6	Eskildsen-ADNI2	Volume and intensity relations	Regression	304	70
7	Eskildsen-Combined	Volume, thickness and intensity relations	Regression	1098	73
8	Eskildsen-FACEADNI1	Volume, thickness and intensity relations	Regression	794	70
9	Eskildsen-FACEADNI2	Volume, thickness and intensity relations	Regression	304	67
10	Franke	VBM	Regression	591	90
11	Ledig-ALL	Volume, thickness and intensity relations	Random forest	734	68
12	Ledig-CORT	Cortical thickness	Random forest	734	58
13	Ledig-GRAD	Intensity relations	Random forest	734	67
14	Ledig-MBL	Intensity relations	Random forest	734	66
15	Ledig-VOL	Volumes	Random forest	734	56
16	Moradi	VBM	SVM	835	77
17	Routier-adni	Shapes	Regression	539	50
18	Routier-train	Shapes	Regression	539	73
19	Sarica	Volume and thickness	SVM	210	70
20	Sensi	Intensity relations	Random forest, SVM	581	73
21	Smith	Volume and raw intensities	Regression	189	80
22	Sørensen-equal	Volume, thickness, shape, intensity relations	LDA	679	73
23	Sørensen-optimized	Volume, thickness, shape, intensity relations	LDA	679	80
24	Tangaro	Volume and thickness	SVM	190	73 5-fold
25	Wachinger-enetNorm	Volume, thickness and shape	Regression	781	73
26	Wachinger-man	Volume, thickness and shape	Regression	781	67
27	Wachinger-step1	Volume, thickness and shape	Regression	781	77
28	Wachinger-step1Norm	Volume, thickness and shape	Regression	781	77
29	Wachinger-step2	Volume, thickness and shape	Regression	781	80

3.2.1. Abdulkadir et al

Algorithm: Abdulkadir (Abdulkadir et al., 2014)

Features: Voxel-based morphometry (VBM) of gray matter (GM).

Classifier: Radial-basis kernel SVM.

Training data: 1289 ADNI subjects and 140 AIBL subjects. The 30 training subjects provided by the challenge were used for parameter selection.

Feature selection: SVM significance maps (Gaonkar and Davatzikos, 2013).

Confounder correction: Yes, for age, sex and intracranial volume (ICV) using kernel regression.

Automatic: Yes. Registration required manual intervention for some subjects.

Computation time: 1 hour per subject.

3.2.2. Amoroso et al

Algorithm: Amoroso (Amoroso et al., 2014)

Features: Volume features (FreeSurfer) and intensity features of the peri-hippocampal region (mean, standard deviation, kurtosis, and skewness).

Classifier: Back propagation neural network (1 hidden layer, 10 neurons). For every pairwise classification, 100 networks were trained on 50 randomly selected features. For final classification, the output scores were averaged.

Training data: 258 ADNI subjects + the 30 training subjects.

Feature selection: Unsupervised filter based on correlation and linear dependencies.

Confounder correction: -

Automatic: Yes.

Computation time: 13 hours per subject, of which 12 hours were due to FreeSurfer processing time.

3.2.3. Cárdenas-Peña et al

Algorithm: Cárdenas-Peña (Cárdenas-Peña et al., 2014)

Features: Features were based on similarities in MRI intensities between subjects. As a first step, similarities between slices of a subject’s scan were calculated along each axis resulting in an interslice kernel (ISK) matrix. Second, pairwise similarities between the subjects’ ISK matrices were computed using the Mahalanobis distance. Third, the dependence between the resulting matrix of the previous step and the class labels was optimized using a kernel centered alignment function. The eigenvalues of the resulting matrix were used as features.

Classifier: Radial-basis kernel SVM.

Training data: 451 ADNI subjects.

Feature selection: -

Confounder correction: -

Automatic: Yes.

Computation time: 22.3 seconds per subject.

3.2.4. Dolph et al

Algorithm: Dolph (Dolph et al., 2014)

Features: Volume ratio of white matter (WM) and CSF for axial slices.

Classifier: Radial-basis kernel SVM.

Training data: The 30 training subjects.

Feature selection: SVM wrapper.

Confounder correction: -

Automatic: Yes, but parameters for skull stripping and tissue segmentation were set manually.

Computation time: 30 minutes per subject.

3.2.5. Eskildsen et al

Algorithm: Eskildsen (Eskildsen et al., 2014, 2015):

Features: Volume and intensity features of the hippocampus (HC) and entorhinal cortex (ERC) were calculated with Scoring by Non-local Image Patch Estimator (SNIPE). By comparing small image patches to a training library, this method segmented these brain regions and computed a grading value per voxel reflecting the proximity between a patch and the classes. As features, the volumes and average grading values for HC and ERC were used.

Cortical thickness was computed with Fast Accurate Cortex Extraction (FACE). As features, the mean cortical thickness was used in regions with large differences in cortical thickness between the classes.

These features were combined:

1. Eskildsen-FACEADNI1: Volume, intensity and cortical thickness features

2. Eskildsen-ADNI1: Volume and intensity features

3. Eskildsen-FACEADNI2: Volume, intensity and cortical thickness features

4. Eskildsen-ADNI2: Volume and intensity features

5. Eskildsen-Combined: A combination of the other four methods by averaging the posterior probabilities

Classifier: Sparse logistic regression. Ensemble learning was used to combine twenty-five models that were trained using different parameters and different sampling of the data.

Training data:

1. Eskildsen-FACEADNI1: 794 ADNI1 subjects

2. Eskildsen-ADNI1: 794 ADNI1 subjects

3. Eskildsen-FACEADNI2: 304 ADNI2 subjects

4. Eskildsen-ADNI2: 304 ADNI2 subjects

5. Eskildsen-Combined: 794 ADNI1 and 304 ADNI2

Regression parameters were optimized on the 30 training subjects.

Feature selection: -

Confounder correction: Yes, for age, sex and differences in class priors.

Automatic: Yes.

Computation time: 55 minutes per subject.

3.2.6. Franke et al

Algorithm: Franke (Franke and Gaser, 2014)

Features: VBM of GM and WM.

Classifier: Relevance vector regression. An age prediction model was trained on healthy controls. Classification of AD, MCI and CN was performed by thresholding the age difference between the predicted age and the real age.

Training data: 561 healthy subjects (IXI cohort¹⁰). The age difference threshold was optimized on the 30 training subjects.

Feature selection: Principal component analysis (PCA).

Confounder correction: Yes. Age was used in the modeling. Separate models were trained for males and females.

Automatic: Yes, except for the optimization of the age difference threshold.

Computation time: 10 minutes per subject.

3.2.7. Ledig et al

Algorithm: Ledig (Ledig et al., 2014):

Features: Five feature sets were used:

1. Ledig-VOL: Volumes of regions-of-interest (ROIs) obtained with multi-atlas label propagation and expectation-maximization-based refinement (MALP-EM).

2. Ledig-CORT: Cortical thickness features (mean and standard deviation) and surface features (surface area, relative surface area, mean curvature, Gaussian curvature) for the whole cortex and cortex regions.

3. Ledig-MBL: Features describing the manifold-based learning (MBL) space. The manifold was trained on intensity texture descriptors for 1701 ADNI subjects.

4. Ledig-GRAD: Intensity patterns in patches. Grading features were learned using data of 629 ADNI and the 30 training subjects. The method was based on SNIPE (Eskildsen et al., 2014).

5. Ledig-ALL: A combination of all features above.

Classifier: Random forest classifier.

Training data: 734 ADNI subjects.

Feature selection: Only for Ledig-MBL and Ledig-Grad. Ledig-MBL: PCA and sparse regression using local binary intensity patterns and mini mental-state examination (MMSE) scores of 292 ADNI subjects. Ledig-Grad: elastic net sparse regression.

Confounder correction: -

Automatic: Yes.

Computation time: 4 hours per subject.

3.2.8. Moradi et al

Algorithm: Moradi (Moradi et al., 2014)

Features: VBM of GM.

Classifier: Transductive SVM. Unsupervised domain adaptation was used to adapt the ADNI data to the 30 training sets. To increase both class separability and within-class clustering, low density separation was applied to both labeled and unlabeled data. The SVM used a graph-distance derived kernel. The classifications were repeated 101 times and combined with majority vote. Classification was performed in two stages: 1) AD/CN classification, 2) a further division of AD/MCI and CN/MCI.

Training data: 835 ADNI subjects.

Feature selection: Elastic net logistic regression.

Confounder correction: Yes. Age effects were removed with linear regression.

Automatic: Yes.

Computation time: 10 minutes per subject.

3.2.9. Routier et al

Algorithm: Routier (Routier et al., 2014)

Features: Features derived from shape models of 12 brain structures: caudate nucleus, putamen, pallidum, thalamus, hippocampus and amygdala of each hemisphere. The segmentations were obtained with FreeSurfer. 3D triangular meshes of the shapes were obtained with a marching-cubes algorithm. Anatomical models of the shapes were built for AD, MCI and CN using Deformetrica¹¹ (Durrleman et al., 2014). The shape models were registered to the test subjects, thus computing the likelihood of the data for each model.

Classifier: Maximum-likelihood regression.

Training data: 509 ADNI subjects.

Thresholds were optimized on:

1. Routier-adni: the ADNI data

2. Routier-train: the 30 training sets

Feature selection: -

Confounder correction: -

Automatic: Yes.

Computation time: 4 days for training the anatomical models and additionally 11 hours per subject.

3.2.10. Sarica et al

Algorithm: Sarica (Sarica et al., 2014)

Features: Volume and cortical thickness features (FreeSurfer).

Classifier: Radial-basis kernel SVM. Pairwise classifications were combined with voting.

Training data: 210 ADNI subjects. The 30 training sets were used for model selection.

Feature selection: Three methods (correlation filter, random forest filter, and SVM wrapper) and their combination were evaluated. The models with best performance on the 30 training subjects were selected: the methods without ICV correction using the random forest filter (AD/CN, AD/MCI) and the correlation filter (CN/MCI).

Confounder correction: Yes. Age and sex were included as features. Experiments were performed with and without ICV correction.

Automatic: Yes, except for the model selection.

Computation time: 5 hours per subject.

Note: Three test subjects were excluded as FreeSurfer failed.

3.2.11. Sensi et al

Algorithm: Sensi (Sensi et al., 2014)

Features: Intensity and textural features of cuboid regions in the medial temporal lobe. The cuboid regions were placed around the entorhinal cortex, perirhinal cortex, hippocampus, and parahippocampal gyrus. In addition, two control regions were placed that are relatively spared by AD (rolandic areas). In each region, voxel intensities were normalized for each tissue by the tissue mean calculated in an additional cuboid region positioned around the corpus callosum in a reference template. To obtain the features, the voxels in the cuboid volumes were processed with 18 filters (e.g., Gaussian mean, standard deviation, range, entropy, mexican hat) with different voxel radii.

Classifier: Radial-basis kernel SVM and random forest classifier, combined by the weighted mean. Using probability density functions estimated on the 30 training subjects, the output probabilities were mapped to the classes.

Training data: 551 ADNI subjects + the 30 training subjects. For the ADNI data, MCIc patients were included in the AD group.

Feature selection: Random forest classifier.

Confounder correction: -

Automatic: Yes.

Computation time: 45 minutes per subject.

3.2.12. Smith et al

Algorithm: Smith (Smith et al., 2014)

Features: Surface area, volume and fragility of a thresholded ROI containing mainly the WM. The fragility originates from network theory and measures how close the structure is from breaking apart into smaller components.

Classifier: Multinomial logistic regression.

Training data: 189 ADNI subjects + the 30 training subjects.

Feature selection: -

Confounder correction: Yes. Age was used as a feature. Separate thresholds for males and females were used for the WM ROI.

Automatic: Yes, except for the optimization of the threshold for the WM ROI.

Computation time: 7–24 minutes per subject.

3.2.13. Sørensen et al

Algorithm: Sørensen (Sørensen et al., 2014)

Features: Five types of features were combined: 1) volumes of seven bilaterally joined regions (amygdala, caudate nucleus, hippocampus, pallidum, putamen, ventricles, whole brain; FreeSurfer), 2) cortical thickness of four lobes and the cingulate gyrus (FreeSurfer), 3) the volume of both hippocampi segmented with a multi-atlas, non-local patch-based segmentation technique (using 40 manual segmentations from the Harmonized Hippocampal Protocol as atlases (Frisoni and Jack, 2011)), 4) two hippocampal shape scores (left and right) computed by a Naive Bayes classifier on the principal components of surface landmarks trained on ADNI and AIBL AD/CN data, 5) a hippocampal texture score computed by a radial-basis kernel SVM on a Gaussian-filter-bank-based texture descriptor trained on ADNI and AIBL AD/CN data.

Classifier: Regularized linear discriminant analysis (LDA).

Different priors were used:

1. Sørensen-equal: equal class priors

2. Sørensen-optimized: class priors optimized on the 30 training subjects ( $p_{CN}=\frac{1}{8},p_{\mathit{MCI}}=\frac{3}{8},p_{AD}=\frac{1}{2}$).

Training data: 504 ADNI and 145 AIBL subjects

Feature selection: -

Confounder correction: Yes. Features were z-score transformed dependent on the age. Volume features were explicitly normalized by dividing by ICV.

Automatic: Yes.

Computation time: 19 hours per subject, of which 18 hours were due to FreeSurfer processing time.

3.2.14. Tangaro et al

Algorithm: Tangaro (Tangaro et al., 2014)

Features: Volume and cortical thickness features (FreeSurfer). Hippocampus segmentations were obtained with random forest classification based on Haar-like features.

Classifier: Linear SVM. Pairwise classifications were combined by multiplication and normalization of the output probabilities.

Training data: 160 ADNI subjects + the 30 training subjects

Feature selection: -

Confounder correction: -

Automatic: Yes.

Computation time: 13 hours per subject, of which 12 hours were due to FreeSurfer processing time.

3.2.15. Wachinger et al

Algorithm: Wachinger (Wachinger et al., 2014a)

Features: Volume, cortical thickness and shape features (FreeSurfer). For computation of shape features, a spectral shape descriptor (‘ShapeDNA’) was derived from volume (tetrahedral) and surface (triangular) meshes obtained from FreeSurfer labels with the marching cubes algorithm. This shape descriptor computes the intrinsic geometry with a method that does not require alignment between shapes (Reuter et al., 2006). Using 50 eigenvalues of the shape descriptor, two types of shape features were computed (Wachinger et al., 2014b): 1) the principal component for 44 brain structures (‘BrainPrint’), and 2) the shape differences between left and right for white matter, gray matter, cerebellum white matter and gray matter, striatum, lateral ventricles, hippocampus and amygdala.

Classifier: Generalized linear model.

Training data: 751 ADNI subjects + the 30 training subjects.

Feature selection: Five methods were used:

1. Wachinger-man: manual selection of ROIs.

2. Wachinger-step1: stepwise selection using the Akaike information criterion on ADNI.

3. Wachinger-step2: stepwise selection using the Akaike information criterion on ADNI and the provided training data.

4. Wachinger-step1Norm: stepwise selection using the Akaike information criterion on ADNI with normalization by the Riemannian volume of the structure.

5. Wachinger-enetNorm: elastic net regularization with normalization by the Riemannian volume of the structure.

Confounder correction: Yes. Age was corrected for by linear regression, volume measures were normalized by the ICV.

Automatic: Yes.

Computation time: 17.4 hours per subject, of which 16.8 hours were due to FreeSurfer processing.

4. Results

The results presented in this section are based on the 29 algorithms presented at the CADDementia workshop (Section 3).

4.1. Classification performance

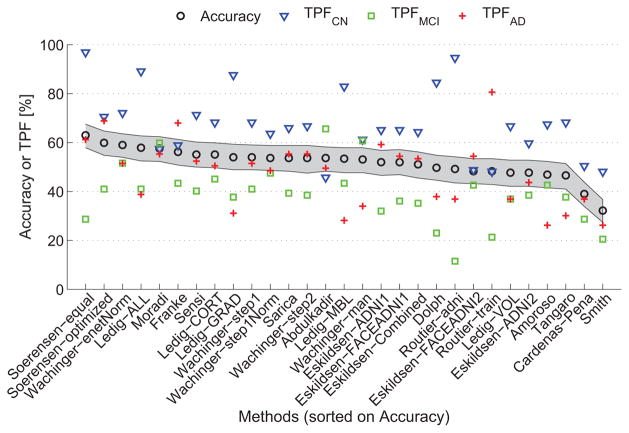
Table 5 and Fig. 1 show the accuracies and TPFs for the algorithms. The algorithms are ranked by accuracy. The accuracies ranged from 32.2% to 63.0%. As a three-class classification problem was analyzed, the accuracy for random guessing would be ~33.3%. If all subjects were estimated to be in the largest class (CN), the accuracy would be n_CN/n = 129/354 = 36.4%. It can thus be observed that 27 out of the 29 algorithms performed significantly better than guessing. The algorithm with the best accuracy was Sørensen-equal, with an accuracy of 63.0%. According to the McNemar test, Sørensen-equal was significantly better than most other algorithms (p < 0.05) except for Sørensen-optimized (p = 0.23), Wachinger-enetNorm (p = 0.21), Moradi (p = 0.14), Ledig-ALL (p = 0.09), and Franke (p = 0.06). The TPFs had a large variability between the algorithms, showing that the different algorithms chose different priors for the classification. Appendix A lists the confusion matrices for all algorithms.

Table 5.

Accuracy and true positive fractions (TPFs) on the test data for the participating algorithms. CI = 95% confidence interval estimated with bootstrapping.

Rank	Algorithm	Accuracy [%] (CI)	TPFCN [%] (CI)	TPFMCI [%] (CI)	TPFAD [%] (CI)
1	Sørensen-equal	63.0 (57.9 – 67.5)	96.9 (92.9 – 99.2)	28.7 (21.3 – 37.4)	61.2 (51.6 – 69.8)
2	Sørensen-optimized	59.9 (54.8 – 64.7)	70.5 (62.8 – 77.8)	41.0 (33.3 – 50.0)	68.9 (59.6 – 77.2)
3	Wachinger-enetNorm	59.0 (54.0 – 63.6)	72.1 (63.4 – 79.2)	51.6 (43.5 – 61.3)	51.5 (41.5 – 61.2)
4	Ledig-ALL	57.9 (52.5 – 62.7)	89.1 (83.7 – 93.8)	41.0 (32.4 – 49.6)	38.8 (30.7 – 50.0)
5	Moradi	57.6 (52.3 – 62.4)	57.4 (48.7 – 66.1)	59.8 (51.3 – 68.1)	55.3 (46.7 – 65.2)
6	Franke	56.2 (50.8 – 61.3)	58.9 (50.4 – 67.5)	43.4 (34.8 – 51.7)	68.0 (58.8 – 77.1)
7.5	Sensi	55.1 (50.0 – 60.2)	71.3 (63.6 – 78.8)	40.2 (31.2 – 49.6)	52.4 (42.7 – 62.0)
7.5	Ledig-CORT	55.1 (49.7 – 59.9)	68.2 (60.5 – 76.0)	45.1 (35.3 – 53.4)	50.5 (41.2 – 60.5)
9.5	Ledig-GRAD	54.0 (48.9 – 59.3)	87.6 (81.7 – 92.6)	37.7 (29.3 – 47.5)	31.1 (22.4 – 40.4)
9.5	Wachinger-step1	54.0 (48.9 – 59.0)	68.2 (60.2 – 75.4)	41.0 (31.9 – 50.9)	51.5 (42.2 – 61.1)
12.5	Wachinger-step1Norm	53.7 (48.6 – 58.8)	63.6 (54.9 – 71.9)	47.5 (38.4 – 56.6)	48.5 (39.6 – 59.1)
12.5	Sarica	53.7 (48.3 – 58.8)	65.9 (57.4 – 74.2)	39.3 (30.0 – 48.2)	55.3 (44.9 – 64.9)
12.5	Wachinger-step2	53.7 (47.5 – 58.8)	66.7 (58.1 – 74.1)	38.5 (30.1 – 48.1)	55.3 (45.5 – 65.0)
12.5	Abdulkadir	53.7 (48.3 – 58.2)	45.7 (37.0 – 53.6)	65.6 (56.1 – 73.0)	49.5 (39.4 – 58.8)
15	Ledig-MBL	53.4 (47.7 – 57.9)	82.9 (76.0 – 88.7)	43.4 (35.1 – 52.9)	28.2 (20.2 – 37.4)
16	Wachinger-man	53.1 (47.7 – 57.9)	61.2 (53.5 – 69.6)	60.7 (51.7 – 70.0)	34.0 (25.7 – 44.7)
17.5	Eskildsen-ADNI1	52.0 (46.6 – 56.8)	65.1 (56.9 – 73.2)	32.0 (24.1 – 40.9)	59.2 (49.5 – 68.3)
17.5	Eskildsen-FACEADNI1	52.0 (46.9 – 57.1)	65.1 (56.6 – 73.1)	36.1 (28.1 – 45.5)	54.4 (44.6 – 63.6)
19	Eskildsen-Combined	51.1 (45.5 – 56.2)	64.3 (56.2 – 72.3)	35.2 (27.1 – 44.3)	53.4 (43.0 – 62.9)
20	Dolph	49.7 (44.6 – 54.8)	84.5 (77.9 – 90.4)	23.0 (16.4 – 31.2)	37.9 (28.9 – 47.3)
21	Routier-adni	49.2 (43.5 – 54.2)	94.6 (89.8 – 97.7)	11.5 (6.2 – 17.7)	36.9 (27.4 – 46.5)
22.5	Eskildsen-FACEADNI2	48.3 (43.2 – 53.4)	48.8 (40.5 – 57.4)	42.6 (33.9 – 51.3)	54.4 (45.5 – 64.0)
22.5	Routier-train	48.3 (42.9 – 53.4)	48.1 (39.8 – 56.9)	21.3 (14.8 – 29.0)	80.6 (72.2 – 87.3)
24.5	Ledig-VOL	47.7 (42.1 – 52.8)	66.7 (57.1 – 74.1)	36.9 (28.9 – 45.9)	36.9 (28.6 – 47.2)
24.5	Eskildsen-ADNI2	47.7 (42.1 – 52.8)	59.7 (51.2 – 68.4)	38.5 (29.9 – 47.3)	43.7 (33.7 – 53.8)
26	Amoroso	46.9 (41.5 – 52.3)	67.4 (58.5 – 75.2)	42.6 (33.6 – 51.1)	26.2 (18.3 – 35.4)
27	Tangaro	46.6 (41.0 – 51.4)	68.2 (60.2 – 76.5)	37.7 (29.2 – 46.3)	30.1 (21.7 – 39.0)
28	Cárdenas-Peña	39.0 (33.9 – 43.8)	50.4 (41.5 – 59.1)	28.7 (21.6 – 38.5)	36.9 (27.4 – 46.8)
29	Smith	32.2 (27.4 – 36.7)	48.1 (39.6 – 57.1)	20.5 (13.9 – 28.3)	26.2 (18.3 – 35.0)

Figure 1.

Accuracy and TPFs on the test data for the participating algorithms. For the accuracy, the 95% confidence interval is shown in grey.

Appendix A.

Confusion matrices of the algorithms

Sørensen-equal		True class			Wachinger-step1Norm		True class			Routier-adni		True class
		CN	MCI	AD			CN	MCI	AD			CN	MCI	AD
Hypothesized class	CN	125	64	15	Hypothesized class	CN	82	49	7	Hypothesized class	CN	122	87	42
	MCI	3	35	25		MCI	47	58	46		MCI	7	14	23
	AD	1	23	63		AD	0	15	50		AD	0	21	38
Sørensen-optimized		True class			Sarica		True class			Eskildsen-FACEADNI2		True class
		CN	MCI	AD			CN	MCI	AD			CN	MCI	AD
Hypothesized class	CN	91	37	5	Hypothesized class	CN	85	43	11	Hypothesized class	CN	63	31	6
	MCI	33	50	27		MCI	41	48	34		MCI	56	52	41
	AD	5	35	71		AD	3	29	57		AD	10	39	56
Wachinger-enetNorm		True class			Wachinger-step2		True class			Routier-train		True class
		CN	MCI	AD			CN	MCI	AD			CN	MCI	AD
Hypothesized class	CN	93	44	6	Hypothesized class	CN	86	51	4	Hypothesized class	CN	62	17	2
	MCI	36	63	44		MCI	41	47	42		MCI	42	26	18
	AD	0	15	53		AD	2	24	57		AD	25	79	83
Ledig-ALL		True class			Abdulkadir		True class			Ledig-VOL		True class
		CN	MCI	AD			CN	MCI	AD			CN	MCI	AD
Hypothesized class	CN	115	57	16	Hypothesized class	CN	59	19	2	Hypothesized class	CN	86	53	11
	MCI	14	50	47		MCI	69	80	50		MCI	41	45	54
	AD	0	15	40		AD	1	23	51		AD	2	24	38
Moradi		True class			Ledig-MBL		True class			Eskildsen-ADNI2		True class
		CN	MCI	AD			CN	MCI	AD			CN	MCI	AD
Hypothesized class	CN	74	30	2	Hypothesized class	CN	107	66	13	Hypothesized class	CN	77	36	7
	MCI	52	73	44		MCI	20	53	61		MCI	49	47	51
	AD	3	19	57		AD	2	3	29		AD	3	39	45
Franke		True class			Wachinger-man		True class			Amoroso		True class
		CN	MCI	AD			CN	MCI	AD			CN	MCI	AD
Hypothesized class	CN	76	48	12	Hypothesized class	CN	79	39	5	Hypothesized class	CN	87	58	32
	MCI	44	53	21		MCI	50	74	63		MCI	36	52	44
	AD	9	21	70		AD	0	9	35		AD	6	12	27
Sensi		True class			Eskildsen-ADNI1		True class			Tangaro		True class
		CN	MCI	AD			CN	MCI	AD			CN	MCI	AD
Hypothesized class	CN	92	45	9	Hypothesized class	CN	84	30	7	Hypothesized class	CN	88	62	18
	MCI	36	49	40		MCI	33	39	35		MCI	31	46	54
	AD	1	28	54		AD	12	53	61		AD	10	14	31
Ledig-CORT		True class			Eskildsen-FACEADNI1		True class			Cárdenas-Peña		True class
		CN	MCI	AD			CN	MCI	AD			CN	MCI	AD
Hypothesized class	CN	88	49	18	Hypothesized class	CN	84	29	8	Hypothesized class	CN	65	51	36
	MCI	32	55	33		MCI	38	44	39		MCI	30	35	29
	AD	9	18	52		AD	7	49	56		AD	34	36	38
Ledig-GRAD		True class			Eskildsen-Combined		True class			Smith		True class
		CN	MCI	AD			CN	MCI	AD			CN	MCI	AD
Hypothesized class	CN	113	59	19	Hypothesized class	CN	83	33	7	Hypothesized class	CN	62	51	44
	MCI	15	46	52		MCI	39	43	41		MCI	39	25	32
	AD	1	17	32		AD	7	46	55		AD	28	46	27
Wachinger-step1		True class			Dolph		True class
		CN	MCI	AD			CN	MCI	AD
Hypothesized class	CN	88	57	7	Hypothesized class	CN	109	73	46
	MCI	40	50	43		MCI	14	28	18
	AD	1	15	53		AD	6	21	39

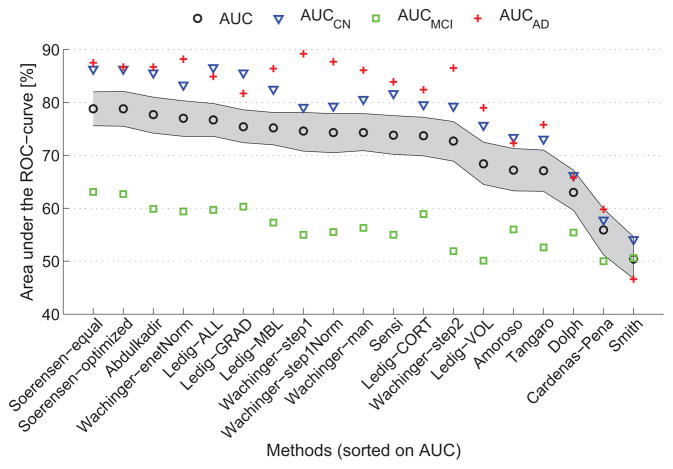
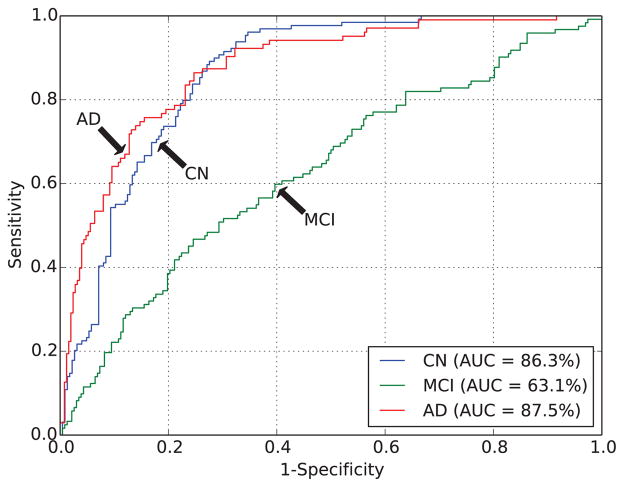
For 19 of the methods, output probabilities were submitted, enabling ROC-analysis. Table 6 and Fig. 2 show the overall AUC and the per-class AUCs (AUC(c_i)) for the algorithms ranked by AUC. The AUC ranged from 50.4% to 78.8%. This was better than random guessing for all algorithms except for one having an AUC of 50.4% (46.7%–54.6%). The two algorithms by Sørensen et al. (Sørensen-equal, Sørensen-optimized) had the highest AUC (78.8%), followed by the algorithm of Abdulkadir (AUC=77.7%). Fig. 3 shows the per-class ROC curves for Sørensen-equal. For most algorithms, the per-class AUCs for CN (range: 54.1%–86.6%) and AD (range: 46.6%–89.2%) were higher than the overall AUC. Except for Smith, AUC_MCI (range: 50.0%–63.1%) was always smaller than the overall AUC.

Table 6.

Area under the ROC-curve (AUC) on the test data for the participating algorithms that computed probabilistic outputs. CI = 95% confidence interval estimated with bootstrapping.

Rank	Algorithm	AUC [%] (CI)	AUCCN [%] (CI)	AUCMCI [%] (CI)	AUCAD [%] (CI)
1.5	Sørensen-equal	78.8 (75.6 – 82.0)	86.3 (81.8 – 89.3)	63.1 (56.6 – 68.3)	87.5 (83.4 – 91.1)
1.5	Sørensen-optimized	78.8 (75.5 – 82.1)	86.3 (81.9 – 89.3)	62.7 (56.8 – 68.4)	86.7 (82.3 – 90.4)
3	Abdulkadir	77.7 (74.2 – 81.0)	85.6 (81.4 – 89.0)	59.9 (54.1 – 66.4)	86.7 (82.3 – 90.3)
4	Wachinger-enetNorm	77.0 (73.6 – 80.3)	83.3 (78.5 – 87.0)	59.4 (52.9 – 65.5)	88.2 (83.8 – 91.4)
5	Ledig-ALL	76.7 (73.6 – 79.8)	86.6 (82.7 – 89.8)	59.7 (53.3 – 65.1)	84.9 (79.7 – 88.7)
6	Ledig-GRAD	75.4 (72.4 – 78.6)	85.6 (81.5 – 88.9)	60.3 (53.9 – 66.5)	81.7 (76.3 – 86.1)
7	Ledig-MBL	75.2 (72.0 – 78.1)	82.5 (77.8 – 86.0)	57.3 (50.9 – 63.6)	86.4 (81.4 – 89.9)
8	Wachinger-step1	74.6 (70.8 – 78.1)	79.1 (73.5 – 83.1)	55.0 (48.5 – 61.4)	89.2 (85.3 – 92.3)
9.5	Wachinger-step1Norm	74.3 (70.5 – 77.9)	79.3 (74.1 – 83.5)	55.5 (48.5 – 61.6)	87.7 (83.7 – 91.1)
9.5	Wachinger-man	74.3 (70.9 – 77.9)	80.6 (75.7 – 84.9)	56.3 (49.7 – 63.0)	86.1 (81.7 – 90.0)
11	Sensi	73.8 (70.2 – 77.5)	81.7 (77.1 – 85.8)	55.0 (48.8 – 61.0)	83.9 (78.8 – 87.7)
12	Ledig-CORT	73.7 (69.9 – 77.2)	79.6 (75.0 – 84.2)	58.9 (52.9 – 64.9)	82.4 (76.7 – 87.3)
13	Wachinger-step2	72.7 (68.9 – 76.4)	79.3 (74.0 – 83.5)	51.9 (45.3 – 58.7)	86.5 (81.9 – 90.3)
14	Ledig-VOL	68.4 (64.5 – 72.5)	75.7 (70.3 – 81.0)	50.1 (44.1 – 56.4)	79.0 (73.3 – 83.5)
15	Amoroso	67.2 (63.3 – 71.3)	73.4 (67.8 – 78.7)	56.0 (49.7 – 61.9)	72.3 (66.2 – 77.5)
16	Tangaro	67.1 (63.2 – 71.0)	73.1 (67.8 – 78.0)	52.6 (45.9 – 58.6)	75.8 (70.2 – 80.6)
17	Dolph	63.0 (59.6 – 67.2)	66.2 (61.3 – 70.3)	55.4 (50.0 – 60.0)	65.8 (60.6 – 71.3)
18	Cárdenas-Peña	55.9 (51.2 – 59.9)	57.8 (51.6 – 63.4)	50.0 (43.9 – 57.1)	59.8 (53.5 – 65.7)
19	Smith	50.4 (46.7 – 54.6)	54.1 (48.0 – 60.0)	50.6 (45.0 – 57.1)	46.6 (40.0 – 53.6)

Figure 2.

Area under the ROC-curve (AUC) on the test data for the participating algorithms. For total AUC, the 95% confidence interval is shown in grey.

Figure 3.

The receiver-operating-characteristic (ROC) curve on all test data for the best performing algorithm: Sørensen-equal.

For the AD and CN classes, the evaluated algorithms obtained relatively high values for TPF and AUC. However, TPF and AUC for the MCI class were lower than those for the other classes, indicating that classification of MCI based on MRI is a difficult problem. This might be due to several factors including the heterogeneity of the MCI class and the use of the clinical diagnosis as reference standard (see Section 5.1.3).

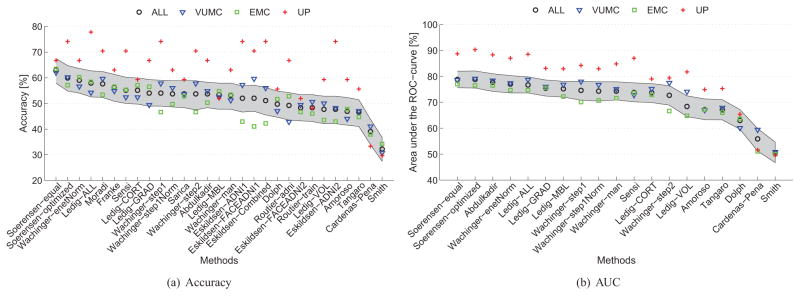
The test data consisted of three subsets of data from three centers (Table 2). Fig. 4 shows how the performances of the algorithms varied between the subsets provided by different centers. The performances on the UP data set were mostly higher than those using all data, but the variation in performance across algorithms was rather high. Performances on the VUMC data were slightly better than those for all data, and performances on the EMC data were slightly worse than those for all data.

Figure 4.

Accuracy (a) and area under the ROC-curve (AUC) (b) on the test data for the participating algorithms on all data (N=354) and on the three subsets of test data from different centers: VUMC (N=166), EMC (N=161), UP (N=27). For accuracy and AUC on all data, the 95% confidence interval is shown in grey.

4.2. Feature extraction and classifiers

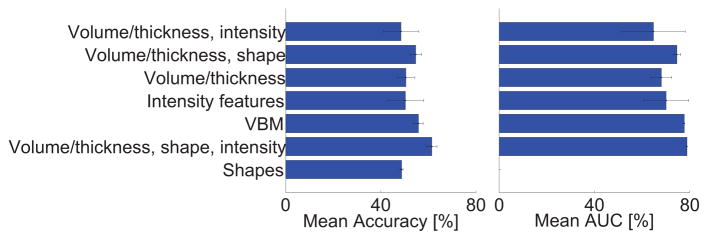
As shown in Table 4, the algorithms used a wide range of approaches. Out of the 29 methods, most methods included features based on volume (N=19), 14 algorithms included features based on cortical thickness, 14 algorithms included features based on intensity (of which two algorithms used raw intensities and the rest more complex intensity relations), 9 algorithms included features based on shape, and 3 algorithms used voxel-based morphometry (VBM). Volume, cortical thickness, intensity and shape features were often combined. The combination of volume, cortical thickness and intensity was most often used (N=8). We noted from Fig. 5 that the performance differences between the different feature extraction strategies were small, but in general we observed that the best performances were achieved with VBM and the combination of volume and cortical thickness with either shape, intensity or both. Also the classifiers differed between the algorithms: 14 algorithms used regression, 7 algorithms used an SVM classifier, 6 used a random forest classifier, 2 used linear discriminant analysis (LDA) and 1 used a neural network for classification. Performance differences between the different classifiers seemed to be small. It should be noted, however, that one should be careful in drawing conclusions based on Table 4 or Fig. 5, as there are multiple differences between the algorithms.

Figure 5.

Mean accuracy and area under the ROC-curve (AUC) on the test data for the different types of features used by the algorithms. The error bars show the standard deviation.

Eight teams incorporated age effects in their algorithms, either by explicitly including age in the model (Franke and Gaser, 2014; Sarica et al., 2014; Smith et al., 2014) or by eliminating age effects using age-dependent normalization (Sørensen et al., 2014) or regression (Abdulkadir et al., 2014; Eskildsen et al., 2014; Moradi et al., 2014; Wachinger et al., 2014a). Three teams used the same strategy to correct for sex (Abdulkadir et al., 2014; Eskildsen et al., 2014; Sarica et al., 2014), two teams trained separate models for males and females (Franke and Gaser, 2014; Smith et al., 2014).

4.3. Training data

Most algorithms, except for Dolph, were trained on more training data than only the 30 provided data sets. Mainly data from ADNI and AIBL were used. Fig. 6 shows the relationship between the number of training data sets and the test set performance. Most algorithms used 600–800 data sets for training.

Figure 6.

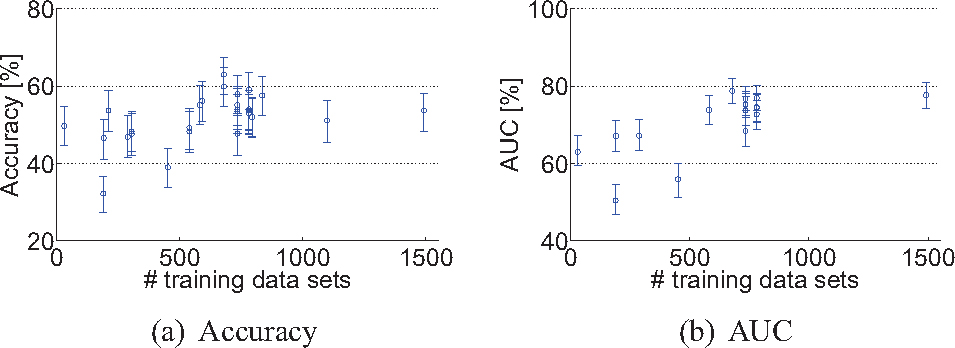
The number of training data sets used plotted against the test set performance of every algorithm: (a) Accuracy, (b) Area under the ROC-curve (AUC). The error bars show the 95% confidence interval.

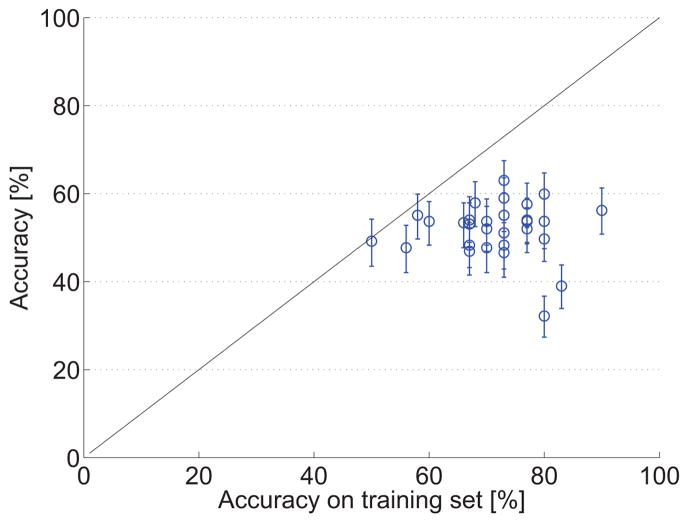
Fig. 7 shows the relationship between the accuracy of the algorithms on the test set and the accuracy on the 30 provided training data sets as reported in the workshop papers. The figure shows that almost all algorithms overestimated accuracy on the training set. However, some of the methods explicitly trained on the 30 provided data sets to ensure optimal performance on the test set. It should be noted that different strategies were used to evaluate the training set accuracy, i.e. train-test evaluation or cross-validation.

Figure 7.

Accuracies for each algorithm estimated on the provided training data plotted against the final accuracy. The error bars show the 95% confidence interval on the test data. The black line (y = x) indicates the expected relationship.

5. Discussion

5.1. Evaluation framework

Although the literature on computer-aided diagnosis of dementia has shown promising results, thorough validation of these algorithms for clinical use has rarely been performed. To enable proper validation of the algorithms, we addressed the following factors in our evaluation framework: comparability, generalizability and clinical applicability.

5.1.1. Comparability

Comparison of different state-of-the-art algorithms is difficult, as most studies use different evaluation data sets, validation strategies and performance measures. According to the literature, little has been done in comparing different algorithms using the same data and methodology. We found two studies that compared multiple algorithms (Cuingnet et al., 2011; Sabuncu and Konukoglu, 2014), of which the work of Cuingnet et al. (2011) does not allow addition of new methods to the comparison. For our evaluation framework, we aimed to increase comparability of the evaluated algorithms by making the testing data set and the validation scripts publicly available. Effort was made to compose a large multi-center data set and to define good evaluation criteria for multi-class classification. One of the main advantages of this evaluation framework is that it can be used by every researcher: anyone who developed a new algorithm can download the data and submit results via our web-based framework¹². Both established and state-of-the-art algorithms can be evaluated and compared to algorithms evaluated by others. The framework remains open for new submissions.

Since the main question that we aimed to address with this framework is how well the current state-of-the-art methods would perform in clinical practice, we specifically chose to use few constraints for the participating methods. Therefore, the framework allows to compare algorithms performing the full analysis, from image to diagnosis. This introduces a lot of variation in the participating algorithms. Participants had a lot of freedom in their choices for the training data and the methods for image processing and classification. Therefore, in discussing the methods we were not able to completely explain the performance differences between methods in all cases. For example, a very good method that uses a small amount of training data may have the same performance as another method that is worse but uses more training data. With the chosen set-up, it is also not possible to assess which part of the algorithm led to the increase in performance. These include a multitude of aspects, such as feature extraction, feature selection, and classification.

At present, a similar challenge is running: the Alzheimer’s Disease Big Data (ADBD) DREAM Challenge #1¹³, of which sub-challenge 3 is similar to the work presented in this paper. In the ADBD DREAM challenge, participants are asked to build a predictive model for MMSE and diagnosis based on T1w MRI data and other variables (i.e., age at baseline, years of education, sex, APOE4 genotype, imputed genotypes). One of the differences with our challenge is that the ADBD DREAM challenge supplies a fixed training set from the ADNI database, instead of leaving this open to the participants. Two test sets, both consisting of 107 subjects from the AddNeuroMed database (Lovestone et al., 2009) are provided. The ADBD DREAM challenge generally made the same choices for their evaluation framework, as they use the same diagnostic groups and reference standard. Preliminary results for the ADBD DREAM challenge are available from their web site. The best predictive model for MMSE yielded a Pearson correlation of 0.602, and the best model for diagnosis yielded an accuracy of 60.2%. The algorithm that was best ranked on average used Gaussian process regression with 20 image features, APOE4 and education (Fan and Guan, 2014).

5.1.2. Generalizability

For new methods, it is important to know how they would generalize to a new, clinically representative data set. Often cross-validation is used to validate the performance of machine learning algorithms (Falahati et al., 2014). Although cross-validation is very useful, especially in the situation when not many scans are available, it optimizes performance on a specific population and can therefore overestimate performance on the general population (Adaszewski et al., 2013). In addition, algorithms are often tuned to specific cohorts which limits their generalizability (Adaszewski et al., 2013). When generalizing an algorithm to other data, variability in the data acquisition protocol, the population or the reference standard can be problematic and can decrease performance (Sabuncu and Konukoglu, 2014). To evaluate generalizability of the algorithms, which is certainly required for clinical implementation, we used a large, new and unseen test set in this work. This data set consisted of scans acquired with GE (n=354) and Siemens (n=30) scanners, so we do not have information on the performance of the algorithms on data from other scanners. However, the data set had some differences in scanning parameters, which allows evaluation of the generalizability of the algorithms to different scanning protocols. The diagnostic labels of the test set were blinded to the authors of the algorithms, which is different from the benchmark papers by Cuingnet et al. (2011) and Sabuncu and Konukoglu (2014). The importance of an independent test is also confirmed by Fig. 7, which shows that all algorithms overestimated the performance by cross-validating or tuning on the training set.

Another factor providing insight into the generalizability of the performance results was the size of the test set. The test set was quite large, consisting of 354 subjects. Not many other studies used an unseen test set. For studies using cross-validation, usually 500–800 data sets from the ADNI database are used (Cuingnet et al., 2011; Falahati et al., 2014; Sabuncu and Konukoglu, 2014). The ADBD DREAM challenge uses an unseen test set, but much smaller than the one used here (107 subjects).

5.1.3. Clinical applicability

For this evaluation framework, the decision was made to split our multi-center data set into a small (n=30) training set and a large test set. This choice resembles a clinical setting, where in a certain hospital only a small training data set is available. On the other hand, a lot of training data are available from publicly available databases like the ADNI and AIBL, which can be used for training the algorithms.

As reference standard for evaluation of the algorithms, the current clinical diagnosis criteria for AD (McKhann et al., 2011) and MCI (Petersen, 2004) were used, which is common practice in studies of computer-aided diagnosis methods (Cuingnet et al., 2011; Klöppel et al., 2008; Falahati et al., 2014; Davatzikos et al., 2008a; Duchesne et al., 2008; Fan et al., 2008a,b; Gray et al., 2013; Koikkalainen et al., 2012; Magnin et al., 2009; Vemuri et al., 2008; Wolz et al., 2011). Ground truth diagnosis of dementia can only be assessed using autopsy and is therefore only rarely available. Of the previously mentioned papers, only one paper included one group of 20 AD patients with an autopsy confirmed diagnosis (Klöppel et al., 2008). Amyloid imaging (Klunk et al., 2004) has also proven to be a good biomarker for AD, as subjects with positive amyloid showed to have a more rapid disease progression (Jack et al., 2010). However, availability of these data is also very limited. The limitation of using clinical diagnosis as the ground truth is that it may be incorrect. In the literature, the reported accuracies of the clinical diagnosis of AD, based on the old criteria (McKhann et al., 1984), compared to postmortem neuropathological gold standard diagnosis were in the range of 70–90% (Mattila et al., 2012; Lim et al., 1999; Petrovitch et al., 2001; Kazee et al., 1993). Although the clinical diagnosis has limitations, we believe it is the best available reference standard. One should also note that this challenge does not aim to assess the diagnostic accuracy of structural MRI, as MRI itself is also included in the criteria for clinical diagnosis. Instead, we focus on comparing computer-aided diagnosis algorithms on an unseen blinded test set with standardized evaluation methods using the clinical diagnosis as the best available reference standard.

This work interprets the differentiation of patients with AD, MCI and controls as a multi-class classification problem. This might not be optimal as there is an ordering of the classes, i.e. classification of an AD patient as an MCI patient might be less bad than classifying as a healthy person. However, addressing only binary problems, such as AD/CN classification, does not reflect the clinical diagnosis making and results in a too optimistic performance estimate. Because the current clinical diagnosis uses the three classes, we chose to focus on multi-class classification in this challenge and did not use the ordering in the evaluation.

According to the criteria of Petersen (2004) and similar to ADNI, only MCI patients with memory complaints, amnestic MCIs, were included in the data set. For classification, all MCI patients were considered to be a single group which is according to current clinical practice (Petersen, 2004). This is debatable, since MCI patients are known to be a clinically heterogeneous group with different patterns of brain atrophy (Misra et al., 2009), of which some cases will not progress to AD. From this point of view, it can be questioned whether MCI is a diagnostic entity or whether MCI describes a stage on a continuum from cognitively normal to AD. If MCI is actually an intermediate between the two other classes, the AD/CN border in three-class classification would be also subject to discussion. Although the usage of the MCI definition is advised for diagnosis in clinical practice (Petersen, 2004), the borders between AD/MCI and MCI/CN based on diagnostic criteria can be unclear. Because of those unclear borders and the heterogeneity in the MCI class, classification accuracies are expected to be reduced. The results of the evaluated algorithms confirmed that distinguishing MCI from AD and CN is difficult. The AUC for all algorithms was the lowest for the MCI class and in most cases also TPF was the lowest for MCI. Despite these limitations, the same choices for the reference standard, classification, and the MCI group were made in the ADBD DREAM challenge. Moreover, since MCI is still used as diagnostic label in current clinical practice, having an objective and automated algorithm that makes such diagnosis based on structural MRI, would already be useful, for example, as a second opinion.

For facilitating clinical implementation of the algorithms, it would be a great benefit to make the evaluated algorithms publicly available for enabling validation on other data without the need for reimplementation. In our evaluation framework, this is not yet possible. Instead, in our framework, all teams were encouraged to make a step-by-step implementation guide¹⁴ to make it possible to run the submitted algorithms on other data sets.

5.2. Evaluated algorithms and results

The best performing algorithm (Sørensen-equal: accuracy = 63.0%, AUC = 78.8%) was based on a combination of features and used a simple linear classifier (LDA). Also, regarding the other top-ranked algorithms, the best performances were achieved by algorithms that incorporated features describing different properties of the scans. Although the performance differences between the different feature extraction strategies were small, algorithms that used shape or intensity features in addition to regional volumes and thickness performed slightly better than algorithms solely based on shape features or on volume features. The VBM-based methods also performed well. Different multivariate analysis techniques were used by the algorithms, mainly regression, SVM, and random forest classifiers. No trend in the best performing type of classifier could be found.

Since hardly any results for three-class classification have been reported, we cannot compare with representative results from the literature. The TPFs and AUCs for the AD and CN classes in this work are a bit lower than those reported previously for AD/CN classification (Falahati et al., 2014), but we expect that this is mainly due to the additional MCI class in the classification and its heterogeneity. The ADBD Dream challenge also evaluated three-class classification, and it reported performances similar to those of this study (see Section 5.1.1).

The methods Sørensen-equal and Sørensen-optimized were ranked highest both based on accuracy and AUC. In general, the rankings by the two performance measures were similar, but there were some exceptions. Abdulkadir, for example, ranked much higher based on AUC (rank=3) than on accuracy (rank=12.5), which means that this method was capable of distinguishing the classes with high sensitivity and specificity at different cut-off points. However, for measuring the accuracy, not the optimal cut-off point was chosen by the classifier. The accuracy of this method could be improved by optimizing the class priors used by the classifier. For classification, it is generally assumed that the training data and its class priors are representative for the test data. Depending on the class distributions of the training data used, this assumption on class priors might not always have been justified. On the other hand, it is difficult to correct for differences in class priors, as the distribution of the test set is often unknown. Of the participating teams, two specifically took the issue of class priors into account. Eskildsen et al. removed the class unbalance of the training set using a resampling technique (Eskildsen et al., 2014; Chawla et al., 2002). Sørensen et al. experimented with two sets of class priors: equal class priors and class priors optimized on the 30 training subjects (Sørensen et al., 2014). However, for most algorithms accuracy and AUC were similar, indicating that reasonable assumptions on the class priors were made.

The provided data set consisted of structural MRI scans from three centers. We noticed a small performance difference between the three subsets. The performance on the UP subset was the highest, but this might be explained by chance given the small size of the UP data set (n=27 in the test set, n=3 in the training set) and a slight selection bias towards more clinically clear-cut cases. Between the two other subsets, a minor performance difference could be noted. The performance differences might be caused by slight differences in inclusion criteria, used scanners and scanning protocols between the centers, emphasizing the importance of a multi-center test set.

The size of the training set is known to have a large influence on the performance of the classifier (Falahati et al., 2014). Although this study does not provide enough information to draw a valid conclusion, as we evaluated only 29 algorithms with the majority of training sets consisting of 600–800 subjects, we see a slight positive relation between the number of training data sets and the test set performance.

The mean age of AD patients in the used data set was 66.1 ± 5.2 years, whereas the age for AD patients in the ADNI cohorts that were used by many algorithms for training was about 10 years higher (Abdulkadir et al., 2014; Amoroso et al., 2014; Eskildsen et al., 2014; Ledig et al., 2014; Sarica et al., 2014; Sensi et al., 2014; Sørensen et al., 2014; Wachinger et al., 2014a). Although the same diagnosis criteria were used in both cohorts, this age difference is most probably due to selection bias. The used dataset consists of clinical data representing the outpatient clinic population, whereas ADNI consists of research data. For clinical practice, MRI may be used more conservatively. In addition, there is a referral bias towards younger patients because the VUMC and the EMC are tertiary centers specialized in presenile dementia. This age difference between training and test data might have had a negative effect on the performances found in this study. To take this into account, eight of the 15 teams incorporated age effects in their algorithms.

5.3. Recommendations for future work

This challenge provided insight on the best strategies for computer-aided diagnosis of dementia and on the performance of such algorithms on an independent clinically representative data set. However, for this challenge, specific choices for the evaluation framework were made. Therefore, for clinical implementation of such algorithms, more validation studies that explore variations of this challenge are necessary.

A limitation of this challenge is that the clinical diagnosis is used as reference standard. For the clinical diagnosis, MCI is used as a diagnostic entity; it could however be questioned whether this can exist as separate diagnosis next to AD. In addition, the accuracy of the clinical diagnosis is limited, but data sets with better reference standards are scarce. The best reference standard is the postmortem diagnosis based on pathology, which is the ground truth for AD diagnosis. A good alternative would be a reference standard based on the clinical diagnosis including amyloid biomarkers or a long-term follow-up. For a validation study, we strongly recommend to have an independent test set with blinded diagnostic labels to promote generalizability.

In this challenge, classification was based on structural MRI using subject age and sex as the only additional information. For a future challenge in which ground truth diagnosis is used for reference, it would be very interesting to use all available clinical data in addition to structural MRI as input for the computer-aided diagnosis algorithms. For the current challenge, this was not yet useful as the reference standard was based directly on these clinical data. For structural MRI, this is not a problem as it is only used qualitatively in clinical diagnosis making.

For the current work, we adopted hardly any constraints resulting in a wide range of participating algorithms. To aid the understanding of the influence of certain methodological choices on the algorithm performance, new projects could decide to focus on comparing specific elements of the algorithms.

We cannot be sure that the included algorithms are the best currently available. Although this challenge was broadly advertised, quite some effort from participants was required which may have kept some researchers from participating. Of the teams that submitted a proposal, two thirds did not participate in the challenge, possibly due to lack of time or resources. To reach a wider audience in future challenges, organizers could reduce the effort required from participants, for example by providing precomputed features.

Another interesting problem to address in a future challenge is that of differential diagnosis of AD and other types of dementia (e.g., frontotemporal dementia (Du et al., 2006; Davatzikos et al., 2008b; Raamana et al., 2014) or Lewy body dementia (Lebedev et al., 2013)). In addition, instead of evaluating diagnostic algorithms, evaluation of prognostic algorithms would be very useful. Future challenges could therefore evaluate the classification of MCI patients that convert to AD and MCI patients that do not convert to AD within a certain time period.

Lastly, new projects could request their participants to make their algorithms publicly available to facilitate clinical implementation of the algorithms for computer-aided diagnosis.

6. Conclusion

We presented a framework for the comparison of algorithms for computer-aided diagnosis of AD and MCI using structural MRI data and used it to compare 29 algorithms submitted by 15 research teams. The framework defines evaluation criteria and provides a previously unseen multi-center data set with the diagnoses blinded to the authors of the algorithms. The results of this framework therefore present a fair comparison of algorithms for multi-class classification of AD, MCI and CN. The best algorithm, developed by Sørensen et al., yielded an accuracy of 63% and an AUC of 78.8%. Although the performance of the algorithms was influenced by many factors, we noted that the best performance was generally achieved by methods that used a combination of features.

The evaluation framework remains open for new submissions to be added to the ranking. We refer interested readers to the web site http://caddementia.grand-challenge.org, where instructions for participation can be found.

We believe that public large-scale validation studies, such as this work, are an important step towards the introduction of high-potential algorithms for computer-aided diagnosis of dementia into clinical practice.

Highlights.

• We objectively compared 29 algorithms for computer-aided diagnosis of dementia

• 15 international teams tested their algorithms on a blinded multicenter dataset

• Algorithms combining types of features performed best: the highest AUC was 78.8%