Lay Summary
Exposure to paroxetine, a commonly prescribed antidepressant, causes mice to produce more daughters than sons. Altering litter sex ratio can provide benefits to parents, and many hypotheses have been offered to explain this phenomenon. Here, we find that maternal exposure negatively influences sons more than daughters and that by biasing the sex ratio of their litters toward daughters, mothers increase their number of grandchildren.
Key words: adaptive sex allocation, cost of reproduction hypothesis, fitness assay, paroxetine, SSRI.
Abstract
While conducting a toxicity assessment of the antidepressant paroxetine (Paxil®), in wild-derived mice (Mus musculus), we observed that exposed dams (P0) produced female biased litters (32:68 M:F). Though numerous experimental manipulations have induced sex ratio bias in mice, none have assessed the fitness of the offspring from these litters relative to controls. Here, we retrospectively analyze experimentally derived fitness data gathered for the purpose of toxicological assessment in light of 2 leading hypothesis (Trivers–Willard hypothesis [TWH] and cost of reproduction hypothesis [CRH]), seeking to test if this facultative sex ratio adjustment fits into an adaptive framework. Control F1 males were heavier than F1 females, but no differences in mass were detected between exposed F1 males and females, suggesting that exposed dams did not save energy by producing fewer males, despite producing 29.2% lighter litters relative to controls. F1 offspring of both treatments were released into seminatural enclosures where fitness was quantified. In enclosures, the relative reproductive success of F1-exposed males (compared with controls) was reduced by ~20% compared with the relative reproductive success of F1-exposed females. Thus, exposed dams increased their fitness by adjusting litters toward females who were less negatively affected by the exposure than males. Collectively, these data provide less support that the observed sex ratio bias results in energetic savings (CRH), and more support for the TWH because fitness was increased by biasing litters toward female offspring. These mammalian data are unique in their ability to support the TWH through the use of relevant fitness data.
INTRODUCTION
In 1973, Trivers and Willard proposed that if parents are capable of facultative sex ratio adjustment of their offspring toward the sex that is likely to have higher reproductive success, then these parents can increase their inclusive fitness. The Trivers–Willard hypothesis (TWH) is based on the observation that in polygynous species, a male of high quality can have substantial reproductive success by mating with several females, whereas low-quality males may not breed at all. In contrast, reproductive success differences are not nearly as extreme in females, where both low- and high-quality females often produce similar numbers of offspring. Trivers and Willard (1973) postulated that high-quality mothers should produce high-quality sons, who will out reproduce their sisters of the same condition; low-quality mothers should produce low-quality daughters, who will out reproduce their brothers of the same condition. An alternative, modern framing of the TWH, is if environmental conditions differentially influence the fitness of males and females, then selection favors sex ratio adjustment (West 2009). Such facultative sex ratio adjustment is adaptive because it will increase the rate at which genes are passed onto future generations.
An alternative hypothesis for adaptive sex ratio adjustment posits that if differential investment in male and female offspring occurs, then parents can skew their litters in favor of the less-expensive sex to reduce the cost of reproduction and increase their own rates of survival and fitness, especially when resources are limited; this idea is known as the cost of reproduction hypothesis (CRH) (Myers 1978). The CRH predicts that low-quality mothers are reluctant to invest resources into the sex with the highest energy demands (often males in mammalian species). By preferentially investing into female offspring, the mother minimizes her own reproductive costs. The importance of parental investment with regard to sex allocation theory has been appreciated since Fisher, though demonstrating its importance relative to the TWH in vertebrate adaptive sex ratio adjustment has been difficult, as often times there is supporting evidence for both hypotheses and they are not mutually exclusive (Cockburn et al. 2002). However, recent studies of birds have been implemented to explicitly disentangle these hypotheses and indicate that differential offspring energetic cost best explains sex ratio bias in the black-legged kittiwake (Rissa tridactyla) (Merkling et al. 2015) and that a combination of both energetics and Trivers–Willard dynamics, driven by male–male competition, explains biases in clutches of house wrens (Troglodytes aedon) (Bowers et al. 2015). For reviews of these hypotheses and others concerning sex allocation theory, see references West (2009) and Komdeur (2012).
The classic ecological example of TWH is the case of the red deer (Cervus elaphus), where dominant females are more likely to produce male offspring that will have higher fitness than subordinate female offspring (Clutton-Brock et al. 1984, 1986). Interestingly, more recent work on this population has revealed that as population densities increase, the biasing of sex ratios toward male offspring in dominant females has disappeared due to the increased difficulty in raising offspring under these conditions; this paired with the observation that male offspring are more likely to die under low resource conditions, indicates that the CRH is also at play in explaining the sex ratios of this population (Kruuk et al. 1999). Similarly, in other observational studies in mammals either the TWH or an iteration of the CRH has been invoked to explain relationships between maternal condition and sex ratio bias occurring in bighorn sheep (Ovis canadensis) (Martin and Festa-Bianchet 2011), Richardson’s ground squirrels (Urocitellus richardsonii) (Ryan et al. 2011) and alpine marmots (Marmota marmota) (Allaine et al. 2000), though it remains largely unclear if one hypothesis or the other is exclusively or even primarily responsible. To disentangle these hypotheses and understand the adaptive basis of sex allocation, empirical measures of both parental investment and offspring fitness are needed (West 2009; Komdeur 2012).
Several experimental manipulations of diets to mimic poor ecological conditions have been successful in causing sex ratio bias and/or inducing differential allocation into one offspring sex over the other in several rodent species. For example, when hamster dams (Mesocricetus auratus) were calorie restricted during pregnancy and lactation, litters were biased toward female offspring and these females weighed more than the male offspring (Labov et al. 1986). Likewise, when wood rat dams (Neotoma floridana) were calorie restricted during lactation, dams invested more into their female offspring than males as measured by offspring mass (McClure 1981). Mice (Mus musculus) consuming a low-calorie diet (Meikle and Drickamer 1986; Dušek et al. 2011) or low-fat diet (Rivers and Crawford 1974; Rosenfeld and Roberts 2004) had female biased litters. Additionally, Cameron (2004) revealed via meta-analysis that maternal condition at the time of conception consistently supported sex ratio bias, where mothers in good body condition produced more male offspring. Though these and other mammalian studies establish a framework to address the adaptive nature of facultative sex ratio adjustment, none have measured the fitness of offspring from the resulting biased litters—measurements that are required to disentangle the leading hypotheses concerning facultative sex ratio adjustment (West 2009; Komdeur 2012).
In a previous experiment, we assessed the safety of the antidepressant paroxetine (Paxil®, GlaxoSmithKline [GSK], Brentford, UK) by conducting fitness assays in wild-derived house mice. To briefly summarize the published experiment (Gaukler et al. 2015), paroxetine-exposed breeders (P0) experienced delayed reproduction and F1 offspring weighed less than their control counterparts. Paroxetine-exposed offspring (F1) were then released into seminatural enclosures where they competed against control animals for mates, resources, and territories over a 28-week period, which represents approximately half of the estimated maximal lifespan for mice in wild populations (Sage 1981). Paroxetine-exposed males had a 13% reduction in mass, dominated 53% fewer territories, had 44% fewer offspring than controls and experienced a 2.5-fold, marginally significant, trend in increased mortality. Paroxetine-exposed F1 females had an initial decline in reproduction relative to controls, but rebounded at later time points (Gaukler et al. 2015).
Here, we examine litter sex ratios of exposed dams (P0) from the aforementioned study and retrospectively utilize the reproductive success data sets generated from the previous experiment to assess 2 hypotheses placing facultative sex ratio adjustment in an adaptive framework. All comparisons, except those involving litter size, within this article are unique from those presented in Gaukler et al. (2015). First, we ask whether paroxetine exposure causes litter sex ratio bias relative to unbiased values and control litters. Second, we ask whether the exposure affects litter size. Third, we ask whether there is differential offspring weaning mass, a proxy for maternal investment, in F1 female versus male offspring and if the degree of this body mass sexual dimorphism differs between exposed and control dams. Finally, we ask whether F1-exposed females and males have differential reproductive success in seminatural enclosures relative to F1 controls, that is, does maternal exposure differentially influence the fitness of male and female offspring.
MATERIALS AND METHODS
Animals
We used wild-derived genetically outbred house mice (Mus musculus) in this experiment, as they exhibit natural behavioral characteristics that allow them to function in natural and seminatural environments, unlike inbred mouse strains (Nelson et al. 2013). In this experiment, animals were from the 12th generation of the colony that is described by Meagher et al. (2000). Cunningham et al. (2013) assessed the relatedness in the 11th generation and found it to be comparable with that in the wild. Individuals were provided access to food and water ad libitum and maintained on a 12:12h light:dark cycle. All procedures were approved by the University of Utah IACUC (protocol number: 07-08002; 10-08002).
Exposure
Paroxetine is a selective serotonin reuptake inhibitor (SSRI) that is prescribed at doses of 20–60mg/day to alleviate depression and other mood disorders (Dunner and Dunbar 1992; GSK 2013). SSRI’s prevent reuptake of serotonin by presynaptic serotonin receptors thereby increasing serotonin availability to postsynaptic serotonin receptors (Stahl 1998). Serotonin is known to have effects on mood, appetite, sexual behavior, and gastrointestinal motility (Stahl 1998). We administered paroxetine (molecular formula: C19H20FNO3·HCl) via diet at a dose of ~22.5mg/kg/day, which is equivalent to a human therapeutic dose of ~1.82mg/kg/day and has been extensively described in Gaukler et al. (2015). The dose we used was to assess toxicity and was selected because it was lower than doses used in previous mouse toxicity assessment studies (Coleman et al. 1999; Rayburn et al. 2000) and was less than 2-fold higher than human therapeutic doses (Dunner and Dunbar 1992; GSK 2013). We selected 60 breeder pairs for this experiment, 20 exposed and 40 controls (there were more controls than exposed because we used control animals in both this and another experiment). When paired (P0) females were 75.8±13.2 (mean [M] ± standard deviation [SD]) weeks old and (P0) males were 70.4±13.8 weeks old. All animals were individually housed, and (P0) females were fed their respective diets 8 days prior and (P0) males 5 days prior to breeding and exposure continued throughout the entire duration of reproduction. Breeders remained together until a maximum of 4 litters were produced (Supplementary Figure S1; panel A). At 28 days of age, we weaned F1 offspring and housed them with same-sex siblings as wild mice become sexually mature at ~6 weeks of age. Upon weaning, we recorded individual mass, litter size, and sex, which we determined by anogenital distance at weaning and later confirmed the majority of individuals again in adulthood (Supplementary Figure S1; panel B). When a mistake was made in sexing at weaning (3 mis-sexed individuals of 70 total offspring), we excluded mass data from those litters from analysis, as a mass measurement could not be directly paired with having come from a male or female offspring because individuals were not uniquely marked. However, all individuals that were selected for the seminatural enclosure portion of the experiment were uniquely ear punched and received a passive integrated transponder tag. After weaning, exposure continued via diet until we released F1 offspring into the seminatural enclosures, at which time males were on average 14.3±4.7 weeks old and females were 18.9±7.0. Once in seminatural enclosures, we provided all animals with the control diet ad libitum because we currently do not have a way to keep exposed and control animals on their respective diets during direct competition in enclosures.
Seminatural enclosures
Enclosures have previously been described in detail in Ruff et al. (2013). Briefly, all enclosures are indoors, measure ~30 m2 and contain 4 defendable optimal territories each with multiple dark nesting sites and having direct access to food. In addition, each enclosure contains 2 suboptimal territories with nest boxes and feeders exposed to light. Territories are separated by hardware mesh that is easily climbed, but adds an element of spatial complexity. Food and water are provided ad libitum in all territories (Figure 1). Animals are kept on a 12:12h light:dark cycle.
Figure 1.
Photograph of a seminatural enclosure. All enclosures are indoors and are ~30 m2. Each enclosure contains 6 territories (4 optimal and 2 suboptimal) that are divided by wire mesh that is easily climbed but adds an element of spatial complexity. The optimal territories have large bins, which contain multiple dark nesting sites and are defendable due to 1 entrance. The suboptimal territories consist of light-exposed nesting sites. All territories have access to food within the chimney-like structures and water (poultry waterers) ad libitum. Passive integrated transponder tag antennas (tennis racket-like structures) are placed above each feeding site. Photograph courtesy D. Cornwall.
We established 5 independent populations (one population per enclosure) and maintained them for 28 weeks. Populations consisted of 8 F1 males and either 14 or 16 F1 females, for a total of 116 animals. Half of each sex were exposed individuals and the remainder were controls. This population structure allows exposed individuals to directly compete with controls for resources, territories, and mates. Enclosure space and population size created a population density reported within the range observed in the wild (Sage 1981).
We released males into the enclosures with nonexperimental females to allow them to establish territories and prevent incidental breeding with experimental females. We removed nonexperimental females and replaced them with experimental females 1 week later. Relatedness at the cousin level or above was generally avoided, but when present, it was balanced between exposed and control groups. Four populations contained 1–2 brother pairs, all populations contained sister pairs and 4 populations contained sister triplets. In a single population, 2 males, 1 each per exposed and control groups, each had 2 sisters in the same population. All of these situations would be found in nature.
Reproductive success and sex determination within seminatural enclosures
We determined reproductive success of F1 individuals by removing and genotyping F2 offspring during 5-week intervals within enclosures as described in Gaukler et al. (2015). In 3 of the 5 populations, we determined reproductive success on a treatment level by examining sex-specific nonoverlapping allelic variants; females were selected on a length variant of the mitochondrial genome (5′-TTGGTTTCACGGAGGATGGT and 5′-CACCACCAGCA CCCAAAGCT) (Meagher et al. 2000). For example, all control females had mitochondrial variant type 1 and all exposed females had mitochondrial variant type 2 within a population. Males were selected on allelic variants in the inverted repeat region near the Sry on the Y-chromosome (5′-CAGGGTTTCTCTCTAGCACA and 5′-CACAACTGGGCTTTGCACATTG) (Meagher et al. 2000). Reciprocal markers were assigned across populations to control for any possible confounding effects. This method allowed us to determine which treatment group (control or exposed) the parents of the F2 individuals came from (Supplementary Figure S1; panels C and D). Using this approach, male F2 offspring were assigned to both a mother treatment group and a father treatment group. However, as females lack the Y-chromosome, F2 female offspring could only be assigned to a mother treatment group. We collected a total of 872 samples with an average of 174.4±38.1 (M ± SD) F2 offspring per population. We also assessed Y-chromosome genotypes in all 5 populations and obtained 414 Y-chromosome genotypes. We assessed mitochondrial genotypes in 626 samples (3 of 5 populations) and obtained genotypes for 100% of these F2 offspring. To gain a better understanding of individual-level reproductive success, we determined reproductive success through genetic parentage analysis in the remaining 2 populations (i.e., 1 mother and 1 father assigned to each F2 offspring) by examining multiple autosomal microsatellite loci. We amplified, scored, and analyzed between 6 and 17 autosomal microsatellite loci in a stepwise fashion. The loci used were d1mit251, d1mit449, d3mit22, d3mit312, d3mit333, d4mit205, d5mit139, d6mit138, d9mit232, d9mit251, d12mit277, d14mit128, d17mit24, d17mit62, d17mit82, d17mit102, and d19mit110 (Gaukler et al. 2015). Primer sequences were obtained from the Mouse Genome Informatics website (The Jackson Laboratory 2013, Bar Harbor, ME). Parentage was assigned in Cervus 3.0 (Kalinowski et al. 2007), and we accepted mother–father–offspring relationships when 95% trio confidence was obtained. Using this rule, we assigned parentage to 91% (187/205) of offspring in one population and 75% (147/195) in the second population. For analysis purposes, we converted the data from the multiple microsatellite parentage determination to treatment-level readouts (total number of F2 offspring per either exposed or control groups within a population vs. total number of F2 offspring per individual (Supplementary Figure S1; panel D)].
Statistical analyses
As offspring can only be female or male, we analyzed sex ratio with a generalized linear mixed model (GLMM) with a binomial distribution and logit link as is recommended (Wilson and Hardy 2002). We set birth cage as a random effect to control for repeated measures as we assessed multiple litters. As reproduction data are discrete counts, we modeled litter size across the fixed effect of treatment in a GLMM with a Poisson distribution and a logarithmic link, the native link for the Poisson distribution in the lme4 library (Bates et al. 2015). The model assessed the fixed effect of treatment on litter size, while breeding cage was modeled as a random effect. A total of 70 (17:53 exposed:control) litters from 28 (8:20 exposed:control) breeding cages were assessed.
For litter mass comparisons, we used a linear mixed-effects model (LMM) to assess the fixed effects of treatment, litter order, litter size, and all interaction of these variables on the litter mass at weaning of 56 (15:41 exposed:control) litters from 25 (8:17 exposed:control) breeding cages, while modeling breeding cage as a random effect. For individual pup mass comparisons, we used a LMM to assess the fixed effects of treatment, sex, a sex by treatment interaction, and litter size on the wean mass of 245 (68:177 exposed:control) pups from 25 (8:17 exposed:control) breeding cages, while modeling breeding cage and litter ID as random effects. For both LMMs that assessed wean mass of litters and individuals, the intercept was set at a litter size of 4, as this was the median litter size for both exposed and control litters.
To determine if the likelihood of an F2 pup being produced by an F1-exposed individual (vs. a F1 control individual) differed between female and male parents within seminatural enclosures, we used a GLMM, assuming a binomial distribution and implementing a logit link. F2 offspring were collected from 5 populations at 5 time points for 25 samplings for both F1 male and female reproductive success counts (observations = 50). For each observation, the count of F2 offspring from exposed parents relative to the count of F2 control offspring was assessed with regard to parental sex. We modeled sex as a fixed effect and modeled population as a random effect to control for repeated measures. We used this relative reproductive success method of analysis, as reproduction assessed in enclosures is based on separate measurement for females and males, mitochondrial and multiple autosomal microsatellite loci for females (total offspring), and the Y-chromosome marker for males (male offspring); thus, making them not directly comparable. By comparing the relative reproductive success of F1-exposed females and males relative to their F1 control counterparts, we can compare the relative reproductive success between F1-exposed females and males as a unitless ratio because we confirmed sex ratios of F2 offspring between treatments did not differ within enclosures (GLMM; z = 0.195, P = 0.846).
To eliminate the possibility that F1-exposed males fathered more daughters than sons and therefore had just as many offspring as F1 control males, we evaluated the sex ratios of individual fathers from the 2 populations where individual parentage assignment was determined. We found no significant difference of sex ratios of F1-exposed fathers compared with F1 control fathers (GLMM; z = −0.645, P = 0.519). We have no reason to suspect that the sex ratios of F1 males to be any different in the 3 of the 5 populations where individual parentage was not determined suggesting that F1 exposed males had reduced reproductive success (in terms of both sons and daughters) compared with F1 control males.
We performed all GLMMs and LMMs in R 3.2.2 using the lme4 library (R Development Core Team 2015; Bates et al. 2015), and all alpha values were 0.05 and tests were 2 tailed. We determined degrees of freedom and resulting P values for LMMs with a Satterthwaite approximation using the lmerTest library (Kuznetsova et al. 2015). For cage-based measures, several candidate models were generated for each analysis that included or excluded litter order, litter size, and their potential interaction with each other and the other fixed effects. In all candidate models, treatment was included, as it was the variable under direct investigation, and in models of wean mass, litter size was always included. Likewise, in the individual, wean mass models a treatment by sex interaction was always included as this interaction was necessary for our inferences. Model selection was done using corrected Akaike information criterion (AICc) scores (Supplementary Table S1), calculated with the AICcmodavg library (Mazerolle 2015), and in all cases, the model with the lowest score was selected. For models concerning litter size, litter wean mass and individual wean mass the best candidate model was selected, and model averaging was not used as ΔAICc >2, a widely used minimum cutoff (Burnham and Anderson 2002). For models concerning litter sex ratio, ΔAICc values were <2 between the 2 leading candidates so a model averaging approach was employed to estimate the parameter of interest incorporating both candidates; however, the interpretation of the fixed effect of treatment did not differ between the candidates (0.72±0.30 vs. 0.74±0.30) or the average (0.73±0.30). Thus, the model with the fewest parameters, which also had the lowest AICc, was selected parsimoniously, because the top 2 candidates were simply more or less complicated versions of the same model; this approach is recommended (Richards 2008).
RESULTS
Sex ratio of F1 litters born in cages
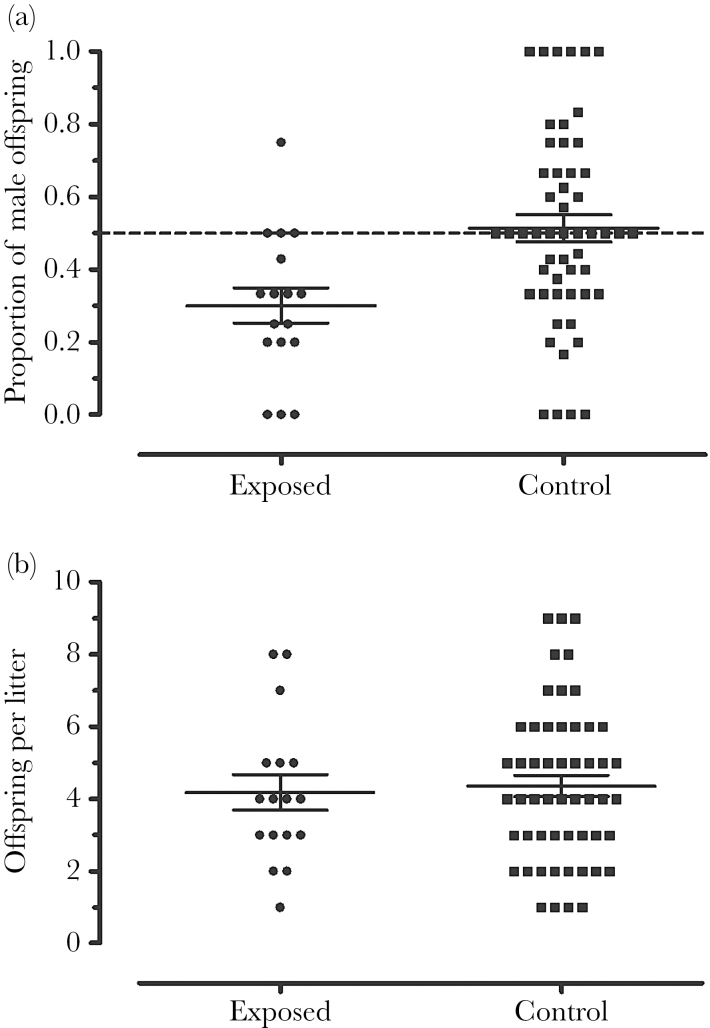
Sex ratio was affected by exposure treatment as exposed dams (P0) produced litters with a sex ratio of 32:68 M:F, whereas control dams (P0) had a sex ratio of 51:49 M:F. Exposed F1 sex ratio was biased toward female offspring when we compared this ratio to an expected 50:50 ratio (GLMM; z = −2.766, P < 0.01; Figure 2a) and when we compared this ratio with control breeders (GLMM; z = 2.380, P < 0.05; Table 1).
Figure 2.
F1 litter sex ratio and litter size from exposed and control dams (P0). (a) Exposed litters were female biased and deviated from the expected 1:1 sex ratio, (dashed line [GLMM, n = 28 cages, observations = 70 litters; z = −2.766, P < 0.01]). Likewise, exposed litter sex ratio differed from that of controls (GLMM, n = 28 cages, observations = 70 litters, z = 2.380, P < 0.05). (b) We did not detect differences in litter size between exposed and control dams (P0) (GLMM; n = 28 cages, observations = 70 litters, z = 0.178, P = 0.859). Points represent individual litters, lines represent means, and error bars represent standard error.
Table 1.
Mixed model results for F1 sex ratio and litter size
| Litter sex ratio | GLMM with binomial distribution and logit link (groups = 28, observations = 70) | |||
|---|---|---|---|---|
| Random effects | Variance | SD | ||
| Cage (intercept) | 0.046 | 0.215 | ||
| Fixed effects | Estimate | Standard error | z value | Pr(> |z|) |
| Intercept (exposure) | −0.743 | 0.269 | −2.766 | 0.006** |
| Control | 0.724 | 0.304 | 2.380 | 0.017* |
| Litter size | GLMM with Poisson distribution and logarithmic link (groups = 28, observations = 70) | |||
| Random effects | Variance | SD | ||
| Cage (intercept) | 0.034 | 0.186 | ||
| Fixed effects | Estimate | Standard error | z value | Pr(> |z|) |
| Intercept (exposure) | 1.425 | 0.138 | 10.324 | <0.001*** |
| Control | 0.028 | 0.160 | 0.178 | 0.859 |
*P < 0.05, **P < 0.01, ***P < 0.001.
F1 litter size
Although we detected a significant bias toward female offspring in the exposed group, we did not observe differences in litter size between exposed and control litters (GLMM; z = 0.178, P = 0.859; Figure 2b). Exposed and control litters had an average of 4.15 (standard error of the mean [SEM] +0.62, −0.53) and 4.28 (+0.74, −0.63) pups per litter, respectively. SEMs are asymmetric, as values have been back-transformed from logarithmic data (Table 1).
F1 litter wean mass
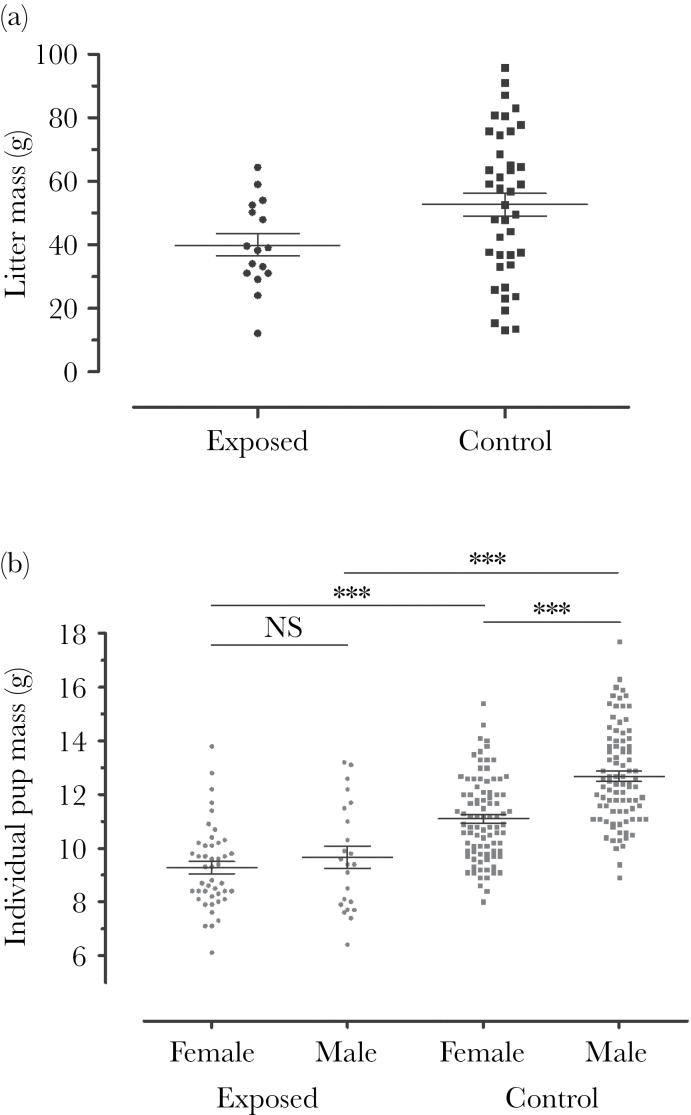
Exposed litters were 29.2% lighter than control litters. The wean mass of exposed litters was 31.8±3.9g (M ± SEM), whereas it was 44.9±2.2g for controls; this difference was statistically significant (GLMM; t = −3.387, P < 0.01; Figure 3a). As expected, litters with larger litter size had higher masses (GLMM; t = 7.847, P < 0.001); however, a marginally significant interaction was detected between treatment and litter size, wherein the discrepancy in mass between exposed and control litters increased with litter size (GLMM; t = −1.981, P = 0.055). Litter order was not found to directly affect litter mass (GLMM; t = 1.521, P = 0.135), and it was not found to significantly interact with exposure treatment (GLMM; t = 1.216, P = 0.231). However, litter order did significantly interact with litter size (GLMM; t = 2.172, P < 0.05), where litter size increased with order, and this interaction did not differ between exposed and control litters (GLMM; t = 0.777, P = 0.442; Table 2).
Figure 3.
Wean mass of exposed and control F1 offspring. (a) Exposed dams (P0) produced lighter litters than did controls (GLMM; n = 25 cages, observations = 56 litters, z = −3.387, P < 0.01). (b) Exposed F1 offspring of both sexes had reduced mass at weaning compared with their control counterparts (Tukey’s post hoc test; n = 25 cages, observations = 245, female P < 0.001, male P < 0.001). F1 control males had greater mass than F1 control females (P < 0.001). However, wean mass did not differ between F1-exposed males and females (P = 0.820). In (a) points represent litters, whereas in (b), points represent individuals. Lines represent means, error bars represent standard error, and ***P < 0.001.
Table 2.
Mixed model results for F1 litter and individual mass
| Litter wean mass | LMM (groups = 25, observations = 56, intercept set at litter size of 4) | |||
|---|---|---|---|---|
| Random effects | Variance | SD | ||
| Cage (intercept) | 7.687 | 2.773 | ||
| Fixed effects | Estimate | Standard error | t value | Pr(> |t|) |
| Intercept (control) | 44.948 | 2.152 | 20.884 | <0.001*** |
| Exposure | −13.168 | 3.888 | −3.387 | 0.001** |
| Litter order | 1.187 | 0.780 | 1.521 | 0.135 |
| Litter size | 8.469 | 1.079 | 7.847 | <0.001*** |
| Exposure × litter order | 2.176 | 1.790 | 1.216 | 0.231 |
| Exposure × litter size | −5.508 | 2.781 | −1.981 | 0.055 |
| Litter order × litter size | 0.852 | 0.392 | 2.172 | 0.035* |
| Exposure × litter order × litter size | 0.970 | 1.247 | 0.777 | 0.442 |
| Individual wean mass | LMM (groups = 25, observations = 245, intercept set at litter size of 4) | |||
| Random effects | Variance | SD | ||
| Cage (intercept) | 0.343 | 0.586 | ||
| Litter ID (intercept) | 0.636 | 0.798 | ||
| Fixed effects | Estimate | Standard error | t value | Pr(> |t|) |
| Intercept (control, female) | 12.613 | 0.448 | 28.128 | <0.001*** |
| Exposure | −1.817 | 0.425 | −4.275 | 0.0002*** |
| Sex (male) | 1.575 | 0.191 | 8.230 | <0.001*** |
| Sex (male) × exposure | −1.008 | 0.373 | −2.701 | 0.008** |
| Litter size | −0.288 | 0.079 | −3.625 | 0.001** |
*P < 0.05, **P < 0.01, ***P < 0.001.
F1 individual wean mass
The relative sexual dimorphism in pup mass was influenced by exposure. Specifically, the increased mass of F1 male offspring relative to their sisters was reduced in litters of exposed dams (P0) relative to controls (LMM; t = −2.701, P < 0.01; Figure 3b) as F1 males were only 0.57±0.37g heavier than F1 females. As we detected a significant effect of treatment, sex and their interaction in the LMM, we performed a post hoc Tukey’s test on all pair-wise combinations and found that all were significant (P < 0.001), except between the masses of exposed F1 females and males (P = 0.820). We found that litter size had an effect on individual wean mass where individuals from larger litters were on average 0.29±0.08g lighter per pup (LMM; t = −3.625, P < 0.01; Table 2).
Relative reproductive success in seminatural enclosures
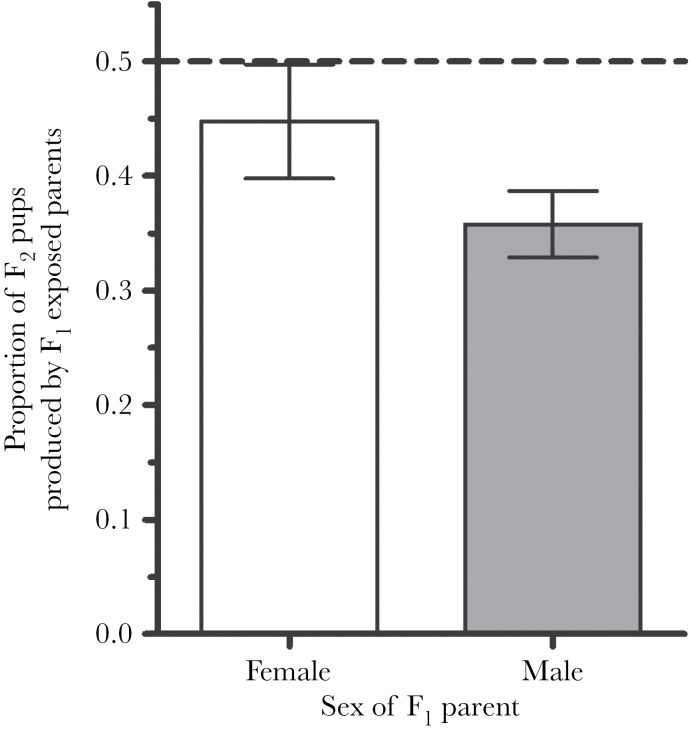
The relative reproductive success of F1-exposed males (compared with F1 control males) was reduced compared with the relative reproductive success of F1-exposed females (compared with F1 control females). Specifically, the probability that an F2 pup was born to a F1-exposed female (44.8%) was higher than that of an F2 pup that was sired by a F1-exposed male (35.8% [GLMM; z = −2.980, P < 0.01; Figure 4]), indicating that F1-exposed females were less affected by exposure than males and out reproduced their brothers of the same condition by ~20% (Table 3).
Figure 4.
Relative reproductive success within seminatural enclosures by sex. The relative reproductive success of exposed F1 males (compared with control males) was reduced compared with the relative reproductive success of exposed females F1 (compared with control females) (GLMM; n = 5 populations, observations = 50, z = −2.980, P < 0.01). The dashed line indicates the level of reproduction required to be equivalent to controls. Error bars represent standard error from 5 samplings of each population in seminatural enclosures. As female and male reproductive success were measured with different techniques, the female bar is informed by twice as many offspring as the male bar.
Table 3.
GLMM results for F2 reproductive success comparisons within seminatural enclosures
| Relative reproductive success (exposed:control) | GLMM with binomial distribution and logit link (groups = 5, observations = 50) | |||
|---|---|---|---|---|
| Random effects | Variance | SD | ||
| Population (intercept) | 0.184 | 0.429 | ||
| Fixed effects | Estimate | Standard error | z value | Pr(> |z|) |
| Intercept (female) | −0.211 | 0.204 | −1.033 | 0.302 |
| Male | −0.374 | 0.126 | −2.980 | 0.003** |
**P < 0.01.
DISCUSSION
Paroxetine exposure caused substantial F1 litter sex ratio bias relative to both unbiased expectations and to control litters. The sex ratio of F1-exposed litters was ~1:2 M:F, and only one litter out of 17 had a sex ratio greater than 50% male. Sex ratio biases have not been detected in other rodent studies assessing the safety and bioactivity of paroxetine, possibly due to the use of laboratory mouse strains (Coleman et al. 1999), which have undergone dozens of generations of selection for consistent and reliable reproduction in cages. As this study used wild-derived mice that have been randomly bred to maintain genetic diversity, it is possible that they still possess the molecular machinery necessary to bias litter sex ratios in response to physiological or environmental stressors, which may have been lost in inbred strains.
It is unknown how paroxetine exposure causes sex ratio bias, though in the largest sense, it is likely due to 1 of 2 explanations—either the exposure adversely affects maternal condition, leading to facultative biasing, or that the exposure to paroxetine itself directly leads to biased litters. The observation that exposed litters weigh less than those of controls supports the notion that exposed dams are of a poorer condition than controls as does our previous finding that F1-exposed males have fewer offspring than F1 control males (Gaukler et al. 2015). However, without a full characterization of the mechanism, we cannot fully eliminate the possibility that paroxetine may lead directly to biased litters, which could occur as a side effect and have no adaptive value. Either of these proposed explanations could be due to endocrine disruption as described in previous studies examining the safety of paroxetine (Gundlah et al. 1998; El-gaafarawi et al. 2005); this endocrine disruption could lead to altered levels of sex hormones that have been associated with sex ratio bias in mammals (Geiringer 1961; Hahn and Hays 1963; Helle et al. 2008). Though endocrine disruption by paroxetine exposure leading to bias directly is possible, it seems unlikely because, though endocrine disrupting chemicals have been shown to alter sex ratios in vertebrates without chromosomal sex determination (Guillette et al. 2000), they have not been shown to do so in mammals where they more commonly result in intersex phenotypes (Yu et al. 2014). Finally, it has yet to be determined if paroxetine exposure consistently biases sex ratios of mice across factors such as age, dose, length of exposure, and maternal body mass, but importantly, in the case, outlined in this study, it resulted in dramatic sex ratio biases.
We found that F1 sex ratio was affected by exposure while not detecting differences in litter size when compared with control litters, suggesting that the sex ratio bias occurred preparturition. Although mechanisms were not evaluated in this study, Rosenfeld and Roberts (2004) propose 4 non-mutually exclusive theoretical hypotheses to explain mechanisms of sex ratio biasing in mammals. Prior to conception, sex ratio bias can occur by 1) differential sperm motility of one class of sperm over the other or 2) one class of sperm may be more effective at fertilizing the egg over the other. Perhaps paroxetine directly and adversely affected Y-bearing sperm, such as motility, or caused a reduction in the number of Y-bearing sperm; additionally, perhaps paroxetine exposure altered the female reproductive tract to favor X-bearing sperm. After fertilization has occurred, bias can occur by 3) a difference in the rate at which XX and XY embryos develop prior to implantation or by 4) an increased arrested development in one embryo sex over the other, a mechanism that has been suggested to be a likely driver in sex ratio bias (Krackow 1995). Hypothesis 3 is unlikely because in litter-bearing mammals, faster developing embryos, such as male mice (Valdivia et al. 1993), have a competitive advantage when it comes to securing a place of attachment to the uterine wall, thus male biased litters would be predicted (Krackow 1995). In terms of hypothesis 4, mice have been observed to resorb ~16–19% of the total implanted embryos (Krackow 1992); perhaps males were selectively aborted. Though our findings offer support for some of these hypotheses, the mechanistic cause of sex ratio adjustment remains unknown; however, paroxetine could potentially be a useful tool to elucidate the still mysterious mechanisms causing sex ratio bias.
Though male mice typically weigh more at weaning than their female littermates (Dewsbury et al. 1980; Nelson et al. 2013), this was not the case for offspring within F1-exposed litters. This finding may suggest that the CRH does not explain the observed sex ratio biasing because the overproduction of female offspring did not result in an energetic savings for exposed dams (P0). In other words, as males and females weighed the same, producing more of one sex than the other does not influence total investment. The reduced mass of F1-exposed offspring, and litters in general, relative to controls is an indication that exposed dams (P0) were in less than optimal condition and unable to invest maximally in their litters; therefore, the observed offspring mass data lend stronger support to the first requirement of the TWH by indicating that exposed dams (P0) are of low quality. However, if exposed dams were in lower condition, then producing fewer sons and investing less in them could be in line with the CRH in the broadest sense. It should be mentioned that wean mass is a rather gross measure of maternal investment especially as offspring typically begin consuming solid food around day 17; however, nursing has been documented up until day 28 (Konig and Markl 1987), which is when these animals were weaned. Factors, such as differential metabolic efficiency between treatments, or differential suckling were not assessed and could also contribute to the observed pattern. Furthermore, other metrics, such as quantifying corticosterone levels, may be a better indicator of parental rearing costs than offspring mass (Love et al. 2014). Because several metrics of maternal investment were not considered and the observation that total litter mass of litters of exposed mothers was reduced, it is not possible to completely rule out the CRH; however, so long as there is a correlation between maternal investment and weaning mass, these data at least, in part, address the question of maternal investment as a function of sex ratio.
Within seminatural enclosures the relative reproductive success of F1-exposed males (compared with F1 control males) was reduced compared with the relative reproductive success of F1-exposed females. The greater consequences of exposure experienced by males are likely due to the high levels of male intrasexual competition within polygynous mating systems. Within seminatural enclosures, it has been demonstrated that territorial dominant males sire ~80% of offspring (Carroll et al. 2004). As observed in Gaukler et al. (2015), exposed males acquired only half as many territories as controls; it is likely that this discrepancy in competitive ability explains the reproductive decline observed between exposed and control male groups and underscores the differential influences of paroxetine exposure on reproductive success between the sexes.
Additional evidence that the sex ratio bias in this study supports the TWH can be found in Gaukler et al. (2015). In seminatural enclosures, exposed F1 individuals competed directly with F1 controls and though exposed F1 offspring of both sexes performed more poorly than their control counterparts, this difference was more pronounced in males (Gaukler et al. 2015), lending support to the TWH as an explanation for the observed sex ratio biasing. More specifically, Gaukler et al. (2015) reports that F1-exposed females had only 19% fewer F2 offspring, whereas F1-exposed males had 44% fewer F2 offspring than controls. These observations support the TWH as an explanation for the observed sex ratio bias as low-quality (exposed) mothers produced low-quality sons, who were out reproduced by their sisters of the same condition.
Here, we have demonstrated that the pharmaceutical agent, paroxetine, can dramatically bias sex ratios in wild-derived mice, and our retrospective analysis of reproductive success supports that this bias is consistent within a Trivers–Willard adaptive framework; however, as this experiment was not designed to directly address the adaptive nature of sex ratio bias, some caveats must be considered when interpreting the data. First, exposure to a pharmaceutical is not a common selective pressure on natural populations; though, paroxetine exposure could induce similar physiological responses that are induced by natural occurring stressors, such as food depredation, thermoregulatory stressors, or exposure to plant secondary compounds. Additionally, as human consumption of pharmaceuticals increases, both parent compounds and metabolites of these drugs are becoming ubiquitous in the environment, thus posing direct potential exposure to wildlife populations. Second, as the initial goal of the experiment was toxicity assessment, the exposure period encompassed, in utero, natal and adult exposure of F1 progeny, allowing for the possibility that differential fitness between male and female F1 offspring and between exposed and control animals could be due to exposure outside the window of in utero development; however, it should be noted that this critique pertains to most ecological studies addressing facultative sex ratio adjustment as offspring developing within females typically find themselves in the same circumstance that decreased her quality (e.g., poor habitat or a low position within the social hierarchy) after birth and throughout development.
Though the data presented in this study suggest support for the TWH, reproductive success data must be gathered from further experiments that are designed to explicitly test these hypotheses concerning facultative sex ratio adjustment as has been done in birds (Bowers et al. 2015; Merkling et al. 2015). Unfortunately, previous empirical studies on facultative sex ratio adjustment in mammals have not incorporated fitness measures of offspring, the metric that is needed to disentangle competing adaptive hypotheses; therefore, this study, despite its imperfections, provides novel insight into the underlying basis of this phenomenon and will hopefully encourage additional experiments in this important, but undertested evolutionary arena. Furthermore, the demonstration that paroxetine exposure induces sex ratio biasing toward female offspring in mice provides a new system in which to pursue the enigmatic mechanisms of facultative sex ratio adjustment.
SUPPLEMENTARY MATERIAL
Supplementary material can be found at http://www.beheco.oxfordjournals.org/
FUNDING
This project was supported by the University of Utah’s Technology Commercialization Program and was partially conducted under the support of the National Institutes of Health (R01-GM109500) and National Science Foundation (DEB 09-18969) to (W.P.), and by a National Science Foundation GK-12 Educational Outreach Fellowship (DGE 08-41233) to (S.G.).
Supplementary Material
Acknowledgments
We thank Dr. J. Seger for his input and suggestions on this manuscript; M. Bartlett, S. Eddy, T. Galland, K. Kandaris, D. Kircher, N. Liu, L. Morrison, E. Schwab, M. Sosa, T. Underwood, and E. Young for enclosure maintenance, data collection, and genotyping; A. Bwika and J. Gale for animal care. We also wish to thank the 2 anonymous reviewers who provided helpful comments and feedback that improved this article.
REFERENCES
- Allaine D, Brondex F, Graziani L, Coulon J, Till-Bottraud I. 2000. Male-biased sex ratio in litters of Alpine marmots supports the helper repayment hypothesis. Behav Ecol. 11:507–514. [Google Scholar]
- Bates D, Maechler M, Bolker B, Walker S, Christensen R, Singmann H, Dai B, Grothendiek G. 2015. lme4: linear mixed-effects models using ‘Eigen’ and S4. R Package. Version 1.1–10. Available from: https://cran.r-project.org/web/packages/lme4/lme4.pdf (Accessed 2 September 2016). [Google Scholar]
- Bowers EK, Thompson CF, Sakaluk SK. 2015. Persistent sex-by-environment effects on offspring fitness and sex-ratio adjustment in a wild bird population. J Anim Ecol. 84:473–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burnham KP, Anderson DR. 2002. Model selection and multimodel inference: a proactical information-theroetic approach. 2nd ed. New York: Springer-Verlag. [Google Scholar]
- Cameron EZ. 2004. Facultative adjustment of mammalian sex ratios in support of the Trivers–Willard hypothesis: evidence for a mechanism. Proc Biol Sci. 271:1723–1728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll LS, Meagher S, Morrison L, Penn DJ, Potts WK. 2004. Fitness effects of a selfish gene (the Mus t complex) are revealed in an ecological context. Evolution. 58:1318–1328. [DOI] [PubMed] [Google Scholar]
- Clutton-Brock TH, Albon SD, Guinness FE. 1984. Maternal dominance, breeding success and birth sex ratios in red deer. Nature. 308:358–360. [Google Scholar]
- Clutton-Brock TH, Albon SD, Guinness FE. 1986. Great expectations: dominance, breeding success and offspring sex ratio in red deer. Anim Behav. 34:460–471. [Google Scholar]
- Cockburn A, Legge S, Double M. 2002. Sex ratios in birds and mammals: can the hypotheses be disentangled? In: Hardy I, editor. Sex ratios concepts and research methods. 1st ed. Cambridge (UK): Cambridge University Press. p. 266–286. [Google Scholar]
- Coleman FH, Christensen HD, Gonzalez CL, Rayburn WF. 1999. Behavioral changes in developing mice after prenatal exposure to paroxetine (Paxil). Am J Obstet Gynecol. 181:1166–1171. [DOI] [PubMed] [Google Scholar]
- Cunningham CB, Ruff JS, Chase K, Potts WK, Carrier DR. 2013. Competitive ability in male house mice (Mus musculus): genetic influences. Behav Genet. 43:151–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dewsbury DA, Baumgerdner DJ, Evans RL, Webster DG. 1980. Sexual dimorphism for body mass in 13 taxa of muroid rodents under laboratory conditions. J Mamm. 61:146–149. [PubMed] [Google Scholar]
- Dunner DL, Dunbar GC. 1992. Optimal dose regimen for paroxetine. J Clin Psychiatry. 53 (Suppl):21–26. [PubMed] [Google Scholar]
- Dušek A, Bartoš L, Sedláček F. 2011. Mixed sex allocation strategies in a polytocous mammal, the house mouse (Mus musculus). Behav Ecol Sociobiol. 65:2209–2217. [Google Scholar]
- El-gaafarawi I, Hassan M, Fouad G, El-komey F. 2005. Toxic effects of paroxetine on sexual and reproductive functions of rats. Egypt J Hosp Med. 21:16–32. [Google Scholar]
- Gaukler SM, Ruff JS, Galland T, Kandaris KA, Underwood TK, Liu NM, Young EL, Morrison LC, Yost GS, Potts WK. 2015. Low-dose paroxetine exposure causes lifetime declines in male mouse body weight, reproduction and competitive ability as measured by the novel organismal performance assay. Neurotoxicol Teratol. 47:46–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geiringer E. 1961. Effect of ACTH on sex ratio of the albino rat. Proc Soc Exp Biol Med. 106:752–754. [DOI] [PubMed] [Google Scholar]
- GSK 2013. Paxil (paroxetine hydrochloride) tablets and oral suspension http://www.apotex.com/us/en/products/downloads/pil/paxil_irtb_ins.pdf (Accessed 2014 March).
- Guillette L, Crain A, Gunderson M, Kools S, Milnes M, Orlando E, Rooney A, Woodward A. 2000. Alligators and endocrine disrupting contaminants: a current perspective. Am Zool. 40:438–452. [Google Scholar]
- Gundlah C, Simon LD, Auerbach SB. 1998. Differences in hypothalamic serotonin between estrous phases and gender: an in vivo microdialysis study. Brain Res. 785:91–96. [DOI] [PubMed] [Google Scholar]
- Hahn EW, Hays RL. 1963. Modification of the secondary sex ratio in the albino rat by progesterone and oestrogen therapy. J Reprod Fertil. 6:409–411. [DOI] [PubMed] [Google Scholar]
- Helle S, Laaksonen T, Adamsson A, Paranko J, Huitu O. 2008. Female field voles with high testosterone and glucose levels produce male-biased litters. Anim Behav. 75:1031–1039. [Google Scholar]
- Kalinowski ST, Taper ML, Marshall TC. 2007. Revising how the computer program CERVUS accommodates genotyping error increases success in paternity assignment. Mol Ecol. 16:1099–1106. [DOI] [PubMed] [Google Scholar]
- Komdeur J. 2012. Sex allocation. In: Royle N, Smiseth P, Kolliker M, editors. The evolution of parental care. 1st ed. Oxford: Oxford University Press. p. 171–188. [Google Scholar]
- Konig B, Markl H. 1987. Maternal care in house mice. Behav Ecol Sociobiol. 20:1–9. [Google Scholar]
- Krackow S. 1992. Sex ratio manipulation in wild house mice: the effect of fetal to the mode of reproduction. Biol Reprod. 47:541–548. [DOI] [PubMed] [Google Scholar]
- Krackow S. 1995. The developmental asynchrony hypothesis for sex ratio manipulation. J Theor Biol. 176:273–280. [DOI] [PubMed] [Google Scholar]
- Kruuk LE, Clutton-Brock TH, Albon SD, Pemberton JM, Guinness FE. 1999. Population density affects sex ratio variation in red deer. Nature. 399:459–461. [DOI] [PubMed] [Google Scholar]
- Kuznetsova A, Brockhoff R, Haubo R., Christensen R. 2015. lmerTest: tests in linear mixed effects models R Package. Version 2.0-29. Available from: https://cran.r-project.org/web/packages/lmerTest/lmerTest.pdf (Accessed 2 September 2016)
- Labov JB, Huck UW, Vaswani P, Lisk RD. 1986. Sex ratio manipulation and decreased growth of male offspring of undernourished golden hamsters (Mesocricetus auratus). Behav Ecol Sociobiol. 18:241–249. [Google Scholar]
- Love OP, Madliger CL, Bourgeon S, Semeniuk CA, Williams TD. 2014. Evidence for baseline glucocorticoids as mediators of reproductive investment in a wild bird. Gen Comp Endocrinol. 199:65–69. [DOI] [PubMed] [Google Scholar]
- Martin JG, Festa-Bianchet M. 2011. Sex ratio bias and reproductive strategies: what sex to produce when? Ecology. 92:441–449. [DOI] [PubMed] [Google Scholar]
- Mazerolle MJ. 2015. AICcmodavg: model selection and multimodel inference based on (Q)AIC(c) R package version 2.0-3. Available from: https://cran.r-project.org/web/packages/AICcmodavg/AICcmodavg.pdf (Accessed 2 September 2016).
- McClure PA. 1981. Sex-biased litter reduction in food-restricted wood rats (Neotoma floridana). Science. 211:1058–1060. [DOI] [PubMed] [Google Scholar]
- Meagher S, Penn DJ, Potts WK. 2000. Male-male competition magnifies inbreeding depression in wild house mice. Proc Natl Acad Sci USA. 97:3324–3329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meikle DB, Drickamer LC. 1986. Food availability and secondary sex ratio variation in wild and laboratory house mice (Mus musculus). J Reprod Fertil. 78:587–591. [DOI] [PubMed] [Google Scholar]
- Merkling T, Welcker J, Hewison JM, Hatch S, Kitaysky S, Speakman JR, Danchin E, Blanchard P. 2015. Identifying the selective pressures underlying offspring sex-ratio adjustments: a case study in a wild seabird. Behav Ecol. 26:916–925. [Google Scholar]
- Myers J. 1978. Sex ratio adjustment under food stress: maximization of quality or numbers of offspring? Am Nat. 112:381–388. [Google Scholar]
- Nelson AC, Cauceglia JW, Merkley SD, Youngson NA, Oler AJ, Nelson RJ, Cairns BR, Whitelaw E, Potts WK. 2013. Reintroducing domesticated wild mice to sociality induces adaptive transgenerational effects on MUP expression. Proc Natl Acad Sci USA. 110:19848–19853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rayburn WF, Gonzalez CL, Christensen HD, Kupiec TC, Jacobsen JA, Stewart JD. 2000. Effect of antenatal exposure to paroxetine (paxil) on growth and physical maturation of mice offspring. J Maternal Fetal Med. 9:136–141. [DOI] [PubMed] [Google Scholar]
- R Development Core Team 2015. R: a language and environment for statistical computing. Vienna (Austria): R Foundation for Statistical Computing. [Google Scholar]
- Richards SA. 2008. Dealing with overdispersed count data in applied ecology. J Appl Ecol. 45:218–227. [Google Scholar]
- Rivers JP, Crawford MA. 1974. Maternal nutrition and the sex ratio at birth. Nature. 252:297–298. [DOI] [PubMed] [Google Scholar]
- Rosenfeld CS, Roberts RM. 2004. Maternal diet and other factors affecting offspring sex ratio: a review. Biol Reprod. 71:1063–1070. [DOI] [PubMed] [Google Scholar]
- Ruff JS, Suchy AK, Hugentobler SA, Sosa MM, Schwartz BL, Morrison LC, Gieng SH, Shigenaga MK, Potts WK. 2013. Human-relevant levels of added sugar consumption increase female mortality and lower male fitness in mice. Nat Commun. 4:2245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryan CP, Anderson WG, Gardiner LE, Hare JF. 2011. Stress-induced sex ratios in ground squirrels: support for a mechanistic hypothesis. Behav Ecol. 23:160–167. [Google Scholar]
- Sage R. 1981. Wild mice. In: Foster H, Small J, Fox J, editors. The mouse in biomedical research. 1st ed. New York: Academic Press. p. 40–90. [Google Scholar]
- Stahl SM. 1998. Mechanism of action of serotonin selective reuptake inhibitors. Serotonin receptors and pathways mediate therapeutic effects and side effects. J Affect Disord. 51:215–235. [DOI] [PubMed] [Google Scholar]
- The Jackson Laboratory; Mouse Genome Informatics 2013. http://www.informatics.jax.org (Accessed March 2014).
- Trivers RL, Willard DE. 1973. Natural selection of parental ability to vary the sex ratio of offspring. Science. 179:90–92. [DOI] [PubMed] [Google Scholar]
- Valdivia RP, Kunieda T, Azuma S, Toyoda Y. 1993. PCR sexing and developmental rate differences in preimplantation mouse embryos fertilized and cultured in vitro. Mol Reprod Dev. 35:121–126. [DOI] [PubMed] [Google Scholar]
- West SA. 2009. Sex allocation. Princeton (NJ): Princeton University Press. [Google Scholar]
- Wilson K, Hardy ICW. 2002. Statistical analysis of sex ratios: an introduction. In: Hardy IC, editor. Sex ratios concepts and research methods. 1st ed. Cambridge (UK): Cambridge University Press. p. 48–92. [Google Scholar]
- Yu M, Wang J, Liu W, Qin J, Zhou Q, Wang Y, Huang H, Chen W, Ma C. 2014. Effects of tamoxifen on the sex determination gene and the activation of sex reversal in the developing gonad of mice. Toxicology. 321:89–95. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.