Finite Element Analysis of Sacroiliac Joint Fixation under Compression Loads

Abstract

Background

Sacroiliac joint (SIJ) is a known chronic pain-generator. The last resort of treatment is the arthrodesis. Different implants allow fixation of the joint, but to date there is no tool to analyze their influence on the SIJ biomechanics under physiological loads. The objective was to develop a computational model to biomechanically analyze different parameters of the stable SIJ fixation instrumentation.

Methods

A comprehensive finite element model (FEM) of the pelvis was built with detailed SIJ representation. Bone and sacroiliac joint ligament material properties were calibrated against experimentally acquired load-displacement data of the SIJ. Model evaluation was performed with experimental load-displacement measurements of instrumented cadaveric SIJ. Then six fixation scenarios with one or two implants on one side with two different trajectories (proximal, distal) were simulated and assessed with the FEM under vertical compression loads.

Results

The simulated S1 endplate displacement reduction achieved with the fixation devices was within 3% of the experimentally measured data. Under compression loads, the uninstrumented sacrum exhibited mainly a rotation motion (nutation) of 1.38° and 2.80° respectively at 600 N and 1000 N, with a combined relative translation (0.3 mm). The instrumentation with one screw reduced the local displacement within the SIJ by up to 62.5% for the proximal trajectory vs. 15.6% for the distal trajectory. Adding a second implant had no significant additional effect.

Conclusion

A comprehensive finite element model was developed to assess the biomechanics of SIJ fixation. SIJ devices enable to reduce the motion, mainly rotational, between the sacrum and ilium. Positioning the implant farther from the SIJ instantaneous rotation center was an important factor to reduce the intra-articular displacement.

Clinical relevance

Knowledge provided by this biomechanical study enables improvement of SIJ fixation through optimal implant trajectory.

Introduction

Sacroiliac joint (SIJ) is known to be involved in 10 to 30% of chronic low-back pain, with pathologies such as degenerative sacroiliitis or sacroiliac joint disruption.^{1, 2} After conservative treatment failure, arthrodesis is the last resort.^{1, 3} The aim of this procedure is to minimize the displacements within the sacroiliac joint to allow bone growth and therefore the fusion of the sacrum and ilium. Sacroiliac joint fusion used to be an open and invasive procedure,⁴ but since the late 2000s, new techniques and implants were introduced enabling a percutaneous minimally invasive surgery (MIS).⁵ Those implants are hollowed to allow their insertion around a guidewire, and the cannula also provides a place to put a bone graft if needed. Several devices specifically designed for SIJ arthrodesis were developed such as the iFuse™ (SI Bone, San Jose, CA, USA), the RIALTO™ Sacroiliac Joint Fusion System (Medtronic, Memphis, TN, USA) and the SImmetry^® SI Joint Fusion System (Zyga Technology Inc., Minnetonka, MN, USA).

The SIJ is a complex bichondylar joint with characteristics of both a diarthrosis and a synarthrosis.⁶ It is a strong bearing joint, with limited movements which are thus difficult to measure and characterize. In the case of chronic pathologies of the SIJ, painful sacroiliac displacements require surgical fixation to establish an arthrodesis. This process needs a minimal displacement of the bones to allow bone growth between the condylar surfaces. The SIJ has an inherently small range of motion, but significant motion reduction is still required to facilitate the bone growth. The efficiency of arthrodesis instrumentation in reducing the displacements within the SIJ as well as the best surgical strategy are yet to be investigated.

Despite promising observations, a strong clinical and radiological evidence supporting the bone ingrowth is currently lacking.^{7, 8} In the short and medium term, the intra-articular movement reduction is mainly ensured by the implant⁹ whose action is not currently well known. A few experimental studies have been carried out to characterize the SIJ biomechanics, but generally in non-physiological conditions.^{10, 11} In the past, the understanding of the SIJ biomechanics was achieved through studies using finite element models (FEM).¹²–²¹ These models generally represent SIJ cartilages and ligaments with 1D elements, and scarcely with 2D elements,¹²–¹⁶ and generally benefit from a dedicated experimental definition of individual ligaments. However, the understanding of the SIJ through the use of numerical models could benefit from accurate 3D representation of its complex morphological features.

The objective of this study was to computationally assess the biomechanics of the stable SIJ fixation in physiological conditions using a detailed FEM. More specifically it aimed at evaluating and comparing the pre- (uninstrumented) to post-instrumented SIJ mobility using different implant configurations.

Methods

A detailed FEM of the pelvis was built to evaluate the biomechanics of SIJ fixation and assess the impact of instrumentation parameters.

Finite Element Model of the Pelvis

The 3-dimensional (3D) geometry used for the FEM was reconstructed using a series of contiguous cross section images (slice thickness: 0.6 mm, slice spacing: 1.2mm, pixel size: 0.8mm) of the pelvis of a 50th percentile human volunteer (32 year-old European male, 75 kg, 1.75 m, with no known spinopelvic pathology).²² The slices were semi-automatically segmented (manual adjustment of iso-surfaces generated by automatic thresholding) to allow for 3D reconstruction of the external surface of bony components of the pelvis using a marching cube type algorithm. The volume obtained was then divided into a cortical layer and a trabecular volume using pelvic cortical thickness values from the literature.¹⁵ The coccyx and the coccygeal ligaments were not included in the model considering their minor influence on the biomechanics of the SIJ.²³

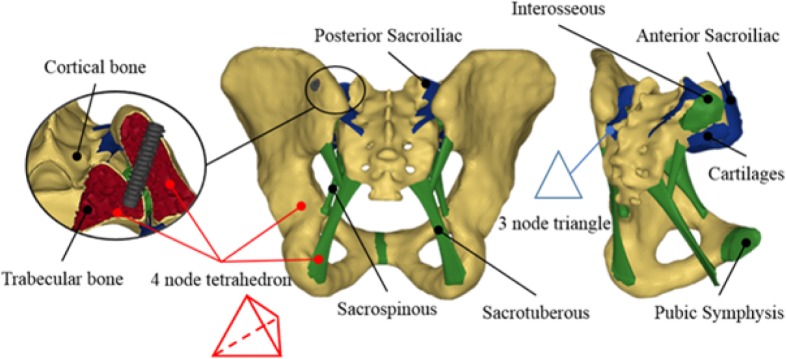
The pelvic bones were modeled as trabecular cores enveloped by an external cortical layer (Figure 2) with its thickness taken and adapted from.^{15, 24, 25} The cortical layer of the iliac bones has regional thicknesses ranging from 0.05 to 5 mm, and the sacral one is 1 mm thick. Both parts were meshed using four node tetrahedral elements of 0.4 mm characteristic length around the SIJ and each screw trajectory and at locations where the radius of curvature of the model was relatively small or there were significant topology changes (sharp change of local surface orientation, etc.). Greater characteristic lengths were used elsewhere (3 and 2 mm on average in the ilium and sacrum respectively) to reduce the computational load when solving the model.

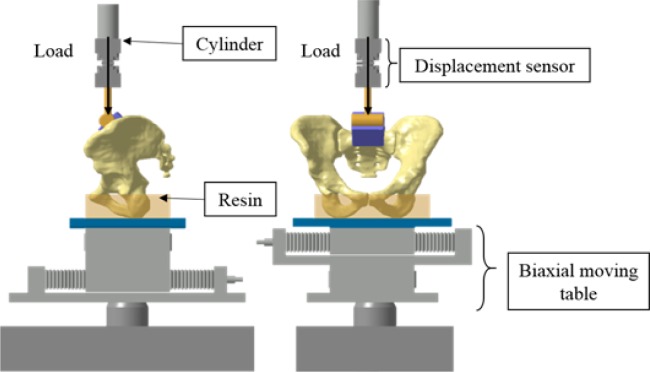
Fig. 2.

Experimental setup (clamps not represented for clarity).

The major pelvic ligaments (interosseous, sacroiliac anterior, sacroiliac posterior, sacrotuberous and sacrospinous) and pubic symphysis geometries were directly implemented from anatomic descriptions.^{26, 27} The sacroiliac posterior and anterior ligaments were meshed using two-dimensional 3 node triangular shell elements with a characteristic length of 2 mm, while the other ligaments and the pubic symphysis were meshed using three-dimensional 4 node tetra-hedrons with a characteristic length of 2 mm (Figure 1). All ligament shell elements were considered as membranes in order to only bear traction loads. There was a continuous mesh between the ligaments and the bones. The sacroiliac articular cartilages were meshed using the elements of the sacrum and iliac bones. The left and right SIJ were considered symmetric and asymptomatic, i.e. no ossification or arthrosis of the joint was modelled. The choice of tetrahedral and triangular elements was based on their ability to conform to complex geometries and their non-warpage properties. The model as a whole contained ∼ 90,000 nodes and ∼ 420,000 elements.

Fig. 1.

Model details (ligaments and mesh).

The material properties of the ligaments were first extracted from a dynamic condition study ^{24, 28} and then calibrated (cf next subsection “Calibration with experimental data”) to quasi-static conditions.

A Johnson-Cook elastoplastic law ²⁹ was used for the bones allowing to represent their non-linear behavior and bone failure. The ligaments and pubic symphysis followed a viscoelastic generalized Kelvin-Voigt material model.^{22, 30} The cartilages were assumed as linear-elastic.^{24, 28} All materials were considered homogenous and isotropic. The material properties are summarized in Table 1.

Table 1.

Material properties used in the FEM.

	Cortical Bone	Trabecular Bone	Ligaments	Pubic Symphysis	SIJ Articular Cartilage
Density (kg.m-3)	2	0.2	2	2	1.05
Young Modulus (MPa)	2625	48.75	40	397	150
Poisson Ratio	0.3	0.25	0.3	0.3	0.2
Yield Stress (MPa)	105	1.95	-	-	-
Hardening modulus (MPa)	875	16.3	-	-	-
Hardening exponent	1	1	-	-	-
Failure plastic strain	0.04	0.04	-	-	-
Tangent Young Modulus (MPa)	-	-	10	155	-
Tangent Poisson ratio	-	-	0.37	0.37	-
Viscoelastic constant	-	-	28	28	-
Navier Constant	-	-	1.105	1.105	-

The simulations were run using the explicit dynamic FEM solver RADIOSS v11 (Altair Engineering, Troy, MI, USA.). A kinetic relaxation scheme was used to perform a quasi-static analysis and reduce dynamic effects of inertia.

Calibration with experimental data

In order to set and calibrate the mechanical properties of the pelvic ligaments of elderly people (who are the most concerned by the SIJ arthrodesis procedure) in physiological conditions, cadaveric tests have been performed. Under IRB approval, two human pelvic specimen (2 women, 88 and 92 years old) were collected from bodies donated for medical research. Care was taken to preserve all major pelvic ligaments (sacroiliac anterior and posterior, sacrotuberous, sacrospinous and interosseous) with a special emphasis on the sacroiliac joint ligaments. The bottom of the iliac bones were casted in a fast cast polyurethane resin (Axson Technologies, Cergy, France) in a physiological standing position with a neutral pelvic tilt, i.e. iliac crests and pubic symphysis in the same vertical plane. They were then fixed to the machine frame using two clamps.

Ten cycles of preconditioning load (0-300 N loading/unloading ramp) were performed to establish a baseline for biological tissue mechanical property measurements.³¹ Subsequently, a 1000 N vertical load was applied on S1-endplate using an uniaxial cylinder connected to a material testing machine (MTS System, Eden Prairie, MN, USA) (Figure 2). The load level was set to represent an important physiological weight in an upright position. The load was applied at a constant rate of 5 N/s, then stayed at the maximal level for 30 s, and released at a constant rate of -20 N/s. The low rates were chosen to minimize the dynamic effects. The S1-endplate displacements were measured at a frequency of 1024 Hz using a LVDT sensor (accuracy 0.01 mm) linked to the cylinder rod (Figure 2).

The same loading conditions were computationally simulated to adjust the mechanical properties of the ligaments in the model using an inverse iterative method to fit the experimental conditions similar to the ones performed by Garcia et al.³² A bisection algorithm was implemented to make the simulated displacement of S1-endplate center matched the experimental data. The bisection method consisted in reducing the Young modulus for the next simulation by 50% if the simulated displacements of the current one were too low, or increasing it by 50% if they were too high. In accordance with the data obtained experimentally, the objective was to simulate a 3 mm (± 5%) S1-endplate displacement with a vertical load of 1000 N. Convergence was obtained after following cycles of bisection, after which a 3.014 mm endplate displacement was simulated, which met the ending criterion of the optimization algorithm (<2% error with experimental data). The resulting Young modulus of 40 MPa, which was within the range of reported data for a younger cohort of subjects,³³ was then used for the ligaments for all the numerical simulations.

SIJ Fixation Modeling

An existing implant was selected for this study (RIALTO™ Sacroiliac Joint Fusion System; Medtronic, Memphis, TN, USA). This implant has a diameter of 12 mm, is cannulated and fenestrated to allow bone ingrowth. Based on the pelvis model size, the 50 mm implant length was selected.

The implant insertion was simplified and modeled in one step consisting in positioning the implant in its instrumentation configuration with respect to the sacrum and the left ilium following the insertion points and orientations of the design of experiments. The sacrum and ilium geometries were modified by subtracting the implant geometry from them. Each implant was meshed using 4 node tetrahedrons with 0.4 mm characteristic length elements. They were modeled as rigid body for computing time optimization, as the stiffness of the implant material is much higher than bone stiffness. Supplementary simulations (the results were not reported here) were performed to ensure that modeling the implants as rigid body had no significant (max difference < 0.05mm) effect on the results. The interface between each implant and the bone was modeled as a contact interface with a point/surface penalty method with a Coulomb friction coefficient set to 0.2.³⁴ Interosseous ligament (IOL) damage induced by the device insertion was modelled by modifying its geometry consistently with the device trajectories.

Model Evaluation

The same specimens used for the calibration data collection were experimentally tested for the model evaluation using the same setup (Figure 2) in different configurations: 1) instrumented with one implant, 2) with two implants. Verification that no damage occurred was made visually after each test on the specimen and the measured F-D curves; the specimens were not put under the following test until complete stress relaxation. The loads applied had the same pattern as the 1000 N load described earlier but two different levels were used (600 N and 800 N). A total of 8 tests were performed (2 specimens x 2 loading levels x 2 implant configurations).

The same configurations and loadings were computationally simulated with the FEM. The percentage of S1 endplate displacement reduction of the instrumented vs. uninstrumented (reference) model was computed and compared with the experimental data.

Simulation and assessment of fixation configurations

Using the FEM, three ramped vertical loads (600, 800 and 1000 N) were computationally applied on the center of S1 endplate, while the bottom part of the two iliac bones was fixed to represent the experimental conditions. For each of the 3 simulations, the load was maintained at a plateau for stabilization purpose and finally released to 0N.

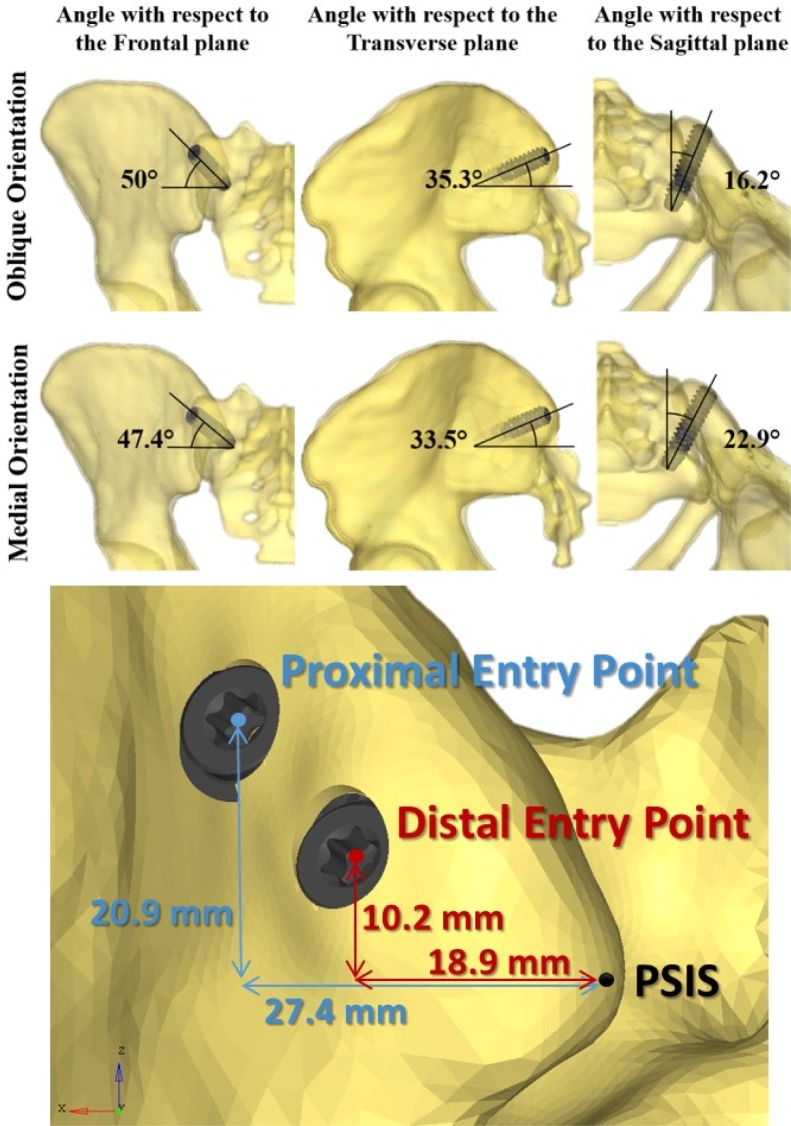
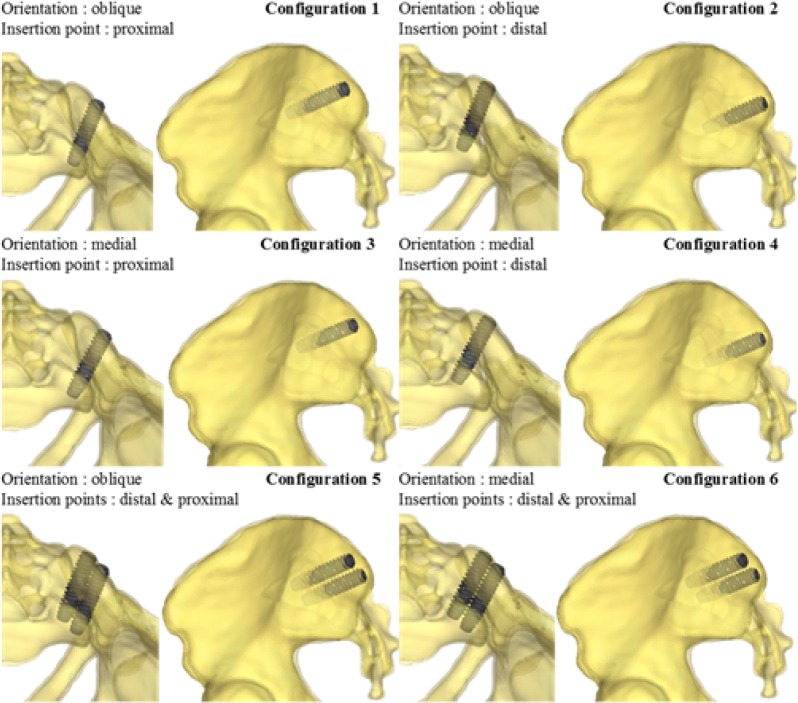
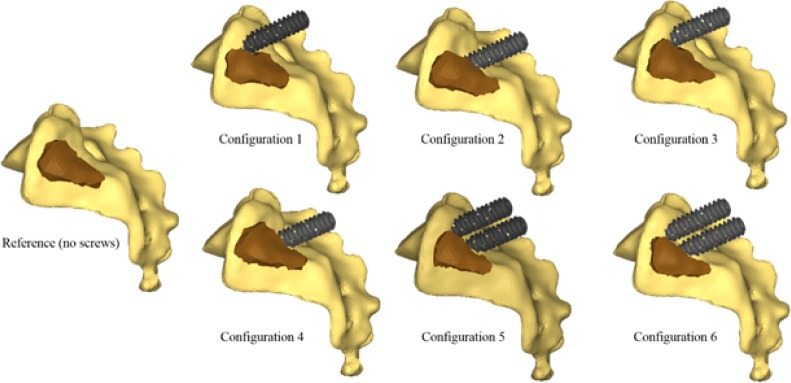
The effects of instrumentation parameters were computationally assessed using a full design of experiments (DOE) with two independent variables related to the implant trajectory (insertion point and orientation of the implant), and the number of implants (one or two), which are three of the parameters involved in the decision-making of the surgeons. The tested orientations (medial or oblique) and insertion points (proximal or distal) are shown on Figure 3. The DOE included 6 configurations of instrumentations (Figure 4). The dependent variables were the local SIJ displacement, i.e. the relative motion between the sacrum and the ilium at the SIJ. This local displacement within the SIJ was computed both in rotation in the sagittal plane and in translation. The rotation was computed using the local axes of the ilium and the sacrum at the SIJ, while the relative translation was computed as the average of the relative linear displacement between 14 pairs of facing points on each part of the articular surfaces after the simulated load. For each simulated configuration, the percentage of displacement reduction (in both rotation and translation) was calculated with respect to the reference uninstrumented configuration.

Fig. 3.

Screw trajectory parameters.

Fig. 4.

Six simulated configurations.

Results

Table 2 presents the results of the model evaluation study. For one implant, the difference between the simulated and experimentally measured S1 endplate displacement reduction in translation was 1.12% and 2.66% respectively at 600 and 800 N, while for two implants, the difference was 3.35% and 1.19%.

Table 2.

Comparison of experimentally measured (mean) and simulated S1 endplate displacement reduction due to the screws.

	1 screw configuration			2 screw configuration
	Experimental	Simulations	Difference	Experimental	Simulations	Difference
600 N	14.98%	13.86%	1.12%	17.71%	14.36%	3.35%
800 N	12.09%	14.75%	2.66%	14.27%	15.46%	1.19%

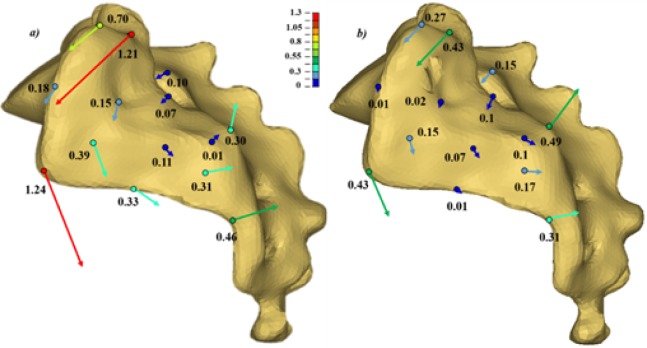
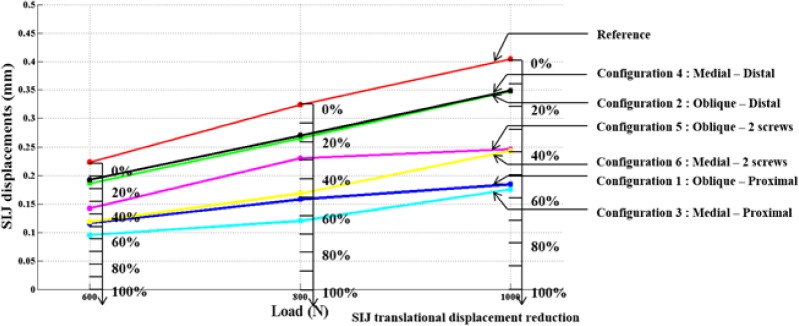
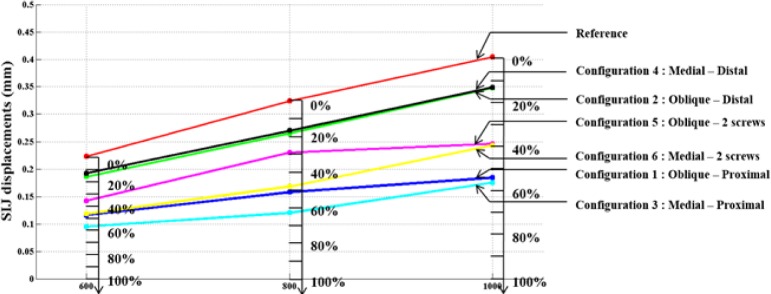
The simulated vertical loading on the uninstrumented model generated a main vertical displacement of the sacrum accompanied with a rotation (nutation) with respect to the ilium. This behavior could be observed when looking at the global displacement (Figure 5) and local displacement vectors of 14 points of the SIJ articular facets (Figure 6). The computed local rotation between the sacral and iliac surfaces in the sagittal plane was 1.38°, 2.05° and 2.80° respectively under vertical loads of 600 N, 800 N and 1000 N, with a combined relative translation below 0.3 mm. The six simulated configurations generated rather different responses to restrain the relative SIJ motion. The local sagittal rotation reduction varied between 21.9% (configuration #2 at 600 N) and 70.2% (configuration #3 at 800 N) for the instrumented simulations, while the translation reduction varied between 13.6% for configuration #4 at 1000 N and 65.2% for configuration #3 at 800 N. The SIJ local translation was more than 40% lower when the proximal entry point was used instead of the distal one. The simulations with two implants (configurations #5 and #6) generated similar or larger displacements as the ones with one implant placed proximally (simulations #1 and #3). In the case of a one implant configuration, the orientation had a negligible effect (< 5%, configuration #1 vs. #3). In the cases of two implant configurations, the medial trajectory reduced the SIJ local translations by an average of 10% more than the oblique trajectory (configuration #5 vs. #6). Figure 7 and Figure 8 summarize the simulated displacements in translation and rotation respectively, of the sacrum with respect to the left iliac bone for all the simulations, and the displacement reduction of the instrumented configurations with respect to the uninstrumented reference.

Fig. 5.

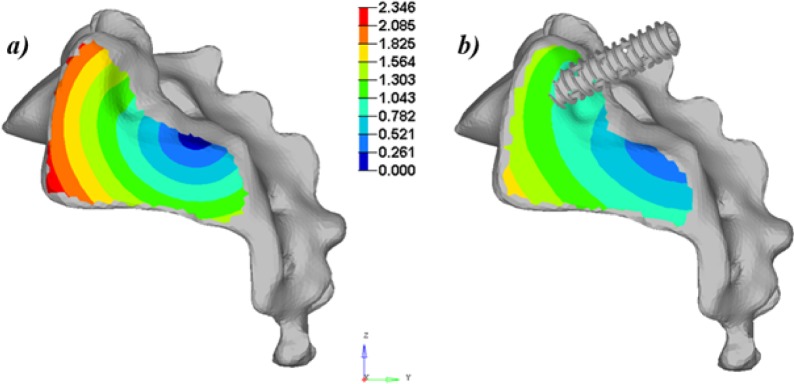
Sagittal view of the global displacements of the SIJ (translations in mm) for the simulations at 1000 N: a) uninstrumented (reference) and b) instrumented with one screw inserted obliquely at the proximal insertion point.

Fig. 6.

Local displacements (translations in mm) of 14 points of the SI facet of the sacrum with respect to the iliac bone after a vertical loading of the sacrum of 1000 N: a) unistrumented; b) instrumented (configuration 1). The displacement vectors are magnified for clarity.

Fig. 7.

SIJ local displacements in the sagittal plane and % of reduction with respect to the uninstrumented reference.

Fig. 8.

Average SIJ local rotations and % of rotation reduction with respect to the uninstrumented reference.

Discussion

The simulated uninstrumented SIJ with vertical loads showed that the SIJ exhibited mainly relative rotational movements (nutation) around an axis perpendicular to the sagittal plane joining the two interosseous ligaments as shown in Figure 5 combined with translational movements and shear stresses occurring in the SIJ plane. This sacroiliac displacement pattern was similar to that described by Farabeuf.³⁵ The SIJ fixation was more efficient with the implant inserted proximally which was located farther from the center of rotation than the distal insertion point.

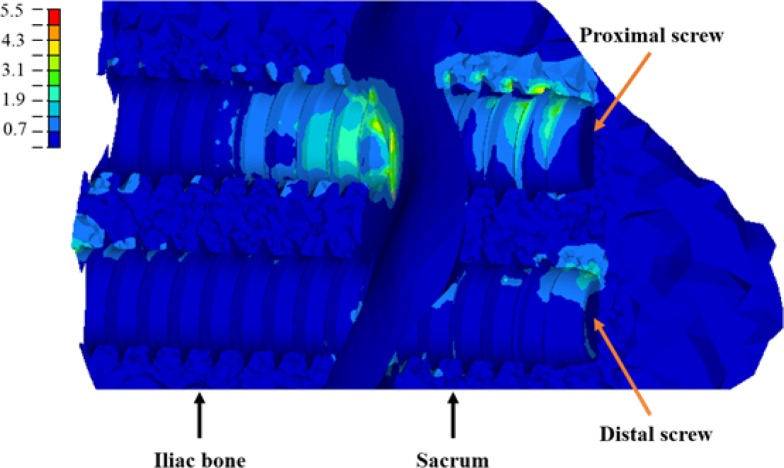
The implant orientation had a slight influence on SIJ displacement reduction in only the two-implant instrumentation scenarios. The instrumentation using the medial orientation (configuration 6) had a better ability to stabilize the SIJ than the one with the oblique orientation (configuration 5), as the implant axis was more parallel to the SIJ axis of rotation. The analysis of the stresses sustained by the implants revealed that the mechanical contribution to the SIJ stabilization was mainly ensured by the implant which is the furthest from the sacrum IRC, i.e. the proximal one (Figure 9).

Fig. 9.

Stresses (MPa) on the left ilium and sacrum trabecular bone (configuration 5, loaded at 800 N). The virtual axis of rotation is located below the figure.

The simulations of the configurations with two implants showed no significant improvement of the stabilization as compared to equivalent configurations with one implant. In fact, larger translational displacements have even been observed with two implants instrumentations. It might be explained by the location of the implants and simulated IOL damage, considering the significant role of this ligament on the SIJ biomechanics. The IOL damage induced by the device insertion (Figure 10) explains the otherwise counter-intuitive displacement reduction. This ligament should be important for the SIJ stability, especially to restrain the shearing movements. Excessive IOL damages induced by certain implant trajectories might thus reduce the SIJ stability. As a result trajectories preserving the IOL integrity should be favored, as also reported in Rahl (2015).³⁶ This explains the difference with a previous study ³⁷ showing an increase in rotational stiffness with two implant instrumentation of a fractured unstable pelvis, in which the IOL might already have been damaged.

Fig. 10.

Interosseous ligament modifications in the model to enable device insertion.

The intra-articular simulated and experimental SIJ displacements were in the same order of magnitude (0.1 – 1 mm) as those published in the literature,³⁸ but with specimens of different ages and conditions. The simulation of the experimental conditions of Miller³⁹ gave a sacral displacement of 0.244 mm which is slightly lower (by 0.03 mm) than the published experimental values.

SIJ devices reduced by up to 50% the articulation local translational movement while the S1-endplate displacement was only lowered by 15%. This difference is mainly due to the iliac bone deformation which makes the two articular facets staying in close contact while the sacrum rotates.

The model was shown to be able to reproduce the reduction of movement between the instrumented configurations vs. the uninstrumented reference given the little difference between the simulated and experimental data (≤3%). Unfortunately, the available specimens were harvested from two elderly females, which resulted in a mean age higher than the population with sacroiliac clinical problems occurrence.⁴⁰

Thus, given the small number, age and inter-individual variability of the experimental cases and their instrumentations, and of the testing conditions, the ability to compare displacements and predict absolute values of motion is limited. Another limitation of this study is from the different geometry and experimental data to calibrate the model. But as it was already shown that the biomechanics of asymptomatic and symptomatic SIJ were not significantly different,⁴¹ therefore, the main effects should be due to the fixation. Also, the SIJ stiffness properties used fell within the corridor of experimental data documented for younger cases.³³ The conclusions of this comparison study between fixation configurations should not be interpreted in terms of absolute values, but rather in term of relative effects. The effects of the different geometry and age related factors remain to be further tested in a future study. Moreover neither the muscle activity nor the nervous system control were taken into account and modeled in this study. This limits the predictive capability of the model to relative assessment of instrumentation configurations, which was close to the experimental findings, vs. absolute quantification of local displacements which would be specific to a given pelvis condition.

There are additional limitations to this computational study. Material properties of the SIJ were all identical, due to insufficient data in the literature on individual ligaments viscoelastic properties. The only mechanical properties available for individual SIJ ligaments are stiffnesses¹⁷ and are dependent on the geometry with which they have been calculated. In the present case, the accurate representation of the ligaments’ geometries coupled to an experimental calibration was assumed to be consistent with literature description of individual SIJ ligaments’ stiffnesses.¹⁷ Bone anisotropy, or bone damage in the bone-implant interface was not considered. Concerning bone damage, future studies should evaluate if, in case of high load bearing, the occurrence of implant loosening could justify the use of 2 implants despite the damage done to the IOL. Patient-specific parameters such as the bone quality, sacrum and ilia dimensions, and joint stiffness should also be further investigated to better understand and characterize the biomechanics of the SIJ instrumentation. Also, the bone-implant interface was idealized and did not model the damages (cracks, micro-fractures) which might be provoked during the device insertion. Including them in a further refined model of the bone-device interface would provide more accurate results and better description and understanding of the local phenomena which could influence the quality of an instrumentation. Finally, the fixation of the sacroiliac joint was only tested on one pelvis geometry and under compression loading of the sacrum, which represent an important and frequent load but do not fully represent all possible physiological loadings and anatomical variability. Additional fixation choices such as the implant length and additional simulations with different physiological loads such as flexion, extension, lateral bending and axial rotation should be performed to better assess the biomechanics of SIJ fixation and perform statistical analyses. However, the conditions tested in this paper are a good starting point, as both single and two-implant fixation are performed by surgeons, and using a 12 mm diameter in both case was compatible with experimental and numerical specimens’ anatomy.

Conclusion

A comprehensive FEM was developed to analyze the biomechanics of SIJ fixation with minimally invasive devices. It allowed to explore and better understand the small motion (below 3° sacro-pelvic rotation), mainly rotational, between the sacrum and ilium.

The insertion point is of major importance toward the reduction of the SIJ displacements. The implants located away from the SIJ axis of rotation showed a better capability to reduce the SIJ motion. The trajectory had an influence in 2 implant instrumentation scenarios. The farther and more parallel the implant was with respect to the sacro-iliac rotation axis, the better was the fixation. Trajectories preserving the interosseous ligament seem to be beneficial to SIJ fixation.

The developed model constitutes a first step toward the comprehension of the SIJ fixation biomechanics. More instrumentation configurations and different loading scenarios should be simulated to better understand and characterize the SIJ fixation surgeries.

Disclosures & COI

Dr. Bianco reports grants from Natural Sciences and Engineering Research Council of Canada and Medtronic of Canada, during the conduct of the study; other from Medtronic, grants from Natural Sciences and Engineering Research Council of Canada, outside the submitted work; Dr. Fradet reports grants from Medtronic, grants from Natural Science and Engineering Research Council of Canada, outside the submitted work; Dr. Aubin reports grants from Natural Sciences and Engineering Research Council of Canada and Medtronic of Canada, during the conduct of the study; other from Medtronic, grants from Natural Sciences and Engineering Research Council of Canada, other from ZimmerCAS, outside the submitted work; Dr. Bruna-Rosso reports grants from Natural Sciences and Engineering Research Council of Canada and Medtronic of Canada, during the conduct of the study; other from Medtronic, grants from Natural Sciences and Engineering Research Council of Canada, outside the submitted work; Dr. Arnoux has nothing to disclose; Mr. Godio-Raboutet has nothing to disclose.