Facing and Overcoming Sensitivity Challenges in Biomolecular NMR Spectroscopy

Abstract

In the Spring of 2013, NMR spectroscopists convened at the Weizmann Institute in Israel to brainstorm on approaches to improve the sensitivity of NMR experiments, particularly when applied in biomolecular settings. This multi-author interdisciplinary Review presents a state-of-the-art description of the primary approaches that were considered. Topics discussed included the future of ultrahigh-field NMR systems, emerging NMR detection technologies, new approaches to nuclear hyperpolarization, and progress in sample preparation. All of these are orthogonal efforts, whose gains could multiply and thereby enhance the sensitivity of solid- and liquid-state experiments. While substantial advances have been made in all these areas, numerous challenges remain in the quest of endowing NMR spectroscopy with the sensitivity that has characterized forms of spectroscopies based on electrical or optical measurements. These challenges, and the ways by which scientists and engineers are striving to solve them, are also addressed.

A new spin on bio-NMR

This Review presents a state-of-the-art description of the leading approaches being considered today to improve the sensitivity of NMR spectroscopy, particularly as applied in biomolecular settings. The focus is on the future of ultrahigh-field NMR systems, emerging NMR detection technologies, new approaches to nuclear hyperpolarization, and progress in sample preparation.

1. The Need To Address Sensitivity Issues

NMR spectroscopy yields a privileged viewpoint of matter. NMR, and its in vivo siblings magnetic resonance spectroscopy (MRS) and magnetic resonance imaging (MRI) have the unique possibility to observe multiple nuclear species and their chemical environments at a site-resolved level, in nearly all kinds of aggregation states and sample conditions. This and other qualities have transformed NMR spectroscopy into a key instrument for advanced research in physics, engineering, chemistry, biochemistry, biology, and medicine. Indeed, systems studied by NMR spectroscopy span a scope ranging from condensed matter solids to biomaterials, from small molecules in solution to megaDalton polymers in the solid state, from biomolecules including metabolites, nucleic acids, and proteins in test tubes to complex aggregates in living cells, from cells and tissues to whole body imaging and localized in vivo spectroscopy. Despite this unparalleled power and versatility, NMR spectroscopy suffers from one drawback, and that is its low sensitivity. Lack of sensitivity is an intrinsic feature of magnetic resonance, which stems from the very weak interaction energies that it involves. While this is a bonus for clinical research and ensures that NMR spectroscopic studies will usually leave the samples under analysis unperturbed, it constrains the applicability of NMR spectroscopy. If it were not because of restricted sensitivity, the potential of NMR spectroscopy would be nearly boundless: nuclei such as ¹³C, ¹⁵N, and ¹⁷O could be observed in natural abundance even in complex and diluted samples, intermediates could be characterized on catalytic surfaces, structural investigations of biomolecules could be carried out within single cells and in subcellular compartments, complex reactions and biological processes could be followed in real time, the metabolic status of humans could be characterized in a non-invasive fashion. Simply fantastic possibilities would open, particularly in the biophysical and biomedical arenas, if the signal-to-noise (S/N) ratio of NMR spectra could be increased.

The limitations of NMR spectroscopy are only too well known to the practitioners of this art, and scientists and engineers invest extensive efforts to overcome these limitations. These sensitivity-enhancing strategies can be subdivided into a number of orthogonal, complementary technologies, and can be summarized as follows:

1. Improvements based on optimization of the way by which NMR experiments are performed with existing hardware. For example, if a sample’s filling factor is increased by raising the concentration of an analyte, so will the S/N ratio. Likewise, if the relaxation properties of the sample can be “optimized” by generating longer-lasting signals or inducing a faster recovery of the spins’ magnetization, gains in the S/N ratio per unit time can also be achieved. Further increases in sensitivity will be achieved by improving the pulse sequences employed and/or the nuclei targeted in the detection.

2. Improving the coupling of the sample’s spins to the radiofrequency (RF) circuitry by optimizing the design of the coils or by reducing the environmental noise can further increase the overall S/N ratio.

3. Increasing the static magnetic field B_o in which the NMR experiment is executed, which dictates both the Boltzmann population of the nuclear spin levels and their Larmor frequency, can increase NMR signals through a B_o^α dependency with α > 1.

4. Enhancing the population differences and, therefore, the polarization of the nuclear spin systems beyond their Boltzmann distributions through physics-based techniques—including the transfer of spin order from unpaired electrons (which have a much larger polarization because of their larger magnetogyric ratio) to nearby nuclei, or from special nuclear states such as para-hydrogen by chemical processes—is another avenue to enhance the S/N ratio. In particular, the transfer of electron spin polarization to nuclear spins by microwave irradiation close to the electron Larmor frequency, commonly referred to as dynamic nuclear polarization (DNP), has become an increasingly important tool in the sensitization of liquid- and solid-state NMR spectroscopy.

These topics were the focus of a recent workshop,^[1] where the authors assembled to brainstorm on the state-of-the-art in these various areas. The following sections focus on each of these avenues of improvement separately, with an emphasis on the unique horizons that either their separate usage or mutual combinations could open in biomolecular NMR spectroscopy.

2. Optimizing Samples and Pulse Sequences

2.1. Sample Optimization for Solid-State NMR Studies

A simple way to maximize signal intensity is to increase the number of active nuclei in the receiving NMR coil, that is, by increasing the amount of sample. At variance with solution NMR spectroscopy, where concentration is dictated by solubility and sample size by stringent field homogeneity demands, solid-state NMR spectroscopy presents a greater flexibility because of the diverse nature of the proteins to be investigated, and because of its usually larger line widths. Sample preparation is thus key to the retrieval of quality line shapes with enhanced sensitivity and resolution for biomolecular solids. Upon considering such systems, a first distinction arises between insoluble and soluble proteins, with the former comprising membrane proteins^[1–3] as well as fibrillar^[4] aggregates.

Soluble proteins can be prepared in a number of ways, but pose the fundamental question of why bother with solid-state NMR spectroscopy in the first place. Although soluble proteins can be studied by solution-phase NMR spectroscopy,^[5] practical limitations arise as the size of the studied protein increases. Signal line-width scales proportionally with the rotational time of the molecule in solution. This rotational correlation time increases linearly with the size of the molecule; hence the larger the protein, the broader its NMR signals. Ingenious solutions to this problem based on TROSY effects^[6] and targeted labeling schemes have been proposed.^[7–11] Despite these successes, the fact remains that such a scaling of line width with rotational correlation time does not occur in the solid state, where line widths are generally independent of protein size.^[12,13] From these considerations, it follows that very large proteins constituted by many identical subunits could be better candidates for solid-than solution-phase NMR spectroscopy.^[14,15] Three main routes have been explored to prepare solid samples of soluble proteins: freeze-drying,^[16–18] freezing,^[19,20] and crystallization^[21,22] (Figure 1). Freeze-dried samples usually provide heterogeneous samples with poor resolution.^[21,23] Freezing also provides poor resolution,^[18,24] even if the addition of proper cryoprotectants^[25,26] yields in many cases reasonably well-resolved solid-state protein spectra from this glassy state.^[24] Finally, if protein microcrystals can be obtained, their quality is often even better than glassy states.^[21,27–30] However, such an approach poses again the problem of rationale: if microcrystals of a protein can be obtained, suitable X-ray structures can also be obtained.^[31]

Figure 1.

Different techniques of sample preparation for solid-state NMR experiments: crystallization, freezing with cryoprotectants, freeze-drying, and sedimentation.

In view of this, it is sensible to concentrate on the optimization of non-microcrystalline samples. A fourth preparation option that has recently been introduced involves sedimenting the protein by ultracentrifugation.^[32,33] The sedimented state is obtained from a clean protein solution, and it is thus clearly different from a precipitate, whose particles are big enough to slowly deposit even under normal gravity. It has long been known that sedimentation is a very mild treatment for extracting a protein, which would not normally precipitate by gravity, out of a solution.^[34] Solid-state NMR experiments have been performed on several sedimented proteins and the quality of the spectra is comparable to that of microcrystalline preparations.^[33,35–38] To optimally fill a rotor with a sediment, the MAS rotor can be placed in ad hoc designed devices that can be hosted in an ultracentrifuge, so that the protein can sediment directly from its solution and fill the rotor completely.^[33,39] Interestingly, it could be shown that the quality of the solid-state NMR spectra of certain freeze-dried proteins was improved by partially rehydrating this powder into a physical state reminiscent, or even equal, to a sediment.^[23,40–42] Sedimentation efficiency depends on the molecular weight and concentration of the protein, as well as on the centrifugal field applied. Since sedimentation promises to become a useful additional option for the preparation of samples for solid-state NMR spectroscopy, prediction tools are being developed to help develop the best sedimentation strategy.^[43]

Sample preparations of insoluble proteins, including preparations of membrane proteins and aggregates, can be even more challenging.^[44,45] In many instances it seems that the optimal preconditioning of these systems needs to be elucidated on a case-by-case basis. However, the benefits that could result from cracking open the investigation of these ubiquitous systems seem so important that efforts to overcome these challenges are active world-wide.

2.2. Optimized NMR Pulse Sequences

NMR spectroscopy has long been known as an extremely flexible tool, where advances in understanding the spin physics underlying the experiment are closely linked to improvements in the quality of the information that can be extracted from it. Biomolecular NMR spectroscopy is the prototypical example of this close relationship, and recent years have witnessed substantial improvements in both the sensitivity of many such experiments as well as in the speed with which such information can be measured. Both of these aspects are in fact somewhat linked, as improvements in S/N ratios bring about reductions in the time needed for an experiment, and vice versa.

One of the most dramatic boosts in sensitivity that happened over the last decade came from strategies that reduce the idle time of an NMR measurement. Indeed, the time course of an NMR experiment is divided between the length of a relatively short pulse sequence, which incorporates pulses, transfers, delays, and measurements of the relevant spin signal, and a much longer recovery delay, where virtually nothing but spin relaxation happens. Whereas the former “action” time usually takes up a few tens of milliseconds, the latter takes a second or more, thereby consuming most of the time of an NMR experiment. Substantial increases in sensitivity per unit signal averaging time can, therefore, result from reducing the recovery times of the excited nuclei. One way of doing so is by adding a suitable relaxation agent, which will shorten the longitudinal relaxation time of the spins without bringing about a concomitant transverse relaxation decrease (i.e. line broadening). This strategy has long been known and used in the NMR spectroscopic analysis of small organic chemicals, were the addition of small amounts of the paramagnetic [Cr(acac)₃] (acac = acetylacetonate) agent has been a common route to deal with long T₁ relaxation times. The use of such strategies has been slower in coming to the biomolecular solution NMR spectroscopy arena, where the addition of charged paramagnetic complexes runs the risk of broadening signals and/or changing the structure of the studied complex. However, the advent of neutral relaxation agents has eased some of these concerns.^[46] Alternative approaches that avoid a direct contact with the biomolecule have also been proposed and realized, whereby lanthanide complexes known to act as very efficient water relaxation agents are inserted to interact with the solvent. The exchange of the water protons with labile NH or OH groups can enhance the longitudinal relaxation properties of the targeted biomolecules.^[47,48] Similar approaches had been explored years ago in solid-state NMR spectroscopy,^[49] but the prospects were not clear because of the introduction of severe dipole-based line broadening, and of problems to reduce the recycle delays for this high-powered, low-repetition-rate kind of experiments. A breakthrough in this area came with the realization by Ishii and co-workers^[50] that, in solid-state NMR spectroscopy, the introduction of MAS rates > 40 kHz obviates the need for high-power heteronuclear decoupling. A main source of stress for both the sample (in terms of heating) and the electronics is thus removed, thereby facilitating the full benefits of faster recycling.^[51,52]

An ingenious way to reduce the recycle delay without having to introduce external agents arises in biomolecular NMR spectroscopy from 1) implementing selective excitations and 2) choosing excitation angles different from 90° and optimized as per the recipe of the Ernst angle settings.^[53] This is a consequence of cross-relaxation phenomena, whereby unexcited nearby nuclei can act as sources of polarization that rapidly rebuild the magnetizations of ¹H-depleted amide or methyl moieties. This idea finds the widest applicability in the case of BEST^[54] and SOFAST^[55] experiments in solution, which during the last few years have become mainstream approaches to collect a wide array of HSQC- or HMQC-based experiments with maximum sensitivity. This combination of selectively exciting only those sites that one intends to measure by doing such excitations with optimized pulse angles can lead to experiments that are 50–100% more sensitive than traditional broad-band, 90° pulse excitation counterparts. While these gains diminish when the complexity and/or dimensionality of a pulse sequence is increased, they are still avenues worth exploiting in numerous 3D and 4D triple-resonance (H/N/C) experiments.^[54,55]

Another sensitivity-enhancing family of experiments that blossomed over the last decade, involves transverse-relaxation-optimized spectroscopy (TROSY).^[56,57] TROSY methods rely on the fact that not all multiplet signal components arising from a J-coupled NMR resonance possess identical line widths. This is a consequence of the nature of the relaxation, whereby it is the sum of all rapidly fluctuating fields felt by a targeted nucleus S that determines the line widths of a resonance. TROSY experiments exploit the fact that opposing fields associated to different fluctuating spin anisotropies may actually interfere destructively, thereby leading to longer-lived, sharper signal components whose observation thus becomes easier. This is the case for amide ¹⁵N-¹H groups in high-molecular-weight proteins, where the effects of dipolar and shielding anisotropies will strengthen one another for one of the doublet components within this two-spin system, but will cancel out for the second component. Something akin happens for ¹³C-¹H groups in aromatic protein side chains as well as in aromatic nucleic acid bases.^[58,59] As a result of these interferences, removing the customary spin decoupling will, instead of splitting signals and bringing about a concomitant sensitivity decrease, yield a multiplet with one of the components much sharper and thus easier to detect. TROSY experiments capitalize on this, by not only avoiding spin decoupling but also selecting correlations arising solely from these longer-lived spin-coupling components. While fine-tuning the destructive interference between dipolar and shielding anisotropies in these two-spin systems requires optimizing the external magnetic field (which varies chemical shielding effects while leaving unchanged that of the dipolar interactions), a field-independent TROSY effect arises within methyl groups in large proteins. This reflects the long-lived states that will originate in the absence of decoupling, as a result of interferences between this group’s ¹H-¹H and ¹H-¹³C dipolar anisotropies.^[60] Embedding such sensitive and often strategically positioned reporter groups within the side chains of otherwise perdeuterated proteins has enabled NMR spectroscopy to target extremely high-molecular-weight biomachines under physiological, solution-state conditions, with unprecedented sensitivity.^[61]

While less directly connected to sensitivity gains, another area that has dramatically gained from coupling improvements in computational power with new algorithms customized to biomolecular NMR spectroscopy, concerns the acquisition of high-dimensional experiments.^[62,63] Indeed, a major research topic in contemporary biomolecular NMR spectroscopy deals with the design of experiments that can provide maximum resolution and minimum ambiguity within the shortest possible times. Such optimized design brings to the forefront the potential advantages that could result from extending the traditional 2D/3D suite of NMR experiments used to resolve and assign residues^[64] to more complex 4D/5D/6D/7D experiments. Besides the need for long coherence lifetimes and good starting sensitivities, as demanded by all the transfers involved in very high-dimensional (nD) NMR experiments, the acquisition of such spectra in a conventional Nyquist-dictated fashion would require a prohibitively large number of scans and astronomical acquisition times. This in turn has stimulated the search for alternatives to reduce the times required for acquiring such spectra, including various forms of projection spectroscopies where different delays are simultaneously evolved,^[65–67] as well as non-uniform-sampling methods which depart from usual Fourier/Nyquist criteria, and avoid measuring a large part of the experimental data points that would normally have to be collected.^[68–70] Customized algorithms are then needed to reconstruct the hyperdimensional spectral distribution that best fits these time-domain data without missing information or generating large amounts of spurious noise. This method has opened up several new applications in both solution- and solid-state NMR spectroscopy, and new sampling schemes based on a priori information or on more sophisticated mathematical reasoning, are constantly introduced. The ultimate step towards increasing the acquisition speed of multidimensional NMR experiments is arguably represented by spatiotemporal encoding methods, capable of delivering arbitrarily high data sets in a single transient.^[71] The sensitivity losses incurred by such “ultrafast” methods as a result of their simultaneous sampling of multiple domains, however, needs to be accounted for in a suitable fashion for biomolecular applications.^[72,73]

3. Optimizing Biomolecular NMR Probes and Coils

Besides improvements in sample preparation and in the “spin gymnastics” of the NMR experiment, improvements in the electronics can make important contributions towards enhancing the sensitivity of the NMR spectrometer. The signal S detected in an NMR experiment based on the inductive coupling of the spins with a pickup coil can be expressed by the classic formula of Hoult and Richards [Eq. (1)].^[214]

$$S\propto k_0\frac{B_1}{I}{V}_{\mathrm{S}}N\gamma \frac{h^2}{4{\pi }^2}S(S+1)\frac{{\omega }_0^2}{3kT\sqrt{2}}$$ (1)

In this equation, V_s is the sample volume, k₀ is a constant which accounts for spatial inhomogeneities in the B₁ field, k is Boltzmann’s constant, S is the spin angular momentum quantum number, γ is the gyromagnetic ratio, N is the spin density (number of spins per unit volume), h is Planck’s constant, T is the absolute temperature measured in Kelvin, and ω₀ is the Larmor frequency. The factor B₁/I, the magnetic field per unit current, is defined as the coil sensitivity, and is inversely proportional to the diameter of the coil. The NMR signal-to-noise ratio is derived by dividing this signal by a noise voltage V_noise [Eq. (2)], where Δf is the receiver bandwidth, and T_N,probe and T_{N,preamplifier} are the respective noise temperatures of these devices, which are defined by Equation (3). Here, NF is the noise factor of the preamplifier, T_coil is the coil temperature, T_sample is the sample temperature, and R_coil and R_sample are the effective resistances of the coil and sample, respectively.

$$V_{\text{noise}}\propto \sqrt{4k(\mathrm{\Delta }f)(T_{N,\text{probe}}+T_{N,\text{preamp}})}$$ (2)

$$T_{N,\text{probe}}=\frac{T_{\text{coil}}{R}_{\text{coil}}+T_{\text{sample}}{R}_{\text{sample}}}{R_{\text{coil}}+R_{\text{sample}}};T_{N,\text{preamp}}=290\left({10}^{\frac{NF}{10}-1}\right)$$ (3)

Equation (1) indicates that the sensitivity of an NMR probe can be increased by reducing the size of the coil, while Equation (2) indicates that the S/N ratio can also increase by reducing the temperature of the NMR probe. The effectiveness of the cryogenic approach depends upon the relative values of the sample and coil resistances. Sample loading reduces the cryogenic advantages, up to the point at which the sample resistance (noise) dominates that of the coil. Sample loading also depends strongly on the diameter of the sample; smaller diameter tubes are more tolerant of salt than larger tubes. De Swiet showed that rectangular tubes with the long axis along the B₁ field will also improve performance in cryogenic probes with lossy dielectric samples.^[74] Equation (3) indicates that additional increases in the S/N ratio may be possible by cooling the preamplifier. For example, a narrow-band gallium arsenide field-effect transistor (GaAs-FET) or high electron mobility transistor (HEMT) based preamplifier can readily be constructed with a noise factor of approximately 0.3 dB, which corresponds to an equivalent noise temperature of about 20 K. Cooling the preamplifier to liquid nitrogen temperatures and below can reduce the preamplifier noise factor to about 0.1 dB, an equivalent noise temperature of around 10 K. Preamplifier cooling is, therefore, advantageous for coils which are cooled to temperatures well below that of liquid nitrogen. These simple equations cited above and the considerations drive much of the contemporary improvements in NMR probe technologies; some of this progress is summarized in the paragraphs below.

3.1. New Coil Designs for Solution-Phase Biomolecular NMR Spectroscopy

Although NMR probes containing small solenoidal coils were developed originally for mass-limited samples of small molecules, they have also been used recently in a number of protein studies.^[75] Solenoids are in fact the most common geometry used for magnetic resonance “microcoils” (Figure 2A). The mass sensitivity of microcoils with diameters of 1–1.5 mm is similar to that of 5 mm cryoprobes, without the requirement of dedicating an entire system to cryogenic operation. Therefore, small volume probes based on such coils are useful for mass-limited (but not for concentration-limited) samples.

Figure 2.

Common NMR coil geometries: A) solenoid, B) saddle coil, C) inductively coupled HTS coils (drawings by Jason Kitchen, NHMFL).

Despite the initial complexity of cryoprobes, recent years have seen a very widespread use of cooled radiofrequency (RF) coils in high-resolution NMR studies of protein structure and dynamics. These probes are cooled to temperatures between 20 K and 77 K, and are most commonly designed using conventional copper-based saddle coils (Figure 2B). Substantial increases in signal-to-noise, up to factors of 4 for standard copper saddle coils, have been achieved using cryogenic cooling technologies in protein NMR studies; commercial cryoprobes are available in most of the standard configurations, for example, triple-resonance inverse-detection, at frequencies up to and including 1000 MHz. An extensive review of cryoprobe applications was published in 2005.^[76]

High-temperature superconductors (HTS), such as yttrium barium copper oxide (YBCO) deposited on sapphire substrates, can provide additional sensitivity enhancements. Brey et al. combined small sample sizes, cryogenic temperatures, and HTS coils to make a 600 MHz 1 mm triple resonance probe with four pairs of HTS coils.^[77] This ¹H-optimized probe can accommodate a total sample volume of between 5 and 10 μL, depending on the wall thickness of the 1 mm outer diameter sample tubes. The overall mass sensitivity of this small volume probe is close to four times greater than a 5 mm cryogenic probe, even if the absolute signal is much less. It should be noted, however, that with current HTS coil designs (e.g. Figure 2C), the largest diameter sample that can be accommodated in a full triple-resonance (¹H, ¹³C, ¹⁵N plus ²H lock) HTS-based probe in a standard bore magnet is about 1.7 mm; new HTS coil designs are necessary to make larger volume probes. The National High Magnetic Field Laboratory (NHMFL) group has also recently designed and built a 1.5 mm ¹³C-optimized probe based on HTS coil technology, which provides over twice the mass sensitivity of any commercial ¹³C-optimized probe; this makes it ideal for ¹³C-based metabolomics and experiments such as INADEQUATE.^[78] The technology and engineering of microcryogenic probes, with particular emphasis on HTS coils, has also been reviewed recently.^[79]

An alternative approach to coil design at very high frequencies involves the use of high permittivity materials. The fact that high permittivity materials can be very high Q-factor devices suggests that they could be used in place of the more traditional conductor-based, metallic RF coils, particularly for high-frequency applications. Recently, and based upon earlier work in electron paramagnetic resonance (EPR) spectroscopy, these types of materials have been applied in high-field magnetic resonance imaging.^[80] It is certainly possible that these types of resonators will also find a niche as NMR frequencies increase above 1 GHz. The key features of a dielectric resonator (DR) are the stable time-invariant electric- and magnetic-field patterns that are formed within it. Cylindrical DRs have transverse electric (TE) and transverse magnetic (TM) modes, as well as hybrid electromagnetic (HEM) modes. A TE mode is defined as one whose electric field vector is normal to the direction of propagation (zero electric field in the propagation direction), a TM mode as one whose magnetic field vector is normal to the direction of propagation (zero magnetic field in the propagation direction), and a HEM mode with non-zero electric and magnetic fields in the propagation direction. Figure 3 shows the distribution of electric and magnetic fields for the most commonly used mode of a cylindrical DR, the TE₀₁ mode. In this mode, the electric and magnetic fields are tangential to one another. Importantly, the electric field is zero at the center of the DR, and is almost entirely constrained within the structure of the DR. An alternative use of dielectric materials is to incorporate them into the structure of a conventional resonator. The dielectric can be used as a “circular” liner in the RF coil to increase the sensitivity and/or shield the sample from the conservative electric field of the RF coil. This is important to avoid heating in experiments requiring high-power proton decoupling, a ubiquitous case when studying biosolid samples endowed with high conductivities. Crum and Zilm^[81] have shown that it is possible to shield the sample from the conservative component of the electric fields that are produced by a solenoid, without significantly altering either the B₁ field distribution or amplitude, by the use of a cylindrical dielectric sleeve which is placed between the sample and coil.

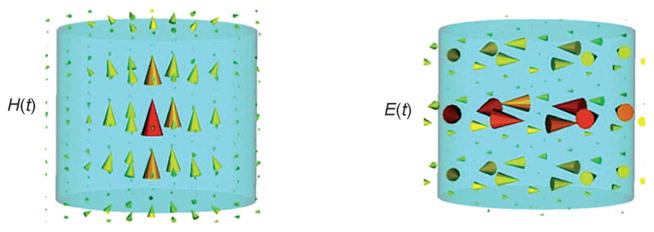
Figure 3.

Distribution of electric (E(t)) and magnetic fields (H(t)) for the most commonly used mode of a cylindrical dielectric resonator, the TE01 mode.

3.2. NMR Probes: Future Directions and Challenges

In all fields of application of magnetic resonance there is a steady trend towards higher static magnetic fields. Commercial high-resolution NMR magnets have reached approximately 23.5 T (1 GHz), with plans for hybrid magnets operating at 1.2 GHz; MRI systems for animals operate at up to 21.1 T (900 MHz), and plans are in place for 11.7 T (500 MHz) systems for human MRI. From a radiofrequency coil point-of-view, both the absolute frequency and the frequency–diameter product are important criteria in design and efficiency. It is interesting to note that millimeter-sized resonators for high-frequency EPR spectroscopy, centimeter-sized coils for high-frequency NMR spectroscopy, and 10–100 cm sized detectors for high-frequency MRI, have the same order-of-magnitude for this frequency–diameter product. In terms of sample properties, dielectric losses increase as a function of frequency for aqueous solutions and tissue, as does conductivity. This means that designs such as dielectric resonators are likely to play a major role not only in MRI coils for animals and humans, but also in high-resolution NMR probes and small resonators for high-frequency dynamic nuclear polarization.

4. Enhancing Sensitivity by Increased Magnetic Fields

4.1. Superconducting NMR Magnets

The signal emitted by the spins increases—as a result of Boltzmann polarization and Faraday induction considerations—quadratically with field. Spectral resolution in an n-dimension NMR experiment grows as the n^th power of B₀, thus explaining the quest for ever-increasing magnetic field strengths for NMR spectroscopy (Figure 4). While current low-temperature superconductors have enabled a 23.5 T field with exquisite stability and resolution to be reached, conventional NMR approaches will likely not be able to exceed 25.9 T (1.1 GHz). This reflects the fact that the superconducting critical current density decreases steeply beyond 23 T (see Figure 5). The use of high-temperature superconductors (HTS) such as Bi₂Sr₂Ca₂Cu₃O_x (Bi-2223), Bi₂Sr₂CaCu₂O_x (Bi-2212), or REBa₂Cu₃O_7-x (i.e. REBCO; RE = rare earth), can provide the high current densities needed to operate above 23 T, thus enabling an NMR magnet to exceed 1 GHz. In fact, a magnetic field strength of 34 T, equivalent to a ¹H NMR frequency of 1.45 GHz, has been achieved using a small Bi-2212 insert coil,^[82] while a 35.4 T (1.5 GHz) field was attained with a small REBCO insert coil placed in the 31 T background field of a water-cooled resistive magnet.^[83] Based upon these successes, a 32 T all-superconducting magnet is being built in the US NHMFL that is based on a conventional low-temperature superconductor (LTS) at 15 T, operating in unison with a 17 T REBCO inner coil.^[84] Thus, an NMR magnet operating beyond 1 GHz is possible by employing an LTS outer coil and a high-field HTS inner coil, or a “LTS/HTS NMR magnet”.

Figure 4.

Increases in the maximum magnetic field strength used in high-resolution NMR spectroscopy over the past 40 years, with emphasis placed on the appearance of the first commercially available field.

Figure 5.

Superconducting critical current density versus applied magnetic field for state-of-the-art Nb₃Sn round wire (red arrow), isotropic Bi-2212 round wire (blue), anisotropic Bi-2223 tape (green), and anisotropic YBCO (REBCO) tape (yellow), for which the upper arrow corresponds to the magnetic field in the Cu-O planes and the lower arrow corresponds to the magnetic field perpendicular to the Cu-O planes. Recent experiments on Bi-2212 round wire have shown dramatic increases in the conductor critical current density following annealing in high-pressure oxygen^[80] (plot by Peter Lee, NHMFL).

High-field magnets generate enormous hoop stresses on the conductors when they are charged. Superconducting materials are typically rather weak, and magnets above about 17 T typically include reinforcement materials such as steel to support the superconductors, which has a subsequent impact on the overall current density of the magnet. For several years, the leading candidate material for attaining fields above 23 T was Bi-2223. However, in 2007 SuperPower delivered a new REBCO tape that included a Hastelloy substrate that can tolerate 450 MPa (twice that of Bi-2223). This material has since been used for several very high field demonstration coils worldwide with minimal additional reinforcement. Several research groups are now focusing on REBCO as the material of choice for NMR magnets up to 1.5 GHz (35 T). However, large-scale application of HTS conductors for NMR magnets may be limited by the high cost of HTS conductors or other technical challenges.

Japan started a project in 2007 to develop an NMR spectrometer operating at 1.02 GHz (24.2 T) by using a high-field Bi-2223 inner coil inserted in a niobium-based LTS NMR magnet. As a consequence of the difficulty in guaranteeing a superconducting joint, such an LTS/HTS NMR magnet is unlikely to provide a persistent current that will be sufficiently stable for NMR measurements. Therefore, this and similar kinds of LTS/HTS NMR magnets will likely be driven by an external DC power supply, as was the case for the first 14.1 T system employed for NMR spectroscopy.^[85] An internal ²H field-frequency lock system stabilizes the magnetic-field fluctuation sufficiently for solution NMR measurements on proteins. The first stage of this program was to develop a 500 MHz NMR spectrometer with an LTS/Bi-2223 magnet which obtained 2D-NOESY, 3D-HNCO, and 3D-HNCACB spectra for a protein;^[86] the spectral qualities were closely equivalent to those achieved by a conventional LTS 500 MHz NMR spectrometer. The second stage, with the goal of developing a 1.02 GHz NMR spectrometer with an LTS/Bi-2223 magnet, was completed during 2015.^[87,216]

An additional Japanese project centered on developing a LTS/REBCO NMR spectrometer that would operate beyond 1 GHz. REBCO conductors were only commercialized in 2009 and, therefore, the magnet technology for REBCO conductors remained relatively undeveloped. During the course of this LTS/HTS project, major technological problems for REBCO coils were encountered, including a) degradation in the superconducting performance for mechanical reasons^[88] and b) large effects of a screening current-induced magnetic field.^[89] Based on a basic investigation of these technological problems, a REBCO coil was impregnated with paraffin wax to suppress degradation in the coil performance; this resulted in the LTS/REBCO magnet successfully achieving 400 MHz operation. However, there was a dramatic difference in the effect of screening currents between the LTS/REBCO 400 MHz NMR spectrometer and the LTS/BSCCO 500 MHz NMR spectrometer as a result of the multilayered tape structure of the REBCO conductor. Further improvements in field homogeneity and stability are still required to make this convenient conductor suitable for NMR magnets. In addition, recent experiments on multifilamentary round wires of Bi-2212 at the NHMFL have shown dramatic increases in the critical current density of the conductor (this critical current density J_E reaches 500 Am⁻¹m² at 30 T, higher than either REBCO or Bi-2223) following high-pressure oxygen reactions (Figure 5).^[90] Such small-diameter round wires may provide higher homogeneity magnetic fields with smaller magnetization currents compared to magnets wound with superconducting tape such as REBCO or Bi-2223. These options are also under exploration within NMR-oriented settings in the US and Japan.

Multiple efforts are in place to develop LTS/HTS NMR magnets for high-resolution NMR spectroscopy. These approaches based on dual-conductor systems hold the promise to revolutionize NMR magnet technology by providing magnets that greatly exceed the present day capabilities. Research and development to advance such magnets is advancing rapidly at laboratories and in industries in Japan, the United States, and Germany.

4.2. Resistive and Hybrid NMR Magnets

The European and US facilities that provide access to ultrahigh magnetic fields are also exploring the options for NMR experiments above 30 T (ca. 1.3 GHz) by using purely resistive magnets. It has been demonstrated, for example, that NMR experiments are feasible in high-field pulsed magnets. Such systems are sited at Dresden and Toulouse^[91,92] and use purely resistive magnets fed by DC currents generated by large power supplies or capacitor banks. These have led to NMR spectra in the 40–70 T range; such pulse magnets, however, have a compact structure that does not provide the field homogeneity and stability required for high-resolution NMR spectroscopy. Typical field variations near the center are 500 ppm in a 1 cm³ volume and their temporal stability is about 10 ppm at approximately 1500 Hz as a result of ripples in the power supply and thermal drift in the cooling system. These systems are, therefore, usually dismissed as alternatives for biomolecular NMR spectroscopy. By contrast, under closer examination are so-called “hybrid magnets”, which consist of a resistive magnet located inside a superconducting coil and operated in series to achieve the highest possible continuous magnetic fields as well as an enhanced inductive-derived stability. The US NHMFL, for example, is currently constructing a 36 T hybrid magnet that is expected to achieve 1 ppm homogeneity over a volume of 1 cm³. Once field shimming and stabilization are optimized, such a system might be suitable for high-resolution solid-state biomolecular NMR spectroscopy. A key feature of this magnet’s design is the connection of the electromagnetic insert in series with a superconducting LTS magnet of very high inductance, thereby providing a formidable damping to the field fluctuations of the power supply. The ultimate challenge in any kind of setup involving an inner resistive component is to achieve the homogeneity and stability required for high-resolution NMR spectroscopy, even in the solid state. Programs to improve field homogeneity and stability exist in several European, Japanese, and American facilities. In general, however, this increases the magnet complexity, decreases the power efficiency, and may reduce the available room-temperature bore diameter. Researchers at Nijmegen, NHMFL, and Japan have pioneered ferromagnetic and paramagnetic shims as an alternative approach without modifications to either the magnet design or to the power supply (Figure 6).^[93,94]

Figure 6.

Homonuclear ¹³C cross-correlation spectrum for L-alanine at 30 T in a standard 33 T Bitter magnet at the HFML in Nijmegen with a 32 mm room-temperature bore with ferroshim and without electrical shims. A 1D digital frequency lock on a ²H reference was used, with feeding hardware controlled phase increments in the indirect dimension. The MAS spinning speed was 45 kHz, and recoupling was achieved by a rotor-synchronized SR6² sequence. Total measurement time about 30 min.

The hurdle arising from the stability issue needs to be counteracted with some kind of custom-built, fast, digital field-frequency lock. In this way one can, in principle, perform most 2D experiments without special modifications to the pulse sequence, since all field-induced phase fluctuations in the evolutions of the different nuclei will be accounted for by changes in the lock.^[95] Another solution to field fluctuations is a “field/frequency” lock using a feedback coil such that signal-average and multidimensional experiments can be performed in resistive magnets much as they are performed in superconducting NMR magnets.^[86] To achieve this, the range of control in the time fluctuations needs to span from milliseconds to seconds. To this end, customized field measurements such as frequency counting and phase measurement of a pulsed lock signal have been developed in the US, Europe, and Japan. However, it should be realized that the operation of resistive and hybrid magnets is much more costly than the nonstop operation offered by superconducting NMR magnets. The costs run into literally thousands of dollars per hour of operation just in terms of electricity. Low sensitivity 2D or 3D NMR experiments requiring relatively long experimental runs raise particular challenges to this kind of concept. For this reason, a major emphasis in optimized biomolecular NMR spectroscopy rests on achieving high fields based on LTS/HTS designs.

In summary, the extra magnetic field strengths already available with nonpersistent magnet designs provide an opportunity for exploring NMR spectroscopy at very high fields. Although these systems do not match the stability or homogeneity of traditional high-resolution NMR spectroscopy, they give a chance to probe experiments in the 30–45 T range, a decade or two before such fields will become available in a purely superconducting format. Their relevance within solid-state biomolecular NMR spectroscopy settings is thus evident, not only on spin ½ nuclei with low gyromagnetic ratios but also on other lower-resolution species such as ¹H atoms in abundant spin networks, or on biologically relevant quadrupolar nuclei such as ¹⁷O or ⁶⁷Zn.

5. Increasing Sensitivity by Spin-Alignment Transfer Strategies: DNP, PHIP, Optical Pumping

The signals to be detected from an ensemble of nuclear spins can be enhanced by transferring spin polarization from electrons which have a large magnetic moment to nuclei. When microwave irradiation of the electron nuclear transitions is used to mediate this process, it is referred to as dynamic nuclear polarization (DNP). The last decade has witnessed the development of microwave sources that permit DNP experiments at the magnetic fields used in contemporary NMR experiments (5–20 T), and therefore DNP has become an integral part of a large variety of NMR studies, including in vivo NMR spectroscopy, NMR/metabolic studies, and high-resolution solid- and liquid-state NMR spectroscopy.^[96–98] Although the DNP concept was introduced theoretically by Overhauser over 60 years ago^[99] and its practical demonstration followed shortly thereafter in metals,^[100] its present practical significance is mainly a result of the implementation of DNP at high field in insulating solids. These experiments include magic angle spinning (MAS) NMR spectroscopy of solids doped with paramagnetic centers,^[101–103] and the use of the large sensitivity enhancement techniques in liquid-state NMR spectroscopy that can be achieved by dissolution of a cryogenically cooled pellet that was subject to solid-state DNP.^[104] As these are currently the most promising strategies for bringing about a dramatic increase in the sensitivity of biomolecular NMR spectroscopy, we devote the main portion of this survey to their recent progress. Moreover, as the principles of DNP are different if executed on solid or liquid samples (regardless of the final state in which the NMR experiment is subsequently done), we further divide these two scenarios.

5.1. Principles of DNP in Solids

The transfer of polarization between microwave-irradiated electrons and their surrounding nuclei is most efficient in the solid state (Figure 7), because of the possibility of implementing it at both high fields and low temperatures, which can yield increases in the resulting nuclear polarization of up to 4–5 orders of magnitude compared to its room-temperature counterpart. This is due to the large differences in the gyromagnetic ratios between the electron and nuclei (γ_e/γ_nuc = 658 for ¹H and γ_e/γ_nuc = 2618 for ¹³C) and the large Boltzmann energy difference that can be induced through a temperature jump (ca. 300 upon going from 1 K to 300 K). The main physical mechanisms driving this solid-state nuclear hyperpolarization process are: 1) the solid effect (SE-DNP),^[105] 2) the cross effect (CE-DNP),^[106–108] and 3) thermal mixing (TM-DNP);^[109–111] even enhancements based on Overhauser effects have recently been reported in insulating solids.^[112] SE-DNP drives the polarization transfer to a nucleus from an isolated unpaired electron.^{[108,111,113–115]} CE-DNP relies on two electrons that transfer polarization in a resonant way to a nucleus.^[116,117] The TM formalism describes the electron-nuclear polarization transfer process in large spin systems containing many dipolar coupled electrons and nuclei, and is usually described using a spin-temperature formalism.^[118–120] In all cases, conditions that maximize the nuclear polarization include starting from the highest possible electron polarization by relying on a high field/temperature ratio, and disturbing this equilibrium by shining microwaves at/near the electron Larmor frequency. In most cases, solid-state DNP experiments are carried out on glassy samples at low temperatures and embedding radicals at concentrations in the 5–40 mM range; measurement of the nuclear polarization enhancement as a function of the microwave irradiation frequency can indicate whether the SE or the CE mechanisms, or a combination of the two, are predominant (Figure 8).^{[117,121–123]} Recent studies have re-derived the specific conditions for efficient signal enhancements and simulated the nuclear polarization build-up times and frequency-swept static DNP experiments.^[116,124] While the SE- and CE-DNP mechanisms are the source of local polarization build-ups, their effect on the polarization of far-removed bulk nuclei must also be considered. This process originates from the dipolar interactions among the nuclei, and can be described by a spin diffusion process.^{[113,115,125–127]} To account for this, a relaxation-like mechanism that incorporates fluctuation operators $I_i^{+}{I}_j^{-}+I_i^{-}{I}_j^{+}$ between pairs of i and j nuclei needs to be considered.^[128] The transport of the polarization across the dipole–dipole-coupled nuclear network should also account for the T₁ relaxation of the bulk nuclei and the dipolar relaxation rates. In this way, and aided by low temperatures that allow for extended DNP “pumping times”, large nuclear spin systems can be polarized in bulk—both by SE (Figure 9) and by CE-DNP. For large systems, the build-up times approach the nuclear relaxation time and the end polarization becomes a function of this relaxation time, as well as of the effective size of the spin system for each DNP-active electron.

Figure 7.

Schematic representation of a DNP experiment: The microwave irradiation drives electronic transitions that, in turn, cause enhancements of the nuclear polarization.

Figure 8.

Interplay between the solid effect and the cross-effect mechanisms in solid-state ¹³C DNP.^[123]

Figure 9.

Solid-effect DNP enhancement profiles simulated for a model system of eight nuclei coupled to a single electron inside a “core” region (shown on the left). The small spheres demonstrate the relative positions of the spins. The curves on the left show their progressive polarization by microwave irradiation.^[124]

An essential difference between the SE and the CE mechanisms concerns the build-up rate of the nuclear polarization in the vicinity of the electron(s). In the SE case, which exploits a forbidden transition, the effective microwave power on the transition is small; the build-up rates are then much smaller than in the CE case, where the electron-driven nuclear spin polarization process is allowed and thus can be directly proportional to the microwave power. In practice, however, the concentration of the electron pairs fulfilling the stringent CE DNP condition—which requires that the two electrons must be properly oriented so that the difference in their resonance frequency exactly matches the nuclear Larmor frequency—is much smaller than the SE-DNP electrons.^[116] Hence, the two types of signal enhancement mechanisms are present simultaneously, with their predominance depending on factors such as radical kind, concentration, and relaxation parameters.

It follows from this description that DNP will benefit from either an EPR line that is sharp and easy to saturate (for SE) or from possessing pairs of coupled electrons (for CE). In all cases, these radicals should be homogeneously distributed over the sample, hence the need to work with amorphous or glassy solids. Several research groups are actively devoted to the development of polarizing molecules and sample preparation procedures that satisfy these conditions.^[129,130] Narrow-line carbon-based radicals such as trityl^[131] and 1,3-bisdiphenylene-2-phenylallyl (BDPA)^[132] are commonly used for exploiting the SE-DNP effect, particularly at cryogenic temperatures; 2,2,6,6-tetramethylpiperidine N-oxyl (TEMPO)^[133] and even metal ions with low orbital momentum have also been used as polarizing agents for SE-DNP.^[134,135] The lower power requirements for achieving efficient CE have made biradicals an appealing option in biomolecular and materials applications.^[136] Biradicals such as TOTAPOL^[136] and AMUPOL^[137] have been shown to lead to good enhancements at about 80 K. In DNP applications, these radicals are usually dissolved in glassing mixtures such as DMSO/water or glycerol/water, which by freezing into an amorphous phase^[102] prevents the segregation of the radical/biradical from the aqueous medium. Remarkably, biomolecule–radical interactions, either specific or aspecific, can also prevent the formation of separate radical grains.^[138–141]

5.2. Instrumental Aspects of DNP-Enhanced MAS NMR Spectroscopy

When applied to the in situ observation of a sample undergoing MAS, solid-state DNP NMR experiments require both a RF circuitry for performing the actual nuclear induction acquisition and a microwave circuitry to promote the electron saturation. In addition, the sample needs to be kept cold by use of cold gases to prolong the electron and nuclear relaxation times, usually by using nitrogen gas cooled to 80 K for implementing the sample spinning. Under such conditions, where the electron T₁ and T₂ times are still relatively short and the fields of observation relatively high (≥9.4 T), an efficient saturation of the electron spin system requires a source of both high-frequency and high-power microwaves. Griffin and co-workers at MIT pioneered the use of cyclotron resonance masers (gyrotrons) to fulfill this role.^[101] Gyrotrons provide much higher powers than alternatives, such as Gunn diodes or Klystrons, with an output power that can be stabilized over the course of a long experiment. A limitation of such sources is their relatively narrow tuning range, which implies that the field rather than the source’s frequency usually needs to be changed if the radical changes, for example, from TEMPO to BDPA. Recent developments, however, have also demonstrated the tunability of certain gyrotron devices based on the selection of different cavity modes.^[142] Tycko et al. have shown that the microwave power requirements can be greatly eased if relaxation times are lengthened by stable spinning at 13–25 K.^[53,215] It remains to be seen if this brings “tunability” to the microwave system.

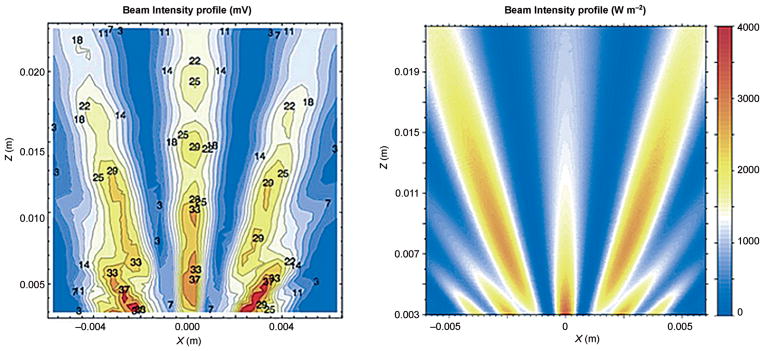
It follows that, in biomolecular applications of DNP MAS NMR spectroscopy, the probe has to provide the ability to irradiate two or three nuclear frequencies simultaneously (e.g. ¹H, ¹³C, and ¹⁵N), as well as the electron spin resonance of the radical in the sample. In current probe technologies, the microwaves are guided as a hybrid mode beam from the gyrotron into the DNP NMR probe through an overmoded waveguide with corrugated walls.^[143] The waveguide terminates in an aperture directed towards an opening in the MAS system, such that the beam is radially incident onto the rf coil and MAS rotor, the latter containing the sample of interest (Figure 10). 3D electromagnetic field simulations of millimeter wave-field distributions^[144] allow one to investigate the electron irradiation inside the rotor. The numbers in the contours shown in Figure 11A represent voltages (in mV) that were measured experimentally, and are in good agreement with computed data (Figure 11B). These simulations reveal that dielectric materials such as zirconia or sapphire (both used as MAS rotor materials) lead to significant refraction of the incident microwave beam. Even the dielectric properties of the DNP NMR sample (consisting, for example, of a frozen glycerol/water mixture) can lead to such effects. Clearly, much remains to be learned about the optimization of the microwave delivery process under such conditions.

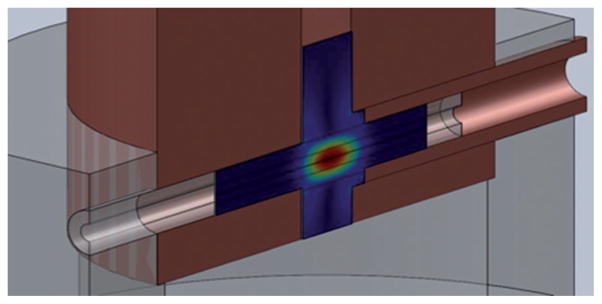
Figure 10.

Top: Computer drawing of the interior of a DNP MAS probe with the waveguide terminal and the MAS stator. Bottom: Cross-section through the MAS stator showing the NMR radiofrequency solenoidal coil, the MAS rotor, and the sample space. The coordinate system y direction is parallel to the MAS rotor and coil axis, the z direction indicates the direction of the incident millimeter wave beam.

Figure 11.

Forward scattering of a millimeter wave beam (Gaussian intensity distribution, hybrid mode HE11, linearly polarized) by a 3.2 mm outside diameter MAS rotor made of zirconia ceramics at a frequency of 263 GHz (wavelength 1.13 mm) in the plane of the incident beam orthogonal to the rotor axis. The rotor is outside of the field of view (below the lower edge of the field plot plane) and the beam propagates from the bottom to the top (along the z axis). Left: Plot of the magnitude of the electric field determined experimentally. Right: Simulated field distribution (magnitude of the Poynting vector field). Measurements and COMSOL simulations by E. de Rijk (EPFL) and SWISSto12, Lausanne.

5.3. Principles and Features of Dissolution (Ex Situ) DNP NMR Spectroscopy

DNP NMR has traditionally been performed at high magnetic fields only under cryogenic conditions. The ground-breaking innovation that brought this kind of DNP into the realm of high-resolution liquid-state NMR spectroscopy and in vivo MRI/MRS, was the introduction of a dissolution procedure that transforms a frozen sample containing highly polarized nuclear spins into a room-temperature solution, in which the spins with sufficiently long longitudinal relaxation time keep their enormous polarizations (Figure 12).^[104] This dissolution is irreversible, and is performed by propelling a hot solvent (e.g. superheated water) onto the frozen sample to rapidly melt it. The resulting solution is chased out of the polarizer using pressurized helium gas and collected for injection into an NMR tube, an animal, or a human. This “dissolution DNP” technique has been used to hyperpolarize ¹H, ⁶Li, ⁷Li, ¹³C, ¹⁵N, ⁸⁹Y, ⁸⁷Rb, and both ¹⁰⁷Ag and ¹⁰⁹Ag,^{[104,145–151]} and may enhance liquid-state nuclear polarization by factors ranging from 1000 to 50000 compared to the room-temperature thermal polarization obtained in the standard magnetic fields used for high-resolution NMR, MRS, and MRI spectroscopy. Thus, although these kinds of experiments cannot be repeated in normal “multiscan” fashion, the rationale behind their application is that, in light of such dramatic sensitivity enhancements, multiscan averaging becomes unnecessary.

Figure 12.

Schematic diagram of the DNP system with the transfer line to the 400 MHz spectrometer. The position of the dissolution stick is shown before (A) and after dissolution (B). The frozen sample is irradiated in the 3.35 T magnet shown on the left, and shuttled rapidly using hot solvent and He chase gas after DNP at low temperature into the high-field system for NMR spectroscopy. Reproduced from Ref. [165] with permission.

In contrast to solid-state DNP MAS NMR, dissolution DNP is inherently an ex situ method. The field strength as well as the temperature at which the DNP processes take place can thus be chosen independently from the parameters used for the post-dissolution NMR measurements. This flexibility allows one to select different temperature and field combinations to obtain the highest polarization in a given amount of time. Typical parameters entail a field of between 3 and 7 T, and a temperature of 1–2 K.^[62–67] Under such conditions, the electron polarization is essentially unity, and nuclear polarizations on the order of 0.1–0.5 can be reached within a few hours. The ex situ character also implies that the role played by the NMR instrumentation is secondary during the polarization process, and a rudimentary coil capable of monitoring the course of the DNP build up by a small flip angle excitation suffices. An exception arises when considering the possibility of enhancing the ¹³C polarization build-up rate through ¹H-¹³C cross-polarization schemes,^[152] something that requires double-resonance high-power circuitry.^[153,154] The low temperatures at which the experiment operates also reduces considerably the demands on the microwave power, with approximately 100 μW (rather than the tens of Watts available from gyrotrons) being suitable for the majority of the cases.^[155]

The solid-to-liquid phase transition and ensuing shuttling of the hyperpolarized liquid from the polarizing to the NMR platforms limits the potential benefits of dissolution DNP to relatively long-lived sites whose T₁ values exceed several seconds. This consideration includes the magnetic fields involved in the hyperpolarizer→spectrometer transfer in the NMR spectrometer field as the sample settles into an NMR tube or in the MRI scanner as a metabolite is perfused and metabolized into an organ of interest. Indeed, following the sample dissolution process and throughout all these different potential events, the nuclear hyperpolarization will begin to decrease back to its thermal equilibrium value. How long the hyperpolarization will remain sufficiently high to be competitive with a normal multiscan acquisition will depend on the nature of the chemical site interrogated, the weight and rigidity of the molecule, and the fields and temperatures involved. Relaxation losses are particularly severe for abundant nuclei such as ¹H, and for large molecules including polypeptides, nucleic acids, and polymers. These systems are generally unsuitable for polarization enhancement by dissolution DNP. Temperature increases will generally prolong the relaxation times of small molecules, although this variable is not always amenable in biomolecular and in vivo studies. A relatively minor chemical change that is often amenable concerns deuteration, which helps reduce the nuclear dipolar relaxation. Extraction or neutralization of the polarizing radicals can also lead sometimes to a reduction of the relaxation rate and hence diminish the transfer-induced losses.^{[132,156–158]} It is also possible to enhance and detect nuclear spins with short relaxation times T₁ by in vitro or in vivo polarization transfer from hyperpolarized nuclear spins with long T₁ values.^{[150,159,160]} Such methods can potentially lead to increased sensitivity or increased spectral resolution, even in vivo.^[161] Further extensions might be enabled by the use of long-lived, singlet-like states,^[162] capable of supporting hyperpolarization by times that exceed the conventional single-spin T₁ values. The most advanced, robust solution when considering chemical or biomolecular applications of fast-relaxing species promises to be the advent of superconducting magnets dedicated to dissolution DNP containing two homogeneous field centers—one for DNP and another for NMR spectroscopy. In this case, sample transfer can occur in hundreds of milliseconds between the two centers, thereby opening a wide array of potential groundbreaking applications.^[163] Although potentially of revolutionary consequences, such an approach would still need to beware of important sample-related issues such as temperature-denaturation of biomolecular samples or solubility/precipitation issues that will arise when considering the preparation of the small-volume but highly concentrated solutions (100–1000 mM) normally utilized in ex situ hyper-polarization.

Another general feature associated with the irreversible decay of the hard-earned DNP hyperpolarization relates to the fact that the NMR experiments that dissolution DNP can support can only include a single or at most a small number of low flip angle scans. This makes it a challenge to collect hyperpolarized 2D NMR acquisitions, of the kind that are ubiquitous in biomolecular NMR spectroscopy. A promising solution rests on employing single-scan “ultrafast” 2D NMR spectra of hyperpolarized compounds; 2D spectra of hyper-polarized liquid samples at sub-μM concentrations can then be acquired within 0.1 s.^{[145,164,165]} Other methods can obtain correlations indirectly, for example from 1D acquisitions using off-resonance decoupling;^[166] these methods are relatively simple, but do not enjoy the resolution benefits of 2D spectroscopy. In the current state of development, it appears that dissolution DNP will not enable the execution of the most complex sequences in the arsenal of contemporary multidimensional NMR spectroscopy. Dissolution DNP should, therefore, not be viewed as a competition but rather as a complement to conventional high-resolution NMR methods of biomolecular characterization.

5.4. Applications of Dissolution DNP: Chemistry, Biochemistry, Medicine

The main area of interest of dissolution DNP is currently aimed at the preparation of hyperpolarized substrates for performing metabolic NMR studies in vivo, to be analyzed by both MRI and MRS. Despite the limited lifetime of the hyperpolarized spin state, application of the technique as a diagnostic tool and for following therapy response in cancer research and cardiology has been widely documented in preclinical studies.^[167,168] Over the last few years dissolution DNP has been used in its first human patient studies.^[169] This development has been impressive and truly multidisciplinary in both scope and execution; it included numerous efforts in terms of pulse-sequence development^[170–174] and led to biological insights which are simply too numerous to describe in this biomolecular-oriented Review.

Significant opportunities for making use of dissolution DNP also arise in the field of high-resolution NMR spectroscopy. Dissolution DNP is particularly well-suited to the observation of transient molecular species in chemical or biochemical reactions away from equilibrium. One way to minimize polarization losses in these transient-state observations is by relying on dedicated, rapid sample injection devices that permit the use of otherwise typical dissolution DNP hardware for spins with sub-second T₁ values.^[175] Drug discovery is an area where this ability to rapidly inject chemicals to target proteins could arise. A number of studies have thus focused on the hyperpolarization of potential ligands by dissolution DNP and their ensuing detection of binding—or even determination of binding constants—from changes in the relaxation and cross-relaxation parameters.^[176,177] From a technological point of view, this may be an almost ideal application for dissolution DNP, since here the inevitable dilution of the sample during dissolution as well as the single-use nature of the technique do not impose significant additional constraints on the experiment. Similar advantages can be argued for following the kinetics of certain chemical and biochemical reactions, including protein and RNA folding. A series of dissolution DNP experiments from a single hyperpolarized sample have allowed, for example, the study of enzyme-catalyzed reactions,^[178] with the possibility to distinguish reagents and reaction products thanks to their different chemical shifts. The availability of customized fast dissolution systems has even allowed for substantial hyper-polarization and observation of transient protein signals. These proteins can, for example, be hyperpolarized in the unfolded state and injected into the NMR instrument for re-folding after a pH jump.^[179,180]

5.5. In Situ Solution-State DNP NMR Spectroscopy

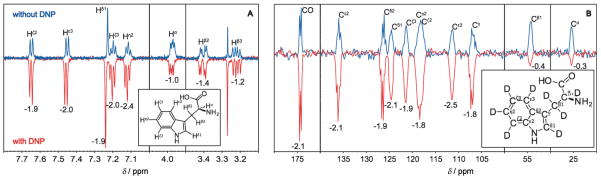
Other than resorting to dissolution, liquids can also be directly polarized in a setup that facilitates fast repetition signal averaging, as the sample always remains in its original state. At variance with what happens in solids, DNP in liquids is driven by electron–nuclear cross-relaxation processes, similar to those in metals, where DNP was first theoretically predicted^[181] and experimentally observed.^[100] This phenomenon is usually also called Overhauser DNP. In most cases the cross-relaxation rate between the DNP agent and target molecule is dominated by the magnetic dipole–dipole interaction between the electron and the nuclear spins. To achieve efficient polarization transfer rates, this interaction has to be modulated on the time scale of the electron-spin Larmor frequency.^[182] Diffusional and rotational correlation times for small organic radicals dissolved in water at room temperature are in the range of tens of picoseconds; this leads to a strong drop in the spectral density, and therefore in the DNP efficiency, above electron Larmor frequencies of about 34 GHz, which corresponds to a magnetic field strength of approximately 1 T. Overhauser DNP has thus been observed at ≤0.5 T fields and utilized within the context of biological investigations to examine the local hydration dynamics in and around complex molecular systems: from the extent of the observed water hyperpolarization, these experiments enabled the translational time of hydration water at the specific sites of the spin probes to be characterized with good sensitivity.^[183,184] However, DNP in liquid samples was believed for a long time to give negligible enhancements at magnetic fields above 1.5 T. Very recently, however, a number of research groups have demonstrated substantial Overhauser DNP enhancements at magnetic fields of 3.4^[185–188] and 9.2 T.^[189–191] A proton polarization enhancement level as high as −165 was observed at 3.4 T in liquid water with TEMPOL nitroxide radicals at concentrations in the 20–100 mM range (Figure 13A,B)^[188] and of −83 at 9.2 T with radical concentrations of 20–1000 mM^[191] (Figure 13C). These enhancements were achieved at and above the boiling point of the solution, as a consequence of the increase in temperature because of the heating of the sample by the microwaves.

Figure 13.

Enhancement at 3.4 T as a function of the microwave power (94 GHz, power given in W) for water and TEMPOL with a concentration of 20 mM (A) and 100 mM (B). The solid line is a prediction from theory with all parameters determined independently from EPR and relaxometery measurements (see van Bentum et al.).^[186] C) DNP enhancement achieved at 9.2 T plotted against the incident microwave power for 1M ¹⁴N-TEMPOL in water for three capillary sizes: 50 (▲), 30 (□), and 20 μm (★) internal diameter. The temperature increase is indicated by the dashed horizontal lines, crossing the curves at the indicated temperatures. Adapted from Ref. [191].

To get a quantitative understanding of the mechanisms at work, a detailed analysis was performed to determine all the relevant parameters intervening in the process. One of these is the degree of saturation of the EPR transition, which depends on the electron spin relaxation rates and the Heisenberg exchange rate.^{[187,188,192]} Annino et al. achieved full saturation at power levels of about 100 μW at 95 GHz with a novel nonradiative resonator^[193] (Figure 14); Neugebauer et al. used the shift resolution available at 9.2 T to determine the saturation parameter by measuring the suppression of the paramagnetic ¹H NMR shift upon irradiation with microwaves.^[191] Another important factor involves the relevant correlation times. There has been a long-standing controversy whether relaxometry data, which is a method of choice to define such microscopic-level dynamics,^{[191,192,194]} are consistent with the observed DNP enhancements at high magnetic fields. Within the Overhauser effect model, they should both be governed by the same relaxation mechanisms. The in situ DNP measurements performed at 3.4 T and 9.2 T on TEMPOL/water mixtures have now shown that these two sides of the coin are indeed consistent with one another, if the ¹H relaxometry data collected from very low (typically 0.01 MHz proton Larmor frequencies) to high magnetic fields are analyzed while including the effect of relaxation as a result of bound radical–water complexes.^[188,191] The resulting model is sufficient to predict quantitatively both the paramagnetic relaxation and the DNP enhancement experienced by water for different radical concentrations and temperatures. The main effect that then explains the high DNP enhancements observed experimentally is the substantial decrease in the diffusion correlation time of water from about 20–30 ps at room temperature to a few picoseconds at temperatures near the boiling point. In this fast mobility conditions, the double-quantum cross-relaxation that drives the Overhauser effect becomes significant even at relatively high fields of 3.4 T or 9.2 T. Similar investigations also reveal such effects for other solvents, even if in cases such as ethanol, the reduced mobility because of the formation of a bound complex results in enhancements that are much lower than in the case of H₂O. Measurements performed in nonpolar solutions indicate that dynamics other than translational diffusion probably contribute substantially to explain the high DNP enhancements observed at 9.2 T.^[195] Molecular dynamics simulations^[196,197] might give more insight into the specific dynamics responsible for the cross-relaxation rates at high frequencies.

Figure 14.

Double resonance structure used by Annino et al. for simultaneous in situ NMR and DNP using a high conversion factor nonradiative resonator.^[193]

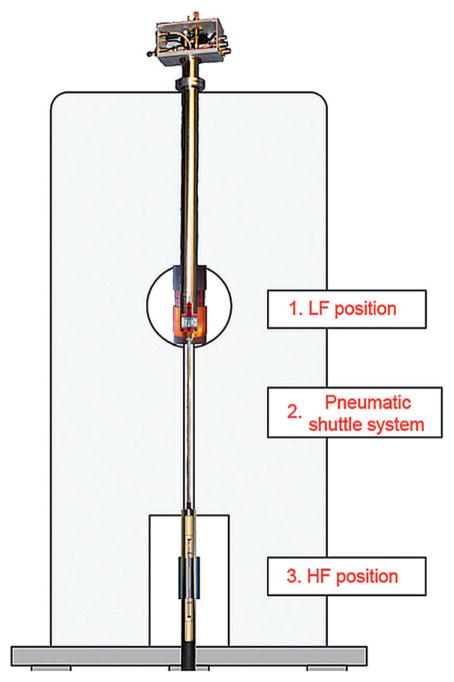
A downside of in situ DNP experiments performed in liquids at high magnetic fields is that they are restricted to small sample volumes. Indeed, although substantial polarization of water can be achieved at high magnetic fields, the dielectric losses in water are huge. This severely limits the penetration depth of the microwaves, and high-field polarizations are only possible for volumes in the nanoliter range that are placed inside a resonant cavity that avoids exposure to the electric field components of the microwave beam. This can, however, be exploited for on-chip NMR detections in a microfluidic context; however, the application for more general biomolecular cases is limited. Another approach that is consequently being explored consists of polarizing the sample at lower magnetic fields, where the sample size is less restricted, and transferring the sample afterwards to the high NMR detection field.^[194,198] Such “shuttle DNP” implementations have included performing Overhauser DNP at low (0.35 T) fields, where radicals such as TEMPOL can be easily saturated and will efficiently transfer their magnetization to nearby protons, followed by sample shuttling to high fields (600 MHz) for final NMR detection. The shuttling is based on a pneumatic operation (Figure 15) that minimizes the distance between the high- and low-field position and ensuring a monotonous increase in the B₀ field between the two positions.^[199] Although this procedure yields high enhancements at low magnetic field, these gains are scaled down by the ratio between the polarizing and detection field, and might be further reduced during the shuttle process.^{[186,194,200]}

Figure 15.

Setup of the shuttle DNP spectrometer, indicating the low-field position (LF, 0.34 T), 47 cm above the high-field position (HF, 14.1 T). The former includes microwave irradiation for DNP and the latter an RF coil for NMR detection. The sample transfers in 60 ms by pneumatic shuttling, with an accurate sample positioning (less than 50 μm). Detection of ¹H and ¹³C signals with a ²H lock and occurs after the container is shuttled.

This approach is susceptible to multiscan averaging, and DNP enhancements of −2.4 have been reached for the ¹H signals of molecules such as tryptophan (Figure 16A). Taking the total measurement time into account, enhancement by up to a factor of −4 is observed.^[201] Recently, ¹³C enhancements were also investigated in a shuttle DNP spectrometer for [¹³C₁₁,¹⁵N₂]-tryptophan as well as [²H₈,¹³C₁₁,¹⁵N₂]-tryptophan (Figure 16B). While in the former case only the carbonyl resonance of Trp shows an expected negative enhancement for a direct Overhauser effect induced by translational and rotational diffusion of the radical with respect to the ¹³C spin of the molecule, the other carbon atoms show a positive enhancement that, if direct, would indicate scalar transfer between the carbon spins and the electron. It should be kept in mind, however, that the protons in tryptophan are also polarized, and that the combination of a positive ¹H,¹³C NOE effect acting on top of the electron,¹H Overhauser effect may also lead to a ¹³C magnetization enhancement that possesses the same sign as the Boltzmann magnetization. Removing the protons from tryptophan removes this dominant transfer for the hydrogen-carrying carbon atoms; all ¹³C resonances then exhibit negative enhancements (Figure 16B), which suggests that indeed through-space Overhauser effects between electrons and carbon atom spins is decisive. Further studies aiming at elucidating these processes in larger biomolecules than tryptophan are under way.

Figure 16.

A) ¹H Enhancement of 10 mM tryptophan in 4.5 μL D₂O in the presence of 10 mM [D₁₆,¹⁵N]-TEMPONE, polarization time of 3 s, T = 52°C. 64 scans. B) ¹³C Enhancement of 50 mM [²H₈,¹³C₁₁,¹⁵N₂]-tryptophan in 4.5 μL D₂O in the presence of 10 mM [D₁₆,¹⁵N]-TEMPONE, polarization time of 3 s, T = 52°C, 4096 scans. All signals now show negative enhancement.

5.6. Spin-Alignment Alternatives: Nuclear Hyperpolarization by para-Hydrogen and Optical Pumping

Polarization transfers from unpaired electrons are not the only way to achieve nuclear hyperpolarization. Another source of polarization can be the H₂ molecule itself. At room temperature, hydrogen exists as two isomers, the ortho-and the para-hydrogen forms, which are present at a statistical ratio of 3:1.^[202] These forms differ in the arrangements that the two ¹H nuclei take in the molecule; there is a correlation between the molecular form and proton spin states, dictated by the overall antisymmetry of the molecular wavefunction. ortho-H₂, which is associated with a symmetric nuclear triplet arrangement, will thus be associated with antisymmetric rotational wavefunctions, whereas the para-H₂ isomer, which is associated to an antisymmetric $(\mid \alpha \beta >-\mid \beta \alpha >)/\sqrt{2}$ nuclear spin singlet, will only arise in molecules with symmetric rotational wavefunctions. The symmetric J = 0 state possesses the lowest energy of the rotational manifold of hydrogen, and therefore the singlet spin wavefunction of para-H₂ dominates at low temperature. Although para-hydrogen itself has no net spin angular momentum and is NMR silent, it can be used as a reagent to create reaction products that possess non-Boltzmann nuclear distributions with high degrees of spin alignment. This results if the two spins making up the invisible $(\mid \alpha \beta >-\mid \beta \alpha >)/\sqrt{2}$ state suddenly become distinguishable, for example, by the addition of the two hydrogen atoms into two chemically inequivalent sites. para-Hydrogen-induced polarization (PHIP) is created in this way,^[203,204] and can achieve enhancement in the 10% range in a simple repetitive fashion, thus opening an interesting route to nuclear hyperpolarization of suitable target molecules. This has allowed the hyperpolarization of a range of organic and biomolecular compounds through their hydrogenation; a number of reviews illustrate the wide range of para-hydrogen-derived applications.^[205–207]

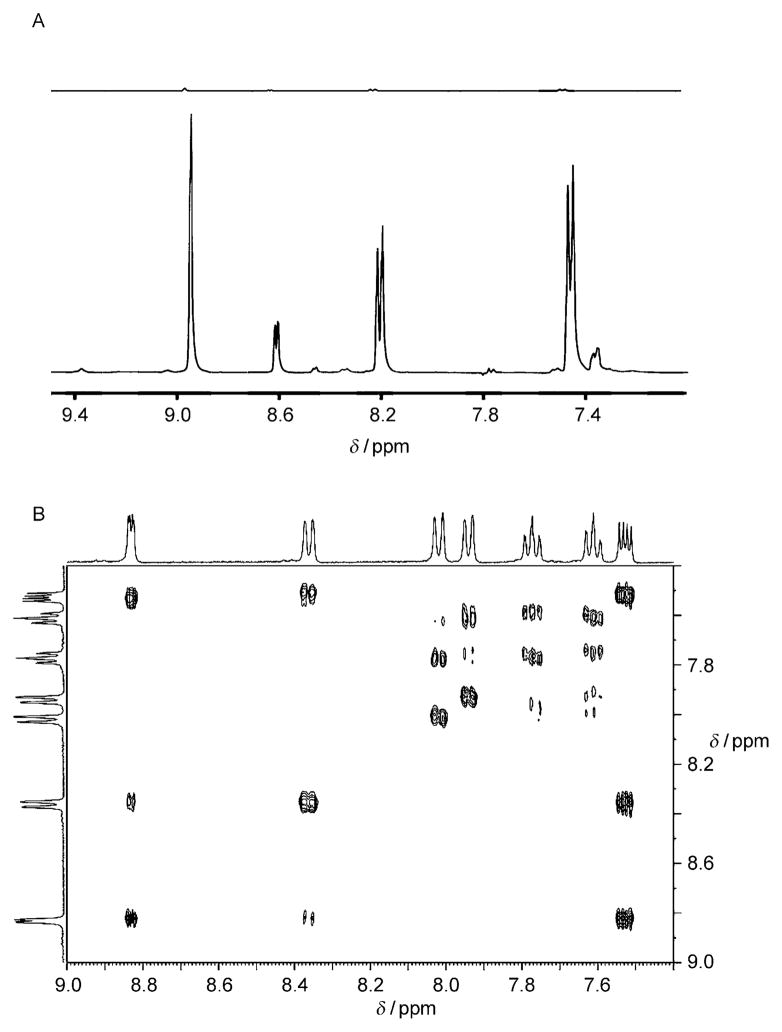
More recently, it has been shown that para-hydrogen can be employed to hyperpolarize a growing range of organic substrates through the establishment of a simple and reversible interaction at a metal center. In this process, the substrate and para-H₂ exchange freely in solution with those of the complex, and a concentration of hyperpolarized product builds up in solution as a result. This process has been termed signal amplification by reversible exchange (SABRE),^[208] and it can typically achieve polarization transfer in a sealed NMR tube over a time period of between 10 and 20 s. Shaking provides a route to the rapid formation of the dihydride complex associated with the SABRE magnetization transfer, whilst simultaneously retaining the highest effective concentration of para-hydrogen in solution throughout the transfer step by facilitating rapid gas equilibration with the headspace. After shaking in this way, the sample is quickly transferred into the magnet of the NMR spectrometer, where data acquisition is undertaken. Figure 17A illustrates 1D enhanced spectra collected by using this strategy. Multipulse sequences that require signal averaging, such as 2D COSY NMR spectroscopy, in conjunction with SABRE have also been demonstrated (Figure 17B).

Figure 17.

A) Bottom: 1D ¹H NMR spectrum of nicotinamide that was hyperpolarized under SABRE. Top: the analogous spectrum collected under Boltzmann controlled populations. B) 2D ¹H-COSY spectrum of hyperpolarized quinolone collected using the SABRE method and the automated polarizer described in Ref. [213].

A final elegant solution that has been presented to achieve hyperpolarization relies on illumination with light: The use of circularly polarized light during promotion to an excited state causes a selection of the spin state of the electron; this is a non-equilibrium electronic polarization that, as in the case of DNP, is in turn reflected by dramatic changes in the nuclear spin polarizations. Optically pumped nuclear enhancements were first (and are most often) achieved in the case of alkali metal atoms, where a single valence outer electron is strongly coupled to the nuclear spin.^[209] The coherent polarization of this electron by a suitably polarized light source can then transfer to nuclei. Electron-spin polarization is transferred, for example, from rubidium to noble gas atoms, such as ¹²⁹Xe, through the hyperfine interaction that is established during the collision of ¹²⁹Xe atoms with the alkali metal. Xenon is an attractive substrate because it is usually not present in living organisms and optical pumping is a rather easy method for imparting hyperpolarization, and because it can resonate over a wide range of chemical shifts, thus being an accurate reporter for changes in its proximity.^[210] Hyperpolarized ¹²⁹Xe gas can, for example, be used as such for imaging of the respiratory apparatus, or it can be used for the creation of biosensors, as a result of the possibility of dissolving xenon in various solvents, either hydrophilic or hydrophobic.^[211] It remains to be seen how many of these optical pumping promises will eventually find translation into the improvement of biomolecular NMR spectroscopic studies

6. Biomolecular NMR Spectroscopy: Sensitivity-Enhancement Perspectives

NMR spectroscopy provides structural and dynamic information on an outstandingly broad range of fields that have an influence on a wide range of biochemical and biophysical investigations ranging from pharmaceutical studies and metabolic profiling to the study of soluble and insoluble proteins, membranes and nucleic acids, crystalline and membrane proteins, and protein aggregates and fibrils. Despite this outstanding track-record of achievement and its unique potential to illuminate the relationship between chemical structure and biological function, NMR spectroscopy faces a number of challenges. Foremost among these, stands its low sensitivity. Indeed, the unique non-invasiveness and extreme site resolution capabilities of NMR spectroscopy derive from the very low energies involved in this magnetic-based spectroscopy. This, however, is also the main Achilles Heel of NMR: as a consequence of the tiny energies it involves, this spectroscopy also has very low sensitivity compared to competing electric-field-based and/or optical technologies. It is clear that unless suitably addressed, this limitation may end up robbing magnetic resonance techniques from being competitive with other rapidly improving forms of spectroscopy and microscopy.

The kind of problems that would become amenable to study by an increased NMR sensitivity can be broadly divided into two scenarios. One includes samples that, in principle, have long-term stability but whose intrinsic sensitivity is low, either because of targeting low-abundance, low-gyromagnetic nuclides, or poorly soluble samples. A second scenario arises in systems that can evolve in time, where increases in the S/N ratio could yield unique information on transiently populated states and on their dynamic changes. Boosting the S/N ratio could yield detailed, unique information for both kinds of scenarios.

Improving the detection limit of NMR spectroscopy would have immediate consequences on our abilities to characterize a wider spectrum of the biological and human metabolomes in health and disease. It would put powerful new structure-elucidation methods at the service of natural products chemistry and it would open rare opportunities to characterize lowly populated but often critically important states of biologically active macromolecules. Low abundance on a per-site basis is a landmark of macromolecular complexes and of membrane-embedded proteins, where low solubility and high molecular weights represent major challenges that a better NMR sensitivity could overcome. Higher sensitivity would also enable the detection of low-magnetogyric nuclei that dominate many chemically and biochemically active sites (³³S, ¹⁷O, ¹⁵N, diamagnetic metal centers), which are usually present at low natural abundance and resonate at very low frequencies. Boosting sensitivity would also make NMR spectroscopy uniquely capable of characterizing the presence, structures, and reactivities of intermediates with lowly populated, but often critically important, dynamic forms. Also within a dynamic biochemistry setting, improving the sensitivity of NMR spectroscopy would push the boundaries of what kind of processes and what size molecules could be observable as these systems evolve in real time. Within in cell settings, atomic-level insight could be gained about the nature and dynamics of post-translational modifications. In metabolic small-molecule research, enhanced sensitivities would enable the quantification of concentration fluxes needed to understand catabolic and metabolic pathways. Further improvements in sensitivity could open new opportunities in methods based on hyphenated NMR spectroscopy, which have become essential ingredients in the search of structure–activity relationships and in many aspects of “omics” sciences. When all these aspects are considered in unison, it is clear that enormous scientific progress could be derived if NMR spectroscopy were to deliver utmost sensitivity per unit time.

It is equally evident that the techniques that will be required to improve the S/N ratio of NMR spectroscopy will be multiple, and differ depending on the method applied and the condition being targeted. This Review attempted to describe contemporary progress in certain key areas that could benefit wide realms of application, regardless of the specific NMR experiment being considered. A traditional solution to the sensitivity problem of NMR spectroscopy has been to increase its operating magnetic field strength B₀. This brings about concomitant increases in sensitivity and in resolution. The last decade, however, has witnessed diminishing returns in the performance of the high-resolution NMR magnet technologies based on the traditional recipe of an all-low-temperature, fully persistent, Nb-based superconductor winding. This diminishing rate of return is manifested by the rapidly increasing sizes and costs of all-LTS systems, in exchange for dwindling improvements in the strengths of the fields delivered. Given this situation, this Review described efforts in the design of alternative magnet technologies capable of fulfilling the stringent homogeneity and stability demands of NMR spectroscopy, while allowing for a quantum jump in the achievable fields. Two models appear promising in this regard: one incorporating a serial arrangement of low-and high-temperature superconducting windings, and another a serial arrangement of superconducting and electromagnets. Both of these models demand changes in the canonical approach of doing NMR spectroscopy, in the sense of requiring the reintroduction of active-field stabilization as a result of the nonpersistent mode by which such systems have so far been operated. Both of these models also pose numerous new challenges to overcome, including construction and operational costs as well as stability demands. This notwithstanding, the benefits that could result from such modes of operation, including the promise of fields reaching up to 40 T and improvements that could trickle down throughout the lower-field NMR spectroscopy and MRI arenas, justify these investments.

The sensitivity of NMR spectroscopy also increased substantially over the last decade as a consequence of the development of better probes for signal detection. These advantages benefited in particular structural biology experiments, where the introduction of cryogenically cooled coils and preamplifiers for solution studies and of low-electric-field probes for biosolid investigations were instrumental in enabling experiments that had hitherto been beyond reach. These technologies are, however, also mature, thus leaving the question of what further progress can be expected in these areas. This Review presented some of the options opening up ahead, including, in the case of liquids, the development of microcoils whose diameters are tailored to the size and kind of sample being analyzed, and coils employing high-temperature superconductors characterized by even lower noise factors than their cryogenically cooled copper counterparts. While these improvements could also have an impact on the execution of solid-state acquisitions, much is determined in these setups by the stringent requirements imposed by fast MAS and by the need to handle high RF powers. However, it is likely that substantial improvements will also benefit the sensitivity of solid-state experiments—particularly as higher fields and higher spinning speeds ameliorate the RF handling requirements. This would, in turn, justify the introduction of cryogenically cooled coils and preamplifiers. Equally crucial in the study of solids and semisolids will be optimizations of the sample preparation procedures, including sedimentation, sample alignment, and new labeling approaches, as well as the introduction of new pulse sequences and experiments endowed with higher sensitivities. In particular, it seems that the methyl-TROSY experiments in solution, of ¹H detection under ultrafast MAS, and of experiments targeting low-magnetogyric species such as ¹⁵N and ¹⁷O where much of the “biochemical action” takes place, should become more widespread as a result of these efforts.

Beyond a focus on improving the performance of traditional components of the NMR experiment—the spectrometer, the pulse sequence, the probe, the sample—the last decade has “rediscovered” the potential that could result from the introduction of hyperpolarization methods into mainstream NMR spectroscopy. These renewed efforts arise from the realization that if the initial nuclear polarizations could be morphed from their usual P ≈ 5×10⁻⁵ thermal equilibrium values at 300 K to P ≈ 0.5, sensitivity gains that could far surpass those of any other technological improvement would result. Standing out in general among all the hyperpolarization approaches capable of delivering this kind of enhancement is DNP, a method that in principle only requires that the sample to be analyzed be mixed with a low dose of a free radical whose EPR signal is then suitably saturated by microwave irradiation. Thanks to a series of remarkable technological developments progressing hand-in-hand with a better understanding of the spin physics involved, DNP has become one of the main focuses of interest in both solution and solid-state NMR spectroscopy. Encouraging advancements in these areas resulted from the advent of commercial systems capable of performing the liquid- and solid-state NMR experiments.

In the case of liquid NMR spectroscopy, the enhancement is brought about under pumped liquid helium conditions, which lead to sensitivity gains of ≥10000 from the combined differences in the gyromagnetic ratio between the electrons and nuclei and in the Boltzmann spin alignment between the cryogenic and room-temperature environments. In solid-state NMR spectroscopy, the temperature of operation is set by cold nitrogen gas, which is better suited to high-power MAS operation, thus leading in principle to more modest gains of 100-fold that are derived mostly from the difference in the gyromagnetic ratio between electrons and nuclei.

These sensitivity enhancements, though unparalleled by any other ongoing technological effort in NMR spectroscopy, have not lead to automatic gains in all realms. Structural biology applications, in particular, still pose a number of significant challenges. The dissolution DNP experiment, at least in its current form, is ill-posed to tackle large biomolecular systems because of the fast relaxation that their spins undergo upon transferring from the polarizing to the observation magnets. Fast-injection devices and shuttling approaches, where the sample never leaves a high magnetic field region, are being explored as solutions to this obstacle; so are approaches based on in situ Overhauser DNP. Solid-state DNP NMR studies are also challenged in large biomolecules, particularly because of the line broadening that low temperatures impart on the ¹³C and ¹⁵N resonances and the decreased enhancements observed at higher fields.^[24,212] The former effects, which derive from the freezing of dynamic averaging modes when biological solids are cooled below about 230 K, do not affect the NMR spectra of inherently heterogeneous systems such as protein aggregates or of inherently broad signals such as those arising from quadrupoles. However, they still remain an obstacle in the generalized use of solid-state DNP to analyze an array of proteins, whose resolution is a topic of active investigation. Alternative roads that may bypass the need for low-temperature operations, perhaps based on new polarizing radicals or on the development of optics-based complements to the traditional DNP experiments, are also being actively considered.

All in all, it is clear that while the mature state of contemporary NMR spectroscopy implies that all the low-lying fruits available to improve this form of spectroscopy may have been harvested, its unparalleled track record also promises valuable new research opportunities to open as new improvements become incorporated into mainstream NMR spectroscopy of biomolecules.

Biographies

Claudio Luchinat, born in Florence, Italy, in 1952, obtained his doctorate in chemistry at the University of Florence in 1976, was a postdoctoral associate and Researcher at the University of Florence, and then Full Professor of Chemistry at the University of Bologna (1986–1996) and Florence (1996 to the present).

Harald Schwalbe completed his PhD (1990–1993) with C. Griesinger, University of Frankfurt, and then carried out postdoctoral research (1993–1995) with C. Dobson, University of Oxford. He was professor for Biological Chemistry at MIT, USA (1999–2001). Since 2001 he has worked at the Johann Wolfgang Goethe University. His research focuses on the development and application of NMR spectroscopy to study the structure and dynamics of proteins, DNA, and RNA.

Lucio Frydman completed his BSc and PhD from the University of Buenos Aires, before being a postdoctoral associate with Prof. Alex Pines in Berkeley (USA). Between 1992 and 2001 he was on the faculty at the University of Illinois—Chicago. He is professor at the Weizmann Institute in Israel and chief scientist for chemistry and biology at the US National High Magnetic Field Laboratory in Tallahassee, Florida. He is the editor of the Journal of Magnetic Resonance, chairman of Euromar’s board of trustees, and director of Weizmann’s Helen L. and Martin S. Kimmel Institute for Magnetic Resonance.