Skip to main content
NCBI home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jul 14;6:29676. doi: 10.1038/srep29676

Universality of the electrical transport in granular metals

Hicham Bakkali 1,2,a, Manuel Dominguez 1, Xavier Batlle 2, Amílcar Labarta 2
PMCID: PMC4944140  PMID: 27411671

Abstract

The universality of the ac electrical transport in granular metals has been scarcely studied and the actual mechanisms involved in the scaling laws are not well understood. Previous works have reported on the scaling of capacitance and dielectric loss at different temperatures in Co-ZrO2 granular metals. However, the characteristic frequency used to scale the conductivity spectra has not been discussed, yet. This report provides unambiguous evidence of the universal relaxation behavior of Pd-ZrO2 granular thin films over wide frequency (11 Hz–2 MHz) and temperature ranges (40–180 K) by means of Impedance Spectroscopy. The frequency dependence of the imaginary parts of both the impedance Z″ and electrical modulus M″ exhibit respective peaks at frequencies ωmax that follow a thermal activation law, ωmax ∝ exp(T1/2). Moreover, the real part of electrical conductivity σ′ follows the Jonscher’s universal power law, while the onset of the conductivity dispersion also corresponds to ωmax. Interestingly enough, ωmax can be used as the scaling parameter for Z″, M″ and σ′, such that the corresponding spectra collapse onto single master curves. All in all, these facts show that the Time-Temperature Superposition Principle holds for the ac conductance of granular metals, in which both electron tunneling and capacitive paths among particles compete, exhibiting a well-characterized universal behavior.

Disordered dielectric materials, consisting of random distributions of conducting and insulating phases, are present in a broad variety of systems such as ceramic composites, polymers, semiconductors or thin films of nanostructured granular metals. The latter have been extensively studied due to their relevant physicochemical properties1,2,3,4,5,6,7, promising optical8,9 and several sensing applications10,11,12. Most of those materials display a similar conductivity-frequency dependence as proposed by Jonscher and known as the universal power law (UPL)13,

graphic file with name srep29676-m1.jpg

Inline graphic being the dc conductivity of the material, A, a pre-exponential constant and n, a fractional exponent which is typically 0 < n < 1. Both A and n are temperature dependent. The ac conductivity of these materials is also found to follow a universal dynamic process, since temperature only changes the number density of charge carriers in ionic conductors14,15 or the electron hopping probabilities in granular metals16,17. Jonscher’s UPL model successfully describes most of disordered dielectric materials when the ac conductivity and permittivity show a dispersive region beyond a critical frequency18,19. Several authors19,20,21,22,23 have applied this model to examine the electrical response of random resistor-capacitor networks, which easily model a heterogeneous microstructure consisting of randomly distributed conducting and insulating regions. Moreover, it has been shown in the case of glasses, amorphous semiconductors and polymers that the conductivity spectra collapse into a single master curve, suggesting the validity of the so-called Time-Temperature Superposition Principle (TTSP), which can be expressed by the following scaling law13,15,24,25,26,27:

graphic file with name srep29676-m3.jpg

where F is a temperature-independent scaling function and ω* is the characteristic frequency corresponding to the onset of the conductivity dispersion, which in turn is the scaling parameter. Hopping conduction is proposed by many studies in order to account for the characteristic frequency ω* acting as the scaling parameter for all conductivity spectra in the measured temperature range28,29. In such works, the onset of the conductivity dispersion is attributed to the relaxation processes related to both grain and grain boundary contributions30. Nevertheless, in the case of granular insulating thin films in the dielectric regime, the ac transport is originated from electron tunneling and capacitive paths among particles in the sample, rather than from ion hopping. Furthermore, the relaxation processes in granular metals are related to competing electron tunneling and capacitive paths among nanoparticles in the material. Previously, it was reported by some of us that capacitance and dielectric loss show scaling behavior in granular metals31. Consequently, the characteristic frequency corresponding to the onset of the conductivity dispersion has been attributed to the frequency at which the magnitudes of the admittances of both the tunneling and capacitive paths become similar4,7,31,32,33. In this report, we determine independently the critical frequency ω* by analyzing the dielectric impedance Z″, electrical modulus M″, and the ac conductivity spectra σ′, respectively, of Pd-ZrO2 granular metal up to room temperature and over a wide frequency range (11 Hz–2 MHz) and we show the scaling behavior of all three spectra at low temperature by applying the TTSP and Jonscher’s UPL models.

Experimental

Pd-ZrO2 samples were evaporated on SiO2 substrates by co-sputtering of Pd and ZrO2 stabilized with 7% volume yttrium oxide (Y2O3) targets, using magnetron sputtering (MS). The distance between the target and sample was fixed at 10.7 cm, argon pressure was 2.3 × 10−5 bar, sample exposure time was 30 second, film thickness was 10 nm and the deposition power was 30 Watts for Pd and 255 Watts for ZrO2. After deposition of the Pd-ZrO2 layer, four parallel Au strips were thermally evaporated on the sample surface to provide the metallic contacts for four-point electrical measurements. These strips were approximately 5 mm long, 1 mm wide, and were separated by a distance of 0.7 mm. The films were initially characterized with a JEOL 2010 high resolution transmission electron microscope (HRTEM) for structural analysis as shown in ref. 32. A bimodal size distribution of Pd particles is observed, with one peak centered at smaller sizes (~2 nm) corresponding to most of the Pd nanoparticles and the other (less clear, shown as a shoulder) at larger sizes (>5 nm) corresponding to fewer Pd nanoparticles (less than about 10% of the overall number of particles32). The average distance among the smaller particles is of about one nanometer, which is excellent for tunneling conductance34,35. Elemental analysis was performed by Energy Dispersive X-ray microanalysis (EDX), leading to a metallic volume fraction of x = 0.28. The contribution to the capacitive conductance is considered to be dominated by the larger particles, which have much smaller impedance than that of the smaller particles32. The modulus of complex impedance (|Z(ω)|) and the phase angle were measured in the frequency range of 11 Hz to 2 MHz and in the temperature range of 40–280 K, using a precision LCR Meter (QuadTech 7600 Plus), a KEITHLEY 6221 AC current source and a KEITHLEY 2182A Nano-Voltmeter in a continuous-flow He cryostat.

Results and Discussion

The real part of the conductivity σ′ for Pd-ZrO2 is calculated using:

graphic file with name srep29676-m4.jpg

where Z′, Z″ are, respectively, the real and imaginary parts of impedance, Inline graphic is the electrode area, and Inline graphic is the inter-electrode separation. σ′ is plotted versus frequency at different temperatures using a log-log scale in Fig. 1 and exhibits two different regions as function of temperature: (i) a dc plateau region and (ii) a frequency-dependent region, which is due to the competition between tunneling and capacitive paths among Pd particles embedded within the ZrO2 amorphous matrix32. This observation is in accordance with Equation (1) proposed by Jonscher. Here, it should be noted that, at very high frequencies (f ≥ 100 kHz), σ′(ω) increases much faster than expected. This anomalous behavior is not caused by any intrinsic phenomenon in the granular system but it arises from the significant contribution at such high frequencies of the measuring leads and electrodes, leading to high electrical losses36,37. Besides, it has been shown in previous works4,7,31,32,33 that, in the case of Pd-ZrO2 granular metals, the onset of the conductivity dispersion corresponds to the frequency at which the magnitudes of the admittances associated with resistive (tunneling) paths between the smallest Pd particles (size ~2 nm), which make up the dc tunneling backbone of the sample, and those associated with the capacitive paths among larger Pd particles (size >5 nm), become similar. This dispersive regime is shifted towards high frequency until it disappears when temperature approaches room temperature (~280 K). The dc resistivity ρdc = 1/σdc has been obtained from the extrapolation of the plateau region to zero frequency and is plotted versus T−1/2 in a semi-log scale in the inset to Fig. 1. At low temperatures, Inline graphic is well described by the inelastic co-tunneling mechanism17,38 for granular metals following thermal activation Inline graphic, which was previously pointed out by Abeles39. The activation energy B is directly related to the Coulomb charging energy of the particles EC, where B = ECdχ, Inline graphic being the interparticle distance associated with the smallest Pd particles and Inline graphic the tunneling barrier energy in units of wave vector. From the linear fit (inset to Fig. 1), we obtain an experimental value of Inline graphic = 12.6 meV. However, at T > 180 K, the dc resistivity deviates from the linear relationship, due to the fact that thermal energy kBT overcomes the charging energy of the particles EC40,41.Therefore, ρdc can no longer be accounted for by the former simple exponential law in the temperature range 200–280 K. Thus, we have focused our study on the temperature range 40–180 K, where the conditions for thermal activated tunneling conduction are fulfilled.

Figure 1. Plot of real part of the conductivity σ′ as a function of frequency in a log-log scale in the temperature range of 40–280 K.

Figure 1

Open in a new tab

The inset shows the dc resistivity ρdc = 1/σdc (obtained from extrapolation of σ′ to zero frequency) versus T−1/2 in a semi-log scale. The solid lines are linear fits.

The electrical impedance has been analyzed by plotting the imaginary part of impedance Z″ versus frequency in a semi-log scale at different temperatures (Fig. 2(a)). This plot provides information on the dielectric processes taking place in the material. One peak at ωmax is observed in Z″ versus frequency which is shifted to higher frequency with increasing temperature, indicating the existence of relaxation processes in the system, while its broadening on increasing temperature suggests that those relaxation processes are temperature-dependent13.

Figure 2.

Figure 2

Open in a new tab

(a) Imaginary part of impedance Z″ as a function of frequency in a semi-log scale, (b) Imaginary part of the electrical modulus M′ as a function of frequency in a semi-log scale. Two peaks are observed in the spectra, at low and high frequency, respectively.

The electrical response of Pd-ZrO2 has also been analyzed using the complex electrical modulus formalism. This method is useful for elucidating the relaxation mechanisms in a material having different magnitudes of resistance and/or capacitance42,43. The imaginary part of the electrical modulus is calculated by using the relationship:

graphic file with name srep29676-m12.jpg

where Inline graphic, and ε0 is the permittivity in free space. Figure 2(b) shows the semi-log plot of M″ versus frequency at different temperatures, where two peaks in M″ are observed, indicating the occurrence of two relaxation processes. Those two relaxation mechanisms can be explained in terms of the competition between parallel tunneling and capacitive paths among the metallic particles, as a consequence of the bimodal size distribution of the Pd particles, explained in more detail elsewhere32. Considering this bimodal size distribution with a larger population of the smaller particles, Fig. 3 shows a simplistic sketch model of the ac electrical conductance in Pd-ZrO2 granular thin film in the dielectric regime. At low frequency, most of the smallest Pd particles are electrically connected through effective resistances due to thermally-activated tunneling. They form the so-called dc tunneling backbone of the sample, whose equivalent resistance is given by Inline graphic, Inline graphic being the tunneling resistance among two small particles. However, there is a certain amount of these smaller particles that are isolated from the dc tunneling backbone at these low frequencies. On the other hand, the set of the largest particles are only connected by capacitive paths Ci, being Inline graphic. At intermediate frequencies (~1 kHz), the larger particles are short-circuited and these capacitive shortcuts provide paths to connect the previously isolated smaller particles to the electrical backbone. Thus, an additional contribution to resistivity Inline graphic arises from this so-called assisted-tunneling process. In this case, Inline graphic is the tunneling resistance among two small particles that become connected to the backbone at this frequency. Here, the low frequency peak ω1max in Fig. 2(b) corresponds to the frequency at which the magnitudes of the admittances of the dc tunneling backbone resistance Inline graphic and capacitive paths (Inline graphic) become similar, i.e., Inline graphic. However, the high frequency peak ω2max in Fig. 2(b) corresponds to the frequency at which the magnitudes of the admittances associated with assisted tunneling resistance paths (Inline graphic), and the capacitive paths (Inline graphic) become similar, i.e., Inline graphic. In this case, it is worth noting that Ra ≪ Rdc since the number of the smaller particles involved in the assisted tunneling process at intermediate frequencies is much smaller than the number of those involved in the dc tunneling backbone. Therefore, the ac response of the sample is assumed to be dominated by the dc tunneling backbone resistance and, as a consequence, the high frequency peaks are not observed in the impedance spectra (see Fig. 2 (a)).

Figure 3. Simplistic sketch of the ac electrical conductance model in Pd-ZrO2 granular thin film in the dielectric regime.

Figure 3

Open in a new tab

At low frequency, most of the smallest Pd particles are electrically connected by the dc tunneling backbone Inline graphic, whereas, at ~1 kHz, an additional contribution of assisted tunneling resistive paths Inline graphic among smaller particles, initially isolated at low frequencies, improves the electrical conductance. The polarized bigger particles only contribute to the capacitive conductance Ci due to the large separation from each other.

The scaling behavior of the electrical impedance was studied by plotting Z″/Z″max versus ω/ωmax in a log-log scale (see Fig. 4(a)). All Z″ curves collapse onto a single master curve following a power law behavior with frequency, both above and below the frequency of the peak, ωmax. This suggests the presence of an absorption process13,18 for which all relaxation times τZ occurring at different temperatures exhibit the same activation energy UZ, indicating that the dynamic process is temperature-independent44. The inset to Fig. 4(a) shows the variation of relaxation time τZ as a function of temperature, calculated using the relationship Inline graphic. Those relaxation times exhibit a characteristic temperature dependence expressed as Inline graphic. Moreover, we showed in a previous work32 that the relaxation process in Pd-ZrO2 granular metals occurs when the condition Inline graphic is fulfilled, i.e., the magnitudes of the admittances of the tunneling and capacitive paths among particles become similar. Therefore, it is reasonable to expect that Inline graphic, since the effective capacitance Inline graphic through the set of the bigger particles is temperature-independent31,32. To confirm this, we obtained the activation energy UZ value from the slope of the linear fit in the semi-log plot of the inset to Fig. 4(a), yielding an experimental value of UZ = 13 meV. This value is in agreement with Inline graphic = 12.6 meV obtained from ρdc.

Figure 4.

Figure 4

Open in a new tab

(a) Scaling plot Inline graphic versus ω/ωmax in a log-log scale. The inset shows the variation of the frequency of the peak in Z″ as a function of T−1/2 in a semi-log scale and (b) Scaling plot Inline graphic versus ω/ωmax in a log-log scale. The inset shows τ1M and τ2M as a function of T1/2 in a semi-log scale. τ1M is the low frequency and τ2M is the high frequency relaxation times, respectively, obtained from the peaks in the main figure. The solid lines are linear fits.

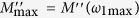Furthermore, the scaling behavior of the sample at low frequency is analyzed by plotting the normalized value of M″, i.e., M″/M″max, versus Inline graphic in a log-log scale (see Fig. 4(b)), where ωmax corresponds to the low frequency peak ω1max and Inline graphic. The normalized spectra around the high frequency regime is not shown since the relaxation frequency of assisted tunneling resistance paths Ra is assumed to be negligible with respect to that of the dc tunneling backbone32. Similar scaling behavior to that previously observed in the peak position of Z″ is shown for M″. The comparison of the data for the impedance and electrical modulus (see Table 1) shows that the peaks observed at low frequency in M″ nearly match the Z″ peaks, suggesting that both peaks are due to the same relaxation process which dominates the conductance. The slight shift observed in the M″ peaks toward higher frequencies with respect to the Z″ peaks is a mathematical result of applying Equation (4) to impedance data in order to calculate the electrical modulus45 (see Table 1). The collapse of all the curves at different temperatures (either Z″ or M″) onto a single master curve indicates that TTSP is fulfilled, and that Inline graphic is the proper choice as scaling parameter. Consequently, the ac electrical transport properties of granular thin films in the dielectric regime show a well-characterized universal behavior.

Table 1. Experimental values of ω max extracted from Z″, and ω 1max and ω 2max extracted from M′, and power law exponent n extracted from σ′ in the dispersive region.

T(K) ωmax(rad/s) ω1max(rad/s) ω2max(rad/s) n
41 748 999 45113 0.71
61 1458 2350 54582 0.65
81 2136 3782 60042 0.59
101 2846 5542 66049 0.55
121 3443 6704 – –
141 4166 8111 – –
161 5039 9814 – –
180 5542 10800 – –
Open in a new tab

Both low frequency Inline graphic and high frequency Inline graphic relaxation times are plotted as a function of temperature in the inset to Fig. 4(b) showing that they are well described by the Abeles model since they follow the characteristic 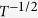Inline graphic dependence. It is thus expected that Inline graphic and Inline graphic, where Inline graphic and Inline graphic are the activation energies corresponding to Inline graphic and Inline graphic, respectively. From these linear fits we may extract the values of Inline graphic = 12.5 meV and Inline graphic = 0.95 meV. The fact that the values of Inline graphic and Inline graphic obtained from Z″ and M″ spectra are very much the same confirms that the relaxation frequency ωmax associated with the dc tunneling backbone completely dominates the ac response of the sample, following Inline graphic.

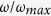Finally, Fig. 5 shows Inline graphic versus Inline graphic in a log-log plot, demonstrating that conductivity also scales with ωmax. Experimental data are plotted up to 10 kHz where the Jonscher’s UPL is fulfilled. The power law of ω is observed above the dc plateau region for all temperatures. According to Equation (1), the ac contribution to the conductivity can be written as Inline graphic, where the exponent n gives the curvature of the dispersive region. The n values obtained from the linear fit of the log-log plot of σ′ versus f (solid lines in the inset to Fig. 5) at different temperatures are shown in Table 1. These values are observed to decrease with increasing temperature. This observation agrees with the case of heterogeneous materials consisting of random distributions of conducting (resistor) and insulating (capacitor) phases, where the parameter n in the power law is directly related to the fraction of capacitive paths involved in the ac conduction mechanism19,20,21,22,23. In our case, the ac response of the sample arises from the competition between the dc tunneling backbone resistance Rdc between smaller particles, and the capacitive reactance XC among bigger particles, Inline graphic, the latter being temperature-independent. In contrast, the resistive paths follow thermal activation, Inline graphic and, therefore, increasing temperature, Rdc decreases. As a consequence, the resistive paths are more favored than capacitive ones and hence n decreases with temperature.

Figure 5. Scaling plot of σ′/σdc versus ω/ωmax in a log-log scale in the temperature range 40–180 K.

Figure 5

Open in a new tab

The inset shows a log-log scale of σ′ versus frequency in the frequency range of 11 Hz–10 kHz. Solid lines indicate the fit of the data to a power law with a fractional exponent n.

The fact that the conductivity curves in Fig. 5 collapse onto a single master curve with an exponent n of 0.71 indicates that TTSP is fulfilled and suggests that the distribution of relaxation times is temperature independent44. Furthermore, the conductivity formalism indicates that ωmax may be regarded as the critical scaling parameter. This confirms our assumption concerning temperature-independent C, since the characteristic frequency that corresponds to the onset of the conductivity dispersion is found to be the same as the relaxation frequency of the tunneling resistance, i.e., Inline graphic. Finally, the power law exponent n extracted from the dispersive region in Fig. 5 (n = 0.71) is in good agreement with the empirical value of the universal law of Jonscher which should be smaller than one19,22,46,47,48.

Conclusions

The scaling behavior of the ac electrical response of the Pd-ZrO2 granular metal in the dielectric regime has been studied in the temperature range 40–180 K. We find that the imaginary part of both the impedance Z″ and the electrical modulus M″, and the real part of the conductivity σ′ spectra collapse onto single master curves using a characteristic frequency ωmax as a scaling parameter. This frequency is associated with the main relaxation processes in the system, which manifests itself through the appearance of low frequency peaks in Z″ and M″, and a dispersive regime in σ′, and it is attributed to competing tunneling and capacitive paths among Pd particles in the amorphous ZrO2 matrix. This scaling behavior confirms the validity of the so-called Time Temperature Superposition Principle (TTSP) for granular metals. Furthermore, the frequency-dependent conductivity σ′ is found to obey the universal power law proposed by Jonscher, with a universal exponent value of 0.71, which agrees with the typical exponents, smaller than one. In summary, the ac electrical transport of Pd-ZrO2 granular metal in the dielectric regime is shown to follow a universal behavior when thermally activated tunneling dominates the conduction mechanism, i.e., Inline graphic.

Additional Information

How to cite this article: Bakkali, H. et al. Universality of the electrical transport in granular metals. Sci. Rep. 6, 29676; doi: 10.1038/srep29676 (2016).

Acknowledgments

This work was supported by the Spanish MINECO (H. Bakkali Ph.D. Grant No. BES-2008-010141 and research project MAT2015-68772-P), European FEDER funds (Una manera de hacer Europa) and the Catalan DURSI (2014SGR220). Dr. M. Kovylina (UB) is acknowledged for sample preparation.

Footnotes

Author Contributions H.B. prepared the samples, made impedance measurement, wrote the main manuscript text, prepared figures, discussed and analyzed results. M.D. wrote the main manuscript text, discussed and analyzed results. A.L. discussed and analyzed results. X.B. discussed and analyzed results. All authors reviewed the manuscript.

References

  1. Ohnuma S., Fujimori H., Mitani S. & Masumoto T. High‐frequency magnetic properties in metal–nonmetal granular films (invited). Journal of Applied Physics 79, 5130–5135, 10.1063/1.361531 (1996). [DOI] [Google Scholar]
  2. Yu M., Liu Y., Moser A., Weller D. & Sellmyer D. J. Nanocomposite CoPt:C films for extremely high-density recording. Applied Physics Letters 75, 3992–3994, 10.1063/1.125516 (1999). [DOI] [Google Scholar]
  3. Watanabe M., Masumoto T., Ping D. H. & Hono K. Microstructure and magnetic properties of FePt–Al–O granular thin films. Applied Physics Letters 76, 3971–3973, 10.1063/1.126838 (2000). [DOI] [Google Scholar]
  4. Batlle X. & Labarta A. Finite-size effects in fine particles: magnetic and transport properties. Journal of Physics D: Applied Physics 35, R15, 10.1088/0022-3727/35/6/201 (2002). [DOI] [Google Scholar]
  5. Hattink B. J. et al. Tunneling magnetoresistance in Co-ZrO2 granular thin films. Physical Review B 73, 045418, 10.1103/PhysRevB.73.045418 (2006). [DOI] [Google Scholar]
  6. Konstantinovic Z., Garcia del Muro M., Varela M., Batlle X. & Labarta A. Particle growth mechanisms in Ag–ZrO 2 and Au–ZrO 2 granular films obtained by pulsed laser deposition. Nanotechnology 17, 4106, 10.1088/0957-4484/17/16/019 (2006). [DOI] [PubMed] [Google Scholar]
  7. Konstantinović Z., García del Muro M., Kovylina M., Batlle X. & Labarta A. AC conductance in granular insulating Co-ZrO2 thin films: A universal response. Physical Review B 79, 094201, 10.1103/PhysRevB.79.094201 (2009). [DOI] [Google Scholar]
  8. Hamanaka Y., Fukuta K., Nakamura A., Liz-Marzán L. M. & Mulvaney P. Enhancement of third-order nonlinear optical susceptibilities in silica-capped Au nanoparticle films with very high concentrations. Applied Physics Letters 84, 4938–4940, 10.1063/1.1760229 (2004). [DOI] [Google Scholar]
  9. Maaza M., Nemraoui O., Sella C., Beye A. C. & Baruch-Barak B. Thermal induced tunability of surface plasmon resonance in Au–VO2 nano-photonics. Optics Communications 254, 188–195, 10.1016/j.optcom.2004.08.056 (2005). [DOI] [Google Scholar]
  10. Huth M., Kolb F. & Plank H. Dielectric sensing by charging energy modulation in a nano-granular metal. Applied Physics A 117, 1689–1696, 10.1007/s00339-014-8631-9 (2014). [DOI] [Google Scholar]
  11. Huth M. Granular metals: From electronic correlations to strain-sensing applications. Journal of Applied Physics 107, 113709, 10.1063/1.3443437 (2010). [DOI] [Google Scholar]
  12. Huth M., Rippert A., Sachser R. & Keller L. Probing near-interface ferroelectricity by conductance modulation of a nano-granular metal. Materials Research Express 1, 046303, 10.1088/2053-1591/1/4/046303 (2014). [DOI] [Google Scholar]
  13. Jonscher A. K. The ‘universal’ dielectric response. Nature 267, 673–679, 10.1038/267673a0 (1977). [DOI] [Google Scholar]
  14. Jain H. & Krishnaswami S. Composition dependence of frequency power law of ionic conductivity of glasses. Solid State Ionics 105, 129–137, 10.1016/S0167-2738(97)00458-X (1998). [DOI] [Google Scholar]
  15. Roling B. Scaling properties of the conductivity spectra of glasses and supercooled melts. Solid State Ionics 105, 185–193, 10.1016/S0167-2738(97)00463-3 (1998). [DOI] [Google Scholar]
  16. Feigel’man M. V. & Ioselevich A. S. Variable-range cotunneling and conductivity of a granular metal. Journal of Experimental and Theoretical Physics Letters 81, 277–283, 10.1134/1.1931015 (2005). [DOI] [Google Scholar]
  17. Beloborodov I. S., Lopatin A. V., Vinokur V. M. & Efetov K. B. Granular electronic systems. Reviews of Modern Physics 79, 469–518, 10.1103/RevModPhys.79.469 (2007). [DOI] [Google Scholar]
  18. Andrew K. J. Dielectric relaxation in solids. Journal of Physics D: Applied Physics 32, R57, 10.1088/0022-3727/32/14/201 (1999). [DOI] [Google Scholar]
  19. Almond D. P. & Bowen C. R. Anomalous Power Law Dispersions in ac Conductivity and Permittivity Shown to be Characteristics of Microstructural Electrical Networks. Physical Review Letters 92, 157601, 10.1103/PhysRevLett.92.157601 (2004). [DOI] [PubMed] [Google Scholar]
  20. Jankowski S. Dielectric Dispersion in Polycrystalline Ferrites: Random Network Model. Journal of the American Ceramic Society 71, C-176–C-180, 10.1111/j.1151-2916.1988.tb05866.x (1988). [DOI] [Google Scholar]
  21. Vainas B., Almond D. P., Luo J. & Stevens R. An evaluation of random R-C networks for modelling the bulk ac electrical response of ionic conductors. Solid State Ionics 126, 65–80, 10.1016/S0167-2738(99)00216-7 (1999). [DOI] [Google Scholar]
  22. Almond D. P. & Vainas B. The dielectric properties of random R-C networks as an explanation of the ‘universal’ power law dielectric response of solids. Journal of Physics: Condensed Matter 11, 9081, 10.1088/0953-8984/11/46/310 (1999). [DOI] [Google Scholar]
  23. Bouamrane R. & Almond D. P. The ‘emergent scaling’ phenomenon and the dielectric properties of random resistor–capacitor networks. Journal of Physics: Condensed Matter 15, 4089, 10.1088/0953-8984/15/24/302 (2003). [DOI] [Google Scholar]
  24. Roling B., Ingram M. D., Lange M. & Funke K. Role of AgI for ionic conduction in AgI-AgPO3 glasses. Physical Review B 56, 13619–13622, 10.1103/PhysRevB.56.13619 (1997). [DOI] [Google Scholar]
  25. Isard J. O. Dielectric dispersion in amorphous conductors. Journal of Non-Crystalline Solids 4, 357–365, 10.1016/0022-3093(70)90063-3 (1970). [DOI] [Google Scholar]
  26. Owen A. E. The electrical properties of glasses. Journal of Non-Crystalline Solids 25, 370–423, 10.1016/0022-3093(77)90099-0 (1977). [DOI] [Google Scholar]
  27. Mansingh A. AC conductivity of amorphous semiconductors. Bull. Mater. Sci. 2, 325–351, 10.1007/BF02908579 (1980). [DOI] [Google Scholar]
  28. Tang R. et al. Impedance spectroscopy and scaling behaviors of Sr3Co2Fe24O41 hexaferrite. Applied Physics Letters 106, 022902, 10.1063/1.4905596 (2015). [DOI] [Google Scholar]
  29. Singh P., Raghvendra, Parkash O. & Kumar D. Scaling of low-temperature conductivity spectra of BaSn1−xNbxO3 (x ≤ 0.100): Temperature and compositional-independent conductivity. Physical Review B 84, 174306, 10.1103/PhysRevB.84.174306 (2011). [DOI] [Google Scholar]
  30. Li W. & Schwartz R. W. AC conductivity relaxation processes in CaCu3Ti4O12 ceramics: Grain boundary and domain boundary effects. Applied Physics Letters 89, 242906, 10.1063/1.2405382 (2006). [DOI] [Google Scholar]
  31. Hattink B. J. et al. Competing tunneling and capacitive paths in Co-ZrO2 granular thin films. Physical Review B 67, 033402, 10.1103/PhysRevB.67.033402 (2003). [DOI] [Google Scholar]
  32. Bakkali H., Dominguez M., Batlle X. & Labarta A. Equivalent circuit modeling of the ac response of Pd-ZrO 2 granular metal thin films using impedance spectroscopy. Journal of Physics D: Applied Physics 48, 335306, 10.1088/0022-3727/48/33/335306 (2015). [DOI] [Google Scholar]
  33. Konstantinović Z., García del Muro M., Batlle X., Labarta A. & Varela M. Nanostructural origin of the ac conductance in dielectric granular metals: The case study of Co20(ZrO2)80. Applied Physics Letters 91, 052108, 10.1063/1.2766858 (2007). [DOI] [Google Scholar]
  34. Mitani S. et al. Enhanced Magnetoresistance in Insulating Granular Systems: Evidence for Higher-Order Tunneling. Physical Review Letters 81, 2799–2802, 10.1103/PhysRevLett.81.2799 (1998). [DOI] [Google Scholar]
  35. Bakkali H. & Dominguez M. Differential conductance of Pd-ZrO 2 thin granular films prepared by RF magnetron sputtering. EPL (Europhysics Letters) 104, 17007, 10.1209/0295-5075/104/17007 (2013). [DOI] [Google Scholar]
  36. Srivastava A., Garg A. & Morrison F. D. Impedance spectroscopy studies on polycrystalline BiFeO3 thin films on Pt/Si substrates. Journal of Applied Physics 105, 054103, 10.1063/1.3078822 (2009). [DOI] [Google Scholar]
  37. Schmidt R., Eerenstein W., Winiecki T., Morrison F. D. & Midgley P. A. Impedance spectroscopy of epitaxial multiferroic thin films. Physical Review B 75, 245111, 10.1103/PhysRevB.75.245111 (2007). [DOI] [Google Scholar]
  38. Sachser R., Porrati F., Schwalb C. H. & Huth M. Universal Conductance Correction in a Tunable Strongly Coupled Nanogranular Metal. Physical Review Letters 107, 206803, 10.1103/PhysRevLett.107.206803 (2011). [DOI] [PubMed] [Google Scholar]
  39. Sheng P., Abeles B. & Arie Y. Hopping Conductivity in Granular Metals. Physical Review Letters 31, 44–47, 10.1103/PhysRevLett.31.44 (1973). [DOI] [Google Scholar]
  40. Balcells Ll., Martínez B., Sandiumenge F. & Fontcuberta J. Low-temperature magnetotransport in nanometric half-metallic ferromagnetic perovskites. Journal of Physics: Condensed Matter 12, 3013, 10.1088/0953-8984/12/13/311 (2000). [DOI] [Google Scholar]
  41. Balcells L., Fontcuberta J., Martínez B. & Obradors X. High-field magnetoresistance at interfaces in manganese perovskites. Physical Review B 58, R14697–R14700, 10.1103/PhysRevB.58.R14697 (1998). [DOI] [Google Scholar]
  42. Morrison F. D., Sinclair D. C. & West A. R. Characterization of Lanthanum-Doped Barium Titanate Ceramics Using Impedance Spectroscopy. Journal of the American Ceramic Society 84, 531–538, 10.1111/j.1151-2916.2001.tb00694.x (2001). [DOI] [Google Scholar]
  43. Macdonald J. R. Impedance spectroscopy. Ann. Biomed. Eng. 20, 289–305, 10.1007/BF02368532 (1992). [DOI] [PubMed] [Google Scholar]
  44. Saha S. & Sinha T. P. Low-temperature scaling behavior of BaFe0.5Nb0.5O3. Physical Review B 65, 134103, 10.1103/PhysRevB.65.134103 (2002). [DOI] [Google Scholar]
  45. Harley G. A. Proton Transport in Lanthanum Phosphates. PhD dissertation, University of California, Berkeley, February (2008). [Google Scholar]
  46. Schrøder T. B. & Dyre J. C. Scaling and Universality of ac Conduction in Disordered Solids. Physical Review Letters 84, 310–313, 10.1103/PhysRevLett.84.310 (2000). [DOI] [PubMed] [Google Scholar]
  47. Dyre J. C. The random free‐energy barrier model for ac conduction in disordered solids. Journal of Applied Physics 64, 2456–2468, 10.1063/1.341681 (1988). [DOI] [Google Scholar]
  48. Lee W. K., Liu J. F. & Nowick A. S. Limiting behavior of ac conductivity in ionically conducting crystals and glasses: A new universality. Physical Review Letters 67, 1559–1561, 10.1103/PhysRevLett.67.1559 (1991). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES