Deducing the Symmetry of Helical Assemblies: Applications to Membrane Proteins

Abstract

Helical reconstruction represents a convenient and powerful approach for structure determination of macromolecules that assemble into helical arrays. In the case of membrane proteins, formation of tubular crystals with helical symmetry represents an attractive alternative, especially when their small size precludes the use of single-particle analysis. An essential first step for helical reconstruction is to characterize the helical symmetry. This process is often daunting, due to the complexity of helical diffraction and to the low signal-to-noise ratio in images of individual assemblies. Furthermore, the large diameters of the tubular crystals produced by membrane proteins exacerbates the innate ambiguities that, if not resolved, will produce incorrect structures. In this report, we describe a set of tools that can be used to eliminate ambiguities and to validate the choice of symmetry. The first approach increases the signal-to-noise ratio along layer lines by incoherently summing data from multiple helical assemblies, thus producing several candidate indexing schemes. The second approach compares the layer lines from images with those from synthetic models built with the various candidate schemes. The third approach uses unit cell dimensions measured from collapsed tubes to distinguish between these candidate schemes. These approaches are illustrated with tubular crystals from a boron transporter from yeast, Bor1p, and a β-barrel channel from the outer membrane of E. coli, OmpF.

1. Introduction

The analysis of helical diffraction from biological assemblies dates back to the original studies of DNA (Franklin and Gosling, 1953; Watson and Crick, 1953; Wilkins et al., 1953) and the folding of polypeptides into an α-helix (Pauling et al., 1951; Perutz, 1951). Those structures were solved by building models based on intensity profiles from X-ray fiber diffraction patterns, and this analysis not only laid the mathematical foundation for helical diffraction theory (Cochran et al., 1952) but also gave rise to Fourier-Bessel reconstruction methods for 3D reconstruction from electron micrographs (DeRosier and Klug, 1968). Since then, electron microscopy (EM) has been a major tool in studying the structural properties of helical assemblies that either appear naturally in a biological context, or are reconstituted in vitro (Egelman, 2015).

There are many examples of naturally occurring helical assemblies, such as actin (Galkin et al., 2015), myosin filaments (Woodhead et al., 2005), microtubules (Li et al., 2002), amyloid fibrils (Schmidt et al., 2015), bacterial flagella (Trachtenberg and DeRosier, 1992), tobacco mosaic virus (Jeng et al., 1989), and filamentous bacteriophages (Wang et al., 2006). Helical assemblies formed by reconstitution of purified proteins include the capsid protein of polyoma virus (Baker et al., 1983), dynamin (Low et al., 2009; Zhang and Hinshaw, 2001), BAR proteins interacting with lipid bilayers (Frost et al., 2008) and integral membrane proteins embedded within such bilayers (Coudray et al., 2013; Toyoshima and Unwin, 1990; Zhang et al., 1998). In the case of membrane proteins, the helical symmetry offers a practical advantage over the alternative planar morphology of conventional 2D crystals formed, for example, by bacteriorhodopsin (Henderson and Unwin, 1975) and light-harvesting complex II (Wang and Kühlbrandt, 1991). In particular, molecules within helical assemblies adopt a complete range of orientations, thus overcoming a major technical hurdle in the analysis of planar crystals by eliminating the need to collect images of tilted specimens. Furthermore, the helical assembly overcomes size limitations of single-particle analysis, which is currently impractical for many membrane proteins due to their small size.

Various reconstitution techniques have been used to produce helical assemblies of membrane proteins. For example, helical arrays of Ca²⁺-ATPase (Young et al., 1997) and the ABC transporter MsbA (Ward et al., 2009) were produced by using BioBeads to rapidly remove detergent, helical arrays of the polytopic mitochondrial outer membrane protein TspO were grown more slowly in Slide-A-Lyzer dialysis cassettes (Pierce) (Korkhov et al., 2010a), and the membrane domain of human erythrocyte band 3 was crystallized in dialysis buttons (Yamaguchi et al., 2010). In recent years, our laboratory has developed a pipeline for automating crystallization screens using 96-well microdialysis plates, which yielded helical crystals for a large number of different membrane protein targets (Lasala et al., 2015).

Although there are different approaches for 3D reconstruction of helical assemblies, they all rely on an initial assignment of the helical symmetry, which is often a difficult process (Egelman, 2014). The conventional parameters used to describe a simple, one-start helix are its rise and the number of subunits per turn (Diaz et al., 2010). However, membrane proteins typically adopt more complex helical assemblies making it more convenient to define an indexing scheme that is comparable to indexing diffraction patterns from 2D and 3D crystals (Toyoshima, 2000). In the case of planar 2D crystals, assignment of indices to diffraction spots is relatively straight-forward and leads directly to an estimate of the size and shape of the unit cell. In contrast, the cylindrical geometry adopted by helical assemblies makes it difficult to establish the number of unit cells that are wrapped around the cylinder (Fig. 1) and thus the parameters that govern the helix (Egelman, 2014). Moreover, the diameter of helical assemblies produced by reconstituted membrane proteins is often variable, thus generating a number of different helical symmetries within a given sample, all of which are derived from the same underlying lattice. In such cases, it is necessary to segregate the helical crystals into classes according to their distinct symmetries. The determination of helical symmetry is facilitated by graphical software tools like Windex (Ward et al., 2003), EMIP (Diaz et al., 2010) and SPRING (Desfosses et al., 2014). However, given ambiguities in this process, it is important to define a set of approaches that can be used not only to establish, but also to validate the indexing scheme, which, if not correct, leads to incorrect structures and inappropriate interpretations of molecular function.

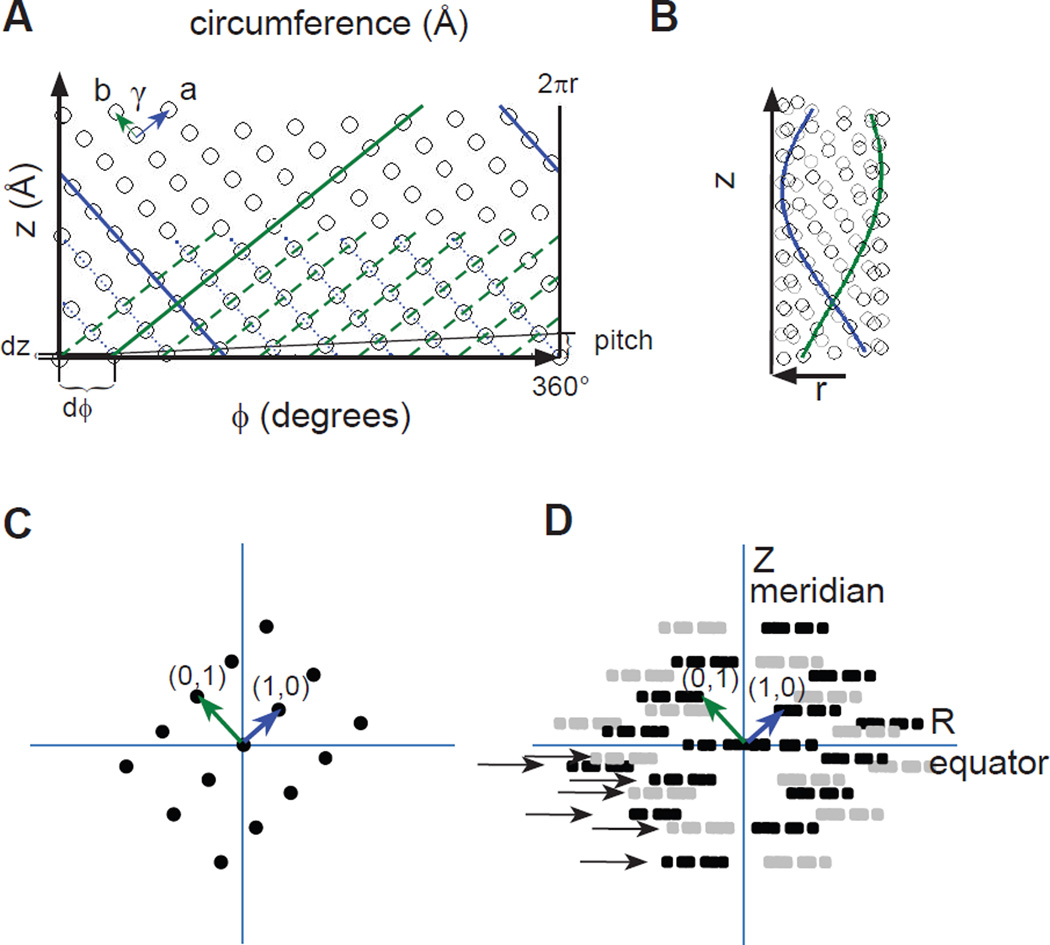
Figure 1.

Relationship between a planar, 2D lattice and a helical assembly. (A) The surface of a helical assembly is composed of a planar lattice, which is characterized by unit cell axes a (blue) and b (green) and the intervening angle γ. The horizontal axis corresponds to the circumference of a cylinder, which can be measured either with azimuthal coordinates (ϕ=0–360°) or a linear dimension (0–2πr, r is the radius) and is depicted as a vector extending from one point in the lattice to another. These two points coincide when the assembly is rolled into a cylinder. The vertical axis corresponds to the longitudinal axis of the cylinder, which has a linear dimension. (B) The same lattice as in A, but rolled up into a cylinder. The solid blue and green lines correspond to those in A and follow a helical path around the surface of the cylinder. Each of these lines belongs to a helical family, which are drawn as parallel, dotted lines in A. The start numbers for each family correspond to the number of parallel lines that cross the circumferential vector, which in this case are 10 for the green helices and 9 for the blue helices. The Bessel orders for these helical families are therefore −9 and 10, with the sign reflecting the handedness of the helices. (C) Mock diffraction pattern from the planar lattice in A showing the principal (1,0) and (0,1) reflections. This pattern of reflections is consistent with Bragg’s law that describes how the lattice lines drawn in A generates this diffraction pattern. (D) Mock diffraction pattern from the helical lattice in B. Each discrete reflection in C generates a Bessel function, depicted as series of three amplitude peaks drawn in black. In addition, the helix generates mirror symmetry about the meridional axis (Z), resulting from the superposition of near and far sides of the assembly. This mirror symmetry gives rise to the amplitude peaks drawn in grey. Together, the black and grey amplitudes constitute a layer line. The rise dz and the azimuthal angle dϕ are shown in panel A, which characterize a one-start helix running through all of the points in the lattice. This one-start helix has a pitch, indicated on the right in panel A, and the distance between the corresponding layer line (with a Bessel order of one) and the equator will equal the reciprocal of this pitch. Such a one-start helix is sometimes referred to as a "genetic helix" and is useful for iterative real-space helical reconstruction methods.

In this report, we start by reviewing the conventional approach to indexing, which relies on the position and phase of the layer lines composing the diffraction pattern. Because this approach leads to ambiguity for the relatively wide tubes formed by membrane proteins, we go on to describe alternative approaches designed to identify and validate the correct scheme. These alternatives include summing diffraction patterns from multiple tubes, analyzing the 2D lattice of collapsed tubes, comparing diffraction patterns from experimental images with those from synthetic images, and comparing density maps from tubes with related helical symmetries. We illustrate the utility of these approaches by analyzing images of two different membrane proteins: the boron transporter from yeast, Bor1p, and an outer membrane protein from E. coli, OmpF.

2. Theoretical background

2.1. Parameters that characterize helical symmetry

A helical crystal can be seen as a planar 2D crystal, which has been rolled up into a cylinder (Figs. 1A, B). Although the 2D lattice is preserved on the surface of this cylinder, the curvature and superposition of near- and far-sides of the cylinder dramatically change the appearance of the Fourier transform relative to that of the planar 2D crystal. Specifically, instead of a 2D lattice of discrete diffraction peaks (Fig. 1C), the helical symmetry elongates each peak in the radial direction to produce a mirror-symmetric pattern of so-called layer lines (Fig. 1D). Each layer line corresponds to a family of parallel helices that pass through all the subunits, much as a given Fourier reflection from a 2D crystal corresponds to a set of lattice planes. Each family of helices, and thus each layer line, is characterized by two parameters, the pitch, which is the distance along the z axis between turns of the helix, and the start number (n), which corresponds to the number of parallel helices that contribute to the family. Whereas the pitch can be readily determined as the reciprocal of the distance between the layer lines and the equator (Z), the start number is more difficult to ascertain and represents the key to indexing of helical symmetry. In the following sections we present first a conventional approach to determine the start numbers of all the layer lines followed by alternative approaches that either facilitate or validate this process.

2.2. Conventional approach to indexing helical symmetry

Whereas the Fourier reflections in a 2D crystal are described by a delta function, the distribution of amplitudes along a given layer line is governed by a Bessel function, J_n(X), where n is an integer that specifies the Bessel order and that also corresponds to the start number for the family of helices. For helical assemblies, the dimensionless argument X for the Bessel function corresponds to 2πRr, where R is the radial coordinate along the layer line in Fourier space and r is the radius of the tube in real space (DeRosier and Moore, 1970). In principle, the position of the maxima along the layer lines can be used to determine the corresponding Bessel orders, because r can be measured from images and J_n(2πRr) can be compared with the amplitude profile of integer Bessel functions. Specifically, the position of the first maximum for Bessel functions (X_max) can be approximated using the following equation (Toyoshima, 2000):

$${\mathrm{X}}_{\text{max}}=2\pi {\mathrm{R}}_{\text{peak }}\mathrm{r}\approx 1.1\mathrm{n}+0.9$$ (1)

where R_peak is the position of the first peak along the layer line. Although r and R_peak are well-determined for point scatterers, the situation with protein subunits is more complex. In particular, Fig. 2A shows a radial density profile of a typical membranous tube and several different positions, where r could be defined. This profile was obtained by defining the center of the tube and using the PRJPLT program from the MRC image processing suite (Crowther et al., 1996) to project the image along the meridional axis, thus producing the mean density of the left and right sides of the tube. The radius can be defined at the middle of the membrane (r_mid), at the outer edge of the tube or including the fringe produced by the contrast transfer function (r_ctf). If r_mid is used, R_peak would roughly correspond to the maximum of the first peak along each layer line, though this is strictly true only if r_mid is replaced for each layer line by the radial center-of-mass of a projection along the path of the corresponding helix. However, this center-of-mass can vary from one layer line to the next, as has been seen for example in bacterial flagella (Trachtenberg and DeRosier, 1992) and is therefore difficult to estimate from a single axial projection, especially when the protein has a domain outside of the membrane. If r_out is chosen, the value for R_peak satisfying equation 1 would be somewhere along the ascending slope before the first peak; when r_ctf is used, the corresponding value of R_peak would coincide with the leading edge of the first peak and would beless dependent on the distribution of mass across the membrane. For this reason, r_ctf is considered to be the most reliable value to use in equation 1 for estimating the Bessel order, n (Toyoshima, 2000).

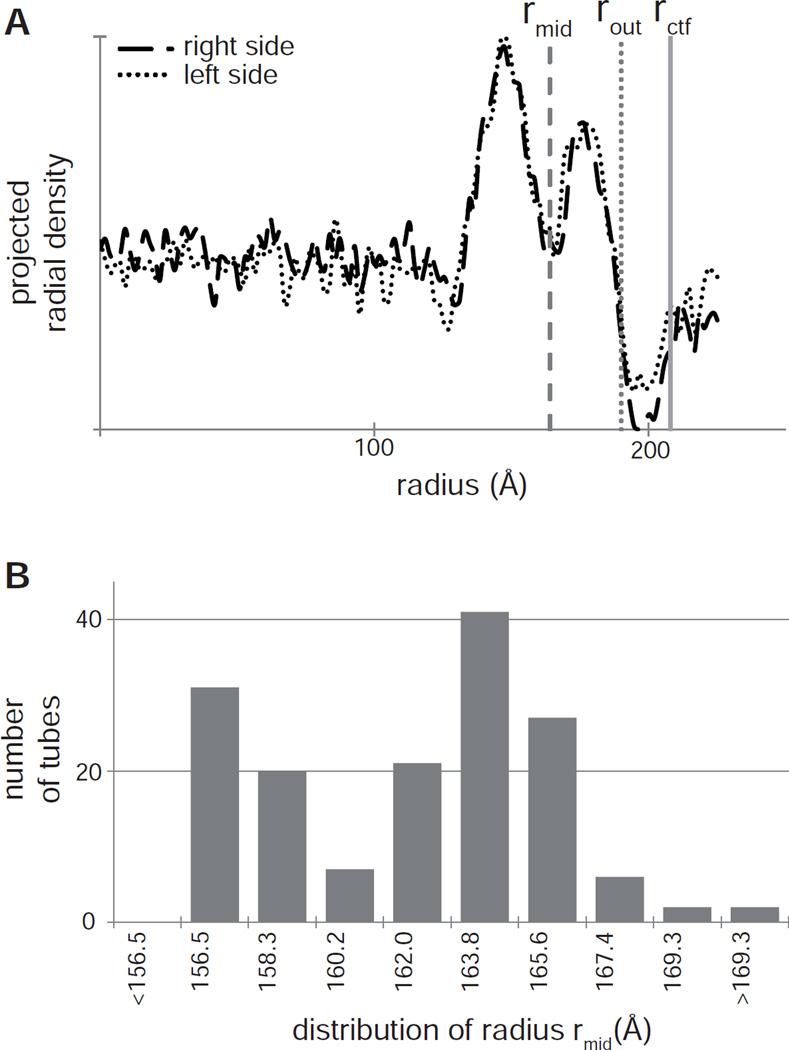
Figure 2.

Measuring the radius of a helical assembly. (A) A typical mean radial density profile from a Bor1p helical tube determined by projecting the image of the helical assembly (typically 100–200 nm long) along its meridional axis using the program PRJPLT. The origin represents the center of the tube and integrated densities are plotted for both the right and left sides of the tube. The two peaks correspond to the inner and outer leaflets of the lipid bilayer (image contrast has been inverted). Measurements of the radius are taken at several different sites, as shown by the vertical, gray lines: r_mid corresponds to the middle of the membrane, r_out to the outer edge of the tube, and r_ctf to the fringe produced by the contrast transfer function. (B) Distribution of radii for Bor1p helical crystals used for helical reconstruction. The distribution illustrates the presence of two classes of tubes, one with radii between 156.5 – 158.3 Å and another one with radii between 163.8 – 165.6 Å.

There are various reasons why the peak positions along individual layer lines may be either shifted or difficult to measure. In particular, tubes that are tilted relative to the imaging plane (i.e., not precisely normal to the electron beam) have characteristic shifts in the layer line peak positions. In tilted tubes, peaks are shifted towards the meridian and the magnitude of this shift depends on the height of the layer line above the equator (value of Z in Fig. 1D). To minimize this problem, it is most reliable to analyze layer lines closest to the equator, which are shifted the least. Another issue is that the presence of Bessel functions along each layer line only occurs for an idealized helix of point scatterers and placing 3D molecules within the unit cell influences the distribution of Fourier amplitudes, thus producing unpredictable shifts in peak positions. For this same reason, some layer lines are strong, some are very weak, and individual peaks along a given layer line may be missing altogether. As a result of these issues, multiple indexing schemes may each produce plausible solutions. This ambiguity is especially problematic for tubes with a large diameter and therefore large values of n; in this case, radii producing n versus n +/− 1 are only slightly different. This problem can be appreciated by selecting a different circumferential vector for the helix shown in Fig. 1. As is discussed more below, changing the circumferential vectors will affect both the pitch and the start numbers of the various helical families, thus producing a different helical symmetry even though the Fourier transform will look rather similar. To resolve such ambiguities, it is essential to use as many layer lines as possible. Layer lines with peaks near the meridian, thus having small Bessel orders, are particularly useful in providing constraints for the entire scheme. Another constraint involves the phase difference of mirror-symmetric peaks from a given layer line that lie on opposite sides of the meridian (i.e., black and grey peaks in Fig. 1D). If the tube is centered and lies parallel to the projection plane, this phase difference is constrained to be 0° when n is even and 180° when n is odd.

The diagrams in Fig.1 show how helical families are derived from the 2D lattice on the surface of the tube and how layer lines can be assigned Miller indices (h,k) that correspond to Fourier reflections from the corresponding 2D reciprocal lattice. These indices provide important constraints for assignment of the Bessel orders. In practice, each layer line is analyzed to measure R_peak and thus to calculate the corresponding Bessel order, n, according to equation 1. Because the Fourier amplitudes are mirror symmetric about the meridian, each layer line provides two independent estimates for R_peak (right and left sides), or the two sides can be averaged in order to increase the signal-to-noise ratio of the amplitude profile (Fig. S1). Then a table is produced in which all of the Bessel orders can be compared. If correctly assigned, there will be consistency between the Bessel order, n, and the height, Z, of each layer line and the corresponding Miller index (Toyoshima, 2000). Specifically, after selecting two principal layer lines and assigning them indices of (1,0) and (0,1), all the other layer lines must be linear combinations of the corresponding values for n and Z (Figs. 3B, C):

$${\mathrm{n}}_{(\mathrm{h},\mathrm{k})}=\mathrm{h}·{\mathrm{n}}_{(\mathrm{1,0})}+\mathrm{k}·{\mathrm{n}}_{(\mathrm{0,1})}$$

$${\mathrm{Z}}_{(\mathrm{h},\mathrm{k})}=\mathrm{h}·{\mathrm{Z}}_{(\mathrm{1,0})}+\mathrm{k}·{\mathrm{Z}}_{(\mathrm{0,1})}$$ (2)

Values for Z can be readily measured, thus providing a strong initial constraint in assigning Miller indices and in distinguishing the two mirror-related lattices produced by the helical symmetry (black and grey reflections in Fig. 1D).

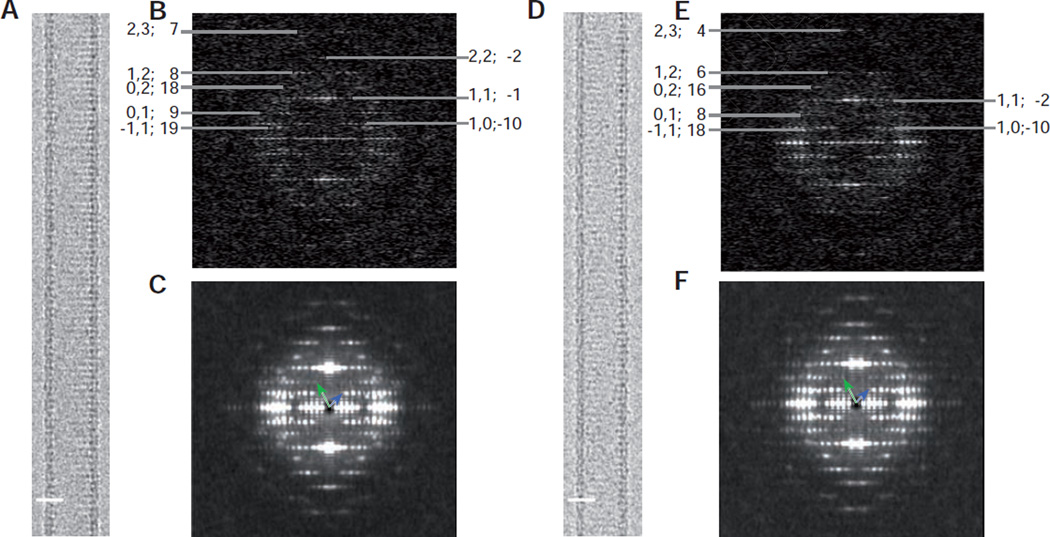
Figure 3.

Image data from Bor1p helical tubes. (A) Typical image of a Type 1 Bor1p helical tube. (B) Diffraction patterns from an individual Type 1 tubes with layer line indices shown at the periphery; each of the layer lines has been assigned Miller indices and a Bessel order (h,k; n). (C) Diffraction pattern resulting from the incoherent sum of diffraction from many overlapping segments (540 Å long) along Type 1 tubes. Small variations in the pitch of layer lines produce a slight blurring in the meridional direction. Blue and green vectors point to the (1,0) and (0,1) layer lines, respectively, and are comparable with the diagram in Fig. 1D. (D–F) Analogous data from Type 2 tubes. Scale bars in A & D correspond to 200 Å.

It should be noted that there are alternative ways to characterize helical symmetry. The integer selection rule represents the classical approach: ℓ = tn + um, where u and t refer to the number of subunits and the number of turns in one full repeat of a fundamental one-start helix that visits all the subunits. This one-start helix is shown as a thin black line in Fig. 1A. Once u and t are established, then ℓ is an integer that refers to the height of a given layer line (Z scaled by the axial repeat distance), n is the corresponding Bessel order and m is an arbitrary integer (Diaz et al., 2010). Based on u and t, one can readily calculate the number of subunits per turn. As a simpler alternative, the one-start helix can be characterized by dϕ and dz, the rotation and translation required to move between consecutive subunits. These two parameters are essential for application of iterative real-space refinement methods (Behrmann et al., 2012; Egelman, 2000; Rohou and Grigorieff, 2014). For the current analysis, however, we will use Miller indices and the corresponding Bessel orders to characterize the helical assembly, as shown in Figs. 3B, C.

3. Methods for analyzing tubular crystals

3.1. Summing data from multiple tubular crystals

Because the Bessel orders of layer lines are estimated from the positions of the initial peak, we took measures to improve the signal-to-noise ratio to better define its location. The first approach involved summing of Fourier transforms from multiple tubes using the SPARX software suite (Hohn et al., 2007). Specifically, the sxhelixboxer command was used to window segments along the tubes, sxali2d was used to center and then rotationally align these segments, and sxprocess was used to sum their Fourier transforms incoherently (i.e., without full translational alignment). This procedure, however, does not account for slight differences in pitch that occur from one tube to the next. As a result, the layer lines in this incoherent sum are somewhat blurry (Figs. 3D, E). Nevertheless, layer line profiles can be extracted from the incoherent sum in order to evaluate the positions of the peaks (Fig. S1).

A second method uses Fourier-Bessel analysis software derived from the MRC software suite (Crowther et al., 1996; DeRosier and Moore, 1970) to extract amplitude and phase data along individual layer lines from multiple tubular crystals. The amplitudes are then summed, irrespective of the phases, to produce an incoherent sum that avoids the blurring of layer lines mentioned above. For both methods, it is essential that all the tubular crystals included in the sum have a common symmetry as indicated by their radius (Fig. 2) and by a matching pattern of layer lines in their Fourier transforms (Fig. 3).

3.2. Synthetic images

In order to validate a specific indexing scheme, synthetic images were created with the desired helical symmetry. We used the atomic structure of uracil transporter UraA (Lu et al., 2011), which has been reported to have the same fold as our target, the boron transporter Bor1p (Barneaud-Rocca et al., 2013; Västermark and Saier, 2014), to produce these images. Most importantly, UraA is likely to have a similar distribution of density across the membrane even though the details of the atomic structure are different. Chimera (Pettersen et al., 2004) was used to position the UraA dimer (PDB code 3QE7) at a radius consistent with our tubular crystals. SPARX (Hohn et al., 2007) routines were used first to apply helical symmetry to this model using sxhelicon_utils and then to generate image densities from this helical model using sxpdb2em. Finally, projection images were created using the prgs command; diffraction patterns were computed and compared either with those from individual electron micrographs of Bor1p tubes, or with the incoherent sums described above. The position of the initial peaks along the layer lines was used to evaluate the different helical symmetries and, to do so, the mean square error (MSE) was computed:

$$\mathit{\text{MSE}}=\frac{1}{L}{\sum }_{\ell =1}^L\frac{1}{P}{\sum }_{p=1}^P{(\frac{S_{\ell ,p}}{\text{max}({\mathrm{S}}_{\ell })}-\frac{R_{\ell ,p}}{\text{max}(R_{\ell })})}^2$$ (3)

where S and R represent the Fourier amplitudes from the synthetic and real images, respectively, normalized by the maximum amplitude along each layer line The index ℓ=1,L refers to the various layer lines and p=1,P refers to points along each of those layer lines.

3.3. Using 2D lattice parameters to evaluate indexing schemes

Knowledge of the 2D lattice dimensions within the membrane plane can help establish the correct helical indexing scheme by predicting the diameter of the helical assembly (Unwin et al., 1988). We make the assumption that, although a given crystallization condition will produce tubes of varying diameters, the underlying 2D lattice on the surface of these tubes are the same. Although the lattice is hard to visualize directly from the tubes due to superposition and curvature, lattice dimensions can be readily measured from collapsed tubes that lie flat on the specimen support. Such collapse is promoted by negative staining and sugar embedding, but also occurs when frozen-hydrated tubes are adsorbed to the carbon film, as opposed to cylindrical tubes which are imaged over holes in this film and thus retain their helical symmetry. For evaluating the lattice dimensions, wider tubes are preferable because they more easily collapse and produce Fourier reflections with a higher signal-to-noise ratio and these dimensions should apply to the entire population of tubes regardless of their diameter.

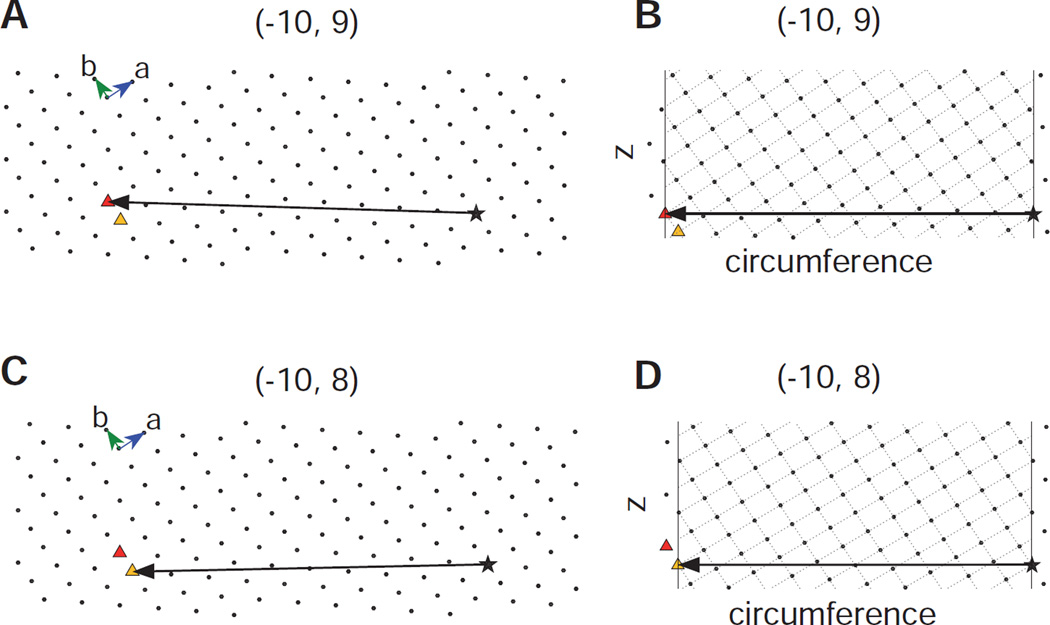
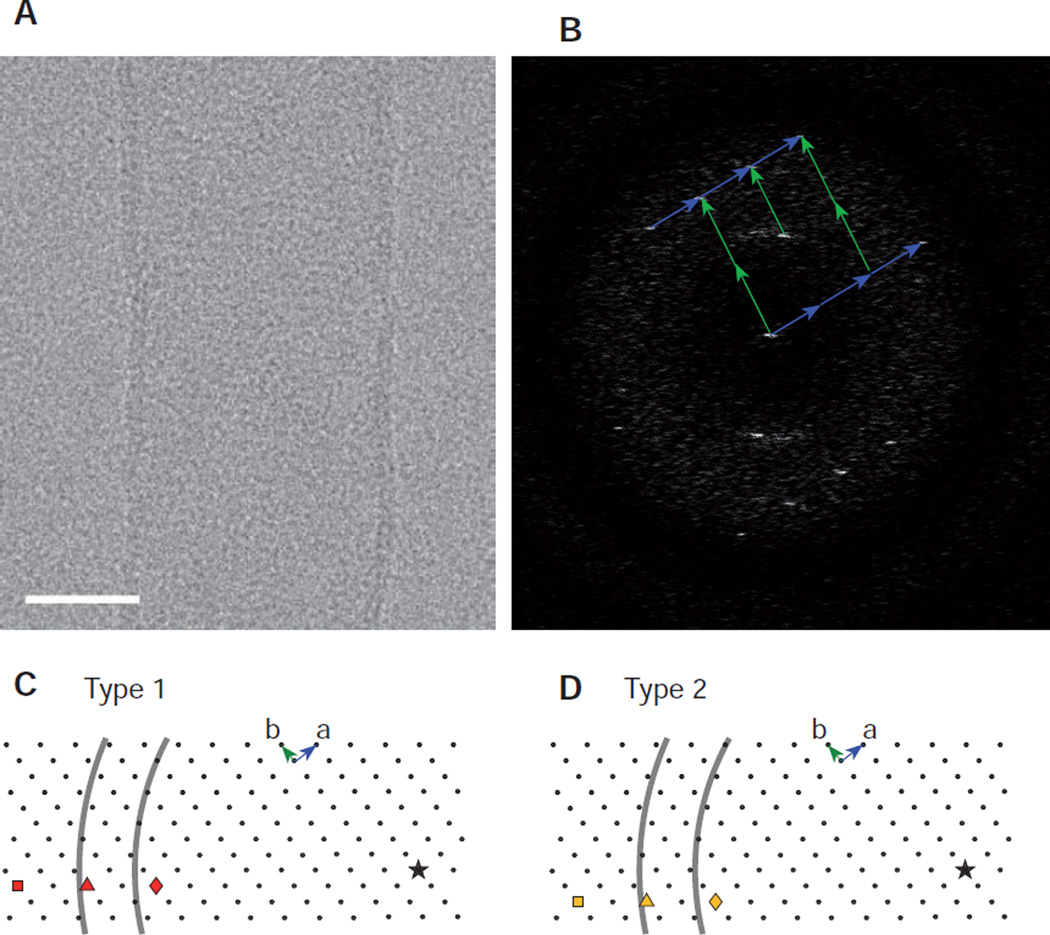
The process of generating helical assemblies from a 2D lattice is illustrated in Fig. 4. Panels A and C show the identical 2D lattice from which two different circumferential vectors have been drawn running from an arbitrary origin (star) to two different lattice points (triangles), which can be indexed as (−10,9) and (−10,8). In panels B and D, the lattice has been reoriented and the azimuthal extent of the cylinder has been delimited by vertical lines. Note that these drawings represent the surface of the tube that has been unrolled into a flat plane and that the vectors correspond to the circumference of the tube. Oblique lines have been drawn through lattice points defining the two principal helical families: (1,0) and (0,1), which result from lines perpendicular to the a and b unit cell axes, respectively. The start numbers correspond to the number of times these lattice lines cross the circumferential vector, which are consistent with (n_1,0,n_0,1) values of (−10,9) and (−10,8), respectively. A key point is that the tube radius measured from the micrographs (Fig. 2) provides a constraint on the length of the circumferential vector, which should approximately equal 2π times that radius.

Figure 4.

Deducing helical symmetry from a 2D surface lattice. (A) The 2D array represents the crystalline lattice of the protein at the surface of the helical assembly; in the case of membrane proteins such as Bor1p and OmpF, this surface corresponds to the membrane plane. A vector representing the circumference of a helical assembly has been drawn from an arbitrary origin (star) to the (−10,9) coordinate in the array (red triangle). (B) After reorienting the circumferential vector to the equatorial plane (horizontal) and delimiting the azimuthal extent of the array (vertical lines), the start number for 30 helical families can be evaluated by the number of times the parallel lines cross the circumferential vector (cf. green and blue lines in Fig. 1A). The helical families that are shown run perpendicular to the a and b vectors and therefore correspond to the (1,0) and (0,1) layer lines. In this case, the chosen circumferential vector generates start numbers of −10 and 9, respectively. (C) The 2D lattice is the same as in A based on the underlying assumption that all the helical assemblies are built from the same lattice. However, the circumferential vector is drawn to the (−10,8) coordinate (yellow triangle) in order to generate a different helical symmetry. (D) The corresponding helical lattice generates start numbers of −10 and 8 for the (1,0) and (0,1) layer lines, respectively.

For the current work, we recorded images of frozen-hydrated Bor1p tubes and negatively stained OmpF tubes that were collapsed on the carbon support. The diffraction patterns from these images were analyzed with the 2dx software suite (Crowther et al., 1996; Gipson et al., 2007) to produce dimensions of the 2D unit cell (a, b and γ).

3.4. Consistency of 3D reconstructions

As discussed in the previous section, it is common to obtain tubular crystals with varying diameters and these tubes typically derive from the same 2D surface lattice. As a result, their helical symmetries are systematically related such that assignment of helical symmetry to one type will uniquely determine the symmetry of a second type. We reasoned that correct helical indexing might produce a more consistent distribution of densities in the independent 3D reconstructions from such tubes, thereby providing a validation for the indexing schemes. To perform 3D reconstructions, we used Fourier-Bessel methods derived from the MRC software developed by Beroukhim and Unwin (Beroukhim and Unwin, 1997) and packaged in the EMIP image processing program (Diaz et al., 2010). For comparison of the resulting densities, unit cells from the two structures were masked and aligned in order to compute the Fourier Shell Coefficient (FSC) curve using SPARX.

3.5 Crystallization of membrane proteins

We used tubular crystals from two different membrane proteins to illustrate our approaches to helical indexing. Bor1p is a presumed boron transporter from the SLC4 family (Jennings et al., 2007; Zhao and Reithmeier, 2001). The Bor1p ortholog from Saccharomyces.mikatae was expressed in the closely-related S.cerevisiae under control of the ADH2 promoter with a C-terminal tag and purified essentially as described previously (Clark et al., 2010; Pryor et al., 2013). Membranes were prepared from cell lysates, then Bor1p was solubilized initially in 1% n-Dodecyl-β-D-maltoside and exchanged into heptaethyleneglycol-n-dodecylether (C₁₂E₇) during affinity chromatography on IgG Sepharose. Following an additional size exclusion chromatography step, the purified protein was extensively screened for 2D crystallization using a high-throughput pipeline (Hu et al., 2010) and the best tubular crystals were obtained using cardiolipin from E. coli (Avanti Polar Lipids) at a lipid-to-protein ratio of 0.44 (w/w). For crystallization, the ternary mixture of protein, lipid and detergent was incubated for 1h at room temperature, and the detergent was removed by dialysis using a 96-well micro-dialysis plate (GN Biosystems) for 1 week at 27°C against a buffer composed of 100 mM HEPES, pH 7, 100 mM NaCl, 2 mM boric acid, 5% NaN₃.

OmpF is a β-barrel channel protein from the outer membrane of E. coli. OmpF was solubilized in 0.5% octyl-POE as previously described (Hoenger et al., 1990), and we screened for crystallization using our high-throughput pipeline together with incomplete factorial and sparse matrices developed in our laboratory (Lasala et al., 2015). Several different conditions produced helical crystals. For this work, we used tubular crystals grown from a mixture of dioleoylphosphatidylcholine and cholesterol (9:1 w/w) solubilized in Triton X100, at a lipid-to-protein ratio of 0.06 (w/w). After 1h incubation at room temperature, the ternary mixture was dialyzed in a 96-well micro-dialysis plate for 1 week at 20°C, using a dialysis buffer of 20 mM MES, pH 6, 150 mM KCl, 5% NaN₃.

For EM, crystallization screens were evaluated by staining samples with 2% uranyl acetate. Suitable samples were prepared for cryo-EM by first diluting them with the crystallization buffer and then applying them to home-made, holey-carbon grids (Diaz et al., 2010) and quick-freezing the grids in liquid ethane. Electron micrographs of Bor1p were acquired on a Tecnai F20 microscope (FEI Corp.) operated at 200 kV with a direct electron detector (Gatan K2). Movies were collected using single-electron counting and super-resolution mode, and motion correction software (Li et al., 2013) was used to produce corrected, binned images with a pixel size of 1.82 Å/pixel. Images of OmpF were recorded on film (Kodak SO-163) using a JE2100F microscope (JEOL Inc.) operated at 200kV, and digitized (Photoscan, Zeiss-Intergraph) with an effective pixel size of 3.06 Å.

4. Experimental results

4.1. Tubular crystals of Bor1p

Bor1p produces tubular crystals with widths from ~30 nm to more than 100 nm. For helical reconstruction, it is desirable to use the narrowest tubes, which are less susceptible to flattening and whose Bessel orders are constrained to smaller values. After selecting the narrowest tubes present in images, the mean radial density distribution was used to measure their radii (Fig. 2). These distributions suggested two discrete types of tubes with radii of 164 Å (Type 1) and 157 Å (Type 2) when measured at the middle of the membrane (r_mid). Alternatively, radii of 190 Å and 183 Å were measured at the outer edge of the two types of tubes (r_out) or 213 Å and 207 Å when the fringe produced by the contrast transfer function was included (r_ctf). The most likely explanation is that these two types represent two different classes of helical symmetry that are derived from a common 2D lattice, but with circumferential vectors of slightly different length, as illustrated in Fig. 4.

Consistent with this explanation, the Fourier transforms from these tubes have layer lines with systematic differences in the peak positions. After assigning Miller indices (h,k) related to the common 2D lattice to the layer lines (Fig. 3B, C), there is a distinct tendency for Type 2 tubes to have smaller Bessel orders. Although the difference is not noticeable for most of the layer lines, the near-meridional layer lines indexed as (1,1) and (2,3) do show distinct differences in the position of the peak amplitudes. Smaller Bessel orders are a consequence of the shorter circumferential vector and thus the lower start number generated by a given set of lattice lines (see Fig. 4). An alternative explanation is that some of the tubes are flattened, which would appear to increase their diameter. However, flattening is unlikely to be isotropic and tends to affect the top and bottom of the tube differently, thus breaking the symmetry of amplitudes across the meridian. Also, flattening would be unlikely to produce two discrete populations of tube diameters, but would instead produce a tail is the distribution of radii extending towards the larger diameters.

Image classification represents another approach to segregate helical particles with different helical symmetries (Skruzny et al., 2015). However, because out-of-plane tilt generates a variety of different views, the projection data for a given helical symmetry is not homogeneous (McCullough et al., 2015). So although this classification may work in some cases, especially when the alternative symmetries produce significant differences in diameter, classification of Bor1p tube generated a multitude of class averages that did not readily fall into discrete groups. On the other hand, neither the diameter nor the phase residuals (discussed below) are affected by out-of-plane tilt and thus represent a more robust sorting of the population of Bor1p tubes.

4.2. Conventional analysis of layer line data from Bor1p crystals

For Type 1 crystals, comparison of phases related by mirror symmetry (i.e., from opposite sides of the meridian) indicates that the Bessel order is odd for the principal layer line assigned as (0,1) and is even for that assigned as (1,0). For Type 2 crystals, both (0,1) and (1,0) layer lines appear to have even Bessel orders. This fundamental difference in phase relationships on the principal layer lines provides additional strong evidence for the presence of two distinct helical symmetries. Furthermore, distinct symmetries are supported by phase residuals resulting from a comprehensive comparison of the mirror symmetric layer line data. These residuals are calculated during the first step of the Fourier Bessel reconstruction process by the SRCH program, which centers the tubes and compensates for out-of-plane tilt (Diaz et al., 2010). These phase residuals are very high (>50 degrees) when layer line parity is not respected.

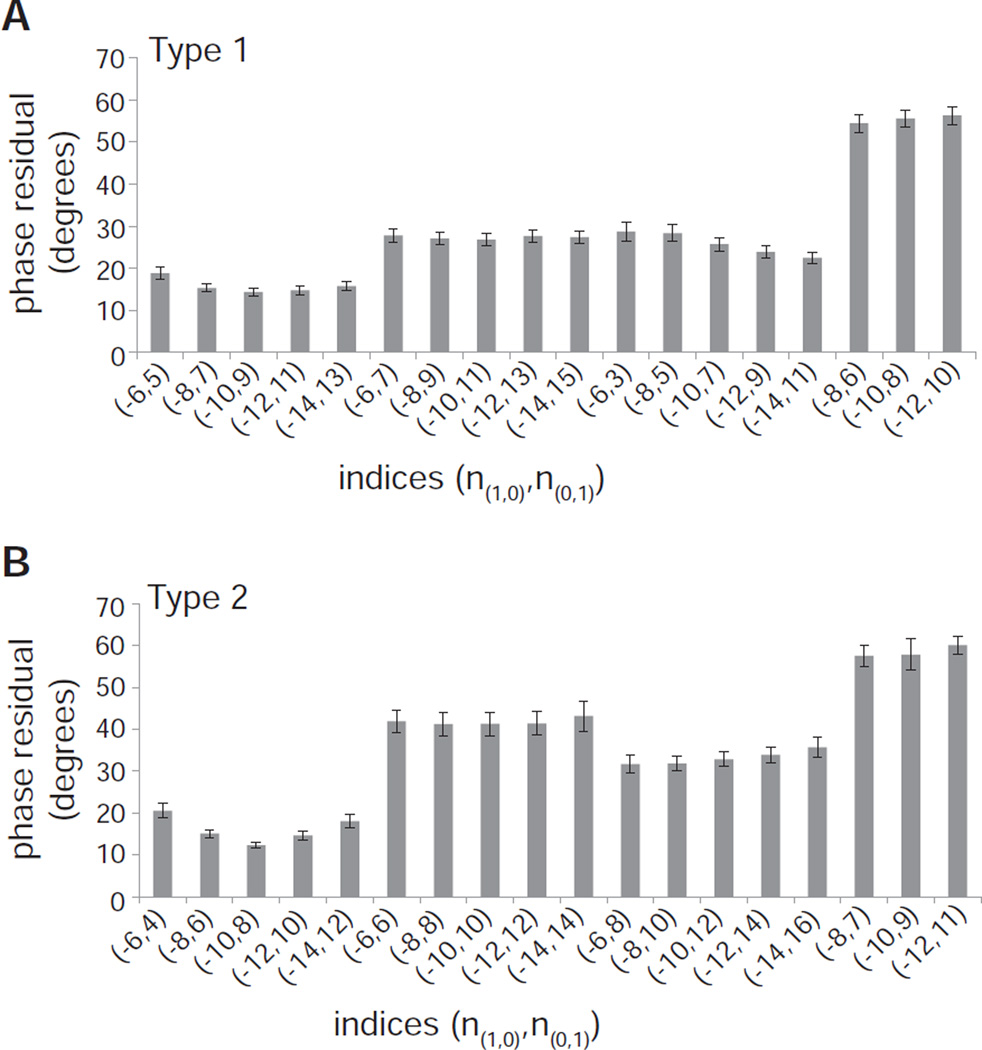
These phase residuals were used to conduct a systematic survey of different combinations of Bessel orders. The (1,1) layer line provides an important constraint in selecting plausible indexing schemes to test, because it is close to but not exactly on the meridian. This location suggests that the corresponding Bessel order (n_(1,1)) should be small, most likely 1 or 2. Given that n_(1,1) = n_(1,0) + n_(0,1), the Bessel orders for the (1,0) and (0,1) should therefore have opposite signs and their absolute value should differ by the corresponding amounts. The results of this survey (Fig. 5) are consistent with n_(1,1) = 1 for Type 1 crystals, with n_(1,1) = 2 for Type 2 crystals, and with |n(1,0)| > |n(0,1)| for both types. However, there is ambiguity regarding the actual value of the Bessel orders because schemes in which n_(1,0) = 8, 10 and 12 all yield similar phase residuals. Note, however, that phase residuals for Type 1 tubes using indexing schemes that are favorable for Type 2 crystals are extremely high (last three schemes shown in Fig. 5A) and visa versa (Fig. 5B), providing yet another confirmation that the two types of tubes have distinct symmetries.

Figure 5.

Phase residuals after refinement of tube center and out-of-plane tilt for the two types of Bor1p helical assemblies. (A) Phase residuals for 57 Type 1 tubes are lowest when |n_(1,0)| = |n_(0,1)|+1. (B) Phase residuals for 34 Type 2 tubes are lowest when |n_(1,0)| = |n_(0,1)|+2, with a slight preference for the (−10,8) indexing scheme. The very high residuals for the last three indexing schemes illustrate that the two types of tubes have distinct helical symmetries. All data represent the mean phase residual and standard error of the mean.

4.3. Summing diffraction data from Bor1p

In principle, this ambiguity in assigning specific Bessel orders could be resolved by accurate measurement of the peak positions along the individual layer lines, as shown by equation 1. However, the signal-to-noise ratio along the layer lines from individual tubes is typically low, making this measurement inaccurate. In order to increase the signal-to-noise ratio, we incoherently summed Fourier data from 57 straight segments using two different techniques: a sum of 2D Fourier transforms and a sum of extracted layer line data (see Section 2.3). Fig. S1 indicates that the two techniques produce almost equivalent results and increase the accuracy with which peak positions are measured. Note that because the first technique does not account for slight variations in pitch, summed layer lines are blurry (Fig. 3C), sometimes leading to spurious peaks that bleed through from an adjacent layer line (e.g., the low resolution peaks on the (2,−1) layer line, which resides just above the equator). Fig. S1 illustrates that although some of the layer lines conform nicely to the expected positions for the (−10,9) indexing scheme, others do not. This situation was also true for other plausible indexing schemes, leading to a certain amount of ambiguity. Nevertheless, after considering all the possibilities, we tentatively concluded that the peak positions for Type 1 and Type 2 crystals of Bor1p are most consistent with the (−10,9) and (−10,8) indexing schemes, respectively. In Fig. S2, incoherent sums from Type 1 and Type 2 layer lines are superimposed, once again demonstrating systematic differences that reflect their differing helical symmetry.

4.4. Synthetic Bor1p images

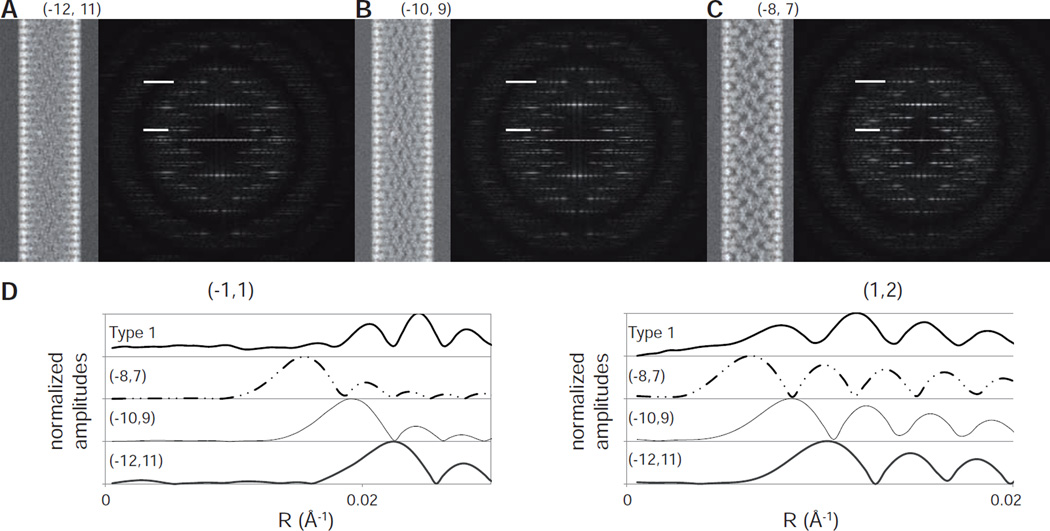
Given that the molecular structure has an influence on the position of the layer line peaks, we constructed synthetic images in an attempt to simulate intensity distributions along the layer lines and thus to evaluate our candidate helical symmetries. A homology model for Bor1p was first created based on the atomic structure of the uracil transporter UraA (Barneaud-Rocca et al., 2013). Both of these transporters have recently been assigned to the Amino acid-Polyamine-Organocation (APC) superfamily with the underlying assumption that they have the same basic fold (Västermark and Saier, 2014). Helical tubes comprising this Bor1p model were then constructed and used to generate noise-free, synthetic projection images and the corresponding Fourier transforms. Although the model assumes a similar dimeric organization and the orientation of these dimers within the unit cell is uncertain, this model should produce a reasonable radial distribution of mass and, if arranged in the correct helical symmetry, should therefore provide a reasonable approximation for the location of the first peak along the layer lines in the experimental Fourier transforms from Bor1p tubes. Figs. 6A–C show synthetic images corresponding to the three candidate helical symmetries for Type 1 tubes. The three images have noticeable differences, but the intensity distributions in the corresponding Fourier transforms look very similar. Amplitude profiles for two strong layer lines are shown in Fig. 6D, illustrating differences in the radial position of peaks and comparisons with data from Type 1 tubes support the (−10,9) indexing scheme. For a more systematic comparison, we calculated the mean square error (MSE, defined by equation 3) from peaks along prominent layer lines from both Type 1 and Type 2 tubes, which indicated that the synthetic models with (−10,9)/(−10,8) indexing schemes were most consistent with the images. Specifically, the MSE between synthetic data and incoherently summed data from Type 1 tubes was 0.083 for the (−10,9) scheme, whereas the (−8,7) and (−12,11) produce MSE = 0.096 and 0.109, respectively. For Type 2 tubes, the MSE for the (−10,8) scheme is 0.077, whereas (−8,6) and (−12,10) schemes produce MSE = 0.104 and 0.096 respectively.

Figure 6.

Data from simulated images of Bor1p. (A–C) Projection images and Fourier transforms from helical assemblies generated using (−12,11), (−10,9) and (−8,7) indexing schemes, respectively. These noise-free images were generated from the X-ray crystallographic structure of the phylogenetically related uracil transporter (UraA) as described in section 3.2. (D) Comparison of the amplitude distribution along the (−1,1) and (1,2) layer lines (indicated on the Fourier transforms). The experimental data from Type 1 tubes are derived from the incoherent sum shown in Fig. 3C.

4.5 Evaluation of the 2D lattice from collapsed Bor1p tubes

If the dimensions of the 2D lattice can be determined, then the length of the circumferential vector that generates a specific helical symmetry (Fig. 4) can be measured and compared with the 2πr_mid, with r_mid being measured from images of the corresponding tubes (Fig. 2). In order to determine the dimensions of the surface lattice for Bor1p, images were acquired from collapsed tubes lying on the carbon support and the values for for a,b, and γ of 87.5 Å, 66.3 Å, and 93.3° were used to generate the 2D lattices in Fig. 7. Although the two lattices in Fig. 7C & D are identical, different candidate circumferential vectors are indicated by symbols: square, triangle and diamond, with the star representing the origin. Based on this origin, the two arcs represent circumferences at the inner and outer leaflets of the bilayer as determined from mean radial density distributions from the two types of tubes (e.g., Fig. 2). This analysis shows that the circumferential vectors from the (−10,9) and (−10,8) indexing schemes (triangles) fall within the boundaries of the bilayer, whereas those from the alternative schemes, in which n_(1,0) is either 8 (diamond) or 12 (square), do not.

Figure 7.

Analysis of surface lattice for Bor1p. (A) Image of a collapsed tube of Bor1p with scale bar of 20 nm. (B) Fourier transform showing lattice that was used to measure the unit cell dimensions. The lattice is from only one side of the tube, probably because absorption to the carbon film caused disordering. (C) Depiction of the surface lattice with an arbitrary origin designated by a star. Three points in the lattice are identified as circumferential vectors that will generate three candidate indexing schemes ((−8,7); (−10,−9); (−12,11), red diamond, triangle, and square, respectively). The correct scheme is expected to generate a circumferential vector consistent with Type 1 tubes. To judge the consistency, black arcs are drawn at a distance from the origin consistent with inner and outer leaflets of the bilayers (calculated as 2πr based on the measured radius of peaks in the mean radial density profile in Fig. 2). (D) A similar analysis of indexing schemes for the Type 2 tubes, comparing (−8,6), (−10,8), and (−12,10) indexing schemes (yellow diamond, triangle, and square, respectively).

4.6. Consistency of the Bor1p reconstructions

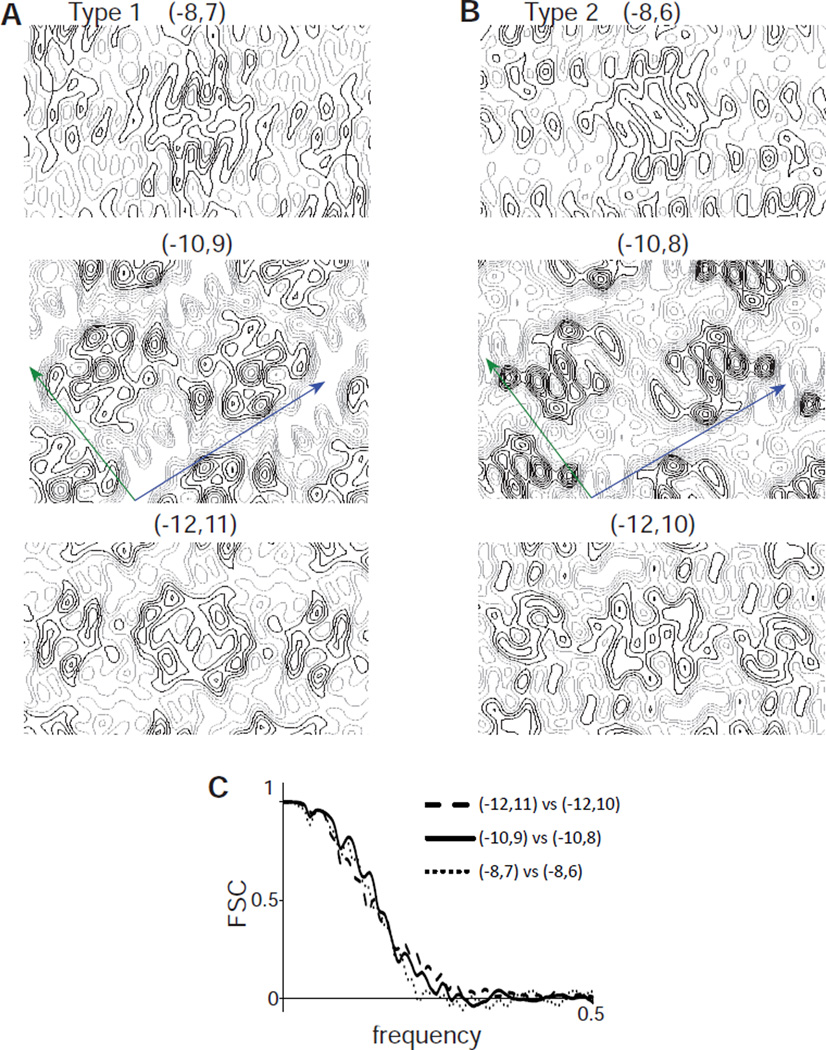
Given the availability of Bor1p tubes with two related helical symmetries, we reasoned that comparison of maps generated with the related schemes might be used to distinguish between the indexing alternatives. Specifically, we compared reconstructions from Type 1 and Type 2 tubes using the following indexing schemes: (−8,7) vs. (−8,6), (−10,9) vs. (−10,8), and (−12,11) vs. (−12,10). We hypothesized that the correct indices would produce consistent density distributions in the two reconstructions, whereas structural artifacts created by incorrect indexing might generate inconsistent features. As expected, helical reconstructions of Type 1 tubes with different indexing schemes produce rather different distributions of density (e.g., comparison of (−8,7), (−10,9) and (−12,11) in Fig. 8A). However, the corresponding reconstructions from Type 2 tubes ((−8,6), (−10,9), and (−12,11)) were in fact rather similar (Fig. 8B). In order to quantify the comparisons, we used Fourier Shell Correlations (Fig. 8C), which clearly illustrate that such comparisons do not provide any basis for distinguishing between the three alternatives for indexing. Inspection of the maps from (−10,9) and (−10,8) reconstructions suggest the densities are consistent with recent dimeric structures of UraA and the anion exchanger Band 3 (Arakawa et al., 2015; Lu et al., 2011). However, a more detailed analysis of these structures will be the subject of a future publication.

Figure 8.

Comparison of maps for Bor1p. (A) Sections from density maps from Type 1 tubes generated with the three candidate indexing schemes. These sections were taken from the middle of the membrane. (B) Sections from density maps from Type 2 tubes from the three candidate indexing schemes. Unit cell axes are drawn in blue (a axis) and green (b axis). (C) Fourier shell correlation curves for the comparison of maps indicated in the legend. The spatial frequency of 0.5 represents the Nyquist frequency, which in this case corresponds to 3.6 Å resolution. This analysis indicates that such comparisons are not able to distinguish between candidate indexing schemes.

4.7. Analysis of OmpF crystals

OmpF is a β-barrel channel from the outer membrane of E. coli. Well-ordered planar 2D crystals are relatively easy to produce (Dorset et al., 1983) and atomic structures have been determined by X-ray crystallography (Pauptit et al., 1991). In testing our 2D crystallization screen (Lasala et al., 2015), we discovered conditions for making novel tubular crystals of OmpF. The diameter of these tubes is large (>100 nm) and highly variable, thus making the determination of helical symmetry particularly challenging. To test our approach to indexing, we used three tubes having a radius r_mid of ~53 nm.

As the first step in indexing, we inspected the symmetry-related phases on either side of the meridian, which suggested that the parity of (1,0) and (0,1) layer lines differed between the three tubes even/odd for the first, odd/even for the second, and even/even for the third. Based on the layer line peak positions, we calculated Bessel orders of ~30 for the (1,0) and ~20 for the (0,1) layer lines (Fig. S3) and then used phase origin refinement (e.g., Fig. 5) to identify candidate indexing schemes corresponding to (−28,21), (−30,21) and (−32,23) for the first tube, (−23,16), (−29,20), (−35,24) for the second tube and (−26,18), (−28,20), (−30,20) and (−30,22) for the third tube, all of which generated relatively low phase residuals.

To discriminate between these alternative indexing schemes, unit cell dimensions were measured from collapsed, negatively stained tubes (Fig. S3) as (a, b, γ ) = (129.5 Å, 129.9 Å, 60°). OmpF has previously been reported to form a p3 lattice in planar 2D crystals, which is consistent with these measurements (Dorset et al., 1983). Using these parameters, we constructed the lattice shown in Fig. S4 and compared the length of the circumferential vectors (between the origin indicated by the star and the lattice points indicated by diamond, triangle and square) with radii measured from the second image (arcs correspond to 2πr for inner and outer leaflets of the bilayers for each tube). This analysis supports the (−23,16), (−29,20), (−35,24) indexing schemes for the three tubes. Finally, we generated 3D maps using the Fourier-Bessel method for the various candidate indexing schemes and maps for one of the tubes are shown in Fig. S5. Because these maps were generated from a single tube, they were relatively noisy. Nevertheless, only the (−29,20) scheme selected by analysis of the surface lattice produced the expected trimeric arrangement of OmpF molecules as seen in previous work (Dorset et al., 1983; Hoenger et al., 1990).

5. Discussion

In this report, we have presented complementary strategies to index diffraction patterns from helical assemblies of membrane proteins, which is an essential first step for 3D reconstruction by either Fourier-Bessel or by iterative, real-space methods. We have illustrated these approaches on tubular crystals comprising the boron transporter, Bor1p, from the SLC4 family, and the β-barrel channel from the outer membrane of E. coli, OmpF. Both are small membrane-embedded proteins that would be impossible to analyze using conventional single-particle EM analysis. Our strategies include measurement of peak positions along the layer lines and parity of their phases, comparison with synthetic images, and wrapping of the 2D surface lattice into a helical assembly (summarized in Table 1). In principle, any of these strategies could solve the problem, but the large Bessel orders that characterize the relatively wide helical tubes produced by membrane proteins make definitive assignment of symmetry difficult. Indeed, our analysis of Bor1p tubes illustrates how individual strategies tend to give ambiguous answers, but overlapping constraints from these independent analyses suggest a unique indexing scheme that, in fact, produced a structure consistent with those of phylogenetically related transporters. Electron tomography represents another approach that has been used not only to characterize helical symmetry but then also to determine a 3D structure by real-space averaging (Bharat et al., 2012). However, analysis of tomograms requires visible features that can be recognized as protruding from the surface of the tubular assembly. Because many transport proteins are largely embedded within the lipid bilayer, they produce a relatively smooth surface at the low resolutions produced by electron tomography.

Table 1.

Workflow for indexing helical symmetry from membrane tubes

procedure	information gained
1. measure tube diameter (Fig. 2)	segregate tubes into classes
2. evaluate phases along layer lines (Fig. 5)	constrain parity of Bessel orders
3. sum layer line data (Figs. S1&S2)	estimate Bessel orders from peak positions
4. create synthetic images (Fig. 6)	validate indexing scheme
5. evaluate surface lattice (Fig. 7)	validate indexing scheme
6. compare 3D reconstructions (Fig. 8)	validate indexing scheme (ineffective)

Analysis of amplitudes and phases along the layer lines represents the conventional approach to indexing (DeRosier and Moore, 1970) and provides constraints that can be tested using the other methods. In favorable cases, a large number of layer lines are visible and can be used to produce a self-consistent set of Bessel orders that uniquely define the helical symmetry. Thus, this analysis is the best place to start, and the process can be greatly aided by incoherent averaging methods, which serve to enhance the signal-to-noise ratio along the layer lines and makes it easier to identify the positions of the relevant peaks. Furthermore, direct inspection of layer line data leads to an understanding of the eccentricities of the helical assembly and helps to identify pathologies that would interfere with the reconstruction process. Eccentricities include the presence of a rotational symmetry axis either parallel or perpendicular to the helical axis, which should then be applied in the reconstruction process. In particular, presence of an n-fold rotational symmetry axis along the meridian (e.g., C3 symmetry) will constrain all Bessel orders to be multiples of n. Presence of two-fold symmetry perpendicular to the meridian (i.e., D1 symmetry), will constrain all of the phases to be 0 or 180°. Common pathologies include the presence of multiple different symmetries and flattening. Different symmetries will produce different patterns of layer line amplitudes (e.g., Fig. 3B, C) and must be segregated prior to analysis. Although there are limitations in using simulated images to evaluate helical symmetry, due to the uncertainty in generating an appropriate structural model, this exercise does at least engender familiarity with the candidate symmetries, which is helpful in the evaluation of the experimental data.

Even slight flattening of tubes will distort the helical symmetry and compromise the resolution. Specifically, flattening will shift the positions of the amplitude peaks along the layer lines and will usually perturb the mirror symmetry because top or bottom surfaces are no longer equivalent. Sharp peaks along the layer lines are a hallmark of flattening and usually grounds for eliminating the corresponding image from the dataset. It is possible that the model-based refinement of helical structures being developed by Rohou and Grigorieff (Rohou and Grigorieff, 2014) could be adapted to account for changes in helical symmetry and flattening, though a precise understanding of the distortions present in a given sample would likely be important. It should be noted, however, that symmetric flattening of the tubes will confuse the analysis of helical symmetry, because of changes both in the apparent tube diameter and in the position of peaks along the layer lines. Because these two effects are interdependent - flattening will increase the measured radius but will also shift the layer line peaks to a lower value for R_peak - one might very well arrive at the correct indexing scheme with moderately flattened tubes (c.f., equation 1). However, these effects will confuse the analysis from unflattened tubes, which will appear to be different even though the underlying helical symmetry is the same.

Our analysis of the 2D lattice is, we believe, a novel approach to assessing helical symmetry. This analysis relies on knowledge of unit cell dimensions for the surface lattice. The hollow tubes formed by reconstituted membrane proteins often grow to a larger diameter and often collapse onto the specimen support, allowing direct visualization of this lattice. In fact, many of the 2D crystallographic studies of membrane proteins have employed collapsed tubes, for which each side of the tube has been analyzed as a planar 2D crystal (Abeyrathne et al., 2010). Given that the radius of cylindrical tubes can be readily measured directly from the images, this analysis is potentially very powerful in selecting between alternative indexing schemes that have been identified by the more conventional approaches. Indeed, indexing of the very wide OmpF crystals would have been very challenging for conventional approaches due to the relatively small number of weak layer lines. It is interesting to note that the lattice points defining the circumferential vectors for alternative schemes tend to lie along a line (Figs. 7 and S4). This is because the spatial relationship of the (1,0) and (0,1) layer lines define the general direction of these vectors, but not necessarily their lengths. For thinner, more rigid tubes produced from cytoskeletal elements or soluble scaffolding proteins, dimensions of the surface lattice will be difficult, if not impossible to ascertain. However, inspection of class averages might be a way to place some constraints on these parameters (Korkhov et al., 2010b), though effects on out-of-plane tilt on the classification process should be taken into consideration.

Direct inspection of the 3D structure can in some cases be used to validate an indexing scheme. In particular, if the structure can be refined to high resolution, then the presence of secondary structure and side-chain densities are a reasonable validation of the symmetry (Egelman, 2014) and is akin to the process by which X-ray crystallographers evaluate an initial set of experimental phases. Similarly, if there is a structure of a related protein, then consistency with this structure might also be used to validate the helical symmetry. Such features can also be used to establish the hand of the helical structure, which is otherwise difficult to accomplish experimentally (Finch, 1972). Without such a priori structural knowledge, however, it is difficult to differentiate the artifacts from the real features of the protein (Egelman, 2014). This is evident from our reconstructions of Type 1 and Type 2 crystals of Bor1p using alternative sets of indexing schemes. Although the individual maps from each type had very different appearances when reconstructed with different symmetries, the artifacts produced by incorrect indexing were similar when the symmetries for the two types were matched.

In summary, helical reconstruction remains a very powerful method for producing 3D structure of proteins that form assemblies with this particular symmetry. Typically, all the necessary orientations of a protein are represented in a helix and the molecular weight of the subunit no longer represents a limiting factor for alignment and reconstruction. Thus, recent advances in detectors for EM offer excellent prospects for achieving atomic resolution from reasonably well-ordered assemblies. Ongoing developments in real-space processing implemented in SPARX (Behrmann et al., 2012; Wu et al., 2014) and FREALIX (Rohou and Grigorieff, 2014) have the potential to address defects such as flattening and variable twist, which would greatly enhance the applicability of helical reconstruction to the large diameter tubes produce by membrane proteins and would thus expand the range of protein structures that can be evaluated by EM. Understanding of the helical symmetry is key to the reconstruction process. Although serious ambiguities can arise in conventional approaches for characterizing the symmetry, a combination of alternative approaches and specifically consideration of the surface lattice of tubular crystals presents an effective way to resolve these ambiguities.