Macromolecular Crowding Modulates Actomyosin Kinetics

Abstract

Actomyosin kinetics is usually studied in dilute solutions, which do not reflect conditions in the cytoplasm. In cells, myosin and actin work in a dense macromolecular environment. High concentrations of macromolecules dramatically reduce the amount of free space available for all solutes, which results in an effective increase of the solutes’ chemical potential and protein stabilization. Moreover, in a crowded solution, the chemical potential depends on the size of the solute, with larger molecules experiencing a larger excluded volume than smaller ones. Therefore, since myosin interacts with two ligands of different sizes (actin and ATP), macromolecular crowding can modulate the kinetics of individual steps of the actomyosin ATPase cycle. To emulate the effect of crowding in cells, we studied actomyosin cycle reactions in the presence of a high-molecular-weight polymer, Ficoll70. We observed an increase in the maximum velocity of the actomyosin ATPase cycle, and our transient-kinetics experiments showed that virtually all individual steps of the actomyosin cycle were affected by the addition of Ficoll70. The observed effects of macromolecular crowding on the myosin-ligand interaction cannot be explained by the increase of a solute’s chemical potential. A time-resolved Förster resonance energy transfer experiment confirmed that the myosin head assumes a more compact conformation in the presence of Ficoll70 than in a dilute solution. We conclude that the crowding-induced myosin conformational change plays a major role in the changed kinetics of actomyosin ATPase.

Introduction

Myosin is a molecular motor that is responsible for force production in muscle, as well as cell trafficking and locomotion, and members of the myosin family participate in a wide range of cellular functions (1). The performance of muscle and the mechanism of the actin-myosin motor function in cells are explained in terms of the kinetics of individual steps of the actomyosin cycle (2). The cycle kinetics is usually studied in dilute solutions at low protein concentrations or in a single-molecule setup, which is dramatically different from the highly structured protein organization of the sarcomere or the dense cytoplasm environment with macromolecular content reaching 20–30% w/v. Such a high macromolecular concentration results in significant volume exclusion (3, 4). Due to the excluded volume, the space available to solutes decreases, which 1) forces the macromolecular solutes to accept a more compact form to minimize their excluded volume (5), and 2) effectively increases the solutes’ concentration, thus increasing their chemical potential. The chemical potential of small solutes is less affected by crowding than that of the large ones, since the excluded volume depends on the sum of radii of the solute and the macromolecular crowder. In the actomyosin cycle, myosin interacts with two ligands: a relatively small nucleotide and a much larger actin. Therefore, the actomyosin cycle potentially can be modulated by crowding, and one can expect different effects of crowding on the activity of myosin ligands.

Our goal in this work was to examine whether macromolecular crowding indeed affects the kinetics of the actomyosin cycle. We used buffered solutions of Dictyostelium discoideum myosin II, rabbit skeletal actin, ATP, ADP, and 25% w/v Ficoll PM 70 (Ficoll70) as a crowding agent to mimic the crowding effect of the intracellular environment (6, 7, 8, 9). Ficoll70 is a nonionic cosolvent with a molecular radius of 5.1 nm and a molecular mass of 70 kDa, and thus is comparable in size and mass to myosin head (89 kDa, prolate spheroid with axes 10.05 nm and 16.25 nm (10)). Ficoll70 stabilizes proteins in solution, but does not form a stable complex with them (8). For the crowded solution, we anticipated 1) a slight increase in the rate of nucleotide binding to myosin and actomyosin, 2) a significant increase in the strong actomyosin complex formation rate, 3) a slight inhibition of ADP dissociation from actomyosin due to the increased effective concentration of ADP in solution, 4) no effect on the rates of actomyosin dissociation and the recovery stroke, and 5) no change in the overall rate of the cycle. A faster entry into strong actomyosin binding and a slower exit from it should affect the myosin duty ratio, which is determined as the time myosin spends being strongly bound to actin relative to the overall time of the cycle.

As a result of detailed kinetic studies, we found that the effect of Ficoll70 on myosin cannot be explained by changes in the ligand chemical potential. The increased viscosity of the crowded solution leads to diffusion control over the myosin-ligand interaction. A transient time-resolved Förster resonance energy transfer (TR²FRET) experiment detected a structural change within the myosin head in the presence of Ficoll70. This structural change could lead to the observed changes in the actomyosin kinetics.

Materials and Methods

Reagents

We obtained 5-((((2-iodoacetyl)amino)ethyl)amino)naphthalene-1-sulfonic acid (IAEDANS) and N-(1-pyrene)iodoacetamide (pyrene) from Life Technologies (Grand Island, NY), DABCYL (4-((4-(dimethylamino)phenyl)azo)benzoic acid) C2 maleimide from AnaSpec (Fremont, CA), and phalloidin, ATP, and ADP from Sigma-Aldrich (Milwaukee, WI). All other chemicals were obtained from ThermoFisher Scientific (Waltham, MA) and VWR (Radnor, PA).

Protein preparation

An A639C:K498C mutant of D. discoideum myosin S1 was expressed and purified as described previously (11, 12). The myosin concentration was determined spectrophotometrically assuming an extinction coefficient of ε_280nm = 0.69 (mg/mL)⁻¹cm⁻¹ (13). For FRET measurements, the protein was labeled in two steps: 1) with the donor (IAEDANS) and 2) with the acceptor (DABCYL) (12, 14). Unreacted probes were removed by spin concentration (Amicon Ultra; EMD Millipore, Billerica, MA). Labeled myosin was centrifuged at 100,000 g for 40 min to remove possible aggregates. The concentration of labeled myosin was determined by a Bradford assay (Bio-Rad Laboratories, Hercules, CA). The experimental buffer contained 20 mM 3-[N-morpholino]propanesulfonic acid (MOPS) pH 7.5, 50 mM KCl, and 3 mM MgCl₂. Actin was prepared from rabbit back and leg muscles as described previously (15). F-actin was labeled with pyrene iodoacetamide or TEMPO maleimide (6:1 label/actin molar ratio), cleaned from the excess label, repolymerized, stabilized with phalloidin at a molar ratio of 1:1, and dialyzed for 2 days at T = 4°C against the experimental buffer. The concentration of unlabeled G-actin was determined spectrophotometrically assuming an extinction coefficient of ε_290nm = 0.63 (mg/mL)⁻¹cm⁻¹ (16). The concentration of labeled G-actin and the labeling efficiency were determined spectroscopically using the following expressions: [G-actin] = (A_290nm – (A_344nm × 0.127))/26,600 M⁻¹ and [pyrene] = A_344nm/22,000 M⁻¹ (17).

Ficoll70 preparation

A 40% w/v Ficoll PM 70 (Amersham Biosciences AB, Uppsala, Sweden) stock solution was prepared first. The Ficoll70 stock solution was diluted to 25% w/v by addition of myosin or actin-buffered solution, or experimental buffer.

ATPase assays

Steady-state basal and actin-activated myosin ATPase activities were measured spectrophotometrically at T = 20°C in the experimental buffer with and without 25% w/v Ficoll70 by the liberation of inorganic phosphate as described previously (18). Both myosin and F-actin were carefully washed before each experiment to avoid any possibility of contamination by products of hydrolysis (phosphate and ADP). Myosin or actomyosin was mixed with ATP, and aliquots were collected at equal time intervals and analyzed for phosphate in an ammonium molybdate-malachite green colorimetric assay (see Supporting Materials and Methods for more details). The rate of basal myosin ATPase was determined as the rate of phosphate production. To determine the maximum velocity of the actomyosin ATPase, the rates of myosin ATPase at different actin concentrations were fitted by the hyperbolic equation v = V_max[actin]/(K_d + [actin]), where v is the rate of the ATPase in the presence of actin, and V_max is the rate of myosin ATPase at an infinite actin concentration (the horizontal asymptote of the hyperbola). We did not account for F-actin ATPase activity because this is a slow process (19) that is significantly inhibited by phalloidin (20). The determined basal and actin-activated myosin ATPase rates were comparable to those reported for other D. discoideum myosin constructs (21, 22, 23, 24, 25).

The transient intrinsic fluorescence of myosin and the fluorescence of pyrene actin were measured with a Bio-Logic SFM-300 stopped-flow transient fluorimeter (Bio-Logic Science Instruments SAS, Claix, France) equipped with an FC-15 cuvette. The mixing unit dead time was 2.6 ms. All experiments were done at T = 20°C. Usually, three syringes and two mixers were used in an experiment. Continuous flow and the smallest intermixer delay line (40 μL) were used except in the weak-to-strong-binding transition experiment, in which intermittent flow and a 60 μL delay line were used. The delay time of the weak-to-strong binding transition experiments was adjusted to make sure that the maximum concentration of myosin in the M^∗∗ state would be produced in the first mixing (Fig. S8). Myosin intrinsic fluorescence was excited by a mercury-xenon lamp at 296 nm and detected using a 320 nm cutoff filter. The pyrene fluorescence was excited at 365 nm and detected using a 420 nm cutoff filter. Multiple transients were usually acquired and averaged to improve the signal/noise ratio. A total of 8000 points were acquired in each experiment.

Analysis of fluorescence transients

The transients obtained in each experiment were fitted globally by the single exponential function S(t) = S_o + A × exp(−k_obs × t), where S(t) is the observed signal at time t, A is the signal amplitude, and k_obs is the observed rate constant. The dependence of the observed rates on the nucleotide or protein concentration was fitted by a hyperbola, v = V_max[ATP]/(K_d + [ATP]), allowing the determination of the maximum rate, V_max (the horizontal asymptote of the hyperbola). To determine the bimolecular rate, the dependence of the observed rates on the nucleotide or protein concentration was fitted by a straight line at small concentrations of the nucleotide or protein. Competitive inhibition of ATP-induced actomyosin dissociation by ADP was measured with pyrene-labeled actin complexed with myosin and incubated with ADP at various concentrations. This solution was rapidly mixed with ATP and the transient fluorescence of pyrene-actin dissociated from myosin was measured. Transients were fitted by single-exponential functions. The observed reaction rates were fitted by the equation k_obs/k₀ = 1/(1+ [ADP]/K′₅) (26, 27, 28), assuming a small [ATP], using the k₀ determined in the experiment without ADP, and varying K′₅, which is the constant of ADP dissociation from actomyosin upon chasing with ATP (see Fig. 2). All data fits were performed with Origin 8 (OriginLab, Northampton, MA). Ficoll70 was fluorescent in the spectral range of our experiments, and its fluorescence exhibited photobleaching (Fig. S9). The transient fluorescence of the Ficoll70-buffered solution was measured before each experiment. The observed transient was fitted with a polynomial function, which was then subtracted from the transients obtained in other experiments.

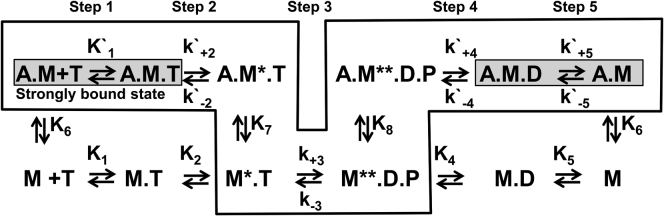
Figure 2.

Actomyosin ATPase cycle reaction scheme. A, actin; M, myosin (M^∗ and M^∗∗ indicate myosin states with increased intrinsic fluorescence); T, ATP; D, ADP; P, phosphate. The asterisk indicates reaction rate constants that describe actomyosin kinetics. Highlighted: the strongly bound actomyosin state. Boxed: the generally accepted pathway of actomyosin interaction.

TR²FRET was measured with an in-house-built transient fluorimeter (14) equipped with an SX-18 stopped-flow unit (Applied Photophysics, Leatherhead, UK), passively Q-switched microchip YAG laser (SNV-20F-100, 355 nm, 20 kHz; Teem Photonics, Meylan, France), photomultiplier (H6779-20; Hamamatsu, Middlesex, NJ), and fast digitizer (Acqiris DC252; Agilent, Santa Clara, CA). A 420 nm cutoff filter and a polarizer set at the magic angle were used in the detection arm. The dead time of the mixing unit was 2.4 ms. All experiments were done at T = 20°C. FRET pair-labeled myosin was rapidly mixed with ATP solution, and the donor fluorescence waveform was acquired after each laser pulse with picosecond resolution. Multiple traces were acquired and averaged to increase the signal/noise ratio. Before each experiment, the fluorescence transients of the Ficoll70-buffered solution were measured. All transients acquired in the experiment were corrected for Ficoll70 fluorescence to account for Ficoll70 photobleaching. The analysis of the donor lifetime in terms of the interprobe distance and myosin structural conformations M^∗ and M^∗∗ (pre- and postrecovery stroke states, respectively) is described in the Supporting Materials and Methods.

Results

Increased rate of actin-activated myosin ATPase in the crowded environment

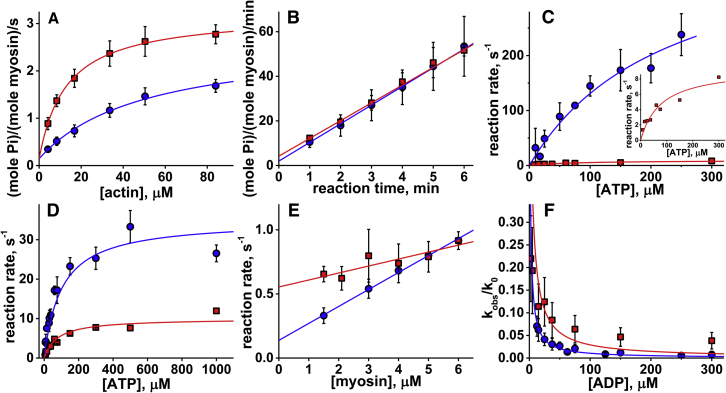
The maximum velocity of steady-state, actin-activated myosin ATPase increased by 30% in the Ficoll70 solution (Fig. 1 A; Table 1). The steady-state myosin ATPase activity was determined at the saturated substrate level, and the velocity of the reaction was described by zero-order kinetics independently of the substrate concentration and the volume excluded by Ficoll70. Addition of Ficoll70 did not affect the rate of basal myosin ATPase activity (Fig. 1 B). Therefore, the actin activation, determined as the ratio of the rates of the actin-activated to the basal myosin ATPase activity, increased from 18-fold without Ficoll70 to 23-fold in the crowded environment.

Figure 1.

(A) Steady-state, actin-activated myosin ATPase activity ([myosin] = 0.8 μM, [ATP] = 5 mM; circles, no Ficoll70; squares, with Ficoll70 in solution). Fit with a hyperbola, V_max = 2.5 ± 0.1 s⁻¹, no Ficoll70; and 3.1 ± 0.1 s⁻¹ with Ficoll70. The data points are averages of N = 6 independent protein preparations. Uncertainties are the standard deviation here and throughout the text. (B) Basal myosin ATPase activity, [myosin] = 3.3 μM. Linear fit, N = 6, v = 0.140 ± 0.007 s⁻¹, no Ficoll70, and 0.133 ± 0.002 s⁻¹ with Ficoll70. (C) ATP-induced actomyosin dissociation. No Ficoll70, N = 6; with Ficoll70 in solution, N = 2. Fit with a hyperbola, V_max = 431.6 ± 120.1 s⁻¹, no Ficoll70; and 9.4 ± 1.4 s⁻¹ with Ficoll70. Inset: data obtained with Ficoll70 in solution. (D) Kinetics of ATP binding and the recovery stroke upon rapid mixing of myosin and ATP; the observed rate constants are fitted with a hyperbola, V_max = 34.9 ± 4.4 s⁻¹, N = 4, no Ficoll70; and 10.0 ± 0.9 s⁻¹, N = 2, with Ficoll70 in solution. (E) Kinetics of the weak-to-strong actomyosin binding transition, N = 4. The observed reaction rates are fitted by a straight line, and the second-order reaction rate constant is determined from the slope of the line. K₈k′₊₄ = 0.13 ± 0.01 μM⁻¹s⁻¹, no Ficoll70; and 0.05 ± 0.01 μM⁻¹s⁻¹ with Ficoll70 in solution. (F) ATP-induced ADP dissociation from actomyosin ([actomyosin] = 0.5 μM, [ATP] = 25 μM; circles, no Ficoll70, N = 3; squares, with Ficoll70, N = 2). Lines: fit by the model of competitive inhibition with variable parameter K′₅, K′₅ = 1.07 ± 0.07 μM, no Ficoll70; and 1.58 ± 0.58 μM with Ficoll70. To see this figure in color, go online.

Table 1.

Actomyosin Kinetic Rate Constants with and without Ficoll70

Kinetic Step	No Ficoll70	With Ficoll70
Actomyosin dissociation, K′1k′+2, μM−1s−1	1.247 ± 0.177	0.094 ± 0.089
Actomyosin dissociation, Vmax, s−1	431.6 ± 120.1	9.4 ±1.4
ATP binding to myosin, K1k+2, μM−1s−1	0.26 ± 0.05	0.11 ± 0.01
Recovery stroke and hydrolysis, Vmax, s−1	34.9 ± 4.4	10.0 ± 0.9
Weak-to-strong-binding transition, K8k′+4, μM−1s−1	0.13 ± 0.01	0.05 ± 0.01
ADP release from actomyosin, K′5, μM	1.07 ± 0.07	1.58 ± 0.58
Basal myosin ATPase, (mole Pi)/(mole myosin)/s	0.140 ± 0.007	0.133 ± 0.002
Actin-activated myosin ATPase, Vmax, (mole Pi)/(mole myosin)/s	2.5 ± 0.1	3.1 ± 0.1
Actin activation, actin-activated/basal ATPase	17.9 ± 1.1	23.3 ± 0.8

Ficoll70 affects ATP-induced actomyosin dissociation

The rate of ATP-induced actomyosin dissociation was measured with 0.5 μM pyrene actomyosin (the concentration in the final mixture, here and throughout the text) rapidly mixed with various concentrations of ATP (steps 1 and 2, Fig. 2). Actomyosin dissociation was monitored via an increase of pyrene fluorescence and fitted by a single exponential function (Fig. S1 A). The obtained dependence of the reaction rates on the ATP concentration was fitted with a hyperbola (the maximum rate of actomyosin dissociation V_max is a horizontal asymptote determined in the fit; Fig. 1 C). V_max decreased 45-fold upon addition of Ficoll70 to the solution (Table 1). The second-order reaction rate constant was determined from the slope of the straight line, fitted to the data points at low [ATP]. Without Ficoll70 in solution, the second-order rate constant was in excellent agreement with the corresponding rates obtained for other D. discoideum constructs (29, 30). With Ficoll70 in solution, the second-order rate constant decreased 12-fold (Table 1).

The hydrolysis rate is affected by Ficoll70

The rate of the recovery stroke and hydrolysis was measured by rapidly mixing 0.5 μM myosin and ATP (12.5–300 μM) and monitoring the increase in myosin intrinsic fluorescence (14) (step 3, Fig. 2). The observed intrinsic fluorescence transients were fitted with single-exponential functions (Fig. S1 B), and the dependence of the obtained reaction rates on [ATP] was fitted by the hyperbolic equation (Figs. 1 D and 2). The maximum rate of myosin fluorescence intensity change (V_max) measures the rate of ATP hydrolysis, k₊₃ + k₋₃ (31, 32), assuming that step 3 consists of two distinct but coupled substeps: the fast and reversible recovery stroke (step 3a) and the hydrolysis step (step 3b), which drives the reaction forward (33). Therefore, the kinetics of the hydrolysis step decreased 3.5-fold in the presence of Ficoll70 (Table 1). Both with and without Ficoll70, V_max was fast enough to be nonlimiting for the overall rate of the actomyosin cycle. The association rate constant, K₁k₊₂, determined from the initial slope, decreased 2.4-fold in the presence of Ficoll70.

Ficoll70 decreases the rate of the actomyosin weak-to-strong-binding transition

The rate of the weak-to-strong-binding transition, K₈k′₊₄, was measured in the double-mixing experiment (step 4, Fig. 2). Initially, myosin at various concentrations was rapidly mixed with 100 μM ATP and the reaction was aged in the delay loop for 2 s to populate myosin in the postrecovery state. After the delay, 0.3 μM pyrene actin with 1 mM ADP was rapidly added to the myosin. Pyrene actin fluorescence is sensitive to strong actomyosin binding (34), and we monitored the formation of a strong actomyosin bond via a decrease in pyrene fluorescence. 1 mM ADP was added to quench the reaction. The observed pyrene fluorescence transients were fitted with single-exponential functions (Fig. S1 C). The obtained dependence of reaction rate constants on the myosin concentration was fitted by a straight line (Fig. 1 E). The rate of the weak-to-strong-binding transition was determined from the slope of the line and was found to be 2.5-fold smaller in the presence of Ficoll70 than in the noncrowded solution.

ADP dissociation from actomyosin

To measure the ADP dissociation constant, K′₅, we first premixed 0.5 μM pyrene-labeled actomyosin with various amounts of ADP and then rapidly mixed the solution with ATP (step 5, Fig. 2). ADP dissociation was monitored via an increase in pyrene fluorescence due to actomyosin dissociation after the dissociation of ADP and ATP binding. ADP dissociation is a slow process compared with ATP-induced actomyosin dissociation (Fig. S1 A), and therefore the rate measured in an experiment is determined by the kinetics of ADP dissociation. The observed transients of pyrene fluorescence were fitted with single-exponential functions. The obtained dependencies of the reaction rates of actomyosin dissociation on [ADP] were fitted using the model of competitive inhibition (28) (Fig. 1 F). We found that K′₅ was the same with and without Ficoll70 (Table 1). The high affinity of ADP for our myosin construct is in good agreement with the literature data for D. discoideum myosin (29).

The structure of myosin head is affected by macromolecular crowding

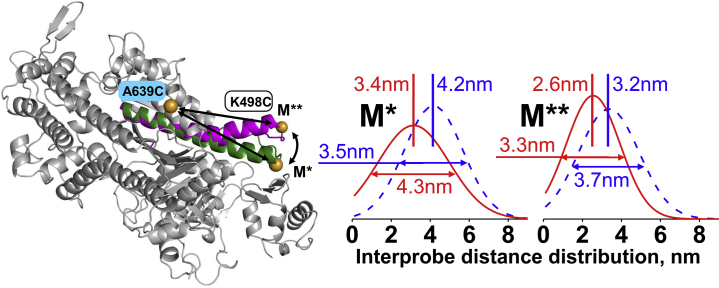
We used TR²FRET (11, 12) to measure the distance between two FRET probes attached to myosin and thus determine the effect of macromolecular crowding on the protein structure. The donor and acceptor probes were attached to K498C (the force-generating region) and A639C (the lower 50 kDa domain) within the myosin head (Fig. 3), and the interprobe distance in the pre- and postrecovery structural states (M, M^∗, and M^∗∗; Fig. 2) was measured in a transient kinetics experiment (14). We mixed myosin (M, 10 μM) with the buffer to measure the interprobe distance in the M state, and detected a 0.8 nm interprobe distance reduction in the presence of Ficoll70 (Fig. 3). We mixed myosin with 300 μM ATP to monitor the formation of the M^∗∗ state via an increased FRET effect. The interprobe distance and Ficoll70-induced distance change of the M^∗ state were similar to those of the M state. We found a 0.6 nm interprobe distance reduction in the M^∗∗ structural state in the presence of Ficoll70 (Fig. 3). The kinetics of the M^∗∗ state formation determined with the FRET pair was the same as the kinetics of the myosin intrinsic fluorescence change. We conclude that the myosin head assumes a more compact form in a crowded solution than in a dilute solution to minimize its excluded volume according to Le Chatelier’s principle. The observed decrease of the ligands’ affinity for myosin in the crowded solution leads us to suggest that the structural change affects the structure or dynamics of the corresponding ligand-binding sites.

Figure 3.

(Left) The myosin head, with overlay of crystal structures 1FMV (M^∗) and 1VOM (M^∗∗), showing a conformational change within the force-generating region. Spheres: engineered labeling sites, showing the predicted shortening of distance between residues 639 and 498 (arrows) during the recovery stroke. (Right) Gaussian distance distributions of the FRET pair within the myosin head (K498C:A639C) without (dashed line) and with (solid line) Ficoll70 in solution. To see this figure in color, go online.

Discussion

According to the excluded-volume theory (4), the rate of the myosin reaction with the ligands actin and ATP is expected to increase in a crowded solution due to the increase in the chemical potential of the solutes. However, we did not observe such a rate increase in our experiments. The observed decrease in the rates of actomyosin and myosin-nucleotide association indicates that other factors affect the myosin-ligand interaction in a crowded solution. Such factors could include the increased ionic strength of the solution, osmotic pressure, viscosity, and structural changes of myosin head or actin induced by macromolecular crowding.

Literature data (35) and our experiments (Supporting Materials and Methods) show that the increased ionic strength decreases the rate of actomyosin association. For our D. discoideum myosin construct, we found that the rate decrease was two times smaller than the effect of macromolecular crowding (Supporting Materials and Methods). Therefore, the effect of increased ionic strength is not dominant when actomyosin is in crowded conditions. The crowding increases the osmotic pressure, which in turn decreases the rate of the rigor complex formation (for example, in a 30% w/v sucrose solution, the rate decreases fivefold due to an increase in osmotic pressure (36)), but the osmotic pressure produced by 25% w/v Ficoll70 is ∼20 times lower than that of the 30% w/v sucrose solution (7), making the effect of the osmotic pressure negligible. Previously, myosin kinetics experiments were performed in the presence of polyethylene glycol (PEG) of different sizes (37, 38, 39). One has to distinguish between a globular crowder (Ficoll) and a polymer (PEG), which forms loose mesh in solution (40). PEG affects osmotic pressure, changing the hydration of solutes, and therefore the effects of PEG and Ficoll70 on myosin kinetics could not be compared. For example, addition of Ficoll70 does not change myosin basal ATPase activity, but addition of PEG decreases ATPase activity (37, 39), as does addition of another known osmolate, sucrose (36).

The macroscopic viscosity of 25% w/v Ficoll70 solution is η = 17 cP (41). Using the Stokes-Einstein relation, we can estimate the coefficient of myosin translational diffusion as 2.5 × 10⁻¹² m²s⁻¹ (assuming for simplicity that the myosin head is a spheroid with a diameter of 10 nm), and that of ATP as 2.5 × 10⁻¹¹ m²s⁻¹. The rate of the myosin-ligand binding can be estimated from the Smoluchowski expression, modified with the statistical weights to account for favorable orientations of interacting molecules (42), k₊₁ = 4πD₁₂R₁₂f₁f₂ (where R₁₂ = R₁ + R₂ is the reaction radius, approximately equal to the sum of the molecular radii of myosin and ligand; D₁₂ = D₁ + D₂ is the relative coefficient of translational diffusion; and f_i = (1/4)sin²(θ_i/2), i = 1,2 is the geometric steric factor, reflecting the angular size θ_i of the reactive spot of interacting molecules, determined as the ratio of the surfaces of the reactive spot and the whole molecule). For the myosin-ATP interaction, assuming f_ATP ∼ 0.5 and f_myosin = 2.5 × 10⁻³ (the reactive spot on the myosin surface on the order of the size of ATP), k₊₁^−F = 1.43 μM⁻¹s⁻¹ without Ficoll70, and k₊₁^+F = 0.08 μM⁻¹s⁻¹ with Ficoll70. The estimated k₊₁^−F is an order of magnitude larger than the observed rate constant K₁k₊₂ (Table 1); therefore, the solvent viscosity does not affect the reaction. With Ficoll70, the estimated k₊₁^+F is close to the experimental rate constant, indicating that the solvent viscosity may affect the reaction rate. Interestingly, the obtained values of K′₁k′₊₂ for the actomyosin-ATP interaction with and without Ficoll70 are close to the calculated values of k′₊₁ (1.25 μM⁻¹s⁻¹ and 1.43 μM⁻¹s⁻¹ without Ficoll70, and 0.09 μM⁻¹s⁻¹ and 0.08 μM⁻¹s⁻¹ with Ficoll70), indicating that the ATP binding to actomyosin may be a diffusion-controlled step. For the actomyosin interaction, assuming f_actin = 0.27 and f_myosin = 0.05 (taking the actin filament as a cylinder with a diameter of 8.4 nm, and the actomyosin interacting spot to have a 2.3 nm radius (43), f_actin = (1/2)sin(θ/2), where θ is the angular size of the interaction spot measured from the axis of the cylinder, and a slow diffusion of actin filament, D_actin << D_myosin, one can estimate k₊₁^−F = 2.5 μM⁻¹s⁻¹ without Ficoll70 and k₊₁^+F = 0.15 μM⁻¹s⁻¹ with Ficoll70. The obtained rate of the actomyosin weak-to-strong binding transition without Ficoll70 is an order of magnitude slower than the calculated diffusion-limited rate, and with Ficoll70 the obtained rate is just three times less than the calculated diffusion-limiting rate, indicating that in the crowded environment the interaction of actin and myosin may be diffusion controlled. Our electron paramagnetic resonance experiments (see Supporting Materials and Methods) show that actin structure is not affected by Ficoll70 in solution, but the TR²FRET experiment shows that the myosin head adopts a more compact structural state compared with that in a dilute solution. It is possible that the structural change in the myosin head affects the kinetics of the actomyosin cycle and therefore may change the duty ratio of myosin molecular motor.

Conclusion

Macromolecular crowding modulates the actomyosin interaction in solution. The overall rate of the actomyosin cycle increases in a crowded solution. The myosin head adopts a more compact conformation than it does in a dilute solution to minimize the excluded volume. Crowding-induced increase of solution viscosity modulates the interaction of the solutes, and the observed decrease in the reaction rates of the myosin-actin and myosin-ATP interactions agrees well with the calculated values of the diffusion-controlled reaction rates.

Author Contributions

Y.E.N., T.A.S., and J.G. designed research; J.G., S.D.B., and A.V.A. performed research; Y.E.N., T.A.S., and A.V.A. contributed analytic tools; Y.E.N., J.G., and S.D.B. analyzed data; and Y.E.N., T.A.S., J.G., and A.V.A. wrote the manuscript.

Editor: James Sellers.