Characterization of Zebrafish Cardiac and Slow Skeletal Troponin C Paralogs by MD Simulation and ITC

Abstract

Zebrafish, as a model for teleost fish, have two paralogous troponin C (TnC) genes that are expressed in the heart differentially in response to temperature acclimation. Upon Ca²⁺ binding, TnC changes conformation and exposes a hydrophobic patch that interacts with troponin I and initiates cardiac muscle contraction. Teleost-specific TnC paralogs have not yet been functionally characterized. In this study we have modeled the structures of the paralogs using molecular dynamics simulations at 18°C and 28°C and calculated the different Ca²⁺-binding properties between the teleost cardiac (cTnC or TnC1a) and slow-skeletal (ssTnC or TnC1b) paralogs through potential-of-mean-force calculations. These values are compared with thermodynamic binding properties obtained through isothermal titration calorimetry (ITC). The modeled structures of each of the paralogs are similar at each temperature, with the exception of helix C, which flanks the Ca²⁺ binding site; this region is also home to paralog-specific sequence substitutions that we predict have an influence on protein function. The short timescale of the potential-of-mean-force calculation precludes the inclusion of the conformational change on the ΔG of Ca²⁺ interaction, whereas the ITC analysis includes the Ca²⁺ binding and conformational change of the TnC molecule. ITC analysis has revealed that ssTnC has higher Ca²⁺ affinity than cTnC for Ca²⁺ overall, whereas each of the paralogs has increased affinity at 28°C compared to 18°C. Microsecond-timescale simulations have calculated that the cTnC paralog transitions from the closed to the open state more readily than the ssTnC paralog, an unfavorable transition that would decrease the ITC-derived Ca²⁺ affinity while simultaneously increasing the Ca²⁺ sensitivity of the myofilament. We propose that the preferential expression of cTnC at lower temperatures increases myofilament Ca²⁺ sensitivity by this mechanism, despite the lower Ca²⁺ affinity that we have measured by ITC.

Introduction

Ectothermic species tolerate a range of acute and seasonal temperatures through plasticity in protein function and changes in gene expression (1, 2). Central to this tolerance is the maintenance of cardiac function across a range of temperatures. The optimal temperature for ectothermic zebrafish (Danio rerio) lies between 25°C and 28°C (3); however, D. rerio cardiac function must be maintained through daily seasonal and geographic temperature fluctuations between 6°C and 38°C (3). Many species of fish, including D. rerio, increase their heart rate up to twofold per 10° increase in temperature in response to acute temperature fluctuations (4, 5, 6, 7, 8, 9, 10, 11). The adaptation to acute temperature changes occurs more quickly than transcriptional changes can account for. Long-term temperature acclimation confers greater tolerance through altered composition of the cardiomyocyte transcriptome, which includes critical proteins of the contractile apparatus such as members of the troponin complex (1, 12).

The cardiac troponin (cTn) complex contains three proteins: cardiac troponin C (cTnC), a Ca²⁺ sensor protein; cardiac troponin I (cTnI), an inhibitory protein; and cardiac troponin T (cTnT), which tethers the complex to the remainder of the thin filament by interacting with tropomyosin (13). cTnC is a two-domain protein with four EF-hand motifs designated as sites I through IV. Site I does not bind Ca²⁺, site II is responsible for the Ca²⁺-sensing function of cTnC, and sites III and IV have a structural role and always bind Ca²⁺ or Mg²⁺ under physiological conditions (14). The bulk-phase cytosolic Ca²⁺ concentration increases from ∼100 nM during diastole to a maximum of 1 μM in systole (15). As the cytosolic Ca²⁺ concentration increases, the regulatory site II of cTnC is bound by Ca²⁺, which leads to a conformational change that exposes a hydrophobic patch. This hydrophobic patch then interacts with cTnI and allows the cTnI inhibitory peptide to withdraw from the actin filament (13). The cTnC-Ca²⁺ binding interaction also interrupts the cTnT-tropomyosin interaction, permits actin/myosin cross-bridge formation, and initiates muscle contraction.

Several structures have been solved for the cTnC protein, including the N-terminal domain of human cTnC in the Ca²⁺-bound (PDB: 1AP4) and Ca²⁺-free (PDB: 1SPY) (16) forms, and in complex with the cTnI switch peptide (PDB: 1MXL) (17), with TnI (PDB: 1J1D), and with TnT (PDB: 1J1E) (18). The N-terminal domain of trout cTnC has also been solved at 7°C (1R6P) and 30°C (PDB: 1R2U) (19). Under similar conditions, these structures differ minimally. The addition of Ca²⁺ causes a slight change in the cTnC structure, although the angle between helices A and B and the status of the hydrophobic patch are unchanged (16). The trout cTnC at 7°C closely resembles mammalian cTnC at 30°C, which suggests a common structure at their respective physiological temperatures (19).

The cardiac contractile element is less sensitive to Ca²⁺ at lower temperatures, an effect that is not observed in skeletal muscle (20, 21). This desensitizing effect was rescued in mammalian cardiomyocytes by introducing four fish-TnC specific amino acid substitutions, Asn2, Ile28, Gln29, and Asp30 (NIQD) (22). The increased sensitivity was attributed to an allosteric effect on the ability of site II of cTnC to bind Ca²⁺ (19), which allows a lower cytosolic Ca²⁺ concentration to trigger cardiac contraction at lower temperatures. A structural explanation was elusive, as there were no obvious differences between the human cTnC structure and that with the NIQD substitutions introduced (23). Because these residues are in the N-helix and hydrophobic patch of cTnC, regions that interact with the other members of the cTn complex (18), the NIQD substitutions may stabilize the Ca²⁺-bound, open conformation of cTnC in the complex.

The fish contractile element adjusts to temperature change in part through the differential expression of a slow-skeletal TnC (ssTnC or TnC1b) variant (1, 24). The slow-skeletal paralog differs from the cardiac paralog (cTnC or TnC1a) at 18 out of 161 amino acid positions. Interestingly, the ssTnC paralog is missing one of the four NIQD residues, where asparagine 2 is replaced by aspartic acid, which is found at that position in mammals (1). The ssTnC paralog in D. rerio is the result of a tandem gene duplication event. Although many redundant duplicate genes are lost, in some cases the ancestral gene function is divided between the duplicates. This process, referred to as subfunctionalization (25), results in the retention of functional paralogs in the genome (26).

The ability of ssTnC to rescue cardiac contraction in a cTnC knockout in D. rerio embryos indicates that the D. rerio TnC paralogs have some overlap in function (24). When D. rerio are acclimated to 18°C, cTnC is expressed preferentially in both chambers of the heart, whereas after 28°C acclimation, the ssTnC is upregulated and becomes the dominantly expressed form in the atrium. ssTnC expression in the ventricle is also increased after 28°C acclimation, but does not supersede cTnC expression (1). The differential expression of TnC paralogs is consistent with a temperature-dependent functional difference.

In this study, we report the thermodynamic properties of the interaction between Ca²⁺ and D. rerio cTnC and that between Ca²⁺ and D. rerio ssTnC at 18°C and 28°C. The TnC-Ca²⁺ interaction was found to be endothermic and entropy driven, similar to the case for human cTnC (27). The ssTnC-Ca²⁺ interaction, measured by isothermal titration calorimetry (ITC), is stronger at both temperatures, despite very limited structural deviation between the simulation-based structural models. Potential-of-mean-force (PMF) calculations, which do not sample the conformational change, yield similar ΔG values for the two paralogs at 28°C and a lower ΔG for ssTnC at 18°C. This discrepancy is resolved through the use of long (μs)-timescale simulations, during which the cTnC protein more readily transitions from the closed to the open state, an unfavorable process that produces lower Ca²⁺ affinity as measured by ITC. We propose that the temperature-dependent change in myofilament Ca²⁺ sensitivity that is expected as a function of paralog selection is dictated by the favorability of the TnC conformational change, which transduces the Ca²⁺ binding signal to the myofilament, rather than the affinity of the regulatory domain of TnC for Ca²⁺.

Materials and Methods

Homology modeling and equilibrium molecular dynamics simulations

The initial models for the TnC constructs were generated using the Swiss-model Workspace (28). These models used the NMR-derived Ca²⁺-bound or Ca²⁺-free N-terminal domain of the human cTnC structure (PDB:1AP4 or PDB: 1SPY, respectively) as a template. Models were built for the N-terminal domain of the cardiac and slow-skeletal paralogs of TnC.

The resulting models were equilibrated with GROMACS 4.6.5 (29), using the AMBER99-sb-ILDN (30) force field. The simulation system was defined as a periodic “cubic” box and was prepared as described in Table S1 in the Supporting Material using the TIP3P water model (31). This was followed by steepest-descent energy minimization to a tolerance of 10 kJ mol⁻¹ nm⁻¹ and conjugate gradient energy minimization for 10,000 steps. The minimized system was restrained with 1000 kJ mol⁻¹ nm⁻¹ absolute position restraints on all of the nonsolvent atoms and equilibrated for 1 ns. The restrained simulations were held at 28°C or 18°C using V-rescale temperature coupling (32) and isotropic Berendsen pressure coupling (33) with a τ_T of 0.1 and τ_P of 1.0, respectively. Interactions were calculated using PME electrostatics (34) and the Verlet cut-off scheme (35). Bond lengths were constrained using the LINCS algorithm (36). Production simulations were done in five replicated 100 ns NPT simulations with no position restraints; other parameters were carried forward from the position-restrained simulations. Long-timescale simulations were identical, with the exception that the run time was extended to 1 μs and snapshots were saved every 100 ps. Simulations of the open conformation of the TnC molecule were stabilized in the open conformation by the presence of the TnI_SW peptide, as described in Genge et al. (37).

The final models were produced by clustering with the Daura algorithm (38) over the backbone and Cβ atoms of each structure across the five trajectory replicates of each paralog-temperature combination; the middle structure of each of the largest clusters from each mutant simulation was used for further analysis. Protein structure superimpositions were performed with VMD (39), and structural quality assessments were carried out using RAMPAGE (40), QMEAN (41), WHATCHECK (42), and MOLPROBITY (43). Quality statistics may be found in Tables S1–S4. Interhelical angles were measured using interhlx (44) over each replicated simulation. Similarly, the hydrophobic solvent-accessible surface areas (h-sasa) of the TnC molecules were calculated with g_sas over each simulation and averaged (45). The TnI_SW was excluded from the complex simulations for the h-sasa calculations of TnC in the open conformation. The number of hydrogen bonds in TnC was calculated with g_hbond, which uses a cutoff radius of 3.5 Å and a 30° angle to enumerate donor/acceptor pairs; these values were averaged over each simulation.

Free-energy calculations

The Ca²⁺-bound TnC model was placed in a “cubic” box with dimensions 6 nm × 6 nm × 15 nm, solvated, and neutralized as in Table S1. This was followed by steepest-descent energy minimization to a tolerance of 10 kJ mol⁻¹ nm⁻¹ and conjugate gradient energy minimization for 1000 steps. The minimized system was restrained with 1000 kJ mol⁻¹ nm⁻¹ absolute position restraints on all of the nonsolvent atoms and equilibrated for 1 ns.

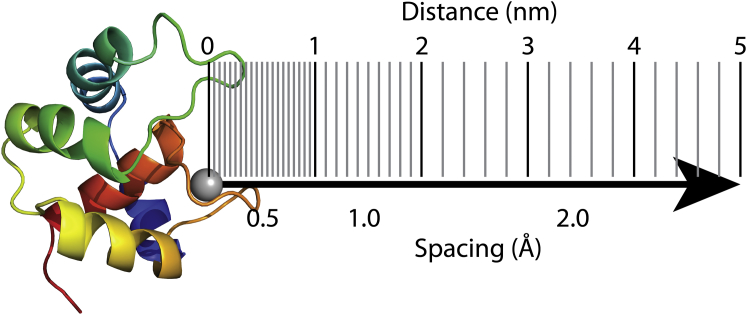
The initial conformations for umbrella sampling were generated as follows: protein α-helical Cα atoms were restrained in three dimensions with a potential with a force constant of 1000 kJ mol⁻¹ nm⁻¹, and the site II Ca²⁺ were restrained only in the y and z dimensions to permit the movement of the ion. A constraint pulling force was applied in the x dimension at 0.001 nm ps⁻¹. Windows for umbrella sampling were extracted from the resulting trajectory at distance intervals of 0.5 Å between 0 and 1 nm, every 1 Å between 1 nm and 2 nm, and every 2 Å between 2 nm and 5 nm.

Umbrella sampling and the weighted-histogram analysis method

Umbrella simulations were run as above, with no restraining potentials aside from the umbrella potential between the Ca²⁺ ion and the center of mass of the α-carbons of the TnC molecule. These simulations used the same parameters as the pull simulations, with the pull rate set to 0, and were run for 30 ns. Analysis was performed using g_wham (46) and the first 5 ns of each sampling window simulation were discarded; errors were estimated with 10,000 bootstraps of the weighted-histogram analysis method of calculation.

Protein expression and purification

Synthetic codon-optimized genes (GeneArt, Regensberg, Germany) encoding full-length D. rerio cTnC (gi 28822163) and ssTnC (gi 50344824) were cloned into the pET-21a(+) expression vector (Novagen, Madison, WI), and the codon corresponding to residue 90 was replaced with a stop codon using the Phusion site-directed mutagenesis protocol (Thermo Scientific, Waltham, MA) to generate N-TnC constructs. The resulting constructs were verified by DNA sequencing and transformed into the Escherichia coli BL21(DE3) expression host strain.

Overnight cultures were diluted 20-fold into lysogeny broth and incubated at 37°C with shaking at 250 rpm. Cultures were induced at OD₆₀₀ = 0.8 with a final concentration of 1 mM isopropyl β-D-1-thiogalactopyranoside followed by 3 h of growth. Cells were harvested by centrifugation, resuspended in 20 mL of 50 mM Tris-HCl pH 8.0, 5 mM EDTA, 1 mM phenylmethylsulfonyl fluoride, and one “c0mplete” protease Inhibitor tablet (Roche, Basel, Switzerland). The cells were lysed by sonication on ice at 80% amplitude using ten 30 s pulses at 30 s intervals. Lysate was clarified by centrifugation at 30,000 × g for 30 min and the supernatant was applied to a fast-flow diethylaminoethyl cellulose column (GE Healthcare, Little Chalfont, UK) equilibrated with 50 mM Tris-HCl, pH 8.0, 5 mM EDTA, and 1 mM dithiothreitol and eluted with a 180 mL gradient between the equilibration buffer and the high-salt buffer comprised of equilibration buffer and 0.55 M NaCl. Fractions containing the TnC protein were pooled and concentrated to 5 mL using an Amicon centrifugal concentrator with a MWCO of 3,000 Da (Millipore, Billerica, MA). The concentrated protein was applied to a HiPrep 26/60 Sephacryl S-100 column (GE Healthcare) equilibrated with 50 mM Tris-HCl pH 8.0, 100 mM NaCl, and 1 mM dithiothreitol. Fractions containing the TnC protein were pooled, concentrated, and stored at −80°C.

Melting-point determination

Protein solutions in the apo state were dialyzed four times against 2 L of MT buffer (150 mM KCl, 10 mM HEPES, pH 7.5, 3 mM MgCl₂, and 2 mM EGTA). Ca²⁺-saturated TnC was dialyzed and diluted similarly with MT buffer supplemented with 3 mM of CaCl₂.

Each melting-temperature replicate contained 3 mg·mL⁻¹ of TnC and 2.5 μL of 100× diluted sypro orange. Temperatures were increased from 4°C to 95°C at 5-s intervals on a CFX96 Touch Real-Time PCR System (BioRad, Hercules, CA). The melting temperature of the protein was determined at the minimum of the first derivative curve, which represents the midpoint of the unfolding transition.

Isothermal titration calorimetry

Protein solutions were dialyzed three times against 2 L of ITC buffer (50 mM HEPES, pH 7.2, and 150 mM KCl) and diluted to a final concentration of 200 μM. Buffers were supplemented with 15 mM, 15 mM, and 2 mM, respectively, of β-mercaptoethanol. Initial buffer contained 2 mM EDTA to generate TnC in the apo state with two subsequent exchanges to remove the EDTA. Concentration was determined using an extinction coefficient of 1490 M⁻¹ cm⁻¹ and a molecular mass of 10.1 kDa. The Ca²⁺ solution was prepared in the dialysis buffer from the final exchange to a final Ca²⁺ concentration of 4 mM. Ca²⁺ was titrated into the protein solution in a series of 19 injections of 2 μL (the first being a dummy injection of 0.4 μL), 2 min apart, with a stirring speed of 1000 rpm. These experiments were repeated at 18°C and 28°C. The heat of dilution of Ca²⁺ into buffer was estimated by averaging three data points after the protein was saturated with Ca²⁺. The average of these three points was subtracted then from the Ca²⁺-protein titration curve. Data were analyzed with Origin 8.0 (OriginLab, Northampton, MA).

Results

Homology models

After 100 ns of simulation, each of the modeled systems had diverged from the starting coordinates (Figs. S1–S4). The middle structure of the largest cluster for each paralog at each temperature was selected as representative for further analysis. The quality indicators for the representative structures used in the PMF calculations may be found in Tables S2–S5.

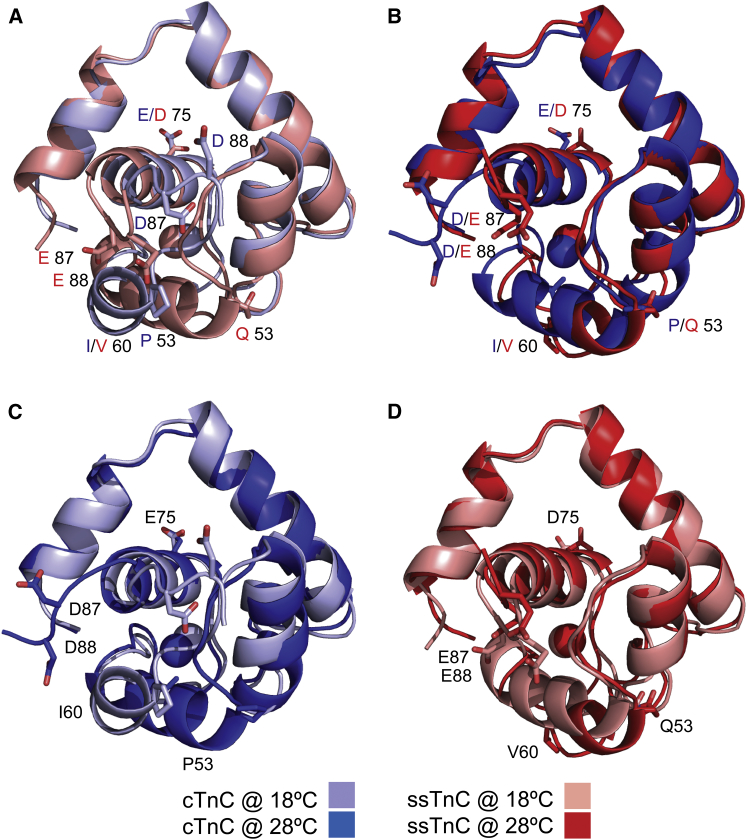
The structures of the equilibrated homology models are very similar to each other, except in their length and orientation of helix C (Fig. 1). Helix C immediately follows the Ca²⁺-binding site II, and changes in this helix may affect the Ca²⁺ interaction. Helix C contains two sequence substitutions between the TnC paralogs: proline 54 in cTnC is replaced with a glutamine in ssTnC, and isoleucine 61 in cTnC is replaced with a valine in ssTnC. The secondary structure is variable between paralog temperature combinations, with helical lengths that vary by up to four residues in the case of helix C (Fig. 2). The difference in orientation of helix C was the greatest between the paralog-temperature combinations. In cTnC at 18°C, helix C is nearly antiparallel to helix D at 153°, whereas in the other representative structures, helices C and D are at angles of 128°, 123°, and 112° for ssTnC at 28°C, ssTnC at 18°C, and cTnC at 28°C, respectively.

Figure 1.

Superimposed structures of the equilibrated representative structures after Daura clustering using backbone and β-carbon atoms during 100-ns equilibration trajectories. Residues that differ between paralogs are labeled. (A) cTnC (light blue) and ssTnC (salmon) at 18°C. (B) cTnC (blue) and ssTnC (red) at 28°C. (C) cTnC at 18°C (light blue) and 28°C (blue). (D) ssTnC at 18°C (salmon) and 28°C (red). The differences between these structures are minimal, but they are most pronounced in the orientation of helix C relative to the remainder of the protein. To see this figure in color, go online.

Figure 2.

Sequence alignment of cTnC and ssTnC, highlighted to visualize the changes in secondary structure after equilibration at each temperature and energy minimization. The most salient change is in helix C, and it is likely due to the temperature-dependent effect of the P55Q, I61V, and E75D substitutions on the stability of helix C and its interaction with helix D. To see this figure in color, go online.

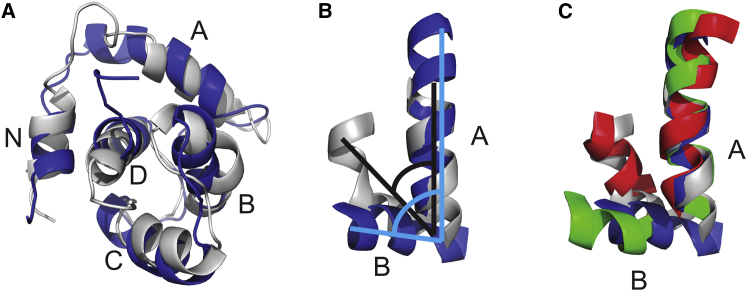
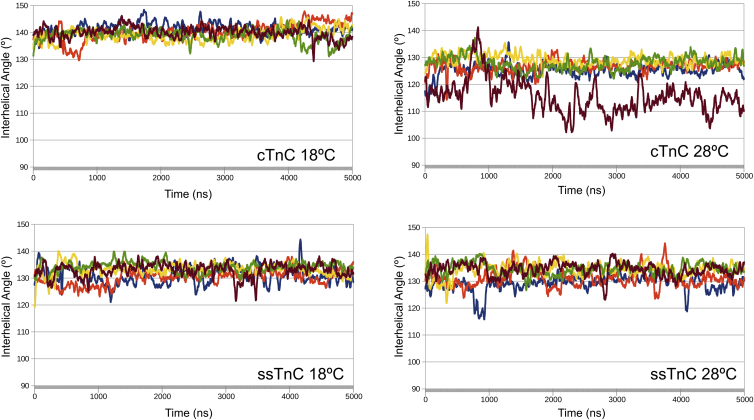
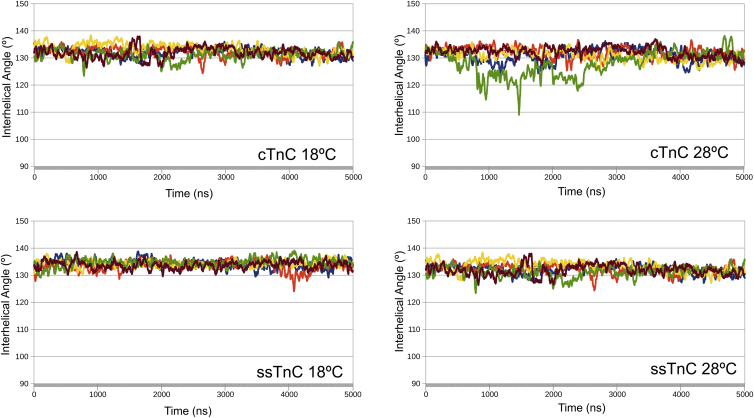
AB interhelical angles were monitored over the course of each simulation. None of the structures reached the open state, defined by an AB interhelical angle below 90° (Fig. 3). During the five replicated 1 μs simulations, the TnC structures at 28°C each had several frames in an intermediate state: seven frames were below 105° in the Ca²⁺-free simulations, whereas 359 frames were below 105° in the Ca²⁺-bound simulations (Figs. 4 and 5). There was a single frame that contained a structure of the ssTnC molecule with an AB interhelical angle below 105° (Table S6).

Figure 3.

(A) Superimposition of snapshots from the 1-μs simulation of cTnC at 28°C, with helices labeled N, A, B, C, and D. The most open conformation from this simulation is shown in blue and the most closed conformation is shown in white. (B) Angles are drawn onto the superimposed and isolated A and B helices. (C) The helices are superimposed with equivalent structures from the NMR-derived human cTnC structures in the Ca²⁺-free, closed form (PDB: 1SPY), shown in red, and in the open conformation in complex with the TnI switch peptide (PDB: 1MXL), shown in green. To see this figure in color, go online.

Figure 4.

The AB interhelical angle over time for 1 μs simulations of TnC + Ca²⁺ at each temperature, plotted as a 25 ns rolling average. To see this figure in color, go online.

Figure 5.

The AB interhelical angle over time for 1 μs apo-TnC simulations at each temperature, plotted as a 25 ns rolling average. To see this figure in color, go online.

When the h-sasa of each structure at each temperature was calculated, there were only slight differences as a function of temperature or sequence substitution; however when the h-sasa were calculated for either the cardiac or slow-skeletal TnC molecule isolated from the TnC/TnI complex and therefore in the open conformation, the average h-sasa of cTnC at 28°C increased by 4.9 nm², whereas the average h-sasa of ssTnC at 28°C increased by 4.1 nm² as a result of the closed-to-open transition. At 18°C, the closed-to-open transition increased the h-sasa by 4.2 nm² and 4.6 nm² for cTnC and ssTnC, respectively. This is in contrast to the effect of Ca²⁺ binding, which had little effect on the average h-sasa of either paralog at each temperature (Table 1).

Table 1.

Average Hydrophobic Solvent-Accessible Surface Area over the Final 50 ns of Five Replicated 100 ns Simulations

	18°C (Ca2+-Bound)	28°C (Ca2+-Bound)	18°C (Ca2+-free)	28°C (Ca2+ free)	18°C (Open)	28°C (Open)
cTnC	22.3 ± 0.4	21.8 ± 0.5	22.6 ± 0.6	22.4 ± 0.7	26.5 ± 0.9	26.8 ± 0.5
ssTnC	21.0 ± 0.5	20.8 ± 0.7	20.8 ± 0.8	21.5 ± 0.5	25.6 ± 0.9	25.0 ± 0.8

Surface area (nm²).

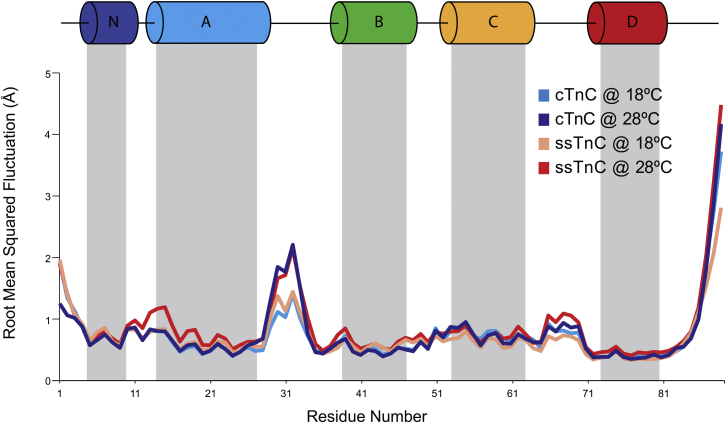
The flexibility of the paralog-temperature combinations is similar (Fig. 6), as represented by the root mean-square fluctuation (RMSF) of each Cα atom sampled over the final 10 ns of each of the simulations and averaged over five replicated simulations. The numbers of hydrogen bonds are identical for the Ca²⁺-free TnC molecules but are increased by ∼1 hydrogen bond in each paralog-temperature combination in the Ca²⁺-bound state (Table 2).

Figure 6.

Average RMSFs per residue (n = 5) are plotted for the final 50 ns of each 100 ns simulations for the paralog-temperature combinations. The protein is most flexible at the termini and EF-hand loops. There is limited variability in RMSFs between paralog-temperature combinations, which suggests that the sequence differences do not greatly influence the protein flexibility. There is a slight effect of temperature on flexibility in the loop regions between helices A and B, as well as in the loop between helices C and D. To see this figure in color, go online.

Table 2.

Average Number of Hydrogen Bonds in Each Structure over the Final 100 ns of Five Replicated 1 μs Simulations for Ca²⁺-Bound and Ca²⁺-free Models of cTnC and ssTnC

	18°C (Ca2+-Bound)	28°C (Ca2+-Bound)	18°C (Ca2+-free)	28°C (Ca2+-free)
cTnC	62.0 ± 1.6	61.0 ± 1.3	60.9 ± 0.6	60.6 ± 1.0
ssTnC	61.8 ± 0.8	61.3 ± 1.6	60.9 ± 1.4	60.6 ± 1.2

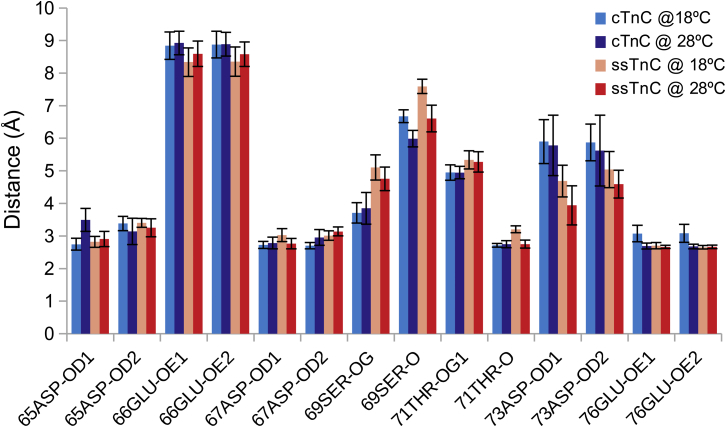
The coordination distances for the Ca²⁺ ions were measured for each of the side-chain ligand atoms, as well as any nearby potential substitutes (Fig. 7). There was very little difference between paralog-temperature combinations, particularly in the distances between ligand atoms that are involved in coordination of the Ca²⁺ ion.

Figure 7.

Ca²⁺ coordination distances for each paralog-temperature combination. Residues that may offer substitute ligands are also included. The distances are similar for the two paralogs at both temperatures. Ser69-OG is slightly closer to the Ca²⁺ ion in the cTnC simulations, whereas Asp73-OD1 is slightly closer to the Ca²⁺ ion in the ssTnC simulations. To see this figure in color, go online.

Free-energy calculations

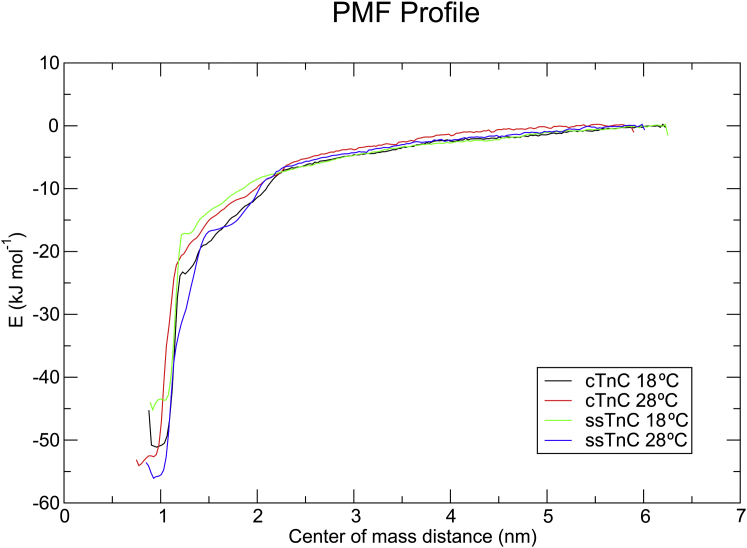
The change in free energy for each of the paralog temperature combinations was determined using PMF calculations (Fig. 8). The PMF profile is plotted in Fig. 9. The free-energy differences indicate little variance between the paralogs at 28°C (−55.5 ± 4.1 kJ mol⁻¹ and −58.0 ± 2.7 kJ mol⁻¹ for cTnC and ssTnC, respectively), whereas at 18°C, cTnC has a higher ΔG of Ca²⁺ interaction than ssTnC (−51.4 ± 3.6 kJ mol⁻¹ vs. −45.5 ± 3.0 kJ mol⁻¹).

Figure 8.

PMF reaction coordinate. The Ca²⁺ ion is removed from the site II binding loop along the x axis. Vertical lines indicate the frequency of PMF sampling windows over the reaction coordinate. Sampling windows were arranged at 0.5 Å below 1.0 nm distance, 1 Å between 1.0 and 2.0 nm, and 2 Å between 2.0 and 5.0 nm. To see this figure in color, go online.

Figure 9.

WHAM-derived umbrella potentials for each temperature-paralog combination. The plots for the two paralogs appear to overlap at each temperature; however, the values at low center-of-mass distance reach minima at different points. At 28°C, the ΔG values of Ca²⁺ interaction for cTnC and ssTnC were −55.5 ± 4.1 kJ mol⁻¹ and −58.0 ± 2.7 kJ mol⁻¹, respectively. At 18°C, the ΔG of Ca²⁺ interaction was −51.4 ± 3.6 kJ mol⁻¹ for cTnC and −45.5 ± 3.0 kJ mol⁻¹ for ssTnC. To see this figure in color, go online.

Melting-point determination

The melting points (Tms) of the Apo-cTnC and Apo-ssTnC were 70.1°C and 65.9°C, respectively. The Tms of the Ca²⁺-bound forms of the proteins were ∼15°C higher in both cases at 84.9°C and 82.3°C for cTnC and ssTnC, respectively.

ITC

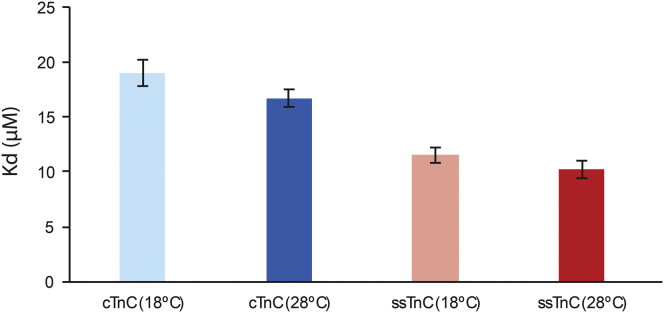
The interactions between TnC and Ca²⁺ were endothermic; in each case, the stoichiometric ratio of Ca²⁺ binding was ∼1, indicating that the regulatory site II was exclusively titrated during these experiments. Representative isotherms are available in Fig. S5. The change in entropy (ΔS) was higher for cTnC at 28°C than at 18°C, and both of these values were greater than the ΔS values for ssTnC, which did not differ significantly with temperature. The change in enthalpy (ΔH) values were greatest for the cTnC paralogs: Ca²⁺ binding to cTnC at 28°C yielded a greater ΔH in response to increased temperature, whereas the ΔH values reported for ssTnC did not differ significantly with temperature. The ΔG values were most favorable for ssTnC at 28°C, followed by ssTnC at 18°C and cTnC at 28°C, which did not differ significantly; the ΔG value for cTnC at 18°C was the least favorable. The thermodynamic parameters are listed in Table 3. The dissociation constant (K_d) value was 2.4 μM higher at 18°C than at 28°C for cTnC, whereas the K_d value for ssTnC was 1.3 μM higher at 18°C than at 28°C (Fig. 10).

Table 3.

Thermodynamic Parameters Derived from ITC for Each Paralog-Temperature Combination

	cTnC (18°C)	cTnC (28°C)	ssTnC (18°C)	ssTnC (28°C)
Kd (μM)	19.0 ± 1.2A	16.7 ± 0.8B	11.5 ± 0.7C	10.2 ± 0.8D
ΔS (J mol–1)	153.9 ± 2.1B	158.6 ± 5.0A	147.7 ± 2.9C	148.1 ± 2.1C
ΔH (kJ mol–1)	18.5 ± 0.5B	20.2 ± 1.4A	15.4 ± 0.8C	15.9 ± 0.5C
ΔG (kJ mol–1)	–26.4 ± 0.2A	–27.6 ± 0.1B	–27.5 ± 0.1B	–28.8 ± 0.2C

Analysis of variance was used to determine that a significant difference existed between mutant-temperature conditions for all four factors. Tukey’s post hoc test was carried out at the level of each factor and is indicated by superscript letters, where mutant-temperature conditions with unique letters are significantly different (p < 0.05). n = 3.

Figure 10.

Plot of the mean K_d values ± SE. cTnC has a higher K_d than ssTnC at each temperature, and at each temperature, the K_d values for each paralog are comparable, though higher at 18°C than at 28°C for each paralog. To see this figure in color, go online.

Discussion

Examination of the effect of sequence substitutions between TnC paralogs on Ca²⁺ interaction has yielded mechanistic insight into the function of TnC. When compared with wild-type human cTnC, the introduction of the fish-specific NIQD molecular phenotype to the human cTnC increases the Ca²⁺ sensitivity of myofilaments (22, 47). The explanation for the increase in sensitivity is that these sequence substitutions allosterically influence the affinity of site II for Ca²⁺. MD-based PMF analysis has shown that the Ca²⁺-binding properties are similar for the two paralogs at both temperatures, with the exception of ssTnC at 18°C, which has a lower ΔG (Fig. 9). The absolute ΔG values from MD simulations are overestimated due to the parameterization of Ca²⁺ in the MD force field and the use of nonpolarizable water; however, the reported values are reasonable as a relative measure (48). ITC measurements indicate that ssTnC has higher affinity for Ca²⁺ at both temperatures, but cTnC is more sensitive to temperature (Fig. 10).

Increased stability of the protein can be conferred by a stronger hydrophobic core or by antiparallel stacking of helices to mutually stabilize helical dipoles (49). The melting temperatures of cTnC and ssTnC indicate that the relative stability of the apo and Ca²⁺-bound forms are similar, since the melting temperature for each was increased by 15°C as a function of Ca²⁺ interaction. Paradoxically, cTnC, which is dominantly expressed at lower temperatures, has a higher melting point than ssTnC despite RMSF values that show that flexibilities of the paralogs are approximately equal (Fig. 6). The MD simulations predict that there is one additional hydrogen bond on average in the Ca²⁺-bound stateas compared to the Ca²⁺-free state, but the total numbers of H-bonds were similar between paralogs at each temperature (Table 2). The h-sasa upon Ca²⁺ binding decreased for each paralog-temperature combination, with the exception of ssTnC at 18°C, which suggests that any stabilizing effect of Ca²⁺ binding was less pronounced in that condition.

The process of Ca²⁺ binding to Ca²⁺-sensing EF-hand proteins is a balance between conformational strain and conformational change (49). The strain induced by Ca²⁺ binding is released by the unfavorable exposure of the hydrophobic patch (49). A more stable closed conformation relative to the open conformation will increase the energetic cost of the closed-open conformational change and decrease the affinity for Ca²⁺. Changes in secondary structure have been noted in response to Ca²⁺ binding of other TnC proteins through the use of CD spectroscopy; greater helical content in the Ca²⁺-bound form conferred greater stability and increased the favorability of the Ca²⁺ interaction (50, 51). The structural differences between the temperature-paralog combinations are primarily found in the length and orientation of helix C, which is adjacent to site II and alters the C/D helical interface (Figs. 1 and 2). This helix is shorter in the representative structure of ssTnC at 28°C than in the others, which suggests that the stability of this helix may be compromised at 28°C while under the conformational strain induced by Ca²⁺ binding. Helices C and D contain three sequence substitutions between cTnC and ssTnC. Residues 54, 61, and 75 are proline, isoleucine, and glutamic acid, respectively, in cTnC, which are replaced by glutamine, valine, and aspartic acid, respectively, in ssTnC. The proline-to-glutamine substitution in particular may increase affinity by destabilizing the closed conformation in ssTnC, and relieve the conformational strain through shortening of helix C. In addition, there is evidence that the I61Q substitution in human cTnC can affect the stability of the helical packing at the B/C helical interface (52).

Sequence substitutions that stabilize the open conformation of N-cTnC produce an increase in Ca²⁺ sensitivity without altered coordination of Ca²⁺ by site II. These substitutions increase the favorability of the conformational change through the release of the Ca²⁺-induced conformational strain on the tertiary structure of the protein, and they minimize the energetic penalty of the conformational change (49, 53, 54). The TnI switch peptide (TnI_SW) binds to the hydrophobic cleft and stabilizes the open conformation of TnC while simultaneously occluding the hydrophobic residues (17). In the absence of TnI_SW, TnC opening and exposure of the hydrophobic patch results in the unfavorable formation of a clathrate water shell. In the cTnC-TnI_SW system, this shell is replaced by hydrophobic interactions between N-cTnC and TnI_SW and by interactions between water and the hydrophilic side chains of the solvent-exposed portion of the TnI_SW. Many fluorescence-based measurements have been used to measure TnC Ca²⁺ affinity in the presence of the other members of the Tn complex and thin filament (53). However, the use of fluorophores such as IAANS (55, 56) or the fluorogenic F27W mutation (57) makes it possible to monitor Ca²⁺ binding by responding to the change in hydrophobicity precipitated by the conformational change, and different results are achieved with the addition of other Tn-complex and thin-filament proteins. The absence of the remainder of the Tn complex and its stabilizing effect on the open conformation of TnC thus constitutes a limitation to this work.

In a population of TnC molecules, Ca²⁺ binding leads to a shift in the equilibrium between the closed and open states, with the proportion shifting from 0% open in the apo-state to between 20% and 27% open in the Ca²⁺-bound state (58, 59). The free-energy cost of this transition has been estimated, through the use of long timescale simulations, at 8 kcal mol⁻¹ (33.5 kJ mol⁻¹) for Ca²⁺-bound human wild-type cTnC (60), which is comparable to the energy of conformational changes in other proteins, such as the ligand-binding domain of an ionotropic glutamate receptor (61) and p38α kinase (62) at 29 kJ mol⁻¹ and 50 kJ mol⁻¹, respectively. The conformational change can confound ITC measurements, as the energetics of the shift in equilibrium between the open and closed states cannot be decoupled experimentally from the Ca²⁺-binding interaction.

The disparity between the ΔG values obtained from ITC and PMF calculations may be attributed to whether the conformational change is included in the measurement. Sequence modifications that affect the relative stability of the closed or open forms, including changes to the size or degree of hydrophobicity of the hydrophobic patch or the packing of the core of the TnC molecule, will influence the affinity of TnC for Ca²⁺. MD-derived ΔG values report the affinity of site II as a function of structural differences due to sequence substitution and equilibration at each temperature, but they do not account for the thermodynamic consequences of the open-to-closed conformational change. ITC measurements of the equilibrium energy include the change in proportion of open and closed TnC molecules as a function of Ca²⁺ titration. The MD simulations presented here indicate that the ΔG of Ca²⁺ binding is similar for both paralogs at 28°C, and for cTnC at 18°C, whereas the ΔG of Ca²⁺ binding for ssTnC at 18°C is less favorable. The timescale of the PMF simulation is inadequate to sample the conformational change of the protein, and therefore, its energetic contribution cannot be included. The ΔG values collected by ITC are in the range −26.4 to −28.8 kJ mol⁻¹ (Table 3) and are similar to those reported for human cTnC, with comparable effects of temperature on binding. The free energy of the Ca²⁺-human-cTnC measured at 10°C and 25°C had ΔG values of −26.6 and −30.5 kcal mol⁻¹, respectively (27). The D. rerio TnC paralogs are much less temperature sensitive than human cTnC, as demonstrated by a 0.3 kcal mol⁻¹ increase in the ΔG of cTnC for Ca²⁺ when temperature is increased from 18°C to 28°C, but this effect is not present in ssTnC due to lower values of ΔS. The lower ΔH values in ssTnC maintain Ca²⁺ binding at a similar ΔG, despite the reduced magnitude of ssTnC ΔS.

In most species, reduced temperature causes a decrease in cardiac myofilament Ca²⁺ sensitivity, an effect that is mediated by cTnC (20, 63). In ectothermic species, cardiac function must be maintained through acute and seasonal temperature change. The differentially expressed ssTnC protein may play a role in this temperature tolerance. The D. rerio ssTnC has higher Ca²⁺ affinity at both temperatures, and its expression is increased in warm-acclimated D. rerio (1). Our work suggests that the changes in TnC Ca²⁺ binding are dictated by three residue substitutions that alter the structure of helices C and D and together modify the energetic landscape of the TnC conformational change, which exposes the hydrophobic patch less frequently in ssTnC than in cTnC. Given that higher relative Ca²⁺ sensitivity is required for survival at lower temperatures (9), and that cTnC is dominantly expressed at low temperatures (1), we expect that cTnC should have higher affinity for Ca²⁺. That is not what was found in this study. Monitoring the AB interhelical angle over 1-μs simulations has shown that the Ca²⁺-bound cTnC molecule is more amenable to conformational change than ssTnC. From this, we infer that cTnC has a less stable closed conformation than ssTnC, and is therefore less able to tolerate the conformational strain induced by Ca²⁺ binding. cTnC is more likely to transition between the closed and open states, which should create higher myofilament Ca²⁺ sensitivity while also accounting for the lower Ca²⁺ affinity we have observed by ITC. In this way, the molecular mechanism that produces higher affinity of the isolated ssTnC molecule for Ca²⁺ may contribute to the lower myofilament Ca²⁺ sensitivity needed for cardiac function at high temperatures through less frequent exposure of the hydrophobic patch (1, 22, 47). Based on the ITC and MD-simulation evidence presented here, we propose that the temperature-dependent effect of TnC paralog substitution is influenced by differences in the favorability of the TnC conformational change, which transduces the Ca²⁺-binding signal to the myofilament rather than being directly related to Ca²⁺ affinity of the TnC molecule.

Author Contributions

Preliminary Experiments, B.L., C.L., J.R., and A.Y.L.; Experimental Design, C.M.S., K.R., C.E.G., G.S., and D.P.T.; Data Collection, C.M.S., K.R., and C.E.G.; Data Analysis, C.M.S., K.R., C.E.G., G.S., and D.P.T.; Manuscript Preparation, C.M.S.; Manuscript Review, C.M.S., K.R., C.E.G., A.Y.L., G.S., D.P.T., F.v.P., and G.F.T.

Editor: David Sept.