Pericellular Brush and Mechanics of Guinea Pig Fibroblast Cells Studied with AFM

Abstract

The atomic force microscopy (AFM) indentation method combined with the brush model can be used to separate the mechanical response of the cell body from deformation of the pericellular layer surrounding biological cells. Although self-consistency of the brush model to derive the elastic modulus of the cell body has been demonstrated, the model ability to characterize the pericellular layer has not been explicitly verified. Here we demonstrate it by using enzymatic removal of hyaluronic content of the pericellular brush for guinea pig fibroblast cells. The effect of this removal is clearly seen in the AFM force-separation curves associated with the pericellular brush layer. We further extend the brush model for brushes larger than the height of the AFM probe, which seems to be the case for fibroblast cells. In addition, we demonstrate that an extension of the brush model (i.e., double-brush model) is capable of detecting the hierarchical structure of the pericellular brush, which, for example, may consist of the pericellular coat and the membrane corrugation (microridges and microvilli). It allows us to quantitatively segregate the large soft polysaccharide pericellular coat from a relatively rigid and dense membrane corrugation layer. This was verified by comparison of the parameters of the membrane corrugation layer derived from the force curves collected on untreated cells (when this corrugation membrane part is hidden inside the pericellular brush layer) and on treated cells after the enzymatic removal of the pericellular coat part (when the corrugations are exposed to the AFM probe). We conclude that the brush model is capable of not only measuring the mechanics of the cell body but also the parameters of the pericellular brush layer, including quantitative characterization of the pericellular layer structure.

Introduction

It is known that the majority of eukaryotic and Gram-negative prokaryotic cells are surrounded by a layer of polysaccharides and glycoproteins attached to the plasma membrane, sometimes called the “pericellular coat” (or “matrix”). The pericellular layer can also include some functional molecule proteins frequently referred as the “glycocalyx”. Sometime these two terms are used synonymously. The presence of a large multimicron pericellular coat was demonstrated with the help of the classical particle exclusion assay (1). Fluorescently labeled or just naturally colored fixed erythrocytes filled empty space between cells of interest (which were fluorescently labeled). The researchers observed a clear space with no fluorescence between the cell membrane and closely packed erythrocytes. This indicated the presence of some nonfluorescent layer around the cells. In the same comprehensive study (1), the researchers demonstrated the key role of hyaluronidase treatment, which entirely removed the nonfluorescent pericellular layer. Hyaluronidase is the enzyme that cleaves hyaluronan (hyaluronic acid, HA), the high-molecular-mass polysaccharide (more specifically, nonsulfated glycosaminoglycan) found in extracellular matrix, bacterial coats, and connective tissues (2). Thus, it was concluded that HA is an essential component of the pericellular coat. It has been also shown that HA is a typical part of the pericellular coat of many eukaryotic cells (2, 3, 4, 5), in particular, fibroblasts (6).

The membrane corrugations, wrinkles, and protrusions (microridges and microvilli) exist on virtually any cell that can go through mitosis. This is because the cell volume increases several times during cell division, and the membrane is stretched; the membrane protrusions serve the protective role to prevent membrane rupture during this process. It was demonstrated that the membrane corrugations are an intrinsic part of the pericellular coat (3), forming a scaffold for the HA-based pericellular coat.

The pericellular coat has an important role in many cell functions because it interacts with the environment through this layer; it influences the flow of nutrients and various controlling factors such as cell adhesion, migration, differentiation, and proliferation (7, 8). The molecular pericellular layer is known to surround neurofilaments to maintain interfilamentous spacing (9, 10). Pericellular layers (4, 11) are also known to be responsible for cell-cell interaction. The size of the pericellular coating was shown (11, 12) to correlate with the degree of invasiveness of cancer (although it is still not clear whether the brush size or the molecular composition, or possibly both, play a major role).

The most common tool to study the pericellular coat relies on the classical particle exclusion assay. The attempts to label general polysaccharides with fluorescent markers based on lectins were unsuccessful (these led to a partial collapse of the pericellular layer). To the best of our knowledge, the HA-specific fluorescent labeling efforts described in Rilla et al. (3), Boehm et al. (13), and Zhang et al. (14) were the only fluorescence studies of the pericellular coat that demonstrated the absence of the collapse of pericellular layer. Optical tweezers (15) and microrheology (13, 16, 17) were demonstrated to be powerful techniques to study pericellular coat.

Atomic force microscopy (AFM) is a quite versatile tool to detect physical presence of molecules on the cell surfaces (18, 19, 20, 21), in particular, the pericellular coat (22, 23, 24, 25, 26). It is due to a broad range of forces the AFM probe can exert on the sample surface. Quantitative methods separating the force response of the cell body from the response of the pericellular coat layer were proposed in Bai and Wang (26), Sokolov et al. (27, 28), and Dokukin et al. (29). The method proposed in Bai and Wang (26) was demonstrated for endothelial cells. It was based on the assumption that the pericellular layer and the cell body can both be treated as simple springs during AFM indentation. The errors due to this oversimplified assumption have not been estimated. A more accurate method, the brush model, developed in Sokolov et al. (27, 28), Dokukin et al. (29), Guz et al. (30), and Iyer et al. (31), was tested for epithelial cells. Its self-consistency (mostly based on the independence of the derived Young’s modulus on the indentation depth) was demonstrated (30). To the best of the authors’ knowledge, the brush model is the only one that demonstrated self-consistency when analyzing cell indentation data. Although the forces due to the pericellular layer were rather distinguishable with the brush model, and their range corresponded to the observed layer of the membrane corrugation (microridges and microvilli), it was not clear if this method is capable of detecting the glycocalyx, polysaccharide/HA part of the pericellular layer. Moreover, the brush model has never been tested for fibroblasts.

In this work, we demonstrate explicitly that the AFM force-separation curves processed through the brush model can be used to produce quantitative information about both the membrane corrugation and polysaccharide/HA parts of the pericellular layer. In addition, we further developed the brush model to make it applicable to the relatively large brush layer, larger than the height of the AFM probe. To demonstrate that the brush model can be used to measure the pericellular glycocalyx, we use guinea pig fibroblast cells. To verify the contribution of the polysaccharide/HA part of the pericellular layer to the force-separation curves, this layer was enzymatically removed using hyaluronidase. The analysis of the force-separation curves demonstrated a clear double-brush behavior of the pericellular layer. Comparing parameters of these two brush layers before and after the enzymatic removal of polysaccharide/HA part, we conclude that the large brush corresponds to the molecular polysaccharide/HA layer, while the small brush is associated with the membrane corrugation layer (which is hidden inside the big molecular layer before the treatment). It is worth noting that this conclusion is in agreement with the observation that the membrane corrugations form a scaffold for the polysaccharide/HA layer (3).

It should be noted that the AFM indentation data is analyzed here on the assumption of quasistatic deformations (so one can assign the Young’s modulus to an elastic material in such measurements). It is obviously an approximation, which is generally accepted these days (32). As was recently shown for neuron cells (33), the cell body can indeed be approximated as an elastic material (up to 10 μm/s speeds of indentation were tested), whereas the pericellular coat demonstrates a clear viscoelastic behavior. The quasistatic approximation makes sense not only because it gives self-consistent results within the brush model (30); it also allows avoiding the need to describe the dynamics of the pericellular (entropic) brush. The entropic brush cannot be characterized with such parameters as an elastic modulus at all. This is because the entropic brush is essentially nonelastic (there is no potential minimum corresponding to the brush equilibrium). The theory describing the viscoelastic properties of an entropic brush has yet to be developed.

Materials and Methods

Cells

Primary skin fibroblasts were isolated from the underarm skin of outbred multicolored guinea pigs (tissues were obtained from a frozen collection) as described in Seluanov et al. (34). Fibroblast is the main cell type producing extracellular matrix in connective tissues. The extracellular matrix holds the tissues together and provides tissue elasticity. Glycocalyx plays an important role in controlling malignant transformation and metastasis. The hyaluronic acid synthesis and degradation process is often perturbed in cancerous cells. The experiments were performed on cells at a low passage number (population doubling 4–10). Cells were grown at 37°C, 5% CO₂, and 5% O₂ on treated polystyrene culture dishes (Corning, Corning, NY) using Eagle’s Minimum Essential Medium supplemented with 15% fetal bovine solution (Gibco/Thermo Fisher Scientific, Waltham, MA) and 1% Penicillin-Streptomycin solution (Gibco/Thermo Fisher Scientific) for 1–2 days. Cells were transported to the AFM lab in flasks (Corning) filled with culture media, overnight without freezing. The amount of the growth medium in the flasks was close to the maximum possible to avoid mechanical damaging of cells during transportation. After receiving, the excessive medium was removed (only 10 mL of the media was kept in each flask). Flasks with cells were placed in an incubator at 37C (5% CO₂) for 12–16 h to let cells relax after transportation. Before the AFM imaging, the top side of the culture bottles was removed. The AFM study was done directly in the medium on the cells attached to the bottom of the culture bottle. A relatively large amount of the medium insured safety of the cell during imaging (run for ∼3 h; no statistical differences between the cell parameters derived from the measurements in the beginning and at the end of the experiments were noted). The study of this work was done on cells close to confluency.

Hyaluronidase treatment of cells

Ten units of hyaluronidase enzyme were added to the 10 mL of cell growth media to achieve the concentration of 1 unit/mL. (One unit of hyaluronidase activity, 1U, is defined as the concentration that causes a change in absorbance/scattering of hyaluronidase at 600 nm of 0.330 per min at pH 5.7 at 37°C in a 2.0 mL reaction mixture.) The original growth medium was substituted with the prepared hyaluronidase-media solution. The treatment was done for 12 h in an incubator at 37C (5% CO₂). All samples were gently washed with a fresh cell growth medium before the AFM imaging.

Confocal fluorescence/Raman microscopy

A confocal Raman microscope (WITec, Ulm, Germany) was used for three-dimensional imaging of cells. A 50× water-immersing objective was used. A 488-nm laser was used for the signal excitation. Lipid membrane was fluorescently labeled with Red Nile dye. The pericellular coat was highlighted with the help of ultrabright fluorescent silica 30-nm nanoparticles (Excitation: 488 nm; Emission: 545 nm), synthesized as described in Cho et al. (35, 36). The particles were used with no further functionalization (having a positively charged surface with Z-potential of 15–20 mV).

Atomic force microscopy

Dimension 3100 and Dimension Icon atomic force microscopes (Bruker Nano/Veeco, Billerica, MA) with Nanoscope V controllers and NPoint close-loop scanners (200 × 200 × 30 μm, X,Y,Z) were used in this study. It is important to use such a large Z-range close loop scanner because of the need to detect a rather large brush layer. Standard cantilever holders for operation in liquids were employed. To obtain the distribution of the properties over the cell surface and simultaneously record cell topography, the force-volume mode of operation was utilized. The force curves were collected with the vertical ramp size of 22 μm. To minimize viscoelastic effects, force-indentation curves were recorded with a frequency of 1.1 Hz (with approach vertical speed of 27 μm/s and retract speed of 140 μm/s). The force-volume images of cells were collected with the resolution of 32 × 32 pixels within a 120 × 120 μm² area.

AFM probe: spherical indenter

Standard V-shaped arrow 200-μm AFM tipless cantilevers (Veeco, Santa Barbara, CA) were used throughout the study, and 5-μm-diameter silica balls (Bangs Laboratories, Fishers, IN) were glued to the cantilevers as described in Berdyyeva et al. (37). The radius of the probe was measured by imaging the inverse grid (Cat. No. TGT1; NT-MDT, Zelenograd, Russia). The cantilever spring constant was measured using the thermal tuning method.

Data processing notes

The models described in the next section were developed for a known geometry such as a sphere over either a plane, a hemisphere, or another sphere. Therefore, we consider only the force curves from the top area of cells (following the previous works (28, 31, 38), we take the force curves in the surface points around the top when the incline of the surface is <10–15°). To identify such curves, the cell height image was used (this image was collected as a part of the force-volume data set). The radius of the cell curvature was derived from these images after correcting the cell heights for deformations (see the Supporting Material for details). A nonlinear curve fitting of corresponding equations allows deriving both the elastic modulus of the cell body and parameters of the pericellular brush (length and grafting density).

Statistical analysis

Statistical analysis was done by using one-side ANOVA test and the confidence level p > 0.05.

AFM modeling of the cell coated with the pericellular brush

It was found that the cell cannot be described as an elastic material when analyzing the force-separation curves collected on living cells (30). The reason for that was attributed to the presence of the essentially nonelastic layer surrounding the cell body, i.e., the pericellular (brush) layer. (The word “brush” was added to stress a distinguishable exponential force dependence attributed to this layer (28), which was similar to a classic entropic brush behavior described with the Alexander de Gennes model (39).) Entropic brushes are held in equilibrium by a nonconservative energy of thermal motion, and therefore do not have the parabolic potential that is a characteristic of any elastic material. As a result, it is impossible to assign the concept of the elastic modulus to this layer in a self-consistent way. However, it was demonstrated that the underlying cell body can still be described as a homogeneous isotropic material (30). The brush model used for that purpose has demonstrated the ability of unambiguous separation between the elastic properties of the cell body and force signature of the pericellular brush layer. This model was described in detail, e.g., in Sokolov et al. (27). Below, we briefly outline the key steps of this model needed for calculation of the brush parameters.

Two-layer model

A two-layer model (later called a “brush” model) was proposed in Sokolov et al. (27, 28) and Iyer et al. (31). It was shown that by separating deformations of the pericellular brush and elastic response of the cell body, one can derive the elastic modulus of the cell body in a self-consistent way (30). Specifically, when the indentation was smaller than 10–20% of the cell body height, the cell body demonstrated behavior consistent with a homogenous and isotropic medium. This model is described in detailed in Sokolov et al. (27, 40), Dokukin et al. (29), and Iyer et al. (31). Here we briefly outline the key steps of this model.

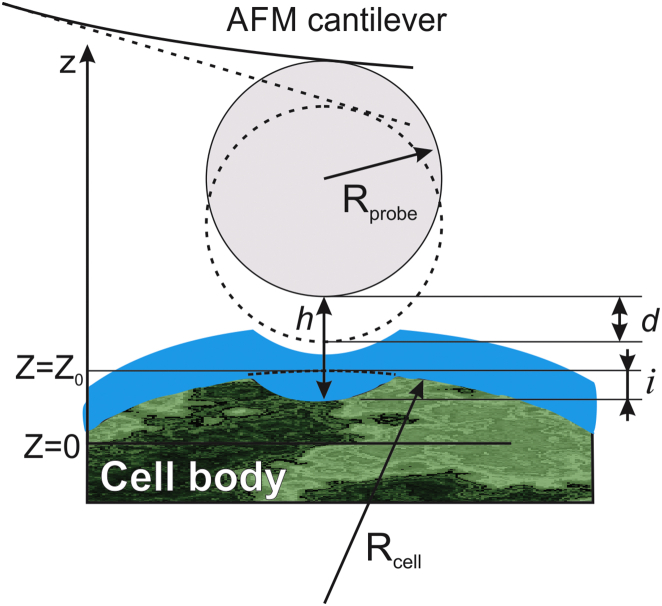
Fig. 1 shows a geometrical schematic of the AFM indentation of a cell body surrounded by the pericellular brush layer. The distance between the cell body and the spherical indenter can be described by the following equation:

$$h=Z-Z_0+i+d,i={\left[\frac{3k\left(1-{\nu }^2\right)}{4E}{\left(\frac{R_{\text{probe}}+R_{\text{cell}}}{R_{\text{probe}}\times R_{\text{cell}}}\right)}^{1/2}\right]}^{2/3}{d}^{2/3},$$ (1)

where Z represents the relative vertical scanner position of the cantilever, d is the cantilever deflection, Z₀ is the undeformed position of the cell body, i is the deformation of the cell body, Z = 0 at the maximum cantilever deflection d, h is the separation between the cell body and AFM probe, E is the elastic modulus of the cell body, ν is the Poisson ratio (hereafter ν = 0.3 is used in this work), and R_probe and R_cell are the radii of curvature of the AFM probe and cell, respectively. Note that R_cell has been measured from the AFM topographical image of the cell obtained in the force-volume mode, and corrected by the cell deformation i (see the Supporting Material for details.)

Figure 1.

A geometrical schematic of the AFM indentation of a cell body surrounded by the pericellular brush layer. The cell is represented as a two-layer structure (pericellular brush and cell body). To see this figure in color, go online.

It is assumed that the pericellular brush layer is softer than the cell body. Then it is possible to reach the load force when the brush layer is almost squeezed (h = 0). It was shown that reaching the residual brush size of ∼10% of its uncompressed value was sufficient within the accuracy of the model. (The value of the load force in the described experiments corresponding to such brush compression is on the order of 2–4 nN.) The elastic modulus E of the cell body is calculated by fitting the deflection-versus-cantilever position data for the region above the squeezed brush threshold (shown in Fig. 4 a) with Eq. 1, in which h = 0. (It is worth noting that up to this point that the only assumption about the brush layer was its “brushy” behavior of having zero Poisson ratio when being squeezed.)

Figure 4.

An example of the analysis of AFM force curves with the brush model. (a) Black circles are the experimental data showing measured deflection of the cantilever versus vertical position of the AFM scanner (d versus Z). The purple circles show the region used to fit Eq. 3 of the brush model to extract E and Z₀. The extrapolated curve from the brush model with h = 0 is shown as a dashed purple line. The red circles show the region of the experimental curve used to fit with the Hertz model. The extrapolation of the traditional Hertz model (which does not take into account the brush layer) is shown as a dotted red line. (b) Measured indentation force versus calculated AFM probe-cell separation distance. The solid (red and green) lines show the fit with the exponential force formulas (Eqs. 2 and 8). (c) Typical dependence of the elastic modulus on the indentation depth. To see this figure in color, go online.

Single- and double-brush models; the case of large pericellular brush

Extrapolating Eq. 1 to the smaller forces that are below the brush-squeezed threshold, one can obtain the force due to the pericellular brush layer from the experimental data. One can see the results of such extrapolation in Fig. 4 a and b of this work. Once plotted in logarithmic scale, a good portion of this force dependence can be approximated with a straight line, which corresponds to the exponential force dependence. One of the known exponential dependence measures of a molecular brush is presented by the Alexander-de Gennes model for an entropic polymer brush (39). Utilizing Derjaguin approximation, one can obtain the force due to the steric repulsion of the entropic brush acting between a spherical probe of radius R_probe and a semispherical cell of radius R_cell (27, 41, 42):

$$F_{\text{single}\text{brush}}=100k_{\text{B}}T{R}^{\ast }{N}^{3/2}{e}^{-\frac{2\pi h}{L}}L,$$ (2)

where k_B is the Boltzmann constant, T is the temperature, $R^{\ast }=\left(R_{\text{probe}}\times R_{\text{cell}}\right)/\left(R_{\text{probe}}+R_{\text{cell}}\right)$, N is the surface density of the brush constituents (effective molecular grafting density), and L is the equilibrium size of the brush layer. Fitting the data with Eq. 2 can only be done within the limits of its applicability, 0.1 < h/L < 0.8. (It should be noted that the coefficient of 100 in this formula is a correction of a previously used factor of 50 that was historically miscalculated.)

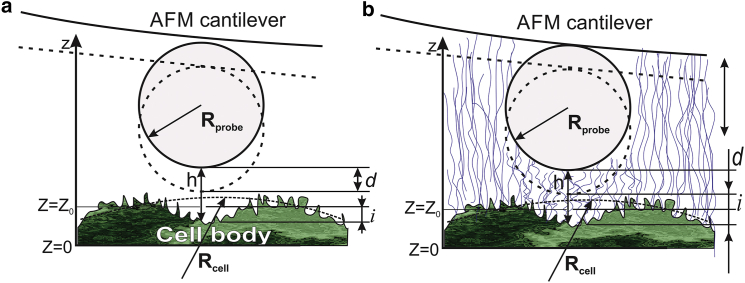
Some of the force curves (see Fig. 4 b) demonstrate double slope behavior in logarithmic scale. This can presumably be explained by the presence of two brush layers, one inside the other. This situation is schematically shown in Fig. 2. The single-brush model described by Eq. 2 is shown in Fig. 2 a. In this case, the brush layer is exampled by corrugations of the cell membrane. The situation when there are two brushes is shown in Fig. 2 b. In such a case, it is exampled by the same small brush as well as a larger brush layer that consists of HA-based pericellular molecules. A longer (and assumedly softer) brush together with a shorter (assumedly more rigid) brush can be described by a simple sum of two brush forces:

$$F_{\text{double}\text{brush}}\approx 100k_{\text{B}}T{R}^{\ast }\left[N_1^{3/2}\text{exp}\left(-2\pi h/L_1\right)L_1+N_2^{3/2}\text{exp}\left(-2\pi h/L_2\right)L_2\right],$$ (3)

where N₁, L₁ and N₂, L₂ are the parameters of the larger and smaller brush, respectively.

Figure 2.

Schematics of the AFM probe deforming (a) single- and (b) double-brush layers on the top of the cell body. According to the conclusion of this work, the single brush is a corrugation of cell membrane, whereas an additional hyaluronan-based pericellular coat creates the second, longer brush. To see this figure in color, go online.

It should be noted that Eq. 3 has been already suggested to describe the double-brush approximation in Iyer et al. (31) and Sokolov et al. (40). However, this formula was described previously for quite a different situation. This formula was applied to describe the force averaged over the cell surface that presumably had a heterogeneous brush consisting of two characteristic lengths and grafting densities. The situation considered in this work is different because we do not observe a noticeable heterogeneity of the brush response. Equation 3 is now applied to each individual force curve without averaging over the different positions on the cell surface. Nevertheless, we assume that Eq. 3 is valid here because of substantial difference between the lengths and grafting densities of two brushes (see Results and Discussion).

Brush equations for the case of large pericellular brush

When one processes the experimental force-separation force curves on the cells used in this article (see the next section), one can see that the size of the (larger) brush can be noticeably larger than the height of the AFM probe (5 μm in our case). Therefore, we need to modify Eqs. 2 and 3 to take into account a possible additional repulsion due to the interaction of the brush with the AFM cantilever itself.

The total steric repulsive force between AFM probe and the cell surface can be estimated as a sum of two forces. The first force is the one acting between the spherical probe and the cell, and the second one is the force between the cell surface and the cantilever excluding the area of the AFM probe. The first term of this sum is the force defined by Eq. 2. The second term is defined using the methodology of the Derjaguin approximation. The force per unit area f between two parallel surfaces, one of which is coated with a brush, can be approximated by (43, 44)

$$f\approx 100k_{\text{B}}T{N}^{3/2}\text{exp}\left(-\frac{2\pi h}{L}\right),$$ (4)

where N is the surface density of the brush constituents (effective molecular grafting density), and L is the equilibrium size of the brush layer.

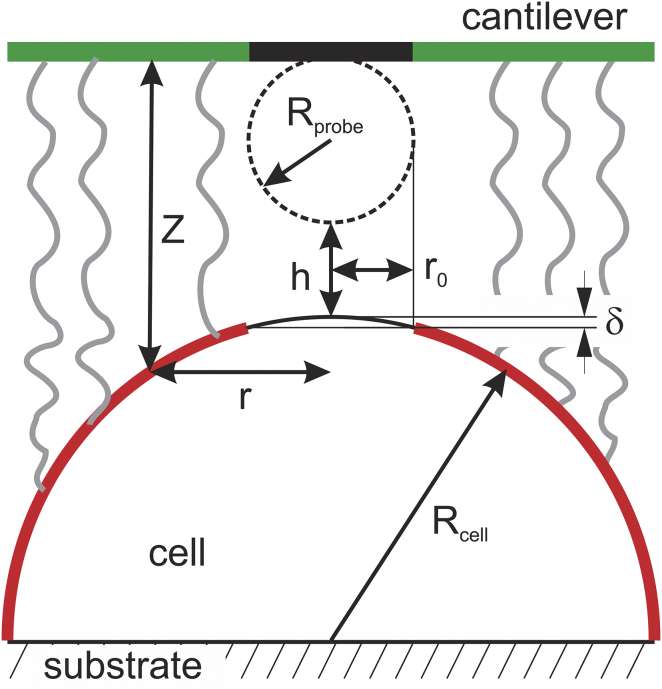
The repulsive force between the cell and AFM cantilever can be found by integrating force (4) over the cell surface directly opposite to the cantilever (highlighted with red in Fig. 3). It should be noted that we assumed that the cantilever is parallel to the substrate. In reality, the AFM cantilever is slightly tilted. Even if we take into account the cantilever deflection, it is still tilted and the angle of 5–10°. This can easily be taken into account by appropriate adjustment of the integrals. However, it would result in complicated integrals that are not taken analytically. It would make nonlinear data fitting extremely complicated. An estimation shows that the error of calculation of the force due to this approximation is <3% for the parameters considered in this work. Thus, the cantilever tilt will be ignored. For a rotationally symmetric case, the cross-sectional area of integration is equal to $2\pi r\text{d}r$, where r is the radius of the cell at a given distance Z from the cantilever (see Fig. 3). Thus, the total additional force acting on the cantilever is then given by

$$F_{\text{additional}}\approx 2\pi \underset{r_0}{\overset{\infty }{\int }}fr\text{d}r=2\pi \underset{h+2R_{\text{probe}}+\delta }{\overset{\infty }{\int }}f\left(Z\right)r\frac{\text{d}r}{\text{d}z}\text{d}z.$$ (5)

If the shape of the cell near its top is parabolic, it is described as $Z-h={r^2/2R}_{\text{cell}}$, where R_cell is the effective radius of the cell near the top. Thus, $\text{d}r/\text{d}z$ = $R/r$. Combining Eqs. 4 and 5, one obtains

$$F_{\text{additional}}\approx 100k_{\text{B}}T{R}_{\text{cell}}{N}^{3/2}\underset{h+2R_{\text{probe}}+\delta }{\overset{\infty }{\int }}{e}^{-\frac{2\pi Z}{L}}\text{d}z=100k_{\text{B}}T{R}_{\text{cell}}{N}^{3/2}{e}^{-\frac{2\pi \left(h+2R_{\text{probe}}+\delta \right)}{L}}L.$$ (6)

Finally, the total force between AFM probe and cell surface in the case of the large (single) brush is given by

$$F_{\text{Large}\text{single}\text{brush}}=100k_{\text{B}}T{R}^{\ast }{N}^{3/2}{e}^{-\frac{2\pi h}{L}}L+100k_{\text{B}}T{R}_{\text{cell}}{N}^{3/2}{e}^{-\frac{2\pi \left(h+2R_{\text{probe}}+\delta \right)}{L}}L.$$ (7)

If we are dealing with a double brush and the larger brush L₁ > 2R_probe, the AFM probe-cell force can now be written as

$$F_{\text{Large}\text{double}\text{brush}}=100k_{\text{B}}T{R}^{\ast }\left[N_1^{3/2}{e}^{-\frac{2\pi h}{L_1}}{L}_1+N_2^{3/2}{e}^{-\frac{2\pi h}{L_2}}{L}_2\right]+100k_{\text{B}}T{R}_{\text{cell}}{N}_1^{3/2}{e}^{-\frac{2\pi \left(h+2R_{\text{probe}}+\delta \right)}{L_1}}{L}_1,$$ (8)

where index 1 is assigned to the large brush. In both equations, $\delta =R_{\text{cell}}-\sqrt{R_{\text{cell}}^2-R_{\text{probe}}^2}$.

Figure 3.

Schematics of the interaction between a large brush and the AFM cantilever. Repulsive force between the cell surface and cantilever was estimated by integrating force over the cell surface that directly faced the cantilever (marked by red and green, respectively). To see this figure in color, go online.

Note that $R_{\text{cell}}>R_{\text{probe}}$ for all cases observed in this work.

Results and Discussion

As a general note about the type of force curves collected for processing, we used only the force curves from the top area of a cell. This is necessary because the Hertz contact model is applicable to two spherical contacts deforming each other along the line connecting their centers. Although a model in which the load force is applied differently can be developed, it has not been done as of yet to the best of the author’s knowledge. Here, following the previous works (29, 30, 31, 37, 38), we take the force curves in the surface points around the top when the incline of the surface is <10–15°. To identify such curves, the AFM image of cell heights was used (the height image was collected as a part of the force-volume data set; the effective radius of the cell was derived from these images after taking into account the cell deformation calculated with Eq. 1.

Fig. 4 shows the results of fitting typical force-curve data. Dark circles show the examples of experimental data. The fit of the elastic deformation of the cell body is shown with purple circles in Fig. 4 a. The dashed purple curve shows the extrapolation of Eq. 1 from the cell-body-fit region to smaller forces (cantilever deflection d) while keeping h = 0. One can see the deviation of such extrapolation from the experimental data due to the presence of the pericellular brush layer. With the parameters E and Z₀ derived from the cell-body-fit region, we can now calculate the cell-AFM probe separation h for any values of the relative vertical scanner position Z (Eq. 1). The force due to the pericellular brush layer can now be found by inverting h(d) in Eq. 1 and using $F\left(h\right)=kd$. The examples of such force curves are shown in Fig. 4 b.

It is worth noting that the traditional Hertz model can in principle be used to fit the raw data without taking into account the brush layer (as done in many articles). However, the extrapolation of this model to low values of Z or larger forces would almost immediately deviate from the experimental data. A typical example is shown in Fig. 4 a. The region of initial contact is fitted with the Hertz model (the fitting region is shown with red circles). The extrapolation beyond the fitted region is presented with a dashed red curve. One can clearly see the deviation from the Hertz model. Any attempt to assign the elastic modulus to a cell for those small forces/deformations would result in values of the modulus that are strongly dependent on the load force (indentation depth). This makes the Hertz model inconsistent because it is built based on the assumption of constancy of the Young’s modulus. At the same time, the constancy of the elastic modulus should be expected for small indentations because any elastic material should demonstrate the linear stress-strain response for sufficiently small deformations, and consequently, allow for a good fitting with the Hertz model. As we described in the Introduction, this is observed because the pericellular brush layer is an essentially nonelastic material that cannot be described by means of moduli of elasticity (see Guz et al. (30) for more detail). Contrary to such behavior, the Young’s modulus is virtually independent of the indentation depth in the case of the brush model described here. Fig. 4 c shows self-consistency of the calculation of the elastic modulus by demonstrating the dependence of the derived elastic modulus on the indentation depth.

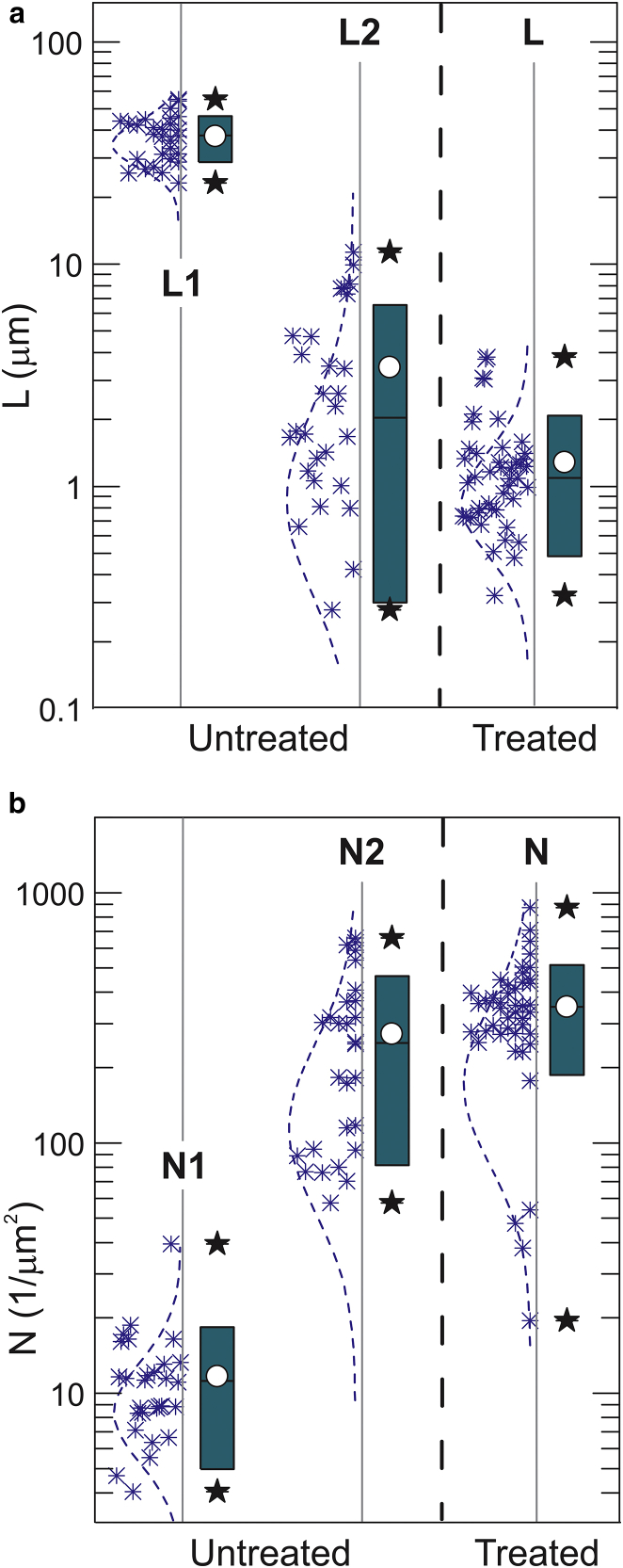
As was suggested in Sokolov et al. (27, 28) and Iyer et al. (31) and described in the Materials and Methods, the pericellular brush layer can be described with such parameters as the equilibrium brush size L and effective grafting density N. Although the pericellular brush was investigated in the previous works for the force curve fitting, it would be more convincing if we demonstrated that these force curves (at least partially) indeed correspond to the pericellular polysaccharides layer surrounding fibroblast cells. To demonstrate it, we cleave the polysaccharide part of the pericellular coat with the help of hyaluronidase. The results of processing of the AFM data with the simple single brush model are shown in Fig. 5 for both cells before and after hyaluronidase treatment. The statistical data processed for 26 cells before the treatment and 44 cells after the treatment are shown.

Figure 5.

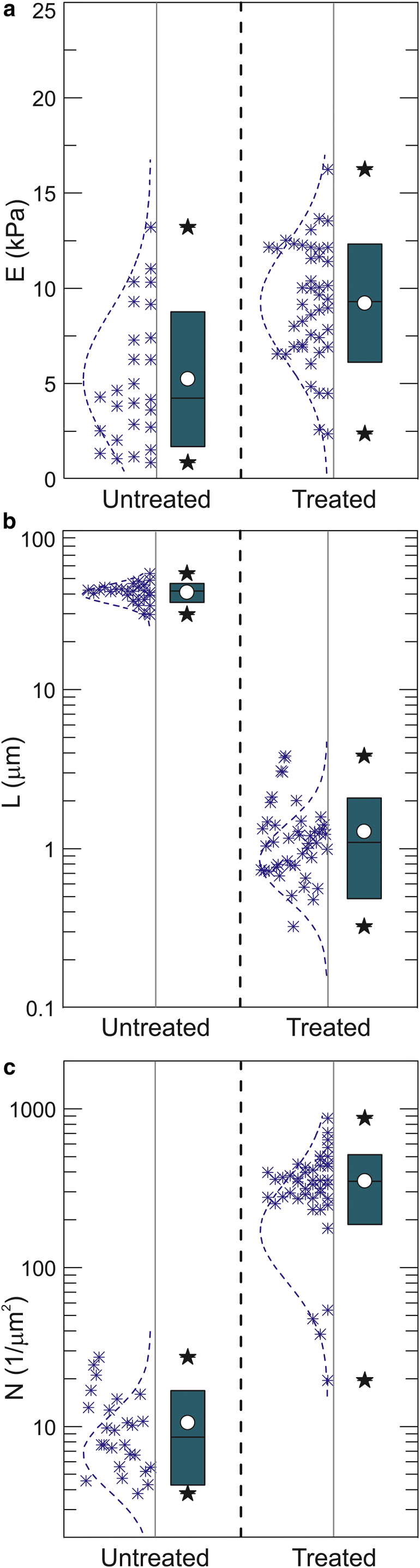
The results of the AFM measurements of cells before and after hyaluronidase treatment. The force curves were processed with the single brush model. (a) The elastic modulus, (b) the length of the pericellular brush, and (c) effective grafting density of the brush are shown. The box height stands for 1 SD at approximately the mean value (white circle); the bar stands for the median; and stars show 10–90% of the distribution. To see this figure in color, go online.

One can clearly see a substantial decrease of the brush length (∼41 times). One can also see the increase of the effective grafting density of the remaining brush layer after the treatment (∼12×). The elastic modulus also changes, although not as significantly as the pericellular brush layer; it increases from 5.4 before to 9.3 kPa after the treatment (significant at p > 0.05).

To process the data shown in Fig. 4, we used the single-brush model (Eq. 2) for the shorter brush and Eq. 7 for the longer brush. However, the majority of the pericellular bush force curves collected from cells before the treatment (Fig. 4 b) show a double-tilt straight lines behavior (in log scale). It corresponds to the double-brush behavior described by Eqs. 3 and 8. Fig. 6 shows the results of the processing of the same data as the one used for Fig. 4, but the force curves collected on cells before the treatment are now processed through the double-brush model (Eq. 8). It should be noted that this new, to our knowledge, data analysis is applied to the processing of the brush layer force only. It does not change the processing of the mechanical response of the cell body. So the elastic modulus of the cell body stays the same when processing with the double-brush model.

Figure 6.

The results of the AFM measurements of cells processed with the double-brush model (untreated cells) and with the single-brush model (cells after the hyaluronidase treatment). (a) Lengths of the pericellular brush; (b) effective grafting densities of the brush. The box height stands for 1 SD at approximately the mean value (white circle); the bar stands for the median; and stars show 10–90% of the distribution. To see this figure in color, go online.

One can see that the double brush, which is seen on the cells before the treatment, consists of two hierarchical brush scales: a large brush (average length of 38 ± 9 μm; grafting density of 11 ± 4 μm⁻²) and a small brush (length of 3.0 ± 3.1 μm; grafting density of 270 ± 190 μm⁻²). Note that the length of the small brush demonstrates a clear non-Gaussian distribution, and therefore, the concept of average and SD are used here as effective for the ease of comparison. One can see that the single brush seen on the cells after the treatment (length of 1.1 ± 0.8 μm; grafting density of 350 ± 160 μm⁻²) is rather similar to the small brush observed before the treatment. Some decrease of the smaller brush should be expected because when the AFM probe squeezes the larger brush to detect the internal small brush, the latter should be decorated with the squeezed molecules of the larger brush. This effectively should increase the size of the smaller brush.

Fig. 7 presents representative confocal fluorescence/Raman optical images of a cell and its pericellular coat. Fig. 7 a shows a vertical profile of the distribution of lipids in a cell, which highlights the lipid pericellular membrane. One can see the surface membrane corrugation of the order of single microns, which is comparable to the size of the internal (smaller) brush. This membrane’s corrugations are presumably the microridges and microvilli reported previously in Sokolov et al. (27, 28), Dokukin et al. (29), Guz et al. (30), and Iyer et al. (31).

Figure 7.

Confocal/Raman images of vertical-cell cross sections. (a) Distribution of lipids in the cell; corrugation of the lipid membrane boundary is seen. (b) Distribution of fluorescent positively charged fluorescent silica nanoparticles are shown above the cell surface; monotonic decrease of the particle’s density seen away from the cell surface is indicative of the decrease of the density of negatively charged HA molecules away from the cell surface. To see this figure in color, go online.

Visualization of the HA pericellular layer is less straightforward. There is a host of literature describing the use of fluorescent dyes to label the HA pericellular layer for endothelial cells (2, 12, 15, 45), in which the HA layer has a rather well-defined boundary. Imaging of the HA layer on fibroblasts seems not to be as straightforward as on endothelial cells. A rather good fitting of the entropic brush model, which was demonstrated in this work, implies that the density of this layer is not constant and monotonically decreases away from the cell body. As a result, it is practically impossible to define the physical border of this layer unambiguously. To demonstrate it, we used bright fluorescent silica nanoparticles that have a positively charged surface. Because HA molecules are negatively charged, the silica particles should electrostatically highlight the HA layer. Fig. 7 b shows an example of the vertical distribution of such particles near the cell surface at 20 min after adding the particles to cells in PBS medium. Fig. 7 b shows a combined fluorescent/Raman image of the culture dish cell and the pericellular cell layer. The bottom layer shows the presence of polystyrene (the material of the culture dish, 134 cm⁻¹ Raman peak), the lipids are highlighted with Red Nile dye (peak intensity at 640 nm), and the density of silica nanoparticles is defined by the intensity of their fluorescence (maximum peak at 545 nm). One can clearly see a monotonic decrease of the fluorescent density of nanoparticles. This is an indication of the decrease of density of HA layer when moving away from the cell surface. (In the case of constant density, the top of the HA layer should be brighter because the particles are entering from the PBS buffer from the top.) More detailed profiles of the fluorescent brightness distribution of silica nanoparticles in the vicinity of cells are shown in Fig. S2 in the Supporting Material, for several times after adding the silica particles. Those profiles are indicative of a rather large extension of the HA layer, which is comparable with numbers shown in Figs. 5 and 6. It should also be noted that a comparable size of HA layer was demonstrated for human lung fibroblast cells (6) (it was also shown there that the size of the HA layer depends on the cell environment).

Based on these results, we can speculate that the brush of treated cells is the small brush that was hidden inside the large brush of untreated cells, which presumably consists of the membrane corrugation decorated with hyaluronic molecules. This is schematically shown in Fig. 8. The small brush seen before the treatment (with the help of the double-brush model) and after the treatment (revealed by using the single-brush model) is presumably the membrane corrugation. This certainly does not exclude the existence of other glycosaccharides and proteins of glycocalyx attached to the cell membrane that survived the hyaluronidase treatment; however, the study of those is beyond the scope of this work.

Figure 8.

A schematic of a double pericellular brush of cells before and after the hyaluronidase treatment. To see this figure in color, go online.

It should be noted that the idea of hyaluronidase-sensitive surface coats attached to membrane protrusions was proposed in Rilla et al. (3) (though they meant quite large protrusions that were found using phase-contrast and optical microscopy). Specifically, the authors showed that slender membrane protrusions in different orientations are a common feature in hyaluronan-secreting cells and that the protrusions form a scaffold for the hyaluronan coat. They also noted that the size of the membrane protrusions was decreased after hyaluronidase treatment. This is in good agreement with our observation. Although the grafting density of the membrane protrusion remains statistically the same after the treatment, its length changes statistically significantly (from ∼3 to ∼1 μm). It is also worth noting that the size of this layer is in good agreement with the thickness of the microvilli layer reported previously (1–5 μm) (13, 28, 29, 31, 46).

Conclusions

Here we demonstrated that the AFM indentation method can be used to extract information about the pericellular brush. This was done by using Guinea pig fibroblast cells. The AFM probe cells’ indentation force curves were analyzed with the help of the brush model, which separates the force contribution of the cell body and the pericellular brush layer. The force curves were collected over both untreated fibroblast cells and cells treated with hyaluronidase to remove hyaluronic content of the pericellular brush. We found that the force signature of the pericellular brush layer changes dramatically after the treatment. The brush-model analysis shows that the pericellular brush of cells before treatment is well described with an extended brush model (i.e., double brush). The analysis shows two brushes, a large one (of 38 ± 9 μm in size, 11 ± 4 μm⁻² grafting density) and a small, much denser one (length of 3.0 ± 3.1 μm; of 270 ± 190 μm⁻² grafting density). After the treatment, we see only one brush with the length of 1.1 ± 0.8 μm and grafting density of 350 ± 160 μm⁻², which is rather similar to the small brush observed before the treatment. We can speculate that the small dense brush consists of membrane protrusions (microvilli and microridges) and maybe the nonhyaluronic part of glycocalyx. This is in agreement with confocal optical measurements as well as the observations previously reported in the literature.

To conclude, we presented the AFM indentation method combined with brush models that can be used to measure both the elastic moduli of cells and the parameters of the pericellular brush layer. When using the double-brush model, it seems to be possible to obtain information about hierarchical structure of pericellular brush layer, to distinguish between the large molecular coat and the membrane protrusion part of the pericellular brush layer.

Author Contributions

I.S. and V.G. designed and supervised the work; Y.A. and A.S. prepared samples; M.D. and I.S. developed theory; V.K. and M.D. conducted the AFM measurements and processed the data; I.S., V.G., and M.D. analyzed the data; V.K., M.D., and I.S. prepared figures; I.S. drafted the article; and all authors discussed the results and commented on the article.

Editor: Christopher Yip.