A systematic framework for exploring the long-term dynamics of a reaction network is applied to a minimal model of ERK regulation that distinguishes both monophosphorylated forms and allows for nonzero enzyme processivity. Bistability and oscillations can be observed at high levels of processivity.
Abstract
Multisite phosphorylation cycles are ubiquitous in cell regulation systems and are studied at multiple levels of complexity, from molecules to organisms, with the ultimate goal of establishing predictive understanding of the effects of genetic and pharmacological perturbations of protein phosphorylation in vivo. Achieving this goal is essentially impossible without mathematical models, which provide a systematic framework for exploring dynamic interactions of multiple network components. Most of the models studied to date do not discriminate between the distinct partially phosphorylated forms and focus on two limiting reaction regimes, distributive and processive, which differ in the number of enzyme–substrate binding events needed for complete phosphorylation or dephosphorylation. Here we use a minimal model of extracellular signal-related kinase regulation to explore the dynamics of a reaction network that includes all essential phosphorylation forms and arbitrary levels of reaction processivity. In addition to bistability, which has been studied extensively in distributive mechanisms, this network can generate periodic oscillations. Both bistability and oscillations can be realized at high levels of reaction processivity. Our work provides a general framework for systematic analysis of dynamics in multisite phosphorylation systems.
INTRODUCTION
Multisite phosphorylation cycles are ubiquitous in cell regulation systems (Lim et al., 2014). A canonical example of such a cycle is provided by the mechanism controlling the enzymatic activity of the extracellular signal-regulated kinase (ERK), an important model for studies of enzyme kinetics in cells (Shaul and Seger, 2007; Futran et al., 2013). Activation of ERK requires phosphorylation at two sites, tyrosine and threonine, within the so-called activation sequence (Payne et al., 1991; Canagarajah et al., 1997). Both sites can be phosphorylated by mitogen-activated protein kinase kinase (MEK), a dual-specificity enzyme that is essential for ERK activation in vivo (Burack and Sturgill, 1997; Ferrell and Bhatt, 1997). Both ERK and MEK exist in two isoforms in mammalian cells (ERK1/2 and MEK1/2); however, the isoforms are functionally redundant (Frémin et al., 2015; Aoidi et al., 2016). ERK activation can be reversed by multiple ERK phosphatases, including PP2A (Ferrigno et al., 1993; Alessi et al., 1995), PAC1 (Ward et al., 1994; Yi et al., 1995), PTP-SL (Hendriks et al., 1995; Ogata et al., 1995; Sharma and Lombroso, 1995; Shiozuka et al., 1995; Pulido et al., 1998), HePTP (Saxena et al., 1999), MKP1 (Keyse and Emslie, 1992; Alessi et al., 1993; Sun et al., 1993; Lewis et al., 1995), MKP2 (Guan and Butch, 1995; King et al., 1995; Misra-Press et al., 1995), MKP3 (Groom et al., 1996; Mourey et al., 1996; Muda et al., 1996), and MKP4 (Dowd et al., 1998), which can dephosphorylate one or both of the sites phosphorylated by MEK (Sohaskey and Ferrell, 1999; Zhao and Zhang, 2001; Zhou et al., 2002).
A large number of similar cycles, with varying numbers of phosphorylation sites and reaction mechanisms, were discovered by studies of intracellular networks and are actively being studied at multiple levels of complexity, from individual molecules and single reactions to organisms (Caunt et al., 2008; Salazar and Höfer, 2009; Kim et al., 2011; Prabakaran et al., 2011; Humphreys et al., 2013). The ultimate goal of these studies is to establish an integrative view of biochemical reactions in vivo, needed for predicting the effects of genetic and pharmacological perturbations of protein phosphorylation networks. For instance, activating mutations in MEK can lead to both developmental abnormalities and cancers, and drugs directly inhibiting MEK are being used in the clinic (Anastasaki et al., 2009; Caunt et al., 2015; Jindal et al., 2015). Understanding the organism-level effects of such mutations and drugs requires systematic analysis of the functional properties of multisite phosphorylation cycles and is essentially impossible without mathematical models (Qiao et al., 2007; Salazar et al., 2010; Ferrell and Ha, 2014; Piala et al., 2014; Prabakaran et al., 2014).
Several models of phosphorylation cycles have received considerable attention from mathematicians and computational biologists (Yang et al., 2004; Salazar and Höfer, 2006; Manrai and Gunawardena, 2008; Kapuy et al., 2009; Thomson and Gunawardena, 2009; Aoki et al., 2011, 2013; Harrington et al., 2012; Conradi and Mincheva, 2014a, b; Hell and Rendall, 2015b; Suwanmajo and Krishnan, 2015). Most of these models do not discriminate between different partially phosphorylated forms and focus on two limiting mechanisms of multisite phosphorylation: processive and distributive (Figure 1, B and C). In a processive mechanism, all of the phosphorylation (or dephosphorylation) reactions happen in one enzyme–substrate binding event (Patwardhan and Miller, 2007). In a distributive mechanism, the catalytic step is followed by rapid dissociation of a partially phosphorylated substrate, and subsequent reactions require a new binding event. Of interest, multisite phosphorylation cycles formed by these two types of mechanisms appear to have qualitatively different systems-level properties. In particular, when the mechanism is processive, the network has a unique steady state for all values of model parameters (Conradi and Shiu, 2015). In contrast, models of cycles formed by distributive mechanisms admit multistability, a regime in which multiple stable steady states, with different relative amounts of the substrate phosphoforms, coexist for the same set of parameters (Wang and Sontag, 2008; Thomson and Gunawardena, 2009; Hell and Rendall, 2015a). A handful of studies have explored the systems-level properties of networks containing both limiting reaction mechanisms as reaction channels (Verdugo et al., 2013; Suwanmajo and Krishnan, 2015).
FIGURE 1:
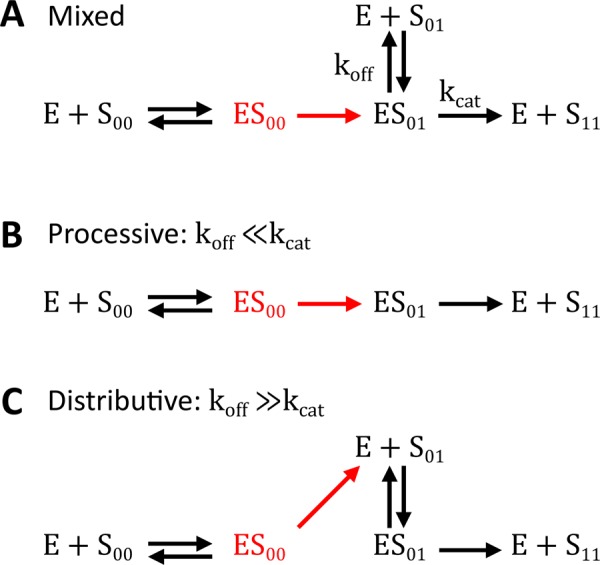
Mixed, processive, and distributive mechanisms. S00, S01, and S11 denote unphosphorylated, monophosphorylated, and bisphosphorylated forms of the substrate, respectively. (A) In our model, dual phosphorylation and dephosphorylation are assumed to occur by a mixed mechanism. Processive and distributive mechanisms are limiting cases of the mixed mechanism. (B) In a processive mechanism, the same enzyme phosphorylates the substrate twice, without dissociating. This corresponds to the limit where  for the complex of enzyme and monophosphorylated substrate. (C) In a distributive mechanism, upon the first phosphorylation event, the enzyme–substrate complex dissociates immediately, allowing the molecules to find new binding partners. This corresponds to the limit where
for the complex of enzyme and monophosphorylated substrate. (C) In a distributive mechanism, upon the first phosphorylation event, the enzyme–substrate complex dissociates immediately, allowing the molecules to find new binding partners. This corresponds to the limit where  for the complex of enzyme and monophosphorylated substrate.
for the complex of enzyme and monophosphorylated substrate.
Much less is known about the general properties of models that both allow the network to operate in the regime between the processive and distributive limits (Figure 1A) and explicitly account for the existence and differential reactivities of different partially phosphorylated forms. Here we use a combination of computational approaches to explore the long-term dynamics in such a model, which is motivated by structural and kinetic studies of ERK regulation. Our approach is readily applicable to a broad class of multisite phosphorylation networks.
RESULTS
Our analysis is based on a mathematical model that is motivated by biochemical studies of ERK regulation. The model describes a perfectly mixed reaction system consisting of ERK, MEK, and MKP3, a dual-specificity phosphatase that dephosphorylates both the tyrosine (Y) and threonine (T) sites within the activation sequence of ERK. Previous studies established that both MEK and MKP3 follow an ordered mechanism (Haystead et al., 1992; Zhao and Zhang, 2001). Specifically, tyrosine is the first site phosphorylated by MEK, and phosphotyrosine (pY) is the first site dephosphorylated by MKP3. As a consequence of this strict order, the unphosphorylated and bisphosphorylated ERK molecules (denoted by TY and pTpY, respectively) give rise to two distinct monophosphorylated forms: the first phosphorylation of ERK leads to tyrosine-phosphorylated ERK (TpY), and the first dephosphorylation of bisphosphorylated ERK leads to threonine-phosphorylated ERK (pTY). At the same time, both of the monophosphorylated forms of ERK can act as substrates for both enzymes (Figure 2A).
FIGURE 2:
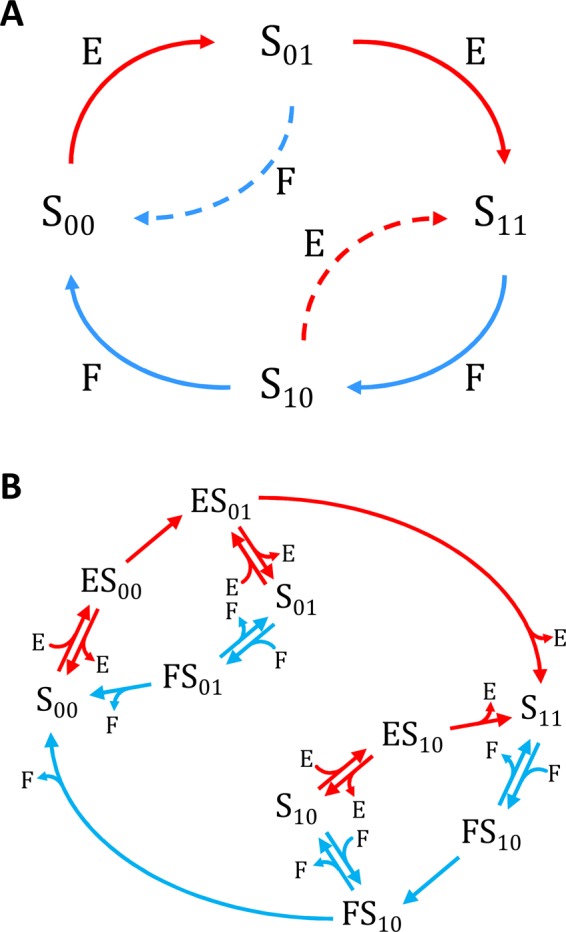
Reaction network (A) and reaction mechanism (B) in the minimal model of ERK regulation by MEK and MKP3. Table 1 gives rate constants associated with each reaction step in B.
The minimal network accounting for these interactions is closely related to the networks considered in two earlier studies. Specifically, Markevich et al. (2004) considered a network with one extra reaction, which resulted from assuming that ERK phosphorylation by MEK follows a random mechanism. Their analysis demonstrated that this network can be bistable. As a consequence of this bistability, continuous variations in the relative levels of kinase and phosphatase can trigger a sharp and irreversible transition between fully unphosphorylated and bisphosphorylated ERK states. Almost a decade later, as a part of computational analysis of circadian rhythms (unrelated to ERK regulation), Jolley et al. (2012) analyzed dynamics in a network with one more reaction, corresponding to a random dephosphorylation mechanism. On the basis of extensive sampling of model parameters, these authors established that their network can generate self-sustained oscillations, a dynamic regime in which the relative levels of different phosphorylated forms change periodically in time. Thus, the two studies most closely related to the network in Figure 2 considered models with one or two extra reactions. As shown later, our results establish that bistability and oscillations can be found in a simpler model.
Of importance, both of these models assumed that the kinase and phosphatase follow a fully distributive mechanism, in which all of the catalytic steps on the way to the fully modified substrate (phosphorylated or dephosphorylated) generate dissociated enzyme and product. As a consequence, all subsequent reactions require de novo formation of complexes between the enzyme and partially modified substrates. This model can be viewed as a limiting regime of a more detailed mechanism in which the enzyme–substrate complex is first transformed into a complex between the enzyme and product of the first reaction (Figure 1A). This complex can either dissociate or continue directly to the next catalytic step. Depending on the relative rates of these steps, this mechanism can behave as fully distributive or fully processive. When the dissociation rate constant of the newly formed complex between the monophosphorylated substrate and enzyme is much larger than the catalytic rate constant for the subsequent reaction, the mechanism behaves as fully distributive. In our model, this corresponds to the limit in which 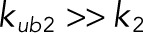 , which makes the kinase fully distributive, and
, which makes the kinase fully distributive, and 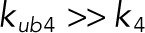 , which makes the phosphatase fully distributive (see Table 1 for the assignment of rate constants to reaction steps). In the opposite extreme, when the catalytic reaction is much faster than dissociation, the mechanism behaves as processive (
, which makes the phosphatase fully distributive (see Table 1 for the assignment of rate constants to reaction steps). In the opposite extreme, when the catalytic reaction is much faster than dissociation, the mechanism behaves as processive (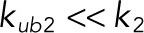 and
and 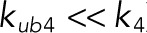 ). Between these extremes, the mechanism, which can be called “mixed,” can accommodate both distributive and processive reaction channels.
). Between these extremes, the mechanism, which can be called “mixed,” can accommodate both distributive and processive reaction channels.
TABLE 1:
Rate constants associated with each reaction step in the reaction diagram in Figure 2B.
| Rate constant | Reaction |
|---|---|
| k1 | 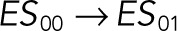 |
| k2 | 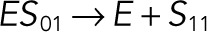 |
| k3 | 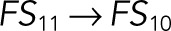 |
| k4 | 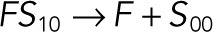 |
| k5 | 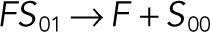 |
| k6 | 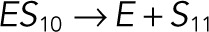 |
| kb1 | 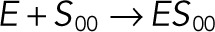 |
| kb2 | 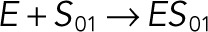 |
| kb3 | 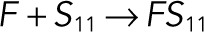 |
| kb4 | 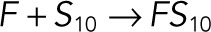 |
| kb5 | 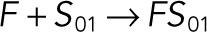 |
| kb6 | 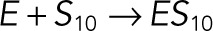 |
| kub1 | 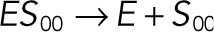 |
| kub2 | 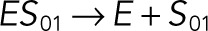 |
| kub3 | 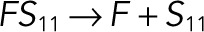 |
| kub4 | 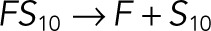 |
| kub5 |  |
| kub6 | 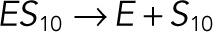 |
We used the mixed reaction mechanism as a building block in constructing the minimal model of ERK regulation (Figure 2B). This model describes six enzymatic reactions that interconvert four different forms of the substrate. To simplify the notation, in the rest of the article, these states are denoted by S00, S01, S10, and S11, which correspond, respectively, to the unphosphorylated (TY), two monophosphorylated (TpY and pTY), and bisphosphorylated (pTpY) molecules. The two enzymes are denoted by E and F, corresponding to MEK and MKP3, respectively. The mass action model of this network leads to a system of 12 coupled ordinary differential equations (ODEs) describing the joint dynamics of two enzymes (E and F), four substrates (S00, S01, S10, S11), and six enzyme–substrate complexes (ES00, ES01, ES10, FS01, FS10, FS11).
The model has 21 free parameters: three rate constants for each of the six enzymatic reactions and three total concentrations of the substrate and two enzymes (Stot, Etot, and Ftot). In the limit when enzymes are much less abundant than substrates (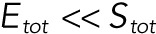 and
and 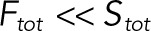 ), the dynamics of the six complexes are slaved to the dynamics of the free substrates, and the model can be reduced to a system of only four ODEs for the substrates (S00, S01, S10, and S11). We developed an efficient approach for applying the steady state approximation for the complexes and deriving reduced models in this and related classes of enzyme–substrate networks. As a result of the steady state approximation, the dynamics of the four remaining variables in the reduced model satisfy the conservation equation
), the dynamics of the six complexes are slaved to the dynamics of the free substrates, and the model can be reduced to a system of only four ODEs for the substrates (S00, S01, S10, and S11). We developed an efficient approach for applying the steady state approximation for the complexes and deriving reduced models in this and related classes of enzyme–substrate networks. As a result of the steady state approximation, the dynamics of the four remaining variables in the reduced model satisfy the conservation equation 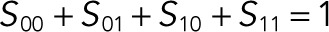 after rescaling the substrate concentrations by Stot. Thus, the dynamics in the reduced model is effectively three-dimensional and can be readily visualized.
after rescaling the substrate concentrations by Stot. Thus, the dynamics in the reduced model is effectively three-dimensional and can be readily visualized.
As a starting point for analyzing the dynamics, we used a combination of computational and algebraic techniques to characterize the steady states in the reduced model. The right-hand sides of the four ODEs contain rational functions of the four variables, and the corresponding steady state problem gives rise to a system of four coupled quadratic equations. Using Gröbner bases, a tool from algebraic geometry that has been applied in the context of dual phosphorylation cycles for mechanism discrimination (Gunawardena, 2007; Manrai and Gunawardena, 2008; Thomson and Gunawardena, 2009; Cox et al., 2010; Harrington et al., 2012), all solutions of this system of polynomials can be calculated for any given set of model parameters. Furthermore, the stability of the resulting steady states can be readily evaluated by examining the eigenvalues of the linearized problem. We implemented this algorithm in Mathematica (Wolfram Research, Champaign, IL) and used it to examine the steady states in our model for 5 × 105 parameter vectors randomly drawn uniformly in logarithm over the 20-dimensional space of model parameters. The Supplemental Materials contain the Mathematica notebooks used to implement parameter sampling and evaluation of long-term dynamics.
Our analysis revealed three classes of outcomes (Figure 3). The first and most abundant class consists of parameter vectors that correspond to steady states that are unique and linearly stable (Figure 3A). The second class contains parameter vectors that predict three steady states—two stable and one unstable (Figure 3B). Of the 5 × 105 parameter sets sampled, 1877 fell into this class, corresponding to a hit rate of ∼1 in 270. Finally, the third and least abundant class of outcomes corresponds to parameter vectors that result in steady states that are unique and linearly unstable. In this case, the linearized problem has at least one eigenvalue with positive real part. This means that any small perturbation to the steady state solution should grow, leading to a periodic solution due to the conservation condition for the total amount of substrate. In principle, it is possible that some of such parameter sets could correspond to more complex dynamics, such as deterministic chaos, but our analysis so far has not revealed such behaviors. By time integration of the full nonlinear problem (without making the steady state approximation for complexes), we confirmed that models with parameters in this class give rise to stable limit cycles in which the relative abundances of the four phosphoforms change periodically in time (Figure 3C). Only 120 parameter sets were found that fell into this class, corresponding to a hit rate of ∼1 in 4300. The Supplemental Materials contain Matlab (MathWorks, Natick, MA) code for numerically integrating the equations of the full and reduced systems at the parameter values used to generate Figure 3.
FIGURE 3:
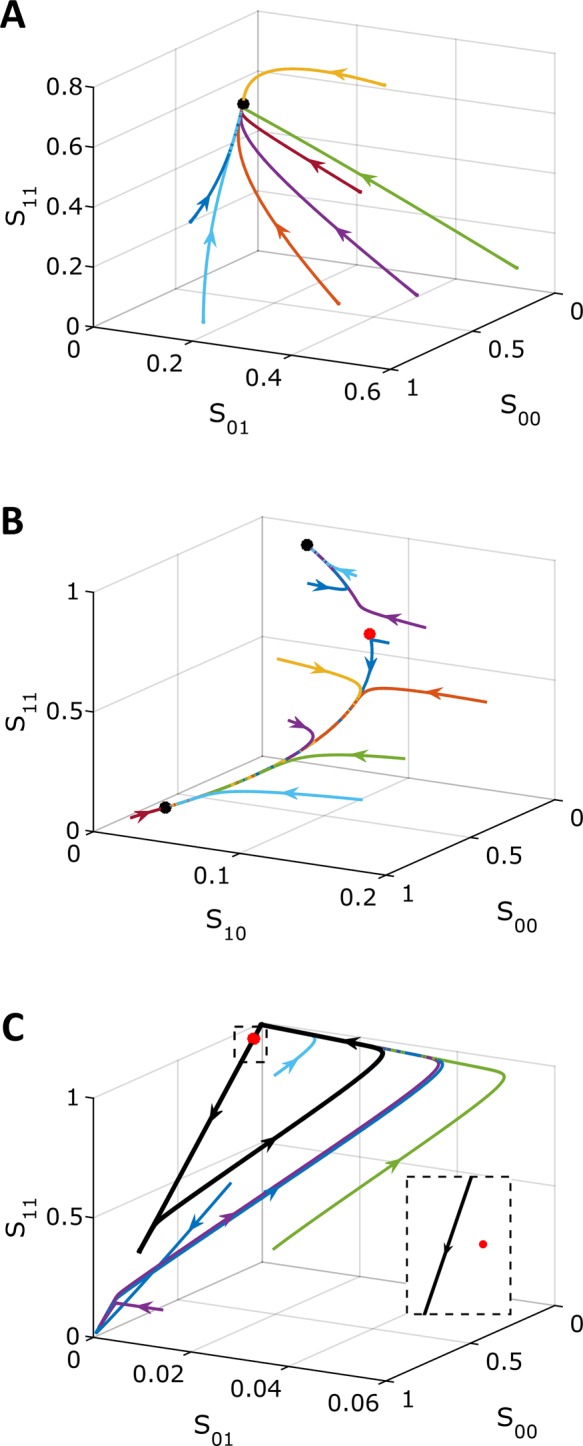
Three types of long-term dynamics in the model: a unique stable steady state (A), bistability (B), and a stable limit cycle (C). Colors are trajectories in phase space from multiple initial conditions. Black dots correspond to stable steady states and red dots to unstable steady states. The black trajectory in C corresponds to the stable limit cycle, which all initial conditions approach after long times. The inset in C zooms in near the unstable steady state, showing that the limit cycle orbit passes very close by the unstable steady state. Phase plots were constructed by numerically integrating the full model. Table 2 gives the parameter values.
The three classes of long-term dynamics identified by our computational screening of model parameters suggest that our network can display three different classes of input–output behaviors. We define the input to be the ratio of the total amounts of kinase and phosphatase (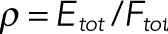 ) and the output to be the long-term concentration of dually phosphorylated substrate, S11. To illustrate this, we used numerical continuation algorithms to compute the branches of steady states and limit cycles as a function of the input to the network (Figure 4). As the starting points for numerical continuation, we used the steady states shown in Figure 3, the parameters for which are given in Table 2. First, we verified that the nonlinear behaviors found in these three cases using the pseudo–steady state approximation carried back to the full model. Then, we calculated the steady state branches using the full model. The three parameter sets with different types of long-term dynamics gave rise to three different types of steady state branches. In all three cases, the state of the substrate transitions from the unphosphorylated form to the fully phosphorylated form as the input to the network is increased, but this transition can pass through robust regions of bistability or oscillations.
) and the output to be the long-term concentration of dually phosphorylated substrate, S11. To illustrate this, we used numerical continuation algorithms to compute the branches of steady states and limit cycles as a function of the input to the network (Figure 4). As the starting points for numerical continuation, we used the steady states shown in Figure 3, the parameters for which are given in Table 2. First, we verified that the nonlinear behaviors found in these three cases using the pseudo–steady state approximation carried back to the full model. Then, we calculated the steady state branches using the full model. The three parameter sets with different types of long-term dynamics gave rise to three different types of steady state branches. In all three cases, the state of the substrate transitions from the unphosphorylated form to the fully phosphorylated form as the input to the network is increased, but this transition can pass through robust regions of bistability or oscillations.
FIGURE 4:
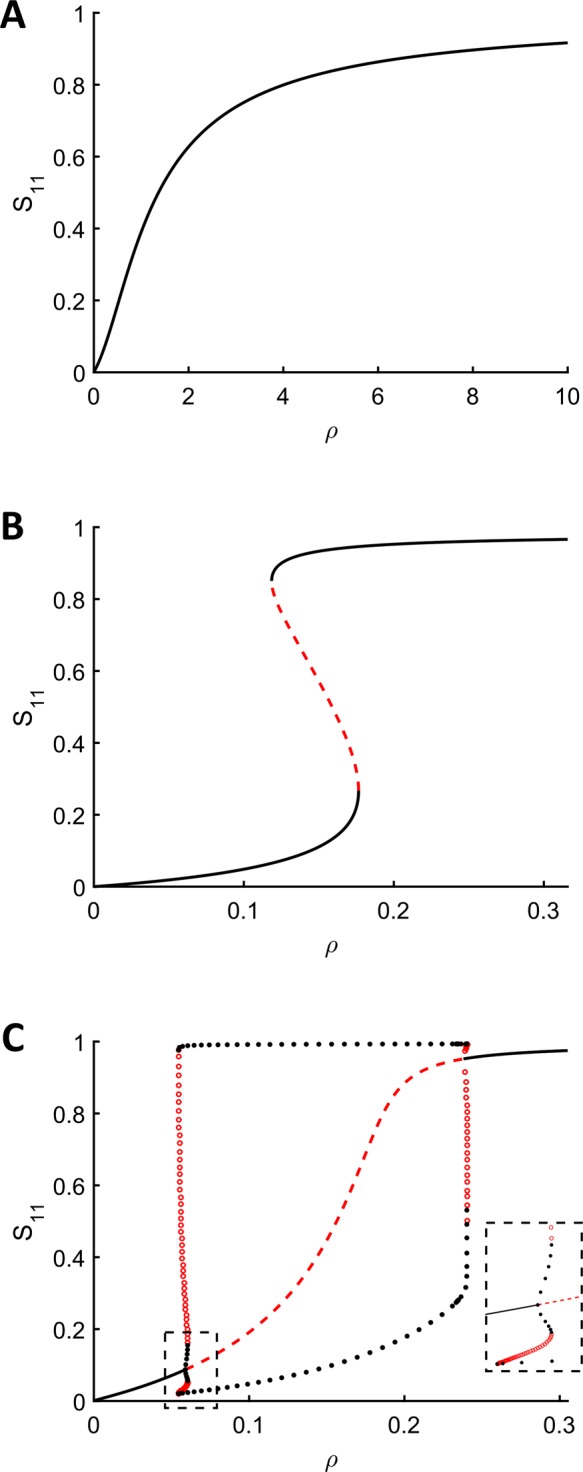
Branches of steady states as a function of the ratio of the total amounts of kinase and phosphatase, 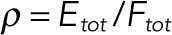 . All parameters other than the total kinase concentration are the same as those in Table 2. (A) The system only has a unique stable steady state for all values of ρ. (B) The system has two stable steady states for some values of ρ and exhibits switch-like behavior and hysteresis. (C) The system exhibits limit cycles for a range of values of ρ. Close to the left bifurcation point, two stable limit cycles can coexist, separated by unstable limit cycles. The Supplemental Materials contain Matlab code for numerically integrating the equations at the parameters and total enzyme concentrations for which two stable limit cycles coexist. The inset zooms in on the region near the left bifurcation point. Note that in all three cases shown here, numerical continuation was performed on the full model of the dual phosphorylation cycle, showing that the nonlinear behaviors found under the pseudo–steady state approximation lift back to the full model in most cases. In addition, Etot and Ftot are both <<Stot for all values of ρ in these bifurcation diagrams.
. All parameters other than the total kinase concentration are the same as those in Table 2. (A) The system only has a unique stable steady state for all values of ρ. (B) The system has two stable steady states for some values of ρ and exhibits switch-like behavior and hysteresis. (C) The system exhibits limit cycles for a range of values of ρ. Close to the left bifurcation point, two stable limit cycles can coexist, separated by unstable limit cycles. The Supplemental Materials contain Matlab code for numerically integrating the equations at the parameters and total enzyme concentrations for which two stable limit cycles coexist. The inset zooms in on the region near the left bifurcation point. Note that in all three cases shown here, numerical continuation was performed on the full model of the dual phosphorylation cycle, showing that the nonlinear behaviors found under the pseudo–steady state approximation lift back to the full model in most cases. In addition, Etot and Ftot are both <<Stot for all values of ρ in these bifurcation diagrams.
TABLE 2:
Parameter values used to generate the phase plots, bifurcation diagrams, and time courses in Figures 3–5.
| Parameter | Figures 3A and 4A: monostable | Figures 3B and 4B: bistable | Figures 3C, 4C, and 5A: limit cycle | Figure 5B: limit cycle |
|---|---|---|---|---|
| k1 | 1 | 1.1994 | 5314.5 | 4.5915 × 105 |
| k2 | 2 | 19,327 | 1291 | 22.28 |
| k3 | 3 | 0.36953 | 44.965 | 3.2585 × 106 |
| k4 | 1 | 29,332 | 9.2497 × 105 | 9.7962 |
| k5 | 1 | 4.1166 × 105 | 1.3334 | 213.71 |
| k6 | 2 | 552.32 | 2.0451 | 14.154 |
| kb1 | 3 | 2733.8 | 5241 | 2531.6 |
| kb2 | 3 | 2.6221 × 106 | 4.0205 | 1.0435 × 105 |
| kb3 | 2 | 109.37 | 64.271 | 19,464 |
| kb4 | 1 | 50.134 | 54.606 | 2.4078 × 106 |
| kb5 | 4 | 6.0968 | 2.1496 × 106 | 8.8294 × 105 |
| kb6 | 3 | 103.34 | 2.7625 × 106 | 1.0831 × 105 |
| kub1 | 2 | 85.59 | 149.19 | 3208.6 |
| kub2 | 1 | 7.9504 | 76.203 | 1.5788 × 106 |
| kub3 | 2 | 10.303 | 2.2707 | 209.83 |
| kub4 | 3 | 1.6602 × 105 | 27,238 | 5.6317 × 105 |
| kub5 | 4 | 28.243 | 6.0681 | 785.47 |
| kub6 | 5 | 0.29981 | 0.40324 | 22.769 |
| Etot | 0.003 | 0.0026087 | 0.0012244 | 0.0068182 |
| Ftot | 0.002 | 0.018996 | 0.0052442 | 0.0084204 |
To summarize, our analysis of the minimal mechanism of the ERK regulation cycle reveals that the system can function as an irreversible switch and as an oscillator. Both of these regimes were previously detected in cycles with additional reactions (Markevich et al., 2004; Jolley et al., 2012). Our results show that oscillations and bistability persist in a simpler model based on the interactions and reactions established in the MEK/ERK/MKP3 system (Haystead et al., 1992; Zhao and Zhang, 2001; Zhou et al., 2002; Aoki et al., 2013). We found that bistability and oscillations in our model can be realized at very different levels of reaction processivity, which can be defined as the probability that a complex between the partially phosphorylated substrate and enzyme will not dissociate and will continue to the next reaction step.
For instance, for the parameter set corresponding the limit cycle shown in Figure 5A, both the phosphorylation and dephosphorylation reactions are highly processive—for both of these reactions, the rate constant of the second catalytic step exceeds, by orders of magnitude, the dissociation rate constant for the partially phosphorylated form. As a consequence, the relative amounts of the monophosphorylated forms at any given time are very low, and the substrate switches between the unphosphorylated and bisphosphorylated forms. A limit cycle in the strongly distributive regime, when partially phosphorylated forms are much more likely to dissociate than continue to the next catalytic step, has a very different structure (Figure 5B). Here all of the four possible phosphoforms are present at appreciable levels at different parts of the oscillating trajectory. Of the 1877 parameter sets that produce bistability, 18 were found for which the probability of the processive reaction channel is at least as likely as the distributive one ( and
and 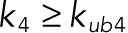 ). However, only one parameter set of the 120 that were found to produce oscillations satisfies this condition.
). However, only one parameter set of the 120 that were found to produce oscillations satisfies this condition.
FIGURE 5:
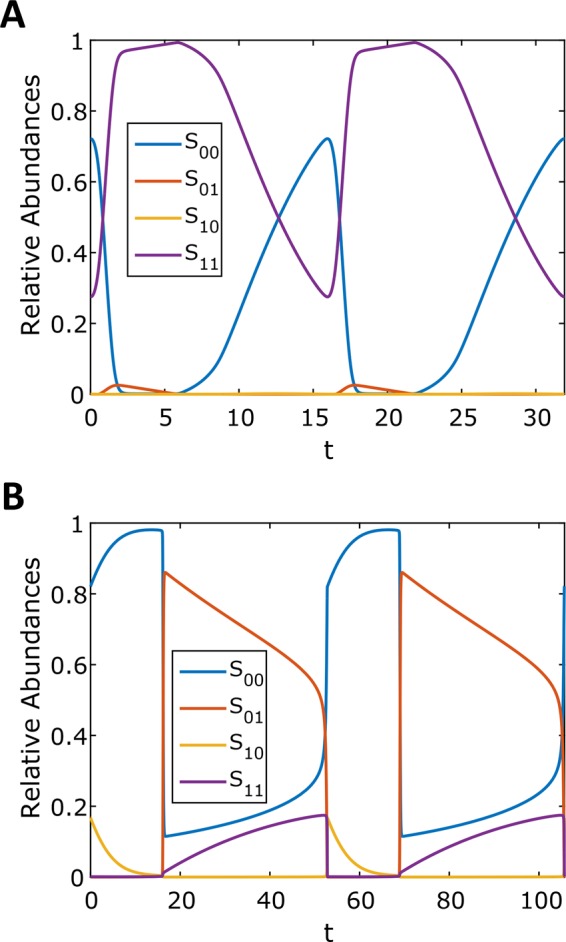
Periodic solutions were found at two different levels of reaction processivity. Time courses and state-space plots of limit cycles found in the processive (A) and distributive (B) regimes. Time courses were generated by numerically integrating the full model. Table 2 gives the parameter values.
Note that earlier analysis of a model that does not distinguish between different partially phosphorylated forms conclusively ruled out bistability in the fully processive regime (Conradi and Shiu, 2015). At the same time, our results obtained for a model with multiple partially phosphorylated forms found that both bistability and oscillations can be realized at high levels of processivity. In the future, it will be interesting to determine how close to the fully processive limit can bistable or oscillatory regimes still exist.
DISCUSSION
We used an idealized mechanism of ERK regulation to explore the long-term dynamics of a model that accounts for all relevant phosphorylation forms and nonzero levels of reaction processivity. In addition to bistability, which has been studied extensively in distributive mechanisms, we found that this model can also generate oscillations. Whether such oscillations can be realized in a single ERK regulation cycle is unclear, but similar oscillations, with ordered appearance of four distinct phosphorylation states, form the basis for robust circadian rhythms in cyanobacteria (Rust et al., 2007). At the same time, several lines of evidence suggest that ERK phosphorylation in cells can be switch-like, in the sense that most of ERK is in fully unphosphorylated or dually phosphorylated forms (Hahn et al., 2013). To interpret these observations from studies in cells, our model must be extended to include additional components (Harrington et al., 2013; Michailovici et al., 2014; Shindo et al., 2016) and interactions, such as the possibility of ERK dephosphorylation by multiple phosphatases (Rintelen et al., 2003).
Another important direction is to include the effects of intracellular crowding, which slows down diffusion. This may result in increased rebinding of partially phosphorylated substrate to the same enzyme. As a consequence, the processive reaction channel becomes more prominent, which may in turn lead to significant changes in the domain of bistability (Takahashi et al., 2010; Gopich and Szabo, 2013; Verdugo et al., 2013; Gopich and Szabo, 2016). Our approach should be readily applicable to kinetic models that include these additional effects, as well as the effects of intracellular compartments and ERK interaction with its substrates, which can protect ERK from phosphatases (Kim et al., 2011; Liu et al., 2011).
Note that while there are multiple techniques for probing the long-term dynamics in multisite phosphorylation cycles, there are no general-purpose tools for probing their transient responses to time-varying inputs. Nevertheless, analysis of transient responses is essential for understanding many of the functional properties of phosphorylation cycles, including their roles during inductive signaling in developing tissues (Lim et al., 2015; Mattingly et al., 2015). In the future, it will be interesting to classify transient responses of multisite phosphorylation cycles to several of the typical inputs encountered by these networks in vivo, starting with pulses provided by the upstream signaling components.
One may ask whether the nonlinear behaviors we found in the model can occur at biologically feasible parameter values. We argue that this question motivates experiments in which isolated components of phosphorylation cycles, such as the ERK-MEK-MKP3 system, are reconstituted in vitro for the purpose of constraining model parameters and determining which long-term behaviors are feasible in such systems.
Another important direction for future work is the systematic analysis of mutations affecting the components of phosphorylation cycles. As an example, it is known that ERK uses the same docking domain to bind to the enzymes that phosphorylate and dephosphorylate it (Tanoue et al., 2000). A well-studied mutation in this domain, which should result in decreased affinity for both kinase and phosphatase, acts as gain of function in vivo (Brunner et al., 1994). Quantitative explanation for this effect is lacking, but it is generally accepted that ERK binding to a phosphatase, such as MKP3, is affected to a greater extent than its binding to the activating enzyme (Bott et al., 1994; Zhou and Zhang, 1999; Zhou et al., 2002; Zhao and Zhang, 2001; Zhang et al., 2003). The relative effects of this mutation on ERK’s interactions with the two enzymes have not been quantified, but once this is done, our approach can be used to predict how these effects influence the systems-level properties of the dual phosphorylation cycle that controls ERK with this mutation.
MATERIALS AND METHODS
Mathematical model of ERK regulation
The following system of equations describe the dynamics of a kinase (E), a phosphatase (F), a substrate with four phosphorylation states (S00, S01, S10, S11), and six enzyme–substrate complexes (ES00, ES01, ES10, FS01, FS10, FS11). Here each index on the substrates and complexes is a phosphorylation site, with 0 denoting unphosphorylated and 1 denoting phosphorylated:
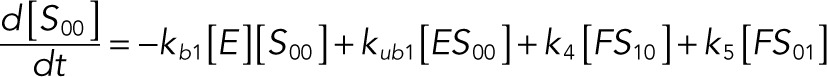 (1.1) (1.1)
|
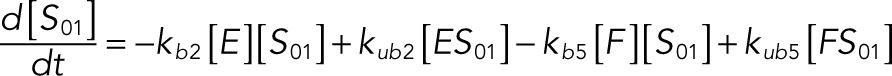 (1.2) (1.2)
|
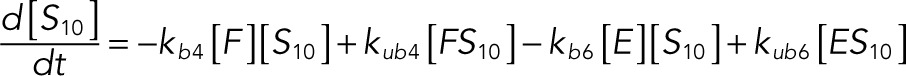 (1.3) (1.3)
|
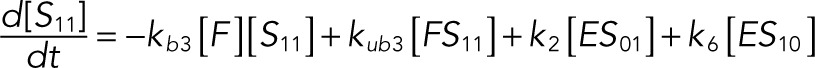 (1.4) (1.4)
|
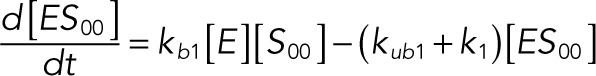 (1.5) (1.5)
|
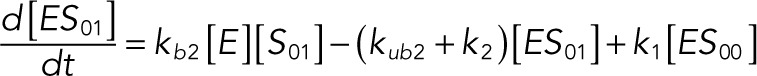 (1.6) (1.6)
|
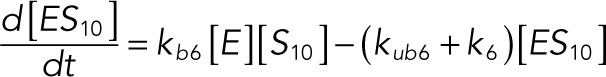 (1.7) (1.7)
|
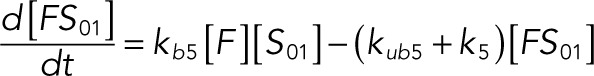 (1.8) (1.8)
|
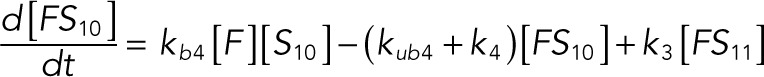 (1.9) (1.9)
|
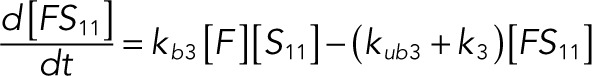 (1.10) (1.10)
|
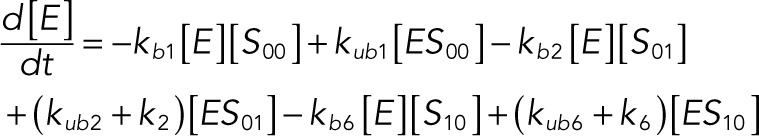 (1.11) (1.11)
|
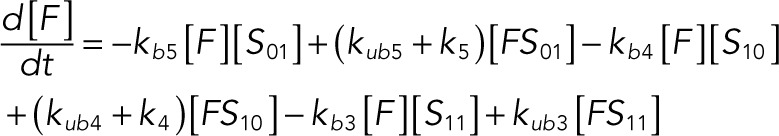 (1.12) (1.12)
|
The conservation laws are as follows:
|
|
|
|
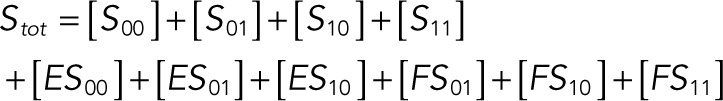 (1.15) (1.15)
|
Matrix representation
It is convenient to write the foregoing system of equations in vector-matrix form:
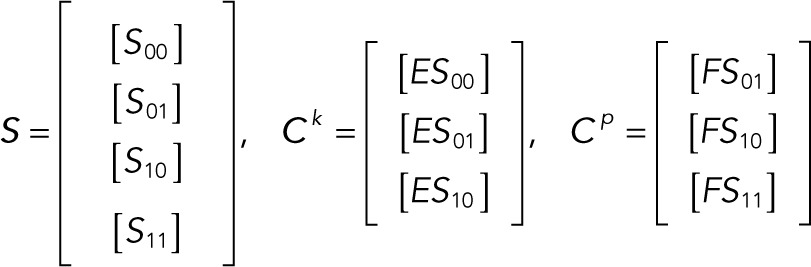 (2.1–2.3) (2.1–2.3)
|
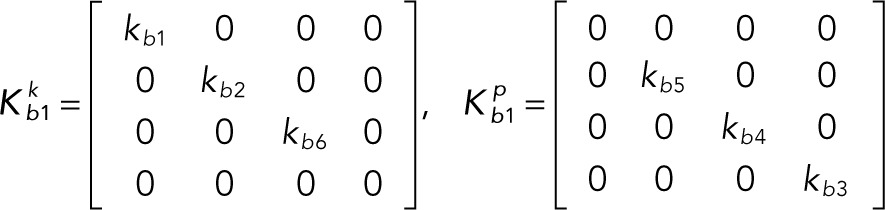 (2.4–2.5) (2.4–2.5)
|
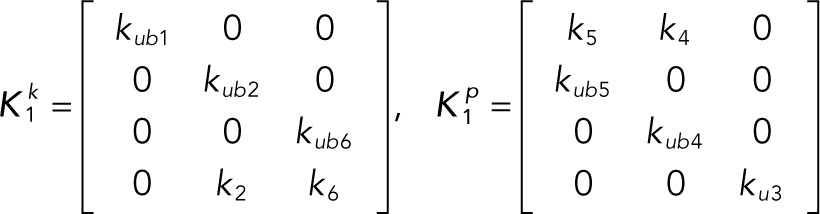 (2.6, 2.7) (2.6, 2.7)
|
 (2.8, 2.9) (2.8, 2.9)
|
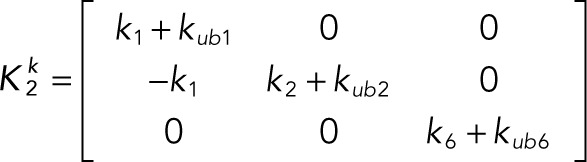 (2.10) (2.10)
|
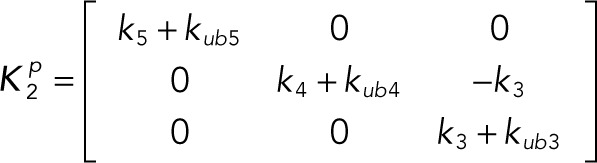 (2.11) (2.11)
|
In terms of these vectors and matrices, the differential equations become
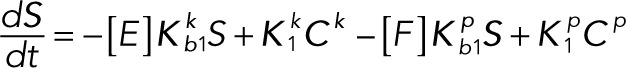 (2.12) (2.12)
|
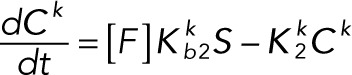 (2.13) (2.13)
|
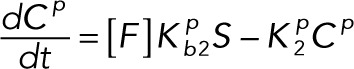 (2.14) (2.14)
|
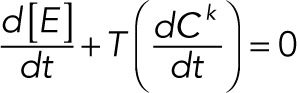 (2.15) (2.15)
|
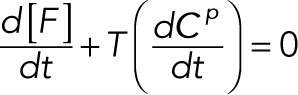 (2.16) (2.16)
|
Here we define the operator T(·), which acts on a vector and takes the sum of the elements of the vector. The conservation laws become
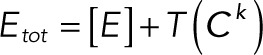 (2.17) (2.17)
|
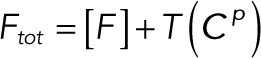 (2.18) (2.18)
|
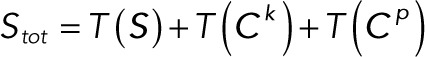 (2.19) (2.19)
|
Pseudo–steady state approximation
In the pseudo–steady state approximation (valid for Etot, Ftot ≪ Stot), we assume that the left-hand side of the differential equations for the complexes vanish, giving
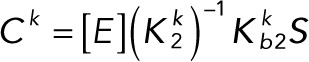 (3.1) (3.1)
|
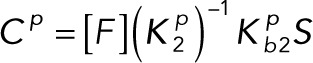 (3.2) (3.2)
|
Substituting Eqs. 3.1 and 3.2 into the conservation laws for [E] and [F] (Eqs. 2.16 and 2.17) and solving for each enzyme concentration gives
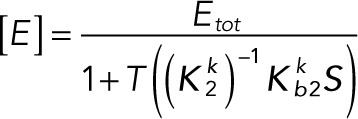 (3.3) (3.3)
|
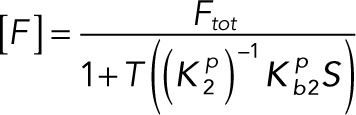 (3.4) (3.4)
|
Substituting the expressions for the enzymes and the complexes into the differential equations for the substrate concentrations gives the reduced system of differential equations:
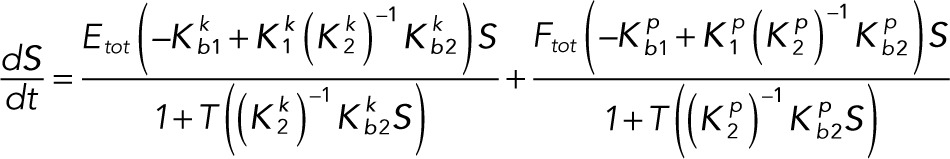 (3.5) (3.5)
|
Lumping together the matrices in the numerator and the denominator gives
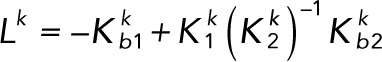 (3.6) (3.6)
|
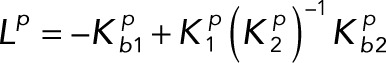 (3.7) (3.7)
|
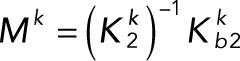 (3.8) (3.8)
|
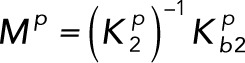 (3.9) (3.9)
|
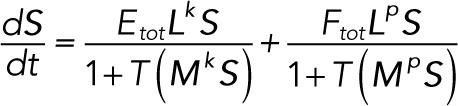 (3.10) (3.10)
|
At this point, we will also nondimensionalize the system. First, we rescale all substrate and complex concentrations by Stot. However, the concentrations of the complexes are bounded above by the total concentrations of their corresponding enzymes, Etot and Ftot. In addition, we take the limit in which Etot/Stot and Ftot/Stot go to zero. Therefore the complexes disappear from the conservation law for the substrate (Eq. 2.19), and the equation becomes
|
|
Rescaling time by k3Ftot/Stot, Lk and Lp by k3/Stot, and Mk and Mp by Stot and introducing the parameter ρ = Etot/Ftot gives the dimensionless system of differential equations:
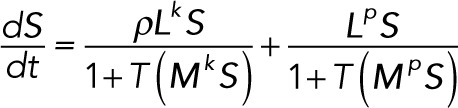 (3.12) (3.12)
|
where all quantities are now understood to be in their dimensionless form.
Sampling of model parameters
Parameters were sampled uniformly in logarithm from a 20-dimensional hypercube. All rate constants were allowed to take on values between 10−1 and 107. The total concentrations of kinase and phosphatase were allowed to vary between 10−4 and 10−1.
Steady state calculations
To solve for the steady states of the foregoing system of differential equations, we set the left-hand sides equal to zero:
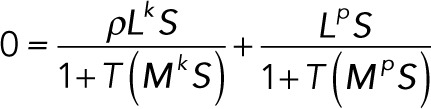 (4.1) (4.1)
|
which is equivalent to
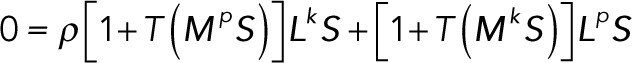 (4.2) (4.2)
|
Note that this is a system of algebraic polynomial equations in the substrate concentrations, with each polynomial being at most degree 2. Using the computer algebra software Mathematica, it is possible to numerically find all solutions to this system of equations. This is done by computation of a Gröbner basis using an efficient monomial ordering, followed by eigensystem methods to extract numerical roots (Cox et al., 2010). The Gröbner basis for a system of polynomials is an equivalent polynomial system that has many useful properties. For example, the set of polynomials in the Gröbner basis has the same set of roots as the original polynomials. In the simplest case, for a linear function of any number of variables, the Gröbner basis computation is equivalent to the Gaussian elimination procedure.
Among the solutions to the polynomial system of equations in Eq. 4.2, the only ones kept were those that had no negative components in the vector S and obeyed conservation of substrate (Eq. 3.11). Continuations of steady states were performed in Matcont (Dhooge et al., 2003), a numerical continuation software for Matlab.
Linear stability analysis
If we define
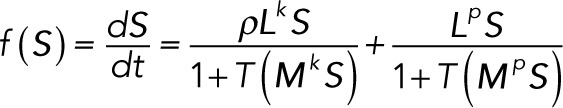 |
then determining the linear stability of a steady state 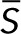 of the reduced system of differential equations requires calculation of the eigenvalues of the Jacobian matrix
of the reduced system of differential equations requires calculation of the eigenvalues of the Jacobian matrix
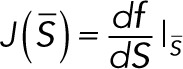 |
evaluated at that steady state. The equation for 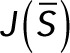 in terms of the matrices defined in the preceding section is
in terms of the matrices defined in the preceding section is
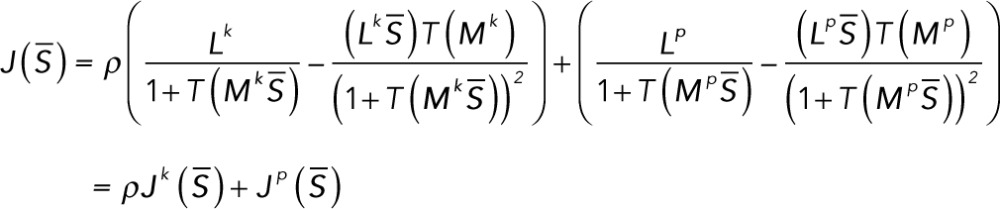 (5.1) (5.1)
|
Here 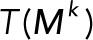 (and similarly
(and similarly 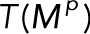 ) means the sum of the columns of
) means the sum of the columns of 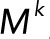 , producing a row vector, so that the product
, producing a row vector, so that the product 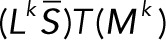 is the outer product of the column vector
is the outer product of the column vector 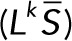 and the row vector
and the row vector 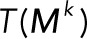 . The denominator of each term is a scalar.
. The denominator of each term is a scalar.
For each parameter set, the linear stability of each nonnegative steady state solution that satisfied the conservation condition was evaluated by substituting it into Eq. 5.1 and calculating the eigenvalues of the Jacobian matrix 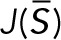 . If one or more eigenvalues had a positive real part, then the steady state was linearly unstable. If all eigenvalues had negative real parts, then the steady state was linearly stable.
. If one or more eigenvalues had a positive real part, then the steady state was linearly unstable. If all eigenvalues had negative real parts, then the steady state was linearly stable.
Supplementary Material
Acknowledgments
We thank Anne Shiu, Jeremy Gunawardena, Heather Harrington, J. Krishnan, Boris Kholodenko, Rony Seger, Elizabeth Goldsmith, Alexey Veraksa, Irina Gopich, Georghe Craciun, and Alan Futran for helpful discussions and comments on the manuscript. H.H.M. and S.Y.S. were supported by National Institutes of Health Grant R01GM086537, and A.M.B. by the Intramural Research Program of the National Institutes of Health, Center for Information Technology.
Abbreviations used:
- ERK
extracellular signal-regulated kinase
- MEK
MAPK/ERK kinase
- MKP3
MAP kinase phosphatase 3.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E16-03-0137) on May 25, 2016.
REFERENCES
- Alessi DR, Gomez N, Moorhead G, Lewis T, Keyse SM, Cohen P. Inactivation of p42 MAP kinase by protein phosphatase 2A and a protein tyrosine phosphatase, but not CL100, in various cell lines. Curr Biol. 1995;5:283–295. doi: 10.1016/s0960-9822(95)00059-5. [DOI] [PubMed] [Google Scholar]
- Alessi DR, Smythe C, Keyse SM. The human CL100 gene encodes a Tyr/Thr-protein phosphatase which potently and specifically inactivates MAP kinase and suppresses its activation by oncogenic ras in Xenopus oocyte extracts. Oncogene. 1993;8:2015–2020. [PubMed] [Google Scholar]
- Anastasaki C, Estep AL, Marais R, Rauen KA, Patton EE. Kinase-activating and kinase-impaired cardio-facio-cutaneous syndrome alleles have activity during zebrafish development and are sensitive to small molecule inhibitors. Hum Mol Genet. 2009;18:2543–2554. doi: 10.1093/hmg/ddp186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aoidi R, Maltais A, Charron J. Functional redundancy of the kinases MEK1 and MEK2: rescue of the Mek1 mutant phenotype by Mek2 knock-in reveals a protein threshold effect. Sci Signal. 2016;9:ra9. doi: 10.1126/scisignal.aad5658. [DOI] [PubMed] [Google Scholar]
- Aoki K, Takahashi K, Kaizu K, Matsuda M. A quantitative model of ERK MAP kinase phosphorylation in crowded media. Sci Rep. 2013;3:1541. doi: 10.1038/srep01541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aoki K, Yamada M, Kunida K, Yasuda S, Matsuda M. Processive phosphorylation of ERK MAP kinase in mammalian cells. Proc Natl Acad Sci USA. 2011;108:12675–12680. doi: 10.1073/pnas.1104030108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bott CM, Thorneycroft SG, Marshall CJ. The sevenmaker gain-of-function mutation in p42 MAP kinase leads to enhanced signalling and reduced sensitivity to dual specificity phosphatase action. FEBS Lett. 1994;352:201–205. doi: 10.1016/0014-5793(94)00958-9. [DOI] [PubMed] [Google Scholar]
- Brunner D, Oellers N, Szabad J, Biggs WH 3rd, Zipursky SL, Hafen E. A gain-of-function mutation in Drosophila MAP kinase activates multiple receptor tyrosine kinase signaling pathways. Cell. 1994;76:875–888. doi: 10.1016/0092-8674(94)90362-x. [DOI] [PubMed] [Google Scholar]
- Burack WR, Sturgill TW. The activating dual phosphorylation of MAPK by MEK is nonprocessive. Biochemistry. 1997;36:5929–5933. doi: 10.1021/bi970535d. [DOI] [PubMed] [Google Scholar]
- Canagarajah BJ, Khokhlatchev A, Cobb MH, Goldsmith EJ. Activation mechanism of the MAP kinase ERK2 by dual phosphorylation. Cell. 1997;90:859–869. doi: 10.1016/s0092-8674(00)80351-7. [DOI] [PubMed] [Google Scholar]
- Caunt CJ, Armstrong SP, Rivers CA, Norman MR, McArdle CA. Spatiotemporal regulation of ERK2 by dual specificity phosphatases. J Biol Chem. 2008;283:26612–26623. doi: 10.1074/jbc.M801500200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caunt CJ, Sale MJ, Smith PD, Cook SJ. MEK1 and MEK2 inhibitors and cancer therapy: the long and winding road. Nat Rev Cancer. 2015;15:577–592. doi: 10.1038/nrc4000. [DOI] [PubMed] [Google Scholar]
- Conradi C, Mincheva M. Catalytic constants enable the emergence of bistability in dual phosphorylation. J R Soc Interface. 2014a;11:20140158. doi: 10.1098/rsif.2014.0158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conradi C, Mincheva M. 2014b. Graph-theoretic analysis of multistationarity using degree theory. ArXiv 1411.2896.
- Conradi C, Shiu A. A global convergence result for processive multisite phosphorylation systems. Bull Math Biol. 2015;77:126–155. doi: 10.1007/s11538-014-0054-4. [DOI] [PubMed] [Google Scholar]
- Cox DA, Little J, Shea DO. Ideals, Varieties, and Algorithms. New York: Springer; 2010. [Google Scholar]
- Dhooge A, Govaerts W, Kuznetsov YA. MATCONT: a Matlab package for numerical bifurcation analysis of ODEs. ACM Trans Math Software. 2003;29:141–164. [Google Scholar]
- Dowd S, Sneddon AA, Keyse SM. Isolation of the human genes encoding the pyst1 and Pyst2 phosphatases: characterisation of Pyst2 as a cytosolic dual-specificity MAP kinase phosphatase and its catalytic activation by both MAP and SAP kinases. J Cell Sci. 1998;111:3389–3399. doi: 10.1242/jcs.111.22.3389. [DOI] [PubMed] [Google Scholar]
- Ferrell JE, Bhatt RR. Mechanistic studies of the dual phosphorylation of mitogen-activated protein kinase. J Biol Chem. 1997;272:19008–19016. doi: 10.1074/jbc.272.30.19008. [DOI] [PubMed] [Google Scholar]
- Ferrell JEJ, Ha SH. Ultrasensitivity part II: multisite phosphorylation, stoichiometric inhibitors, and positive feedback. Trends Biochem Sci. 2014;39:556–569. doi: 10.1016/j.tibs.2014.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrigno P, Langan TA, Cohen P. Protein phosphatase 2A1 is the major enzyme in vertebrate cell extracts that dephosphorylates several physiological substrates for cyclin-dependent protein kinases. Mol Biol Cell. 1993;4:669–677. doi: 10.1091/mbc.4.7.669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frémin C, Saba-El-Leil MK, Levesque K, Ang SL, Meloche S. Functional redundancy of ERK1 and ERK2 MAP kinases during development. Cell Rep. 2015;12:913–921. doi: 10.1016/j.celrep.2015.07.011. [DOI] [PubMed] [Google Scholar]
- Futran AS, Link AJ, Seger R, Shvartsman SY. ERK as a model for systems biology of enzyme kinetics in cells. Curr Biol. 2013;23:R972–979. doi: 10.1016/j.cub.2013.09.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gopich IV, Szabo A. Diffusion modifies the connectivity of kinetic schemes for multisite binding and catalysis. Proc Natl Acad Sci USA. 2013;110:19874–19879. doi: 10.1073/pnas.1319943110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gopich IV, Szabo A. Influence of diffusion on the kinetics of multisite phosphorylation. Protein Sci. 2016;25:244–254. doi: 10.1002/pro.2722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groom LA, Sneddon AA, Alessi DR, Dowd S, Keyse SM. Differential regulation of the MAP, SAP and RK/p38 kinases by Pyst1, a novel cytosolic dual-specificity phosphatase. EMBO J. 1996;15:3621–3632. [PMC free article] [PubMed] [Google Scholar]
- Guan KL, Butch E. Isolation and characterization of a novel dual specific phosphatase, HVH2, which selectively dephosphorylates the mitogen-activated protein kinase. J Biol Chem. 1995;270:7197–7203. doi: 10.1074/jbc.270.13.7197. [DOI] [PubMed] [Google Scholar]
- Gunawardena J. Distributivity and processivity in multisite phosphorylation can be distinguished through steady-state invariants. Biophys J. 2007;93:3828–3834. doi: 10.1529/biophysj.107.110866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahn B, D’Alessandro LA, Depner S, Waldow K, Boehm ME, Bachmann J, Schilling M, Klingmüller U, Lehmann WD. Cellular ERK phospho-form profiles with conserved preference for a switch-like pattern. J Proteome Res. 2013;12:637–646. doi: 10.1021/pr3007232. [DOI] [PubMed] [Google Scholar]
- Harrington HA, Feliu E, Wiuf C, Stumpf MP. Cellular compartments cause multistability and allow cells to process more information. Biophys J. 2013;104:1824–1831. doi: 10.1016/j.bpj.2013.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrington HA, Ho KL, Thorne T, Stumpf MP. Parameter-free model discrimination criterion based on steady-state coplanarity. Proc Natl Acad Sci USA. 2012;109:15746–15751. doi: 10.1073/pnas.1117073109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haystead TA, Dent P, Wu J, Haystead CM, Sturgill TW. Ordered phosphorylation of p42mapk by MAP kinase kinase. FEBS Lett. 1992;306:17–22. doi: 10.1016/0014-5793(92)80828-5. [DOI] [PubMed] [Google Scholar]
- Hell J, Rendall AD. A proof of bistability for the dual futile cycle. Nonlinear Analysis: Real World Appl. 2015a;24:175–189. [Google Scholar]
- Hell J, Rendall AD. Dynamical features of the MAPK cascade. ArXiv 1508.07822. 2015b.
- Hendriks W, Schepens J, Brugman C, Zeeuwen P, Wieringa B. A novel receptor-type protein tyrosine phosphatase with a single catalytic domain is specifically expressed in mouse brain. Biochem J. 1995;305:499–504. doi: 10.1042/bj3050499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphreys JM, Piala AT, Akella R, He H, Goldsmith EJ. Precisely ordered phosphorylation reactions in the p38 mitogen-activated protein (MAP) kinase cascade. J Biol Chem. 2013;288:23322–23330. doi: 10.1074/jbc.M113.462101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jindal GA, Goyal Y, Burdine RD, Rauen KA, Shvartsman SY. RASopathies: unraveling mechanisms with animal models. Dis Model Mech. 2015;8:769–782. doi: 10.1242/dmm.020339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jolley CC, Ode KL, Ueda HR. A design principle for a posttranslational biochemical oscillator. Cell Rep. 2012;2:938–950. doi: 10.1016/j.celrep.2012.09.006. [DOI] [PubMed] [Google Scholar]
- Kapuy O, Barik D, Sananes MR, Tyson JJ, Novak B. Bistability by multiple phosphorylation of regulatory proteins. Prog Biophys Mol Biol. 2009;100:47–56. doi: 10.1016/j.pbiomolbio.2009.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keyse SM, Emslie EA. Oxidative stress and heat shock induce a human gene encoding a protein-tyrosine phosphatase. Nature. 1992;359:644–647. doi: 10.1038/359644a0. [DOI] [PubMed] [Google Scholar]
- Kim Y, Paroush Z, Nairz K, Hafen E, Jiménez G, Shvartsman SY. Substrate-dependent control of MAPK phosphorylation in vivo. Mol Syst Biol. 2011;7:467. doi: 10.1038/msb.2010.121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King AG, Ozanne BW, Smythe C, Ashworth A. Isolation and characterisation of a uniquely regulated threonine, tyrosine phosphatase (TYP 1) which inactivates ERK2 and p54jnk. Oncogene. 1995;11:2553–2563. [PubMed] [Google Scholar]
- Lewis T, Groom LA, Sneddon AA, Smythe C, Keyse SM. XCL100, an inducible nuclear MAP kinase phosphatase from Xenopus laevis: its role in MAP kinase inactivation in differentiated cells and its expression during early development. J Cell Sci. 1995;108:2885–2896. doi: 10.1242/jcs.108.8.2885. [DOI] [PubMed] [Google Scholar]
- Lim B, Dsilva CJ, Levario TJ, Lu H, Schupbach T, Kevrekidis IG, Shvartsman SY. Dynamics of inductive ERK signaling in the Drosophila embryo. Curr Biol. 2015;25:1784–1790. doi: 10.1016/j.cub.2015.05.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim W, Meyer B, Pawson T. Cellular signaling: principles and mechanisms. Garland Sci. 2014.
- Liu P, Kevrekidis IG, Shvartsman SY. Substrate-dependent control of ERK phosphorylation can lead to oscillations. Biophys J. 2011;101:2572–2581. doi: 10.1016/j.bpj.2011.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manrai AK, Gunawardena J. The geometry of multisite phosphorylation. Biophys J. 2008;95:5533–5543. doi: 10.1529/biophysj.108.140632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markevich NI, Hoek JB, Kholodenko BN. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J Cell Biol. 2004;164:353–359. doi: 10.1083/jcb.200308060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattingly HH, Chen JJ, Arur S, Shvartsman SY. A transport model for estimating the time course of ERK Activation in the C. elegans germline. Biophys J. 2015;109:2436–2445. doi: 10.1016/j.bpj.2015.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michailovici I, Harrington HA, Azogui HH, Yahalom-Ronen Y, Plotnikov A, Ching S, Stumpf MP, Klein OD, Seger R, Tzahor E. Nuclear to cytoplasmic shuttling of ERK promotes differentiation of muscle stem/progenitor cells. Development. 2014;141:2611–2620. doi: 10.1242/dev.107078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misra-Press A, Rim CS, Yao H, Roberson MS, Stork PJ. A novel mitogen-activated protein kinase phosphatase. Structure, expression, and regulation. J Biol Chem. 1995;270:14587–14596. doi: 10.1074/jbc.270.24.14587. [DOI] [PubMed] [Google Scholar]
- Mourey RJ, Vega QC, Campbell JS, Wenderoth MP, Hauschka SD, Krebs EG, Dixon JE. A novel cytoplasmic dual specificity protein tyrosine phosphatase implicated in muscle and neuronal differentiation. J Biol Chem. 1996;271:3795–3802. doi: 10.1074/jbc.271.7.3795. [DOI] [PubMed] [Google Scholar]
- Muda M, Boschert U, Dickinson R, Martinou JC, Martinou I, Camps M, Schlegel W, Arkinstall S. MKP-3, a novel cytosolic protein-tyrosine phosphatase that exemplifies a new class of mitogen-activated protein kinase phosphatase. J Biol Chem. 1996;271:4319–4326. doi: 10.1074/jbc.271.8.4319. [DOI] [PubMed] [Google Scholar]
- Ogata M, Sawada M, Fujino Y, Hamaoka T. cDNA cloning and characterization of a novel receptor-type protein tyrosine phosphatase expressed predominantly in the brain. J Biol Chem. 1995;270:2337–2343. doi: 10.1074/jbc.270.5.2337. [DOI] [PubMed] [Google Scholar]
- Patwardhan P, Miller WT. Processive phosphorylation: mechanism and biological importance. Cell Signal. 2007;19:2218–2226. doi: 10.1016/j.cellsig.2007.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payne DM, Rossomando AJ, Martino P, Erickson AK, Her JH, Shabanowitz J, Hunt DF, Weber MJ, Sturgill TW. Identification of the regulatory phosphorylation sites in pp42/mitogen-activated protein kinase (MAP kinase) EMBO J. 1991;10:885–892. doi: 10.1002/j.1460-2075.1991.tb08021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piala AT, Humphreys JM, Goldsmith EJ. MAP kinase modules: the excursion model and the steps that count. Biophys J. 2014;107:2006–2015. doi: 10.1016/j.bpj.2014.09.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prabakaran S, Everley RA, Landrieu I, Wieruszeski JM, Lippens G, Steen H, Gunawardena J. Comparative analysis of Erk phosphorylation suggests a mixed strategy for measuring phospho-form distributions. Mol Syst Biol. 2011;482 doi: 10.1038/msb.2011.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prabakaran S, Gunawardena J, Sontag ED. Paradoxical results in perturbation-based signaling network reconstruction. Biophys J. 2014;106:2720–2728. doi: 10.1016/j.bpj.2014.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pulido R, Zuniga A, Ullrich A. PTP-SL and STEP protein tyrosine phosphatases regulate the activation of the extracellular signal-regulated kinases ERK1 and ERK2 by association through a kinase interaction motif. EMBO J. 1998;17:7337–7350. doi: 10.1093/emboj/17.24.7337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiao L, Nachbar RB, Kevrekidis IG, Shvartsman SY. Bistability and oscillations in the Huang-Ferrell model of MAPK signaling. PLoS Comput Biol. 2007;3:1819–1826. doi: 10.1371/journal.pcbi.0030184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rintelen F, Hafen E, Nairz K. The Drosophila dual-specificity ERK phosphatase DMKP3 cooperates with the ERK tyrosine phosphatase PTP-ER. Development. 2003;130:3479–3490. doi: 10.1242/dev.00568. [DOI] [PubMed] [Google Scholar]
- Rust MJ, Markson JS, Lane WS, Fisher DS, O’Shea EK. Ordered phosphorylation governs oscillation of a three-protein circadian clock. Science. 2007;318:809–812. doi: 10.1126/science.1148596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salazar C, Brümmer A, Alberghina L, Höfer T. Timing control in regulatory networks by multisite protein modifications. Trends Cell Biol. 2010;20:634–641. doi: 10.1016/j.tcb.2010.08.012. [DOI] [PubMed] [Google Scholar]
- Salazar C, Höfer T. Kinetic models of phosphorylation cycles: a systematic approach using the rapid-equilibrium approximation for protein-protein interactions. Biosystems. 2006;83:195–206. doi: 10.1016/j.biosystems.2005.05.015. [DOI] [PubMed] [Google Scholar]
- Salazar C, Höfer T. Multisite protein phosphorylation—from molecular mechanisms to kinetic models. FEBS J. 2009;276:3177–3198. doi: 10.1111/j.1742-4658.2009.07027.x. [DOI] [PubMed] [Google Scholar]
- Saxena M, Williams S, Brockdorff J, Gilman J, Mustelin T. Inhibition of T cell signaling by mitogen-activated protein kinase-targeted hematopoietic tyrosine phosphatase (HePTP) J Biol Chem. 1999;274:11693–11700. doi: 10.1074/jbc.274.17.11693. [DOI] [PubMed] [Google Scholar]
- Sharma E, Lombroso PJ. A neuronal protein tyrosine phosphatase induced by nerve growth factor. J Biol Chem. 1995;270:49–53. doi: 10.1074/jbc.270.1.49. [DOI] [PubMed] [Google Scholar]
- Shaul YD, Seger R. The MEK/ERK cascade: from signaling specificity to diverse functions. Biochim Biophys Acta. 2007;1773:1213–1226. doi: 10.1016/j.bbamcr.2006.10.005. [DOI] [PubMed] [Google Scholar]
- Shindo Y, Iwamoto K, Mouri K, Hibino K, Tomita M, Kosako H, Sako Y, Takahashi K. Conversion of graded phosphorylation into switch-like nuclear translocation via autoregulatory mechanisms in ERK signalling. Nat Commun. 2016;7:10485. doi: 10.1038/ncomms10485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shiozuka K, Watanabe Y, Ikeda T, Hashimoto S, Kawashima H. Cloning and expression of PCPTP1 encoding protein tyrosine phosphatase. Gene. 1995;162:279–284. doi: 10.1016/0378-1119(95)00306-q. [DOI] [PubMed] [Google Scholar]
- Sohaskey ML, Ferrell JEJ. Distinct, constitutively active MAPK phosphatases function in Xenopus oocytes: implications for p42 MAPK regulation in vivo. Mol Biol Cell. 1999;10:3729–3743. doi: 10.1091/mbc.10.11.3729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun H, Charles CH, Lau LF, Tonks NK. MKP-1 (3CH134), an immediate early gene product, is a dual specificity phosphatase that dephosphorylates MAP kinase in vivo. Cell. 1993;75:487–493. doi: 10.1016/0092-8674(93)90383-2. [DOI] [PubMed] [Google Scholar]
- Suwanmajo T, Krishnan J. Mixed mechanisms of multi-site phosphorylation. J R Soc Interface. 2015;12:20141405. doi: 10.1098/rsif.2014.1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi K, Tanase-Nicola S, ten Wolde PR. Spatio-temporal correlations can drastically change the response of a MAPK pathway. Proc Natl Acad Sci USA. 2010;107:2473–2478. doi: 10.1073/pnas.0906885107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanoue T, Adachi M, Moriguchi T, Nishida E. A conserved docking motif in MAP kinases common to substrates, activators and regulators. Nat Cell Biol. 2000;2:110–116. doi: 10.1038/35000065. [DOI] [PubMed] [Google Scholar]
- Thomson M, Gunawardena J. Unlimited multistability in multisite phosphorylation systems. Nature. 2009;460:274–277. doi: 10.1038/nature08102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verdugo A, Vinod PK, Tyson JJ, Novak B. Molecular mechanisms creating bistable switches at cell cycle transitions. Open Biol. 2013;3:120179. doi: 10.1098/rsob.120179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Sontag ED. On the number of steady states in a multiple futile cycle. J Math Biol. 2008;57:29–52. doi: 10.1007/s00285-007-0145-z. [DOI] [PubMed] [Google Scholar]
- Ward Y, Gupta S, Jensen P, Wartmann M, Davis RJ, Kelly K. Control of MAP kinase activation by the mitogen-induced threonine/tyrosine phosphatase PAC1. Nature. 1994;367:651–654. doi: 10.1038/367651a0. [DOI] [PubMed] [Google Scholar]
- Yang L, MacLellan WR, Han Z, Weiss JN, Qu Z. Multisite phosphorylation and network dynamics of cyclin-dependent kinase signaling in the eukaryotic cell cycle. Biophys J. 2004;86:3432–3443. doi: 10.1529/biophysj.103.036558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi H, Morton CC, Weremowicz S, McBride OW, Kelly K. Genomic organization and chromosomal localization of the DUSP2 gene, encoding a MAP kinase phosphatase, to human 2p11.2-q11. Genomics. 1995;28:92–96. doi: 10.1006/geno.1995.1110. [DOI] [PubMed] [Google Scholar]
- Zhang JL, Zhou B, Zheng CF, Zhang ZY. A bipartite mechanism for ERK2 recognition by its cognate regulators and substrates. J Biol Chem. 2003;278:29901–29912. doi: 10.1074/jbc.M303909200. [DOI] [PubMed] [Google Scholar]
- Zhao Y, Zhang ZY. The mechanism of dephosphorylation of extracellular signal-regulated kinase 2 by mitogen-activated protein kinase phosphatase 3. J Biol Chem. 2001;276:32382–32391. doi: 10.1074/jbc.M103369200. [DOI] [PubMed] [Google Scholar]
- Zhou B, Wang ZX, Zhao Y, Brautigan DL, Zhang ZY. The specificity of extracellular signal-regulated kinase 2 dephosphorylation by protein phosphatases. J Biol Chem. 2002;277:31818–31825. doi: 10.1074/jbc.M203969200. [DOI] [PubMed] [Google Scholar]
- Zhou B, Zhang ZY. Mechanism of mitogen-activated protein kinase phosphatase-3 activation by ERK2. J Biol Chem. 1999;274:35526–35534. doi: 10.1074/jbc.274.50.35526. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


