Abstract
Lactate dehydrogenase (LDH) catalyzes the interconversion of pyruvate and lactate. Recent isotope-edited IR spectroscopy suggests that conformational heterogeneity exists within the Michaelis complex of LDH, and this heterogeneity affects the propensity toward the on-enzyme chemical step for each Michaelis substate. By combining molecular dynamics simulations with Markov and hidden Markov models, we obtained a detailed kinetic network of the substates of the Michaelis complex of LDH. The ensemble-average electric fields exerted onto the vibrational probe were calculated to provide a direct comparison with the vibrational spectroscopy. Structural features of the Michaelis substates were also analyzed on atomistic scales. Our work not only clearly demonstrates the conformational heterogeneity in the Michaelis complex of LDH and its coupling to the reactivities of the substates, but it also suggests a methodology to simultaneously resolve kinetics and structures on atomistic scales, which can be directly compared with the vibrational spectroscopy.
INTRODUCTION
It has been long recognized that proteins are highly dynamic entities and their structures are best described as an ensemble of interconverting conformations on different time scales. The same holds true for the enzyme–substrate (Michaelis) complex which contains an ensemble of interconverting conformations, each with its own reactivity (kcat) as shown by recent single-molecule experiments,1–3 despite that it is usually assumed as a single active conformation in virtually all the textbooks.
Lactate dehydrogenase catalyzes the interconversion of pyruvate and lactate, using the cofactors NADH and NAD+, respectively, and it has been studied to characterize the conformational heterogeneity in the Michaelis complex and the coupling of this heterogeneity to enzymatic catalysis.4–10 Recently, the conformational heterogeneity of the ternary complex of LDH (LDH·NADH·pyruvate) was revealed through isotope-edited IR spectroscopy.9 The C=O stretching vibration of pyruvate was used as the vibrational probe, which is a direct measure of the strength of the electric field on the bond in a particular conformation and it is also highly correlated with the propensity toward the on-enzyme chemical reaction of that conformation.11 For local high-frequency vibration such as the C=O stretch, the vibration is assumed to behave as a one-dimensional oscillator. Vibrational Stark spectroscopy12 and theoretical computations13 have shown that the C=O stretching vibration responds to electric fields in a linear fashion, as suggested by linear Stark effect theory,14 which is believed to be an intrinsic property of the oscillator. Recently, it has been shown that a good linear correlation can be captured between the C=O frequencies and the ensemble-average electrostatic fields calculated by using the classical molecular dynamics (MD) with fixed-charge force fields.15
Isotope-edited IR spectroscopy has been proven to be a valuable tool to probe the conformational heterogeneity of the Michaelis complex and measure the reactivity of each Michaelis substate. Temperature-jump experiments combined with a kinetics model has been proposed for the Michaelis complex of LDH,10 in which four distinct Michaelis substates were resolved. However, structural information about degrees of freedom other than the probing carbonyl is mostly unknown. This information might shed light on important mechanisms such as how the enzyme interacts with the substrate in each Michaelis substate. It is a challenging problem to obtain a detailed kinetic network on atomistic scales for straightforward MD simulations, since the time scales of the involved motions range from nanosecond to microsecond, even millisecond. Markov state models (MSMs) have been shown to be able to reproduce long-time conformational dynamics of biomolecules using data from MD simulations that are individually much shorter. MSMs have been successfully applied to study the coupling of conformational dynamics of enzyme and substrate bindings in the lysine-, arginine-, ornithine-binding,16 choline-binding,17 and trypsin18 proteins.
Previously, we studied the catalytically relevant loop motions in purine nucleoside phosphorylase19 and lactate dehydrogenase20,21 using straighforward MD simulations. Recently, we estimated the free energy surface of the Michaelis complex of LDH using the cut-based free energy profile (FEP) method.22 Even though different substrate binding modes were resolved, the basins on the FEP and the substates resolved by vibrational spectroscopy were only compared indirectly through hydrogen bond analysis. Due to the limitation of the method, the relaxation time scales of the system were underestimated by about 4 orders of magnitude. In this work, 80 μs trajectories of MD simulations have been analyzed with a Markov model which is further coarse-grained into a hidden Markov model (HMM) to obtain the metastable states. A total of 13 substates which differ in protein conformations as well as the substrate binding modes were resolved. The structural features of the substates were analyzed, and a kinetic network was established between them. The relaxation time scales are closer to the experimental values. Ensemble-average electric fields were calculated for each substate and compared with the vibrational spectroscopy to assign the IR bands to the Michaelis substates quantitatively. Our results not only support the experiment-observed conformational heterogeneity in the Michaelis complex of LDH but also provide a detailed view of the interactions between LDH and pyruvate in each observed Michaelis substate.
METHODS
Molecular Dynamics Simulations
The MD simulation and force field parameters are identical to the settings used in ref 22. The initial structure was built on the X-ray crystal structure of human heart LDH complexed with the cofactor NADH and the substrate mimic oxamate (PDB ID: 1I0Z). Two asymmetric units were included to form the tetramer model, and the substrate pyruvate was created by manually substituting the oxamate nitrogen atom with a carbon atom. The proteins and the cofactors were modeled using the CHARMM36 force field,23,24 and the force field parameters for pyruvate were obtained using the CHARMM general force field.25 The system was solvated in a cubic TIP3P26 water box, and neutralized with sodium ions. To prevent the substrate from diffusing too far away from the active site, a soft wall potential was added to the hydride donor–acceptor distance at 15 Å. A total of 25 independent simulations of 0.8 μs were conducted with different initial velocities using the NAMD program.27 The coordinate trajectories of each subunit in the tetramer were treated as independent trajectories and saved every 100 ps for analysis, resulting in a total simulation time of 80 μs (8 × 105 snapshots).
Markov State Models
The first step of estimating an MSM is to transform the trajectories in Cartesian coordinate space into trajectories in a preselected feature space which can capture the conformational changes of the protein. After various descriptors were tested, we found that methods only including the backbone atoms (Cα) of the protein were not sufficient to resolve different conformations of the protein. Thus, we defined a feature set to describe the contacts between a set of 28 active site residues which includes the active site loop (residues 98–110 and 112), important active site residues (residues 138–139, 168, 193–195), and the contacting helix (residues 237–239, 242–243, and 246–248). First, the minimum inter-residue distance rmin, which is defined as the distance of the closest pair of heavy atoms between two residues, is calculated for each pair of the selected residues which are at least two residues apart from each other. The minimum inter-residue distance rmin can capture the conformational changes involving the backbones as well as the side chains of the protein. Then, instead of using a cutoff value (step function) to turn rmin into a binary contact indicator, we used a continuous function
where tanh is the hyperbolic tangent function and r1/2 = 5 Å, to transform rmin into a contact value x between 0 and 1 which captures the degree of contact of two residues. Next, we exclude the pairs of residues which have no contact with each other (x < 0.02) through the whole trajectories. In this way, each snapshot of protein can be represented by a 261-dimensional vector . Similar procedures were also applied to get the contact values between the carbonyl O of pyruvate and the selected active site residues, resulting in a 28-dimensional vector which was used as the input features to build the MSM to resolve different substrate binding states.
For the next step, a time-lagged independent component analysis (TICA)28,29 was performed on the featurized trajectories to find the slow linear subspace of the input features, and each TICA component was scaled according to its corresponding eigenvalue to obtain a kinetic map30 in which Euclidean distances are proportional to kinetic distances, providing an optimal space to perform clustering. When projecting the featurized trajectories, instead of keeping a selected number of TICA components, we chose to keep the TICA components which have eigenvectors that can account for 90% of the total variation in kinetic distance. Then, the k-means clustering method was employed to group the snapshots into microstates. Finally, the reversible transition matrix was estimated using the maximum likelihood estimator.31 All the estimations and analysis of MSM were done by using the PyEMMA 2 program.32
We first analyzed the microstates obtained by using combined with as the input features, which contains the protein conformations as well as the substrate binding. While the microstates resolved different protein conformations, they did not distinguish different binding states of the substrate, because the protein motions are on much slower time scales than the substrate motions in the current simulation system. Thus, we obtained another set of 500 microstates by using only as the input features, and then manually dividing each microstate by giving each snapshot an additional label which incorporated the substrate binding states. We determined the substrate binding states of each snapshot by estimating a MSM with 500 microstates using only as the input features, and lumping the microstates into four metastable states with the Perron cluster cluster analysis (PCCA) method.33,34 The metastable states were used as the label describing the substrate binding states. Thus, each microstate obtained by using as the input features was further divided into up to four possible new microstates, which yielded a new set of 758 microstates. We calculated the implied relaxation time scales as a function of the lag time τ which showed that the time scales become constant starting at a lag time of ~30 ns (Figure S4a). Therefore, τ = 30 ns was used as the lag time to estimate the final MSM.
Coarse-Grained Kinetic Model
By using the same set of 758 microstates, we also estimated a coarse-grained kinetic model using a HMM.35 First, the original MSM was coarse-grained into four metastable states using the PCCA+ method36 to obtain an initial guess for the hidden transition matrix the output probability matrix χ.35 Then, maximum likelihood HMM was estimated using the Baum–Welch method37,38 as implemented in the PyEMMA 2 program. Implied relaxation time scale as a function of lag time for the HMM was also calculated (Figure S4c), which shows reasonably converged time scales except for the time scales at a lag time of 10 ns where the reversible transition matrix estimation did not converge. Because the HMM was estimated by coarse-graining the MSM, the lag time of the HMM is the same as the lag time of the MSM (30 ns).
The expected value and variance of observable A in hidden state i can be estimated as
| (1) |
| (2) |
where χIi is the output probability of hidden state I to observed state (microstate) i and ⟨A⟩i is the expected value of A in the observed state i, which can be calculated as the mean of A for all the members of i. When the metastable state I was further divided into substates In on the basis of the substrate binding states n, the output probability of In to observed state i is
Then, the expected value and variance of observable A in substate In can be estimated using eqs 1 and 2. The transition probability between the substates is
| (3) |
where , and πI is the stationary probability of I. χI,In is the output probability of I to In, which can be calculated as
The stationary probability of In is
| (4) |
Bayes Factor Analysis
Bayes factor analysis39 was used to identify the key contacts defining each metastable state. The Bayes factor for a specific contact between residues i and j in state k can be calculated as
| (5) |
where cij is the contact indicator; i.e., cij = 1 if a contact is present between residues i and j and cij = 0 otherwise. Thus, for a specific contact in a specific state, the Bayes factor is the ratio of the probability of finding the system in this state given that the contact exists and the probability of finding the system in this state given that the contact does not exist. The Bayes factor can be seen as the degree of uniqueness for a contact to define a state. In this work, Bayes factors were calculated for the contacts between the same set of 28 active site residues used to define rmin, and cij was calculated as a step function of rmin(i, j)
In practice, the probability of observing cij = 1 in state k, P(cij = 1∣k), was estimated as the expected value of cij in state k using eq 1. The unconditional probability of observing cij = 1, P(cij = 1), was estimated as the average of P(cij = 1∣k) over all k’s, weighted by the stationary distribution of k. Then, P(cij = 0∣k) = 1 – P(cij = 1∣k) and P(cij = 0) = 1 – P(cij = 1). To avoid the contacts with small P(cij = 1∣k) from showing large Bayes factors, P(cij = 1∣k) was regularized by 10−4, which will suppress Bayes factors of rare contacts without affecting the others.
Electric Field Calculation
The electric field exerted onto the C=O stretching vibration of pyruvate by the environment (the whole system except for pyruvate) can be calculated from the electrostatic forces on the carbonyl atoms of pyruvate. Because the electrostatic forces are not readily available through the Tcl interface of the NAMD program, we adopted a similar strategy as in ref 15 to get the electrostatic forces on the carbonyl atoms for each snapshot using eqs 6–8.
| (6) |
| (7) |
| (8) |
First, the snapshots were postprocessed using the same simulation parameters as in the MD simulations to extract the total forces on the C and O atoms of the carbonyl in pyruvate, , where i denotes the C or O atom. Then, the snapshots were postprocessed again with the partial charges of all atoms of the environment set to zero, and the total forces on the C and O atoms, , which did not include the electrostatic forces exerted by the environment due to the lack of partial charges of the environment atoms, were also extracted. By taking the difference between the total forces from the two rounds of postprocessing calculations for the C or O atom (eq 6), we can get the electrostatic forces on the C or O atom exerted by the environment, . The electric field at the position of the C or O atom, , can be calculated as the electrostatic force on the corresponding atom dividing by the partial charge qi of the same atom (eq 7). Finally, the electric field experienced by the C=O stretching vibration, ∣Fvib∣, is calculated by projecting the electric field at the C or O atom onto the unit vector along the C=O bond, , and then averaging the two projections between the two atoms (eq 8).
RESULTS AND DISCUSSION
Multiple Metastable Substrate Binding States
Multiple substates of the Michaelis complex of LDH have been shown in experiment by vibrational spectroscopy. The C=O stretching vibration of the substrate pyruvate has been used as the vibrational probe in these experiments. The frequency shifts of the probe in different substates can show their propensities toward the chemical step, and can provide a direct measurement of the local electrostatic environments of the probe, which is ultimately determined by the interactions between the substrate and the protein/solvent such as hydrogen bonds. Thus, it is important to resolve the metastable substrate binding states in the MSM in order to compare with the experiments.
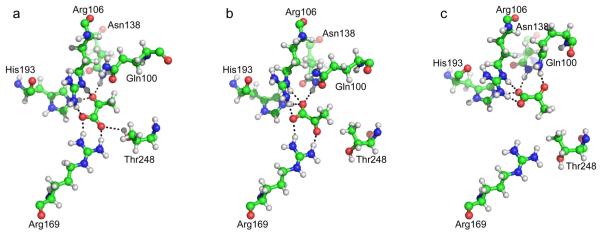
In this work, we first built an MSM on the basis of the contacts between the protein and the substrate only (the information about protein conformations not included explicitly; see Methods for details) and then lumped the microstates of the MSM into four metastable states. The first two metastable states are the same two binding states we found previously,22 the substrate binding state in the X-ray structure Sxray in which the carbonyl O of pyruvate forms hydrogen bonds with Arg106, Asn138, and His193 (Figures 1a and S1a) and the carboxyl O forms hydrogen bonds with Arg106, Arg169, and His193 (Figures 1a and S2a) and an alternative binding state Sflip in which pyruvate flips around its main chain by 180°, the carbonyl O forms a hydrogen bond with Arg169 (Figures 1b and S1b), and the carboxyl O forms hydrogen bonds with Arg106, Asn138, Arg169, and His193 (Figures 1b and S2b). The third metastable state is a newly resolved binding state Srotate in which the substrate rotates in the molecular plane by ~90° and shifts away from Arg169, the carbonyl O forms hydrogen bonds with Asn138 and a loop residue Gln100 (Figures 1c and S1c), and the carboxyl O forms hydrogen bonds with Arg106, Asn138, and His193 (Figures 1c and S2c). Furthermore, the methyl group of pyruvate also forms a nonpolar contact with Thr248 (Figures 1c and S3c) which could help in stabilizing the binding. In the last metastable state Sa/u, the substrate cannot form a metastable binding to the protein, and is only weakly associated with or unbound from it, so this state is very heterogeneous (Figures S1d, S2d, and S3d) in terms of substrate binding, and should not have significant contributions to the vibrational spectra of the probe.
Figure 1.
Representative structures from (a) the state of X-ray structure Sxray, (b) the flipped state Sflip, and (c) the rotated state Srotate.
The slowest time scales of the MSM are at sub-microseconds (Figure S4b). However, it should be noted that the MSM built upon the contacts between the enzyme and the substate should only be considered to be qualitative, since the time scales of the slowest motions in the system actually correspond to the protein motions which is neglected deliberately in this model, so we did not draw any quantitative conclusions from this model and only used the metastable states as an additional label for the microstates built upon the enzyme conformations to resolve different binding states of the substrate (see Methods).
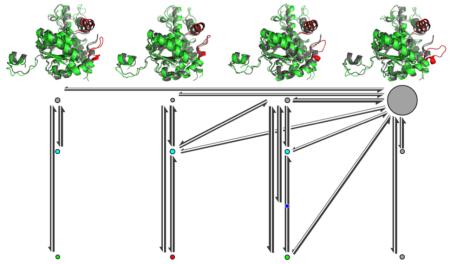
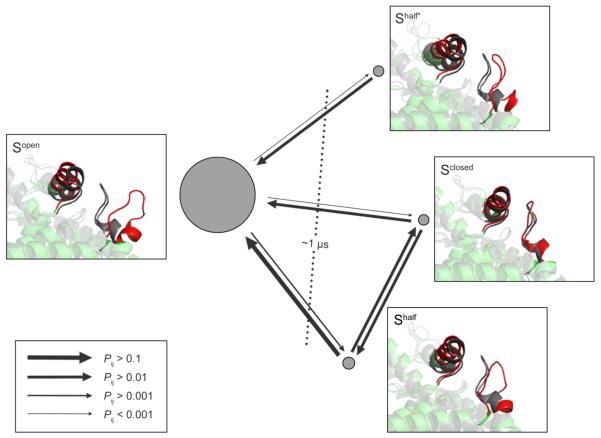
Microsecond Time Scale Protein Motions
By manually incorporating the substrate binding states into the discretization of the input feature space, we obtained a set of 758 microstates which were used to estimate a MSM. The MSM was further coarse-grained into a four-state HMM because there is a gap after the third relaxation time scales (Figure S4a) which indicates there are four metastable states in the model. Figure 2 shows the metastable states of the protein conformations. Representative structures for the metastable protein states are shown with the active site loop and its contacting helix highlighted and the crystal structure 1I0Z (in black) superimposed for comparison. By visual inspection, we found the overall structural differences between the metastable states mainly came from the active site loop region. At equilibrium, the vast majority (over 95%) of the system is in the open state Sopen, while each of the remaining states only accounts for 1–2% of the whole population. The slowest conformational change in the system is governed by a relaxation time scale of ~1 μs, which corresponds to the transition between the open state Sopen and the remaining (closed and half-open) states. This is in agreement with the previous experiments which showed the rate-limiting step in the turnover of LDH is the closure of the active site loop over the substrate binding pocket.40 At the currently used lag time (30 ns), Sclosed and Shalf can interconvert with each other, while Shalf* cannot interconvert with Sclosed or Shalf directly without going through Sopen. Shalf and Shalf* have similar conformations of the active site loop in terms of the loop–helix distances, but the inter-residue contacts defining each state are different (Figure 3; see below).
Figure 2.
Representative structures, equilibrium distribution, and kinetics of the four metastable protein states. The arrowed lines represent the transition probabilities between the metastable states. The areas of the discs are proportional to the probabilities of the corresponding metastable states at equilibrium. The dashed line represents the slowest relaxation time scale and its corresponding transition process.
Figure 3.
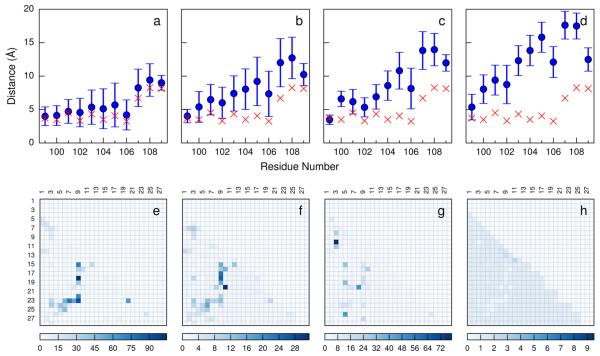
Structural features of the protein metastable states. HMM-weighted distributions of the minimum distances between the active site loop residues and the contacting helix in (a) Sclosed, (b) Shalf, (c) Shalf*, and (d) Sopen. The red markers represent the minimum distances calculated from the crystal structure; Bayes factors for the contacts used to define the protein conformation features for (e) Sclosed, (f) Shalf, (g) Shalf*, and (h) Sopen.
To compare the overall structures of the metastable states, we calculated the HMM-weighted distributions of the minimum distances between the active site loop residues and the contacting helix in each metastable state (Figure 3a–d). In Sclosed, the active site loop fluctuates around its position in the crystal structure, and remains in the closed position, while, in Sopen, the active site loop is in a wide open position compared with its position in the crystal structure, especially toward the end of the loop where the average minimum distances exceed 15 Å for Leu107 and Asn108. In both of the states Shalf and Shalf*, the active site loop is slightly more open than in the crystal structure.
To compare the structural features of the metastable states on a more detailed level, we calculated the Bayes factors39 (using eq 5; see Methods) for all of the inter-residue contacts used to define the protein conformation features (261 dimensions) to find what set of contacts uniquely define each metastable state. Parts e–h of Figure 3 show the results of the Bayes factor analysis, in which the magnitudes of the Bayes factors for the contacts in each metastable state reflect the degrees of uniqueness of the contacts with respect to other metastable states. There are two sets of contacts uniquely defining Sclosed (Figure 3e). One consists of the contact between Arg106 and Asn138 and the contact between Arg106 and His193, which also exist in the crystal structure. These residues are also important substrate binding residues. The other set of contacts that uniquely define Sclosed is formed by the helix residue Tyr239 and the loop residues 103–106, which suggests that these inter-residue contacts play an important role in stabilizing the closed conformation of the protein. In Shalf, the overall Bayes factors are quite similar to those in Sclosed (Figure 3f), though the values are much lower for Shalf, which suggests the similarities of the contacts in the two metastable states and is consistent with the fact that Sclosed and Shalf are kinetically close to each other (Figure 2). For Shalf* (Figure 3g), the contact with the largest Bayes factor is between two loop residues Gln100 and Leu107. There are also two contacts with relatively large Bayes factors: the contact between Ser105 and Asp195 and the contact between the loop residue Glu102 and the helix residue Gly246. There are no contacts with significant Bayes factors in Sopen (Figure 3h), which suggests that the conformations in Sopen are mostly unstructured, so there are no contacts that can uniquely define this metastable state.
Substates of the Michaelis Complex
Due to the separation of time scales between protein and substrate motions, the HMM mainly captured the protein motions; i.e., the substrate binding states are still mixed in each of the metastable protein states. To compare with the substates resolved in experiment, each of the four states in the HMM were further divided into up to four substates on the basis of the additional labels (substrate binding states) of the microstates, which resulted in 13 substates because some combinations of the substrate binding states and protein states were not observed in this model. Figure 4 shows the kinetic network of the substates, where the transition probabilities and stationary distribution are calculated using eqs 3 and 4. The majority of the population is in (~94%), which suggests that LDH is not a strong binder for pyruvate, whereas the populations of the remaining substates range from 0.1 to 1%. The substrate binding state Srotate only exists in the metastable state Shalf. The intermetastable transitions happen mainly when the substrate is in Sa/u or Sflip, which are not reactive binding states, and mainly through , which works like a central hub in the kinetic network. The reactive substates (, , , and ) cannot interconvert directly without going through a nonreactive substate (see below), which supports the experimental observations.10
Figure 4.
Kinetic network of substates of the metastable states.
Direct Comparison with Substates Resolved by Vibrational Spectroscopy
To have a direct comparison with vibrational spectroscopy, the electric field exerted onto the vibrational probe (the C=O stretching vibration of pyruvate) for each snapshot was calculated using eqs 6–8, and then the expected value and variance of the electric field for each substate were estimated using eqs 1 and 2. By excluding the substates with the protein in the open state or the substrate in the associated/unbound state, the remaining states can be grouped into four clusters on the basis of their expected values of the electric field. If we assign the four clusters to the four peaks of the IR spectrum of the LDH·NADH·pyruvate complex (1673, 1679, 1686, and 1699 cm−1),9 we can find a reasonably good linear correlation (R2 = 0.96) between the peak vibrational frequencies and the ensemble-average electric field (Figure 5), which suggested that the substates resolved in our model could be assigned to the observed substates of the Michaelis complex. It should be noted that the correlation between the standard deviation of the electric field distribution and the IR band’s line width is rather poor, as can be seen in Figure 5. One potential source of such large errors is that, even though the fixed-charge force field can describe the average properties of the electric field quite well, it is not adequate to capture the field heterogeneity. It has been suggested that reliable estimations of the IR line width for the C=O bond can be achieved by incorporating the polarizable force field.41 Another potential source is the limitation of the Stark effect theory itself due to its rather primitive form. More rigorous and well-parametrized models like the amide frequency maps,42 the solvatochromic charge model,43 or the more recent SolEFP method44 have been proposed to model the vibrational solvatochromism more versatilely and reliably.
Figure 5.
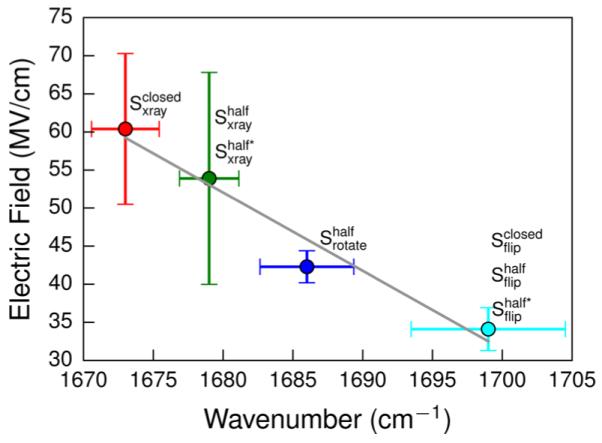
Correlation between calculated electric fields and the C=O stretching vibration of pyruvate for the substates of the metastable states. Error bars along the x- and y-axes correspond to the standard deviations of the IR spectrum and the electric field, respectively.
It has been suggested that each C=O band could potentially represent more than one substate,9 which is indeed the case as has been seen in our model. The C=O band with the largest frequency shift (1673 cm−1) corresponds to in which the active site is highly structured with the loop closed and C=O of pyruvate is highly polarized by the three hydrogen bonds formed with Arg106, Asn138, and His193. The C=O band at 1679 cm−1 corresponds to two substates and in which the substrate is still bound in a similar fashion as in the crystal structure but the active site loop is more open due to the loss of some key contacts in the closed state. The hydrogen bonds between the carbonyl O of pyruvate and the residues Arg106, Asn138, and His193 were weakened because of the higher flexibility of the active site, so the C=O band in and is less shifted than that in . The C=O band at 1686 cm−1 corresponds to in which the substrate rotates in the molecular plane and can only form two hydrogen bonds with Gln100 and Asn138, so the C=O is less polarized. The fitting of the C=O band at 1686 cm−1 is slightly worse than those of the other three bands, which could be caused by the fact that the band near 1686 cm−1 also contains the out-of-phase C=C stretch motions of the reduced nicotinamide moiety of NADH.9 The C=O band at 1699 cm−1 can be assigned to the substates with the substrate flipped regardless of the protein state (, , and ) in which the substrate flips around its main chain, and can only form one hydrogen bond with Arg169, so it has the least frequency shift. It has been proposed that the observed substates at 1673, 1679, and 1686 cm−1 are all reactive, whereas the observed substate at 1699 cm−1 is nonreactive.10 On the contrary to our previous proposal in which the substates with the flipped substrate were assigned to one of the three reactive observed substates,22 by comparing the calculated electric field and IR bands directly in this work, we found that the substates with the flipped substrate actually corresponded to the nonreactive substate at the IR band of 1699 cm−1.
CONCLUSIONS
The Markov and hidden Markov models have been shown to be a powerful tool to obtain a detailed kinetic network of the protein conformations and the coupled substrate bindings. When combining with the electric field calculations, they can provide a way to compare with the vibrational spectroscopy directly, which can help in interpreting and complementing the experiments on atomistic scales. In this work, we explored the conformational dynamics of LDH and its coupling to the interactions between LDH and pyruvate by combining MD simulations and Markov/hidden Markov models. Besides the associated/unbound state, three substrate binding states are resolved, which differ in the hydrogen bond network formed with the protein, including a previously unresolved binding mode in which the substrate rotates in the molecular plane by ~90° and shifts away from Arg169 compared to the crystal structure. For protein conformations, a hidden Markov model resolved four metastable states including closed state, two half-open states, and open state. The closed state resembles the crystal structure in terms of loop–helix distances and residue contacts in the active site, and the contacts between the helix residue Tyr239 and the loop residues 103–106 help in stabilizing the closed conformation. For the two half-open states, the loop–helix distances are slightly larger than the closed state. One half-open state is kinetically closer to the closed state, and has similar inter-residue contacts, while the other one has different contacts with the closed state. For the open state, the active site loop is fully open in terms of the loop–helix distances, and the conformations of the active site loop are unstructured.
To have a direct comparison with the vibrational spectroscopy, each of the metastable states was further divided into up to four substates according to the substrate binding states of the microstates, and the expected value of the electric field exerted onto the vibrational probe was calculated for each substate. We found a good linear correlation between the calculated electric field and the peaks of the infrared spectra, so we can assign the substates resolved in our model to the IR bands, and the structural features of substates corresponding to each IR band can be obtained. The IR bands with the largest three frequency shifts correspond to the binding state as in the crystal structure while the protein is in the closed state (1673 cm−1), or in either of the two half-open states (1679 cm−1), and the binding state with the rotated substrate while the protein is in one of the half-open states (1686 cm−1). These substates are all reactive but differ in the propensities toward the chemical reaction according to experiments. The IR band with the smallest frequency shift (1699 cm−1) corresponds to the binding state with the flipped substrate while the protein is not in the open states. The transition probabilities between the substates support the proposal that the reactive substates cannot interconvert directly without going through the nonreactive substates.
Our work supports the dynamical point of view of enzymatic catalysis45 and suggests a methodology to determine the detailed kinetic network of the Michaelis complex on atomistic scales which can be directly compared with the vibrational spectroscopy. For LDH, there is heterogeneity in the Michaelis complex in terms of protein conformations and substrate bindings, and the femtosecond on-enzyme chemical step46 is modulated by the microsecond protein conformational changes and the coupled nanosecond substrate binding mode changes. Thus, the conventional picture of enzymatic catalysis in which the on-enzyme chemical step is initiated from a single species, presumably the one resembling the crystal structures of the enzyme–substrate complex, might not provide the whole picture of the reaction. The methodology used in this work can be used to resolve all the distinct reactive substates which can be used as the starting structures in the study of the on-enzyme chemical step. Furthermore, the methodology used in this work can also be used in studying evolutionary adaptation of function such as adaptation to varying thermal environments, and allosteric regulation of enzyme, which are believed to be through the modulation of the Michaelis complex ground state ensemble distribution.47
Supplementary Material
ACKNOWLEDGMENTS
The authors acknowledge the support from National Institutes of Health Grant GM068036.
Footnotes
Box plots of the distributions of the minimum distances between carbonyl oxygen (Figure S1)/carboxyl oxygens (Figure S2)/methyl carbon (Figure S3) of pyruvate, and active site residues in different substrate binding states; implied relaxation time scales as a function of lag time (Figure S4); and output probabilities from hidden to observable discrete states (Figure S5) (PDF)
Notes
The authors declare no competing financial interest.
REFERENCES
- (1).Min W, English BP, Luo G, Cherayil BJ, Kou SC, Xie XS. Fluctuating Enzymes: Lessons from Single-Molecule Studies. Acc. Chem. Res. 2005;38:923–931. doi: 10.1021/ar040133f. [DOI] [PubMed] [Google Scholar]
- (2).Min W, Gopich IV, English BP, Kou SC, Xie XS, Szabo A. When Does the Michaelis-Menten Equation Hold for Fluctuating Enzymes? J. Phys. Chem. B. 2006;110:20093–20097. doi: 10.1021/jp065187g. [DOI] [PubMed] [Google Scholar]
- (3).Xie XS. Enzyme Kinetics, Past and Present. Science. 2013;342:1457–1459. doi: 10.1126/science.1248859. [DOI] [PubMed] [Google Scholar]
- (4).Gulotta M, Deng H, Deng H, Dyer RB, Callender RH. Toward an Understanding of the Role of Dynamics on Enzymatic Catalysis in Lactate Dehydrogenase. Biochemistry. 2002;41:3353–3363. doi: 10.1021/bi016009a. [DOI] [PubMed] [Google Scholar]
- (5).McClendon S, Vu DM, Clinch K, Callender R, Brian Dyer R. Structural Transformations in the Dynamics of Michaelis Complex Formation in Lactate Dehydrogenase. Biophys. J. 2005;89:L07–L09. doi: 10.1529/biophysj.105.064675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Deng H, Brewer S, Vu DM, Clinch K, Callender R, Dyer RB. On the Pathway of Forming Enzymatically Productive Ligand-Protein Complexes in Lactate Dehydrogenase. Biophys. J. 2008;95:804–813. doi: 10.1529/biophysj.108.128884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Zhadin N, Gulotta M, Callender R. Probing the Role of Dynamics in Hydride Transfer Catalyzed by Lactate Dehydrogenase. Biophys. J. 2008;95:1974–1984. doi: 10.1529/biophysj.108.132464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Deng H, Vu DV, Clinch K, Desamero R, Dyer RB, Callender R. Conformational Heterogeneity within the Michaelis Complex of Lactate Dehydrogenase. J. Phys. Chem. B. 2011;115:7670–7678. doi: 10.1021/jp2015929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Peng H-L, Deng H, Dyer RB, Callender R. Energy Landscape of the Michaelis Complex of Lactate Dehydrogenase: Relationship to Catalytic Mechanism. Biochemistry. 2014;53:1849–1857. doi: 10.1021/bi500215a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Reddish MJ, Peng H-L, Deng H, Panwar KS, Callender R, Dyer RB. Direct Evidence of Catalytic Heterogeneity in Lactate Dehydrogenase by Temperature Jump Infrared Spectroscopy. J. Phys. Chem. B. 2014;118:10854–10862. doi: 10.1021/jp5050546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Deng H, Zheng J, Clarke A, Holbrook JJ, Callender R, Burgner JW. Source of Catalysis in the Lactate Dehydrogenase System. Ground-State Interactions in the Enzyme·Substrate Complex. Biochemistry. 1994;33:2297–2305. doi: 10.1021/bi00174a042. [DOI] [PubMed] [Google Scholar]
- (12).Park ES, Andrews SS, Hu RB, Boxer SG. Vibrational Stark Spectroscopy in Proteins: A Probe and Calibration for Electrostatic Fields. J. Phys. Chem. B. 1999;103:9813–9817. [Google Scholar]
- (13).Choi J-H, Cho M. Vibrational Solvatochromism and Electrochromism of Infrared Probe Molecules Containing C≡O, C≡N, C=O, or C-F Vibrational Chromophore. J. Chem. Phys. 2011;134:154513. doi: 10.1063/1.3580776. [DOI] [PubMed] [Google Scholar]
- (14).Bublitz GU, Boxer SG. Stark Spectroscopy: Applications in Chemistry, Biology, and Materials Science. Annu. Rev. Phys. Chem. 1997;48:213–242. doi: 10.1146/annurev.physchem.48.1.213. [DOI] [PubMed] [Google Scholar]
- (15).Fried SD, Bagchi S, Boxer SG. Measuring Electrostatic Fields in Both Hydrogen-Bonding and Non-Hydrogen-Bonding Environments Using Carbonyl Vibrational Probes. J. Am. Chem. Soc. 2013;135:11181–11192. doi: 10.1021/ja403917z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Silva D-A, Bowman GR, Sosa-Peinado A, Huang X. A Role for Both Conformational Selection and Induced Fit in Ligand Binding by the LAO Protein. PLoS Comput. Biol. 2011;7:e1002054. doi: 10.1371/journal.pcbi.1002054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Gu S, Silva D-A, Meng L, Yue A, Huang X. Quantitatively Characterizing the Ligand Binding Mechanisms of Choline Binding Protein Using Markov State Model Analysis. PLoS Comput. Biol. 2014;10:e1003767. doi: 10.1371/journal.pcbi.1003767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Plattner N, Noé F. Protein Conformational Plasticity and Complex Ligand-binding Kinetics Explored by Atomistic Simulations and Markov Models. Nat. Commun. 2015;6:7653. doi: 10.1038/ncomms8653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Núñez S, Wing C, Antoniou D, Schramm VL, Schwartz SD. Insight into Catalytically Relevant Correlated Motions in Human Purine Nucleoside Phosphorylase. J. Phys. Chem. A. 2006;110:463–472. doi: 10.1021/jp051277u. [DOI] [PubMed] [Google Scholar]
- (20).Pineda JRET, Callender R, Schwartz SD. Ligand Binding and Protein Dynamics in Lactate Dehydrogenase. Biophys. J. 2007;93:1474–1483. doi: 10.1529/biophysj.107.106146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Pineda JRET, Antoniou D, Schwartz SD. Slow Conformational Motions That Favor Sub-picosecond Motions Important for Catalysis. J. Phys. Chem. B. 2010;114:15985–15990. doi: 10.1021/jp1071296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Pan X, Schwartz SD. Free Energy Surface of the Michaelis Complex of Lactate Dehydrogenase: A Network Analysis of Microsecond Simulations. J. Phys. Chem. B. 2015;119:5430–5436. doi: 10.1021/acs.jpcb.5b01840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Best RB, Zhu X, Shim J, Lopes PEM, Mittal J, Feig M, MacKerell AD. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 2012;8:3257–3273. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- (25).Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, Shim J, Darian E, Guvench O, Lopes P, Vorobyov I, et al. CHARMM General Force Field: A Force Field for Drug-like Molecules Compatible with the CHARMM All-atom Additive Biological Force Fields. J. Comput. Chem. 2010;31:671–690. doi: 10.1002/jcc.21367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- (27).Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Peréz-Hernández G, Paul F, Giorgino T, Fabritiis GD, Noé F. Identification of Slow Molecular Order Parameters for Markov Model Construction. J. Chem. Phys. 2013;139:015102. doi: 10.1063/1.4811489. [DOI] [PubMed] [Google Scholar]
- (29).Schwantes CR, Pande VS. Improvements in Markov State Model Construction Reveal Many Non-Native Interactions in the Folding of NTL9. J. Chem. Theory Comput. 2013;9:2000–2009. doi: 10.1021/ct300878a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Noé F, Clementi C. Kinetic Distance and Kinetic Maps from Molecular Dynamics Simulation. J. Chem. Theory Comput. 2015;11:5002–5011. doi: 10.1021/acs.jctc.5b00553. [DOI] [PubMed] [Google Scholar]
- (31).Prinz J-H, Wu H, Sarich M, Keller B, Senne M, Held M, Chodera JD, Schütte C, Noé F. Markov Models of Molecular Kinetics: Generation and Validation. J. Chem. Phys. 2011;134:174105. doi: 10.1063/1.3565032. [DOI] [PubMed] [Google Scholar]
- (32).Scherer MK, Trendelkamp-Schroer B, Paul F, Pérez-Hernández G, Hoffmann M, Plattner N, Wehmeyer C, Prinz J-H, Noé F. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput. 2015;11:5525–5542. doi: 10.1021/acs.jctc.5b00743. [DOI] [PubMed] [Google Scholar]
- (33).Schütte C, Fischer A, Huisinga W, Deuflhard P. A Direct Approach to Conformational Dynamics Based on Hybrid Monte Carlo. J. Comput. Phys. 1999;151:146–168. [Google Scholar]
- (34).Weber M. Improved Perron Cluster Analysis. ZIB-Report. 2003;03–04 [Google Scholar]
- (35).Noé F, Wu H, Prinz J-H, Plattner N. Projected and Hidden Markov Models for Calculating Kinetics and Metastable States of Complex Molecules. J. Chem. Phys. 2013;139:184114. doi: 10.1063/1.4828816. [DOI] [PubMed] [Google Scholar]
- (36).Deuflhard P, Weber M. Robust Perron Cluster Analysis in Conformation Dynamics. Linear Algebra Appl. 2005;398:161–184. [Google Scholar]
- (37).Baum LE, Petrie T, Soules G, Weiss N. A Maximization Technique Occurring in the Statistical Analysis of Probabilistic Functions of Markov Chains. Ann. Math. Stat. 1970;41:164–171. [Google Scholar]
- (38).Welch LR. Hidden Markov Models and the Baum-Welch Algorithm. IEEE Inf. Theory Soc. Newsl. 2003;53:1–13. [Google Scholar]
- (39).Zhou G, Voelz VA. Using Kinetic Network Models To Probe Non-Native Salt-Bridge Effects on α-Helix Folding. J. Phys. Chem. B. 2016;120:926–935. doi: 10.1021/acs.jpcb.5b11767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Dunn CR, Wilks HM, Halsall DJ, Atkinson T, Clarke AR, Muirhead H, Holbrook JJ. Design and Synthesis of New Enzymes Based on the Lactate Dehydrogenase Framework. Philos. Trans. R. Soc., B. 1991;332:177–184. doi: 10.1098/rstb.1991.0047. [DOI] [PubMed] [Google Scholar]
- (41).Fried SD, Wang L-P, Boxer SG, Ren P, Pande VS. Calculations of the Electric Fields in Liquid Solutions. J. Phys. Chem. B. 2013;117:16236–16248. doi: 10.1021/jp410720y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).la Cour Jansen T, Dijkstra AG, Watson TM, Hirst JD, Knoester J. Modeling the Amide I Bands of Small Peptides. J. Chem. Phys. 2006;125:044312. doi: 10.1063/1.2218516. [DOI] [PubMed] [Google Scholar]
- (43).Lee H, Choi J-H, Cho M. Vibrational Solvatochromism and Electrochromism. II. Multipole Analysis. J. Chem. Phys. 2012;137:114307. doi: 10.1063/1.4751477. [DOI] [PubMed] [Google Scholar]
- (44).Błasiak B, Cho M. Vibrational Solvatochromism. III. Rigorous Treatment of the Dispersion Interaction Contribution. J. Chem. Phys. 2015;143:164111. doi: 10.1063/1.4934667. [DOI] [PubMed] [Google Scholar]
- (45).Callender R, Dyer RB. The Dynamical Nature of Enzymatic Catalysis. Acc. Chem. Res. 2015;48:407–413. doi: 10.1021/ar5002928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Basner JE, Schwartz SD. How Enzyme Dynamics Helps Catalyze a Reaction in Atomic Detail: A Transition Path Sampling Study. J. Am. Chem. Soc. 2005;127:13822–13831. doi: 10.1021/ja043320h. [DOI] [PubMed] [Google Scholar]
- (47).Hochachka PW, Somero GN. Biochemical Adaptation: Mechanism and Process in Physiological Evolution. Oxford University Press; Oxford, U.K.: 2002. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.