Abstract
Mathematical disabilities (MD) have a negative life-long impact on professional success, employment, and health outcomes. Yet, little is known about the intrinsic functional brain organization that contributes to poor math skills in affected children. It is now increasingly recognized that math cognition requires coordinated interaction within a large-scale fronto-parietal network anchored in the intraparietal sulcus (IPS). Here we characterize intrinsic functional connectivity within this IPS-network in children with MD, relative to a group of typically developing (TD) children who were matched on age, gender, IQ, working memory, and reading abilities. Compared to TD children, children with MD showed hyper-connectivity of the IPS with a bilateral fronto-parietal network. Importantly, aberrant IPS connectivity patterns accurately discriminated children with MD and TD children, highlighting the possibility for using IPS connectivity as a brain-based biomarker of MD. To further investigate regional abnormalities contributing to network-level deficits in children with MD, we performed whole-brain analyses of intrinsic low-frequency fluctuations. Notably, children with MD showed higher low-frequency fluctuations in multiple fronto-parietal areas that overlapped with brain regions that exhibited hyper-connectivity with the IPS. Taken together, our findings suggest that MD in children is characterized by robust network-level aberrations, and is not an isolated dysfunction of the IPS. We hypothesize that intrinsic hyper-connectivity and enhanced low-frequency fluctuations may limit flexible resource allocation, and contribute to aberrant recruitment of task-related brain regions during numerical problem solving in children with MD.
Strong foundational skills in mathematics are indispensable not only for educational and professional success, but also for quantitative reasoning in everyday life (Butterworth, Varma, & Laurillard, 2011; Geary, Nugent, & Bailey, 2013; Parsons & Bynner, 2005). Critically, disabilities in numerical and mathematical problem solving, including developmental dyscalculia, are widespread (Butterworth et al., 2011; Shalev, Auerbach, Manor, & Gross-Tsur, 2000; Szucs & Goswami, 2013). Yet, despite its negative consequences for employability, academic performance, and socio-economic well-being (Butterworth et al., 2011; Parsons & Bynner, 2005), the etiology of mathematical disabilities (MD) and its neural underpinnings remain unclear.
It has been argued that MD originates from a core dysfunction in the representation of quantity and the inability to access numerical magnitude information conveyed by number symbols or words (Butterworth et al., 2011; Noel & Rousselle, 2011). Converging evidence from adults, children and, non-human primates suggests that the representation of approximate quantity is a foundational ability supported by the intraparietal sulcus (IPS) subdivision of the dorsal posterior parietal cortex (for reviews, see e.g., Ansari, 2008; Brannon, 2006; Cohen Kadosh, Lammertyn, & Izard, 2008). An emerging body of research has led to the hypothesis that the IPS is a key locus of deficits in children with MD (e.g., Cohen Kadosh et al., 2007; Price, Holloway, Rasanen, Vesterinen, & Ansari, 2007). However, while task-based functional MRI (fMRI) studies have consistently demonstrated aberrant IPS recruitment in children with MD (Ashkenazi, Rosenberg-Lee, Tenison, & Menon, 2012; Kaufmann, Vogel, Starke, Kremser, Schocke, et al., 2009; Kucian et al., 2006; Molko et al., 2003; Mussolin et al., 2010; Price et al., 2007; Rosenberg-Lee et al., 2014), it is the case that multiple distributed regions within posterior parietal, prefrontal and, ventral temporal-occipital cortices show impairments as well (Ashkenazi et al., 2012; Kaufmann, Wood, Rubinsten, & Henik, 2011; Kucian, 2011; Mussolin et al., 2010). Furthermore, children with MD show aberrant task-related functional connectivity between IPS and multiple brain systems during arithmetic problem-solving (Rosenberg-Lee et al., 2014). These findings have led to the hypothesis that MD may involve an intrinsic network-level aberration, rather than an isolated dysfunction of the IPS (Fias, Menon, & Szucs, 2014).
There is growing evidence to suggest that numerical cognition relies on interactions within and between multiple functional brain systems, including those subserving quantity processing, episodic and semantic memory, working memory, and cognitive control (e.g., Arsalidou & Taylor, 2011; Fias et al., 2014; Figure 1). While the IPS plays a key role in building representations of numerical quantity, it is also part of an intrinsically connected dorsal fronto-parietal system that includes the superior parietal lobe (SPL), frontal eye fields, supplementary motor area (SMA), insula, and middle frontal gyrus (MFG) (Corbetta, Patel, & Shulman, 2008; Corbetta & Shulman, 2002; Menon & Uddin, 2010; Supekar & Menon, 2012; Uddin et al., 2010). This system is thought to be important for top-down goal-driven attention, including performance monitoring and manipulation of numerical information in working memory. In contrast, the ventral attention system, which includes the supramarginal gyrus (SMG), insula and inferior frontal gyrus, is thought to be involved in saliency processing and attentional filtering (Corbetta et al., 2008; Corbetta & Shulman, 2002; Fox, Corbetta, Snyder, Vincent, & Raichle, 2006; Menon & Uddin, 2010; Supekar & Menon, 2012). Finally, memory systems anchored in the medial and anterior temporal lobe, as well as in the angular gyrus, are important for encoding and retrieval of math facts (Grabner et al., 2009; Qin, Cho, et al., 2014). It is currently not known whether functional circuits associated with the IPS are aberrant in MD and crucially, whether they impact the multiple dorsal and ventral fronto-parietal and memory circuits that are involved in numerical cognition.
Figure 1. Schematic diagram of math-related brain circuits.
It is increasingly recognized that mathematical processing requires interaction within and between multiple interacting brain systems, including systems involved in processing lower-order visual information and number form (brown), numerical quantity (green), episodic and semantic memory (blue), and attentional control (red and black). Adapted from Fias et al. (2014). AG = angular gyrus, AI = anterior insula, ATL = anterior temporal lobe, FEF = frontal eye fields, IFG = inferior frontal gyrus, IPS = intraparietal sulcus, ITC = inferior temporal cortex, MFG = middle frontal gyrus, MTL = medial temporal lobe, SMA = supplementary motor area, SMG = supramarginal gyrus, SPL = superior parietal lobe.
Although most studies of numerical cognition in children with MD have found aberrations within the IPS, as well as multiple other parietal and prefrontal cortical areas, the exact profile of aberrations has varied considerably from study to study. For example, some studies have reported hypo-activity in IPS and associated fronto-parietal brain areas in children with MD (e.g., Kucian, 2011; Kucian et al., 2006; Price et al., 2007), while others have found hyper-activity (e.g., Davis et al., 2009; Iuculano et al., 2015; Kaufmann, Vogel, Starke, Kremser, Schocke, et al., 2009; Rosenberg-Lee et al., 2014). Such inconsistencies may arise from differences in the numerical tasks (e.g., non-symbolic number comparison, symbolic number comparison, addition, subtraction) and baseline (“control”) conditions (e.g., fixation, mental rotation, manipulation of task complexity) used in various studies, as well as differences in task performance between the MD and typically developing groups (see Menon, 2015 for a detailed review). Intrinsic functional connectivity (e.g., Fox & Raichle, 2007) has the potential to address broader questions related to functional brain organization in MD and to circumvent methodological issues arising from differences in the type of numerical task and control conditions used, as well as confounding effects of task performance and strategy use (e.g., Church et al., 2009; Fair et al., 2007; Finn et al., 2014; Koyama et al., 2011; Supekar, Uddin, et al., 2013; Uddin et al., 2013).
Here we use task-free fMRI to address critical gaps in our knowledge of aberrant parietal networks in children with MD. Specifically, we investigated intrinsic functional connectivity of the IPS in 7 to 9 year old children with MD, and contrasted it with functional connectivity of a well-matched group of typically developing (TD) children, who differed on math achievement, but not on age, gender, IQ, reading abilities, or working memory. We hypothesized that functional circuits associated with the IPS would be aberrant in children with MD, and that IPS connectivity patterns could be used to discriminate children with MD from TD controls.
Methods
Participants
Data from two ongoing research projects (Project 1: Ashkenazi, Rosenberg-Lee, Metcalfe, Swigart, & Menon, 2013; Ashkenazi et al., 2012; Rosenberg-Lee et al., 2014; Project 2: Iuculano et al., 2015; Supekar, Swigart, et al., 2013) examining mathematical cognition in children with and without MD were included in the present study. Participants were recruited from a wide range of schools in the San Francisco Bay Area using mailings to schools, and postings at libraries and community groups. We included second and third grade children (7–9 years old) with no history of developmental disabilities and with a full-scale IQ above 80, assessed using the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999). In the absence of agreement about the exact definition and diagnostic criteria of MD (Kaufmann et al., 2013; Szucs & Goswami, 2013), here MD was defined as mathematical achievement at or below the 25th percentile (Ashkenazi et al., 2013; Ashkenazi et al., 2012; Davis et al., 2009; Swanson, Jerman, & Zheng, 2009), which corresponds to 90 points on a standardized test scale. This is in line with cut-off criteria used in fMRI studies of developmental dyslexia (e.g., Finn et al., 2014; Tanaka et al., 2011). Nineteen children (8.91 years (SD 0.60), 13 girls and 6 boys) who scored at or below 90 on the Numerical Operations subtest of the Wechsler Individual Achievement Test, Second Edition (WIAT-II; Wechsler, 2001) were included in the MD group. In addition, we performed follow-up analyses on a subset of 14 children with the most severe math disabilities, scoring at or below 85 on Numerical Operations (i.e., at least one standard deviation lower than the population average). MD children with co-morbid reading disabilities, i.e., children who scored at or below 90 on the Word Reading or Reading Comprehension subtests of the WIAT-II (Wechsler, 2001) were excluded from the study, as were children with excessive head movement (for movement characteristics see below). The TD group consisted of nineteen children (8.75 years (SD 0.75), 9 girls, 10 boys), who scored at or above 95 (37th percentile) on the Numerical Operations subtest of the WIAT-II. TD children were selected using a genetic algorithm (Uddin et al., 2013) designed to ensure that the two groups did not differ on age, gender, full-scale IQ, and reading ability (based on the Word Reading subtest of the WIAT-II).
To control for variations in data acquisition and scan parameters across the two research studies, we ensured that the MD and TD groups included the same number of children from each study cohort – the MD and TD groups included 13 children from one cohort (Ashkenazi et al., 2013; Ashkenazi et al., 2012; Rosenberg-Lee et al., 2014) and 6 children from the other (Iuculano et al., 2015; Supekar, Swigart, et al., 2013). Furthermore, all analyses included “cohort” as a covariate of no interest. To further examine the robustness of our findings, we performed additional region of interest (ROI) analyses in the two cohorts separately. Informed consent was obtained from the legal guardian of each child participant, and study protocols were approved by the Stanford University Institutional Review Board.
Standardized Cognitive Assessments
Mathematical abilities
Mathematical abilities were assessed using the WIAT-II (Wechsler, 2001). This achievement battery includes nationally standardized measures of K-12 academic skills and problem-solving abilities, which are normed by grade and time of academic year (Fall, Spring, or Summer). The Numerical Operations subtest is a paper-and-pencil test that measures number writing and identification, rote counting, number production, and simple addition, subtraction, multiplication, and division problems. For example, 4 – 2 = ___ and 37+54 = ___ (presented horizontally and vertically, respectively) are two problems in the 2nd and 3rd grade range. The Mathematical Reasoning subtest is a verbal problem-solving test that measures counting, geometric shape identification, and single- and multi-step word problem-solving involving time, money, and measurement with both verbal and visual prompts. The child is required to solve problems with whole numbers, fractions or decimals, interpret graphs, identify mathematical patterns, and solve problems of statistics and probability. For example, a dime is presented and the child is asked, “How many pennies does it take to equal the value of one dime?” An example of a probability problem is: “If you flipped a coin ten times, how many times would the coin be most likely to land on heads?”
Reading abilities
The WIAT-II was also used to assess reading abilities. The Word Reading subtest involves reading individual words presented visually to the child, and was used for matching the MD and TD groups on reading ability. In addition, the Reading Comprehension subtest was administered, which involves reading passages and answering questions about them.
Working memory
Four subtests of the Working Memory Test Battery for Children (WMTBC) (Pickering & Gathercole, 2001) were used to assess working memory abilities: 1) Counting Recall and 2) Backward Digit Recall, which are thought to measure the central executive, 3) Digit Recall, which is thought to measure phonological loop, and 4) Block Recall, a variant of the Corsi block tapping test which is thought to measure the visuo-spatial sketch pad (Pickering & Gathercole, 2001).
FMRI data acquisition
Functional imaging data were acquired at a 3T General Electric Signa Scanner at The Richard M. Lucas Center for Imaging at Stanford University. Participants were instructed to lay still with their eyes closed for the duration of the entire scan. For the first study cohort (13 MDs and 13 TDs), the resting-state scan contained 240 volumes and was acquired using a single-channel head-coil. Data for the second study cohort (6 MDs and 6 TDs) contained 180 volumes and was acquired using an 8-channel head-coil. All other scanning parameters were similar as noted below. Twenty-nine axial slices (4.0 mm thickness, 0.5 mm skip) were collected parallel to the AC-PC line, using a T2* weighted gradient echo spiral in-out pulse sequence (Glover & Lai, 1998) (TR = 2000ms; TE = 30ms, flip angle =80°, 1 interleave). Scans were acquired with a field of view of 20 x 20 cm and a matrix size of 64 x 64, providing an in-plane spatial resolution of 3.125 mm. To reduce blurring and signal loss from field in-homogeneity, an automated high-order shimming method based on spiral acquisitions was used before acquiring the functional MRI scan (Kim, Adalsteinsson, Glover, & Spielman, 2002).
Movement
Head movement was minimized during scanning by a comfortable, custom-built restraint. Before group matching, we excluded children with movement larger than 5 mm in either the x, y, or z directions. In the examined MD sample, the movement range was on average 0.41 (SD 0.27), 0.74 (SD 0.58), and 1.54 (SD 1. 33) mm in the x, y, and z direction, with 0.71 (SD 0.50), 1.76 (SD 1.54), 0.68 (SD 0.64) degrees of roll, pitch, and yaw. In TDs, the movement range was on average 0.43 (SD 0.51), 0.69 (SD 0.63), 1.39 (SD 1.19) mm in the x, y, and z direction, with 0.80 (0.74), 1.71 (SD 1.46), 0.70 (SD 0.63) degrees of roll, pitch, and yaw. There were no significant differences in movement between the groups on any of the six movement parameters (all ps ≥.649, η2p ≤ .006). Mean frame-wise displacement did not exceed > .5, and was almost identical across groups (p = .955, η2p < .001).
FMRI data preprocessing
The first 6 volumes were not analyzed to allow for signal equilibration. A linear shim correction was applied separately for each slice during reconstruction using a magnetic field map acquired automatically by the pulse sequence at the beginning of the scan (Glover & Lai, 1998). FMRI data were preprocessed and analyzed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm). Preprocessing procedures included slice time correction, normalization to the standard Montreal Neurological Institute (MNI) T1 template, and spatial smoothing using a Gaussian kernel (6 mm full-width at half-maximum). For the functional connectivity analyses, a bandpass filter (0.008 to 0.1 Hz) was applied to the smoothed data to remove high frequency artifacts.
Functional connectivity analysis
Seed regions of interest
We defined the IPS seed ROIs using observer-independent cytoarchitectonic regions, combining the maximum probability maps of hIP1, hIP2, and hIP3 of the Anatomy Toolbox in SPM8. Detailed information about the anatomical boundaries of these maps has been published elsewhere (Caspers et al., 2008; Caspers et al., 2006; Choi et al., 2006). The MarsBar toolbox (http://marsbar.sourceforge.net/) was used to create a binary ROI from these maps (Figure 2).
Figure 2. IPS seed regions of interest (ROIs).
ROIs were defined based on unbiased observer-independent cytoarchitectonic regions (Caspers et al., 2006, 2008; Choi et al., 2006). IPS = intraparietal sulcus. Coordinates are in MNI space.
Whole-brain functional connectivity analysis
For the whole-brain functional connectivity analysis, we used a seed-correlation approach similar to that described in Uddin et al. (2010). First-level analyses were performed on a subject-by-subject basis. For each ROI, we separately extracted the first eigenvector time course, and then calculated how strongly that time course fit the data at each voxel using a General Linear Model (GLM). The global mean signal, computed across all voxels of the brain, as well as 6 motion parameters were included as additional covariates of no interest in the model to take into account the effects of physiological noise and participant movement. Individual contrast images were then submitted to group-level analyses.
Group comparisons of functional connectivity were performed using two-sample t-tests, with study cohort as a covariate of no interest. In addition, to examine whether severity of MD was related to the level of aberrant brain connectivity, we performed regression analyses within the MD group using demeaned scores of math ability (WIAT-II Numerical Operations subtest) as a covariate of interest. Cohort was again included here as a covariate of no interest. This analysis addresses an important question regarding the neural correlates of heterogeneity and individual differences in MD. Note that performing this analysis across the entire sample would have been minimally informative, as we would have likely found results similar to the categorical MD versus TD analysis since these same math ability scores were used as an inclusion criterion for group membership.
Results were masked using a gray matter image and thresholded at p < 0.01 height, with family-wise error (FWE) corrections for multiple comparisons at the cluster level (p < 0.01, spatial extent 128 voxels). The cluster size was determined using Monte Carlo simulations implemented in MatLab (cf. Rosenberg-Lee, Barth, & Menon, 2011).
Network-based classification of children with MD
To examine whether children with MD could be discriminated from their TD peers based on IPS functional connectivity patterns, we used a linear, hard-margin SVM classifier implemented in the R package e1071 (http://cran.r-project.org/web/packages/e1071/). Before running the classification analysis, connectivity maps were normalized, voxel-wise, within each cohort by subtracting the mean and then dividing by the standard deviation. Next, individual subject maps were masked to include only voxels that were significant at the group level (p < 0.01 FWE correction at the whole-brain level, spatial extent 100 voxels; Supplementary Figure S1). A linear, hard-margin SVM with cost parameter C fixed to 10e9 was used to avoid over-fitting, which might occur in cases where the predictors (number of voxels) outnumber the observations (participants) (Uddin et al., 2013). Classification accuracy was estimated using a leave-one-out cross validation. The data were divided into N folds (N = 38). N-1 folds were used to build a classifier, and classification was tested on the left-out sample. This procedure was repeated N times, and the average classification accuracy was computed. We used permutation tests (10000 permutations) to compute the p-values associated with the classification accuracy of each IPS-network by randomly assigning subjects into TD and MD groups. Further, confidence intervals for classification accuracy were computed via a bootstrapping procedure. For each of 10000 iterations, 19 subjects from each group were sampled with replacement to generate a surrogate sample which was then submitted to the same cross-validation procedure outlined above. This produces an empirical distribution of classification accuracies from which we derived the 95% confidence interval.
Fractional Amplitude of Low Frequency Fluctuations (fALFF) analysis
To investigate group differences in regional low frequency fluctuations, we performed voxel-wise analyses of fractional Amplitude of Low Frequency Fluctuations (fALFF), which provides a measure of the BOLD signal amplitude within a specific brain region, and is defined by the power of the signal in the low frequency range relative to the power across all frequencies (Mennes et al., 2011; Zang et al., 2007; Zou et al., 2008; Zuo et al., 2010). Unlike functional connectivity, which examines the interactions of investigator-specified brain regions, fALFF is a regional measure that does not require a priori definition of specific ROIs, and can therefore be used to explore aberrant intrinsic brain dynamics outside our hypothesized IPS-network. Compared to ALFF (i.e., the power of the fluctuations in the low frequency range, irrespective of the power in the other frequencies), fALFF is thought to have better sensitivity and specificity in detecting the spontaneous signal fluctuations because it is less affected by physiological noise (Zou et al., 2008). Preprocessing procedures for the fALFF analyses involved the same steps as the functional connectivity analyses, including slice time correction, normalization to the MNI template, and spatial smoothing. Because fALFF involves computation of the power across the entire frequency spectrum, bandpass filtering was not applied to the time series. Following Zou et al. (2008) we computed the power spectrum at each voxel by transforming the time series to the frequency domain. Then, we calculated the square root of the amplitude at each frequency (which is proportional to the power at that frequency). Finally, we divided the sum of the amplitude across the low frequencies (0.008 to 0.1 Hz) by the sum of the amplitudes across the entire frequency range.
Results were masked using a gray matter image and thresholded at p < 0.01 height, with FWE corrections for multiple comparisons at the cluster level (p < 0.01, spatial extent 128 voxels).
Results
Neuropsychological profile
Table 1 shows standardized measures of math, reading, IQ, and working memory for the MD and TD groups. These groups were a priori matched on age, gender, full-scale IQ, and Word Reading. Beyond the difference in Numerical Operations by design, groups also differed on the Mathematical Reasoning subtest of the WIAT-II. None of the non-math measures showed a significant difference between groups, including working memory and Reading Comprehension, suggesting that the groups were very well matched for general cognitive abilities.
Table 1.
Participant characteristics of the MD and TD groups
| MD | TD | ||
|---|---|---|---|
| Age* | 8.91 (0.60) | 8.75 (0.75) | p = 0.480, η2p = .014 |
| Gender* | 13F/ 6M | 9F/ 10M | p = 0.325, ϕ = .213 |
| WASI | |||
| Performance IQ | 103.1 (11.8) | 106.6 (10.3) | p = 0.334, η2p = .026 |
| Verbal IQ | 104.9 (12.7) | 100.8 (11.2) | p = 0.292, η2p = .031 |
| Full-scale IQ* | 104.1 (8.9) | 104.5 (9.0) | p = 0.900, η2p < .001 |
| WIAT-II | |||
| Numerical Operations** | 83.5 (4.4) | 110.7 (8.1) | p < .001, η2p = .821 |
| Mathematical Reasoning | 94.3 (9.5) | 106.2 (11.4) | p = .001, η2p = .256 |
| Word Reading* | 102.9 (8.2) | 103.7 (5.8) | p = 0.734, η2p = .003 |
| Reading Comprehension | 103.6 (6.1) | 104.1 (9.6) | p = 0.841, η2p = .001 |
| WMTB-C | |||
| Digit Recall | 100.9 (17.2) | 104.9 (19.1) | p = 0.502, η2p = .013 |
| Block Recall§ | 91.6 (11.8) | 97.6 (11.5) | p = 0.125, η2p = .066 |
| Counting Recall§ | 81.8 (18.3) | 83.3 (16.5) | p = 0.789, η2p = .002 |
| Backward Digit Recall | 92.4 (17.9) | 91.2 (12.2) | p = 0.809, η2p = .002 |
Note:
Used for group assignment;
Used for matching;
For Block recall and count recall, data from one participant were lost.
For all other analyses, N = 38. Gender differences were assessed using a chi-square test. All other differences were examined using univariate ANOVAs. MD = children with mathematical disabilities, TD = typically developing children.
Children with MD show IPS hyper-connectivity compared to TD children
Across the MD and TD groups, the IPS showed strong intrinsic functional connectivity with multiple bilateral prefrontal, parietal, and ventrotemporal occipital areas, including IPS, SPL, SMG, MFG, superior frontal gyrus (SFG), SMA, insula, and fusiform gyrus (Supplementary Figure S1). Comparison of IPS connectivity patterns between the groups revealed greater functional connectivity in children with MD in a number of regions within this fronto-parietal network (p < 0.01, spatial extent 128 voxels; Tables 2 and 3; Figure 3A). Specifically, children with MD showed increased inter-hemispheric connectivity between left and right IPS, as well as between IPS and other dorsal fronto-parietal regions, including bilateral SPL/lateral occipital cortex and left SFG/ MFG. In addition, both the left and right IPS showed greater functional connectivity with right SMG and superior temporal gyrus (STG). In addition to these regions, the right IPS also showed greater connectivity with right SFG, precentral gyrus, and SMA, while the left IPS showed greater connectivity with the left frontal pole and right putamen in children with MD. Only one cluster showed reduced IPS connectivity in children with MD compared to TD children (Tables 2 and 3; Supplementary Figure S2). Because of the close vicinity of this region to the lateral ventricle, this finding should be interpreted with caution.
Table 2.
Group differences in functional connectivity of the left IPS
| Local Maxima | Clustersize | Peak (T) | Coordinates | ||
|---|---|---|---|---|---|
| x | y | z | |||
| MD > TD | |||||
| L frontal pole* | 354 | 4.52 | −34 | 50 | 16 |
| L frontal pole | 3.80 | −48 | 42 | 12 | |
| L frontal pole | 3.35 | −36 | 52 | 24 | |
| R SMG, angular gyrus, SPL (IPS)* | 760 | 4.27 | 42 | −46 | 48 |
| R SMG (IPS) | 4.09 | 44 | −36 | 44 | |
| R SMG (IPS) | 3.84 | 52 | −28 | 42 | |
| L SFG* | 336 | 3.99 | −12 | 4 | 70 |
| L SFG, MFG | 3.97 | −28 | 6 | 62 | |
| L SFG | 3.70 | −16 | 0 | 56 | |
| L precuneous cortex, SPL, lateral occipital cortex* | 391 | 3.91 | −8 | −58 | 66 |
| L lateral occipital cortex | 3.65 | −18 | −66 | 64 | |
| L precuneous cortex, lateral occipital cortex | 3.40 | −6 | −72 | 52 | |
| R putamen* | 376 | 3.55 | 28 | −4 | 10 |
| R putamen | 3.48 | 30 | −2 | −6 | |
| R putamen | 3.35 | 30 | 6 | 8 | |
| R Heschl's gyrus | 141 | 3.41 | 54 | −8 | −2 |
| R STG | 3.36 | 58 | 0 | −6 | |
| TD > MD | |||||
| L precuneous/ posterior hippocampus* | 268 | 4.10 | −24 | −42 | 10 |
| L precuneous/ posterior hippocampus | 3.82 | −16 | −42 | 18 | |
| L precuneous/ posterior hippocampus | 3.74 | −30 | −48 | 8 | |
Note: Results are reported at p < .01, 128 voxels. MNI coordinates are labeled according to the Harvard-Oxford atlas. IPS is defined based on the Juelich atlas. For each cluster, 3 sub-peaks are reported which are more than 8mm apart.
= cluster also found in a subset children who scored at or below 85 on the Numerical Operations subtest of the WIAT-II compared with typically developing children. MD = children with mathematical disabilities, TD = typically developing children, IPS = intraparietal sulcus, MFG = middle frontal gyrus, SFG = superior frontal gyrus, SMG = supramarginal gyrus, SPL = superior parietal lobule, STG = superior temporal gyrus.
Table 3.
Group differences in functional connectivity of the right IPS
| Local Maxima | Clustersize | Peak (T) | Coordinates | ||
|---|---|---|---|---|---|
| x | y | z | |||
| MD > TD | |||||
| R SMG* | 163 | 4.25 | 68 | −22 | 30 |
| R STG | 3.56 | 64 | −32 | 12 | |
| R SPL* | 411 | 3.99 | 28 | −46 | 64 |
| R SPL, SMG, angular gyrus (IPS) | 3.60 | 44 | −46 | 56 | |
| R lateral occipital cortex, SPL | 3.22 | 16 | −58 | 62 | |
| R STG* | 161 | 3.96 | 60 | −2 | −4 |
| R precentral gyrus* | 485 | 3.61 | 30 | −18 | 68 |
| R SFG, precentral gyrus | 3.24 | 20 | −8 | 72 | |
| R precentral gyrus | 3.14 | 36 | −10 | 64 | |
| L SMG (IPS)* | 295 | 3.55 | −50 | −34 | 40 |
| L SMG, SPL (IPS) | 3.44 | −44 | −46 | 54 | |
| L SPL, postcentral gyrus | 3.20 | −34 | −40 | 66 | |
| L SFG, MFG* | 218 | 3.42 | −26 | 8 | 64 |
| L SFG | 3.36 | −24 | 0 | 64 | |
| L precentral gyrus, SFG | 3.18 | −16 | −14 | 68 | |
| L precuneous cortex, SPL, lateral occipital cortex | 186 | 3.16 | −8 | −58 | 62 |
| L lateral occipital cortex, SPL (IPS) | 3.10 | −30 | −62 | 60 | |
| L lateral occipital cortex | 2.95 | −28 | −72 | 52 | |
| TD > MD | |||||
| L precuneous cortex* | 252 | 3.91 | −20 | −52 | 10 |
| L precuneous cortex | 3.58 | −28 | −54 | 8 | |
| L precuneous cortex | 3.57 | −18 | −44 | 16 | |
Note: Results are reported at p < .01, 128 voxels. MNI coordinates are labeled according to the Harvard-Oxford atlas. IPS is defined based on the Juelich atlas. For each cluster, 3 sub-peaks are reported which are more than 8mm apart.
= cluster also found in a subset children who scored at or below 85 on the Numerical Operations subtest of the WIAT-II compared with typically developing children. MD = children with mathematical disabilities, TD = typically developing children, IPS = intraparietal sulcus, MFG = middle frontal gyrus, SFG = superior frontal gyrus, SMG = supramarginal gyrus, SPL = superior parietal lobule, STG = superior temporal gyrus.
Figure 3. Brain areas that showed greater IPS connectivity in children with mathematical disabilities (MD) compared to typically developing (TD) children.
(A) Children with MD showed hyper-connectivity between bilateral IPS and multiple dorsal frontal and parietal cortical regions, between bilateral IPS and right hemisphere SMG and STG, and between left IPS and right putamen. (B) Results were almost identical when examining a subset of 14 MD children who scored at or below 85 on the Numerical Operations subtest of the WIAT-II (MD*). All results are thresholded at p < 0.01 height, with family-wise error (FWE) corrections for multiple comparisons at the cluster level (p < 0.01, spatial extent 128 voxels). Greater connectivity for MD > TD in red (left IPS), blue (right IPS), and green (both left and right IPS). Coordinates are in MNI space. FP = frontal pole; IPS = intraparietal sulcus; SFG = superior frontal gyrus; SMG = supramarginal gyus; SPL = superior parietal lobe; STG = superior temportal gyrus.
Next, to examine IPS functional connectivity in children with the most severe math difficulties, we performed a follow-up analysis in a subset of 14 MD children who scored at or below 85 on the Numerical Operations subtest of the WIAT-II (i.e., at least one standard deviation lower than the population average), in comparison to the original TD sample (n = 19). The MD and TD groups remained matched on age, gender, IQ, reading, working memory, and movement (all ps ≥.241, η2p ≤.044). Results in the MD subgroup were in line with the original analysis (see Tables 2 and 3 and Figure 3B). As in the original analysis, children with the most severe MD showed greater functional connectivity between IPS and regions of the dorsal fronto-parietal network, as well as right SMG and STG, compared to TD children. A notable difference between the results was the extension of the right SMG cluster to posterior middle temporal gyrus/ lateral occipital cortex in the subsample of children with more severe MD. Taken together, our results reveal a consistent and robust pattern of hyper-connectivity in left and right IPS circuits in children with MD.
IPS functional connectivity is negatively correlated with math ability in children with MD
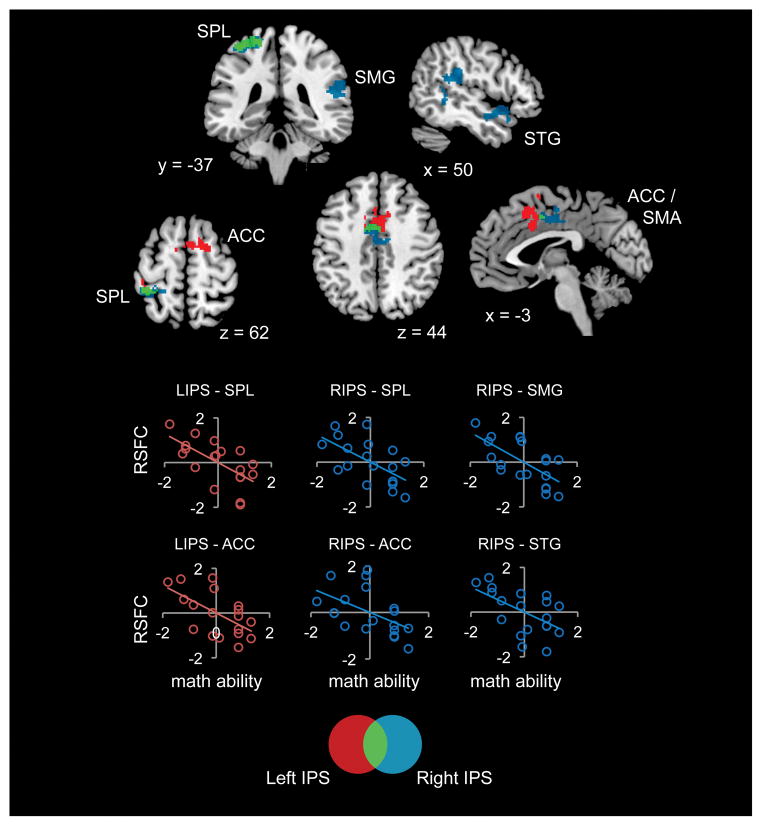
To further investigate the relation between IPS connectivity and math ability in MD children, we performed regression analyses within the MD group. For this purpose, we included demeaned scores of the WIAT-II Numerical Operations test as a covariate of interest in the whole-brain analysis. Study cohort was included as a covariate as well. In agreement with the results of the group comparison, we found a negative correlation between math ability and IPS functional connectivity (Figure 4). More specifically, in children with the lowest math abilities, bilateral IPS showed the highest functional connectivity with left SPL and anterior cingulate gyrus, extending into the SMA. In addition, children with the lowest math abilities showed highest connectivity between right IPS and two large right hemisphere clusters: one in the right temporal parietal junction (including SMG and middle temporal gyrus) and the other in right anterior STG and temporal pole. The patterns of brain-behavior correlations partially overlapped with the results of the group comparison in left SPL, SMA, and right SMG. These results reveal greater hyper-connectivity in low functioning children with MD.
Figure 4. Negative correlation between IPS connectivity and math ability within the group of children with mathematical disabilities (MD).
Results are thresholded at p < 0.01 height, with family-wise error (FWE) corrections for multiple spatial comparisons at the cluster level (p < 0.01, spatial extent 128 voxels). Brain-behavior correlations are displayed in red (left IPS), blue (right IPS), and green (both left and right IPS). Coordinates are in MNI space. Graphs (created for illustrative purposes) depict the correlation between math ability (WIAT-II Numerical Operations) and functional connectivity measures, after scores were normalized across children within each cohort. RSFC = resting state functional connectivity; ACC = anterior cingulate gyrus; IPS = intraparietal sulcus; SMA = supplementary motor area; SMG = supramarginal gyrus; SPL = superior parietal lobe; STG = superior temporal gyrus.
IPS-connectivity based classification of MD and TD children
Next, we used a linear hard-margin SVM classifier to examine whether IPS connectivity patterns could be used to distinguish MD status in children. IPS connectivity maps (which were masked to include only voxels that were significant at the group level) served as features in the classification analysis. Using leave-one-out cross-validation, the classifier was trained on N-1 participants and tested on the remaining participant. We found that left IPS connectivity-based classification yielded a significant cross-validation accuracy of 84.2% (p = 0.0098). The 95% confidence interval of left IPS was 76.3%–94.7% (Supplementary Figure S3). Cross-validation accuracy of right IPS connectivity-based classification was 76.3%, which did not reach significance (p = 0.0564). The 95% confidence interval for right IPS was 76.3%–94.7% (Supplementary Figure S3). These results reveal that aberrant IPS connectivity patterns can be used to discriminate children with MD from their TD peers.
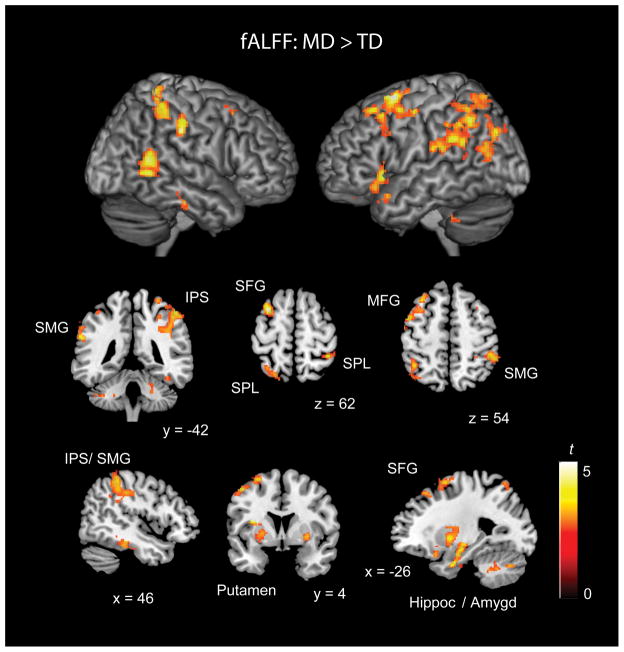
Children with MD show increased fractional Amplitude of Low Frequency Fluctuations compared to TD children
Finally, we investigated group differences in the amplitude of the low frequency BOLD fluctuations. To measure BOLD signal fluctuation, we used fALFF, a regional measure that does not require a priori definition of seed ROIs. A two-sample t-test of group differences in fALFF indicated that children with MD show increased BOLD signal amplitude in multiple brain regions relative to their TD peers, particularly in the fronto-parietal network, including bilateral IPS, SPL/ lateral occipital cortex, and MFG/ SFG (Table 4; Figure 5). Children with MD also showed elevated fALFF in right SMG and middle temporal gyrus, as well as in temporal occipital fusiform cortex, left inferior frontal gyrus/ orbitofrontal cortex, and medial prefrontal cortex. Increased fALFF was also found in subcortical regions, including bilateral putamen, hippocampus, and amygdala.
Table 4.
Group differences in fALFF (MD > TD)
| Local Maxima | Clustersize | Peak (T) | Coordinates | ||
|---|---|---|---|---|---|
| x | y | z | |||
| L MFG, SFG | 569 | 5.51 | −30 | 8 | 64 |
| L precentral gyrus | 3.97 | −54 | −8 | 52 | |
| L MFG | 3.89 | −32 | 26 | 52 | |
| R SMG | 959 | 5.42 | 68 | −24 | 38 |
| R SMG (IPS) | 4.15 | 50 | −28 | 40 | |
| R SMG, angular gyrus | 3.76 | 48 | −40 | 56 | |
| R cerebellum | 1547 | 5.26 | 18 | −52 | −30 |
| R cerebellum | 4.00 | 20 | −70 | −32 | |
| L cerebellum | 3.65 | −20 | −70 | −32 | |
| L central opercular cortex | 831 | 5.03 | −32 | 2 | 16 |
| L putamen | 4.35 | −24 | 0 | 0 | |
| L hippocampus, parahippocampal gyrus | 4.07 | −18 | −8 | −32 | |
| L angular gyrus | 716 | 4.56 | −58 | −56 | 44 |
| L SMG, parietal operculum cortex | 4.21 | −60 | −42 | 28 | |
| L SMG | 4.19 | −62 | −46 | 44 | |
| R MTG, angular gyrus | 345 | 4.41 | 58 | −52 | 12 |
| R MTG | 4.27 | 62 | −52 | 0 | |
| L lateral occipital cortex | 401 | 4.31 | −46 | −78 | 34 |
| L lateral occipital cortex | 3.69 | −40 | −66 | 24 | |
| L lateral occipital cortex | 3.36 | −42 | −70 | 16 | |
| L frontal operculum cortex, IFG pars triangularis, IFG pars opercularis | 166 | 4.16 | −48 | 18 | −4 |
| L frontal orbital cortex | 3.36 | −50 | 24 | −12 | |
| L frontal operculum cortex, IFG pars triangularis, IFG pars opercularis | 3.17 | −44 | 18 | 6 | |
| L thalamus | 262 | 3.79 | −4 | −22 | −6 |
| brain stem | 3.60 | 0 | −22 | −14 | |
| R brain stem | 2.97 | 4 | −14 | −16 | |
| L SPL, SMG, angular gyrus (IPS) | 259 | 3.78 | −40 | −52 | 54 |
| L lateral occipital cortex | 3.32 | −44 | −62 | 56 | |
| L lateral occipital cortex | 3.31 | −22 | −68 | 64 | |
| R MFG | 146 | 3.77 | 28 | 14 | 48 |
| R MFG | 2.46 | 34 | 12 | 56 | |
| R temporal fusiform gyrus, temporal occipital fusiform cortex | 233 | 3.73 | 40 | −38 | −20 |
| R ITG | 3.46 | 46 | −28 | −18 | |
| R ITG | 3.45 | 54 | −22 | −24 | |
| L frontal orbital cortex | 143 | 3.64 | −30 | 18 | −20 |
| L temporal pole | 3.30 | −50 | 14 | −18 | |
| L insular cortex | 3.08 | −28 | 14 | −10 | |
| L frontal medial cortex | 278 | 3.42 | −10 | 50 | −12 |
| R frontal pole | 3.41 | 18 | 50 | −14 | |
| L frontal medial cortex | 3.36 | −10 | 42 | −16 | |
| R putamen | 161 | 3.37 | 30 | 4 | −2 |
| R amygdala, hippocampus | 3.13 | 26 | −8 | −12 | |
Note: Results are reported at p < .01, 128 voxels. MNI coordinates are labeled according to the Harvard-Oxford atlas. IPS is defined based on the Juelich atlas. For each cluster, 3 sub-peaks are reported which are more than 8mm apart. MD = children with mathematical disabilities, TD = typically developing children, IFG = inferior frontal gyrus, IPS = intraparietal sulcus, ITG = inferior temporal gyrus, MFG = middle frontal gyrus, MTG = middle temporal gyrus, SFG = superior frontal gyrus, SMG = supramarginal gyrus, SPL = superior parietal lobule.
Figure 5. Greater fALFF in children with mathematical disabilities (MD) compared to typically developing (TD) children.
Results are thresholded at p < 0.01 height, with family-wise error (FWE) corrections for multiple spatial comparisons at the cluster level (p < 0.01, spatial extent 128 voxels). Coordinates are in MNI space. fALFF = Fractional Amplitude of Low Frequency Fluctuations; IPS = intraparietal sulcus; MFG = middle frontal gyrus; SFG = superior frontal gyrus; SMG = supramarginal gyus; SPL = superior parietal lobe.
To examine the relationship between intrinsic functional connectivity to the IPS and fALFF results, we performed ROI analyses based on the regions that showed increased functional connectivity with both left and right IPS. There were 6 clusters that showed overlap between left and right IPS connectivity of at least 30 voxels: right IPS/SPL, left SPL/lateral occipital cortex, two clusters in left SFG, right STG and right SMG. Because the two SFG clusters were very close in space, only the largest cluster was examined. We found that, across the whole sample, there was a positive correlation between fALFF and functional connectivity in each of the five ROIs examined (all rs≥.371; ps ≤.024, controlling for cohort; Supplementary Table S1), indicating an overlap and correspondence in brain areas that showed hyper-activity and hyper-connectivity. Next, to examine whether group differences in functional connectivity could be accounted for by differences in fALFF, we performed a set of ANCOVA analyses to examine functional connectivity differences, including regional fALFF and cohort as covariates. We found that for most ROIs, group differences in functional connectivity remained significant after covarying out fALFF (Supplementary Table S2). These results indicate that IPS hyper-connectivity in children with MD cannot simply be explained by enhanced levels of low frequency fluctuations.
Additional analyses to demonstrate the robustness of our findings
Although the motion parameters between the MD and TD groups were closely matched, we performed a number of additional analyses to examine the robustness of our findings against potential head motion-related confounds. First, we excluded five participants (2 MD, 3 TD) who had head motion in excess of 3 mm and reran the functional connectivity and fALFF group analyses on data from the remaining thirty-three participants (17 MD, 16 TD). Second, we implemented a procedure recommended by Power and colleagues to compute framewise displacement (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012; Power et al., 2014; Power, Schlaggar, & Petersen, 2015). To control for head motion, we included framewise displacement as a covariate of no interest in the first level functional connectivity analyses and reran the entire analysis. Results from these analyses (reported in Supplementary Figures S4 to S6 of the Supplementary Material) were consistent with the results from the original analysis, suggesting that our findings are robust against motion-related confounds.
Next, to examine the robustness of our findings against potential cohort related confounds, group means were plotted for the two study cohorts separately. For the functional connectivity data, we examined the five clusters that showed increased functional connectivity with both left and right IPS (as described in the previous section). For the fALFF data, we examined all fifteen clusters that showed increased fALFF in MD > TD. Results from these analyses are reported in Figures S7 and S8 of the Supplementary Material. Briefly, for cohort 1, mean connectivity of both left and right IPS seed ROIs was higher for MD > TD in all five clusters. Furthermore, the MD group showed higher fALFF in all fifteen clusters. For cohort 2, MDs showed higher right IPS connectivity in all five clusters and higher left IPS connectivity in four out of five clusters. Similar to cohort 1, MDs showed higher fALFF in all fifteen clusters. Taken together, these results point to a consistent pattern of differences across the two cohorts.
Discussion
While task-based fMRI studies of numerical cognition have provided important information about the neural correlates of MD, findings from these studies have been inconsistent with respect to the profile of IPS and fronto-parietal function in affected children (Ashkenazi et al., 2012; Davis et al., 2009; Kaufmann, Vogel, Starke, Kremser, Schocke, et al., 2009; Kaufmann et al., 2011; Kucian, 2011; Kucian et al., 2006; Molko et al., 2003; Mussolin et al., 2010; Price et al., 2007). Moreover, little is known about intrinsic brain circuits that contribute to poor math skills in children with MD. Here, we investigated intrinsic functional connectivity and regional low-frequency signal fluctuations in a well-characterized group of 7–9 year-old children with MD. Importantly, the MD group did not have co-morbid reading difficulties or other developmental disabilities, which have been shown to have unique aberrations in intrinsic connectivity (e.g., Finn et al., 2014; Koyama et al., 2013). Furthermore, children with MD were closely matched to a group of TD children on age, gender, IQ, reading ability, and working memory.
We demonstrate for the first time that, rather than being under-connected, functional circuits associated with the IPS are intrinsically hyper-connected in children with MD. Furthermore, novel machine learning algorithms revealed that aberrant IPS connectivity patterns could be used to discriminate children with MD from TD children with high levels of accuracy, suggesting that IPS connectivity is a distinguishing neurobiological feature of the disorder. Finally, we found evidence for spontaneous regional hyper-activity in the IPS as well as multiple other brain regions in children with MD. Our findings of aberrant IPS connectivity and widespread aberrations in low frequency fluctuations advance the view that MD is best characterized as a network-level deficit, affecting the IPS and its functional circuits (Fias et al., 2014). More generally, our findings are consistent with an interactive specialization model which suggests that neurodevelopmental disorders are likely to be characterized by dysfunction in multiple functional circuits, rather than isolated dysfunction of a particular brain area, as typically seen in adult patients with focal brain injuries (Johnson, 2011; Menon, 2013; Rubinsten & Henik, 2009; Schlaggar & McCandliss, 2007).
Parietal hyper-connectivity in children with MD
Compared to their TD peers, children with MD showed aberrant IPS connectivity with multiple regions, notably in frontal and parietal cortex. Specifically, children with MD showed greater functional connectivity between left and right IPS, as well as between IPS and other dorsal fronto-parietal regions, including bilateral SPL, SFG/MFG, and SMA. In addition, children with MD showed increased IPS connectivity with right temporo-parietal cortex, including the SMG and STG. Importantly, results were almost identical when more stringent criteria of MD were used, suggesting that the broad pattern of hyper-connectivity observed was not caused by the relatively lenient MD criteria used in this study. Additional analysis within the MD group revealed a negative correlation between IPS connectivity and individual math scores, particularly with the anterior cingulate cortex, SMA, left SPL, and right SMG and STG, further demonstrating the robustness of our findings of hyper-connectivity in childhood MD.
Many brain regions that showed aberrant connectivity in the MD group overlapped with prefrontal and parietal cortex regions typically engaged during numerical cognition (Arsalidou & Taylor, 2011; Kaufmann et al., 2011). It is plausible that intrinsic hyper-connectivity in the fronto-parietal network in children with MD may underlie the increased activation and connectivity of these regions reported in several studies of numerical problem-solving (Iuculano et al., 2015; Kaufmann, Vogel, Starke, Kremser, & Schocke, 2009; Kaufmann, Vogel, Starke, Kremser, Schocke, et al., 2009; Kaufmann et al., 2011; Rosenberg-Lee et al., 2014). Interestingly, not all studies have found greater fronto-parietal activation in children with MD, but discrepancies between studies may be explained the type of baseline conditions used (Menon, 2015). Specifically, it has been suggested that MD is characterized by reduced modulation of brain responses with increasing task complexity, rather than reduced activation per se (Ashkenazi et al., 2012). For example, children with MD show reduced activation in fronto-parietal regions for small versus large distances in number comparison tasks (Mussolin et al., 2010; Price et al., 2007; but see Kucian et al., 2011), and for complex versus simple problems in arithmetic tasks (Ashkenazi et al., 2012). Moreover, multivariate representational similarity analyses have indicated that IPS response patterns are less differentiated between complex versus simple arithmetic problems in children with MD (Ashkenazi et al., 2012), which is also indicative of reduced task-complexity-related modulation of brain response. We suggest that in children with MD, IPS hyper-connectivity may limit their ability to flexibly and efficiently engage and modulate task-relevant fronto-parietal circuits.
Beyond their involvement in numerical cognition, prefrontal and posterior parietal regions identified as being hyper-connected in MD, have also been associated with more general attention and cognitive control mechanisms (e.g., Corbetta & Shulman, 2002; Duncan, 2006; Niendam et al., 2012). Aberrant connectivity within these fronto-parietal areas in children with MD is consistent with deficits in spatial attention that have been reported in MD even in domains outside mathematical problem-solving (Ashkenazi & Henik, 2010; Szucs, Devine, Soltesz, Nobes, & Gabriel, 2013). The dorsal frontal and parietal regions that typically show high functional connectivity with the IPS show close resemblance to the dorsal spatial network thought to be involved in top-down, goal-driven attention (Figure 1; Corbetta et al., 2008; Corbetta & Shulman, 2002). It has been argued that this network can be distinguished from a ventral attention system anchored in the right hemisphere temporal parietal junction and inferior frontal gyrus, which plays a more prominent role in stimulus-driven reorienting (Figure 1; Corbetta et al., 2008; Corbetta & Shulman, 2002; Fox et al., 2006). Children with MD showed IPS hyper-connectivity not only with dorsal prefrontal and parietal cortex, but also with right temporo-parietal regions, including SMG, suggesting that their dorsal and ventral attention streams are less differentiated in affected children. Consistent with this hypothesis, a recent meta-analysis has found greater right SMG engagement in children with MD during numerical processing (Kaufmann et al., 2011). Further studies with both intrinsic and task-based fMRI are needed to investigate how intrinsic hyper-connectivity in dorsal and ventral attentional systems may contribute to both mathematical difficulties as well as domain-general cognitive deficits.
Hyper- as opposed to hypo-connectivity in children with MD
Our findings of increased functional connectivity in MDs compared to TDs might seem contradictory with the notion that greater functional connectivity reflects greater neuronal efficiency (Van Den Heuvel & Hulshoff Pol, 2010). Studies in children with neurodevelopmental disorders, including autism (Supekar, Uddin, et al., 2013; Uddin et al., 2013), anxiety disorders (Qin, Young, et al., 2014) and schizophrenia (Whitfield-Gabrieli et al., 2009) have, however, pointed to hyper-connectivity as a prominent feature of aberrant functional circuits in children. We have suggested that hyper-connectivity may result in an inability to flexibly engage and disengage brain circuits in a context dependent manner (Uddin et al., 2014), thereby contributing to impaired cognition. Our finding of hyper-connectivity is also noteworthy in the context of fronto-parietal and parieto-temporal white matter deficits that have been reported in children with MD (Kucian et al., 2014; Rykhlevskaia, Uddin, Kondos, & Menon, 2009). The relation between structural connectivity and intrinsic brain dynamics is not, however, as straightforward as one might expect (Damoiseaux & Greicius, 2009; Horwitz, Hwang, & Alstott, 2013). In a review of the literature on large-scale neural modeling of functional-structural relationships, Horowitz et al. concluded that weakening of a structural connection could lead to both decreases and increases of functional connectivity between brain regions that are not directly affected (Horwitz et al., 2013). Furthermore, increased functional connectivity can also result from changes in alternate multi-synaptic pathways that link areas with structural deficits. Further research is needed to examine how white matter tract deficits influence functional connectivity in MD and how hyper-connectivity of intrinsic functional circuits disrupts math problem solving.
IPS connectivity patterns discriminate MD and TD children
Multivariate classification analyses demonstrated that brain connectivity can be used to discriminate TD children and children with MD. Using left IPS connectivity maps as features in a SVM classifier, MD status could be determined with greater than 80% accuracy. These results illustrate the robustness of IPS-related connectivity differences between the MD and TD groups, and suggest that functional connectivity could be used as a brain-based biomarker to predict learning disabilities such as MD in children. Critically, our findings provide the strongest evidence to date that IPS connectivity may be a distinguishing neurobiological feature of the disorder.
Aberrant local signal fluctuations in children with MD
Next, to investigate aberrant brain organization in local neural circuits, as measured at the individual voxel level, and its potential links to atypical IPS functional connectivity in children with MD, we performed fALFF analyses on the same task-free fMRI data (Mennes et al., 2011; Zang et al., 2007; Zou et al., 2008; Zuo et al., 2010). fALFF is a voxel-wise measure of spontaneous BOLD signal fluctuations and can be used to examine intrinsic brain dynamics without a priori selection of ROIs. We found that compared to TD children, children with MD showed greater fALFF levels in multiple brain regions, most prominently in the IPS, SPL, MFG/ SFG, and SMG, providing additional evidence for fronto-parietal circuit dysfunction extending beyond the IPS. FALFF differences partly overlapped with fronto-parietal areas that showed hyper-connectivity with the IPS. Convergent on these findings, we found a significant correlation between fALFF and functional connectivity in fronto-parietal cortex. Nevertheless, despite the relation between fALFF and functional connectivity, group differences in functional connectivity could not completely be accounted for by group differences in fALFF. Moreover, fALFF also identified additional abnormalities in subcortical regions, notably bilateral putamen and left anterior hippocampus. It is noteworthy, in this context, that memory-based fact retrieval, which relies in part on the hippocampus (Qin, Cho, et al., 2014), is known to be weaker in children with MD (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007). The extent to which aberrations in procedural and associative memory systems contribute to impaired fact retrieval in children with MD remains to be investigated. We suggest that extensive enhancements of spontaneous low-frequency fluctuations in children with MD reflects aberrations in multiple brain regions that extend beyond the IPS, which may limit their ability to flexibly and efficiently engage task-relevant brain areas and distributed circuits (cf. Supekar, Uddin, et al., 2013).
Limitations and future directions
One important challenge for future studies is addressing heterogeneity in the clinical profile of MD (Kaufmann et al., 2013; Rubinsten & Henik, 2009). This heterogeneity may reduce the likelihood of finding robust neural deficits within a study sample of children with MD, and give rise to inconsistent findings between studies with different sample characteristics. In this study, we focused on a well-characterized group of children with MD without co-morbid reading difficulties or developmental disabilities, matched to TD children on IQ, reading, and working memory. By using strict selection- and matching criteria, we hoped to identify an intrinsic connectivity and brain organization profile that could be specifically attributed to math difficulties. An important avenue of future research is to investigate whether the same neurobiological deficits are found in children across heterogeneous clinical profiles, e.g. in children with comorbid reading disabilities (Menon, 2015). Moreover, with regards to the practical applications of using functional connectivity as a brain-based biomarker, further studies are needed to examine whether classification is possible in a broader sample, including children of different ages and co-morbid learning disabilities.
It is also important to take into account the specific cut-off criteria that are used to define MD, as it has been argued that children who meet the most stringent criteria of MD (i.e., math scores below the 10th percentile) have a different etiology compared to children with less severe difficulties (Mazzocco, Feigenson, & Halberda, 2011; Murphy, Mazzocco, Hanich, & Early, 2007). Here, only a minority of children (n = 7) scored at or below the 10th percentile, which precluded us from studying this subgroup separately. However, our brain-behavior analyses provide preliminary evidence that parietal hyper-connectivity is most evident in children with more severe math difficulties. Further studies are necessary to replicate our findings in larger samples, to examine similarities and differences in the functional network architecture of children with different learning profiles, and to investigate the influence of aberrant intrinsic functional circuits on cognitive information processing in affected children.
Conclusions
Our study reveals aberrant intrinsic functional brain organization in a well-characterized group of 7-9 year old children with MD. Our findings provide novel insights into the neurobiology of the disorder, and open up new opportunities for using brain connectivity-based biomarkers of specific learning disabilities. Crucially, our findings demonstrate that, even in a relatively pure sample of children with math difficulties, aberrant brain organization is not confined to focal IPS regions. Rather, our findings indicate that the neurobiology of childhood MD is characterized both by aberrant regional signals and inter-regional functional connectivity. We hypothesize that high levels of spontaneous activity and IPS hyper-connectivity may make it difficult for children with MD to modulate brain circuits in a context-dependent manner, thereby limiting flexible resource allocation in response to changing task demands (cf. Supekar, Uddin, et al., 2013; Uddin et al., 2014).
Supplementary Material
Research highlights.
Mathematical disabilities (MD) have a negative life-long impact on professional success, employment, and health outcomes, yet, little is known about the intrinsic functional brain organization that contributes to poor math skills in affected children.
Intrinsic functional hyper-connectivity of the intraparietal sulcus (IPS) – a brain region critical for numerical cognition – is a distinguishing and behaviorally relevant neurobiological feature of children with MD.
Childhood MD is also associated with higher levels of spontaneous low frequency fluctuations in multiple frontal and parietal areas.
Our findings advance the view that MD is best characterized as a network-level deficit; we hypothesize that IPS hyper-connectivity and high levels of spontaneous activity may limit flexible resource allocation in response to changing task demands.
Acknowledgments
This work was supported by NIH grants (HD047520, HD059205, MH101394) and NWO (446-12-001). We thank Xujun Duan and Lucina Uddin for assistance with data analysis.
References
- Ansari D. Effects of development and enculturation on number representation in the brain. Nature Reviews Neuroscience. 2008;9(4):278–291. doi: 10.1038/nrn2334. nrn2334. [DOI] [PubMed] [Google Scholar]
- Arsalidou M, Taylor MJ. Is 2+2=4? Meta-analyses of brain areas needed for numbers and calculations. Neuroimage. 2011;54(3):2382–2393. doi: 10.1016/j.neuroimage.2010.10.009. S1053-8119(10)01301-7. [DOI] [PubMed] [Google Scholar]
- Ashkenazi S, Henik A. Attentional networks in developmental dyscalculia. Behavioral and Brain Functions. 2010;6(1):2. doi: 10.1186/1744-9081-6-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashkenazi S, Rosenberg-Lee M, Metcalfe AW, Swigart AG, Menon V. Visuo-spatial working memory is an important source of domain-general vulnerability in the development of arithmetic cognition. Neuropsychologia. 2013;51(11):2305–2317. doi: 10.1016/j.neuropsychologia.2013.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashkenazi S, Rosenberg-Lee M, Tenison C, Menon V. Weak task-related modulation and stimulus representations during arithmetic problem solving in children with developmental dyscalculia. Developmental Cognitive Neuroscience. 2012;2(0):S152–S166. doi: 10.1016/j.dcn.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brannon EM. The representation of numerical magnitude. Current Opinion in Neurobiology. 2006;16(2):222–229. doi: 10.1016/j.conb.2006.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butterworth B, Varma S, Laurillard D. Dyscalculia: From brain to education. Science. 2011;332(6033):1049–1053. doi: 10.1126/science.1201536. [DOI] [PubMed] [Google Scholar]
- Caspers S, Eickhoff SB, Geyer S, Scheperjans F, Mohlberg H, Zilles K, Amunts K. The human inferior parietal lobule in stereotaxic space. Brain Structure and Function. 2008;212(6):481–495. doi: 10.1007/s00429-008-0195-z. [DOI] [PubMed] [Google Scholar]
- Caspers S, Geyer S, Schleicher A, Mohlberg H, Amunts K, Zilles K. The human inferior parietal cortex: cytoarchitectonic parcellation and interindividual variability. Neuroimage. 2006;33(2):430–448. doi: 10.1016/j.neuroimage.2006.06.054. S1053-8119(06)00697-5. [DOI] [PubMed] [Google Scholar]
- Choi HJ, Zilles K, Mohlberg H, Schleicher A, Fink GR, Armstrong E, Amunts K. Cytoarchitectonic identification and probabilistic mapping of two distinct areas within the anterior ventral bank of the human intraparietal sulcus. Journal of Comparative Neurology. 2006;495(1):53–69. doi: 10.1002/cne.20849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Church JA, Fair DA, Dosenbach NUF, Cohen AL, Miezin FM, Petersen SE, Schlaggar BL. Control networks in paediatric Tourette syndrome show immature and anomalous patterns of functional connectivity. Brain. 2009;132(1):225–238. doi: 10.1093/brain/awn223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen Kadosh R, Cohen Kadosh K, Schuhmann T, Kaas A, Goebel R, Henik A, Sack AT. Virtual dyscalculia induced by parietal-lobe TMS impairs automatic magnitude processing. Current Biology. 2007;17(8):689–693. doi: 10.1016/j.cub.2007.02.056. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R, Lammertyn J, Izard V. Are numbers special? An overview of chronometric, neuroimaging, developmental and comparative studies of magnitude representation. Progress in Neurobiology. 2008;84(2):132–147. doi: 10.1016/j.pneurobio.2007.11.001. S0301-0082(07)00211-0. [DOI] [PubMed] [Google Scholar]
- Corbetta M, Patel G, Shulman GL. The reorienting system of the human brain: from environment to theory of mind. Neuron. 2008;58(3):306–324. doi: 10.1016/j.neuron.2008.04.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbetta M, Shulman G. Control of goal-directed and stimulus-driven attention in the brain. Nature Reviews Neuroscience. 2002;3(3):201–215. doi: 10.1038/nrn755. citeulike-article-id:919645. [DOI] [PubMed] [Google Scholar]
- Damoiseaux JS, Greicius MD. Greater than the sum of its parts: a review of studies combining structural connectivity and resting-state functional connectivity. Brain Structure and Function. 2009;213(6):525–533. doi: 10.1007/s00429-009-0208-6. [DOI] [PubMed] [Google Scholar]
- Davis N, Cannistraci CJ, Rogers BP, Gatenby JC, Fuchs LS, Anderson AW, Gore JC. Aberrant functional activation in school age children at-risk for mathematical disability: a functional imaging study of simple arithmetic skill. Neuropsychologia. 2009;47(12):2470–2479. doi: 10.1016/j.neuropsychologia.2009.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan J. EPS Mid-Career Award 2004: brain mechanisms of attention. The Quarterly Journal of Experimental Psychology. 2006;59(1):2–27. doi: 10.1080/17470210500260674. [DOI] [PubMed] [Google Scholar]
- Fair DA, Dosenbach NUF, Church JA, Cohen AL, Brahmbhatt S, Miezin FM, … Schlaggar BL. Development of distinct control networks through segregation and integration. Proceedings of the National Academy of Sciences of the United States of America. 2007;104(33):13507–13512. doi: 10.1073/pnas.0705843104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fias W, Menon V, Szucs D. Multiple components of developmental dyscalculia. Trends in Neuroscience and Education. 2014;2(2):43–47. [Google Scholar]
- Finn ES, Shen X, Holahan JM, Scheinost D, Lacadie C, Papademetris X, … Constable RT. Disruption of functional networks in dyslexia: a whole-brain, data-driven analysis of connectivity. Biological Psychiatry. 2014;76(5):397–404. doi: 10.1016/j.biopsych.2013.08.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Corbetta M, Snyder AZ, Vincent JL, Raichle ME. Spontaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(26):10046–10051. doi: 10.1073/pnas.0604187103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nature Reviews Neuroscience. 2007;8(9):700–711. doi: 10.1038/nrn2201. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Nugent L, Numtee C. Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development. 2007;78(4):1343–1359. doi: 10.1111/j.1467-8624.2007.01069.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Nugent L, Bailey DH. Adolescents’ functional numeracy is predicted by their school entry number system knowledge. PLoS One. 2013;8(1) doi: 10.1371/journal.pone.0054651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover GH, Lai S. Self-navigated spiral fMRI: interleaved versus single-shot. Magnetic Resonance in Medicine. 1998;39(3):361–368. doi: 10.1002/mrm.1910390305. [DOI] [PubMed] [Google Scholar]
- Grabner RH, Ansari D, Koschutnig K, Reishofer G, Ebner F, Neuper C. To retrieve or to calculate? Left angular gyrus mediates the retrieval of arithmetic facts during problem solving. Neuropsychologia. 2009;47(2):604–608. doi: 10.1016/j.neuropsychologia.2008.10.013. [DOI] [PubMed] [Google Scholar]
- Horwitz B, Hwang C, Alstott J. Interpreting the effects of altered brain anatomical connectivity on fMRI functional connectivity: a role for computational neural modeling. Frontiers in Human Neuroscience. 2013;7 doi: 10.3389/fnhum.2013.00649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iuculano T, Rosenberg-Lee M, Richardson J, Tenison C, Fuchs L, Supekar K, Menon V. Cognitive tutoring induces widespread neuroplasticity and remediates brain function in children with mathematical learning disabilities. Nature Communications. 2015 doi: 10.1038/ncomms9453. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson MH. Interactive Specialization: A domain-general framework for human functional brain development? Developmental Cognitive Neuroscience. 2011;1(1):7–21. doi: 10.1016/j.dcn.2010.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufmann L, Mazzocco MM, Dowker A, von Aster M, Gobel SM, Grabner RH, … Nuerk HC. Dyscalculia from a developmental and differential perspective. Frontiers in Psychology. 2013;4:516. doi: 10.3389/fpsyg.2013.00516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufmann L, Vogel SE, Starke M, Kremser C, Schocke M. Numerical and non-numerical ordinality processing in children with and without developmental dyscalculia: Evidence from fMRI. Cognitive Development. 2009;24(4):486–494. doi: 10.1016/j.cogdev.2009.09.001. [DOI] [Google Scholar]
- Kaufmann L, Vogel SE, Starke M, Kremser C, Schocke M, Wood G. Developmental dyscalculia: compensatory mechanisms in left intraparietal regions in response to nonsymbolic magnitudes. Behavioral and Brain Functions. 2009;5(1):35. doi: 10.1186/1744-9081-5-35. 1744-9081-5-35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufmann L, Wood G, Rubinsten O, Henik A. Meta-analyses of developmental fMRI studies investigating typical and atypical trajectories of number processing and calculation. Developmental Neuropsychology. 2011;36(6):763–787. doi: 10.1080/87565641.2010.549884. [DOI] [PubMed] [Google Scholar]
- Kim D, Adalsteinsson E, Glover GH, Spielman DM. Regularized higher-order in vivo shimming. Magnetic Resonance in Medicine. 2002;48(4):715–722. doi: 10.1002/mrm.10267. [DOI] [PubMed] [Google Scholar]
- Koyama MS, Di Martino A, Kelly C, Jutagir DR, Sunshine J, Schwartz SJ, … Milham MP. Cortical signatures of dyslexia and remediation: an intrinsic functional connectivity approach. PLoS One. 2013;8(2):e55454. doi: 10.1371/journal.pone.0055454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koyama MS, Di Martino A, Zuo XN, Kelly C, Mennes M, Jutagir DR, … Milham MP. Resting-state functional connectivity indexes reading competence in children and adults. Journal of Neuroscience. 2011;31(23):8617–8624. doi: 10.1523/JNEUROSCI.4865-10.2011. 31/23/8617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucian K. Non-symbolic numerical distance effect in children with and without developmental dyscalculia: a parametric fMRI study. Developmental Neuropsychology. 2011;36(6):741. doi: 10.1080/87565641.2010.549867. [DOI] [PubMed] [Google Scholar]
- Kucian K, Ashkenazi SS, Hänggi J, Rotzer S, Jäncke L, Martin E, von Aster M. Developmental dyscalculia: a dysconnection syndrome? Brain Structure and Function. 2014;219(5):1721–1733. doi: 10.1007/s00429-013-0597-4. [DOI] [PubMed] [Google Scholar]
- Kucian K, Loenneker T, Dietrich T, Dosch M, Martin E, von Aster M. Impaired neural networks for approximate calculation in dyscalculic children: a functional MRI study. Behavioral and Brain Functions. 2006;2(1):31. doi: 10.1186/1744-9081-2-31. 1744–9081-2-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzocco MM, Feigenson L, Halberda J. Impaired acuity of the approximate number system underlies mathematical learning disability (dyscalculia) Child Development. 2011;82(4):1224–1237. doi: 10.1111/j.1467-8624.2011.01608.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mennes M, Zuo XN, Kelly C, Di Martino A, Zang YF, Biswal B, … Milham MP. Linking inter-individual differences in neural activation and behavior to intrinsic brain dynamics. Neuroimage. 2011;54(4):2950–2959. doi: 10.1016/j.neuroimage.2010.10.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menon V. Developmental pathways to functional brain networks: emerging principles. Trends in Cognitive Sciences. 2013;17(12):627–640. doi: 10.1016/j.tics.2013.09.015. [DOI] [PubMed] [Google Scholar]
- Menon V. Neurocognitive basis of math disabilities and their comorbidity with reading disabilities. In: Eden G, editor. The Wiley Handbook on the Cognitive Neuroscience of Developmental Dyslexia. John Wiley & Sons Press; 2015. [Google Scholar]
- Menon V, Uddin LQ. Saliency, switching, attention and control: a network model of insula function. Brain Structure and Function. 2010;214(5–6):655–667. doi: 10.1007/s00429-010-0262-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molko N, Cachia A, Riviere D, Mangin JF, Bruandet M, Le Bihan D, … Dehaene S. Functional and structural alterations of the intraparietal sulcus in a developmental dyscalculia of genetic origin. Neuron. 2003;40(4):847–858. doi: 10.1016/s0896-6273(03)00670-6. S0896627303006706. [DOI] [PubMed] [Google Scholar]
- Murphy MM, Mazzocco MM, Hanich LB, Early MC. Cognitive characteristics of children with mathematics learning disability (MLD) vary as a function of the cutoff criterion used to define MLD. Journal of Learning Disabilities. 2007;40(5):458–478. doi: 10.1177/00222194070400050901. [DOI] [PubMed] [Google Scholar]
- Mussolin C, De Volder A, Grandin C, Schlogel X, Nassogne MC, Noël MP. Neural correlates of symbolic number comparison in developmental dyscalculia. Journal of Cognitive Neuroscience. 2010;22(5):860–874. doi: 10.1162/jocn.2009.21237. [DOI] [PubMed] [Google Scholar]
- Niendam TA, Laird AR, Ray KL, Dean YM, Glahn DC, Carter CS. Meta-analytic evidence for a superordinate cognitive control network subserving diverse executive functions. Cognitive, Affective, & Behavioral Neuroscience. 2012;12(2):241–268. doi: 10.3758/s13415-011-0083-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noel MP, Rousselle L. Developmental changes in the profiles of dyscalculia: An explanation based on a double exact-and-approximate number representation model. Frontiers in Human Neuroscience. 2011;5:165. doi: 10.3389/fnhum.2011.00165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parsons S, Bynner J. Does numeracy matter more? London: NRDC; 2005. [Google Scholar]
- Pickering S, Gathercole S. Working Memory Test Battery for Children. San Antonio, TX: PsyCorp; 2001. [Google Scholar]
- Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage. 2012;59(3):2142–2154. doi: 10.1016/j.neuroimage.2011.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Mitra A, Laumann TO, Snyder AZ, Schlaggar BL, Petersen SE. Methods to detect, characterize, and remove motion artifact in resting state fMRI. Neuroimage. 2014;84:320–341. doi: 10.1016/j.neuroimage.2013.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Schlaggar BL, Petersen SE. Recent progress and outstanding issues in motion correction in resting state fMRI. Neuroimage. 2015;105:536–551. doi: 10.1016/j.neuroimage.2014.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price GR, Holloway I, Rasanen P, Vesterinen M, Ansari D. Impaired parietal magnitude processing in developmental dyscalculia. Current Biology. 2007;17(24):R1042–1043. doi: 10.1016/j.cub.2007.10.013. S0960-9822(07)02072-6. [DOI] [PubMed] [Google Scholar]
- Qin S, Cho S, Chen T, Rosenberg-Lee M, Geary DC, Menon V. Hippocampal-neocortical functional reorganization underlies children's cognitive development. Nature Neuroscience. 2014;17(9):1263–1269. doi: 10.1038/nn.3788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin S, Young CB, Duan X, Chen T, Supekar K, Menon V. Amygdala subregional structure and intrinsic functional connectivity predicts individual differences in anxiety during early childhood. Biological Psychiatry. 2014;75(11):892–900. doi: 10.1016/j.biopsych.2013.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg-Lee M, Ashkenazi S, Chen T, Young CB, Geary DC, Menon V. Brain hyper-connectivity and operation-specific deficits during arithmetic problem solving in children with developmental dyscalculia. Developmental Science. 2014;18(3):351–372. doi: 10.1111/desc.12216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg-Lee M, Barth M, Menon V. What difference does a year of schooling make? Maturation of brain response and connectivity between 2nd and 3rd grades during arithmetic problem solving. Neuroimage. 2011;57(3):796–808. doi: 10.1016/j.neuroimage.2011.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinsten O, Henik A. Developmental dyscalculia: heterogeneity might not mean different mechanisms. Trends in Cognitive Sciences. 2009;13(2):92–99. doi: 10.1016/j.tics.2008.11.002. S1364-6613(08)00264-7. [DOI] [PubMed] [Google Scholar]
- Rykhlevskaia E, Uddin LQ, Kondos L, Menon V. Neuroanatomical correlates of developmental dyscalculia: combined evidence from morphometry and tractography. Frontiers in Human Neuroscience. 2009;3:51. doi: 10.3389/neuro.09.051.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlaggar BL, McCandliss BD. Development of neural systems for reading. Annual Review of Neuroscience. 2007;30:475–503. doi: 10.1146/annurev.neuro.28.061604.135645. [DOI] [PubMed] [Google Scholar]
- Shalev R, Auerbach J, Manor O, Gross-Tsur V. Developmental dyscalculia: prevalence and prognosis. European Child & Adolescent Psychiatry. 2000;9(0):S58–S64. doi: 10.1007/s007870070009. [DOI] [PubMed] [Google Scholar]
- Supekar K, Menon V. Developmental maturation of dynamic causal control signals in higher-order cognition: a neurocognitive network model. PLoS Computational Biology. 2012;8(2):e1002374. doi: 10.1371/journal.pcbi.1002374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Supekar K, Swigart AG, Tenison C, Jolles DD, Rosenberg-Lee M, Fuchs LS, Menon V. Neural predictors of individual differences in response to math tutoring in primary-grade school children. Proceedings of the National Academy of Sciences of the United States of America. 2013;110(20):8230–8235. doi: 10.1073/pnas.1222154110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Supekar K, Uddin LQ, Khouzam A, Phillips J, Gaillard WD, Kenworthy LE, … Menon V. Brain hyperconnectivity in children with autism and its links to social deficits. Cell Reports. 2013;5(3):738–747. doi: 10.1016/j.celrep.2013.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swanson HL, Jerman O, Zheng X. Math disabilities and reading disabilities: Can they be separated? Journal of Psychoeducational Assessment 2009 [Google Scholar]
- Szucs D, Devine A, Soltesz F, Nobes A, Gabriel F. Developmental dyscalculia is related to visuo-spatial memory and inhibition impairment. Cortex. 2013;49(10):2674–2688. doi: 10.1016/j.cortex.2013.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szucs D, Goswami U. Developmental dyscalculia: Fresh perspectives. Trends in Neuroscience and Education. 2013;2(2):33–37. [Google Scholar]
- Tanaka H, Black JM, Hulme C, Stanley LM, Kesler SR, Whitfield-Gabrieli S, … Hoeft F. The brain basis of the phonological deficit in dyslexia is independent of IQ. Psychological Science. 2011;22(11):1442–1451. doi: 10.1177/0956797611419521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uddin LQ, Supekar K, Amin H, Rykhlevskaia E, Nguyen DA, Greicius MD, Menon V. Dissociable connectivity within human angular gyrus and intraparietal sulcus: evidence from functional and structural connectivity. Cerebral Cortex. 2010;20(11):2636–2646. doi: 10.1093/cercor/bhq011. bhq011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uddin LQ, Supekar K, Lynch CJ, Cheng KM, Odriozola P, Barth ME, … Menon V. Brain state differentiation and behavioral inflexibility in autism. Cerebral Cortex. 2014:bhu161. doi: 10.1093/cercor/bhu161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uddin LQ, Supekar K, Lynch CJ, Khouzam A, Phillips J, Feinstein C, … Menon V. Salience network-based classification and prediction of symptom severity in children with autism. JAMA Psychiatry. 2013;70(8):869–879. doi: 10.1001/jamapsychiatry.2013.104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Den Heuvel MP, Hulshoff Pol HE. Exploring the brain network: a review on resting-state fMRI functional connectivity. European Neuropsychopharmacology. 2010;20(8):519–534. doi: 10.1016/j.euroneuro.2010.03.008. [DOI] [PubMed] [Google Scholar]
- Wechsler D. Wechsler abbreviated scale of intelligence. San Antonio, TX: Psychological Corporation; 1999. [Google Scholar]
- Wechsler D. The Wechsler Individual Achievement Test — Second Edition (WIAT-II) The Psychological Corporation; 2001. [Google Scholar]
- Whitfield-Gabrieli S, Thermenos HW, Milanovic S, Tsuang MT, Faraone SV, McCarley RW, … LaViolette P. Hyperactivity and hyperconnectivity of the default network in schizophrenia and in first-degree relatives of persons with schizophrenia. Proceedings of the National Academy of Sciences of the United States of America. 2009;106(4):1279–1284. doi: 10.1073/pnas.0809141106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zang YF, He Y, Zhu CZ, Cao QJ, Sui MQ, Liang M, … Wang YF. Altered baseline brain activity in children with ADHD revealed by resting-state functional MRI. Brain & Development. 2007;29(2):83–91. doi: 10.1016/j.braindev.2006.07.002. [DOI] [PubMed] [Google Scholar]
- Zou QH, Zhu CZ, Yang Y, Zuo XN, Long XY, Cao QJ, … Zang YF. An improved approach to detection of amplitude of low-frequency fluctuation (ALFF) for resting-state fMRI: fractional ALFF. Journal of Neuroscience Methods. 2008;172(1):137–141. doi: 10.1016/j.jneumeth.2008.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo XN, Di Martino A, Kelly C, Shehzad ZE, Gee DG, Klein DF, … Milham MP. The oscillating brain: complex and reliable. Neuroimage. 2010;49(2):1432–1445. doi: 10.1016/j.neuroimage.2009.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.