On the Equivalence of FCS and FRAP: Simultaneous Lipid Membrane Measurements

Abstract

Fluorescence correlation spectroscopy (FCS) and fluorescence recovery after photobleaching (FRAP) are widely used methods to determine diffusion coefficients. However, they often do not yield the same results. With the advent of camera-based imaging FCS, which measures the diffusion coefficient in each pixel of an image, and proper bleaching corrections, it is now possible to measure the diffusion coefficient by FRAP and FCS in the exact same images. We thus performed simultaneous FCS and FRAP measurements on supported lipid bilayers and live cell membranes to test how far the two methods differ in their results and whether the methodological differences, in particular the high bleach intensity in FRAP, the bleach corrections, and the fitting procedures in the two methods explain observed differences. Overall, we find that the FRAP bleach intensity does not measurably influence the diffusion in the samples, but that bleach correction and fitting introduce large uncertainties in FRAP. We confirm our results by simulations.

Introduction

Fluorescence correlation spectroscopy (FCS) and fluorescence recovery after photobleaching (FRAP) belong to the most commonly used types of techniques for studying molecular diffusion in biological and biomimetic systems (1). They mainly owe their popularity to their straightforward integration with fluorescence imaging by a confocal or a wide-field microscope and their noninvasive nature, allowing diffusion measurements in living cells and organisms. Both techniques measure the diffusion coefficient (D) of fluorescent tracer molecules and their application ranges largely overlap. However, a number of studies reported significant differences between parameters obtained by FRAP and FCS when applied, although not simultaneously, to the same system (2, 3, 4, 5, 6, 7, 8, 9). The observed discrepancies potentially originate from multiple methodological differences. The most common factors cited are the different length- and timescales accessible by the respective methods. Diffusive movement of molecules in complex environments such as biological membranes is very often hindered by transient trapping and/or semipermeable barriers (1, 10). In such cases, the apparent diffusion coefficient strongly depends on the observation area within which it is probed. Other factors include the much higher laser power used in FRAP during photobleaching, which could lead to sample damage, and data fitting, which is very different between the two methods. Here we use imaging total internal reflection FCS (ITIR-FCS) (11, 12, 13, 14), a camera-based FCS modality that records correlation functions in each pixel of an image, to simultaneously measure FCS and FRAP on the exact same data. We compare the techniques on three different systems: 1) simulated images, 2) DOPC (dioleoylphosphatidylcholine)-supported lipid bilayers (SLBs), and 3) plasma membranes of living cells expressing fluorescent analogs of membrane proteins (a glycosylphosphatidylinositol anchored protein, GFP-GPI, and plasma membrane targeting sequence, PMT-GFP). In contrast to previous studies that applied FRAP and FCS to the same systems sequentially, we perform FRAP and FCS analysis on the exact same data. This approach is, to our knowledge, the first truly simultaneous application of FRAP and FCS, and it qualitatively improves the relevancy of the comparison of the two techniques. The most important advantage lies in the fact that we perform FCS analysis on the data recorded during the fluorescence recovery. This enables us to detect potential transient changes in molecular diffusion induced by the FRAP bleaching pulse. While any such transient changes would affect the results of FRAP, sequential FCS measurements performed before or after the FRAP experiment would not be influenced by them. While this study deals entirely with two-dimensional diffusion in biological and biomimetic membranes, an analogous approach could be extended to compare the results of imaging FCS and FRAP when measuring diffusion in three-dimensional systems, such as the cell nucleus. The only alterations needed would be the implementation of imaging FCS in a single-plane illumination configuration (15, 16) and a suitable bleaching illumination for FRAP.

Materials and Methods

Materials and sample preparation

The protocols for SLB preparation and cell cultivation, transfection, and preparation for imaging together with the specifications of all materials used are given in Bag et al. (10). The SLBs used in this study were prepared from DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine) and headgroup-labeled RhoPE (1,2-dimyristoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (ammonium salt)) purchased from Avanti Polar Lipids (Alabaster, AL). DOPC and RhoPE solutions in chloroform were mixed to achieve a RhoPE/DOPC ratio of ∼1:50,000; the solvent was evaporated under vacuum and the dried lipid film was suspended in buffer (10 mM HEPES, 150 mM NaCl, pH 7.4), the total lipid concentration being 0.5 mM. The lipid suspension was then sonicated to clarity, yielding a suspension of small unilamellar vesicle liposomes. The small unilamellar vesicle suspension was then exposed to a clean glass surface (a microscope coverslip cleaned by 2 M sulfuric acid and thoroughly rinsed with deionized water) and incubated for 20 min at 65°C. After cooling down to room temperature, the excessive unfused liposomes were removed from the SLB by rinsing with excess of the buffer.

CHO-K1 cells were obtained from the American Type Culture Collection (Manassas, VA). GFP-GPI plasmid (referred to as GPI-GFP-AP in Bag et al. (10)) was a gift from John Dangerfield (Anovasia, Singapore). The cells were cultivated in DMEM medium (Dulbecco’s Modified Eagle Medium, Invitrogen; Singapore) supplemented with 1% penicillin G and streptomycin (PS:PAA; Sigma-Aldrich Handels, Vienna, Austria), and 10% FBS (fetal bovine serum; Invitrogen; Singapore) at 37°C in a 5% (v/v) CO₂ environment. Electroporation was used for transfection of the cells, during which ∼90% confluent cells in a 75-cm² flask were washed twice with 1 × PBS and trypsinized with 0.25% trypsin, 0.03% EDTA solution for ∼1 min at 37°C, and then resuspended in culture medium. Cells were precipitated by centrifugation and resuspended in a small amount of resuspension R buffer (Neon Transfection System; Life Technologies, Singapore). One-half of the suspension was transferred into an electroporation cuvette (2-mm wide; Bio-Rad, Hercules, CA) for a single transfection. After the electroporation pulse, cells were seeded back to a prewashed cover-glass (30-mm diameter; Lakeside, Monee, IL) in a 35-mm culture dish. Transfected cells grew in the culture medium for 24–36 h before measurement. Cells were imaged in Phenol Red-free DMEM medium containing 10% FBS.

Experimental setup and data acquisition

The imaging setup was based on an IX81 inverted microscope (Olympus, Tokyo, Japan) equipped with iLas² illumination system (Roper Scientific, Trenton, NJ) allowing simultaneous objective-based total internal reflection fluorescence illumination and FRAP bleaching by a focused laser in the same region of interest. A 491-nm (for cells expressing GFP) or a 561-nm (for SLBs labeled by RhoPE) solid-state laser was used as the excitation source. The sample was illuminated and the fluorescence emission was collected by a high numerical-aperture oil immersion objective (UAPON 100×, NA 1.49; Olympus). The excitation and emission beams were separated by a 416/500/582/657-nm BrightLine Quad-Edge Dichroic Beamsplitter (Semrock, Rochester, NY) and the emission passed through a 440/521/607/700-nm BrightLine Quad-Band Bandpass Filter (Semrock) before being recorded by an electron multiplying charge-coupled device camera (Evolve 512; Photometrics, Tucson, AZ). The exposure time was 3 ms (3.4 ms per frame) and the spinning of the laser beam on the iLas² module was synchronized with the frame-rate of the camera. The image acquisition was controlled by MetaMorph Premier Version 7.7.9 (Molecular Devices, Sunnyvale, CA). Each recorded stack consisted of 60,000 frames with a time resolution of 3.4 ms. The dimensions of the acquired regions of interest were 512 × 40 pixels (41 × 6.4 μm). The FRAP bleaching pulse was applied after ∼1/3 of the stack had been recorded (around the 20,000th frame). The FRAP bleaching was done by rapidly scanning a focused laser beam over a circular area with a diameter of either 16 μm for SLBs, or 6.4, 4.8, or 3.2 μm for cells. The beam was scanned five times over the area; the bleaching pulse duration was 86 ms for 16-μm, 70 ms for 6.4-μm, 40 ms for 4.8-μm, and 20 ms for 3.2-μm diameter circles. The temperature of the sample was maintained at 37°C by a temperature-control chamber (Chamlide TC; Live Cell Instrument, Seoul, Korea).

Diffusion and bleaching simulations

Simulated stacks of 60.000 frames of 40 × 40 pixels were generated by a self-written Fiji (17) plug-in (18). The simulated area was a square with sides 1.5 times longer than those of the final image. In the beginning, molecules were randomly positioned within the simulated area and in each simulation step (corresponding to each frame) all molecules were moved with a Gaussian distributed random displacement centered at 0 and having a variance of 4 D t_f, where t_f is the time-step of the simulation (corresponding to the time between two consecutive frames). If a molecule moved out of the simulated area, a new molecule was placed at a random location along the boundary of the simulated area. The number of photons emitted by a molecule per second was a Poisson random number with a mean of 2000. The points in which individual photons were detected were selected randomly from a Gaussian distribution centered at the position of the emitter and having the width of the Gaussian approximation of the microscope point-spread function (PSF). The photon then contributed a single count to the pixel in which its location fell. Besides the photon counts, each pixel contained simulated noise and background (a Gaussian random number with a mean of 500 and standard deviation of 100). The simulation parameters were selected based on the parameters of our data acquisition: t_f was 3.4 ms, the pixel dimensions 0.16 × 0.16 μm (in the sample space), the noise and background were determined by recordings in samples of cells not expressing any fluorescent protein, and the PSF width (1/e² radius) was set to 277 nm according to the ITIR-FCS calibration of our system (see the following section).

Continuous bleaching (due to excitation used for imaging) was simulated in the following way: at each step, each emitter was switched off (it did not contribute any counts to any of the subsequent frames) with a probability of 1 – exp(−t_f/t_B); t_B is the exponential decay time of the bleaching. The FRAP bleaching pulse was simulated by switching off all emitters within a circle of diameter ω in the 20,000th frame of the stack. Simulations were performed for different values of D, t_B, and ω; D ranged from 0.07 to 1 μm² s⁻¹, t_B ranged from 5 to 100 s, and ω from 1.6 to 3.2 μm.

ITIR-FCS data treatment

The image stacks were analyzed by a self-written Fiji plug-in (the same one that was used for the simulations) analogous to our previously described program, ImFCS (13). It calculates an autocorrelation function (ACF) from the intensity trace in each pixel of a selected region of interest and fits it with a model for two-dimensional diffusion derived previously in Sankaran et al. (12). The values of apparent particle number N and diffusion coefficient D are extracted from each fit. In this way a value of N and D is assigned to each pixel, giving rise to particle number and diffusion coefficient maps. The size of the microscope PSF was calibrated by measurements in supported lipid bilayers, as described earlier in Bag et al. (14). The background was set to 500 counts based on recordings in samples of cells not expressing any fluorescent protein. Four pixels (2 × 2) were binned for the analysis to ensure a better signal/noise. This corresponds to an effective observation area of 0.35 μm² (for GFP-labeled proteins) or 0.42 μm² (for Rho-PE); the observation area is calculated as the area of the binned pixels in the sample space convoluted with the microscope PSF (11).

Intensity trace correction in ITIR-FCS

The intensity traces were corrected for long-term trends caused by bleaching or fluorescence recovery by a variance conserving intensity trace correction (19):

$$F_{\text{corr}}\left(t\right)=F\left(t\right){\left(\frac{f\left(t\right)}{f\left(0\right)}\right)}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+f\left(0\right)\left[1-{\left(\frac{f\left(t\right)}{f\left(0\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right].$$ (1)

F(t) and F_corr(t) are the raw and the corrected intensity traces, respectively, and f (t) is an analytic function that approximates the trend in the intensity trace. An exponential function (i.e., exponential correction) is frequently used to correct for bleaching, which is expected to result in an exponential decay of intensity. In this study, we used polynomial functions (i.e., polynomial correction), because they offer more flexibility in correcting for arbitrary trends in intensity traces caused by long-term trends in the concentration of fluorescent molecules in the observation area. We applied the same procedure to correct for the obvious bleaching as well as for the fluorescence recovery after the FRAP pulse. Correction by polynomials of order not higher than 6 was used to treat almost all the experimental data; in a few cases (as specified) 8th-order polynomials were used because polynomials of the 6th order were not sufficient to approximate the measured intensity trends. Higher-order polynomials were needed to correct the trends in some of the simulated data because of very steep gradients in the intensity trends (for details, see the Supporting Discussion in the Supporting Material).

The Supporting Discussion provides an analysis of the performance of the polynomial trace correction and its comparison with related correction strategies. We propose a simple guideline for the choice of the polynomial order used for the correction: to use the lowest order of the polynomial providing sufficient correction for undesirable trends (the intensity trace after the correction is stationary and the ACFs converge to 0). Following this guideline, polynomial correction offers an efficient and very straightforward way to correct an arbitrary long-term trend in the intensity time trace. Importantly, it requires only the intensity traces themselves and does not rely on any additional measurements or assumptions concerning the character of the trends.

FRAP data treatment

The average intensity in the FRAP-bleached region in all frames from the first frame after the end of the bleaching pulse until the last frame of the stack was plotted against time from the end of the bleaching pulse and analyzed in OriginPro (OriginLab, Northampton, MA). The appropriate model for fitting fluorescence recovery in a circular uniformly bleached area is the Soumpasis model (20):

$$F\left(t\right)=F\left(0\right)+C\text{exp}\left(-\frac{{\omega }^2}{2Dt}\right)\left[I_0\left(-\frac{{\omega }^2}{2Dt}\right)+I_1\left(-\frac{{\omega }^2}{2Dt}\right)\right].$$ (2)

F(0) is the intensity immediately after the bleaching pulse; C is the difference between the asymptotic value of the intensity at t = ∞ (the endpoint of the recovery) and F(0); ω is the radius of the bleached area; and I_α (α = 0; 1) values are modified Bessel functions of the first kind. F(0) can be determined from the recovery trace (we used the average of the first 10 points of the trace), and C and D are free parameters of the fit.

Equation 2 can be modified in a straightforward manner to account for two populations of diffusing molecules with two different diffusion coefficients (see the Supporting Material). We have tested fitting our data with the model with two diffusion coefficients; however, the inclusion of a second diffusion coefficient did not significantly improve the fit, and in most cases both diffusion coefficients either converged to the same value or the fractional contribution of the second diffusion coefficient was negligible, suggesting that a model with a single diffusion coefficient provides an adequate description.

Correction for continuous bleaching in FRAP

All experimental intensity traces suffered from continuous bleaching, which had to be corrected in the analysis of the recoveries. We employed three different strategies:

• (1)External exponential correction is based on approximating the bleaching trend in the region of interest with an exponential decay f(t) and using Eq. 1 to correct the recovery trace. Only those parts of the intensity trace of the region of interest that are not affected by the recovery can be used to find the exponential approximation of the bleaching trend. That means the part of the intensity trace before the FRAP bleaching pulse (prebleach sequence) and the part after the recovery has (almost completely) converged. As an almost complete convergence, we understood for this purpose that at least 94% of the original fluorescence intensity has recovered. We estimated the time point of the 94% recovery using Eq. 2 into which we inserted for D the diffusion coefficient determined by FCS. We then interpolate the exponential intensity decay in the time interval in which the recovery has taken place. We refer to this approach as “prebleach and tail approximation”. Another option is to approximate only the prebleach sequence with an exponential decay and extrapolate the decay until the end of the measurement (i.e., “prebleach approximation”). As we show in Results and Discussion, the latter approach is in most cases inadequate and we have, therefore, used only the prebleach and tail approximation.
• (2)In the internal exponential correction, we include an exponential bleaching factor into Eq. 2. The modified fitting function then has the following form:

$$F\left(t\right)=A+\left[F\left(0\right)-A+C\text{exp}\left(-\frac{{\omega }^2}{2Dt}\right)\left[I_0\left(-\frac{{\omega }^2}{2Dt}\right)+I_1\left(-\frac{{\omega }^2}{2Dt}\right)\right]\right]\text{exp}\left(-t/t_B\right),$$ (3)

where t_B is the bleaching time and A is the steady intensity reached when an equilibrium has been established between the depletion of fluorophores due to continuous bleaching and the influx of fresh fluorophores via diffusion.

• (3)Reference area correction relies on measuring the intensity trace in a reference area located outside of the FRAP bleach region. The recovery trace F(t) is then corrected by the reference trace F_R(t):

$$F_{\text{corr}}\left(t\right)=F\left(t\right)\frac{F_R\left(0\right)}{F_R\left(t\right)}.$$ (4)

Here, F_R(0) is the intensity in the reference area in the first frame after the FRAP bleaching pulse. F_corr(t) is then fitted by Eq. 2.

Results and Discussion

FRAP bleaching pulse does not affect molecular diffusion

First we tested whether the high intensity illumination during the FRAP bleaching pulse induces any transient changes in the molecular diffusion, because any such effects would influence the diffusion coefficients obtained by FRAP. This we did by comparing the values of D obtained by FCS from the parts of each stack recorded before and after the FRAP bleaching pulse, respectively. We divided each stack of 60,000 frames into three substacks of ∼20,000 frames each: 1) the sequence before the FRAP pulse, 2) the sequence after the end of the FRAP pulse in which most of the fluorescence intensity recovery takes place, and 3) the last part in which most of the fluorescence intensity has already recovered. We refer to them in the following discussion as prebleach, recovery, and postrecovery substacks, respectively (Fig. 1 C).

Figure 1.

Illustration of a simultaneous FRAP and ITIR-FCS experiment performed on living CHO cells expressing GFP-GPI. The particle number (N) and diffusion coefficient (D) maps are given in (A) for the three substacks (prebleach, recovery, and postrecovery). The dimensions of the cell images are 25.6 × 6.4 μm. A color-scale bar of N and D is next to the maps. (B) Autocorrelation functions (gray curves) for each observation area (2 × 2 binned pixels, 0.35 μm²) in each of the three substacks. The best fits of the correlation curves are also shown (black lines) together with the average values of D obtained from all the fits. The whole intensity trace in the FRAP bleach region (a circle of 3.2-μm radius) is plotted in (C) and the definition of the prebleach, recovery, and postrecovery are schematically depicted. The recovery trace corrected for bleaching by reference area correction is shown in (D) (gray line) together with a fit by Eq. 2 (black line) and the fitted value of D. To see this figure in color, go online.

The results for all investigated samples and simulations are summarized in Table 1; an example of a live cell experiment is illustrated in Fig. 1. In all cases, the D values obtained from the recovery and postrecovery substacks are within the margins of error identical to the values obtained from the respective prebleach substacks. It can be also noted in Fig. 1 that the bleached region does not differ from its surroundings in the distribution of D values. On the other hand, the bleached region is very distinct in the particle number map for the recovery phase; in agreement with expectations, it exhibits significantly lower particle numbers compared to its surroundings. It can, therefore, be concluded, in agreement with other authors, that the FRAP bleaching pulse does not affect the molecular diffusion in any measurable way (21, 22). However, this does not exclude long-term damage due to phototoxicity induced by the FRAP bleaching pulse.

Table 1.

Comparison of D Values Obtained by ITIR-FCS from Different Segments of the Acquired Image Stacks

	Prebleach DPB/μm2 s−1	Recovery	Postrecovery
Relative D (D/DPB)
Simulation (10)	0.21–1.07	0.99 ± 0.08	1.08 ± 0.11
DOPC SLB (5)	2.6 ± 0.2	0.99 ± 0.11	1.03 ± 0.10
PMT-GFP in CHO cells (4)	0.69 ± 0.20	0.93 ± 0.10	0.99 ± 0.03
GFP-GPI in CHO cells (13)	0.36 ± 0.11	1.00 ± 0.16	1.04 ± 0.10

The value for the prebleach substack (D_PB) and the relative values (normalized to the D_PB of each respective stack) for the other two substacks are given for the samples studied experimentally. Thus, in the ideal case the relative D is expected to be 1. Simulations were performed over a range of D values (0.2–1 μm² s⁻¹); therefore, only a range is given for D_PB instead of a mean value. The intensity traces were corrected by polynomials of the orders of 2 or 4 for the prebleach substacks; 4, 6, or 8 for the recovery substacks (8th order was used only in the cases of simulated stacks); and order 2 or not corrected for the postrecovery substacks. Mean ± standard deviation are shown; the number of measurements (regions in SLBs or simulated stacks, each containing 400 individual ACFs, or cells, each containing typically >1000 individual ACFs) from which they were calculated is given in parentheses next to the sample description.

There is a slight trend in the D values though; the values for the postrecovery substacks tend to be on average higher and the values from the recovery substacks on average lower compared to the values from the prebleach substacks. This is most likely caused by the polynomial intensity trace correction applied on the data before performing FCS analysis to remove any long-term trends in intensity (see Materials and Methods and the Supporting Discussion). As shown in the Supporting Discussion, using a polynomial of higher or lower order than optimal can result in over- or underestimation of D, respectively. Moreover, values obtained from stacks with a restricted number of frames (∼20,000 in this case) are more sensitive to the order of the polynomial used for correction (see the Supporting Discussion). Because we restricted ourselves to even orders in choosing the optimal polynomial order, we cannot exclude introducing a small bias in D. Nevertheless, the differences in the three values of D are smaller than the experimental error and, therefore, insufficient to explain any potential discrepancies between FRAP and FCS results.

An additional explanation of the higher D for the postrecovery phase compared to the prebleach phase can be seen in Figs. 1 and S1. Some ACFs obtained from the prebleach segment are very broad, indicating very slowly diffusing molecules, possibly clusters of molecules. Such broad ACFs are absent among ACFs obtained from the postrecovery substack, because most of the very slowly diffusing particles have been bleached by that time. Slowly diffusing particles were present even in the SLBs, where they probably correspond to unfused liposomes adhering to the SLB surface. Those could not be completely avoided in the relatively large regions of interest captured here. However, the broad ACFs (D < 10% of the average diffusion coefficient) represent <3% (31 curves out of 1160) of all the curves shown in Fig. 1 and the situation was similar or better in other datasets. Furthermore, the simulated data (free from any slow moving particles) follow the same trend in D, i.e., the value from the postrecovery substack is on average slightly higher and the value from the recovery substack is on average lower compared to the prebleach substacks (Table 1). This proves that the slow-moving particles were sufficiently rare in the experimental data to have any significant impact on the measured D values. In cases where outliers have a significant influence on the data, they can be filtered by applying thresholds on the D values to be included in any evaluation.

Comparison of FRAP and FCS results for simulated data and testing of bleaching correction strategies in FRAP

To compare the performance of the two techniques, we calculated D_FRAP by fitting the fluorescence recoveries extracted from the image stacks. The recoveries consisted of the average intensities in the bleached region for each frame beginning with the first frame after the end of the bleaching pulse and ending with the last frame of the stack. D_FCS was calculated from the same substack from which the recovery was extracted (that means a substack comprising the recovery and postrecovery sequences defined above). D_FCS was obtained by analysis of the whole substack of ∼40,000 frames instead of averaging the two values (for the recovery and the postrecovery sequence) obtained in the previous section. The reason for that is the increasing accuracy and precision of D_FCS determination with increasing number of frames in the stack and its increasing robustness toward over- and undercorrection artifacts of the polynomial trace correction, as shown in the Supporting Discussion. However, we also show in the Supporting Discussion that the D_FCS values obtained from stacks with as few as 20,000 frames are not significantly biased and, therefore, their use in the previous section does not invalidate the conclusions drawn from them.

The more complex intensity trends encountered in the larger stacks containing a part with a very steep increase in intensity as well as an almost stationary part (or even a slight decrease in some cases) required a higher order of polynomial trace correction. Polynomials of 6th order and in a few cases of the live cells data of 8th order were used to correct experimental intensity traces. Polynomials of orders from 6 to 12 were used to correct the simulated traces.

For simulations, the ratio of the actual value of D used in the simulations to D_FCS was 0.99 ± 0.03; therefore D_FCS can in that case be regarded as the true value of D.

First, we tested the FRAP fitting on simulated stacks without continuous bleaching. Fig. S2 A shows recovery extracted from a simulated stack with D = 0.5 μm² s⁻¹. The fit with C as a free fitting parameter gives D = 0.40 ± 0.01 μm² s⁻¹. The fit is not an ideal approximation of the simulated recovery, as can be seen from the residuals in the lower panel of Fig. S2 A. In the absence of continuous bleaching or immobile emitters, it can be assumed that the intensity recovery will converge to a value equal to the average intensity in the prebleach phase. We performed, therefore, a fit with C fixed accordingly, leaving D as the sole free parameter. The fit is evidently unsatisfactory, as seen in Fig. S2 A, although the fitted value of D is closer to the expected value (0.51 ± 0.01 μm² s⁻¹). Recovery extracted from a simulated stack with D = 0.2 μm² s⁻¹ is shown in Fig. S2 B. Although the fitted D agrees well with the expected value (0.19 ± 0.01 μm² s⁻¹), the residuals clearly show that the fit is not a perfect one. These observations indicate that Eq. 2 describes the recovery only approximately, even in the ideal case of the simulated data without continuous bleaching.

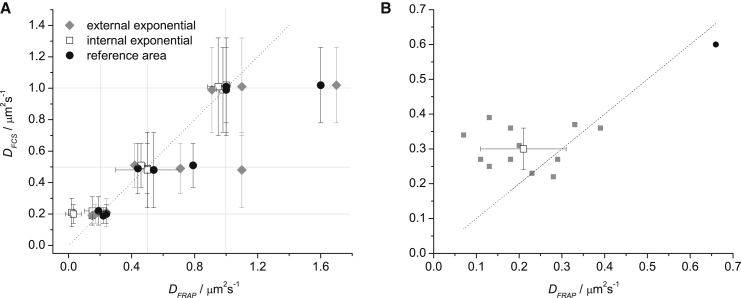
For simulated stacks with continuous bleaching, we tested all three correction strategies. We compare their performance and discuss their applicability for experimental data. A summary of the requirements and applicability of the correction strategies is given in Table 2. A comparison of D_FRAP for the different correction strategies with D_FCS is shown in Fig. 2 A and Table 3. Note that while the errors in D_FCS in Fig. 2 A are typically much larger than those of D_FRAP, they represent not just the uncertainty in D_FRAP determination but also the heterogeneity of D distribution within the imaged (or simulated) area. The standard errors of mean (representing the uncertainty in determination of the average D_FCS) are negligible, due to the large number of averaged values for individual pixels.

Table 2.

A Comparison of the Three Bleach Correction Strategies Used in this Study to Correct for the Continuous Bleaching in FRAP

Correction Strategy	Assumptions	Requirements on data	Suitable experimental systems
External Exponential	Complete recovery of fluorescence	FRAP recovery recorded until a high degree of convergence	In vitro molecular structures (e.g., SLBs)
Internal Exponential	Monoexponential bleaching	FRAP recovery recorded until a very high degree of convergence needed for reliable fitting with Eq. 3	In vitro molecular structures (e.g., SLBs)
Reference Area	The FRAP region and the reference area have almost identical bleaching profile	Intensity trace from a reference area (optimally recorded simultaneously with the FRAP recovery)	Cells and in vitro systems

Figure 2.

Comparison of D_FCS with D_FRAP for simulations (A) and living CHO cells (B). (A) Comparison of D_FCS with D_FRAP values obtained for simulated stacks using the three bleach correction strategies. The horizontal and vertical lines correspond to the actual values of D used in the simulations. The dotted line corresponds to D_FRAP = D to facilitate comparison. (B) Comparison of D_FCS and D_FRAP values obtained for living CHO cells expressing GFP-GPI. All recovery traces were bleach-corrected using reference area correction. (Solid symbols) Results from one individual cell each. (Open square) Average D_FCS and D_FRAP with respective standard deviations. Note that for one of the cells (black circle) both the D_FRAP and D_FCS are considerably larger than the average of the rest of the cells; this cell was excluded from calculating the average displayed by the open square. Dotted line corresponds to D_FCS = D_FRAP to facilitate comparison.

Table 3.

Average D_FCS and D_FRAP Values for Simulations and Measurements in SLBs and Live Cells for Different Bleach Correction Strategies in FRAP

Correction Strategy	DFCS/μm2 s−1	DFRAP/μm2 s−1
(1)	(2)	(3)
Simulation (0.2 μm2 s−1)	0.20 ± 0.01	0.19 ± 0.05	0.09 ± 0.08	0.22 ± 0.03
Simulation (0.5 μm2 s−1)	0.49 ± 0.02	0.74 ± 0.34	0.49 ± 0.02	0.59 ± 0.18
Simulation (1.0 μm2 s−1)	1.00 ± 0.01	1.24 ± 0.41	0.98 ± 0.03	1.20 ± 0.35
DOPC SLB	2.6 ± 0.2	4.0 ± 0.3	3.9 ± 0.5	7.2 ± 1.0
GFP-GPI in CHO	0.33 ± 0.10	—	—	0.24 ± 0.16

(1) External and (2) internal exponential correction and (3) reference area correction.

External exponential correction performs well in most cases; however, it sometimes overestimates D by a factor > 2. Fig. S3 shows the importance of considering the end of the trace in the exponential approximation of the bleaching trend. The prebleach approximation proves to be inadequate even for simulated stacks with ideally monoexponential bleaching. It is even more likely to fail for experimental data that frequently require a biexponential decay to approximate the bleaching trend (Fig. S3).

External exponential correction assumes a complete recovery. In the presence of immobile fluorophores that are bleached by the FRAP bleaching pulse and do not recover, the intensity trace exhibits a discontinuity at the point of the FRAP pulse. It is, therefore, applicable to correct recovery traces recorded in SLBs, where the assumption of a complete recovery is reasonable; however, it is not suitable for cell data, in which case the presence of immobile fluorophores is not unlikely.

The performance of the internal exponential correction was improving with increasing D. We obtained very good agreement between D_FRAP and D for simulated stacks with D of 0.5 and 1.0 μm² s⁻¹. On the other hand, analysis of simulated stacks with D = 0.2 μm² s⁻¹ sometimes gave results very far from the expected value (e.g., 0.03 ± 0.06 μm² s⁻¹). Two examples of recoveries extracted from simulated stacks and corrected by bleaching factor strategy are shown in Fig. S4. While Eq. 3 gave in all cases better fits than Eq. 2 (thanks to the higher number of free parameters), the fitted parameter values were in many cases (especially in the cases of slower diffusion) determined with extremely large uncertainty due to high interdependency of the parameters (>99%), suggesting the fitting problem is ill-posed. The improved performance with increasing D indicates that a high degree of convergence of the recovery curve is needed for a reliable fit with Eq. 3. This conclusion is further supported by the fact that for simulations with D = 0.2 μm² s⁻¹, the average D_FCS/D_FRAP ratio decreases from ∼8 to ∼1.3 when the diameter of the FRAP bleach area decreases from 4.8 to 3.2 μm (a smaller bleached area meaning a higher level of recovery convergence within a given measurement time for a given D).

This indicates that internal exponential correction is not well suited for the cell data, where, due to slow diffusion, only incomplete recovery was reached within the time-frame of our measurements. Moreover, Eq. 3 contains the assumption of a monoexponential nature of the bleaching trend; this may not be the case in cell membranes, where complex intensity trends are common. However, including a biexponential bleaching factor in Eq. 3 increases the number of free fitting parameters and further compromises the numerical stability of the fits.

When applying reference area correction on simulated data, we used as a reference the corresponding area in a reference stack simulated without the FRAP bleaching pulse but with otherwise identical simulation parameters. With this strategy we obtained overall the best agreement between D_FCS and D_FRAP, although in some cases D_FRAP was also considerably overestimated. Interestingly, the datasets for which D_FRAP was overestimated with reference area correction were the same ones for which it was overestimated with external exponential correction. Note that, in the case of simulations, the reference areas had exactly the same bleaching trend as the FRAP bleached region; this is not likely to be perfectly true for experimental data, where an increased uncertainty in D_FRAP is, therefore, expected.

Comparison of FRAP and FCS results for SLBs

In the case of the SLBs, external exponential correction gave D_FRAP = (4.0 ± 0.3) μm² s⁻¹, which is larger than D_FCS = (2.6 ± 0.2) μm² s⁻¹. D_FCS is consistent with our previous results (14, 23) as well as with reported values obtained by single-particle tracking (24) or equilibrating lipid gradients (25); we, therefore, consider it more reliable. A possible reason for the overestimation of D in FRAP is an imperfect bleach correction; this is suggested by the overestimation of D_FRAP when applying external exponential correction on some of the simulated stacks (Fig. 2 A). External exponential correction using the prebleach and tail approximation always required a biexponential decay to correct the bleaching trend in the SLB data (Fig. S3). The bleaching trend is not likely to be monoexponential due to the differences in continuous bleaching trends between different parts of the FRAP bleach region, which was rather large in the case of SLBs (16-μm diameter), as required by the comparatively fast diffusion of lipids in a SLB. Another possible reason for the higher D_FRAP value is reversible bleaching of a fraction of the fluorophores (26, 27, 28, 29); reversibly bleached fluorophores resume fluorescence emission after residence in a dark state, and thus can accelerate the fluorescence recovery. Internal exponential correction gave D_FRAP = (3.9 ± 0.5) μm² s⁻¹, in agreement with external exponential correction.

Reference area correction did not perform well on SLB data, overestimating the D value (the average D_FRAP = (7.2 ± 1.0) μm² s⁻¹) not only in comparison with FCS but also in comparison with the other two bleaching correction strategies in FRAP. We have tested two ways of selecting the reference area: in the same stack as the FRAP bleached region in a belt between 6.4 and 11.2 μm from the border of the FRAP bleached region; and in a reference stack recorded without a FRAP bleaching pulse. The reference stack was recorded in the same SLB under the same conditions and the reference area was, in that case, selected in the center of the illuminated area and having the same dimensions as the FRAP bleached region. In the first case, there was a mismatch between the bleaching kinetics in the reference area and the FRAP bleached region, respectively (Fig. S5). This is most likely caused by the excitation intensity being the highest in the center of the illuminated area and decreasing toward the periphery, resulting in a dependence of the bleaching kinetics on the distance from the center of the illuminated area. In the second case, a better agreement in the bleaching kinetics was achieved; however, the D_FRAP values are similarly overestimated (D_FRAP = (8.1 ± 0.5) μm² s⁻¹ on average). It seems, therefore, that the reference area correction is not well suited for the combination of bleached area and diffusion coefficient present in our SLB data and that under those circumstances it is prone to overestimate the D_FRAP similarly to the case of the simulated data with D = 1 μm² s⁻¹.

Comparison of FRAP and FCS results for living cells

As we have already noted above when discussing the applicability of bleach correction strategies in FRAP, external and internal exponential corrections are not well suited for application on our data from living cells. The absence of immobile fluorophores central to external exponential correction is not necessarily satisfied for proteins in the plasma membrane of cells and, due to slow diffusion, the ≥94% recovery may not be reached in a long enough portion of the trace needed for reliable exponential fitting of the bleaching trend. Internal exponential correction requires a high degree of convergence of the recovery curve for reliable fitting with Eq. 3; however, only incomplete recovery was reached within the time-frame of our cell measurements due to slow diffusion of the membrane proteins. Furthermore, a monoexponential bleaching trend assumed in Eq. 3 is not likely a good description of the bleaching in the cell membrane, where complex intensity trends are common.

We, therefore, used reference area correction. The average intensity trace of two regions outside of the bleached region within the same cell was used as the reference. The inherent assumption behind this correction strategy is that the bleaching in the reference area approximates well the bleaching in the region of interest. This may not be the case in a system as heterogeneous as a cell membrane and the arbitrary choice of the reference area may introduce a considerable uncertainty in the determination of D. Fig. 3 shows the intensity traces from two different reference regions in the cell membrane. Correcting the recovery trace with either of the two traces leads to a different corrected trace and a different value of D. D obtained with correction by the average trace of both reference areas lies between the two values. It can be also noted that out of the three traces, the one corrected by the average of both reference regions can be best fitted by Eq. 2, suggesting that the average reference trace describes the actual bleaching trend in the region of interest better than either of the two individual traces. Nevertheless, a considerable uncertainty in D connected with the choice of the reference area remains.

Figure 3.

An example of the influence of the selection of the reference area on bleach correction by the reference area strategy. The two reference areas are schematically depicted in (A) superimposed on the image of a CHO cell expressing GFP-GPI (average projection of 100 frames immediately following the end of the FRAP bleaching pulse). The dimensions of the cell image are 25.6 × 6.4 μm. The average intensity traces from each of the reference areas are plotted in (B) (for the frames starting with the first frame after the FRAP bleaching pulse and ending with the last frame of the stack). The recovery trace was corrected by the two individual reference traces and by the average reference trace (the average intensity trace of both areas) (C). The best fits of the traces with Eq. 2 are also plotted and the fitted values of D are given in the figure legend.

The average values of D_FRAP and D_FCS of GFP-GPI in cell membranes, (0.24 ± 0.16) μm² s⁻¹ and (0.33 ± 0.10) μm² s⁻¹, respectively, agree within the margin of error and are consistent with our previous results from Bag et al. (10). Fig. 2 B shows the comparison of D_FRAP and D_FCS for individual cells. At D_FRAP > 0.2 μm² s⁻¹, FRAP and FCS are quite consistent with D_FCS/D_FRAP = 1.2 ± 0.4. In cells with D_FRAP < 0.2 μm² s⁻¹ they do not agree well, with D_FRAP varying much more strongly and D_FCS being more constant and higher than D_FRAP. This can be interpreted in two different ways. Either FCS cannot measure correctly very slow diffusion and D_FCS is overestimated in those cells, or D_FRAP is underestimated in those cells, possibly due to incorrect bleach correction, while FCS gives a better estimate of D, closer to the average value from all the cells investigated. To test the former hypothesis, we simulated a stack with D = 0.07 μm² s⁻¹ (the lowest value of D_FRAP). D_FCS = (0.07 ± 0.02) μm² s⁻¹ is in perfect agreement with the expected value, providing support for the latter hypothesis. An additional support for the latter hypothesis is provided by our other FCS studies of membrane protein diffusion in living cells, in which diffusion coefficients as low as (0.07 ± 0.01) μm² s⁻¹ were reproducibly measured (30). Fig. 3 shows that different reference areas used for the bleach correction can result in values of D_FRAP differing by a factor >2; a reference area with bleaching trend different from the region of interest may, therefore, account for the discrepancy. Another possible explanation of the lower D_FRAP in those cells is the hindrance of diffusion on length scales longer than those probed in FCS. Both methods in that case return a correct value of D on their respective length-scale, demonstrating the heterogeneity of the cell membrane. An argument in favor of this explanation is that GPI-GFP is a known lipid-raft marker (10, 31). On the other hand, the length-scales probed by either of the techniques are much larger than expected dimensions of lipid rafts. Structures hindering GPI-GFP diffusion on length-scales larger than those probed by ITIR-FCS could be readily resolved in our fluorescence images; if not in the intensity images, then very likely in the D maps. The absence of any such structures in the cells exhibiting low D_FRAP values compared to the other cells allows for the possibility that GPI-GFP diffusion probed by ITIR-FCS is not different from that probed by FRAP.

On the other hand, it can be seen in Fig. 2 B that, for one of the cells, both the D_FRAP and D_FCS values are considerably larger than the average of the rest of the cells; this indicates that both techniques sense the same relative changes in D.

Interestingly, Stasevich et al. (3) also found the continuous bleaching to be an important source of the discrepancies they observed between FRAP and confocal FCS. In that case, the cryptic bleaching in confocal FCS was the main issue. The authors reached a good agreement with FRAP when using temporal image correlation spectroscopy instead of confocal FCS. This suggest cryptic bleaching as a potential cause of previously reported discrepancies between confocal FCS and FRAP. ITIR-FCS, similarly to temporal image correlation spectroscopy, is less prone to cryptic bleaching-related artifacts and we show in the Supporting Discussion that the influence of those artifacts on our data is insignificant. The above-mentioned work focused primarily on binding quantification by FRAP and FCS; this study, therefore, provides complementary information by concentrating on diffusion coefficient measurements.

Conclusions

We have shown that the FRAP bleaching pulse does not induce any transient changes in the molecular diffusion; therefore, diffusion probed by FRAP during the recovery does not differ from the diffusion in equilibrium probed by FCS. We show that both methods give the same relative changes in D and we obtained a good agreement between the average D_FRAP and D_FCS for a membrane protein in living cells. However, both techniques are sensitive to bleaching caused by the continuous excitation used for fluorescence observation. Correction for the bleaching is straightforward in FCS and, contrary to the bleach correction in FRAP, does not require any additional data or assumptions (19, 32). The uncertainties connected with bleach correction in FRAP increase the uncertainty with which D_FRAP is determined. For some of our simulated data, D_FRAP differed from the correct value by a factor larger than 2. Similarly, for protein diffusion in cell membranes, we show that for different reference areas used for the bleach correction, we may get values of D differing by more than a factor of 2 (Fig. 3).

The uncertainties in D_FRAP introduced by the bleach correction may account for the discrepancies between D_FRAP and D_FCS in cells exhibiting D_FRAP < 0.2 μm² s⁻¹. Another possible explanation of the discrepancy is the higher prominence of barriers hindering diffusion on longer scales in the membranes of those cells. On the other hand, FCS has higher requirements on signal/noise than FRAP. Fig. S5 shows an example of FRAP recovery obtained from a stack that gave correlation curves too noisy to be analyzed. The lower requirements on signal/noise reduce the requirements on excitation power and, thus, lessen to some degree the problems with bleaching. Another advantage of FRAP is the ability to quantify the fraction of immobile fluorophores from the difference between the prebleach intensity and the intensity after complete recovery; this information is not directly accessible in FCS. In other situations, ITIR-FCS offers the advantages of a straightforward bleach correction and, above all, of mapping the distribution of D and particle number in every pixel of an image. The latter feature is especially important in studies seeking to establish a relation between structure and molecular mobility in living cells. Overall we find that FRAP measurements are not influenced by the application of a strong bleaching pulse, not taking into account any long-term photodamage beyond the FRAP measurement time of the sample due to phototoxicity. Furthermore, FRAP and imaging FCS techniques provide similar diffusion coefficient values. However, imaging FCS provides better and more stable diffusion coefficients with also much better spatial and temporal resolution, partly due to the ease of intensity trace correction even for strongly varying cases. This is especially the case for slow diffusion and on live cells. FRAP, on the other hand, has a lower requirement on the signal/noise and the concentration in the sample and can obtain results even in cases where imaging FCS might not be applicable anymore.

Author Contributions

T.W. designed the study; R.M. and Y.H.F. performed the experiments; R.M. analyzed the data; and R.M. and T.W. wrote the article.

Editor: Ana-Suncana Smith.