Accelerated High Bandwidth MR Spectroscopic Imaging Using Compressed Sensing

Abstract

Purpose

To develop a compressed sensing (CS) acceleration method with a high spectral bandwidth exploiting the spatial-spectral sparsity of MR spectroscopic imaging (MRSI).

Methods

Accelerations were achieved using blip gradients during the readout to perform non-overlapped and stochastically delayed random walks in k_x-k_y-t space, combined with block-Hankel matrix completion for efficient reconstruction. Both retrospective and prospective CS accelerations were applied to ¹³C MRSI experiments, including in vivo rodent brain and liver studies with administrations of hyperpolarized [1-¹³C] pyruvate at 7T and [2-¹³C] dihydroxyacetone at 3T, respectively.

Results

In retrospective undersampling experiments using in vivo 7T data, the proposed method preserved spectral, spatial and dynamic fidelities with R² ≥ 0.96 and ≥ 0.87 for pyruvate and lactate signals, respectively, 750-Hz spectral separation and up to 6.6-fold accelerations. In prospective in vivo experiments, with 3.8-fold acceleration, the proposed method exhibited excellent spatial localization of metabolites and peak recovery for pyruvate and lactate at 7T as well as for dihydroxyacetone and its metabolic products with a 4.5-kHz spectral span (140 ppm at 3T).

Conclusion

This study demonstrated the feasibility of a new CS approach to accelerate high spectral bandwidth MRSI experiments.

Introduction

In hyperpolarized ¹³C experiments, MR spectroscopic imaging (MRSI) techniques provide real-time assessment of ¹³C labeling in multiple metabolites and their distribution in different organs or tissue types, leading to the measurement of enzyme kinetics, tissue perfusion, pH, redox state, and more (1–4). The major technical challenges facing hyperpolarized ¹³C MRSI with in vivo applications are the sub-minute lifetime of the hyperpolarized ¹³C signal and the relatively broad dispersion of ¹³C spectra. The short lifetime of the hyperpolarized ¹³C signal requires MRSI techniques that capture the dynamics of metabolites in a rapid manner and make efficient use of the ¹³C hyperpolarization. Therefore, it is desirable to reduce the number of phase encodings and excitations. Meanwhile, the broad spectral dispersion of many hyperpolarized ¹³C probes and their metabolic products make it necessary to develop high bandwidth methods. For example, monitoring [1-¹³C] lactate and ¹³C-bicarbonate production using hyperpolarized [1-¹³C] pyruvate requires a spectral dispersion of 20 ppm (5,6); hyperpolarized [2-¹³C] dihydroxyacetone and one of its metabolic products, [2-¹³C] glycerol-3-phosphate, have a spectral dispersion of 140 ppm, with several other products within this bandwidth (4); and even more challenging, a spectral dispersion of 180 ppm is necessary to follow [5-¹³C] glutamate and [2-¹³C] lactate production after injection of hyperpolarized [2-¹³C] pyruvate (6–8).

Previous hyperpolarized ¹³C studies have utilized several MRSI techniques, such as phase-encoded MRSI (2,5,9,10), echo planar spectroscopic imaging (EPSI) and compressed sensing (11–14), spiral spectroscopic imaging (spiral SI) (8,10,15), concentric rings spectroscopic imaging (16) and model-based spectral reconstruction (17–19). Although phase-encoded MRSI is slow, its intrinsically high spectral bandwidth is advantageous for many hyperpolarized ¹³C applications. The fast MRSI techniques, including EPSI, spiral SI, and concentric rings, utilize high-slew-rate gradient waveforms to cover k-t space repetitively (16,20,21). These techniques rapidly sample k-space, but have relatively low spectral bandwidths on clinical MRI systems (i.e. <1 kHz) due to limitations in gradient hardware performance. Model-based spectral reconstruction utilizes constraints based on the known chemical shifts of images that are acquired with multiple echo times (TEs) (17–19), but requires specific knowledge of the resonant frequencies and B₀ inhomogeneity.

Compressed sensing (CS) is a promising tool for accelerating MRSI with two fundamental criteria: sparsity and incoherence (22). The capability of CS has been demonstrated in hyperpolarized ¹³C EPSI (11–14) as well as in ¹H (23–29), ²³Na (30), ³¹P (31) and ¹⁹F (32) MRSI applications. The spectral dimension of MRSI data is the sparsest, and several methods exploit this sparsity for substantial acceleration using incoherent spatial and spectral undersampling and CS reconstruction (11–14). Several reconstruction methods have also been successfully used in previous CS MRSI studies, e.g. L₁-minimization (11–14,23,24), total variation minimization (25,27–29), and maximum entropy reconstruction (26), and group sparsity based reconstruction (33). Recently, Hankel or block-Hankel matrix completion has been used for recovering undersampled spectral data (34–36) as well as accelerating dynamic MRI (37,38) and calibrationless parallel imaging reconstruction (39–41).

Previously, random blip gradients have been utilized in hyperpolarized ¹³C studies to accelerate EPSI via randomizing the undersampling in the spatial (k_x, k_y), spectral (t), and dynamic (frame) dimensions (11–14). In the present study, four major improvements were made. First, the random blip scheme was optimized based on 2D random walks within the entire k-space sampling region. Second, random blip gradients were combined with stochastic time delays to preserve the inherent bandwidth of MRSI. Third, the CS reconstruction was formulated as a low rank matrix completion to efficiently exploit spatial-spectral sparsity and shared information along the dynamic dimension. Fourth, the proposed method was combined with calibrationless parallel imaging reconstruction (39–41). A retrospective study with varied acceleration factors was performed on an in vivo hyperpolarized ¹³C MRSI dataset. Then prospective accelerations were demonstrated in two hyperpolarized ¹³C MRSI experiments in vivo with hyperpolarized [1-¹³C] pyruvate at 7T and hyperpolarized [2-¹³C] dihydroxyacetone at 3T. We also evaluated the feasibility of CS MRSI with calibrationless parallel imaging in a phantom experiment.

Methods

Compressed Sensing MRSI

Random walk trajectory

The proposed method combined random blip gradients with random walk trajectories and stochastic time delays, allowing incoherent undersampling in k-t space. As shown in Figure 1a, triangular blip gradients were added to a MRSI sequence (FIDCSI, DV24 version at 3T, and DV23 at 7T, GE Healthcare, Waukesha, WI). In each repetition time (TR, Figure 1a), the modified MRSI sequence consisted of a slice selective RF excitation pulse followed by 20 pairs of G_x and G_y blip gradients (0.8 ms duration each) with random amplitudes and time delays. Each pair of G_x and G_y blip gradients moved the k-space trajectory in k_x and k_y, and a series of random blip gradients created a random walk trajectory in k_x-k_y-t space. The random walk trajectory was kept on Cartesian grid points when blip gradients were off, and MRSI data was continuously acquired during both blip gradient on and off periods. However, only the data sampled on the Cartesian grid during the blip off periods were used in reconstruction. Of note, time delays between blip gradients (in Fig. 1a) were randomized to create incoherent undersampling along the t dimension.

Figure 1.

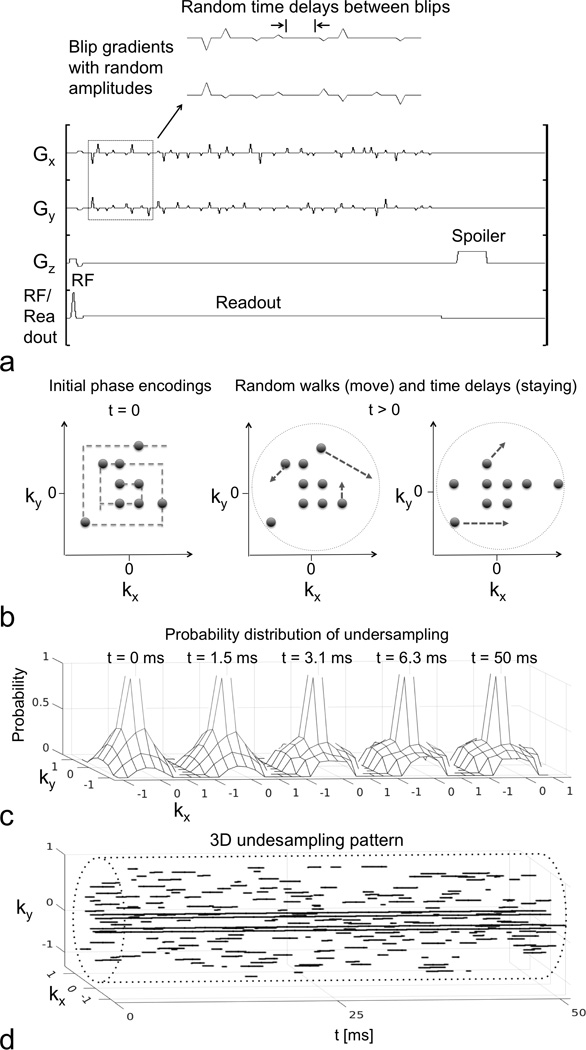
CS MRSI sequence, random walk and time delay scheme and undersampling pattern. (a) CS MRSI sequence for a single acquisition. Blip gradients with random amplitudes and time delays were applied on G_x and G_y during the readout period, which facilitated a random walk trajectory in the k_x-k_y plane. (b) The initial phase encoding locations followed a random spiral-out order. During the readout, some phase encodings were performing random walks, and some were not, due to the random time delays or the full sampling at the center. Random walks moved slower near the center, creating variable density sampling. Four phase encodings in the center were fully sampled along t dimension. (c) The probability distribution of undersampling at various time points. The central peak indicated full sampling. The sampling distribution due to the random walks in peripheral k-space became increasingly flat from t = 0 to 3.1 ms, and was relatively stationary with t > 3.1 ms. (d) The 3D k_x-k_y-t undersampling pattern (3.8-fold) for the first frame, with the cylindrical sampling boundary (dashed line).

Random walk trajectories with the blip gradients were designed with the following constraints (as illustrated in Fig. 1b): 1) initial phase encoding locations were randomly selected and followed a spiral-out order; 2) different random time delay and blip gradient schemes were used for each phase encoding; 3) trajectories in each frame were non-overlapped in k_x-k_y-t space; 4) trajectories were all confined within a cylinder boundary in k_x-k_y-t space; and 5) trajectories moved slower when they were closer to the center of the k_x-k_y plane to create variable density sampling. Probability distributions of this undersampling scheme were generated by Monte Carlo simulation with 1000 realizations, as shown in Figure 1c. The distribution became increasingly flat in the peripheral k_x-k_y plane from t = 0 to 3.1 ms and was relatively stationary for t > 3.1 ms.

Dynamic 3D undersampling pattern

The undersampling pattern was randomized along k_x, k_y, t and frame dimensions. Figure 1d shows the 3D undersampling pattern in k_x-k_y-t space for the first frame, and the undersampling factor was 3.8. For each frame, the undersampling scheme consisted of 14 phase encodings (i.e., 14 excitations). Among them, 10 phase encodings followed the random walk trajectories in k_x-k_y-t space with stochastic time delays as described above. The other 4 phase encodings fully sampled the t dimension for the center of the k_x-k_y plane. For different frames, the 3D undersampling patterns were all independently generated to create randomness along the frame dimension (as shown in Supporting Figure S1). These undersampling patterns were used in all prospective in vivo experiments.

Reconstruction

Block-Hankel reconstruction matrix

A concatenated Hankel matrix (or block-Hankel matrix) was used in this study to represent the dynamic MRSI data in a low-rank manner and to exploit the spatial-spectral sparsity and shared information along the dynamic dimension. As shown on the right side of Figure 2, a 3D sliding window with a size of 5 × 5 × 40 for retrospective experiment or 5 × 5 × 20 for prospective experiments was applied on k_x, k_y and t dimensions of MRSI data to form the block-Hankel matrix H.

Figure 2.

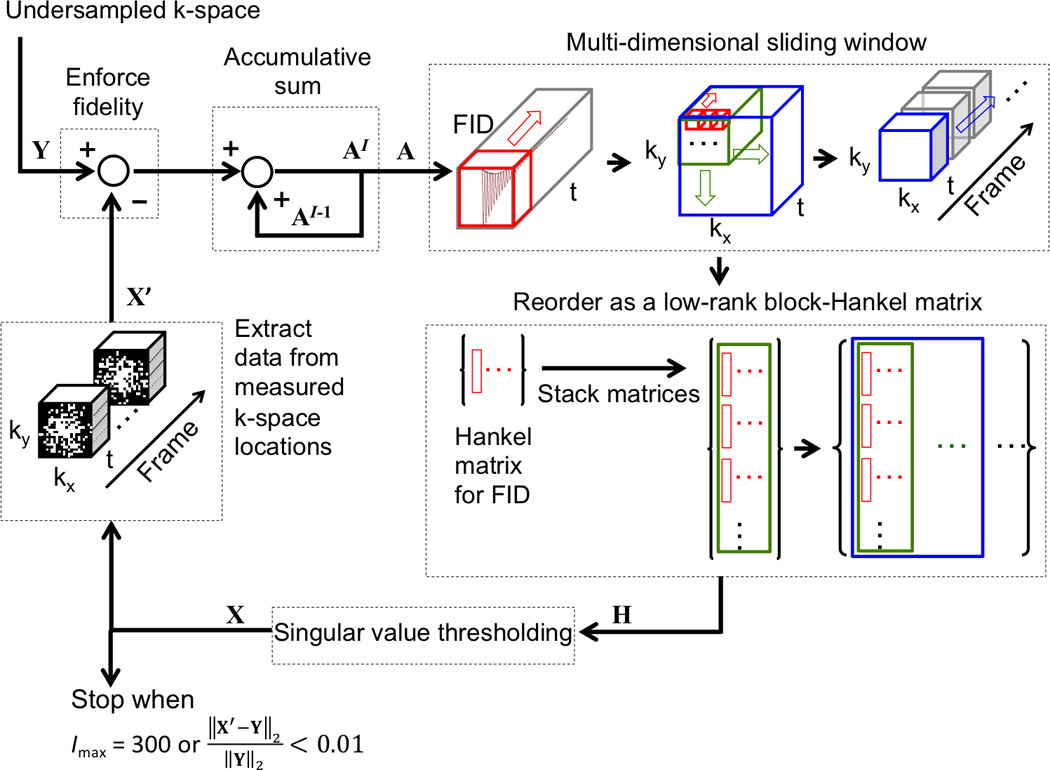
Illustration of the singular value thresholding method used to reconstruct CS datasets. Y is the undersampled k-space; X is the estimated or reconstructed k-space data; X’ the k-space data at measured locations extracted from X; A is the accumulative sum of the difference between Y and X’; H is the block-Hankel matrix of A and the input of the singular value thresholding operation; and I_max for maximum iteration number. Hankel matrices for FIDs (red windows) are first stacked in a column-wise order for all voxels within a k_x-k_y window (green window). Then, the column-wise block matrices for all k_x-k_y windows and frames (blue window indicates one frame) are concatenated along each row to form a large block-Hankel matrix, H.

To characterize the rank of this block-Hankel matrix, we modeled the MRSI data in x-y-frequency (f) space as a linear combination of spatial-spectral peaks that have Lorentzian line-shapes. In k_x-k_y-t space, signal contributed by a spatial-spectral peak at (x_l, y_l, f_l) is the product of three separable exponential functions, that is

$$s_l({\mathrm{k}}_{\mathrm{x}},{\mathrm{k}}_{\mathrm{y}},\mathrm{t})=d_{l,u}{e}^{-(i2\pi x_l+A_l){\mathrm{k}}_{\mathrm{x}}}{e}^{-(i2\pi y_l+B_l){\mathrm{k}}_{\mathrm{y}}}{e}^{-(i2\pi f_l+R_2^{*})t}$$ Eq. 1

where l=1, 2, …, L is the index of peak, d_l,u is the amplitude for frame u, A_l and B_l are decay rates of the k-space signal along k_x and k_y (or line-broadening/blurring factors for spatial Lorentzian peak profiles), and R₂* is the decay rate of the FID (or line-broadening/blurring factor for spectral Lorentzian peak profile). In this model, the block-Hankel matrix H for MRSI data is a linear combination of block-Hankel matrices for each spatial-spectral peak as given by

$$\mathbf{H}={\sum }_{l=1}^L{\mathbf{H}}_{\mathit{l}}$$ Eq. 2

where L is the number of spatial-spectral peaks in the x-y-f space. Here rank(H_l) = 1 for l = 1, 2, …, L (see Appendix for details). Using subadditivity of rank, the rank of H has the following upper bound, that is

$$\text{rank}(\mathbf{H})\le {\sum }_{l=1}^L\text{rank}({\mathbf{H}}_{\mathit{l}})=L.$$ Eq. 3

Therefore, the rank of block-Hankel matrix is not greater than the number of spatial-spectral peaks.

Block-Hankel matrix completion

The nuclear norm minimization for the block-Hankel matrix completion (34,36) can be written as

$$\underset{\mathbf{X}}{\text{argmin}}{\Vert H(\mathbf{X})\Vert }_{*}\mathrm{s}.\mathrm{t}.M(\mathbf{X})=\mathbf{Y}$$ Eq. 4

where M is a k-space undersampling operator, H a 3D sliding window and concatenation operator describing the conversion into a block-Hankel matrix, X the reconstructed MRSI dataset and Y the undersampled MRSI dataset. This nuclear norm minimization can be solved by a singular value thresholding method (42), as shown in Figure 2. The singular value thresholding S(H, μ) was defined as

$$S(\mathbf{H},\mathrm{a})={\mathbf{U}}_{\mathbf{H}}{S}_{\mu }({\mathbf{\Lambda }}_{\mathbf{H}}){{\mathbf{V}}_{\mathbf{H}}}^{*}$$ Eq. 5

where S_μ(Λ) was the soft thresholding on the diagonal entries of Λ with a threshold level μ, and U_HΛ_HV_H* was the singular value decomposition (SVD) of H. In this study, the threshold level μ was set to a large value to ensure accuracy (42).

All the SVD calculations were performed based on a randomized SVD algorithm for reducing the computation cost (43), using the source code that is available online (https://github.com/cvxr/TFOCS/randomizedSVD.m). Only 300 singular values were computed since the other singular values were normally below the threshold. All numerical calculations were carried out in MATLAB (Mathworks Inc., Natick, MA) on a desktop computer.

Broadband spatial-spectral (SPSP) selective RF excitation pulse

In this study, a broadband SPSP pulse was designed for the in vivo hyperpolarized [2-¹³C] dihydroxyacetone (DHAc) experiments. This pulse utilized aliased spectral bands to excite resonances that had a large spectral span (140-ppm, or 4.5-kHz at 3T). A method based on L₂-regularization of an initial RF waveform using an echo-planar trajectory ensured the accuracy of spatial selectivity at several bands of interest across the large spectral span. The SPSP pulse was designed to apply small flip angles for [2-¹³C] DHAc and its hydrate, and large flip angles for its metabolic products: ≤ 0.3° at [2-¹³C] DHAc (213 ppm), 26° at phsophoenolpyruvate (151 ppm), 2.3° at DHAc hydrate (96 ppm) and 20° at glycerol 3-phosphate (G3P) (73 ppm). Additional details of this broadband SPSP pulse are presented in another paper (44).

MR experiments

In vivo mouse brain experiments

The in vivo mouse brain datasets were collected from a 7T whole-body MRI scanner (GE Healthcare, Waukesha, WI). A mouse head RF surface coil was used for both transmission and reception. Two in vivo 2D dynamic hyperpolarized ¹³C MRSI experiments with circular full k-space coverage (n = 1) or prospective 3.8-fold undersampling (n = 1) were performed in two nude mice. All animal experiments were carried out under a protocol approved by the Institutional Animal Care and Use Committee. Both the full k-space and prospectively accelerated MRSI scans were performed with slab thickness = 15 mm, matrix = 8 × 8, field of view (FOV) = 24 × 24 mm², and spectral bandwidth = 5 kHz. For the full k-space MRSI, the other parameters were echo time (TE)/TR = 2.7/80 ms, flip angle = 5°, FID points = 256, readout time = 51.2 ms, excitations per frame = 54, number of frames = 10 and dynamic resolution = 4.1 s/frame. The phase encodings were sampled in a spiral-out order in k-space. The prospectively accelerated MRSI was performed with TE/TR = 2.6/140 ms, flip angle = 10°, FID points = 512, readout time = 102.4 ms, excitations per frame = 14, number of frames = 20, dynamic resolution = 3 s/frame, and undersampling factor = 3.8. The SNR efficiency for undersampling was 92% accounting for duty-cycle losses due to the blip gradients. All the dynamic MRSI data were acquired starting at the beginning of a bolus injection of approximately 0.35 mL hyperpolarized [1-¹³C] pyruvate solution (80 mM, pH = 7.0), produced using HyperSense polarizer (Oxford Instruments). T₂-weighted ¹H images were acquired with TE/TR = 17/4000 ms, FOV = 40 × 40 mm², matrix size = 512 × 512, and slice thickness = 1 mm.

In vivo rat liver experiment

The in vivo rat liver dataset was collected from a 3T whole-body MRI scanner (GE Healthcare, Waukesha, WI). A quadrature volume RF coil was used for both transmission and reception. A Sprague-Dawley rat was examined after 24-hr food deprivation with ad libitum access to water. 3D balanced steady-state free precession anatomical ¹H imaging was performed with TE/TR = 2.2/5.3 ms, FOV = 16 × 8 × 48 mm³ and matrix size = 256 × 256 × 80. Prospectively accelerated hyperpolarized ¹³C MRSI was performed with TE/TR = 10/150 ms, slice thickness = 20 mm, matrix = 8 × 8, FOV = 64 × 64 mm², spectral bandwidth = 10 kHz, FID points = 512, excitations per frame = 14, number of frames = 20, and dynamic resolution = 3 s/frame. The readout time was 51.2 ms, undersampling factor = 3.8, and the SNR efficiency for undersampling was 83%. The data acquisition started at 15 s from the beginning of a bolus injection of approximately 3 mL hyperpolarized [2-¹³C] DHAc solution (80 mM, pH = 7.0), produced using HyperSense (Oxford Instruments).

Calibrationless parallel imaging experiment

A human-head-size thermal ¹³C phantom was filled with ethylene glycol (HOCH₂CH₂OH, anhydrous, 99.8%, Sigma-Aldrich, St. Louis, Missouri) and was scanned on the abovementioned 3T whole-body MRI. An eight channel ¹³C RF surface coil was used for signal reception (45). MRSI data has TE/TR = 2.8/1000 ms, matrix size = 12 × 12, voxel size = 16.6 × 16.6 × 50 mm³, spectral bandwidth = 5 kHz, no averages and no dynamics. The 4-fold undersampling pattern was generated according to the principles illustrated in Figure 1.

Data Analysis

For the phantom MRSI datasets, neither spectral nor spatial filters were used. Signal intensity was quantified by an integration method on absolute spectra. For all in vivo MRSI datasets, a 9 Hz line-broadening spectral filter was applied without spatial filtering. Signal intensities were obtained using the area integration method on the real part of complex spectra. All spectra were displayed in absolute form. In the prospective undersampling experiments, metabolite maps were linearly interpolated and were overlaid on anatomical references. In the retrospective undersampling experiment, metabolite maps were plotted without interpolation.

Results

Phantom experiments

We first performed thermal ¹³C phantom experiments where prospectively undersampled k-space with the proposed CS reconstruction and full k-space data showed a strong linear correlation with a slope = 1.02 and R² = 0.94. Further details can be found in the Supporting Figure S2.

In vivo mouse brain experiments

In Figure 3, a full k-space in vivo dataset was reordered into the proposed block-Hankel matrix structure, which could be approximated by a few singular values (in Figure 3b). In Figure 3c, the different singular values and vectors of the block-Hankel matrix after low-rank approximation correspond to distinct spectral, dynamic and spatial features of this hyperpolarized [1-¹³C] pyruvate experiment. The first and second singular values and vectors were mostly [1-¹³C] pyruvate signal, with similar dynamics corresponding to the bolus injection and subsequent decay but slightly different spatial distributions. The sixth singular value was mostly [1-¹³C] lactate signal with dynamics shifted to later frames corresponding to the progressive build up of this metabolic product.

Figure 3.

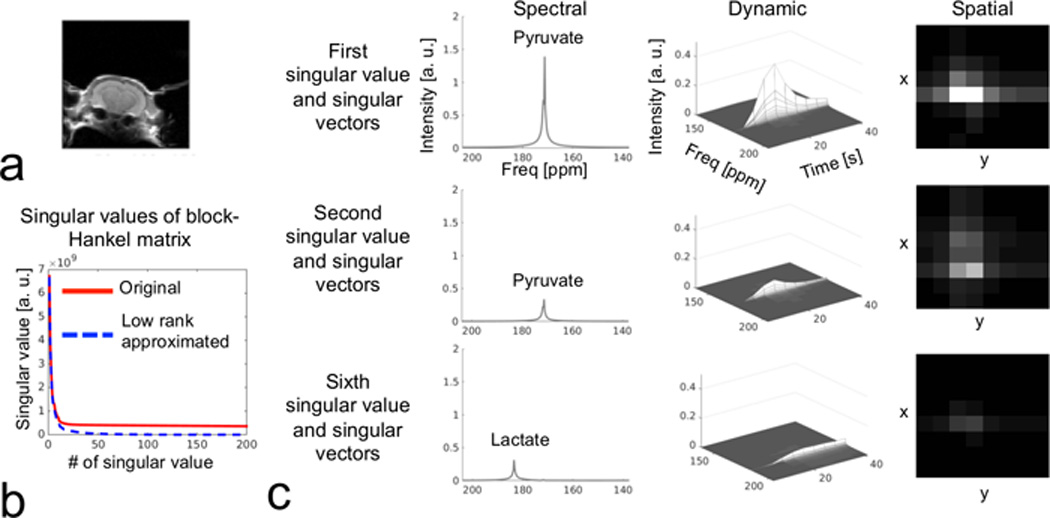
A typical full k-space in vivo hyperpolarized [1-¹³C] pyruvate MRSI dataset, reordered as a block-Hankel matrix with size of 1000 × 30000 (via sliding window and reordering as illustrated in Fig. 2). (a) The T₂-weighted MRI depicts the field of view for the 2D 8 × 8 MRSI. (b) The first 200 singular values from the singular value decomposition of original block-Hankel matrix (red solid line) and its low-rank approximation (blue dash line) are plotted. Low-rank approximation (by Cadzow denoising on block-Hankel matrix) iteratively extracted the top 100 singular values and vectors, and was repeated 300 times. (c) Singular values and vectors from the block-Hankel matrix decomposition after low-rank approximation, showing distinct spectral, dynamic and spatial features.

The performance of the proposed method was examined by retrospective undersampling of the full k-space ¹³C MRSI dataset acquired on a normal mouse brain in vivo. In Figure 4, the reconstructed dynamic spectra with undersampling factors of 2, 2.7, 3.8 and 6.6 were compared with full k-space ground truth. The CS reconstruction preserved the spectral fidelity with acceleration factors up to 6.6-fold, even with the SNR losses introduced by retrospectively throwing away data. Spatial distributions of pyruvate and lactate were preserved in all undersampled datasets with CS reconstruction, resulting in similar lactate to pyruvate ratios within the studied brain region. Time courses of pyruvate and lactate signals in the undersampled datasets were linearly correlated with that in the full k-space dataset. For pyruvate, slopes of correlations were 0.96, 1.02, 0.98 and 0.96 for undersampling factors of 2, 2.7, 3.8 and 6.6, with R² of 0.98, 0.98, 0.98 and 0.96, respectively. For lactate, slopes of correlations were 0.97, 0.85, 0.94 and 0.78 for undersampling factors of 2, 2.7, 3.8 and 6.6, with R² of 0.96, 0.93, 0.95 and 0.87, respectively. The poorer lactate correlation at an undersampling factor of 6.6 led us to choose an undersampling factor of 3.8 for prospective experiments.

Figure 4.

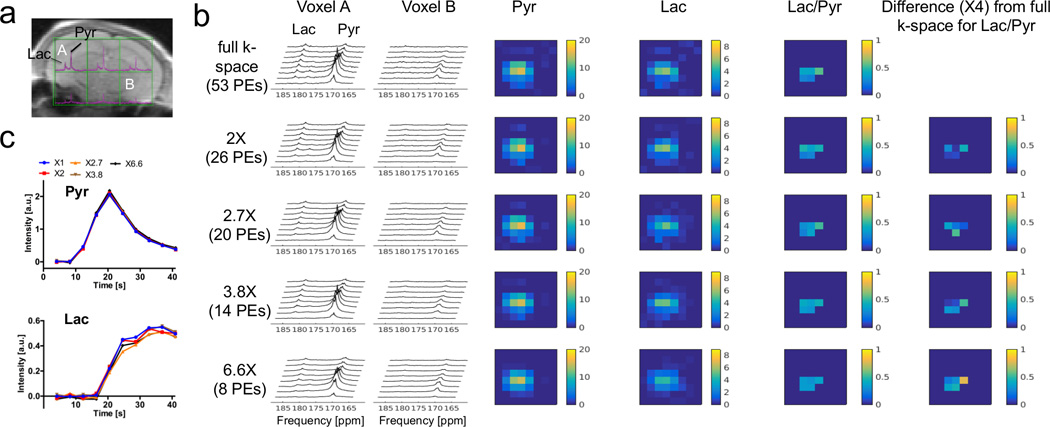
Retrospective CS experiment on a full k-space ¹³C mouse brain MRSI dataset following intravenous administration of hyperpolarized [1-¹³C] pyruvate (same as Fig. 3). The reconstructed dynamic spectra with undersampling factors of 2, 2.7, 3.8 and 6.6 were compared with full k-space ground truth. (a) Fully sampled k-space spectra are overlaid on top of a reference ¹H image. Voxel A was selected as a high SNR voxel, and B was a low SNR voxel. (b) Dynamic spectra and metabolic maps with different undersampling factors. PEs stands for phase encodings. The pyruvate (Pyr) and lactate (Lac) peaks and their spatial features were well-preserved in all undersampled datasets. (c) The pyruvate and lactate time courses from the sum of six voxels on brain. CS largely preserved dynamic features as well.

Figure 5 shows the results of the prospective CS hyperpolarized [1-¹³C] pyruvate MRSI experiment with 3.8-fold undersampling on another normal mouse brain. Both pyruvate and lactate maps showed excellent agreement with the anatomical reference images, with metabolites primarily localized within the brain (5,9). The lactate and pyruvate also had dynamics typical of a bolus injection and metabolic conversion, and lactate was observed for over 54 s.

Figure 5.

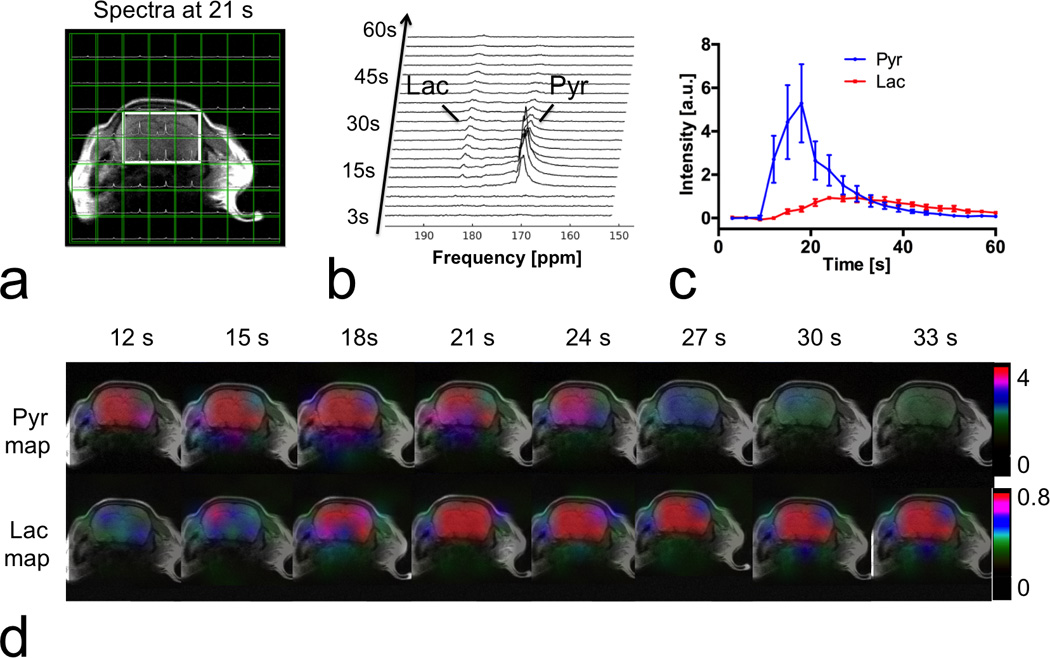
Prospectively 3.8-fold accelerated CS MRSI on mouse brain, following intravenous administration of hyperpolarized [1-¹³C] pyruvate. (a) A mosaic view of spectra and T₂ weighted MRI. Spectra were spatially localized within the head area. (b) Dynamic spectra from the sum of six voxels marked by the solid box in (a). Lactate (Lac) and pyruvate (Pyr) peaks were clearly observed. (c) Time courses of pyruvate and lactate from the marked area. (d) The ¹³C metabolic maps showed pyruvate and lactate dynamics, with the majority of signal localized to the brain.

In vivo rat liver experiment

Figure 6 shows the results from the in vivo dynamic hyperpolarized [2-¹³C] DHAc MRSI experiment in a rat liver with a prospective acceleration factor of 3.8. Metabolites in the reconstructed spectra were spatially localized primarily within the liver. The spectra and time courses, summed among four voxels in the liver, revealed the metabolic conversion from hyperpolarized [2-¹³C] DHAc to G3P was primarily occurring in the rat liver. ¹³C resonances with a 140-ppm (or 4.5-kHz at 3T) span were effectively recovered by the proposed method.

Figure 6.

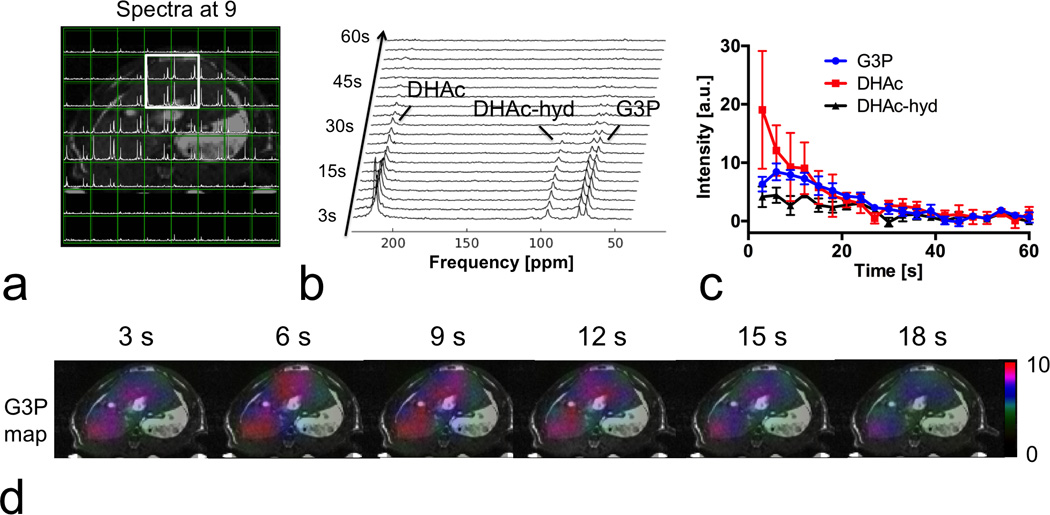
Prospectively 3.8-fold accelerated CS MRSI on rat liver, following intravenous administration of hyperpolarized [2-¹³C] dihydroxyacetone (DHAc), which results in a 140-ppm (4.5 kHz at 3T) range of metabolite chemical shifts. (a) A mosaic view of spectra and abdominal T₂-weighted MRI. Spectra were spatially localized primarily within the liver as expected. (b) Dynamic spectra from the marked area in (a). The three peaks in the dynamic spectra are DHAc (≤0.3° flip, 213 ppm), DHAc hydrate (DHAc-hyd, 2.3° flip, 96 ppm) and glycerol 3-phosphate (G3P, 20° flip, 73 ppm), all of which were recovered by the proposed method. (c) Time courses of DHAc, DHA-hyd and G3P from the marked liver area. (d) The ¹³C metabolic map showed that G3P generated from DHAc was primarily distributed within the liver, indicating accurate reconstruction by our method.

Discussion

Compressed sensing MRSI with hyperpolarized ¹³C applications

The proposed undersampling scheme combined random blip gradients with random walk trajectories and stochastic time delays, allowing incoherent spatial and spectral undersampling for in vivo hyperpolarized ¹³C MRSI experiments. Meanwhile, the presented reconstruction method exploited the spatial-spectral sparsity and shared information along the dynamic dimension, where we extended the application of block-Hankel matrix completion to MRSI. The capability of the proposed method was demonstrated in the in vivo hyperpolarized ¹³C MRSI experiments with retrospective CS acceleration. Furthermore, in the prospective mouse brain experiment, CS was shown to preserve the spectral, spatial and dynamic characteristics of hyperpolarized [1-¹³C] pyruvate and lactate (which have 750-Hz spectral separation at 7T) with good sensitivity and high spectral bandwidth. Lactate and pyruvate signals were observed for over 54 s at 7T, a relatively long duration for in vivo experiments. In the prospective rat liver experiment, reconstructed spectra were spatially localized within the abdominal tissue area (G3P was mostly detected within the liver region). The recovered spectral peaks (with 4.5-kHz spectral separation at 3T) demonstrated the feasibility of CS acceleration for high spectral bandwidth MRSI in hyperpolarized ¹³C experiments in vivo.

The 15-mm slice thickness in the two mouse brain experiments and 20-mm slice thickness in the rat liver experiment likely caused partial volume effects, e.g. contaminations of DHAc and DHAc hydrate signals from the kidney in the rat liver experiment. In the retrospective experiment, the lactate had larger discrepancies with acceleration than pyruvate, likely due to the low SNR of [1-¹³C] lactate (typical in normal brain). The metabolite and ratio maps in Figure 4 also show some spatial smoothing with high acceleration factors. We used this experiment to choose the retrospective undersampling factor of 3.8, although we expect slightly better performance with prospective undersampling because throwing away data in the retrospective analysis results in SNR losses.

Calibrationless parallel imaging for compressed sensing MRSI

Figure 7 shows that the proposed CS MRSI method can be combined with the calibrationless parallel imaging reconstruction (39–41), since both are based on block-Hankel matrix completion. This only required changes to the construction of the block-Hankel matrix, where block-Hankel matrices for coils are concatenated as shown in Figure 7a. The combined CS and parallel imaging acceleration generally preserved the most of the spectral and spatial features of the ¹³C MRSI phantom dataset. This combination could be valuable for hyperpolarized ¹³C and other X-nuclear MRSI applications, where the coil calibration data and coil sensitivity maps are not available or technically difficult to acquire.

Figure 7.

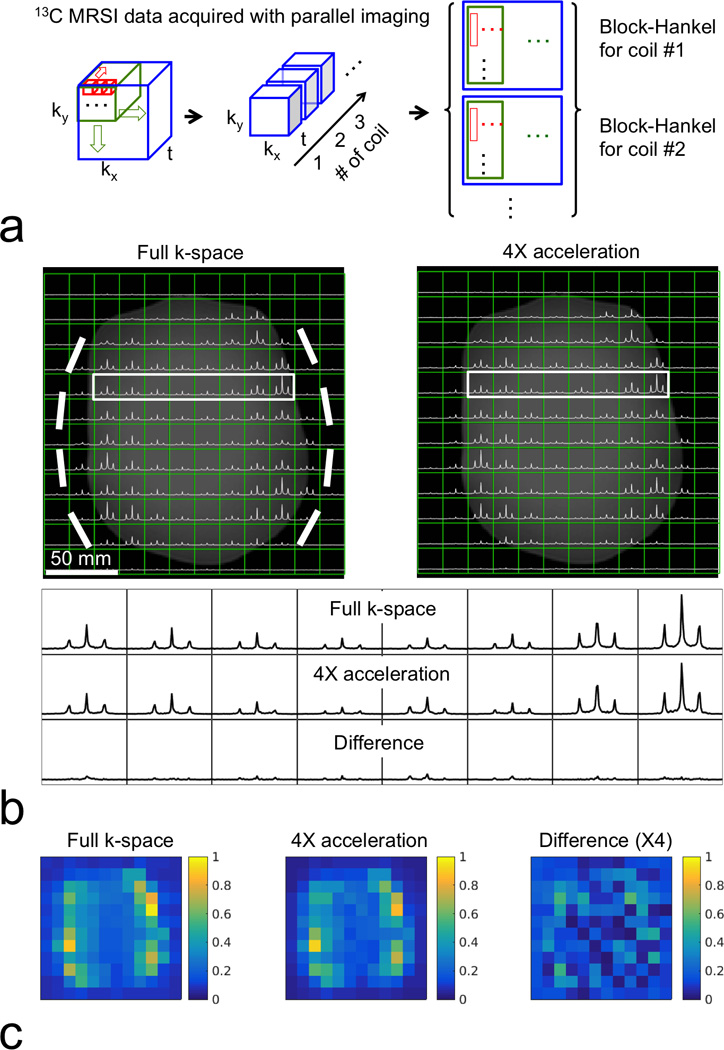
Retrospectively 4-fold accelerated 2D MRSI on a thermal ¹³C phantom (containing 99.8% ethylene glycol) including calibrationless parallel imaging. (a) For reconstruction incorporating calibrationless parallel imaging, Hankel matrices for FIDs (red windows) are stacked in a column-wise order, and k_x-k_y windows (green windows) are concatenated along each row, as done when not using parallel imaging (Fig. 2). Then, block-Hankel matrices for coils (blue windows) are concatenated along column. (b) Full k-space and CS accelerated spectra after the sum of squares coil combination. Bright bold lines indicate eight elements of the surface ¹³C RF receiver coil. The bottom panel shows the comparison of spectra from marked area (solid boxes). The triplet spectra of ethylene glycol (J_C-H = 150 Hz) were well recovered by the combined CS and calibrationless parallel imaging, with most obvious differences occurring in the low SNR region in the middle of the phantom. (c) Integrated spectra maps comparison. The combined CS and parallel imaging acceleration generally preserved the most of spectral and spatial features of the ¹³C MRSI phantom dataset.

Conclusion

This study developed a CS method that uniquely combined random blip gradients with stochastic time delays, and exploited the spatial-spectral sparsity with a block-Hankel matrix completion reconstruction to accelerate high bandwidth MRSI. In retrospective hyperpolarized ¹³C experiments, CS preserved spectral, spatial and dynamic fidelities with up to 6.6-fold accelerations. In prospective experiments, 3.8-fold acceleration for dynamic MRSI was successfully performed in vivo in a mouse brain and a rat liver with hyperpolarized [1-¹³C] pyruvate and hyperpolarized [2-¹³C] dihydroxyacetone, respectively. These results demonstrated the feasibility of the proposed CS approach to accelerate high bandwidth MRSI in hyperpolarized ¹³C experiments in vivo.

Appendix

In k_x-k_y-t space, signal contributed by a Lorentzian spatial-spectral peak, l, at (x_l, y_l, f_l) is given by the outer product (designated “◦”) of 4 vectors, that is

$${\mathbf{S}}_{\mathit{l}}={\mathit{d}}^{\mathit{T}}◦\left[\begin{array}{c}\hfill e^{q\mathrm{\Delta }{\mathrm{k}}_{\mathrm{x}}(i2\pi x_l+A_l)}\hfill \\ \hfill e^{(q-1)\mathrm{\Delta }{\mathrm{k}}_{\mathrm{x}}(i2\pi x_l+A_l)}\hfill \\ \hfill ⋮\hfill \\ \hfill e^{-q\mathrm{\Delta }{\mathrm{k}}_{\mathrm{x}}(i2\pi x_l+A_l)}\hfill \end{array}\right]◦\left[\begin{array}{c}\hfill e^{a\mathrm{\Delta }{\mathrm{k}}_{\mathrm{y}}(i2\pi y_l+B_l)}\hfill \\ \hfill e^{(a-1)\mathrm{\Delta }{\mathrm{k}}_{\mathrm{y}}(i2\pi y_l+B_l)}\hfill \\ \hfill ⋮\hfill \\ \hfill e^{-a\mathrm{\Delta }{\mathrm{k}}_{\mathrm{y}}(i2\pi y_l+B_l)}\hfill \end{array}\right]◦\left[\begin{array}{c}\hfill e^{-\mathrm{\Delta }\mathrm{t}(i2\pi f_l+R_2^{*})}\hfill \\ \hfill e^{-2\mathrm{\Delta }\mathrm{t}(i2\pi f_l+R_2^{*})}\hfill \\ \hfill ⋮\hfill \\ \hfill e^{-m\mathrm{\Delta }\mathrm{t}(i2\pi f_l+R_2^{*})}\hfill \end{array}\right]$$ Eq. A1

where d = [d_l,1 ⋯ d_l,u] a vector that contains the dynamic amplitudes for u frames, [−q, q] and [−a, a] the ranges of k_x and k_y dimensions, A_l, B_l, and R₂* are the decay rates (or line-broadening/blurring factors) and Δk_x, Δk_y and Δt the minimal sampling intervals for k_x, k_y and t dimensions.

The 3D sliding window operation with a window size of p × b × n in k_x, k_y and t dimensions can apply to S_l, creating a block-Hankel matrix, H_l ∈ ℂ^{(2q−p+2)(2a−b+2)(m−n+1)×upbn}. H_l can be written as the Kronecker product (designated “⊗”) of three Hankel matrices, i.e. H_t ∈ ℂ^(m−n+1)×n, H_kx ∈ ℂ^{(2q−p+2)×p} and H_ky ∈ ℂ^{(2a−b+2)×b}, and they are given respectively as

$${\mathbf{H}}_{\mathit{k}\mathit{x}}=\left[\begin{array}{ccc}\hfill e^{q\mathrm{\Delta }{\mathrm{k}}_{\mathrm{x}}{x}_l(i2\pi x_l+A_l)}\hfill & \hfill \cdots \hfill & \hfill e^{(q-p+1)\mathrm{\Delta }{\mathrm{k}}_{\mathrm{x}}(i2\pi x_l+A_l)}\hfill \\ \hfill e^{(q-1)\mathrm{\Delta }{\mathrm{k}}_{\mathrm{x}}(i2\pi x_l+A_l)}\hfill & \hfill \cdots \hfill & \hfill e^{(q-p)\mathrm{\Delta }{\mathrm{k}}_{\mathrm{x}}(i2\pi x_l+A_l)}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill e^{(p-q-1)\mathrm{\Delta }{\mathrm{k}}_{\mathrm{x}}(i2\pi x_l+A_l)}\hfill & \hfill \cdots \hfill & \hfill e^{-q\mathrm{\Delta }{\mathrm{k}}_{\mathrm{x}}(i2\pi x_l+A_l)}\hfill \end{array}\right],$$

$${\mathbf{H}}_{\mathit{k}\mathit{y}}=\left[\begin{array}{ccc}\hfill e^{a\mathrm{\Delta }{\mathrm{k}}_{\mathrm{y}}(i2\pi y_l+B_l)}\hfill & \hfill \cdots \hfill & \hfill e^{(a-b+1)\mathrm{\Delta }{\mathrm{k}}_{\mathrm{y}}(i2\pi y_l+B_l)}\hfill \\ \hfill e^{(a-1)\mathrm{\Delta }{\mathrm{k}}_{\mathrm{y}}(i2\pi y_l+B_l)}\hfill & \hfill \cdots \hfill & \hfill e^{(a-b)\mathrm{\Delta }{\mathrm{k}}_{\mathrm{y}}(i2\pi y_l+B_l)}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill e^{(b-a-1)\mathrm{\Delta }{\mathrm{k}}_{\mathrm{y}}(i2\pi y_l+B_l)}\hfill & \hfill \cdots \hfill & \hfill e^{-a\mathrm{\Delta }{\mathrm{k}}_{\mathrm{y}}(i2\pi y_l+B_l)}\hfill \end{array}\right],$$

$${\mathbf{H}}_{\mathit{t}}=\left[\begin{array}{ccc}\hfill e^{-\mathrm{\Delta }\mathrm{t}(i2\pi f_l+R_2^{*})}\hfill & \hfill \cdots \hfill & \hfill e^{-n\mathrm{\Delta }\mathrm{t}(i2\pi f_l+R_2^{*})}\hfill \\ \hfill e^{-2\mathrm{\Delta }\mathrm{t}(i2\pi f_l+R_2^{*})}\hfill & \hfill \cdots \hfill & \hfill e^{-(n+1)\mathrm{\Delta }\mathrm{t}(i2\pi f_l+R_2^{*})}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill e^{-(m-n+1)\mathrm{\Delta }\mathrm{t}(i2\pi f_l+R_2^{*})}\hfill & \hfill \cdots \hfill & \hfill e^{-m\mathrm{\Delta }\mathrm{t}(i2\pi f_l+R_2^{*})}\hfill \end{array}\right],\text{and}$$

$${\mathbf{H}}_l=\mathit{d}\otimes {\mathbf{H}}_{\mathit{k}\mathit{x}}\otimes {\mathbf{H}}_{\mathit{k}\mathit{y}}\otimes {\mathbf{H}}_{\mathit{t}}.$$ Eq. A2

Notably in this model H_kx, H_ky, and H_t are all rank-1 matrices, and rank(H_l) = rank(d)rank(H_kx)rank(H_ky)rank(H_t) = 1.