Nanonet Force Microscopy for Measuring Cell Forces

Abstract

The influence of physical forces exerted by or felt by cells on cell shape, migration, and cytoskeleton arrangement is now widely acknowledged and hypothesized to occur due to modulation of cellular inside-out forces in response to changes in the external fibrous environment (outside-in). Our previous work using the non-electrospinning Spinneret-based Tunable Engineered Parameters’ suspended fibers has revealed that cells are able to sense and respond to changes in fiber curvature and structural stiffness as evidenced by alterations to focal adhesion cluster lengths. Here, we present the development and application of a suspended nanonet platform for measuring C2C12 mouse myoblast forces attached to fibers of three diameters (250, 400, and 800 nm) representing a wide range of structural stiffness (3–50 nN/μm). The nanonet force microscopy platform measures cell adhesion forces in response to symmetric and asymmetric external perturbation in single and cyclic modes. We find that contractility-based, inside-out forces are evenly distributed at the edges of the cell, and that forces are dependent on fiber structural stiffness. Additionally, external perturbation in symmetric and asymmetric modes biases cell-fiber failure location without affecting the outside-in forces of cell-fiber adhesion. We then extend the platform to measure forces of (1) cell-cell junctions, (2) single cells undergoing cyclic perturbation in the presence of drugs, and (3) cancerous single-cells transitioning from a blebbing to a pseudopodial morphology.

Introduction

Biophysical influences on cell shape, cytoskeletal organization, and migration speed make it necessary to accurately quantify the forces that underlie cell-substrate interactions (1, 2). Cells receive physical and chemical cues from their surrounding microenvironment known as the extracellular matrix (ECM), a primarily fibrous network with composition and structure that varies temporally and spatially in the body (3, 4, 5). Mechanical communication between a cell and its substrate occurs bidirectionally through integrin-mediated focal adhesions. Cells generate forces via actomyosin contractions that act on their surroundings (inside-out, or IO) but also respond to forces originating outside the ECM that are transmitted through adhesion sites to the cytoskeletal network (outside-in, or OI) (6, 7, 8, 9). Both directions are physiologically relevant, as seen in the example case of arteries: smooth muscle cells generate IO contractile forces that control vessel constriction to modulate blood pressure, but also experience OI forces from vessel expansion with each heartbeat that cause the cell to reorient actin stress fibers (10, 11). Therefore, force measurement platforms that are able to capture both modes can allow distinguishing forces that cells exert from those that they can withstand. This can provide new insights into understanding disease states where progression from normal function to failure either occurs rapidly or without warning or detection (bone fracture, muscle or ligament tears, blood vessel aneurysms).

IO forces are commonly measured by substrates that contain deformable objects such as traction force gels or micropillar arrays (12, 13, 14, 15, 16, 17, 18). Cells pull on these objects as they migrate, resulting in deflections that can be measured and converted to forces (19). Conversely, OI platforms require an active component that applies forces to the cell or its substrate. Such approaches include active stretching of traction force gels or micropillar arrays, atomic force microscopy (AFM) cantilevers, microfluidic devices that incorporate fluid shear, and other microelectromechanical systems devices (20, 21, 22, 23, 24, 25, 26). Recent in vitro studies by us and by others have shown that on ECM-mimicking suspended fibers, cells migrate by applying contractile forces, as evidenced by the deflection of fibers (27, 28). Very little is known on the link between fibrous environmental cues and force generation, which necessitates development of contextually relevant platforms to measure single and multicell forces. In this regard, we have previously observed that nanofiber curvature induces cell elongation with associated focal adhesion clustering at the periphery of the cell, a phenomenon that is responsible for altered cell-nucleus aspect ratio and migration speed (27, 29). Additionally, improvements to our non-electrospinning spinneret-based tunable engineered parameters (STEP) technique (Fig. 1; (30, 31)) has allowed us to produce fibrous nanonets of tunable structural stiffness (N/m) for measuring cellular forces (32); we term this method “nanonet force microscopy”.

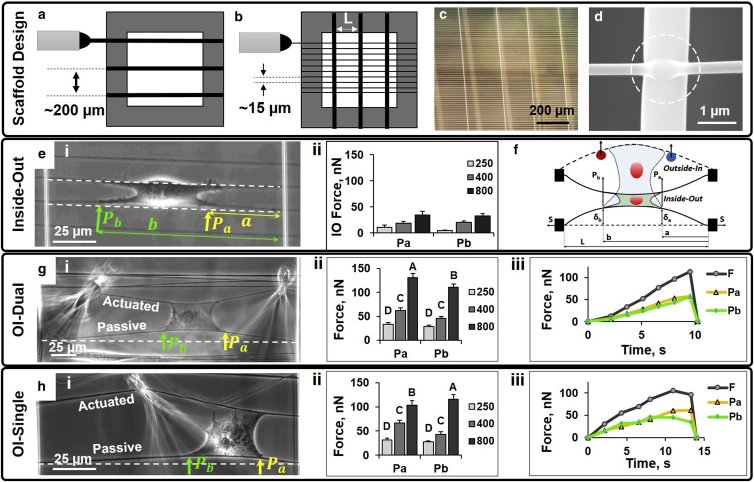
Figure 1.

(a) Schematic of large-diameter fibers (∼1200 nm) spun with interfiber spacing (∼200 μm) over a hollowed-out substrate, resulting in suspended fibers; (b) schematic of small diameter fibers spun with spacing (∼15 μm) perpendicular to the first layer; (c) optical image of an assembled nanonet; (d) fiber intersections are fused together, resulting in fixed boundary conditions; (e) IO force measurement, showing (i) representative parallel cell and (ii) forces P_a and P_b for different fiber diameters; (f) schematic of IO and OI modes showing use of two point load model and selection of locations for a and b; (g) OI-Dual platform, with (i) representative optical image, (ii) force distribution, and (iii) representative force-time plot of abrupt breaking failure with resultant force calculated as $\left(F=P_a+P_b\right)$; and (h) OI-Single platform, with (i) representative optical image, (ii) force distribution, and (iii) representative force-time plot of peeling failure. Letters above bars represent groups of statistical significance. Shared letters indicate insignificant differences (n = 242). White dashed lines indicate undeflected fiber position. To see this figure in color, go online.

In addition to observing contractile IO forces generated by cells attached to nanonet fiber segments, we present here the development and application of external probe-based perturbation (symmetric and asymmetric) to measure the cell’s mechanical response and load distribution. Perturbations of single cells and cell-cell pairs attached to nanonets of different diameters reveal that bias (asymmetric loading) does not affect the maximum adhesion force of the cell, but rather shifts the failure location and probability of failure in a diameter-dependent manner. We propose that these effects are due to curvature-induced orientation and distribution of focal adhesion sites. We then demonstrate the power of the platform by extending the studies to measure 1) cell-cell junctional force response to external perturbation, revealing stronger adhesion formation at the cell-fiber interface than the cell-cell junction; 2) single cell force response from the onset of exposure to a cytoskeletal drug; and 3) reduction in forces of cancerous glioma cells undergoing a blebbing-to-pseudopodial transition caused by physical stretching of the cell in the absence of drugs.

Materials and Methods

Nanonet manufacturing and cell culture

The previously reported non-electrospinning STEP technique (33, 34) was used to manufacture suspended criss-cross polystyrene nanonet scaffolds with fused fiber intersections. Scaffolds were placed in 35-mm glass-bottom dishes (MatTek, Ashland, MA) and sterilized in 70% ethanol for 10 min. Fibers were coated in 2 μg/mL fibronectin (Invitrogen, Carlsbad, CA) to promote cell attachment (35). C2C12 mouse myoblasts (American Type Culture Collection (ATCC), Manassas, VA) were cultured in DMEM cell culture media (Invitrogen) supplemented with 10% fetal bovine serum and 1% penicillin/streptomycin (HyClone Laboratories, Logan, UT). Cells were seeded by placing 35-μL droplets of 100,000 cells/mL on the scaffolds and 300 μL DMEM around the dish edges to prevent evaporation. After incubating 4 h for attachment, 2 mL of HEPES-buffered RPMI 1640 media (ATCC) was added to the dishes due to its ability to maintain pH longer than DMEM (36). Cancer cell blebbing experiments were performed with DBTRG-05MG glioma cells using RPMI 1640 media (ATCC).

Force modeling

Similar to previously reported force measurement strategies involving inverse methods, we model the fibers as prismatic beams under uniform tension with fixed ends. We assume that a cell applies two point loads on the beam, one on each end of the cell-fiber interface (where the focal adhesions cluster) that both contribute to overall fiber deflection. Therefore, by modifying Timoshenko’s single point load model to incorporate both point loads (37), the experimentally measured deflections ${\delta }_a$ and ${\delta }_b$ (Fig. 1) can be related to their associated loads P_a and P_b (see the Supporting Material):

$$\begin{array}{c}{\delta }_a=\left(-\frac{P_a\text{sinh}\left[\lambda \left(L-a\right)\right]}{S\lambda \text{sinh}\left[\lambda L\right]}\text{sinh}\left[\lambda a\right]+\frac{P_a\left(L-a\right)}{SL}a\right)\\ -\frac{P_b\text{sinh}\left[\lambda \left(L-b\right)\right]}{S\lambda \text{sinh}\left[\lambda L\right]}\text{sinh}\left[\lambda a\right]+\frac{P_b\left(L-b\right)}{SL}a,\end{array}$$

$$\begin{array}{c}{\delta }_b=-\frac{P_a\text{sinh}\left[\lambda a\right]}{S\lambda \text{sinh}\left[\lambda L\right]}\text{sinh}\left[\lambda \left(L-b\right)\right]+\frac{P_a\left(L-b\right)}{SL}a\\ +\left(-\frac{P_b\text{sinh}\left[\lambda \left(L-b\right)\right]}{S\lambda \text{sinh}\left[\lambda L\right]}\text{sinh}\left[\lambda b\right]+\frac{P_b\left(L-b\right)}{SL}b\right),\end{array}$$

with the dependent variables defined in the following subsections (Table 1).

Table 1.

STEP Nanonet Force Microscopy Model Parameters

Variable	Significance	Value
L	segmental length of the fiber (distance between adjacent fixed ends)	variable; 100–500 (μm)
a	location of point load nearest to fiber-fiber intersection	0 < a < L (μm)
b	location of other point load	0 < a < b < L (μm)
${\delta }_a$	fiber deflection at $a$	variable (μm)
${\delta }_b$	fiber deflection at $b$	variable (μm)
λ	shape-dependent mechanics parameter	$\sqrt{S/EI}$ (m−1)
S	uniform pretensional load	S = π(d2/4)∗T (μN)
T	uniform pretensional stress, calculated from AFM residual stress measurements	4.1 MPa (70)
d	fiber diameter	250, 400, and 800 nm
E	elastic modulus of the polymer (polystyrene)	E = 0.97 (GPa) (70)
I	area moment of inertia	$I=\frac{\pi d^4}{64}$ (m4)

Probe design and operation

Micropipette probes were pulled to 1-μm-diameter tips from 1.0-mm-diameter capillary glass rods (Sutter Instrument, Novato, CA) using the P-1000 Flaming/Brown micropipette puller (Sutter Instrument). Using an MP-285 motorized manipulator (Sutter Instrument), probes were positioned near parallel-shaped cells and then preprogrammed for strain rate, end-state position, and number of cycles. A strain rate of 3 μm/s was used unless otherwise noted because it was the fastest rate at which cells did not exhibit viscoelastic effects (Supporting Material).

Time-lapse and scanning electron microscopy imaging

Nanonets were placed in an incubating microscope with a digitally controlled three-axis stage (AxioObserver Z1; Carl Zeiss, Jena, Germany). Time-lapse movies were created by capturing still images approximately once per 600 ms. Both 20× and 40× images were captured with an AxioCam MRm camera (Carl Zeiss). Data was analyzed using AxioVision (Carl Zeiss) and the software ImageJ (National Institutes of Health, Bethesda, MD).

Immunohistochemistry and immunofluorescence imaging

Scaffolds containing cells were fixed in 4% paraformaldehyde, permeabilized in 0.1% Triton X100 solution, and blocked in 10% goat serum. Primary rabbit anti-paxillin antibodies (Invitrogen) were diluted 1:250 and incubated at 4°C for 1 h. Secondary goat anti-rabbit Alexa Fluor 488 (Invitrogen) antibodies were then incubated for 45 min at room temperature protected from light. Nuclei were counterstained with 300 nM of DAPI (Invitrogen) for 5 min. Scaffolds were kept hydrated in 1 mL of PBS (phosphate-buffered saline) during imaging. Fluorescent images were taken with the Axio Observer Z1 microscope (Carl Zeiss).

Statistical analysis

Sample populations were tested for statistical significance using Student’s t-test in the software JMP 11 (http://www.jmp.com/en_us/software.html). A p-value ≤ 0.05 was used (unless otherwise noted) to determine significant differences. Error bars represent standard error unless otherwise noted. Values are reported as an average of mean ± 1 SE.

Results and Discussion

Nanonet scaffold design enables force measurement

Using the non-electrospinning STEP technique, suspended polystyrene nanofibers are fabricated in aligned arrays of desired diameter, spacing, and orientation. Previous work from our group has demonstrated that cells on suspended nanofibers tend to spread between two parallel fibers if the gap between the two fibers is approximately <20 μm (29, 38). Cells configured in this manner interact exclusively with two suspended fibers and not the underlying substrate, making the resulting isolation of cell-fiber interactions repeatable, convenient, and accessible to external perturbation. To increase the occurrence of this cell shape, large strutlike 1200-nm-diameter fibers are spun at an average spacing of 200 μm and smaller diameter fibers are fabricated on top of and orthogonal to the previous layer with shorter interfiber spacing (∼15 μm; Fig. 1, a–c). Fiber intersections are then fused to each other (Fig. 1 d, white dotted circle), ensuring fixed boundary conditions that allow the fibers to bend. Forces applied by cells are then calculated by measuring fiber deflection. Thus, scaffolds simultaneously encourage parallel cell configuration and allow for both IO observation and OI manipulation. In addition to having an elastic modulus (E, units: N/m²), fibers present cells with structural stiffness (k, units: N/m) that accounts for the fiber diameter and position of cell along the suspended length. Three different diameters (250, 400, and 800 nm) were used in this study to obtain a wide range of curvature and structural stiffness values (3–50 nN/μm) as measured by AFM ramp tests (27, 39). The structural stiffness values permit optically measurable deflection (>2 μm) under cell-scale loads while remaining in the elastic limit (deflection ≤ 5% of the span length; (40, 41); see the Supporting Material).

IO fiber deflections measure contractile forces

As cells attach and spread between two parallel nanonet segments, individual fibers deflect (Fig. 1 e i), which can be used to calculate forces. Cells in such configurations form cell-fiber adhesion clusters in two separate locations at the periphery of the cell (29). Because of this observation, we can approximate the distributed load as a single load at both cell peripheries on the fiber. Load location a with associated load P_a is assigned such that it is located nearest to the fixed fiber intersection, which makes location b with associated load P_b synonymous with the probe side in OI-single mode. We recorded 70 C2C12 cells and their associated IO fiber deflections at a and b, and calculated the forces exerted by cells at P_a (21.6 ± 3.9 nN) and P_b (22.3 ± 2.7 nN; Fig. 1 e ii). The two point loads can then be represented by an equivalent single point load (P_resultant) at an intermediate location located at the geometrical center of the cell (45.0 ± 5.4 nN). Comparing P_a and P_b, it is seen that forces are essentially equally distributed across the cell. Furthermore, IO forces were also found to be dependent upon fiber diameter and structural stiffness, a trend similar to both micropillars of varying pillar stiffness and flat substrates with tunable modulus of elasticity (E, units: N/m²; (42, 43)). For instance, cells attached to smaller fibers (250 nm) only exerted an average IO force of 16.0 ± 4.2 nN, whereas those on larger (800 nm) fibers exerted 67.9 ± 9.4 nN (Fig. 1 e ii).

OI perturbation measures cell adhesion strength

To measure OI cell adhesion forces, a probe system was designed to perturb single parallel-shaped cells via programmable micromanipulated motions. Two different modes of operation were designed to determine the effect of biased loading on cell adhesion: symmetric dual probes (i.e., OI-Dual) positioned on either side of a parallel-shaped cell, actuating the cell symmetrically (Fig.1 g i); and a single probe (i.e., OI-Single) actuating one side of the cell to induce bias (unsymmetric mode; Fig. 1 h i). To determine cell adhesion strength, the cell was stretched to failure (detachment from fiber) by pushing the leading active fiber while recording the deflection of trailing passive fiber. The cytoskeletal network experiences increasing force in this configuration as the cell is stretched, and eventually the cell detaches with the passive fiber returning to its original nondeflected state. The maximum force value reached during this test was taken to be the adhesion force of the cell.

OI-Dual manipulation (Fig. 1 g ii) results in comparatively even force distribution within the cell, with averages of P_a = 33.4 ± 3.8 nN and P_b = 29.1 ± 2.5 nN on 250-nm fibers, P_a = 62.0 ± 5.6 nN and P_b = 45.8 ± 4.0 nN on 400-nm fibers, and P_a = 131.5 ± 8.3 nN and P_b = 111.0 ± 6.6 nN on 800-nm fibers. These forces correspond to fiber deflections averaging 3.2% of their span length, falling within the suggested elastic limit for polystyrene nanofibers (40, 41). The force-time plot from a dual probe perturbation typically shows a steady rise in force as the cell is stretched while maintaining adhesion integrity, which is followed by a sharp drop as the cell-fiber adhesion fails, representative of the abrupt breaking failure typically observed (Fig. 1 g iii). The failure locations averaged over all diameters demonstrated cell-fiber failure to occur equally on each side of the cell (a: 29%; b: 29%; both simultaneously: 42% of the time), further suggesting even distribution of forces within the cell (Movie S1).

OI-Single manipulation results in averages of P_a = 31.4 ± 4.1 nN and P_b = 27.6 ± 1.7 nN on 250-nm fibers, P_a = 66.3 ± 5.7 nN and P_b = 43.3 ± 5.2 nN on 400-nm fibers, and P_a = 103.5 ± 9.8 nN and P_b = 115.4 ± 9.9 nN on 800-nm fibers (Fig. 1 h ii). By using a single probe that actuates the fiber on just one side of the cell, forces are more asymmetrically distributed or biased and cause failure to initiate on probe side b more frequently (a: 17%; b: 58%; both simultaneously: 25% of the time). Force-time plots from OI-single tests also steadily rise over time, but instead of dropping sharply as seen in cells perturbed with dual probes, a peeling-type failure mechanism is often observed wherein forces level off before failing (Fig. 1 h iii; Movie S2). The ability to control single cell force distribution and detachment location may prove valuable in understanding certain cell events, such as leader cell formation in metastasis from primary tumors or single cell injury models. Care was taken to ensure equidistant probe placement from the edge of the cell (single: 47 ± 3 μm; dual: 44 ± 5 μm), and as a result, we found the distance from the probe to the cell body to be insensitive to resultant adhesion force in our dataset. The force of adhesion (P_resultant) averaged over all diameters remained similar (dual actuation: 126.6 ± 8.7 nN; single actuation: 121.0 ± 8.6 nN), which compare favorably to forces obtained through other OI approaches (44, 45).

Effects of nanofiber curvature

We next wanted to determine whether fiber curvature could explain diameter-dependent bias effects. Having previously observed cells on smaller diameter fibers to cluster adhesions over a longer distance (presumably due to the reduced available adhesion area per unit fiber length; (27, 29, 46)), we hypothesized that curvature-induced adhesion orientation was at least partially responsible for diameter-dependent bias effects. Furthermore, as evidenced by the breaking versus peeling-type of failure observed, bias may be perturbing focal adhesions differently on fibers of different diameters due to spatial orientation, polarization, and/or structural stiffness effects.

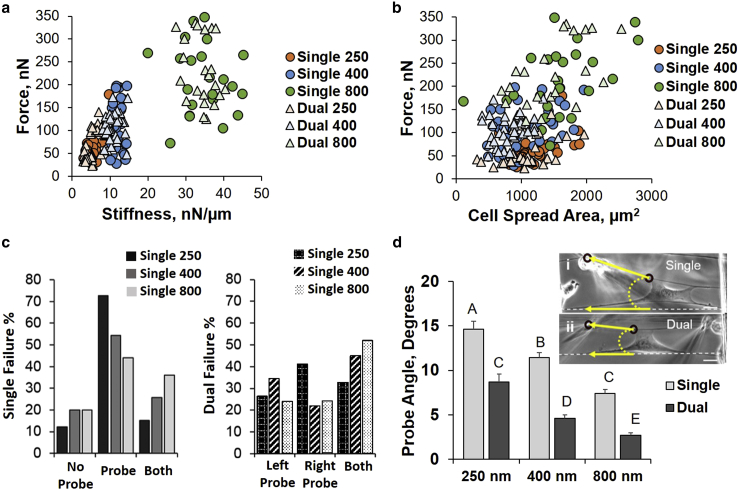
We found that increasing fiber structural stiffness k (N/m) values were associated with increased adhesion forces, where a linear trend was seen for lower stiffnesses that began to saturate after ∼35 nN/μm (Fig. 2 a). Cell spread area was also measured at the time of failure and found to be only weakly correlated with total force, in good agreement with findings from literature (Fig. 2 b; (43)). The average detachment forces for all diameters $\left(F_{\text{Resultant}\text{Dual}}/F_{\text{Resultant}\text{Single}}\right)$ remained close to unity (250 nm: 1.06; 400 nm: 0.98; and 800 nm: 1.12), thus suggesting that probe based bias ultimately dictates location of the initiation of failure (Fig. 2 c). Probe perturbation also created an angle between the leading active and trailing passive fiber. To quantify this angle (taken just before cell detachment from fiber), a line was drawn between the probe and cell-fiber interface on the actuated fiber (yellow arrow connecting circles) and compared to the original position of the trailing fiber serving as reference (yellow arrow overlaying white dashed lines; Fig. 2 d (insets i and ii)). Averaged over all diameters tested, OI-dual manipulation resulted in an angle of 5.3°, whereas the single probe created an angle of 11.5° between the actuated and passive fibers before cell failure (Fig. 2 d). These angles were largest for the 250-nm diameter fibers and smallest for the 800-nm fibers, suggesting that adhesions perhaps experience different loading angles as a function of fiber diameter.

Figure 2.

(a) Force as a function of structural stiffness; (b) force as a function of cell spread area; (c) failure occurrence locations for OI-Single mode (probe side, no probe side, and both sides) and OI-Dual mode (left probe side, right probe side, and both sides); and (d) the angle created between the actuated and passive fiber (probe angle) shows that the single probe angle is larger than dual probe angle for each diameter (scale bar, 25 μm; n = 188). To see this figure in color, go online.

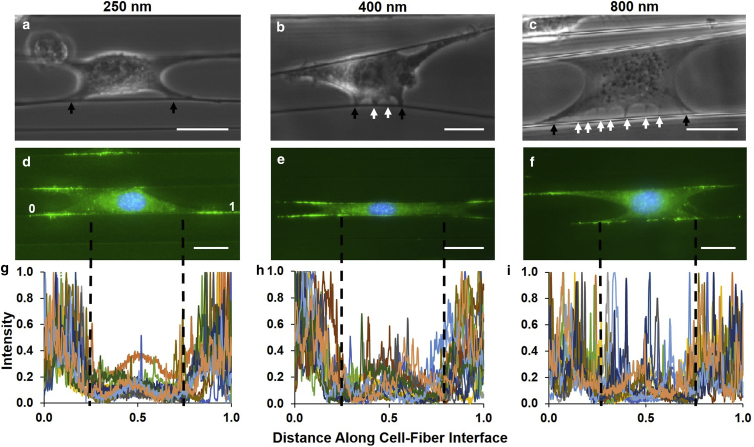
Immunostaining cells for focal adhesion protein paxillin revealed clusters of paxillin located primarily at the poles of the cell on small-diameter fibers. With increasing fiber diameter, additional adhesion clustering was found along the intermediate locations of the cell (Fig. 3), thus, strongly suggesting the role of curvature in failure distribution using biased perturbation.

Figure 3.

Focal cluster distribution along the cell-fiber interface as a function of selected diameters. (a–c) Optical images of cells being pulled on 250-, 400-, and 800-nm-diameter fibers, respectively, with the two primary peripheral clusters (black arrows) shown distinctly from intermediary groups (white arrows), which increase with increasing diameter; (d–f) fluorescence images showing paxillin signal presence along the cell-fiber axis; and (g–i) corresponding intensity of the paxillin signal with primary cluster zones separated from intermediary zones by black dashed lines. As fiber diameter increases, signal intensity within this region increases as well (scale bar, 25 μm; n = 42). To see this figure in color, go online.

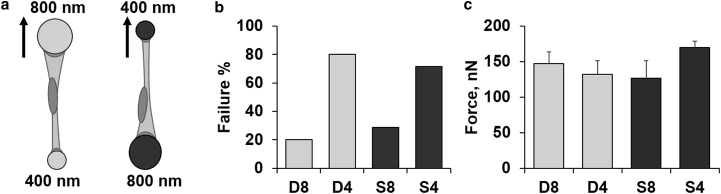
To investigate the role of bias further, we made nanonets having different diameters (400 and 800 nm) to which cells could attach to simultaneously (Fig. 4; and Movie S3). Both the OI-Dual and OI-Single modes were used to determine whether diameter-dependent bias effects observed previously on same-diameter fibers would be conserved when the cell was attached to mismatched diameters.

Figure 4.

(a) Sketch of mismatch diameter orientations (solid arrows represent location and direction of probe actuation), as well as data showing (b) failure occurrence, and (c) adhesion forces at failure (as measured on the passive fiber) for each case. The letter D indicates that the cell was pulled with the dual probe system, and the letter S indicates that the cell was pulled with a single probe (D8 = dual 800 nm; D4 = dual 400 nm; S8 = single 800 nm; S4 = single 400 nm; n = 51).

In both the OI-Dual (light shading) and OI-Single (dark shading) modes, cells failed more often on the smaller diameter fiber (D4 and S4) compared to the large diameter fiber (D8 and S8, Fig. 4 b). We found that the forces of adhesion remained similar for each location of failure (Fig. 4 c), thus further supporting our findings on the role of fiber curvature on focal adhesion clustering and its implications in a cell’s ability to modulate force response to external perturbation.

Platform applications

Cell-cell junction behavior on nanonets

In their native environment, cell-cell junctions allow cells to adhere to one another to maintain proper tissue functionality. Cell-ECM contacts occur through integrins while cell-cell junctions are anchored by cadherins (47). Physical cues that drive cell-ECM adhesion growth are typically reported to be similar for cell-cell contacts; for instance, enhanced contractility due to increased substrate stiffness causes stronger cell-cell adhesion (48, 49). In contrast to other systems exploring cell-cell adhesion on micropillars or using an AFM cantilever (48, 50), or those that explore full monolayer behavior (51), the nanonet probe system allows simultaneous investigation of cell-cell junctions and cell-ECM contacts (Fig. 5).

Figure 5.

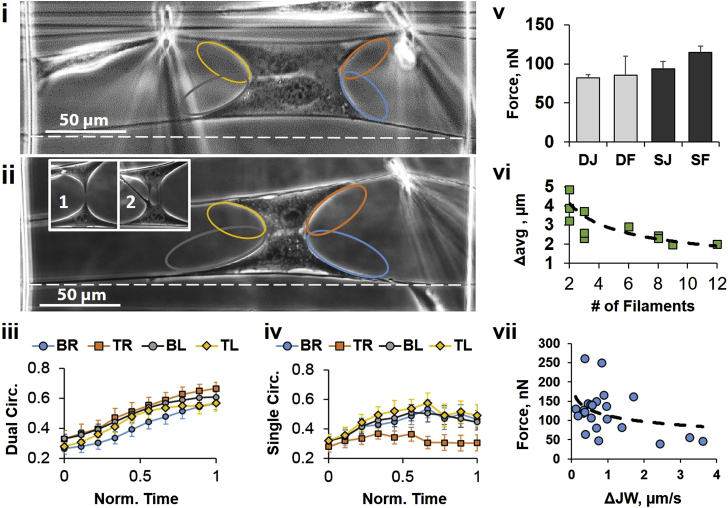
Cell-cell junction tests are performed with (i) the dual probe and (ii) the single probe and show the effect of bias via circularity measurements, wherein (iii) dual probe causes steady increase in circularity on all four edges of the cell (top-left (TL), top-right (TR), bottom-left (BL), bottom-right (BR)), while (iv) the single probe causes circularity reduction at the edge closest to the probe (orange oval; n = 37). Forces (v) are higher when failing on fibers (F) compared to cell-cell junctions (J) for both systems (n = 52); (vi) spacing of the filaments spanning the cell-cell junction (inset 1 and 2 of ii) correlates with number of filaments seen (n = 11), and (vii) forces decrease when the junction width decreases more rapidly (n = 23). To see this figure in color, go online.

Cell-cell pairs formed spread morphologies similar to those of single cells except with a fusion plane running parallel to the fiber axis (Movie S4). When actuated with the OI-Dual system, cells were pulled evenly on both sides. This was confirmed by circularity analysis of the curvatures between the cell-cell junction and the cell-fiber adhesions located at the top-left (TL), top-right (TR), bottom-left (BL), and bottom-right (BR) of the cell-cell pair (Fig. 5 i). Cell configuration was initially slightly elongated (low circularity) but became more circular throughout the stretch, and did so evenly on each side (Fig. 5 iii). On the other hand, OI-Single actuation (Fig. 5 ii) induced uneven cell stretching as evidenced by saturation and eventual decrease in the top-right circularity (closest to the probe; Fig. 5 iv).

While failure occurred more often at the cell-cell junction for both actuation modes (65% of the time for single and 90% for dual) in agreement with other recent studies (48, 52), bias again did not significantly affect total force at detachment (Fig. 5 v). During failure, long filamentous structures were seen spanning the gap of the junction as it failed (Fig. 5, insets 1 and 2; Movie S5). Several groups have shown the formation of these structures, which are composed primarily of actin surrounded by the plasma membrane during junction formation, but have not described the plasma membrane behavior during junction failure (49, 53, 54). We noted that as the number of filaments spanning the gap between the two cells increased, the average distance between each filament decreased (Fig. 5 vi). A thin filament could often be seen holding the entire cell-cell junction together before failure (Fig. 5 ii, inset 1). We speculate that this behavior may arise from the distribution and clustering of cadherin throughout the junction (55, 56). Lastly, the cell-cell junction width often narrowed during the pull (initial width = 18.2 ± 6.2 μm; width immediately before failure = 7.6 ± 5.6 μm). Perturbing at the same strain rate, the rate at which junction-width narrowing occurred appears to correlate with the force required to break the junction, with faster decreases in cell-cell junction width (ΔJW) associating with reduced forces (Fig. 5 vii).

Force response to cyclic perturbation and cytoskeletal drug

Having characterized the effects of probe bias, we next sought to determine whether the nanonet platform is able to capture the temporal force response of cells attached to nanonets undergoing physical perturbation at different timepoints and frequencies in the presence and absence of drugs. If subjected to cyclic stretch at subfailure amplitudes, we hypothesized that the cell would weaken over time and exhibit decreased force with each successive stretch. This idea was based on studies performed on flat substrates, wherein cells are seeded on thin elastic films and a uniaxial or biaxial stretch amplitude (∼10–15%) is applied to the entire film at 0.1–1 Hz (57, 58).

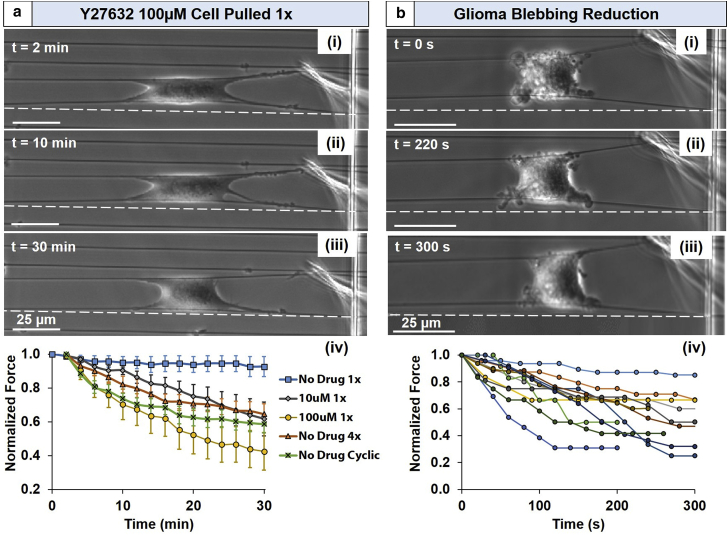
Using a constant strain rate of 2 μm/s, the probe stretched cells to a subfailure amplitude and then returned to its original resting position (Movie S6). This process was repeated every 2 min for a 30-min duration. The effect of stretching frequency was also examined: in addition to only stretching the cell once per 2-min window (1×), cells were stretched four times (4×) as well as continuously (Fig. 6 a). We found that when the cell was stretched a single time (1×) and then allowed to rest the remainder of the 2 min, force was not significantly reduced (decrease of 7%). However, if the cell was either cycled four times (4×, Movie S7) in that same 2-min window (1 min of perturbation once every 15 s, 1 min of rest) or continuously perturbed, force significantly decreased (4× = 37% reduction, continuous = 41%).

Figure 6.

(a) Time-lapse images (i–iii) of the effect of cycle frequency and drug administration on cell force. (iv) Increasing cycle frequency decreases cell force (1× = 7% force reduction, 4× = 37%; continuous = 41%). Similarly, increasing drug concentration while cycling at 1× also decreases force (10 μM = 38%; 100 μM = 57%). Despite force magnitude reduction being similar, ROCK inhibition does not appear to reach steady state within 30 min. Error bars represent standard error (n = 6 for each case). (b) Reduction of cancer cell blebbing through probe-induced stretch, as shown by (i–iii) time-lapse images and (iv) force evolution upon onset of transition from blebbing to lamellipodial behavior (n = 11). To see this figure in color, go online.

To further evaluate the nanonet probe system for efficacy as a drug testing platform at high magnifications and temporal resolutions, we subjected cells to varying concentrations of the Rho-kinase (ROCK)-inhibitor Y27632 and monitored its force evolution over the same 30-min period. In uninhibited cells, ROCK pathway activation leads to increased cytoskeletal tension through F-actin stress fiber formation and focal adhesion development, thereby allowing cells to generate contractile forces (59, 60). Y27632 competes with ATP for binding sites on ROCK, preventing this pathway’s initiation and resulting in decreased cytoskeletal tension (61, 62). Y27632 was added at either normal (10 μM; (22, 63)) or oversaturated (100 μM; (64)) concentrations at the start of experiment (time = 0 min; Fig. 6 a) to quantify ROCK-inhibited force evolution. Cells treated with 10-μM Y27632 cycled at 1× (38% reduction) followed similar trends to the cyclically perturbed control cells, and cells treated with 100-μM Y27632 that cycled at 1× experienced a further reduction in force (57%). These data demonstrate the nanonet force platform’s flexibility in applying forces in varying modes, while simultaneously being able to detect changes in cell forces from the time that external perturbations (mechanical or chemical) were introduced in the system.

Cancer cell blebbing reduction with probe stretching

One of the identified hallmarks of cancer is the evasion of apoptosis (65). Glioma cells have been observed to exhibit reversible membrane blebbing, a phenomenon in which increased hydrostatic pressure drives cytoplasm through local ruptures in the actin cortex (66). It has recently been reported that blebbing cells exist in a state of simultaneous hypercontractility and reduced actin polymerization, but when corrected through the use of various cytoskeletal drugs, these same cells can revert to pseudopodial/lamellipodial protrusions (67). Previous work in our group has shown that blebbing ceases when the cell takes on a spread area >1400 μm² (38). Taken together, these works suggest that blebbing can be reduced in the absence of drugs via prolonged subfailure stretch.

Thus, a step strain was applied to single-blebbing Denver Brain Tumor Research Group (DBTRG-05MG) cells and was held constant while cells transitioned from blebbing to lamellipodia (Movie S8; Fig. 6 b). Onset of transition, evidenced by the first observed force decrease, required ∼5–10 min to take place. Upon initializing transition, blebbing ceased and lamellipodia were observed after another 200–400 s. This transition was marked by decreased cell contractility wherein the average force reduced by ∼20 nN (40% of blebbing force; n = 11). These tests confirm that hypercontractility is partially responsible for producing blebs, and we believe that this demonstrates the mechanical stretch-based quantification of forces involved in this reversal for the first time.

Conclusions

In this work we have developed a suspended nanofiber-based force measurement system (nanonet force microscopy) capable of capturing single-cell IO contractile forces (average 45.0 ± 5.4 nN) and OI adhesion forces in the absence (symmetric average 126.6 ± 8.7 nN) and presence of bias (asymmetric average 121.0 ± 8.6 nN). By using a single probe, asymmetric loading from one side increases failure probability on the side of the cell nearest the probe by >30%. Paxillin clusters on fibers of different diameters show greater intercluster scattering on larger fibers. This phenomenon is thought to be responsible for alterations to single-cell adhesion force as shown by novel diameter mismatch studies. Cyclic loading, cell-cell adhesion, and cancer cell blebbing reversal phenomena further emphasize the uniqueness and power of the platform.

Nanonet force scaffolds use suspended and aligned nanofibers to investigate single-cell mechanics on ECM-like substrates and represent, to our knowledge, the first fiber-based substrate able to capture both IO and OI modes. To the best of our knowledge, electrospinning is currently unable to reproducibly form these suspended structures with robust control on fiber diameter, spacing, and orientation. Traction force gels, microelectromechanical systems devices, and micropillar arrays offer comparable quantifications of forces but do not present cells with ECM-like nanofiber curvature effects. We show here that these effects manifest in cell modifications to FAC distribution and ultimately cell adhesion force. In its current stage of development, we can accurately measure nanoNewton and higher forces. With use of nanonets of smaller diameters, softer material such as polyurethane, and fibers of longer length, it is conceivable that the nanonet platform will be able to measure forces in the range of hundreds of picoNewtons or less. We further emphasize that our platform enables fiber networks to be integrated with ultrasensitive force measurement methods such as AFM or laser traps, thus providing new capabilities to measure multiscale forces. Continual development of the nanonet platform will allow us to pose questions regarding onset, progression, and eventual treatment of disease at the single- and multicell level. For instance, future studies could address the mechanism behind preferential myofibroblast adhesion to larger and more organized native tissue in wound healing applications (68, 69). Additionally, we anticipate combining these tools with chemical stimuli to develop contextually relevant in vitro platforms that measure cell response to comprehensive physio-chemical cues.

Author Contributions

A.S.N. designed research; K.S. performed research; K.S. and A.S.N. analyzed data; J.W., W.Z., and R.K. contributed analytic tools; and K.S. and A.S.N. wrote the article.

Editor: Jochen Guck.