Mapping dynamic social networks in real life using participants' own smartphones

Abstract

Interpersonal relationships are vital for our daily functioning and wellbeing. Social networks may form the primary means by which environmental influences determine individual traits. Several studies have shown the influence of social networks on decision-making, behaviors and wellbeing. Smartphones have great potential for measuring social networks in a real world setting. Here we tested the feasibility of using people's own smartphones as a data collection platform for face-to-face interactions. We developed an application for iOS and Android to collect Bluetooth data and acquired one week of data from 14 participants in our organization. The Bluetooth scanning statistics were used to quantify the time-resolved connection strength between participants and define the weights of a dynamic social network. We used network metrics to quantify changes in network topology over time and non-negative matrix factorization to identify cliques or subgroups that reoccurred during the week. The scanning rate varied considerably between smartphones running Android and iOS and egocentric networks metrics were correlated with the scanning rate. The time courses of two identified subgroups matched with two meetings that took place that week. These findings demonstrate the feasibility of using participants' own smartphones to map social network, whilst identifying current limitations of using generic smartphones. The bias introduced by variations in scanning rate and missing data is an important limitation that needs to be addressed in future studies.

1. Introduction

Humans are highly social beings. Not only do we like to be surrounded by friends, many of our activities require interaction with other people. Given its pervasive role in our functioning, there has been a longstanding scientific interest in the analysis of social interactions. In 1934, Moreno introduced ‘sociograms’ – a diagram of points and lines used to represent relationships within a group of people – which laid the foundation of sociometry [1]. The development of methodologies to quantify social interactions, such as the use of matrix algebra and graph theory, made it possible to formalize fundamental social-psychological concepts such as groups and social circles in network terms and to objectively discover emergent groups in network data [2] [3]. Social network analysis has found a wide range of applications, such as quantifying social capital in organizations [4] [5], to determine how diseases spread in the community [6] [7], investigate the role of social networks in the development of brain diseases such as dementia [8], or the protection social support can offer for mental heath [9] [10] [11]. Much of this interest can be attributed to the appealing focus of social network analysis on the relationships among people, and on the patterns and implications of these relationships.

Networks are defined by nodes and the edges between them. In the case of social networks, the nodes represent individual people and the edges the relationships between them. Quantifying the relationships between people is hence fundamental in characterizing social networks. To estimate these relationships, most studies have tended to follow the lead of the pioneering study by Moreno, who used questionnaires to investigate friendship choices among selected children [1]. In these studies, researchers simply ask respondents to identify their friends and use these data to define the edges of the social network. For example, in the Framingham Heart study – a long-term, ongoing cardiovascular study of the residents of the town of Framingham, Massachusetts – researchers used contact information provided by subjects over a 30-year period to map the social network of friends and family in the study. These data have been used to investigate how the behavior of individual people is influenced by their social network and has demonstrated how their happiness [12], obesity [7], and smoking behavior [12] spreads as a function of their social network. This approach to define the edges is time consuming, subjective and depends on the nature of the questions – or name generators – that are asked [13] [14] [15]. That is, respondents will describe networks of varied size and the characteristics of relationships will vary considerably depending on the questions asked [13].

Sensor-enabled mobile phones have the potential to collect vast amounts of objective data at low cost [16] [17] [18] [19], and are particularly suited to ecological momentary assessment, i.e. monitoring and assessment in real-time and real-world conditions [20]. Smartphones have been used to map social networks by assessing physical proximity using either Bluetooth [21], location data [22] or by combining different data modalities [23] [24] [25] [26]. It was shown that physical proximity data can be used to accurately infer friendships between participants [21]. It has hence been well established that smartphones can be used to efficiently map face-to-face interactions and provide valuable information about the dynamics of social interactions, which may have many applications. For instance, if we understand the principles that govern social networks and how egocentric networks – the local network surrounding an individual – influence behavior, we may be able to use network metrics to inform the design of interventions to prevent social withdrawal or the spread of negative and stigmatizing attitudes.

However, most studies have handed out specially programmed mobile phones to study participants [19] [21] [22] [23] [24] [25] [27] [28]. Using people's own smartphones will be critical for scaling up this technology for potential mHealth applications. This will also provide the ability to provide users with feedback on their own social connectedness, which fits in the wider trend of using mobile phones for continuous self-monitoring of physical and mental health [20] [29] [30]. Here we assess the feasibility of using people's own smartphones as a data collection platform to gather information about the dynamics of their individual social network via Bluetooth. We developed an application for iOS and Android to collect Bluetooth data from participants' own smartphones and tested the application on participants within our organization to validate the social network dynamics obtained using their own smartphone against the events that occurred during the period of data acquisition. The study aims to identify potential limitations of the technology and methodology that can inform larger studies on the role of social networks in mental health.

2. Materials and methods

2.1. Procedure

We collected data for one working week (24–28 November 2014). A team meeting was planned on Monday and a staff meeting on Wednesday, enabling validation of the proposed methodology. We used the Bluetooth scanning statistics to quantify the connection strength between participants and to define a weighted, undirected social network. Graph metrics were used to quantify the structure of relationships and the position of participants within the social network. Non-negative matrix factorization (NMF) was used to decompose the dynamic connectivity matrix and identify a small number of factors that capture the dominant recurring network configurations.

2.2. Participants

Staff and research students within the Black Dog Institute were sent an email via the general distribution email list, inviting them to participate in the study. The email contained a link to a participant information sheet, and participants were asked to sign an online consent form. This study was reviewed and approved by the University of New South Wales Human Research Ethics Committee (HC14172).

2.3. Data acquisition

Custom applications were developed for the Android and iOS operating systems. The Android application was based on the Purple Robot open-source data collection platform [31]. For the iOS application we used the BluetoothManager private API. Both versions of the application asked the user to confirm consent prior to the commencement of Bluetooth data collection. Bluetooth is a short-range communication protocol designed to allow a wireless connection between nearby devices, such as smartphones. A key feature of a Bluetooth device is the ability to scan for other nearby devices. When a Bluetooth device conducts a discovery scan, other Bluetooth devices within a range of 5–10 m respond with their user-defined name, the device type, and a unique 12-hexadecimal-digit hardware media access control (MAC) address. A device's MAC address is fixed and can be used to differentiate one device from another, irrespective of the device name and type. When a participant's MAC address is discovered by a periodic Bluetooth scan performed by another participant, it indicates that the two smartphones are within 5–10 m of each other (see also [21]).

The Android application was configured to perform a Bluetooth discovery scan every five minutes during the study period. It was not possible to specify a scan frequency in the iOS application due to operating system restrictions on background execution; therefore data was collected on a best-effort basis, as often as permitted by the handset.

As the Bluetooth MAC address of a device is potentially personally identifiable information, to ensure the privacy of participants these data were cryptographically hashed on the handset to prevent re-identification. Hashing generates a consistent ‘signature’ for each data item that cannot be reversed to reveal the original data value.

2.4. Connectivity analysis

We estimate the connectivity between participants based on the Bluetooth scanning statistics of their smartphones, and from these statistics we define the connection strengths between participants and thus the weights of the network. Smartphones scan at irregular intervals and the scanning behavior {t_i} can be regarded a point process. It is completely specified by a series of scanning times and the start and end points of the recording interval [0, T]. It is convenient to introduce some notation that enables formulae to be written in a compact form [32]. The counting process N(t) is defined as the number of scans that occur between the start of the interval (t = 0) and time t. The average connection strength between device i and j can then be represented as

$$R_{ij}=\frac{N_{ij}\left(T\right)+N_{ji}\left(T\right)}{N_i\left(T\right)+N_j\left(T\right)}$$ (1)

where N_ij is the number of scans where device i detected device j and N_i the number of times device i scanned on time interval T. By normalizing the number of times one of the devices detected the other by the number of times each device scanned, the connection strength R_ij is bound on the interval [0,1], where 1 indicates that both devices always detected each other when they scanned and 0 indicates that the devices never detected each other. If both devices did not scan during the interval of interest, R_ij is set to zero. By defining the connection strengths as a ratio we regard the particular scores as stochastic or probabilistic realizations drawn by random sampling from an underlying true tendency or probability distribution of relationship strengths [33] [34].

To obtain a time-resolved definition of Eq. (1), we convert the point process into a time series using a binning method to make it accessible for methods of time series analysis [35] [36]. We hence define a time series

$$x_i\left(t\right)=\{\begin{array}{c}\hfill 1,ifdeviceiscannedattimet\hfill \\ 0,elsewhere\end{array}$$ (2)

that represents the times device i scanned and

$$x_{ij}\left(t\right)=\{\begin{array}{c}\hfill 1,ifdeviceidetectedjattimet\hfill \\ \hfill 0,elsewhere\hfill \end{array}$$ (3)

as the times device i detected device j. Using a time-domain smoothing operator, we can then define connectivity strength between device i and device j in a time-resolved manner as

$${\mathrm{\Gamma }}_{ij}\left(t\right)=\frac{S\left\{x_{ij}\left(t\right)+x_{ji}\left(t\right)\right\}}{S\left\{x_i\left(t\right)+x_j\left(t\right)\right\}},t=\mathrm{1,2},\dots ,T$$ (4)

where S{.} is a suitable smoothing operator (see also [37]). Here we use a Gaussian window of either 10 min or 2 h duration to estimate connectivity dynamics at short and longer time scales. Smoothing was implemented by convolving the smoothing window with the time series.

2.5. Network analysis

We then use graph theory to examine the structure of relationships detected using Bluetooth (see [38] for an introduction to graph theory). The participants are the nodes and the connectivity matrix defines the edges of the network. The connectivity (adjacency) matrix can be determined by estimating the connection strength between all pairs of smartphones. As the connection strengths in Eqs. (1) and (4) are ratios and symmetric (the connection strength between device i and j is equal to the connection strength between j and i), the connection matrix defines a weighted undirected graph. A wide range of network metrics are available to quantify the topology of weighted undirected graphs (see [39] for an overview). Networks metrics quantify either global or local properties of a graph, which characterize how the network is organized and how specific actors are positioned within this network [2]. For instance, measures of ‘centrality’ quantify how central an actor is within a network, which is thought to determine its influence on the network. In particular, betweenness centrality indexes the percentage of all shortest paths from neighbor to neighbor that pass through a particular node and hence measures the potential for control of communication [40]. Nodes with high betweenness centrality are often referred to as hubs. The clustering coefficient quantifies the density of the neighborhood of each node and is equivalent to the fraction of the node's neighbors that are also neighbors of each other [41]. The clustering coefficient is used to detect the presence of clusters or cliques within a network.

Network metrics can be used to quantify both static and dynamic networks. For dynamic networks, static ‘snapshots’ can be generated for particular time points or time intervals and the network topology at that time point can be assessed. If the network topology is assessed at each time point (t =1,2,…, T), this yields time series of the network metrics that specify if and how the position of specific actors within the network changes over time. Rather than analyzing these snapshots separately, the dynamic connectivity matrix can be analyzed as a whole. Matrix factorization techniques can be used to decompose the connectivity matrix into its basic building blocks and hence obtain a low-dimensional representation that makes its analysis tractable [34] [42]. Non-negative matrix factorization has been used to detect overlapping communities in social networks [43] [44]. As it provides a low-dimensional approximation of the data, non-negative matrix factorization is particularly useful to recover large recurring network configurations and separate these distinct network states from continuous data. Here we use non-negative matrix factorization (NMF) to decompose the dynamic connectivity matrix (time-resolved connectivity for each pair of participants) into two non-negative matrices reflecting the connectivity matrices (basis vectors) and the corresponding time courses, respectively. The basis vectors delineate the communities or subgroups that are present in the data and the time courses when these subgroups were observed. NMF is distinguished from other methods by its non-negativity constraints [45] and both the time courses and the connectivity matrices are hence non-negative. For the estimation of most network metrics it is required that the connectivity matrix does not contain any negative entries [39].

We used Gephi for visualization of the network topologies [46].

3. Results

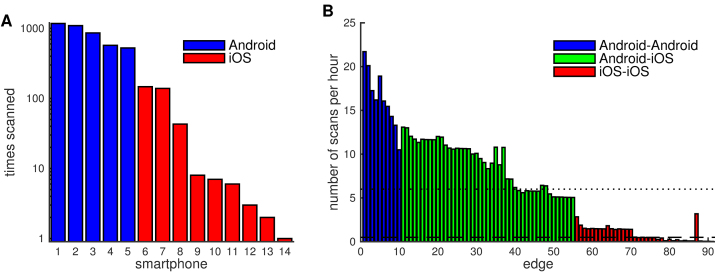
Fourteen participants agreed to join the study; five participants had Android handsets and 9 participants had iPhones. The smartphones scanned a total of 4581 times and detected 381 unique devices. Here we only analyze the connections between the fourteen participants that entered the study. The scanning behavior differed considerably between smartphones (Fig. 1A). Smartphones running Android scanned more often (on average 845 ± 294 scans during the 5-day period) than smartphones running iOS (40 ± 60). To estimate the connection strength between two participants – the weights of the network edges – we combined the data from both smartphones, improving the scanning rate for each edge of the network (Fig. 1B). The scanning rate per edges, determined based on the inter-scan intervals, was on average 6.5 scans/h (Android-Android: 16.4 ± 3.3 scans/h, Android-iOS: 8.8 ± 2.7 scans/h, iOS-iOS: 0.89 ± 0.82 scans/h). Of the 91 edges, 73 edges were assessed at least once every 2 h on average (dashed line) and 42 edges were assessed at least once every 10 min (dotted line).

Fig. 1.

Bluetooth scanning statistics. A) The total number of scans made by each smartphone in the 5-day period displayed on a logarithmic scale. B) Scanning rate for each edge of the network. The scanning rate between node A and B is determined by the number of scans by smartphone A and B combined, as the edges are undirected (symmetric). The horizontal dotted line reflects a scanning rate of 1 scan every 10 min; the dashed line 1 scan every 2 h.

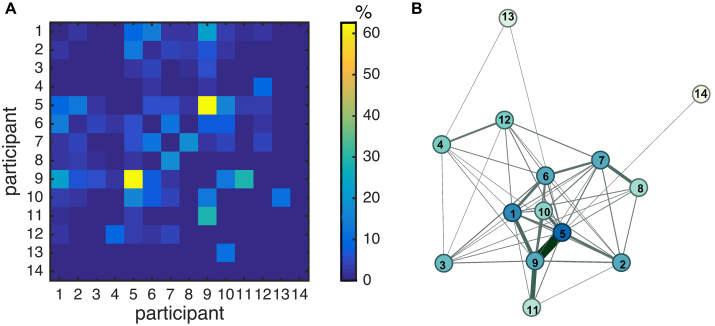
We first determined the static social network by pooling the data across the whole 5-day period (see Eq. (1)). By estimating the connection strength R_ij between each pair of participants, the connectivity matrix was determined (Fig. 2A). The connectivity matrix shows the percentage of time each pair of participants was connected, that is, that both participants were in close physical proximity such that their smartphones could detect each other via Bluetooth. The connection strength varied considerably between pairs of participants: the devices of some participants never detected each other, whereas some devices detected each other up to 60% of the times their devices scanned (participants 5 and 9). Fig. 2B shows the weighted undirected graph that is defined by this connectivity matrix. The graph shows that some nodes are more strongly connected than others, such as participants 1, 5 and 9.

Fig. 2.

Static social network. A) Connectivity matrix in which the weights are determined by the total of number times two devices detected each other divided by the total number of scans (Eq. (1)). Participants 1–5 had Android handsets; participants 6–14 had iPhones. B) Network topology of the corresponding graph: The color of the nodes reflects the weighted degree and the width and color of the edges reflect the weights. The network topology is generated using ForceAtlas 2.

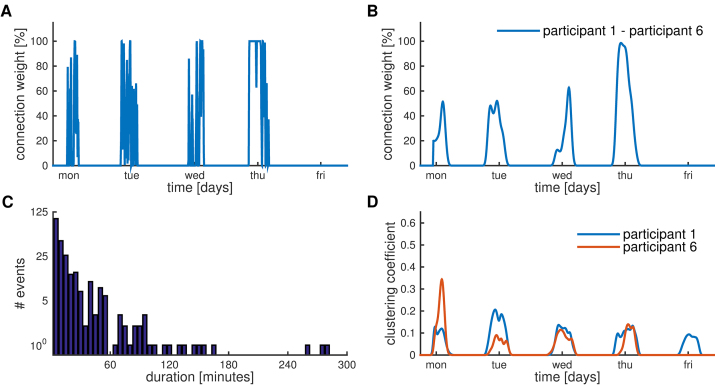
We then analyzed the dynamic social network by estimating the connection strength in a time-resolved manner. Temporal changes in connection strength were estimated by convolving the scanning behavior with a Gaussian smoothing window (Eq. (4)). We used a 10-min and a 2-h smoothing window to assess the fast and slower network dynamics, respectively. Fig. 3A shows the fast changes in connection strength between participants 1 and 6 as example. A short smoothing window can be used when high temporal resolution is required, e.g. to determine the duration of interactions (Fig. 3C). This shows that, across all participants, shorter interactions are more frequent, although some people were in close proximity for longer durations up to 280 min (about 4.5 h). Such information can be used to investigate the natural time scale of face-to-face interactions [47].

Fig. 3.

Connectivity dynamics. Temporal changes in connection strength were determined by convolving the scanning events with a Gaussian smoothing window (Eq. (4)). A) Change in connection strength between two exemplar participants over the 5-day period when smoothed over 10-min intervals. B) Change in connection strength when smoothed over 2-h intervals. C) Histogram of the duration of interactions across all pairs of participants. Events reflect a period during which two smartphones detected each other without interruptions. A 10-min smoothing window was used and only edges with at least 6 scans/h were included. D) Change in clustering coefficient of two nodes of the network (participants 1 and 6) over the 5-day period using a 2-h smoothing window.

Fig. 3B shows slower changes in connection strength obtained using the 2-h smoothing window. Although the temporal resolution is reduced, the precision of the estimate is improved, as connection strength is determined based on a larger number of scanning events. By estimating dynamic connectivity between all pairs of participants we obtain a dynamic connectivity matrix that defines how the social network develops over time. The changes in network configuration can then be quantified by estimating network metrics at each point in time. In Fig. 3D we show the change in the clustering coefficient over time for two nodes of the network (participants 1 and 6). The clustering coefficient is a measure of the degree to which nodes in a graph tend to cluster together [41]. In particular in social networks, nodes tend to create tightly knit groups characterized by a relatively high density of edges. The local clustering coefficient of a node quantifies how close its neighbors are to being a clique.

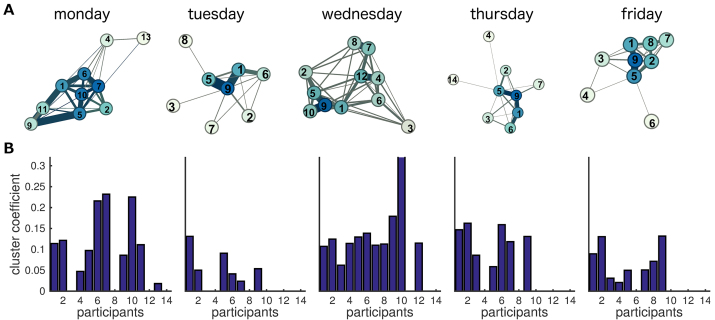
To explore the temporal changes in network topology, we computed the connectivity matrices for each of the five days separately. The static connectivity matrix was determined over the time interval from 9 am to 5 pm using Eq. (1). Fig. 4 shows the network topology for each day as well as the cluster coefficients for all the nodes. The network topologies differed considerable between days. On Monday group of strongly connected nodes was observed including participants 1, 2, 5, 6, 7 and 10. A much sparser network was observed on Tuesday revealing strong connections between participants 1, 5 and 9. On Wednesday a broadly connected network consisting of most of the participants was observed, whereas on Thursday a similar network configuration as on Tuesday was observed. Friday showed again strong coupling between participants 1, 5 and 9, but now also included strong connections to participants 2, 7 and 8.

Fig. 4.

Dynamics of network topology. The connectivity matrix is estimated for each day of the week to assess the corresponding network topology. A) Network topology: The color of the nodes reflects the weighted degree and the width and color of the edges reflect the weights. The network topologies are generated using ForceAtlas 2. B) The local clustering coefficient at each day of the week.

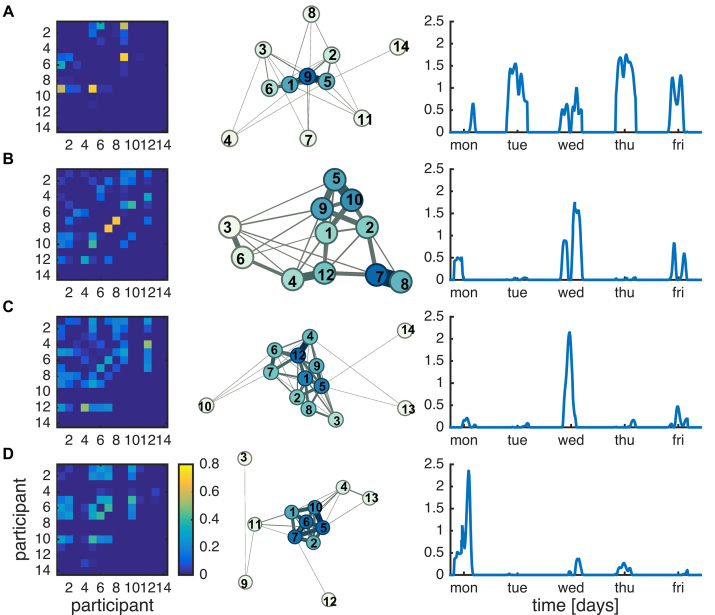
In addition to providing these snapshots of the social network as shown in Fig. 4, the dynamic connectivity matrix can be analyzed at each time point. Video S1 shows the evolution of the network configuration over time. To assess the network configurations that commonly reoccurred during the week, we decompose the complete dynamic connectivity matrix using NMF. NMF yields a low-dimensional approximation of a dataset by minimizing the squared error [45], and will hence only recover the coarse structure of social networks. Four factors were extracted that each consist of the time courses of dynamic connectivity and the corresponding network weights. The first factor reveals a sparse network with strong connections between participants 1, 5, 6 and 9 (Fig. 5A). This network configuration is consistently observed each day of the week, but most strongly expressed on Tuesday and Thursday. The second factor captures a larger network, which in addition to participants 1, 5 and 9 also includes strong connections to other participants such as 7, 8 and 10. This network configuration is observed on Monday, Wednesday and Friday. The third factor shows a large clique of most of the participants. This network configuration was mainly observed on Wednesday and peaked during lunchtime, while the first two factors showed a distinct dip at this time. The peak in the expression of factor 3 coincided with the staff meeting at the Black Dog Institute at which most employees were present. Finally, the fourth factor shows a smaller clique consisting of participants 1, 2, 5, 6, 7, and 10 and this configuration was mainly observed on Monday and peaked in the afternoon. This coincided with the research group team meeting and several team members were participants in this study.

Fig. 5.

Factorization of network dynamics. The connectivity matrix is estimated in a time-resolved manner using a 2-h smoothing window and decomposed into 4 factors (A-D) using non-negative matrix factorization. Each factor is characterized by the extracted featured (the time courses in the right column) and the loadings of this feature in the original time-resolved connectivity matrix. The left column shows the loadings that give the weights of the connectivity matrix. The middle column shows the corresponding network topology. The color of the nodes reflects the weighted degree and the width and color of the edges reflect the weights. The network topologies are generated using ForceAtlas 2.

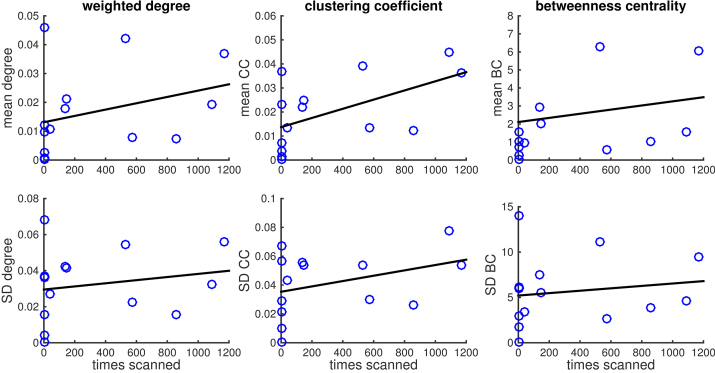
Finally, we test whether differences in scanning rates may have introduced a bias in the estimation of the social network metrics. The scanning rate differed significantly between devices from as low as 1 scan to almost 1200 scans during the 5-day period (see Fig. 1A). A low scanning rate increases the chance that a connection was not observed even though the participants were in close physical proximity. This problem is partly resolved, because even if a device itself does not scan regularly, other devices are still able to detect it. The scanning rates per edge are therefore more consistent, although 18 of the 91 edges were assessed less than once every 2 h (Fig. 1B). To test whether this affects the accuracy and precision of estimating networks metrics, we correlated the scanning rate with the mean and SD of three commonly used network metrics (weighted degree, clustering coefficient and betweenness centrality). The means and SDs of all three network metrics were positively correlated with the number of times the smartphone scanned during the 5-day period (r = 0.29 ± 0.15), but only the correlation between the mean clustering coefficient and the times scanned was significant (r = 0.55, p = 0.04, Fig. 6).

Fig. 6.

Correlation between network metrics and the number of times a smartphone scanned. Three network metrics (weighted degree, clustering coefficient and betweenness centrality) are estimated at each time point using a 2-h smoothing window. The mean and standard deviation of the network metrics are correlated against the number of times the smartphones scanned during the 5-day period. Each panels shows the 14 data points as well the linear regression line.

4. Discussion

We tested the feasibility of using people's own smartphones as a data collection platform to map dynamic social networks. We developed an application for iOS and Android to collect Bluetooth data and tested the application on participants within our organization to validate the social network dynamics obtained using their own smartphone against the events that occurred during the period of data acquisition. One week of data was collected from 14 participants, five of whom had Android handsets and 9 had iPhones. Time-resolved connectivity was derived from the Bluetooth scanning statistics and used to define the dynamic weights of an undirected network. Network metrics such as the weighted degree, clustering coefficient and betweenness centrality provided quantitative measures of how the topology of the network evolves over time. Non-negative matrix factorization was used to extract network configurations that commonly reoccurred during the week. This data-driven approach revealed a core network that was consistently observed throughout the week, as well as two networks that were only observed on a single day. These latter two networks correspond to a team meeting on Monday and a staff meeting on Wednesday and provide face validity of the proposed methodology. These findings demonstrate the feasibility of using participants' own smartphones to map dynamic social networks in real life. The ability to use personal smartphones will be vital for the translation of this technology to clinical applications.

The present study uses Bluetooth to measure physical proximity and define the edges of the network. It hence belongs to a wider group of studies using physical proximity or location-based features as a proxy for social ties [21] [22] [23] [24] [26] [48] [49]. While previous studies used designated smartphones that were handed out to the participants, the current study is the first to use participants' own smartphones to map social networks. This approach to define social networks is supported by studies showing that similarities between two individuals' movements strongly correlate with their proximity in the social network and that such correlations can be exploited to predict which new links will develop in a social network [21] [50] [51]. In fact, one study found that the decision to install an app on a phone relies more on the face-to-face interaction ties than the self-perceived friendship ties [27]. Here we use graph theory to quantify the relationships between multiple participants, rather than focusing on dyadic relationships between pairs of participants. Although we only tested the approach on a limited number of participants (n = 14) during a 5-day period, we were able to identify four distinct network configurations. The structure of these cliques or subgroups and in particular the position or centrality of individuals within these cliques may be important determinants of the effect of social relationships on individual behavior [40] [52] [53] [54]. Network metrics such as the clustering coefficient and betweenness centrality may hence provide important predictors of individual characteristics and behaviors.

We obtained dynamic networks by integrating Bluetooth scanning statistics across short time intervals (see Eq. (4)). The ability to define time-resolved connectivity critically depends on the scanning rate of the data collection platform. We observed large variability in scanning rates between smartphones: smartphones running Android performed on average 7.5 scans/h, whereas iPhones performed 0.35 scans/h. App development on the Android OS and iOS platform requires different approaches and programming languages [55]. In an attempt to ensure a particular overall user experience, iOS imposes restrictions on the background execution of apps, restricting the scope for passive data collection applications that can be achieved on Android devices. Further development of the app is required to increase the scanning rate on iPhones. A next step may be using Bluetooth Low Energy (BLE) to act as a ‘beacon’ to share a unique ID. However, it is currently not feasible to use BLE to map social networks, due to the inability of iOS devices to detect another iOS device when both are in a locked state [56]. In the current study we therefore used the BluetoothManager private API, as the public CoreBluetooth API only contains functions for interacting with low-energy devices. The use of private APIs prevents distribution via the App Store and hence obstructs the application of this technology at scale.

Even if the differences between platforms can be resolved, differences in scanning behavior and missing data will be unavoidable when mapping social networks in real life, as participants forget to bring their smartphones or to charge them before the battery runs out. These variations in scanning behavior may introduce a bias in the estimation of social networks. Here we assessed the extent of this bias and found weak correlations between the scanning rate and egocentrically defined networks metrics. Only the correlation between the scanning rate and the mean clustering coefficient was moderate and statistically significant. These weak correlations are surprising given the large variations in scanning rates. This is partly due to the symmetric measure of connectivity strength that was used: even if a device does not scan regularly itself, the other devices can still detect it. However, this will not resolve the edges between two iOS devices with low scanning rates. In addition, the network metrics are defined over all the edges connecting a particular node: even if the weights of a few edges are underestimated, the effect on network metrics is limited. Although these properties of network metrics may partly compensate for the effects of variations in scanning rate, this bias will affect the network that is obtained [57]. The bias introduced by variation in scanning rate and missing data may be addressed by using connectivity measures that are robust against missing data [58] or by compensating for missing data in the statistical model used for comparing network metrics [59]. It demonstrates the importance of monitoring scanning statistics rather than just recording the times two devices detect each other, as missing data will otherwise be overlooked.

These finding are a step towards using a participant's own handset in the passive detection of social network structures. We present an application for Android and iOS to collect Bluetooth data and methods for mapping dynamic social networks and to quantify the position of individual participants within multiple subgroups in which they engage. Social network analysis provides important information about the natural and externally imposed social mechanisms related to behavior and decision making [27], which could help to design and evaluate new tools for helping people with mental health problems. Several studies have shown that emotional states strongly depend on the structure of social networks and that people with similar levels of happiness, loneliness and depressive symptoms cluster together [12] [60] [61]. This clustering is caused both by direct peer-to-peer influence (contagion) as well as the tendency of individuals to connect with similar people (homophily) [60] [62] [63]. In addition to direct peer-to-peer influence, mental health may also be affected by the location of individuals within their social network or the number and strength of their connections. For instance, lonely people are disproportionately represented at the periphery of the social network [60] and adolescent girls with more depressive symptoms have a smaller network size [28].

Social networks are not stable; the creation and dissolution of relationships are fundamental social processes with profound implications for human outcomes [64]. Most individuals display a distinctive and robust pattern of social interactions that tends to persist over time irrespective of the changes in the identity of peers [65]. Changes in the structure of egocentric social networks may hence provide key indicators of developing mental health issues (see also [66]). The ability to map dynamic social networks using participants' own smartphones offers a non-intrusive and scalable method to investigate the influence of changes in social interactions on mental health. Social withdrawal is a common telltale sign of depression and several studies have shown that socially withdrawn children at risk for a wide range of negative adjustment outcomes [67]. Dynamic network analysis may help to objectively quantify social withdrawal and investigate its consequences on mental health. Future studies are needed to determine if and how the shorter timescales (durations of interactions, switching between subgroups) and the longer timescales (creation and dissolution of relationships, social withdrawal) of dynamic social networks relate to the development of mental health problems.

Declarations

Author contribution statement

Tjeerd Boonstra: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Mark Larsen: Conceived and designed the experiments; Performed the experiments; Wrote the paper.

Helen Christensen: Conceived and designed the experiments; Wrote the paper.

Funding statement

Helen Christensen was supported by a National Health and Medical Research Council John Cade Fellowship in Mental Health Research (APP1056964). Tjeerd Boonstra was supported by a Veni Fellowship from the Netherlands Organization for Scientific Research (NWO #45110-030). This work was supported by the Young and Well CRC (youngandwellcrc.org.au), established under the Australian Government’s Cooperative Research Centres Program.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.

Supplementary content

The following are Supplementary data to this article:

Supplementary Video S1

Changes in network topology over the 5-day period. Temporal changes in connection strength were determined by convolving the scanning events with a 2 h Gaussian smoothing window and the connectivity matrix was estimated at half-h intervals. The video was developed in Gephi and the network topologies are generated using ForceAtlas 2.