Nanomechanics of Type I Collagen

Abstract

Type I collagen is the predominant collagen in mature tendons and ligaments, where it gives them their load-bearing mechanical properties. Fibrils of type I collagen are formed by the packing of polypeptide triple helices. Higher-order structures like fibril bundles and fibers are assembled from fibrils in the presence of other collagenous molecules and noncollagenous molecules. Curiously, however, experiments show that fibrils/fibril bundles are less resistant to axial stress compared to their constituent triple helices—the Young’s moduli of fibrils/fibril bundles are an order-of-magnitude smaller than the Young’s moduli of triple helices. Given the sensitivity of the Young’s moduli of triple helices to solvation environment, a plausible explanation is that the packing of triple helices into fibrils perhaps reduces the Young’s modulus of an individual triple helix, which results in fibrils having smaller Young’s moduli. We find, however, from molecular dynamics and accelerated conformational sampling simulations that the Young’s modulus of the buried core of the fibril is of the same order as that of a triple helix in aqueous phase. These simulations, therefore, suggest that the lower Young’s moduli of fibrils/fibril bundles cannot be attributed to the specific packing of triple helices in the fibril core. It is not the fibril core that yields initially to axial stress. Rather, it must be the portion of the fibril exposed to the solvent and/or the fibril-fibril interface that bears the initial strain. Overall, this work provides estimates of Young’s moduli and persistence lengths at two levels of collagen’s structural assembly, which are necessary to quantitatively investigate the response of various biological factors on collagen mechanics, including congenital mutations, posttranslational modifications and ligand binding, and also engineer new collagen-based materials.

Introduction

Collagen is the primary constituent of the extracellular matrix of animal connective tissue (1, 2, 3, 4, 5, 6, 7). To date, 28 different types of collagen have been identified in vertebrates and higher invertebrates (4, 5, 6, 7). Among these collagen types, type I is the most abundant in vertebrates. It combines with other molecules in varying ratios to form a variety of tissue scaffolds, such as basal membranes, ligaments, tendons, skin, and blood vessels, where it gives them their load-bearing mechanical properties.

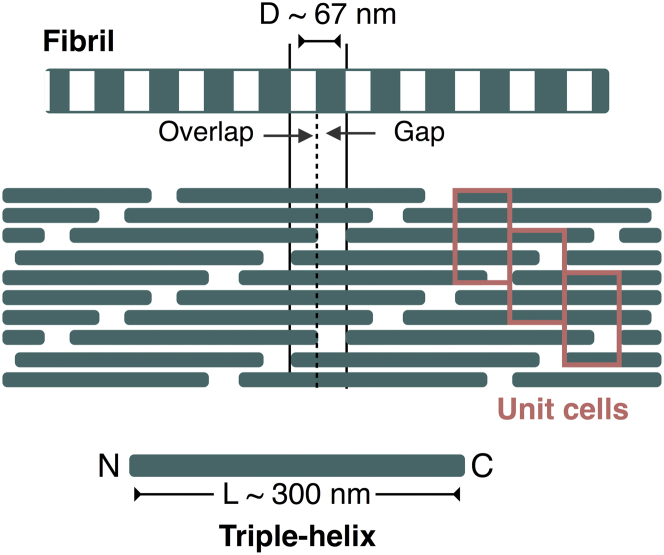
The building block of type I collagen is a 300-nm-long triple helix, which is made up of three parallel polypeptide chains wound around each other. These triple helices assemble to form fibrils. The arrangement of triple helices in a fibril is such that the N-termini of two axially adjacent triple helices are separated by D = 67 nm and the N-termini of two collaterally adjacent triple helices are separated axially by 0.54 D (8, 9, 10, 11, 12, 13, 14). This staggered arrangement creates alternating regions of low and high protein density along the fibril axis with a repeating unit of length D (Fig. 1). These D-periods are, in fact, signature structural features of several collagen types, and are visible as alternating dark and light bands in transmission electron microscopy (TEM) and atomic force microscopy (AFM). Fibrils, in turn, combine with other collagenous and noncollagenous molecules, such as proteoglycans, to form fibril bundles and fibers, which then assemble with each other to form tissue scaffolds.

Figure 1.

Structural hierarchy of type I collagen fibril. The fibril is drawn at two different spatial resolutions. While the lower-resolution cartoon highlights the repeating dark and light bands visible in TEM and AFM, the higher-resolution cartoon shows the two-dimensional arrangement of the triple-helices (green rectangles) within a fibril. The higher-resolution representation also outlines three representative crystallographic unit cells of the fibril. Note that a crystallographic unit cell is not a microfibril. To see this figure in color, go online.

How do the mechanical properties of collagen vary across this structural hierarchy? Table 1 summarizes the mechanical properties of triple helices and fibrils/fibril bundles obtained from experiments and molecular dynamics (MD) simulations (15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26). The first trend we note is that the persistence lengths of triple helices are significantly smaller than those of fibrils/fibril bundles. This trend reflects the fact that thermal fluctuations bend triple helices over much shorter lengths compared to fibrils/fibril bundles. This is, nonetheless, expected because triple helices are three orders-in-magnitude thinner than fibrils/fibril bundles. Surprisingly, however, we also note that the Young’s modulus of triple helix, determined by mapping its mechanics on to an elastic rod, is an order-of-magnitude larger than the moduli of fibrils and fibril bundles. This observation implies that it is easier to stretch fibrils/fibril bundles compared to triple helices, at least in the limit of small strains. What explains this differential mechanical response?

Table 1.

Mechanical Properties of Type I Collagen at Different Structural Levels

Structural Level	r (nm)	Y (GPa)	$l_p$ (nm)	Method	T (K)	Reference
Triple helix	0.62	2.9 ± 0.12	83.2∗	X-ray	293	(15)
	—	4.5∗	14.5	optical tweezers	298	(16)
	—	3.7–7.8∗	12–25	AFM	298	(17)
	0.78	1.3–2.4	—	energy minimization	NA	(18)
	0.36	4.2∗	12.9	accelerated MD	310	present work
Collagen-like triple helix	—	4.8 ± 1.0	15.3∗	steered MD	300	(19)
	0.36	7.0	22.3∗	steered MD	300	(20)
	0.36	4.0	12.7∗	steered MD	310	(21)
	0.35	1.8–2.3	5.1–6.5∗	MD (force-extension)	300	(22)
Fibril core	1.75	2.34	4.0 × 103∗	MD (constant-strain)	310	present work
Fibril/fibril bundle	—	0.43	—	SAXS	293	(23)
	280–426	0.07–0.17	0.8–10.7 × 1011∗	AFM	—	(24)
	220–570	0.123 ± 0.046	0.6–24.7 × 1011∗	MEMS	—	(25)
	116–200	0.1–0.36	0.03–1.1 × 1011∗	optical tweezers	298	(26)

The values of Young’s moduli (Y) marked by asterisks (^∗) are computed from their reported respective persistence lengths $\left(l_p\right)$ using the relationship given by Eq. 1. Similarly, the values of $l_p$ marked by asterisks are computed from their reported respective Y using Eq. 1. Interconversion between Y and $l_p$ through Eq. 1 requires values of temperature (T) and radius (r). In cases where temperature was not reported, it is assumed to be 298 K, and in cases where the radius of the triple helix was not reported, it is assumed to be 0.36 nm.

We note first that the experiments that report the mechanical properties of fibrils/fibril bundles, including ours (26), do not differentiate between fibrils and fibril bundles. Consequently, the lower Young’s moduli of fibrils/fibril bundles could either be due to the packing of fibrils into fibril bundles, and/or due to the packing of triple helices into fibrils. Recent experiments show that the flexibility of type I triple helix is sensitive to solvent conditions, and can modulate its Young’s modulus by an order in magnitude (17, 27). This suggests the possibility that the packing of triple helices into fibrils, a process accompanied by partial dehydration of triple helices, perhaps reduces the Young’s modulus of individual triple helix, which results in a fibril having smaller Young’s moduli. It is also conceivable that the interaction between triple helices in a fibril is sufficiently weak that straining a fibril alters the relative arrangements between triple helices, but does not affect the structures of the individual triple helices. This could lead to a fibril being less resistant to axial deformation compared to a triple helix.

To explore these possibilities, we first determine, using accelerated MD, the Young’s modulus of an isolated triple helix in salt solution. This serves as a control and also assesses the performance of MD against experiment. This is particularly important because we have demonstrated that the structural organization of triple helices in the fiber diffraction unit cell is sensitive to the employed MD protocol (28), and the question remains as to how well our protocol predicts the mechanics of isolated triple helices. We then determine the Young’s modulus of the buried core of a fibril. The underlying idea is that if the Young’s modulus of the buried core is found to be similar to that of fibrils/fibril bundles obtained from experiment, then we will conclude that the relatively lower Young’s moduli of fibrils/fibril bundles can be attributed to the specific packing of triple helices in the core of a fibril.

Materials and Methods

Potential of mean force

The potential of mean force, U(R), where R is the end-to-end distance of a triple helix, is determined using well-tempered metadynamics (29, 30, 31). Gaussian hills of height h₀ = 2 kJ/mol and width w = 0.2 nm are deposited over R using a scaling factor s = 6 at regular intervals of 100 integration time steps. Geometrically, R is defined as the distance between the centers of masses of the backbone atoms of the N- and C-termini of the triple helix fragment.

The N- and C-termini of all three peptides in a triple helix are capped individually, and the peptides are described using the all-atom Amber99sb-ildn force field (28, 32, 33, 34). The triple helix is placed in a cubic box containing explicit water molecules (∼136 K), and water is described using SPC/E parameters (35). NaCl salt concentration is set at 10 mM, and there are four extra Cl⁻ ions compared to Na⁺ to balance the net charge on the triple helix. Electrostatic interactions are computed using the particle mesh Ewald scheme (36) with a Fourier grid spacing of 0.1 nm, a fourth-order interpolation, and a direct space cutoff of 10 Å. van der Waals interactions are computed explicitly for interatomic distance up to 10 Å. Temperature is regulated at 310 K and pressure at 0.1 MPa using extended ensemble approaches (37, 38) and with coupling constants of 1 ps. Bonds in the peptides are constrained using the P-LINCS algorithm (39), and the geometries of the water molecules are constrained using SETTLE (40). These constraints permit use of an integration time step of 2 fs. Before subjecting the triple helix to well-tempered metadynamics, the triple helix is subjected to 10 ns of standard MD.

MD simulations of fibril core

The details of our MD simulation protocol are provided elsewhere (28), and here we provide only the salient points. Because the resolution of the crystal structure (PDB: 3HR2) was insufficient to reveal atomic level details, including side chain orientations and interpeptide hydrogen bonds (12, 13), an atomically detailed model was constructed by incorporating the high-resolution crystallographic data of collagen-related peptides (12, 28, 41). The model includes all known hydroxylated forms of prolines and lysines, but not any glycosyl groups, as their specific sites remain unknown. We leave out all cross-links between triple helices, and this is to allow the packed triple helices sufficient flexibility to rearrange under applied strains. It should be noted that the computed value of Young’s modulus in the absence of cross-links serves as a lower limit. The overall system contains 70,606 particles, which includes the peptide, explicit water (∼11 K molecules), and 31 Cl⁻ ions to counter the positive charge of the peptide. The resulting ratio of Cl⁻ ions and water in the unit cell corresponds, roughly, to a salt concentration of 150 mM. With the exception of one simulation parameter, namely the pressure coupling scheme, all the simulation parameters are the same as those used in the MD simulation of the triple helix. In this case, we employ an anisotropic pressure coupling scheme wherein the components of the virial pressure tensor are regulated separately. While the diagonal components, σ_ii, are regulated at a pressure of 0.1 MPa, the nondiagonal components, σ_i≠j, are regulated at zero pressure to emulate a zero-shear condition.

This MD simulation protocol preserves the dimensions of the triclinic unit cell, the gap/overlap ratio of the fibril, and the pitch of the constituent triple helix (28). In addition, the average D-band length is D₀ = 66.28 ± 0.08 nm, which is in close correspondence with the values obtained from AFM, TEM, and x-ray diffraction studies (8, 9, 10, 11, 12, 13, 14).

We use Gromacs v4.5 (http://www.gromacs.org/) for all MD simulations (42).

Results and Discussion

Young’s modulus of triple helix

To determine the Young’s modulus of an isolated triple helix, we assume that its thermal fluctuations can be described by the wormlike chain model. The Young’s modulus (Y) of the triple helix can then be obtained from the persistence length $\left(l_p\right)$ using the relationship (43)

$$Y=4k_{\text{B}}T{l}_p/\pi r^4,$$ (1)

where T is the temperature, $k_{\text{B}}$ is the Boltzmann constant, and r is the radius of the triple helix. The persistence length $l_p$ is obtained by solving numerically the relationship (44)

$${\langle R\rangle }^2+\langle \Delta R^2\rangle =2l_p{L}_c\left[1-\frac{l_p}{L_c}\left(1-e^{-L_c/l_p}\right)\right],$$ (2)

where R and $L_c$ are, respectively, the end-to-end distance and the contour length of the triple helix.

To solve Eq. 2 for a triple helix of contour length $L_c$, we need to determine the averages ${\langle R\rangle }^2$ and $\langle \Delta R^2\rangle$. From a theoretical standpoint, these averages can be obtained using any conformational sampling method that is coupled to a temperature bath. This can, however, be practically challenging when the solvent is described explicitly and when free energy barriers are large. To circumvent these issues, we compute these averages from the potential of mean force, U(R), a thermodynamic quantity whose convergence with respect to conformational sampling is tractable. We use U(R) as Boltzmann weights and determine

$$\langle R\rangle =\frac{\int R{e}^{-U\left(R\right)/k_{\text{B}}T}dR}{\int e^{-U\left(R\right)/k_{\text{B}}T}dR}$$ (3)

and

$$\langle \Delta R^2\rangle =\langle R^2\rangle -{\langle R\rangle }^2,$$ (4)

We determine U(R) not for the entire collagen triple helix, whose contour length exceeds 300 nm, but for a fragment of the triple helix that has a contour length of $L_c$ = 15.3 nm (Fig. 2 a). For even such a small fragment, the simulation cell containing explicit solvent has close to half a million particles. Nevertheless, the length of the fragment is chosen such that it extends beyond two true pitch lengths of the triple helix—the true pitch of a 7/2 helix spans 21 amino-acid triplets, and our fragment contains 45 amino-acid triplets. While the choice of the primary sequence of the fragment can be expected to affect the computed Young’s modulus, other simulation studies (18, 22) suggest that the effect will not be significant enough to alter the conclusions of this study.

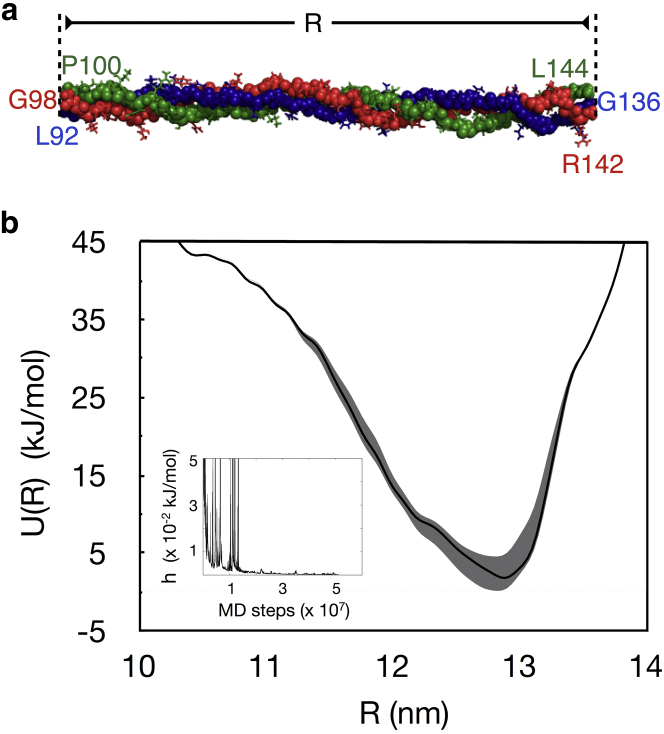
Figure 2.

(a) Representative 45-residue fragment of the collagen molecule. The backbone atoms are drawn as spheres and the side chains are drawn as sticks. The primary sequences of the two α1 chains are $P_{100}^{h}GM{K}^h\dots PRG{L}_{144}$ and $G_{98}L{P}^{h}G\dots MGP{R}_{142}$, and the primary sequence of the α2 chain is $L_{92}{P}^{h}GF\dots GAK{G}_{136}$. The h superscript over selected residues refers to their posttranslationally modified hydroxylated forms, and the subscript on the terminal residues of the chains matches their specific numbers in the primary sequence taken from the fiber diffraction structure of the fibril (PDB: 3HR2). Note that the residue numbers in the three chains are different, and this is because the three chains in the triple helix are staggered. (b) Potential of mean force (U(R)) of this fragment evaluated as a function of its end-to-end distance (R) from well-tempered metadynamics. (Solid line) Estimate from a trajectory comprising 5 × 10⁷ MD steps (100 ns of metadynamics time). (Shaded area) Range bounded by two estimates, one from a smaller trajectory comprising 4.5 × 10⁷ MD steps and the other from a longer trajectory comprising of 5.5 × 10⁷ MD steps. (Inset) Time evolution of the dynamic hill height (h). To see this figure in color, go online.

Fig. 2 b shows the U(R) determined using well-tempered metadynamics (29, 30, 31) where conformational sampling is conducted for 5 × 10⁷ MD steps. Using this U(R) profile in Eq. 3, we find that $\langle R\rangle =12.78\text{nm}$, which corresponds roughly to the position of the lowest energy in U(R). Using Eq. 4, we find that $\langle \Delta R^2\rangle =0.04{\text{nm}}^2$. Convergence is estimated in three ways. First, we track the dynamic hill height in metadynamics (Fig. 2 b, inset), which does not take up a value greater than 0.001 kJ/mol during the entire second half of the trajectory, and it continues to decease asymptotically, as expected theoretically (45). Second, we compute $\langle R\rangle$ and $\langle \Delta R^2\rangle$ using U(R) profiles from shorter and longer metadynamics trajectories (29). The U(R) profiles from these trajectories are also shown in Fig. 2 b. The shorter trajectory is comprised of 10% fewer MD steps (4.5 × 10⁷ MD steps) and yields $\langle R\rangle =12.69\text{nm}$ and $\langle \Delta R^2\rangle =0.04{\text{nm}}^2$. The longer trajectory, which is comprised of 10% more MD steps (5.5 × 10⁷ MD steps), yields $\langle R\rangle =12.74\text{nm}$ and $\langle \Delta R^2\rangle =0.04{\text{nm}}^2$. $\langle R\rangle$ values computed from the three trajectory lengths are within 1% of each other, with no correlation between the averages and trajectory length. Finally, we compute the averages following a time-independent reconstruction of U(R) (46), and find $\langle R\rangle =12.61\text{nm}$, which is also within 1% of the values obtained from the unweighted U(R) profiles.

Numerical solution of Eq. 2 using $\langle R\rangle =12.78\text{nm}$ and $\langle \Delta R^2\rangle =0.04{\text{nm}}^2$ yields $l_p=12.85\text{nm}$. Plugging this value of $l_p$ in Eq. 1, and using $r=0.36\pm 0.01$, which is one-half of the average width of the triple helix (28) in the well-tempered metadynamics simulation, yields a corresponding Y = 4.2 GPa. Decreasing $\langle R\rangle$ by 1% yields $l_p=12.09\text{nm}$ nm and Y = 3.95 GPa, and increasing $\langle R\rangle$ by 1% yields $l_p=13.70\text{nm}$ and Y = 4.50 GPa. These values of persistence lengths and Young’s moduli fall within the range of the most recent estimates from AFM and optical tweezer experiments (Table 1). We also note that while there are other simulation-based studies of the mechanical properties of collagen-like triple helices (Table 1), the Young’s moduli in all, but one, of those studies are obtained using steered MD, where decoupling the effects of kinetics from static thermodynamic properties is challenging (47, 48).

Young’s modulus of fibril core

We determine the Young’s modulus of the fibril core from its stress-strain relationship. To emulate the fibril core, we simulate the crystallographic unit cell of the fibril (12, 13) under periodic boundary conditions. The crystallographic unit cell, which is the smallest repeating unit in a fibril, is a triclinic cell whose longest lattice constant is equal to the D-band length of the fibril. The unit cell contains exactly one triple helix wrapped 4.46 times about the fibril axis, that is, the length of the triple helix L = 4.46 D (Fig. 1). Such a periodic system represents an infinitely wide and infinitely long fibril that lacks an interface with bulk solvent and, therefore, it represents the buried core of a fibril. We note that simulating a single crystallographic unit cell under periodic conditions is an approximate representation of the buried core in that it does not incorporate aperiodic variations across multiple unit cells. Nevertheless, because the unit cell we employ is, in fact, the smallest periodic repeating unit observed in fiber diffraction studies (12, 13), we consider it as an appropriate initial model of the fibril core.

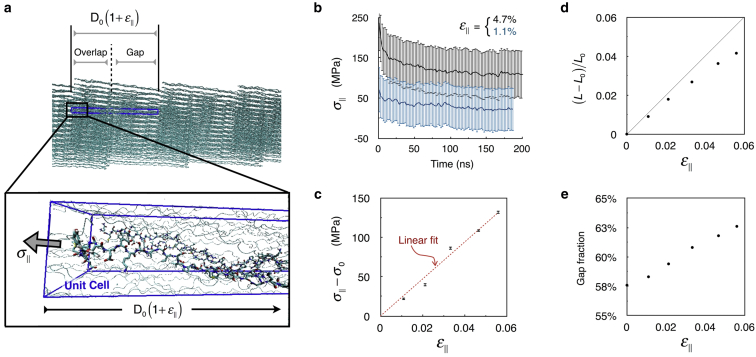
The stress-strain relationship is obtained by simulating the unit cell after straining it along the fibril axis $\left({ϵ}_{\parallel }>0\right)$ and recording the resulting stress ${\sigma }_{\parallel }$ (Fig. 3 a). Specifically, we carry out five separate MD simulations of the unit cell, and in each simulation, the lattice constant parallel to the fibril axis (or the D-band length) is held fixed at a length $D=D_0\left(1+{ϵ}_{\parallel }\right)$. The details of our MD simulation protocol are provided elsewhere (28), and are also described briefly in the Materials and Methods. The evolution of the stress as a function of simulation time is shown in Fig. 3 b. We find that in all cases stress-equilibration requires >150 ns of equilibration time. Assuming that these strains are in the linear regime, we obtain the Young’s modulus using Hooke’s law, $Y=\left(\langle {\sigma }_{\parallel }\rangle -{\sigma }_0\right)/{ϵ}_{\parallel }$, where ${\sigma }_0=0.1\text{MPa}$ (Fig. 3 c). The values of $\langle {\sigma }_{\parallel }\rangle$ are obtained by averaging ${\sigma }_{\parallel }$ over the final 20 ns of each trajectory. A linear fit between $\left(\langle {\sigma }_{\parallel }\rangle -{\sigma }_0\right)$ and ${ϵ}_{\parallel }$ yields Y = 2.34 GPa. Inserting this value in Eq. 1 and taking $r=\sqrt{\mathbf{b}\times \mathbf{c}/\pi }=1.75$ nm, where $\mathbf{b}$ and $\mathbf{c}$ are the two smallest lattice constants of the unit cell under zero-stress condition, yields a persistence length $l_p=4.0\times {10}^3$ nm. The values of the unit cell vectors $\mathbf{b}$ and $\mathbf{c}$ are taken from our earlier work (28).

Figure 3.

Constant-strain MD simulations of the crystallographic unit cell under periodic boundary conditions. (a) Snapshot of the MD simulation illustrating the unit cell (blue box), the strained lattice constant $\left|\mathbf{a}\right|=D_0\left(1+{ϵ}_{\parallel }\right)$, and the component of the virial stress tensor parallel to the fibril axis, ${\sigma }_{\parallel }$. (b) Time evolution of the ${\sigma }_{\parallel }$ in two different constant-strain simulations, one in which ${ϵ}_{\parallel }=0.011$, and the other in which ${ϵ}_{\parallel }=0.047$. The vertical lines represent fluctuations in ${\sigma }_{\parallel }$ observed over 2 ns time intervals. (c) Stress-strain relationship estimated for five different strain values. $\langle {\sigma }_{\parallel }\rangle$ values are averages over the final 20 ns of the constant-strain simulations, and the standard errors are obtained via block averaging. (d) Relationship between the fractional change in the length of the triple-helix (L), and the applied strain, estimated from the final 20 ns of constant-strain simulations. $L_0$ is the length of the triple helix in the zero-strain simulation. (e) Relationship between the gap fraction and the applied strain, estimated from the final 20 ns of constant-strain simulations. To see this figure in color, go online.

Analysis of the equilibrated portions of the MD simulations reveals that the fractional increase in triple helix length is not correlated linearly with the applied strain (Fig. 3 d), implying that straining also induces slippage between triple helices. For the maximum applied strain, the gap fraction, estimated from axial mass densities (28), increases by 5% from 0.58 to 0.63 (Fig. 3 e). Such slippage is less likely to occur under physiological conditions when the triple-helices are cross-linked. Including cross-linking in the model will only increase the Young’s modulus of the fibril core, and therefore, the computed Young’s modulus serves as a lower limit. Nevertheless, despite the slippage, the computed Young’s modulus of the fibril core is comparable to the Young’s modulus of a triple helix and is an order-of-magnitude larger than the Young’s moduli of fibrils/fibril bundles (Table 1).

Conclusions

Results from our simulations suggest that the smaller Young’s moduli of fibrils/fibril bundles relative to that of their constituent triple helices cannot be attributed to the specific packing of triple helices in the fibril core. Therefore, it is not the fibril core that yields initially to axial stress. Rather, it must be the portions of the fibril exposed to the solvent and/or the fibril-fibril interface that get strained in response to the initial stress. It is conceivable that the fibril portion exposed to the solvent is packed loosely compared to the fibril core and may yield to relatively smaller axial stresses. It is also plausible that the fibril-fibril interface slips first in response to applied axial stresses. As such, the packing of fibrils into fibril bundles is facilitated by the binding of noncollagenous molecules, such as proteoglycans, which are expected to interact with fibrils weakly compared to the interaction that holds triple helices together within fibrils (5). This explanation is supported by our recent experiments (26), which show broad distributions in both the Young’s moduli (0.1–0.36 GPa) and the diameters (116–200 nm) of type I collagen fibril/fibril bundles extracted from a single tissue-type. It is unlikely that the organization of the fibril core varies within a tissue-type (5), and it may be that the distribution in Young’s moduli is systematically related to the distribution in the sizes fibrils/fibril bundles, or the packing of the fibrils within fibril bundles. Indeed, statistical modeling of interfibrillar interactions suggests that the arrangement of interfibrillar cross-link forming sites contributes to the broadening of the denaturation transition in fibrillar collagen (49). Additionally, studies based on a wormlike bundle model suggest that competition between the elastic properties of the filaments and those of the cross-links leads to renormalized effective bend and twist rigidities, at least for microtubule- or actinlike filament bundle geometries (50). Further study is, however, required to establish causality, and toward that end, this work lays the foundation by providing converged estimates of Young’s moduli and persistence lengths at two levels of collagen’s structural hierarchy. In general, this work provides the necessary baseline (or control) to quantitatively investigate the effect of various biological factors on the mechanical properties of collagen, such as congenital mutations, post-translational modifications, and ligand binding (1, 2, 3, 4, 5, 6, 7), and also engineer new collagen-based materials (51).

Author Contributions

S.V., J.P.R.O.O., and J.D.S. designed research; S.V. performed research; S.V. analyzed data; and S.V., J.P.R.OO., and J.D.S. wrote the article.

Editor: David Sept.