Time Cells in Hippocampal Area CA3

Abstract

Studies on time cells in the hippocampus have so far focused on area CA1 in animals performing memory tasks. Some studies have suggested that temporal processing within the hippocampus may be exclusive to CA1 and CA2, but not CA3, and may occur only under strong demands for memory. Here we examined the temporal and spatial coding properties of CA3 and CA1 neurons in rats performing a maze task that demanded working memory and a control task with no explicit working memory demand. In the memory demanding task, CA3 cells exhibited robust temporal modulation similar to the pattern of time cell activity in CA1, and the same populations of cells also exhibited typical place coding patterns in the same task. Furthermore, the temporal and spatial coding patterns of CA1 and CA3 were equivalently robust when animals performed a simplified version of the task that made no demands on working memory. However, time and place coding did differ in that the resolution of temporal coding decreased over time within the delay interval, whereas the resolution of place coding was not systematically affected by distance along the track. These findings support the view that CA1 and CA3 both participate in encoding the temporal and spatial organization of ongoing experience.

SIGNIFICANCE STATEMENT Hippocampal “time cells” that fire at specific moments in a temporally structured memory task have so far been observed only in area CA1, and some studies have suggested that temporal coding within the hippocampus is exclusive to CA1. Here we describe time cells also in CA3, and time cells in both areas are observed even without working memory demands, similar to place cells in these areas. However, unlike equivalent spatial coding along a path, temporal coding is nonlinear, with greater temporal resolution earlier than later in temporally structured experiences. These observations reveal both similarities and differences in temporal and spatial coding within the hippocampus of importance to understanding how these features of memory are represented in the hippocampus.

Introduction

The hippocampus plays a critical role in the temporal organization of memories (Eichenbaum, 2014), and a potential mechanism for this temporal organization are hippocampal “time cells,” neurons in hippocampal area CA1 that fire at specific moments in temporally structured experiences (Pastalkova et al., 2008; MacDonald et al., 2011, 2013; Kraus et al., 2013; Modi et al., 2014; Wang et al., 2015). So far, time cells have been examined only in CA1, and it is currently unknown whether other areas of the hippocampus have time cells or where the temporal properties of CA1 time cells originate within the hippocampal circuitry. One intriguing possibility is that CA1 receives temporal information directly from the medial entorhinal cortex (MEC) and is specialized for the temporal organization of memories within the hippocampus. Consistent with this possibility, time cells are also observed in MEC (Kraus et al., 2015), MEC lesions disrupt fine timing of CA1 neuronal activity (Schlesiger et al., 2015), and MEC cells that project directly to the CA1 are critical for memory requiring an association across time (Kitamura et al., 2014). Also, other studies have distinguished a selective role for CA1 and not CA3 in associating events across time (Kesner et al., 2005; Farovik et al., 2010) and in the reorganization of spatial representations over prolonged periods (Mankin et al., 2012). Conversely, within CA1, temporal coding properties parallel those of spatial coding properties, including that time and place cells are found in the same neuronal population and the same cells can encode both place and time, that both CA1 and CA3 neurons encode specific events along with place or time, and both respond to a change in the relevant spatial or temporal cues by a “remapping” or “retiming,” respectively. Place cells are prevalent in CA3, as they are in CA1, so the parallels between time and place cells suggests that the entire hippocampal circuitry is involved in both temporal and spatial processing (Eichenbaum, 2014).

Also, when the properties of place and time cells are compared, a striking difference is that time cells have thus far only been reported in tasks that involve a strong working memory demand (Pastalkova et al., 2008). In contrast, place cells fire in a spatially tuned manner whenever there is a fixed spatial environment regardless of whether or not the rat is engaged in a memory task. In the previous study, the control task without a memory demand also lacked a fixed temporal structure of events, perhaps preventing expression of stable temporal firing fields.

Here, we examined whether temporal processing within the hippocampus is limited to area CA1, or extends to CA3, by recording from CA1 and CA3 neurons in rats running on a treadmill in between alternating paths in a delayed alternation T-maze task, thus placing a demand on working memory. We also recorded from rats running a simplified task almost identical in structure except without working memory demands. The results show that CA3 neurons exhibit robust temporal coding, and CA1 and CA3 neurons equivalently code time and space and do so equivalently both with and without a working memory demand. Within both areas, temporal coding does differ from spatial coding in that time representation is decreased in resolution over the delay interval, whereas spatial coding had the same resolution over the length of the track.

Materials and Methods

Subjects

Neural activity data were collected from 11 male Long–Evans rats weighing 400–550 g. All rats were water deprived but provided with food ad libitum. The weight of the rats was monitored regularly as a means of regulating good health. All animal procedures were approved by the Boston University Institutional Animal Care and Use Committee.

Task

The apparatus was a 122 × 92 cm rectangular track with a “stem” in the middle of the long dimension onto which the treadmill was inserted. Water ports were located at the end of the treadmill and on each long arm (see Fig. 4C). On the first day of training, rats were allowed to freely explore the maze and forage for scattered water rewards. On the next day, rats were allowed to run only in the forward direction on right-turn trials for water rewards (henceforth called “looping”). Then they were shaped on treadmill running by providing rewards on the treadmill while progressively increasing the treadmill speeds for longer periods until the rat completed a 20 s run at 20 cm/s. Subsequently, the rats were trained without the treadmill activated to alternate left and right turns at the choice point to receive rewards after each successful alternation. Once the rat consistently performed over 90% correct on alternation, treadmill activation was reinstated and the animals were retrained to alternate with treadmill running. In this final phase of training, rats were given a small 0.05 ml water reward for entering the treadmill and a large reward of 0.1 ml after a 20 s run at 20 cm/s on the treadmill on each trial. They then approached a choice point and were required to turn in the direction opposite to that where they entered the stem to receive another reward of 0.05 ml after correct alternations.

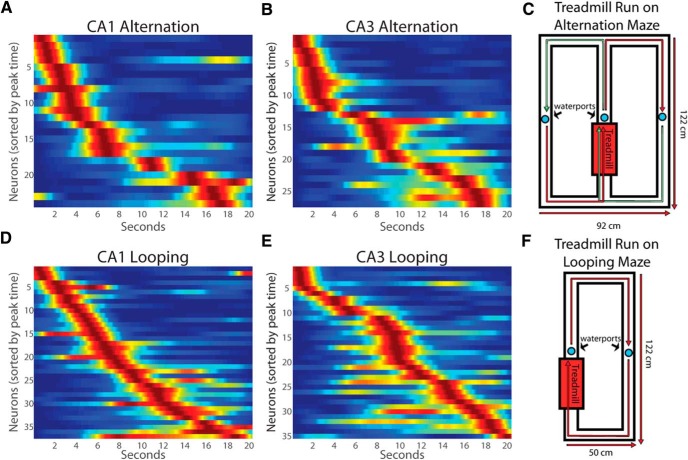
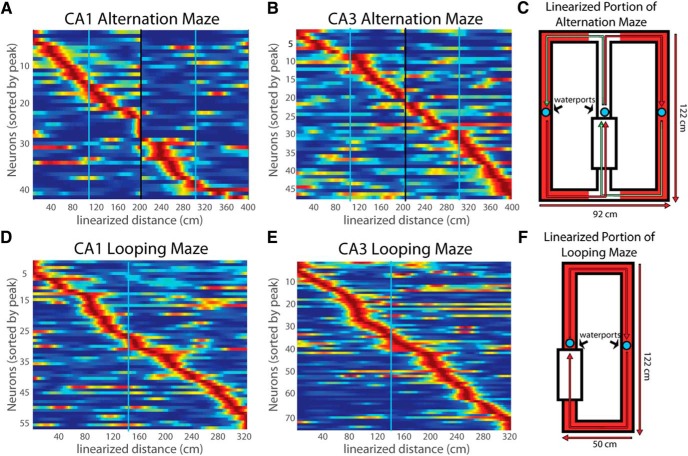
Figure 4.

Time cell firing patterns in CA1 and CA3 during treadmill running in alternation (A, B) and looping (D, E) sessions. C, F, Representations of the alternation and looping mazes.

Electrode implants and physiological recording

Once rats performed above 90% correct over 1 week of testing, electrode drives were implanted. Five rats were trained in alternation before implantation, and neuronal activity was recorded during separate sessions of alternation and looping. Three other rats were implanted after training on looping (right-turn) only, and then subsequently neuronal activity was recorded during the looping task. Then these animals were trained on the alternation task and subsequently recordings were taken as they performed this task. Three additional rats were trained and recordings were taken only during the looping task. The findings in the experiments described below did not differ among these training regimens.

Each tetrode comprised four 12 μm nichrome wires (Sandvik Heating Technology) and was gold plated until an impedance of 200–250 kΩ at 1000 Hz was reached (Komorowski et al., 2009). The microdrive was implanted 1 mm into the cortex above the hippocampus unilaterally in seven rats [anteroposterior (AP), −3.3 mm; mediolateral (ML), +2.8 mm] and bilaterally in four rats (AP, −3.4 mm; ML, ±3.0 mm). After at least 1 week of surgical recovery, tetrodes were gradually lowered into CA1 and later into CA3. Electrical recordings were made using a 96 channel multichannel acquisition processor (Plexon) in which spike channels were referenced to another ipsilateral electrode to remove movement-related artifacts. Action potentials were detected by threshold crossing and digitized at 40 kHz. Preliminary identification of CA1 and CA3 recordings was made by a combination of tracking the electrode depth and observation of spike bursting at the theta rhythm, strong theta power, and the presence of sharp wave ripples during sleep. Position data were captured using light-emitting diodes situated on the rat's head stage that were monitored at 30 Hz by a Cineplex Digital Capture System (Plexon) and synchronized to neural data.

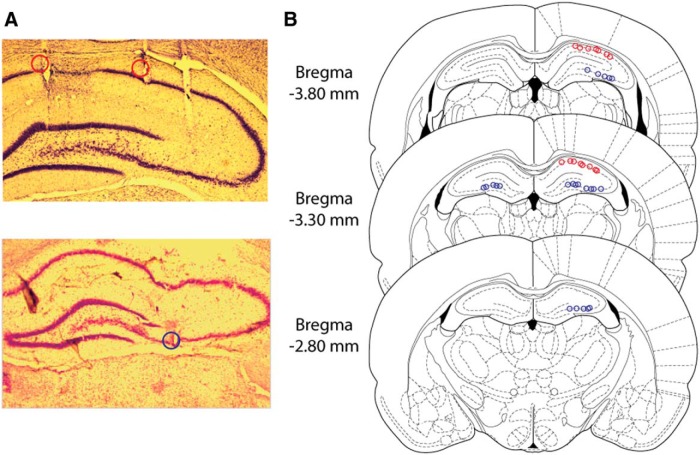
After completion of the experiments, rats were anesthetized with 2.5% isoflurane, and small lesions were made at the end of the tetrodes by passing 40 μA of direct current through each wire. Animals were then injected with an overdose of pentobarbital sodium/phenytoin sodium (Euthasol; Virbac Animal Health) and transcardially perfused with 0.05 m PBS, followed by 4% paraformaldehyde in 0.05 m PBS. The brain was removed, postfixed in 4% paraformaldehyde, and then cryoprotected using a 30% sucrose solution in 0.05 m K-PBS. Slices were then stained with cresyl violet to perform histological confirmation of tetrode locations in CA1 and CA3 (Fig. 1).

Figure 1.

Tetrode location in CA3. A, Representative coronal slices of CA1 (red circles) and CA3 (blue circle) recording lesion sites. B, Reconstruction of all recording sites in CA1 (red circles) and CA3 (blue circles) with sections taken from the atlas of Paxinos and Watson (2007).

Analysis of temporal and spatial firing patterns

Individual neurons were isolated by manually sorting clusters of waveforms using Offline Sorter (Plexon). Sorting was performed using the relative amplitudes across each wire, the waveform width, and the peak-to-valley distance. The sorted clusters were screened for interspike intervals shorter than the neuronal refractory period, indicating that there could multiple units. Spiking and tracking data were imported into MATLAB 2015b for additional analysis with custom scripts.

Maximum likelihood estimation of temporally modulated firing.

We analyzed cell firing patterns while rats ran on a treadmill to identify temporally modulated cells. We classified time cells by comparing nested maximum likelihood models of the spike train of a cell, with models that included or did not include time. For each model, we performed the maximum likelihood fit across all the treadmill runs. Nested models were compared using a likelihood ratio test to assess the probability that adding parameters significantly (p < 0.02, Bonferroni's corrected for the number of cells) improved the fit.

We compared the following four models to find the model that best fit the spiking data. First, we calculated the maximum likelihood estimation of a spike train assuming constant firing across the whole treadmill run. This model, p₁(t; θ₁), gives the probability of a spike at any given time point t but did not include any temporal terms, so the set of parameters θ₁ only includes a constant term (a₁):

This model was compared with a nested four-parameter model, p₂(t; θ₂) (Eq. 2), that includes a temporally modulated term T, which modeled a Gaussian time field with two parameters:

where T is just a Gaussian field controlled by μ and σ:

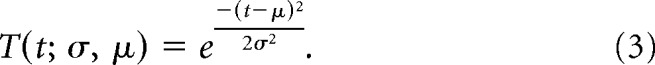To be classified as a time cell, we required that model p₂, which included a term for temporal modulation, provide a better fit than the constant model p₁. In addition, we evaluated another set of models. The three-parameter p₃ included a temporal term but did not include a constant background firing rate:

and a seven-parameter model, p₄(t; θ₄) (Eq. 5), includes a constant term with amplitude a₁ along with two Gaussian time fields, T₁ and T₂, defined using the function T(t; σ, μ) as defined in Equation 3. Each time field is defined with separate parameters for the amplitude of the two time fields (a₆, a₇), the temporal shift of the peak of each of the time fields (μ₁, μ₂), and the SD for each of the time fields (σ₁, σ₂):

Cells that significantly improved their fit with a model that included temporal parameters were considered time cells if they passed a reliability test. Reliability of the firing field of a time cell was tested by separating even and odd trials and performing the analysis separately using the above procedures. Cells that were significantly fit by models with temporal parameters in both even and odd trials and whose even and odd fits had a Pearson's correlation coefficient r > 0.4 were considered to have reliable firing and labeled time cells. We did not find any cells for which p₄ fit better than p₂ so we will not consider multiple time fields further. Sixty-one cells were fit better by p₃ than p₂. For these cells, we used the estimates of μ and σ taken from p₃.

Implementation of maximum likelihood estimation.

We allowed μ to vary between −20 and 40 s, and σ had to be <40 s. Given that the duration of each treadmill run was 20 s and the temporal resolution was 1 ms for each trial, there are 20,000 points per trial. If a spike was observed in a particular 1 ms time bin, f(t) was set to 1; otherwise, it was set to 0. For each time bin, the model gives us probability that a spike occurs. To avoid numerical errors, instead of using the likelihood, we computed the negative log-likelihood (nLL):

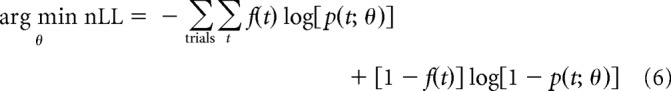To find the best fitting model in a maximum likelihood sense in an automated and efficient way, we searched the parameter space using a combination of particle swarming and the Quasi-Newton method. Particle swarming (Poli et al., 2007) was performed first (with the swarm size equal to 50), and its output was used to initialize the Quasi-Newton method, which was performed second (the number of maximum function evaluations was set to 10,000).

To ensure that a model had an accurate assessment of the center and width of a time field, we only considered cells that clearly peaked during the treadmill run. For the beginning of the treadmill run, only cells with a model parameter μ that was greater than σ were included for additional analysis. Because fields at the end of the treadmill run are much wider than cells in the beginning of the run, the largest σ that was used to remove a cell at the beginning of the treadmill, σ_max, was used as the cutoff for μ for all cells at the end of the treadmill run (20 s − σ_max). For a model with two time fields to be considered, both fields had to have their centers during the treadmill run as above. Additionally, the two fields had to be non-overlapping such that μ₁ and μ₂ were separated by at least σ₁ + σ₂.

Analysis of spatial firing patterns.

Spatial firing patterns were also analyzed as animals traversed the maze outside the treadmill. For the analysis of spatial firing, the maze path was linearized by transforming the tracking signals into polar coordinates, and maze segments were binned using the angle of the tracking and a 2 cm binned linear definition of the maze. Spatial activity patterns were assessed for periods when the rat was moving 4 cm/s or faster on the arms of the maze excluding the stem and areas where rats slowed before entering or leaving the stem. The total linearized distance during alternation trials was 400 cm, the same distance rats ran on the treadmill. For looping sessions, we linearized the entire maze traversed, except the treadmill, for a total linearized distance of 330 cm.

Cells were categorized as place cells using a similar method to the method used to define time cells above. The identical equations were used, except time was replaced with x(t), the path across the linearized portion of the maze interpolated to 1 ms resolution. In alternation sessions, the two linearized sections of the maze are separated by an intersection with the stem. To avoid treating the two maze segments as one unified segment, the two maze segments were treated separately. The other difference in methodology was the model parameter μ was bounded by an extra maze length larger and smaller than the range of the maze definition in x, and σ was bounded between 0 and twice the maze length. After the maximum likelihood estimation was completed, to only include cells with clear centers and widths, place cells were only considered if the center of field parameter μ was σ from all the maze edges. Only 12 place cells were fit by the model including two fields. Because of the small number of place cells with two fields, we did not analyze these cells.

Other analysis methods.

Spatial tuning curves for each neuron were created for periods when the rat was moving at a speed of 4 cm/s or greater by comparing firing rate as a function of linearized spatial position on the linearized maze in 2 cm spatial bins. The spike counts and occupancy times in each bin were independently smoothed for time or space by convolving with a Gaussian smoothing kernel of 6 s time or 60 cm distance, respectively. Session average tuning curves were compiled in an identical way but by averaging bins across trials before smoothing.

When comparing the firing fields of time cells and place cells between different distributions, we used a two-sample t test along with Hedges' g effect size and its 95% confidence interval. This effect size is a variation on Cohen's D that corrects for biases attributable to small sample sizes (Hedges and Olkin, 2014) and is calculated using the following formulas:

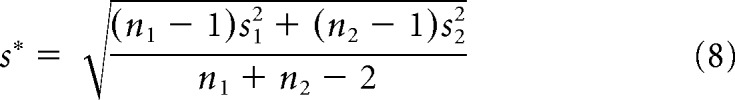These controlled effect sizes may be conservatively interpreted with Borenstein and Cohen's (1988) convention of small (0.2), medium (0.5), and large (0.8) (Hedges and Olkin, 2014). Exact analytical confidence intervals for Hedges' g were calculated by iteratively calculating how far the centrality of the distribution deviates from the null hypothesis. Hedges' g was calculated using the “Measures of Effect Size” toolbox for MATLAB version 1.4. In case these measures were biased from non-normal distributions, we also tested for differences between these distributions by running a two-sample Kolmogorov–Smirnov (KS) test.

When comparing two nominal variables for independence, we performed Fisher's exact test to calculate the two-tailed p value. Descriptive statistics are listed with ±SEM. Information scores were calculated in bits per second in space using the linear maze in 4 cm bins and during the treadmill run in 200 ms bins (in which rats traveled 4 cm distance) using Equation 9.

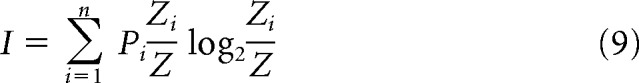where P_i is the probability of occupying the ith spatial or temporal bin, Z_i is the firing rate in the ith bin, and Z̄ is the mean firing rate across all bins (Skaggs and McNaughton, 1998).

Results

Analyses were performed on data from 11 rats in 74 recording sessions that yielded a total of 463 CA1 cells and 481 CA3 cells. Examples of recording sites and their distribution are shown in Figure 1. Neurons with an average firing rate over the entire session >5 Hz were considered interneurons and excluded from additional analysis, leaving 386 putative CA1 pyramidal cells and 379 putative CA3 pyramidal cells.

Time cells in CA3

Time cells are equally prevalent in CA1 and CA3

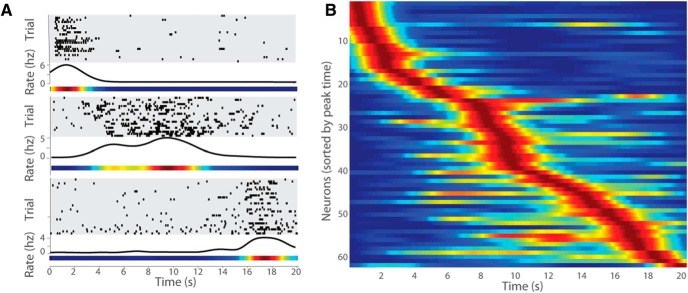
Of all putative pyramidal cells, 206 CA1 cells and 227 CA3 cells that had an average firing rate of at least 0.2 Hz during treadmill running were considered in analyses aimed to determine whether their activity was temporally modulated. Time cells were identified as neurons with temporally modulated firing patterns by comparing nested maximum likelihood estimation models (for details, see Materials and Methods). Using this operational definition, 62 of 227 (27.3%) CA3 cells qualified as time cells. This proportion of CA3 cells that were time cells was not different from the proportion of CA1 cells that were time cells [61 of 206 (29.6%); Fisher's exact test, p = 0.670, two-tailed]. Examples of CA3 time cells that fired at three different moments of the treadmill run are shown in Figure 2A, and the time fields of all recorded CA3 time cells are depicted in Figure 2B. Also, there was no reliable difference in mean firing rate between CA1 and CA3 time cells (CA1, 4.20 ± 0.42 Hz; CA3, 4.25 ± 0.32 Hz; two sample t test, t₍₁₂₂₎ = −0.05, p = 0.96).

Figure 2.

Time cell firing patterns of CA3 neurons. A, Three CA3 neurons are represented on top of each other, each with the following three graphs: (1) raster plots showing temporally modulated spiking during all the individual trials over the duration of the treadmill run; (2) perievent time histogram showing the average firing rate (Hertz) across the treadmill run; and (3) normalized firing rate map of the neuron over the treadmill run. Red correlates to the highest firing rate observed, and blue correlates to the lowest firing rate observed. B, The firing patterns of all identified CA3 time cells, including both alternation and looping sessions. Each row represents the normalized firing rate of one neuron over the duration of the treadmill run (as seen in A), and the order of neurons presented is determined by the peak firing times.

Time cell sequences represent time with decreasing resolution with increasing time

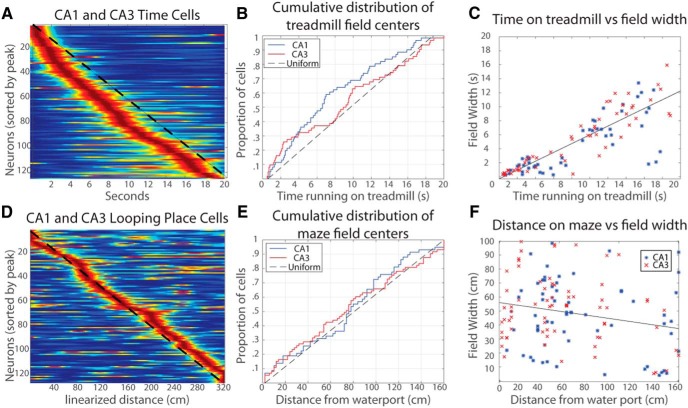
A striking aspect of time cells coding is an overabundance of time cells early in the treadmill run and an accompanying expansion of the duration of elevated activity later in the run (Fig. 2B). By combining CA1 and CA3 time cells, the non-uniform distribution of time cells centers is evident when compared with the uniform distribution (Fig. 3A,B, dashed line). These relationships are most apparent in the cumulative distributions of CA1 and CA3 time field centers, in which it can be seen that the distributions for CA1 and CA3 rise faster than the uniform distribution (dashed line) early in the delay interval and overlap with one another (Fig. 3B). The distributions of combined CA1 and CA3 time cells significantly differed from uniform (KS test, D₍₁₂₃₎ = 0.17, p = 0.001), but the distributions for CA1 and CA3 did not significantly differ from each other (KS test, D_(61,62) = 0.14, p = 0.57).

Figure 3.

Distribution of time and place fields and field widths. A, Firing patterns of all recorded time cells. Dashed line = uniform distribution of time field centers. B, Cumulative distribution function of CA1 and CA3 distributions on the treadmill. For a description of how to read this graph, see Results. C, Scatter gram of the center in time of firing fields on the treadmill run and the width of those fields. D, Same as A except distance traveled along the looping maze. E, Same as B except the x-axis is distance traveled from the previous water ports on the looping maze. Note that neither CA1 or CA3 stray far from the uniform distribution. F, Same as C except the x-axis is distance traveled from the previous water ports on the looping maze.

In addition, a scatter plot of time field widths over the period of treadmill running suggests that the width of time fields increases during running on the treadmill (Fig. 3C). A multiple linear regression of field widths in CA1 and CA3 along with times of the field centers confirmed a strong linear relationship (F_(1,121) = 301.66, p < 0.001, r² = 0.71) such that width of a time field increased 0.62 ± 0.04 s for every second of treadmill running. The intercept of the regression was not significant. To explore potential differences between regions, we performed a multiple regression of width onto center location interacting with region. Because we did not observe a reliable intercept in the previous regression, we did not allow an intercept term in this model. The interaction of region and the field center was significant, indicating that time field widths of cells in CA1 and CA3 are significantly different from each other (F_(1,121) = 11.12, p < 0.01, r² = 0.89). An analogous multiple regression analysis on temporal information scores with field center as a covariate showed a nonsignificant interaction between region and the location of the center of fields, indicating there was no significant difference between the information scores of the two regions (F_(1,119) = 1.46, p = 0.23).

Time cells are equally prevalent with and without a working memory demand

We also recorded CA3 and CA1 time cells in animals performing a “looping” task that did not require that animals remember the path of the previous trial (Fig. 4). During treadmill running in the looping task, robust time cell patterns were apparent throughout the delay in both CA1 and CA3 neurons (Fig. 4A,B and D,E). Time cells in CA1 and CA3 were equally prevalent in both looping and alternation sessions [CA1: looping, 37 of 116 (31.9%); alternation, 24 of 89 (27.0%); CA3: looping, 35 of 130 (27.0%); alternation, 27 of 97 (27.8%); Fisher's exact test, p = 0.82, two-tailed].

Comparison of time and place cell firing properties in CA1 and CA3

Place cells are equally prevalent in CA1 and CA3

We also examined the spatial firing properties of the same population of recorded neurons as animals traversed the maze outside the treadmill (Fig. 5). Of all the recorded putative pyramidal cells, 249 CA1 cells and 322 CA3 cells that had an average firing rate of at least 0.2 Hz on the linearized portions of the maze were included in spatial analyses. Using a similar methodology with a linearized maze that was used with time, cells were tested using the maximum likelihood estimation criteria for reliable spatial modulation (see Materials and Methods). With this metric, 122 of 322 (37.9%) CA3 cells and 99 of 249 (39.8%) CA1 cells were considered spatially modulated, and these proportions were not statistically different (Fisher's exact test, p = 0.67, two-tailed). CA3 place cells had significantly higher peak firing rates than CA1 place cells (CA1, 3.91 ± 0.33 Hz; CA3, 5.23 ± 0.39 Hz; two-sample t test, t₍₂₂₀₎ = −2.5, p = 0.02, Hedges g = −0.36). Conversely, as observed for time cells, CA3 and CA1 place field widths were not significantly different from each other (CA1, 41.39 ± 3.21 cm; CA3, 48.20 ± 3.01 cm; two-sample t test, t₍₂₂₀₎ = −1.54, p = 0.12, Hedges g = −0.21), and information scores of CA3 place cells were not significantly different from those of CA1 place cells (CA1, 2.81 ± 0.40 bits/s; CA3, 3.70 ± 0.41 bits/s; two-sample t test, t₍₂₂₀₎ = −1.53, p = 0.13, Hedges g = −0.21).

Figure 5.

Place cell firing patterns in CA1 and CA3 during alternation (A, B) and looping (D, E) sessions. C, F, Diagram of the alternation and looping mazes with red areas indicating parts of the mazes in which spatial firing patterns were analyzed.

Time cells in CA1 and CA3 are sometimes also place cells

Some neurons that were time cells on the treadmill were also place cells on the maze. To compare the proportions of cells that had fields on the maze and fields during the treadmill run, only cells that had a firing rate average of at least 0.2 Hz on both the treadmill and the maze were considered. This resulted in 155 cells [155 of 386 (40.2%)] in CA1 and 168 cells [168 of 379 (44.3%)] in CA3 that fired under both conditions. In CA3, 13 of 168 (7.7%) of these cells had both a time field when the rat ran in the treadmill and a place field when the rat traversed the maze. In comparison, in CA1, 16 of 155 (10.3%) cells had a reliable time field and place field. These proportions did not significantly differ (Fisher's exact test, p = 0.44, two-tailed), and these proportions did not differ from the expectation of random conjoint coincidence of time and place coding by the same neuron in CA1 (Fisher's exact test, p = 0.24, two-tailed) or CA3 (Fisher's exact test, p = 0.17, two-tailed). These findings are consistent with the possibility that time cells and place cells were drawn from the same population of cells with a global remapping between the treadmill run and the maze.

Time cells differ from place cells on some basic firing properties

Place cells and time cells in CA1 and CA3 were compared to explore the possibility of differences between their firing properties during the treadmill run and when traversing the maze. There were no significant differences between the peak firing rate of cells on the treadmill or maze in CA1 (treadmill, 4.20 ± 0.42 Hz; maze, 3.87 ± 0.32 Hz; two-sample t test, t₍₁₆₀₎ = 0.64, p = 0.52, Hedges g = 0.11) or CA3 (treadmill, 4.25 ± 0.32 Hz; maze, 5.12 ± 0.38 Hz; two-sample t test, t₍₁₈₃₎ = −1.57, p = 0.12, Hedges g = −0.25). Information scores of cells were not significantly different between the maze and the treadmill in both CA1 (treadmill, 2.43 ± 0.13 bits/s; maze, 2.81 ± 0.41 bits/s; two-sample t test, t₍₁₆₀₎ = −0.73, p = 0.47, Hedges g = −0.12) and CA3 (treadmill, 2.90 ± 0.15 bits/s; maze, 3.70 ± 0.41 bits/s; two-sample t test, t₍₁₈₃₎ = −1.37, p = 0.17, Hedges g = −0.21). Because the distribution of information scores on the treadmill may not be normal, we also compared the distribution of information scores on the maze and the treadmill and found that they were significantly different in CA1 (KS test, D_(61,99) = 0.32, p = 5e⁻⁰⁴) and CA3 (KS test, D_(62,122) = 0.37, p = 1e⁻⁰⁵). Finally, the widths of firing fields on the maze and treadmill were compared with each other by converting the time running on the treadmill into distance traveled on the treadmill. Field widths of cells were significantly larger on the treadmill than on the maze in both CA1 (treadmill, 87.37 ± 9.40 cm; maze, 41.39 ± 3.21 cm; two-sample t test, t₍₁₆₀₎ = 5.46, p = 2e⁻⁰⁷, Hedges g = 0.88, KS test, D_(61,99) = 0.37, p = 4e⁻⁰⁵) and CA3 (treadmill, 115.23 ± 11.56 cm; maze, 48.20 ± 3.01 cm; two-sample t test, t₍₁₈₃₎ = 7.25, p = 1e⁻¹¹, Hedges g = 1.13, KS test, D_(62,122) = 0.47, p = 1e⁻⁰⁸).

Place coding did not show a systematic decrease in resolution with distance traveled

The firing fields of place cells covered the entire maze, and the distribution of those fields was not reliably different from a uniform distribution across the maze (Fig. 3D,E; KS test, D₍₁₃₁₎ = 0.10, p = 0.12). To directly compare distributions of firing fields on the maze and the treadmill, the distance traveled during the treadmill run was considered instead of the time passed during the treadmill run. Because the distance traveled on the treadmill run was substantially longer than the length of the maze segments, the comparison was approached in three ways. First, only the firing fields on the first 160 cm traveled on the treadmill were compared with the firing fields on the same-sized maze segments between water ports on looping trials used above, and these distributions were significantly different (KS test, D_(57,116) = 0.23, p = 0.02). In case the distribution is scaled between reward events, the analysis was redone by rescaling the distance until the center of firing fields by the proportion of the run on the treadmill and maze segment, and the difference in distributions was also significant (KS test, D_(57,116) = 0.21, p = 0.004). The final possibility tested was that the boundaries of the distributions of fields on the treadmill and maze was not the water reward but the beginning and end of the treadmill run. This comparison was made between the full linearized looping maze of 330 cm, including the reward location, and the first 330 cm of the treadmill run. The maze and treadmill distributions were still significantly different (KS test, D_(110,221) = 0.21, p = 0.003).

Place field width does not vary with distance traveled on the maze

We examined whether place field width varies with distance run along segments of the maze between water ports during looping sessions. In Figure 3F, a scatter plot of place field widths and the distance from the previous water port did not reveal an obvious difference in place field size along the maze run, and this observation was confirmed in a simple linear regression (r² = 0.005, F_(1,129) = 0.67, p = 0.41). Unlike time fields during the treadmill run that grow wider with elapsed time, the width of place fields on the maze do not significantly vary with the distance traveled on the maze since the previous reward.

Place cells and time cells are equally prevalent regardless of working memory demands

Time cells were shown previously to be equally prevalent regardless of working memory load and region. Place cells in CA1 and CA3 were also active on the maze in both looping and alternation sessions (Fig. 5). Similar to the findings on time cells, working memory load did not affect the proportion of cells that were place cells [CA1: looping, 57 of 137 (41.6%); alternation, 42 of 112 (37.5%); CA3: looping, 72 of 183 (39.3%); alternation, 49 of 139 (35.3%); Fisher's exact test, p = 0.74, two-tailed]. When directly comparing the proportion of cells in CA1 and CA3 that had fields on the treadmill run in looping and alternation sessions and the proportion of cells in CA1 and CA3 that had fields on the maze in looping and alternation sessions, the proportions of place cells were all higher than the proportions of time cells, but this difference failed to reach significance (χ_7,n=1003² = 13.25, p = 0.07).

Discussion

The present findings provide evidence that CA3 neurons fire at specific, successive moments during a fixed interval, indicating that temporal coding within the hippocampus is not exclusively supported by CA1. The system of temporal processing instead mirrors spatial processing such that time and place are both robustly represented in CA3 and CA1, as well as MEC (Kraus et al., 2015). Furthermore, the firing properties of time cells in CA3 were quite similar to those in CA1, just as place cells from the two regions also were mostly similar. Notwithstanding these general similarities, the distribution of time cells and their firing field widths resulted in a temporal representation that decreased in resolution with the passage of time on the treadmill, whereas there was no analogous tendency for place cells as a function of distance along the maze.

This overrepresentation of time early in the treadmill run confirms previous reports on CA1 time cells (MacDonald et al., 2011; Kraus et al., 2013) and extends the finding to CA3 and is in stark contrast to place cells, which were evenly distributed on the maze without any bias of field width along the maze arm. This difference between temporal and spatial representation may be attributable to absence of temporal cues beyond the onset of running in contrast to the prevalence of spatial cues throughout traversal of the maze. This account is consistent with reports that, when environmental cues are reduced, spatial information in place cell activity is diminished (Wang et al., 2015). Increasing field width and decreasing representation over time is a central feature of temporal coding that enables increased efficiency when encoding in a scale invariant manner (Howard et al., 2014).

This difference in the organization of network coding of time and space is paralleled by a recent observation that, whereas hippocampal time cell representations depend on the theta rhythm, place cell representations do not (Wang et al., 2015). Thus, although time and space coding are very similar in many ways described here, the circuit mechanisms and consequent organization of network representation may be distinct and adaptive to differing demands for internal information processing in the time domain as contrasted with external information processing in the spatial domain.

The observation of time cells in both CA1 and CA3 in the absence of a working memory demand differs from a previous report that time cells are evident only when a working memory demand is imposed (Pastalkova et al., 2008). A possible explanation for the discrepancy of these results is that the control task of the previous study lacked a fixed temporal structure of events within trials. Additional work will be necessary to define exactly what task elements are necessary and sufficient to produce time cells. We speculate that these elements will be related to the regular spatiotemporal aspects of a task. On a network level, a reliable history of temporal structure might place the network into a experience-specific initial state at the outset of a delay, allowing the network thereafter to read out a reliable sequence of cells without a changing external stimulus driver of the system.

The present findings of similar time coding in CA1 and CA3 contrast with reports of differential effects of selective CA1 and CA3 damage on tasks that involve temporal processing demands (Kesner et al., 2005; Farovik et al., 2010). This discrepancy mirrors many observations on the robust appearance of place cells in both CA1 and CA3 in tasks that do not require navigation or spatial memory (e.g., random foraging for food, running in a linear track), contrary to the common finding that damage to either area impairs spatial memory. Thus, hippocampal areas may encode both the spatial and temporal organization of experiences regardless of whether these representations are required for current task performance.

Mankin et al. (2012, 2015) reported that place cell patterns in CA1 and CA2, but not CA3, evolve over periods of several hours and days and have suggested that a temporal signal for long periods might be selectively represented in the final stages of intrinsic hippocampal processing. In contrast, the current findings indicate similar temporal processing in CA1 and CA3, in addition to MEC (Kraus et al., 2015), suggesting that mechanisms for temporal organization of specific experiences and neural drift over long periods of time may involve distinct coding mechanisms.

Together, the present results are consistent with the view that the properties of time cells parallel those of place cells, such that, like spatial processing, temporal processing is prevalent throughout the hippocampus regardless of distinctions in memory demands. These observations are consistent with the view that the hippocampus performs the same computations on spatial and temporal information to construct an organization of experience, and both dimensions require only consistency of temporal and spatial input (Eichenbaum, 2014).