Stimulus Dependence of Correlated Variability across Cortical Areas

Abstract

The way that correlated trial-to-trial variability between pairs of neurons in the same brain area (termed spike count or noise correlation, r_SC) depends on stimulus or task conditions can constrain models of cortical circuits and of the computations performed by networks of neurons (Cohen and Kohn, 2011). In visual cortex, r_SC tends not to depend on stimulus properties (Kohn and Smith, 2005; Huang and Lisberger, 2009) but does depend on cognitive factors like visual attention (Cohen and Maunsell, 2009; Mitchell et al., 2009). However, neurons across visual areas respond to any visual stimulus or contribute to any perceptual decision, and the way that information from multiple areas is combined to guide perception is unknown. To gain insight into these issues, we recorded simultaneously from neurons in two areas of visual cortex (primary visual cortex, V1, and the middle temporal area, MT) while rhesus monkeys viewed different visual stimuli in different attention conditions. We found that correlations between neurons in different areas depend on stimulus and attention conditions in very different ways than do correlations within an area. Correlations across, but not within, areas depend on stimulus direction and the presence of a second stimulus, and attention has opposite effects on correlations within and across areas. This observed pattern of cross-area correlations is predicted by a normalization model where MT units sum V1 inputs that are passed through a divisive nonlinearity. Together, our results provide insight into how neurons in different areas interact and constrain models of the neural computations performed across cortical areas.

SIGNIFICANCE STATEMENT Correlations in the responses of pairs of neurons within the same cortical area have been a subject of growing interest in systems neuroscience. However, correlated variability between different cortical areas is likely just as important. We recorded simultaneously from neurons in primary visual cortex and the middle temporal area while rhesus monkeys viewed different visual stimuli in different attention conditions. We found that correlations between neurons in different areas depend on stimulus and attention conditions in very different ways than do correlations within an area. The observed pattern of cross-area correlations was predicted by a simple normalization model. Our results provide insight into how neurons in different areas interact and constrain models of the neural computations performed across cortical areas.

Introduction

The extent to which trial-to-trial variability is shared between pairs of neurons in the same cortical area (termed spike count or noise correlation, or r_SC) has been used for the past two decades to infer properties of local circuits and to understand the computations performed by groups of neurons (for review, see Cohen and Kohn, 2011). In visual cortex, the way that r_SC depends on stimulus and cognitive factors is remarkably consistent across studies, brain areas, and tasks (for review, see Cohen and Kohn, 2011). For example, spike count correlations between pairs of neurons in primary visual cortex (V1) do not depend on the orientation of the stimulus (Kohn and Smith, 2005), and correlations between pairs of neurons in the middle temporal area (MT) do not depend on the direction of the stimulus (Huang and Lisberger, 2009), even though those stimulus factors strongly affect mean firing rate. Paying attention to the joint receptive fields of neurons in the same visual cortical area has been associated with decreases in r_SC in several cortical areas and studies (Cohen and Maunsell, 2009, 2011; Mitchell et al., 2009; Zénon and Krauzlis, 2012; Herrero et al., 2013; Gregoriou et al., 2014; Ruff and Cohen, 2014a; Luo and Maunsell, 2015). An appealing hypothesis is that the consistency of the way stimulus and cognitive factors affect correlated variability in different areas could imply the existence of canonical computations performed across visual cortex (for review, see Carandini and Heeger, 2012).

However, there are both anatomical and functional reasons to think that the way correlations between pairs of neurons in different cortical areas depend on stimuli and cognitive factors might be different than for correlations between pairs of neurons in the same area. The anatomy and patterns of connectivity between neurons in different cortical areas is very different than connectivity within a cortical area (Maunsell and van Essen, 1983; Ungerleider and Desimone, 1986). These differences likely cause differences in patterns of correlations within and across cortical areas. Furthermore, sensory and cognitive processes likely involve the coordinated activity of neurons in many brain areas. For example, neurons in both V1 and MT respond to moving stimuli and are important for motion perception (Parker and Newsome, 1998; Born and Bradley, 2005). One possibility is that motion perception is based on the combined responses of all motion selective neurons, regardless of which area they come from. Alternatively, perception may involve computations that take into account the boundaries between areas (e.g., feedforward computations).

We reasoned that these possibilities might be distinguished by determining whether r_SC between pairs of neurons in different cortical areas depends on stimuli and task conditions in the same way as r_SC within the same cortical area. We recorded simultaneously from neurons in V1 and MT and found that r_SC between areas depends on many stimulus factors that do not affect correlations within an area. Combined with our finding that attention has opposite effects on correlations within and across areas (Ruff and Cohen, 2016), these findings suggest that the neural computations that give rise to perception treat neurons differently depending on which area they come from. We found that both the stimulus and attention dependence of r_SC between areas can be explained by a model of divisive normalization in which V1 provides feedforward inputs to MT that are passed through a divisive nonlinearity. Together, our results provide insight into interactions between neurons in different areas and provide a framework for using correlated variability to probe the computations performed by networks of neurons across the brain.

Materials and Methods

Electrophysiological recordings.

A subset of these data (from 2 of 10 stimulus/attention conditions, which allowed us to measure attention-related correlations between V1 and MT) are presented elsewhere (Ruff and Cohen, 2016). The subjects in this experiment were two adult male rhesus monkeys (Macaca mulatta, 8 and 9 kg). All animal procedures were approved by the Institutional Animal Care and Use Committees of the University of Pittsburgh and Carnegie Mellon University. Before behavioral training, we implanted each animal with a titanium head post. After the animal learned the task (4–5 months), we implanted a 10 × 10 microelectrode array (Blackrock Microsystems) in area V1 and a recording chamber that gave us access to area MT. The V1 array was connected to a percutaneous connector that allowed simultaneous recordings from 96 electrodes. The distance between adjacent electrodes on the array was 400 μm, and each electrode was 1 mm long. We identified area V1 using stereotactic coordinates and by visually inspecting the sulci. During each recording session, we inserted a single electrode (Fred Haer) into area MT. We identified MT using stereotactic coordinates, gray and white matter transitions, and receptive field properties.

We recorded neuronal activity from V1 and MT simultaneously during daily experimental sessions for several months in each animal. We included recording sessions for analysis when the MT unit's receptive field largely overlapped the envelope of receptive fields of the units we recorded on the V1 array (Fig. 1A) and when the animal completed at least 150 behavioral trials (mean, 648 completed trials from 32 recording sessions; 12 from Monkey 1 and 20 from Monkey 2). We optimized the direction and speed of the visual stimuli for the tuning properties of the MT unit.

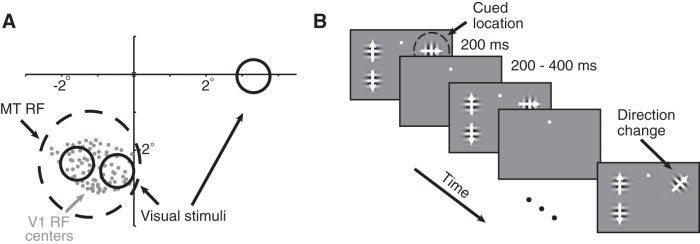
Figure 1.

Recording and psychophysical methods. A, Receptive fields from an example experimental session. We recorded simultaneously from a 96 channel chronically implanted microelectrode array in area V1 and a single electrode in area MT. We selected MT units whose receptive fields (black dashed circle) overlapped the envelope of receptive fields of the units we recorded in V1 (centers denoted by the gray dots). The locations and approximate sizes of the three visual stimuli are denoted by the solid black circles. Spatial receptive fields were estimated by rapidly presenting a single, small Gabor patch at a range of locations while the monkey fixated. B, Schematic of the motion direction change detection task. Once the monkey fixated a central spot, either two or three small Gabor stimuli synchronously flashed on for 200 ms and off for a randomized 200–400 ms period. Two of the stimuli were positioned inside the joint receptive fields of the V1 and MT neurons we recorded, and the third, when present, was placed in the opposite hemifield. After an unsignaled and randomized number of stimulus presentations (picked from an exponential distribution; minimum, 2 stimulus presentations; mean, 6 stimulus presentations; maximum, 14 stimulus presentations), the direction of one of the stimuli changed. The monkeys were cued in blocks of 50–100 trials to detect changes in (and therefore attend to) one of the stimuli and ignore motion direction changes in the other stimulus. The monkeys were rewarded for making a saccade to the attended stimulus within 500 ms of the stimulus change. Responses to distractor changes were never rewarded. The two stimuli within the receptive field moved in opposite directions (the preferred and null directions of the MT cell under study), and which of the two stimuli moved in the preferred direction varied randomly from trial to trial. The stimulus in the opposite hemifield moved in a direction that was orthogonal to the MT neuron's preferred direction. We assessed the stimulus dependence of r_SC on trials in which attention was directed to the stimulus in the opposite hemifield as the receptive fields of the neurons we recorded (for the stimulus conditions we recorded, see Fig. 3), and we assessed attention by comparing r_SC on blocks of trials when attention was directed to one of the two stimuli within the MT neuron's receptive fields.

To measure correlations between pairs of MT units (as in Fig. 2), in a subset of experiments, we recorded using a movable 24 channel probe (Alpha Omega or Plexon). This data set consisted of a total of 652 MT units recorded during 32 recording sessions (mean, 20.4 units per recording session). These data were not included in the normalization model (see below, Normalization model of MT responses) because we did not record V1 activity simultaneously.

Figure 2.

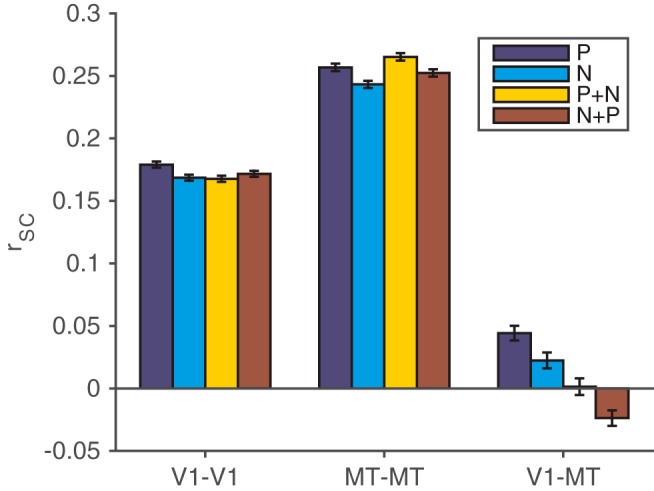
Spike count correlations between pairs of units in different, but not the same, cortical areas depend on the visual stimulus. We compared r_SC between units with similar direction tuning in four stimulus conditions: a single stimulus moving in the preferred direction (dark blue bars), a single stimulus moving in the null or antipreferred direction (light blue bars), a preferred stimulus in the V1 unit's receptive field combined with a null stimulus outside the V1 unit's receptive field (but still inside the MT neuron's receptive field; yellow bars), and a null stimulus in the V1 unit's receptive field combined with a preferred stimulus outside the V1 unit's receptive field (red bars). Spike count correlations did not substantially depend on the visual stimulus for pairs of V1 units (left bars) or pairs of MT units (middle bars), but they did depend on the stimulus for pairs of V1 and MT units (right bars; t tests on rate-matched distributions, p < 0.05; for detailed statistics, see Data analysis). Error bars represent SEM.

Visual stimuli and behavior.

We presented visual stimuli using custom software (written in Matlab using the Psychophysics Toolbox; Brainard, 1997; Pelli, 1997) on a CRT monitor (calibrated to linearize intensity; 1024 × 768 pixels; 120 Hz refresh rate) placed 57 cm from the animal. We monitored eye position using an infrared eye tracker (Eyelink 1000, SR Research) and recorded eye position and pupil diameter (1000 samples/s), neuronal responses (30,000 samples/s), and the signal from a photodiode to align neuronal responses to stimulus presentation times (30,000 samples/s) using hardware from Ripple.

The monkeys performed a motion direction change detection task (Fig. 1B). A trial began when the monkey fixated a small spot within a 1° square fixation window in the center of the video display. Monkeys typically maintained fixation within a much smaller window than was allotted (the median SD of eye position during analyzed stimulus presentations was 0.18°). Stimulus presentations when we detected a microsaccade were excluded from our analyses (see below, Data analysis). The visual stimuli were achromatic Gabor patches whose size and location were picked so that two stimuli lay within the receptive field of a single MT unit under study (Fig. 1A). These two stimuli were approximately equidistant from the fixation spot (their distances from the fixation never differed by >0.3°). The stimuli were centered ∼2.5–3.5° eccentric (median, 2.9°), and each stimulus typically subtended <1° of visual angle. The visual stimuli flashed on for 200 ms and off for an interval that was randomly selected from a uniform distribution whose range was 200–400 ms. The stimuli drifted at the same speed, which was selected from a range between 6 and 12° per second (picked to elicit large responses in the MT unit). The two stimuli within the receptive field of the MT unit moved in opposite directions (the preferred and null directions of the MT cell under study), and which of the two stimuli moved in the preferred direction varied randomly from trial to trial.

During blocks of trials when the animal was cued to attend to one of the two stimuli in the MT receptive field, both stimuli presented at either 8% contrast or 100% contrast, and their contrast was randomly interleaved on each stimulus presentation. In separate blocks of trials, the animal was instructed to direct its attention to a third stimulus in the opposite hemifield (“attend opposite” blocks; see Fig. 1B). In these blocks of trials, the two stimuli in the MT receptive field were independently presented at 0, 50, or 100% contrast. The third, attended stimulus was presented at either 8 or 100% contrast, with its contrast randomly interleaved on each stimulus presentation and independently selected from the contrasts of the stimuli in the MT receptive field. When the third stimulus was present, it moved in an orthogonal direction to those in the opposite hemifield.

After an unsignaled number of stimulus presentations picked from an exponential distribution (minimum, 2 stimulus presentations; mean, 6 stimuli; maximum 14 stimuli), the direction of one of the stimuli changed. During each experimental session, we selected a single magnitude of the direction change designed to get the animal to perform near psychophysical threshold (range, 10–45°). The probability of direction change was independent at each location (the unattended stimuli each changed on ∼12% of trials). Before the start of each block of trials, the monkey performed 5–10 instruction trials (which were not included in any of the analyses) in which there was only a single stimulus. The location of this stimulus constituted a cue as to the attended location. In the upcoming block of trials, if the attended stimulus was the one that changed, the monkey was given a liquid reward for making a saccade to that stimulus within 500 ms of the change. To account for saccadic latency and to avoid rewarding the monkey for guessing, the monkey was rewarded only for saccades beginning at least 100 ms after the change. If no saccade occurred within 500 ms of the direction change at the cued location, the trial was classified as a miss and terminated with no reward. If no change occurred within the maximum 14 stimulus presentations, the monkey was rewarded simply for maintaining fixation. Attention was cued to one of the three stimulus locations in blocks of 50–100 trials. The monkey was never rewarded for making a saccade to distractor changes.

Overall, the monkeys correctly detected the stimulus changes on 66% of completed trials during the 32 experimental sessions where we collected neuronal data from both V1 and MT. When alternating attention between two stimuli placed within the receptive field of the MT unit, the monkeys detected 90% of the full-contrast direction changes and 42% of the low-contrast direction changes that occurred at the attended location. The monkeys responded to 21% of the unattended orientation changes, but were not rewarded for these responses. During blocks of trials when the animals were instructed to direct attention to the hemifield opposite the joint receptive fields of the V1 and MT units (“attend away” conditions, which were much easier for the animals since the distractors were far away from the attended stimuli), they detected direction changes at full contrast 99% of the time and responded to direction changes at the unattended location 5% of the time.

We fit our model to each MT unit's responses to preferred and null stimuli separately (see Normalization model of MT responses). We therefore treated each stimulus configuration (e.g., preferred stimulus at Location 1 and null at Location 2, or the opposite) separately. Our data set therefore consisted of 64 MT units/conditions (32 units recorded in separate sessions, each with two different stimulus configurations). None of our results failed to reach significance, and none of our conclusions differed if we restricted analysis to one stimulus configuration per unit. We felt it was most conservative to consider both stimulus configurations to account for differences in the location of each stimulus within the MT unit's receptive field or the number of V1 units whose receptive field overlapped each stimulus.

We included a V1 unit for analysis and assigned it to a “pool” if it responded significantly more to a full-contrast stimulus at one location than the other, collapsed across the two directions of motion (t test, p < 0.01). Across the 64 recording sessions/stimulus configurations, 3262 V1 units satisfied this criterion (1631 unique units). The mean number of V1 units per pool from each recording session was 25.

Data analysis.

All spike sorting was done off-line manually using Offline Sorter (version 3.3.2, Plexon). We based our analyses on both single units and multiunit clusters and use the term unit to refer to either. Using chronically implanted microarrays (as we used for our V1 recordings), it is nearly impossible to tell whether we recorded from the same single or multiunit clusters on subsequent days. However, the MT units were recorded on different electrodes each day, so each MT unit or V1–MT pair was unique.

Our analyses of neuronal data are based on spike counts from 30 to 230 ms after stimulus onset for V1 and 50 to 250 ms after stimulus onset for MT to account for the visual latencies of neurons in both areas. Using identical windows for both areas led to qualitatively similar results to those presented here.

We computed spike count correlations (r_SC) between pairs of units (Fig. 2) or between the averaged activity of pools of V1 units and the MT unit (see Fig. 4) using a standard Pearson's correlation coefficient. Because this measure is sensitive to outliers, we excluded stimulus presentations on which either unit (or group of units) in the pair responded more than three SDs differently than its mean (according to the convention in the study by Kohn and Smith, 2005). Stimulus presentations where a microsaccade was detected anywhere between 10 ms before until 10 ms after the stimulus was shown were excluded from analysis. We identified microsaccades using a velocity detection algorithm (Engbert and Kliegl, 2003). The activity of pools of V1 units (used to calculate correlations in Fig. 4 and as inputs to the model in Figs. 3–5) was defined as the average response of all V1 units that responded significantly more to a full-contrast stimulus presented alone at one of the two locations inside the receptive field of the MT unit than the other (t test, p < 0.01).

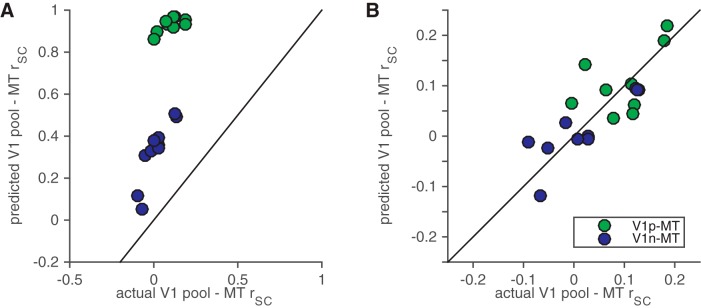
Figure 4.

The modified normalization model accounts for much of the stimulus and attention dependence of V1–MT correlations. A, Predicted versus actual correlations between the MT unit and the pool of V1 units whose receptive fields overlapped the stimulus moving in the MT unit's preferred direction (green) or the stimulus moving in the MT unit's null direction (blue). B, The same model but with independent noise added to match the average correlation across all conditions.

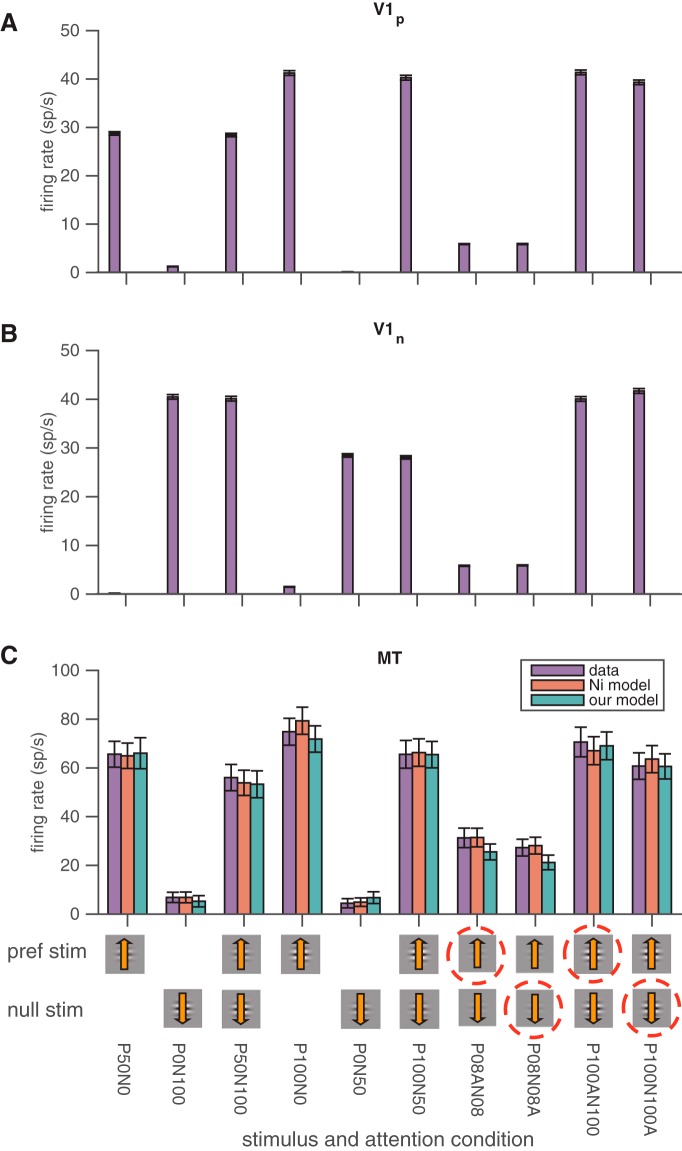
Figure 3.

Actual and modeled trial-averaged responses to different stimulus and attention conditions. A, Average firing rates of V1 units whose receptive fields overlap the stimulus moving in the MT unit's preferred direction. The icons on the x-axis represent the contrasts of the stimulus moving in the MT unit's preferred direction (top row) and null direction (bottom row). The dashed red circle represents the cued attention location. For the conditions where no dashed red circle is present, the monkey was cued to attend to the third stimulus in the hemifield opposite the MT unit's receptive field. The shorthand below the icons states the exact contrast and attention conditions (e.g., P100AN100 means 100% contrast stimuli in both the preferred and null directions with attention directed toward the stimulus moving in the MT unit's preferred direction). Error bars represent SEM. B, The same model for V1 units whose receptive fields overlap the stimulus moving in the MT unit's null direction. C, Both normalization models account well for the trial-averaged responses of MT units in different stimulus and attention conditions. The different colored bars depict the actual responses of the MT units (purple) and the predicted responses of the normalization model by Ni et al. (2012) (red) and of our modified normalization model (green) in a variety of stimulus and attention conditions. None of the model fits were significantly different from the actual responses or from each other (t tests, p > 0.05). Other conventions are as in A and B.

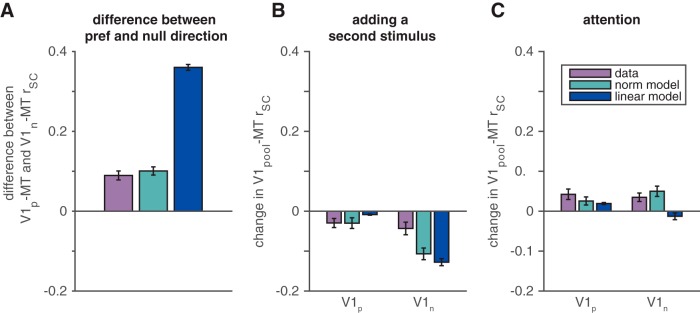
Figure 5.

The modified normalization model accounts better for the stimulus and attention dependence of V1–MT r_SC than a linear model. A, V1–MT r_SC depends on the motion direction of the stimulus. Shown are observed (purple) and predicted (green and blue for the normalization and linear models, respectively) differences between V1–MT correlations for the pool of V1 units whose receptive fields overlap the stimulus moving in the MT unit's preferred direction (V1_p) and the pool of V1 units whose receptive fields overlap the stimulus moving in the MT unit's null direction (V1_n). Error bars represent SEM. B, V1–MT r_SC depends on the presence of a second stimulus. Shown are observed and predicted changes in correlation when a second stimulus is added outside the V1 unit's receptive field and inside the MT unit's receptive field for the V1 pool whose receptive fields overlapped the preferred (left bars) and null stimuli (right bars). We compared V1–MT correlations in response to a full-contrast stimulus alone with correlations in response to that stimulus paired with a 50% contrast stimulus moving in the opposite direction. Conventions are as in A. C, V1–MT r_SC depends on attention. We compared correlations in responses to pairs of full-contrast stimuli when the monkey attended into and out of the V1 units' receptive fields. Conventions are as in A and B.

The distribution matching procedure to control for mean firing rate in our analysis of spike count correlations was described in detail previously (Churchland et al., 2010; Ruff and Cohen, 2014b). Briefly, the goal of this analysis was to have the same distribution of geometric mean firing rates (but not covariances) in each of the stimulus or task conditions being compared, so we used a different subdistribution of unit pairs in each stimulus and attention condition. We compare distributions of geometric mean firing rates in each stimulus or task condition and select the greatest common distribution. We then subsample our pairs of units in each condition to match that distribution and analyze spike count correlations for those subdistributions. We repeat the resampling process 1000 times and report average r_SC values from these resampled distributions and do statistics on the median resampled distribution.

Normalization model of MT responses.

To determine whether a simple neural computation could account for the stimulus and task dependence that we observed in V1–MT r_SC, we adapted a normalization model of attention that was used previously to describe the average responses of MT neurons in a variety of stimulus and attention conditions (Ni et al., 2012). This class of models provides the best known description of the trial-averaged responses of sensory neurons in different stimulus and task conditions (Boynton, 2009; Lee and Maunsell, 2009; Reynolds and Heeger, 2009; Carandini and Heeger, 2012; Sanayei et al., 2015), so we reasoned that it would be a good place to start looking for a description of the computations underlying the stimulus and task dependence of cross-area r_SC. We picked the Ni et al. (2012) model as a starting point for our efforts because it was designed for a similar experiment as ours and because it includes only five free parameters.

In the instantiation of the model in the Ni et al. (2012) paper (which is very similar to other normalization models; Boynton, 2009; Lee and Maunsell, 2009; Reynolds and Heeger, 2009; Carandini and Heeger, 2012; Ni et al., 2012; Sanayei et al., 2015), the mean response of an MT cell to a combination of stimuli moving in the MT neuron's preferred (P) and null (N) directions is given by the following:

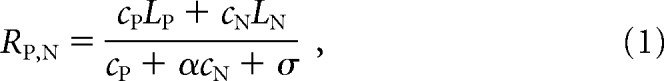where R_P,N is the mean response of the MT neuron; c_P and c_N are the contrasts of the preferred and null stimuli, respectively; L_P and L_N represent the responses of the neuron's linear receptive field to a full-contrast stimulus moving in the preferred and null directions, respectively; and σ is a semisaturation constant. The numerator of Equation 1 therefore represents the linear response of the neuron, and the neuron's preference for the preferred direction of motion over the null direction is determined by L_P and L_N. The denominator, which represents divisive normalization, depends only on the contrasts of the stimuli and on the tuned normalization parameter α. The parameter α captures the observation that MT neurons vary in the extent to which they exhibition normalization.

Attention is instantiated in the model using the scaling parameter β, such that the response of the MT neuron is given by

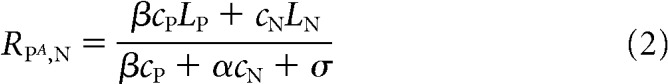when attention is directed to the stimulus moving in the MT neuron's preferred direction, and by

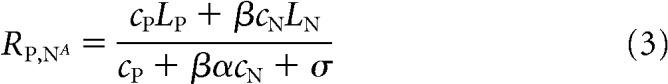when attention is directed to the stimulus moving in the null direction. In this model, attention acts to scale both the sensory evidence (numerators in Eqs. 2 and 3) and the relevant normalization terms (denominators in Eqs. 2 and 3). Together, Equations 1–3 have five free parameters (L_P, L_N, α, β, and σ), which are fit to the average responses of the MT neuron in different stimulus and attention conditions.

We hypothesized that the tuned component of the MT neuron's response might come from its V1 inputs. We therefore replaced the terms related to the MT neuron's tuning in Equations 1–3 (c_PL_P and c_NL_N) with the average firing rates of the V1 neurons whose receptive fields overlap the preferred and null stimuli. In our model, Equations 1–3 are replaced by the following:

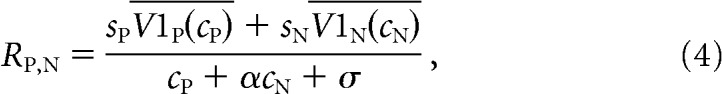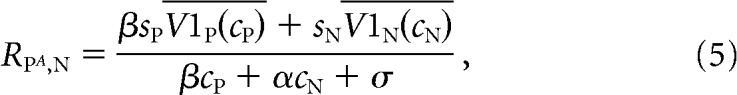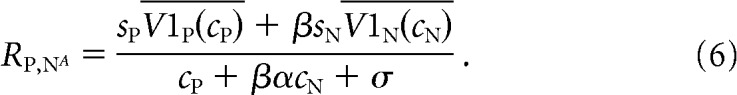In this model, V1_P(c_P) and V1_N(c_N) represent the trial-averaged (measured) responses of the pools of V1 neurons whose receptive fields overlap the preferred or null stimuli, respectively, whose contrast is given by c_P or c_N. The parameters s_P and s_N are scaling parameters that reflect the direction tuning of the MT neuron. Like the original model, this modified model has five free parameters (s_P, s_N, α, β, and σ).

In this model, the mean V1 responses we recorded replace the contrast-dependent terms in the numerator of Equations 1–3, and the scaling parameters s_P and s_N account for the MT neuron's direction selectivity. This model is not a mechanistic description of how direction tuning arises in MT (in which feedforward inputs from V1 might be themselves direction selective; Movshon and Newsome, 1996). Instead, our logic relies on the observation that the responses of V1 neurons are, on average, correlated with a wide range of other V1 neurons (Smith and Kohn, 2008). Therefore, the responses of the V1 units we recorded are likely correlated with the responses of the V1 neurons that provide direct inputs to MT.

We fit our modified model to the trial-averaged responses of the MT unit in the 10 stimulus and attention conditions using the measured trial-averaged responses of the V1 units whose receptive fields overlapped each stimulus (Fig. 3). We then predicted the response of the MT unit on each trial using the fitted model parameters and the actual responses of the V1 units recorded on that trial. We used the predicted MT responses to calculate predicted spike count correlations between the modeled MT unit and the recorded V1 units (Fig. 4).

Results

Spike count correlations between, but not within, cortical areas depend on visual stimuli

One of our primary goals was to compare the dependence of r_SC between pairs of neurons in the same or different cortical areas on the visual stimulus. Consistent with previous results (Kohn and Smith, 2005; Huang and Lisberger, 2009), we found that correlations between pairs of units in the same area did not depend strongly on the direction the stimulus was moving. Figure 2 shows correlations between pairs of V1 units (left) and pairs of MT units (middle) that responded more strongly to the same one of the two motion directions presented (t test, p < 0.05) and, in the case of V1, were in the same spatial pool (see Materials and Methods). These correlations are based on stimulus presentations when the animal's attention was directed to a stimulus in the opposite hemifield as the receptive fields of the recorded units (the “attend opposite” condition; see Materials and Methods). Overall, correlations were very slightly higher when the single stimulus in the joint receptive field moved in the units' preferred direction than when it moved in the null direction (t test, p < 10⁻⁴ for V1 and p < 10⁻³ for MT). However, correlations are known to covary with firing rate (Cohen and Kohn, 2011), and the difference in r_SC between preferred and null stimuli was not significant for MT (t test, p = 0.12) and only barely significant for V1 (t test, p = 0.04) when we considered distributions of pairs for which the distributions of firing rates was matched for preferred and null stimuli (see Materials and Methods). Similarly, adding a second stimulus outside the receptive fields of the V1 units and within the receptive fields of the MT units had little effect on r_SC between pairs of units in the same area (t tests, p values for rate matched pairs were >0.05 for all comparisons).

However, correlations between pairs of units in different areas depended strongly on the direction of the stimulus and on the presence of a second stimulus (Fig. 2, right). Correlations between V1 and MT were greater when a stimulus moved in the MT neuron's preferred direction compared to its null direction (t test, p < 10⁻³ for rate-matched pairs) and were lower for pairs of stimuli than for either stimulus alone (t tests, p < 10⁻³ for rate matched pairs). The reduction in cross-area correlation for pairs of stimuli was not simply because the second stimulus was nonpreferred; V1–MT r_SC was lower when a preferred stimulus was added to a null stimulus than for the null stimulus alone (t test, p < 10⁻³ for rate matched pairs; compare the turquoise and red bars on the right side of Fig. 2). Therefore, two different stimulus manipulations (changing the motion direction and adding a second stimulus), which both have substantial effects on the mean firing rates of V1 and MT units, have substantial effects on cross-area, but not within-area, spike count correlations.

Attention has opposite effects on spike count correlations between pairs of neurons in the same or in different cortical areas

We also compared the dependence of within- versus cross-area correlations on a factor that is associated with changes in r_SC within a cortical area: visual attention. In the same animals and in the same recording sessions as in Figure 2, we measured the effects of switching attention between two stimuli within the MT unit's receptive field (Fig. 1; Materials and Methods) on V1–V1 and V1–MT correlations. These two stimuli always moved in opposite directions (the preferred and null directions of the MT cell under study) and were either both 8% contrast or both 100% contrast, and contrast was randomly interleaved on each stimulus presentation. On these trials, there was no third stimulus in the opposite hemifield.

Consistent with previous results, we found that attention affected the responses of V1 and MT units in several ways. Attention was associated with increases in the rates (Maunsell and Cook, 2002; Yantis and Serences, 2003; Reynolds and Chelazzi, 2004) of units in both areas (Fig. 3) and with decreases in spike count correlations (Cohen and Maunsell, 2009, 2011; Mitchell et al., 2009; Zénon and Krauzlis, 2012; Herrero et al., 2013; Gregoriou et al., 2014; Ruff and Cohen, 2014a; Luo and Maunsell, 2015) between pairs of V1 units (pairwise attention-related V1 correlation decrease, 0.008; Wilcoxon rank sum test, p = 4.9 × 10⁻⁶; Ruff and Cohen, 2016) as well as between pairs of MT units (pairwise attention-related MT correlation decrease, 0.019; Wilcoxon rank sum test, p = 0.017; Ruff and Cohen, 2016). Importantly, attention was also associated with the opposite pattern of changes in cross-area correlations: shifting attention toward the joint receptive fields of a pair of V1 and MT neurons increased, rather than decreased, their spike count correlation (pairwise attention-related V1–MT correlation increase, 0.018; Wilcoxon rank sum test, p = 1.4 × 10⁻⁴; Ruff and Cohen, 2016; these data are shown in Fig. 5C averaged within simultaneously recorded groups, see Normalization accounts for the stimulus and attention dependence of V1–MT correlations).

Together, our results show that spike count correlations between pairs of units in different cortical areas depend very differently on stimulus and task conditions. The two stimulus manipulations we tried (changing the direction of the stimulus, which is thought to affect feedforward inputs to neurons in visual cortex, or adding a second stimulus, which is thought to invoke divisive normalization; Carandini and Heeger, 2012) had no effect on correlations between pairs of units in the same areas, but were associated with changes in V1–MT correlations. In contrast, attention affected both within- and cross-area correlations, but in opposite ways.

A modified normalization model explains the average responses of MT neurons in different stimulus and attention conditions

We wondered whether the stimulus and task dependence of cross-area correlations could provide insight into the neuronal computations that occur between different levels of processing. The simplest prevailing hypothesis concerning the relationship between V1 and MT responses is that the activity of MT neurons reflect summed inputs from V1 that have been passed through a divisive nonlinearity (Carandini and Heeger, 1994; Rust et al., 2006). A simple model of divisive normalization has become the premiere framework for understanding the trial-averaged responses of neurons in many sensory, cognitive, and motor systems (Carandini and Heeger, 2012) and for relating MT responses to stimulus and attention properties in particular (Lee and Maunsell, 2009; Reynolds and Heeger, 2009; Ni et al., 2012).

To determine whether the same simple computation could account for the stimulus and attention dependence of cross-area correlations, we adapted a standard normalization model of attention (Ni et al., 2012) to include trial-to-trial variability (for details of how our model relates to the previously published model, see Materials and Methods). Our logic was to substitute the trial-averaged responses of V1 units for the stimulus parameters in the published model, fit the free parameters in the model to the trial-averaged responses of V1 and MT units, and determine whether the resulting function captured the stimulus and attention dependence of V1–MT r_SC that we observed (Fig. 2).

Because our normalization model predicts MT responses as a function of the average rate of a pool of V1 units, we first calculated the average activity of an MT unit and the pools of V1 units we recorded (for details of pool assignment, see Materials and Methods) in each of the 10 stimulus and attention conditions in our task (Fig. 3). As expected, firing rates were affected by attention, the presence of a second stimulus, and the contrasts and motion directions of the stimuli.

Standard normalization models explain the trial-averaged responses of MT responses as a function of the response of the linear receptive field to preferred and null stimuli (which accounts for direction tuning; the numerators in Eqs. 1–3), tuned normalization (which accounts for nonlinearities in the responses to combinations of stimuli, which differ from neuron to neuron; the denominators in Eqs. 1–3), and weighting by attention (the parameter β in Eqs. 1–3). To determine whether the normalization model could account for shared trial-to-trial variability between V1 and MT, we substituted the responses of the pools of V1 units whose receptive fields overlapped the stimulus moving in the MT unit's preferred or null direction for the responses of the linear receptive field (Eqs. 4–6).

Like the original normalization model, our modified normalization model did a good job capturing the trial-averaged responses of MT units across the 10 stimulus and attention conditions in our study (Fig. 3C; note that both models have five free parameters). Across the 64 MT units/stimulus configurations in our study, the original model (Eqs. 1–3) captured, on average, 95% of the variance in the trial-averaged responses of the MT units, and our modified model captured 92% of the variance. The difference between the variance accounted for by the two models was small but significant (mean difference, 3%; paired t test, p = 0.015). The saturating nonlinearity in the contrast response functions of the V1 units likely accounts for most of the difference between the two models. Even so, the modified model accounts for a large proportion of the variance, and basing its predictions on the responses of V1 units allows us to test whether it can also account for shared trial-to-trial variability.

The modified normalization model explains shared variability between V1 and MT

After we fitted the model using the trial-averaged responses of the V1 and MT units we recorded, we predicted the response of the MT unit on each trial using the fitted model parameters and the actual responses of the V1 units recorded on that trial. On each trial, we therefore recorded three responses (the response of the MT unit and the average responses of both of the pools of V1 units whose receptive fields respectively overlapped the stimuli moving in the MT unit's preferred and null directions), and we used the model to predict the MT unit's response. We used these data and predictions to calculate four correlation coefficients for each stimulus and attention condition: between the actual and modeled MT units and the pools of V1 units whose receptive fields overlapped the preferred and null stimuli, respectively.

Our modified normalization model accounts well for many aspects of the V1–MT correlations we measured. The green and blue points in Figure 4A depict the predicted and measured correlations between MT and the pool of V1 units whose receptive fields overlapped the stimulus moving in the MT unit's preferred or null direction, respectively. Each point represents the average predicted and the average measured correlation for one of the 10 stimulus/attention conditions in our task (Fig. 3). The model accounts for 49% of the variance in the mean correlations between the MT cell and the V1 pool whose receptive fields overlap the stimulus moving in the MT unit's preferred direction across different stimulus and attention conditions and 81% of the variance in the mean correlations between the MT cell and the V1 pool whose receptive fields overlap the stimulus moving in the MT unit's null direction. Another strategy would have been to use the fitted parameters from the model by Ni et al. (2012) and substitute, after fitting, scaled versions of the contrast responses curves of the V1 pools for the linear functions of contrast in the numerators of Equations 1–3. This version of the model accounts for 44% of the variance in the mean correlations between the MT cell and the V1 pool whose receptive fields overlap the stimulus moving in the MT unit's preferred direction across different stimulus and attention conditions and 78% of the variance in the mean correlations between the MT cell and the V1 pool whose receptive fields overlap the stimulus moving in the MT unit's preferred direction. This performance is similar but slightly worse than the model we used (t tests, p < 0.05 for both the preferred and null pools), perhaps because fitting the parameters to the V1 responses allows the fits to partially compensate for nonlinearities in the V1 contrast response functions.

The models' poorer performance predicting correlations between MT and the pool of V1 units whose receptive fields overlap the preferred stimulus is likely caused by a saturation in the predicted correlations (many of the predicted correlations in Fig. 4A were near 1). Considering that the model was fit only to average firing rates (and therefore did not take any aspect of trial-to-trial variability into account), the model captures an impressive amount of the available stimulus and attention dependence of V1–MT correlations.

Although the normalization model captures much of the way that V1–MT correlations vary depending on the visual stimuli or the attention condition, the absolute magnitude of the model's predicted and actual correlations is notably different. In our model, the only source of trial-to-trial variability in MT responses comes from V1. Because the V1 inputs to the model represent averages of dozens of units, the predicted variability is low. The total amount of predicted trial-to-trial variability in our modeled neurons is much less than in the MT units we recorded (quantified using the Fano factor, which is the ratio of variance to mean responses, 0.59 for modeled units and 1.41 for recorded MT units, which are significantly different, paired t tests, p < 10⁻¹⁰), and all of that variability comes from V1. If (as is almost certainly the case) the MT units have trial-to-trial response variability from any source besides the V1 units we happened to record, the predicted correlations will always be higher than the actual ones.

Consistent with this idea, we found that adding independent, zero-mean Gaussian noise to the responses of the MT unit made it possible for the model to quantitatively match V1–MT correlations. For each recording session, we added enough independent noise to match the average V1–MT correlation across all stimulus and task conditions. Figure 4B depicts the results of this exercise. The average magnitude of the predicted and actual correlations (across all of the points along x- and y-axes in Fig. 4B) was therefore by definition equal, but the condition-by-condition correlation between the predicted and actual correlations was not trivial. Similar to the noise-free version of the model, this version of the model accounts for 51% of the variance in the mean correlations between the MT cell and the V1 pool whose receptive fields overlap the stimulus moving in the MT unit's preferred direction across different stimulus and attention conditions and 82% of the variance in the mean correlations between the MT cell and the V1 pool whose receptive fields overlap the stimulus moving in the MT unit's null direction.

Although the modified model in Figure 4B accounts well for the stimulus and attention dependence of V1–MT correlations, we had to add too much noise to quantitatively match the observed correlations. The average Fano factor of the modeled MT units was 106, which is much larger than for the recorded MT units (which was 1.41). Therefore, the existence of independent noise is not a satisfactory explanation for why our normalization model predicted much higher than observed V1–MT correlations. Adding independent noise did not affect the extent to which the model captured stimulus and attention dependence of V1–MT correlations, so this dependence must arise from the covariance, rather than from the variance of the responses of the units we recorded. Consistent with this idea, we found that in the empirical data, the mean V1–MT covariance and r_SC in each condition were highly correlated (r = 0.95 for interactions between the MT unit and the V1 and the V1 pool whose receptive fields overlap the stimulus moving in the MT unit's preferred direction, r = 0.96 for interactions between the MT cell and the V1 pool whose receptive fields overlap the stimulus moving in the MT unit's null direction).

Together, these results suggest that normalization provides a good account of the stimulus and attention dependence of r_SC by affecting the covariance of V1 and MT units, but that the variance of cortical neurons is affected by some mechanism other than simple summation of feedforward inputs that go through a divisive nonlinearity combined with independent noise. An attractive possibility is the cancellation of correlated inputs in a balanced inhibitory–excitatory network (van Vreeswijk and Sompolinsky, 1996; Amit and Brunel, 1997; Renart et al., 2010). Because our model is descriptive rather than mechanistic, we are unable to test this idea in the current framework.

Normalization accounts for the stimulus and attention dependence of V1–MT correlations

Even when overestimating the magnitude of V1–MT correlations, our normalization model (Fig. 4A) accounts for many of the ways that sensory and cognitive factors influenced our measured V1–MT correlations. For example, it correctly predicts that correlations would be higher between the MT unit and the V1 units whose receptive fields overlap the stimulus moving in the MT unit's preferred direction than with V1 units whose receptive fields overlap the null stimulus (Fig. 5A, compare green, purple bars). This observation is contrary to observed correlations between pairs of units in the same cortical area, which were indistinguishable for preferred and null stimuli (Fig. 2). In the model, this stimulus dependence comes about because of the parameter s_P > s_N in Eqs. 4–6. This relationship leads to the direction tuning of the MT unit (greater responses to preferred than null stimuli) and also means that the responses of V1 units whose receptive fields overlap the preferred stimulus have a greater effect on the predicted MT responses than the responses of the V1 units whose receptive fields overlap the null stimulus.

The model also correctly predicts that correlations between V1 and MT will be lower when there are two stimuli within the MT unit's receptive field than when there is only one (Fig. 5B, compare green, purple bars). The model also predicts that this effect will be smaller for V1 units whose receptive fields overlap the preferred stimulus than those whose receptive fields overlap the null stimulus. When there is only one stimulus, the units whose receptive fields overlap the location where there is no stimulus fire at a very low rate, so the MT units' variability is almost entirely inherited from the V1 units whose receptive fields overlap the stimulus that is present. The asymmetry in this effect on V1 units whose receptive fields overlap the preferred and null stimuli comes again from the asymmetry in the parameters s_P and s_N in Eqs. 4–6. Adding a more highly weighted preferred stimulus has a greater effect on the predicted MT response than adding a null stimulus.

Although there is a hint of asymmetry in the effects of adding a preferred or null stimulus in our data, the model predicts a greater asymmetry than we observed. One possibility is that tuned normalization (which does not affect the predicted V1–MT correlations in our model because it occurs in the denominator of Eqs. 4–6, which does not have trial-to-trial variability) corrects for the preferred-null asymmetry to a certain extent. Consistent with this idea, the units that exhibit a greater degree of tuned normalization (higher α in Eqs. 4–6) tended to have a greater difference between the predicted and observed asymmetry (correlation between α and the difference between the two purple bars and the two green bars in Fig. 5B of 0.20, which is significantly greater than 0, p < 0.05).

Finally, the model correctly predicts that attention should increase V1–MT correlations (Fig. 5C, compare green, purple bars). The predicted and actual attention-related increases in V1–MT correlations were statistically indistinguishable (t tests, p = 0.80 for V1_P–MT correlations, p = 0.84 for V1_N–MT correlations). In the model, attention-related changes in V1–MT correlations can be accounted for either by changes to the activity of V1 inputs or by changes in the effective weighting of V1 inputs (the parameter β in Eqs. 4–6).

A linear model fails to account for the effects of stimulus direction, adding a second stimulus, or attention on V1–MT correlations

We focused on a normalization model because normalization has become an accepted framework for explaining the trial-averaged responses of neurons in a wide range of systems and conditions (Carandini and Heeger, 2012). However, it remains possible that a simpler model would also account for the stimulus and attention dependence of V1–MT correlations.

To investigate this possibility, we constructed a linear model of MT responses. This model is identical to our normalization model without the normalization step. Therefore, the mean response of an MT cell to a combination of stimuli moving in the MT neuron's preferred or null direction is given by the following:

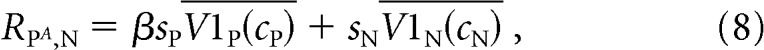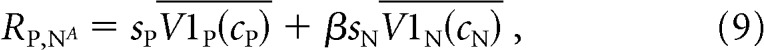where the conventions in Equations 7–9 are identical to those in Equations 4–6.

Overall, this model captures the majority of the variance in mean MT responses (85% of the variance compared with 92% in the normalization model). It did substantially worse, however, at capturing the stimulus and attention dependence of V1–MT correlations (Fig. 5, blue bars). The linear model substantially overpredicts the difference in correlation in response to stimuli in the MT neuron's preferred versus null directions (which is larger than the actual difference in the data and the difference predicted by the normalization model; t tests, p < 0.05; Fig. 5A, blue bar). This difference causes the linear model to predict an even larger asymmetry in the effect of adding a second stimulus in the preferred versus null direction than the normalization model, which already overestimates this asymmetry (predicted difference between the linear and normalization models is >0, t test, p < 0.05; Fig. 5B). Furthermore, the linear model predicts that the sign of the attention-related change in correlation depends on the direction of the stimulus (Fig. 5C, compare blue bars, left, right), whereas the observed attention-related correlation change did not depend on the direction of the stimulus (t test, p > 0.05).

These failures can be explained by differences in the fitted parameters in the linear and normalization models. The normalization model has three tuned parameters (s_P, s_N, and α), whereas the linear model has only two (s_P and s_N). Therefore, the ratio of s_P to s_N is the only source of tuning in the linear model. Unsurprisingly, the ratio of the fitted values of s_P and s_N are larger in the linear model than in the normalization model (mean ratio of s_P to s_N is 7.56 in the linear model and 2.97 in the normalization model). This large ratio accounts for the larger than observed stimulus dependence in the linear model. Because attention is instantiated in the linear model only by weighting the tuned terms, the large ratio also accounts for the incorrect prediction of the linear model that the sign of the attention-related change in correlation depends on the direction of the stimulus.

Overall, the failure of the linear model to account for the stimulus and attention dependence of V1–MT correlations suggests that a nonlinearity such as divisive normalization is necessary to describe the pattern of correlation changes we observed.

Discussion

Using shared variability to understand neuronal computations

We show here that correlations between pairs of units within the same and different cortical areas depend on visual stimuli and task conditions in qualitatively different ways. We used a modified normalization model to show that the stimulus and attention dependence of cross-area correlations could be accounted for by a scenario in which MT responses are described as a weighted sum of V1 responses that have been passed through a divisive nonlinearity. Critically, we fit the model only to the trial-averaged responses of the V1 and MT units, and these fits could be used to explain the patterns of correlations we observed.

Our results suggest that understanding the way that the shared trial-to-trial variability of neuronal responses depends on different sensory, motor, and cognitive factors can help identify the computations performed by networks of neurons within and across brain areas. In particular, our results support the hypothesis that normalization is a good description of the relationship between the responses of neurons in visual cortex in different stimulus and task conditions, and the responses of neurons in other areas. Although many models include multiple layers (an analogy to multiple brain areas), our results suggest that viable models will have to account for shared variability in a way that follows the predictions of a normalization model.

Differences between sensory normalization and attention

Two of our manipulations, adding a second stimulus and attending to one of multiple stimuli, are part of a long list of processes in a variety of species, brain areas, and experimental conditions that affect the trial-averaged responses of individual neurons in ways that are well described by normalization, which has been proposed to be a canonical neural computation (for review, see Carandini and Heeger, 2012). In particular, normalization accurately describes the divisive (or multiplicative) scaling of neuronal responses associated with a wide variety of modulatory processes such as the contrast of visual stimuli (Rust et al., 2006; Carandini and Heeger, 2012), multisensory integration (Ohshiro et al., 2011), reward (Louie et al., 2013), and attention (Boynton, 2009; Lee and Maunsell, 2009; Reynolds and Heeger, 2009; Ni et al., 2012). Many of the same modulatory processes that scale neuronal responses are also associated with changes in response covariability (for review, see Cohen and Kohn, 2011), and the extent to which a given neuron's average response is modulated by adding a second stimulus is highly correlated with the extent to which its response is affected by shifting attention (Lee and Maunsell, 2009; Ni et al., 2012; replicated in our data set, data not shown). These observations are consistent with the hypothesis that this whole class of modulatory processes, including adding a second stimulus and attention, share underlying neuronal mechanisms.

However, one aspect of our results is inconsistent with this idea. We observed that adding a second stimulus affects spike count correlations between pairs of units in different, but not the same, cortical area. In contrast, attention affects both within- and cross-area correlations, but in different directions. The normalization model may help explain this difference. In the model, adding a second stimulus affects both the numerator and denominator of Equations 4–6 in an additive way, while attention is instantiated by the scaling parameter β. A literal interpretation of this model is that attention acts on inputs that have already passed through the divisive nonlinearity. This possibility is consistent with the neuron-by-neuron correlation between modulation by attention and adding a second stimulus because neurons whose inputs are not passed through the nonlinearity would not show attention effects (Ni et al., 2012). Our results support this idea by showing that the effects of both adding a second stimulus and attention on V1–MT correlations are consistent with the normalization model (Fig. 5).

Implications for the mechanisms underlying sensory and cognitive processes

Because normalization is so ubiquitous, any constraints on its underlying neuronal mechanism are very valuable. It is important to note that the normalization model (both the original model and our modified version) describes a computation, not a neuronal mechanism. However, our observations concerning the stimulus and cognitive dependence of cross-area spike count correlations, and the fact that they are largely predicted by the normalization model, place constraints on possible mechanisms.

Theoretical models of how information is communicated from one area to another make very different predictions about shared variability. For example, strictly feedforward models in which excitation and inhibition are not differentiated predict unphysiologically high spike count correlations (Kriener et al., 2008). Incorporating a nonlinearity such as divisive normalization into a feedforward model decreases correlated variability and improves estimates of the stimulus dependence of correlations (Tripp, 2012). Models in which excitation and inhibition are balanced and independent have near-zero correlations (van Vreeswijk and Sompolinsky, 1996; Amit and Brunel, 1997), and recurrent networks with excitatory–inhibitory balance exhibit correlation cancellation that leads to a high variance in correlation coefficients but near-zero mean correlations (Renart et al., 2010). Furthermore, the spiking nonlinearity can make correlations scale with firing rates (de la Rocha et al., 2007), which our mean matching controls show is not sufficient to account for our results.

Our correlation results therefore place constraints on potential models about interarea communication. Our results are broadly consistent with a feedforward network in which the inputs go through a divisive nonlinearity (Tripp, 2012), combined with some mechanism that reduces correlations overall (such as excitatory–inhibitory correlation canceling; or see Tripp, 2012). Any viable model will need to simultaneously account for the stimulus and task dependence of correlations within the same area as well as between areas.

Thousands of neurons in many brain areas respond to any sensory stimulus or contribute to any cognitive or motor processes. In the last two decades, improvements in multineuron recording techniques have led to a dramatic increase in the number of studies that measure shared variability as a way to gain insight into the computations and mechanisms underlying such sensory, cognitive, and motor processes. Because we found such different dependence of correlated variability within and across areas on sensory and cognitive processes, our results suggest that a full understanding will require simultaneous recordings in multiple areas.