Conditions for Valid Empirical Estimates of Cancer Overdiagnosis in Randomized Trials and Population Studies

Abstract

Cancer overdiagnosis is frequently estimated using the excess incidence in a screened group relative to that in an unscreened group. However, conditions for unbiased estimation are poorly understood. We developed a mathematical framework to project the effects of screening on the incidence of relevant cancers—that is, cancers that would present clinically without screening. Screening advances the date of diagnosis for a fraction of preclinical relevant cancers. Which diagnoses are advanced and by how much depends on the preclinical detectable period, test sensitivity, and screening patterns. Using the model, we projected incidence in common trial designs and population settings and compared excess incidence with true overdiagnosis. In trials with no control arm screening, unbiased estimates are available using cumulative incidence if the screen arm stops screening and using annual incidence if the screen arm continues screening. In both designs, unbiased estimation requires waiting until screening stabilizes plus the maximum preclinical period. In continued-screen trials and population settings, excess cumulative incidence is persistently biased. We investigated this bias in published estimates from the European Randomized Study of Screening for Prostate Cancer after 9–13 years. In conclusion, no trial or population setting automatically permits unbiased estimation of overdiagnosis; sufficient follow-up and appropriate analysis remain crucial.

Research articles on overdiagnosis—the detection of disease that would not present clinically in the absence of screening—have proliferated in recent years. In many of these studies, investigators considered the higher observed incidence (hereafter referred to simply as incidence) of disease in the presence of screening as a proxy for overdiagnosis (1–5). In such “excess incidence” studies, it has been estimated that overdiagnosis accounts for 31% of all breast cancer cases in the United States (1), 59% of screen-detected prostate cancer cases in the European Randomized Study of Screening for Prostate Cancer (ERSPC) (6, 7), and 22% of the cases detected in the mammography arm of the Canadian National Breast Screening Study (2). Concerns have been raised about the reliability of these estimates (8–11), although the precise conditions required for valid estimation are not well understood.

Overdiagnosis studies conducted in the population setting are challenging because, once screening has started, it is impossible to observe what the incidence would have been in the absence of screening. Counterfactual background incidence must therefore be extrapolated from historical trends or imputed by other means. The background incidence is critical in the calculation of excess incidence, because excess incidence is calculated as the difference between the observed incidence under screening and the background incidence. Population-based excess incidence estimates without a verifiably accurate estimate of background incidence should therefore be interpreted with great caution, particularly those involving extrapolation over a lengthy time interval.

Given that it can be difficult to determine background incidence in the population setting, assessments of overdiagnosis using incidence data from randomized screening trials may seem more reliable. Unlike population studies, trials offer an opportunity to validly estimate background incidence using data from the control group, so long as randomization is successful and there is no screening in the control arm (contamination). Because of the availability of a control group and perhaps because screening trials are considered gold-standard sources of evidence, the reliability of overdiagnosis estimates from these trials has not been thoroughly investigated.

In the present study, we examined conditions for valid estimation of cancer overdiagnosis based on excess incidence in both trial and population settings. To do so, we extended an early conceptual model (12) to quantitatively link cancer natural history, test sensitivity, and receipt of tests with the effects of a new screening program on observed disease incidence. Using the model, we derived conditions for valid empirical estimates of the number of overdiagnosed cancers and illustrated these conditions in common trial designs and plausible population settings. We concluded by evaluating empirical estimates in the ERSPC. We offer general recommendations below.

METHODS

Overview

In this section, we describe a model of the effects of a screening test on disease incidence that we can use to replicate the changes in incidence in trials and population settings under screening and to investigate bias associated with excess-incidence estimates of overdiagnosis. In general, the introduction of a screening program has predictable effects (12) on the incidence of relevant cancers, that is, cancers that would present clinically in the absence of screening. Initially, this incidence increases as the program reaches into the pool of preclinical cancers not detectable without the test. How far it reaches into the pool and how many preclinical cancers it nets—and therefore how much incidence increases and for how long—depends on the size of the pool and the characteristics of the program. Over time, however, as testing patterns stabilize and the pool of newly detectable cancers is emptied, incidence eventually falls. We used the model to formalize this process and develop expressions for the incidence of relevant cancers under screening and overdiagnosis, allowing us to derive the waiting time needed for unbiased empirical estimation of overdiagnosis using annual or cumulative incidence.

The model

The model comprises 5 components: 1) the rate of onset of relevant cancers, 2) the distribution of preclinical detectable time periods after onset, 3) the episode sensitivity of a new screening test, 4) the receipt of screening tests, and 5) the fraction of screen-detected cancers that are overdiagnosed. Components 1 and 2 determine the size of the pool of relevant cancers that are detectable by screening. In the absence of trends in risk factors or clinical practice before screening begins, the rate of onset of relevant cancers (r) will equal the rate of cancer diagnosis. In the United States, the annual incidence of breast cancer in 1975, before mammography screening was widely adopted, was 105 per 100,000 women (13). The annual incidence of prostate cancer in 1985, before prostate-specific antigen screening was introduced, was 116 per 100,000 men (13). Although clinical practice patterns were not constant before screening for these cancers began (12, 14), these incidence rates provide first approximations of the rates of onset of relevant breast and prostate cancers. In general, a higher rate of onset creates a larger reservoir of preclinical cancers that can be detected by screening.

Because relevant cancers are destined to be clinically diagnosed within the lifetime of the patient, the longest possible preclinical period for these cancers is finite. Let [0, D] denote the range of these periods in years. The periods when cancers are detectable by screening are sometimes called “sojourn times” (15–17). A closely related idea is the lead time, or the time by which screening advances diagnosis; the longest lead time provides a conservative approximation to the longest preclinical period (D). Lead time distributions have been estimated for several cancers (15, 16, 18) and average 2–4 years for invasive breast cancers and 5–7 years for prostate cancers in the United States. A longer preclinical period permits screening to detect relevant cancers earlier and to advance diagnosis of cancers that would have presented further in the future.

Components 3 and 4 determine how quickly the latent pool is depleted. Episode sensitivity (19) p represents the probability of diagnosis due to the test among individuals with preclinical disease. A more sensitive test, a greater frequency of compliance with biopsy recommendations, and a more sensitive biopsy all increase the episode sensitivity, which in turn more quickly depletes the pool of preclinical cancers. Similarly, a greater number of tests drains the pool more quickly. In a randomized trial, receipt of tests reflects attendance at invited screens q. In a population setting, receipt of tests reflects dissemination into clinical practice. Note that only in the unrealistic situation in which a test is done continuously and has perfect sensitivity is sojourn time equal to lead time.

Component 5 determines the number of overdiagnosed cancers each year, which we express as a constant fraction b of screen detections. We make no distinction between overdiagnosed cancers that would have progressed to symptomatic presentation were it not for death from another cause, cancers that are indolent, or cancers that would have regressed spontaneously. These distinctions do not impact our results.

Using these model components, we can derive expressions for cancer incidence with and without screening. Let $N_y^k$ denote the number of new relevant cancers that develop in year y with preclinical period k years, so that a total of $N_y={\sum }_{k=0}^D{N}_y^k$ cancers develop in year y, of which $N_y^0$ are diagnosed in year y, $N_y^1$ are diagnosed in year y + 1, and so on, until $N_y^D$ are diagnosed in year y + D. Thus, in each year y before screening begins, $C_y={\sum }_{k=0}^D{N}_{y-k}^k$ cancers reach the end of their preclinical periods and are clinically diagnosed. Figure 1 shows how incidence and prevalence of relevant cancers at a point in time are composed of cancers that developed during or before this time.

Figure 1.

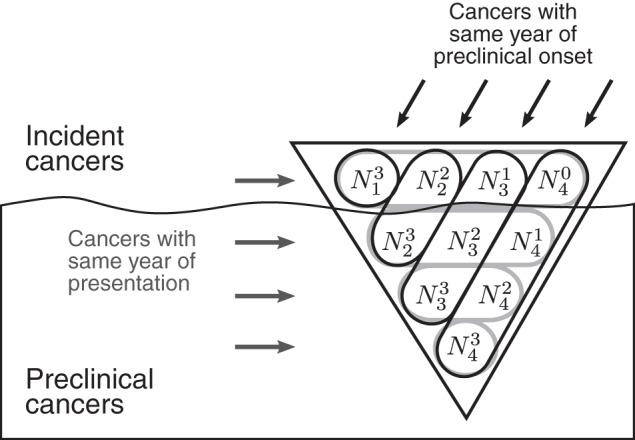
Conceptual “iceberg” of prevalence and clinical incidence of relevant cancers in year 4 when the range of preclinical detectable periods is 0–3 years. The symbol $N_y^k$ denotes the number of relevant cancers that develop in year y with preclinical period k years and therefore would present in year y + k if they are not detected earlier by screening. For example, $N_4^0$ cancers develop in year 4 with preclinical period <1 year, $N_3^1$ cancers develop in year 3 with a preclinical period of at least 1 year but less than 2 years, and so on.

Suppose an annual screening program is introduced in year y*. Assume, without loss of generality, 100% attendance by the population. After screening begins, the number of cancers that reach the end of their preclinical period without being detected by screening and are clinically diagnosed in year y is:

$$C_y=\sum _{k=0}^D{(1-p)}^{min\{k,y-y^{\ast }\}}{N}_{y-k}^k,$$ (1)

where y − y* is the number of years since the screening program began. Here min{k, y − y*} represents the number of screening tests given when preclinical disease is present, each of which must be a false negative and thus occurs with probability 1 − p. This formulation assumes that test results are independent and sensitivity is constant; generalizations in which sensitivity depends on the preclinical period or with proximity to clinical diagnosis can be readily derived. The incidence of screen-detected cancers is:

$$S_y=\sum _{k=1}^D\sum _{j=0}^{k-1}p{(1-p)}^{min\{j,y-y^{\ast }\}}{N}_{y-j}^k.$$ (2)

In words, screen-detected incidence in year y is comprised of cancers that had not yet reached the end of their preclinical periods, that were not detected by previous tests, and that were detected by the test in year y. Finally, let O_y = bS_y denote the number of overdiagnosed cancers diagnosed in year y, so that total incidence in year y is:

$$I_y=C_y+S_y+O_y.$$ (3)

Example trial and population settings

Given suitable inputs, the model can project total incidence and its components across years. We demonstrate these projections in trial and population settings for episode sensitivity p = 0.5 and overdiagnosis fraction b = 0.25. For simplicity, the number of preclinical cancers is determined by assuming that relevant cancers develop at an annual rate of r = 100 per 100,000 individuals for a population with fixed size P = 50,000 or 100,000 and the preclinical period follows a discrete uniform distribution so that $N_y^k=rP/(D+1)$ for all k and y. The starting year of screening y* can vary between the screen and control arm in each trial design and across subpopulations that adopt annual screening in each population setting.

The trial designs are as follows. 1) In a stop-screen trial, the screen arm receives 4 annual tests and then screening stops. 2) In a continued-screen trial, the screen arm receives annual tests indefinitely. 3) In a delayed-screen trial, the screen arm receives annual tests indefinitely, and the control arm receives annual tests indefinitely after a 4-year delay. Similar designs have been used to study breast or prostate cancer screening. We assume an attendance rate of q = 0.8 at each screen test and a maximum preclinical period of D = 6 years.

The population settings are as follows. 1) Screening disseminates over a ramping-up period in which cumulative percentages of the population that adopt annual screening are 5%, 15%, 30%, 45%, and 50% in years 2, 3, 4, 5, and 6, respectively, and D = 6 years. 2) Annual screening is adopted by 10%, 30%, and 50% of the population in years 2, 3, and 4, respectively, and D = 6 years. 3) Screening is as in setting 1 and D = 12 years.

In both trial and population settings, the model projects annual and cumulative incidence over specified time periods. In each setting, we compute excess incidence in screened groups relative to unscreened groups, compare this with the true number of overdiagnosed cancers, and identify the earliest time point at which the empirical estimate is unbiased.

RESULTS

The introduction of a new screening program induces a bulge in the incidence of relevant cancers relative to background incidence. General results about the height and width of the bulge are derived in the Appendix. To summarize, for a given rate of onset, the height of the bulge is determined by the episode sensitivity and the receipt of tests, and the end of the bulge is given by the first point that screening stabilizes plus the maximum preclinical period. Thus, even when accurate information about background incidence is available, an unbiased empirical estimate of the number of overdiagnosed cancers requires follow-up at least as long as the longest preclinical period once screening stabilizes.

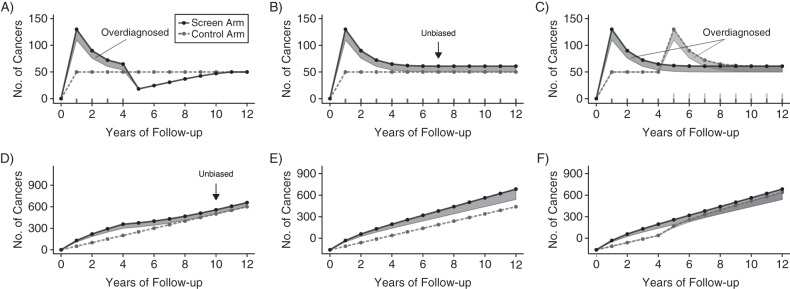
Figure 2 shows annual and cumulative incidence in the screen and control arms for each trial design, with overdiagnosed cancers highlighted in shaded areas. In the stop-screen design, when participants in the screen arm stop undergoing screening, its annual incidence (Figure 2A) falls below control-arm incidence because relevant cancers that would have presented then have already been detected. The annual incidence in the screen arm then gradually rises back to control-arm incidence. Excess cumulative incidence (Figure 2D) first equals the number of overdiagnosed cancers at 10 years of follow-up, corresponding to the first year screening stops (year 4) plus the 6-year maximum preclinical period.

Figure 2.

Hypothetical annual (A–C) and cumulative (D–F) cancer incidence in screen (solid lines) and control (dashed lines) arms in 3 trial designs. In the stop-screen design (A and D), the screen arm receives tests during years 1–4 and the control arm receives no tests. In the continued-screen design (B and E), the screen arm receives tests in years 1–12 and the control arm receives no tests. In the delayed-screen design (C and F), the screen arm receives tests in years 1–12 and the control arm receives tests in years 5–12. In each design, 50,000 individuals are randomized to each arm, relevant cancers develop at an annual rate of 100 per 100,000 individuals, the range of preclinical periods is 0–6 years, episode sensitivity is 50%, and 25% of cancers detected by screening are overdiagnosed (shaded areas). If available, minimum follow-up for unbiased estimation of overdiagnosis using excess incidence in the screen relative to the control arm is shown (black arrows).

If the screen arm continues screening, excess annual incidence (Figure 2B) first equals the number of overdiagnosed cancers at 7 years of follow-up, corresponding to the 6-year maximum preclinical period after screening starts (year 1). However, in contrast with the stop-screen design, excess cumulative incidence always overstates overdiagnosis (Figure 2E).

If the control arm starts screening after a delay (Figure 2F), it no longer provides information about incidence in an unscreened group, and no unbiased empirical estimate of overdiagnosis is available. If the frequency of overdiagnosis is the same in the 2 arms, annual incidence in the control and screened groups converge after 11 years (Figure 2C), corresponding to the first year screening begins in the control arm (year 5) plus the 6-year maximum preclinical period.

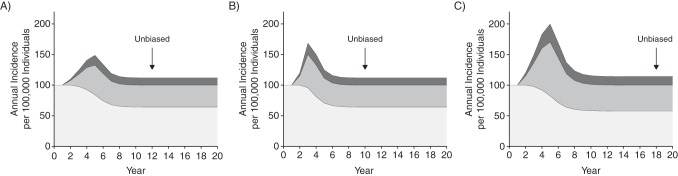
Figure 3 shows annual incidence in the population settings partitioned into screen and clinical diagnoses and overdiagnoses (equation 3 above). Once screening stabilizes, the effects of screening on incidence resemble patterns in a continued-screen trial. The first point the bulge in relevant cancers returns to the background level, so that excess incidence provides an unbiased estimate of overdiagnosed cancers, occurs 5 + 6 = 11 (Figure 3A), 3 + 6 = 9 (Figure 3B), and 5 + 12 = 17 (Figure 3C) years from the start of screening (year 2), reflecting the time for screening uptake to stabilize plus the maximum preclinical period. In general, the first point that excess incidence provides an unbiased estimate of overdiagnosis, as well as the bias before this point, is a complicated function of cancer natural history, episode sensitivity, and screening uptake.

Figure 3.

Hypothetical annual incidence rates for relevant cancers detected without screening (light gray), relevant cancers detected early by screening (medium gray), and overdiagnosed cancers (dark gray) in 3 population settings. Cumulative percentages of the population that adopted annual screening are 5%, 15%, 30%, 45%, and 50% in years 2, 3, 4, 5, and 6, respectively (A and C) or 10%, 30%, and 50% in years 2, 3, and 4, respectively (B). The maximum preclinical detectable period is 6 years (A and B) or 12 years (C). In each setting, relevant cancers develop at an annual rate of 100 per 100,000 individuals, episode sensitivity is 50%, and 25% of cancers detected by screening are overdiagnosed. Black arrows indicate minimum follow-up for unbiased estimation of overdiagnosis using excess incidence relative to background incidence.

Although excess annual incidence in a continued-screen trial or population setting eventually provides an unbiased estimate of the number of overdiagnosed cancers in a given year, excess cumulative incidence does not yield an accurate result, even after many years. This is because screening is continually advancing the diagnosis of relevant cancers that would have been diagnosed in the future, and background incidence under the same follow-up has not yet caught up. This is shown in Table 1, in which we report excess cumulative incidence and the true incidence of overdiagnosis in the 3 population settings in Figure 3. In each setting, the selected study period ranges from the start of screening to the first point that an unbiased estimate is available using excess annual incidence. We found that, in each setting, excess cumulative incidence was nearly double the true incidence of overdiagnosed cancers over this period.

Table 1.

Hypothetical Excess Cumulative Incidence and the True Incidence of Overdiagnosis in 3 Population Settings, Years 2–20

Population Settinga	Setting Characteristics							Cumulative Incidence (Cases per 100,000)		Overdiagnosis Estimate (Cases per 100,000)		Error in Excess Incidence Estimate
	Cumulative Population Starting Annual Screening by Year, %					Maximum Preclinical Detectable Period, Years	Study Years	Without Screening	With Screening	Excess Incidenceb	True Incidence of Overdiagnosis	Absolutec	Relatived
	2	3	4	5	6
1	5	15	30	45	50	6	2–12	1,100	1,339.1	239.1	124.9	114.2	1.91
2	10	40	50			6	2–10	900	1,128.3	228.3	114.2	114.2	2.00
3	5	15	30	45	50	12	2–18	1,700	2,228.1	528.1	270.4	257.7	1.95

^a Setting 1 involves slow dissemination of screening and a short maximum preclinical period; setting 2 involves fast dissemination of screening and a short preclinical period; and setting 3 involves slow dissemination of screening and a long maximum preclinical period. In each setting, relevant cancers develop at an annual rate of 100 per 100,000 individuals, episode sensitivity is 50%, and 25% of screen-detected cancers are overdiagnosed.

^b Excess incidence is cumulative incidence with screening minus cumulative incidence without screening.

^c Absolute error is excess incidence minus true incidence of overdiagnosis.

^d Relative error is excess incidence divided by true incidence of overdiagnosis.

DISCUSSION

Using excess incidence to estimate the number of overdiagnosed cancers is intuitive and relatively common. The potential for this approach to be misleading has been noted (20–22), but formal conditions for valid estimates have not been established. Our examination shows that, even in an uncontaminated screening trial or a population setting with perfect knowledge about background incidence, excess incidence yields a biased estimate of overdiagnosed cancers except under fairly specific circumstances. In particular, excess incidence in a stop-screen trial requires using cumulative incidence, whereas a continued-screen trial or population setting requires using annual incidence. Either setting further requires that excess incidence be calculated only after screening patterns have stabilized plus the maximum preclinical period. This finding confirms and formalizes results from prior studies (11, 20, 23) regarding the importance of adequate follow-up in excess-incidence studies of overdiagnosis.

The model involves several simplifying assumptions that were useful for deriving these general conditions. First, we assumed a discrete uniform distribution for the preclinical periods and did not allow this distribution to change over time. Further, incidence and screening frequencies did not vary with age. These assumptions did not affect our main conclusions, but the absence of an age structure limited our ability to interrogate proposed adjustments to excess incidence that use age-specific results to reduce bias (e.g., 8, 9). Test sensitivity was assumed independent of prior tests and of time to clinical diagnosis, though this assumption can be generalized. We made no assumptions about whether overdiagnoses represented cancers that were progressive, indolent, or regressive; in certain contexts, a practitioner may wish to represent competing mortality explicitly, for example, to tease out information about the proportion of overdiagnosed cancers that are progressive.

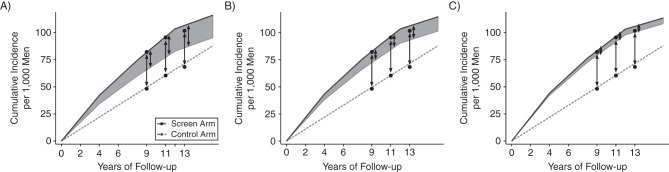
In certain settings, the model can be used to evaluate existing studies of excess incidence for their likely validity and to explore the potential magnitude of bias. To illustrate, we consider the ERSPC, a continuous-screen trial with limited screening in the control arm (24). ERSPC investigators reported cumulative incidence differences between the screen and control arms of 34, 36, and 33 cancers per 1,000 men at 9, 11, and 13 years of follow-up, respectively (6, 25, 26), and used these to approximate overdiagnosis when calculating the number needed to detect to prevent 1 prostate cancer death. Figure 4 shows reported cumulative excess incidence (black dots) and corresponding model projections for each arm (solid and dashed lines). For specified values of the maximum preclinical period, we identified overdiagnosis frequencies that yielded projected incidence that was similar to observed incidence in the screen arm. As expected, longer maximum preclinical periods among relevant cancers required a lower overdiagnosis frequency. Under a 12-year maximum preclinical period (Figure 4A), a 40% overdiagnosis frequency was required, corresponding to 16, 19, and 21 overdiagnoses per 1,000 men, approximately half the published excess cases at 9, 11, and 13 years, respectively. Under a 20-year maximum preclinical period (Figure 4C), which is more consistent with prevailing knowledge about prostate cancer natural history (27), a 10% overdiagnosis frequency was required, implying even greater bias in published estimates. Because our model relies on simplifying assumptions, this examination of ERSPC estimates should only be interpreted as suggestive of the potential magnitude of bias in published results. In practice, reliable empirical estimates of overdiagnosis in this trial can only be obtained by calculating the excess using annual instead of cumulative incidence, with reliability increasing with increasing length of follow-up.

Figure 4.

Reported (black dots) and modeled cumulative prostate cancer incidence rates in the screen (solid lines) and control (dashed lines) arms of the European Randomized Study of Screening for Prostate Cancer under 3 values for the maximum preclinical period: A) 12 years; B) 16 years; and C) 20 years. In each setting, model inputs were selected to match the trial. Relevant cancers developed at an annual rate of 550 per 100,000 men to match incidence in the control arm, episode sensitivity was 48% (19), 76% of men in the screen arm attended 3 quadrennial screens (39), and there was no control arm screening. Combining these inputs with the maximum preclinical period implied overdiagnosis frequencies (shaded areas) of 40% (A), 25% (B), and 10% (C). Reported excess-incidence estimates of overdiagnosis were 34, 36, and 33 per 1,000 men after 9, 11, and 13 years of follow-up. Corresponding model-based estimates were 16, 19, and 21 (A), 10, 12, and 13 (B), and 4, 5, and 5 (C).

In contrast with the ERSPC, the use of cumulative incidence in the Canadian National Breast Screening Study is appropriate given its stop-screen design and 20 years of follow-up after the end of the screening given published estimates of the preclinical period for breast cancer (16). However, screening was not tracked after the intervention period. If the screen arm continued screening and/or the control arm started screening, the validity of any estimate becomes difficult to judge.

Similarly, our findings can be used to evaluate empirical estimates from population studies. For instance, in a study of mammography screening in the United States, Bleyer and Welch (1) compared observed breast cancer incidence with assumed background rates over 30 years and estimated that 31% of breast cancers were overdiagnosed in 2008. Although the assumed background rates have been criticized (28, 29), follow-up for this calculation after stabilization of mammography screening may be sufficient in principle for valid estimation of overdiagnosis in 2008. However, in the same study (1), the authors found 1.3 million excess cumulative breast cancers among women during 1978–2008. By using excess cumulative incidence from the introduction of screening, the estimated overdiagnoses frequency likely includes relevant in addition to overdiagnosed cancers.

Although we zeroed in on the issues of study design, calculation metric, and follow-up duration, we did not consider modifications that have been suggested to reduce bias associated with excess-incidence estimates when screening is restricted to specific age strata (30). These modifications include comparing incidence under screening with incidence in an older population (to account for lead time) (8) and considering incidence under screening that includes ages beyond the screening age range (to account for the compensatory drop in incidence that occurs among persons older than those who are offered screening) (23). In principle, our model can be extended to investigate these modifications, but this will require imposing an age structure on the modeled population.

In previous work, researchers have identified the need for sufficient follow-up before an unbiased estimate of overdiagnosis is available (20, 23). Duffy and Parmar (23) conducted a quantitative investigation into the follow-up needed in a hypothetical population setting, but we know of no investigation in trial settings. Rather, there seems to be a prevailing confidence in overdiagnosis results from trials due to the randomization of subjects to intervention groups. Our work indicates that this is misplaced. Alternative approaches have also been used to estimate overdiagnosis, including statistical (17, 31, 32), analytic (33), microsimulation (34), and decision analysis (35) models. Strengths and limitations of these approaches have been previously discussed (10, 36–38). Further research is needed to identify the conditions under which model-based estimates provide valid estimates of overdiagnosis.

In conclusion, we offer the following recommendations for estimating overdiagnosis using the excess incidence in a screened relative to an unscreened group. 1) Calculate the difference only after the initial years of screening uptake. Use annual incidence in a continued-screen trial and cumulative incidence in a stop-screen trial. Note that the wait time condition requires sufficient follow-up for all individuals, and the often-reported median follow-up in a trial can be substantially longer than the complete follow-up necessary for valid estimation. In a population setting, compelling information is needed about a trend in background incidence for an empirical estimate of overdiagnosis to be plausible. 2) Review estimates of cancer natural history to evaluate consistency of overdiagnosis estimates with prevailing understanding of natural history and lead-time distributions (37). The maximum lead time is a useful lower bound for the maximum preclinical period. 3) Recognize that a trial setting provides a valid comparison group provided that noncompliance and contamination are minimal. However, this does not automatically mean that overdiagnosis estimates from a trial are valid. In fact, even in the trial setting, sufficient follow-up and appropriate analytic methods are necessary to correctly interpret excess incidence as an estimate of the frequency of overdiagnosis.

APPENDIX

Minimum Follow-Up for Unbiased Empirical Estimation of Overdiagnosis

Using the model, we determine the minimum follow-up necessary for excess incidence to yield an unbiased estimate of the number of overdiagnosed cancers. Because this is equivalent to the first time point at which relevant cancers return to the background level after screening begins, we determine the earliest year y′ (with y′ ≥ y*) in which the number of new cancers that develop and enter the preclinical pool (N_y′) equals the number of cancers detected and removed from the pool (C_y′ + S_y′). Symbolically, this condition is:

$$\sum _{k=0}^D{N}_{y^{\mathrm{\prime }}}^k=\sum _{k=0}^D{(1-p)}^{min\{k,y^{\mathrm{\prime }}-y^{\ast }\}}{N}_{y^{\mathrm{\prime }}-k}^k+\sum _{k=1}^D\sum _{j=0}^{k-1}p{(1-p)}^{min\{j,y^{\mathrm{\prime }}-y^{\ast }\}}{N}_{y^{\mathrm{\prime }}-j}^k.$$ (1)

(We assume here 100% attendance with no loss of generality.) Under a stationary distribution of preclinical periods, in which the same number of relevant cancers with a given preclinical period develop each year, the steady state is reached precisely when it is reached for each preclinical period k = 1, 2, …, D, that is, when

$$N_{y^{\mathrm{\prime }}}^k=(1-p{)}^{min\{k,y^{\mathrm{\prime }}-y^{\ast }\}}{N}_{y^{\mathrm{\prime }}-k}^k+\sum _{j=0}^{k-1}p{(1-p)}^{min\{j,y^{\mathrm{\prime }}-y^{\ast }\}}{N}_{y^{\mathrm{\prime }}-j}^k.$$ (2)

(We can ignore k = 0 because the $N_{y^{\mathrm{\prime }}}^0$ cancers that develop in year y′ are diagnosed in that year.) Under a stationary distribution of preclinical periods, the number of cancers with the same preclinical period k cancels from both sides, and equation 2 holds precisely when

$$1=(1-p{)}^{min\{k,y^{\mathrm{\prime }}-y^{\ast }\}}+\sum _{j=0}^{k-1}p{(1-p)}^{min\{j,y^{\mathrm{\prime }}-y^{\ast }\}}.$$ (3)

To see that this condition holds when y′ − y* ≥ D, first notice that when k = 1, it is trivial that 1 = (1 − p) + p. If this condition holds when k = n, then

$$(1-p{)}^{n+1}+\sum _{j=0}^{n}p{(1-p)}^j=(1-p)\left({(1-p)}^n+\sum _{j=0}^{n-1}p{(1-p)}^j\right)+p=(1-p)+p=1,$$ (4)

and so the condition holds by mathematical induction. In contrast, when 0 ≤ y′ − y* < D, 1 or more terms necessary for equality in equation 3 are missing from the right side, which implies that the number of cancers detected exceeds the number of new cancers that develop during this period. In other words, once screening begins, incidence of relevant cancers first increases above the background level and then eventually returns to this level after the maximum preclinical period has elapsed.

If screening disseminates into the population over time, it is necessary to wait until screening stabilizes across the population plus the maximum preclinical period. Before this point, the number of cancers being detected and removed from the population is still ramping up. Similarly, if test sensitivity improves over time, screening will reach progressively deeper into the pool of preclinical cancers, and incidence of relevant cancers will achieve a long-term steady state only after sensitivity has stabilized. In general, an unbiased estimate of overdiagnosis requires a new batch of cancers with the full range of preclinical periods to develop and be diagnosed under stable screening practices.

If the distribution of preclinical periods is not stationary, for example, because the population is open and includes entrance of individuals with different distributions of preclinical periods than the initial population or because there is a secular trend in factors associated with cancer risk, the situation is more complicated. The wait time necessary for the incidence of relevant cancers to achieve a steady state will depend on the effects of the new entrants on the pool of preclinical cancers. Similarly, if test sensitivity depends on the preclinical period or proximity to clinical diagnosis, dynamic effects on the necessary wait time will depend on the specific details of these relationships. Broadly speaking, however, time-varying effects of screening will tend to lengthen the wait time necessary for incidence of relevant cancers to return to the background level. Even in the simplest setting, convergence to background incidence is a complicated function of the rate of onset, the distribution of preclinical periods, test sensitivity, and receipt of tests.