Viral epidemiology of the adult Apis Mellifera infested by the Varroa destructor mite

Abstract

The ectoparasitic mite Varroa destructor has become one of the major worldwide threats for apiculture.

Varroa destructor attacks the honey bee Apis mellifera weakening its host by sucking hemolymph. However, the damage to bee colonies is not strictly related to the parasitic action of the mite but it derives, above all, from its action as vector increasing the transmission of many viral diseases such as acute paralysis (ABPV) and deformed wing viruses (DWV), that are considered among the main causes of CCD (Colony Collapse Disorder).

In this work we discuss an $SI-SI$ model that describes how the presence of the mite affects the epidemiology of these viruses on adult bees. The acronym $SI-SI$ means that the disease affects both populations. In fact it accounts for the bee and mite populations, that are each divided among the S (susceptible) and I (infected) states. We characterize the system behavior, establishing that ultimately either only healthy bees survive, or the disease becomes endemic and mites are wiped out. Another dangerous alternative is the Varroa invasion scenario with the extinction of healthy bees. The final possible configuration is the coexistence equilibrium in which honey bees share their infected hive with mites.

The analysis is in line with some observed facts in natural honey bee colonies. Namely, these diseases are endemic. Further, if the mite population is present, necessarily the viral infection occurs.

The findings of this study indicate that a low horizontal transmission rate of the virus among honey bees in beehives will help in protecting bee colonies from Varroa infestation and viral epidemics.

1. Introduction

Pathogens, e.g. viruses, fungi and bacteria, significantly affect the dynamics of invertebrates. Experimental evidence reveals that some naturally harmless honey bee viruses turn instead epidemic via new transmission routes [17]. Specifically, the parasitic mite Varroa jacobsoni, that normally affects the eastern honey bee Apis cerana, switched host and started to attack the western honey bee Apis mellifera. This caused large outbreaks of mites, in particular of Varroa destructor, larger in A. mellifera than in A. cerana. These mite populations act as bee viruses vectors and are presumed to be the cause of the worldwide loss of mite-infested honey bee colonies, because they induce a much faster spread of the viruses than occurred before.

In order to better understand the Varroa-infested colony response to these viruses, it is necessary to study the joint effects of mites and viral diseases, since both appear simultaneously in fields conditions. The goal of this paper is to formulate and investigate a mathematical model able to describe how the mite presence affects the virus epidemiology on adult bees. To this end, we consider all the possible transmission routes for honey bee viral diseases.

In the literature models for the study of the decline of honey bees colonies have been introduced. For instance, in [10] the attention focuses on brood, hive bees and foragers as main variables, finding a forager mortality threshold beyond which the colony failure is ensured. This fact induces also their replacement by younger hive bees, which is a further endangerment for the rapid disappearance of the colony. A model just for the mite Varroa destructor has been described in [11], consisting of the mites, workers and drones populations. It uses a phenomenological type of function for the eggs laying rate. Effects on the bees are not accounted for, but the model may turn to be useful to evaluate control strategies. An extensive work has been carried out in [7], from the modeling phase to the validation using field data. Colony survival depends on thresholds for the Varroa population, the brood rearing and the effectiveness of the insecticides used to kill the mites, which are found to be best effective when applied at the end of the summer. If treated in the spring, in fact, the Varroa population will recover by the end of the season and constitute a renewed threat in the following year. On a more applied side, sampling methods for the assessment of the mite population are discussed in [4]. The very recent paper [14] accounts for healthy and infected bees, the whole set of mites in the beehive, and the infected mites. The model contains essentially a Leslie–Gower submodel for the mites, whose carrying capacity depends on the bee population size. In fact a crucial parameter is here represented by the number of mites that can be sustained per single bee, on average. Further, since a sufficiently high number of worker bees must be present to ensure for brood rearing and for the operation of the beehive, a Hill function is used to model this kind of switching behavior, and in the bees birthrate formulation also the mite influence is accounted for. In particular this models the fact that the infected mites can kill the pupa before it becomes an adult bee. Finally, the effect of seasonality is taken into account, via 4 different sets of parameter values.

The paper is organized as follows. In the next Section we present the biological background, briefly describing the host Apis Mellifera, the vector Varroa destructor, the honey bee viral diseases and their three-species interactions. In Section 3 the model is formulated, assessing its basic properties. Its equilibria are investigated in Section 4 for feasibility and in the following Section 5 for their stability, where also bifurcations are investigated. These connect all the equilibria together and are shown to completely capture the system's behavior, as persistent oscillations among the populations are proven to be impossible for equilibria when global stability results hold. In Section 6 we perform numerical simulations based on a set of parameter values, some of which are obtained from field data. An interpretation of the results is also provided. Sensitivity analysis is carried out in the following Section 7. A final discussion concludes the paper, Section 8. The Appendix contains the technical details of the global stability analysis.

2. Materials

We briefly present in this section the three actors playing a major role in the beehive.

2.1. The host: the honey bee Apis mellifera

In the summer season a honey bee colony harbors generally a single reproductive queen, living on average 2 to 3 years, with about 60000 adult female worker bees, 10000 to 30000 individuals at the brood stage (egg, larvae and pupae) and a few hundreds of male drones, [14]. The workers take care of the colony by foraging, producing honey, caring for and rearing the brood and the bees new generation. The queen lays fertilized eggs producing worker bees and, rather seldom, other queens, as well as non-fertilized eggs from which drones are born. During the winter the queen and around 8000 to 15000 adult workers thrive feeding only on the honey produced and stored in the previous summer. Because of the very high population density experienced in such an environment, the honey bee colonies can very easily be affected by pathogens, [12].

Honey bees possess many defenses against diseases: for instance, grooming the mites away from their bodies, or removing the Varroa-infested brood. However, colonies are still affected by diseases and pests.

2.2. The vector: the mite Varroa destructor

An adult Varroa mite can be either in the phoretic or in the reproductive life stage. It is in the phoretic one, when it thrives attacking a bee and sucking its hemolymph. To this end, it pierces the cuticle of the bee with its specialized mouth-parts. As the mite can switch host during this phase, it may spread viruses in the colony by sucking them from one host and then injecting them into a healthy individual, [13].

Essentially, no honey bee mortality can be ascribed to the damages related in the sucking operation, i.e. hemolymph subtraction and tearing of tissues. Instead, the bee colonies damage comes from the mite being the vector of many seriously harmful viral diseases. As a defense, the bees groom, biting the mites, that as a consequence may fall off to the bottom of the hive, constituting the “natural mite drop”. This however represents just a small part of the phoretic mites and above all of the whole mite population, as the reproductive mites are confined in the capped cells.

The mites second life stage is indeed the reproductive one, [13]. To lay eggs, a mature female mite moves from an adult bee into the cell of a larva. When the brood cell is capped, the larva begins pupating and the mite starts to feed. About three days later the mite lays its eggs: one is unfertilized and produces a male, four to six are fertilized and give rise to females. After hatching, the females feed on the pupa and mate with the male. The surviving mature female mites remain attached to the host bee when the latter becomes adult and leaves the cell.

2.3. The viral pathogens

Scientists have found viruses in honey bees since decades, but in general they were considered harmless. Only when about thirty years ago Varroa became a widespread problem, about twenty different viruses have been associated with the vectors Varroa mites, [13]. Most of honey bee viruses commonly cause covert infections, i.e. the virus can be detected at low titers within the honey bee population in the absence of obvious symptoms in infected individuals or colonies. However, when injected into the open circulatory system of the insects, in which the heart pumps blood into the space in between the organs rather than in closed vessels as in vertebrates, these diseases are extremely virulent: just a few viral particles per bee are sufficient to kill the infected individual within a few days.

The transmission of viral diseases to honey bees represents the most serious problem caused by Varroa destructor, for whose pathogens they constitute their main physical or biological vectors. This can easily occur when a virus-carrying mite attaches to the healthy bee during its phoretic phase. Further, viral diseases can also spread among bees by contact e.g. from queen to egg or from drone to queen, or through the environment and food.

On the other hand, a healthy phoretic mite may turn into a virus carrier by horizontal contacts with other infected mites, but also by contact with an infected bee. Therefore to control the viruses, the Varroa population in a hive should be kept in check, while symptoms of viral diseases usually suggest the presence of Varroa in the colony, [13].

From epidemiological surveys and laboratory experiments, especially two viruses can successfully be transmitted between honey bees during mite feeding activities and are therefore described in the next Subsections: deformed wing virus (DWV) and acute paralysis virus (ABPV).

2.3.1. Deformed wing virus (DWV)

This syndrome in infected bees is rather benign, causing covert infections with no visible symptoms, [9]. But in the presence of Varroa destructor, overt DWV infections are much more common. The affected bees show deformed wings, bloated and shortened abdomens, discoloration and are bound to die within three days from the infection. The outcome could even be the whole colony destruction. Further, DWV appears to replicate in Varroa, rendering it also a biological vector, [9]. Winter colony mortality also appears to be strongly associated with DWV presence.

2.3.2. Acute paralysis virus (ABPV)

ABPV was present at low concentrations as a covert infection in adult bees, but never caused paralysis outbreaks. However, when Varroa destructor established in the European honey bee populations, the virus has been found in the bees worldwide and is now geographically distributed as the A. mellifera. It is considered a primary cause of pupae and adult bees fast mortality, [9]. The main symptoms of bees affected by this virus are inability to fly, hair loss from the body, uncontrollable trembling.

3. Theory

In view of the biological scenario discussed in the previous Section, we present now the mathematical model. As a first assumption, we disregard to explicitly account for the viruses. We instead focus on the remaining other two populations, bees and mites, that are distinguished among healthy and infected individuals.

Let thus B denote the healthy bees, I the infected ones, M the healthy mites, N the infected ones. The model, accounting for all the possible population interactions described in detail below, reads as follows:

$$X^{\prime }=g(X)={(g_B,g_I,g_M,g_N)}^T,g:{\mathcal{D}}^0\to {\mathbb{R}}_{+}^4,$$ (1)

where ${\mathcal{D}}^0$ is defined below and $X=(B,I,M,N)$ is the population vector. The components of the right hand side g are explicitly given by:

$$\begin{array}{c}{g}_B=\hat{b}(B,I)\frac{B}{B+I}-\lambda BN-\gamma BI-mB-aBM-qBN,\hfill \\ g_I=\hat{b}(B,I)\frac{I}{B+I}+\lambda BN+\gamma BI-(m+\mu )I-cIM-dIN,\hfill \\ g_M=\tilde{R}(M+N,B+I)-\beta MI-\delta MN-eMB,\hfill \\ g_N=-nN-pN(N+M)+\beta MI+\delta MN-eNB.\hfill \end{array}$$ (2)

Note that the right-hand side of (2) is not well-defined at the set of points Θ where $B+I=0$. Defining the subset ${\mathcal{D}}^0\subset {\mathbb{R}}_{+}^4$ of the points away from the singularity, namely

$${\mathcal{D}}^0=\{X=(B,I,M,N)\in {\mathbb{R}}_{+}^4:B+I\ne 0\},$$

the domain of g is thus ${\mathcal{D}}^0$.

The first equation expresses the dynamics of healthy bees. The function $\hat{b}(B,I)$ represents the bees daily birth rate. Newborns are assumed to be born healthy in proportion to the fraction of healthy bees in the colony, since the disease is transmitted to larvae mainly by infected nurse bees that contaminate royal jelly.

The second term models the situation in which, if attacked by infected mites, the healthy bees may contract the virus carried by the mite at transmission rate λ. Horizontal transmission among the bees at rate γ occurs either via small wounds of the exoskeleton, e.g. as a result of hair loss, or ingestion of feces. The fourth term in the equation describes the bees' natural mortality, occurring at rate m, while the last ones model the mite parasitism, at respective rates a and q for healthy and infected mites.

The second equation describes the evolution of infected bees. As for the healthy bees, they reproduce at rate $\hat{b}(B,I)$, but in proportion now to the fraction of infected bees in the population. The second and third terms account for the new recruits in this class due to contacts of healthy bees, respectively with infected mites and infected bees. Infected bees are subject to both their natural m and disease-related μ mortalities. The remaining terms describe again mite parasitism, now at rates c and d respectively for healthy and infected mites.

The third and fourth equations model respectively the dynamics of healthy and infected mites.

The mites are born always healthy, as no viral infection is transmitted to the offsprings, i.e. no viruses are passed vertically from parents to offsprings. The mites reproduction is described by the function $\tilde{R}$, that depends on the whole mite and bee populations. When attacking the infected bees, mites can, in turn, contract the virus at rate β. Furthermore, healthy mites can acquire the virus also horizontally from other infected mites at rate δ. The last term models the grooming behavior of healthy bees at rate e. We exclude this behavior for the infected bees, as they are weakened by the virus and not able to perform any resistance against Varroa mites.

Note that in formulating the fourth equation we account for the fact that the virus does not cause any harm to the infected Varroa population, but individuals remain infected until their natural death, that occurs at rate n, hence there cannot be any disease recovery. On the other hand, we consider the effect of intraspecific competition between healthy and infected mites at rate p. The remaining terms once again describe the new recruits in this class, from horizontal contacts with infected bees or mites, and finally the healthy bees grooming at the same rate e as for the healthy mites, as this activity depends only on the bees.

Finally, in this general model, we further make the following simplifying assumptions:

• •the daily bees birth rate is constant, $\hat{b}(B,I)=b$;
• •
  the honey bee mortality induced by the presence of Varroa mite can be neglected when compared with their natural and disease-related mortality, so that we set

  $$a=q=c=d=0;$$ (3)
• •
  healthy mites grow in a logistic fashion with reproduction rate $\hat{r}$, natural mortality n, for which the net reproduction rate becomes $r=\hat{r}-n$; for this to happen, we take

  $$\begin{array}{ccc}\hfill p& \hfill =\hfill & \frac{r}{K},\tilde{R}(M+N,B+I)=\hat{r}(M+N)-nM-\frac{r}{K}M(M+N)\hfill \\ \hfill & \hfill =\hfill & rM+(r+n)N-\frac{r}{K}M(M+N)=r(1-\frac{M}{K})(M+N)+nN.\hfill \end{array}$$ (4)

Therefore, system (2) reduces to the following one, written in shorthand as

$$X^{\prime }=f(X)={(f_B,f_I,f_M,f_N)}^T,f:{\mathcal{D}}^0\to {\mathbb{R}}_{+}^4,$$ (5)

where the components of the right hand side f are those of g in which (3) and (4) are used. Explicitly,

$$\begin{array}{c}{f}_B=b\frac{B}{B+I}-\lambda BN-\gamma BI-mB,\hfill \\ f_I=b\frac{I}{B+I}+\lambda BN+\gamma BI-(m+\mu )I,\hfill \\ f_M=r(1-\frac{M}{K})(M+N)+nN-\beta MI-\delta MN-eMB,\hfill \\ f_N=-nN-\frac{r}{K}N(N+M)+\beta MI+\delta MN-eNB.\hfill \end{array}$$ (6)

Note that summing the last two components of (5) we obtain

$$f_M+f_N=r(M+N)(1-\frac{M+N}{K})-e(M+N)B,$$

i.e. exactly the logistic growth term for the whole Varroa population, for which the parameter K thus represents the carrying capacity.

3.1. Well-posedness and boundedness

In view of the above remarks, in this section we need to study the well-posedness, following basically the path of [16]. The results show that the solutions are always bounded away from the set $\mathrm{\Theta }=\{(B,I,M,N)\in {\mathbb{R}}_{+}^4:B+I=0\}$.

Theorem 3.1 Well-posedness and boundedness —

If $X_0\in {\mathcal{D}}^0$, then there exists a unique solution of (5) defined on $[0,+\infty )$ such that $X(0)=X_0$. Moreover, for any $t>0$, $X(t)\in {\mathcal{D}}^0$, and

$$\frac{b}{\tilde{m}}\le \underset{t\to +\infty }{\lim \inf }(B(t)+I(t))\le \underset{t\to +\infty }{\lim \sup }(B(t)+I(t))\le \frac{b}{m}$$ (7)

where $\tilde{m}=m+\mu$. Further,

$$M(t)+N(t)\le L,\forall t\ge 0,$$ (8)

where $L=\max \{M(0)+N(0),K\}$.

Proof

The right-hand side of the system is globally Lipschitz continuous on ${\mathcal{D}}^0$, so that existence and uniqueness of the solution of system (5) is ensured for every trajectory that is at a finite distance of this boundary. We now show that (7) and (8) hold for all the trajectories originating from a point where $B+I\ne 0$. From the boundedness of the variables, it will follow that all trajectories are defined on an infinite horizon and they stay away from the set Θ.

Summing the first two equations in (5), for any point inside ${\mathcal{D}}^0$ we obtain

$$B^{\prime }+I^{\prime }=b-mB-(m+\mu )I\ge b-\tilde{m}(B+I),\tilde{m}=m+\mu .$$

Integrating this differential inequality between $X(0)=X_0$ and $X(t)$, points of a trajectory for which $X(\tau )\in {\mathcal{D}}^0$ for all $\tau \in [0,t]$, we get

$$B(t)+I(t)\ge \frac{b}{\tilde{m}}(1-e^{-\tilde{m}t})+(B(0)+I(0))e^{-\tilde{m}t},$$ (9)

where the right-hand side is positive for any $t>0$.

Proceeding similarly as above, we have

$$B^{\prime }+I^{\prime }\le b-m(B+I),$$

and therefore

$$B(t)+I(t)\le \frac{b}{m}(1-e^{-mt})+(B(0)+I(0))e^{-mt}.$$ (10)

From (9) and (10), it is easy to see that the inequalities in (7) hold for any portion of trajectory remaining inside ${\mathcal{D}}^0$.

We now consider the evolution of M and N. Defining the whole Varroa mite population V as follows

$$V=M+N$$ (11)

and summing the last two equations in (2), for any point inside ${\mathcal{D}}^0$ we obtain

$$V^{\prime }=rV-\frac{r}{K}MV-eBV-\frac{r}{K}NV\le rV(1-\frac{V}{K}).$$ (12)

The latter is a logistic term, thus the solution trajectory moves toward the stable equilibrium point $V=K$. Hence, we get $V(t)\le \max \{V(0),K\}$ for all $t\ge 0$, proving (8).

From the results on $B+I$ and V the boundedness of all populations follows, [16]. Thus all trajectories originating in ${\mathcal{D}}^0$ remain in ${\mathcal{D}}^0$ for all $t>0$.  □

Theorem 3.1 shows that the compact set ${\mathcal{D}}^1$, defined as the largest subset of ${\mathcal{D}}^0$ satisfying the inequalities of Theorem 3.1,

$${\mathcal{D}}^1\doteq \{(B,I,M,N)\in {\mathbb{R}}_{+}^4:\frac{b}{\tilde{m}}\le B+I\le \frac{b}{m},0\le M+N\le L\},$$

is a positively invariant attractor for all the system's trajectories. As all the equilibria lie in this set, as it will be clear in the next section, this result indicates that the equilibria analysis contains the ultimate behavior of the system.

4. Methods

In this section we will find the equilibria of the model (5) and assess their feasibility.

Since the domain of definition of f in (5) is ${\mathcal{D}}^0$, we exclude solutions of the equilibrium equations, i.e. (5) in which the components of f are set equal to zero, not included in it. The admissible equilibria are then the points at which at least one of the two bees subpopulations thrive. Explicitly, we find

$$E_1=(\frac{b}{m},0,0,0),E_2=(0,\frac{b}{m+\mu },0,0),$$

which are always feasible and

$$E_3=(\frac{b}{m},0,\frac{K}{r}(r-\frac{eb}{m}),0)$$

which is feasible for

$$r\ge \frac{eb}{m}.$$ (13)

We then find

$$E_4=(\frac{{\mu }^2-b\gamma +m\mu }{\mu \gamma },\frac{b\gamma -m\mu }{\mu \gamma },0,0),$$ (14)

so that feasibility for $E_4$ is given by

$$0<b\gamma -m\mu <{\mu }^2.$$ (15)

There are two more equilibria, coexistence, $E^{⁎}=(B^{⁎},I^{⁎},M^{⁎},N^{⁎})$ which is analyzed numerically, and the equilibrium $E_5$ with no healthy bees which we now investigate.

4.1. The healthy-bees-free equilibrium

To find the point $E_5$, we set $B=0$ in the equilibrium equations, and proceed as follows. From the second equation of (5), we find

$$I_5=\frac{b}{m+\mu }.$$

Substituting the value of I and rearranging, the last two equations provide two conic sections: ${\psi }_1(M,N)=0$ which explicitly is

$$\frac{r}{K}{M}^2+(\frac{r}{K}+\delta )MN-(r-\frac{\beta b}{m+\mu })M-(r+n)N=0$$ (16)

and ${\psi }_2(M,N)=0$, given by

$$(\delta -\frac{r}{K})MN-\frac{r}{K}{N}^2+\frac{\beta b}{m+\mu }M-nN=0.$$ (17)

Thus, the equilibrium is obtained as intersection of these two conic sections that lie in the first quadrant of the $M-N$ phase plane.

We begin by classifying the conic sections.

4.1.1. The conic section ${\psi }_1$

Computing the invariants of ${\psi }_1(M,N)$, we find in particular that

$$-\frac{{(r+\delta K)}^2}{4K^2}<0,$$

from which we conclude that ${\psi }_1$ is a hyperbola. Its center $C_1(x_{C_1},y_{C_1})$ is

$$x_{C_1}=K\frac{r+n}{r+\delta K}>0,y_{C_1}=\frac{r(m+\mu )(K-2x_{C_1})-b\beta K}{(m+\mu )(r+\delta K)}.$$

There is one vertical asymptote

$$M_{\infty }=\frac{(r+n)K}{r+\delta K}>0,$$

and the following oblique asymptote

$$N=-\frac{r}{r+\delta K}M+K\frac{r(r+\delta K)(m+\mu )-b\beta (r+\delta K)-r(r+n)(m+\mu )}{(m+\mu ){(r+\delta K)}^2}.$$

Looking for the intersections of ${\psi }_1$ with respectively the M and N axes, we observe that ${\psi }_1$ crosses the vertical axis only at the origin and the horizontal one also at the abscissa

$$M_1=\frac{K}{r}(r-\frac{\beta b}{m+\mu }),$$

which is positive if the following inequality holds

$$r>\frac{\beta b}{m+\mu }.$$ (18)

Figures 1, 2 and 3 show the three cases for which there is a feasible branch: for $M_{\infty }<M_1$ the hyperbola ${\psi }_1$ decreases from +∞ to zero in the corresponding interval, Case 1, Figure 1; for $0<M_1<M_{\infty }$ it raises up from zero to +∞ in $[M_1,M_{\infty }]$, Case 2, Figure 2; for $M_1<0<M_{\infty }$ from the origin it grows to the vertical asymptote, Case 3, Figure 3. The change in the two different shapes of the hyperbola ${\psi }_1$ occurs when $M_1$ and $M_{\infty }$ coalesce, for which the hyperbola degenerates into its asymptotes, which occurs for the critical value

$${\beta }_d=\frac{r}{b}(m+\mu )(K-\frac{(r+n)K}{r+\delta K)}).$$ (19)

Figure 1.

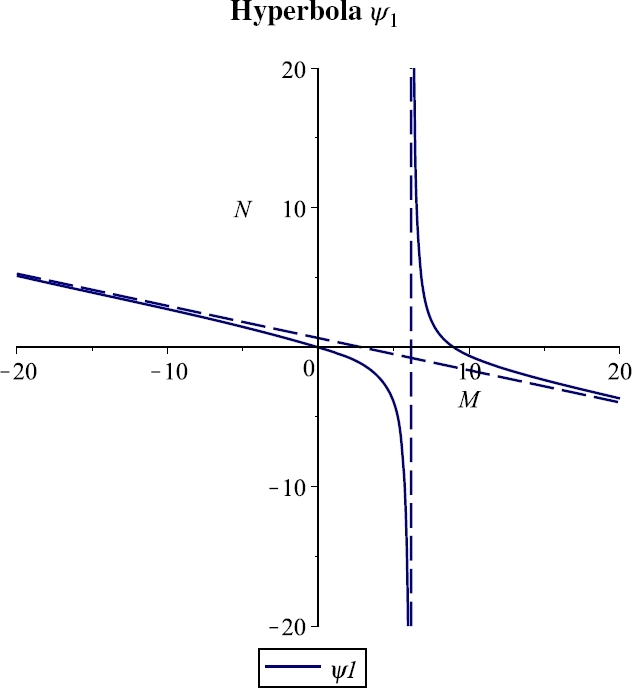
Case 1. M_∞ < M₁, for the parameter values r = 0.06, e = 0.001, λ = 0.03, b = 250, K = 10, β = 0.0002, m = 0.04, μ = 8, δ = 0.02, n = 0.1.

Figure 2.

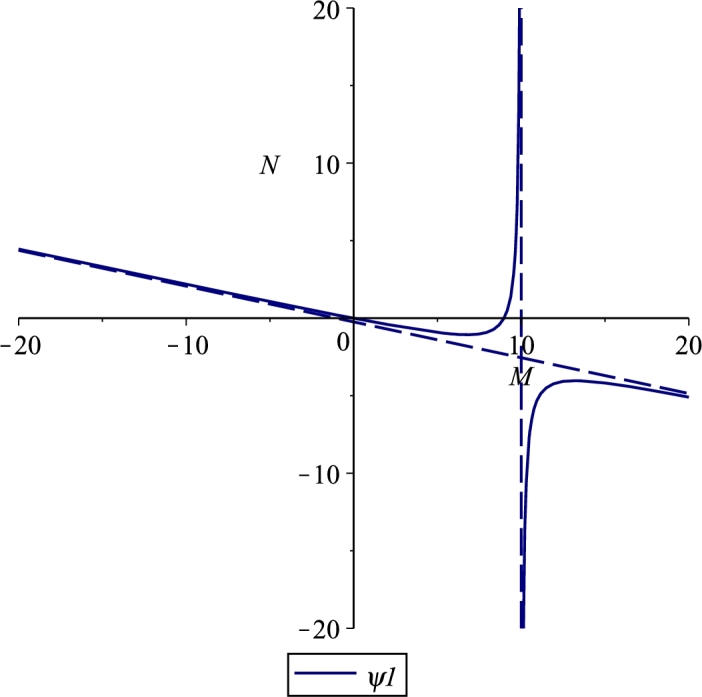
Case 2. 0 < M₁ < M_∞, for the parameter values r = 0.06, e = 0.001, λ = 0.03, b = 250, K = 10, β = 0.0002, m = 0.04, μ = 8, δ = 0.02, n = 0.2.

Figure 3.

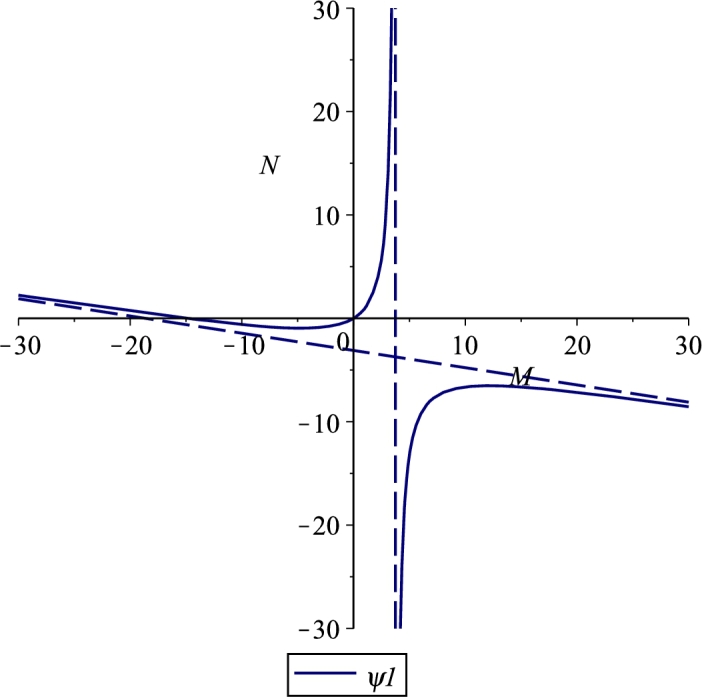
Case 3. M₁ < 0 < M_∞, for the parameter values r = 0.04, e = 0.001, λ = 0.03, b = 1000, K = 10, β = 0.001, m = 0.04, μ = 10, δ = 0.02, n = 0.05.

4.1.2. The conic section ${\psi }_2$

For the second conic section, the second invariant is always negative,

$$-\frac{1}{4}{(\delta -\frac{r}{K})}^2<0,$$

showing that also ${\psi }_2$ is a hyperbola. Its center is $C_2(x_{C_2},y_{C_2})$,

$$x_{C_2}=\frac{2K}{(\delta K-r)}[\frac{n}{2}-\frac{br\beta }{(m+\mu )(\delta K-r)}],y_{C_2}=\frac{\beta bK}{(r-\delta K)(m+\mu )}.$$

The slopes of the asymptotes solve the quadratic equation $(\delta K-r)\ell -r{\ell }^2=0$, which provides immediately ${\ell }_1=0$, ${\ell }_2=(\delta K-r)r^{-1}$, so that ${\psi }_2$ has the horizontal asymptote

$$N=\frac{\beta bK}{(r-\delta K)(m+\mu )}.$$

Further, the hyperbola ${\psi }_2$ goes through the origin and crosses the negative vertical axis. There are two possible cases, $r>\delta K$ and $r<\delta K$. In the former, Case A, Figure 4, the feasible branch raises up monotonically from the origin to the horizontal asymptote, in the latter, Case B, Figure 5, instead it raises up again from the origin to the oblique asymptote. The transition among them occurs when the hyperbola degenerates into its asymptotes, as the parameter value δ crosses the critical threshold value

$${\delta }_d=\frac{r}{K}(1+\frac{\beta b}{n(m+\mu )}).$$ (20)

Figure 4.

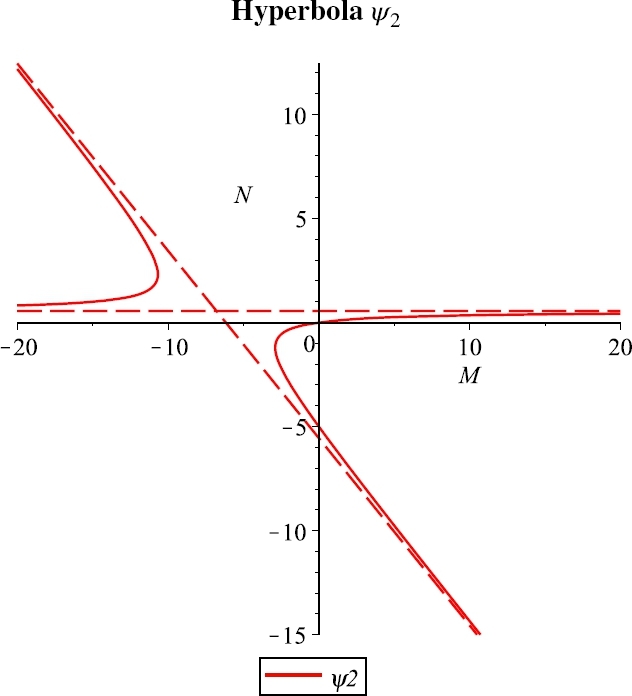
Case A. r > δK, for the parameter values r = 0.2, e = 0.001, λ = 0.03, b = 40, K = 10, β = 0.002, m = 0.04, μ = 8, δ = 0.002, n = 0.1.

Figure 5.

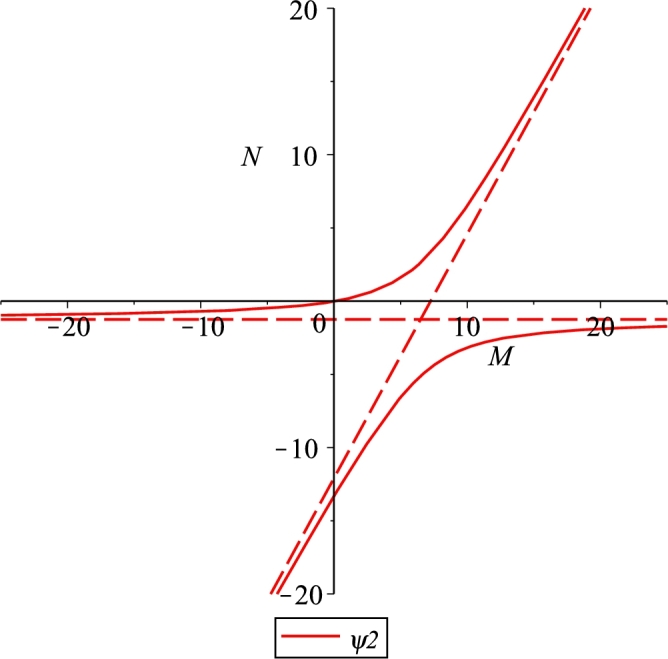
Case B. r < δK, for the parameter values r = 0.3, e = 0.001, λ = 0.03, b = 250, K = 10, β = 0.002, m = 0.04, μ = 8, δ = 0.08, n = 0.4.

4.1.3. Feasibility of the healthy-bees-free equilibrium

Evidently, the hyperbolae ${\psi }_1$ and ${\psi }_2$ intersect at one point at least, which we require to be located in the first quadrant for feasibility. The following cases may arise.

• Case 1A.

  If $\delta K<r<\frac{\beta b\delta K}{(m+\mu )(\delta K-n)-\beta b}$, there is a feasible intersection point.

• Case 2A.

  If $r>\max \{\delta K,\frac{\beta b\delta K}{(m+\mu )(\delta K-n)-\beta b},\frac{\beta b}{m+\mu }\}$, the hyperbolae cross the origin and they further intersect at a feasible intersection point.

• Case 1B.

  If $r<\min \{\delta K,\frac{\beta b\delta K}{(m+\mu )(\delta K-n)-\beta b}\}$, there is a feasible intersection point.

• Case 2B.

  If $\max \{\frac{\beta b\delta K}{(m+\mu )(\delta K-n)-\beta b},\frac{\beta b}{m+\mu }\}<r<\delta K$, the hyperbolae cross the origin and they further intersect at a feasible intersection point.

• Case 3A.
  If $\delta K<r<\frac{\beta b}{m+\mu }$, the hyperbolae cross the origin and they further intersect at a feasible point if and only if the slope at the origin of ${\psi }_2$ is larger than that of ${\psi }_1$, namely $N_{{\psi }_2}^{\prime }(0)>N_{{\psi }_1}^{\prime }(0)$. The slopes of the two hyperbolae at the origin are

  $$N_{{\psi }_1}^{\prime }(0)=\frac{\beta b-r(m+\mu )}{(r+n)(m+\mu )},N_{{\psi }_2}^{\prime }(0)=\frac{\beta b}{n(m+\mu )}.$$ (21)

  Hence, the explicit condition that they must be satisfied is

  $$\beta br+rn(m+\mu )>0,$$ (22)

  which clearly always holds.
• Case 3B.

  If $r>\min \{\delta K,\frac{\beta b}{m+\mu }\}$, a similar situation as for Case 3A arises, again depending on the slopes at the origin of the two conic sections. Condition (22) is found once again to be necessary, but again always satisfied.

In summary, the equilibrium point $E_5$ is feasible always. Note that the intersection at the origin gives $M=N=0$, so that in such case we are back to equilibrium $E_2$.

The coexistence equilibrium will finally be analyzed numerically.

5. Calculation

The aim now is to verify the stability of equilibria determined in the previous section and to find their possible mutual relations.

The Jacobian matrix for the system (5) at a generic point is given by

$$J=\left(\begin{array}{cccc}\hfill J_{11}\hfill & \hfill -\frac{bB}{{(B+I)}^2}-\gamma B\hfill & \hfill 0\hfill & \hfill -\lambda B\hfill \\ \hfill -\frac{bI}{{(B+I)}^2}+\lambda N+\gamma I\hfill & \hfill J_{22}\hfill & \hfill 0\hfill & \hfill \lambda B\hfill \\ \hfill -eM\hfill & \hfill -\beta M\hfill & \hfill J_{33}\hfill & \hfill J_{34}\hfill \\ \hfill -eN\hfill & \hfill \beta M\hfill & \hfill J_{43}\hfill & \hfill J_{44}\hfill \end{array}\right),$$ (23)

where

$$\begin{array}{cc}\hfill & J_{11}=\frac{b}{B+I}-\frac{bB}{{(B+I)}^2}-\lambda N-m-\gamma I,\hfill \\ \hfill & J_{22}=\frac{b}{B+I}-\frac{bI}{{(B+I)}^2}-m-\mu +\gamma B,\hfill \\ \hfill & J_{33}=-\frac{r(M+N)}{K}+r(1-\frac{M}{K})-\beta I-eB-\delta N,\hfill \\ \hfill & J_{34}=r(1-\frac{M}{K})-\delta M+n,\hfill \\ \hfill & J_{43}=\delta N-\frac{r}{K}N+\beta I,\hfill \\ \hfill & J_{44}=-n-eB+\delta M-\frac{r}{K}(M+N)-\frac{r}{K}N.\hfill \end{array}$$

We now turn to the stability analysis of each equilibrium. However, in view of the difficulty of analytically assessing even its existence, as already stated above, the stability of the coexistence equilibrium $E^{⁎}$ is investigated by means of simulations.

5.1. Local stability analysis of $E_1$

For the equilibrium point $E_1$ the eigenvalues are

$${\mathrm{\Lambda }}_1=-m,{\mathrm{\Lambda }}_2=\frac{b\gamma -m\mu }{m},{\mathrm{\Lambda }}_3=\frac{mr-be}{m},{\mathrm{\Lambda }}_4=-\frac{be+mn}{m}.$$

Therefore, the equilibrium $E_1$ is stable if and only if

$$\gamma <\frac{m\mu }{b},r<\frac{be}{m}.$$ (24)

5.2. Local stability analysis of $E_2$

Two of the eigenvalues of J evaluated at $E_2$ are immediately found,

$${\mathrm{\Lambda }}_1=\mu -\frac{\gamma b}{m+\mu }=\frac{m\mu +{\mu }^2-\gamma b}{m+\mu },{\mathrm{\Lambda }}_2=-m-\mu .$$

The other two eigenvalues are the roots of the equation

$${\mathrm{\Lambda }}^2-\mathrm{tr}{\hat{J}}^{⁎}(E_2)\mathrm{\Lambda }+\det {\hat{J}}^{⁎}(E_2)=0,$$ (25)

where $\mathrm{tr}{\hat{J}}^{⁎}(E_2)$ and $\det {\hat{J}}^{⁎}(E_2)$ are respectively the trace and the determinant of the submatrix

$${\hat{J}}^{⁎}(E_2)=\left(\begin{array}{cc}\hfill r-\frac{b\beta }{m+\mu }\hfill & \hfill r+n\hfill \\ \hfill \frac{\beta b}{m+\mu }\hfill & \hfill -n\hfill \end{array}\right),$$

obtained from (23) deleting the first two rows and the first two columns. The Routh–Hurwitz criterion ensures that the eigenvalues have negative real part if and only if the trace is negative and the determinant is positive. However, the latter condition is never satisfied, namely

$$\mathrm{tr}{\hat{J}}^{⁎}(E_2)=r-\frac{b\beta }{m+\mu }-n<0,\det {\hat{J}}^{⁎}(E_2)=-rn-\frac{r\beta b}{m+\mu }<0,$$ (26)

showing that $E_2$ is therefore unconditionally unstable.

5.3. Local stability analysis for $E_3$

Also for the equilibrium point $E_3$ two eigenvalues are explicit, ${\mathrm{\Lambda }}_1=-m$, ${\mathrm{\Lambda }}_2=-r+be{m}^{-1}<0$ by the feasibility condition (13). The other two eigenvalues are those of the remaining minor of the Jacobian ${\tilde{J}}^{⁎}(E_3)$, obtained by deleting its first and third rows and columns. They are the roots of the quadratic

$${\mathrm{\Lambda }}^2-\mathrm{tr}{\tilde{J}}^{⁎}(E_3)\mathrm{\Lambda }+\det {\tilde{J}}^{⁎}(E_3)=0.$$ (27)

Again, by the Routh–Hurwitz criterion, at $E_3$ stability is achieved for

$$\begin{array}{c}\frac{\gamma b}{m}+\frac{\delta K}{r}(r-\frac{be}{m})<\mu +n+r,\hfill \\ (\frac{\gamma b}{m}-\mu )[\frac{\delta K}{r}(r-\frac{eb}{m})-n-r]>\frac{\lambda b}{m}\frac{\beta K}{r}(r-\frac{be}{m}).\hfill \end{array}$$ (28)

5.4. Local stability analysis for $E_4$

The characteristic equation at $E_4$ factorizes into the product of two quadratic equations. The first is

$${\mathrm{\Lambda }}^2-\mathrm{tr}{J}^{⁎}(E_4)\mathrm{\Lambda }+\det J^{⁎}(E_4)=0,$$ (29)

where $J^{⁎}(E_4)$ is the submatrix

$$J^{⁎}(E_4)=\left(\begin{array}{cc}\hfill \frac{b\gamma (b\gamma -m\mu -{\mu }^2)}{{\mu }^3}\hfill & \hfill \frac{(b\gamma -m\mu -{\mu }^2)(b\gamma +{\mu }^2)}{{\mu }^3}\hfill \\ \hfill -\frac{(b\gamma -m\mu )(b\gamma -{\mu }^2)}{{\mu }^3}\hfill & \hfill -\frac{b\gamma (b\gamma -m\mu )}{{\mu }^3}\hfill \end{array}\right).$$

Thus, the Routh–Hurwitz conditions give the first set of inequalities needed for stability, the first one of which holds unconditionally:

$$\mathrm{tr}{J}^{⁎}(E_4)=\frac{b\gamma (b\gamma -m\mu -{\mu }^2)}{{\mu }^3}-\frac{b\gamma (b\gamma -m\mu )}{{\mu }^3}=-\frac{b\gamma }{\mu }<0,$$ (30)

$$\begin{array}{cc}\hfill \det J^{⁎}(E_4)=& \frac{b\gamma (b\gamma -m\mu -{\mu }^2)}{{\mu }^3}(-\frac{b\gamma (b\gamma -m\mu )}{{\mu }^3})\hfill \\ \hfill & +\frac{(b\gamma -m\mu -{\mu }^2)(b\gamma +{\mu }^2)(b\gamma -m\mu )(b\gamma -{\mu }^2)}{{\mu }^6}>0.\hfill \end{array}$$ (31)

Dividing (31) by $(b\gamma -m\mu -{\mu }^2)(b\gamma -m\mu )$, which is negative from the feasibility condition (15), the inequality is reduced to

$$-\frac{1}{{\mu }^2}<0,$$

so that it always holds. The second quadratic is

$${\mathrm{\Lambda }}^2-\mathrm{tr}{J}_{⁎}(E_4)\mathrm{\Lambda }+\det J_{⁎}(E_4)=0,$$ (32)

where

$$J_{⁎}(E_4)=\left(\begin{array}{cc}\hfill r-\frac{\beta (b\gamma -m\mu )-e(b\gamma -m\mu -{\mu }^2)}{\mu \gamma }\hfill & \hfill r+n\hfill \\ \hfill \frac{\beta (b\gamma -m\mu )}{\mu \gamma }\hfill & \hfill \frac{e(b\gamma -m\mu -{\mu }^2)}{\mu \gamma }-n\hfill \end{array}\right).$$ (33)

Once again, the associated Routh–Hurwitz conditions

$$\begin{array}{c}\mathrm{tr}{J}_{⁎}(E_4)=r-\frac{\beta (b\gamma -m\mu )}{\mu \gamma }+\frac{2e(b\gamma -m\mu -{\mu }^2)}{\mu \gamma }-n<0,\hfill \\ \begin{array}{cc}\hfill \det J_{⁎}(E_4)=& (r-\frac{\beta (b\gamma -m\mu )-e(b\gamma -m\mu -{\mu }^2)}{\mu \gamma })(\frac{e(b\gamma -m\mu -{\mu }^2)}{\mu \gamma }-n)\hfill \\ \hfill & -\frac{\beta (r+n)(b\gamma -m\mu )}{\mu \gamma }>0,\hfill \end{array}\hfill \end{array}$$

upon rearranging, provide the following stability conditions:

$$\begin{array}{c}r+\frac{2e(b\gamma -m\mu -{\mu }^2)}{\mu \gamma }<n+\frac{\beta (b\gamma -m\mu )}{\mu \gamma },\hfill \\ (r-\frac{\beta (b\gamma -m\mu )-e(b\gamma -m\mu -{\mu }^2)}{\mu \gamma })(\frac{e(b\gamma -m\mu -{\mu }^2)}{\mu \gamma }-n)\hfill \\ >\frac{\beta (r+n)(b\gamma -m\mu )}{\mu \gamma }.\hfill \end{array}$$ (34)

5.5. Local stability analysis for $E_5$

For the equilibrium point $E_5$ the analytic expression of the mite populations $M_5$ and $N_5$ is not known. Anyway, we can evaluate the Jacobian matrix (23) for $B=0$ and $I=b{(m+\mu )}^{-1}$. The characteristic equation factorizes to provide immediately two eigenvalues, namely

$${\mathrm{\Lambda }}_1=\mu -\lambda N_5-\frac{\gamma b}{m+\mu },{\mathrm{\Lambda }}_2=-m-\mu <0,$$

yielding the first stability condition

$$N_5>\frac{1}{\lambda }(\mu -\frac{\gamma b}{m+\mu }).$$ (35)

The other two eigenvalues are the roots of

$${\mathrm{\Lambda }}^2-\mathrm{tr}{\bar{J}}^{⁎}(E_5)\mathrm{\Lambda }+\det {\bar{J}}^{⁎}(E_5)=0$$

where ${\bar{J}}^{⁎}(E_5)$ is the submatrix

$${\bar{J}}^{⁎}(E_5)=\left(\begin{array}{cc}\hfill {\bar{J}}_{33}\hfill & \hfill r+n-\frac{r}{K}{M}_5-\delta M_5\hfill \\ \hfill \delta N_5-\frac{r}{K}{N}_5+\frac{\beta b}{m+\mu }\hfill & \hfill {\bar{J}}_{44}\hfill \end{array}\right),$$

obtained from (23) deleting the first two rows and columns and

$${\bar{J}}_{33}=r-\frac{r}{K}(2M_5+N_5)-\frac{\beta b}{m+\mu }-\delta N_5,{\bar{J}}_{44}=-n+(\delta -\frac{r}{K})M_5-2\frac{r}{K}{N}_5.$$

The Routh–Hurwitz criterion provides the remaining stability conditions

$$\begin{array}{c}{M}_5(-3\frac{r}{K}+\delta )+N_5(-\delta -3\frac{r}{K})+r<n+\frac{\beta b}{m+\mu },\hfill \\ [r-\frac{r}{K}(2M_5+N_5)-\frac{\beta b}{m+\mu }-\delta N_5][(\delta -\frac{r}{K})M_5-n-2\frac{r}{K}{N}_5]\hfill \\ >[r+n-\frac{r}{K}{M}_5-\delta M_5][(\delta -\frac{r}{K})N_5+\frac{\beta b}{m+\mu }].\hfill \end{array}$$ (36)

5.6. Transcritical bifurcations

Direct analytical considerations on the feasibility and stability conditions are only possible between a few pairs of equilibria. Some other transcritical bifurcations are instead found with the help of numerical simulations.

• •$E_1$–$E_4$
  Comparing (24) and the left inequality in (15), we find that $E_4$ becomes feasible exactly when $E_1$ is unstable, and vice versa. There is thus a transcritical bifurcation for which $E_4$ emanates from $E_1$ when the bifurcation parameter γ crosses from below the critical value ${\gamma }^{\mathrm{†}}$ given by

  $${\gamma }^{\mathrm{†}}=\frac{m\mu }{b}.$$ (37)

  The simulation reported in Figure 6 shows it explicitly. For the chosen parameter values, ${\gamma }^{\mathrm{†}}=m\mu b^{-1}\approx 0.000096$.

Figure 6.

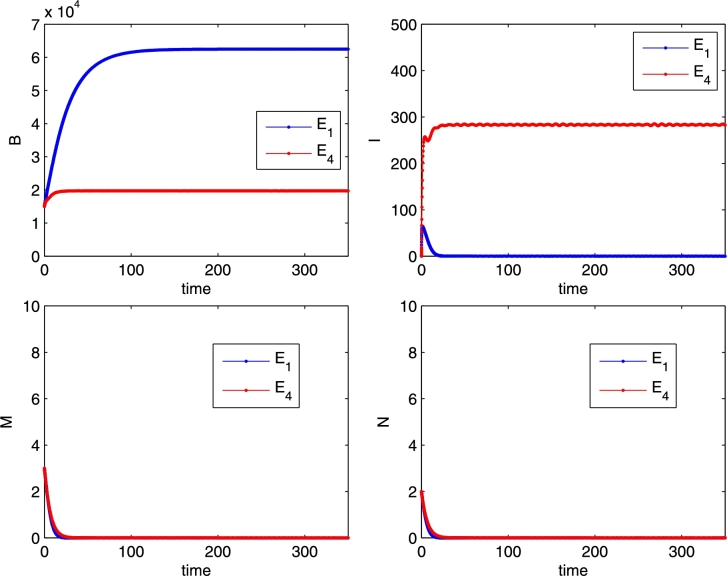
Transcritical bifurcation between E₁ and E₄, for the parameter values r = 0.02, K = 15000, b = 2500, m = 0.04, n = 0.007, e = 0.00001, μ = 6, λ = 0.01, δ = 0.0005, β = 0.00006, γ = 0.000094 (blue), γ = 0.0003 (red), p = 0.001. Initial conditions B = 15000, I = 0, M = 3, N = 2.

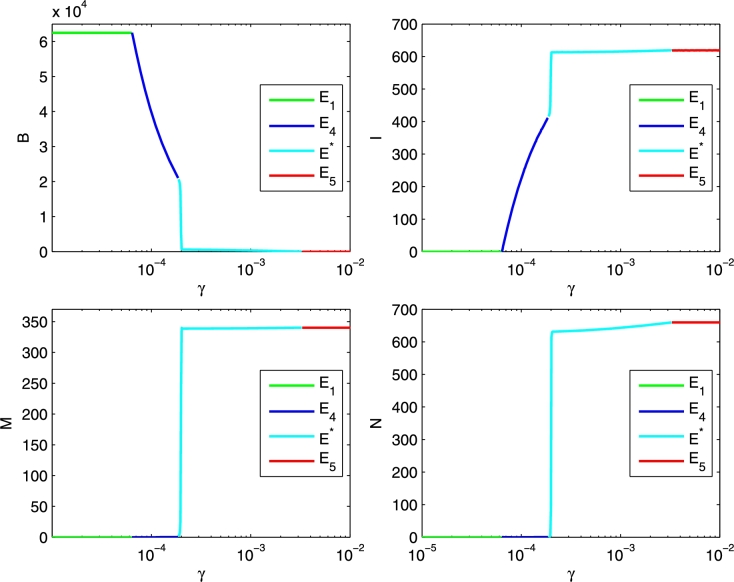
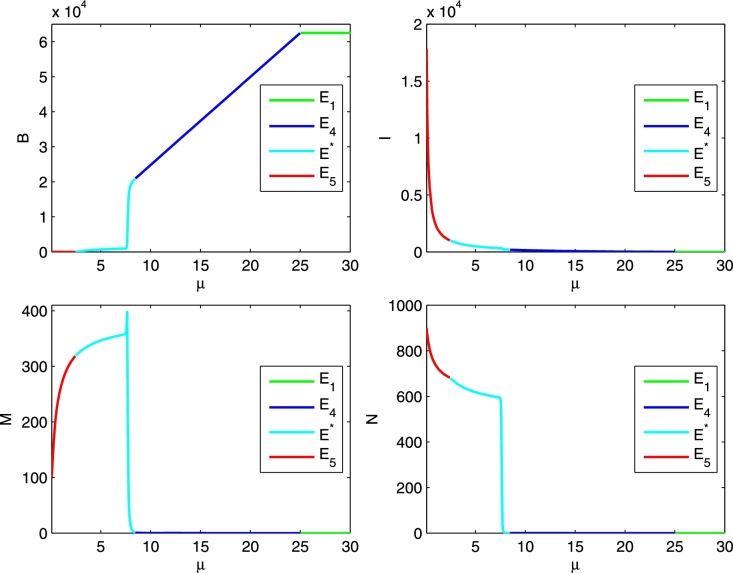
We also provide two bifurcation diagrams for the four populations as a function of the bifurcation parameters γ, in Figure 7, and μ, in Figure 8.

Figure 7.

Semilogarithmic bifurcation diagram, in terms of the bifurcation parameter γ, for the parameter values r = 0.02, K = 1000, b = 2500, m = 0.04, n = 0.007, e = 0.000001, μ = 4, λ = 0.003, δ = 0.0007, β = 0.00001. Initial conditions B = 15000, I = 0, M = 3, N = 2.

Figure 8.

Bifurcation diagram, as a function of μ, for the parameter values r = 0.02, K = 1000, b = 2500, m = 0.04, n = 0.007, e = 0.000001, γ = 0.0004, λ = 0.003, δ = 0.00007, β = 0.00001. Initial conditions B = 15000, I = 0, M = 3, N = 2.

Looking at Figure 7, starting from very low values of γ, we find at first the healthy-bees-only equilibrium $E_1$. Note that only the healthy bee population B thrives when $\gamma <{\gamma }^{\mathrm{†}}\approx 5\cdot {10}^{-5}$. Then in the range ${\gamma }^{\mathrm{†}}<\gamma <{\gamma }_1\approx 1.4\cdot {10}^{-4}$ the disease becomes endemic, thus $I>0$, while mites keep on being wiped out. The system is found thus at equilibrium $E_4$. For values of γ larger than ${\gamma }_1$ and up to ${\gamma }_2\approx 3\cdot {10}^{-3}$, the system quickly settles at the equilibrium $E^{⁎}$. Here we have coexistence of bees and mites in an endemic hive, all the populations survive. Past the threshold value ${\gamma }_2$ the healthy bee population vanishes. In this situation, the disease remains endemic and affects all the bees. This transition shows numerically the last transcritical bifurcation between coexistence and the Varroa invasion situations, namely the equilibria $E^{⁎}$ and $E_5$.

In Figure 8, starting from low values of the bifurcation parameter μ, we find instead the equilibria $E_5$, then coexistence followed by $E_4$ and finally the Varroa-free and disease-free equilibrium $E_1$.

Furthermore, comparing the μ-values in the bifurcation diagram, we discover an interesting and seemingly counter-intuitive phenomenon: a higher level of infection in the hive is obtained for a lower value of the disease-related mortality and vice versa. This can be interpreted by observing that a higher survival of infected bees makes them longer available for the transmission of the virus and inevitably leads to an increase of the viral titer in the colony. Hence, when transmitted by Varroa mites, the most virulent diseases at the colony level become the least harmful for the single bees. Thus the number of mites required for vectoring an epidemic spread is higher for the most harmful viruses. For instance, it has indeed been shown that the acute paralysis virus (APBV), which is rapidly lethal to infected bees, for its epidemic outbreak requires a much larger mite population than the mite population needed for the deformed wing virus (DWV) outbreak, which instead allows a greater survival of infected bees, [17].

5.7. Hopf bifurcations

We now try to establish whether there are special parameter combinations for which sustained population oscillations are possible.

Clearly at $E_1$ no Hopf bifurcation arises, since the eigenvalues are all real.

At $E_3$ a similar situation arises, with the quadratic (27). Annihilating the coefficient of the linear term, we have

$$-\mu +\frac{\gamma b}{m}=n+r-\frac{\delta K}{r}(r-\frac{be}{m})$$

from which, upon substitution into the constant term, we find

$$-{[-n-r+\frac{\delta K}{r}(r-\frac{be}{m})]}^2-\frac{\lambda b}{m}\frac{\beta K}{r}(r-\frac{be}{m})>0$$

which cannot be satisfied, recalling the feasibility condition (13), showing once again that no Hopf bifurcations are possible.

At $E_4$ the characteristic equation factorizes into the product of two quadratics. The first one, namely the equation (29), has a strictly positive linear term (30) so we exclude the possibility for a Hopf bifurcation to occur.

The second one has the form (32). To see whether Hopf bifurcations arise, we need the trace to vanish and the determinant to be positive. Thus, imposing the condition on the trace we are led to

$$r-\frac{\beta (b\gamma -m\mu )}{\mu \gamma }+\frac{2e(b\gamma -m\mu -{\mu }^2)}{\mu \gamma }-n=0.$$ (38)

This condition however contradicts the second stability condition (34). Indeed, note that solving for n the equation (38), we find

$$n=r-\frac{\beta (b\gamma -m\mu )}{\mu \gamma }+\frac{2e(b\gamma -m\mu -{\mu }^2)}{\mu \gamma },$$ (39)

and the second inequality in (34) becomes

$$-{(r-\frac{\beta (b\gamma -m\mu )-e(b\gamma -m\mu -{\mu }^2)}{\mu \gamma })}^2-\frac{\beta (r+n)(b\gamma -m\mu )}{\mu \gamma }>0,$$

which is never satisfied, using the left inequality in the feasibility condition (15). We conclude that also at $E_4$ no Hopf bifurcations can arise.

5.8. Global stability results

We now investigate the system's global behavior at each equilibrium, by constructing a suitable Lyapunov function in each case.

Let us define the following auxiliary quantities for each equilibrium $E_i$, $i=1,4,5$ and $E^{⁎}$:

$$\begin{array}{c}{A}_1(Z)=\frac{{\eta }^{(i)}Z}{B_i+I_i}+Z\frac{{\eta }^{(i)}\lambda B_i{N}_i}{b{I}_i},A_2={\rho }^{(i)}\delta +\frac{r({\rho }^{(i)}+{\sigma }^{(i)})}{K},\hfill \\ A_3=\frac{(r+n){\rho }^{(i)}}{M^{(i)}}+{\sigma }^{(i)}\delta ,A_4(Z)=\frac{{\eta }^{(i)}\lambda N_{i}Z}{b}+\gamma {\eta }^{(i)},A_7={\sigma }^{(i)}e+\lambda {\varphi }^{(i)},\hfill \\ A_5(Z)=\frac{({\varphi }^{(i)}+{\eta }^{(i)})Z}{B_i+I_i}+\gamma {\varphi }^{(i)},A_6(Z,W)=\frac{{\eta }^{(i)}\lambda Z}{W}+\frac{{\sigma }^{(i)}\beta M_i}{N_i}.\hfill \end{array}$$ (40)

5.8.1. Equilibrium $E_1$

At $E_1$, consider the nonnegative function

$$L_{(1)}={\varphi }^{(1)}{B}_1[\frac{B-B_1}{B_1}-\log (1+\frac{B-B_1}{B_1})]+{\eta }^{(1)}I+{\rho }^{(1)}M+{\sigma }^{(1)}N.$$ (41)

Differentiating, using (6) and bounding from above, we find

$$\begin{array}{ccc}\hfill L_{(1)}^{\prime }& \hfill =\hfill & \sum _{i=1}^4{T}_i^{(1)}={\varphi }^{(1)}\frac{B^{\prime }}{B}(B-B_1)+{\eta }^{(1)}{I}^{\prime }+{\rho }^{(1)}{M}^{\prime }+{\sigma }^{(1)}{N}^{\prime }\hfill \\ \hfill & \hfill \le \hfill & -b{\varphi }^{(1)}\frac{B-B_1+I}{(B+I)B_1}(B-B_1)-[\lambda {\varphi }^{(1)}N+\gamma {\varphi }^{(1)}I](B-B_1)\hfill \\ \hfill & \hfill \hfill & -{\eta }^{(1)}b\frac{I+B-B_1}{(B+I)B_1}I+({\eta }^{(1)}\lambda -{\sigma }^{(1)}e)(B-B_1)N-\frac{{\rho }^{(1)}r}{K}{M}^2\hfill \\ \hfill & \hfill \hfill & +(B-B_1)[{\eta }^{(1)}\gamma I-{\rho }^{(1)}eM]-MN(\frac{({\rho }^{(1)}+{\sigma }^{(1)})r}{K}+\delta {\rho }^{(1)}-\delta {\sigma }^{(1)})\hfill \\ \hfill & \hfill \hfill & -\frac{{\sigma }^{(1)}r}{K}{N}^2+MI\beta ({\sigma }^{(1)}-{\rho }^{(1)})+N({\eta }^{(1)}\lambda B_1+{\rho }^{(1)}r-n{\sigma }^{(1)}-e{\sigma }^{(1)}{B}_1)\hfill \\ \hfill & \hfill \hfill & +M{\rho }^{(1)}(r-e{B}_1+n)+I({\eta }^{(1)}\gamma B_1-(m+\mu ){\eta }^{(1)}+\frac{{\eta }^{(1)}b}{B_1}).\hfill \end{array}$$ (42)

Introducing $U^{(1)}={(B-B_1,I,M,N)}^T$ and requiring

$${\eta }^{(1)}\lambda B_1+{\rho }^{(1)}r\le n{\sigma }^{(1)}+e{\sigma }^{(1)}{B}_1,r+n\le e{B}_1,\gamma B_1+\frac{b}{B_1}\le m+\mu ,$$ (43)

it is possible then to write the estimate

$$L_{(1)}^{\prime }\le -U^{(1)T}{\mathrm{\Lambda }}^{(1)}{U}^{(1)},$$

with

$${\mathrm{\Lambda }}^{(1)}=\left[\begin{array}{cccc}\hfill \frac{b{\varphi }^{(1)}}{(B+I)B_1}\hfill & \hfill {\mathrm{\Lambda }}_{12}^{(1)}\hfill & \hfill \frac{1}{2}{\rho }^{(1)}e\hfill & \hfill {\mathrm{\Lambda }}_{14}^{(1)}\hfill \\ \hfill {\mathrm{\Lambda }}_{21}^{(1)}\hfill & \hfill \frac{{\eta }^{(1)}b}{(B+I)B_1}\hfill & \hfill \frac{1}{2}({\rho }^{(1)}-{\sigma }^{(1)})\beta \hfill & \hfill 0\hfill \\ \hfill \frac{1}{2}{\rho }^{(1)}e\hfill & \hfill \frac{1}{2}({\rho }^{(1)}-{\sigma }^{(1)})\beta \hfill & \hfill \frac{r{\rho }^{(1)}}{K}\hfill & \hfill {\mathrm{\Lambda }}_{34}^{(1)}\hfill \\ \hfill {\mathrm{\Lambda }}_{41}^{(1)}\hfill & \hfill 0\hfill & \hfill {\mathrm{\Lambda }}_{43}^{(1)}\hfill & \hfill \frac{{\sigma }^{(1)}r}{K}\hfill \end{array}\right]$$

and

$$\begin{array}{c}{\mathrm{\Lambda }}_{12}^{(1)}={\mathrm{\Lambda }}_{21}^{(1)}=\frac{1}{2}\frac{b({\varphi }^{(1)}+{\eta }^{(1)})}{(B+I)B_1}+\frac{1}{2}\gamma ({\varphi }^{(1)}-{\eta }^{(1)}),\hfill \\ {\mathrm{\Lambda }}_{14}^{(1)}={\mathrm{\Lambda }}_{41}^{(1)}=\frac{1}{2}{\sigma }^{(1)}e-\frac{1}{2}{\eta }^{(1)}\lambda +\frac{1}{2}\lambda {\varphi }^{(1)},\hfill \\ {\mathrm{\Lambda }}_{34}^{(1)}={\mathrm{\Lambda }}_{43}^{(1)}=\frac{1}{2}\frac{({\rho }^{(1)}+{\sigma }^{(1)})r}{K}+\frac{1}{2}\delta ({\rho }^{(1)}-{\sigma }^{(1)}).\hfill \end{array}$$

Now ${\mathrm{\Lambda }}^{(1)}$ is positive definite, if we require the principal minors ${\mathrm{\Delta }}_i^{(1)}$, $i=1,\dots ,4$ to be positive. For ${\mathrm{\Delta }}_1^{(1)}={\mathrm{\Lambda }}_{11}^{(1)}$ it is trivial. Deferring to the Appendix the technical details, we make here the following claims.

Theorem 5.1

$E_1$ is globally asymptotically stable if the conditions (43), (64), (66), (68) are satisfied.

5.8.2. Equilibrium $E_4$

For equilibrium $E_4$ we follow the same pattern using

$$\begin{array}{ccc}\hfill L_{(4)}& \hfill =\hfill & {\varphi }^{(4)}{B}_4[\frac{B-B_4}{B_4}-\log (1+\frac{B-B_4}{B_4})]\hfill \\ \hfill & \hfill \hfill & +{\eta }^{(4)}{I}_4[\frac{I-I_4}{I_4}-\log (1+\frac{I-I_4}{I_4})]+{\rho }^{(4)}M+{\sigma }^{(4)}N\hfill \end{array}$$ (44)

and differentiate

$$L_{(4)}^{\prime }=\sum _{i=1}^4{T}_i^{(4)}={\varphi }^{(4)}\frac{B^{\prime }}{B}(B-B_4)+{\eta }^{(4)}\frac{I^{\prime }}{I}(I-I_4)+{\rho }^{(4)}{M}^{\prime }+{\sigma }^{(4)}{N}^{\prime }.$$ (45)

Taking upper bounds for each term we have

$$T_1^{(4)}=-\frac{{\varphi }^{(4)}b{(B-B_4)}^2}{(B+I)(B_4+I_4)}-\lambda {\varphi }^{(4)}(B-B_4)N-\gamma {\varphi }^{(4)}(B-B_4)(I-I_4),$$ (46)

$$\begin{array}{cc}\hfill T_2^{(4)}=& -{(I-I_4)}^2\frac{{\eta }^{(4)}b}{(B+I)(B_4+I_4)}-\frac{{\eta }^{(4)}b}{(B+I)(B_4+I_4)}(B-B_4)(I-I_4)\hfill \\ \hfill & +(\lambda {\eta }^{(4)}\frac{N}{I}+\gamma {\eta }^{(4)})(B-B_4)(I-I_4)+\frac{{\eta }^{(4)}\lambda }{I}{B}_4(I-I_4)N,\hfill \end{array}$$ (47)

$$\begin{array}{cc}\hfill T_3^{(4)}=& -M^2\frac{{\rho }^{(4)}r}{K}-{\rho }^{(4)}\beta M(I-I_4)-e{\rho }^{(4)}M(B-B_4)\hfill \\ \hfill & -{\rho }^{(4)}MN(\delta +\frac{r}{K})+{\rho }^{(4)}(r+n)N-{\rho }^{(4)}\beta M{I}_4-{\rho }^{(4)}eM{B}_4,\hfill \end{array}$$ (48)

$$\begin{array}{cc}\hfill T_4^{(4)}=& -{\sigma }^{(4)}{N}^2\frac{r}{K}+{\sigma }^{(4)}NM(\delta -\frac{r}{K})+\beta {\sigma }^{(4)}M(I-I_4)\hfill \\ \hfill & -e{\sigma }^{(4)}N(B-B_4)-n{\sigma }^{(4)}N-e{\sigma }^{(4)}N{B}_4+\beta {\sigma }^{(4)}M{I}_4.\hfill \end{array}$$ (49)

Introducing $U^{(4)}={(B-B_4,I-I_4,M,N)}^T$ and imposing

$$\beta {\sigma }^{(4)}{I}_4\le {\rho }^{(4)}\beta I_4+{\rho }^{(4)}e{B}_4,{\rho }^{(4)}(r+n)\le {\sigma }^{(4)}(n+e{B}_4),$$ (50)

we have the estimate $L_{(4)}^{\prime }\le -U^{(4)T}{\mathrm{\Lambda }}^{(4)}{U}^{(4)}$, with

$${\mathrm{\Lambda }}^{(4)}=\left[\begin{array}{cccc}\hfill \frac{b{\varphi }^{(4)}}{(B+I)(B_4+I_4)}\hfill & \hfill {\mathrm{\Lambda }}_{1,2}^{(4)}\hfill & \hfill \frac{1}{2}{\rho }^{(4)}e\hfill & \hfill {\mathrm{\Lambda }}_{1,4}^{(4)}\hfill \\ \hfill {\mathrm{\Lambda }}_{2.1}^{(4)}\hfill & \hfill \frac{{\eta }^{(4)}b}{(B+I)(B_4+I_4)}\hfill & \hfill (\frac{{\rho }^{(4)}}{2}-\frac{{\sigma }^{(4)}}{2})\beta \hfill & \hfill -\frac{1}{2}\frac{{\eta }^{(4)}\lambda B_4}{I}\hfill \\ \hfill \frac{1}{2}{\rho }^{(4)}e\hfill & \hfill (\frac{{\rho }^{(4)}}{2}-\frac{{\sigma }^{(4)}}{2})\beta \hfill & \hfill \frac{r{\rho }^{(4)}}{K}\hfill & \hfill {\mathrm{\Lambda }}_{3,4}^{(4)}\hfill \\ \hfill {\mathrm{\Lambda }}_{4,1}^{(4)}\hfill & \hfill -\frac{1}{2}\frac{{\eta }^{(4)}\lambda B_4}{I}\hfill & \hfill {\mathrm{\Lambda }}_{4,3}^{(4)}\hfill & \hfill \frac{{\sigma }^{(4)}r}{K}\hfill \end{array}\right]$$

where

$$\begin{array}{c}{\mathrm{\Lambda }}_{1,2}^{(4)}={\mathrm{\Lambda }}_{2,1}^{(4)}=\frac{1}{2}\gamma ({\varphi }^{(4)}-{\eta }^{(4)})+\frac{1}{2}\frac{{\eta }^{(4)}b}{(B+I)(B_4+I_4)}-\frac{1}{2}\frac{{\eta }^{(4)}\lambda N}{I},\hfill \\ {\mathrm{\Lambda }}_{3,4}^{(4)}={\mathrm{\Lambda }}_{4,3}^{(4)}=\frac{1}{2}\frac{({\rho }^{(4)}+{\sigma }^{(4)})r}{K}+\frac{1}{2}\delta ({\rho }^{(4)}-{\sigma }^{(4)}),\hfill \\ {\mathrm{\Lambda }}_{1,4}^{(4)}={\mathrm{\Lambda }}_{4,1}^{(4)}=\frac{1}{2}({\sigma }^{(4)}e+\lambda {\varphi }^{(4)}).\hfill \end{array}$$

Theorem 5.2

$E_4$ is globally asymptotically stable provided the conditions (50), (69), (70), (71) hold.

5.8.3. Equilibrium $E_5$

At $E_5$ we take

$$\begin{array}{ccc}\hfill L_{(5)}& \hfill =\hfill & {\varphi }^{(5)}B+{\eta }^{(5)}{I}_5[\frac{I-I_5}{I_5}-\log (1+\frac{I-I_5}{I_5})]\hfill \\ \hfill & \hfill \hfill & +{\rho }^{(5)}{M}_5[\frac{M-M_5}{M_5}-\log (1+\frac{M-M_5}{M_5})]\hfill \\ \hfill & \hfill \hfill & +{\sigma }^{(5)}{N}_5[\frac{N-N_5}{N_5}-\log (1+\frac{N-N_5}{N_5})]\hfill \end{array}$$ (51)

and differentiate

$$\begin{array}{ccc}\hfill L_{(5)}^{\prime }=\sum _{i=1}^4{T}_i^{(5)}& \hfill =\hfill & {\varphi }^{(5)}{B}^{\prime }+{\eta }^{(5)}\frac{I^{\prime }}{I}(I-I_5)\hfill \\ \hfill & \hfill \hfill & +{\rho }^{(5)}\frac{M^{\prime }}{M}(M-M_5)+{\sigma }^{(5)}\frac{N^{\prime }}{N}(N-N_5).\hfill \end{array}$$ (52)

Requiring

$$\frac{b}{I_5}+\gamma I_5\le \lambda N_5+m$$ (53)

we obtain the bound

$$T_1^{(5)}\le -\frac{{\varphi }^{(5)}{B}^2}{(B+I)I_5}-{\varphi }^{(5)}B(I-I_5)(\frac{b}{(B+I)I_5}+\gamma )-\lambda {\varphi }^{(5)}B(N-N_5),$$ (54)

as well as

$$\begin{array}{cc}\hfill T_2^{(5)}\le & -{\eta }^{(5)}{(I-I_5)}^2\frac{b}{(B+I)I_5}\hfill \\ \hfill & +{\eta }^{(5)}B(I-I_5)(\frac{\lambda N_5}{I_5}+\gamma -\frac{b}{(B+I)I_5})+{\eta }^{(5)}(I-I_5)(N-N_5)\frac{\lambda B}{I_5},\hfill \end{array}$$ (55)

$$\begin{array}{cc}\hfill T_3^{(5)}\le & -\frac{{\rho }^{(5)}r}{K}{(M-M_5)}^2-{\rho }^{(5)}\beta (M-M_5)(I-I_5)\hfill \\ \hfill & -{\rho }^{(5)}(M-M_5)(N-N_5)(\frac{r}{K}-\frac{r+n}{M_5}+\delta )-e{\rho }^{(5)}B(M-M_5),\hfill \end{array}$$ (56)

$$\begin{array}{cc}\hfill T_4^{(5)}\le & -\frac{{\sigma }^{(5)}r}{K}{(N-N_5)}^2+{\sigma }^{(5)}\beta \frac{M_5}{N_5}(N-N_5)(I-I_5)\hfill \\ \hfill & +{\sigma }^{(5)}(M-M_5)(N-N_5)(\delta +\frac{\beta I}{N_5}-\frac{r}{K})-e{\sigma }^{(5)}B(N-N_5),\hfill \end{array}$$ (57)

so that with $U^{(5)}={(B,I-I_5,M-M_5,N-N_5)}^T$ we have the estimate $L_{(5)}^{\prime }\le -U^{(5)T}{\mathrm{\Lambda }}^{(5)}{U}^{(5)}$, with

$${\mathrm{\Lambda }}^{(5)}=\left[\begin{array}{cccc}\hfill \frac{{\varphi }^{(5)}}{(B+I)I_5}\hfill & \hfill {\mathrm{\Lambda }}_{1,2}^{(5)}\hfill & \hfill \frac{1}{2}{\rho }^{(5)}e\hfill & \hfill {\mathrm{\Lambda }}_{1,4}^{(5)}\hfill \\ \hfill {\mathrm{\Lambda }}_{2,1}^{(5)}\hfill & \hfill \frac{{\eta }^{(5)}b}{(B+I)I_5}\hfill & \hfill \frac{1}{2}{\rho }^{(5)}\beta \hfill & \hfill {\mathrm{\Lambda }}_{4,2}^{(5)}\hfill \\ \hfill \frac{1}{2}{\rho }^{(5)}e\hfill & \hfill \frac{1}{2}{\rho }^{(5)}\beta \hfill & \hfill \frac{r{\rho }^{(5)}}{K}\hfill & \hfill {\mathrm{\Lambda }}_{3,4}^{(5)}\hfill \\ \hfill {\mathrm{\Lambda }}_{4,1}^{(5)}\hfill & \hfill {\mathrm{\Lambda }}_{4,2}^{(5)}\hfill & \hfill {\mathrm{\Lambda }}_{4,3}^{(5)}\hfill & \hfill \frac{{\sigma }^{(5)}r}{K}\hfill \end{array}\right]$$

where

$$\begin{array}{c}{\mathrm{\Lambda }}_{1,2}^{(5)}={\mathrm{\Lambda }}_{2,1}^{(5)}=\frac{b}{2}\frac{{\varphi }^{(5)}+{\eta }^{(5)}}{(B+I)I_5}+\frac{1}{2}\gamma ({\varphi }^{(5)}-{\eta }^{(5)})-\frac{1}{2}\frac{{\eta }^{(5)}\lambda N_5}{I_5},\hfill \\ {\mathrm{\Lambda }}_{1,4}^{(5)}={\mathrm{\Lambda }}_{4,1}^{(5)}=\frac{1}{2}({\sigma }^{(5)}e+\lambda {\varphi }^{(5)}),{\mathrm{\Lambda }}_{2,4}^{(5)}={\mathrm{\Lambda }}_{4,2}^{(5)}=-\frac{1}{2}(\frac{{\eta }^{(5)}\lambda B}{I_5}+\frac{{\sigma }^{(5)}\beta M_5}{N_5}),\hfill \\ {\mathrm{\Lambda }}_{3,4}^{(5)}={\mathrm{\Lambda }}_{4,3}^{(5)}=\frac{r}{2}\frac{{\rho }^{(5)}+{\sigma }^{(5)}}{K}-\frac{1}{2}\frac{{\rho }^{(5)}(r+n)}{M_5}-\frac{1}{2}\frac{{\sigma }^{(5)}\beta I}{N_5}+\frac{1}{2}\delta ({\rho }^{(5)}-{\sigma }^{(5)}).\hfill \end{array}$$

In summary we have

Theorem 5.3

If the conditions (53), (72), (73), (74) are valid, equilibrium $E_5$ is globally asymptotically stable.

5.8.4. Equilibrium $E^{⁎}$

It is possible to investigate the global stability of the equilibrium $E^{⁎}$, under certain conditions, once again by constructing a suitable Lyapunov function. Consider the nonnegative function

$$\begin{array}{ccc}\hfill L_{⁎}& \hfill =\hfill & {\varphi }^{⁎}{B}^{⁎}[\frac{B-B^{⁎}}{B^{⁎}}-\log (1+\frac{B-B^{⁎}}{B^{⁎}})]\hfill \\ \hfill & \hfill \hfill & +{\eta }^{⁎}{I}^{⁎}[\frac{I-I^{⁎}}{I^{⁎}}-\log (1+\frac{I-I^{⁎}}{I^{⁎}})]\hfill \\ \hfill & \hfill \hfill & +{\rho }^{⁎}{M}^{⁎}[\frac{M-M^{⁎}}{M^{⁎}}-\log (1+\frac{M-M^{⁎}}{M^{⁎}})]\hfill \\ \hfill & \hfill \hfill & +{\sigma }^{⁎}{N}^{⁎}[\frac{N-N^{⁎}}{N^{⁎}}-\log (1+\frac{N-N^{⁎}}{N^{⁎}})].\hfill \end{array}$$ (58)

Upon differentiation, we find

$$\begin{array}{ccc}\hfill L_{⁎}^{\prime }& \hfill =\hfill & \sum _{i=1}^4{T}_i^{⁎}\hfill \\ \hfill & \hfill =\hfill & {\varphi }^{⁎}\frac{B^{\prime }}{B}(B-B^{⁎})+{\eta }^{⁎}\frac{I^{\prime }}{I}(I-I^{⁎})+{\rho }^{⁎}\frac{M^{\prime }}{M}(M-M^{⁎})+{\sigma }^{⁎}\frac{N^{\prime }}{N}(N-N^{⁎}),\hfill \end{array}$$ (59)

and using the equations of (6), collecting similar terms, we find for the first two terms the following expressions

$$\begin{array}{c}\begin{array}{cc}\hfill T_1^{⁎}=& -\frac{{\varphi }^{⁎}b(B-B^{⁎})[(B-B^{⁎})+(I-I^{⁎})]}{(B+I)(B^{⁎}+I^{⁎})}\hfill \\ \hfill & -{\varphi }^{⁎}(B-B^{⁎})[\gamma (I-I^{⁎})+\lambda (N-N^{⁎})],\hfill \end{array}\hfill \\ \begin{array}{cc}\hfill T_2^{⁎}=& (I-I^{⁎})(B-B^{⁎})[\gamma {\eta }^{⁎}-\frac{{\eta }^{⁎}b}{(B+I)(B^{⁎}+I^{⁎})}+\frac{{\eta }^{⁎}\lambda N^{⁎}}{I}]\hfill \\ \hfill & -{(I-I^{⁎})}^2[\frac{{\eta }^{⁎}b}{(B+I)(B^{⁎}+I^{⁎})}+\frac{{\eta }^{⁎}\lambda B^{⁎}{N}^{⁎}}{I{I}^{⁎}}]+{\eta }^{⁎}\lambda \frac{B}{I}(I-I^{⁎})(N-N^{⁎}).\hfill \end{array}\hfill \end{array}$$

For the remaining terms we have the following bounds

$$\begin{array}{c}\begin{array}{cc}\hfill T_3^{⁎}=& -{\rho }^{⁎}{(M-M^{⁎})}^2[\frac{(r+n)N}{M{M}^{⁎}}+\frac{r}{K}]\hfill \\ \hfill & +{\rho }^{⁎}(M-M^{⁎})[(N-N^{⁎})(\frac{(r+n)}{M^{⁎}}-\frac{r}{K}-\delta )-\beta (I-I^{⁎})-e(B-B^{⁎})]\hfill \\ \hfill \le & -{\rho }^{⁎}{(M-M^{⁎})}^2\frac{r}{K}+{\rho }^{⁎}(M-M^{⁎})(N-N^{⁎})[\frac{(r+n)}{M^{⁎}}-\frac{r}{K}-\delta ]\hfill \\ \hfill & -{\rho }^{⁎}(M-M^{⁎})[\beta (I-I^{⁎})+e(B-B^{⁎})],\hfill \end{array}\hfill \\ \begin{array}{cc}\hfill T_4^{⁎}=& -{\sigma }^{⁎}{(N-N^{⁎})}^2[\frac{MI\beta }{N{N}^{⁎}}+\frac{r}{K}]\hfill \\ \hfill & +{\sigma }^{⁎}(N-N^{⁎})[(M-M^{⁎})(\frac{\beta I}{N^{⁎}}-\frac{r}{K}+\delta )+\beta \frac{M^{⁎}}{N^{⁎}}(I-I^{⁎})-e(B-B^{⁎})]\hfill \\ \hfill \le & {\sigma }^{⁎}\frac{r}{K}{(N-N^{⁎})}^2+{\sigma }^{⁎}(N-N^{⁎})[(M-M^{⁎})(\frac{\beta I}{N^{⁎}}-\frac{r}{K}+\delta )\hfill \\ \hfill & +\beta \frac{M^{⁎}}{N^{⁎}}(I-I^{⁎})-e(B-B^{⁎})].\hfill \end{array}\hfill \end{array}$$

Letting $U^{⁎}={(B-B^{⁎},I-I^{⁎},M-M^{⁎},N-N^{⁎})}^T$, once again it therefore follows $L_{⁎}^{\prime }\le -U^{⁎T}{\mathrm{\Lambda }}^{⁎}{U}^{⁎}$, with the symmetric matrix ${\mathrm{\Lambda }}^{⁎}$ with entries

$$\begin{array}{c}{\mathrm{\Lambda }}_{11}^{⁎}=\frac{{\varphi }^{⁎}b}{(B+I)(B^{⁎}+I^{⁎})},{\mathrm{\Lambda }}_{13}^{⁎}={\mathrm{\Lambda }}_{31}^{⁎}=\frac{1}{2}e{\rho }^{⁎},{\mathrm{\Lambda }}_{14}^{⁎}={\mathrm{\Lambda }}_{41}^{⁎}=\frac{1}{2}(\lambda {\varphi }^{⁎}+e{\sigma }^{⁎}),\hfill \\ {\mathrm{\Lambda }}_{12}^{⁎}={\mathrm{\Lambda }}_{21}^{⁎}=\frac{1}{2}[\frac{({\varphi }^{⁎}+{\eta }^{⁎})b}{(B+I)(B^{⁎}+I^{⁎})}+\gamma ({\varphi }^{⁎}-{\eta }^{⁎})-\frac{{\eta }^{⁎}\lambda N^{⁎}}{I}],\hfill \\ {\mathrm{\Lambda }}_{22}^{⁎}=\frac{{\eta }^{⁎}b}{(B+I)(B^{⁎}+I^{⁎})}+\frac{{\eta }^{⁎}\lambda B^{⁎}{N}^{⁎}}{I{I}^{⁎}},{\mathrm{\Lambda }}_{23}^{⁎}={\mathrm{\Lambda }}_{32}^{⁎}=\frac{1}{2}\beta {\rho }^{⁎},\hfill \\ {\mathrm{\Lambda }}_{24}^{⁎}={\mathrm{\Lambda }}_{42}^{⁎}=-\frac{1}{2}(\frac{{\eta }^{⁎}\lambda B}{I}+\frac{\beta {\sigma }^{⁎}{M}^{⁎}}{N^{⁎}}),{\mathrm{\Lambda }}_{33}^{⁎}=\frac{{\rho }^{⁎}r}{K},\hfill \\ {\mathrm{\Lambda }}_{34}^{⁎}={\mathrm{\Lambda }}_{43}^{⁎}=-\frac{1}{2}[{\rho }^{⁎}\frac{r+n}{M^{⁎}}-\frac{r}{K}({\rho }^{⁎}+{\sigma }^{⁎})-\delta ({\rho }^{⁎}-{\sigma }^{⁎})+\frac{\beta {\sigma }^{⁎}I}{N^{⁎}}],{\mathrm{\Lambda }}_{44}^{⁎}=\frac{{\sigma }^{⁎}r}{K}.\hfill \end{array}$$

Now ${\mathrm{\Lambda }}^{⁎}$ is positive definite if all its principal minors ${\mathrm{\Delta }}_i^{⁎}$, $i=1,\dots ,4$ are positive. This is ensured by the following conditions. For ${\mathrm{\Delta }}_1^{⁎}$, it is clear, as ${\mathrm{\Lambda }}_{11}^{⁎}>0$.

The final result is the following.

Theorem 5.4

Assuming conditions (75), (76), (77), the coexistence equilibrium is globally asymptotically stable.

6. Results

In this section, after describing the set of parameter values used, we carry out numerical simulations using the Matlab built-in ordinary differential equations solver ode45.

6.1. The known model parameters

We take the known model parameters from the literature, [2], [6], §8.2.3.5, [8] and [12], while we simulate the remaining ones.

Taking the day as the time unit, the birth rate of worker honey bees is taken as $b=2500$, while their natural mortality rate is $m=0.04$, equivalent to a life expectancy of 25 days, [8].

The literature does not provide a precise value for the grooming behavior, but from [8] a range of reasonable values of e lies between ${10}^{-6}$ and ${10}^{-5}$.

During the bee season, i.e. spring and summer, the mite population doubles every month, so we fix $r\approx {30}^{-1}\ln 2$, that is $r=0.02$, [6], p. 225.

Their carrying capacity is taken as $K=15000$ mites, [12], while their natural mortality rate in the phoretic phase is estimated to be $n=0.007$ during the bee season, [2].

Table 1 summarizes the values used in the numerical simulations.

Table 1.

Model parameters and their values from the literature. Bees and mites are measured in pure numbers.

Parameter	Interpretation	Value	Unit	Source
b	Bee daily birth rate	2500	day−1	[8]
e	Grooming rate of healthy bee	10−6 − 10−5	day−1	[8]
m	Bee natural mortality rate	0.04	day−1	[8]
K	Varroa carrying capacity	15000		[12]
r	Varroa growth rate	0.02	day−1	[6]
n	Varroa natural mortality rate in the phoretic phase	0.007	day−1	[2]

6.2. Initial conditions and free parameters

The initial conditions for the colony are given from field data. All the bees are healthy since the infected, having a lower longevity, cannot survive the winter. Further, the acaricide treatments against Varroa performed in the autumn and winter theoretically allow to eradicate the infestation, so that the mite population usually does not exceed 10 units at the beginning of the bee season, see Table 2.

Table 2.

Initial condition for the simulations.

Population	Value
Sound bees	15000
Infected bees	0
Mites	≤10

For the known parameters we use the reference values from field data reported in Table 1. For the remaining free parameters, the values are arbitrarily chosen to simulate a hypothetical hive.

6.3. Equilibrium $E_1$

At equilibrium $E_1$ only the healthy bees survive. It represents the best situation for the hive. Healthy and infected mites are wiped out while the healthy bee population increases to a level of 62500 units, which matches field observations on the size of actual beehives.

The equilibrium $E_1$ is stably attained for the following choice of the free parameters: $\mu =4$, $\lambda =0.003$; $\delta =0.00007$, $\beta =0.00001$, $\gamma =0.00001$. Initial conditions are set as follows: $B=15000$, $I=0$, $M=3$, $N=2$.

The second stability condition (24) is always satisfied by the field data. Infected bees become extinct in view of the remaining stability condition (24), that, rewritten in the form

$$\gamma <\frac{m\mu }{b},$$ (60)

establishes an upper bound on the horizontal transmission rate of the virus among the bees.

6.4. Equilibrium $E_3$

The disease-free equilibrium point $E_3$, where also healthy mites are present, is impossible in the field conditions, since the feasibility condition (13) is not satisfied.

This result is well substantiated by the empirical beekeepers observations in natural honey bee colonies. Namely, the viral infection occurs whenever the mite population is present.

6.5. Equilibrium $E_4$

At the mite-free equilibrium point $E_4$ the disease remains endemic among the bees.

Rearranging (15), we can see that in this situation the opposite condition of equilibrium $E_1$ must be verified, namely

$$\frac{m\mu }{b}<\gamma <\frac{\mu +m}{b}\mu$$ (61)

imposing a lower and an upper bound on the disease horizontal transmission rate among bees. It is indeed reasonable to expect that with a high enough contact rate also the population of infected bees survives, as opposed to the equilibrium $E_1$, while a too low one instead becomes insufficient for the infected bees to thrive, compare indeed (61) with the alternative condition (60). If instead the horizontal transmission rate becomes too large, exceeding its upper bound in (61), the point $E_4$ is not feasible, showing therefore that the mites must invade the beehive. These remarks are clearly visible in Figure 7.

The equilibrium $E_4$ is obtained for the free parameter values: $\mu =6$, $\lambda =0.01$, $\delta =0.0005$, $\beta =0.00006$, $\gamma =0.0002$ and the initial conditions $B=15000$, $I=0$, $M=3$, $N=2$. The eigenvalues of the Jacobian matrix for these parameter values are

$${\mathrm{\Lambda }}_1\approx -0.0416+0.5i,{\mathrm{\Lambda }}_2\approx -0.0416-0.5i,{\mathrm{\Lambda }}_3\approx -0.28,{\mathrm{\Lambda }}_4\approx -0.32,$$

showing that $E_4$ is approached via damped oscillations.

6.6. Equilibrium $E_5$

The equilibrium $E_5$ represents the Varroa invasion scenario. It is always feasible and can be obtained with the following choice for the free parameters: $\mu =5$, $\lambda =0.004$, $\delta =0.0005$, $\beta =0.0001$, $\gamma =0.3$ and the initial conditions $B=15000$, $I=0$, $M=3$, $N=2$.

Also in this case, the viral infection remains endemic. The effective virulence of the disease is increased by the presence of mites, since the virus is directly vectored into the hemolymph of the honey bees. As a consequence, the healthy bee population becomes extinct.

Since $E_2$ is unstable, it seems much more likely that an epidemic could affect all the bees in a Varroa-infested colony than in a Varroa-free colony, as reported in [12], where it is stated in fact that “the mite is a far more effective vector than nurse bees are”. Further, detailed studies show that most of the honey bee viruses are present at low levels but do not cause any apparent symptoms in Varroa-free colonies. Only important stressors, such as the introduction of Varroa destructor, can convert the silent infection into a symptomatic one, [9], [18].

6.7. The coexistence equilibrium $E^{⁎}$

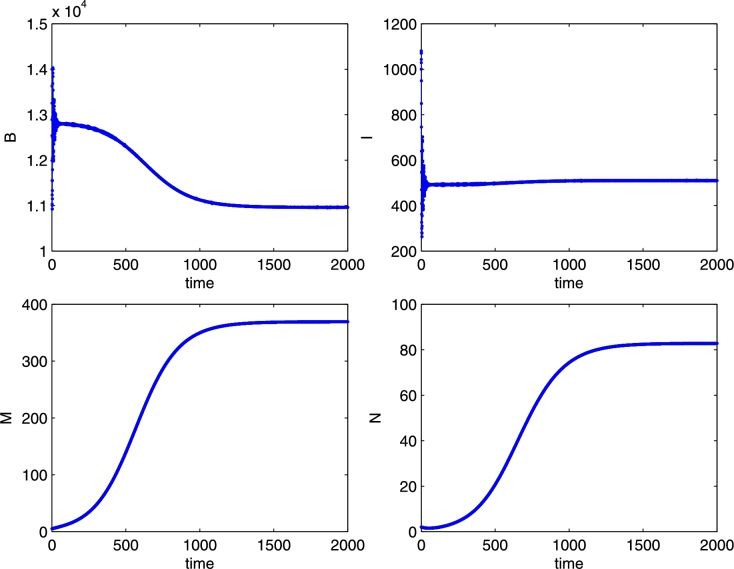
At coexistence the honey bees share their infected hive with mites.

Figures 9 and 10 show two different levels of infection in the mites. The spread of the virus throughout the colony depends on the model parameters describing the disease transmission, namely λ, γ, β, δ. Reasonably, smaller values of these parameters lead to a rather higher proportion of healthy bees and mites with respect to the infected ones, Figure 10, while the opposite situation is depicted in Figure 9 with a higher disease prevalence in the presence of higher disease transmission rates.

Figure 9.

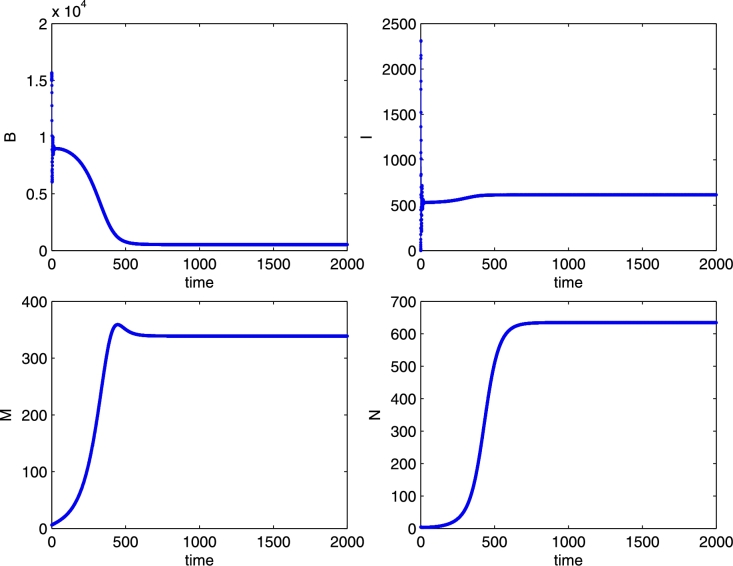
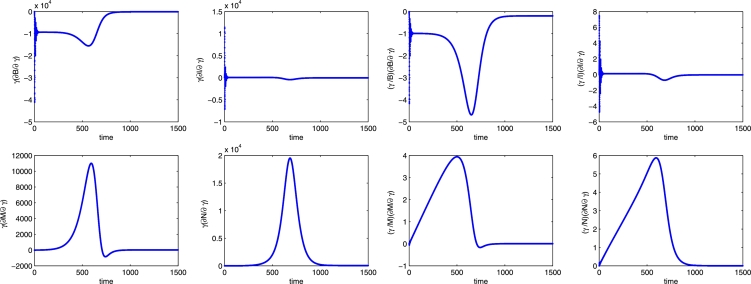
The coexistence equilibrium E*, for the parameter values: r = 0.02, K = 1000, b = 2500, m = 0.04, n = 0.007, e = 0.000001, μ = 4, λ = 0.003, δ = 0.00007, β = 0.00001, γ = 0.0004. Initial conditions B = 15000, I = 0, M = 6, N = 4. Note the sharp decrease of the healthy bee population as the mites rapidly increase in the early times of the simulation.

Figure 10.

The coexistence equilibrium E*, for the parameter values: r = 0.02, K = 1000, b = 2500, m = 0.04, n = 0.007, e = 0.000001, μ = 4, λ = 0.0003, δ = 0.00003, β = 0.000007, γ = 0.0003. Initial conditions B = 14000, I = 1000, M = 5, N = 2. Here we use lower transmission rates and a different initial condition from the previous simulations, in particular a nonzero value for the infected bees, to highlight the effect of Varroa infestation on honey bee viral infections: indeed, for early times, there is a decrease of both bee populations as the number of mites increases.

6.8. Summary

We sum up the feasibility and stability conditions of the equilibrium points in Table 3.

Table 3.

Summarizing feasibility and stability conditions table of the equilibria.

Equilibrium	Feasibility	Stability	In field conditions
$E_1$	Always	(24)	Allowed
$E_2$	Always	Unstable	Unstable
$E_3$	(13)	(28)	Infeasible
$E_4$	(15)	(34)	Allowed
$E_5$	Always	(35), (36)	Allowed
$E^{⁎}$	Numerical simulations	Numerical simulations	Allowed

7. Discussion

In this section we perform the sensitivity analysis on (5) in order to assess the parameters that most influence the system dynamics. We illustrate the concepts following the ideas presented in [15].

The sensitivity equations are obtained by differentiating the model equations with respect to all the parameters. Since our model consists of 4 equations with 11 parameters, we obtain a sensitivity system of 44 equations. Letting α denote the vector of the 11 parameters, [5], the sensitivity system for (5) can be formulated as follows

$$\frac{d}{dt}\left(\frac{\partial X_i(\alpha ,t)}{\partial {\alpha }_j}\right)=\sum _{s=1}^4\frac{\partial f_i(X,\alpha ,t)}{\partial X_s}\frac{\partial X_s(\alpha ,t)}{\partial {\alpha }_j}+\frac{\partial f_i(X,\alpha ,t)}{\partial {\alpha }_j},$$ (62)

for $i=1,\dots ,4$ and $j=1,\dots ,11$, with initial conditions

$$\frac{\partial X_i(\alpha ,0)}{\partial {\alpha }_j}=0,i=1,\dots ,4,j=1,\dots ,11.$$ (63)

Solving such system requires the knowledge of the state variables $X_i$, $i=1,\dots ,4$, which come from the solution of the original system (5). We are finally led to solve a system of 48 differential equations. Thus, the rate of change of each state as a function of the change in the chosen parameter is obtained from the value of the sensitivity solution evaluated at time t, [3].

The parameters and thus also the sensitivity solutions for different parameters, are however measured in different units. This means that without further action, any comparison is futile. To make a valid comparison of the effect that parameters with different units have on the solution, the sensitivity solution is multiplied by the parameter under consideration, obtaining the so-called semi-relative sensitivity solution, [1]. It provides information concerning the amount of change that the variable will experience when the parameter of interest is subject to a positive perturbation, [3].

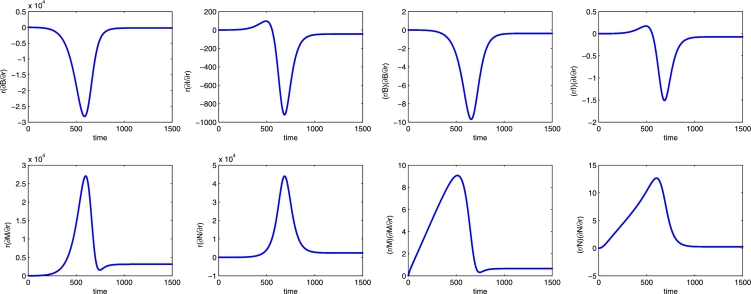
Computing the semi-relative solutions and making a comparison of the scales on the vertical axis of these plots, i.e. ranking the parameters according to the ∞-norm, we deduce that the parameters most affecting the system are r, μ, e and γ.

Specifically, an increase of the Varroa growth rate dramatically influences the solutions and has a negative effect on the bee populations and a positive influence on the mite populations, consistently with Figure 11 (left frame). Furthermore, the effect of perturbing r can best be observed on the transient dynamics of the populations B, M and N. It corresponds respectively to a reduction of about 28200 healthy bees after 590 days and an increment of 27000 (at $t=600$) and 44000 (at $t=685$) units for the mite populations.

Figure 11.

Semi-relative solutions (left) and the logarithmic sensitivity solutions (right) with respect to the parameter r. In each frame the populations are B, I, M, N in clockwise order.

From Figure 11 (right frame), we can approximately obtain the expected percentage changes from an increase of r. In particular, [3], we compute the logarithmic sensitivity solutions, namely

$$\frac{\partial \log (X_i(\alpha ,t))}{\partial \log ({\alpha }_j)}=\frac{{\alpha }_j}{X_i(\alpha ,t)}\frac{\partial X_i(\alpha ,t)}{\partial {\alpha }_j},$$ (64)

for $i=1,\dots ,4$ and $j=1,\dots ,11$.

Calculating (64), we find that a positive perturbation of r leads to a decrease of up to 970% in the healthy bee population at $t=655$ days, a 150% decrease in the infected bee population at $t=685$ days, a 900% increase in the healthy mite population at $t=510$ days, and over 1250% increase in the infected mite population at $t=600$ days.

However, note that the changes in the populations of more than 100% in the time interval $[500,700]$ are reasonable as their level in such time interval is quite low, i.e. each population does not exceed 2000 units. This is shown in Figure 9 for the set of parameter values used in the sensitivity analysis.

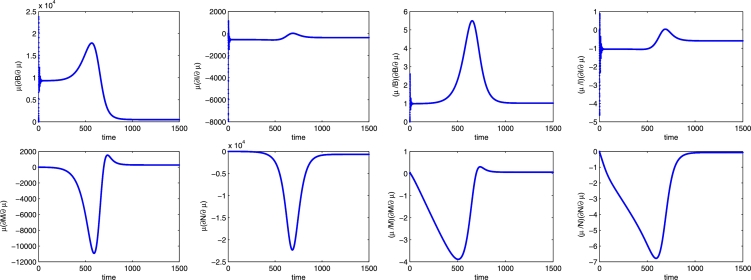
We now turn to the parameter μ, second in order of sensitivity. Let us focus on the bee populations B and I. From Figure 12, it is clear that a higher value of the bees disease-related mortality has a positive impact on the healthy bee population and a negative influence on the infected bee population. It also depresses both mite populations.

Figure 12.

Semi-relative solutions (left) and the logarithmic sensitivity solutions (right) with respect to the parameter μ. In each frame the populations are B, I, M, N in clockwise order.

From our results, an increase in μ leads to a decrease in the infected bee population. In particular, we find an increase of 17900 healthy bees at time $t=565$ (peak of about 550% expected change) and a reduction of 370 infected bees (60%) at the end of the observation period. Indeed, the shorter survival time means that the virus has less time to be transmitted, thus explaining the positive impact on the healthy bee population. This is also in line with our earlier observations: when transmitted by Varroa mites, the most virulent diseases at the colony level are the least harmful ones to the single bees.

Looking at the mite populations, a positive perturbation of μ shows its greatest effect on the healthy mites population at time $t=590$, with a decrease of 10900 units (peak of 390%), and leads to a decrease of 22300 infected mites at time $t=685$ (peak of 680%). Note that the negative influence of μ on the mite populations quickly decreases by time $t=700$ and its effect becomes negligible at the end of the observation period.

A comparison between the scales on the vertical axes in Figure 11 and Figure 12 suggests that positive changes in μ have a more considerable influence on the long term dynamics of the bee populations rather than changes in r. Conversely, the long term dynamics of the mite populations are more affected by positive perturbations of r rather than by perturbations of μ. To check this fact, it is enough to observe that in the long run, the curves for r attain values closer to zero and in any case smaller than those attained by the curves for μ, for the bees, while the opposite holds for the mites.

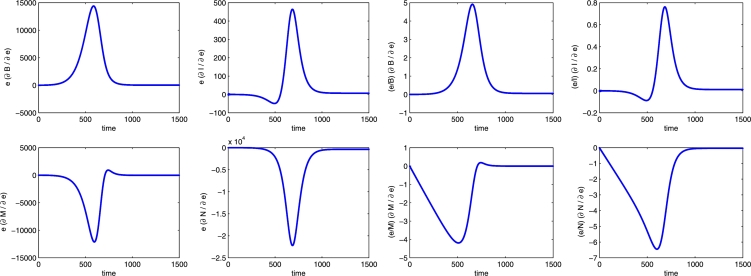
Furthermore, the semi-relative sensitivity solutions and the logarithmic sensitivity solutions for all the state variables with respect to the parameter e are shown in Figure 13. As expected, the grooming rate of healthy bees has a positive impact on the bee populations and a negative influence on the mite populations. The large peaks show that the transient dynamics of the system is really sensitive to e, with an increase by 14400 healthy bees at time $t=585$ (peak of 490%), an increase by 465 infected ones at time $t=685$ (peak of 76%), a decrease by 12100 healthy mites at time $t=595$ (peak of 420%) and a decrease by 22200 infected ones at time $t=685$ (peak of 645%). As for the other parameters, after the peak the influence decreases over time and the plot suggest that the long term dynamics of the system is almost insensitive to e.

Figure 13.

Semi-relative solutions (left) and the logarithmic sensitivity solutions (right) with respect to the parameter e. In each frame the populations are B, I, M, N in clockwise order.

Lastly, we find that a positive change in the horizontal transmission rate among bees has a negative effect on the bee populations, and a positive effect on the mite populations, as shown in Figure 14. We note that perturbations of γ especially influence the populations B, M, and N, respectively with an expected decrease of 15500 healthy bees at time $t=565$ (peak of 470%), an increase of 11000 healthy mites at time $t=590$ (peak of about 400%) and an increase of 19500 infected ones at time $t=685$ (peak of 590%).

Figure 14.

Semi-relative solutions (left) and the logarithmic sensitivity solutions (right) with respect to the parameter γ. In each frame the populations are B, I, M, N in clockwise order.

To conclude the analysis, we compare Figure 13 and Figure 14. Looking at the peaks in the logarithmic sensitivity solutions, we discover that e influences the transient dynamics of all the populations more than γ, while at the end of the observation period γ shows a greater impact on the solutions, except for the infected mite population. This result in the long term is perhaps difficult to see on the plot, but it can be gathered from the simulation values.

The knowledge of the most influential parameters tells us on which ones of them we could act in order to drive the system to a possibly safer situation. Theoretically, the sensitivity analysis shows that the population of healthy bees would highly benefit from a reduction of the Varroa growth rate, as well as a reduction of the horizontal transmission rate among bees. Also a higher bees disease related mortality and a greater rate of the grooming behavior would help in protecting the colonies.

8. Conclusion

Field and research evidence indicate that the long-term decline of managed honey beehives in the western countries is associated with the presence of viruses in the honey bee populations, [9]. While formerly the viruses produced only covert infections, their combination with the invading parasite Varroa destructor has triggered the emergence of overt viral infections. These cause concern because they entail fatal symptoms at both the individual bee level and at the colony level, constituting a major global threat for apiculture and at large for agriculture, as bees are among the most important pollinators.

In the model presented here we combine bee and mite population dynamics with viral epidemiology, to produce results that well match field observations and give a clear explanation of how Varroa affects the epidemiology of certain naturally occurring bee viruses, causing considerable damages to colonies.

The model allows only four possible stable equilibria, using the known field parameters, see Table 3. The first one contains only the thriving healthy bees. Here the disease is not present and also the mites are wiped out. Alternatively, we find the equilibrium still with no mite population, but with endemic disease among the thriving bee population. Thirdly, infected bees coexist with the mites in the Varroa invasion scenario; in this situation the disease invades the hive, affecting all the bees and driving the healthy bees to extinction. The final coexistence equilibrium is also possible, with both populations of bees and mites thriving and with an endemic disease in the beehive among both species. Transcritical bifurcations relate these points while Hopf bifurcations have been shown never to arise, since each equilibrium in suitable circumstances is also globally asymptotically stable, when locally stable.

Further, two alternatives turn out to be impossible.

On one hand, the endemic disease cannot affect all the bees in a Varroa-free colony. However, in agreement with the fact that the presence of V. destructor increments the viral transmission, the analytic results indicate that the whole bee population may become infected when this disease vector is present in the beehive.

On the other hand, the healthy mites cannot thrive only with healthy bees. Namely, if the Varroa population is present, then necessarily the bees viral infection occurs. This is another result that is in agreement with observations of honey producers, who assume the beehive to be infected in the presence of V. destructor.

The findings of this study also indicate that a low horizontal virus transmission rate among honey bees in beehives will help in protecting the bee colonies from the Varroa infestation and the viral epidemics. In fact, from (24), for a low γ the disease- and mite-free equilibrium $E_1$ is stable. Further, Figure 8 substantiates the empirical remark mentioned in the previous section, that the most harmful diseases at the colony level are those that least affect the single bees. In fact, we can observe that for a very low bee mortality μ, the equilibrium toward which the system settles is the healthy-bee-free point, in which only infected bees and mites thrive.

The model presented here gives good qualitative insight into the spread of the bee disease. However, in its assumptions certain effects that can be relevant are omitted. For instance, the Varroa carrying capacity K, taken here as constant, could reasonably be considered as a bee-population-dependent function, since mites essentially carry out their life on the host's body. Similarly the bee daily birth rate b could become a function of the bee population size, as the egg-laying rate of the queen depends on the amount of food the worker bees bring in the hive. Nevertheless, despite this simplicity the model presented here will be a good starting point for the development of other more sophisticated models, that for instance include seasonality and other aspects relevant for the bee colony health, or further to investigate the effectiveness of various Varroa treatment strategies.

Declarations

Author contribution statement

Sara Bernardi, Ezio Venturino: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This work was supported by the project: ‘Metodi numerici nelle scienze applicate’ of the Dipartimento di Matematica “Giuseppe Peano”, Università di Torino.

Competing interest statement

The authors declare no conflict of interest.

Additional information

Supplementary content related to this article has been published online at 10.1016/j.heliyon.2016.e00101.

No additional information is available for this paper.

Appendix

The following Appendix is associated with this article:

Appendix

Global stability analysis.