Abstract
Stochastic chemical kinetics has become a staple for mechanistically modeling various phenomena in systems biology. These models, even more so than their deterministic counterparts, pose a challenging problem in the estimation of kinetic parameters from experimental data. As a result of the inherent randomness involved in stochastic chemical kinetic models, the estimation methods tend to be statistical in nature. Three classes of estimation methods are implemented and compared in this paper. The first is the exact method, which uses the continuous-time Markov chain representation of stochastic chemical kinetics and is tractable only for a very restricted class of problems. The next class of methods is based on Markov chain Monte Carlo (MCMC) techniques. The third method, termed conditional density importance sampling (CDIS), is a new method introduced in this paper. The use of these methods is demonstrated on two examples taken from systems biology, one of which is a new model of single-cell viral infection. The applicability, strengths and weaknesses of the three classes of estimation methods are discussed. Using simulated data for the two examples, some guidelines are provided on experimental design to obtain more information from a limited number of measurements.
Keywords: parameter estimation, systems biology, stochastic chemical kinetics, computational modeling, Bayesian inference
Introduction
The classical method to simulate the time evolution of reacting molecules is based on the continuum assumption. When the number of molecules of all reacting species in a set of chemical reactions is of the order of Avogadro’s number, the concentration can be assumed to be a continuous real variable. In such cases, classic mass action kinetics can be used to describe the rates of reaction. When the number of molecules of one or more species is on the order of hundreds or thousands, however, we can no longer use the continuum assumption. As a result, instead of real-valued concentrations we need to consider the integer-valued number of molecules. Another effect of such low number of molecules is that the classical mass action kinetics is no longer valid. The reaction rates are no longer deterministic, and a probabilistic approach is required. Instead of accounting for amount of reactants consumed (and products produced) in a time interval, we need to account for the probability that a reaction occurs in a time interval. This approach of modeling chemical reactions has come to be known as stochastic chemical kinetics.1–4
Another difference between the deterministic and stochastic regimes of chemical kinetics is seen in the simulation methods. While the classical, deterministic regime involves solving a system of coupled ordinary differential equations (ODEs), the stochastic regime requires a probabilistic method involving repeated generation of random numbers. Various algorithms have been developed to simulate stochastic chemical kinetics starting with the stochastic simulation algorithm (SSA), also known as Gillespie’s algorithm.2,5 Note that unlike the solution of a system of ODEs, the SSA produces a different (random) trajectory for every simulation. Considerable research has been devoted to developing alternative algorithms6,7 and approximations with applications to various problems.8–12
Cellular processes in systems biology frequently demonstrate intrinsic noise or randomness,13–15 which is caused by the presence of low number of reacting molecules. Arkin and coworkers16,17 used stochastic chemical kinetic models to explain how a homogeneous population of λ-infected E. coli cells can partition into subpopulations that follow different pathways. Weinberger et al.18 demonstrated that the otherwise unexplained phenotypic bifurcation observed in HIV-1 infected T-cells could be accounted for by the presence of low molecular concentrations and a stochastic transcriptional feedback loop. Hensel et al.19 developed a detailed model of intracellular growth of vesicular stomatitis virus (VSV) to demonstrate that stochastic gene expression contributes to the variation in viral yields.
The acceptance of stochastic reaction kinetics as a standard approach to explain intrinsic noise and the advances in experimental measurement techniques, especially fluorescence microscopy, led to the inverse problem of estimating parameters from data. Golding et al.20 used fluorescence microscopy to measure the number of mRNA molecules in a single cell at a sampling rate of two measurements per minute. They showed that the average number of mRNA transcripts per cell was between zero and 10 and proposed a stochastic gene expression model to explain the observed behavior.
Initial attempts to estimate model parameters (usually the reaction rate constants) were rather ad hoc—the parameters were set to biologically plausible values and then tuned by eye so that the model simulation resembled the experimental data.17 Another approach is to use the continuum assumption and treat the reaction kinetics as deterministic instead of stochastic. In this case, parameter estimates can be easily obtained by least-squares fitting or maximum likelihood estimation. Tian et al.21 demonstrated that this approach does not produce good parameter estimates when the number of molecules is small. Later approaches maintained the stochasticity of the model and utilized various statistical Monte Carlo methods to estimate parameters. These estimation methods may be classified into two familiar categories—maximum likelihood methods and Bayesian inference methods. Maximum likelihood methods include simulated maximum likelihood,21 density function distance,22 and approximate maximum likelihood22,23 methods. All of these methods maximize an approximation of the true likelihood to obtain parameter estimates. Stochastic gradient descent, proposed by Wang et al.,24 estimates the gradients of the likelihood function with respect to the parameters using a reversible jump Markov chain Monte Carlo (RJMCMC) method. By contrast, Bayesian inference methods attempt to obtain the posterior distribution of the parameters, which can then be maximized to obtain maximum a posteriori (MAP) estimates. Most Bayesian inference methods rely on MCMC techniques. Rempala et al.25 utilize MCMC-enabled Bayesian inference to estimate parameters in a specific model of gene transcription. Wilkinson and coworkers26–30 have developed a range of Bayesian inference algorithms, all of which use MCMC methods. In many cases, they replace the stochastic chemical kinetic model with another statistical model26 or approximate it using the diffusion approximation.27–29 In other cases, they use the true stochastic model.30,31 Similar to the MCMC method of Wilkinson,30 Choi and Rempala32 proposed a Bayesian inference algorithm based on Gibbs sampling. All of these estimation methods suffer from their own particular shortcomings and have restricted applicability. We will discuss these issues in this article.
Many of the examples in the references above come from systems biology—Prokaryotic gene-autoregulation,17,24,29 gene transcription models,23,25 RNA expression,20,22,23 and single-cell mtDNA dynamics.26 Other examples include the Lotka–Volterra model29–31 and epidemic models.32 These models consist of 2–8 reactions involving 2–5 species.
In this article, we first start with the formulation of the true (exact) likelihood of the data without any approximations. We demonstrate that for a very restricted class of models and data, the true likelihood may be computed and then numerically maximized to obtain maximum likelihood estimates (MLE). In further restricted cases, the posterior may be obtained by numerically integrating the relevant expressions. We then move on to implement and compare some of the Bayesian inference methods available in the literature. We consider only the methods that utilize the true stochastic chemical kinetic model (instead of using a diffusion approximation or a statistical substitute). These methods are based on Gibbs sampling and use either a Metropolis– Hastings (MH) step30 or the uniformization32,33 technique. Finally, we describe a novel Bayesian inference method that we call conditional density importance sampling (CDIS), which uses importance sampling instead of MCMC techniques. We implement these three classes of methods (exact, MCMC and CDIS) on two examples from systems biology. The first example is a novel model of early viral gene expression, and the second example is a reduction of the RNA expression model studied by,20,22,23 which we call the gene on-off model. Each of these models exemplifies a quintessential feature of systems biology models that complicates parameter estimation. We use simulated datasets for each example and estimate the parameters using the different parameter estimation methods. Through these estimation exercises, we provide some general guidelines on how to utilize limited number of measurements to obtain maximum information. Finally, we compare all estimation methods and enumerate their strengths and weaknesses.
This article is organized as follows. We start with a brief review of stochastic chemical kinetic models and corresponding parameter estimation methods in the Background section. Following that, in the Examples section, we demonstrate the application of these parameter estimation methods on two systems biology models—early viral gene expression and gene on-off.
Background
Stochastic kinetic models
We provide only a brief description of stochastic chemical kinetics here. Consider a system of nr reactions, denoted by ℛ1, ℛ2, …, ℛnr and ns species, denoted by χ1, χ2, …, χns. The system of reactions is written in standard notation
in which, each reaction has an associated rate constant, ki. We denote the set of rate constants using the nr × 1 vector, θ = [k1 k2 ⋯ knr]T. Similar to the deterministic case, the nr × ns stoichiometric matrix, ν may be written as
Let X(t) be the ns × 1 state vector representing the number of molecules of each species at time t. Let R be the nr × 1 vector denoting the number of times each reaction ℛi is fired during the time interval [0, T]. Given R, the state of the system at time T may be obtained from the equation
| (1) |
But given X(T) and X(0), we can recover R only if νT has full column rank. Equation 1 is not very different from the corresponding deterministic equation (see Rawlings and Ekerdt34 p. 45, Eq. 2.30). Instead of using reaction rates and concentration of species, we use the number of reactions fired and number of molecules of each species. Note that both X(t) and R are vector-valued random variables whose elements can assume only nonnegative integer values. At time t, each reaction ℛi has an associated reaction propensity defined as
| (2) |
For example, a bimolecular reaction of the form would have reaction propensity h(X(t), θ) = kA(t)B(t). Reaction propensity is similar to the rate of reaction in deterministic kinetics albeit with some differences as described in.2 The total reaction propensity at time t is the sum of propensities of P all reactions and is denoted by .
The set of all possible states of the system is called the state space, denoted by S. As the state is an integer-valued vector, the state space S is discrete containing |S| states. Here, |S| represents the number of states in the state space. Thus, the state vector forms a stochastic (or random) process X = {X(t) : t ∈ [0, T]} in a discrete state space and continuous time. This stochastic process is essentially a continuous-time discrete-space (homogeneous) Markov chain that has the following Markov property
| (3) |
Equation 3 can be converted to a system of ODEs by rearranging the terms and taking a limit of dt → 0. One form of these ODEs is the Kolmogorov’s forward equation
| (4) |
| (5) |
in which P(t) is an |S| × |S| transition matrix. Each element (P(t))i, j represents the probability of the system being in state j at time s + t given that the system was in state i at time t. The |S| × |S| matrix Q is called the transition rate matrix. Elements of Q are composed of the reaction propensities defined in Eq. 2. For a detailed description, we refer the reader to Ref. 30 (p. 137). Another form of the Kolmogorov forward equation, which is more common in the chemical and physical sciences literature, is the chemical master equation (CME).4,5,11,22,35,36 The exact method and the uniformization technique, discussed in the next subsection, use Kolmogorov’s forward equation as defined in Eq. 4.
The state of the system, x(t), remains constant over time until a reaction event occurs, thus forming a staircase plot of x(t) versus t. As a result, the stochastic process X = {X(t) : t ∈ [0, T]}, which has uncountably infinite (time) dimensions, can be completely defined by recording only the reaction events. The simulation techniques2,6,7 exploit this characteristic by simulating reaction events or firings starting from an initial condition. For every reaction firing, two quantities are simulated from appropriate probability distributions— the time at which the reaction occurs and the index number of the reaction that occurs. Different trajectories of X(t) are generated using different random numbers. We denote one such trajectory or instance of X by the variable x. Note that x contains the complete reaction event data, which may be used to recreate the entire, continuously varying stochastic process. Unlike a simulation, laboratory experiments only measure the full (or partial) state of the system at discrete time points. These measurements constitute the discretetime data and are collectively denoted by y. Note that y does not necessarily contain information about reaction events and is, therefore, a subset of the complete event data x.
Our aim is to estimate the parameter vector θ using a stochastic chemical kinetic model and discrete-time data y. In this article, we consider only the case of full measurements in which all species are measured at discrete time points. Let {s0, s1, …, sm} be the times at which measurements {y0, y1, …, ym} are available. Each measurement yi is an ns × 1 vector. We also assume that the initial condition y0 is known, that is, not random. Thus, the discretetime data y can be defined as
| (6) |
Parameter estimation methods
We begin with a brief review of Bayesian inference as it applies to our problem. We assume that parameter vector θ is a random variable with a prior distribution π(θ). The posterior distribution of θ, denoted by π(θ|y), represents the updated distribution of θ after taking the data y into account. The prior and posterior are related via Bayes’ rule
| (7) |
in which π(y|θ) denotes the likelihood of data. Throughout this article, we use the following gamma prior
| (8) |
| (9) |
We intend to obtain the posterior π(θ|y), or an approximation of it, using the gamma prior and the likelihood. MAP estimates, θ̂, may then be obtained by maximizing the posterior with respect to θ, either analytically or numerically. Unlike Bayesian estimation, MLE maximizes the likelihood π(y|θ) with respect to theta. We denote the estimates obtained by MLE as θ̂MLE.
Exact Method
The exact method obtains the likelihood by solving Kolmogorov’s forward equation described in (4) for a given value of θ, either numerically or analytically. The likelihood may then be maximized to obtain the MLE estimates θ̂MLE, or the posterior may be obtained up to a constant, using Eq. 7. The likelihood π(y|θ) may be obtained as follows
| (10) |
Note that the term P(yi|yi−1, θ) is nothing but the (yi−1, yi)-element of the matrix P(si+1 − si), which may be obtained by solving Eq. 4.
The solution to Eq. 4 requires a matrix exponentiation of (si+1 − si)Q, which becomes computationally expensive if the number of states, |S|, is large. As Q depends on θ, at least one matrix exponentiation is required to calculate the likelihood value for every θ. As many as m matrix exponentiations may be required if the time points {s0, s1, …, sm} are not equally spaced. While some research has been done to solve the CME (and equivalently Kolmogorov’s forward equation) analytically under special cases,37 it is usually not possible to do so. This means that the likelihood value at a given θ has to be evaluated numerically which further increases the computational cost to obtain MLE estimates. The MAP estimates may be obtained by maximizing the product of likelihood and prior at a similar computational cost. To completely determine the posterior as a distribution, we require the normalizing constant π(y), which is given by
| (11) |
In general, the integration in Eq. 11 is not analytically possible and numerical methods have to be used. Numerical integration of Eq. 11 is usually tractable when the number of parameters nr is small (less than three). The gene on-off example in Examples section is one such case. In other cases, for example, early viral gene expression in the Examples section, the state space S is unbounded making Q infinite dimensional and an analytical solution to Eq. 4 is essential to be able to use the exact method.
MCMC Methods
The MCMC methods and the CDIS method described in this section are in the same vein and utilize the same analytical expressions that are available under special circumstances. We begin with the general formulation of the estimation problem and describe relevant analytical expressions.
Given the complete event data x (instead of the discrete measurement data y), it is possible to write down the likelihood analytically [30, p. 279]
| (12) |
in which
n represents the total number of reaction events occurred in the time interval [s0, sm],
nj represents the index number of the jth reaction event,
tj represents the time at which jth reaction event occurred.
Note that Eq. 12 computes the likelihood of the continuously varying stochastic process using only the information about reaction events. When the reaction propensity is separable, that is, as described in Eq. 2, the likelihood expression becomes
| (13) |
in which
| (14) |
and ri is the ith element of r representing the number of times reaction ℛi occurs in the time interval [s0, sm]. This expression of likelihood motivates the use of the gamma prior defined in Eq. 8. The posterior given complete reaction event data may be written analytically as
| (15) |
in which
| (16) |
Thus, the prior and complete data posterior are conjugate, that is, they come from the same family of distributions.
The problem is that we have the discrete-time (measurement) data y instead of the complete (reaction) event data x. As y ⊆ x, an obvious approach is to first appropriately simulate and average over the hidden or missing data represented by x\y, and then infer the parameters θ using the “averaged” x. Both the MCMC and CDIS methods essentially perform this averaging in very different ways. We will now describe the MCMC methods and delay the description of CDIS until later in this subsection.
MCMC methods aim to obtain the joint distribution of θ and x given y, that is, π(θ, x|y) by using Gibbs sampling [30, p. 255]. A basic Gibbs-style algorithm may be written as:
Sample x ~ π(x|y)
Sample θ ~ π(θ|x, y) = π(θ|x) using Eq. 16
Sample x ~ π(x|θ, y)
Return to Step 2
This algorithm may be iterated to produce samples of θ that can then be binned to produce a histogram representing the posterior π(θ|y). Note that the samples of θ and x generated by this algorithm come from the true joint distribution π(θ, x|y). There are two problems with this method. First, the distribution π(x|y) is not available. So, we initialize the iterative procedure by replacing Step 1 with any method (not necessarily statistical) that can generate a sample of x that satisfies y. Obviously, when the initial x does not come from the true distribution π(x|y), the samples of θ and x are no longer distributed as π(θ, x|y). In this case, the samples of (θ, x) form a Markov chain whose stationary distribution is π(θ, x|y). Thus, the Markov chain can be run until stationarity is achieved and then samples of θ may be generated to produce a histogram. The second problem is to sample x from π(x|θ, y). This problem can either be solved using endpoint-conditioned simulation methods33 or using a MH step [30, p. 282].
Endpoint-conditioned simulation methods, such as uniformization,33 can generate samples of x from the true conditional distribution π(x|θ, y). This method, which we refer to as Gibbs-uniformization, was used by32 to estimate parameters in epidemic models. Similar to the exact method, the uniformization technique uses the solution to Kolmogorov’s forward equation and, therefore, suffers from similar associated issues of a large (or unbounded) state space. Other endpoint-conditioned simulation methods such as direct sampling33 or bisection sampling38 may be used to produce similar estimation methods.
Using a MH step, [30, p. 282] makes the overall algorithm a Metropolis-within-Gibbs-style algorithm. The MH step generates a proposed sample of x from an approximate conditional distribution πA(x|θ, y) instead of the true conditional, and then, accepts or rejects the proposed sample x based on a suitably defined acceptance probability. This class of estimation methods was proposed by Wilkinson and coworkers.26,28–30 There are two major variations of this overall scheme—RJMCMC method31 and the block updating method.30,31 In this article, we consider only the block updating method as described in Ref. 30 [pp. 281–287], which we call MCMC-MH.
CDIS Method
We present here an alternative and novel method, CDIS, to perform the “averaging” over x as discussed previously in this section. Instead of attempting to obtain the joint posterior distribution of (θ, x) given y, we aim to obtain only the posterior π(θ|y) using importance sampling
| (17) |
in which, q(x) represents the importance or proposal distribution. Instead of generating samples of x from the target distribution π(x|y), we generate samples from the importance distribution. Note that as y ⊆ x, the reverse conditional π(y|x) is either 1 (when x agrees with y) or zero (otherwise). The distribution of complete event data π(x) may be obtained using Bayes’ rule as follows
| (18) |
Using Eqs. 17, 13, and 18, the posterior may be approximated by a weighted sum of gamma distributions
| (19) |
in which the weights wk are given by
| (20) |
Note that the complete data likelihood π(θ|x) is known analytically in Eq. 15, and the weights wk can be numerically computed, thus, providing a semianalytical expression for the joint posterior in Eq. 19.
As is usually the case with importance sampling, the choice of the importance function is critical to numerical efficiency. The importance function q(x) should “mimic” the target distribution π(x|y). In this article, we present the importance sampling procedure in brief and refer the reader to Ref. 39 for a detailed description with statistical analysis. To obtain q(x), we start with the target distribution
| (21) |
As we discussed previously in this section, x contains the information about the time and the index number of reaction events that occur in the time interval [s0, sm]. To simulate x, we first generate the random variable R, using the distribution q(r). Conditioned on r, we generate reaction sequence {n1, n2, ⋯, nn} in which nj represents the index number of j th reaction event and . Finally, conditioned on r and {n1, n2, ⋯, nn}, we generate a set of reaction times {t1, t2, ⋯, tn}, which represent the times corresponding to the reaction events. Thus, the q(x) is given by
| (22) |
Note that both Gibbs-uniformization and MCMC-MH methods generate samples of x for a given θ, from the (target) distribution π(x|θ, y). This requires an iteration over θ and produces the posterior π(θ|y) as a histogram. By contrast, CDIS method generates samples of x from the (target) distribution π(x|y) in which θ has been integrated out. Thus, the CDIS method produces a semianalytical posterior distribution that can be evaluated for every θ value.
Examples
The reaction kinetics in systems biology (whether deterministic or stochastic) differ from the reaction kinetics in chemistry in one large respect—systems biology models usually violate mass balance.17,20–26,29–32 Such reaction kinetics can result in an unbounded number of molecules (usually as a result of a synthesis reaction) causing the state space S to become unbounded as well. Violation of mass balance is an ease-of-use approximation in which we do not explicitly model species (e.g., amino acids and nucleic acids) that (1) are present in large amounts, (2) are not expected to not vary appreciably, and (3) are not critical to the reaction system we intend to model. Balancing the reactions by explicitly modeling “missing” species does not improve the situation. The state space, S, remains prohibitively large (although bounded) due to the species present in large amounts, and the increased number of species causes an unnecessary increase in model complexity and computation. Unboundedness of state space, S, usually rules out the application of exact and Gibbs-uniformization methods, except when an analytical solution to Eq. 4 is available. Our first example, early viral gene expression, in the Examples section has this feature.
Another common feature that complicates parameter estimation is cyclical kinetics. Cyclical kinetics includes reversible reactions as well as oscillatory kinetics such as the Lotka–Voltera model. We define cyclical kinetics as the set of reactions whose transposed stoichiometric matrix νT has less than full column rank. As discussed in the Background section, when νT does not have full column rank, Eq. 1 cannot be solved uniquely for R, thus, resulting in at least one degree of freedom. In such a case, a large, possibly infinite, number of (hidden) reaction events may occur between two measurements. As a result, the amount of hidden data to be “averaged” over is much larger, which demands more computational effort. The gene on-off example in the Examples section has this feature.
Early viral gene expression model
The motivation for this example comes from the virus infection experiments performed by Timm and Yin.40 The following model describes the viral infection of a single baby hamster kidney (BHK-21) cell by VSV. The rationale behind this reaction mechanism comes from both the VSV-BHK biology and the characteristics of the data
| (23) |
The viral infection process takes place in five distinct stages41: adsorption to the host cell and entry, uncoating of the genome, transcription and translation, genome replication, assembly and release of virus progeny. The first two stages, namely, adsorption/entry and uncoating must occur before the viral genome undergoes transcription or replication. A delay is observed before viral protein begins to appear.
In (23), V represents unactivated viral genome and G represents activated viral genome. The species G1. G2, …, Gn represent various intermediate (or delay) states of the viral genome. Unactivated viral genome, V, has to undergo adsorption, entry, and uncoating before it is ready for transcription and replication. The reactions in (23) converting V to G represent these initial stages of adsorption, entry, and uncoating. The species M and P represent Red Fluorescent Protein (RFP) mRNA and red fluorescent protein, respectively. The transcription reaction creates more mRNA, M from activated genome G. Translation creates more red fluorescent protein, P from mRNA, M. Observed RFP signal is proportional to the amount of red fluorescent protein P present in the cell. Here, any delays associated with maturation of the RFP signal are embedded in the translation rate.
During the early stages of infection, the degradation of G, M, and P is not important. Therefore, we further reduce the model in (23) to represent only the early stages of infection and remove the delay states. This leads to the following reduced model
| (24) |
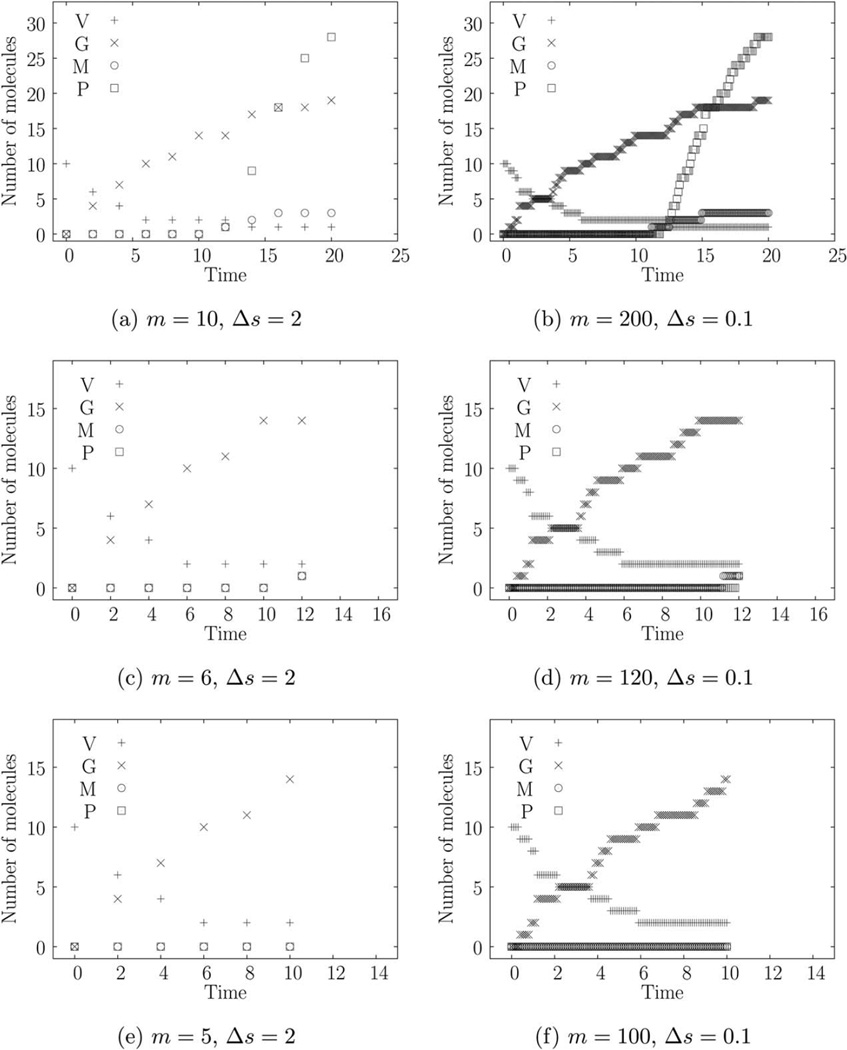
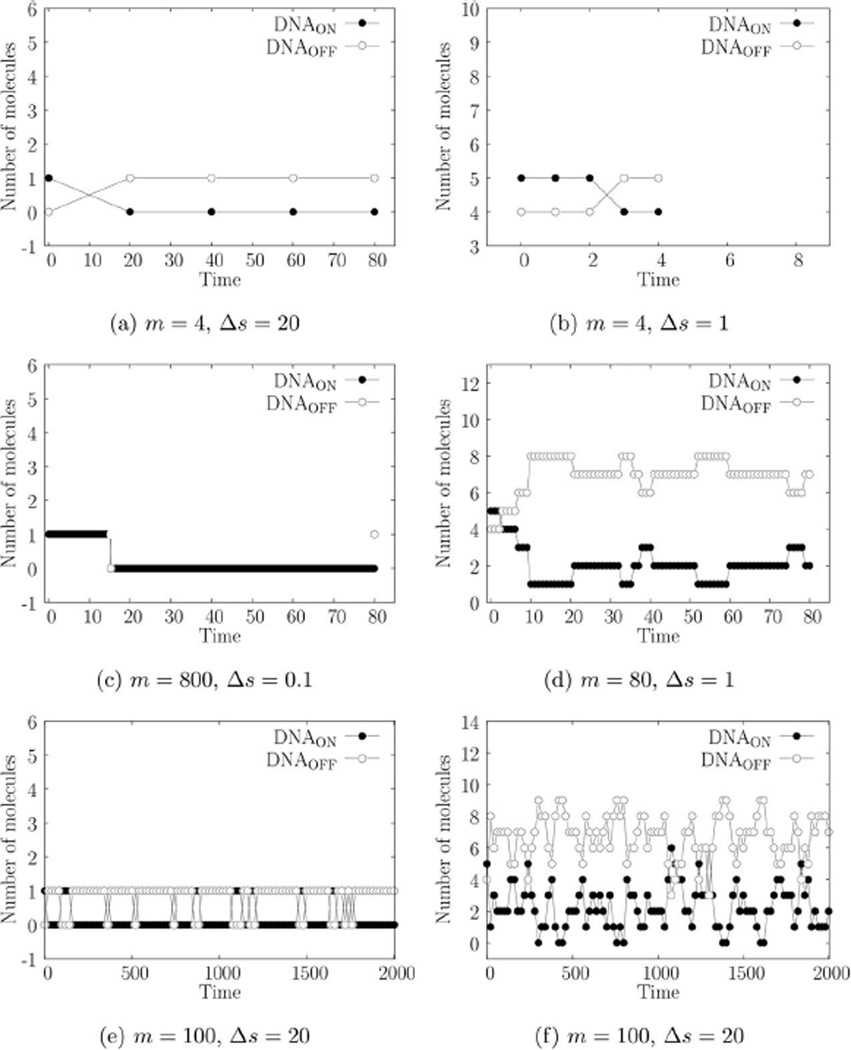
Using true parameter values θ0 as shown in Table 1 and an initial condition of X(0) = [V0 G0 M0 P0]T = [10 0 0 0]T (corresponding to a multiplicity of infection or MOI of 10), we generate six simulated trajectories with Gillespie’s direct method.2 These trajectories, shown in Figure 1, use the same random numbers but have different sampling frequency (Δs) and different number of time points (m). Note that Figures 1a, b span the same time interval of [0, 20] but Figure 1b has 20 times larger measurement frequency. The same is true for the next two rows of Figure 1.
Table 1.
True Rate Constants and Gamma Prior Parameters
| True Values |
Prior Parameters |
||||
|---|---|---|---|---|---|
| Reactions | Parameters | θ0 | θ̂prior | a | b |
| Activation | ka | 0.15 | 10 | 1.01 | 0.0010 |
| Transcription | kt | 0.02 | 20 | 1.01 | 0.0005 |
| Replication | kr | 0.05 | 1 | 1.01 | 0.0100 |
| Translation | kf | 1.00 | 30 | 1.01 | 0.0003 |
Figure 1.
(A–F) VSV early gene expression.
True parameter values of θ0 = [ka kt kr kf]T = [0.15 0.02 0.05 1]T. Initial condition of X(0) = [V0 G0 M0 P0]T = [10 0 0 0]T corresponding to an MOI of 10. m = number of points, Δs = sampling time.
As we can see in (24), all reactions except the activation reaction violate mass balance. This rules out the application of exact and Gibbs-uniformization methods and we only compare the MCMC-MH and CDIS methods. We use a gamma prior as described in Eq. 8 with shape (a) and rate (b) parameters shown in Table 1. The mode (or peak) of the gamma prior, denoted by θ̂prior is also shown in Table 1. Note that θ̂prior is chosen to be very different than θ0 so as to not bias the posterior toward the true values. The shape parameter is chosen so that the prior is essentially uniform over a large range of parameter values.
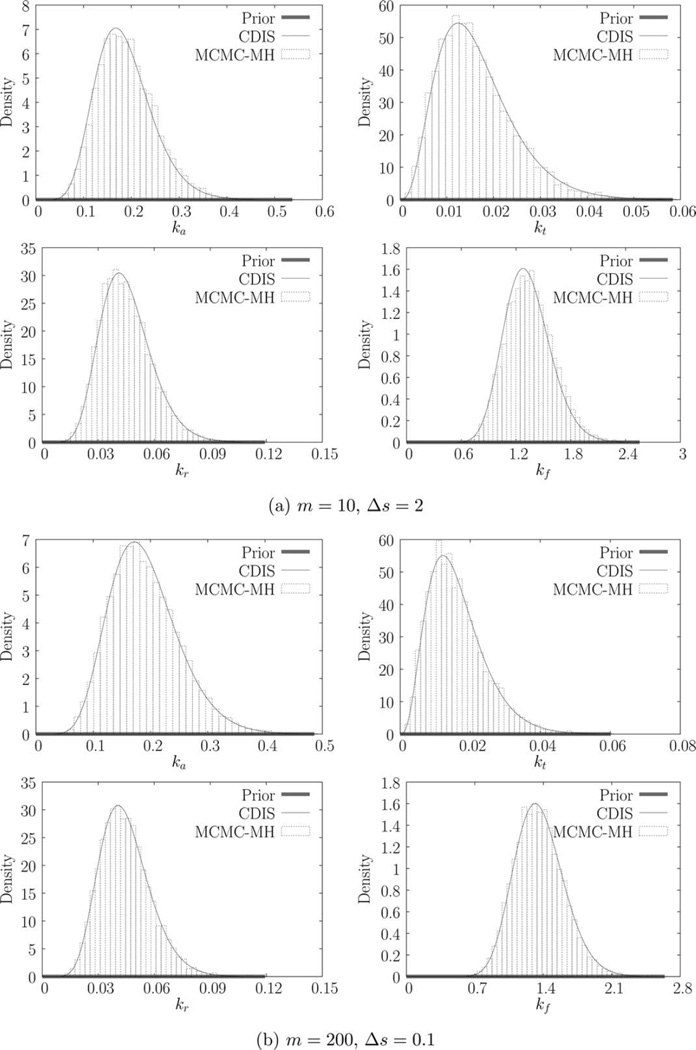
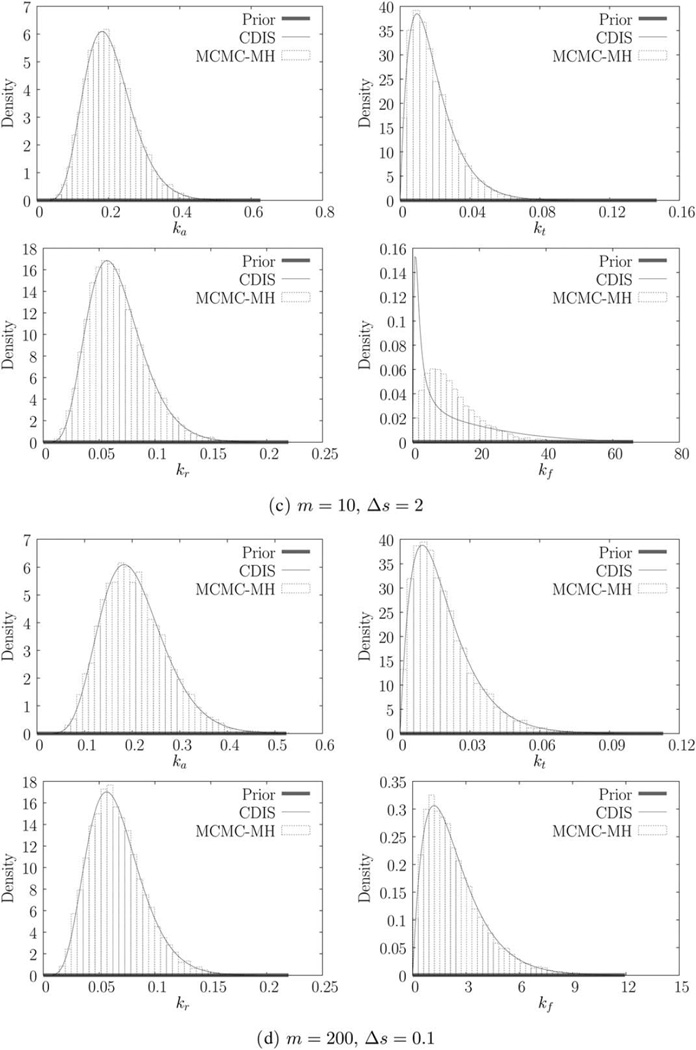
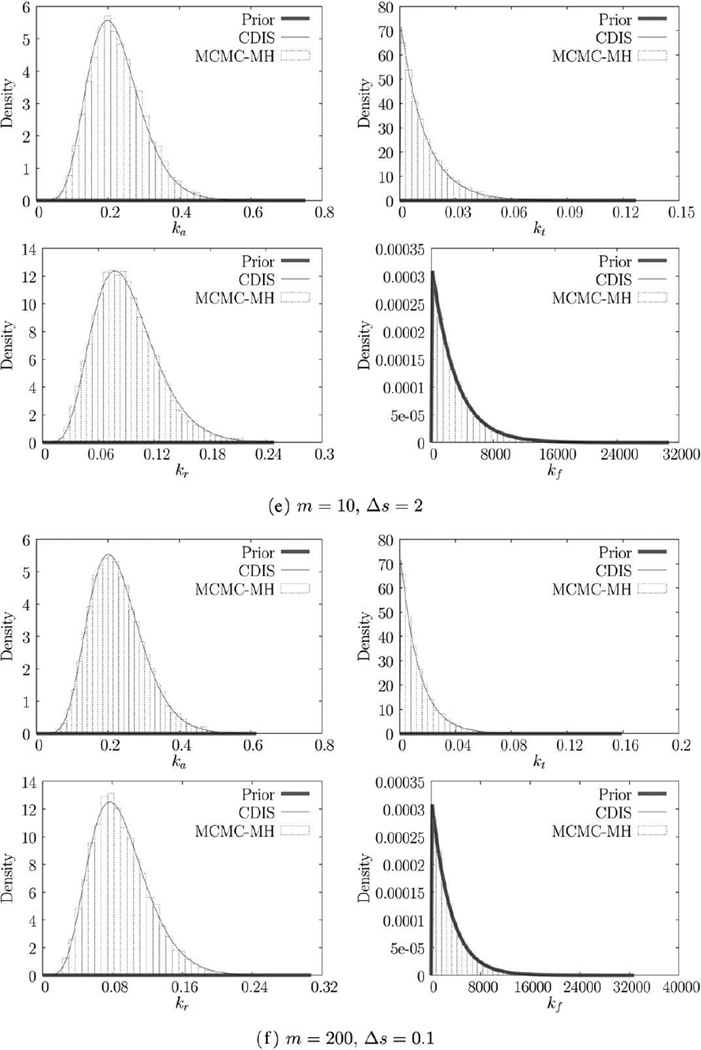
We estimate the parameters for each of the six trajectories using both CDIS (with N = 1000 samples) and MCMC-MH methods (with N = 10,000 steps). The resulting parameter estimates (MAP estimates) are shown in Table 2. The marginal posteriors π(ki|y) are shown in Figure 2. As discussed before, CDIS produces a semianalytical expression for the marginal posterior while the MCMC-MH method produces samples of θ, which are then binned to produce the histogram. Parameter estimates for the CDIS method are obtained by numerical optimization. The estimates for MCMC-MH method are obtained by simply finding the bin with the largest probability (or height). Histogram estimation suffers from the problem of bias-variance tradeoff [42, p. 303]. As a result, MCMC-MH estimates have an inherent error corresponding to the width of the bin (~10−2 – 10−5 for this example). CDIS estimates in contrast are accurate up to any desired level of accuracy (~10−10 due to machine precision).
Table 2.
Parameter Estimates from CDIS and MCMC-MH
| Dataset | CDIS (N = 1000) | MCMC-MH (N = 10,000) |
|---|---|---|
| (1a) | (0.1674, 0.0124, 0.0411, 1.2767) | (0.1457, 0.0117, 0.0380, 1.3568) |
| (1b) | (0.1716, 0.0122, 0.0407, 1.3163) | (0.1768, 0.0112, 0.0387, 1.3871) |
| (1c) | (0.1825, 0.0096, 0.0572, 0.8019) | (0.1907, 0.0082, 0.0597, 6.4541) |
| (1d) | (0.1832, 0.0095, 0.0567, 1.2069) | (0.1752, 0.0121, 0.0549, 1.1623) |
| (1e) | (0.1994, 0.0001, 0.0778, 30.0000) | (0.2012, 0.0006, 0.0700, 155.6734) |
| (1f) | (0.2018, 0.0001, 0.0770, 30.0000) | (0.2010, 0.0008, 0.0759, 166.1711) |
True values (ka0, kt0, kr0, kf0) = (0.15, 0.02, 0.05, 1).
Figure 2.
Marginal priors and posteriors obtained using CDIS and MCMC-MH.
We begin by comparing the results for trajectories in Figures 1a, b. Figures 2a, b show the corresponding marginal posteriors and priors. In comparison to the posteriors, the priors are essentially uniform, indicating that the priors have little effect on the MAP estimates. The CDIS and MCMC-MH methods agree quite well. The first two rows of Table 2 provide the parameter estimates. The parameter estimates θ̂ are close to the true values θ0 indicating that the estimation methods are reasonably accurate. For any statistical estimation method, even the exact method, there is some estimator error (or bias) due to the finite amount of data. Thus, we do not expect the estimates in Table 2 to track the true values. However, we expect the parameter estimates, θ̂ to converge as the number of samples (N) increases.
Note that increasing the number of measurements by a factor of 20 (from 1a to 1b) does appreciably change the parameter estimates. Looking at the next trajectory in Figure 1c we see that the CDIS and MCMC-MH posteriors for translation rate constant, kf, are different (Figure 1c). In this case, increasing the number of measurements causes the two posteriors to agree with each other (Figure 2d). Looking at the corresponding parameter estimates in Table 2, we can see that increasing the measurement frequency changes the estimates for kf significantly but the other parameter estimates do not change. Finally, for the last two trajectories in Figures 1e, f, increased measurement frequency does not change the parameter estimates as well. However, for these trajectories, there are two interesting outcomes—(1) the parameter estimates for kt and kf are very different from their corresponding true values and (2) the posteriors for kf are the same as the prior.
MCMC-MH and CDIS methods use the complete data posterior π(θ|x) (in Eqs. 15–16) to generate an approximation of the required posterior π(θ|y). Equation 16 offers some explanation about behavior of estimates. The marginal complete data posterior, π(ki|x) uses the information in x only through ri and Gi. Here, ri is the number of times reaction ℛi occurs in time interval [s0, sm] and can be obtained uniquely by solving Eq. 1 because νT has full column rank. Changing the measurement frequency while keeping the same end points y0 and ym does not change ri. But increasing the measurement frequency does provide a better (lower variance) estimate of Gi (defined in Eq. 14). This observation explains why the increasing measurement frequency has a weak effect on the posterior and estimates.
We now compare the data in Figures 1e, c, a. The trajectory in Figure 1e shows that the mRNA (M) and protein (P) measurements remain at zero and neither transcription nor translation reaction events occur during the given [0, 5] time interval. As a result, every (event data) sample x generated by the CDIS or MCMC-MH method has r4 = 0 and G4 = 0. Looking back at Eq. 16, we can see that this dataset provides no information at all for the translation reaction. Consequently, the posterior of kf is exactly equal to the posterior. While the CDIS method provides this information analytically, the MCMC-MH method provides this information through samples of kf. In such a case, the model in (24) should be further reduced by removing the translation reaction. While r2 is also equal to zero, G2 > 0, which means that there is some information available regarding the transcription rate constant kt. Consequently, the estimate k̂t in Table 2, while being very different than kt,0, is not equal to k̂t,prior. Figures 1c, a have larger (nonzero; ri, Gi) values and provide better estimates.
In Table 3, we present the computational time spent in terms of seconds taken to generate one sample of x for both methods. All simulations were performed using Octave on an Intel(R) Core(TM) 2 Quad 2.66GHz, 8GB RAM machine running Lubuntu 13.04. For both methods, the computational time per sample is directly proportional to the number of time points, m and is (roughly) inversely proportional to the sampling interval, Δs. Table 3 shows that when m is low (in 1a, c, e), the CDIS method takes much longer to generate one sample of x than MCMC-MH. However, when m is high (in 1b, d, f), MCMC-MH is slower than CDIS. Irrespective of the per sample computational time, CDIS requires at least 10 times fewer samples than MCMC-MH. In fact, CDIS method produces a semianalytical posterior with just one sample while a large (~1000) samples are required to obtain a histogram using MCMC methods. Even further, a significant number of samples (~10–50%) have to be burned-in while using MCMC methods to ensure convergence of the Markov chain to stationarity. The CDIS method, by contrast, may have problems with convergence if the importance distribution q(x) is not “close enough” to the target distribution π(x|y). We have not encountered convergence issues for this example (see Supporting Information).
Table 3.
Sampling Time (Seconds per Sample) for CDIS and MCMC-MH
| Dataset | CDIS (N = 1000) | MCMC-MH (N = 10,000) |
|---|---|---|
| (1a) | 0.54 | 0.12 |
| (1b) | 0.54 | 1.35 |
| (1c) | 0.30 | 0.06 |
| (1d) | 0.37 | 0.83 |
| (1e) | 0.30 | 0.05 |
| (1f) | 0.35 | 0.66 |
Gene on-off
The RNA expression model was first proposed by Golding et al.20 and later studied by Reinker et al.23 and Poovathingal and Gunawan.22 This model, as shown in reactions (25), has three species and three reactions
| (25) |
As discovered by Golding et al.,20 the number of RNA molecules in a single cell was around 0–10. This simple model also violates mass balance, which makes the exact and Gibbs-uniformization methods inapplicable. To demonstrate the exact and Gibbs-uniformization methods and compare them to MCMC-MH and CDIS methods, we consider only the first two reactions in the model. This simplification creates the reduced, gene on-off model presented in reactions (26)
| (26) |
While this model is no longer suited to study mRNA expression, it can be used to study the switching—activation (ON) and deactivation (OFF)—of a gene. As this model now has only two parameters to be estimated, we can plot likelihood and joint posterior values, which is another motivation for choosing this reduced model.
We generate six simulated trajectories using true parameter values θ0 = [k1 k−1]T = [0.03 0.01]T with Gillespie’s direct method,2 as shown in Figure 3. Trajectories in the first column (Figures 3a, c, e) are simulated using an initial condition of X(0) = [DNAON, 0 DNAOFF, 0]T = [1 0]T, which corresponds to only one copy of the gene. The second column (Figures 3b, d, f) is simulated using X(0) = [DNAON, 0 DNAOFF, 0]T = [5 4]T, which corresponds to nine copies of the gene.
Figure 3.
Gene on-off model.
True parameter values of θ0 = [k1 k−1]T = [0.03 0.01]T. First column: X(0) = [DNAON, 0 DNAOFF, 0]T = [1 0]T. Second column: X(0) = [DNAON, 0 DNAOFF, 0]T = [5 4]T. m = number of points, Δs = sampling time.
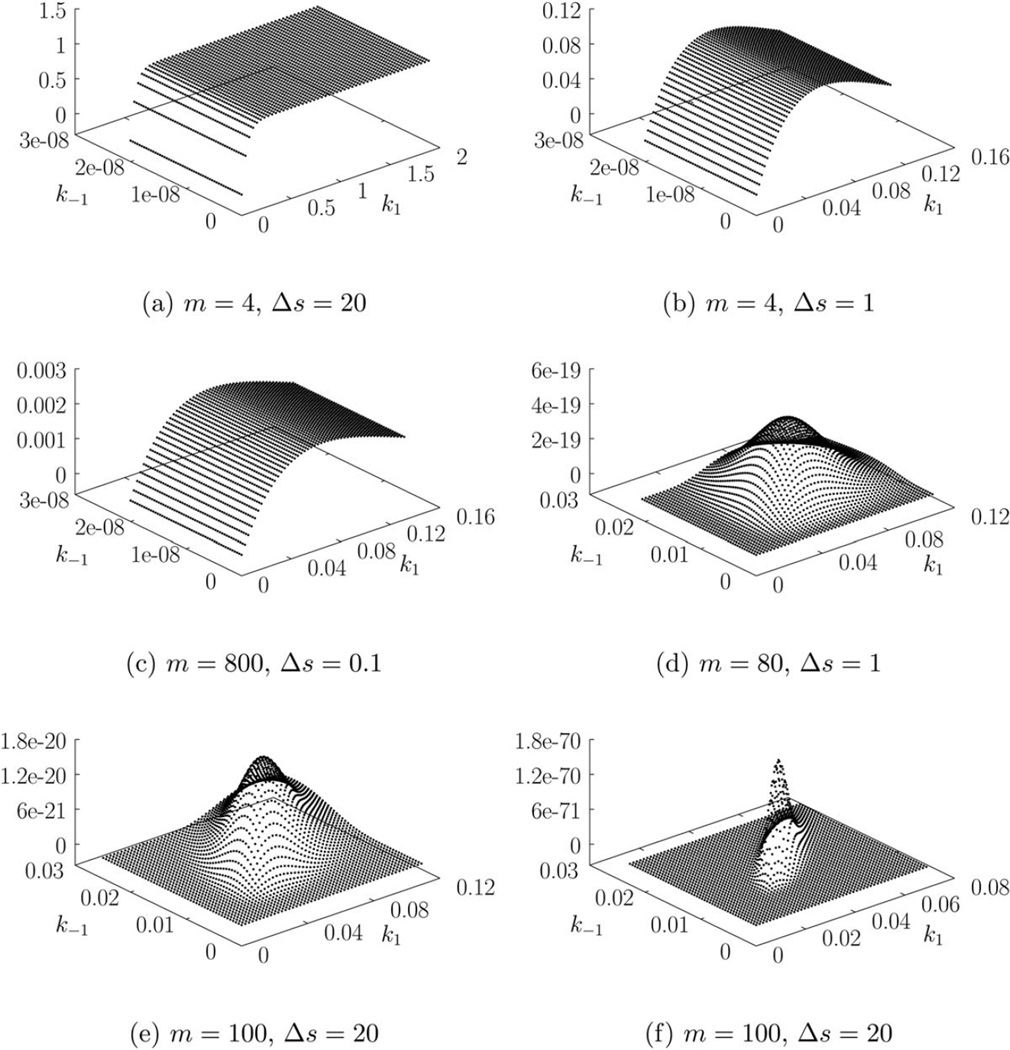
We begin by computing the likelihood π(y|θ) for each trajectory using the exact method as described in the Background section. The resulting three-dimensional (3-D) likelihood plots, corresponding to each of the trajectory, are presented in Figure 4. We can see that for the data in Figure 3a, the likelihood is essentially flat when k−1 is small and k1 is large enough. The likelihood plots for Figure 3b, c are flat when k−1 is small but have a peak in k1. The data in Figures 3d, e produce likelihood curves, which are peaked in both k1 and k−1 while the data in Figure 3f the most sharply peaked likelihood surface.
Figure 4.
Gene on-off model. Exact likelihood plots for data in Figure 3.
Intuitively, the likelihood in Figure 4a seems reasonable. The corresponding trajectory in Figure 3a may be recreated, with probability 1, if we set k1 = ∞ and k−1 = 0, that is, π(y|θ = [∞ 0]T) = 1. Therefore, the only information we can obtain is that k1 ≫ k−1; we cannot obtain independent estimates of both parameters. Figure 3b has the same number of measurements as Figure 3a but k1 = ∞ is no longer possible because we observe that ℛ1 does not occur until t = 2. This observation provides some information about k1. As ℛ2 does not occur in Figure 3b, it is still possible for k−1 to be zero. Data in Figure 3c has a large number of finely sampled measurements (m = 800, Δs = 0.1) but it still does not provide more information than Figure 3b, which has far fewer measurements. Figure 3c indicates that the gene switched off (i.e., ℛ1 occurred) once around t = 15. While the increased measurement frequency provides an accurate time of the switch (compared to Figures 3a, b), the trajectory can still be simulated when k−1 = 0. Thus, Figure 3c provides no information about ℛ2. In fact, a reduced model consisting of ℛ1 alone may be used to explain this data. Figure 3d has 10 times fewer measurements than Figure 3c and spans the same time interval of [0, 80], but it provides a better estimate of k−1. This is because both ℛ1 and ℛ2 occur often. Figure 3e also provides better estimates for the same reason. Note that the data in Figures 3d, e do not allow the possibility of k−1 = 0. Figure 1f provides the sharpest likelihood surface (and the best estimates) among all trajectories in spite of having a sampling time of Δs = 20.
Unlike the previous example, νT for this example does not have full column rank. This means, as we intuitively expect, that we cannot uniquely obtain the number of times each reaction occurred (i.e., ri) between two measurements. For example, in Figure 3a, the number of times ℛ1 and ℛ2 occurred between t = 0 and t = 20 is given by (r1, r2) = (n + 1, n), n = 0, 1, 2 …. Therefore, we define ri,min as the observed (or minimum) number of times a reaction ℛi must occur. As we can see, for Figures 3a, b, c, (r1,min, r2,min) = (1, 0), which indicates that these datasets do not provide information about k−1. Figures 3d, e, f have larger (nonzero) values of (r1,min, r2,min) and provide better estimates.
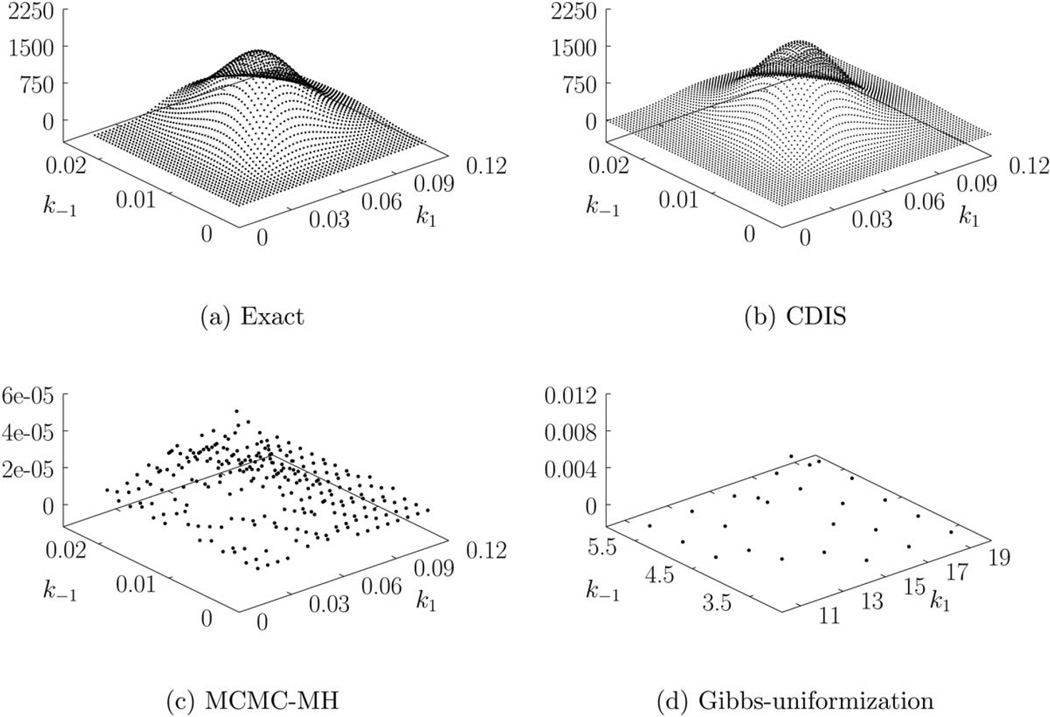
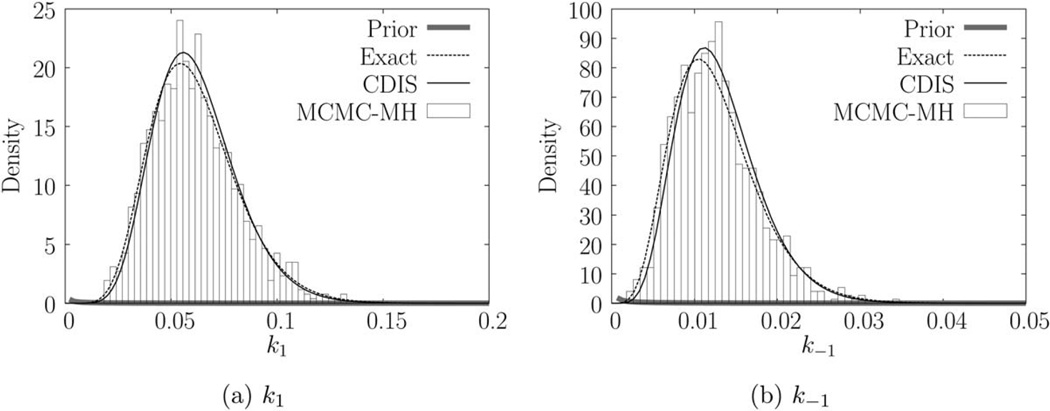
We compare other estimation methods with the exact method for the data in Figure 3d. The joint posterior for all four estimation methods is presented in Figure 5. Parameter estimates obtained by (exact) maximum likelihood estimation and other methods are provided in Table 4. The estimates obtained by exact Bayesian estimation are close to the exact MLE estimates, which indicate that the prior does not bias the estimation. The sampling times are also presented in Table 4. Gibbs-uniformization method performs the worst due to slow mixing of the Markov chain (see Supporting Information). Furthermore, the uniformization step is extremely slow, which limits the number of Markov chain steps that can be used. Detailed analysis of computation time required by uniformization and other similar methods may be found in Ref. 33. As we can see from Figure 5d, 1000 Markov chain steps were not enough to produce a 3-D histogram. Consequently, the Gibbs-uniformization estimates are not accurate. Gibbs-uniformization must be run for a much larger number of steps to obtain reliable estimates. By contrast, CDIS (N = 100 samples) and MCMC-MH (N = 1000 steps) estimates are close to the exact (Bayesian) estimates. A burn-in of 100 steps was used for MCMC-MH method. Variance in CDIS estimates (using N = 100 samples) was lower than the variance in MCMC-MH estimates (using N = 1000 steps). Reducing the number of Markov chain steps used by the MCMC-MH method increases the variance in the resulting histogram and parameter estimates. Thus, the CDIS method requires 10 times fewer numbers of samples compared to the MCMC-MH method to obtain the same accuracy in estimates. The computational expense in terms of seconds/sample is higher for CDIS compared to the MCMC-MH method but the overall computation time is still ~85% lower for CDIS method than MCMC-MH method. In this article, we implemented the block update version of the Metropolis-within-Gibbs-style estimation methods (see MCMC methods in the Background section). It is possible that the RJMCMC method31 may perform better. For cyclical kinetics, both the CDIS and the Metropolis-within-Gibbsstyle methods require a tuning parameter to generate samples of ri. We followed the recommended tuning parameter as suggested by Boys et al.31 and Wilkinson.30 More details are provided in the Supporting Information. The marginal posteriors for both parameters are presented in Figure 6. We used a = [1.01 1.01]T, b = [0.00067 0.00125]T as the parameters for gamma prior.
Figure 5.
Joint posteriors for Figure 3d.
Table 4.
Parameter Estimates and Sampling Time (Seconds per Sample) for Figure 3d
| Parameter | Exact | Exact | CDIS | MCMC-MH | GibbsUnif |
|---|---|---|---|---|---|
| (MLE) | (BE) | (N = 100) | (N = 1000) | (N = 1000) | |
| k1 | 0.0533 | 0.0534 | 0.0557 | 0.0556 | 11.9865 |
| k−1 | 0.0103 | 0.0103 | 0.0111 | 0.0115 | 3.5485 |
| Sampling time (s/sample) | – | – | 0.76 | 0.53 | 9.01 |
True values θ0 = (k1,0, k−1,0) = (0.03, 0.01).
Figure 6.
Marginal posteriors and priors for Figure 3d.
Experimental and Model Design
Only a limited number of measurements can be performed in the laboratory due to resource limitations. The analysis presented in the previous section may be used to develop general guidelines on both experimental and model design that will help in parameter estimation. As we have shown, performing more measurements at a higher frequency does not necessarily improve estimates of some parameters. In both examples, we obtained inaccurate estimates of a rate constant ki when the corresponding reaction ℛi was not observed to occur, that is, ri,min was zero. In cases where both ri and Gi are zero, we obtained no information about the rate constant at all (see data in Figure 1c). Note that Gi is zero indicating that the reaction cannot occur at all during the corresponding time interval and, therefore, implies that ri = 0, but the converse does not hold.
To obtain good estimates, our aim is to ensure large values of both ri,min and Gi by designing the experiment (i.e., manipulating the times at which measurements are taken). The guidelines we provide here are specific to stochastic chemical kinetic models and are not applicable during the exploratory phase of research when no reliable information is available about the system being measured. These guidelines are useful in the later stages of experimentation when we have a set of candidate reaction models in mind.
(1) As the parameter estimation depends on Gi (Eq. 14), it is more important to measure the reactants than the products. If the reactants are not measured, then the numbers of reactant molecules have to be inferred using Eq. 1 and statistical sampling, thereby increasing the computational burden, (2) measuring a reactant species that remains at zero does not provide information about the corresponding reaction(s). As we have seen in the early viral gene expression example, the mRNA (M) remains at zero in Figures 1e, f. The corresponding estimates of translation reaction rate constant kf were close to zero. The measurement effort spent during the interval [0, 10] when M was at zero, could have been better spent later during the experiment when the M was large enough. In some experiments, the measurements are left-censored, that is, we cannot measure them accurately until the measurement is above a certain threshold value. Obviously, measuring left-censored values provides little information, which is especially true for a stochastic chemical kinetic model, (3) estimation of a rate constant is difficult when we do not observe the occurrence of the corresponding reaction event. We have shown in the gene on-off example that estimates of k−1 were close to zero until we were able to observe ℛ2 occurring, that is, until r2,min > 0. The same is true for the data in Figure 1e. For the early viral gene expression example, we know from VSV-BHK biology that the translation occurs later in the experiment, which allows us to reserve more resources for later measurements. For systems like the gene on-off model, the “gene switching on reaction” (ℛ2) does not have such time dependence. Thus, the only way to observe the reaction events occur is by increasing the number of measurements. From the data in Figures 3d, f, we can see that it is better to perform the same number measurements spread sparsely over a longer period of time instead of finely spread over a shorter period of time, and (4) increased measurement frequency does provide some benefit. Likelihood plots in Figures 4a, c show that increased measurement frequency does improve the estimate of k1. This increased measurement frequency does not change the observed number of events, r1,min, but it does improve the value of G1, thus providing the improvement.
It is also important to choose the correct set of models for which to estimate parameters. If the model has a νT with full column rank, then we can obtain the number of observed reaction events uniquely (i.e., ri = ri,min) using the data and Eq. 1. If we can further identify that Gi is zero for a particular reaction (e.g., kf in Figures 1e, f) then the data provides no information about the corresponding reaction, and we should simplify the model by removing the reaction. Even if Gi > 0 but ri = 0, then the estimate of the corresponding reaction rate constant is likely to be zero (e.g., kr in Figures 1e, f) and this reaction may be removed as well. If the model’s νT does not have full column rank, the observed number of reaction events ri,min provides similar guidelines. Using the exact likelihood method, we observed that estimates of k−1 were zero when r2,min = 0. In such cases, the “gene switching on” reaction ℛ2 may be removed to simplify the model.
Conclusions and Future Work
In this article, we have demonstrated the use of three classes of parameter estimation methods, one of which is a new method. Using two examples from systems biology, we have demonstrated some strengths and weaknesses of all three methods. The exact method is intractable when the state space in large or unbounded (except in very special cases), which frequently happens in systems biology models. Even with a finite (and small) state space, Bayesian inference using the exact method requires numerical integration in nr dimensions, which is also computationally expensive. The Gibbs-uniformization MCMC method, similar to the exact method, also uses the solution to Kolmogorov’s forward equation and is not usually applicable. Furthermore, the uniformization technique requires enormous computation, which makes the overall MCMC algorithm slow. More research is required to generate better endpoint-conditioned simulation methods. By comparison, the MCMC-MH method works well. All MCMC methods may sometimes have issues with convergence of Markov chains and require that a considerable fraction of Markov chain steps be burned-in, which increases the computational effort required. Even if these issues are resolved, MCMC methods provide the user with a histogram of the posterior that has the usual bias-variance tradeoff issues. The CDIS method, by contrast, provides a semianalytical expression for the posterior, which may be used for further analysis. We have shown that the CDIS method has good convergence properties and requires much less overall computation time than MCMC methods. Convergence of the CDIS method depends on the ability of the importance distribution to mimic the target distribution. There may be examples where the importance distribution we proposed is sufficiently different from the target distribution to require significantly more computation, but we have not yet encountered this issue.
Parameter estimation in stochastic chemical kinetics is a new area of research when compared to deterministic kinetics. Estimating parameters for a wide range of models using experimental data is a challenge that has two major bottlenecks. The first bottleneck is the measurements—only a partial set of species (usually one) can be measured at a time and even these measurements suffer from unknown measurement noise. The case of partial measurements is similar to the case of cyclical kinetics and may be solved by both CDIS and MCMC-MH methods. With the advancements in experimental techniques, the measurements are becoming more accurate and eventually it may be possible to obtain full measurements with low or at least characterized measurement noise. The second bottleneck is the computation time required. More measurements usually require more computation. Even with a small amount of “perfect data,” the computation time required may be large. In the future, when large amounts of imperfect data are available, computation is expected to be prohibitive, and fast, albeit approximate, estimators will be required.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge funding for this research from a University of Wisconsin WARF Named Professorship Award. Andrea Timm and John Yin provided helpful comments and discussions. We are also grateful for support from the National Institutes of Health (AI071197 and AI091646)
Footnotes
Additional Supporting Information may be found in the online version of this article.
Literature Cited
- 1.McQuarrie DA. Stochastic approach to chemical kinetics. J Appl Probab. 1967;4:413–478. [Google Scholar]
- 2.Gillespie DT. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comput Phys. 1976;22:403–434. [Google Scholar]
- 3.Zheng Q, Ross J. Comparison of deterministic and stochastic kinetics for nonlinear systems. J Chem Phys. 1991;94:3644–3648. [Google Scholar]
- 4.van Kampen NG. Stochastic Processes in Physics and Chemistry. 2nd. Amsterdam, The Netherlands: Elsevier Science Publishers; 1992. [Google Scholar]
- 5.Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81:2340–2361. [Google Scholar]
- 6.Gibson MA, Bruck J. Efficient exact stochastic simulation of chemical systems with many species and many channels. J Phys Chem A. 2000;104:1876–1889. [Google Scholar]
- 7.Anderson DF. A modified next reaction method for simulating chemical systems with time dependent propensities and delays. J Chem Phys. 2007;127:214107. doi: 10.1063/1.2799998. [DOI] [PubMed] [Google Scholar]
- 8.Srivastava R, Haseltine EL, Mastny E, Rawlings JB. The stochastic quasi-steady-state assumption: reducing the model but not the noise. J Chem Phys. 2011;134:154109. doi: 10.1063/1.3580292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mastny EA, Haseltine EL, Rawlings JB. Two classes of quasisteady-state model reductions for stochastic kinetics. J Chem Phys. 2007;127:094106. doi: 10.1063/1.2764480. [DOI] [PubMed] [Google Scholar]
- 10.Cao Y, Gillespie DT, Petzold LR. The slow-scale stochastic simulation algorithm. J Chem Phys. 2005;122:014116. doi: 10.1063/1.1824902. [DOI] [PubMed] [Google Scholar]
- 11.Haseltine EL, Rawlings JB. On the origins of approximations for stochastic chemical kinetics. J Chem Phys. 2005;123:164115. doi: 10.1063/1.2062048. [DOI] [PubMed] [Google Scholar]
- 12.Haseltine EL, Rawlings JB. Approximate simulation of coupled fast and slow reactions for stochastic chemical kinetics. J Chem Phys. 2002;117:6959–6969. [Google Scholar]
- 13.Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- 14.Blake WJ, Kaern MA, Cantor CR, Collins JJ. Noise in eukaryotic gene expression. Nature. 2003;422:633–637. doi: 10.1038/nature01546. [DOI] [PubMed] [Google Scholar]
- 15.Raser JM, O’Shea EK. Control of stochasticity in eukaryotic gene expression. Science. 2004;304:1811–1814. doi: 10.1126/science.1098641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.McAdams HH, Arkin A. Stochastic mechanisms in gene expression. Proc Natl Acad Sci USA. 1997;94:814–819. doi: 10.1073/pnas.94.3.814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Arkin A, Ross J, McAdams HH. Stochastic kinetic analysis of developmental pathway bifurcation in phage λ-infected Escherichia coli cells. Genetics. 1998;149:1633–1648. doi: 10.1093/genetics/149.4.1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Weinberger LS, Burnett JC, Toettcher JE, Arkin AP, Schaffer DV. Stochastic gene expression in a lentiviral positive-feedback loop: HIV-1 tat fluctuations drive phenotypic diversity. Cell. 2005;122:169–182. doi: 10.1016/j.cell.2005.06.006. [DOI] [PubMed] [Google Scholar]
- 19.Hensel SC, Rawlings J, Yin J. Stochastic kinetic modeling of Vesicular stomatitis virus intracellular growth. Bull Math Biol. 2009;71:1671–1692. doi: 10.1007/s11538-009-9419-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Golding I, Paulsson J, Zawilski SM, Cox EC. Real-time kinetics of gene activity in individual bacteria. Cell. 2005;123:1025–1036. doi: 10.1016/j.cell.2005.09.031. [DOI] [PubMed] [Google Scholar]
- 21.Tian T, Xu S, Gao J, Burrage K. Simulated maximum likelihood method for estimating kinetic rates in gene expression. Bioinformatics. 2007;23:84–91. doi: 10.1093/bioinformatics/btl552. [DOI] [PubMed] [Google Scholar]
- 22.Poovathingal SK, Gunawan R. Global parameter estimation methods for stochastic biochemical systems. BMC Bioinf. 2010;11:1–12. doi: 10.1186/1471-2105-11-414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Reinker S, Altman RM, Timmer J. Parameter estimation in stochastic biochemical reactions. IEE Proc Syst Biol. 2006;153:168–178. doi: 10.1049/ip-syb:20050105. [DOI] [PubMed] [Google Scholar]
- 24.Wang Y, Christley S, Mjolsness E, Xie X. Parameter inference for discretely observed stochastic kinetic models using stochastic gradient descent. BMC Syst Biol. 2010;4:1–16. doi: 10.1186/1752-0509-4-99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rempala GA, Ramos KS, Kalbfleisch T. A stochastic model of gene transcription: an application to L1 retrotransposition events. J Theor Biol. 2006;242:101–116. doi: 10.1016/j.jtbi.2006.02.010. [DOI] [PubMed] [Google Scholar]
- 26.Henderson DA, Boys RJ, Krishnan KJ, Lawless C, Wilkinson DJ. Bayesian emulation and calibration of a stochastic computer model of mitochondrial DNA deletions in substantia nigra neurons. J Am Stat Assoc. 2009;104:76–87. [Google Scholar]
- 27.Golightly A, Wilkinson DJ. Bayesian sequential inference for stochastic kinetic biochemical network models. J Comput Biol. 2006;13:838–851. doi: 10.1089/cmb.2006.13.838. [DOI] [PubMed] [Google Scholar]
- 28.Golightly A, Wilkinson D. Bayesian inference for nonlinear multivariate diffusion models observed with error. Comput Stat Data Anal. 2008;52:1674–1693. [Google Scholar]
- 29.Golightly A, Wilkinson DJ. Bayesian parameter inference for stochastic biochemical network models using particle Markov chain Monte Carlo. Interface Focus. 2011;1:807–820. doi: 10.1098/rsfs.2011.0047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wilkinson DJ. Stochastic Modelling for Systems Biology. Vol. 44. Boca Raton, FL: CRC press; 2012. [Google Scholar]
- 31.Boys RJ, Wilkinson DJ, Kirkwood TBL. Bayesian inference for a discretely observed stochastic kinetic model. Stat Comput. 2008;18:125–135. [Google Scholar]
- 32.Choi B, Rempala GA. Inference for discretely observed stochastic kinetic networks with applications to epidemic modeling. Biostatistics. 2012;13:153–165. doi: 10.1093/biostatistics/kxr019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hobolth A, Stone EA. Simulation from endpoint-conditioned, continuous-time Markov chains on a finite state space, with applications to molecular evolution. Ann Appl Stat. 2009;3:1204–1231. doi: 10.1214/09-AOAS247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rawlings JB, Ekerdt JG. Chemical Reactor Analysis and Design Fundamentals. Madison, WI: Nob Hill Publishing; 2004. p. 640. [Google Scholar]
- 35.Chen W-Y, Kulkarni A, Milum JL, Fan LT. Stochastic modeling of carbon oxidation. AIChE J. 1999;45:2557–2570. [Google Scholar]
- 36.Graham MD, Rawlings JB. Modeling and Analysis Principles for Chemical and Biological Engineers. Madison, WI: Nob Hill Publishing; 2013. p. 552. [Google Scholar]
- 37.Jahnke T, Huisinga W. Solving the chemical master equation for monomolecular reaction systems analytically. J Math Biol. 2007;54:1–26. doi: 10.1007/s00285-006-0034-x. [DOI] [PubMed] [Google Scholar]
- 38.Asmussen S, Hobolth A. Bisection ideas in end-point conditioned Markov process simulation. Proceedings of the 7th International Workshop on Rare Event Simulation; Rennes, France. 2008. pp. 7499–7506. [Google Scholar]
- 39.Gupta A. Ph.D. thesis. Madison, WI: University of Wisconsin- Madison; 2013. Parameter estimation in deterministic and stochastic models of biological systems. [Google Scholar]
- 40.Timm A, Yin J. Kinetics of virus production from single cells. Virology. 2012;424:11–17. doi: 10.1016/j.virol.2011.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Rose JK, Whitt MA. Rhabdoviridae: The viruses and their replication. In: Knipe DM, Howley PM, editors. Fields Virology. 4th. Vol. 1. Philadelphia: Lippincot Williams & Wilkins; 2001. pp. 1221–1244. [Google Scholar]
- 42.Wasserman L. All of Statistics: A Concise Course in Statistical Inference. Springer; 2004. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.