Feedback Regulation in a Cancer Stem Cell Model can Cause an Allee Effect

Abstract

The exact mechanisms of spontaneous tumor remission or complete response to treatment are phenomena in oncology that are not completely understood. We use a concept from ecology, the Allee effect, to help explain tumor extinction in a model of tumor growth that incorporates feedback regulation of stem cell dynamics, which occurs in many tumor types where certain signaling molecules, such as Wnts, are upregulated. Due to feedback and the Allee effect, a tumor may become extinct spontaneously or after therapy even when the entire tumor has not been eradicated by the end of therapy. We quantify the Allee effect using an ‘Allee index’ that approximates the area of the basin of attraction for tumor extinction. We show that effectiveness of combination therapy in cancer treatment may occur due to the increased probability that the system will be in the Allee region after combination treatment versus monotherapy. We identify therapies that can attenuate stem cell self-renewal, alter the Allee region and increase its size. We also show that decreased response of tumor cells to growth inhibitors can reduce the size of the Allee region and increase stem cell densities, which may help to explain why this phenomenon is a hallmark of cancer.

1 Introduction

Feedback control of cell growth and differentiation plays a central role in tissue development and homeostasis (Buchmann et al. 2014; Freeman 2000; Lander et al. 2009). It is increasingly recognized that in tumors, feedback regulation may also influence cancer cell proliferation and differentiation through signaling pathways used in normal tissues via biochemical signaling factors and mechanotransduction. However, in cancer, these feedback mechanisms are either abrogated or altered by the cancer cells to help promote tumor growth (e.g., see Carracedo et al. 2008; Chen and Hughes-Fulford 2001; Massagué et al. 2000). In the intestinal epithelium, for example, Wnt proteins and their downstream effectors are critical regulatory molecules in development and homeostasis of intestinal epithelial cells. Wnts are produced at the base of intestinal crypts by intestinal stem cells and Paneth cells and act on the stem and transit-amplifying cells to increase self-renewal and proliferation rates (Clevers et al. 2014; Pinto and Clevers 2005). These cells also produce Wnt inhibitors such as Dkk in response to Wnt signal (González-Sancho et al. 2005). Maintenance of tissue homeostasis is aided by production of bone morphogenetic proteins (BMPs), members of the TGFβ superfamily, by differentiated cells at the top of the villi that promote differentiation of the stem and transit-amplifying cells (Radtke and Clevers 2005). In normal physiology, this highly regulated program allows for maintenance of an intestinal lineage hierarchy, whereas overactivation of Wnt signal occurs in a majority of hereditary and sporadic colorectal cancers (Bienz and Clevers 2000; Reya and Clevers 2005). Wnts, Wnt inhibitors and BMPs play similar roles in other tissues such as skin, breast (Clevers et al. 2014) and the brain (Bayin et al. 2014; Caja et al. 2015), although other members of the TGFb superfamily, such as TFGb-1 and TGFb-2, may upregulate stem cell self-renewal and promote tumor invasiveness. Additionally, other signaling factors such as notch, fibroblast growth factors, sonic hedgehog and epidermal growth factors may also influence stem cell self-renewal (e.g., Ciurea et al. 2014; Matchett and Lappin 2014; Mertins 2014).

Analogous to normal tissues, in many types of cancer, cells appear to be hierarchically organized. Examples include leukemias and solid tumors such as breast, brain, prostate, ovarian and colon (Meacham and Morrison 2013; O'Connor et al. 2014). In particular, a small fraction of tumor cells, called cancer stem cells (CSCs), seem to be capable of initiating and maintaining cancer and are more resistant to therapy. CSCs give rise to cells that do not have these capabilities.

Mathematical models of CSCs reveal a variety of surprising behaviors. For example, agent-based model simulations by Enderling et al. (2009) identified a so-called tumor growth paradox where tumors with larger death rates of non-stem cancer cells might grow bigger than tumors with smaller death rates for non-CSCs. This effect results from a competition for space between CSCs and non-CSCs, which can be interpreted as a form of negative feedback. As soon as non-CSCs are removed, CSCs may divide symmetrically to increase the number of CSCs, thereby increasing the size of the tumor. In Hillen et al. (2013) a basic CSC model was used to explain the tumor growth paradox. Further, mathematical models also predict that hierarchically organized tumors exhibit a greater degree of heterogeneity and invasiveness than models that do not consider CSCs (e.g., Poleszczuk et al. 2015; Scott et al. 2014; Sottoriva et al. 2010, 2011).

Intriguingly, using a continuum model of CSCs that accounted for biochemically mediated feedback regulation of CSC dynamics, Youssefpour et al. (2012) showed that therapies that exploit feedback regulation, such as therapies that combine radiation or chemotherapy (that target differentiated cells) with differentiation therapy (that targets cancer stem cells), are capable of fully eradicating a tumor even if each therapy applied individually would not be successful. In the specific cases of metastatic brain cancer, head and neck cancer and breast cancer, Bachman and Hillen (2012) investigated the combination therapy proposed by Youssefpour et al. using a simplified mathematical model similar to that studied here. Bachman and Hillen demonstrated that treatment benefits can be achieved through a combination of a differentiation promotor and radiation treatment for metastatic brain cancer and for head and neck cancer. The effect of combination therapy on breast cancer was less clear.

One of the recently identified feedback mechanisms of CSCs involves the protein survivin. Survivin is considered to promote dedifferentiation of non-stem cancer cells into CSCs. In experiments of non-small cell lung cancer in mice (Iwasa et al. 2006) it was found that survivin is expressed upon radiation treatment, leading to enhanced dedifferentiation and to enhanced radio-resistance. The survivin effect is then controlled by administration of YM155. In (Rhodes and Hillen 2016) a mathematical model was developed to investigate the combination of YM155 administration and radiation therapy on the CSC dynamics.

Motivated by these studies, we develop a simplified model of feedback-regulated tumor growth to better understand the underlying mechanisms of how feedback in tumors can contribute to treatment success or even to spontaneous regression, which occurs in about 1/80,000–1/100,000 cases of cancer (Challis and Stam 1900). We show that the feedback mechanisms can induce an Allee effect, which is a phenomenon, studied in ecology, where there exists a positive correlation between population density and individual fitness (Stephens et al. 1999). In the case of a tumor, the Allee effect can manifest itself through treatment, which can cause the CSC count to fall below a threshold such that the tumor cannot sustain itself and dies out, or in spontaneous tumor remission when CSC numbers may naturally fall below the sustainability threshold (Korolev et al. 2014). The existence of a sustainability threshold belies an important conclusion: treatment does not need to kill all the CSCs to be successful in eradicating a tumor. In our reduced system, we prove that such an Allee effect exists and we analyze the dependence of the Allee region and the sustainability threshold on model parameters and initial conditions.

2 Model Development

Our model focuses on the interplay between CSCs, represented by S(t), and a self-renewal activator a(t), which represents the combined activity of self-renewal promoters (e.g., Wnts) in a spatially homogeneous setting. This is a simplification of a more complicated model that includes S(t), a(t), and two other variables: the differentiated cells, represented by D(t), and concentration of the differentiation promoter, T(t). We begin by considering the more complex model, which itself is a spatially homogeneous version of the model considered by Youssefpour et al. (2012).

The dynamics of S(t) and D(t) can be given by (e.g., Lander et al. 2009; Youssefpour et al. 2012)

$$\stackrel{.}{S}=\stackrel{\text{Stem cell self-renewal}}{\overbrace{(2p(T,a)-1)kS}},$$ (1)

$$\stackrel{.}{D}=\stackrel{\text{Differentiation of stem cells}}{\overbrace{2(1-p(T,a))kS}}-\stackrel{\text{Cell death}}{\overbrace{dD}},$$ (2)

where the overdot denotes the time derivative, k is proliferation rate of CSCs and is taken to be constant and nonnegative, and d is the death rate of differentiated cells, which incorporates both apoptosis and necrosis. The variable p(T, a) denotes the probability of self-renewal of CSCs and depends on concentration of T, a differentiation promoter (e.g., a member of the TGFβ superfamily), and on the activator, a. We can take p to be (Youssefpour et al. 2012)

$$p(T,a)=p_{\min }+(p_{\max }-p_{\min })\left(\frac{\xi a}{1+\xi a}\right)\left(\frac{1}{1+\psi T}\right),$$ (3)

where the minimum and maximum rates of self-renewal are p_min and p_max, respectively, and ξ and ψ are the positive, by a, and negative, by T, feedback strengths on p. In our reduced model we assume a linear relationship between T and S. Indeed, we first consider a model for the dynamics of T as

$$\stackrel{.}{T}=vD-\mu T,$$ (4)

where ν is the production rate of T by D, and μ is the effective decay rate of T (which could include uptake by CSCs or differentiated cells). Assuming that T and D are in a quasi-steady state we obtain

$$T=(v∕\mu )D,$$ (5)

$$D=(1∕d)2(1-p)S.$$ (6)

The former can be justified since the diffusional dynamics of T occurs on a faster timescale (minute) than that of cell proliferation (day), e.g., Youssefpour et al. (2012), although here we neglect spatial variation. The latter assumes that differentiated cells do not perpetually accumulate. Combining Eqs. (5) and (6), we obtain T~S, and so we simplify Eq. (3) to yield

$$p(S,a)=\left(\frac{{\xi }_{1}a}{1+{\xi }_{1}a}\right)\left(\frac{1}{1+{\xi }_{2}S}\right),$$ (7)

where we have taken p_min = 0 and p_max = 1 and the parameter ξ₂ has absorbed the linear shift to S.

Self-renewal promoters such as Wnts can have multiple downstream effectors (Najdi et al. 2011) that can upregulate the production of the promoters. This can be modeled as a positive feedback of the promoter on its own production (Crosnier et al. 2006). Further, cells with high self-renewal promoter activity (e.g., CSCs) can produce factors (e.g., Dkk) that inhibit the production of self-renewal promoters. Here, we assume for simplicity that the level of inhibitor is constant. Accordingly, we consider the production rate of a as β = γ/b, where γ is the production rate and b corresponds to a constant level of inhibitor. To mitigate the blow-up of a that a model with constant inhibitor levels can produce, we introduce the linear saturation term λ, which forces ȧ to saturate to a linear rate. We note that since the effect of a on p is bounded by 1 (Eq. (7)), forcing a to saturate to a high value would produce qualitatively similar results. We thus study

$$\stackrel{.}{a}=a\left(\frac{\beta Sa}{1+\lambda a}-1\right),$$ (8)

where we have taken the decay rate of a to be 1, without loss of generality (e.g., take the timescale to be the inverse of the characteristic decay rate of a). The reduced model, which describes feedback-regulated stem cell dynamics, is given by

$$\begin{array}{cc}\hfill \stackrel{.}{S}=& (2p(S,a)-1)kS=f_1(S,a),\hfill \\ \hfill \stackrel{.}{a}=& a\left(\frac{\beta Sa}{1+\lambda a}-1\right)=f_2(S,a),\hfill \\ \hfill p(S,a)=& \frac{{\xi }_{1}a}{1+{\xi }_{1}a}\frac{1}{1+{\xi }_{2}S}.\hfill \end{array}$$ (9)

The variables and parameters for system (9) are summarized in Table 1.

Table 1.

Variables and parameters for system (9)

Symbol	Description	Relative change in more aggressive tumors	Parameter profile
			Pr1 (less aggres.)	Pr2 (more aggres.)
Variables
S = S(t)	Cancer stem cell (CSC) concentration	–	–	–
a = a(t)	CSC activator concentration	–	–	–
p = p(S, a)	Probability of stem cell self-renewal	–	–	–
Parameters
ξ 1	Positive feedback strength of a on p	↑	1	5
ξ 2	Negative feedback strength of S on p	↓	1	0.5
λ	Saturation term for ȧ	↓	1	1
k	CSC division rate	↑	1	1
β	Production rate of a	↑	2	4

To model more aggressive tumors, parameters can be adjusted as indicated. The sample parameter profiles Pr₁ and Pr₂ described in Sects. (4)–(6) are also shown, where the text (less aggres.) and (more aggres.) indicates the relative aggressive profile of the tumor

3 Analysis of the Allee Effect

In this section, we demonstrate that the system (9) shows an Allee effect. To begin, we calculate the following partial derivatives, which we will need in the analysis:

$$\begin{array}{cc}\hfill p_S& ≔\frac{\partial p}{\partial S}=-\frac{{\xi }_1{\xi }_{2}a}{(1+{\xi }_{1}a){(1+{\xi }_{2}S)}^2}\le 0\text{where}{p}_S=0\text{only when}a=0,\hfill \\ \hfill p_a& ≔\frac{\partial p}{\partial a}=\frac{{\xi }_1}{(1+{\xi }_{2}S){(1+{\xi }_{1}a)}^2}>0,\hfill \\ \hfill {\left(f_2\right)}_S& ≔\frac{\partial f_2}{\partial S}=\frac{\beta a^2}{1+\lambda a}\ge 0\text{where}{\left(f_2\right)}_S=0\text{only when}a=0,\hfill \\ \hfill {\left(f_2\right)}_a& ≔\frac{\partial f_2}{\partial a}=\frac{\beta Sa(2+\lambda a)}{{(1+\lambda a)}^2}-1.\hfill \end{array}$$

where we use subscripts to denote partial derivatives. Note that the sign of (f₂)_a depends upon β, S, a and λ.

Theorem 1

Existence of an Allee region.

• (i)The domain Ω = [0, ∞) × [0, ∞) is positively invariant for (9).
• (ii)
  The system (9) has two steady states in Ω, P₁(0, 0) and P₂(S₂, A₂), where P₂ is the unique intersection of the curves

  $$\{p(S,a)=0.5\}\text{and}\{f_2(S,a)=0\}.$$
• (iii)P₁ is asymptotically stable, and P₂ is a saddle point.
• (iv)There exists a separatrix that separates the basin of attraction of P₁ from an attractor with nonzero S when λ/β < 1/ξ₂. This separatrix forms the threshold between population extinction P₁ and population sustainability.

Proof

• (i)We observe that Ṡ ≥ –kS and ȧ ≥ –a. Setting Ṡ+kS = l₁ and ȧ+a = l₂ and solving each differential equation under the condition that (l₁, l₂) ≥ (0, 0) gives us the condition that (S(t), a(t)) ≥ (0, 0) for all initial (S, a) ≥ (0, 0). Thus, Ω = [0, ∞) × [0, ∞) is positively invariant for (9).
• (ii)
  We find Ṡ = 0 if and only if S = 0, p(S, a) = 0.5, or k = 0. The second equation is in steady state if a = 0 or a = a*(S) = (βS–λ)^–1, S > 0. We note that when S = 0, $a^{\ast }\left(S\right)=\frac{-1}{\lambda }<0$ since λ is assumed to be nonnegative. This cannot be a steady state since a ≥ 0. Similarly, if a = 0, then p(S, 0) = 0. Hence, the only steady state with S = 0 or a = 0 is P₁(0, 0).

  • We next want to determine whether there exist, and if yes how many, pairs of (S, a) such that p(S, a) = 0.5 and f₂(S, a) = 0. This can be found by solving the system:

    $$\{\begin{array}{c}\frac{{\xi }_{1}a}{1+{\xi }_{1}a}\frac{1}{1+{\xi }_{2}S}=0.5\hfill \\ \frac{\beta Sa}{1+\lambda a}=1\hfill \end{array}\phantom{\}}$$ (10)

    Solving the first equation S, we obtain S = (ξ₁a – 1)/(ξ₂(1 + ξ₁a)). We first note that the function is monotone increasing in a, since S′ = (2ξ₁)/(ξ₂(1 + ξ₁a)²) > 0 where the prime denotes the derivative with respect to a. Moreover, we have

    $$\underset{a\to 0}{\lim }\left(\frac{{\xi }_{1}a-1}{{\xi }_2(1+{\xi }_{1}a)}\right)=-\frac{1}{{\xi }_2}\text{and}\underset{a\to \infty }{\lim }\left(\frac{{\xi }_{1}a-1}{{\xi }_2(1+{\xi }_{1}a)}\right)=\frac{1}{{\xi }_2}$$

    Repeating the process for the second equation, we obtain $S=(1+\lambda a)∕\left(\beta a\right)=1∕\left(\beta a\right)+\lambda ∕\beta ,S^{\prime }=\frac{-1}{\beta a^2}<0$; hence, the function is monotone decreasing, and

    $$\underset{a\to 0}{\lim }\left(\frac{1}{\beta a}+\frac{\lambda }{\beta }\right)=\infty \text{and}\underset{a\to \infty }{\lim }\left(\frac{1}{\beta a}+\frac{\lambda }{\beta }\right)=\frac{\lambda }{\beta }.$$

    Therefore, the nonnegativity constraints on (S, a) and the parameters guarantee existence of a unique solution if

    $$\lambda ∕\beta <1∕{\xi }_2.$$ (11)

    In the linear stability analysis below, whenever we discuss P₂(S₂, A₂), the steady state corresponding to (9), we assume that the inequality (11) is satisfied.
• (iii)
  The Jacobian of f = (f₁(S, a), f₂(S, a)) in Eq. (9) is

  $$\mathit{J}(S,a)=\left(\begin{array}{cc}\hfill 2p_{S}kS+(2p-1)k\hfill & \hfill 2p_{a}kS\hfill \\ \hfill {\left(f_2\right)}_S\hfill & \hfill {\left(f_2\right)}_a\hfill \end{array}\right)$$ (12)

  For P₁(0, 0) we have p(0, 0) = 0, ps = 0, pa = ξ₂, (f₂)_s = 0 and (f₂)_a = –1. Therefore, we have

  $$\mathit{J}(0,0)=\left(\begin{array}{cc}\hfill -k\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill \end{array}\right),$$

  which has two negative eigenvalues. Hence P₁(0, 0) is an asymptotically stable node.

  • For P₂(S₂, A₂), where we denote p_(S,2) = p_S(S₂, A₂), p_(a,2) = p_a(S₂, A₂), (f₂)_(S,2) = (f₂)_S(S₂, A₂) and (f₂)_(a,2) = (f₂)_a(S₂, A₂), the Jacobian is

    $$\mathit{J}(S_2,A_2)=\left(\begin{array}{cc}\hfill 2p_{(S,2)}k{S}_2\hfill & \hfill 2p_{(a,2)}k{S}_2\hfill \\ \hfill {\left(f_2\right)}_{S,2}\hfill & \hfill {\left(f_2\right)}_{a,2}\hfill \end{array}\right)$$

    We recall that p_S < 0, p_a > 0, and (f₂)_S > 0. Since we also have (βS₂ A₂)/(1 + λA₂) = 1 by (10), we obtain

    $${\left(f_2\right)}_{a,2}=\frac{\beta S_2{A}_2(2+\lambda A_2)}{{(1+\lambda A_2)}^2}-1=\frac{2+\lambda A_2}{1+\lambda A_2}-1=\frac{1}{1+\lambda A_2}>0.$$

    Therefore, we have (f₂)_a,2 > 0, and hence the determinant of J(S₂, A₂) is

    $$\det \mathit{J}(S_2,A_2)=2p_{(S,2)}k{S}_2{\left(f_2\right)}_{(a,2)}-2p_{(a,2)}k{S}_2{\left(f_2\right)}_{(S,2)}<0,$$ (13)

    which makes P₂ a saddle point.
• (iv)System (9) thus satisfies the assumptions of the Stable Manifold Theorem (SMT) (see Theorem 2 in Appendix 1), which then guarantees existence of a separatrix, M, separating the basins of attraction of P₁ from a nonzero attractor when (11) is satisfied.

4 Dependence of the Separatrix on Parameters

For the system (9) to have a steady state other than P₁(0, 0), the inequality λ/β < 1/ξ₂ in (11) must be satisfied. Recall that λ is the saturation term for ȧ, and β is the rate of a auto-activation, normalized by a constant level of stem cell-derived Wnt inhibitor, b. Therefore, λ/β is increased when there is strong saturation and/or low self-activation strength, and is decreased when the saturation strength is low and/or self-activation strength is high. In more advanced cancers, it has been shown that the Wnt cascade may be constitutively activated and response to growth inhibitors is lowered (Hanahan and Weinberg 2011; Krausova and Korinek 2014), which means that a-saturation strength decreases and β increases; hence, λ/β tends to decrease as the cancer progresses. Moreover, if the inhibitory effect of S on p, modeled by the parameter ξ₂, is strong, then 1/ξ₂ will be small, and the inequality is less likely to be satisfied, thereby leading to one steady state of P₁(0 0). On the other hand, a low strength of p-inhibition (hence giving a relatively large 1/ξ₂) occurs with more advanced cancers. Thus, we see that as a cancer progresses, the inequality (11) is more likely to be satisfied, thereby altering the long-term system dynamics toward a higher probability that (S, a) $\nrightarrow$ (0, 0).

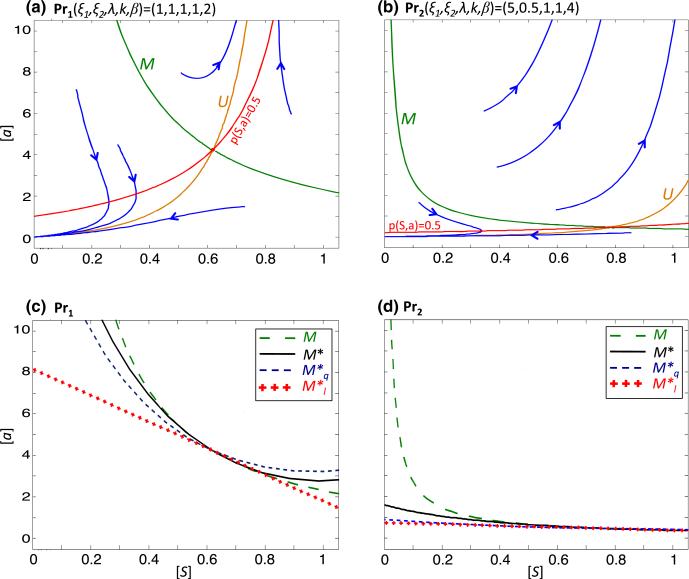
The Stable Manifold Theorem (SMT) allows us to iteratively approximate the separatrix, M, when the inequality (11) is satisfied. In Appendix 1, an approximation to M is given, which we obtain by stopping at the second iteration. We refer to this approximation as M*. Since it is cumbersome to further improve the approximation iteratively by the SMT, we check whether M* is a good approximation of M by comparing M* with the separatrix predicted for a given set of parameters by a numerical ODE analysis program (here we have used pplane8 in MATLAB; Arnold and Polking 1999). We choose two sets of parameters, Pr₁(ξ₁, ξ₂, λ, k, β) = (1, 1, 1, 1, 2) and Pr₂ = (5, 0.5, 1, 1, 4), where Pr₂ represents a more aggressive tumor than Pr₁. Using pplane8, we observe that the separatrix for Pr₂ is shifted southwest of the separatrix for Pr₁, with the result that the Pr₂ system will have a nonzero steady state for a lower threshold of (S, a) than Pr₁ (Fig. 1a, b). We also plot the contour p = 0.5 and observe that even if (S, a) lies below the separatrix (in the Allee region), S can increase in time transiently if p(S, a) > 0.5, with the amount of increase dependent on the system parameters. The more aggressive tumor parameters can lead to a larger transient increase in S. In Fig. 1c, d we plot M* for Pr₁ and Pr₂, overlay these results with the separatrix predicted by pplane8 and note that the shape and location of M* are close to the numerically predicted separatrix. We proceed to analyze M* in order to establish a dependence between the parameters of the model and behavior of the separatrix.

Fig. 1.

The separatrix and its approximations for system (9). a, b pplane8 plots of (9) with parameters a Pr₁ and b Pr₂. The descending green curve in each graph is the pplane approximation of the stable manifold (separatrix M), and the ascending orange curve is the pplane approximation of the unstable manifold, U. The blue curves represent forward solutions of the system. The red curves represent the contours at which the self-renewal probability p = 0.5. Note that solutions to the right of the separatrix tend to nonzero (S, a), whereas solutions to the left tend to P₁(0, 0). In each region, however, if the current values (S, a) are above the p = 0.5 contour, then S increases in time. Analogously, if (S, a) lies below the p = 0.5 contour, then S decreases. c, d The separatrices predicted by pplane8 (large dash, green) of c Pr₁ and d Pr₂ are plotted along with the SMT approximation of the separatrix, M* (solid black), the quadratic approximation, $M_q^{\ast }$ (small dash, blue), and the linear approximation, $M_l^{\ast }$ (cross, red) (Color figure online)

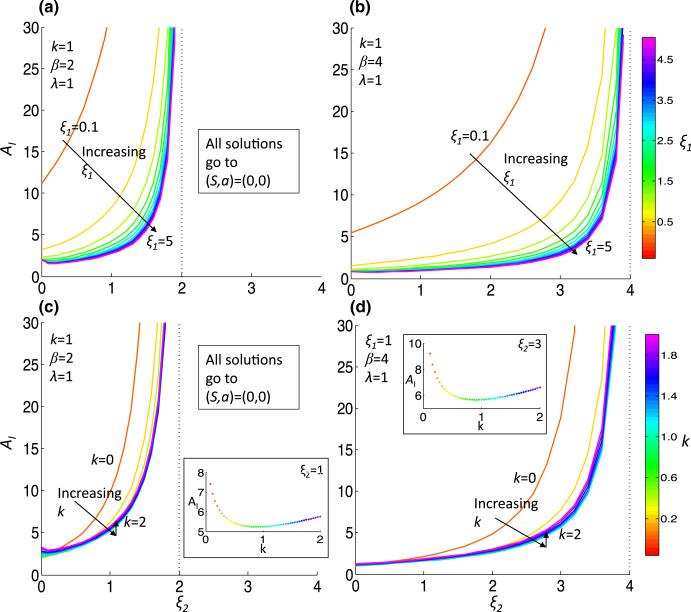
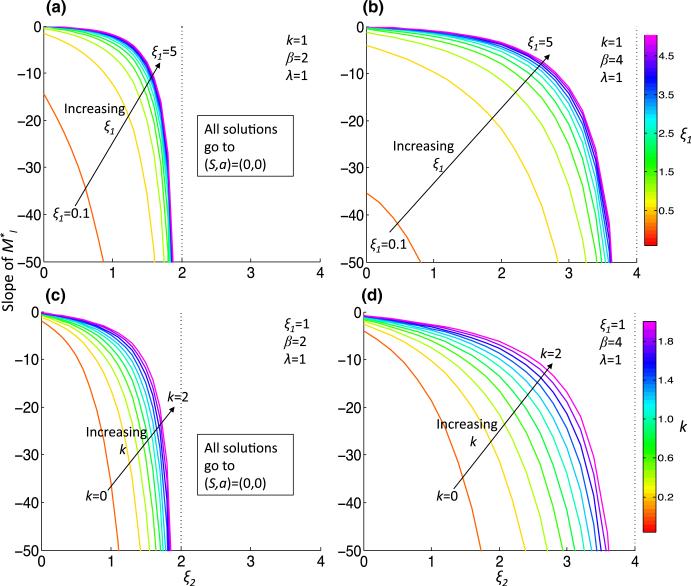
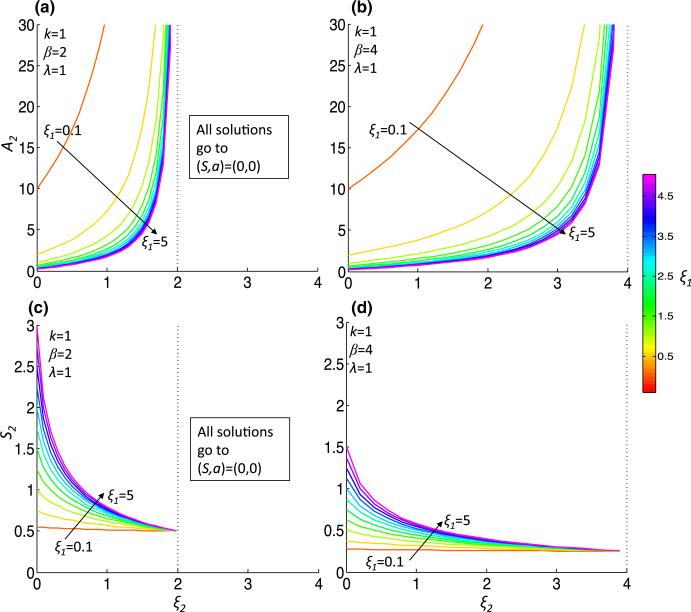
Due to the complicated dependence of M* on the parameters, we take linear and quadratic approximations of M*, which we call $M_l^{\ast }$ and $M_q^{\ast }$, respectively, given in Eqs. (42) and (44) in Appendix 1. We plot $M_l^{\ast }$ and $M_q^{\ast }$ for the two parameter sets, Pr₁ and Pr₂, in Fig. 1c, d. Noting that $M_l^{\ast }$ gives an approximation of the tangent line to the separatrix, we concentrate our analysis on the parameter dependence of $M_l^{\ast }$. To quantify the Allee effect, we develop an ‘Allee index,’ which we refer to as A_I, that is given by the area below $M_l^{\ast }$, which is an estimation of the size of the Allee region. This ‘Allee region’ is the basin of attraction for the steady state representing tumor extinction, P₁(0, 0), and hence A_I = A_I (ξ₁, ξ₂, λ, k, β) is inversely correlated with tumor sustainability. Indeed, the more aggressive tumor Pr₂ has A_I (Pr₂) = 0.77, which is just 14% of A_I(Pr₁) = 5.24 for the less-aggressive tumor. The dependence of A_I on various parameter regimes provides information on how parameter values influence the susceptibility of the tumor to the Allee effect (Fig. 2). We find that increasing ξ₂, the strength of inhibition of p by S increases A_I for all parameter regimes. The increase in A_I comes about due to a ξ₂-dependent increase in the steady-state value A₂ and magnitude of m_l, the slope of $M_l^{\ast }$ (which is always negative) (Figs. 3, 4). Although the steady-state value S₂ decreases as ξ₂ increases, it does not tend to zero; indeed, as ξ₂ → β/λ, by (10), S₂ → λ/β. Conversely, increasing ξ₁, the strength of activation of p by a, results in a decreased A_I by the opposite mechanisms as decreasing ξ₂: there is an increase in magnitude of m_l, a decrease of A₂ and an increase of the steady-state value S₂ that cannot compensate for the decrease in A_I (Figs 2a, b, 3a, b, 4a, b). Generally, increasing β from 2 to 4 also decreases A_I due to the same mechanisms as when increasing ξ₁, and the increase also extends the range of ξ₂ that satisfies (11) (Fig. 2). For smaller values of ξ₂ and ξ₁, increasing β from 2 to 4 decreases A_I by a different mechanism. For example, at ξ₂ = 0, λ = 1 and k = 1, the m_l increases in magnitude from approximately –15 to –35 (Fig. 3). The steady-state value A₂ does not change significantly, but S₂ decreases from approximately 0.5 to 0.25 (indeed, lim (S₂)_ξ1→0 = λ/β) (Fig. 4). We also consider the dependence of A_I on k, the stem cell division rate. Unlike the other parameters, (A₂, S₂) is not dependent on k. As k initially increases from 0, there is a drop in A_I (except for very small ξ₂), but afterward there is a minor increase in A_I with increasing k (Fig. 2c, d, inset), indicating a non-monotonic dependence of A_I on k. The slope, m_l, decreases in magnitude with increasing k (Fig. 3c, d).

Fig. 2.

The Allee index as a function of parameters. The Allee index (A_I), the area in the region bounded above by $M_l^{\ast }$, is plotted for increasing ξ₂ and for increasing ξ₁ (a, b) or k (c, d) under less (β = 2, (a, c)) or more (β = 4, (b, d)) aggressive conditions. Insets in (c, d) show non-monotonic behavior of A_I with respect to k. Note that the range of ξ₂ is dependent on β and λ, since for the system to have a non-trivial attractor, the inequality λ/β < 1/ξ₂ must be satisfied (Color figure online)

Fig. 3.

The slope of $M_l^{\ast }$, m_l, as a function of parameters. The slope of $M_l^{\ast }$, m_l, is plotted for increasing ξ₂ and for increasing ξ₁ (a, b) or k (c, d) under less (β = 2, (a, c)) or more (β = 4, (b, d)) aggressive conditions (Color figure online)

Fig. 4.

The steady-state P₂(S₂, A₂) as a function of parameters. The steady-state P₂(S₂, A₂) is plotted for increasing ξ₂ and for increasing ξ₁ (a, b) or k (c, d) under less (β = 2, (a, c)) or more (β = 4, (b, d)) aggressive conditions (Color figure online)

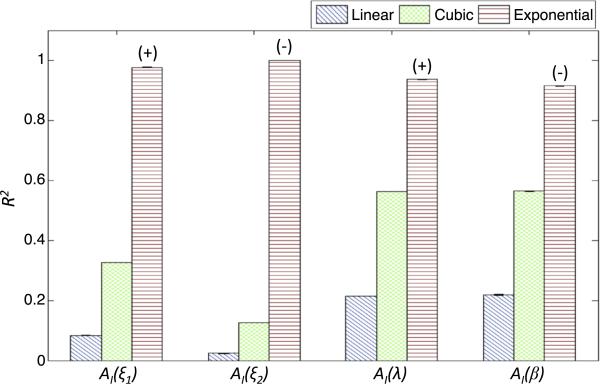
To analyze the dependence of A_I on model parameters, we fit A_I using linear, cubic and exponential functions in the parameters ξ₁,ξ₂, β and λ individually. For each fit, we then vary another parameter to obtain a distribution for the adjusted coefficient of determination (R², see Appendix 2) (Greene 2003), which we use to measure the goodness of fit. The results are shown in Fig. 5. We observe that for all parameters, the fit is best for an exponential function. We find that A_I exponentially increases with ξ₂ and λ and decreases with ξ₁ and β, indicating that therapy that changes these parameters in the indicated direction will incur exponential gains in effectivity (i.e., the probability to push the tumor into the Allee region) with a linearly increasing dosage (see Sect. 6 for an example). We do not perform this fit with k due to the non-monotonic dependence of A on k.

Fig. 5.

Estimating global dependence of A_I on parameters. Fixing all parameters but one, A_I is calculated for increasing ξ₂, ξ₁, λ and β. A linear, cubic or exponential regression curve is fit to A_I as a function of each parameter. The adjusted coefficient of determination, R², is plotted, with its color corresponding to the curve type. The sign above the exponential curve R² corresponds to the sign of the estimated curve and represents whether A_I, as a function of the respective parameter, decreases or increases with the increasing parameter value. Error bars are calculated by varying one other parameter and re-fitting the parametric functions (error bars may not be visible due to low variability of R² with respect to the varied parameter). Choice of the varied parameter does not alter the results in a qualitative manner. Ranges of parameters used are: ξ₁ ∈ [0, 5], ξ₂ ∈ [0, 2], β ∈ [1, 4], λ ∈ [0, 4]. When fixed, parameters are taken to be (ξ₁, ξ₂, λ, β) = (1, 1, 1, 2). k is set to k = 1 and not varied due to the non-monotonic dependence of A_I on k (see text)

5 Long-Term System Behavior

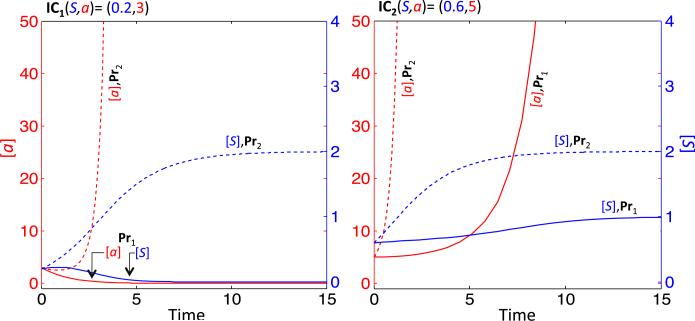
We now consider how the system (9) behaves for longer time. Returning to our two parameter sets, Pr₁(ξ₁, ξ₂, λ, k, β) = (1, 1, 1, 1, 2) and Pr₂(ξ₁, ξ₂, λ, k, β) (5, 0.5, 1, 1, 4), we consider two sets of initial conditions. We take IC₁(S, a) = (0.2, 3) and IC₂(S, a) = (0.5, 5), noting that IC₁ lies in the Allee region for Pr₁, but not Pr₂ (Fig. 1). We plot the trajectories obtained from solving (9) numerically (using the ode45 function in MATLAB) for initial conditions IC₁ at Pr₁ (solid lines) and Pr₂ (dashed lines) (Fig. 6a). For Pr₁, (S, a) predictably tend to (0, 0), whereas for Pr₂, a continues to increase, while S stabilizes at S = 2. For initial conditions IC₂ (Fig. 6b), a increases for both Pr₁ and Pr₂, but the rate of increase is higher for Pr₁. S stabilizes for both Pr₁ (at S = 1) and Pr₂ (at S = 2). When the initial conditions are in the sustainability region, the limiting behavior on ȧ is a linear function in a proportional to (βS)/λ.

Fig. 6.

Sample trajectories for Pr₁ and Pr₂. Plotting the numerical solutions of (9) with initial conditions IC₁(S, a) = (0.2, 3) (left panel) and IC₂(S, a) = (0.6, 5) (right panel) with parameters Pr₁(ξ₁, ξ₂, λ_k, β) = (1, 1, 1, 1, 2) (solid lines) and Pr₂(ξ₁, ξ₂, λ_k, β) = (5, 0.5, 1, 1, 4) (dashed lines) (Color figure online)

The limiting behavior on S as a increases can be found by considering Ṡ_lima→∞ = {(2p(S, a) – 1)kS}_lima→∞,

$${\stackrel{.}{S}}_{{\lim }_{a\to \infty }}=\left(\frac{2}{1+{\xi }_{2}S}-1\right)kS$$ (14)

This is a separable differential equation with positive solution

$$S^{\star }\left(t\right)=\frac{2{\xi }_2+e^{(-kt)-c}(\sqrt{4{\xi }_2{e}^{kt+c}+1}+1)}{2{\xi }_2^2}$$ (15)

where c is an arbitrary constant and S^★(t) is the solution to (14). We observe that lim_t→∞ S^★(t) = 1/ξ₂, indicating that the long-term behavior of S in the sustainability regime is inversely proportional to ξ₂. We note that for Pr₁, where ξ₂ = 1, lim_t→∞ S*(t) = 1 and for Pr₂, where ξ₂ = 0.5, lim_t→∞ S*(t) = 2.

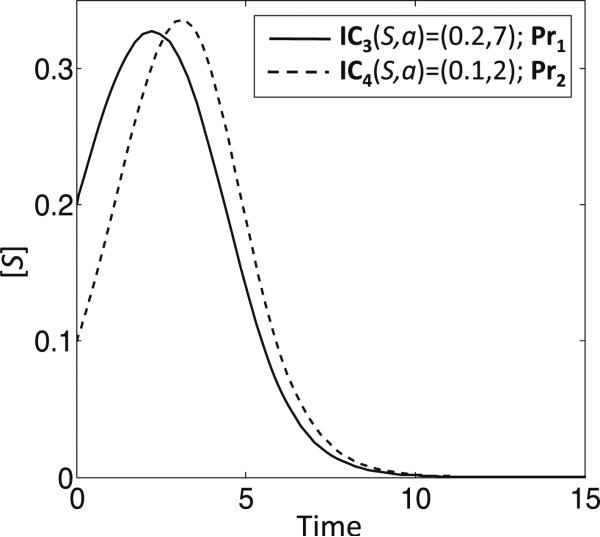
We make another observation with regard to behavior of system (9) in the Allee region. In Fig. 1, we note that the sample trajectories in the respective Allee regions for Pr₁ and Pr₂ can show a transient increase in S before tumor extinction if the initial conditions lie above the p = 0.5 curve. Indeed, taking IC₃(S, a) = (0.2, 7) for Pr₁ and IC₄(S, a) = (0.1, 2) for Pr₂, there is a transient increase in S, although at longer times the tumor is extinguished (Fig. 7). These non-monotone trajectories that reside in the Allee regions of tumors may help to explain some cases of spontaneous tumor regression (see Sect. 6).

Fig. 7.

Non-monotonic trajectories in the Allee regions for Pr₁ and Pr₂. Examples of non-monotonic trajectories of S for initial conditions in the respective Allee regions for Pr₁ (IC₃(S, a) = (0.2, 7)) and Pr₂ (IC₄(S, a) = (0.1, 2))

6 Therapy, Spontaneous Regression and the Allee Effect

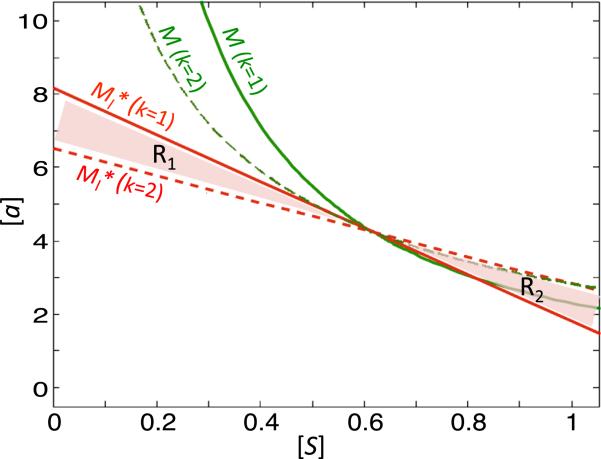
Classical chemotherapeutic drugs against cancer are cytotoxic drugs that target rapidly dividing cells (Malhotra and Perry 2003; Mathijssen et al. 2014). In our model, such drugs would correspond to lowering the k and S values of a system. We have observed that lowering k decreases the slope of $M_l^{\ast }$ without changing (A₂, S₂). Following a sample parameter scheme (Pr₁), we find that lowering k from 2 to 1 changes region 1, R₁, which has high a and small S values, from a sustainability regime to a regime that is susceptible to the Allee effect (Fig. 8). Thus, our model predicts that cytotoxic chemotherapy may make the tumor more susceptible to extinction even in the presence of high levels of activator. Moreover, while the region 2, R₂, which has large S and small a values, changes from an extinction regime to a sustainability regime, the tumor is less likely to be in this region after cytotoxic chemotherapy since the level of S will be reduced. Since chemotherapy is often administered alongside radiation and surgery, both therapies that reduce S (see below), our system shows that these types of therapy may cause tumor extinction not only by lowering S until the (S, a) values lie in the Allee region, but also by expanding the Allee region to be more inclusive of tumors with high levels of activator. This is an important consideration, since in addition to an overactive Wnt cascade, which occurs in a majority of colon cancers (Bienz and Clevers 2000; Reya and Clevers 2005) and may allow for high a levels even after reduction of S due to very high production rates, Wnt activity is further increased in colon tumor cells due to stromal-produced HGF (Hanahan and Weinberg 2011; Nakamura et al. 1997).

Fig. 8.

Example of dependence of system (9) on k. We consider the system (9) with Pr₁ = (ξ₁, ξ₂, λ, k, β) = (1, 1, 1, 1, 2) (solid lines) and ${\mathbf{Pr}}_1^{\ast }=({\xi }_1,{\xi }_2,\lambda ,k,\beta )=(1,1,1,2,2)$ (dashed lines) and plot M (green) and $M_l^{\ast }$ (red). R₁ represents the tumor substainability region in the phase space for ${\mathbf{Pr}}_1^{\ast }$, but the Allee region for Pr₁. Conversely, R₂ represents the tumor sustainability region for Pr₁, but the Allee region for ${\mathbf{Pr}}_1^{\ast }$ (Color figure online)

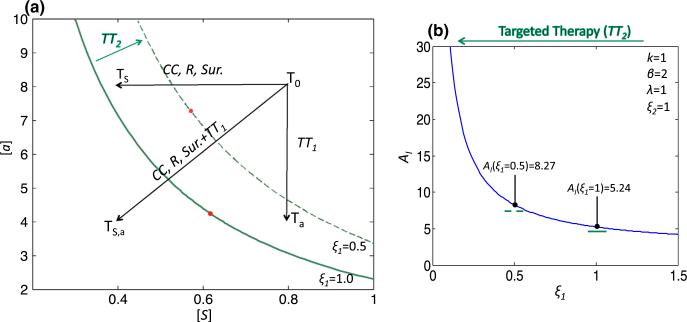
Another major modality in cancer treatment is what is known as targeted therapy, which acts by interfering with proteins involved in carcinogenesis (Kwak et al. 2007). A number of Wnt pathway inhibitors are currently in preclinical development and have shown promise in slowing growth and inducing cell death in both in vitro and in vivo experimental systems (Anastas and Moon 2013). In our model, targeted Wnt therapy may move the system into the Allee region by decreasing a directly and/or by decreasing ξ₁, the strength of a-dependent positive feedback on p, which will increase A_I. We use the system (9) to model how radiation, surgery and targeted therapy can impact tumor growth and how combination therapy can either move a tumor into or increase the Allee region (Fig. 9a). We begin with the parameter set Pr₁ and the initial condition T₀(S, a) = (0.8, 8). We note that T₀, which represents an untreated tumor, is in the sustainability region for Pr₁. We model different therapies by grouping them by the effect they have on S, a, or the model parameters. Radiation, surgery and cytotoxic chemotherapy all reduce S and can be modeled by shifting T₀ to the left in the phase space. As discussed above, cytotoxic chemotherapy also increases the magnitude of the slope of $M_l^{\ast }$, but for this discussion we neglect this effect. Targeted therapy that lowers a shifts T₀ downward in the phase space. Let us take T_s to be the tumor T₀ after treatment with a therapy that reduces S by 50% and T_a to be the tumor T₀ after treatment with a targeted therapy that reduces a by 50%. While both T_s and T_a are still in the sustainability region, for a combination therapy that reduces both S and a by 50%, the resulting tumor, T_(S,a), is now in the Allee region. Additionally, we find that targeted therapy that reduces ξ₁ by 50% (from 1.0 to 0.5) increases A_I, such that now a therapy which reduces S or a by 50% can move T₀ into the Allee region. As discussed in Sect. 4, this increase in A_I is exponential with respect to a linear decrease in ξ₁ (Fig. 9b), indicating that targeted therapy, especially in combination with other treatment modalities, can have a significant impact on the probability that the tumor will reside in the Allee region post-treatment.

Fig. 9.

Impact of therapy on tumor behavior. a The separatrix for Pr₁(ξ₁, ξ₂, λ, k, β) (1, 1, 1, 1, 2) is plotted in solid green, and for (ξ₁, ξ₂, λ, k, β) = (0.5, 1, 1, 1, 2), the separatrix is plotted in dashed green. T₀ represents an untreated tumor, and T_s, T_a and T_(S,a) represent tumors where treatment reduces S, a or both S and a, respectively, by 50%. Different treatments are in italics: CC refers to cytotoxic chemotherapy, R to radiation, Sur. to surgery, TT₁ to targeted therapy that reduces a and TT₂ to targeted therapy that reduces ξ₁. b The effect of TT₂ on A_I follows an exponential curve. The two plotted points A_I (ξ₁ = 1) and A_I (ξ₁ = 0.5) indicate the respective A_I of the system in (a) corresponding to no therapy (solid green separatrix) and TT₂ therapy (dashed green separatrix) (Color figure online)

The spontaneous regression of cancer has been defined as ‘the partial or complete disappearance of a malignant tumor in the absence of all treatment, or in the presence of therapy that is considered inadequate to exert a significant influence on neoplastic disease’ (Everson and Cole 1968). Although difficult to ascertain, the incidence rate is estimated to be approximately 1/80,000–1/100,000 cases (Challis and Stam 1900). Reviews of such cases have shown that a primary coincidental event in the personal history of a patient with spontaneous regression is an acute/feverish infection, which stimulates acute immune activity that is able to target the cancer in addition to the infection (Hobohm 2001; Jessy 2011). In our model, such acute immune stimulation, and associated cancer cell death, corresponds to a reduction in S that may push the system into the Allee region of the tumor. For example, if we again consider T₀ in Fig. 9 with system parameters (ξ₁, ξ₂, λ_k, β) = (0.5, 1, 1, 1, 2) (the separatrix is dashed green), a shift to T_s by acute immune stimulation would be sufficient to induce tumor regression. Moreover, our model also shows how cases of spontaneous regression can arise without acute infection. In Sect. 5, we found that, given a parameterization for system (9), a subset of the Allee region has non-monotone trajectories in S. Specifically, while S is eventually extinguished, there is a transient increase in S at early times. If such a tumor is thus initially clinically evaluated during the transient increase phase, the long-term behavior follows the classical definition of spontaneous regression.

One can also use our model to consider why the occurrence of spontaneous regression is so low by examining three scenarios: (1) The tumor is in the Allee region, (2) the tumor is deep in the sustainability region, and (3) the tumor is in the sustainability region but near the separatrix M. The first scenario can occur when the tumor is observed to be of non-negligible size but will eventually go extinct via either a monotonic or non-monotonic trajectory, without additional external inputs (such as an increased immune response). Since neither of these situations is a steady state, the probability that the tumor will be detected at a non-negligible size before it becomes extinct is small; otherwise, such cases would be reported more often. Indeed, the prevalence of spontaneous regression may be higher than reported since many monotonic and non-monotonic extinction events can go undetected either because the maximum tumor size reached is too small for detection or that the temporal course of the trajectory is too fast to be frequently observed or cause symptoms. In the second scenario, where the tumor is deep in the sustainability region, an immune response that would move it to the Allee region would have to be significant. Since cancer cells employ immunoevasive techniques to successfully evade both specific and non-specific immune responses (Dunn et al. 2002), one would expect the number of cases where this occurs to be extremely low as well. Finally, for the third scenario, where the tumor lies near the sustainability region, there are a number of considerations. First, due to heterogeneity and noise in the system, part or all of the tumor may actually be or move into (and out of) the Allee region. It is in this scenario that an immune response, which would push the system more deeply into the Allee region, would be most likely to result in spontaneous regression of the tumor. But for this to occur, ‘the stars must align’ for the system, i.e., it would have to be near M, which may not be likely if it is large enough to be detected and/or not expected to respond to therapy, and an immune response would have to occur that propels it into the Allee region.

7 Discussion

It has recently been suggested that exploitation of the Allee effect in tumor growth should be considered for therapy development (Korolev et al. 2014). We have simplified a model of tumor growth in order to understand the principles under which a tumor can die out at low density, i.e., exhibit an Allee effect. In our system, the Allee effect occurs due to the following reasons: low level of activator, a, will lower the probability of stem cell self-renewal, p. A low p will result in lower stem cell production and hence less a production. For low enough S and a, the system will thus tend toward tumor extinction. Using the Stable Manifold Theorem, we have shown that there can exist a separatrix which distinguishes between trajectories of (S, a) tending to (0, 0) and trajectories that tend to nonzero solutions. The location of the separatrix depends on the various parameters in the model, which are the strength of a-dependent activation (ξ₁) and S-dependent inhibition (ξ₂) of the probability of self-renewal p, the stem cell division rate (k) and the strength of a self-activation (β) and saturation (λ). A linear approximation of the separatrix by the Stable Manifold Theorem has allowed us to quantify the susceptibility of the tumor to the Allee effect by introducing an Allee index.

Given that there can be an Allee effect, one can ask how a tumor of appreciable size can develop at all before the Allee effect leads to extinction? As we have observed, our model allows for the transient growth of stem cell numbers, and hence tumor size, even when the system is in the Allee region (recall Figs. 1a, b, 7). The amount by which S can increase depends on system parameters. In addition, following the hypothesis that cancer stem cells act as cancer-initiating cells (Zhou et al. 2009), one can imagine that at very early times, the tumor is made almost entirely of cancer stem cells, which does not correspond to the system we present, since we assume a linear relationship between stem (S) and differentiated (D) cell populations, and concentration of differentiation promoter (T) (see Eqs. (1)–(7)). Such an assumption is valid for a system that already has an appreciable, quasi-steady, population of D and T. At early time points, when D and T are negligible, the system exhibits an effective probability of stem cell self-renewal p that is dependent only on concentration of a, specifically a higher p than would be predicted by the model, thereby allowing S to increase even more than predicted by our model. This may also enable the tumor to escape the Allee region for a finite period of time until a sufficient amount of T accumulates to provide negative feedback on p, which could push the tumor back into the Allee region and ultimately toward tumor extinction.

Our model and associated analysis can give insight into patient outcomes. For example, elevated levels of nuclear β-catenin, a downstream signaling target of the Wnt cascade, in the excised tumors of patients who had undergone surgery and therapy for colorectal cancer, were strongly correlated with poor patient survival (Cheah et al. 2002). We can translate this phenomenon to a system where lowered levels of S and k via surgery and therapy do not induce tumor extinction because high a levels maintain the system in the sustainability regime. It follows that treatments that combine traditional cancer therapy (surgery and cytotoxic chemotherapy) with targeted Wnt inhibitors may be especially effective for the patients with elevated Wnt levels because the lowered a levels would allow the system to enter the Allee region.

This simplified model may also help to explain why the combination treatment in the more complex system developed by Youssefpour et al. (2012) was successful in tumor eradication, whereas the individual therapies were not. The combination therapy consisted of cyclical radiation therapy (intermittent killing of tumor cells) and differentiation therapy (addition of TGFβ to the system). This combination therapy can be interpreted in our model as a combination of decreased S (which shifts the system toward the Allee region) and increased ξ₂ (which increases the Allee region and A_I), thus increasing the probability that the tumor will be extinguished by the Allee effect over individual therapy.

Additionally, the dependence of the system behavior on the strength of the negative feedback on stem cell self-renewal, ξ₂, is of particular interest since tumor response to growth inhibitors decreases throughout tumor progression (Hanahan and Weinberg 2000). A decrease in ξ₂ in our system decreases A_I and increases the limiting value of S in the sustainability region. Therefore, a decrease in response to growth inhibitors has the combined effect of decreasing the probability that traditional chemotherapy and/or surgery will cause the tumor to become extinct, and increasing the long-term population of stem cells. It may be this dual action in promoting tumor survival and growth that has selected the decreased response to growth inhibitors to be a major hallmark of cancer.

8 Conclusions

We have shown, with a simple stem cell and chemical activator model, that a tumor can undergo the Allee effect either spontaneously or after treatment when the system is in the basin of attraction for extinction (what we term the Allee region). By considering tumor remission in the language of dynamical systems, we have been able to quantify and observe how various parameters of the system contribute to defining the Allee region in the phase space of the tumor and activator. Moreover, we have shown why combination therapy may be especially effective with respect to treatment and tumor eradication (e.g., see Chinnaiyan et al. 2000; Cassidy et al. 2004; Uno et al. 2006; Mangsbo et al. 2010), as it can increase the probability that the treated tumor will lie in the Allee region (by moving the tumor into and/or increasing the Allee region).

We have purposefully kept the model simple in order to allow an analytical approach to the question of tumor eradication. Extensions to include full cell lineages, non-constant concentrations of the inhibitor and/or differentiation promoters, microenvironmental interactions (such as host-produced HGF upregulation of a) or more complex parameter dependencies (e.g., the cell division rate k may be positively correlated with a) should yield qualitatively similar results. Spatial effects can also be incorporated. In particular, it is expected that the Allee index will vary throughout space. This suggests that depending on the microenvironmental conditions and the spatial distribution of feedback factors, some parts of the tumor may be in the Allee region, while other parts may not. Applying combination therapy increases the probability that the whole tumor will lie in the Allee region.

Appendix 1: Approximation of the Separatrix for System (9) using the Stable Manifold Theorem

We use the Stable Manifold Theorem (SMT) to prove that the separatrix described in Theorem 1 near the equilibrium point P₂(S₂, A₂) of system (9) exists and to approximate it. We follow the technique presented in (Perko 2001). We recall that P₂ occurs at the unique intersection of the curves {p(S, a) = 0.5} and {F(S, a) = 0}. We state the SMT here for reference.

Theorem 2

(The Stable Manifold Theorem). Let E be an open subset of ${\mathbb{R}}^n$ containing the origin, let f ∈ C¹(E), and let ϕ_t be the flow of the nonlinear system ẋ = f(x). Suppose that f(0) = 0 and that Df(0) has k eigenvalues with negative real part and n–k eigenvalues with positive real part. Then there exists a k-dimensional differentiable manifold M tangent to the stable subspace E^m of the linear system ẋ = Ax at 0 where A = Df(0), such that for all t ≥ 0, ϕ_t(M) $\subset$ M for all x₀ ∈ M and

$$\underset{t\to \infty }{\lim }{\varphi }_t\left({\mathbf{x}}_0\right)=0.$$

In our case, we make an affine change of coordinates to system (9) which sends P₂ → 0 and use the constructive proof of the SMT (see Perko 2001, p. 108) to find the separatrix M.

Affine Change of Coordinates

To apply the SMT, we need to first make the affine change of coordinates: c (S, a) → (S, a) – (S₂, A₂). We let (S*, a*) c(S, a). Then, applying c to (9), and nothing that (S, a) = (S*, a*) + (S₂, A₂), and $\frac{\partial }{\partial t}(S,a)=\frac{\partial }{\partial t}((S^{\ast },a^{\ast })+(S_2,A_2))=\frac{\partial }{\partial t}(S^{\ast },a^{\ast })$, we obtain

$$\begin{array}{cc}\hfill {\stackrel{.}{S}}^{\ast }& =(2p^{\ast }(S^{\ast },a^{\ast })-1)k(S^{\ast }+S_2)=f_1^{\ast }(S^{\ast },a^{\ast }),\hfill \\ \hfill {\stackrel{.}{a}}^{\ast }& =(a^{\ast }+A_2)\left(\frac{\beta (S^{\ast }+S_2)(a^{\ast }+A_2)}{1+\lambda (a^{\ast }+A_2)}-1\right)=f_2^{\ast }(S^{\ast },a^{\ast }),\hfill \\ \hfill p^{\ast }(S^{\ast },a^{\ast })& =\frac{{\xi }_1(a^{\ast }+A_2)}{1+{\xi }_1(a^{\ast }+A_2)}\frac{1}{1+{\xi }_2(S^{\ast }+S_2)}.\hfill \end{array}$$ (16)

The Jacobian for (16) is

$${\mathit{J}}^{\ast }(S^{\ast },a^{\ast })=\left(\begin{array}{cc}\hfill 2p_{S^{\ast }}^{\ast }k(S^{\ast }+S_2)+(2p^{\ast }-1)k\hfill & \hfill 2p_{a^{\ast }}^{\ast }k(S^{\ast }+S_2)\hfill \\ \hfill {\left(f_1\right)}_{S^{\ast }}\hfill & \hfill {\left(f_1\right)}_{a^{\ast }}\hfill \end{array}\right),$$

where

$$\begin{array}{cc}\hfill p_{S^{\ast }}^{\ast }& =\frac{-{\xi }_1{\xi }_2(a^{\ast }+A_2)}{(1+{\xi }_1(a^{\ast }+A_2)){(1+{\xi }_2(S^{\ast }+S_2))}^2},\hfill \\ \hfill p_{a^{\ast }}^{\ast }& =\frac{{\xi }_1}{(1+{\xi }_2(S^{\ast }+S_2)){(1+{\xi }_1(a^{\ast }+A_2))}^2},\hfill \\ \hfill {\left(f_2^{\ast }\right)}_{S^{\ast }}& =\frac{\beta {(a^{\ast }+A_2)}^2}{1+\lambda (a^{\ast }+A_2)},\hfill \\ \hfill {\left(f_2^{\ast }\right)}_{a^{\ast }}& =\frac{\beta (S^{\ast }+S_2)(a^{\ast }+A_2)(2+\lambda (a^{\ast }+A_2))}{{(1+\lambda (a^{\ast }+A_2))}^2}-1.\hfill \end{array}$$ (17)

In this coordinate system, (S*, a*) = (0, 0) is an equilibrium point and P*(0, 0) corresponds to P₂(S₂, A₂). To use the SMT, we need to first determine A = Df(0) = J* (0, 0). We have

$$\mathit{A}={\mathit{J}}^{\ast }(0,0)=\left(\begin{array}{cc}\hfill 2p_{S^{\ast }}^{\ast }(0,0)k{S}_2\hfill & \hfill 2p_{a^{\ast }}^{\ast }(0,0)k{S}_2\hfill \\ \hfill {\left(f_2\right)}_{S^{\ast }}(0,0)\hfill & \hfill {\left(f_2\right)}_{a^{\ast }}(0,0)\hfill \end{array}\right).$$ (18)

We first note, as in the original J(S₁, S₂), that since $p_{S^{\ast }}^{\ast }<0$ and ${\left(f_2^{\ast }\right)}_{a^{\ast }}(0,0)>0$, $2p_{S^{\ast }}^{\ast }(0,0)k{S}_2{\left(f_2\right)}_{a^{\ast }}(0,0)<0$ and since $p_{a^{\ast }}^{\ast }>0$ and ${\left(f_2^{\ast }\right)}_{S^{\ast }}>0$, $2p_{a^{\ast }}^{\ast }(0,0)k{S}_2{\left(f_2\right)}_{S^{\ast }}(0,0)>0$. Therefore,

$$\det {\mathit{J}}^{\ast }(0,0)=2p_{S^{\ast }}^{\ast }(0,0)k{S}_2){\left(f_2^{\ast }\right)}_{a^{\ast }}(0,0)-2p_{a^{\ast }}^{\ast }(0,0)k{S}_2{\left(f_2^{\ast }\right)}_{S^{\ast }}(0,0)<0,$$

and hence J*(0,0) has one positive and one negative eigenvalue, and P* is a saddle-point. We also recall that S₂ and A₂ satisfy

$$\{\begin{array}{c}\frac{{\xi }_1{A}_2}{1+{\xi }_1{A}_2}\frac{1}{1+{\xi }_2{S}_2}=0.5,\hfill \\ \frac{\beta S_2{A}_2}{1+\lambda A_2}=1.\hfill \end{array}\phantom{\}}$$ (19)

Using (19), we simplify (17) to calculate the elements of A,

$$\begin{array}{cc}\hfill p_{S^{\ast }}^{\ast }(0,0)& =\frac{-A_2{\xi }_1{\xi }_2}{(1+{\xi }_1{A}_2){(1+{\xi }_2{S}_2)}^2}=\frac{-{\xi }_2}{2(1+{\xi }_2{S}_2)},\hfill \\ \hfill p_{a^{\ast }}^{\ast }(0,0)& =\frac{1}{(1+{\xi }_2{S}_2){(1+{\xi }_1{A}_2)}^2}=\frac{1}{2A_2(1+{\xi }_1{A}_2)},\hfill \\ \hfill {\left(f_2^{\ast }\right)}_{S^{\ast }}(0,0)& =\frac{\beta A_2^2}{1+\lambda A_2}=\frac{A_2}{S_2},\hfill \\ \hfill {\left(f_2^{\ast }\right)}_{a^{\ast }}(0,0)& =\frac{\beta S_2{A}_2(2+\lambda A_2)}{{(1+\lambda A_2)}^2}-1=\frac{2+\lambda A_2}{1+\lambda A_2}-1=\frac{1}{1+\lambda A_2}.\hfill \end{array}$$ (20)

Substituting (20) into (18), we have the following expression for A = J*(0, 0),

$$\mathit{A}=\left(\begin{array}{cc}\hfill \frac{-{\xi }_{2}k{S}_2}{1+{\xi }_2{S}_2}\hfill & \hfill \frac{k{S}_2}{A_2(1+{\xi }_1{A}_2)}\hfill \\ \hfill \frac{A_2}{S_2}\hfill & \hfill \frac{1}{1+\lambda A_2}\hfill \end{array}\right).$$ (21)

Preliminary Calculations for the SMT

Following (Perko 2001) and taking x = (S*, a*), we can rewrite the system (16) as

$$\stackrel{.}{\mathbf{x}}=\mathbf{Ax}+\mathbf{F}\left(\mathbf{x}\right),$$ (22)

where A = J*(0,0) and F(x) = f*(x) – Ax. We next need to find an invertible matrix C such that

$$\mathit{B}={\mathit{C}}^{-1}\mathit{AC}=\left(\begin{array}{cc}\hfill L_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill L_2\hfill \end{array}\right),$$ (23)

where L₁ and L₂ are the negative and positive eigenvalues, respectively, of A = (A_{i j}). We first calculate the trace, T, and determinant, D, of A,

$$\begin{array}{cc}\hfill T& =A_{11}+A_{22}=\frac{-{\xi }_{2}k{S}_2}{1+{\xi }_2{S}_2}+\frac{1}{1+\lambda A_2},\hfill \\ \hfill D& =A_{11}{A}_{22}-A_{12}{A}_{21}=\frac{-{\xi }_{2}k{S}_2}{1+{\xi }_2{S}_2}\frac{1}{1+\lambda A_2}-\frac{k{S}_2}{A_2(1+{\xi }_1{A}_2)}\frac{A_2}{S_2}=\frac{-{\xi }_{2}k{S}_2}{(1+{\xi }_2{S}_2)(1+\lambda A_2)}-\frac{k}{1+{\xi }_1{A}_2}.\hfill \end{array}$$

We note, from the calculations above, that D < 0. We proceed to calculate 0 = det(A – LI) to obtain the quadratic equation

$$0=L^2-(A_{11}+A_{22})L+(A_{11}{A}_{22}-A_{12}{A}_{21})=L^2-TL+D.$$

The quadratic formula gives us:

$$L_{1,2}=\frac{T\mp {(T^2-4D)}^{1∕2}}{2}=T∕2\mp {(T^2∕4-D)}^{1∕2}.$$

Since D < 0, we find that L_1,2 are both real and have opposite sign; hence, L₁ < 0 < L₂. It can be verified that v₁ = [(L₁ – A₂₂), A₂₁]^T and v₂ = [(L₂ – A₂₂), A₂₁]^T are eigenvectors corresponding (respectively) to L₁ and L₂. Here the superscript T denotes the transpose. Therefore, we have

$$\mathit{A}={\mathit{CBC}}^{-1}=\frac{1}{A_{21}(L_1-L_2)}\left(\begin{array}{cc}\hfill L_1-A_{22}\hfill & \hfill L_2-A_{22}\hfill \\ \hfill A_{21}\hfill & \hfill A_{21}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill L_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill L_2\hfill \end{array}\right)\left(\begin{array}{cc}\hfill A_{21}\hfill & \hfill -L_2+A_{22}\hfill \\ \hfill -A_{21}\hfill & \hfill L_1-A_{22}\hfill \end{array}\right)$$

We make another change of variables, taking y = C^–1(x), and writing (22) as

$$\stackrel{.}{\mathbf{y}}=\mathbf{By}+\mathbf{G}\left(\mathbf{y}\right),$$ (24)

where B is from (23) and G(y) = C^–1F(Cy).

Applying the SMT

By the SMT (taking a = (a₁, a₂)),

$$\mathbf{u}(t,\mathbf{a})=\mathit{U}\left(t\right)\mathbf{a}+{\int }_0^t\mathit{U}(t-s)\mathbf{G}\left(\mathbf{u}(s,\mathbf{a})\right)ds-{\int }_t^{\infty }\mathit{V}(t-s)\mathbf{G}\left(\mathbf{u}(s,\mathbf{a})\right)ds$$ (25)

is the solution to (24), where

$$\mathit{U}\left(t\right)=\left(\begin{array}{cc}\hfill e^{L_{1}t}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\text{and}\mathit{V}\left(t\right)=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill e^{L_{2}t}\hfill \end{array}\right).$$

We solve for u using the method of successive approximation. We let u⁽⁰⁾ (t, a) = 0 and

$${\mathbf{u}}^{(j+1)}(t,a)=\mathit{U}\left(t\right)\mathbf{a}+{\int }_0^t\mathit{U}(t-s)\mathbf{G}\left({\mathbf{u}}^{\left(j\right)}(s,\mathbf{a})\right)ds-{\int }_t^{\infty }\mathit{V}(t-s)\mathbf{G}\left({\mathbf{u}}^{\left(j\right)}(s,\mathbf{a})\right)ds.$$ (26)

To solve for j = 1, we note that G(0) = C^–1F(C · 0) = C^–1F(0) = 0 since f₁(0, 0) = f₂(0, 0) = 0. Therefore,

$${\mathbf{u}}^{\left(1\right)}(t,\mathbf{a})=\left(\begin{array}{c}\hfill e^{L_{1}t}{a}_1\hfill \\ \hfill 0\hfill \end{array}\right).$$

For the next approximation, we first calculate U(t – s)G(u⁽¹⁾(s, a)) = U(t – s)C^–1F(Cw) = H₁F(Cw) where H₁ = U(t – s)C^–1 and w = (e^L₁s a₁, 0)^T. Simplifying H₁ gives us:

$${\mathit{H}}_1=\mathit{U}(t-s){\mathit{C}}^{-1}=\frac{1}{A_{21}(L_1-L_2)}\left(\begin{array}{cc}\hfill e^{L_1(t-s)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{cc}\hfill A_{21}\hfill & \hfill A_{22}-L_2\hfill \\ \hfill -A_{21}\hfill & \hfill L_1-A_{22}\hfill \end{array}\right)=e^{L_1(t-s)}\left(\begin{array}{cc}\hfill \frac{1}{L_1-L_2}\hfill & \hfill \frac{A_{22}-L_2}{A_{21}(L_1-L_2)}\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right).$$

Then,

$${\mathit{H}}_1\mathbf{F}\left(\mathit{C}\mathbf{w}\right)=e^{L_1(t-s)}\left(\begin{array}{cc}\hfill \frac{1}{L_1-L_2}\hfill & \hfill \frac{A_{22}-L_2}{A_{21}(L_1-L_2)}\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\times \left[\left(\begin{array}{c}\hfill f_1\left(\mathbf{Cw}\right)\hfill \\ \hfill f_2\left(\mathbf{Cw}\right)\hfill \end{array}\right)-e^{L_{1}s}{a}_1\left(\begin{array}{cc}\hfill A_{11}\hfill & \hfill A_{12}\hfill \\ \hfill A_{21}\hfill & \hfill A_{22}\hfill \end{array}\right)\left(\begin{array}{c}\hfill L_1-A_{22}\hfill \\ \hfill A_{21}\hfill \end{array}\right)\right]=e^{L_1(t-s)}\left(\begin{array}{c}\hfill \frac{f_1\left(\mathbf{Cw}\right)}{(L_1-L_2)}+\frac{f_2\left(\mathbf{Cw}\right)A_{22}-L_2}{A_{21}(L_1-L_2)}\hfill \\ \hfill 0\hfill \end{array}\right)-e^{L_{1}t}{a}_1\left(\begin{array}{c}\hfill \frac{L_1(T-L_2)-D}{L_1-L_2}\hfill \\ \hfill 0\hfill \end{array}\right).$$ (27)

Hence,

$${\int }_0^t\mathit{U}(t-s)\mathbf{G}\left({\mathbf{u}}^{\left(1\right)}(s,\mathbf{a})\right)={\int }_0^t{e}^{L_1(t-s)}\left(\begin{array}{c}\hfill \frac{f_1\left(\mathbf{Cw}\right)}{(L_1-L_2)}+\frac{f_2\left(\mathbf{Cw}\right)A_{22}-L_2}{A_{21}(L_1-L_2)}\hfill \\ \hfill 0\hfill \end{array}\right)ds-t\left[e^{L_{1}t}{a}_1\left(\begin{array}{c}\hfill \frac{L_1(T-L_2)-D}{L_1-L_2}\hfill \\ \hfill 0\hfill \end{array}\right)\right].$$ (28)

We note that our stable manifold will be of the form $y_2={\psi }_2^{\left(2\right)}\left(y_1\right)$, where ${\psi }_2^{\left(2\right)}\left(a_1\right)=u_2^{\left(2\right)}(0,a_1,0)$. Since U(t)a and (28) only contribute trivially to $u_2^{\left(2\right)}$, we will not perform further calculations on them.

Next, we calculate V(t – s)G(u⁽¹⁾(s, a)) = V(t – s)C^–1F(Cw) = H₂F(Cw). As before, we first calculate H₂:

$${\mathit{H}}_2=\mathit{V}(t-s){\mathit{C}}^{-1}=\frac{1}{A_{21}(L_1-L_2)}\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill e^{L_2(t-s)}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill A_{21}\hfill & \hfill A_{22}-L_2\hfill \\ \hfill -A_{21}\hfill & \hfill L_1-A_{22}\hfill \end{array}\right)=e^{L_2(t-s)}\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{-1}{L_1-L_2}\hfill & \hfill \frac{L_1-A_{22}}{A_{21}(L_1-L_2)}\hfill \end{array}\right).$$

We thus have,

$${\mathit{H}}_2\mathbf{F}\left(\mathbf{Cw}\right)=e^{L_2(t-s)}\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{-1}{L_1-L_2}\hfill & \hfill \frac{L_1-A_{22}}{A_{21}(L_1-L_2)}\hfill \end{array}\right)\times \left[\left(\begin{array}{c}\hfill f_1\left(\mathbf{Cw}\right)\hfill \\ \hfill f_2\left(\mathbf{Cw}\right)\hfill \end{array}\right)-e^{L_{1}s}{a}_1\left(\begin{array}{cc}\hfill A_{11}\hfill & \hfill A_{12}\hfill \\ \hfill A_{21}\hfill & \hfill A_{22}\hfill \end{array}\right)\left(\begin{array}{c}\hfill L_1-A_{22}\hfill \\ \hfill A_{21}\hfill \end{array}\right)\right]=e^{L_2(t-s)}\left(\begin{array}{c}\hfill 0\hfill \\ \hfill \frac{-f_1\left(\mathbf{Cw}\right)}{L_1-L_2}+\frac{f_2\left(\mathbf{Cw}\right)(L_1-A_{22})}{A_{21}(L_1-L_2)}\hfill \end{array}\right)-e^{s(L_1-L_2)}{e}^{L_{2}t}\left[\begin{array}{c}\hfill 0\hfill \\ \hfill g(L_1,L_2,A_{21},A_{22})\hfill \end{array}\right].$$ (29)

Taking the integral of the right-hand term on the domain [t, ∞) gives us $\frac{e^{L_{1}t}}{L_2-L_1}{(0,g(\cdot ))}^T$. We find that $g(\cdot )=L_1^2-T{L}_1+D=0$. Therefore, this term does not contribute to the stable manifold.

The SMT allows us to calculate the second approximation to the separatrix, ${\mathrm{M}}^{\ast }=u_2^{\left(2\right)}(0,a_1,0)$, as

$${\mathrm{M}}^{\ast }=\frac{1}{L_1-L_2}\left({\int }_0^{\infty }-e^{-L_{2}s}{f}_1^{\ast }\left(\mathbf{Cw}\right)ds+\frac{L_1-A_{22}}{A_{21}}{\int }_0^{\infty }{e}^{-L_{2}s}{f}_2^{\ast }\left(\mathbf{Cw}\right)ds\right).$$ (30)

where Cw = e^L₁s a₁(L₁ – A₂₂, A₂₁)^T, and by (16),

$$f_1^{\ast }\left(\mathbf{Cw}\right)=\left(\frac{2{\xi }_1(e^{L_{1}s}{a}_1{A}_{21}+A_2)}{(1+{\xi }_1(e^{L_{1}s}{a}_1{A}_{21}+A_2))(1+{\xi }_2(e^{L_{1}s}{a}_1(L_1-A_{22})+S_2))}-1\right)k(e^{L_{1}s}{a}_1(L_1-A_{22})+S_2),$$ (31)

$$f_2^{\ast }\left(\mathbf{Cw}\right)=(e^{L_{1}s}{a}_1{A}_{21}+A_2)\left(\frac{\beta (e^{L_{1}s}{a}_1(L_1-A_{22})+S_2)(e^{L_{1}s}{a}_1{A}_{21}+A_2)}{1+\lambda (e^{L_{1}s}{a}_1{A}_{21}+A_2)}-1\right).$$ (32)

We now solve $-{\int }_0^{\infty }{I}_{1}ds={\int }_0^{\infty }{e}^{-L_{2}s}{f}_1^{\ast }\left(\mathbf{Cw}\right)ds$ and ${\int }_0^{\infty }{I}_{2}ds={\int }_0^{\infty }{e}^{-L_{2}s}{f}_2^{\ast }\left(\mathbf{Cw}\right)ds$. Substituting (31) into I₁, we obtain

$$I_1=\left(\frac{2{\xi }_1{e}^{-L_{2}s}(e^{L_{1}s}{a}_1{A}_{21}+A_2)}{(1+{\xi }_1(e^{L_{1}s}{a}_1{A}_{21}+A_2))(1+{\xi }_2(e^{L_{1}s}{a}_1(L_1-A_{22})+S_2))}-e^{-L_{2}s}\right)k(e^{L_{1}s}{a}_1(L_1-A_{22})+S_2).$$ (33)

We split I₁ into three parts:

$$I_1=I_{11}+I_{12}+I_{13}=\frac{(2{\xi }_1{e}^{-L_{2}s}(e^{L_{1}s}{a}_1{A}_{21}+A_2)k(e^{L_{1}s}{a}_1(L_1-A_{22})+S_2)}{(1+{\xi }_1(e^{L_{1}s}{a}_1{A}_{21}+A_2))(1+{\xi }_2(e^{L_{1}s}{a}_1(L_1-A_{22})+S_2)}-k{e}^{(L_1-L_2)s}{a}_1(L_1-A_{22})-e^{-L_{2}s}k{S}_2.$$

We can directly integrate I₁₂ and I₁₃ to obtain

$$-{\int }_0^{\infty }{I}_{1}ds=-{\int }_0^{\infty }{I}_{11}ds-\frac{k{a}_1(L_1-A_{22})}{L_1-L_2}+\frac{k{S}_2}{L_2}.$$ (34)

We now work to simplify I₁₁ by taking u = e^L₁s. The change of variables gives us

$$-{\int }_0^{\infty }{I}_{11}ds=-\frac{2k}{L_1}{\int }_{u_1}^{u_2}{u}^{-T∕L_1}\times \frac{(u{a}_1{A}_{21}+A_2)(u{a}_1{(}_1-A_{22})+S_2)}{(1+{\xi }_1(u{a}_1{A}_{21}+A_2))(1+{\xi }_2(u{a}_1(L_1-A_{22})+S_2))}du=\frac{2{\xi }_{1}k}{L_1}{\int }_0^1{u}^{-T∕L_1}\frac{(u{c}_1+A_2)(u{c}_2+S_2)}{(1+{\xi }_1(u{c}_1+A_2))(1+{\xi }_2(u{c}_2+S_2))}du,$$ (35)

where we find that u₁ = 1 and $u_2={\lim }_{s\to \infty }{e}^{L_{1}s}=0$ since L₁ < 0. We take c₁ = a₁A₂₁ and c₂ = a₁(L₁ – A₂₂).

We would like to do a partial fraction decomposition for the integrand term in (35) not containing u^–T/L₁, $I_{11}^{\ast }$. Noting that both the numerator and denominator are of degree 2, we first perform long division to obtain a fraction p/q where deg p < deg q. Fully multiplying the terms in the fraction, and setting c₃ = A₂c₂ + S₂c₁ and c₄ = A₂ξ₁ + S₂ξ₂ + A₂S₂ξ₁ξ₂ + 1 gives us

$$I_{11}^{\ast }=\frac{u^2{c}_1{c}_2+u{c}_3+A_2{S}_2}{u^2{\xi }_1{\xi }_2{c}_1{c}_2+u({\xi }_1{\xi }_2{c}_3+{\xi }_2{c}_2+{\xi }_1{c}_1)+c_4}=\frac{1}{{\xi }_1{\xi }_2}-\frac{u(c_2∕{\xi }_1+c_1∕{\xi }_2)+(A_2∕{\xi }_2+S_2∕{\xi }_1+1∕\left({\xi }_1{\xi }_2\right))}{(1+{\xi }_1(u{c}_1+A_2))(1+{\xi }_2(u{c}_2+S_2))}.$$ (36)

Setting c₅ = c₂/ξ₁ + c₁/ξ₂ and c₆ = A₂/ξ₂ + S₂/ξ₁ + 1/(ξ₁ξ₂), the second term of (36) becomes

$$\frac{u{c}_5+c_6}{(1+{\xi }_1(u{c}_1+A_2))(1+{\xi }_2(u{c}_2+S_2))}=\frac{N_1}{(1+{\xi }_1(u{c}_1+A_2))}+\frac{N_2}{(1+{\xi }_2(u{c}_2+S_2))},$$

where

$$\begin{array}{cc}\hfill N_1=& \frac{-c_5({\xi }_1{A}_2+1)+c_1{c}_6{\xi }_1}{{\xi }_1{\xi }_2(c_1{S}_2-A_2{c}_2)+c_1{\xi }_1-c_2{\xi }_2},\hfill \\ \hfill N_2=& \frac{-c_5({\xi }_2{S}_2+1)+c_2{c}_6{\xi }_2}{{\xi }_1{\xi }_2(-c_1{S}_2+A_2{c}_2)-c_1{\xi }_1+c_2{\xi }_2}.\hfill \end{array}$$

Therefore, the integrand in (35), $u^{-T∕L_1}{I}_{11}^{\ast }$, can be written as

$$u^{-T∕L_1}{I}_{11}^{\ast }=u^{-T∕L_1}\left(\frac{1}{{\xi }_1{\xi }_2}-\frac{N_1}{(1+{\xi }_1(u{c}_1+A_2))}-\frac{N_2}{(1+{\xi }_2(u{c}_2+S_2))}\right).$$

We note that the first term can be integrated,

$$\frac{2{\xi }_{1}k}{L_1{\xi }_1{\xi }_2}{\int }_0^1{u}^{-T∕L_1}du=\frac{-2k}{L_2{\xi }_1{\xi }_2}{u}^{-L_1∕L_2},$$

where the first equality comes about from the observation that –T/L₁ = –1 –L₂/L₁. To summarize, if we set

$$I_{11}^{\ast \ast }=u^{-T∕L_1}\left(\frac{N_1}{(1+{\xi }_1(u{c}_1+A_2))}+\frac{N_2}{(1+{\xi }_2(u{c}_2+S_2))}\right),$$

we can rewrite (34) as

$$-{\int }_0^{\infty }{I}_{1}ds=\frac{k{S}_2}{L_2}-\frac{k{C}_2}{L_1-L_2}-\frac{2{\xi }_{1}k}{L_2{\xi }_1{\xi }_2}-\frac{2{\xi }_{1}k}{L_1}{\int }_0^1{I}_{11}^{\ast \ast }du.$$ (37)

To solve ${\int }_0^1{I}_{11}^{\ast \ast }du$, we will need to use a hypergeometric function and the beta function. Indeed, we have the formula

$${\int }_0^1{t}^{b-1}{(1-t)}^{c-b-1}{(1-tx)}^{-a}dt=B{(b,c-b)}_2{F}_1(a,b;c;x),$$

where $B(a,b)={\int }_0^a{t}^{a-1}{(1-t)}^{b-1}dt$ and ${}_{2}F_1(a_1,a_2;b_1;x)={\sum }_{k=0}^{\infty }\frac{{\left(a_1\right)}_k{\left(a_2\right)}_k}{{\left(b_1\right)}_k}\frac{x^k}{k!}$. In our case, we split $I_{11}^{\ast \ast }$ naturally as a sum of two terms, and for the first integral, we have b – 1 = –T/L₁, hence b = 1 – T/L₁ = –L₂/L₁, 0 = c – b – 1, hence c = b + 1 = 2 – T/L₁, a = 1, and x = (–ξ₁C₁)/(ξ₁A₂ + 1), where we have pulled (ξ₁ A₂ + 1)^–1 from the denominator. We want to first find an explicit representation for B(b, c – b),

$$B(b,c-b)=B(-T∕L_1+1,1)={\int }_0^1{t}^{-T∕L_1}dt=\frac{1}{-L_2∕L_1}{t}^{-T∕L_1+1}{\mid }_0^1=\frac{-L_1}{L_2}.$$

Using the hypergeometric function and (37), our final formula for $-{\int }_0^{\infty }{I}_{1}ds={\int }_0^{\infty }-e^{L_{2}s}{f}_1^{\ast }\left(\mathbf{Cw}\right)ds$ is

$$-{\int }_0^{\infty }{I}_{1}ds=k\left(\frac{S_2}{L_2}-\frac{C_2}{L_1-L_2}-\frac{2}{L_2{\xi }_2}+\frac{2{\xi }_1{N}_1}{L_2({\xi }_1{A}_2+1)}2F_1^1+\frac{2{\xi }_1{N}_2}{L_2({\xi }_2{S}_2+1)}2F_1^2\right),$$ (38)

where

$${}_{2}F_1^1=2F_1\left(1,-L_2∕L_1;1-L_2∕L_1;\frac{-{\xi }_1{c}_1}{{\xi }_1{A}_2+1}\right)$$

and

$${}_{2}F_1^2=2F_1\left(1,-L_2∕L_1;1-L_2∕L_1;\frac{-{\xi }_2{c}_2}{{\xi }_2{S}_2+1}\right)$$

We now begin work to solve ${\int }_0^{\infty }{I}_{2}ds={\int }_0^{\infty }{e}^{-L_{2}s}{f}_2\left(\mathbf{Cw}\right)ds$. Using the same substitution as earlier, i.e., u = e^L₁s, and again taking c₁ = a₁ A₂₁ and c₂ = a₁(L₁ – A₂₂), we obtain

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{I}_{2}ds=& \frac{-1}{L_1}{\int }_0^1{u}^{-T∕L_1}(u{c}_1+A_2)\left(\frac{\beta (u{c}_2+S_2)(u{c}_1+A_2)}{1+\lambda (u{c}_1+A_2)}-1\right),\hfill \\ \hfill =& \frac{-\beta }{L_1}{\int }_0^1{u}^{-T∕L_1}\frac{(u{c}_2+S_2){(u{c}_1+A_2)}^2}{1+\lambda (u{c}_1+A_2)}du+\frac{1}{L_1}{\int }_0^1{u}^{-T∕L_1+1}{c}_1+u^{-T∕L_1}{A}_{2}du,\hfill \\ \hfill =& \frac{-\beta }{L_1}{\int }_0^1{u}^{-T∕L_1}\left(c_3^{\ast }{u}^2+c_4^{\ast }u+c_5^{\ast }+\frac{c_6^{\ast }}{\lambda u{c}_1+\lambda A_2+1}\right)du+\frac{c_1}{L_1-L_2}+\frac{-A_2}{L_2},\hfill \end{array}$$ (39)

where the last equality comes from long division in the first integral and full integration of the second. The constants are as follows:

$$c_3^{\ast }=\frac{c_1{c}_2}{\lambda },c_4^{\ast }=\frac{c_2{A}_2+c_1{S}_2}{\lambda }-\frac{c_2}{{\lambda }^2},c_5^{\ast }=\frac{c_2}{c_1{\lambda }^3}+\frac{S_2(A_2-1)}{{\lambda }^2},c_6^{\ast }=\frac{-1}{{\lambda }^3}+\frac{S_2-(A_2{c}_2∕c_1)}{{\lambda }^2}.$$

We concentrate now on the first integral in (39). The first three terms multiplied by u^–T/L₁ can be integrated in a straightforward manner. The last one can be integrated using a hypergeometric function as described earlier. We thus obtain

$${\int }_0^{\infty }{I}_{2}ds=-\beta \left(\frac{c_3^{\ast }}{2L_1-L_2}+\frac{c_4^{\ast }}{L_1-L_2}-\frac{c_5^{\ast }}{L_2}\right)+\frac{\beta c_6^{\ast }}{L_2(1+\lambda A_2)}{}_{1}F_2^3+\frac{c_1}{L_1-L_2}-\frac{A_2}{L_2},$$ (40)

where ${}_{1}F_2^3={}_{2}F_1(1,-L_2∕L_1;1-L_2∕L_1;\frac{-\lambda c_1}{1+\lambda A_2})$. Therefore, using (30), (38) and (40) we obtain an explicit solution for M*,

$$M^{\ast }=\frac{k}{L_1-L_2}\left(\frac{S_2}{L_2}-\frac{c_2}{L_1-L_2}-\frac{2}{L_2{\xi }_2}+\frac{2N_1{\xi }_1}{L_2({\xi }_1{A}_2+1)}{}_{1}F_2^1+\frac{2N_2{\xi }_1}{L_2({\xi }_2{S}_2+1)}{}_{1}F_2^2\right)+\frac{L_1-A_{22}}{(L_1-L_2)A_{21}}\left(-\beta \left(\frac{c_3^{\ast }}{2L_1-L_2}+\frac{c_4^{\ast }}{L_1-L_2}-\frac{c_5^{\ast }}{L_2}\right)+\frac{\beta c_6^{\ast }}{L_2(1+\lambda A_2)}{}_{1}F_2^3+\frac{c_1}{L_1-L_2}-\frac{A_2}{L_2}\right),$$ (41)

where the constants and hypergeometric functions were specified earlier.

Linear and Quadratic Approximation of M*

We take a linear and quadratic portion of M* in order to more easily ascertain the effects of the system parameters. Using the expansion for the hypergeometric function, and noting that the untransformed stable manifold will intersect (0, 0), we remove all nonlinear terms and rewrite M* as y₂ = my₁, where m is the slope of the line y₂ to obtain

$$y_2=\frac{-y_1}{{(L_1-L_2)}^2}{c}_7,$$ (42)

where c₇ is the constant

$$c_7=\frac{2N_1{\xi }_1^2{A}_{21}k}{{({\xi }_1{A}_2+1)}^2}+\frac{2N_2{\xi }_1{\xi }_{2}k(L_1-A_{22})}{{({\xi }_2{S}_2+1)}^2}-(L_1-A_{22})+\frac{L_1-A_{22}}{A_{21}}\left(-\beta c_4^{\ast \ast }+A_{21}+\frac{\beta c_6^{\ast \ast }{A}_{21}\lambda }{{(1+\lambda A_2)}^2}\right),$$ (43)

where $c_4^{\ast \ast }=c_4^{\ast }∕y_1$ and $c_6^{\ast \ast }=c_6^{\ast }∕y_1$. Next, since (S*, a*) = x = Cy, we can obtain

$$a^{\ast }=S^{\ast }\left(\frac{{(L_1-L_2)}^2-c_7}{(L_1-A_{22}){(L_1-L_2)}^2+(-L_2+A_{22})c_7}\right)A_{21}.$$

Keeping all quadratic terms, we obtain

$$y_2=\frac{-{\left(y_1\right)}^2}{(L_1-L_2)(2L_1-L_2)}{c}_8-\frac{-y_1}{{(L_1-L_2)}^2}{c}_7,$$ (44)

where

$$c_8=-2{\xi }_1\left(\frac{N_1{\xi }_1^{2}k{A}_{21}^2}{{({\xi }_1{A}_2+1)}^3}+\frac{N_2{\xi }_2^2{(L_1-A_{22})}^2}{{({\xi }_2{S}_2+1)}^3}\right)+\frac{L_1-A_{22}}{A_{21}}\left(\frac{-\beta }{\lambda }{A}_{21}(L_1-A_{22})-\frac{\beta c_6^{\ast \ast }{A}_{21}^2{\lambda }^2}{{(1+\lambda A_2)}^3}\right).$$

The system can be solved for x = (S*, a*) using the quadratic formula.

In Fig. 1, we plot M*, $M_l^{\ast }$ and $M_q^{\ast }$ for specific parameter values in the original coordinate system (S, a). To plot M* and $M_q^{\ast }$ in the original coordinate system (S, a), we input a discreet set of values for y₁ and use Eqs. (41) or (44), respectively, to find y₂. We can then find (S*, a*) = C^–1y and hence (S, a) (S* + S₂, a* + A₂). To plot $M_l^{\ast }$ in the original coordinate system (S, a), we directly find (S*, a*) using Eq. (42) and translate to (S, a). To simplify notation, when we refer to M*, $M_l^{\ast }$ and $M_q^{\ast }$ in the main text, we are referring to these functions after coordinate transformation to (S, a).

Appendix 2: Calculation of the Coefficient of Determination, R²

Here, we briefly describe the calculation of the coefficient of determination, or R², as a measure of the goodness of fit of a regression model to the data. One can find more in depth development and analysis of R² in Greene (2003).

The coefficient of determination is calculated as follows. Define the dependent variables as ${\left\{y_i\right\}}_{i=1}^n$ (in our case, the y_i correspond to the values of A_I for a given parameter input); taking $\stackrel{‒}{y}={\sum }_i{y}_i∕n$, we define the total variation in y as

$$S{S}_t=\sum _i{(y_i-\stackrel{‒}{y})}^2,$$

which is just the sum of squared deviations. For each y_i, we associate a b_i, which is the value of the regression equation at independent variable x_i. We similarly define the residual sum of squares as

$$S{S}_{res}=\sum _i{(y_i-b_i)}^2.$$

The unadjusted R² is calculated as

$$R^2=1-\frac{S{S}_{res}}{S{S}_t}.$$

Note that if the data perfectly fit the model (i.e., $y_i=b_i\forall i$), then R² = 1, indicating that a model with a perfect fit to the data has R² = 1, and decreases to 0 as the goodness of fit is reduced. The adjusted R², R̄², corrects to an increase in R² that can occur due to incorporation of additional degrees of freedom into a model and thus should be used in lieu of R² when comparing goodness of fit between models with different degrees of freedom. It is defined as

$${\stackrel{‒}{R}}^2=1-\frac{S{S}_{res}∕(n-d)}{S{S}_t∕(n-1)},$$

where n is the total number of observations, d is the number of regression coefficients, n – d is the degrees of freedom of SS_res, and n – 1 is the degrees of freedom of SS_t. In the main text, the adjusted R² is presented without the bar notation.