Early accretion of protoplanets inferred from a reduced inner solar system ²⁶Al inventory

Abstract

The mechanisms and timescales of accretion of 10–1000 km sized planetesimals, the building blocks of planets, are not yet well understood. With planetesimal melting predominantly driven by the decay of the short-lived radionuclide ²⁶Al (²⁶Al→²⁶Mg; t_1/2 = 0.73 Ma), its initial abundance determines the permissible timeframe of planetesimal-scale melting and its subsequent cooling history. Currently, precise knowledge about the initial ²⁶Al abundance [(²⁶Al/²⁷Al)₀] exists only for the oldest known solids, calcium aluminum-rich inclusions (CAIs) – the so-called canonical value. We have determined the ²⁶Al/²⁷Al of three angrite meteorites, D’Orbigny, Sahara 99555 and NWA 1670, at their time of crystallization, which corresponds to (3.98 ± 0.15)×10⁻⁷, (3.64 ± 0.18)×10⁻⁷, and (5.92 ± 0.59)×10⁻⁷, respectively. Combined with a newly determined absolute U-corrected Pb–Pb age for NWA 1670 of 4564.39 ± 0.24 Ma and published U-corrected Pb–Pb ages for the other two angrites, this allows us to calculate an initial (²⁶Al/²⁷Al)₀ of $({1.33}_{-0.18}^{+0.21})\times {10}^{-5}$ for the angrite parent body (APB) precursor material at the time of CAI formation, a value four times lower than the accepted canonical value of 5.25 × 10⁻⁵. Based on their similar ⁵⁴Cr/⁵²Cr ratios, most inner solar system materials likely accreted from material containing a similar ²⁶Al/²⁷Al ratio as the APB precursor at the time of CAI formation. To satisfy the abundant evidence for widespread planetesimal differentiation, the subcanonical ²⁶Al budget requires that differentiated planetesimals, and hence protoplanets, accreted rapidly within 0.25 ± 0.15 Ma of the formation of canonical CAIs.

1. Introduction

Planet formation is thought to occur in stages, where the accretion of dust to form planetesimals is an intermediate step to form the first large bodies. Consequently, understanding the timescales and efficiency of planetesimal accretion can lead to a better understanding of planet formation processes. Although the accretion mechanisms are not understood, rapid and efficient accretion of dust to ten to hundred km-sized planetesimals is a common prediction of all numerical models (Weidenschilling, 2000; Johansen et al., 2007; Cuzzi et al., 2008; Morbidelli et al., 2009). This is supported by the meteorite record that suggests crystallization of basaltic material as early as 3 Ma after CAI formation (Bizzarro et al., 2005; Schiller et al., 2010, 2011; Baker et al., 2012), indicating that accretion, differentiation and cooling of their parent bodies occurred early. For example, isotopic and chemical evidence from diogenite meteorites, igneous products of differentiation, requires parent body wide cooling within 1 Ma after CAI formation (Schiller et al., 2011).

The primary heat source driving planetesimal melting is the decay of the short-lived radionuclide ²⁶Al (²⁶Al→²⁶Mg; t_1/2 = 0.73 Ma). Knowledge about the initial ²⁶Al abundance [(²⁶Al/²⁷Al)₀] at the beginning of our solar system only exists for calcium aluminum-rich inclusions (CAIs). This so-called canonical value is based on the ²⁶Al/²⁷Al abundances of 5.25 × 10⁻⁵ determined for CAIs from CV meteorites at the time of their crystallization (Jacobsen et al., 2008; Larsen et al., 2011). However, planetesimals with a radius larger than a few tens of km that accreted with a (²⁶Al/²⁷Al)₀ of 5.25 × 10⁻⁵ contained sufficient energy to maintain temperatures in excess of their liquidus over several million years (e.g., Hevey and Sanders, 2006; Moskovitz and Gaidos, 2011; Elkins-Tanton et al., 2011; Golabek et al., 2014). To achieve diminished ²⁶Al/²⁷Al ratios in the accreting matter, which allow for early cooling, thermal models of accreting planetesimals assume a delay time between CAI formation and planetesimal accretion (e.g., Golabek et al., 2014). Thus, a ubiquitous canonical (²⁶Al/²⁷Al)₀ throughout the protoplanetary disk at the time of CAI formation is problematic. First, early planetesimal cooling <2 million years of CAI formation is not possible if a planetesimal with a radius larger than few tens of kilometers accreted with a canonical (²⁶Al/²⁷Al)₀ ratio due to the energy released by ²⁶Al decay (e.g., Hevey and Sanders, 2006). Second, the presence of undifferentiated planetesimals requires a protracted time span of planetesimal accretion to avoid melting of chondritic parent bodies. However, this conflicts with the prediction of rapid and efficient planetesimal accretion by numerical models. As such, a ubiquitous canonical (²⁶Al/²⁷Al)₀ throughout the protoplanetary disk at the time of CAI formation is inconsistent with the meteorite record. However, the prediction of rapid accretion of planetesimal and early melting and cooling of these bodies could be met if the terrestrial planet forming region was characterized by a lower (²⁶Al/²⁷Al)₀ relative to that of canonical CAIs.

Canonical CAIs do not contain the same nucleosynthetic inventory as chondrites, achondrites and the Earth (e.g., Trinquier et al., 2007, 2009; Moynier et al., 2012; Paton et al., 2013; Kruijer et al., 2014; Schiller et al., 2015). For example, in canonical CAIs the abundance of ⁵⁰Ti is enhanced by ~0.1% when compared to bulk Earth (Trinquier et al., 2009). Although this appears small, most of the dust in the proto-solar molecular cloud that formed our solar system was isotopically homogenized during its residence in the interstellar medium prior to the formation of the solar systems progenitor molecular cloud (Jones and Nuth III, 2011; Schiller et al., 2015) and, thus, only a small portion of dust that preserved its original nucleosynthetic signature caused the nucleosynthetic variability observed in our solar system. When compared to CI chondrites, CAIs are enriched in ⁵⁰Ti by a factor of five compared to the deficit present in the Earth. This suggests a large relative difference in the abundance of nucleosynthetic enriched ⁵⁰Ti carriers between CAIs and the Earth. The presence of live ²⁶Al in our solar system implies that its carrier is a fresh contribution to the dust reservoir of the presolar molecular cloud. Given that nucleosynthetic variations in other elements, such as ⁵⁰Ti, exist, it appears likely that ²⁶Al variability is also present. Therefore, it is unreasonable to accept the current paradigm of a solar system wide canonical (²⁶Al/²⁷Al)₀ based on CAIs without independent determination of the (²⁶Al/²⁷Al)₀ of other solar system reservoirs at a resolution appropriate for the short half-life of ²⁶Al. Importantly, the only independent estimate of the (²⁶Al/²⁷Al)₀ comes from a correlation of ⁵⁴Cr and the mass-independent component of ²⁶Mg (µ²⁶Mg*) in bulk meteorites (Larsen et al., 2011). Based on this correlation, Larsen et al. (2011) calculated an (²⁶Al/²⁷Al)₀ for the precursor of non-carbonaceous meteorites of (1–2) × 10⁻⁵. In particular, their calculated APB (²⁶Al/²⁷Al)₀ of (1.61 ± 0.32) × 10⁻⁵ is significantly lower than the canonical abundance. However, this estimate assumes that the Mg isotope composition of young angrites is representative of the bulk APB (i.e. that their precursors ²⁷Al/²⁴Mg was not altered by melting and differentiation prior to complete ²⁶Al decay) and that no Mg isotope heterogeneity exists. These assumptions can be overcome by combining a precise, assumption free, U-corrected absolute Pb–Pb age and ²⁶Al/²⁷Al ratio determined by an internal mineral isochron of an achondrite that crystallized while ²⁶Al was alive. This allows determination of the theoretical (²⁶Al/²⁷Al)₀ ratio of the precursor material at the time of CAI formation by back calculating the measured ²⁶Al/²⁷Al to the age of CAIs. Consistency between the calculated initial (²⁶Al/²⁷Al)₀ for multiple individual samples with different ages from a single parent body gives confidence in the accuracy of the result. Although this approach is not new (e.g., Nyquist et al., 2009), earlier Pb–Pb ages were calculated assuming a constant and inappropriate ²³⁸U/²³⁵U. Recently, Brennecka et al. (2010) demonstrated that variable ²³⁸U/²³⁵U exists in CAIs and, thus, accurate Pb–Pb ages for CAIs and early solar system matter require a ²³⁸U/²³⁵U correction.

In an effort to test the (²⁶Al/²⁷Al)₀ reported by Larsen et al. (2011) and independently determine the (²⁶Al/²⁷Al)₀ of the APB, we revisit the Pb–Pb and ²⁶Al–²⁶Mg systematics of the volcanic angrites D’Orbigny and Sahara 99555 (Sah99555) and complement this data with new Pb–Pb and ²⁶Al–²⁶Mg data for a third volcanic angrite, NWA 1670 (NWA1670). These volcanic angrite meteorites are ideally suited because: 1) their volatile depleted nature ensures high U/Pb ratios that allow for precise Pb–Pb dating, 2) their basaltic bulk composition and petrology provides both high and low Al/Mg phases that are required for precise internal ²⁶Al–²⁶Mg isochrons, and 3) they are quenched and largely unshocked rocks (Keil, 2012), suggesting that closure temperatures of different chronometers were reached closely in time and were not reset after initial closure. Based on their similar chemistry as well as indistinguishable Δ¹⁷O signatures (Keil, 2012; Greenwood et al., 2005), it is also believed that all three meteorites stem from a common parent body.

2. Samples

The samples analyzed here have already been thoroughly studied for their petrology, geochemistry and isotope systematics (Keil, 2012 and references therein). Both D’Orbigny and Sah99555 are unbrecciated, unshocked and contain vesicles (Mittlefehldt et al., 2002), whereas only D’Orbigny contains glass. U-corrected (assuming a ²³⁸U/²³⁵U = 137.786 ± 0.013; Connelly et al., 2012) Pb–Pb ages for Sah99555 and D’Orbigny are 4563.43 ± 0.18 Ma and 4563.59 ± 0.20 Ma, respectively (Amelin, 2008a, 2008b; Connelly et al., 2008). Reported internal ²⁶Al–²⁶Mg mineral isochrons for both these meteorites yield indistinguishable ²⁶Al/²⁷Al ratios of (5.13 ± 1.90) × 10⁻⁷ and (5.06 ± 0.92) × 10⁻⁷ (Spivak-Birndorf et al., 2009) and (4.45 ± 0.56) × 10⁻⁷ and (3.88 ± 0.27) × 10⁻⁷ (Schiller et al., 2010), respectively. Similarly, no resolvable chronological difference exist in their initial ¹⁸²Hf/¹⁸⁰Hf and ⁵³Mn/⁵⁵Mn ratios (Kleine et al., 2012; Sugiura et al., 2005).

NWA1670 has a bulk chemical composition similar to that of other angrites but also contains abundant and large olivine xenocrysts embedded in a cryptocrystalline matrix of intergrown feldspar, pyroxene and olivine (Jambon et al., 2008). The high magnesian olivine xenocrysts are typically overgrown by less Mg-rich olivine. The similar geochemistry and indistinguishable oxygen isotope composition of NWA1670 with respect to other angrites confirms their common ancestry (Greenwood et al., 2005). The ⁵³Mn/⁵⁵Mn abundance determined for NWA1670 suggests a crystallization age similar to D’Orbingy and Sah99555 (Sugiura et al., 2005). NWA1670 is one of the few angrites that may have experienced some shock (Keil, 2012, and references therein).

3. Methods

3.1. ²⁶Al–²⁶Mg isotope measurements

Whole rock fragments of D’Orbigny, Sah99555 and NWA1670 weighing around 1 g were mildly crushed with an agate mortar and pestle, rinsed in acetone and distilled water and sieved. Whole rock samples of approximately 20 mg were taken from the 250–500 µm size fraction of D’Orbigny and Sah99555. Feldspar separates were generated from the remaining size fraction of these two meteorites with a Frantz isodynamic magnetic separator whereas olivine and pyroxene separates were handpicked from the crushed bulk sample. Due to the cryptocrystalline nature of the NWA1670 groundmass, only olivine and cryptocrystalline ground-mass separates of a few mg each were handpicked. Samples were digested using HF–HNO₃ acid mixtures and, after complete dissolution, Al/Mg ratios were determined on an aliquot of the digested sample to 2% accuracy using a ThermoFisher X-Series II inductively coupled plasma source mass spectrometer (ICPMS).

Magnesium was purified by ion-exchange chromatography and its isotopic composition analyzed using a ThermoFisher Neptune Plus multiple collector ICPMS (MC-ICPMS) equipped with a Sampler Jet and Skimmer X-cone and an Apex sample introduction system following protocols outlined in Bizzarro et al. (2011). The Mg isotope composition was measured in high resolution mode using a 50 μm entrance slit (M/ΔM > 5000). At an uptake rate of ~50 μL/min, the sensitivity of the instrument was ~200 V/ppm. Depending on sample size signal intensities were typically 100 V or 25 V on mass ²⁴Mg (see Table 1). Faradays cups that received signals larger than 50 V were connected to an amplifier with a 10¹⁰ Ω feedback resistor, whereas Faradays cups collecting smaller signals were connected to an amplifier with a 10¹¹ Ω feedback resistor. Single analyses comprised 1667 s of data acquisition and each sample was bracketed by standard analyses and analyzed ten times when permissible. Mg isotope data are reported in the μ-notation as relative deviations from the DTs-2b standard (µ²⁵Mg_DSM-3 = −122 ± 17 ppm (2 sd); Bizzarro et al., 2011) according to the following formula:

$${\mathrm{\text{μ}}}^{\text{25}}\text{Mg=}\left[\frac{{{(}^{25}{\text{MG/}}^{\text{24}}\text{Mg)}}_{sample}}{{{(}^{25}{\text{Mg/}}^{\text{24}}\text{Mg)}}_{DTS-2b}}-1\right]\times {10}^6.$$ (1)

Table 1.

Mg isotope data and ²⁷Al/²⁴Mg ratios for NWA1670, D’Orbigny and Sah99555.

Meteorite/mineralogy	µ26Mg* ± 2 se (ppm)	µ25Mg ± 2 se (ppm)	n	24Mg (V)	27Al/24Mg	Mg# (ol)
NWA1670
ol	−10.6 ± 0.8	+100 ± 9	10	117	0.003	0.84
ol	−12.7 ± 1.7	+33 ± 4	10	74	0.004	0.85
ol	−11.2 ± 2.2	+13 ± 13	10	80	0.008	0.90
ol	−8.1 ± 2.3	0 ±4	10	86	0.009	0.73
ol	−11.4± 0.9	+ 63 ± 4	10	71	0.010	0.84
ol	−10.5 ± 2.6	−4 ± 6	10	75	0.015	0.90
ol	−9.1 ± 1.4	+14±3	10	82	0.016	0.83
ol	−12.7 ± 1.2	+2 ± 9	10	85	0.018	0.88
ol	−11.8 ± 1.2	+35 ± 6	10	111	0.022	0.89
ol	−9.0 ± 2.0	+19 ± 11	10	100	0.034	0.79
fsp/px	−5.3 ± 1.5	+36 ± 22	10	116	1.93
fsp/px	−0.8 ± 1.6	+177 ± 9	10	113	2.18
fsp/px	−1.3 ± 1.6	+57 ± 11	10	123	2.48
fsp/px	−0.4 ± 1.5	+15 ± 18	10	117	2.60
fsp/px	+1.8 ± 1.6	+77 ± 3	10	96	2.73
fsp/px	+0.9 ± 0.9	+81 ± 3	10	94	2.83
fsp/px	+3.0 ± 2.3	+56 ± 7	10	92	3.02
fsp/px	+0.5 ± 3.3	+65 ± 7	10	64	3.11
fsp/px	+4.3 ± 2.4	+56 ± 5	10	69	3.20
D’Orbigny
ol	+3.9 ± 3.8	−161 ± 23	4	27	0.220
ol	+4.0 ± 1.1	−4 ± 14	10	102	0.240
ol	+4.4 ± 1.3	+60 ± 4	10	139	0.721
px	+5.7 ± 1.4	+ 71 ± 17	10	116	1.36
WR	+9.2 ± 1.6	+26 ± 20	10	117	1.78
fsp	+29.2 ± 3.6	+62 ± 17	8	61	8.27
fsp	+93.3 ± 4.1	−15 ± 21	10	28	29.5
fsp	+121.5 ± 3.3	−191 ± 8	10	32	43.3
Sah99555
ol	+1.2 ± 3.6	−205 ± 13	10	30	0.085
WR	+11.5 ± 2.3	−14 ± 9	10	38	2.14
fsp	+121.4 ± 5.8	−11 ± 23	10	26	45.0
fsp	+168.8 ± 11	−151 ± 84	3	26	64.1

Notes: ol = olivine, fsp = feldpspar, px = pyroxene, WR = whole rock.

The mass-independent component in ²⁶Mg (µ²⁶Mg*) is reported in the same fashion, but represents deviations from the internally normalized ²⁶Mg/²⁴Mg of the sample from the reference standard, normalized to ²⁵Mg/²⁴Mg = 0.126896 using the exponential mass fractionation law. We used the exponential law (β = 0.511) to correct for instrumental mass bias and potential natural mass fractionation experienced by the samples. Two lines of evidence indicate that this approach yields accurate ²⁶Mg* values. First, the rock samples analyzed here are rapidly cooled magmatic lavas and, under such conditions, equilibrium mass fractionation is believed to be negligible (Teng et al., 2007). Second, instrumental mass fractionation under typical analytical conditions in our laboratory is driven by kinetic processes rather than equilibrium (i.e., Bizzarro et al., 2011). As such, variable instrument-related mass fractionation in samples relative to the standard can be accurately corrected for using our approach. We note that, similar to earlier studies (Spivak-Birndorf et al., 2009; Schiller et al., 2010), stable isotope variability exists between individual mineral fractions, typically for samples containing little Mg. We infer that this reflects analytical artifacts in the stable isotope data during analysis by MC-ICPMS induced by the presence of residual organics accumulated in the purification process rather than true isotope variability. Thus, we caution that the reported internal uncertainties for ²⁵Mg do not reflect the true reproducibility of the data, which may be significantly larger for small samples.

All Mg data reduction was conducted off-line using Iolite (Paton et al., 2011) and changes in mass bias with time were interpolated using a smoothed cubic spline. For each analysis, the mean and standard error of the measured ratios were calculated using a 3 sd threshold to reject outliers. Individual analyses of a sample were combined to produce a weighted average by the propagated uncertainties of individual analyses and reported final uncertainties are the 2 se of the mean. ²⁶Al–²⁶Mg isochrons were calculated based on ²⁷Al/²⁴Mg and Mg isotope data reported in Table 1 using Isoplot applying an external reproducibility of the μ²⁶Mg* data of 2.5 ppm for samples analysed systematically ten times at signal intensities of ~80 V for ²⁴Mg (Bizzarro et al., 2011). Samples measured at intensities of ~25 V for ²⁴Mg yielded a larger external reproducibility of 5 ppm that is predicted by counting statistics for approximately four times lower signals.

3.2. ²⁰⁶Pb–²⁰⁷Pb analysis of NWA1670

Pb data was collected in two sessions, one for a whole rock sample and one for a purified pyroxene separate. The whole rock aliquot was coarsely crushed with an agate mortar and pestle. The pyroxene fraction was generated by crushing fragments with a mortar and pestle to a sieve size of 60–150 mesh, passing this material through a Frantz isodynamic separator before picking a final fraction with a binocular microscope. The pyroxene separate was >99% pure. Both samples were washed in 5 cycles of distilled water, ethanol and acetone that included 5 min on a hotplate (110 °C) and 5 min of ultrasonication. This was followed by 3 steps of 0.01 M HBr that included 5 min on a hotplate (110 °C) and 5 min of ultrasonication. Final cleaning was accomplished using 1 M HBr and 2 M HNO₃ as prescribed in Table 2. These washing steps contained a total of 9.4 ng of Pb, which was analysed for Pb isotopes as two separate aliquots. Each sample was then subjected to a progressive dissolution using increasing acid strengths and varying hotplate times (Table 2) following modified procedures outlined in Connelly and Bizzarro (2009). Lead was separated from matrix elements by passing the samples twice through a HBr–HNO₃-based chemistry with Eichrom anion resin (Connelly and Bizzarro, 2009). The purified Pb was analyzed on a ThermoFisher Triton thermal ionization mass spectrometer. Pb was loaded onto previously outgassed zone-refined Re filaments with silica gel made from silicic acid. All analyses were made by sequentially peak jumping the ion beams into the axial secondary electron multipler–ion counting system (SEM-IC). Samples were spiked with a ²⁰²Pb–²⁰⁵Pb double tracer to allow for an internal correction for instrumental mass fractionation assuming a linear mass fractionation law. The ²⁰²Pb–²⁰⁵Pb tracer was calibrated against SRM-981 assuming a ²⁰⁸Pb–²⁰⁶Pb ratio of 2.1677 (Amelin and Davis, 2006). Samples are corrected for Pb blank added during the chemical separation according to replicate blanks run during the same session. Pb blanks from the chemistry during this work ranged from 0.2 to 0.5 pg. Samples are also corrected for a 0.1 pg Pb loading blank.

Table 2.

Step wise dissolution protocol and Pb isotope data for NWA1670

Sample	Fraction	Acid	Treatment	Pb (ng)	$\frac{{206}_{\text{Pb}}}{{204}_{\text{Pb}}}$ uncorr.	$\frac{{204}_{\text{Pb}}}{{206}_{\text{Pb}}}$* corr.	%2σ	$\frac{{207}_{\text{Pb}}}{{206}_{\text{Pb}}}$* corr.	%2σ	$\frac{{208}_{\text{Pb}}}{{206}_{\text{Pb}}}$* corr.	%2σ	Rho**
Whole rock	W1	1 M HBr	5US/5HP/5US	4722.2	97.28	0.0102425	0.094	0.666491	0.010	1.119692	0.004	0.003
Whole rock	W2	2 M HN03	5US/5HP/5US	4683.5	82.30	0.0121038	0.060	0.674524	0.010	1.173223	0.005	0.004
Whole rock	L1	4 M HN03	30HP/5US	2886.7	195.41	0.0050993	0.102	0.645063	0.010	0.996108	0.020	0.016
Whole rock	L2	2 M HCl	20HP/5US	997.6	178.02	0.0055837	0.107	0.647081	0.010	1.008311	0.021	0.103
Whole rock	L3	6 M HCl	5US/5HP/5US	494.6	177.83	0.0055698	0.153	0.647250	0.016	0.970794	0.027	0.174
Whole rock	L4	6 M HCl	100HP/5US	795.9	492.37	0.0020038	0.246	0.632382	0.016	1.154197	0.036	0.156
Whole rock	L5	1MHF	40HP/5US	699.2	1432.50	0.0006707	0.850	0.626966	0.020	1.468536	0.060	0.171
Whole rock	L6	1MHF	30HP/5US	477.4	554.57	0.0017599	0.436	0.631292	0.015	1.530029	0.040	0.357
Whole rock	L7	6 M HCl	5US/60HP/5US	187.6	1214.00	0.0007282	2.533	0.627212	0.025	1.454022	0.024	0.543
Whole rock	L8	28 M HF	5US	248.3	895.00	0.0010477	1.281	0.627801	0.024	1.314198	0.057	0.415
Whole rock	R	28 M HF/7 M HNO3	3 days HP/5US	26.1	185.35	0.0048291	2.269	0.643563	0.082	1.091098	0.185	0.849
Clinopyroxene	C-L3	6 M HCl	60HP/5US	204.3	360.28	0.0026868	0.602	0.635160	0.034	1.770295	0.028	0.334
Clinopyroxene***	C-L4	1 M HF	15HP/5US	113.5	769.21	0.0011291	2.944	0.628250	0.042	1.426170	0.041	0.582

Notes:

US = ultrasonication, HP = hot plate.

^*Isotope ratios corrected for fractionation (internally normalized with a ²⁰⁵Pb/²⁰²Pb tracer, tracer Pb and blank Pb.

^**Rho corresponds to the error correlation between the ²⁰⁴Pb/²⁰⁶Pb vs. ²⁰⁷Pb/²⁰⁶Pb ratios.

^***The final digestion of the residue after step L4 of the clinopyroxene yielded less than 0.5 pg of total Pb.

4. Results

4.1. Mg isotope data

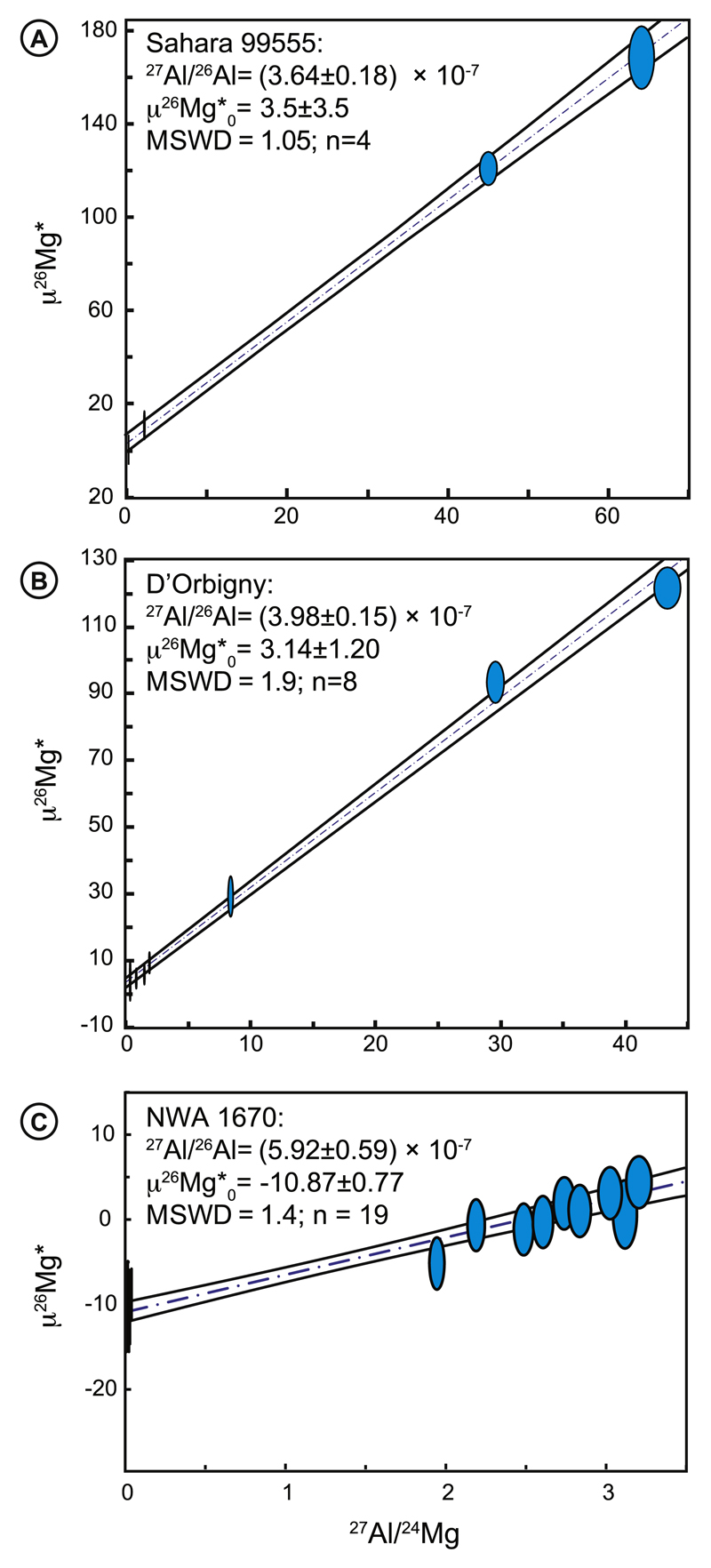
All mineral separates and whole rock samples from D’Orbigny and Sah99555 have positive µ²⁶Mg* values that range from +1.2 ± 3.6 to +168.8 ± 11 and correlate with their respective ²⁷Al/²⁴Mg (Table 1). Eight fragments from D’Orbigny form a linear array with a slope equivalent to a ²⁶Al/²⁷Al of (3.98 ± 0.15) × 10⁻⁷ (MSWD = 1.9) and a positive intercept ${(\mu }^{\text{26}}{\text{Mg}}_{\text{0}}^{\text{*}}=+3.14\pm 1.20)$. Similarly, four fragments from Sah99555 form a linear array with a slope equivalent to a ²⁶Al/²⁷Al of (3.64 ± 0.18) × 10⁻⁷ (MSWD = 1.05) and a positive intercept ${(\mu }^{\text{26}}{\text{Mg}}_{\text{0}}^{\text{*}}=+3.5\pm 3.5)$.

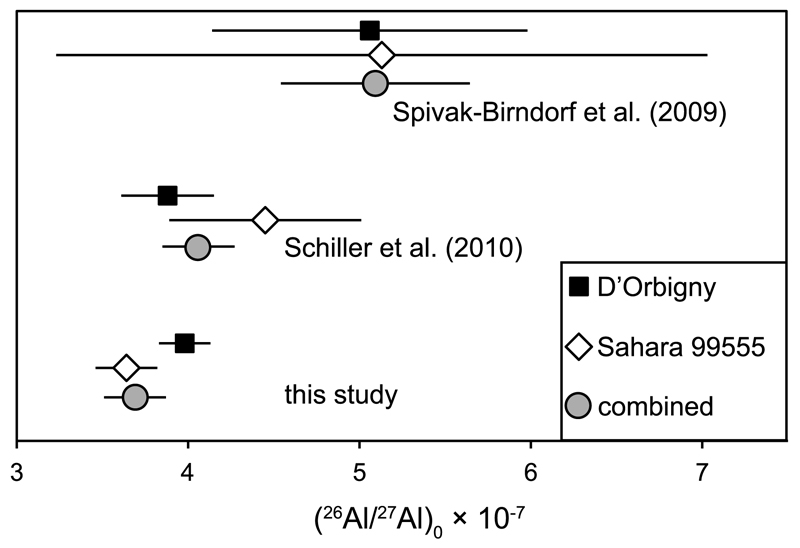
Although the Mg isotope systematics of D’Orbigny and Sah99555 have already been studied before, the new ²⁶Al/²⁷Al reported for D’Orbigny and Sah99555 represent a significant improvement in precision for both angrites. In detail, the new data reported here improves the current uncertainties for D’Orbigny’s ²⁶Al/²⁷Al ratio at the time of its crystallization by a factor of 6 and 3.7 and for Sah99555 by a factor of 10.5 and 1.5 compared to previous data by Spivak-Birndorf et al. (2009) and Schiller et al. (2010), respectively (Fig. 1). Notably, an isochron of the combined data for D’Orbigny and Sah99555 returns a ²⁶Al/²⁷Al of (3.70 ± 0.18) × 10⁻⁷, which is within uncertainties of the data reported by Schiller et al. (2010) but translates into a relative age that is 0.33 ± 0.13 Ma younger than the value reported by Spivak-Birndorf et al. (2009) for the same meteorites.

Fig. 1.

Comparison of ²⁶Al/²⁷Al ratios of D’Orbigny and Sah99555 determined here and that reported in the literature for the same meteorites.

In contrast to the Mg data for D’Orbigny and Sah99555, most of the 19 individual samples analysed from NWA1670 have µ²⁶Mg* values that are lower than that of Earth. In particular, all ten olivine separates have values that cluster around −10.7, whereas the highest measured µ²⁶Mg* value is +4.3 ± 2.4. The total range in µ²⁶Mg* for NWA1670 is much smaller than for D’Orbigny and Sah99555 but µ²⁶Mg* correlate with their respective ²⁷Al/²⁴Mg ratio. Consequently, the combined Mg isotope and ²⁷Al/²⁴Mg data of all samples from NWA1670 form a linear array with a slope equivalent to a ²⁶Al/²⁷Al of (5.92 ± 0.59) × 10⁻⁷ (MSWD = 1.4) and an intercept of ${\mathrm{\text{μ}}}^{\text{26}}{\text{Mg}}_{\text{0}}^{\text{*}}=-10.87\pm 0.77$ (see Fig. 2).

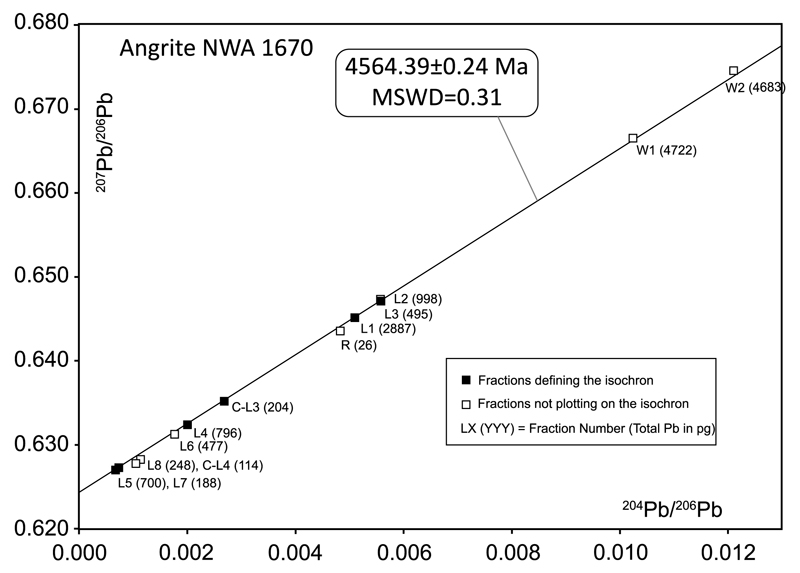
Fig. 2.

Pb–Pb isochron diagram for NWA1670. Errors are smaller than symbols shown. Isochron age errors are 95% confidence intervals. MSWD = Mean square of weighted deviations. Labels indicate the sample name including in brackets the calculated amount of Pb present in each step. All data presented in this figure can be found in Table 2.

4.2. Pb–Pb age of NWA1670

The Pb–Pb data for six out of thirteen individual dissolution steps (including initial washes) of a sample of NWA1670 reported in Table 2 form a linear array that is equivalent to a Pb–Pb age of 4564.39 ± 0.24 Ma, when using a U-isotope composition of ²³⁸U/²³⁵U = 137.786 ± 0.013 (Fig. 3, Connelly et al., 2012). Most meteoritic material contains at least three reservoirs of Pb: a) initial Pb (Pb_i), b) radiogenic Pb (Pb_r) and c) terrestrial contaminant Pb (Pb_c). An accurate age is most commonly defined by a spread of points along an isochron representing a mixture of Pb_i and Pb_r, with the initial washing steps intended to remove Pb_c. However, an accurate age can also be calculated from the y-intercept value in a ²⁰⁴Pb/²⁰⁶Pb vs ²⁰⁷Pb/²⁰⁶Pb diagram from two-component system of Pb_r and Pb_c, provided the fractions defining the isochron contain no Pb_i such as has been documented for Sah99555 (Amelin, 2008a; Connelly et al., 2008). We infer that this is the case for NWA1670 given that the isochron defined by the six fractions regresses to a Pb isotopic composition consistent with modern terrestrial contamination as estimated by Stacey and Kramers (1975) and projects well below the solar system initial as represented by Canyon Diablo Pb (Tatsumoto et al., 1973). The points that fall above the isochron are interpreted to contain a minor, but measurable, amount of Pb_i. Points falling below the isochron are interpreted to represent domains of minerals that lost a minor amount of accumulated radiogenic Pb_r during thermal alteration on the parent body such that they now lie slightly below the isochron. It should be noted that the points defining the isochron represent six of 11 fractions but 81% of the total Pb derived from the stepwise dissolution steps of the whole rock sample and the pyroxene mineral separate.

Fig. 3.

Internal mineral ²⁶Al–²⁶Mg isochron diagrams for (A) Sah99555, (B) D’Orbigny, and (C) NWA1670. Uncertainties for µ²⁶Mg* are either the external reproducibility or the internal error, whichever is larger. The estimated uncertainty for ²⁷Al/²⁴Mg ratio is 2%. Calculating the µ²⁶Mg* values using the equilibrium (β = 0.521) rather than the exponential (β = 0.511) mass fractionation law increases the scatter of the linear regressions, which results in an MSWD of 7.5, 4.9, and 9.3 for the Sah99555, D’Orbigny and NWA1670 regressions, respectively. Given the simple thermal history of these volcanic rocks, this observation supports our proposal that the exponential law is more appropriate to account for stable isotope differences between minerals of each sample.

5. Discussion

5.1. Comparison of absolute Pb–Pb and relative ²⁶Al–²⁶Mg ages

Based on the chemical and isotopic similarities of the three analysed angrites, little doubt exist about their common origin from the same parent body and, thus, relative age differences based on Pb–Pb or ²⁶Al/²⁷Al cannot be caused by differences in their pre-cursor (²⁶Al/²⁷Al)₀ or U isotopic composition. The precise and U-corrected Pb–Pb isochron for NWA1670 defines an age of 4564.39 ± 0.24 Ma (Fig. 2), which is 0.88 ± 0.28 Ma older than the average age of the other two angrites (4563.51 ± 0.13 Ma; Amelin, 2008b, 2008a; Connelly et al., 2008, 2012). The older age of NWA1670 agrees with the primitive chemistry of cores of olivine and pyroxene xenocrysts in NWA1670 that cluster at the least evolved spectrum of the angrite trend (Jambon et al., 2008). Also in agreement with the Pb–Pb ages, the differences in measured ²⁶Al/²⁷Al between the angrites indicates that NWA1670 crystallized ${0.50}_{-0.29}^{+0.27}$ Ma before Sah99555 and D’Orbigny, a range that is within error of the offset in absolute Pb–Pb ages of 0.88 ± 0.28 Ma. Based on these comparable age offsets using ²⁶Al–²⁶Mg and Pb–Pb chronology, the incorporation of potentially less radiogenic (i.e. older) ²⁶Mg isotope signatures of the xenocryst olivine in the isochron of NWA1670, which can only increase the calculated ²⁶Al/²⁷Al of NWA1670, has no resolvable effect.

5.2. The initial ²⁶Al/²⁷Al of the APB

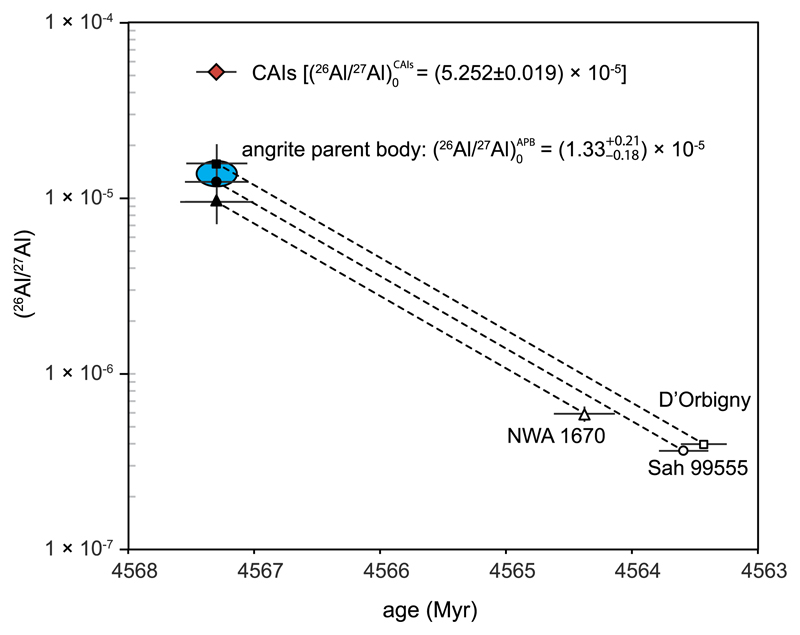
Considering that the Pb–Pb ages and ²⁶Al/²⁷Al of all three meteorites are internally consistent, the (²⁶Al/²⁷Al)₀ ratio of their precursor is simply a function of the relative Pb–Pb age difference between CAIs and the angrites and the half-life of ²⁶Al. When back calculating the measured ²⁶Al/²⁷Al of all three meteorites to the age of CAIs (4567.30 ± 0.16 Ma; Connelly et al., 2012) D’Orbigny, Sah99555 and NWA1670 each predict an (²⁶Al/²⁷Al)₀ of their precursor of ${1.56}_{-0.33}^{+0.41}\times {10}^{-5}$, ${1.23}_{-0.27}^{+0.34}\times {10}^{-5}$ and ${0.95}_{-0.25}^{+0.32}\times {10}^{-5}$, respectively. Combined, the weighted average indicates that their common APB precursor had an (²⁶Al/²⁷Al)₀ of ${1.33}_{-0.18}^{+0.21}\times {10}^{-5}$, lower by a factor of ~4 relative to the value for canonical CAIs (Fig. 4). The calculated mean is in agreement with the independently determined value of (1.61 ± 0.32) × 10⁻⁵ for the APB by Larsen et al. (2011) based on younger, plutonic angrites. The model of ²⁶Al heterogeneity proposed by Larsen et al. (2011) predicts variability in the initial (²⁶Al/²⁷Al)₀ of disk solids ranging from the solar value of (2.81 ± 0.30) × 10⁻⁵ down to values as low as 1 × 10⁻⁵. Luu et al. (2015) recently reported comparable variability in chondrules Allende, which is apparently in agreement with the model of Larsen et al. (2011) if the majority of chondrules formed shortly after CAIs. However, absolute age dating of the chondrules studied by Luu et al. (2015) is required to support this proposal.

Fig. 4.

Shown is the evolution of ²⁶Al/²⁷Al on a logarithmic scale versus time starting from the measured ²⁶Al/²⁷Al of the angrites Sah99555, D’Orbigny and NWA1670 at the time of their crystallization projected backwards to the time of CAI formation using U-corrected, absolute Pb–Pb ages for angrites and CAIs (Amelin, 2008b, 2008a; Connelly et al., 2008, 2012) and a ²⁶Al half-life of 0.73 Ma, which establish an (²⁶Al/²⁷Al)₀ of the APB of $({1.33}_{-0.18}^{+0.21})\times {10}^{-5}$. Also shown is the canonical (²⁶Al/²⁷Al)₀ of CAIs with U-corrected Pb–Pb age (Connelly et al., 2012; Larsen et al., 2011).

The discrepancy of our calculated (²⁶Al/²⁷Al)₀ with the canonical value measured in CAIs requires that either the absolute Pb–Pb chronology, the assumption of concurrent closure of the ²⁶Al–²⁶Mg and Pb–Pb decay systems of volcanic angrites and/or the assumption of solar system-wide canonical (²⁶Al/²⁷Al)₀ is incorrect. As outlined above, the quenched textures of the analysed volcanic angrites have been interpreted to indicate rapid cooling, requiring that closure temperatures of the ²⁶Al–²⁶Mg and Pb–Pb decay systems were reached well within the resolution of these chronometers. Furthermore, all three angrites have a pristine mineralogy and preserve mineral zoning that lacks signs of metamorphic overprint, arguing against late resetting of the ²⁶Al–²⁶Mg system for all these samples.

5.3. Accuracy of the Pb–Pb ages

Based on several lines of independent reasoning, the Pb–Pb ages of angrites are interpreted to be accurate to within their stated uncertainties. First, each Pb–Pb age is defined by well-correlated linear arrays defined by multiple individual analyses in ²⁰⁷Pb/²⁰⁶Pb–²⁰⁴Pb/²⁰⁶Pb space and/or highly radiogenic fractions that constrain the ²⁰⁷Pb_r/²⁰⁶Pb_r. Second, the Pb–Pb ages based on linear arrays of multiple individual analyses are indistinguishable from model ages based on the most radiogenic fractions and primordial Pb, thus demonstrating that the ages are not sensitive to the existence of terrestrial Pb that comprises the non-radiogenic Pb in some samples. Third, the Pb–Pb analyses of Sah99555 by two independent groups using different sample digestion methods have yielded identical ages for this meteorite within analytical uncertainty (Amelin, 2008a; Connelly et al., 2008). Fourth, the Pb–Pb ages of all three angrites have been corrected for their U-isotope composition, making their Pb–Pb ages assumption free. Similar arguments can also be made for the accuracy of the absolute Pb–Pb age of CAIs, which are discussed in depth by Connelly et al. (2012). We emphasize that the current best estimate of the absolute formation age of CAIs at 4567.30 ± 0.16 Ma reflects the weighted mean of four individual inclusions analysed in two different laboratories (Amelin et al., 2010; Connelly et al., 2012). Importantly, the four inclusions investigated defined U-isotope variability, with compositions that are isotopically heavy and light relative to the solar ²³⁸U/²³⁵U value of 137.786 ± 0.013. The age concordancy of these inclusions, despite the wide range of their ²³⁸U/²³⁵U ratios, supports the interpretation that the U-corrected Pb–Pb age of 4567.30 ± 0.16 Ma dates the timing of CAI condensation and not a secondary event. As such, we conclude that the discrepancy between the measured (²⁶Al/²⁷Al)_cryst. in angrites and that projected from the canonical value to their respective Pb–Pb age reflects a reduced ${{(}^{26}\text{Al}{/}^{27}\text{Al})}_0^{APB}$ ratio of the precursor material in the APB accretion region relative to that of the CAI forming region. Collectively, these data require an inhomogeneous distribution of the (²⁶Al/²⁷Al)₀ within the protoplanetary disk.

5.4. Assessing the level of (²⁶Al/²⁷Al)₀ homogeneity in the protoplanetary disk using ¹⁸²Hf–¹⁸²W chronology

The successful application of a short-lived radionuclide chronometer requires homogeneous distribution of the parent isotope throughout space and time in the protoplanetary disk. Testing the assumption of homogeneity has proven difficult and mainly relies on checking concordancy between different short-lived and long-lived chronometers (e.g., Nyquist et al., 2009; Spivak-Birndorf et al., 2009; Kleine et al., 2012; Kruijer et al., 2014). The angrites D’Orbigny and Sah99555 have been central to the debate of whether ²⁶Al was homogeneously distributed given their antiquity, presumed rapid cooling and relatively pristine nature.

The most recent contributions to this debate attempted to use the ¹⁸²Hf–¹⁸²W system to test for homogeneity of (²⁶Al/²⁷Al)₀ in the protoplanetary disk. Kleine et al. (2012) reported a 4.3 ± 0.7 Ma offset for the average ¹⁸²Hf/¹⁸⁰Hf value for D’Orbigny and Sah99555 relative to that for CAIs as defined by Burkhardt et al. (2008). This time span agrees within error with the average age offset between these two angrites and CAIs as defined by their published U-corrected Pb–Pb ages (Fig. 5), namely 3.8 ± 0.2 Ma (Amelin, 2008b, 2008a; Connelly et al., 2008, 2012). But these age offsets are distinctly smaller than the average ²⁶Al–²⁶Mg age of 5.22 ± 0.05 Ma for these two angrites relative to the canonical CAI based on a canonical (²⁶Al/²⁷Al)₀ abundance (Larsen et al., 2011). To explain the discrepant ²⁶Al–²⁶Mg age relative to both the Pb–Pb and ¹⁸²Hf–¹⁸²W ages, Kleine et al. (2012) concluded that the (²⁶Al/²⁷Al)₀ ratio was heterogeneously distributed such that the APB precursor material had a lower initial inventory of ²⁶Al than the CAI forming reservoir.

Fig. 5.

Comparison of relative ages of Sah99555 and D’Orbigny with respect to CAIs. To test for (²⁶Al/²⁷Al homogeneity a canonical (²⁶Al/²⁷Al)₀ was assumed. Data sources: Amelin (2008b, 2008a), Connelly et al. (2008, 2012), Kleine et al. (2012), Burkhardt et al. (2008), Kruijer et al. (2014), Larsen et al. (2011) and this work.

More recently, Kruijer et al. (2014) revised the (¹⁸²Hf/¹⁸⁰Hf)₀ to a slightly higher value [but within error of Burkhardt et al. (2008)] resulting in the angrites becoming 0.5 Ma younger than the previous results of Kleine et al. (2012). This translates into an increased age difference between the average age for D’Orbigny and Sah99555 relative to CAIs of 4.8 ± 0.6 Ma (Fig. 5). This revised relative age is now outside that defined by published Pb–Pb ages but agrees better with ²⁶Al–²⁶Mg relative age for the two angrites of 5.20 ± 0.05 Ma after CAI formation and canonical (²⁶Al/²⁷Al)₀ ratio. They infer that the concordance of these ¹⁸²Hf–¹⁸²W and ²⁶Al–²⁶Mg relative ages supports homogeneous distribution of ²⁶Al. To explain the discordance of the Pb–Pb ages, they suggest that the concordant ages of four CAIs presented by Amelin et al. (2010) and Connelly et al. (2012) are too young and that an unpublished age for a single CAI by Bouvier et al. (2011) that is 0.64 ± 0.45 Ma older may be a better age estimate for CAIs in CV chondrites.

A critical assumption of all short-lived relative chronometers is the homogeneous initial abundance of the parent isotope throughout the protoplanetary disk. As mentioned earlier, concordance between relative ages obtained by different chronometers, such as the relative age difference between CAIs and angrites, has traditionally been used to argue for homogeneity of the parent isotopes. The most rigorous test using this approach is concordance of a relative age with an assumption free absolute age, such as that obtained by the U-corrected Pb–Pb system. In the case of the new (¹⁸²Hf/¹⁸⁰Hf)₀ by Kruijer et al. (2014), the relative ¹⁸²Hf–¹⁸²W age of angrites and CAIs are not consistent with published absolute Pb–Pb ages. Although Kruijer et al. (2014) argue that this is due to an uncertain absolute Pb–Pb age of CAIs, much more obvious reasons for this discrepancy could be an overestimation of (¹⁸²Hf/¹⁸⁰Hf)₀, an underestimation of the uncertainty of the (¹⁸²Hf/¹⁸⁰Hf)₀, or heterogeneity in (¹⁸²Hf/¹⁸⁰Hf)₀ that is subequal to the uncertainty on the initial (¹⁸²Hf/¹⁸⁰Hf)₀ ratio of CAIs. Considering the fact that the (¹⁸²Hf/¹⁸⁰Hf)₀ reported by Kruijer et al. (2014) requires secondary corrections for nucleosynthetic effects on W isotopes in CAIs and the relatively large uncertainties involved in the ¹⁸²Hf–¹⁸²W system itself, either of these alternatives appear viable. Consequently, the assumption of homogeneous (¹⁸²Hf/¹⁸⁰Hf)₀ and the lack of consistency with the assumption-free, significantly more precise U-corrected Pb–Pb chronology using published Pb–Pb ages for CAIs makes the ¹⁸²Hf–¹⁸²W chronometer a poor choice compared to the Pb–Pb system to test (²⁶Al/²⁷Al)₀ homogeneity in the protoplanetary disk. In addition, the typical ¹⁸²Hf–¹⁸²W age uncertainty of ≥0.6 Ma cannot resolve (²⁶Al/²⁷Al)₀ variability in the early solar system similar to almost two half-lives of ²⁶Al decay or a potential difference by a factor of four in the (²⁶Al/²⁷Al)₀, which is similar to the (²⁶Al/²⁷Al)₀ heterogeneity documented here. Given these serious concerns, we submit that age comparisons based on the ¹⁸²Hf–¹⁸²W system (Kleine et al., 2012; Kruijer et al., 2014) are not robust and, therefore, cannot be used to rigorously test the assumption of (²⁶Al/²⁷Al)₀ homogeneity.

5.5. µ²⁶Mg* evidence for prolonged magmatic residence preserved in D’Orbigny and Sah99555

During the lifetime of ²⁶Al, magmatic processes such as partial melting or fractional crystallization will alter the bulk ²⁷Al/²⁴Mg of a magma body and, thus, alter the rate of ²⁶Mg ingrowth in the residue and melt. As Mg is more compatible in olivine and pyroxene than Al, basaltic partial melts will have an increased ²⁷Al/²⁴Mg relative to the bulk parent body. As such, production of basaltic melts during the lifespan of ²⁶Al will results in the accumulation of ²⁶Mg* in these relative to the average bulk parent body. The magnitude of the accumulated ²⁶Mg* is dependent on the relative increase of the ²⁷Al/²⁴Mg ratio of the magma compared to the average bulk parent body, the ²⁶Al/²⁷Al at the time of magma formation and the lifetime of the magma until final crystallization.

The signature of such magmatic evolution may be preserved in the positive ${\mathrm{\text{μ}}}^{26}{\text{Mg}}_{\text{0}}^{\ast }$ of D’Orbigny and Sah99555. The indistinguishable ${\mathrm{\text{μ}}}^{26}{\text{Mg}}_{\text{0}}^{\ast }$ combined with similar ²⁶Al/²⁷Al and indistinguishable Pb–Pb ages of Sah99555 and D’Orbigny indicates a very similar magmatic history of these two angrites. Although the Mg isotope composition of the APB precursor is not known, the elevated µ²⁶Mg*₀ of Sah99555 and D’Orbigny suggest a prolonged residence time of their parental magma with elevated ²⁷Al/²⁴Mg ratios prior to eruption, which may include a prolonged period of melt migration (Moskovitz and Gaidos, 2011). Alternatively, these positive µ²⁶Mg*₀ could also be explained if the bulk APB had a Mg isotope composition that is slightly enriched in ²⁶Mg compared to Earth or if D’Orbigny and Sah99555 are products of re-melting of an older magma. The former is unlikely due to the fact that NWA1670 and young angrites have a negative (or lower) bulk µ²⁶Mg* (Table 1; Larsen et al., 2011), whereas the latter cannot be strictly ruled out but requires an even earlier (albeit potentially shorter) magmatic evolution of a precursor magma.

Assuming a composition of the APB of ${\mathrm{\text{μ}}}^{\text{26}}{\text{MG}}_{\text{0}}^{\ast }=-15.9$, ²⁷Al/²⁴Mg = 0.09781 ± 0.00029 and (²⁶Al/²⁷Al)₀ of ${1.33}_{-0.18}^{+0.21}\times {10}^{-5}$ (Larsen et al., 2011; Paton et al., 2012) at the time of CAI formation and a Al/Mg of the final magma given by the bulk Al/Mg of D’Orbigny and Sah99555, respectively, one can calculate that their precursor magma must pre-date the crystallization of both angrites by ~1 Ma to generate their µ²⁶Mg* isochron intercepts. Considering that the Al/Mg acts as a multiplier of the ²⁶Al-to-²⁶Mg ingrowth and the bulk ²⁷Al/²⁴Mg of D’Orbigny and Sah99555 likely represent a maximum ²⁷Al/²⁴Mg of the parental magmas, the estimated magma residence time is most likely a lower limit. Importantly, the required residence time of the magma rules out that the parental magmas to D’Orbigny and Sah99555 are the result of impact melting just prior their crystallization, but are internally derived magmas that cooled rapidly after extrusion.

5.6. Thermodynamical constraints

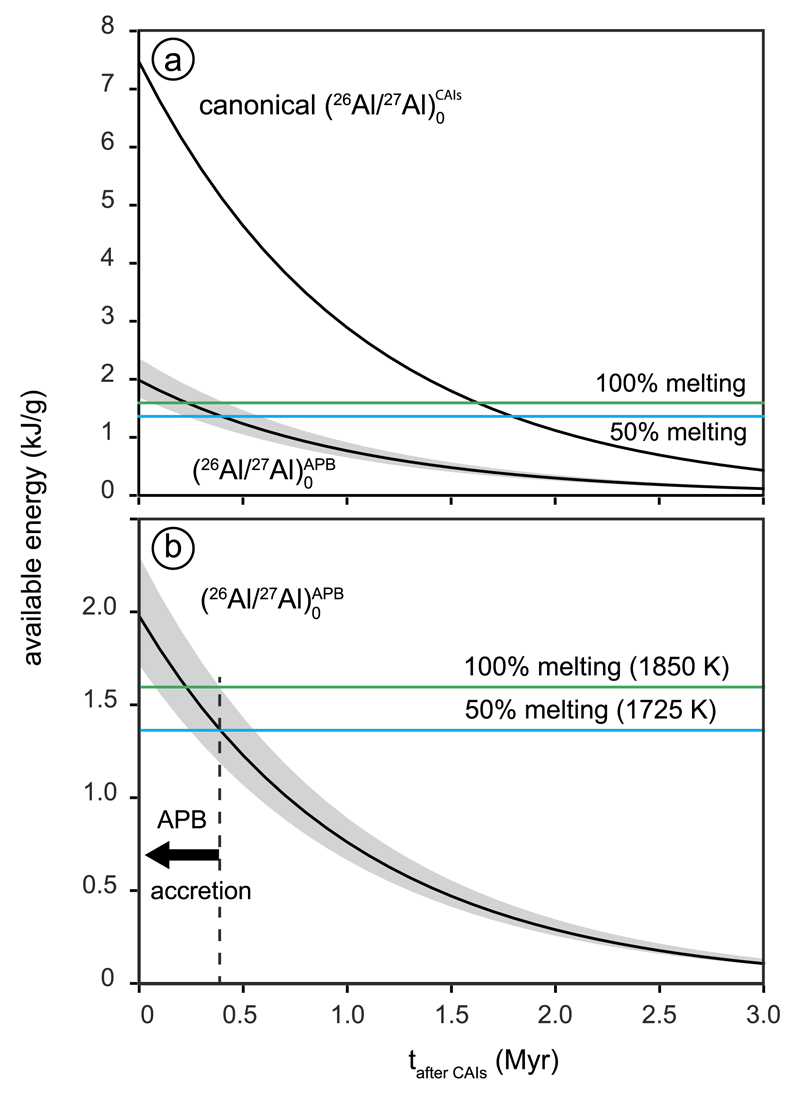
The observation that angrites are products of magmatic differentiation and, in some cases, may have evolved over a prolonged time span is a key constraint on the timing of APB accretion. Approximately 1.6 kJ of energy is required to completely melt 1 g of dry primitive solar dust from ambient temperatures (Hevey and Sanders, 2006). This represents about a fifth of the energy present as ²⁶Al in dust with a solar ²⁶Al/²⁴Mg and canonical (²⁶Al/²⁷Al)₀ at the time of CAI formation. This amount of energy would allow for extensive melting in any planetesimals with a radius larger than a few tens of kilometers if it accreted as late as 2–3 ²⁶Al half-lives or ~1.7 Ma after CAI formation (Fig. 6a). However, our newly-determined (²⁶Al/²⁷Al)₀ for the APB shortens this time frame substantially. Assuming APB accretion from de-volatized CI-type dust with an Al abundance of 1.34%, the revised (²⁶Al/²⁷Al)₀ equates to 2.0 ± 0.3 kJ/g of energy stored in the dust. This requires accretion within 0.25 ± 0.15 Ma of CAIs to allow for large scale melting driven solely by ²⁶Al decay (Fig. 6b). Variability in the Al abundance in parent bodies also affects their total ²⁶Al budget. However, non-carbonaceous chondrites show little variability in their Al concentration (Kallemeyn and Wasson, 1981; Kallemeyn et al., 1989) and, thus, Al variability in differentiated planetesimal is expected to have only a minor effect on their internal energy budgets. Thus, energetic considerations based on ²⁶Al limit the accretion of the APB to the first 0.25 ± 0.15 Ma of CAI formation, an estimate consistent with predictions of early coremantle differentiation from ¹⁸²Hf–¹⁸²W systematics (Kleine et al., 2012).

Fig. 6.

The available energy resulting from ²⁶Al decay is shown in (a) versus time for a canonical (²⁶Al/²⁷Al)₀ and that the (²⁶Al/²⁷Al)₀ for the APB, while the same figure is shown expanded in (b) indicating also the allowable time window of APB accretion. APB accretion is assumed to occur while sufficient energy is available for large scale melting to satisfy the differentiated character of angrites. The required energy for melting and respective temperatures are from Hevey and Sanders (2006).

Most differentiated meteorites as well as Earth and Mars have isotopic signatures (e.g., ⁵⁴Cr, ⁵⁰Ti, ^43,46,48Ca) similar to angrites but significantly different than CAIs (Trinquier et al., 2007, 2009; Schiller et al., 2015) and it appears that (²⁶Al/²⁷Al)₀ broadly correlates with these nucleosynthetic signatures (Larsen et al., 2011). As such, planetesimal and planets forming in the same region and from similar material as the APB, identifiable by their nucleosynthetic signatures (e.g., ⁵⁴Cr), are inferred to have formed with comparable levels of (²⁶Al/²⁷Al)₀. Having a subcanonical (²⁶Al/²⁷Al)₀ in the planetesimal and terrestrial planet forming region comparable to that of the APB supports the predicted rapid accretion of planetesimals (e.g., Johansen et al., 2007) and removes the inevitability of late cooling of planetesimals larger than a few tens of kilometer.

However, if planetesimal formation is a rapid and efficient process, it is unlikely that undifferentiated meteorites, chondrites, are the products of a late generation of forming planetesimals, but rather supports the idea that they are products of late accretionary layers forming an unmelted outer crust of older, internally differentiated planetesimals (Elkins-Tanton et al., 2011). Notably, the lower (²⁶Al/²⁷Al)₀ for the planetesimal and terrestrial planet forming region significantly reduces the planetesimal accretion time scales to allow for an outer, undifferentiated crust to occur on internally molten, differentiated bodies to a few hundred thousand years.

6. Conclusions

²⁶Al–²⁶Mg systematics based on mineral separates from the volcanic angrites D’Orbigny, Sah99555 and NWA1670 indicate ²⁶Al/²⁷Al ratio at the time of their crystallization of (3.98 ± 0.15) × 10⁻⁷, (3.64 ± 0.18) × 10⁻⁷ and (5.92 ± 0.59) × 10⁻⁷, respectively. The higher ²⁶Al/²⁷Al ratio in NWA1670 translates into an older crystallization age of ${0.50}_{-0.29}^{+0.27}$ Ma compared to D’Orbigny/Sah99555. This age difference is in agreement with the newly-determined U-corrected Pb–Pb age of 4564.39 ± 0.24 Ma for NWA1670, which is 0.88 ± 0.28 Ma older than the published U-corrected Pb–Pb ages for D’Orbigny/Sah99555, making it the oldest dated angrite. Utilizing the internally consistent Pb–Pb and ²⁶Al–²⁶Mg systematics to calculate the (²⁶Al/²⁷Al)₀ of their precursor, the APB, at the time of CAI formation yields an (²⁶Al/²⁷Al)₀ of ${1.33}_{-0.18}^{+0.21}\times {10}^{-5}$. This value is in perfect agreement with an independent estimate by Larsen et al. (2011) and supports the suggestion that the bulk of the µ²⁶Mg* variability observed in solar system reservoirs reflects initial ²⁶Al variability rather than Mg isotope heterogeneity. This interpretation is further strengthened by the homogeneous distribution of silicon isotopes in bulk solar system reservoirs, which suggest limited Mg heterogeneity as Mg and Si are synthesized by similar nucleosynthetic processes (Pringle et al., 2013). Considering the similar nucleosynthetic signature of angrites and other inner solar system reservoirs, the (²⁶Al/²⁷Al)₀ of APB is likely representative of material accreting in the terrestrial planet forming region. On the other hand, the nucleosynthetic enrichments in CAIs might indicate that the gas from which they condensed was also characterized by a significantly enhanced (²⁶Al/²⁷Al)₀ compared to the bulk solar system. This enhancement can be understood in the concept of an unmixing of a physically well mixed reservoir that contains isotopically homogenized old dust that has been processed in the interstellar medium and a relatively young component of freshly synthesized stellar dust (Schiller et al., 2015). Due to the short half-life of ²⁶Al it will solely be associated with the young dust component and consequently the resulting ²⁶Al variability in different solar system reservoirs will be orders of magnitude larger than for other, stable, neutron-rich isotopes that show correlated variability such as ⁵⁰Ti, ⁵⁴Cr and ⁴⁸Ca (Trinquier et al., 2007, 2009), whose abundance in the young dust represents only a minute contribution to their overall solar system budget. A prediction of this model is that the initial solar system abundance of ⁶⁰Fe should also be variable and enhanced in CAIs relative to the inner disk solids providing that this nuclide also resides in the new dust component (Holst et al., 2013). However, this requires the direct determination of the initial ⁶⁰Fe/⁵⁶Fe value of a CAI, which is currently lacking.

The low (²⁶Al/²⁷Al)₀ of the APB and the differentiated nature of angrites requires planetesimal accretion to have taken place within 0.25 ± 0.15 Ma of the age of CAIs. Such early accretion is in perfect agreement with numerical simulations that require early and efficient accretion of larger bodies within the protoplanetary disk (Weidenschilling, 2000; Johansen et al., 2007; Cuzzi et al., 2008). Considering the short time window allowed for planetesimal melting with a (²⁶Al/²⁷Al)₀ akin to the APB, material accreting within only a few hundred thousand years onto already internally differentiated planetesimal is unlikely to undergo further differentiation, allowing for preservation of chondritic material as an outer shell. Further, heating driven by ²⁶Al decay becomes insignificant ~2 Ma after CAI formation, allowing for early cooling and fractional crystallization of magmas on these planetesimals such as demonstrated by the ancient Pb–Pb age of NWA1670.