Cellular biomechanics of central nervous system injury

INTRODUCTION

Biomechanics is considered one of the core disciplines to understand principles of physiology and pathophysiology in the human. Decades of biomechanics research revealed many primary principles regulating growth, tissue formation, organism morphogenesis, and tissue regeneration. Not surprisingly, biomechanics is one of the core sciences used to understand how dynamic loading in the central nervous system (CNS) causes injury. This key transition from physiology to pathophysiology is especially important, as early pathophysiologic changes to the CNS can strongly influence cellular decisions to survive, reintegrate, and repair the injured CNS. This long-term response, initiated when forces are transferred to the cellular/molecular scale at the time of injury, is a key contributor in the outcome of head-injured and spinal cord-injured patients.

Compared to nearly every other application of biomechanics and human body, biomechanics of traumatic loading has three unique components. First, the mechanical event is nearly always considered as a single event, rather than a series of cyclical loadings that are applied to organ/tissue/cellular preparations. In other areas of biomechanics, cyclical loading of tissue/cellular components is critical in defining the homeostatic response and the adaptation of this response during disease. Examples include the periodic distension of the vascular wall during the cardiovascular cycle, or the frequent loading and unloading of orthopedic soft tissues during gait. In contrast, the brain and spinal cord are considered “mechanically protected” organs and do not have a clear constant level of mechanical stimulation. Second, traumatic loading is probably the fastest event studied in biomechanics, especially considering the very recent work on blast injury biomechanics. The very brief nature of the event – the acceleration/deceleration event in a blunt impact event is typically delivered in less than 50 milliseconds, while the mechanical loading in a blast event lasts only a few milliseconds – present enormous technical challenges because traditional biomechanical tools to study the forces, displacements, deformations, and stresses in tissue/cellular structures are often lacking. Third, the functional and physical wiring of the brain and spinal cord remain largely a mystery and are the focus of many efforts across the neuroscience and neurologic sciences. Any biomechanically based study of events at the cellular and molecular scale must consider the physical wiring of the structure and our ability to mechanically interrogate individual components of these circuits to lay the groundwork for a more integrative view of how the brain and spinal cord will respond to the mechanical forces occurring during injury.

Given this unique set of circumstances, it is not surprising that there has been a large increase in the use and development of simplified laboratory models to deconstruct some of these experimental complexities. Foremost among these challenges is developing new simplified laboratory models that develop repeatable, reproducible, and informative models of the clinical condition. The animate models of traumatic brain injury developed over the past several decades are explained in Chapter 8 of this volume. Certainly, as we know more about how mechanical loading affects the function of the brain and spinal cord at many length scales – at the organ level, at the tissue level, and at the cellular/molecular level – we will become much more facile with developing models that accurately reproduce these loadings in vitro.

The conversion of the mechanical input to the resulting biochemical cascades – termed mechanotransmission – triggers the evolving injury patterns in the brain and spinal cord after traumatic injury. The concept of mechanotransmission has transformed biomechanics from a study of structure-property relationships into a more integrated structure-function-property triad across lengths scales in the CNS. At the most reductionist level, this means that we are now beginning to explore how some cells respond directly to the mechanical load with a set of biochemical signatures, even now extending these into genomic signatures. Not surprisingly, as the mechanical load is adjusted to either individual cells or clusters of cells, one may find that some cell types respond while others do not.

In this chapter, we review the state of the field in understanding how the cellular components of the CNS respond to the biomechanical loading that occurs at the moment of traumatic injury. It is not meant to be an exhaustive review of all work generated to date. Several other recent reviews can be collected and reviewed in their own right for this purpose (LaPlaca et al., 2007; Kumaria and Tolias, 2008; Chen et al., 2009; Morrison et al., 2011). Moreover, another chapter in this volume (Ch. 6) provides a more detailed description of the macroscopic biomechanics associated with mild TBI. In this chapter, we intend to provide a broad overview of the basic principles that led to our current understanding of how cells in the nervous system respond to mechanical force. We also discuss some of the emerging frontiers for this discipline as we move from understanding macroscopic events to integrating the micro- and meso-scale responses of neural circuits. The collective goal of these efforts is to bring a more mechanistic understanding of how mechanotransmission in the CNS can shape the neurobehavioral response of the organism after traumatic CNS injury, potentially highlighting new therapeutic opportunities to improve outcome after CNS injury.

MECHANICAL LOADING IN THE BRAIN: HOW IT OCCURS, AND WHAT INFLUENCES IT

It is widely believed that the most important event dictating immediate post-traumatic consequences is the mechanical loading itself. The nature and underlying conceptual framework for traumatic loading in the nervous system is reviewed in detail in other portions of this textbook. However, a brief review of these principles will help provide context for some of the concepts described in later portions of this chapter.

Several decades of work has shown us three general loading characteristics are critical in determining the post-traumatic neurologic sequelae for traumatic brain injury. First, the direction of the acceleration loading will strongly influence the brain regions affected during an injury and, thus, the resulting neurologic sequelae. Second, the duration of these acceleration events can vary across a broad spectrum and contribute to the location of structures damaged within the brain after loading. In general, extremely brief accelerations are more likely to affect cortical regions, while longer duration accelerations can cause damage to cortical and deeper brain structures. Third, and perhaps most importantly, the type of acceleration – rotational and/or translational – clearly contributes to the mechanics of loading within the intracerebral tissues.

The use of computer models to predict the bulk head motions in either blunt or protected head impact conditions has progressed considerably, and is now a common approach to estimate how different “real world” impact and blast scenarios will cause head linear/rotational accelerations and deformation of the intracranial contents, providing guidelines on how these conditions can be recreated in experimental models (recent studies include Ho and Kleiven, 2009; Nyein et al., 2010; Zhu et al., 2010; Chatelin et al., 2011; Lamy et al., 2011; Coats et al., 2012; Kimpara and Iwamoto, 2012; Panzer et al., 2012; Sundaramurthy et al., 2012; Cloots et al., 2013; reviews can be found in King et al., 1995; Voo et al., 1996; Cohen et al., 2007). These computational approaches provide the design corridor for in vitro models of CNS trauma that, in turn, will provide critical biological response information at the millimeter and micron scale. In the next section, we review the salient features of the traumatic mechanical loading that need to be reproduced in any in vitro representation of CNS trauma.

RECREATING TRAUMA IN VITRO

Certainly, in vitro models attempt to maintain some level of biomechanical fidelity to the “real world” event. However, since the real world event can be so unique and complex, these models often reduce the complex input into a series of well prescribed, controllable, and repeatable inputs at the cellular and tissue scale. Ideally, these models have the ability to independently control both the stress and strain applied to the in vitro preparation. In studying the cellular biomechanics of injury, an investigator often faces a series of very pragmatic decisions which we outline below.

The first decision is the choice of the culture preparation. Early work in this field used cell lines, primarily because of the difficulty in successfully culturing primary neurons and astrocytes. Techniques for isolating a large number of diverse primary cell types are now available, and these methods are sufficiently detailed to provide long-term cultures of nearly pure cellular populations (e.g., primary hippocampal neurons; primary cortical astrocytes),or a mixture of neural and glial cell types found within the living brain. One may choose a more complex preparation by isolating living slices of brain tissue, thereby preserving the architecture of the brain at the time of slice removal. These preparations – termed organotypic cultures – represent the most fidelity to the living, in vivo environment. However, even these preparations lack an intact vasculature. To date, though, no investigator has provided an in vitro model that contains an active vascular system to mimic the potential interaction of vascular perfusion on outcome of tissue injured in vitro.

Once an in vitro platform is selected, the second decision is defining the mechanical input. From a practical standpoint, the selection of the input condition is influenced partly by the desired output measurement. Acute signatures of the traumatic loading event often include some measure of ion imbalance; examples include fluorescence-based ion indicators to indirectly assess ion flux immediately after injury, release of neurotransmitters, or changes in the membrane potential (Tavalin et al., 1995; LaPlaca and Thibault, 1998; Geddes et al., 2003; Lusardi et al., 2004a). For these measures, testing systems often mount directly to a microscope (Cargill and Thibault, 1996; McKinney et al., 1996; Morrison et al., 1998; Smith et al., 1999; Lusardi et al., 2004b). This requirement often means that the mechanical input is relatively simple, reliable and may have less fidelity to the complex loading that occurs within the in vivo brain. However, the advantages of drawing relationships between these acute events and longer term assays of cellular and organelle viability make these simple models the most widely used. To date, the most versatile of the in vitro models provide the flexibility to challenge the in vitro preparations with more “real world” mechanical inputs (Morrison et al., 2006). However, the practical constraints of exploring this parametric space – there are literally millions of combinations that one could explore – limit the utility of these more flexible architectures.

An additional feature to consider is how much of the cellular population will be injured, and the mechanical uniformity of this injury. During the in vivo loading scenario, it is clear that some brain regions are deformed far more than neighboring regions. Nearly every investigation has examined how populations of cells respond to mechanical stimulation. Many studies apply the injury to the entire population of cells, while a smaller number apply the injury only to a subregion of the culture (see reviews: Kumaria and Tolias, 2008; Chen et al., 2009; Morrison et al., 2011). These in vitro preparations, since they contain several different cell types, are useful surrogates of the integrated response approximating small regions in the brain. Recently, the ability to mechanically stimulate single individual cells has appeared, opening up new opportunities to explore how single cells can influence the behavior of small neuronal ensembles. Therefore, a closer simulation of the in vivo environment can be targeted by studying how spatially defined patterns of mechanical stimulation can affect the broad behavior of cellular networks.

WHAT ARE THE CRITICAL CELLULAR INPUTS FOR RECREATING THE MECHANICAL SPECTRUM?

In the biomechanics literature, there is considerable discussion on the types of deformation that occur in vivo. The high bulk modulus and low shear modulus of brain tissue makes the brain much more likely to experience shear deformation during impact mechanical loading. In addition to these shear strains, high pressures can be produced throughout the parenchyma during impact. Although the effects of pressure are not often studied, this loading scales easily to in vitro systems and it does not depend on the orientation of the cells within the tissue. There is often a misconception, though, when understanding how shear deformation can be represented with in vitro systems. A primary challenge is that it is not easy to predict how macroscopic shear will translate to deformations of cellular structures within the complex CNS tissue.

A few examples will help illustrate the complexity of the macro to micro transformation. In a simple shear deformation of a cube, consider a cellular process such as a dendrite or axon that is oriented along the diagonal of this cube. If the dendrite/axon was oriented along the diagonal that lengthens during the shear deformation, then the dendrite/axon would experience a tensile strain during shear. In comparison, if the dendrite/axon was oriented along the opposite diagonal, the dendrite or axon is compressed along its axis. Finally, if the dendrite/axons aligns along one edge of the cube, it would experience no deformation during this shear. These modes of subcellular deformation are shown in Figure 7.1.

Fig. 7.1.

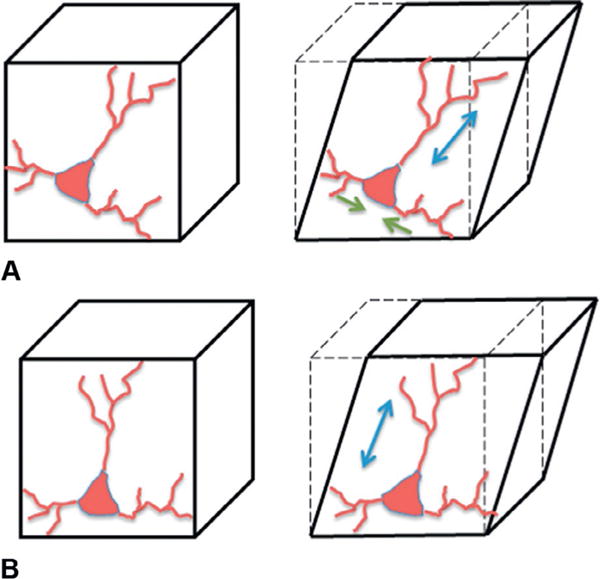
Transformation of the macroscopic mechanical input (shear) to the cellular components of CNS tissue. (A) If a neuron has dendritic elements aligned along the major axis of elongation (blue), these structures will elongate in shear. Other structures (green arrows) will compress. (B) If a neuron has structures oriented along the bottom edge of the element, they will not deform. If structures align along the side of the element, these structures will elongate.

The correct prediction of how bulk or macroscopic mechanical loading causes deformation of cellular structures is an enormously significant problem in CNS mechanics. Indeed, a key knowledge gap now being filled is building structurally accurate models of CNS tissue that can be used to understand how an applied mechanical loading at the macroscopic scale – i.e., a sample of excised tissue, or a small volume of brain tissue in vivo – results in the deformation of cellular and sub-cellular structures (Bain et al., 2003; Meaney, 2003; Cohen et al., 2008; Karami et al., 2009; Pan et al., 2011). Even simple models of composite material behavior show that cellular/subcellular deformation is very heterogeneous, depends critically on the mechanical coupling among cellular populations, and may vary substantially across different brain regions subject to the same macroscopic loading because of differences in tissue microstructure. Experimental platforms are also showing how subcellular structures are deformed uniquely in response to the applied mechanical loading (LaPlaca et al., 2005).

The broad emphasis on understanding the effect of cellular deformations on CNS tissue has generated several technologies to study this phenomenon in vitro. For example, fluid flowing quickly past a monolayer of cells will induce a deformation, and this deformation can be severe enough to activate glutamate receptors and, at higher levels, cause an immediate increase in plasma membrane permeability and changes in network dynamics (LaPlaca and Thibault, 1997; Prado et al., 2005). Alternatively, cells in two-dimensional culture can be moved rapidly and then stopped very suddenly (Murphy and Horrocks, 1993). In this model, the different densities of subcellular organelles and nuclear components will cause intracellular deformation. In both of these techniques, it is difficult to establish the in vivo biomechanical fidelity of these models. Rather, the techniques are useful to study input/output responses in ways not possible with other methods.

The most widely used approach to deform cellular populations is culturing either dissociated cell monolayers or organotypic slice cultures onto flexible substrates, and deforming the substrates to indirectly deform the culture/slice sample (Cargill and Thibault, 1996; McKinney et al., 1996; Morrison et al., 1998; Smith et al., 1999; Lusardi et al., 2004b). Two general types of deformation are studied most commonly: a method where the substrate is deformed in two perpendicular directions simultaneously (termed “biaxial”), and a second method where the substrate is deformed primarily along one axis (“uniaxial”). The uniaxial configuration is most readily comparable to shear deformation in vivo, as the principal directions of stretch are identical to a pure shear deformation. The biaxial method is more complex, because it involves a mixture of planar expansion and pure shear. Some differences appear when comparing these techniques directly: the uniaxial model of deformation requires higher peak deformations to cause immediate alterations in plasmalemma permeability, while biaxial deformation offers a symmetric deformation field that can apply a more homogeneous input to dissociated or organotypic culture networks (Geddes and Cargill, 2001; Geddes-Klein et al., 2006).

Applying deformations to cells in vitro is a relatively straightforward technique, and has been the study of several past laboratories. However, the application of a defined stress, both the direction and magnitude of the stress, is a much more difficult technical challenge. One must first define the stress level that is appropriate. Next, one should consider how to focally apply these controlled stresses without affecting neighboring cells. Third, the varied material properties of the cellular and subcellular constituents means the loading regime will differ uniquely among individual cells, as well as across regions within individual cells. It is perhaps for this reason that models to accurately apply stresses at the micron and submicron scale are lacking still in the literature.

ARE THERE IMPORTANT MECHANOSENSORS?

Once an investigator decides on the mechanical inputs that they would like to recreate in vitro, a next question is whether cells of the CNS possess any unique mechanosensors for these inputs. We use the term mechanosensors to describe receptors and channels in the CNS that respond directly to the mechanical stimulation. In many perspectives, we envision these receptors to express a dose-response to an applied mechanical force similar to how a dose-response curve will describe the property of a ligand-receptor binding interaction. Similarly, we envision this dose-response curve to change when the rate of applied force is adjusted. This property of rate sensitivity is partly analogous to the kinetics of receptor binding, where the traditional receptor response is influenced the timing of receptor activation in response to periodic, temporally varying impulses of agonist. Models for these “mechanokinetics” of receptor activation have been proposed for some ligand-receptor interactions (Bell, 1978), but none have been applied to channels and receptors expressed in neurons and glia.

Much like developing a set of criteria to define the agonist binding affinity and, alternatively, the pharmacologic inhibition efficacy for receptors expressed on any cell type, we view these mechanical sensors as having a similar force and rate activation curve. In addition, mechanosensors may respond differently to competing mechanical inputs – for example, some receptors may be sensitive only to the pressure applied, while other receptors will be sensitive to a certain type of deformation (i.e., tension), and still yet others may change their sensitivity to deformation based on the applied input pressure. Despite their potential importance, we know very little about the mechanoactivation profiles for most receptors expressed in the brain. Evidence shows that the NMDA receptor can respond or “sense” mechanical forces that are applied during traumatic injury (Paoletti and Ascher, 1994; Zhang et al., 1996; Kloda et al., 2007). One important physiologic consequence of this mechanical loading is the loss of magnesium block in the NMDA receptor, a feature that normally limits the ion flux across the receptor at normal resting membrane potentials. Moreover, the agonist affinity of the NMDAR is altered after mechanical stretch. The molecular tethering of the receptor to the cytoskeleton is key for this mechanosensing property, and there is a potentially intriguing control of this mechanosensitivity within a single serine residue of the NR2B subunit of the receptor (Singh et al., 2012). Controlling mechanosensitivity through the NR2B subunit is potentially significant because of the association between NR1/NR2B receptor subtypes and neuronal demise after mechanical injury (DeRidder et al., 2006).

A second mechanosensor is the α-subunit of the voltage-gated sodium channel (Wolf et al., 2001; Iwata et al., 2004; von Reyn et al., 2009). The initial mechanosensing response of the sodium channel elicits changes in calcium homeostasis and subsequent proteolytic cleavage of this channel, contributing to an impairment of the networks in the acute phase following injury. Remarkably, the selected activation of this pathway in the axonal compartment can lead to a relatively rapid proteolysis of the channel along domains controlling inactivation of the sodium channel after depolarization. Moreover, this channel proteolysis is influenced by the stability of the microtubule network in the axon, suggesting that the mechanical structure of the axon confers some level of protection against degenerative changes in the axon. This rapid change (<15 minutes) in channel integrity is contrasted with a later stage degradation phase (4–6 hours) that precedes any evidence of neuronal death (von Reyn et al., 2012). However, it is not yet clear if this later phase of degradation can be blocked to rescue neurons in the network, or if this later degradation is part of a larger irreversible sequence of events leading to the removal of the neuron from the injured network.

Other receptors are known to either activate rapidly and/or change their properties after mechanical injury, yet it is not clear if these are activated directly by the mechanical force. For example, AMPA receptors demonstrate a loss in the desensitization property of the receptor (Goforth et al., 1999). The molecular reason(s) for this loss in desensitization of the receptor are not completely known, but it may owe more to the upstream mechanoactivation of the NMDAR than the molecular structure of the receptor and any postsynaptic tethering to the cytoskeleton (Goforth et al., 2004). Thus, there is no direct evidence that AMPA receptors are direct mechanosensors. In addition, changes in GABA receptor currents appear after injury, but they also depend directly on NMDAR activation (Kao et al., 2004). Similarly, in glial cells it is known that a focal mechanical stimulation can elicit broad intercellular waves that are mediated by release of ATP and glutamate (Charles et al., 1991). Although the mechanism(s) responsible for intercellular wave transmission is well known, specific mechanoactivated receptors in astrocytes are not well described for this phenomenon.

Once activated, these mechanosensors can have broad implications in the function of neuroglial circuitry. A good description of many of these molecular-based mechanisms of injury appears in Chapter 5 of this volume. Despite this broad impact, though, only scant evidence appears for mechanosensing properties of other glutamate receptors and channels in neurons. Knowledge of sensors that are associated with specific neuronal subtypes is also lacking, and could be important for adjusting the balance between inhibitory and excitatory circuitry in the brain after trauma. Similarly, there is very little knowledge available on mechanosensors expressed in glial cell types, the activation of which may be particularly important for shaping networks in ensuing hours to days after the initial injury.

DO THESE MECHANOSENSORS CAUSE FUNCTIONAL CHANGES?

The ability of mechanosensors to affect function within neuroglial circuits can occur at the level of individual cells within the network, multicellular clusters, or even more broadly throughout the brain. Several past studies now show a clear mechanical tolerance for neuronal survival, and these estimates span both dissociated and organotypic slice culture preparations (Geddes and Cargill, 2001; Cater et al., 2006; Elkin and Morrison, 2007). There is also new evidence showing that the spontaneous electrical activity of the network can be impaired with mechanical stimulation (LaPlaca et al., 2005; Patel et al., 2012), yet there is no consensus yet on how these thresholds for activity impairments correspond to the thresholds for neuronal death. Several changes in the neural circuit state can now be traced back to mechanoactivation of the NMDA receptor, including a slow, neuronal depolarization that can lead to altered network excitability, the loss of AMPAR desensitization that can also change excitability, and the insertion of new glutamate receptor subtypes that appear over several hours (Bell et al., 2007; Spaethling et al., 2008; Chen et al., 2009; Goforth et al., 2011). At this time, though, little data exists on how the function of individual neurons within the network contributes to the overall network dynamics of the circuit.

It is also likely that the neural circuit evolves its function over time, yet there is little information on how these changes occur. The advent of new methods in network science provide measures of functional connectivity in neuronal ensembles, and these have been applied to study changes in the wiring of networks that occur during development (Soriano et al., 2008). With new optogenetic tools available to either activate or inhibit individual neurons within a population (Bernstein et al., 2012), there is a significant new opportunity to extend the information from this connectivity analysis and draw functional relationships to identify neurons driving rhythms in networks, or shaping the complex patterns that emerge in these networks. The recovery of patterns after in vitro injury does occur, and the persisting patterns are certainly influenced by neuronal loss (Patel et al., 2012). One emerging and potentially important property is how these injured networks retain their ability to synchronize their activity across ensembles following injury, and how the ability to synchronize these networks are critically dependent on the wiring architecture of these injured circuits.

CAN WE USE IN SILICO SIMULATIONS AS A COMPLEMENT TO IN VITRO SYSTEMS?

Over the past decade, there have been a series of studies to evaluate precisely the most fundamental building block of neurotransmission: the release of a glutamate vesicle from the presynaptic terminal and its subsequent binding to glutamate receptors on the postsynaptic surface. In a series of studies, it is now clear that the binding of glutamate to its cognate receptors is a stochastic phenomenon at the single synaptic scale and is influenced heavily by several parameters: the amount of glutamate released, the frequency at which this glutamate is released, and the relative number and diversity of glutamate receptors appearing on the postsynaptic face (Franks et al., 2002, 2003; Santucci and Raghavachari, 2008; Singh et al., 2011). Many, if not all, of these features are likely altered in the traumatically injured brain. Already, there is evidence that the loss of the magnesium block can provide an important functional consequence for the NMDA receptor in the traumatically injured network (DeRidder et al., 2006). Moreover, the appearance of new receptor populations occurs within hours of traumatic injury and may change the timing of signals in neural circuits. In parallel with these postsynaptic models of neurotransmission, relatively recent models of the presynaptic and postsynaptic signaling networks show how changes at the pre-/postsynaptic terminal can also contribute to the precise timing and duration of signaling network activation in the postsynaptic zone (Keller et al., 2008; Santucci and Raghavachari, 2008; Volman et al., 2009; Nadkarni et al., 2010; Faas et al., 2011).

With the integration of multiple synaptic inputs onto individual neurons, the next level of analysis involves how these individual dendritic inputs, regardless of their noisy behavior, will influence the activation signal propagation throughout neuronal networks. A large number of simple models of different neuronal types can be developed and solved analytically, using approximations of the neural connectivity that appears in vivo. These computational models can become increasingly complex by incorporating features that one measures at the individual dendritic and synaptic scale, building models of networks with high anatomic fidelity. The use of these more elegant models to understand post-traumatic signaling, though, is not available in the literature. One recent analysis using a simple, reductionist model from our group revealed that a key feature of injury is the loss in ability to synchronize signals among neuronal ensembles (Volpicelli-Daley et al., 2011). This ability to synchronize was critically dependent on the activation of calpain, a common calcium-activated neutral protease capable of cleaving the α-subunit of the sodium channel to disrupt the timing of networks (Patel et al., 2012). Expanding the use of these simple models, adapted to include the stochastic properties of receptor activation at the single spine, represents great promise for the future to ultimately decode how single cell scale changes can influence the behavior of broader neuronal networks.

This combination of in silico and in vitro data provides an added perspective to predict how changes over time will impact the transmission of information through the brain circuits. These changes will likely occur in at least three phases – an immediate phase, a network remodeling phase, and a final, augmented plasticity phase (Table 7.1). The immediate phase includes the primary changes to the receptors, channels, and neuronal function (i.e., ability to fire an action potential) and the resulting impact on generalized network activity. With the changes that we know already in some of the mechanosensitive channels and receptors, the immediate phase is generally characterized as a period of less synchronized, and lower, activity across a network. Thus, the immediate phase may be described as a period in which information transmission though the network is somewhat limited. The network remodeling phase is mediated by the consequences of the immediate phase, and can be characterized by the permanent removal of neurons from the network, the adjustment of synaptic strength among remaining neurons, an increase or decrease of connectivity within the network, and the appearance of different synaptic receptor subtypes. The impact on information transfer through the network is dependent upon the degree of each of these changes. For example, the removal of neurons in the network could lead to the more reliable transmission of information through the network because the neurons removed may have acted as an undesirable source of desynchronization in the network. Alternatively, the increase in connectivity of the remodeled network may lead to the transmission of more patterned inputs through the network, thereby increasing information flow in the network. The augmented plasticity phase would include the period where the remodeled network is now responding to sensory and cognitive inputs, with the expectation that these inputs would serve to further adjust the connection strengths among neurons remaining in the network. There is abundant evidence showing deficits in synaptic plasticity for weeks to months after the initial injury (Chs 5, 21, and 42). However, there is little knowledge in the exact state of plasticity for individual neurons in the network within the damaged circuit. A key consideration in this third phase is determining whether the remodeled network retains its original “dynamic range” – i.e., whether the circuit undergoes the same reshaping of its connections that occurred prior to injury. These changes should also not be viewed only in the areas of initial injury, as the brain has a well-established and complex series of interconnections among brain regions. Therefore, it is very possible that small changes to networks within specific regions of the brain can have very widespread consequences to initially undamaged regions of the brain.

Table 7.1.

Three phases of network changes

	Immediate phase	Remodeling phase	Augmented plasticity phase
Factor	Mechanoactivated receptors	Neuronal loss	Synaptic strength adjustment – new range?
	Altered neurotransmitter release	Synaptic strength changes	Circuit synchronization?
	Neuronal connectivity changes Altered pattern input	Excitatory/inhibitory balance	Adjustment to sensory/cognitive input
Timing	~seconds to hours	~days to weeks(?)	~weeks to months(?)
Information flow	Less synchronized	Variable, depending on effect	Alteration in dynamic range of circuits is key
	Reduced information		Interconnection of regions; more widespread effects

Three phases of network changes that can affect the information flow in brain circuitry after traumatic brain injury. The immediate phase reflects changes to the circuit information flow caused by immediate changes to receptors, channels, synaptic release, and neuronal integrity. The remodeling phase is when the circuits adjust both their network structure and synaptic strength as aberrant receptors and channels are replaced. The augmented plasticity phase describes how the remodeled circuitry responds to cognitive and/or sensory input, thereby establishing the dynamic range of the remodeled circuit.

LOOKING INTOTHEFUTURE: MULTISCALEQUESTIONSANDTHEKEY FORTHEFUTURE

Using in vitro models of neurotrauma to examine the multiscale behavior of function in the brain after trauma eventually lead us back to the beginning. Namely, can we use these models understand how the neurobehavior of an animal or human is altered after trauma? This multiscale question is certainly not unique to neurotrauma; this is one of the penultimate questions broadly across neuroscience. We are moving towards this level of understanding in the traumatically injured brain with a newfound appreciation of how events at the synaptic, dendritic, single neuron, and the neuronal/glial ensemble levels integrate to affect this overlying behavior. Moreover, we may soon realize that the coordinated activation of ensembles across major pathways in the brain may provide one of the keys in recovery after injury. As we look forward to the future, it is likely that our information at the in vitro scale will feed into important insights into how the consequences of traumatic mechanical loading condition will help synchronize the activity of neural circuits in vivo, and also how the cellular/molecular mechanotransmission process will influence the capacity of these circuits to relay information across this frequency spectrum. In concert with understanding how these circuits are synchronized to optimize information transfer, we will be in a much better position to understand how behaviors can change after traumatic injury, as well as understanding effective therapies to improve outcome after these injuries.