Mapping the Orientation of White Matter Fiber Bundles: A Comparative Study of Diffusion Tensor Imaging, Diffusional Kurtosis Imaging, and Diffusion Spectrum Imaging

GR Glenn; L-W Kuo; Y-P Chao; C-Y Lee; JA Helpern; JH Jensen

doi:10.3174/ajnr.A4714

. 2016 Jul;37(7):1216–1222. doi: 10.3174/ajnr.A4714

Mapping the Orientation of White Matter Fiber Bundles: A Comparative Study of Diffusion Tensor Imaging, Diffusional Kurtosis Imaging, and Diffusion Spectrum Imaging

GR Glenn ^a,^b,^c, L-W Kuo ^d,^✉, Y-P Chao ^e, C-Y Lee ^a,^c, JA Helpern ^a,^b,^c, JH Jensen ^a,^c,^✉

PMCID: PMC4946981 NIHMSID: NIHMS750778 PMID: 26939628

The authors evaluated fiber bundle orientations from DTI and diffusional kurtosis compared with diffusion spectrum imaging as a criterion standard to assess the performance of each technique. DTI, diffusional kurtosis imaging, and diffusion spectrum imaging datasets were acquired during 2 independent sessions in 3 volunteers. While orientation estimates from all 3 techniques had comparable angular reproducibility, diffusional kurtosis imaging decreased angular error throughout the white matter compared with DTI. Diffusion spectrum imaging and diffusional kurtosis imaging enabled the detection of crossing-fiber bundles. They conclude that fiber bundle orientation estimates from diffusional kurtosis imaging have less systematic error than those from DTI.

Abstract

BACKGROUND AND PURPOSE:

White matter fiber tractography relies on fiber bundle orientation estimates from diffusion MR imaging. However, clinically feasible techniques such as DTI and diffusional kurtosis imaging use assumptions, which may introduce error into in vivo orientation estimates. In this study, fiber bundle orientations from DTI and diffusional kurtosis imaging are compared with diffusion spectrum imaging as a criterion standard to assess the performance of each technique.

MATERIALS AND METHODS:

For each subject, full DTI, diffusional kurtosis imaging, and diffusion spectrum imaging datasets were acquired during 2 independent sessions, and fiber bundle orientations were estimated by using the specific theoretic assumptions of each technique. Angular variability and angular error measures were assessed by comparing the orientation estimates. Tractography generated with each of the 3 reconstructions was also examined and contrasted.

RESULTS:

Orientation estimates from all 3 techniques had comparable angular reproducibility, but diffusional kurtosis imaging decreased angular error throughout the white matter compared with DTI. Diffusion spectrum imaging and diffusional kurtosis imaging enabled the detection of crossing-fiber bundles, which had pronounced effects on tractography relative to DTI. Diffusion spectrum imaging had the highest sensitivity for detecting crossing fibers; however, the diffusion spectrum imaging and diffusional kurtosis imaging tracts were qualitatively similar.

CONCLUSIONS:

Fiber bundle orientation estimates from diffusional kurtosis imaging have less systematic error than those from DTI, which can noticeably affect tractography. Moreover, tractography obtained with diffusional kurtosis imaging is qualitatively comparable with that of diffusion spectrum imaging. Because diffusional kurtosis imaging has a shorter typical scan time than diffusion spectrum imaging, diffusional kurtosis imaging is potentially more suitable for a variety of clinical and research applications.

White matter fiber tractography is used clinically to visualize functionally important WM tracts and aid neurosurgeons during presurgical planning.^1,2 Tractography is also an important research tool for studying structural connectivity because tractography is currently the only noninvasive technique for in vivo mapping of anatomic neural connections in the human brain.³ However, tractography relies on fiber bundle orientation estimates derived from particular DWI techniques, which may have inherent methodologic limitations, potentially resulting in clinically misleading information.^4,5

Of the several proposed DWI methods for estimating the orientation of WM fiber bundles, a common approach uses the diffusion orientation distribution function (dODF), which quantifies the relative degree of diffusion mobility along a given direction from physical properties of water diffusion.^6–9 Diffusion of water is assumed to be least restricted parallel to the orientation of WM fiber bundles, resulting in local maxima of the dODF. The dODF may be defined by

where n is a normalized orientation vector, r is a radial displacement magnitude, P(rn, t) is the diffusion displacement probability distribution function (dPDF) for diffusion displacement rn over a diffusion time t, α is a constant radial weighting power, and Z is a normalization constant.

Several distinct techniques exist for reconstructing the dODF from DWI data, which differ in their theoretic assumptions and optimal experimental implementation. These include DTI, which assumes that the diffusion of water can be completely described by Gaussian (normal) diffusion^10–12; diffusional kurtosis imaging (DKI), which extends the DTI model to account for non-Gaussian diffusion effects^13–16; Q-ball imaging, which applies the Funk transform to DWI data from high-angular-resolution diffusion-weighted imaging^6,7; and diffusion spectrum imaging (DSI).^8,9

In contrast to other methods, DSI quantifies the dODF by using an exact (in the narrow gradient pulse limit) Fourier transform relationship between the DWI signal and the dPDF. To accomplish this requires a dense sampling of q-space with relatively high maximum b-values. Thus, DSI effectively characterizes complex intravoxel microarchitecture without the need for intricate tissue models or ancillary approximations, though it tends to have more demanding data-acquisition requirements than alternative methods. Due to its rigorous mathematic formulation and comprehensive description of intravoxel diffusion dynamics, DSI may be considered a reference standard for validating other dODF techniques for in vivo experiments.¹⁷ Nonetheless, even the exact dODF may not give the precise orientation of WM fiber bundles, reflecting the complex and subtle relationship between diffusion and microstructure.

The DTI dODF has the same information as the diffusion tensor ellipsoid, and the global maximum of the DTI dODF gives the direction identical to the principal eigenvector of the diffusion tensor.^7,16 Although efficient in terms of image-acquisition time, DTI is not capable of directly resolving intravoxel fiber crossings,^10–12 which can lead to increased errors in orientation estimates from regions with complex tissue architecture.^5,18

The motivation for considering the kurtosis dODF is 2-fold. First, there have been a considerable number of prior studies using DKI to investigate neuropathology, including stroke,^19–23 Alzheimer disease,^24–28 cancer,^29–31 and numerous others.³² Therefore, a tractography method that is compatible with DKI can be of value. Second, DKI shares some of the practical advantages of DTI that make it particularly attractive for clinical settings, such as small maximum b-values and protocol options with relatively short scan times.^14,21,33 For example, in clinical settings, a whole-brain DKI dataset with good image quality may be acquired in approximately 7 minutes,²¹ and respectable whole-brain DKI tractography has been demonstrated with acquisition times as short as 5.3 minutes.³³ Moreover, DKI inherently provides measures of the diffusion and kurtosis tensors as well as all the corresponding tensor-derived quantitative measures (eg, mean diffusivity and mean kurtosis), which are of interest for characterizing tissue microstructure.³⁴

In this study, dODFs derived from DSI, DKI, and DTI by using in vivo human measurements are directly compared, particularly with regard to their estimates of fiber bundle orientation. The errors intrinsic to the dODF orientations from DTI and DKI are calculated using the DSI orientations as benchmarks. In addition, the intrasubject variabilities of dODF orientation estimates are calculated across independent sessions for all 3 methods. A primary goal of this study is to assess the degree to which the DKI dODF approximates the DSI dODF and improves the DTI dODF. Tractography results are also compared qualitatively for the 3 dODF reconstruction techniques.

Materials and Methods

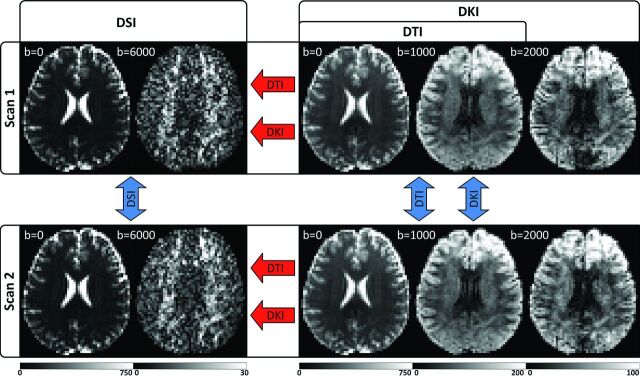
The study was approved by the institutional review board at the National Health Research Institutes (Taiwan), and informed consent was obtained from all participants before enrollment in the study. Experiments were performed on 3 healthy volunteers on a 3T MR imaging system (Tim Trio; Siemens, Erlangen, Germany); and for each participant, 2 full DSI and DKI datasets were obtained, with the DTI dataset being taken as a subset of the DKI dataset. Angular variabilities in the orientation estimates were quantified as the absolute, voxelwise angular difference for each reconstruction between repeat scans, and for DKI and DTI, angular errors were quantified as the absolute, voxelwise angular differences from the corresponding DSI scan. For each subject, T1-weighted magnetization-prepared rapid acquisition of gradient echo images were also acquired for anatomic reference. The experimental design is illustrated in Fig 1, and the angular variability and error measures are illustrated in Fig 2. A detailed description of our image-acquisition protocol and image-analysis steps is given in the On-line Appendix.

Fig 1. — Experimental design illustrated with sample images from a single subject. For each subject, 2 separate scans are obtained, which include independent DSI and DKI acquisitions optimized for the respective reconstructions. The DTI reconstruction is calculated from a subset of the DKI acquisition and is fully independent of the DSI scan but not the DKI scan. Angular variability is calculated between scans (*blue arrows*), and angular error is calculated for DKI and DTI in reference to the corresponding DSI scan (*red arrows*). Units for the b-value are second/square millimeter, and the signal intensity ranges for each image are given by the corresponding color bar (in arbitrary units). DWIs from the highest b-value for each acquisition are given to illustrate the range of diffusion-weighting applied.

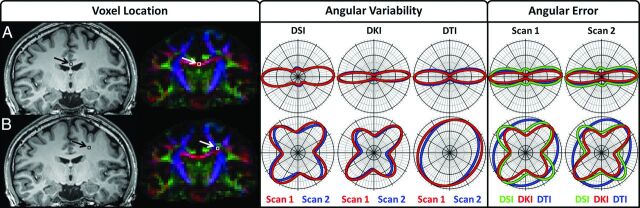
Fig 2. — Polar 2D dODF cross-section plots illustrate angular variability and angular error measures. Row A illustrates dODFs taken from a single voxel in the corpus callosum where 1 predominant fiber bundle orientation is expected, and row B illustrates dODFs taken from a single voxel where multiple fiber bundles are expected to occur between cortical projections from the corpus callosum and the ascending and descending fiber bundles in the corona radiata. The “Voxel Location” tab illustrates the location of the voxels overlaid on the corresponding section from the MPRAGE image and the FA color map for anatomic reference; the “Angular Variability” tab illustrates angular variability measures, which are taken between scans for each reconstruction; and the “Angular Error” tab illustrates the angular error measures, which are taken relative to the corresponding DSI dODF for each scan. The section plane for the polar plots is rotated to contain the first and second largest orientations of the DSI dODF, because DSI is used as a reference. For visualization, each dODF is scaled to a maximum value of 1.

The angular error estimates, as quantified in this study, include contributions from both random and systematic errors. Random error may result from thermal noise, incomplete q-space sampling distributions, and physiologic effects such as pulsatile flow and bulk subject motion, while systematic errors arise from the approximations inherent to the DTI and DKI dODFs. Although it is difficult to rigorously isolate the random and systematic components of the angular error, a rough index of systematic error is given by the difference between the angular error and angular variability for a given reconstruction because the angular variability is a measure of random error. We used this heuristic approach as a practical means of comparing systematic errors for the DTI and DKI dODFs.

Fiber-tracking results were assessed qualitatively by looking at the reconstructed tracts in specific regions with complex fiber bundle geometries and over the whole brain (On-line Video). To aid the qualitative assessment, a color-encoding scheme was used, in which each individual tract was colored by its overall displacement from the starting point to the ending point of the tract, with red indicating a left-right displacement, blue indicating an inferior-superior displacement, and green indicating an anteroposterior displacement. Similar colors represent similar overall trajectories, whereas differing colors indicate tracts following different overall trajectories.

Results

Summary statistics for each subject and ROI are given in the On-line Table. DTI has the lowest angular variability in both the inclusive and conservative WM ROIs as well as the single fiber bundle ROI, while DSI has the lowest angular variability in both the 2 and ≥3 crossing-fibers ROIs. Conversely, DKI has the highest angular variability in all ROIs, with the exception of the ≥3 crossing-fibers ROI, where DTI has the highest angular variability. However, the angular variabilities for all reconstructions are comparable within each of the ROIs, differing by, at most, 2.1° in the single fiber bundle ROI (On-line Table, “Single-fiber ROI”). On the other hand, DKI consistently improves angular error compared with DTI in all ROIs. Moreover, the DKI systematic errors are all substantially smaller than the DTI systematic errors, consistent with a higher degree of accuracy for the DKI dODFs.

For the ROIs tested, dODF performance measures are influenced by the fractional anisotropy (FA) value, with the smaller angular variability and angular error for regions with higher FA. Conversely, the occurrence of crossing fibers increased angular variability and angular error in dODF-derived orientation estimates. However, the accuracy of the DKI dODF is less affected than the DTI-derived dODF in crossing-fiber regions. Properties of the dODF reconstructions are explored further in On-line Figs 1 and 2.

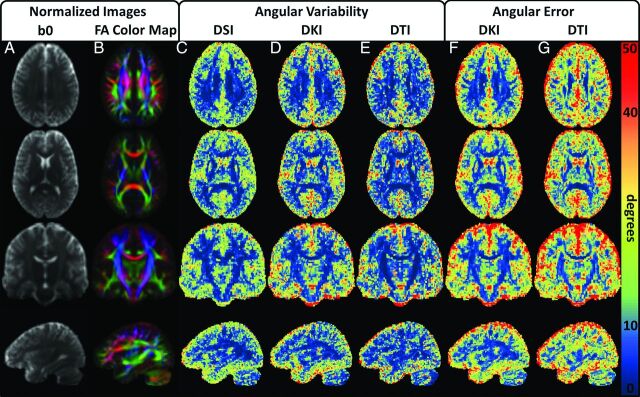
Mean normalized parameter maps are given in Fig 3 to illustrate the group-wise performance of the dODF reconstructions. All 3 of the reconstruction techniques demonstrate similar angular variability throughout the WM, but DTI shows improvement in angular variability in regions with high FA (eg, note the corpus callosum and corticospinal tracts in rows 2 and 3, which show high FA contrast). The DKI angular error estimates are relatively consistent throughout the WM, whereas the DTI angular error estimates show distinct WM regions where the angular error deteriorates. When one compares these regions with the normalized FA color maps, it is likely that these regions represent voxels with more complex fiber bundle geometries owing to influences from multiple fiber bundle orientations within a voxel (eg, note the intersecting regions between the corpus callosum and corona radiata, which are apparent in rows 1 and 3).

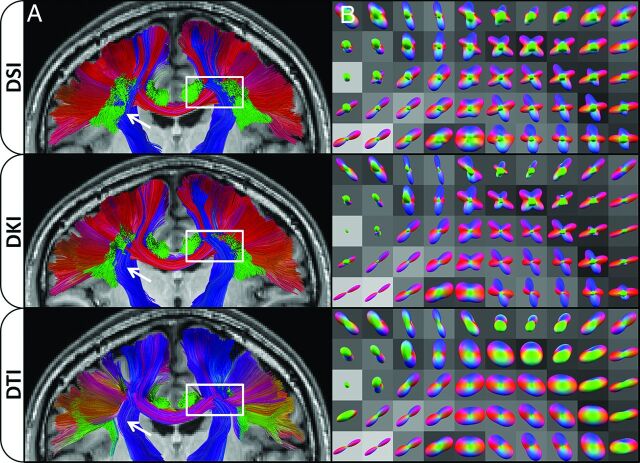
Exemplary tractography results are given in Fig 4. A cross-sectional view of the fiber tracts has been selected to highlight the effects of interactions that occur in regions with complex tissue architecture. This particular section contains noticeable influences from the corpus callosum, which is mainly along the left-right orientation, and the corticospinal tracts (among others), which are mainly along the inferosuperior orientation. This section also shows effects from the superior longitudinal fasciculus and the cingulum bundle, which are mainly oriented along the anteroposterior direction. In the tractography panels for DSI and DKI, the corpus callosum can be seen crossing through the corona radiata as it passes from one hemisphere to the next. However, these trajectories are obscured by the DTI dODFs, with the corpus callosum tracts either being prematurely truncated or swept into the corticospinal tracts. It can also be seen from these images that the DSI dODF approximation is more sensitive at detecting multiple peaks (note the extent of the superior longitudinal fasciculus fibers indicated by the white arrows and the predominance of green lobes in the respective 3D dODF renderings). DTI is not capable of directly resolving crossing fibers; this scenario markedly affects tractography through complex regions such as those shown in Fig 4. Full-brain tractography results are compared in the On-line Video.

Discussion

In this study, we have used DSI as a reference standard to assess the angular error in orientation estimates from DKI and DTI and quantified the intrasubject angular variability of WM fiber bundle orientation estimates from DTI, DKI, and DSI. We have focused primarily on comparing the estimated fiber orientations that the dODFs identify, because these are the inputs needed for constructing tractography. However, these are only approximations for the true fiber orientations, which are, in general, not known, even if the dODF is measured exactly.

A primary motivation for this study is to help assess the potential of DKI tractography for data obtained with clinical MR imaging scanners. By estimating both the diffusion and kurtosis tensors, DKI more fully characterizes diffusion in complex neural tissue than conventional DTI; this feature, theoretically, should improve tractography. Our experimental results support this proposition because both the angular and systematic errors are markedly lower for DKI (On-line Table and Fig 3). Moreover, tractography generated with DKI is qualitatively much more similar to that obtained with DSI than is DTI tractography (Fig 4 and On-line Video). Given that DKI, in comparison with DTI, also provides several additional diffusion measures (eg, mean kurtosis) that are sensitive to neuropathologic changes associated with a variety of diseases,^19–32 there are potentially compelling advantages to DKI vis-à-vis DTI.

Overall, the angular variability estimates are comparable for all 3 reconstructions in all ROIs, differing by, at most, 2.1° in the single-fiber ROI (On-line Table, “Single-fiber ROI”). However, DKI tends to have increased angular variability compared with both DTI and DSI in all ROIs except for the ROI with ≥3 crossing-fiber bundles. Although the precise origin of the increased angular variability of DKI is unclear, this could result from a trade-off between estimation error from incomplete q-space sampling distributions and subject motion. DTI, for example, requires the shortest acquisition time, which may result in the lowest contributions of subject motion to angular variability. DSI, on the other hand, uses a large number of diffusion-encoding vectors to characterize diffusion dynamics, which could have lower angular variability from the dODF reconstruction but an increased likelihood of subject motion. DKI is also known to be sensitive to reconstruction artifacts resulting from Gibbs ringing^35,36 and noise bias,³⁷ though these are also expected to affect DSI.

To acquire high-quality, whole-brain DSI and DKI datasets for evaluation, we optimized our protocol for high SNR rather than a short acquisition time. Consequently, the total scan time used in this study was relatively long compared with typical clinical protocols. To improve scan efficiency, one or more of several different strategies may be used. For example, there has been a successful effort to reduce the q-space sampling burden of DSI, including decreasing the q-space sampling density by sampling fewer points,^38,39 sampling only one-half of the q-space by assuming symmetry of the q-space data,^40,41 or sampling only a quarter of the q-space by using compressed sensing.⁴² The acquisition time can also be reduced with simultaneous multisection EPI,^43–47 while stronger diffusion-encoding gradients can be used to reduce the TE to improve the SNR.⁴⁷ Although DSI may show the largest improvement in acquisition time, these considerations are generally applicable to DKI as well. There may be an increase in the angular error and variability if SNR is reduced, as may occur with accelerated acquisition schemes,⁴⁵ or if sparse q-space sampling schemes are used.⁴⁰ Nevertheless, DKI may be presumed to have shorter typical scan times than DSI because DKI requires only the second and fourth cumulants of the dPDF,⁴⁸ while DSI uses the full dPDF with the inherent greater data-acquisition burden. A valuable follow-up study would be to quantitatively investigate the differences in the orientation estimates by using protocols with acquisition times that are more suitable for routine clinical scanning.

A variety of alternative techniques can resolve the orientations of crossing-fiber bundles for tractography. Compared with several other dODF reconstructions, the kurtosis dODF has been shown to have a comparable or improved resolving power⁴⁹; however, numeric simulations indicate that the kurtosis dODF may sometimes have a greater angular error than other dODFs for larger fiber-crossing angles.^16,49 Fiber bundle orientations can also be estimated from directional diffusional kurtosis estimates provided by DKI without estimating the dODF directly,⁵⁰ or the white matter fiber bundles may be modeled mathematically and used to estimate a model-dependent fiber orientation distribution function—for example, by using fiber ball imaging⁵¹ or constrained spherical deconvolution.^52,53 Because none of these techniques are directly analogous to the dODF, they were not included in the present study. In addition, model-based approaches make detailed assumptions about the relationship between WM and the DWI signal that have yet to be fully validated. Nevertheless, the directional diffusional kurtosis approach has been shown to increase fiber detection through the corpus callosum,⁵⁰ and constrained spherical deconvolution can be highly sensitive to crossing fibers.^18,54

To summarize, in this study we acquired, from 3 healthy volunteers, a unique dataset with 6 full DSI and DKI acquisitions, to quantify dODF performance measures from DTI, DKI, and DSI. In general, DKI substantially decreases the error of dODF orientation estimates relative to DTI. Moreover, DKI enables the detection of crossing fibers, which results in pronounced improvement relative to DTI for tractography throughout regions with complex fiber bundle geometries.^15,16,33,36 Indeed, our results indicate that the tractography obtained with DKI is qualitatively quite comparable with that for DSI, despite DKI sampling a much smaller portion of q-space. With enhanced tractography relative to DTI and shorter typical scan times than DSI, DKI-based tractography is potentially advantageous, particularly in clinical settings where time considerations are crucial. However, further study will be needed to more fully investigate the comparative utility of DKI-based tractography.

Conclusions

The higher order information provided by the kurtosis tensor enables DKI to directly resolve crossing fibers and improves the accuracy of DKI relative to DTI for tractography. Both DKI and DTI are capable of mapping the single predominant fiber bundle orientation, but the angular error of DTI deteriorates in regions with complex fiber orientations due to its theoretic limitation under the assumption of Gaussian diffusion. DSI, DKI, and DTI all have comparable angular variabilities; however, DKI has decreased angular error in the dODF fiber orientation estimates relative to DTI. Unlike DTI, DKI is thus able to generate white matter fiber tractography comparable with that of DSI, and due to its shorter typical scan time than DSI, DKI is potentially more suitable for a variety of clinical and research applications.

Supplementary Material

Tractography_Comparison.mov

Download video file^{(51.9MB, mov)}

15-00938.pdf

15-00938.pdf^{(1.7MB, pdf)}

ABBREVIATIONS:

b0: image in DWI dataset with no diffusion weighting
DKI: diffusional kurtosis imaging
dPDF: diffusion displacement probability distribution function
dODF: diffusion orientation distribution function
DSI: diffusion spectrum imaging
FA: fractional anisotropy

Footnotes

Disclosures: Li-Wei Kuo—RELATED: Grant: NHRI-BN-104-PP-06*; MOST-103-2221-E-400-001.* Joseph A. Helpern—RELATED: Grant: Litwin Foundation*; UNRELATED: Grants/Grants Pending: National Institutes of Health.* Jens H. Jensen—RELATED: Grant: Litwin Foundation,* Comments: I have partial salary support from this grant; UNRELATED: Patents (planned, pending or issued) and Royalties: US Patent 8811706, Comments: I am a coinventor on a patent that covers one of the imaging methods investigated in this article (DKI). The patent is owned by my former employer (New York University), but I could be entitled to royalties at some point. To date, I have not received royalties from this patent. *Money paid to the institution.

This work was supported by the National Institutes of Health research grant T32GM008716 (to P. Halushka), the Litwin Foundation (to J.A.H.), and grants NHRI-BN-104-PP-06 and MOST-103-2221-E-400-001 (to L.-W.K).

REFERENCES

1. Romano A, D'Andrea G, Minniti G, et al. Pre-surgical planning and MR-tractography utility in brain tumour resection. Eur Radiol 2009;19:2798–808 10.1007/s00330-009-1483-6 [DOI] [PubMed] [Google Scholar]
2. Mormina E, Longo M, Arrigo A, et al. MRI tractography of corticospinal tract and arcuate fasciculus in high-grade gliomas performed by constrained spherical deconvolution: qualitative and quantitative analysis. AJNR Am J Neuroradiol 2015;36:1853–58 10.3174/ajnr.A4368 [DOI] [PMC free article] [PubMed] [Google Scholar]
3. Lazar M. Mapping brain anatomical connectivity using white matter tractography. NMR Biomed 2010;23:821–35 10.1002/nbm.1579 [DOI] [PMC free article] [PubMed] [Google Scholar]
4. Tournier JD, Mori S, Leemans A. Diffusion tensor imaging and beyond. Magn Reson Med 2011;65:1532–56 10.1002/mrm.22924 [DOI] [PMC free article] [PubMed] [Google Scholar]
5. Farquharson S, Tournier JD, Calamante F, et al. White matter fiber tractography: why we need to move beyond DTI. J Neurosurg 2013;118:1367–77 10.3171/2013.2.JNS121294 [DOI] [PubMed] [Google Scholar]
6. Tuch DS, Reese TG, Wiegell MR, et al. Diffusion MRI of complex neural architecture. Neuron 2003;40:885–95 10.1016/S0896-6273(03)00758-X [DOI] [PubMed] [Google Scholar]
7. Tuch DS. Q-ball imaging. Magn Reson Med 2004;52:1358–72 10.1002/mrm.20279 [DOI] [PubMed] [Google Scholar]
8. Wedeen VJ, Hagmann P, Tseng WY, et al. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med 2005;54:1377–86 10.1002/mrm.20642 [DOI] [PubMed] [Google Scholar]
9. Wedeen VJ, Wang RP, Schmahmann JD, et al. Diffusion spectrum magnetic resonance imaging (DSI) tractography of crossing fibers. Neuroimage 2008;41:1267–77 10.1016/j.neuroimage.2008.03.036 [DOI] [PubMed] [Google Scholar]
10. Basser PJ, Mattiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson 1994;103:247–54 10.1006/jmrb.1994.1037 [DOI] [PubMed] [Google Scholar]
11. Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor-MRI. J Magn Reson B 1996;111:209–19 10.1006/jmrb.1996.0086 [DOI] [PubMed] [Google Scholar]
12. Basser PJ, Pajevic S, Pierpaoli C, et al. In vivo fiber tractography using DT-MRI data. Magn Reson Med 2000;44:625–32 [DOI] [PubMed] [Google Scholar]
13. Jensen JH, Helpern JA, Ramani A, et al. Diffusional kurtosis imaging: the quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med 2005;53:1432–40 10.1002/mrm.20508 [DOI] [PubMed] [Google Scholar]
14. Jensen JH, Helpern JA. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed. 2010;23:698–710 10.1002/nbm.1518 [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Lazar M, Jensen JH, Xuan L, et al. Estimation of the orientation distribution function from diffusional kurtosis imaging. Magn Reson Med 2008;60:774–81 10.1002/mrm.21725 [DOI] [PMC free article] [PubMed] [Google Scholar]
16. Jensen JH, Helpern JA, Tabesh A. Leading non-Gaussian corrections for diffusion orientation distribution function. NMR Biomed 2014;27:202–11 10.1002/nbm.3053 [DOI] [PMC free article] [PubMed] [Google Scholar]
17. Hagmann P, Jonasson L, Maeder P, et al. Understanding diffusion MR imaging techniques: from scalar diffusion-weighted imaging to diffusion tensor imaging and beyond. Radiographics 2006;26(suppl 1):S205–23 10.1148/rg.26si065510 [DOI] [PubMed] [Google Scholar]
18. Jeurissen B, Leemans A, Tournier JD, et al. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging. Hum Brain Mapp 2013;34:2747–66 10.1002/hbm.22099 [DOI] [PMC free article] [PubMed] [Google Scholar]
19. Jensen JH, Falangola MF, Hu C, et al. Preliminary observations of increased diffusional kurtosis in human brain following recent cerebral infarction. NMR Biomed 2011;24:452–57 10.1002/nbm.1610 [DOI] [PMC free article] [PubMed] [Google Scholar]
20. Fung SH, Roccatagliata L, Gonzalez RG, et al. MR diffusion imaging in ischemic stroke. Neuroimaging Clin N Am 2011;21:345–77, xi 10.1016/j.nic.2011.03.001 [DOI] [PubMed] [Google Scholar]
21. Hui ES, Fieremans E, Jensen JH, et al. Stroke assessment with diffusional kurtosis imaging. Stroke 2012;43:2968–73 10.1161/STROKEAHA.112.657742 [DOI] [PMC free article] [PubMed] [Google Scholar]
22. Grinberg F, Ciobanu L, Farrher E, et al. Diffusion kurtosis imaging and log-normal distribution function imaging enhance the visualisation of lesions in animal stroke models. NMR Biomed 2012;25:1295–304 10.1002/nbm.2802 [DOI] [PubMed] [Google Scholar]
23. Umesh Rudrapatna S, Wieloch T, Beirup K, et al. Can diffusion kurtosis imaging improve the sensitivity and specificity of detecting microstructural alterations in brain tissue chronically after experimental stroke? Comparisons with diffusion tensor imaging and histology. Neuroimage 2014;97:363–73 10.1016/j.neuroimage.2014.04.013 [DOI] [PubMed] [Google Scholar]
24. Falangola MF, Jensen JH, Tabesh A, et al. Non-Gaussian diffusion MRI assessment of brain microstructure in mild cognitive impairment and Alzheimer's disease. Magn Reson Imaging 2013;31:840–46 10.1016/j.mri.2013.02.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Benitez A, Fieremans E, Jensen JH, et al. White matter tract integrity metrics reflect the vulnerability of late-myelinating tracts in Alzheimer's disease. Neuroimage Clin 2013;9:64–71 10.1016/j.nicl.2013.11.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
26. Fieremans E, Benitez A, Jensen JH, et al. Novel white matter tract integrity metrics sensitive to Alzheimer disease progression. AJNR Am J Neuroradiol 2013;34:2105–12 10.3174/ajnr.A3553 [DOI] [PMC free article] [PubMed] [Google Scholar]
27. Vanhoutte G, Pereson S, Delgado Y, Palacios R, et al. Diffusion kurtosis imaging to detect amyloidosis in an APP/PS1 mouse model for Alzheimer's disease. Magn Reson Med 2013;69:1115–21 10.1002/mrm.24680 [DOI] [PubMed] [Google Scholar]
28. Gong NJ, Wong CS, Chan CC, et al. Correlations between microstructural alterations and severity of cognitive deficiency in Alzheimer's disease and mild cognitive impairment: a diffusional kurtosis imaging study. Magn Reson Imaging 2013;31:688–94 10.1016/j.mri.2012.10.027 [DOI] [PubMed] [Google Scholar]
29. Raab P, Hattingen E, Franz K, et al. Cerebral gliomas: diffusional kurtosis imaging analysis of microstructural differences. Radiology 2010;254:876–81 10.1148/radiol.09090819 [DOI] [PubMed] [Google Scholar]
30. Van Cauter S, Veraart J, Sijbers J, et al. Gliomas: diffusion kurtosis MR imaging in grading. Radiology 2012;263:492–501 10.1148/radiol.12110927 [DOI] [PubMed] [Google Scholar]
31. Rosenkrantz AB, Sigmund EE, Johnson G, et al. Prostate cancer: feasibility and preliminary experience of a diffusional kurtosis model for detection and assessment of aggressiveness of peripheral zone cancer. Radiology 2012;264:126–35 10.1148/radiol.12112290 [DOI] [PubMed] [Google Scholar]
32. Steven AJ, Zhuo J, Melhem ER. Diffusion kurtosis imaging: an emerging technique for evaluating the microstructural environment of the brain. AJR Am J Roentgenol 2014;202:W26–33 10.2214/AJR.13.11365 [DOI] [PubMed] [Google Scholar]
33. Glenn GR, Helpern JA, Tabesh A, et al. Optimization of white matter fiber tractography with diffusional kurtosis imaging. NMR Biomed 2015;28:1245–56 10.1002/nbm.3374 [DOI] [PubMed] [Google Scholar]
34. Tabesh A, Jensen JH, Ardekani BA, et al. Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magn Reson Med 2011;65:823–36 10.1002/mrm.22655 [DOI] [PMC free article] [PubMed] [Google Scholar]
35. Veraart J, Fieremans E, Jelescu IO, et al. Gibbs ringing in diffusion MRI. Magn Reson Med 2015. August 10. [Epub ahead of print] 10.1002/mrm.25866 [DOI] [PMC free article] [PubMed] [Google Scholar]
36. Perrone D, Aelterman J, Pižurica A, et al. The effect of Gibbs ringing artifacts on measures derived from diffusion MRI. Neuroimage 2015;120:441–55 10.1016/j.neuroimage.2015.06.068 [DOI] [PubMed] [Google Scholar]
37. Glenn GR, Tabesh A, Jensen JH. A simple noise correction scheme for diffusional kurtosis imaging. Magn Reson Imaging 2015;33:124–33 10.1016/j.mri.2014.08.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
38. Kuo LW, Chen JH, Wedeen VJ, et al. Optimization of diffusion spectrum imaging and q-ball imaging on clinical MRI system. Neuroimage 2008;41:7–18 10.1016/j.neuroimage.2008.02.016 [DOI] [PubMed] [Google Scholar]
39. Tefera GB, Zhou Y, Juneja V, et al. Evaluation of fiber tracking from subsampled q-space data in diffusion spectrum imaging. Magn Reson Imaging 2013;31:820–26 10.1016/j.mri.2013.02.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
40. Kuo LW, Chiang WY, Yeh FC, et al. Diffusion spectrum MRI using body-centered-cubic and half-sphere sampling schemes. J Neurosci Methods 2013;212:143–55 10.1016/j.jneumeth.2012.09.028 [DOI] [PubMed] [Google Scholar]
41. Yeh CH, Cho KH, Lin HC, et al. Reduced encoding diffusion spectrum imaging implemented with a bi-Gaussian model. IEEE Trans Med Imaging 2008;27:1415–24 10.1109/TMI.2008.922189 [DOI] [PubMed] [Google Scholar]
42. Menzel MI, Tan ET, Khare K, et al. Accelerated diffusion spectrum imaging in the human brain using compressed sensing. Magn Reson Med 2011;66:1226–33 10.1002/mrm.23064 [DOI] [PubMed] [Google Scholar]
43. Feinberg DA, Setsompop K. Ultra-fast MRI of the human brain with simultaneous multi-slice imaging. J Magn Reson 2013;229:90–100 10.1016/j.jmr.2013.02.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
44. Larkman DJ, Hajnal JV, Herlihy AH, et al. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J Magn Reson Imaging 2001;13:313–17 [DOI] [PubMed] [Google Scholar]
45. Setsompop K, Cohen-Adad J, Gagoski BA, et al. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. Neuroimage 2012;63:569–80 10.1016/j.neuroimage.2012.06.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
46. Reese TG, Benner T, Wang R, et al. Halving imaging time of whole brain diffusion spectrum imaging and diffusion tractography using simultaneous image refocusing in EPI. J Magn Reson Imaging 2009;29:517–22 10.1002/jmri.21497 [DOI] [PMC free article] [PubMed] [Google Scholar]
47. Setsompop K, Kimmlingen R, Eberlein E, et al. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. Neuroimage 2013;80:220–33 10.1016/j.neuroimage.2013.05.078 [DOI] [PMC free article] [PubMed] [Google Scholar]
48. Kiselev VG. The cumulant expansion: an overarching mathematical framework for understanding diffusion NMR. In: Jones DK, ed. Diffusion MRI: Theory, Methods and Applications. New York: Oxford University Press; 2011:152–68 [Google Scholar]
49. Jensen JH, Helpern JA. Resolving power for the diffusion orientation distribution function. Magn Reson Med 2015. October 7. [Epub ahead of print] 10.1002/mrm.25900 [DOI] [PubMed] [Google Scholar]
50. Neto Henriques R, Correia MM, Nunes RG, et al. Exploring the 3D geometry of the diffusion kurtosis tensor: impact on the development of robust tractography procedures and novel biomarkers. Neuroimage 2015;111:85–99 10.1016/j.neuroimage.2015.02.004 [DOI] [PubMed] [Google Scholar]
51. Jensen JH, Russell Glenn G, Helpern JA. Fiber ball imaging. Neuroimage 2016;124:824–33 10.1016/j.neuroimage.2015.09.049 [DOI] [PMC free article] [PubMed] [Google Scholar]
52. Tournier JD, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. Neuroimage 2007;35:1459–72 10.1016/j.neuroimage.2007.02.016 [DOI] [PubMed] [Google Scholar]
53. Tournier JD, Yeh CH, Calamante F, et al. Resolving crossing fibres using constrained spherical deconvolution: validation using diffusion-weighted imaging phantom data. Neuroimage 2008;15:617–25 10.1016/j.neuroimage.2008.05.002 [DOI] [PubMed] [Google Scholar]
54. Wilkins B, Lee N, Gajawelli N, et al. Fiber estimation and tractography in diffusion MRI: development of simulated brain images and comparison of multi-fiber analysis methods at clinical b-values. Neuroimage 2015;109:341–56 10.1016/j.neuroimage.2014.12.060 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Tractography_Comparison.mov

Download video file^{(51.9MB, mov)}

15-00938.pdf

15-00938.pdf^{(1.7MB, pdf)}

[B1] 1. Romano A, D'Andrea G, Minniti G, et al. Pre-surgical planning and MR-tractography utility in brain tumour resection. Eur Radiol 2009;19:2798–808 10.1007/s00330-009-1483-6 [DOI] [PubMed] [Google Scholar]

[B2] 2. Mormina E, Longo M, Arrigo A, et al. MRI tractography of corticospinal tract and arcuate fasciculus in high-grade gliomas performed by constrained spherical deconvolution: qualitative and quantitative analysis. AJNR Am J Neuroradiol 2015;36:1853–58 10.3174/ajnr.A4368 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B3] 3. Lazar M. Mapping brain anatomical connectivity using white matter tractography. NMR Biomed 2010;23:821–35 10.1002/nbm.1579 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B4] 4. Tournier JD, Mori S, Leemans A. Diffusion tensor imaging and beyond. Magn Reson Med 2011;65:1532–56 10.1002/mrm.22924 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B5] 5. Farquharson S, Tournier JD, Calamante F, et al. White matter fiber tractography: why we need to move beyond DTI. J Neurosurg 2013;118:1367–77 10.3171/2013.2.JNS121294 [DOI] [PubMed] [Google Scholar]

[B6] 6. Tuch DS, Reese TG, Wiegell MR, et al. Diffusion MRI of complex neural architecture. Neuron 2003;40:885–95 10.1016/S0896-6273(03)00758-X [DOI] [PubMed] [Google Scholar]

[B7] 7. Tuch DS. Q-ball imaging. Magn Reson Med 2004;52:1358–72 10.1002/mrm.20279 [DOI] [PubMed] [Google Scholar]

[B8] 8. Wedeen VJ, Hagmann P, Tseng WY, et al. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med 2005;54:1377–86 10.1002/mrm.20642 [DOI] [PubMed] [Google Scholar]

[B9] 9. Wedeen VJ, Wang RP, Schmahmann JD, et al. Diffusion spectrum magnetic resonance imaging (DSI) tractography of crossing fibers. Neuroimage 2008;41:1267–77 10.1016/j.neuroimage.2008.03.036 [DOI] [PubMed] [Google Scholar]

[B10] 10. Basser PJ, Mattiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson 1994;103:247–54 10.1006/jmrb.1994.1037 [DOI] [PubMed] [Google Scholar]

[B11] 11. Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor-MRI. J Magn Reson B 1996;111:209–19 10.1006/jmrb.1996.0086 [DOI] [PubMed] [Google Scholar]

[B12] 12. Basser PJ, Pajevic S, Pierpaoli C, et al. In vivo fiber tractography using DT-MRI data. Magn Reson Med 2000;44:625–32 [DOI] [PubMed] [Google Scholar]

[B13] 13. Jensen JH, Helpern JA, Ramani A, et al. Diffusional kurtosis imaging: the quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med 2005;53:1432–40 10.1002/mrm.20508 [DOI] [PubMed] [Google Scholar]

[B14] 14. Jensen JH, Helpern JA. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed. 2010;23:698–710 10.1002/nbm.1518 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B15] 15. Lazar M, Jensen JH, Xuan L, et al. Estimation of the orientation distribution function from diffusional kurtosis imaging. Magn Reson Med 2008;60:774–81 10.1002/mrm.21725 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B16] 16. Jensen JH, Helpern JA, Tabesh A. Leading non-Gaussian corrections for diffusion orientation distribution function. NMR Biomed 2014;27:202–11 10.1002/nbm.3053 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B17] 17. Hagmann P, Jonasson L, Maeder P, et al. Understanding diffusion MR imaging techniques: from scalar diffusion-weighted imaging to diffusion tensor imaging and beyond. Radiographics 2006;26(suppl 1):S205–23 10.1148/rg.26si065510 [DOI] [PubMed] [Google Scholar]

[B18] 18. Jeurissen B, Leemans A, Tournier JD, et al. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging. Hum Brain Mapp 2013;34:2747–66 10.1002/hbm.22099 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B19] 19. Jensen JH, Falangola MF, Hu C, et al. Preliminary observations of increased diffusional kurtosis in human brain following recent cerebral infarction. NMR Biomed 2011;24:452–57 10.1002/nbm.1610 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B20] 20. Fung SH, Roccatagliata L, Gonzalez RG, et al. MR diffusion imaging in ischemic stroke. Neuroimaging Clin N Am 2011;21:345–77, xi 10.1016/j.nic.2011.03.001 [DOI] [PubMed] [Google Scholar]

[B21] 21. Hui ES, Fieremans E, Jensen JH, et al. Stroke assessment with diffusional kurtosis imaging. Stroke 2012;43:2968–73 10.1161/STROKEAHA.112.657742 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B22] 22. Grinberg F, Ciobanu L, Farrher E, et al. Diffusion kurtosis imaging and log-normal distribution function imaging enhance the visualisation of lesions in animal stroke models. NMR Biomed 2012;25:1295–304 10.1002/nbm.2802 [DOI] [PubMed] [Google Scholar]

[B23] 23. Umesh Rudrapatna S, Wieloch T, Beirup K, et al. Can diffusion kurtosis imaging improve the sensitivity and specificity of detecting microstructural alterations in brain tissue chronically after experimental stroke? Comparisons with diffusion tensor imaging and histology. Neuroimage 2014;97:363–73 10.1016/j.neuroimage.2014.04.013 [DOI] [PubMed] [Google Scholar]

[B24] 24. Falangola MF, Jensen JH, Tabesh A, et al. Non-Gaussian diffusion MRI assessment of brain microstructure in mild cognitive impairment and Alzheimer's disease. Magn Reson Imaging 2013;31:840–46 10.1016/j.mri.2013.02.008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B25] 25. Benitez A, Fieremans E, Jensen JH, et al. White matter tract integrity metrics reflect the vulnerability of late-myelinating tracts in Alzheimer's disease. Neuroimage Clin 2013;9:64–71 10.1016/j.nicl.2013.11.001 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B26] 26. Fieremans E, Benitez A, Jensen JH, et al. Novel white matter tract integrity metrics sensitive to Alzheimer disease progression. AJNR Am J Neuroradiol 2013;34:2105–12 10.3174/ajnr.A3553 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B27] 27. Vanhoutte G, Pereson S, Delgado Y, Palacios R, et al. Diffusion kurtosis imaging to detect amyloidosis in an APP/PS1 mouse model for Alzheimer's disease. Magn Reson Med 2013;69:1115–21 10.1002/mrm.24680 [DOI] [PubMed] [Google Scholar]

[B28] 28. Gong NJ, Wong CS, Chan CC, et al. Correlations between microstructural alterations and severity of cognitive deficiency in Alzheimer's disease and mild cognitive impairment: a diffusional kurtosis imaging study. Magn Reson Imaging 2013;31:688–94 10.1016/j.mri.2012.10.027 [DOI] [PubMed] [Google Scholar]

[B29] 29. Raab P, Hattingen E, Franz K, et al. Cerebral gliomas: diffusional kurtosis imaging analysis of microstructural differences. Radiology 2010;254:876–81 10.1148/radiol.09090819 [DOI] [PubMed] [Google Scholar]

[B30] 30. Van Cauter S, Veraart J, Sijbers J, et al. Gliomas: diffusion kurtosis MR imaging in grading. Radiology 2012;263:492–501 10.1148/radiol.12110927 [DOI] [PubMed] [Google Scholar]

[B31] 31. Rosenkrantz AB, Sigmund EE, Johnson G, et al. Prostate cancer: feasibility and preliminary experience of a diffusional kurtosis model for detection and assessment of aggressiveness of peripheral zone cancer. Radiology 2012;264:126–35 10.1148/radiol.12112290 [DOI] [PubMed] [Google Scholar]

[B32] 32. Steven AJ, Zhuo J, Melhem ER. Diffusion kurtosis imaging: an emerging technique for evaluating the microstructural environment of the brain. AJR Am J Roentgenol 2014;202:W26–33 10.2214/AJR.13.11365 [DOI] [PubMed] [Google Scholar]

[B33] 33. Glenn GR, Helpern JA, Tabesh A, et al. Optimization of white matter fiber tractography with diffusional kurtosis imaging. NMR Biomed 2015;28:1245–56 10.1002/nbm.3374 [DOI] [PubMed] [Google Scholar]

[B34] 34. Tabesh A, Jensen JH, Ardekani BA, et al. Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magn Reson Med 2011;65:823–36 10.1002/mrm.22655 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B35] 35. Veraart J, Fieremans E, Jelescu IO, et al. Gibbs ringing in diffusion MRI. Magn Reson Med 2015. August 10. [Epub ahead of print] 10.1002/mrm.25866 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B36] 36. Perrone D, Aelterman J, Pižurica A, et al. The effect of Gibbs ringing artifacts on measures derived from diffusion MRI. Neuroimage 2015;120:441–55 10.1016/j.neuroimage.2015.06.068 [DOI] [PubMed] [Google Scholar]

[B37] 37. Glenn GR, Tabesh A, Jensen JH. A simple noise correction scheme for diffusional kurtosis imaging. Magn Reson Imaging 2015;33:124–33 10.1016/j.mri.2014.08.028 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B38] 38. Kuo LW, Chen JH, Wedeen VJ, et al. Optimization of diffusion spectrum imaging and q-ball imaging on clinical MRI system. Neuroimage 2008;41:7–18 10.1016/j.neuroimage.2008.02.016 [DOI] [PubMed] [Google Scholar]

[B39] 39. Tefera GB, Zhou Y, Juneja V, et al. Evaluation of fiber tracking from subsampled q-space data in diffusion spectrum imaging. Magn Reson Imaging 2013;31:820–26 10.1016/j.mri.2013.02.006 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B40] 40. Kuo LW, Chiang WY, Yeh FC, et al. Diffusion spectrum MRI using body-centered-cubic and half-sphere sampling schemes. J Neurosci Methods 2013;212:143–55 10.1016/j.jneumeth.2012.09.028 [DOI] [PubMed] [Google Scholar]

[B41] 41. Yeh CH, Cho KH, Lin HC, et al. Reduced encoding diffusion spectrum imaging implemented with a bi-Gaussian model. IEEE Trans Med Imaging 2008;27:1415–24 10.1109/TMI.2008.922189 [DOI] [PubMed] [Google Scholar]

[B42] 42. Menzel MI, Tan ET, Khare K, et al. Accelerated diffusion spectrum imaging in the human brain using compressed sensing. Magn Reson Med 2011;66:1226–33 10.1002/mrm.23064 [DOI] [PubMed] [Google Scholar]

[B43] 43. Feinberg DA, Setsompop K. Ultra-fast MRI of the human brain with simultaneous multi-slice imaging. J Magn Reson 2013;229:90–100 10.1016/j.jmr.2013.02.002 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B44] 44. Larkman DJ, Hajnal JV, Herlihy AH, et al. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J Magn Reson Imaging 2001;13:313–17 [DOI] [PubMed] [Google Scholar]

[B45] 45. Setsompop K, Cohen-Adad J, Gagoski BA, et al. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. Neuroimage 2012;63:569–80 10.1016/j.neuroimage.2012.06.033 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B46] 46. Reese TG, Benner T, Wang R, et al. Halving imaging time of whole brain diffusion spectrum imaging and diffusion tractography using simultaneous image refocusing in EPI. J Magn Reson Imaging 2009;29:517–22 10.1002/jmri.21497 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B47] 47. Setsompop K, Kimmlingen R, Eberlein E, et al. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. Neuroimage 2013;80:220–33 10.1016/j.neuroimage.2013.05.078 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B48] 48. Kiselev VG. The cumulant expansion: an overarching mathematical framework for understanding diffusion NMR. In: Jones DK, ed. Diffusion MRI: Theory, Methods and Applications. New York: Oxford University Press; 2011:152–68 [Google Scholar]

[B49] 49. Jensen JH, Helpern JA. Resolving power for the diffusion orientation distribution function. Magn Reson Med 2015. October 7. [Epub ahead of print] 10.1002/mrm.25900 [DOI] [PubMed] [Google Scholar]

[B50] 50. Neto Henriques R, Correia MM, Nunes RG, et al. Exploring the 3D geometry of the diffusion kurtosis tensor: impact on the development of robust tractography procedures and novel biomarkers. Neuroimage 2015;111:85–99 10.1016/j.neuroimage.2015.02.004 [DOI] [PubMed] [Google Scholar]

[B51] 51. Jensen JH, Russell Glenn G, Helpern JA. Fiber ball imaging. Neuroimage 2016;124:824–33 10.1016/j.neuroimage.2015.09.049 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B52] 52. Tournier JD, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. Neuroimage 2007;35:1459–72 10.1016/j.neuroimage.2007.02.016 [DOI] [PubMed] [Google Scholar]

[B53] 53. Tournier JD, Yeh CH, Calamante F, et al. Resolving crossing fibres using constrained spherical deconvolution: validation using diffusion-weighted imaging phantom data. Neuroimage 2008;15:617–25 10.1016/j.neuroimage.2008.05.002 [DOI] [PubMed] [Google Scholar]

[B54] 54. Wilkins B, Lee N, Gajawelli N, et al. Fiber estimation and tractography in diffusion MRI: development of simulated brain images and comparison of multi-fiber analysis methods at clinical b-values. Neuroimage 2015;109:341–56 10.1016/j.neuroimage.2014.12.060 [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Mapping the Orientation of White Matter Fiber Bundles: A Comparative Study of Diffusion Tensor Imaging, Diffusional Kurtosis Imaging, and Diffusion Spectrum Imaging

GR Glenn

L-W Kuo

Y-P Chao

C-Y Lee

JA Helpern

JH Jensen