Compressed sensing for rapid late gadolinium enhanced imaging of the left atrium: A preliminary study

Abstract

Current late gadolinium enhanced (LGE) imaging of left atrial (LA) scar or fibrosis is relatively slow and requires 5–15 minutes to acquire an undersampled (R=1.7) 3D navigated dataset. The GeneRalized Autocalibrating Partially Parallel Acquisitions (GRAPPA) based parallel imaging method is the current clinical standard for accelerating 3D LGE imaging of the LA and permits an acceleration factor ~R=1.7. Two compressed sensing (CS) methods have been developed to achieve higher acceleration factors: a patch based collaborative filtering technique tested with acceleration factor R~3, and a technique that uses a 3D radial stack-of-stars acquisition pattern (R~1.8) with a 3D total variation constraint. The long reconstruction time of these CS methods makes them unwieldy to use, especially the patch based collaborative filtering technique. In addition, the effect of CS techniques on the quantification of percentage of scar/fibrosis is not known.

We sought to develop a practical compressed sensing method for imaging the LA at high acceleration factors. In order to develop a clinically viable method with short reconstruction time, a Split Bregman (SB) reconstruction method with 3D total variation (TV) constraints was developed and implemented. The method was tested on 8 atrial fibrillation patients (4 pre-ablation and 4 post-ablation datasets). Blur metric, normalized mean squared error and peak signal to noise ratio were used as metrics to analyze the quality of the reconstructed images, Quantification was performed on the undersampled images and compared with the fully sampled images. Quantification of scar from post-ablation datasets and quantification of fibrosis from pre-ablation datasets showed that acceleration factors up to R~3.5 gave good 3D LGE images of the LA wall, using a 3D TV constraint and constrained SB methods. This corresponds to reducing the scan time by half, compared to currently used GRAPPA methods. Reconstruction of 3D LGE images using the SB method was over 20 times faster than standard gradient descent methods.

1. INTRODUCTION

Atrial fibrillation (AF) affects over 7 million people in Europe and the US and is the most common cardiac arrhythmia. Acquisition of Late Gadolinium Enhancement (LGE) images of the left atrium (LA) is becoming a valuable tool for assessing the degree of fibrosis in the left atrium before and after treatment. Radio frequency (RF) ablation therapy is a promising procedure for treating AF and restoring sinus rhythm. Pre-ablation images have been used to detect fibrosis and are reported to be predictive of ablation outcome [1]. Post-ablation images can be used to detect the degree of ablation-induced scar in the LA wall [2, 3]. While LGE images are very useful for non-invasive assessment of the LA wall, the image acquisition is relatively slow.

Current LGE acquisition methods for the LA use a 3D Cartesian inversion recovery pulse sequence with ECG gating and a respiratory navigator. In every heartbeat, after an inversion pulse has been applied, segments of 3D k-space are acquired while the heart is in the diastolic phase of the cardiac cycle and the diaphragm position is within a window. This acquisition process is inherently slow. The high spatial resolution required to assess the thin LA wall prolongs the acquisition further. Currently, the relatively long acquisition time of the 3D LGE sequence is a challenge to clinical workflow, particularly if an inversion time is chosen that does not give good results or the scan has to be repeated for other reasons such as patient motion.

Parallel imaging techniques like GRAPPA have been employed for faster acquisition, though reported acceleration factors for imaging the LA are less than R=2 [2]. Advancements in compressed sensing (CS) [4, 5] have made it possible to reconstruct good quality images from relatively few k-space samples by leveraging sparsity constraints. To the best of our knowledge, only two groups have looked at faster 3D LGE imaging. A 3D radial stack of stars acquisition with R~1.8 (144 rays x 36 slab encodes) with a total variation (TV) constraint was used in [6], and a collaborative filtering method where the properties of similarity patches learned from the image were used as constraints with R=3 [7, 8]. Both methods are computationally intensive, especially the process of learning from patches. The reconstruction time for the patch-based method was reported as 98 minutes using a non GPU based implementation [8]. These two CS reconstruction methods do not use rapid minimization techniques and hence suffer from long reconstruction times. In addition, the use of accelerated acquisitions could lead to loss of information about the amount of scar or fibrosis in the LA wall. The published CS techniques do not perform quantification of percentage of scar/fibrosis to study the effect of CS techniques on the quantification procedure.

The aim of this paper is to develop a rapid compressed sensing method and evaluate the acceleration factors that can be achieved, while maintaining good quality reconstructions and practical reconstruction times. Recently, several optimization methods such as the primal-dual algorithm [9], Split Bregman (SB) [10], and Augmented Lagrangian (AL) [11] have been developed, which can rapidly minimize compressed sensing objective functionals. Variable splitting methods like SB involve decoupling of the L₂ norm term from the L₁ norm term, which allows for rapid convergence of the minimization problem. Variable splitting techniques have been used to accelerate other compressed sensing methods for MRI. In [12], an AL based approach was developed for dynamic multicoil reconstruction with a Cartesian variable density sampling pattern. In [13], AL was used to accelerate sparse SENSE reconstructions where spatial TV and wavelets were used as sparsifying transform. Here we focus on the use of the Split Bregman (SB) approach to reconstruct LGE images of the LA with 3D TV, although the AL, dual algorithms and Split Bregman techniques are closely related, as shown in [11].

2. METHOD

2.1. Data Acquisition

2.1.1. Patient data

To study the reconstruction method on human data, 8 fully sampled (4 post-ablation and 4 pre-ablation) datasets from atrial fibrillation patients were acquired with a Siemens 3T Verio scanner. Acquisition parameters were TR=3.8ms, TE=2.1ms, TI=300–400ms, 36–40 slice encodings, a slice thickness of 2.5mm and flip angle=14 degrees with 1.25×1.25×2.5 mm³ resolution. The TI was chosen based on the nulling point of the myocardium. To reduce respiratory motion ghosting, the phase encoding direction was left-right. The size of the data matrix acquired from the scanner was ~320×320×(36–40), transaxial slices. A 32 channel phased array coils were used to acquire the data and a contrast agent dose of 0.1 mmol/kg of Gd-BOPTA was used. The images were acquired ~20 minutes after injection. A respiratory navigator (trailing) was used during the acquisition. It took ~ 10–15 minutes to acquire full k-space data.

2.2. Undersampling Pattern

To produce undersampled data from the fully sampled data, a variable density sampling pattern was used, fully sampled along k_x, while directions k_y, k_z were undersampled using a bell shaped polynomial variable density distribution given by P(y, z) = (1− r(k_y,k_z))^p, where r is the normalized distance from the center of the sampling mask, given by $r(k_y,k_z)=(\frac{2}{\sqrt{{n_1}^2+{n_2}^2}})\sqrt{k_y^2+k_z^2};\frac{-n_1}{2}<k_y\le \frac{n_1}{2}$ and $\frac{-n_2}{2}<k_z\le \frac{n_2}{2}$. Here n₁ and n₂ are the sizes of the measured data matrix in the y and z directions, respectively. Points that are closer to the center have a higher probability of being sampled while points further away from the center have a lower probability of being sampled. The polynomial order (p) controls how densely the center of k-space is sampled. The higher the polynomial order, the smaller is the central k-space region being sampled.

2.3. Reconstruction

The standard compressed sensing approach can be written in a constrained form as

$${{}_{argmin\mathit{m}}\left|\right|\varphi m\left|\right|}_1\mathrm{s}.\mathrm{t}.{\left|\right|Em-k\left|\right|}_2^2<{\sigma }^2$$ (1)

Where k is the measured k-space data, σ is the noise or artifact level in the measured k-space data, m is the (3D) image to be minimized, || ||₁ is the L₁ norm, || ||₂ is the L₂ norm, and E is the encoding matrix that includes the Fourier operator and an undersampling pattern. The symbol ϕ is a sparsity-promoting transform. In this paper, ϕ is the spatial gradient operator, which gives the total variation (TV) constraint.

Using the Bregman iterations technique, equation (1) can be reduced to a sequence of unconstrained optimization problems as shown in [14]

$$C_1={{}_{argmin\mathit{m}}\left|\right|\varphi m\left|\right|}_1+\frac{\mu }{2}{\left|\right|Em-k^j\left|\right|}_2^2$$ (2)

$$k^{j+1}=k^j+k^0-{Em}^{j+1}$$ (3)

Here μ is the weight that controls the tradeoff between sparsity of the image (the L₁ norm term) and closeness to the measured data (the L₂ norm term). Eq. (2) is a mixture of L₁ and L₂ norms, and using traditional methods like gradient descent for minimizing (2) have a slow rate of convergence. As shown in [10], (2) can be reduced to a series of unconstrained problems by introducing an intermediary variable d, such that ϕm=d so that eq. (2) can be written as:

$${{}_{argmin\mathit{m},d,b}\left|\right|d\left|\right|}_1+\frac{\mu }{2}{\left|\right|Em-k^j\left|\right|}_2^2+\frac{\lambda }{2}{\left|\right|d-\varphi m-b\left|\right|}_2^2$$ (4)

Where b comes from optimizing the Bregman distance [10]. The Bregman distance based on a convex function E between any two points u and v is given by, $D_E^p(u,v)=E(u)-E(v)-<p,u-v>$, where p is the subgradient of E at v.

Using the Split Bregman formulation, fast convergence for L₁ regularized problems like those used in compressed sensing has been shown [10]. The measured k-space data k⁰, which is updated as k^j+1 = k^j+k⁰− Em^j+1 in eq. (3), is equivalent to an “adding-the-noise-back” iterative step [15]. The derivation for this “adding noise back” step, based on Bregman distance and Bregman iterations is shown in [14]. By minimizing (4) and updating k as in (3), the constrained L₁ problem in (1) can be minimized in fewer iterations as compared to standard gradient descent based methods. Others have shown for denoising and deblurring applications that this type of “adding- the-noise-back” implementation produces images with less error and with edges that are sharper as compared to TV without the adding noise back step [15]. The SB method which includes “adding noise back” has been called the constrained version of SB [10] and the method that does not include “adding noise back” has been called the unconstrained version of SB. The “adding noise back” step is a method to ensure that edges and fine textures that are lost due to TV regularization are included in the reconstruction. This adding noise back step can help improve the sharpness of edges in the reconstructed images.

The equation used to implement 3D TV based image reconstruction using SB is given as

$$\underset{m,dx,dy,dz,bx,by,bz}{min}{\left|\right|\sqrt{{(dx)}^2+{(dy)}^2+{(dz)}^2}\left|\right|}_1+\frac{\mu }{2}{\left|\right|Em-k^j\left|\right|}_2^2+\frac{\lambda }{2}{\left|\right|dx-{\nabla }_{x}m-bx\left|\right|}_2^2+\frac{\lambda }{2}{\left|\right|dy-{\nabla }_{y}m-by\left|\right|}_2^2+\frac{\lambda }{2}{\left|\right|dz-{\nabla }_{z}m-bz\left|\right|}_2^2$$ (5)

Here dx, dy and dz are the dummy variables introduced by the SB technique to enforce dx=∇_xm, dy=∇_ym and dz=∇_zm, for the three directions x,y and z respectively. A minimum solution for m is found by alternatively minimizing m, dx, dy and dz. Algorithm 1 shows the steps followed to minimize the different variables. When trying to minimize m, the L₁ term (first term in eq. (5)) that does not contain m is removed. By decoupling m from the L₁ norm term, fast convergence can be achieved. The update for m while dx, dy, and dz are held fixed is given as:

$$m^{i+1}=\underset{m}{min}\frac{\mu }{2}{\left|\right|Em-k^j\left|\right|}_2^2+\frac{\lambda }{2}{\left|\right|{dx}^i-{\nabla }_{x}m-{bx}^i\left|\right|}_2^2+\frac{\lambda }{2}{\left|\right|{dy}^i-{\nabla }_{y}m-{by}^i\left|\right|}_2^2+\frac{\lambda }{2}{\left|\right|{dz}^i-{\nabla }_{z}m-{bz}^i\left|\right|}_2^2$$ (6)

The terms dx, dy and dz can then be minimized quickly by using the generalized shrinkage operator [10]. The minimization of the surrogate variables is performed in the inner loop of Algorithm 1 while the “adding noise back” step is performed in the outer loop of Algorithm 1.

2.4. Implementation of Reconstruction

After undersampling the k-space data, coil compression with principal component analysis [16, 17] was performed on the measured k-space data and the data was compressed into 4 virtual coils. Each coil was reconstructed separately and then the results combined with the square root of sum of squares. As discussed in [16, 17], coil compression reduces the total number of coils required to reconstruct the image and hence reduces the reconstruction time. Experiments were performed to see how many virtual coils are necessary to reconstruct images without any loss of image quality due to coil compression. No loss of image quality was seen when 4 virtual coils were used to reconstruct the images. For some datasets it was possible to achieve good images with 3 virtual coils, but in order to maintain uniformity, 4 virtual coils were used to reconstruct all of the datasets.

The code was implemented in MATLAB. Parallel toolbox as well as Jacket 2.3.0 (AccelerEyes, Atlanta, GA) were used to run the reconstruction on GPU’s. The code was run on an Nvidia Tesla C2070 with a total dedicated memory of 6GB. The value of p was chosen as 1.6 and the weights for the reconstruction were chosen as λ=0.9 and μ=0.6. These weights were chosen empirically to give the best visual image quality. Different weights were tested on the 8 datasets. Changing the weights by ±50% did not cause any major change in the visual quality of the image, though the convergence was slower when μ<0.45 was used. The set of weights chosen allowed for fast convergence of the reconstructed images.

2.5. Comparison Metrics

(a) Visual inspection

The images were visually inspected for overall quality and also for sharpness and the ability to distinguish fine structures. The inverse Fourier transform (IFT) of the fully sampled data from each coil followed by square-root-of-sum-of-squares coil combination was used as “truth” to compare the reconstruction quality of images for different undersampling factors.

(b) Line profiles and difference images

To compare the sharpness of the LA wall in the reconstructed images with the fully sampled image, plots of intensities of a line across the LA were used. Image differences between the reconstructed image and fully sampled image were also computed to see if the residual difference image had any structures present or had a noise like pattern, especially in the LA.

(c) Normalized mean squared error and peak signal to noise ratio (PSNR)

The normalized mean squared error (NMSE) and PSNR give a sense of how different the reconstructed images are from the fully sampled image. Here NMSE was computed as

$$\mathit{NMSE}(m_{\mathit{Full}},m)={\left|\right|m_{\mathit{Full}}-m\left|\right|}_2^2/{\left|\right|m_{\mathit{full}}\left|\right|}_2^2,$$

where m_full is the fully sampled image, m is the reconstructed image.

PSNR was computed as

$$\mathit{PSNR}=20log(\frac{{\mathit{Max}}_{m_{\mathit{Full}}}}{\sqrt{\mathit{MSE}}}),$$

where Max_mFull is the maximum intensity in the fully sampled image and mean squared error (MSE) is defined as

$$\mathit{MSE}(m_{\mathit{Full}},m)=\frac{1}{({\mathit{Dim}}_X\ast {\mathit{Dim}}_y\ast {\mathit{Dim}}_z)}({\left|\right|m_{\mathit{full}}-m\left|\right|}_2^2),$$

where Dim represents the dimension/size of the image in x, y and z directions.

(d) Blur metric

The metrics described above use the fully sampled reference image in order to compute the metric. In contrast, the blur metric [18] is a reference image free metric that can be used to assess the quality of an image. The variation of an image with respect to a low pass filtered version of the same image can be used as an estimate for the amount of blurring in the image. After the low pass filtering process is performed, the difference is normalized to quantify the blur. An image with sharp edges would have a large variation with respect to the low pass filtered version while a smoother image would have smaller variation. The range of the blur metric is from 0 to 1, and a larger blur metric corresponds to a blurrier image.

(e) Quantification of the extent of LGE in the LA

The two CS techniques published for accelerating 3D LGE imaging do not perform quantification of the 3D LGE images to estimate the percentage of scar or percentage of fibrosis, which is part of the clinical procedure here and in some other locations. In order to study the effects of undersampling on the quantification procedure, the fully sampled images and the undersampled images were independently quantified and the results were compared.

The entire quantification procedure for the LGE images was performed by the Comprehensive Arrhythmia Research and Management (CARMA) center, University of Utah. The 3D LGE post-ablation images were used to calculate the percentage of scar present in the LA. The LA wall was first manually segmented. Manual segmentation was a laborious process for the ~40 slices. In order to make the process of quantification less laborious, comparisons were only made between the fully sampled image and images reconstructed using R=3.5. Contours were manually drawn on the fully sampled image and separately on images reconstructed using R=3.5 and then the percentage of scar quantified for the four post-ablation datasets. In order to estimate inter-observer variability, two of the four fully sampled post-ablation datasets were segmented by two users independently. An automated classification software [19] developed at the CARMA center, took the segmented images as input and calculated the percentage of scar in the post-ablation datasets. This automatic classification algorithm, based on clustering of voxels in the image, has been shown to have good correlation with manual scar classification by expert observers [19].

To quantify the pre-ablation datasets, a semi-automated classification software [20] was used. The images were segmented manually as described above. After segmentation, classification of voxels was performed by thresholding the intensities in the LA wall. This thresholding was performed independently on each slice. A threshold was temporarily chosen by the semiautomated software by estimating the mean and standard deviation of non-fibrotic tissue. A final threshold was then manually chosen by the user at two to four standard deviations above the mean of the non-fibrotic tissue. Based on the extent of enhancement of the pre-ablation images, the patient was then classified into four groups [21]: stage I, stage II, stage III or stage IV. This type of classification can be used to help select appropriate medical strategies. It is important that undersampling the images does not lead to a different classification.

3. RESULTS

3.1. Reconstruction of human datasets

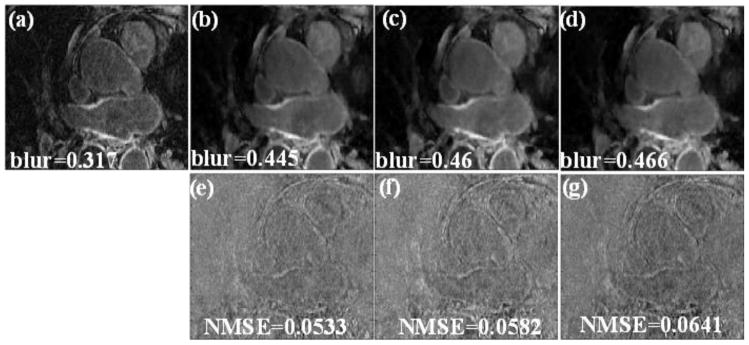
Fig 1 shows a comparison between a fully sampled image and undersampled versions of the data reconstructed with the unconstrained SB that does not include “adding-noise-back” for a post-ablation dataset. When the “adding noise back” step is not used, blurring is visible in the reconstructed images. This is especially visible for higher acceleration factors of R=3.5 and 4. In the difference image shown in Fig 1 (e)–(g), fine texture is visible. This shows that sharp transitions in the reconstructed image have been smoothed. The blur metric and NMSE further show that the reconstructed images do not match the fully sampled image well. In addition, when the unconstrained SB method is used on the pre-ablation dataset, the loss of fine texture and smoothing of sharp transitions is even more evident (not shown). This is because in pre-ablation data, the relative enhancement in the LA wall is typically less than in post-ablation datasets.

Fig 1.

(a) Cropped LA region in one slice from a fully sampled image. (b), (c) and (d) reconstructions using the unconstrained SB method with no “adding noise back” term (only using eq. (6)). The blur metric for the truth and the reconstructed images are reported along with the images. (e), (f) and (g) Difference image between the truth and the images reconstructed in (b), (c) and (d) respectively. The MSD of the individual slice is shown along with the difference image. Blurring of the LA wall was visible in these reconstructions that use the unconstrained SB method.

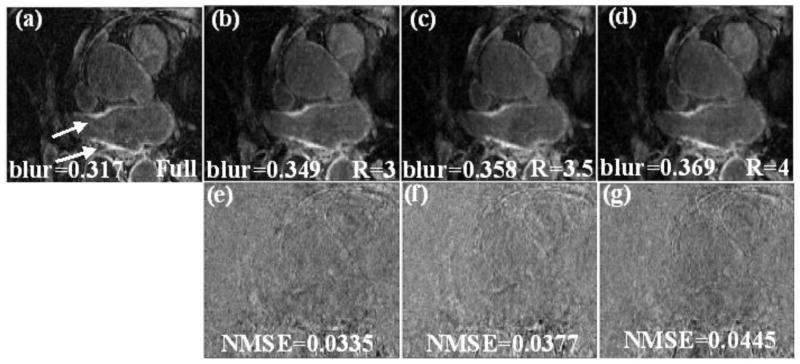
Reconstruction of the post-ablation dataset shown in Fig 1 using the constrained version of SB that uses “adding noise back” is shown in Fig 2. The LA wall is better visualized and fine textures are better preserved in Fig 2 than the images in Fig 1. The lower NMSE and lower blur metric show that images in Fig 2 match the truth better. For the post ablation datasets reconstructed using R=3.5, the MSE and standard deviation on average were (8.9 ±4.5).

Fig 2.

(a) Cropped LA region in one slice from a fully sampled image, the arrows point to the enhancement in the LA wall. (b), (c) and (d) Reconstruction using the proposed method with “adding noise back” for R=3, R=3.5 and R=4 respectively (using eq. (6) and (3)). The blur metric for the truth and the reconstructed images are reported along with the images. (e), (f) and (g) Difference image between the truth and the images reconstructed in (b), (c) and (d) respectively. The MSE of the individual slice is shown along with the difference image.

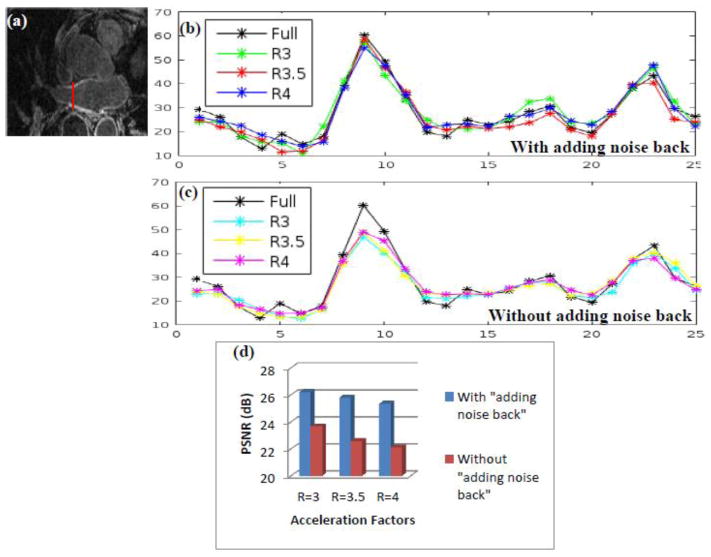
To compare the unconstrained SB and constrained SB reconstructions further, intensities of a vertical line across the LA wall are plotted in Fig 3 for the three reconstructions with undersampling factors R=3, 3.5 and 4, to compare edge profiles with the truth. The location of this vertical line is shown by a thin red line in Fig 3 (a). In Fig 3 (b), the peaks of the curves that correspond to the constrained SB formulation match the truth well for the three acceleration factors R=3, 3.5 and R=4. The curves that correspond to the unconstrained SB formulation in Fig 3 (c) have lower peaks as compared to the truth. This shows that the unconstrained SB formulation is not able to reconstruct the LA wall faithfully and there is a loss of contrast. This is further confirmed by the comparison of the PSNR for the three acceleration factors in Fig 3 (d). For the unconstrained SB formulation, where the “adding noise back step” is not used, the PSNR is lower than the constrained SB formulation for all three acceleration factors.

Fig 3.

A comparison of the constrained SB formulation (with “adding noise back” step) with the unconstrained SB formulation (without “adding noise back” step). (b) Plot of a line across of the LA wall for the images in Fig 2 that correspond to the constrained SB formulation, the location shown by the thin red vertical line in (a). For all of the three acceleration factors, the peaks of the curves from the reconstructed images match the truth. (c) Plot of a line across the LA wall for the images in Fig 1 that correspond to the unconstrained SB formulation. For all of the three acceleration factors, the peaks of the curves from the reconstructed images are lower than the truth. (d) The comparison of PSNR for the unconstrained SB images in Fig 1 and constrained SB images in Fig 2. The PSNR with constrained SB formulation is higher than the unconstrained SB formulation for all three acceleration factors. These results show that the constrained SB formulation that uses the “adding noise back” step can reconstruct images with better contrast and sharper edges.

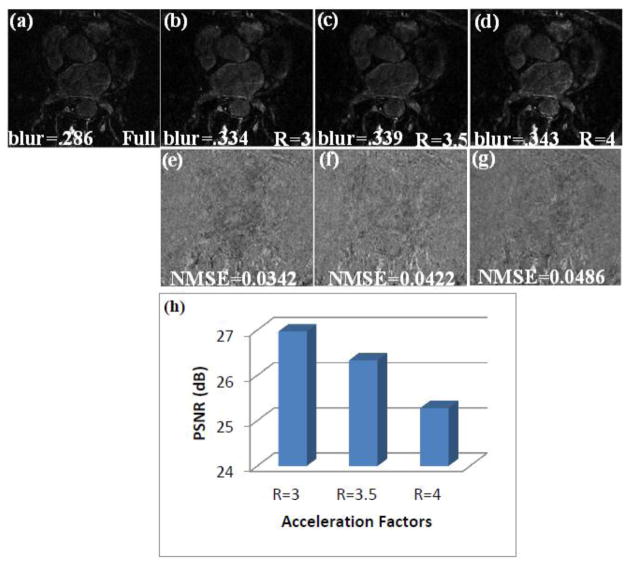
The reconstructions from R=3, 3.5 and 4 using the constrained SB approach for a pre-ablation dataset are shown in Fig 4. The images show that the reconstructed images match the fully sampled image well. At undersampling factors of R=4 some minimal smoothing is seen, though the enhancement in the LA wall is still visible. For the pre-ablation datasets reconstructed using R=3.5, the MSE and standard deviation on average were (11.7±5.5).

Fig 4.

(a) A slice from a fully sampled image from a pre-ablation dataset. (b), (c) and (d) Reconstruction using the proposed constrained SB method for R=3, R=3.5 and R=4 respectively. The blur metric for the truth and the reconstructed images are reported along with the images. (e), (f) and (g) Difference image between the truth and the images reconstructed in (b), (c) and (d) respectively. (h) Bar chart comparing the PSNR of images reconstructed using R=3, R=3.5 and R=4.

The difference images in Fig 2 and Fig 3 show few fine structures, as the reconstructions closely matched the truth. The blur metrics calculated on the reconstructed images for the 3 acceleration factors are close to the blur metric calculated on fully sampled image. This shows that the sharpness of the edges in the reconstructed images matched the sharpness of the fully sampled image well and that there was not much increase in smoothing beyond that present in the fully sampled image.

3.3 Quantification of enhancement

3.3.1 Quantification of ablation on post-ablation datasets

3.3.1.1 Study of inter-user variability

The result of the two fully sampled post-ablation images quantified by two independent users is shown in Table I. The difference between the two observers was ~ 2.5% on average. While the number of datasets used was small, the inter-user variability seen here was similar to the inter-user and intra-user variability of about ±3% reported in [1], where a much larger number of datasets was used. When 3D rendering [2] of the segmented images was performed, it was seen that there was a small change in shape, location and degree of scarring detected by the two users. This gave an estimate of the inter-user variability in both the estimation of percentage of scar and locations where scarred tissue is detected.

Table I.

Comparison of percentage fibrosis calculated from the fully sampled images for two post-ablation datasets which were independently segmented by two users. The percentage fibrosis calculated by the two users matched well. The small variation in the percentage of scar calculated by the two users is mostly due to the intra-user variability in the segmentation process.

User 1	User 2
15.9%	18.5%
9.8%	12.2%

3.3.1.2 Quantification of percentage of scar from R=3.5 images

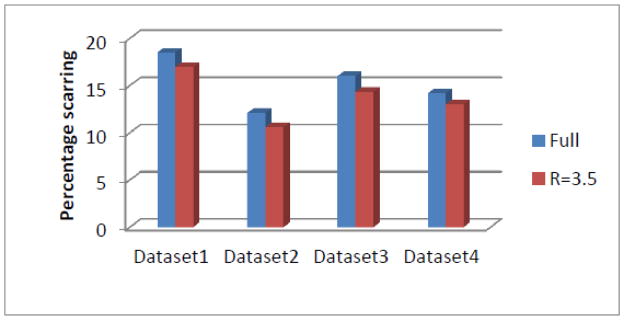
A comparison of quantification of the fully sampled image and the images reconstructed using R=3.5 for the four post-ablation datasets are shown in Fig 5. It was found that the difference between the values calculated was ~2% on average. When 3D rendering of the fully sampled image and the image reconstructed using R=3.5 was performed after segmentation, the percentage scarring and location of scar estimated from the fully sampled images and the R=3.5 images were similar.

Fig 5.

The comparison of percentage scarring calculated from the fully sampled image and the images reconstructed from R=3.5. The difference between the values calculated from the fully sampled image and the images reconstructed from R=3.5 is within the expected inter and intra-user variability.

3.3.2 Quantification of pre-ablation data

The percent enhancement estimated by the quantification procedure using R=3.5 closely matched those estimated from the fully sampled image for the four pre-ablation datasets. For all of the four datasets, the classification of the patient based on the quantification of enhancement was the same for the fully sampled image and for R=3.5 images. The results for the four datasets are shown in Table II. When 3D rendering of the segmented images was performed, the location of enhancement and the percentage fibrosis detected matched well between the fully sampled image and R=3.5 images.

Table II.

Comparison of percentage fibrosis calculated from the fully sampled image and the image reconstructed from R=3.5 for four pre-ablation datasets. The percentage fibrosis calculated from the fully sampled data matches those calculated from R=3.5 well. The classification of patients based on the percentage fibrosis calculated from R=3.5 matches the classification from the fully sampled data.

	Full Image	Classification	R=3.5	Classification
Dataset Pre-1	14.3%	Utah II	17.9%	Utah II
Dataset Pre-2	7.2%	Utah I	6.2%	Utah I
Dataset Pre-3	8.4%	Utah I	6.4%	Utah I
Dataset Pre-4	15.5%	Utah II	15.4%	Utah II

3.3 Convergence and reconstruction time

For all of the datasets the number of iterations for the inner loop in Algorithm 1 was fixed to 10 iterations. It was necessary to perform the outer loop for updating k only 4–8 times to reach convergence, assuming a convergence criterion of $\frac{\left|\right|m^{i+1}-m^i\left|\right|}{\left|\right|m^{i+1}\left|\right|}\le 5\times {10}^{-3}$. Similar findings were reported in [10]. To be conservative, 10 iterations were used for both the inner and outer loops; a total of 100 iterations were performed to reconstruct each dataset. The average reconstruction time for the SB method to reconstruct a 3D dataset with 44 slices was 8 seconds on a Linux platform, 16 CPU cores (Intel Xeon CPU E5620 @ 2.40Ghz), 2 GPU cards (NVIDIA Tesla C2070) and 96 GB RAM. This was much faster compared with the gradient descent method, which on average took about 170 seconds to reconstruct the images on the same platform. This corresponds to a speedup of over 20 using SB.

4. DISCUSSION

We developed a rapid SB 3D total variation reconstruction method for fast acquisition of 3D LGE images of the LA that outperformed gradient descent based methods. The gradient descent based implementation used a smooth approximation of the L₁ norm by adding a small positive constant to avoid singularities that occur when the magnitude of the gradient is close to zero. This smooth approximation caused smoothing of edges in the reconstructed image. When the SB method without the “adding noise back” step was considered, it performed slightly better at edge locations compared to the gradient descent based implementation of the same minimization problem, though the overall image quality was similar. The use of soft thresholding to minimize the L₁ norm in SB based implementations performs better than the smooth approximation used while implementing the L₁ norm in gradient descent based implementation. When compared to the unconstrained SB method that does not use the “adding noise back” step, the constrained SB method with “adding noise back” helped reconstruct good quality images that matched the fully sampled image better.

The constrained SB method that uses the “adding noise back” step has an equivalent AL version that can be shown to also have this “adding noise back” step; the near equivalence between SB and AL is shown in [11, 14]. “Noise” which is added back also contains information about edges and other sharp transitions in the image. By infusion of this information back into the reconstruction algorithm, better quality reconstructions are achieved. Some of the published methods that utilize AL or SB do not use this “adding noise back” step [12, 13, 22]. Our experiments show that the addition of this step improved image quality beyond that achieved by the unconstrained SB formulation. Similar findings were reported in [15] for image denoising and deblurring applications.

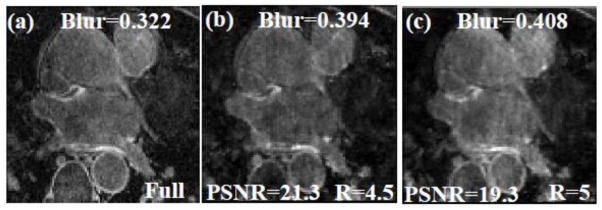
In general, acceleration factors could not be increased beyond R=4 for the resolution acquired here without causing loss of contrast and sharpness of edges, especially in the LA. As good visualization of the LA wall is essential, 3D SB TV at R=4 is the maximum acceleration factor that could be achieved without much loss of structure and edge sharpness in the LA. At high acceleration factors of R=4.5 and above, the reconstructed images have less edge sharpness and relatively poor quality, an example is shown in Fig 6.

Fig 6.

An example where the acceleration factors are too high and the reconstruction algorithm fails to reconstruct images with good quality. (a) A slice from a fully sampled post-ablation dataset, (b) and (c) Images reconstructed using R=4.5 and R=5 respectively. Significant blurring is seen in the LA wall and there is also an overall loss in contrast. The MSE, blur metric and PSNR are reported on the images.

The published CS methods do not study the effect of regularization on quantification of percentage scar from post-ablation and quantification of percentage of fibrosis from pre-ablation images. We found that when the images were segmented and the quantification procedure was performed, the percentage of scar/fibrosis from the undersampled images matched those estimated from the fully sampled images. The small difference seen in the estimates were not considered significant as they were within the reported intra-user and inter-user variability [1]. To study the inter-user variability for our data, 2 out of the 4 fully sampled post-ablation images were quantified by two independent users. There was 2.5% difference on average between the estimates of the two users. Though it would appear as though one of the users is consistently underestimating the percentage of scar, this variation could be due to the inter-user variability in the segmentation process.

4.1 Resolution

There is a difference in resolution between the data used here and the data used in [7]. The data acquired here had a resolution of 1.25×1.25×2.5 mm³, while the resolution in [7] was 1.4×1.4×1.4 mm³. Having high resolution in the x-y dimension is necessary to accurately detect and analyze the thin LA wall; especially if segmentation has to be performed to quantify the images for the percentage of RF ablation induced scar or percentage of fibrosis.

4.2 Limitations and future improvements

The comparisons made in this preliminary study were based on retrospectively undersampled data. For future study it is necessary to acquire undersampled data on the scanner directly, and to acquire a large number of such prospectively undersampled datasets - the number of datasets here was limited and designed to give an initial evaluation of the approach. This work is a preliminary study to show that is possible to achieve good quality images from data acquired with acceleration factors greater than R=3 and also show that a 3D TV constraint is useful for this type of data. This work is the first to study the effect of CS based reconstruction techniques on the quantification of fibrosis/scar. Adding other constraints like the wavelet transform, low rank constraints [23] or data reordering constraints [24] could help in increasing the acceleration factors further. The downside of including additional constraints would be an increase in reconstruction time. The use of multicoil TV reconstructions, instead of the coil-by-coil reconstructions used here, could also help improve the image quality and achieve higher acceleration factors. If a multicoil TV formulation is used, the SB formulation would have to be modified as the SB framework used here cannot be directly applied to multicoil reconstructions. The existing CS techniques developed for accelerating LGE imaging of the LA [6, 7] do not use a multicoil reconstruction formulation.

5. CONCLUSIONS

A SB total variation reconstruction method was developed and implemented for application to 3D LGE images of the LA. This study showed that it was possible to accelerate 3D LGE acquisitions beyond R=3 while achieving high quality reconstructions within a short reconstruction time. The short reconstruction time of the SB approach is advantageous and might permit the method to be used in the routine clinical setting. This study showed the effectiveness of the “adding noise back” step in improving the reconstructed image quality beyond the unconstrained SB formulation.

We also analyzed the effect of accelerated acquisitions on the quantification of percentage of scar/fibrosis. The results showed that the percentage of scar or percentage of fibrosis estimated from the undersampled images matched those estimated from fully sampled data and the small variation seen was within the intra-user and inter-user variability. This implies that compared to the current 3D LGE method with GRAPPA and R=1.7 [2, 21], the data can be acquired in half of the time, which could significantly increase the usage of such LA imaging. Alternatively, higher resolution could be obtained with the current acquisition time. While further testing is needed, 3D TV with SB is a promising approach to rapidly reconstruct good quality images from undersampled (R~3.5) 3D LGE LA scans.

Appendix

Algorithm 1.

The algorithm above shows the steps to reconstruct the 3D LGE images using a 3D TV constraint with Split Bregman. Derivation of these steps and implementation details are given in [10].

To minimize (5)

$$\underset{m,dx,dy,dz,bx,by,dz}{min}{\left|\right|\sqrt{{(dx)}^2+{(dy)}^2+{(dz)}^2}\left|\right|}_1+\frac{\mu }{2}{\left|\right|Em-k^j\left|\right|}_2^2+\frac{\lambda }{2}{\left|\right|dx-{\nabla }_{x}m-bx\left|\right|}_2^2+\frac{\lambda }{2}{\left|\right|dy-{\nabla }_{y}m-by\left|\right|}_2^2+\frac{\lambda }{2}{\left|\right|dz-{\nabla }_{z}m-bz\left|\right|}_2^2$$

Initialize m1 = E*k0,dx1 = dy1 = dz1 = bx1 = by1 = bz1 = 0

For j=1:N1

For i=1:N2

mi+1 = F−1Q−1FHi

${dx}^{i+1}=max(S^i-\frac{1}{\lambda },0)\frac{{\nabla }_x{m}^i+{bx}^i}{S^i}$

${dy}^{i+1}=max(S^i-\frac{1}{\lambda },0)\frac{{\nabla }_y{m}^i+{by}^i}{S^i}$

${dz}^{i+1}=max(S^i-\frac{1}{\lambda },0)\frac{{\nabla }_z{m}^i+{bz}^i}{S^i}$

bxi+1 = bxi + (∇xmi+1−dxi+1)

byi+1 = byi + (∇ymi+1−dyi+1)

bzi+1 = bzi + (∇zmi+1−dzi+1)

End

kj+1 = kj + k0−Emj+1

End

Here F is the Fourier transform and $S^i=\sqrt{{\mid {\nabla }_x{m}^i+{bx}^i\mid }^2+{\mid {\nabla }_y{m}^i+{by}^i\mid }^2+{\mid {\nabla }_z{m}^i+{bz}^i\mid }^2}$

$$H^i={\mu E}^{\ast }{k}^j+\lambda {\nabla }_x^T({dx}^i-{bx}^i)+\lambda {\nabla }_y^T({dy}^i-{by}^i)+\lambda {\nabla }_z^T({dz}^i-{bz}^i)$$

and Q = RT R−λFΔF−1

where m is the image being estimated, N1 is the number of outer iterations, N2 is the number of inner iterations, k the measured k-space, Δ is the Laplacian, R is the sampling pattern, dx, dy and dz are dummy variables added to enforce dx = ∇xm, dy = ∇ym and dz = ∇zm respectively. μ is the weight on the fidelity term and λ is the weight used to enforce d = ∇m for the three directions x, y and z using SB.