Analysis of Pharmacokinetics of Gd-DTPA for Dynamic Contrast-enhanced Magnetic Resonance Imaging

Abstract

The pharmacokinetics (PK) of the contrast agent Gd-DTPA administered intravenously (i.v.) for contrast-enhanced MR imaging (DCE-MRI) is an important factor for quantitative data acquisition. We studied the effect of various initial bolus doses on the PK of Gd-DTPA and analyzed population PK of a lower dose for intra-subject variations in DCE-MRI. First, fifteen subjects (23–85 years, M/F) were randomly divided into four groups for DCE-MRI with different Gd-DTPA dose: group-I, 0.1mmol/kg, n=4; group-II, 0.05 mmol/kg, n=4; group-III, 0.025mmol/kg, n=4; and group-IV, 0.0125 mmol/kg, n=3. Sequential fast T1 mapping sequence, after a bolus i.v. Gd-DTPA administered, and a linear T1-[Gd-DTPA] relationship were used to estimate the PK of Gd-DTPA. Secondly, MR-acquired PK of Gd-DTPA from 58 subjects (28–80 years, M/F) were collected retrospectively, from an ongoing study of the brain using DCE-MRI with Gd-DTPA at 0.025 mmol/kg, to statistically analyze population PK of Gd-DTPA. We found that the PK of Gd-DTPA (i.v. 0.025 mmol/kg) had a half-life of 37.3 ± 6.6 mins, and was a better fit into a linear T1-[Gd-DTPA] relationship than higher doses (up to 0.1 mmol/kg). The area under the curve (AUC) for 0.025 mmol/kg was 3.37± 0.46, which was a quarter of AUC of 0.1 mmol/kg. In population analysis, a dose of 0.025 mmol/kg of Gd-DTPA provided less than 5% subject-dependent variation in the PK of Gd-DTPA. Administration of 0.025 mmol/kg Gd-DTPA enable us to estimate [Gd-DTPA] from T1 by using a linear relationship that has a lower estimation error compared to a non-linear relationship. DCE-MRI with a quarter dose of Gd-DTPA is more sensitive to detect changes in [Gd-DTPA].

1. INTRODUCTION

Dynamic contrast-enhanced MRI (DCE-MRI) studies, which are also called bolus-tracking studies, commonly implemented by a bolus intravenous injection (i.v.) of an exogenous paramagnetic contrast agent, such as widely used Gadolinium diethylene triamine pentaacetic acid (Gd-DTPA) [1–3] or iron nanoparticles [4, 5], followed by a time series acquisition of intensity-enhanced images. Either relaxation rate constant (R1 or R2) or relaxivity (the slope of change in R1 or R2 versus the concentration in mM⁻¹s⁻¹; r1 or r2) of Gd-DTPA were used to determine the concentration of Gd-DTPA ([Gd-DTPA]).

The initial concentration of Gd-DTPA in the plasma ([Gd-DTPA₀]) is an important parameter for DCE-MRI because of its important role in the PK of Gd-DTPA. [Gd-DTPA₀] is related to the administered bolus dose and varies with subjects. There are no standard guidelines for the bolus dose of Gd-DTPA for DCE-MRI. Although the dose of 0.1 mmol/kg is being routinely used for contrast-enhanced clinical studies [1, 6], other doses of Gd-DTPA have been also administered for experimental and clinical MRI [7]. Despite its apparent safe use at this dose, there are controversies about its safety [8–10], especially on the organ and intracranial deposition of Gd-DTPA [11, 12]. These concerns point to the importance of reducing the subject exposure to Gd-DTPA. Therefore, reducing the area under the curve (AUC) of Gd-DTPA in the plasma—a measure of how much Gd-DTPA stays in the body before it clears out, is desirable [13].

Effective way to reduce AUC of Gd-DTPA is to lower the administered bolus dose. To investigate the use of a lower bolus for DCE-MRI, it is important to understand the relationship between [Gd-DTPA] and MR parameters of interest. Linear models were commonly used to relate [Gd-DTPA] to MR signals such as T1 and T2. These models were challenged [14, 15] by showing that r1 depends on many variables such as tissue structure of the compartment of interest in the brain [16], pH, temperature and instrument model e. g. magnetic field strength [17]. Moreover, it was shown that nonlinearity between 1/T1 and [Gd-DTPA] is more pronounced at higher [Gd-DTPA] [18]. These evidences suggest that shortening the range of [Gd-DTPA] may reduce the nonlinearity in MR signal-[Gd-DTPA] relationship.

This study had a two-fold purpose: (a) to find a more accurate model for the PK of Gd-DTPA by investigating Gd-DTPA time-concentration data acquired from patients and phantoms at different [Gd-DTPA], and (b) to analyze the PK of Gd-DTPA for AUC and the inter-subject variability of the PK of Gd-DTPA, after administering lower than 0.1 mmol/kg doses of Gd-DTPA.

2. MATERIALS and METHODS

2.1. Phantom Experiments

A phantom was made by 7 cylinders filled with Gd-DTPA (MW= 938 Da; Bayer Healthcare) in 500 ml of regular water with the following amounts of Gd-DTPA: 8.0, 4.0, 1.6, 0.8, 0.4, 0.2, and 0.0 ml. These values were calculated to mimic the following doses of Gd-DTPA for the human experiment; 0.5, 0.25, 0.1, 0.05, 0.025, 0.0125, and 0.0 mmol/kg, respectively. Phantom data were acquired with the same imaging protocol that was used to acquire human data.

2.2. Clinical Laboratory Data

Concentration-time data of Gd-DTPA for four different aqueous solution i.v. bolus-injected dose of 0.25, 0.1, 0.05, and 0.025 mmol/kg was acquired from the manufacturer (Bayer Healthcare) for comparison with acquired MRI data. Each dose was i.v. bolus administered to a group of 5 controls. Concentration of Gd-DTPA was sampled by drawing blood and recording for two hours after the i.v. injection. [Gd-DTPA] was analytically determined by inductively coupled plasma atomic emission spectrometry (ICP). For more details on the data collection and analysis see ([19, 20]). Data were fitted with a biexponential clearance model for modeling the PK of Gd-DTPA in blood for different bolus injection dose Gd-DTPA₀.

2.3. Subjects

Time-concentration data collection by MR was performed in two parts. First, we studied 15 healthy controls (mean ± SD age 54 ± 23 years M/F), which were a subgroup of controls from an ongoing MR blood-brain barrier permeability study. Subjects were randomly divided into four groups (group-I, 0.1mmol/kg, n=4; group-II, 0.05 mmol/kg, n=4; group-III, 0.025mmol/kg, n=4; and group-IV, 0.0125 mmol/kg, n=3) for DCE-MRI. Secondly, Gd-DTPA time-concentration data from 58 subjects participating in an ongoing DCE-MRI study of the brain (mean ± SD age 63.6 ± 15.6 years) with a dose of 0.025 mmol/Kg Gd-DTPA was collected for population PK analysis. None of the participants has a history of blood filtration problem at the start of the study. The study was approved by the Human Research Review Committee at the University of New Mexico Health Sciences Center, and all participants gave informed consent as approved by the Institutional Review Board.

2.4. MR Imaging

MRI data were acquired using a 1.5 - Tesla Siemens whole-body clinical scanner with a standard eight-channel array head coil (Siemens AG, Erlangen, Germany). The MR imaging protocol consisted of three anatomical and eight T1 maps for DCE-MRI in axial orientation to capture the concentration of Gd-DTPA in the superior sagittal sinus. The first T1 map was acquired pre-injection and the rest were acquired post-injection of Gd-DTPA.

T1 mapping with partial inversion recovery (TAPIR), a fast T1 mapping sequence [21, 22], was used to estimate T1 maps for a series of four different Gd-DTPA concentrations (0.1 – 0.0125 mmol/kg). Data acquisition using TAPIR was performed with the following parameters: TR = 15ms; banded readout scheme with 3 echoes at TE1/TE2/TE3 = 2.8/5.1/7.4ms; α = 25°; FOV = 220 mm × 220 mm, slice thickness = 5.0 mm, slice gap = 5 mm; interleaved, number of slices= 6, number of averages = 1, Matrix size = 128 × 128, receiver bandwidth = 50 kHz; number of time points sampled on the relaxation curve = 20; TI = 30 ms and preparation delay τ= 2s. Imperfections due to the non-perfect inversion of the magnetization in TAPIR were corrected which is required for an unbiased determination of T1 [21, 22].

Gd-DTPA (MW= 938 Da; Bayer Healthcare) was injected automatically within 2 seconds as a rapid bolus i.v. after the acquisition of first T1 image. Subsequent T1 images were acquired post-injection of Gd-DTPA.

2.5. Data processing

Data processing were performed with custom software written in MATLAB (Mathworks, Natick, MA) and implemented on a PC running Ubuntu Linux12.4. The first step in data processing was to create the time series of T1 maps from echo images [23]. After the reconstruction of T1 maps, post-processing for de-noising and motion correction were done to prepare data for further analysis [24].

For a human study, MR signal intensity was sampled from a volume of interest (VOI) placed on the superior sagittal sinus. Within this volume a voxel with a maximum dynamic range of intensity and a minimum noise was selected by evaluating the time activity curve of all voxels in this volume. Likewise, to obtain T1-[Gd-DTPA] data from the phantom a VOI was selected by placing a circle in the center of the cross section of each bottle in the image with a radius less than the radius of the circles (to avoid noise in the boundary of images). Within this VOI the average of the signal intensity was selected to represent the MR signal dynamics for [Gd-DTPA] calculation. A commonly accepted constant-relaxivity relationship between T1 and [Gd-DTPA] was used to estimate [Gd-DTPA] in the VOI in T1 images.

$$\mathrm{\Delta }\left(\frac{1}{T1\left(t\right)}\right)={\mathrm{r}}_1\left[\text{Gd}-\text{DTPA}\right].$$ (1)

Where r₁ is the relaxivity (mM⁻¹s⁻¹; which is reported for water experiment to be 4.79 [17], and 4.7±1 [25] and 5.1 for cell culture medium [25]) and [Gd – DTPA] is the concentration of Gd-DTPA in mmol at time t. This equation linearly relates the deviation of the inverse of T1 from the baseline T1₀ to the [Gd-DTPA] in the tissue regardless of the exchange limits.

2.6. Pharmacokinetic Study

Pharmacokinetic parameters of Gd-DTPA were calculated using R statistical environment (version 3.0.2, R Development Core Team 2013) [26]. We used two PK approaches [27]: 1) non-compartmental PK analysis for single accessible compartment, and 2) compartmental PK analysis of time-concentration data for two accessible compartment model. Non-compartmental PK analysis were conducted with the assumption of a single accessible compartment for Gd-DTPA. As a measure of Gd-DTPA exposure, we calculated the area under the time-concentration curve $\left(\text{AUC}\right)\text{AUC}={\displaystyle {\int }_0^{\infty }c\left(t\right)dt}$, and the area under the first moment of the time-concentration curve $\left(\text{AUMC}\right)\text{AUMC}={\displaystyle {\int }_0^{\infty }tc\left(t\right)dt}$. The mean residence time (MRT), $\text{MRT}=\frac{AUMC}{AUC}$, and the clearance (CL) were also calculated from AUC and AUMC. We used Bootstrap-t resampling approach implemented in PK package of R to estimate these PK parameters. We also used segmented liners fit package of R to estimate segmented linear relationships between 1/T1 and [Gd-DTPA].

For compartmental analysis, biexponential modeling of Gd-DTPA data were employed with the assumption that Gd-DTPA is cleared from the plasma compartment into tissue and renal compartments. In compartmental analysis, indexes of Gd-DTPA persistence; two-phase half-life [28, 29] of Gd-DTPA for a dose of 0.025 mmol/kg were estimated by using a biexponential model,

$$y={\mathrm{a}}_1{e}^{-{\mathrm{b}}_{1}t}+{\mathrm{a}}_2{e}^{-{\mathrm{b}}_{2}t}\text{with}{\mathrm{b}}_1>{\mathrm{b}}_2>0.$$ (2)

All four parameters of the model a₁, a₂, b₁, and b₂ were estimated by best fitting the data to the model. Four different measures have been investigated for best fitting the data to biexponential functions: ordinary least square on normal data, weighted least square, iteratively reversed weighted least square, and ordinary least square on logarithmic data.

3. RESULTS

3.1. Phantom Experiment

Different doses of Gd-DTPA in aqueous environment resulted in different relaxation curves (Fig 1A). These relaxation curves were used to calculate T1 values and generate T1 maps (Fig 1B). The relationship between 1/T1 values and [Gd-DTPA] in the aqueous environment of phantoms was nonlinear for doses between 0.0 to 0.5 mmol/kg (Fig 1C). Figure 1C shows that data fitted to a segmented linear function around a quarter dose with a lower mean square error than nonlinear model. While the rate of change of T1 in response to change in [Gd-DTPA] in aqueous environment of phantom was higher for a lower [Gd-DTPA], it was lower for a higher [Gd-DTPA] (>0.1mmol/kg, Fig 1D).

Figure 1. Relationship between [Gd-DTPA] and T1 acquired by a fast T1 mapping is nonlinear.

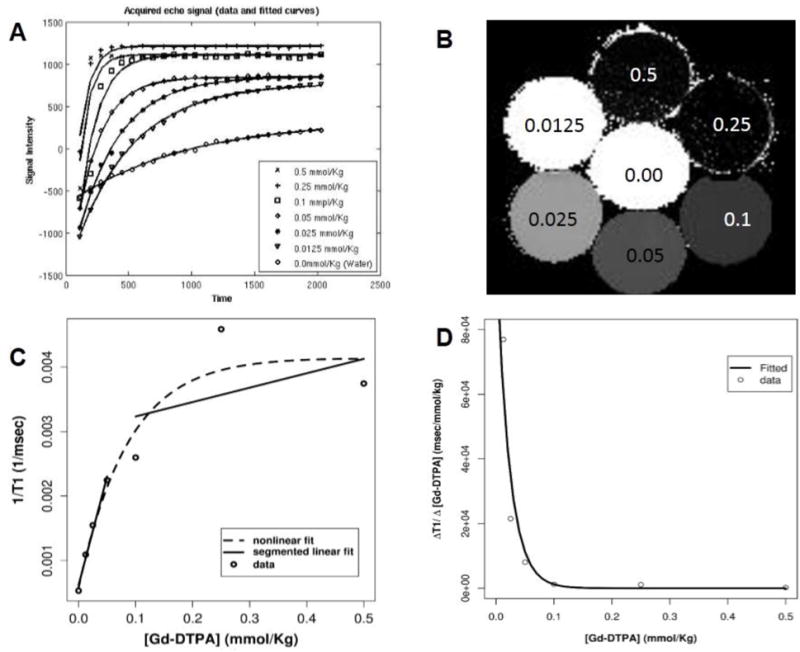
A) The acquired echo signals with the fitted curves to calculate T1 for different [Gd-DTPA]. B) Illustration of T1 map of coronal section of the phantom (2mm thickness). [Gd-DTPA] (mmol/kg) for each bottle of the phantom is shown over each circle for various concentrations from zero to 0.5 mmol/kg. C) Relationship between T1 and [Gd-DTPA] for concentrations less than 0.5 mmol/kg is represented. Open circles represent sampled values for 1/T1 for different doses of Gd-DTPA. Dotted line represent a biexponential fit to the data. Solid lines represent a segmented linear fit to the data. There are two linear models for the lower dose and higher dose of Gd-DTPA. D) The ratio of changes of T1 over the change of [Gd-DTPA] for different dose of Gd-DTPA is illustrated.

3.2. Blood Experiment

Fitting clinical time-[Gd-DTPA] data to biexponential functions shows that the coefficients of exponents are linearly dependent on the dose of bolus injection (Fig 2). While one of the exponents of the model was dose-dependent, the other exponent was dose-independent. By fitting linear functions to values obtained for each parameter of the biexponential model for all concentrations we obtain the following time-concentration equation for Gd-DTPA. This model shows that the PK of Gd-DTPA not only depends on time but it also depends on the initial concentration.

$$\left[CRp\right]\left(t\right)=0.4\ast C{R}_0\ast (e^{-\left(CR0\ast 2\ast t\right)}+e^{-\left(0.008\ast t\right)})$$ (3)

In this equation CR₀ is the initial [Gd-DTPA] in the plasma, which is sampled immediately after the bolus injection. Note that for simplicity the exponents of the model were obtained by a linear regression on all exponents of models of different doses.

Figure 2. Time-concentration profile of clinical laboratory data of Gd-DTPA after an i.v. bolus administration of four different boluses of Gd-DTPA.

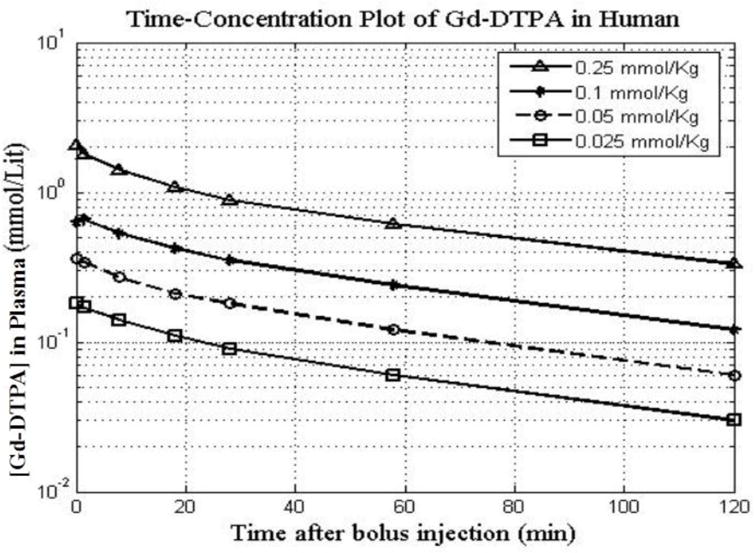
Data and fitted curves for 120 mins after the bolus injection are represented. Concentration-time data of Gd-DTPA for four different aqueous solution i.v. bolus-injected dose of 0.25, 0.1, 0.05, and 0.025 mmol/kg with the fitted curves for 120 mins after the bolus administration are represented. Each dose was i.v. bolus administered to a group of 5 controls. Concentration of Gd-DTPA was sampled by drawing blood and recording for two hours after the i.v. injection. It is safe to assume that in a healthy condition Gd-DTPA homogenously distributed through the body with body tissue density of 1 kg/L, thus the concentration of mmol/kg is equal to mmol/L.

3.3. MR-acquired Data

Dynamics of T1 values measured with TAPIR, a sequence developed for the accurate determination of T1 [22] every 3 mins for four [Gd-DTPA] shows the difference in T1 values and the difference in change in T1 values (Fig 3). The following biexponential functions were best fitted to the data represented in Fig 3 for bolus doses of 0.1, 0.05, 0.025, and 0.012 respectively.

$$\begin{array}{c}{[Gd-DTPA]}_{0.1}=0.099e^{-0.099t}+e^{-0.008t}\\ {[Gd-DTPA]}_{0.05}=0.038e^{-0.046t}+e^{-0.008t}\\ {[Gd-DTPA]}_{0.025}=0.018e^{-0.062t}+e^{-0.008t}\\ {[Gd-DTPA]}_{0.012}=0.009e^{-0.056t}+e^{-0.008t}\end{array}$$ (4)

The lack of linear relationship (as also observed with clinical data) between exponents and coefficient of concentration equations for different doses indicates that the linear relation between T1, as acquired by TAPIR, and [Gd-DTPA] for a range of 0.1 – 0.012 mmol/kg does not exist.

Figure 3. Dynamics of T1 for different dose of i.v. bolus of Gd-DTPA as sampled from inferior and superior sagittal sinuses.

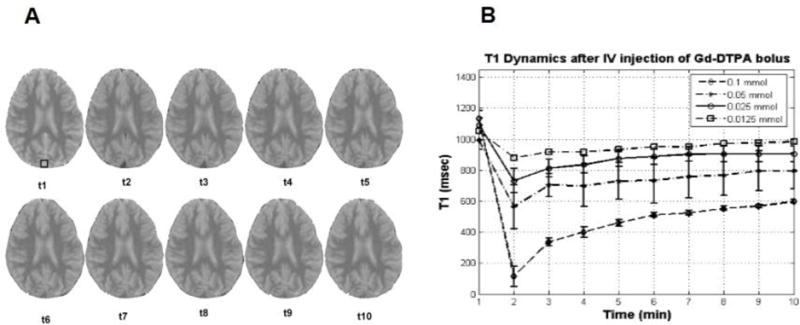
A) A representative series of T1 maps showing changes in the contrast as a result of Gd-DTPA dynamics. Inferior and superior sagittal sinuses sampled to represent the concentration of Gd-DTPA in the plasma. B) T1 changes for four different doses of Gd-DTPA are represented. For each dose the first T1 is sampled before the bolus injection. The nine other consecutive samples of T1 acquired after the bolus injection. In this figure T1 dynamics is shown with error bars for four groups of subjects. The curve is connecting the mean values for each group and represents the mean of T1 dynamics.

3.4. Pharmacokinetic Analysis

The estimate of parameters of the PK of Gd-DTPA for four different bolus i.v. doses, by employing a non-compartmental model, are summarized in Table 1. The non-compartmental half-life was higher for dose of 0.025 mmol/kg Gd-DTPA and was inversely proportional to the dose except for the dose of 0.012 mmol/kg. As expected, the value of AUC was reduced in proportion to the bolus dose, but the clearance (CL) decreases as bolus dose decreases except for the dose of 0,012 mmol/kg.

Table 1.

Pharmacokinetic parameters of Gd-DTPA after i.v. injection with different bolus doses in four groups of healthy controls calculated by employing a non-compartmental model.

Dose (mmol/Kg)	CL (mL/min)	MRT (min)	AUC0-to-infinity (mmol.min/L)	AUMC0-to-infinity (mmol.min2/L)	Non-compartment half (min)
0.100	0.075	33.48	13.39	448.0	23.23
0.050	0.012	40.23	4.05	163.0	28.58
0.025	0.009	43.11	2.80	121.0	30.00
0.012	0.014	28.40	0.89	25.4	19.70

AUC = area under the time-concentration curve; AUMC = area under the first moment of time-concentration curve; CL = clearance; MRT = mean residence time.

Point estimates of parameters of the PK of Gd-DTPA with a bolus of 0.025 mmol/kg dose for 58 cases along with standard errors (SE), and bootstrap-t confidence intervals are given in Table 2. The non-compartmental half-life was 38.4 mins with 95% confidence interval ranging from 29.75 to 57.47. Comparison between values of MRT, AUC and AUMC estimated at different doses of Gd-DTPA (Table 1) and corresponding values estimated from 58 subjects at 0.025 mmol/kg dose (Table 2) shows that the values represented in Table 1 are within the confidence interval of corresponding values represented in Table 2.

Table 2.

Pharmacokinetic parameters of Gd-DTPA after i.v. injection of bolus of 0.025 mmol/Kg for 58 healthy volunteer calculated by employing a non-compartment model.

PK Parameter	Estimate	SE	95% boott-CI
AUC0-to-24 (mmol.min/L)	1.078	0.0091	(1.067; 1.09)
AUC0-to-infinity (mmol.min/L)	3.3725	0.4658	(2.77; 4.6575)
AUMC0-to-infinity (mmol.min2/L)	181.53	57.278	(120.27; 362.413)
MRT (min)	53.82	9.5624	(41.6314; 80.305)
non-comp. half-life (min) 37.309	6.628	(28.84; 55.6633)
CL (mmol/min)	0.0741	0.0102	(0.0516; 0.0929)
VSS (mmol)	3.9901	0.1648	(3.7043; 4.3684)

AUC = area under the time-concentration curve; AUMC = area under the first moment of time-concentration curve; CL = clearance; MRT = mean residence time; SE = standard errors; VSS = volume of distribution at steady state.

Samples of the PK of Gd-DTPA for bolus dose of 0.025 mmol/kg and the fitted biexponential function for all 58 subjects are shown as a scatter plot in Fig 4. Though the bolus size was the same in this experiment, variation was observed in post-injection T1 values (Fig 4). This variation in T1 values reduces slightly over time but not significantly. Moreover, longitudinal analysis of individual data revealed that higher T1 values tend to stay higher over the time. The slope of dynamics of T1 in individuals follow the same pattern as others. In population analysis, a dose of 0.025 mmol/kg of Gd-DTPA provided less than 5% subject-dependent variation in the PK of Gd-DTPA (Fig 5).

Figure 4. Population PK of a single dose (0.025 mmol/kg) of Gd-DTPA as administered via an i.v. bolus and measured indirectly by measuring T1 alterations in inferior and superior sagittal sinuses.

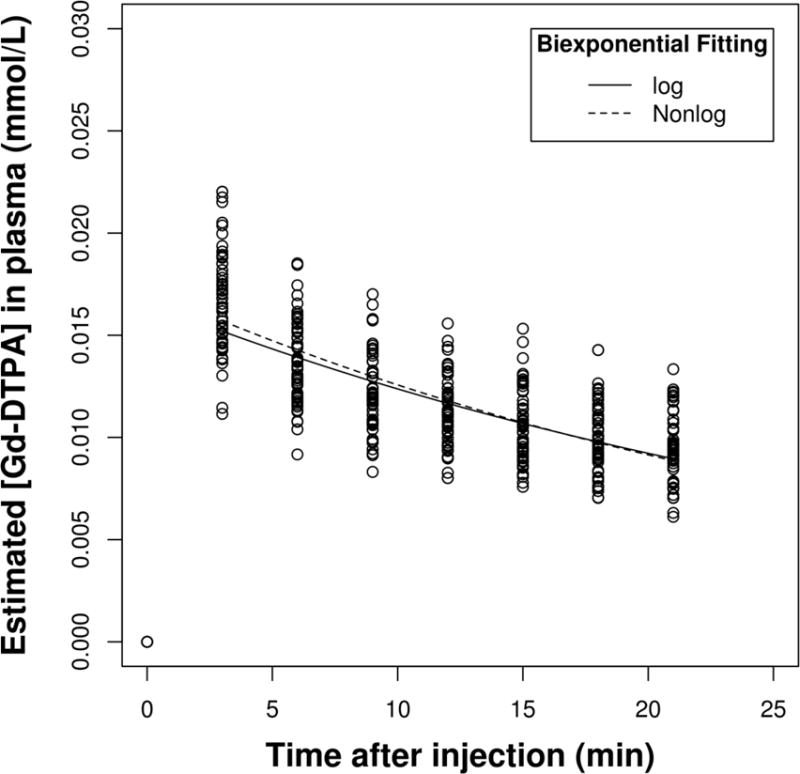
MR-acquired PK of Gd-DTPA from 58 subjects (28–80 years, M/F) were collected retrospectively, from an ongoing study of the brain using DCE-MRI with Gd-DTPA at 0.025 mmol/kg. Nonlinear fitting of population time-concentration data to biexponential functions for a bolus of a 0.025 mmol/kg dose of Gd-DTPA is represented in normal and logarithmic scale for clarity.

Figure 5. Intra-Subject variation in time series of T1 acquired after a bolus dose of 0.025 mmol/kg Gd-DTPA.

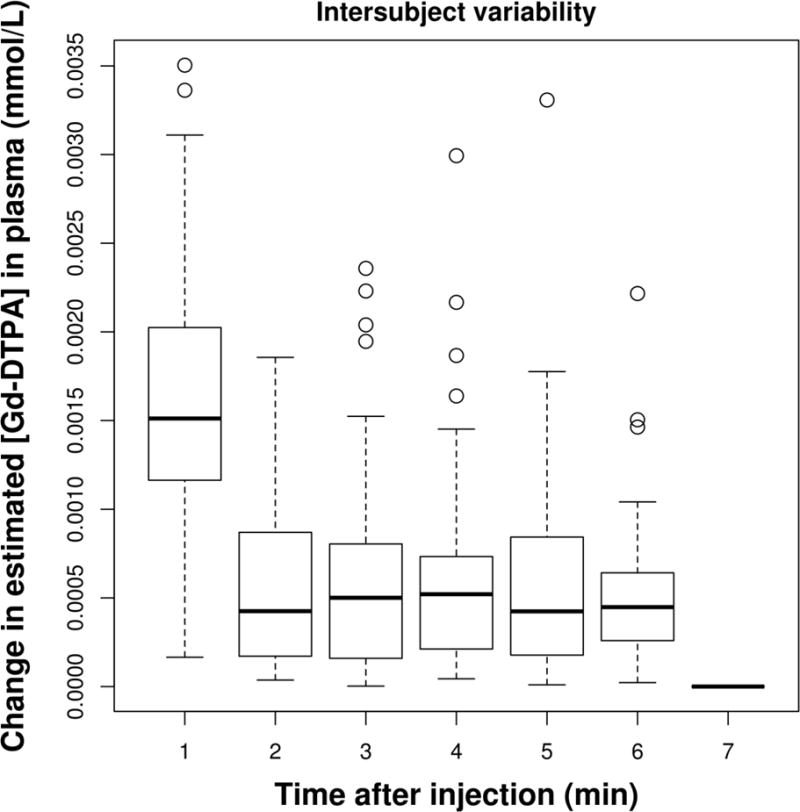
MR-acquired PK of Gd-DTPA from 58 subjects (28–80 years, M/F) were collected retrospectively, from an ongoing study of the brain using DCE-MRI with Gd-DTPA at 0.025 mmol/kg. The rate of change of T1 time series were compared between 58 subjects of the study. The rate of change of T1 for a bolus dose of 0.025 mmol/Kg of Gd-DTPA provided less than 5% subject-dependent variation.

Results of two-compartment analysis of time-concentration data of Gd-DTPA with 0.025 mmol/kg dose in all of the 58 subjects are shown in Table 3. A two-phase half-life estimation of terminal half-life of Gd-DTPA is given in this table along with slope and intercept of phases. The second phase half-life is smaller than the half-life calculated in non-compartmental model. Weighted least square model has the least standard error in parameter estimation when a biexponential model is used to model the PK of Gd-DTPA (Table 4).

Table 3.

The estimate of initial and terminal half-life of Gd-DTPA with slope and intercept for normal and log scale of data.

	Normal Scale		Logarithmic Scale
	initial	terminal	initial	terminal
half-life (min)	0.03824025	23.58440083	0.03346895	21.80187352
slope	18.12611655	0.02939007	20.71015629	0.03179301
intercept	0.12526617	0.05595425	0.18371797	0.05823089

Table 4.

Estimated parameters of biexponential function fitted to time-concentration data.

Estimate	Std. Error	t value	Pr(>|t|)
a1 0.033640	0.006747	4.986	9.38e-07***
b1 0.299737	0.140316	2.136	0.0333*
a2 0.044781	0.005588	8.013	1.38e-14***
b2 0.015764	0.006391	2.467	0.0141*

4. DISCUSSION

The major outcomes of the present report can be summarized as follows: (1) The relationship between [Gd-DTPA] and R1 (1/T1) for a bolus dose of 0.025 mmol/kg i.v. administered Gd-DTPA can be well approximated by a segmented linear model; (2) the clearance of Gd-DTPA is dose-dependent; (3) the rate of change of T1 for a bolus dose of 0.025 mmol/Kg of Gd-DTPA provided less than 5% subject-dependent variation.

The reciprocal relationship between T1 and [Gd-DTPA] is complex, a best existing estimate of this relationship is a nonlinear function. However, this estimate, as can be also observed from our data (Fig 1C), is not a comprehensive, accurate estimation of T1 and [Gd-DTPA] relationship. The use of a model that accurately results the [Gd-DTPA] is important for DCE-MRI data processing. This only happens if the model has least estimation error around the [Gd-DTPA] in the area on interest. We found that the use of segmented linear estimation method around a lower dose of Gd-DTPA results a least estimation error in the T1-[Gd-DTPA] relationship. By using this estimation technique we found that for lower doses of [Gd-DTPA] the estimated relationship has the least estimation error.

We also investigated the rate of change of T1 over the change of [Gd-DTPA] for doses around this lower dose. We found that the ratio is at its highest for this dose as it is shown in Fig 1D. This is an important observation since in DCE-MRI it is desirable to amplify the dynamics of [Gd-DTPA]. Comparing the PK of Gd-DTPA for four different doses, we found that the half-life of Gd-DTPA in plasma, when administered as a bolus i.v., depends on the primary dose; higher doses of injected Gd-DTPA caused a greater reduction on T1 by the end of wash-in period. More importantly, the effect of Gd-DTPA on signal intensity in the washout period does not follow a linear relationship with the primary dose. Twenty-one minutes after the injection of Gd-DTPA, the percentage of T1 that recovered from the original reduction after 3 minutes is 43% for higher than and 48% for lower than 0.1 mmol/kg dose.

Gd-DTPA similar to many other MR contrast agents designed to influences solvent water relaxation. This depends on the magnetic field strength and molecular environment parameters [30]. Unpaired electrons around metal creates dipole-dipole effects that draws magnetization and shortens T1. In an in vivo experiment with Gd-DTPA Kalavagunta et. al. have observed a quadratic relationship between T1 relaxivity, r_1, and [Gd-DTPA] below the dose of 2mM and a linear relationship for concentration higher than 2mM [31]. Similar to their observation For [Gd-DTPA] below 1mM (we tested here in an aqueous phantom) we did not observe a linear relationship for the whole range.

The difference between the aqueous and the plasma environment effect on T1-[Gd-DTPA] relation was tested here. Our data from aqueous phantoms, as well as the data obtained directly from plasma, were in agreement with time-concentration data that we acquired by using MRI. All these three data sets confirming the dose-dependent nature of the clearance of Gd-DTPA. Not only the bolus dose, but also other parameters such as the influence of macromolecular content [32] and compartmentalization of brain extracellular space, complicate the relationship between r₁ and [Gd-DTPA] [16].

Using a higher relaxivity contrast agent is another option to reduce the bolus dose of contrast agent. For example, gadobenate dimegulumine (Gd-BOPTA) with a 0.05 mmol/kg dose, was used to attain a comparable contrast enhancement in the brain [7]. A contrast agent with a higher relaxivity generates higher signal intensity than the lower relaxivity one, but the dynamics of the generated signal may be the same as the signal generated by a low-relaxivity contrast agent. Therefore, for the applications that are based on the dynamics of a contrast agent using a high-relaxivity agent may not offer a big improvement. Here, we tested the possibility of reducing the dose of Gd-DTPA to attain a linear relationship between signal intensity and [Gd-DTPA]. We observed that the lower dose of Gd-DTPA (0.025 mmol/kg), at 1.5T magnetic field and 3T (data are not shown here), offers a segmented linear relationship between [Gd-DTPA] and R1.

This relationship can be used to calculate the rate of [Gd-DTPA] change correctly in the tissue of interest by having the MR data. This relationship is not valid for a higher [Gd-DTPA] as it can be observed from the phantom data (Fig 1). It is possible that for a higher dose the effect of individual variations become significant. For comparative studies with T1 DCE-MRI it is important to attain a reduced intra-subject variability in r1. For this reason, we investigated the lower dose for its relaxivity and also intra-subject variability in human.

Individual differences are an important consideration for studies involving PK of a contrast agent. Though the bolus size per kilogram of body weight was constant in this experiment, the T1 effect of Gd-DTPA was not the same (Fig 4). However, the slopes of the dynamics of T1 in individuals follow the same pattern as others. Results of two-compartment analysis of time-concentration data of Gd-DTPA with a dose of 0.025 mmol/kg in 58 subjects are shown in Table 3. A two-phase half-life estimation of terminal half-life of Gd-DTPA is given in this table along with slope and intercept of phases. The second phase half-life is smaller than the half-life calculated in non-compartmental model. Weighted least squares model has the least standard error in parameter estimation when a bi-exponential model is used to model the PK of Gd-DTPA (Table 4).

The present study also has some caveats: the very limited number of patients for each sub-group of Gd-DTPA doses is a limitation of this study. However, for the purpose of this study, a large number of patients in the final dose is important where we conducted statistical analysis. In this study we selected Gd-DTPA because of its popular use in clinics, however, more studies with different contrast agent, specifically with high relaxivity contrast agents are needed to understand the variation of R1-[contrast agent] relationship. The present study was carried out on a 1.5T magnet and part of the experiments were repeated with 3T all under normal room temperature. In this study we did not investigate the effect of temperature, pH, and magnetic field strength on R1-[Gd-DTPA] relationship. In addition, we collected T1w data by using TAPIR sequence, using a different T1 mapping sequences may result a different outcome; it is nevertheless noted that TAPIR has been demonstrated to have a very high accuracy and precision [21, 22]. We selected the dose of 0.1 mmol/kg as the standard dose in the present study because it has been largely used in clinics without any serious side effects [33]. For this study we halved this dose 3 times (0.1, 0.05, 0.025, and 0.0125) to investigate the effect of dose on T1-[Gd-DTPA] relationship.

Another limitation of this study is the lack of absolute determination of [Gd-DTPA] in the plasma independent of MRI data. The absolute data acquired from the manufacturer were used to investigate the dynamics of [Gd-DTPA] this absolute data then was used to build a model for pharmacokinetics of Gd-DTPA. This model then was used to estimate [Gd-DTPA] from the MR data.

5. CONCLUSIONS

The dose of bolus i.v. administered Gd-DTPA is an important parameter in DCE-MRI studies because of the importance of Gd-DTPA PK parameters. We conclude that a quarter dose of 0.1 mmol/Kg of Gd-DTPA offers a minimum error in estimation of [Gd-DTPA] by using T1 values. Moreover, the administration of this dose renders a higher change in T1 in relation to change in [Gd-DTPA]. This is a desired property for DCE-MRI.

A bolus of 0.025 mmol/kg Gd-DTPA, with a half-life of 37.3 ± 6.6 mins, a mean residence time of 53.8 ± 9.5, and an AUC of 3.37 ± 0.47 mmol.min/L, which is less than the AUC of higher doses, results in less exposure of patients to Gd-DTPA, Lower dose of Gd-DTPA together with optimized acquisition of DCE-MRI, offers shorter acquisition time and less exposure of subjects.