Rheology of clustering protein solutions

Abstract

High viscosity is a major challenge with protein therapeutics at extremely high concentrations. To overcome this obstacle, it is essential to understand the relationship between the concentration of a protein solution and its viscosity as a function of shear rate and temperature. Here, lysozyme is a model charged globular protein having both short-ranged attraction (SA) and long-ranged repulsion (LR) that promote the formation of dynamic clusters at high concentrations. We report viscosity measurements from a micro-capillary rheometer (using only several microliters of solution) over a wide range of lysozyme solution concentrations, shear rates, and temperatures. Solution structural relaxation dynamics are also probed by dynamic light scattering (DLS). As a result of lysozyme's SALR interactions, the viscosity increased dramatically across all shear rates with increasing concentration and decreasing temperature. While most of the solutions exhibited Newtonian behavior, shear thinning was exhibited at the highest concentration (480 g/l) and lowest temperatures at shear rates above approximately 10⁴s⁻¹. The onset shear rate for thinning and a structural relaxation rate estimated from a slow-mode measured by DLS are compared. These measurements provide insights into the properties of protein solutions and their microscopic structural origins.

I. INTRODUCTION

Over the past 30 years, multiple advances have been made in the field of immunology. One of the notable advances has been the use of monoclonal antibodies (mAbs) to treat various diseases.^1,2 However, as effective as mAbs may be at countering many diseases, their potency must not be compromised by certain manufacturing or storing processes.³ In order to meet dosage and volume requirements of subcutaneous injections, antibody solutions are prepared at concentrations exceeding 100 g/l.⁴ Such high concentrations also occur naturally in intracellular environments for endogenous proteins. Thus, the high concentration solution behavior of proteins is broadly of interest. In concentrated solutions, the relationships between molecular conformation, intermolecular interaction, clustering (reversible and irreversible aggregation), and viscosity are complex.^5,6

In comparison with mAbs, lysozyme has similar interactions but a much simpler structure and shape. Lysozyme is a globular protein whose tertiary structure resembles an ellipsoid.⁷ For simplicity, its excluded volume can be approximated as a hard sphere colloid.⁸ Unlike most synthetic colloidal particles, however, a lysozyme molecule is not uniformly charged,⁹ which produces an appreciable dipole moment. These non-uniformities and other local hydrophobic and van der Waals interactions cause lysozyme to have an attractive potential at short range.^10,11 The significant net charge of lysozyme (approximately +9/molecule at low salt conditions¹²) produces repulsive interaction at long range. The interplay between these short and long range forces is common for some proteins, including mAbs,¹³ and it governs clustering, phase behavior, and solution viscosity.^14,15 Short-ranged attraction (SA) drives clustering and long-ranged repulsion (LR) limits the local range of association, producing supramolecular strands of so-called intermediate range order (IRO),⁸ i.e., local concentrations of protein molecules clustered together, sometimes forming interconnected percolated filamentous networks.^14,16 With such clustering, the solution often becomes more viscous.¹⁷ Both concentration and temperature play a role in the local dynamics and thus viscosity.

Specifically, in a recent neutron-spin-echo scattering study of high-concentration salt-free lysozyme solutions that exhibit IRO, we observed localized glassy-like dynamics at high protein concentrations and low temperatures.¹⁸ Under these conditions, the structure and dynamics resemble attractive colloidal gels,¹⁹ but lysozyme is at equilibrium (or quasi equilibrium at the highest concentrations, when crystallization is the equilibrium state) and thus exhibits Newtonian behavior at long times. These results motivate the present search for viscoelastic behavior of the system. This anticipated viscoelasticity was not observed in our previous study because of pressure and flow rate limitations of the rheometer used then. Instead, the steady shear rheology over a broad parameter space of temperatures, concentrations, and shear rates was Newtonian. The primary objective therefore of the current study is to use a similar microcapillary rheometer with expanded dynamic range to test lysozyme solutions at higher shear rates comparable to inherent diffusion and relaxation time scales in dense solutions. With this new capability, shear rates exceeding 10⁵s⁻¹ are accessible. Since it was not necessary to test many different concentrations, we sample only a few here. Although shear rates of this magnitude occur during injection of drug products through small diameter needles, this study is not motivated specifically by such applications. Rather, it aims to elaborate the dynamics of clustering fluids which exhibit localized glassy dynamics.¹⁸ These measurements shed light on the inherent dynamic characteristics of lysozyme solutions with IRO structure and of clustering protein solutions in general.

II. MATERIALS AND METHODS

A. Instrumentation

A detailed description of the microfluidic rheometer was published previously.²⁰ Briefly, we describe the salient features of the microcapillary rheometer. A hydrostatic pressure difference is applied to drive protein sample through a narrow (approximately 30 μm diameter) borosilicate glass microcapillary, whose hydrodynamic resistance is calibrated with water (see details below). The protein solution pushes water through a flow meter. The recorded pressure, flow rate, and calibration determine the shear stress, shear rate, and viscosity at the microcapillary wall.

To access higher shear rates and stresses, some components of the previous rheometer were replaced. Here, we use the following components: an OB1 (Elvesys, see Acknowledgments) pressure controller (equipped with low pressure channels up to 2 × 10⁴ Pa and high pressure channels up to 8 × 10⁵ Pa) and Flowell, MFS-2 and MFS-3 flow meters (Fluigent and Elvesys, up to 0.13 μl/s and 0.9 μl/s, respectively). Measurements from different flow meters were consistent within uncertainty. The length L and diameter d of the narrow section of a microcapillary are selected to achieve high shear rates, depending on the limits set by the maximum flow rate (0.9 μl/s) and pressure (8 × 10⁵ Pa). If the primary limitation is volumetric flow rate, high shear rate is achieved by small d. If, however, the primary limitation is pressure (e.g., when sample viscosity is high), high shear rate is achieved by relatively small L/d. Based on the latter consideration, microcapillaries with L/d ranging from 9 to 50 were used here. In contrast to the previous rheometer,²⁰ higher flow velocities and smaller L/d meant that kinetic energy of the fluid must now be accounted for. At the highest flow rates here, the residence time of the fluid in the narrow section of the microcapillary is approximately 1 ms; the flow velocity is approximately 1 m/s and the Re number may be up to 30. In such circumstances, the viscosity is no longer given by the Hagen-Poiseuille equation. An additional term arises from kinetic energy, and the viscosity of the sample η_s(T) is given by:²¹

$${\eta }_s\left(T\right)=\frac{\Delta P}{K_{c}Q}-{\eta }_w\left(T_{\mathit{m}\mathit{e}\mathit{t}\mathit{e}\mathit{r}}\right)\frac{K_{\mathit{m}\mathit{e}\mathit{t}\mathit{e}\mathit{r}}}{K_c}-C\left|Q\right|,$$ (1)

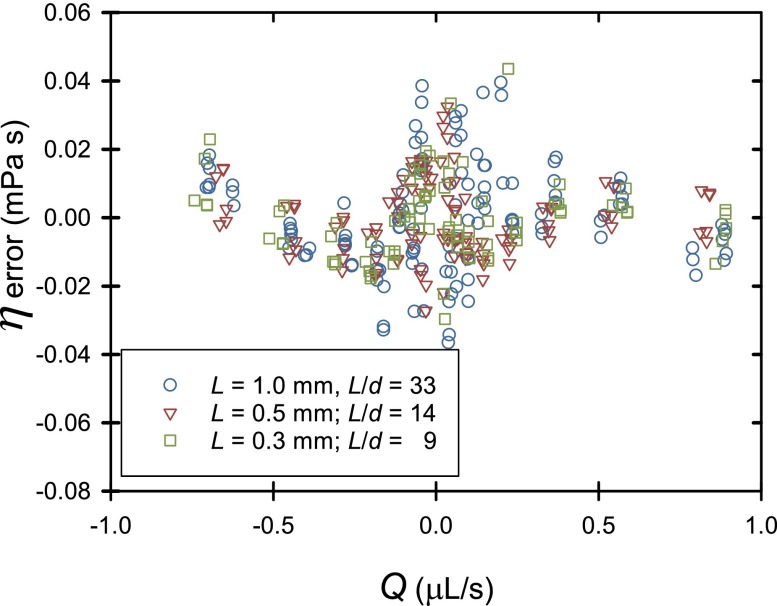
where ΔP here is the total pressure drop across the system and the 2^nd term accounts for the pressure drop across the flow meter. Q is the flow rate through the rheometer, and the factors K_i are calibration constants that are approximately the Hagen-Poiseuille constants $\frac{128L_i}{\pi d_i^4}$, considering the length and diameter of microcapillary c or meter. The 3^rd term is the kinetic energy (Bernoulli) contribution. Since the two ends of the microcapillary have different shape (one tapered the other not), the calibrated value of C depends on the flow direction. Residual errors are a few percent (see Fig. 1). These errors were not further corrected. The similarity of these residuals for different microcapillaries suggests that their source may be in calibration of the flow meter readings. In other work, NIST is addressing these concerns.

FIG. 1.

Residual errors after calibration of microcapillaries with water to determine best fit values of K_meter, K_c, and C.

Temperature is maintained as before²⁰ with an insulated multishell temperature chamber, heated or cooled by a Peltier plate. Peltier power and pneumatic pressure are both controlled through a program written in LabVIEW that in turn reads pressure output, temperature (through Pt-resistance thermometers), and flow rate. Using these readings, the Rabinowitsch correction for shear rate²² is applied and an accurate viscosity can be determined.

B. Preparation of lysozyme solutions

Purified lysozyme²³ (MW = 14.3 kDa) powder was stored at −20 °C. The container of lysozyme was allowed first to equilibrate to room temperature to avoid condensation of humidity. The solutions were prepared gravimetrically and the mass data were converted to g/l using the partial specific volume of lysozyme (0.717 cm³/g) and the density of D₂O (1.107 g/cm³). When making dilute solutions with concentration less than 350 g/l, lysozyme powder and D₂O are mixed in a vial using a vortex mixer at room temperature. Such solutions are at equilibrium. Vortex mixing creates bubbles and causes shearing. The shear rate there is rather modest. As the container is rotated rapidly (2800 rpm or 47 Hz), the swirling liquid is estimated to be sheared roughly 10 strain units or less per cycle. The shear rate during mixing is therefore of the order of 500 s⁻¹. Once all visible clumps disappear, the solution is then filtered (for scattering experiments) and stored in another vial at 4 °C. Filtering did not change the concentration when checked occasionally by uv-vis spectroscopy, and it is performed merely to remove any large foreign particles that would disturb scattering measurements. Filtering did not change viscosity results. In order to form more concentrated solutions (greater than 350 g/l), the same procedure is followed while all equipment and solutions are handled at 50 °C. Details of this procedure can be found elsewhere.¹⁸ These solutions are metastable for 6 h to 21 h, depending on the concentration and the temperature.

Significant unexplained differences in diffusivity and viscosity were observed between different batches of lysozyme powder, i.e., the results reported here from one batch of lysozyme are less viscous than those reported previously¹⁸ from an older batch. The cause of this difference may be some salt impurity, but we have not resolved this question.

C. Testing and analysis

The parameter space covered in this study includes lysozyme solution concentrations ranging from 140 g/l to 480 g/l, shear rates ranging from 10¹s⁻¹ to 10⁵s⁻¹, and temperatures ranging from 5 °C to 50 °C. Protocols for operating the rheometer and its data acquisition were both handled by a program written in LabVIEW. This program directly controls the two pressure channels used, thus dictating the flow rate. The pressures are adjusted automatically to geometrically scan a wide range of pressure drops. The operator can select whether the system begins at low magnitude pressure drop and scans to high magnitude, or the reverse. At each setting, flow rate is monitored over time to determine when the flow reaches steady state.²⁰ Further, the flow rate, pressures, and chamber temperature are monitored during the time period of steady flow to calculate the mean and uncertainty of each parameter. These measurements are used to obtain the solution viscosity. Tests were run multiple times to check the reproducibility of the results, and the sequence of pressure drops was changed to determine if the measurements depend on the shear rate history.

D. Dynamic light scattering (DLS)

Dynamic light scattering (DLS) of lysozyme solutions was performed using a Wyatt DynaPro NanoStar to measure collective diffusivity.²⁴ The intermediate scattering function, $I(q,\tau )$, was calculated from the intensity autocorrelation function according to the Siegert relation

$$I\left(q,\tau \right)={\left(\frac{1}{\beta }\left[\frac{〈I\left(t\right)I(t+\tau )〉}{{〈I\left(t\right)〉}^2}-1\right]\right)}^{1/2}\approx A_0+A_1\hspace{0.17em}\text{exp}\left(-q^2{D}_1\tau \right)+A_2\hspace{0.17em}\text{exp}\left(-q^2{D}_2\tau \right).$$ (2)

As shown, $I(q,\tau )$ is represented by a double exponential to capture the two relaxation modes that appear at elevated protein concentrations. Alternatively, a stretched exponential A₂ exp(−(q²D₂τ)^α) replaced the last term. Here, α is the stretching exponent, $D_1$ and $D_2$ are the diffusion coefficients associated with each relaxation mode, $A_1$ and $A_2$ are the corresponding relative intensities, and $q=(4\pi n/\lambda )\hspace{0.17em}\text{sin}\hspace{0.17em}(\theta /2)$ is the scattering vector, where $n$ is the refractive index, $\theta$ is the scattering angle, and $\lambda$ is the wavelength. τ is the delay time and β is an instrument factor.

III. RESULTS AND DISCUSSION

At relatively low shear rates, all solutions had a constant viscosity which could be averaged to determine the zero shear rate viscosity η_o. As we reported previously,¹⁸ η_o increased markedly with increasing concentration of lysozyme and decreasing temperature. The substantial increase in viscosity was attributed to both caged diffusive dynamics at a length scale smaller than IRO and larger scale supramolecular clusters, which may percolate throughout. A similar increase in viscosity observed in concentrated mAb solutions has been attributed likewise to such supramolecular clustering.¹⁷ The dynamics of these structures will be elaborated by several observations below.

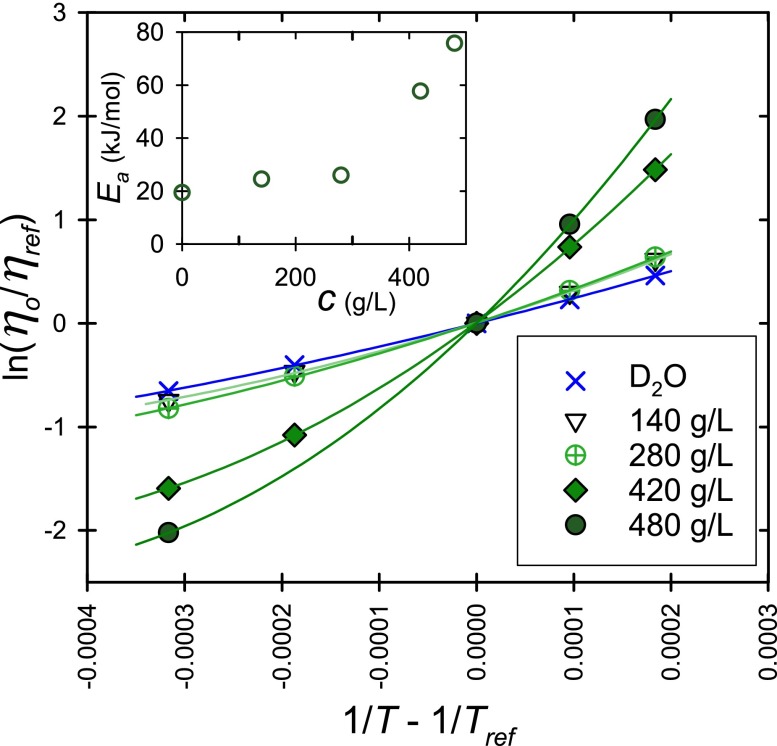
First, this previous detailed analysis¹⁷ of clustering and the localized slow dynamics at the IRO length scale in concentrated lysozyme solutions is complimented by an Arrhenius analysis (Fig. 2). In particular, effects of clustering become apparent in an Arrhenius plot of the solution viscosity by changes in activation energy and by an onset of non-linear behavior. Arrhenius behavior is represented by

$$\eta ={\eta }_{\mathit{r}\mathit{e}\mathit{f}}{e}^{\frac{E_a}{R}\left(\frac{1}{T}-\frac{1}{T_{\mathit{r}\mathit{e}\mathit{f}}}\right)},$$ (3)

where η is the viscosity of the sample, R is the gas constant, T is the temperature, and E_a is the activation energy for the motion of lysozyme molecules and clusters passing each other. The subscript “ref” indicates that the data can be expressed relative to the data at an arbitrary reference temperature, e.g., η_ref at T_ref = 20 °C. D₂O and dilute solutions of lysozyme have viscosity-temperature relationships that appear nearly linear in Fig. 2 and they thus approximate Arrhenius behavior.

FIG. 2.

Arrhenius plot of the natural logarithm of η_o as a function of the inverse of temperature, and lysozyme in solution concentration ranging from 140 g/l to 480 g/l. T_ref here is 20 °C. Inset in upper left is a plot of the apparent E_a v. protein concentration c. Standard uncertainties are smaller than the symbol size.

Two aspects of the rheology of concentrated lysozyme solutions are apparent from Figure 2. When the protein concentration increases, the slope of the Arrhenius plot, the apparent E_a, increases and the departure from linear Arrhenius behavior intensifies. For pure D₂O at 20 °C,²⁵ E_a and the second-order coefficient of a polynomial fit are (19.4 ± 0.1) kJ/mol and (61.0 ± 2.8) (kJ/mol)², respectively. The uncertainties here are estimated by a doubling of the mean square error. The corresponding values for the lysozyme solutions are larger and grow with increasing concentration. For example, at 480 g/l, the apparent E_a = (75.7 ± 0.1) kJ/mol and the second order coefficient is (591 ± 3) (kJ/mol)². The apparent E_a increases markedly at the highest concentrations (Fig. 2 inset), indicating that protein mobility within the solution microstructure is hindered and may even be locally trapped. The sizeable second order coefficient indicates significant departures from Arrhenius behavior. These departures from linearity indicate that the type of local motion (for example, the length scale of cooperative motion) changes with temperature.²⁶ Consequently, the marked increase in activation energy and non-Arrhenius behavior with increasing protein concentration observed in Fig. 2 are likely manifestations of the appearance of the localized glassy like behavior.

This Arrhenius analysis sheds further light on the IRO structure and its dynamics. The IRO as indicated by a peak observed by small angle neutron scattering experiments (at the length scale of approximately 2 to 3 protein diameters) forms in lysozyme solutions. This IRO peak has a larger magnitude at low temperatures, such as at 5 °C compared to 50 °C.¹⁸ The IRO induces local dense regions with small cage size and can be thought of as internal structures within larger protein clusters, whose extent grows with protein concentration, eventually leading to percolation.¹⁶ At low protein concentration, the protein monomers exchange in and out of the clusters and the apparent E_a is modest (Fig. 2 inset), but at elevated protein concentrations, corresponding with the largest activation energies found here, lysozyme mobility is locally caged. Moreover, the large second-order coefficient indicates that the size of local structural rearrangements is temperature-dependent.²⁶ These results are consistent with the decreased local dynamics of proteins observed by our recent neutron scattering study.¹⁸

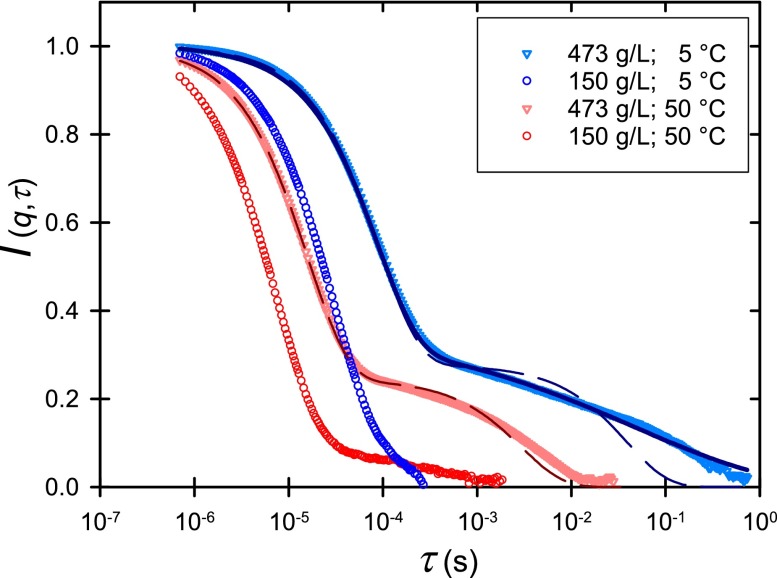
While η_o was used previously through the generalized Stokes-Einstein equation to estimate lysozyme long-time mobility,¹⁸ here we examine DLS measurements and higher shear rate rheology to identify the timescale of the relaxation of structure of these solutions. A single relaxation was observed by DLS at low and moderate concentrations (Fig. 3, Table I). In some cases, a few percent of relaxation of I(q,τ) occurs by a second mode, indicating weak changes in the solution with time despite the fact that the solutions are macroscopically stable (see supplementary material). At high concentration, an additional slow mode becomes an appreciable fraction of the relaxation process (Fig. 3). The fast relaxation is fit well by an exponential, but the slow relaxation is not a simple exponential at low temperature. The physical mechanisms of such stretched exponential relaxation have been explored elsewhere²⁶ and need future investigations. The two relaxation times themselves do not hold material significance, because they reflect the time required to dissipate fluctuations on the scale prescribed by the scattering vector q, which is much larger than the molecular, the IRO, or in some cases even the extended cluster length scale. The relevant material information therefore is in the diffusivities associated with the two relaxation modes. We assume that the fast diffusion associated with the first relaxation (D₁) is due to the relatively fast albeit caged fluctuation of proteins at the IRO length scale and that the slower mode (D₂) is possibly associated with relaxation of large clusters beyond the IRO length scale. This is qualitatively consistent with the apparent stretched exponential behavior of D₂ that can be associated with a distribution of relaxation times resulting from the variety of caged and structured environments an individual protein experiences within the heterogeneous microstructure formed under conditions with IRO.

FIG. 3.

The first-order auto correlation function from dynamic light scattering of lysozyme solution at concentrations and temperatures indicated. Dashed lines show double exponential fits and the solid line is a stretched exponential fit of the relaxation observed at 5 °C and 473 g/l.

TABLE I.

DLS data and analysis. (Uncertainties of D₂/a² can be determined simply by propagation from the respective uncertainties reported here.)

c (g/l)	T ( °C)	D1 (μm2/s)	D2 (μm2/s)	α	a (nm)	D2/a2 (s−1)
1	5	57 ± 1			1.80 ± 0.03
1	25	102 ± 3			1.95 ± 0.06
150	5	90 ± 3			1.14 ± 0.04
	20	164 ± 3			1.04 ± 0.02
	25	190 ± 4			1.04 ± 0.02
	50	346 ± 10			1.05 ± 0.03
473	5	31 ± 2	0.07 ± 0.08	1	3.3 ± 0.2	6.5 × 103
	5	31.9 ± 0.6	0.057 ± 0.009	0.30 ± 0.01	3.21 ± 0.06	5.5 × 103
	25	73.9 ± 2.3	0.23 ± 0.12	1	2.7 ± 0.1	3.2 × 104
	50	175 ± 3	0.94 ± 0.25	1	2.07 ± 0.04	2.2 × 105

From the fast diffusivity, an apparent material size can be approximated from the equivalent hydrodynamic radius a = kT/(6πμD₁), where μ is the viscosity of the solvent D₂O. Although this Stokes-Einstein relation appears to break down at time scales O(10 ns),¹⁸ it is a reasonable approximation for longer time behavior.¹⁸ At low concentrations, e.g., 1 g/l, the size a is equal to the hydrodynamic radius of the monomer (Table I).²⁷ At intermediate concentrations, repulsions between the monomers increase their cooperative diffusivity and decrease the apparent hydrodynamic size. At still higher concentrations and low temperatures, attractions, clustering, and hydrodynamic effects slow the diffusion so that the apparent size (a) becomes intermediate between the hydrodynamic radius of the monomer and of the IRO filament.

The second mode is much slower than the first. The rate of this relaxation can be estimated from the slower diffusion coefficient and the same length scale a, i.e., D₂/a² (see Table I). Similar two-step relaxation is predicted from Rouse-like dynamics of associating solutions that form equilibrium linear clusters.²⁶ In that example, like here, the first relaxation is exponential and the second relaxation is described by a cluster-size-dependent stretched exponential. In the limit of large clusters, the stretching exponent is one-third, approximately consistent with the measured relaxation at 5 °C, where α = 0.30 ± 0.01.

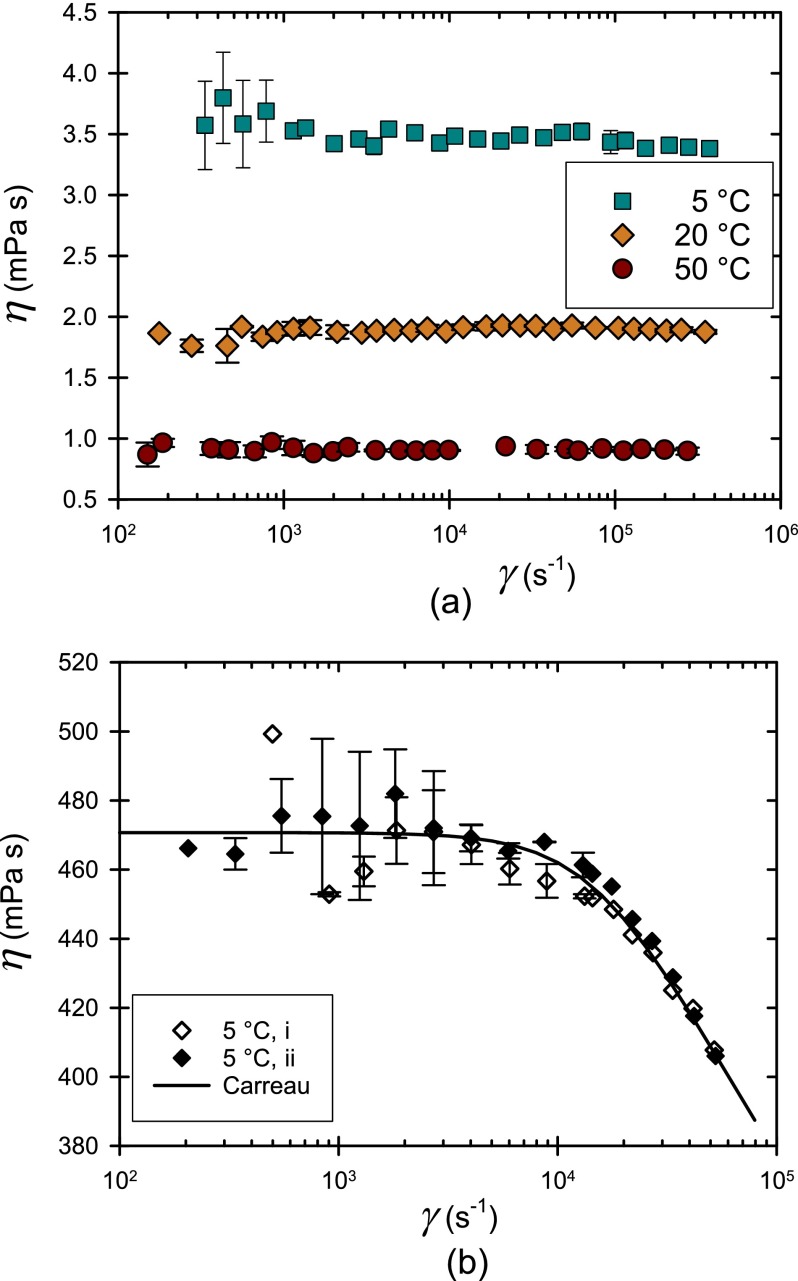
Here, we directly relate this long-time relaxation rate in concentrated lysozyme solutions to the high shear rate rheology (see Fig. 5). To do so, we tested the conditions at which lysozyme solutions exhibited non-Newtonian behavior. All but the most concentrated solutions exhibited Newtonian behavior up to the highest shear rate tested (e.g., Figure 4a shows constant viscosity as a function of shear rate for a 140 g/l lysozyme solution up to 4 × 10⁵s⁻¹). In these cases, all of the data could be averaged to determine η_o, reported above.

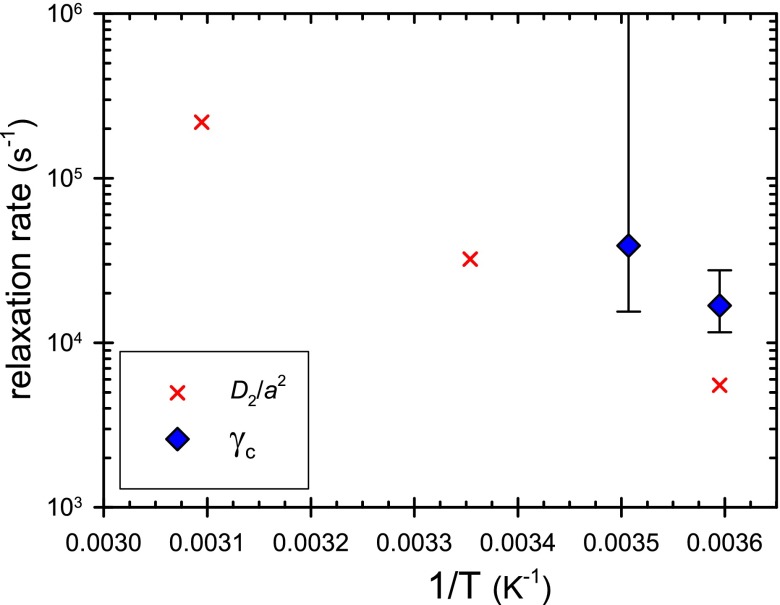
FIG. 5.

Estimates of the rate of structure relaxation in concentrated lysozyme solution (approximately 480 g/l), comparing ${\dot{\gamma }}_c$ (the onset of shear thinning in steady shear flow) and D₂/a² (the slow relaxation rate estimated by DLS).

FIG. 4.

(a) Plot of viscosity as a function of shear rate η($\dot{\gamma }$) for a 140 g/l lysozyme solution at (5, 20, and 50)  °C. This solution exhibits Newtonian behavior at all temperatures. (b) η($\dot{\gamma }$) for 480 g/l lysozyme solution at 5 °C. Data were acquired first (i) from high to low shear rate and then (ii) the reverse. Standard uncertainties of multiple measurements are reported.

Only solutions at 480 g/l and low temperature (5 °C and 12 °C) exhibited non-Newtonian behavior at high shear rates (Fig 4 b). For these solutions, viscosities measured at lower shear rate were therefore segregated and averaged to determine η_o. At the highest shear rate, the viscosity at 5 °C is approximately 18% below η_o (Fig. 4b), well outside of uncertainty. The data collected at other temperatures are reported in supplementary material. To check whether the observed behavior was steady state, shear rates were applied in both ascending and descending order (Fig. 4 b). Repeatability and reversibility were observed within experimental uncertainty, suggesting that shear thinning reflects the behavior of the equilibrium solution structure. The shear thinning rheology is inherent to the solution and not caused by viscous heating, which is here always negligible. Furthermore, changes in lysozyme conformation should be negligible, since the Peclet number (a²γ̇/D₁) remains less than 0.02 under all conditions. Only a Peclet number (Pe) associated with the slow mode (a²γ̇/D₂) becomes appreciable (reaching values up to approximately 10), suggesting distortions and rearrangements of the supramolecular structure only, as elaborated below.

The shear rate dependence of the viscosity data was fit to the Carreau model,²⁸ chosen for its simplicity to describe Newtonian behavior at low shear rates and power-law shear thinning at high rates.

$$\eta =\frac{{\eta }_o}{{\left(1+{\left(\dot{\gamma }/{\dot{\gamma }}_c\right)}^2\right)}^{\left(1-n\right)/2}}$$ (4)

The three model parameters include η_o, ${\dot{\gamma }}_c$ the shear rate at the onset of shear thinning, and n the power law index which describes the degree of non-Newtonian behavior or how steep the decrease is in the viscosity for shear rates greater than ${\dot{\gamma }}_c$ (note that n = 1 is Newtonian, n < 1 is shear thinning, and n = 0 is a yield stress fluid). At 5 °C, η_o, ${\dot{\gamma }}_c$, and n were determined by best fit to minimize least square errors. The extracted power law n value of 0.88 ± 0.05 indicates mild shear thinning. The fitted value of ${\dot{\gamma }}_c$ is approximately 17 000 s⁻¹ (with a standard uncertainty range between 12 000 s⁻¹ and 28 000 s⁻¹). Weaker shear thinning is observed at 12 °C (see supplementary material), and its onset is at a slightly higher shear rate of roughly 40 000 s⁻¹. At 20 °C and 50 °C, thinning was not observed with the current rheometer capability (see supplementary material). Shear thinning behavior returned when measurements were repeated at 5 °C. As noted above, this repeatability and reversibility argue against permanent aggregates and for dynamic equilibrium clusters.

As noted above, the onset of shear thinning should indicate the long-time internal relaxation rate of large clusters. It is common to assume that the starting point of the shearing thinning behavior is when Pe is approximately unity, from which a characteristic size can be estimated. This estimated size is about 33 times that of the monomer, i.e., much larger than the IRO length scale. Hence, it is unlikely that the IRO is distorted in the shear rate investigated in this paper. Instead, the relaxation occurs on the much larger length scale, by rearrangement of the percolated clusters, where IRO is the internal structure. The fact that the shear thinning occurs at such a high shear rate indicates that the percolated clusters are not strongly bound to allow rearrangement on that time scale. It would be very useful to test this hypothesis by measuring the possible changes of the structure in situ during flow. Unfortunately, instruments to conduct those studies are currently unavailable, since it would require shear rates in excess of 10 000 s⁻¹ on a SANS instrument. NIST is currently developing a rheometer for simultaneous in situ scattering of fluids under such high shear rate.

Having determined γ̇_c and D₂/a², the values can now be compared (Fig. 5). It appears that the relaxation rate during shear is roughly a factor of three faster than the thermal quiescent process measured by DLS. The relaxation processes in steady shear and those at rest (during DLS) may or may not be topologically different. The respective relaxation rates may therefore be somewhat different. The near agreement of these two and their similar trend with temperature will motivate further investigation concerning the measurement of the relaxation and dynamics of supramolecular clusters formed in SALR colloids.

IV. CONCLUSION

Using a microcapillary rheometer with expanded capabilities, we investigated the rheology of lysozyme solutions over a broad parameter space of temperatures, concentrations, and shear rates. The low concentration solutions exhibited Newtonian behavior even up to shear rates approximately 10⁵s⁻¹. We observed that η_o increased with an increase in protein concentration and a decrease in temperature which is in general a reflection of increased interaction between molecules and the growth of clusters within solution. Although the dependence of η_o on temperature approximates an Arrhenius relationship at low protein concentrations, significant departures are observed at high solution concentrations corresponding with the onset of localized glassy like behavior recently observed using neutron spin echo.¹⁸

At high shear rates, concentrated solutions of 480 g/l exhibited shear thinning and the onset and extent of shear thinning depends on the temperature of the solution. The characteristic size associated with the onset of the shearing thinning behavior is significantly larger than the IRO length scale. The Carreau model was used to quantify the shear rate at the onset of shear thinning. This critical shear rate correlates roughly to a secondary relaxation observed by DLS, both of which are likely to correspond to internal relaxation of equilibrium clusters.

SUPPLEMENTARY MATERIAL

See supplementary material for additional data concerning sample stability and shear thinning.