Abstract
Purpose:
The image quality of dedicated cone beam breast CT (CBBCT) is limited by substantial scatter contamination, resulting in cupping artifacts and contrast-loss in reconstructed images. Such effects obscure the visibility of soft-tissue lesions and calcifications, which hinders breast cancer detection and diagnosis. In this work, we propose a library-based software approach to suppress scatter on CBBCT images with high efficiency, accuracy, and reliability.
Methods:
The authors precompute a scatter library on simplified breast models with different sizes using the geant4-based Monte Carlo (MC) toolkit. The breast is approximated as a semiellipsoid with homogeneous glandular/adipose tissue mixture. For scatter correction on real clinical data, the authors estimate the breast size from a first-pass breast CT reconstruction and then select the corresponding scatter distribution from the library. The selected scatter distribution from simplified breast models is spatially translated to match the projection data from the clinical scan and is subtracted from the measured projection for effective scatter correction. The method performance was evaluated using 15 sets of patient data, with a wide range of breast sizes representing about 95% of general population. Spatial nonuniformity (SNU) and contrast to signal deviation ratio (CDR) were used as metrics for evaluation.
Results:
Since the time-consuming MC simulation for library generation is precomputed, the authors’ method efficiently corrects for scatter with minimal processing time. Furthermore, the authors find that a scatter library on a simple breast model with only one input parameter, i.e., the breast diameter, sufficiently guarantees improvements in SNU and CDR. For the 15 clinical datasets, the authors’ method reduces the average SNU from 7.14% to 2.47% in coronal views and from 10.14% to 3.02% in sagittal views. On average, the CDR is improved by a factor of 1.49 in coronal views and 2.12 in sagittal views.
Conclusions:
The library-based scatter correction does not require increase in radiation dose or hardware modifications, and it improves over the existing methods on implementation simplicity and computational efficiency. As demonstrated through patient studies, the authors’ approach is effective and stable, and is therefore clinically attractive for CBBCT imaging.
Keywords: breast, computed tomography, cone-beam breast CT, scatter correction, Monte Carlo simulation
1. INTRODUCTION
Mammography screening plays an important role in early breast cancer detection.1 However, the nature of 2D projection in mammograms results in tissue superposition, leading to compromised specificity and sensitivity in cancer detection, especially for dense breasts.1,2 Dedicated cone beam breast CT (CBBCT) is a newly developed technique and does not use physical breast compression as used in mammography.3,4 It produces high quality tissue-superposition-free volumetric images, demonstrating a potential to substantially improve breast cancer detection and diagnosis.5–8 A fundamental limitation of CBBCT image quality is the high scatter contamination stemming from the large irradiation volume in each x-ray projection. In this paper, we propose a practical approach for effective scatter correction on CBBCT.
Scatter-induced errors typically appear in reconstructed images as global cupping artifacts, local streaking artifacts around dense objects, as well as contrast reduction.9–12 Inaccurate reconstruction values of CBBCT impede its quantitative use in clinical tasks, including glandular/adipose segmentation13 and computer-aided cancer detection/diagnosis,12 while contrast reduction reduces the conspicuity of calcifications and soft-tissue lesions. Suppression of scatter signals has been an active research field since the early days of x-ray and CT imaging.12,14–16 Briefly, existing methods can be divided into two main categories: scatter rejection by preventing the scattered photons from reaching the detector17 and scatter correction by estimating the scatter content after projection data acquisition.14–16,18,19 It is worth mentioning that the latter methods are only able to remove the mean scatter signals, leaving statistical scatter noise in the corrected images. Thus, it is inherently more dose-efficient to prevent scatter from reaching the detector than to correct for scatter on scatter contaminated projections. Comprehensive reviews of general scatter correction methods can be found in Refs. 20 and 21. Despite their success demonstrated in certain scenarios, these methods have different drawbacks including low efficacy, dose or scan time increase, need for hardware modification, and intensive computation. An optimal scatter correction approach is yet to be established. In current CBBCT imaging, the most investigated method for scatter correction is probably scatter measurement. The measurement-based methods insert a sheet of beam-stop or beam-pass array to sparsely measure scatter or primary signals.12,16,18 Scatter estimation is then obtained via interpolation, based on the fact that scatter contains dominant low-frequency components. In addition to modifications of the imaging geometry, due to the inevitable loss of primary signals inside the blocker shadows, these methods require extra data acquisition and therefore additional imaging dose. Shading correction on CBBCT images as a postreconstruction processing step removes global cupping artifacts,10,13 but fails to reduce high-frequency image errors. The corrected images therefore still suffer from contrast loss.
In a clinical setting, the following properties are desired on a practical scatter correction method for CBBCT: (1) high correction efficacy and reliability across general populations; (2) no requirement of imaging time increase or imaging hardware modifications; (3) high computational efficiency. None of the existing approaches on CBBCT achieves the above three goals simultaneously. Although it seems challenging to design a generic scatter correction method with these properties for different CT scanners, in this work, we aim to develop such a practical technique for CBBCT by exploiting its unique feature of relatively small variations in scatter properties with heterogeneous tissue distribution and the relatively simple geometry of the imaged object (i.e., breast). Inspired by Ref. 14, where scatter database for one patient is premeasured and modified for scatter correction of subsequent scans for the same patient, we propose to precompute a library of scatter distributions via Monte Carlo (MC) simulations on breasts with different dimensions. On patient data acquired from a clinical research prototype CBBCT system with no hardware modification or scan time increase, we first select the scatter distribution according to the breast size measured on a first-pass CBBCT reconstruction. The selected scatter distribution is modified to account for the geometric transformation between the MC simulation and the physical scan, and then subtracted from the measured projections for effective scatter correction. In general CT imaging, a large scatter library is needed for the success of the proposed method, especially for complex objects, increasing the computational burden. In CBBCT, however, we find that a scatter library with only one input parameter of the breast size is sufficient for effective scatter correction. The computationally intensive MC simulation can therefore be greatly reduced. Furthermore, the MC simulations for generating the scatter library are precomputed and do not need to be repeated for each patient dataset. The signal processing time for scatter correction is therefore much less than the CBBCT reconstruction time. We investigate the efficacy and robustness of the proposed library-based scatter correction on 15 clinical research patient datasets, with a wide range of breast sizes and geometric complexities. Image spatial nonuniformity (SNU) and the separation in linear attenuation coefficients between adipose and fibroglandular tissue, herein referred to as contrast to signal deviation ratio (CDR) are used as quality metrics for evaluating the performance of the method.
2. METHODS AND MATERIAL
2.A. Breast model and parameterization of the scatter library for CBBCT
Besides correction accuracy, the practical value of the proposed library-based method is determined by the size of the precomputed library. On a CT scanner with a fixed imaging protocol, the scatter distribution is dependent on the unknown anatomical structures (i.e., shapes and heterogeneous distributions) of the imaged object. A large set of parameters are therefore needed to specify the object geometry, which in general can be arbitrary and complex, and hence, a large number of possible scatter distributions. In addition, each scatter distribution on a 2D detector of a CT scan has three dimensions: the lateral and longitudinal detector coordinates (u, v) as well as the projection angle β, which typically covers 360°. As such, an ideal scatter library has a tremendously large size and requires huge memory consumption on a computer.
Although library-based scatter correction seems infeasible for general CT imaging, we find that the library size for effective scatter correction can be very small for breast imaging on the current clinical research CBBCT systems. Figure 1 shows the geometry of the clinical research CBBCT used in our studies.22 The breast with a semiellipsoidal shape is positioned pendant along the y-axis of rotation through an aperture in the patient support table, while the x-ray tube and detector rotate around the breast simultaneously to acquire the projection data. The reconstructed CT image of the breast typically resembles a simple semiellipsoid, with no other background objects. In addition to the relatively simple shape, another unique feature of the breast is that it is mainly composed of soft tissue, including glandular and adipose tissue. It has been shown that these two materials lead to small differences in the resulting scatter distributions.9 We can therefore generate the library of scatter distributions for a simplified breast model with a semiellipsoidal shape and a homogenous composition. Note that such a simplified model has also been implemented in previous studies to obtain the dosimetric characteristics of CBBCT.4,23–26
FIG. 1.
Imaging geometry of the clinical research CBBCT system used in the presented studies.
In this work, we further simplify the breast model by assuming rotational symmetry about the rotation axis of the CBBCT. As shown in Fig. 1, we assume that the breast is centered at the rotation axis and the lengths of principle axes are equal in the x and z directions, denoted as Deff. Hereafter in the paper, we refer to Deff as the effective breast diameter. On a real breast CBBCT image, Deff can be determined as the effective diameter of the breast at the chest wall. The length of semiprincipal axis in the y direction of the breast model, which is the distance from the chest wall to nipple, is set to 0.75Deff. The breast composition is modeled as a homogenous fibroglandular/adipose mixture with different densities simulating the effects of different volumetric glandular fractions (VGF). As shown in a later section, our investigations reveal that the performance of the proposed library-based scatter correction is insensitive to the breast density value used in our model. Therefore, we fix VGF as 15% (i.e., the population average27,28) in the generation of the scatter library, unless otherwise stated. Note that due to the rotational symmetry of the breast model, the resultant scatter remains unchanged for different projection angles. As such, only one 2D image is needed to describe the scatter distribution for a CBBCT scan for one specific breast size. The precomputed scatter library consists of a set of 2D scatter images for different Deff, each denoted as SDeff(u, v).
After aggressive simplification of the breast geometry, the scatter library has a small size with only one input parameter, Deff. We will validate the proposed empirical breast model for scatter generation on patient data. One particular concern regarding the inaccuracy of our approach is the chest wall, which is not included in the breast model. As shown later in the evaluation studies, we find that ignoring the chest wall in the breast model has negligible effect on the scatter correction performance, mainly due to the strong signal attenuation in the chest wall region.
2.B. Library-based scatter correction for CBBCT
2.B.1. Scatter library generation
Different methods, such as scatter measurement18,19,29 or analytical modeling,30–32 can be used to obtain scatter distributions on the simplified breast model. In this work, we choose to use the c++ based geant4 Monte Carlo toolkit (www.geant4.org) to generate our scatter library.
Figure 1 shows screen shots of the MC simulation. In the simulation, we use the geometry of the clinical research prototype CBBCT system on which the patient data are acquired. The source to axis of rotation distance (SAD) is 65 cm and the source to detector distance (SDD) is 89.8 cm, resulting in a magnification factor of 1.38. The detector model is based on an ideal flat-panel detector with a dimension of 30 × 40 cm. To reduce the variance in the scatter estimate, we use a large pixel size of 1 mm. The simulated photons are emitted from a point x-ray source to irradiate the entire breast with a half cone beam shape. Note that we do not model the bowtie filter as the system used to acquire the clinical datasets does not employ one.
To acquire SDeff(u, v), a series of monoenergetic simulations are performed with photon energy ranging from 10 keV to the kVp value used in the clinical research CBBCT system, in increments of 2 keV. The Livermore low energy physics model of geant4 is used for radiation transport. The physical processes for x-ray photon interactions include photo-electric effect, Compton scattering, and Rayleigh scattering. For each simulation, a total number of 1.2 × 107 photons per energy bin are emitted from the point source and the physical interactions are tracked along their trajectories. Position-dependent scatter and primary x-ray photon fluence incident on the detector are recorded. The scoring methodology is based on the interaction type, where each x-ray photon reaching the detector is considered as a scatter event if it undergoes at least one scatter (Compton or Rayleigh scatter) interaction. For a primary event, the incident x-ray photon must satisfy the following conditions: (1) it does not undergo Compton or Rayleigh scatter, (2) its energy does not change before hitting on the detector, and (3) its direction does not change. The scatter distribution for a polyenergetic x-ray beam is generated by weighting the map from each energy bin with the x-ray spectrum normalized to unit area that is used for data acquisition.
MC simulation is computationally intensive, with the total simulation time proportional to the number of emitted photons. The simulated scatter distribution contains Poisson noise. An open-source matlab function, Gridfit,33 is applied to reduce the noise on the scatter map via surface fitting in a similar way as in the existing literature.34,35 The Gridfit function is based on the concept of “approximant” map and it controls the amount of smoothness via a smoothing parameter, which is empirically chosen to minimize the root mean square difference in the scatter distribution prior to and after fitting. The resultant scatter distribution is considered noise-free and is finally archived in the scatter library.
The aforementioned methods are repeated for different Deff to generate the entire scatter library. As shown in the evaluation studies, we find that the performance of the proposed scatter correction does not require a high accuracy of the Deff value. Considering the range of Deff in the general population, we use 6–22 cm, with an interval of 2 cm. The scatter library therefore consists of nine scatter images, each with a size of 1024 × 768 pixels after interpolating the original map with a size of 400 × 300. The total computation time of the library generation is about 30 h on a 2.5 GHz Intel Core i7 MacBook. Note that this computation cost should be considered as part of the system calibration or precomputation stage. Once the library is generated, it can be repetitively used for scatter correction on different patient datasets.
2.B.2. Library-based scatter estimation on patient data
We propose two steps to obtain an estimated scatter distribution for each patient dataset based on the precomputed scatter library. First, we select a proper scatter distribution from the scatter library with a Deff value matching that of the imaged breast. Second, the selected scatter distribution is modified to compensate for the difference in breast geometry between that used in MC simulation and that of the real breast.
2.B.2.a. Library selection scheme.
Only one parameter, Deff, is needed to select a scatter distribution from the scatter library. To select the appropriate Deff, we perform a first-pass CBBCT reconstruction on the scatter-contaminated projections. The chest wall region is then segmented from the reconstructed volume. For the coronal slice closest to the chest wall, the number of voxels within the breast, A, is determined and with known voxel dimension of ΔV, we estimate Deff as in Ref. 36,
| (1) |
2.B.2.b. Scatter modification based on object translation and magnitude conversion.
During MC simulation, the semiellipsoidal breast is centered at the rotation of axis. This condition, however, may not necessarily hold in a patient scan. Although the breast aperture on the clinical research CBBCT system is centered at the rotation of axis, variation in patient positioning results in translation of breast from the rotation axis. To compensate for the effects of different breast center positions in the simulated MC data and in the patient scan, we assume that the scatter distribution translates with the projection of the object center on the detector with an unchanged shape. Although this shift-invariance property is theoretically inaccurate for a divergent x-ray projection, our previous publication has shown that this approximation leads to sufficient accuracy for scatter estimation.14
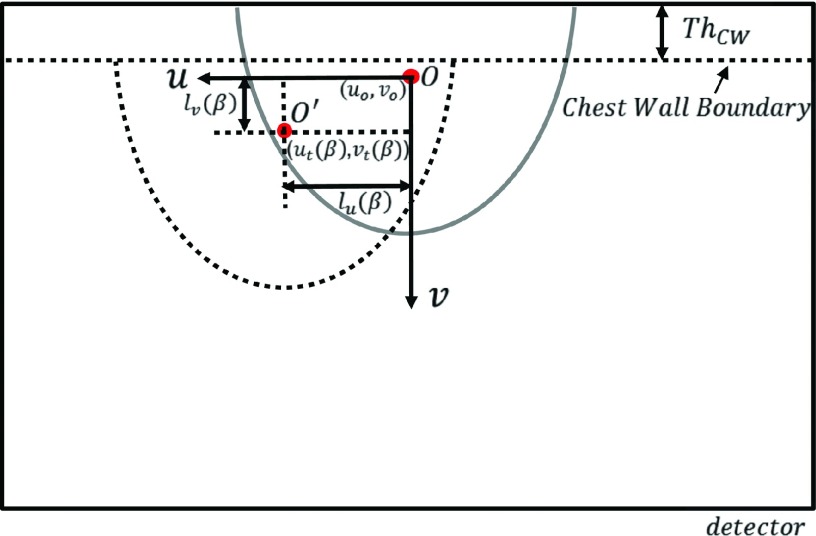
Figure 2 illustrates the coordinate system and the breast projections on the detector. The semiellipse outlined in gray represents the projection after the logarithmic operation (i.e., the line integrals) of the modeled breast in MC simulation. The center of mass (COM) projected onto the detector is denoted as the point O(u0, v0). The region in dashed line represents the clinical research CBBCT projection acquired on a patient after the logarithmic operation, with the COM at point O′(ut, vt). Note that the chest wall region is segmented and removed from the image, and therefore is not used in the COM calculation.
FIG. 2.
CBBCT projection coordinate system for describing the spatial translation of SDeff(u, v).
To obtain the scatter distribution at each projection angle β, for correction on the clinical data, , we spatially shift the scatter distribution SDeff(u, v) selected from the library by the distance between the COMs calculated for each projection angle β, i.e.,
| (2) |
The shifting distance along the lateral and longitudinal directions, lu and lv, is calculated as
| (3) |
| (4) |
where ThCW is the thickness of the chest wall. Note that the COM of the breast projection varies for different projection angles β, leading to a β-dependent lu. ThCW typically remains unchanged for different projections, and thus lv is constant over different β. When the translated coordinate is outside the domain of the scatter distribution stored in the scatter library, pixel values are obtained via extrapolation.
The obtained scatter distribution, , needs to be multiplied by a conversion ratio, k(β), to match the magnitude or the unit of scatter signals in a patient scan. This ratio can be calculated by comparing the total signal levels of the raw projection data before the logarithmic operation in a simulated projection and in a patient projection. Denote the raw projection on a patient as T(u, v, β), which contains both primary and scatter signals, and one obtains the conversion ratio for each projection angle as
| (5) |
where is the primary distribution obtained via translating the original simulated primary signals in the same way as the calculation of from SDeff. To increase the estimation accuracy, we calculate the conversion ratio using pixels only inside the projected breast on the detector, defined as a region of interest (ROI), Ω, in Eq. (5).
To prevent overcorrection of scatter, which results in negative values of estimated primary signals, we apply a softcut function, f, on the scatter estimate after magnitude conversion to obtain the final scatter estimate. The softcut function ensures that the estimated scatter is always less than the measured projection data. If the estimated scatter is larger than a user-defined threshold, which is close to but smaller than the measured raw projection, an empirical exponential function is applied to limit the output value below the measured raw projection. Details of the softcut function can be found in Ref. 19. The scatter corrected projection data are finally obtained as
| (6) |
2.B.3. Summary of the workflow
Figure 3 summarizes the workflow of the proposed library-based scatter correction algorithm as the following steps:
FIG. 3.
Flowchart of the proposed library-based scatter correction.
Step 1: Reconstruct first-pass CBBCT images using uncorrected raw projection data.
Step 2: Determine the chest wall boundary from CBBCT projection and then locate its corresponding coronal slice from the first-pass reconstructed image acquired in Step 1.
Step 3: Determine the Deff from the selected slice using Eq. (1).
Step 4: Select the proper SDeff(u, v) from MC scatter library according to Deff.
Step 5: For each projection view, perform spatial translation on SDeff(u, v) via Eqs. (2)–(4), adjust the magnitude by multiplying the factor calculated via Eq. (5), and apply the softcut function to obtain the scatter estimate.
Step 6: Subtract the scatter estimate from the measured CBBCT projection to obtain the scatter corrected projection using Eq. (6).
Step 7: Reconstruct to obtain scatter-corrected CBBCT images.
2.C. Evaluation
2.C.1. Validation of Monte Carlo simulation
We first use a large number of photons (7 × 107 photons per energy bin) in the MC simulation to generate scatter distributions with low noise levels. Based on Poisson statistics, we estimate the average statistical precision (i.e., uncertainty) as 4.47% for a breast with a 14-cm diameter and 4.87% for a large breast with an 18-cm diameter. These results are considered as the ground truths. To shorten the computational time, we generate our library using reduced number of photon (1.2 × 107 photons per energy bin) and a surface fitting algorithm (i.e., Gridfit), as discussed in Sec. 2.B.1. The resulting scatter distributions are compared with the ground truths for validation.
2.C.2. Patient evaluation
We demonstrate the feasibility and evaluate the performance of the proposed library-based scatter correction via a retrospective study with 15 clinical research patient datasets. These patient data were from a clinical study which was conducted in accordance with a protocol that was approved by the institutional review boards of the University of Rochester Medical Center and the University of Massachusetts Medical School. All these cases were highly suspicious for malignancy and were assigned category 4 or 5 according to the breast imaging-reporting and data system (BI-RADS) of the American College of Radiology.37
The clinical research CBBCT prototype system (Koning Corporation, West Henrietta, NY, USA) uses a 49 kVp tungsten anode spectrum with a first half-value layer of 1.39 mm Al and a mean energy of 30.4 keV.38 The tungsten target x-ray tube (RAD71SP, Varian Medical Systems, Salt Lake City, UT) is powered by a high frequency generator (Sedecal, USA) and the detector is a thallium-doped cesium iodine (CsI:Tl) flat-panel detector (PaxScan® 4030CB, Varian Medical Systems, Salt Lake City, UT). Each CBBCT scan acquires 300 projections over 360°, each with a size of 1024 × 768 pixels. The reconstructed CBBCT images have an isotropic voxel size of 0.273 mm. Except for the generation of the scatter library via MC simulation, all other steps of our method are implemented in matlab. The standard FDK reconstruction is implemented using graphics processing unit (GPU) acceleration. On a 1.6 GHz 64-bit windows 7 workstation with NVIDIA Quadro 620 GPU, it takes an average of 3.5 min to reconstruct the volumetric CBBCT images with a typical size of 1024 × 1024 × 450. The time for reconstruction slightly varies depending on the breast length along the y direction. The other processing steps to generate scatter-corrected projections (including library selection, spatial translation and soft-cut) currently do not use the GPU-based parallel computing and take about 1 min total for each patient dataset.
One focus of our evaluation studies is to investigate the effects of the simple breast model on the efficacy of scatter correction, and to optimize the method parameters. No beam hardening correction has been implemented. In particular, we aim to find out: (1) whether ignoring the chest wall in the generation of scatter library results in significant errors in scatter correction; (2) whether breast size and VGF, the two parameters used in typical MC studies of breast imaging,4,24,26,39 are both needed as the input parameters of the scatter library; (3) what precision is required on the input parameter(s) of the scatter library.
2.C.2.a. Chest wall effect.
For generality of the scatter library and computation simplicity, we do not include the chest wall in the MC simulations for generating the scatter library. To investigate if the presence of chest wall in clinical data affects the scatter correction performance, additional MC simulations are conducted with the chest wall modeled as a cylinder of 2 cm height and 28 cm diameter, corresponding to the maximum scanner field-of-view. We compare the scatter corrected images of two patient cases (Deff = 14 and 18 cm) using the scatter distribution obtained with and without the chest wall in MC simulation.
2.C.2.b. Effect of volumetric glandular fraction.
A previous study showed that the distribution of scatter-to-primary ratio (SPR) is minimally affected by different values of VGF in breast CT imaging.9 Since CT image error in the presence of scatter is a function of SPR,40 we hypothesize that the scatter correction performance of the proposed library-based method is insensitive to VGF values, and VGF can therefore be fixed in all MC simulations.
To verify our hypothesis, we compare the scatter-corrected images on one patient using the library-based method with different VGF values (2%, 15%, 35%, 50%, and 75%) in the generation of the scatter library using MC simulation. The patient has a true VGF value of 15%, which is estimated from the first-pass reconstructed images by using a Gaussian-kernel based fuzzy C-mean (KFCM) algorithm that had been previously published.28
2.C.2.c. Effect of breast size.
The breast diameter, Deff, has the largest effect on the scatter correction result using our method. The breast diameters from 10 to 18 cm represent 95% of general population in the United States,26 with an average of 14 cm.4 We therefore use a Deff range of 6–22 cm for generating the scatter library. To investigate the required precision of Deff for accurate scatter estimation, we compare the scatter correction results on the same patient using different Deff values with an interval of 2 cm. To investigate the impact of breast length, Leff, MC simulations are performed with varying Leff (0.5, 0.75, and 1.0 times the Deff). The resultant scatter distributions are used for scatter correction on the same patient for comparison.
2.C.2.d. Test of method robustness and image quality metrics.
We test the robustness of our method with 15 clinical research patient datasets. The focus is to evaluate the performance of the scatter correction method on patient datasets that included large variations in breast sizes and VGF, and irregular breast shapes.
In all of the evaluation studies, we use SNU and CDR as quantitative metrics. The SNU is calculated using five selected ROIs randomly distributed in the adipose tissue area on the reconstructed image,
| (7) |
where and are the maximum and the minimum of the mean CT values of the selected ROIs, respectively, and is the average of the mean CT values of the ROIs. The SNU well quantifies the global cupping artifacts on the CBBCT images.
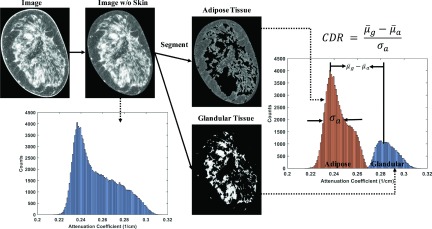
To compute the CDR, we first segment glandular and adipose tissues on the reconstructed image using the KFCM segmentation method.28 The image contrast is defined as the mean signal difference between the attenuation coefficients of the glandular and adipose tissues, and the CDR is calculated as
| (8) |
where and are the mean attenuation coefficients of the segmented glandular and adipose tissues, respectively. σa is the signal standard deviation measured on the segmented adipose tissue. Figure 4 illustrates the above procedures of CDR calculation. We calculate image contrast in a conventional way as the mean signal difference between adipose and glandular tissues. Since we investigate our method performance on clinical images, it is difficult to select an absolutely uniform area and then measure the image noise. σa in Eq. (8) is different from the statistical image noise, and it actually includes two more terms, image nonuniformity due to existing image artifacts and small background structures. Readers should be aware that our definition of CDR is different from that of the contrast-to-noise ratio (CNR).
FIG. 4.
Illustration of the CDR calculation.
3. RESULTS
3.A. Validation of Monte Carlo simulation
The computation time of each simulation with a large number of photons (7 × 107 photons per energy bin) takes approximately 21 h, which is reduced to 3.3 h (i.e., by a factor of nearly 7) using the proposed method with a reduced number of photons (1.2 × 107 photons per energy bin) and surface fitting. Compared with the ground truth, the scatter distribution obtained by our method has a root-mean-squared difference (RMSD) of 0.04% for a 14 cm diameter breast and 0.08% for a large 18 cm diameter breast. This result has been reported in our prior work.41
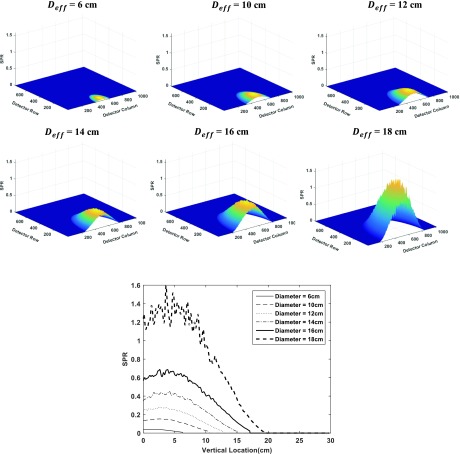
Figure 5 shows the SPR maps inside the breast region on the detector for different breast diameters Deff, along with the comparison of their central column profiles in the chest wall to nipple direction. These simulated SPR maps are consistent with published results from other research groups.9
FIG. 5.
SPR maps for different breast sizes and comparison of the central line profiles in the chest wall to nipple direction.
3.B. Chest wall effect
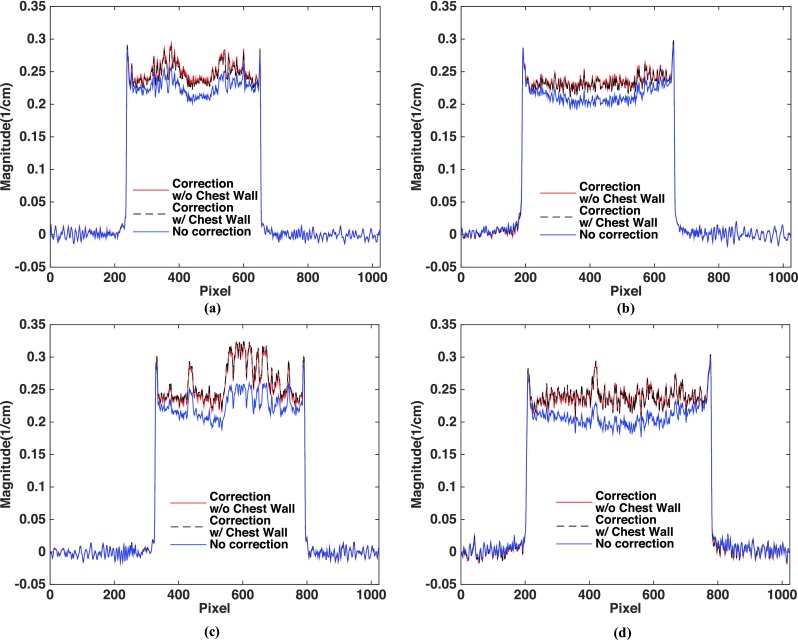
Two sets of clinical research patient data, one with an average breast [Deff = 14 cm, shown in Fig. 6(A) columns (a) and (b)] and the other with a large breast [Deff = 18 cm, shown in Fig. 6(A) columns (c) and (d)] are used to investigate the scatter correction performances when the chest wall is included or excluded during MC-based generation of the scatter library. Figure 6 compares the images without correction, corrected using the library-based method with and without including the chest wall in the MC simulation, and the difference between the two correction schemes. The proposed library-based correction significantly improves the overall image uniformity and contrast. The extracted 1D profiles taken at the dashed lines shown in the first row of Fig. 6(A) are compared in Fig. 7. As shown in the fourth row of Fig. 6(A) as well as in Fig. 7, inclusion of the chest wall in the generation of the scatter library leads to negligible difference on the image quality. The RMSD between the scatter-corrected images with and without including the chest wall in the MC simulation is 0.98% and 1.58% for the coronal and sagittal views of the average-size breast, respectively, and 1.09% and 1.96% for the large breast. Most of the large differences lie in the area behind the chest wall. Figure 6(B) shows the same comparison as Fig. 6(A) for a near-chest wall coronal slice with tissue truncation. The maximum percentage difference and RMSD between the two scatter-corrected images are 3.34% and 0.27% for the average breast, and 5.80% and 1.31% for the large breast, respectively. This study indicates that it is practical to ignore the chest wall during the generation of scatter library for the implementation simplicity of the proposed algorithm without much degradation of scatter correction accuracy.
FIG. 6.
Demonstration of the chest wall effect in the proposed library-based scatter correction. (A) Comparison of patient images without correction (first row), corrected using the library-based method without and with the inclusion of the chest wall in the MC simulation (second and the third row, respectively), and the difference between the two correction schemes (fourth row). Columns (a) and (b): Coronal and sagittal views for an average size breast with Deff of 14 cm. Columns (c) and (d): for a large size breast with Deff of 18 cm. Display window: [0.2 0.3] cm−1 for the first three rows, [−0.01 0.01] cm−1 for the last row. The dashed lines in the first row indicate where the 1D profiles of Fig. 7 are taken. (B) Comparison of scatter corrected images near chest wall. Top row shows the results for an average breast size of 14 cm and bottom row for a large breast size of 18 cm. The display windows for uncorrected/corrected images and difference images are the same as those in (A).
FIG. 7.
1D profiles taken on the images of Fig. 6(A). The location where the 1D profiles are taken is shown as the dashed lines in the first row of Fig. 6(A).
3.C. Effect of VGF
Figure 8 demonstrates the effect of VGF on the performance of our method. The first column of Fig. 8 shows the uncorrected image (top row) and the image corrected by the library-based approach using the true VGF value of 15% (bottom row). The proposed correction greatly improves the image quality. The SNU calculated from the selected ROIs is reduced from 7.70% to 2.50%, and the CDR is improved from 5.48 to 9.26, a nearly two-fold increase. Figure 8 also includes the images corrected by the library-based approach using incorrect VGF of 2%, 35%, 50%, and 75%, and their differences compared with the result using the true VGF value of 15% is shown in the bottom row. It is seen that the performance of our method is insensitive to the accuracy of the VGF value. Table I summarizes the quantitative analysis on the images of Fig. 8. Although the correction result using the true VGF value has the best (lowest) image SNU and high CDR, the error on the VGF value results in very small differences on the image quality. Even with an inaccurate VGF value of 75%, the image SNU is degraded by less than 0.8% and the image CDR is reduced by less than 4%. The above comparison indicates that the performance of the library-based scatter correction is minimally affected by the VGF. Hence, we fix the VGF at 15% in all subsequent implementations presented in this paper. During MC simulation for the scatter library generation, this scheme reduces the library size and therefore the computation burden.
FIG. 8.
Demonstration of the effect of different VGF values on the performance of the library-based scatter correction. The first column shows the uncorrected original image (upper) and corrected image (bottom) using the true VGF value of 15%. The rest of the upper row: image corrected using different VGF values. Display window: [0.2 0.3] cm−1. The rest of the bottom row: difference images compared with the result using a VGF value of 15%. Display window: [−0.003 0.002] cm−1. The five white squared ROIs defined in the uncorrected image are used to calculate the SNU values shown in Table I.
TABLE I.
Comparison of SNU, CDR, and CDR increase ratio on the uncorrected and the corrected images using different VGF values.
| Correction with different VGF values | ||||||
|---|---|---|---|---|---|---|
| No correction | 2% | 15% | 35% | 50% | 75% | |
| SNU (%) | 7.70 | 2.79 | 2.52 | 3.21 | 3.13 | 3.28 |
| CDR | 5.48 | 9.38 | 9.26 | 9.19 | 9.09 | 8.89 |
| CDR increase ratio | 1.00 | 1.71 | 1.69 | 1.68 | 1.66 | 1.62 |
3.D. Effect of effective breast diameter (Deff) and breast length (Leff)
We use one randomly selected breast to investigate the effect of Deff on the correction performance of the proposed method. Based on Eq. (1), the breast has a measured Deff of 14.1 cm. We therefore use 14 cm as the “true” Deff in the proposed library-based scatter correction. The first column of Fig. 9(A) shows the uncorrected image and the image corrected by the library-based method using the true Deff value. The Leff used for this evaluation is fixed at 0.75Deff. The rest of Fig. 9(A) are the images corrected by the library-based method using different Deff values (6, 10, 12, 16, 18, 22 cm; top row) and their corresponding difference compared to the result using the true Deff (bottom row). The quantitative analysis of the uncorrected and the corrected images is summarized in Table II(a). The Deff has a larger effect on the scatter correction performance for our algorithm than the VGF. In general, using a Deff smaller (or larger) than the estimated value leads to under (or over) correction of scatter with the proposed algorithm. As shown in Table II(a), a Deff estimated using Eq. (1) indeed achieves an optimal image quality with both low SNU and high CDR. It is worth noting that the results around the true Deff values (i.e., using Deff values of 12, 14, and 16 cm) have small differences in these metrics. This finding indicates that the scatter library does not need high precision of Deff for the success of our method. We therefore propose to precompute the scatter library using breast models with Deff in 2 cm intervals.
FIG. 9.
Demonstration of the effect of different Deff and Leff values on the performance of the library-based scatter correction. (A) The scatter correction results using different values. The first column shows the uncorrected image (upper) and the corrected image (bottom) using an estimated Deff of 14 cm. The rest of the upper row: image corrected using different Deff values. Display window: [0.2 0.3] cm−1. The rest of the bottom row: difference images compared with the result using a Deff value of 14 cm. Display window: [−0.03 0.04] cm−1. (B) The scatter correction results using different Leff value. The first column shows the uncorrected image (upper) and the corrected image (bottom) using an estimated Leff of 0.75Deff. The rest of the upper row: images corrected with 0.5Deff and 1Deff. The bottom row: the corresponding difference images compared with the result using a Leff of 0.75Deff. The display windows for uncorrected/corrected images and difference images are the same as those in (A).
TABLE II.
(a) Comparison of SNU, CDR and CDR increase ratio on the uncorrected image and the corrected images using different Deff values. (b) Comparison of SNU, CDR, and CDR increase ratio on the uncorrected image and the corrected images using different Leff values.
| (a) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Correction with different Deff values | ||||||||
| No correction | 6 cm | 10 cm | 12 cm | 14 cm | 16 cm | 18 cm | 22 cm | |
| SNU (%) | 6.30 | 4.25 | 2.26 | 1.77 | 1.79 | 2.07 | 2.58 | 7.40 |
| CDR | 5.36 | 5.70 | 5.94 | 5.81 | 5.95 | 5.76 | 5.69 | 4.92 |
| CDR increase ratio | 1.00 | 1.06 | 1.11 | 1.08 | 1.11 | 1.08 | 1.06 | 0.92 |
| (b) | ||||
|---|---|---|---|---|
| Correction with different Leff values | ||||
| No correction | 0.50Deff | 0.75Deff | 1.00Deff | |
| SNU (%) | 6.302 | 1.806 | 1.789 | 2.408 |
| CDR | 5.358 | 5.598 | 5.937 | 5.942 |
| CDR increase ratio | 1.000 | 1.045 | 1.108 | 1.109 |
The same patient data are used to investigate the effect of Leff on the scatter correction performance. By fixing the Deff at the true value of 14 cm, we carry out scatter correction using scatter maps generated with Leff equal to 0.5Deff and 1Deff. The first column of Fig. 9(B) shows the uncorrected image and the image corrected using a scatter map with Leff of 0.75Deff. The rest two columns of Fig. 9(B) are the images corrected using scatter maps with Leff of 0.5Deff and 1Deff, and their corresponding differences compared to the result using 0.75Deff. The quantitative comparison, Table II(b), shows that the discrepancy between corrected images using different Leff values is less than 0.7% on SNU and is less than 5.6% on CDR. This finding indicates that the Leff has a small effect on the proposed method. Therefore it is practical to fix the Leff at 0.75Deff during the MC simulation for better computation efficiency.
3.E. Patient-group studies
To demonstrate the efficacy and robustness of the proposed method, Table III summarizes the results on 15 breast patients. For all the cases, we compare the SNU and CDR in both coronal and sagittal views without and with scatter correction. For coronal views, the proposed method improves the CDR on average by a factor of 1.49 and the SNU is reduced from 7.14% to 2.47%, on average. Similar performance is also observed in sagittal views, where the CDR is improved on average by a factor of 2.12 and the SNU is reduced from 10.14% to 3.02%, on average.
TABLE III.
Comparison of SNU, CDR, and CDR increase ratio on the 15 patient CBBCT datasets without and with scatter correction. Note that the VGF values, estimated via the KFCM method, are listed for reference only. They are not used in the proposed library-based scatter correction.
| Coronal view (x–z) | Sagittal view (x–y) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Patient # | Deff (cm) | VGF (%) | SNU (%) (before/after) | CDR (before/after) | CDR increase ratio | SNU (before/after) | CDR (before/after) | CDR increase ratio | ||||
| 1 | 14 | 41 | 6.43 | 1.07 | 5.32 | 6.77 | 1.27 | 7.49 | 2.87 | 4.28 | 5.27 | 1.23 |
| 2 | 14 | 5 | 11.92 | 2.83 | 2.56 | 5.48 | 2.14 | 14.07 | 2.12 | 3.02 | 8.66 | 2.86 |
| 3 | 14 | 18 | 7.41 | 3.38 | 6.76 | 10.07 | 1.49 | 20.18 | 2.32 | 1.16 | 8.52 | 7.32 |
| 4 | 14 | 14 | 6.79 | 2.70 | 6.80 | 9.12 | 1.34 | 11.48 | 3.15 | 5.01 | 5.70 | 1.14 |
| 5 | 14 | 7 | 5.66 | 1.90 | 5.47 | 7.50 | 1.37 | 6.59 | 3.34 | 4.71 | 7.17 | 1.52 |
| 6 | 14 | 16 | 7.89 | 2.99 | 4.06 | 5.93 | 1.46 | 11.74 | 3.09 | 3.72 | 6.31 | 1.70 |
| 7 | 14 | 13 | 13.03 | 3.30 | 4.91 | 6.44 | 1.31 | 8.64 | 2.17 | 6.56 | 7.65 | 1.17 |
| 8 | 14 | 34 | 5.24 | 3.10 | 5.23 | 7.35 | 1.41 | 9.38 | 2.98 | 4.60 | 6.28 | 1.36 |
| 9 | 12 | 15 | 5.19 | 2.15 | 5.17 | 7.36 | 1.42 | 11.02 | 1.55 | 4.92 | 7.74 | 1.57 |
| 10 | 18 | 12 | 12.62 | 2.82 | 2.45 | 6.69 | 2.73 | 16.18 | 6.89 | 2.38 | 5.97 | 2.51 |
| 11 | 10 | 7 | 5.20 | 1.93 | 9.47 | 12.94 | 1.37 | 9.73 | 2.13 | 5.11 | 9.42 | 1.84 |
| 12 | 10 | 1 | 2.96 | 1.92 | 5.08 | 6.72 | 1.32 | 5.60 | 4.79 | 4.72 | 6.53 | 1.38 |
| 13 | 14 | 19 | 4.35 | 1.70 | 7.51 | 9.60 | 1.28 | 9.81 | 2.18 | 4.73 | 7.61 | 1.61 |
| 14 | 10 | 15 | 6.65 | 3.23 | 6.14 | 6.18 | 1.01 | 4.42 | 2.72 | 6.93 | 7.71 | 1.11 |
| 15 | 16 | 21 | 5.78 | 1.96 | 6.43 | 9.21 | 1.43 | 5.84 | 3.07 | 1.88 | 6.58 | 3.50 |
| Average | 7.14 | 2.47 | 5.56 | 7.82 | 1.49 | 10.14 | 3.02 | 4.25 | 7.14 | 2.12 | ||
| STD | 2.94 | 0.68 | 0.40 | 4.10 | 1.26 | 1.54 | ||||||
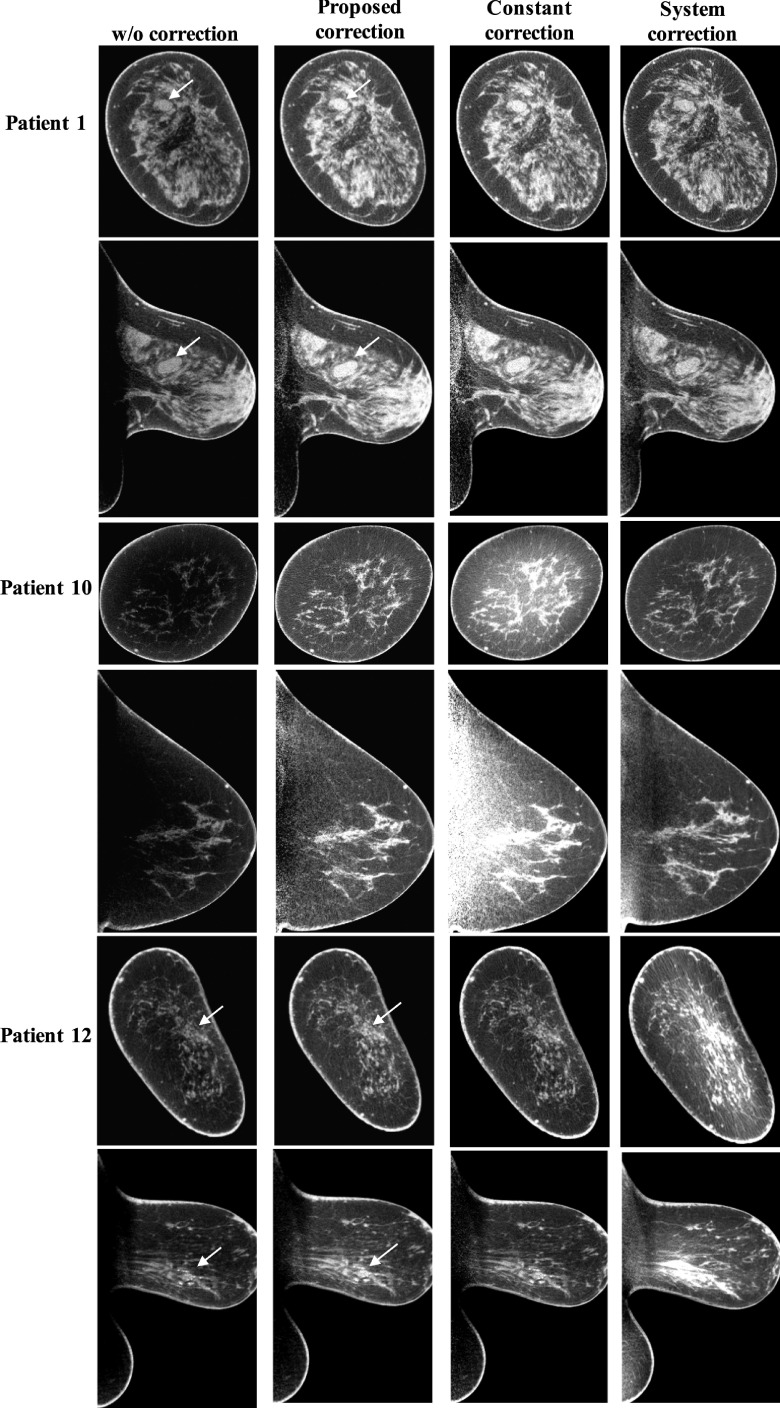
To scrutinize the method performance, we compare the library-based scatter correction method with two other correction methods: constant correction and system correction. In the constant correction method, we assume that scatter has a uniform distribution and scatter correction is carried out by subtracting a constant value from the measured projection. The constant, i.e., the scatter level, is estimated from the simulated SPR (shown in Fig. 5) according to the breast size and fixed as 75% of the maximum scatter signal for a balanced performance for all patient cases. The system correction method is an algorithm embedded in the imaging software of the commercial CBBCT scanner which we use to acquire all the patient data. In Fig. 10, we show representative results on three patient cases, and a comparison of image SNU is listed in Table IV. It is found that only the library-based approach stably removes the shading artifacts and obtains corrected images with low SNU for all patient cases. The soft tissue abnormalities (indicated by white arrows on patient 1) and calcification clusters (indicated by white arrows on patient 12) become more discernible after the proposed scatter correction. The other two correction methods have unpredictable inferior performances with either scatter overestimation or underestimation.
FIG. 10.
Comparison of typical correction results using the proposed library-based method, the constant correction method, and the software-embedded method (system correction). The lesions are indicated by the white arrows. Display window: [0.2 0.3] cm−1.
TABLE IV.
Comparison of SNU using different scatter correction methods for coronal and sagittal views shown in Fig. 10.
| Coronal view (x–z) SNU (%) | Sagittal view (x–y) SNU (%) | |||||
|---|---|---|---|---|---|---|
| Patient no. | Proposed correction | Constant correction | System correction | Proposed correction | Constant correction | System correction |
| 1 | 1.11 | 1.56 | 1.31 | 2.54 | 3.70 | 6.24 |
| 10 | 2.64 | 11.61 | 2.29 | 5.26 | 28.65 | 7.85 |
| 12 | 2.53 | 3.61 | 7.64 | 4.79 | 6.37 | 9.79 |
To further demonstrate the reliability of the library-based scatter correction, Fig. 11 shows the correction results for patients with different breast sizes (i.e., Deff) and shapes. It is seen that our method robustly corrects for scatter on CBBCT for a large range of breast diameters from 10 to 18 cm.
FIG. 11.
The correction results for breasts with different sizes and shapes. Display window: [0.2 0.3] cm−1.
4. CONCLUSIONS AND DISCUSSION
In this work, we propose a highly efficient and effective scatter correction method for CBBCT imaging by estimating the scatter based on a precomputed scatter library using MC simulations. The method performance has been demonstrated on a group of 15 patient datasets acquired from a clinical research CBBCT prototype system. The proposed method effectively reduces the image SNU from 7.14% to 2.47% in the selected ROIs and improves the CDR by a factor of about 1.8 on average. Increased visibility has been observed for soft tissue lesions and calcification clusters, two important indications for breast cancers.
The proposed library-based scatter correction has the following attractive features. First, our method requires no change of the imaging protocol (i.e., no scan time or dose increase) or the system hardware, and therefore can be used as software plug-in in the signal processing chain of current CBBCT systems. Second, due to the simplicity of the CBBCT imaging geometry, we substantially minimize the size of the scatter library without degradation of the method performance, which improves the method practicality by reducing the computation complexity and memory consumption. Third, as the scatter library is precomputed and stored in a system calibration stage, the scatter correction step is efficiently performed on the real patient data (200 ms per projection in our matlab implementations). These combined advantages together with the high effectiveness and robustness as demonstrated on patient studies make our method distinct from the existing scatter correction approaches. By developing an effective yet practical scatter correction method, our research potentially promotes the clinical role of dedicated CBBCT.
The performance of the proposed library-based scatter correction can be further enhanced by refining the method design, although the results presented in this paper on clinical data indicate a small margin of possible improvements. For example, the scatter library is currently generated via MC simulation on a simplified breast model with only one parameter. We can increase the accuracy of scatter estimation by using a sophisticated breast model with more geometric parameters to account for different breast deformations in a clinical scan. The size of scatter library will increase accordingly by including more breast parameters and one parameter of projection angle due to the loss of rotational symmetry. In the MC simulation engine, the current physics model, which includes only basic collisional interactions, can be improved by more realistic modeling of the x-ray source and the detector. For example, inclusion of the heel effect on the x-ray tube, a dedicated beam shaping filter,42 and a nonideal energy response curve on the detector in the MC simulation further increases the scatter estimation accuracy. The proposed correction only removes the low-spatial-frequency component of scatter, and the high-frequency statistical noise of the scatter is inevitably left in the scatter-corrected image. We will implement a penalized weighted least square method previously designed for scatter correction algorithms40 together with the library-based method to further enhance the image CDR.
In addition to the above algorithmic advancements on scatter correction, our future research will include statistical validation of the method accuracy and reliability on more patient studies. As another major source of CT imaging errors, beam hardening effect also causes cupping artifacts on CBBCT, as well as streaks around dense objects.5 We will design and implement beam hardening correction algorithms to reduce the residual artifacts on the images shown in this paper. After these studies, we will investigate the improvements in detection and classification of breast tumors on CBBCT images achieved by our methods, using both human and numerical observers43 and computer-aided techniques.44–47
ACKNOWLEDGMENTS
Research reported in this publication was partially supported by the National Institute of Biomedical Imaging and Bioengineering, and the National Cancer Institute, of the National Institutes of Health under Award Nos. R21EB019597, R21 CA134128, and R01 CA195512.
CONFLICT OF INTEREST DISCLOSURE
The authors have no COI to report. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
REFERENCES
- 1.Berry D. A., Cronin K. A., Plevritis S. K., Fryback D. G., Clarke L., Zelen M., Mandelblatt J. S., Yakovlev A. Y., Habbema J. D. F., and Feuer E. J., “Effect of screening and adjuvant therapy on mortality from breast cancer,” N. Engl. J. Med. 353(17), 1784–1792 (2005). 10.1056/NEJMoa050518 [DOI] [PubMed] [Google Scholar]
- 2.McCormack V. A. and dos Santos Silva I., “Breast density and parenchymal patterns as markers of breast cancer risk: A meta-analysis,” Cancer Epidemiol., Biomarkers Prev. 15(6), 1159–1169 (2006). 10.1158/1055-9965.EPI-06-0034 [DOI] [PubMed] [Google Scholar]
- 3.Chen B. and Ning R., “Cone-beam volume CT breast imaging: Feasibility study,” Med. Phys. 29(5), 755–770 (2002). 10.1118/1.1461843 [DOI] [PubMed] [Google Scholar]
- 4.Boone J. M., Nelson T. R., Lindfors K. K., and Seibert J. A., “Dedicated breast CT: Radiation dose and image quality evaluation,” Radiology 221(3), 657–667 (2001). 10.1148/radiol.2213010334 [DOI] [PubMed] [Google Scholar]
- 5.O’Connell A. M., Karellas A., and Vedantham S., “The potential role of dedicated 3D breast CT as a diagnostic tool: Review and early clinical examples,” Breast J. 20(6), 592–605 (2014). 10.1111/tbj.12327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lindfors K., Boone J., and Nelson T., “Dedicated breast CT: Initial clinical experience,” Radiology 246(3), 725–733 (2008). 10.1148/radiol.2463070410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Prionas N. D., Lindfors K. K., Ray S., Huang S.-Y., Beckett L. A., Monsky W. L., and Boone J. M., “Contrast-enhanced dedicated breast CT: Initial clinical experience,” Radiology 256(3), 714–723 (2010). 10.1148/radiol.10092311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cole E. B., Campbell A. S., Vedantham S., Pisano E. D., and Karellas A., “Clinical performance of dedicated breast computed tomography in comparison to diagnostic digital mammography [abstract # SSA01-09],” in 101st Scientific Assembly and Annual Meeting of the Radiological Society of North America (Radiology Society of North America, Chicago, IL, 2015). [Google Scholar]
- 9.Kwan A. L., Boone J. M., and Shah N., “Evaluation of x-ray scatter properties in a dedicated cone-beam breast CT scanner,” Med. Phys. 32(9), 2967–2975 (2005). 10.1118/1.1954908 [DOI] [PubMed] [Google Scholar]
- 10.Altunbas M. C., Shaw C. C., Chen L., Lai C., Liu X., Han T., and Wang T., “A post-reconstruction method to correct cupping artifacts in cone beam breast computed tomography,” Med. Phys. 34(7), 3109–3118 (2007). 10.1118/1.2748106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen Y., Liu B., O’Connor J. M., Didier C. S., and Glick S. J., “Characterization of scatter in cone-beam CT breast imaging: Comparison of experimental measurements and Monte Carlo simulation,” Med. Phys. 36(3), 857–869 (2009). 10.1118/1.3077122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yang K., Burkett G., and Boone J. M., “A breast-specific, negligible-dose scatter correction technique for dedicated cone-beam breast CT: A physics-based approach to improve Hounsfield unit accuracy,” Phys. Med. Biol. 59(21), 6487–6505 (2014). 10.1088/0031-9155/59/21/6487 [DOI] [PubMed] [Google Scholar]
- 13.Yang X., Wu S., Sechopoulos I., and Fei B., “Cupping artifact correction and automated classification for high-resolution dedicated breast CT images,” Med. Phys. 39, 6397–6406 (2012). 10.1118/1.4754654 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhu L., Xie Y., Wang J., and Xing L., “Scatter correction for cone-beam CT in radiation therapy,” Med. Phys. 36(6), 2258–2268 (2009). 10.1118/1.3130047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Niu T., Sun M., Star-Lack J., Gao H., Fan Q., and Zhu L., “Shading correction for on-board cone-beam CT in radiation therapy using planning MDCT images,” Med. Phys. 37(10), 5395–5406 (2010). 10.1118/1.3483260 [DOI] [PubMed] [Google Scholar]
- 16.Sechopoulos I., “X-ray scatter correction method for dedicated breast computed tomography,” Med. Phys. 39(5), 2896–2903 (2012). 10.1118/1.4711749 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Siewerdsen J. H., Moseley D. J., Bakhtiar B., Richard S., and Jaffray D. A., “The influence of antiscatter grids on soft-tissue detectability in cone-beam computed tomography with flat-panel detectors,” Med. Phys. 31(12), 3506–3520 (2004). 10.1118/1.1819789 [DOI] [PubMed] [Google Scholar]
- 18.Ning R., Tang X., and Conover D., “X-ray scatter correction algorithm for cone beam CT imaging,” Med. Phys. 31(5), 1195–1202 (2004). 10.1118/1.1711475 [DOI] [PubMed] [Google Scholar]
- 19.Zhu L., Bennett N. R., and Fahrig R., “Scatter correction method for x-ray CT using primary modulation: Theory and preliminary results,” IEEE Trans. Med. Imaging 25(12), 1573–1587 (2006). 10.1109/TMI.2006.884636 [DOI] [PubMed] [Google Scholar]
- 20.Niu T. and Zhu L., “Overview of x-ray scatter in cone-beam computed tomography and its correction methods,” Curr. Med. Imaging Rev. 6(2), 82–89 (2010). 10.2174/157340510791268515 [DOI] [Google Scholar]
- 21.Rührnschopf E.-P. and Klingenbeck K., “A general framework and review of scatter correction methods in x-ray cone-beam computerized tomography. Part 1: Scatter compensation approaches,” Med. Phys. 38(7), 4296–4311 (2011). 10.1118/1.3599033 [DOI] [PubMed] [Google Scholar]
- 22.O’Connell A., Conover D. L., Zhang Y., Seifert P., Logan-Young W., Lin C. F. L., Sahler L., and Ning R., “Cone-beam CT for breast imaging: Radiation dose, breast coverage, and image quality,” Am. J. Roentgenol. 195(2), 496–509 (2010). 10.2214/ajr.08.1017 [DOI] [PubMed] [Google Scholar]
- 23.Sechopoulos I., Vedantham S., Suryanarayanan S., D’Orsi C. J., and Karellas A., “Monte Carlo and phantom study of the radiation dose to the body from dedicated CT of the breast,” Radiology 247(1), 98–105 (2008). 10.1148/radiol.2471071080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Vedantham S., Shi L., Karellas A., O’Connell A. M., and Conover D. L., “Personalized estimates of radiation dose from dedicated breast CT in a diagnostic population and comparison with diagnostic mammography,” Phys. Med. Biol. 58(22), 7921–7936 (2013). 10.1088/0031-9155/58/22/7921 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Thacker S. C. and Glick S. J., “Normalized glandular dose (DgN) coefficients for flat-panel CT breast imaging,” Phys. Med. Biol. 49(24), 5433–5444 (2004). 10.1088/0031-9155/49/24/003 [DOI] [PubMed] [Google Scholar]
- 26.Boone J. M., Shah N., and Nelson T. R., “A comprehensive analysis of DgNCT coefficients for pendant-geometry cone-beam breast computed tomography,” Med. Phys. 31(2), 226–235 (2004). 10.1118/1.1636571 [DOI] [PubMed] [Google Scholar]
- 27.Yaffe M. J., Boone J. M., Packard N., Alonzo-Proulx O., Huang S. Y., Peressotti C. L., Al-Mayah A., and Brock K., “The myth of the 50-50 breast,” Med. Phys. 36(12), 5437–5443 (2009). 10.1118/1.3250863 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Vedantham S., Shi L., Karellas A., and O’Connell A. M., “Dedicated breast CT: Fibroglandular volume measurements in a diagnostic population,” Med. Phys. 39(12), 7317–7328 (2012). 10.1118/1.4765050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Siewerdsen J. H., Daly M. J., Bakhtiar B., Moseley D. J., Richard S., Keller H., and Jaffray D. A., “A simple, direct method for x-ray scatter estimation and correction in digital radiography and cone-beam CT,” Med. Phys. 33(1), 187–197 (2006). 10.1118/1.2148916 [DOI] [PubMed] [Google Scholar]
- 30.Wiegert J., Bertram M., Rose G., and Aach T., “Model based scatter correction for cone-beam computed tomography,” Proc. SPIE 5745, 271–282 (2005). 10.1117/12.594520 [DOI] [Google Scholar]
- 31.Kolb T. M., Lichy J., and Newhouse J. H., “Comparison of the performance of screening mammography, physical examination, and breast US and evaluation of factors that influence them: An analysis of 27 825 patient evaluations,” Radiology 225(1), 165–175 (2002). 10.1148/radiol.2251011667 [DOI] [PubMed] [Google Scholar]
- 32.Spies L., Evans P. M., Partridge M., Hansen V. N., and Bortfeld T., “Direct measurement and analytical modeling of scatter in portal imaging,” Med. Phys. 27(3), 462–471 (2000). 10.1118/1.598914 [DOI] [PubMed] [Google Scholar]
- 33.D’Errico J., Surface Fitting using gridfit, 2010, available online at http://www.mathworks.com/matlabcentral/fileexchange/8998-surface-fitting-using-gridfit.
- 34.Zbijewski W. and Beekman F. J., “Efficient Monte Carlo based scatter artifact reduction in cone-beam micro-CT,” IEEE Trans. Med. Imaging 25(7), 817–827 (2006). 10.1109/TMI.2006.872328 [DOI] [PubMed] [Google Scholar]
- 35.Colijn A. P. and Beekman F. J., “Accelerated simulation of cone beam x-ray scatter projections,” IEEE Trans. Med. Imaging 23(5), 584–590 (2004). 10.1109/TMI.2004.825600 [DOI] [PubMed] [Google Scholar]
- 36.Huang S.-Y., Boone J. M., Yang K., Packard N. J., McKenney S. E., Prionas N. D., Lindfors K. K., and Yaffe M. J., “The characterization of breast anatomical metrics using dedicated breast CT,” Med. Phys. 38(4), 2180–2191 (2011). 10.1118/1.3567147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.ACR, Breast Imaging Reporting and Data System, Breast Imaging Atlas, 4th ed. (American College of Radiology (ACR), Reston, VA, 2004). [Google Scholar]
- 38.Vedantham S., Shi L., Karellas A., and Noo F., “Dedicated breast CT: Radiation dose for circle-plus-line trajectory,” Med. Phys. 39(3), 1530–1541 (2012). 10.1118/1.3688197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sechopoulos I., Feng S. S. J., and D’Orsi C. J., “Dosimetric characterization of a dedicated breast computed tomography clinical prototype,” Med. Phys. 37(8), 4110–4120 (2010). 10.1118/1.3457331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhu L., Wang J., and Xing L., “Noise suppression in scatter correction for cone-beam CT,” Med. Phys. 36(3), 741–752 (2009). 10.1118/1.3063001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shi L., Vedantham S., Karellas A., and Zhu L., “Library-based scatter correction for dedicated cone beam breast CT: A feasibility study,” Proc. SPIE 9783, 978330 (2016). 10.1117/12.2217327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Vedantham S., Shi L., and Karellas A., “Dedicated cone-beam breast CT: Design of a 3-D beam-shaping filter (abstract # TU-CD-207-10),” Med. Phys. 42(6), 3612 (2015). 10.1118/1.4925629 [DOI] [Google Scholar]
- 43.Sanchez A. A., Sidky E. Y., and Pan X., “Task-based optimization of dedicated breast CT via Hotelling observer metrics,” Med. Phys. 41(10), 101917 (16pp.) (2014). 10.1118/1.4896099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jalalian A., Mashohor S. B. T., Mahmud H. R., Saripan M. I. B., Ramli A. R. B., and Karasfi B., “Computer-aided detection/diagnosis of breast cancer in mammography and ultrasound: A review,” Clin. Imaging 37(3), 420–426 (2013). 10.1016/j.clinimag.2012.09.024 [DOI] [PubMed] [Google Scholar]
- 45.Malich A., Fischer D. R., Facius M., Petrovitch A., Boettcher J., Marx C., Hansch A., and Kaiser W. A., “Effect of breast density on computer aided detection,” J. Digital Imaging 18(3), 227–233 (2005). 10.1007/s10278-004-1047-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Rangayyan R. M., Ayres F. J., and Leo Desautels J. E., “A review of computer-aided diagnosis of breast cancer: Toward the detection of subtle signs,” J. Franklin Inst. 344(3–4), 312–348 (2007). 10.1016/j.jfranklin.2006.09.003 [DOI] [Google Scholar]
- 47.Castellino R. A., “Computer aided detection (CAD): An overview,” Cancer Imaging 5(1), 17–19 (2005). 10.1102/1470-7330.2005.0018 [DOI] [PMC free article] [PubMed] [Google Scholar]