Role of structural inhomogeneities in resting-state brain dynamics

Abstract

Brain imaging methods allow a non-invasive assessment of both structural and functional connectivity. However, the mechanism of how functional connectivity arises in a structured network of interacting neural populations is as yet poorly understood. Here we use a modeling approach to explore the way in which functional correlations arise from underlying structural connections taking into account inhomogeneities in the interactions between the brain regions of interest. The local dynamics of a neural population is assumed to be of phase-oscillator type. The considered structural connectivity patterns describe long-range anatomical connections between interacting neural elements. We find a dependence of the simulated functional connectivity patterns on the parameters governing the dynamics. We calculate graph-theoretic measures of the functional network topology obtained from numerical simulations. The effect of structural inhomogeneities in the coupling term on the observed network state is quantified by examining the relation between simulated and empirical functional connectivity. Importantly, we show that simulated and empirical functional connectivity agree for a narrow range of coupling strengths. We conclude that identification of functional connectivity during rest requires an analysis of the network dynamics.

Introduction

Complex but highly structured patterns of correlated fluctuations have been observed in spontaneous/task-free brain activity measured by brain imaging techniques in healthy (Biswal et al. 1995; Damoiseaux et al. 2006) and diseased brain (Zhou et al. 2010). It has been shown that dynamical patterns of these correlations are shaped by a complex interplay between underlying anatomical connections and ongoing activity of the interacting regions (Deco et al. 2011; Ghosh et al. 2008). Thus, allowing for long-distance co-activity of functionally segregated brain areas and forming the basis of cognitive functions (Werner 2009). However, the exact mechanisms contributing to the long-range cortical interactions still remain largely unknown. It has been suggested that, together with the collective effects governed by the network properties, inter-regional distances and indirect connections may also play significant roles. Recent studies on large-scale functional connectivity have begun to demonstrate the role of dynamic reconfiguration of resting-state functional connections over multiple time scales (Hansen et al. 2015; Hutchison et al. 2013) and of such reconfiguration when brain moves between task-free and task-dependent state (Dimitriadis et al. 2015).

Theoretical models of the resting-brain dynamics allow for exploration of these mechanisms, with the focus on the relationship between large-scale anatomical connectivity and either local or global dynamics (see Cabral et al. (2014) for a recent review). The common approach of these models is to consider the brain as a complex dynamical system operating in so called metastable regime (Shanahan 2010; Tognoli and Kelso 2014). The key properties of the brain metastability is flexible network dynamics, which allow for synchronization patterns that change over time.

In this paper, we utilize these approaches and additionally introduce anatomical inhomogeneities into cortical interactions. Thus, making our model physiologically more plausible, we explore conditions that allow long-distance functional correlations.

Modeling functional connectivity

We use structural connectivity derived from diffusion weighted Magnetic Resonance Imaging (dMRI) data (Iturria-Medina et al. 2008) to numerically simulate resting-state functional correlations between brain areas. To closely match empirical findings, a blood-oxygen-level-dependent (BOLD) fMRI signal is inferred from the simulated activity of the node corresponding to the respective brain region (Cabral et al. 2011, 2014; Deco et al. 2009; Ghosh et al. 2008). This is done using a Balloon-Windkessel hemodynamic model (Friston et al. 2000; Seth et al. 2013), which is a widely used model of neurovascular coupling, and has been implemented in existing models of large-scale brain functional connectivity (Cabral et al. 2011; Ghosh et al. 2008; Honey et al. 2009). We extend this modeling approach by utilizing the following Kuramoto-type equation, whose neurobiological implications are well established (Breakspear et al. 2010; Cabral et al. 2011), to simulate the dynamics of brain regions:

$$\begin{array}{c}\hfill {\dot{\mathit{\theta }}}_i(t)={\mathit{\omega }}_i+c\sum _{j=1}^N{A}_{ij}sin[{\mathit{\theta }}_j(t)-{\mathit{\theta }}_i(t)-{\mathit{\alpha }}_{ij}],\end{array}$$ 1

where ${\mathit{\theta }}_i(t)$ describes the state of the brain region (network node) i over time, N is the number of regions considered ($N=90$), and c is a sufficiently strong global coupling chosen from a range of values to (i) engage phase interactions (Izhikevich and Kuramoto 2006; Nicosia et al. 2013; Strogatz 2000)) and (ii) influence correlated amplitude fluctuations at lower frequencies (Cabral et al. 2014; Vuksanović and Hövel 2014). The parameter ${\mathit{\omega }}_i$ is the natural frequency of the ith oscillator, set in the $\mathit{\gamma }$ frequency range (drawn randomly from a Gaussian distribution with the mean ${\mathit{\omega }}_0=30\text{Hz}$) to facilitate the emergence of the desired dynamical network state (Cabral et al. 2014, 2011; Vuksanović and Hövel 2014) and relate local node dynamics to the neurophysiology (Leopold et al. 2003; Logothetis et al. 2001).

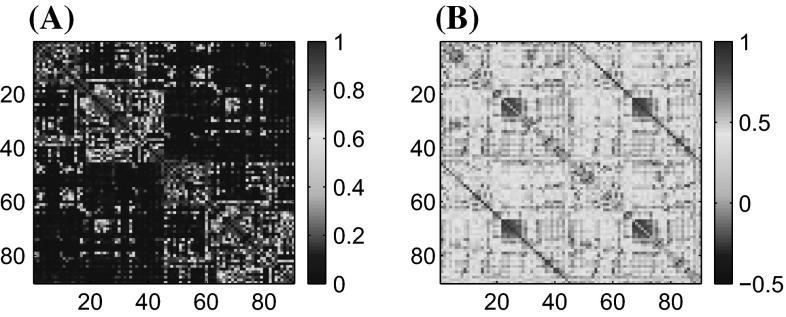
The connectivity matrix, $\left\{A_{ij}\right\}$, determining the coupling topology, represents a structural connectivity matrix estimated from dMRI data, according to the procedure described in Iturria-Medina et al. (2008). The procedure maps out probabilities for the presence of the direct neural connections between all pairs of the 90 considered anatomical regions of interest. We will therefore refer to this map as the anatomical connectivity (AC) map or matrix (Iturria-Medina et al. 2008), whose weighted entries ranges from 0 to 1 (Fig. 1A). Structural inhomogeneities are introduced in the coupling term by distance-dependent phase offsets ${\mathit{\alpha }}_{ij}$. The element ${\mathit{\alpha }}_{ij}$ makes network interactions biologically more plausible translating neural signal transmission delays into corresponding phase offsets (Breakspear et al. 2010), thus preventing full synchronization of the network (Keane et al. 2012; Nicosia et al. 2013). Heterogeneous phase-offsets are scaled into interval $\left(0,\mathit{\pi }/2\right)$ according to the distances between the brain regions of interests. We aim to explore synchrony between neural populations that arises as a result of these inhomogeneities in the coupling term1.

Fig. 1.

A Anatomical and B functional connectivity obtained from DTI and fMRI data, respectively. The connectivity analysis is performed on the 90 brain regions according to the list in Table 1

We quantify the degree of network synchrony using order parameter R, defined in the following way:

$$\begin{array}{c}\hfill R(t)=\left|〈e^{i{\mathit{\theta }}_j(t)}〉\right|j=1,\dots ,N.\end{array}$$ 2

Extreme values of the order parameter, $R(t)=1$ and $R(t)=0$, indicate the network’s complete synchrony or asynchrony, respectively. Values between 0 and 1 represent network’s transition from less to more synchronized state, i.e. network metastable regime (Shanahan 2010).

Table 1.

Cortical and sub-cortical regions as defined in the automated anatomic labeling (AAL) template image

Index R/L	Anatomical description	Label
1/46	Precentral	PRE
2/47	Frontal Sup	F1
3/48	Frontal Sup Orb	F10
4/49	Frontal Mid	F2
5/50	Frontal Mid Orb	F20
6/51	Frontal Inf Oper	F30P
7/52	Frontal Inf Tri	F3T
8/53	Frontal Inf Orb	F30
9/54	Rolandic Oper	RO
10/55	Supp Motor Area	SMA
11/56	Olflactory	OC
12/57	Frontal Sup Medial	F1M
13/58	Frontal Mid Orb	SMG
14/59	Gyrus Rectus	GR
15/60	Insula	IN
16/61	Cingulum Ant	ACIN
17/62	Cingulum Mid	MCIN
18/63	Cingulum Post	PCIN
19/64	Hippocampus	HIP
20/65	ParaHippocampal	PHIP
21/66	Amygdala	AMYG
22/67	Calcarine	V1
23/68	Cuneus	Q
24/69	Lingual	LING
25/70	Occipital Sup	O1
26/71	Occipital Mid	O2
27/72	Occipital Inf	O3
28/73	Fusiform	FUSI
29/74	Postcentral	POST
30/75	Parietal Sup	P1
31/76	Parietal Inf	P2
32/77	Supra Marginal Gyrus	SMG
33/78	Angular	AG
34/79	Precuneus	PQ
35/80	Paracentral Lobule	PCL
36/81	Caudate	CAM
37/82	Putamen	PUT
38/83	Pallidum	PAL
39/84	Thalamus	THA
40/85	Heschi	HES
41/86	Temporal Sup	T1
42/87	Temporal Pole sup	T1P
43/88	Temporal Mid	T2
44/89	Temporal Pole Mid	T2P
45/90	Temporal Inf	T3

Indexes from 1–45 indicate right (R) and 46–90 left (L) hemisphere regions

Characterization of brain networks

Simulated functional connectivity

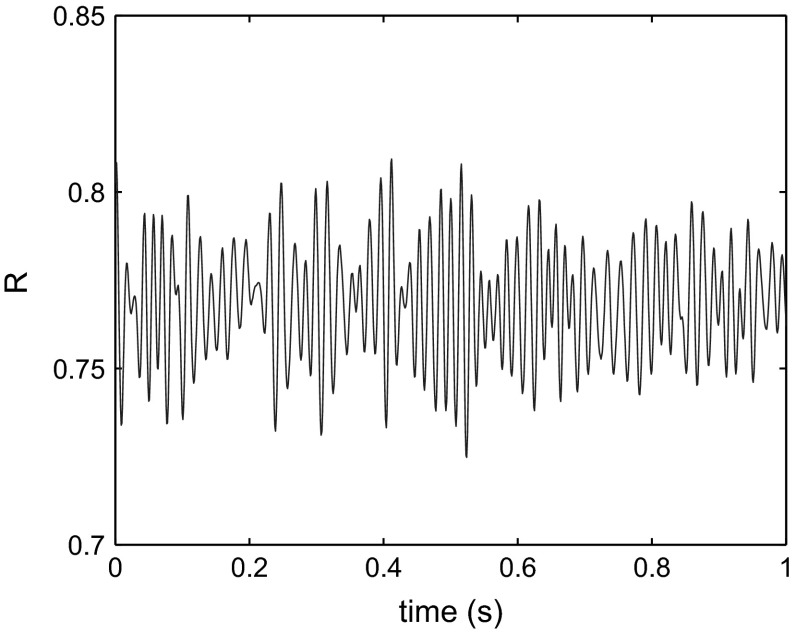
For assessment of the simulated functional connectivity (FC) we employed the simple linear (Pearson) coefficient of correlation of the simulated BOLD time series. The representative examples of simulated FCs for different values of the coupling strength c are given in Fig. 2. We find that scaling the global coupling strength within the range from 23.3 to 23.4, in steps of 0.01, affects functional correlations between simulated time series and therefore FCs so as to agree with the empirical FC. Visually, patterns of correlated activity between empirical and simulated FC matrices agree best for $c=23.32$ with a correlation coefficient $\mathit{\rho }=0.32$ and mean squared error of 0.12 [compare Figs. 1B and 2]. At the same time, global network synchrony, measured via Eq. (2), displays a considerable amount of variation over time (Fig. 3). Variations in level of network synchrony represent an important property of the resting-state brain dynamics, that allow flexible network interactions. This is, again, the range of global coupling strength values where simulated FCs show best agreement with experiment.

Fig. 2.

Simulated functional connectivity according to Eq.  (1) obtained for five different values of the coupling strength c

Fig. 3.

Global synchrony R given by Eq. (2) as a function of time for a coupling strength $c=23.32$

Anatomical and functional connectivity

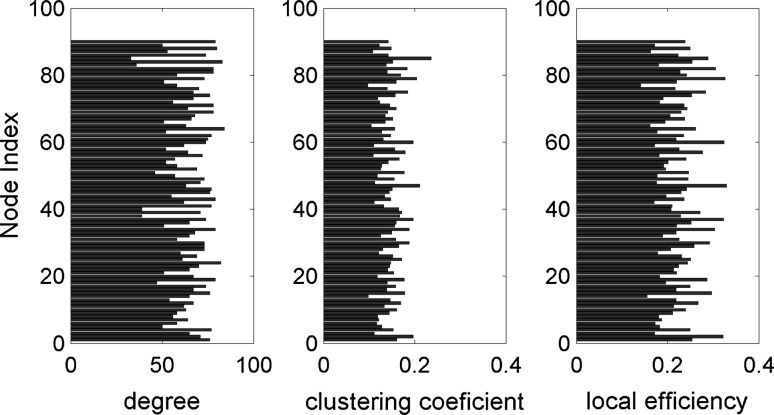
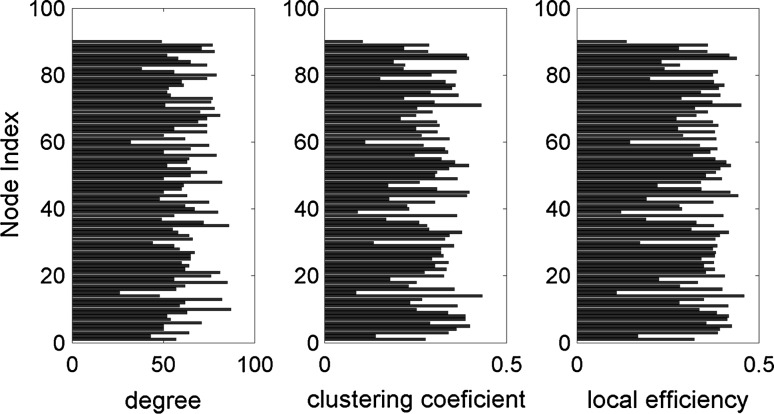
For exploration of the relation between structural connectivity and simulated functional connectivity, we consider a graph-theoretic approach (Bullmore and Sporns 2009). Here, we used standard methods to compute some of the most commonly used network characteristics: node degree, clustering coefficient and local efficiency. (See Rubinov and Sporns 2010 for details of these measures). All calculations are performed on weighted matrices – empirical AC and simulated FC – for $c=23.32$. Figure 4 represents the above mentioned network measures obtained on the AC network. The same network measures calculated on simulated FC are represented in Fig. 5. Our analysis shows that calculated network measures for simulated FC are on average higher than those for the empirical AC. Furthermore, the degrees based on the simulated FC exhibit a larger variability demonstrating self-organizing dynamics in the network. These results suggest that an anatomical connectivity analysis requires also an analysis of network dynamics in order to provide insight into large-scale brain connectivity.

Fig. 4.

Characterization of the weighted anatomical connectivity matrix: node degree, clustering coefficient and local efficiency

Fig. 5.

Characterization of the weighted simulated functional connectivity matrix (coupling strength $c=23.32$): node degree, clustering coefficient and local efficiency

Conclusion

In this study we have shown that functional connectivity within a network of neural oscillators depends on the parameters of the populations: coupling strength and structural inhomogeneities. Moreover, the dependence for the agreement between empirical and simulated FCs, as well as for the global functional network properties, has been investigated. In particular, in the parameter regions where the simulated FC resembles the empirical FC, relation with the underlying structural connectivity is examined. The functional network shows a rich pattern of activity, dependent on the underlying topology and connections strength.