A model of cooperative effect of AMPA and NMDA receptors in glutamatergic synapses

Abstract

Glutamatergic synapses play a pivotal role in brain excitation. The synaptic response is mediated by the activity of two receptor types (AMPA and NMDA). In the present paper we propose a model of glutamatergic synaptic activity where the fast current generated by the AMPA conductance produces a local depolarization which activates the voltage- and [Mg²⁺]-dependent NMDA conductance. This cooperative effect is dependent on the biophysical properties of the synaptic spine which can be considered a high input resistance specialized compartment. Herein we present results of simulations where different values of the spine resistance and of the Mg²⁺ concentrations determine different levels of cooperativeness between AMPA and NMDA receptors in shaping the post-synaptic response.

Introduction

Glutamatergic are the large majority of the brain excitatory synapses constituting the basic structures for the integration, elaboration and transmission of the information among neurons in the brain. Moreover, the spike sequences produced by a neuron are the resulting effect of the dendritic and somatic synaptic activity and, hence, these synapses represent the main origin of the neural code and neural computation. It is not surprising, then, that a huge amount of experimental and theoretical researches focus on the mechanisms of regulation of the glutamatergic synaptic response and that a great attention is paid to the structure/function relations of these synapses.

The glutamatergic synaptic complex, although in principle is very simply structured, has several regulatory mechanisms, both at pre- and post-synaptic side, which are not yet fully clarified. It is formed by a pre-synaptic Active Zone (AZ) and a corresponding post-synaptic area called Post Synaptic Density (PSD). The AZ contains vesicles filled by glutamate (Glu) docked to the pre-synaptic cell membrane. The PSD contains co-localized $\mathit{\alpha }$-amino-3-hydroxy-5-methyl-D-aspartate receptors (AMPARs) and N-methyl-D-aspartate receptors (NMDARs). The PSD is positioned on the upper surface (head) of a protrusion of the dendritic membrane called spine. This kind of organization is peculiar of this synaptic type since usually other types of synapses connect directly on dendritic shaft as for example the GABAergic synapses. This morphological organization suggests a possible role of the glutamatergic synaptic structure on its functionality (Wickens 1988; Harnett et al. 2012; Tønnesen et al. 2014).

The mechanism of transmission is also apparently simple. The arrival of a pre-synaptic spike produces a Ca⁺⁺ influx into the pre-synaptic terminal triggering the fusion of a docked vesicle to the cell membrane which produces the fusion pore through which Glu molecules freely diffuse, by Brownian motion, into the synaptic cleft. The hitting of freely moving Glu molecules to post-synaptic AMPARs and NMDARs may produce the binding AMPAR-Glu and NMDAR-Glu. AMPARs and NMDARs have two binding sites for Glu. Both receptor types are ionotropic channels that, if opened, permit the flow of a depolarizing current. To have a good open probability each receptor need to be connected to two molecules of Glu (AMPAR-2Glu and NMDAR-2Glu). The ionic current flowing into these receptors is contributed mainly by Na⁺, K⁺ and Ca⁺⁺ ions and is called Excitatory Post Synaptic Current (EPSC). The EPSC produces a variation of the membrane potential called Excitatory Post Synaptic Potential (EPSP) which, filtered by the the cable properties of the dendrites (Rall 1962b; Rall and Rinzel 1973), arrives to the neuron soma. The integration of the EPSPs arriving from the dendritic districts at the initial segment of the axon (hillock), can drive the membrane potential to the threshold value for the spike generation.

Despite this apparent simplicity, all the synaptic events are very finely regulated by complex mechanisms. Moreover, for a single presynaptic event, a large variability of the responses (5–100 pA for the EPSC) is observed although synaptic transmission is defined as of “quantal” type (Forti et al. 1997; Hanse and Gustafsson 2001; Auger and Martin 2000; Boucher et al. 2010). The observed variability in several cases can be attributed to stochastic factors. For example, vesicles position (eccentricity) and the amount of Glu molecules they store, can be sources of pre-synaptic stochastic variability that influences synaptic response both when only AMPARs (Clements et al. 1992; Raastad et al. 1992; Liu et al. 1999; McAllister and Stevens 2000; Ventriglia and Di Maio 2002, Ô2003a, b; Ventriglia 2011; Ventriglia and Di Maio 2013a, b) and when also NMDARs contribute to the response (Dobrunz and Stevens 1997; Schikorski and Stevens 1997, 2001; Ventriglia and Di Maio 2002, 2003a, b). Examples of variability due to post-synaptic factors can be the number of receptors (Ventriglia and Di Maio 2000a, b, 2002, 2003a, b) and their subunits composition. It is well known, in fact, that the assembly of receptors with different subunits produces channels with different conductance and this is true for both types of receptors (see for example Traynelis et al. 2010; Table 2).

Table 2.

Basic EPSC simulation parameters

Parameter	Value
C	$1\mathit{\mu }F/c{m}^2$
$V_r$	$-65m{V}^a$
$V_u$	$+40m{V}^b$
$V_E$	0mV
$R_s$	$500M{\mathit{\Omega }}^c$
$P_{o_{AMPA}}$	$0.{67}^d$
$P_{o_{NMDA}}$	$0.{42}^d$
$g_{AMPA}$	$15\pm 10p{S}^e$
$g_{NMDA}$	$40\pm 15p{S}^e$
${\mathit{\alpha }}_{AMPA}$	5ms
${\mathit{\alpha }}_{NMDA}$	150ms
$\mathit{\delta }t$	${10}^{-3}ms$

C specific membrane capacitance, $V_r$ resting potential, $V_u$ complete Mg²⁺ unblocking potential, $V_E$ synaptic reverse potential, $R_s$ synaptic resistance, $P_{o_{AMPA}}$ mean AMPAR open probability, $P_{o_{NMDA}}$ mean NMDAR open probability, $g_{AMPA}$ AMPAR conductance, $g_{NMDA}$ NMDAR conductance, ${\mathit{\alpha }}_{AMPAR}$ mean AMPAR-Glu binding duration, ${\mathit{\alpha }}_{NMDAR}$ mean NMDAR-Glu binding duration, $\mathit{\delta }t$ simulation time step

^a (Planert et al. 2013); ^b (Kupper et al. 1998; Jahr and Stevens 1990; Vargas-Caballero and Robinson 2004); ${}^c$ (Wickens 1988); ${}^d$ (Traynelis et al. 2010; Dingledine et al. 1999; Zito and Scheuss 2009); ${}^e$ (Dingledine et al. 1999; Traynelis et al. 2010)

The variability of EPSC amplitude can also depend on factors external to the synapse as for the case of dopamine regulation of glutamatergic synapses on medium spiny neurons (MSNs) of the striatum (Umemiya and Raymond 1997; Dingledine et al. 1999; Di Maio et al. 2015) and activity of neighbor synapses (both excitatory and inhibitory) that, by changing locally the membrane potential, modify the driving force for current generation (Di Maio 2008).

The EPSC variability of the glutamatergic response represents a key obstacle for the understanding of the neural codes because it is one of the main factors influencing the stochasticity observed in spike sequences of neurons also in the case of the same presynaptic stimulation.

Another key factor that must be considered in physiological condition is the relative role of AMPARs and NMDARs in shaping the post-synaptic response. Although the contribution to the EPSC consists for both of them in a depolarizing current, they contribute with different dynamics in shaping the EPSC time course. AMPARs have lower affinity for Glu and a lower mean single receptor conductance with respect to the NMDARs (Dingledine et al. 1999; Traynelis et al. 2010) but they produce a very fast response (peak at ~0.3 ms) and, on average, they represent the majority of receptors (see Ventriglia 2011, among others). The NMDARs at resting level of the membrane potential (~−65 to −75 mV) are completely blocked by Mg²⁺ and, consequently, their conductance is 0 also in the case they are in the configuration NMDAR-2Glu. Unblocking of these receptors depends on membrane voltage such that the complete removal of the Mg²⁺ block occurs only for very positive values of the membrane voltage ($V_m\simeq$+40 mV) (Jahr and Stevens 1990; Kupper et al. 1998; Vargas-Caballero and Robinson 2004). These properties of NMDARs are very important for phenomena as Long Term Potentiation (LTP) and Long Term Depression (LTD) which are the base for cognitive processes as learning and memory. For a given number of NMDARs in a given synapse, in fact, changes in $V_m$ can modulate the progressive activation of NMDAR producing effect both in amplitude and time course of the synaptic response since, once activated, a NMDAR has a long activity time (up to ~500 ms) due to its higher affinity to Glu compared to that of AMPARs (less than ~10 ms for full EPSC decay) (Clements et al. 1992, among many others). Consequently, we can assume that, in physiological conditions, the rising phase of EPSC is mainly contributed by AMPARs activity while the decay phase by the NMDARs activity that maintain the memory of the occurred (pre-synaptic) event.

On the role of NMDARS, however, some considerations are needed. Both AMPA and NMDA currents have a reversal potential (the value of membrane potential above which current inverts the direction) of ~0 mV. This means that membrane potentials too close to this value would produce non significant NMDA contribution to the synaptic EPSC. Activation of NMDA conductance has been observed for levels of depolarization (below 0 mV) depending on $V_m$ and on (Mg²⁺) according to sigmoid functions (Jahr and Stevens 1990; Vargas-Caballero and Robinson 2004). Moreover, despite the fact that AMPA EPSP registered at soma is usually less than 1 mV of amplitude, local variation of $V_m$ can be much more consistent if we consider that the synaptic spine, for its morphology, can be considered as a separate compartment with a high impedance (Wickens 1988; Harnett et al. 2012; Tønnesen et al. 2014). It follows that in the spine compartment, also for low level of synaptic current produced during the synaptic transmission, it is possible a variation of $V_m$ in the order of tens of mVs (Wickens 1988; Harnett et al. 2012; Tønnesen et al. 2014). The synaptic resistance ($R_s$) has been computed in the range ~100–1000 M$\mathit{\Omega }$ (Segev 1998; Harnett et al. 2012; Tønnesen et al. 2014). An important question then is: “Can the fast AMPA-dependent membrane depolarization at the spine level be responsible for the activation of NMDA conductance for a single synaptic event?”. If so, a cooperative effect between AMPA and NMDA in physiological conditions can be assumed also for a single synaptic event (Jahr and Stevens 1990; Vargas-Caballero and Robinson 2004; Di Maio et al. 2015).

In the present paper, in order to answer the above question we propose a model of glutamatergic synapse where the mutual regulation of AMPA and NMDA activities are considered as depending on the probability that local variations of $V_m$ induced by the fast AMPA current can induce, according to probabilistic rules, the unblocking of Mg²⁺ from NMDA receptors freeing their conductance. We assumed as a probabilistic function for the freeing of the single NMDAR a modification, in terms of probability, of the sigmoid relationship $V_m/g_{\mathrm{N}\mathrm{M}\mathrm{D}\mathrm{A}\mathrm{R}}$ (being $g_{\mathrm{N}\mathrm{M}\mathrm{D}\mathrm{A}\mathrm{R}}$ the single receptor conductance) experimentally found by Jahr and Stevens (1990) and Vargas-Caballero and Robinson (2004).

Methods

We used, in sequence, two different simulation systems, one for the diffusion of glutamate in the synaptic cleft and binding to the post-synaptic receptors and one that, by using the results of the diffusion model produces the simulation of the post-synaptic activity.

Diffusion simulation was implemented by a Fortran program based on MPICH parallelizing routines. This program uses a fine description of the synaptic geometry and Langevin equations (Gillespie 1996) for the Brownian diffusion of the neurotransmitter molecules (Ventriglia and Di Maio 2000a, b, 2002, 2003a, b, 2013a, b; Di Maio et al. 2015). The post-synaptic activity has been simulated by a C++ program which used, off line, the matrix of the second Glu molecule binding to the receptors, produced during the diffusion simulation. This matrix is used to simulate the post-synaptic electrical activity.

Model

The model used can be essentially divided into two parts. The diffusion model and the EPSC-EPSP model.

Synaptic model

The diffusion model has been based on Brownian motion of Glut molecules solely constricted by the synaptic structure. In our simulations, the diffusion process starts into a vesicle docked at the pre-synaptic Active Zone (AZ). The arrival of a pre-synaptic spike (not simulated) induces the formation of a fusion pore between a pre-synaptic vesicle and the pre-synaptic neuron membrane. The opening of this pore permits the free diffusion of Glut molecules into the synaptic cleft (Ventriglia and Di Maio 2000a, b, 2002, 2003a, b, 2013a, b; Di Maio et al. 2015).

Geometry of the synaptic space

We used a very fine time step (40 fs) without space discretization which requires a very fine geometrical description of the synaptic space since the molecule pathway is followed, for very narrow positions, step by step. The geometry of the synaptic space includes a pre-synaptic (spherical) vesicle docked at the AZ having an inner diameter ($d_{vesicle}$) of 26.6 nm and containing 770 Glu molecules ($N_{Glu}$). When the vesicle fuses with the pre-synaptic membrane, a fusion pore is formed. This pore was modeled as a cylinder with height ($h_{pore}$) of 12 nm (the sum of two lipid bilayers) and a radius expanding with a areal velocity ($V_{areal}$) (see Table 1; Ventriglia and Di Maio 2000a, b). The AZ, on the pre-synaptic side, and the PSD, on the head of a spine, form a flat cylinder the height of which ($h_{syn}$) was 20 nm (the synaptic cleft) and diameter of 220 nm. This cylinder is enclosed in a larger one with a diameter of 400 nm delimiting the whole synaptic space. The space between the two cylinders contains fibrils which anchor, to each other, the pre- and post-synaptic membrane (Zuber et al. 2005; Ventriglia and Di Maio 2013a, b). Fibrils are modeled as cylinders with diameter of 14 nm regularly inter-spaced every 22 nm (Zuber et al. 2005; Ventriglia 2011). AMPA and NMDA receptors are considered as cylinders, protruding from the post-synaptic membrane of 7 nm, each having two binding sites (of circular shape) for Glu on the upper part. The wall of the external cylinder is assumed to be an absorbing boundary because the probability that molecules spilled over of the synaptic space return back is negligible because captured by Glu receptors of the glial cells surrounding all the synaptic area (Boucher et al. 2010).

Table 1.

Parameters used for the diffusion simulation

$N_{Glu}$	770
$d_{vesicle}$	26.6 nm
T	298.16 K
D	$7.6\times {10}^{-6}$cm${}^2$s${}^{-1}$
m	$2.4658025\times {10}^{-25}$ Kg
$\mathit{\Delta }$	$40\times {10}^{-15}$ s
$h_{pore}$	12 nm
$h_{syn}$	20 nm
$V_{areal}$	31.4 nm${}^2$ms${}^{-1}$
$P_{\mathit{\gamma }}$	$3\times {10}^{-6}$

Among the many different options (Ventriglia and Di Maio 2002, 2003a), in order to standardize the results, for the present work we simulated a diffusion origin from a vesicle centered at the central axis passing from AZ and PSD (i.e., central coordinates of vesicles are $x_0=y_0=0.0$). Different positions of vesicle could, in fact, one of the causes of post-synaptic response variability (Ventriglia and Di Maio 2002, 2003a).

Diffusion model

The diffusion of Glutamate molecules is based on free Brownian motion restricted only by the synaptic structures. We implemented a numerical simulation system based on Langevin equations (Gillespie 1996) which in the standard form are written as:

$$\begin{array}{cc}\hfill \frac{d}{dt}{\mathbf{r}}_i(t)& ={\mathbf{v}}_i(t)\hfill \end{array}$$ 1

$$\begin{array}{cc}\hfill m\frac{d}{dt}{\mathbf{v}}_i(t)& =-\mathit{\gamma }{\mathbf{v}}_i(t)+\sqrt{2\mathit{ϵ}\mathit{\gamma }}\mathbf{\Lambda }(t)\hfill \end{array}$$ 2

where ${\mathbf{r}}_i(t)$ is the position and ${\mathbf{v}}_i(t)$ is the velocity of the generic ith molecule, m is the molecular mass of the neurotransmitter. $\mathit{\gamma }$ is a friction parameter depending on the absolute temperature [$\mathit{\gamma }=k_B\frac{T}{D}$ with $k_B$ being the Boltzman constant, D the diffusion coefficient for glutamate ($\mathit{ϵ}=k_{b}T$) and T the temperature in ${}^{o}K$]. As stochastic force we supposed a Gaussian white noise $[⟨{\mathit{\Lambda }}_i(t){\mathit{\Lambda }}_j(t+\mathit{\Delta })⟩={\mathit{\delta }}_{i,j}\mathit{\delta }(\mathit{\Delta })]$ with intensity $2\mathit{ϵ}\mathit{\gamma }$.

The above equations have been discretized for numerical simulation in the parallel Fortran program as follow

$$\begin{array}{cc}\hfill {\mathbf{r}}_i(t+\mathit{\Delta })& ={\mathbf{r}}_i(t)+{\mathbf{v}}_i(t)\mathit{\Delta }\hfill \end{array}$$ 3

$$\begin{array}{cc}\hfill {\mathbf{v}}_i(t+\mathit{\Delta })& ={\mathbf{v}}_i(t)-\mathit{\gamma }\frac{{\mathbf{v}}_i}{m}\mathit{\Delta }+\frac{\sqrt{2\mathit{ϵ}\mathit{\gamma }\mathit{\Delta }}}{m}{\mathbf{\Omega }}_i\hfill \end{array}$$ 4

where ${\mathbf{\Omega }}_i$ is a random vector with three Gaussian components $x_i,y_i,z_i$ having all mean $\mathit{\mu }=0$ and $\mathit{\sigma }=1$ with final $\mathit{\sigma }$ being dependent on the multiplicative value. $\mathit{\Delta }$ is the time step that we have chosen to have a good dumping term in the above equation ($\mathit{\Delta }=40\times {10}^{-15}s$). The space position ${\mathbf{r}}_i(t)=[x_i(t),y_i(t),z_i(t)]$ was saved for the analysis every $5\times {10}^4$ iterations, corresponding to a simulation time of $2\times {10}^{-9}s$. In Table 1, a summary of the main parameters used for diffusion simulation is presented. During the diffusion process, Glu molecules were considered as dimensionless (dots) except when their position approached one of the the binding site of the receptors. In this case, the geometry of Glu molecule was considered to compute the binding probability by geometrical considerations. In fact, we consider not accurate the binding probability normally used (Clements et al. 1992; Jonas et al. 1993) because they are usually obtained at equilibrium which is not the case of the synaptic space during the neurotransmitter vesicle release in physiological conditions (Ventriglia 2011; Ventriglia and Di Maio 2013a, b). Even more, normal binding probability would be not adequate for the small time step we used ($40\times {10}^{-15}s$). We considered that the Glu molecule has an ovoid shape and that only the $\mathit{\gamma }-$carboxyl side of the molecule can bind to glutamatergic receptors. Since we modeled the binding site as of circular shape, we assumed that all useful orientations of the Glu molecule that can produce a binding are enclosed in a cone angle and we computed the binding probability as the ratio between the cone angle and the sphere which contains all the possible orientations (Ventriglia and Di Maio 2013a, b; Ventriglia 2011; Di Maio et al. 2015).

For computational purposes, the PSD was considered as a matrix $\mathbf{R}$ of size $(10\times 10)$. In the present simulations we used a total of 68 receptors. Of these 55 were AMPARs, 13 NMDARs and 32 positions of the matrix, segregated into the corners, did not contain any receptor. This arrangement produced a representation of the PSD of a circular shape in the squared matrix [see Fig. 1 of Ventriglia and Di Maio (2013a)]. This number was chosen considering the size of our simulated synapse, the size of the single receptors and a proportion $\frac{N_{AMPAR}}{N_{NMDAR}}$ considered reasonable for a mean mature synapse of CA1 area of mammalian hyppocampus (Ventriglia 2011).

The receptors were randomly positioned on the matrix $\mathbf{R}$ such that any locations $i,j\in \mathbf{R}$ was defined as

$$R_{i,j}\in \mathbf{R}=\left\{\begin{array}{cc}0\hfill & \text{if}{R}_{i,j}\in \mathbf{R}\text{has}\text{no}\text{receptor}\\ 1\hfill & \text{if}{R}_{i,j}\in \mathbf{R}\text{is}\text{AMPAR}\\ 2\hfill & \text{if}{R}_{i,j}\in \mathbf{R}\text{is}\text{NMDAR}\end{array}\right.$$

The matrix $\mathbf{R}$ can be defined as identity matrix.

Two additional matrices ${\mathbf{T}}_{\mathbf{1}}$ and ${\mathbf{T}}_{\mathbf{2}}$, of the same size of $\mathbf{R}$, were used to register respectively the binding time of a first and a second molecule of Glu to each receptor such that $\forall R_{i,j}\in \mathbf{R}\exists [T_{1_{i,j}}\in {\mathbf{T}}_{\mathbf{1}},T_{2_{i,j}}\in {\mathbf{T}}_{\mathbf{2}}]$.

All the process described above essentially correspond to simplified classical Markov chain of the receptor transition which can be summarized as $B_0\rightleftharpoons B_1\rightleftharpoons B_2\rightleftharpoons A_2$. Here $B_0$ denotes the non bound state. $B_1$ represents the binding of a single Glu to the receptor and the time of transition was registered in the matrix ${\mathit{T}}_{\mathbf{1}}$. $B_2$ represents the state with two molecules bound and the transition time was registered in the matrix ${\mathit{T}}_{\mathbf{2}}$. The probabilistic transitional rules for the states $B_0\rightleftharpoons B_1\rightleftharpoons B_2$ are based on the geometrical considerations described above. The state $A_2$ represents the active state when two molecules of Glu are bound. Although in some more complex schema of receptor transition also the probability that a single bound receptor can open is included (i.e., transition $B_1\rightleftharpoons A_1$), we neglected the contribution of the $A_1$ state because the probability that one of such receptors open with a single bound molecule of Glu is negligible. Since we are interested only in the overt response and not in the single receptor dynamic, in our simplified schema we considered as equivalent to the non active states all the transitions (as for example desensitization) which do not produce synaptic current and hence the event of transition $B_2\rightleftharpoons A_2$ is the only one contributing in shaping the synaptic responses.

Post-synaptic response model

The binding of two molecules of glutamate to AMPARs produces their opening while for the NMDARs the same occurs only in the case it has been freed of Mg${}^{2+}-$block. We then used the matrix ${\mathbf{T}}_{\mathbf{2}}$ containing the binding time of the second molecule of Glu to the receptors to generate the post-synaptic electrical activity (EPSP and EPSC) according to the following equations:

$$\begin{array}{c}\hfill I_s(t)=g_s(t)(V_m(t)-V_E)\end{array}$$ 5

where $I_s(t)$ is the synaptic current(EPSC), $g_s(t)$ is the total synaptic conductance and $V_m(t)$ the membrane potential at time t. $V_E$ is the synaptic equilibrium (reversal) potential ($\sim 0mV$). Although negligible, a capacitative current $I_c(t)$ has been computed considering only the spine surface as unique capacitative component according to

$$\begin{array}{c}\hfill I_c(t)=C\frac{dV}{dt}\end{array}$$ 6

with C being the membrane capacitance. Since the value of $I_c<1pA$ it was not included in the following computation.

The value of $V_m(t)$ has then been computed as

$$\begin{array}{c}\hfill V_m(t)=V_r-R_s{I}_s(t)\end{array}$$ 7

Here $V_r$ is the resting potential, $I_s$ is the synaptic current due to the receptor opening and $R_s$ the spine resistance that we varied across the simulations. In the time discretized version [time step $\mathit{\delta }t=1\times {10}^{-6}s$ ($1\mathit{\mu }s$)] we have:

$$\begin{array}{c}\hfill I_s(t)=g_s(t)(V_m(t-\mathit{\delta }t)-V_E)\end{array}$$ 8

To compute the total synaptic conductance ($g_s(t)$) different criteria need to be used between AMPARs and NMDARs. While for AMPARs $B_2\rightleftharpoons A_2$ transition depends only on the open (and closing) probability of this receptors (see below), NMDARs are blocked by Mg${}^{2+}$ at the resting level and, hence, depends also on the probability that they can be unblocked. Some authors have shown that NMDA-conductance activation depends on Mg${}^{2+}$ concentration and on the depolarization level of the membrane according to a sigmoid function (Jahr and Stevens 1990; Vargas-Caballero and Robinson 2004). We have transformed this function in terms of probability of Mg${}^{2+}$ unblocking ($P_u$) from the membrane potential by using a similar sigmoid function as follows

$$\begin{array}{cc}\hfill P_u(V_m,X)& =\frac{1}{1+X{e}^{-k{V}_m)}}\hfill \\ \hfill P_u(V_m,X)& =\left\{\begin{array}{cc}=1\hfill & \text{if}X:X=0;V_m:V_m\in (-\infty ,\infty )\hfill \\ \in (-\infty ,\infty )\hfill & \text{if}X:X>0;V_m:V_m\in (-\infty ,\infty )\hfill \end{array}\right.\hfill \end{array}$$ 9

where X is the $M{g}^{2+}$ concentration (in mM), $V_m$ the membrane potential (in mV) and k is a steepness parameter we used to adjust the probabilistic function such to resemble the relationship voltage/conductance found by Jahr and Stevens (1990) and Vargas-Caballero and Robinson (2004). For a given value of Mg${}^{2+}$ then

$$\begin{array}{c}\hfill P_u(V|X)=\frac{1}{1+[M{g}^{2+}]e^{-(0.1V_m)}}\end{array}$$ 10

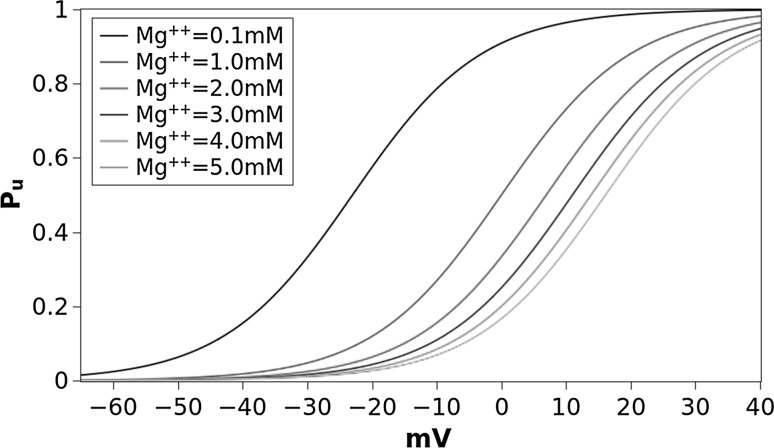
The probability function for the different values of [Mg${}^{++}$] is shown in Fig. 1. The steepness was chosen to ensure that $P_u\sim 0$ when membrane is at the resting potential ($-65$ mV) and $P_u\sim 1$ for the almost complete Mg${}^{2+}$ unblocking ($V_u\sim +40mV$) observed by Jahr and Stevens (1990) and Vargas-Caballero and Robinson (2004). For $[M{g}^{2+}]=0$ we have $P_u=1$ that means no Mg${}^{2+}$, no block of NMDARs the dynamic of which, with the appropriate parameters, becomes similar to that of AMPARs. For values of [Mg${}^{2+}]>0$, into the physiological range of $V_m$ ($-65\text{to}+40mV$), $P_u$ is never 0 and never 1 ensuring that at $-65$ mV there is a low probability ($P_u\le {10}^{-3}\text{for}[M{g}^{2+}]=1mM$) that some NMDAR, for molecular stochastic processes, can be spontaneously unblocked and that at $V_m=+40mV$, for the same reason, some receptors can remain still blocked.

Fig. 1.

Probability function for unblocking of Mg${}^{2+}$ from NMDAR as function of $V_m$

We used a Heaviside function applied to the uniform probability distribution (U(0, 1)) as a probabilistic rule for the transition $B_2\rightleftharpoons A_2$ both for AMPARs and for unblocked NMDARs by using the appropriate open probability $P_o$ (see Table 2). Given $P_o$ (Table 2), the closing probability will be $P_c=1-P_o$.

At any time t the total conductance was computed considering the state and the individual conductance of receptors in the state $A_2$ as

$$\begin{array}{cc}\hfill g(t)& =\sum _{i=1}^{10}\sum _{j=1}^{10}{g}_{r_{i,j}}(t)\hfill \\ \hfill g_{r_{i,j}}(t)& =\left\{\begin{array}{cc}0\hfill & \text{if}{R}_{i,j}\in \mathbf{R}=0\text{or in}{B}_0,B_1,B_2\text{state}\hfill \\ g_{AMPA}\hfill & \text{if}{R}_{i,j}\in \mathbf{R}=1\text{in state}{A}_2;T_{2_{i,j}}<t<T_{u_{i,j}}\hfill \\ g_{NMDA}\hfill & \text{if}{R}_{i,j}\in \mathbf{R}=2\text{in state}{A}_2;T_{2_{i,j}}<t<T_{u_{i,j}}\hfill \end{array}\right.\hfill \end{array}$$ 11

where $g_{r_{i,j}}(t)$ is the conductance of $R_{i,j}\in \mathbf{R}$ and $T_{u_{i,j}}\in {\mathbf{T}}_{\mathbf{u}}:T_{u_{i,j}}=T_{2_{i,j}}+t_b$ is the duration of binding of two molecules of Glu to a receptor independently of the condition open ($A_2$) or close ($B_2$). The value of $t_b$ was considered as depending on a Poisson process where the time at which a molecule of Glu unbinds from the receptor is a second event after the binding event. Distribution of $t_b$ has been chosen according to a probability density function of the Exponential Distribution of the type $f(x;{\mathit{\alpha }}_R)=\frac{1}{{\mathit{\alpha }}_R}{e}^{-\frac{x}{{\mathit{\alpha }}_R}}$ which is the base of such Poisson’s processes. The parameter ${\mathit{\alpha }}_R$ depends on the affinities for Glu and is notoriously larger for NMDARs than for AMPARs (see Table 2). At each iteration the matrix ${\mathbf{T}}_{\mathbf{u}}$ was renewed so that $T_{u_{i,j}}\in {\mathbf{T}}_{\mathbf{u}}=T_{2_{i,j}}+t_b$. In summary, $\forall T_{2_{i,j}}\le t\le T_{u_{i,j}}$ the receptor $R_{i,j}\in \mathbf{R}$ undergoes to the transition $B_2\rightleftharpoons A_2$ while for $t=T{u}_{i,j}+\mathit{\delta }t$ it definitively goes into the state $B_1$ and its contribution to the conductance become 0. Transitions probability $B_2\rightleftharpoons A_2$ were computed at each time step and $\forall R_{i,j}\in \mathbf{R}$ in the interval $\{T_{2_{i,j}}\le t\le T_{u_{i,j}}\}$ using the Heavised function such that

$$\begin{array}{cc}\hfill P_{B_2\to A_2}& =\left\{\begin{array}{cc}0\hfill & \text{if}U(0,1)>P_o\hfill \\ 1\hfill & \text{if}U(0,1)\le P_o\hfill \end{array}\right.\hfill \\ \hfill P_{A_2\to B_2}& =\left\{\begin{array}{cc}1\hfill & \text{if}U(0,1)>P_o\hfill \\ 0\hfill & \text{if}U(0,1)\le P_o\hfill \end{array}\right.\hfill \end{array}$$

where $P_o$ is the probability to open the specific value of which are reported in Table 2 both for AMPARs ($P_{o_{AMPA}}$) and for NMDARs ($P_{o_{NMDA}}$). If receptor is in $A_2$ state (open) the appropriate conductance ($g_{i,j}$) depends on the receptor type and its subunits composition. It is well known, in fact, that AMPARs and NMDARs are tetramers that can have different assembly configurations (usually dimers of dimer) and that the single channel conductance depends on the subunit composition (Dingledine et al. 1999; Traynelis et al. 2010). To account for this differences we randomized single channel conductances by a Gaussian distribution $G({\overline{g}}_r,\mathit{\sigma }$) with $\overline{g_r}$ being the mean single receptor conductance averaged among those known for the different subunits composition of AMPARs or NMDARs, respectively [see Table 2 and Dingledine et al. (1999) and Traynelis et al. (2010)]. Single receptor conductance has been computed anew at each iteration.

In the different simulations we varied the synaptic resistance $R_s$ in steps of $100M\mathit{\Omega }$ in the range 100–1000 M$\mathit{\Omega }$.

For each value of $R_s$ the $M{g}^{2+}$ concentration was varied in the range 1–5 mM in steps of 1 mM. A comparative test with $[M{g}^{2+}]=0.1mM$ was added to simulate the almost Mg${}^{2+}-$free condition and for the comparison of the NMDA current obtained in our simulations with the experimental results on conductance reported by Jahr and Stevens (1990) and Vargas-Caballero and Robinson (2004).

Being interested only to the peak amplitude of the EPSC, the total simulation time was limited to 50 ms. Simulation time step ($\mathit{\delta }t$) was 0.001 ms ($1.0\mathit{\mu }s$). EPSCs ad EPSPs were computed by averaging over 10000 runs.

Results

Our results consisted of EPSCs and EPSPs of a simulated glutamatergic synapse obtained for different values of $R_s$ and $M{g}^{2+}$ concentrations.

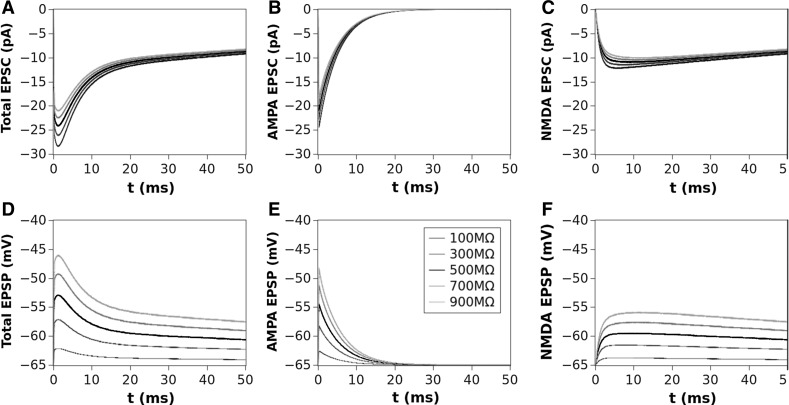
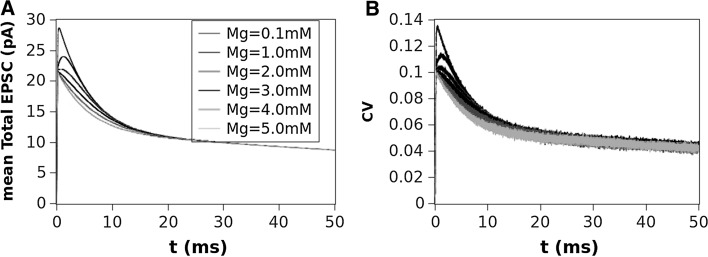
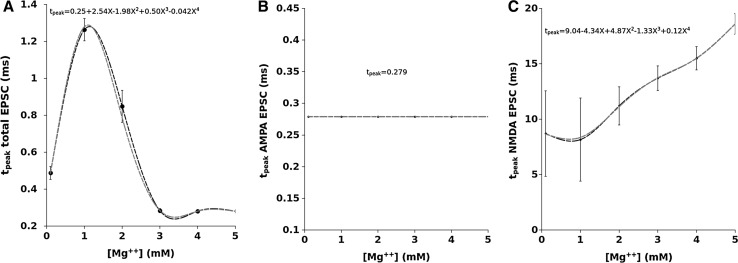
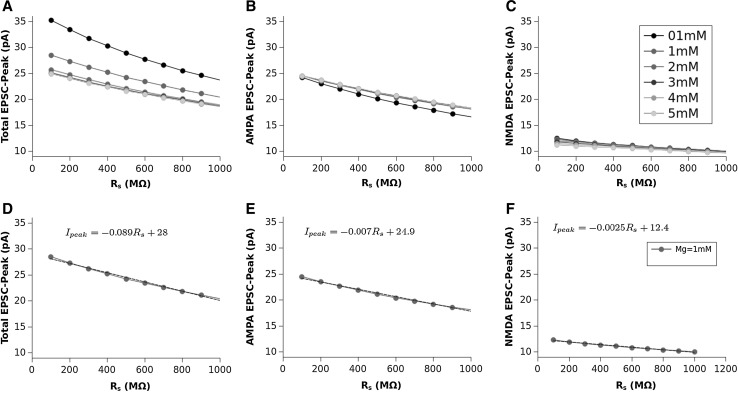
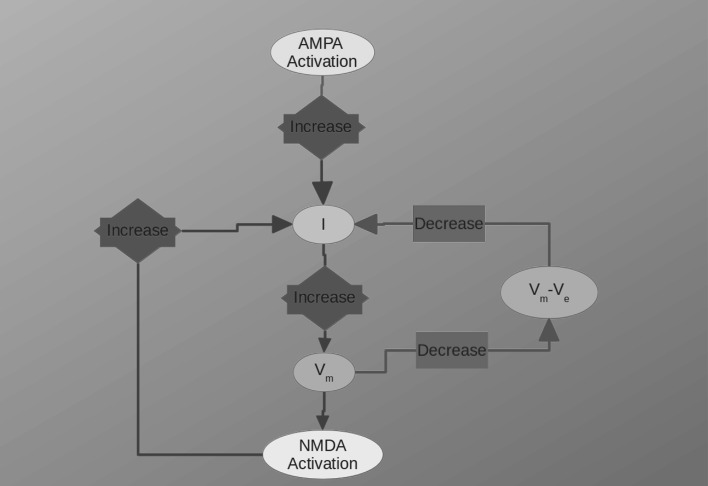
In Fig. 2 we show, as an example, the EPSCs (panels A,B and C) and corresponding EPSPs (panels D,E and F) computed for a value of $[M{g}^{2+}]=1mM$, which is considered the most close to the physiological concentration, for values of $R_s$ ranging from 100 to 1000 M$\mathit{\Omega }$. The AMPA (second column) and NMDA (third column) contributions are also shown in this figure. The dependence of the total EPSC and EPSP from $R_s$ is evident as well as for the AMPA and NMDA components. The time course and amplitude of our simulated EPSCs, adequately scaled for the cable properties, fit very well those of experimental data reported in literature (see Forti et al. 1997; Zito and Scheuss 2009, for example) showing that our model is enough robust. Figure 3 shows the EPSC time course (left panel) averaged over all the range of resistances we used (100–1000 M$\mathit{\Omega }$) compared for the different values of Mg${}^{2+}$ concentration. In this figure can be noted that the highest peak amplitude of the total EPSC is obtained for Mg${}^{2+}$ = 0.1 mM. This effect is due because the very low Mg${}^{2+}$ concentration permits the NMDA-component to grow very fast such that summation occurs when both components are almost at peak (best condition). By increasing $M{g}^{2+}$ the NMDA peak decreases while increases its time to peak (see in comparison with Fig. 5). The combined effect of these two factors reduces the total EPSC peak in the range $1-2mM$ of the $M{g}^{2+}$ concentration. The increasing of the $M{g}^{2+}$ concentration, in fact, increases the temporal separation of the two components peaks reducing the efficacy of the summation such that the peak of the total EPSC reduces in amplitude. As a general rule we can assume that “the larger the peaks separation of the two components, the lower peak amplitude of the total EPSC”. This general rule applies for concentrations of $M{g}^{2+}$ less than 3mM. For the higher concentrations (3, 4 and $5mM$) the separation of NMDA and AMPA peaks become such that only the AMPA-component contributes to the total EPSC (see also Fig. 5). The right panel of Fig. 3 shows the coefficient of variation (CV) computed as $CV=\frac{SD}{\left|\overline{I}\right|}$ being $\left|\overline{I}\right|$ the absolute value of the mean current and SD the standard deviation. The shape of the CV resembles that of the corresponding EPSC for all the values of $M{g}^{2+}$ concentration showing that the larger variability depending on $R_s$ occurs at the peak. The variation of the CV peaks is $0.10-0.14$ indicating that spine resistance can contribute for a $10-14\%$ of the total stochastic variability observed in recordings from different synapses (which can have different spine resistances). In Fig. 4, left panels, the dependence of peak amplitude for the total, AMPA- and NMDA-EPSCs are shown for all the concentration of $M{g}^{2+}$ and for all the values of $R_s$. These results, compared with those of Fig. 3, suggest that the cooperative modulation of AMPA and NMDA in producing the total EPSC is restricted to a range of values of $[M{g}^{2+}]\le 3mM$. Panels D, E and F of this figure show the peak amplitudes of the total, AMPA and NMDA EPSCs for a concentration of $M{g}^{2+}=1mM$ which, in general, is considered the most physiological one. The same panels show the fitting curves with relative equations. Comparing the fitting models, it is clear that the trend of the total EPSC is more similar to that of the AMPA-component than to that of the NMDA-component. These results suggest a major contribution of the AMPA with respect to the NMDA component to the total EPSC peak amplitude. This is not a direct consequence of the different number of AMPARs and NMDARs since single channel conductance for NMDARs is much higher than the AMPARs one (see, Table 2). Figure 5 shows the dependence of the time to peak on $M{g}^{2+}$ concentration for the total, AMPA and NMDA EPSCs. Time to peak has been averaged over all the values of $R_s$ and the fitting curves with the corresponding equations are superimposed. It is well clear that AMPA time to peak is a horizontal line (a constant) because AMPA component has no dependences. Conversely, both the total and NMDA time to peak are fitted by a 4th order polynomial as function of Mg⁺⁺ concentration although with different parameters. These results suggests that the component which maximally influences the time to peak of the total EPSC is the NMDA-component. As for the case of the amplitude, also the complex pattern of the time to peak of the total EPSC depends on the different times to peak of the AMPA- and NMDA-components. Also in this case the larger observed variability (see SD bars in Fig. 5) has been obtained for concentrations of $M{g}^{2+}<3mM$ suggesting that in this range there can be a significant regulatory effect. Figure 6 shows a schematic simplified description of the whole model and it is intended to help the understanding of the complex pattern of cooperativeness AMPARs/NMDARs in shaping the post-synaptic response. In brief, the fast activation of AMPARs produces the local depolarization of the membrane which can partially activate NMDAR conductance. The total (AMPA/NMDA) current increases the depolarization but decrease the driving force ($V_m-V_E$) moderating, in this way, both AMPA and NMDA dependent currents. In this regulatory system, the spine resistance play a pivotal role because the amplitude of the membrane depolarization depends on this parameter.

Fig. 2.

Total EPSC (A) and AMPA (B) and NMDA (C) contributions for a concentration of Mg${}^{2+}$ = 1 mM and values of $R_s$ ranging 100–1000 M$\mathit{\Omega }$; Panels D, E and F show the corresponding EPSPs

Fig. 3.

A Mean EPSC peak amplitude mediated over all the values of $R_s$ and compared for the different concentration of $M{g}^{2+}$. B the coefficient of variation ($CV=\frac{SD}{\left|\overline{I}\right|}$) for the mediated EPSCs of a

Fig. 5.

EPSC time to peak as a function of [Mg⁺⁺] mediated for all the values of $R_s$. A Total EPSC and polynomial curve fitting. B AMPA–EPSC (it is a constant). C NMDA–EPSC and polynomial curve fitting. The bars represent the standard deviation for all panels

Fig. 4.

Total EPSC (A), AMPA EPSC (B) and NMDA EPSC (C) peak amplitudes as function of $R_s$ for different values of [Mg${}^{2+}$]. Total (D), AMPA (E) and NMDA (F) EPSCs for $[M{g}^{2+}]=1mM$ as function of $R_s$ and corresponding liner fittings

Fig. 6.

Schematic representation of AMPA/NMDA cooperation to the EPSC and EPSP

Discussion

The progression of knowledge on glutamatergic synapse shows constantly how this structure, which is the base of information transmission among neurons and neuronal computation, is extremely complex and very finely regulated. The variability of the synaptic morphology (the size of the spine and of the PSD), the total number of receptors, the relative proportion AMPARs/NMDARs and many other parameters, influence the synaptic response contributing to the observed variability of the recorded EPSC.

In the present paper we have used our model of glutamatergic synapse to test the influence of some biophysical parameters on its activity. Several point need to be discussed.

The fact that this kind of synapse is organized as a spine, with an head that can be variable in size and a neck which can vary in length and diameter, in some way must be connected to its functionality (Wickens 1988; Harnett et al. 2012; Tønnesen et al. 2014). A biophysical parameter that can play a reasonable role and is connected to the spine morphology is the total electric resistance. For this reason the spine has been considered as a separate electrical compartment (Wickens 1988; Harnett et al. 2012; Tønnesen et al. 2014; Di Maio et al. 2015). In the present paper, we assumed that spines with different resistance $R_s$ can produce a different regulatory effect on membrane voltage and consequently on the relative contribution of AMPARs and NMDARs to the total EPSC. AMPARs and NMDARs contribution to the membrane depolarization reduces the driving force for the current formation ($V_m-V_E)$ which, in turn, reduces both AMPARs and NMDARs currents regulating in this way the total EPSC. Thus, the AMPA/NMDA cooperation consists in a mutual regulation of the respective currents mediated by the spine resistance which influences the driving force ($V_m-V_e$). The resulting effect is an EPSC which is essentially AMPA-dependent for its amplitude and NMDA-dependent for its time to peak and its rising phase. The dependence of NMDA receptors from the Mg${}^{2+}$ block is another important point. The probability that Mg${}^{2+}$ unblocks from NMDARs depends on its concentration and on membrane potential. In turn, membrane potential depends on synaptic resistance independently from the origin of the membrane potential modification (i.e., if AMPA or retrograde spike, or neighbor synaptic activity).

In the present simulations, we have considered a range of values for the spine resistance of hundreds of $M\mathit{\Omega }$ (Wickens 1988; Harnett et al. 2012; Tønnesen et al. 2014) which can produce local variations of membrane potential sufficient to activate, at least partially, the NMDAR conductance. This means that, in physiological conditions, a single synaptic event can have both AMPA and NMDA components which cooperate in shaping the EPSC. As a whole, the system can be considered as a feedback mechanism which regulates AMPA and NMDA currents for the production of the total EPSC. In summary, for a given resistance, the increase of total conductance rises the total current which in turn enlarges the value of $V_m$ reducing the driving force for ionic current ($V_m(t)-V_E$) and resulting in a regulation of the current itself (Fig. 6).

In conclusion, the AMPA–NMDA cooperativeness can produce very different shapes of EPSC and EPSP depending on local modifications of the biophysical properties of the synapse. The EPSC peak amplitude and its time to peak can have a continuous range of values in the same synapse depending on the regulatory effect of each single biophysical parameter such that a small variation of one parameter can produce significantly different synaptic outputs.

Our results show that the main contribution to the peak amplitude of the EPSC is given by the AMPA component, the variation of which, for any resistance and any Mg${}^{2+}$ concentration, essentially follows the same trend of the total EPSC amplitude.

Conversely, the AMPA component never affects the time to peak of the total EPSC being the AMPA time to peak a constant, independently of its amplitude, of the Mg${}^{2+}$ concentration and of the spine resistance. This role is essentially due to the NMDA component. It is well known that NMDA component shapes the decay phase of the total EPSC because its activity lasts much longer than AMPA; from our results is also evident that it shapes the rising phase too.

Although in our knowledge there are no evidences that Mg${}^{2+}$ concentration in the synaptic space is variable in physiological conditions, our results suggest that a possible mechanism of regulation of glutamatergic synapse could be dependent on a local fine regulation of the Mg${}^{2+}$ concentration. Our results show that if such regulation exists, it must be confined in the range between 0 and 3 mM because the EPSC time to peak becomes almost constant for values greater than 3 mM. Possible candidates for this regulation could be the glial cells which very closely surround the synaptic space and act as regulatory systems of other substances involved in synaptic activity including the regulation of synaptic Glu concentration.

The problem of Mg${}^{2+}$ concentration can also be important when comparing electrophysiological data from different authors because some differences in the synaptic responses, as well as in whole neuron activity, can be due to different Mg${}^{2+}$ concentration used for the experiments.

In addition, small changes in morphology of the synaptic spine can produce a variation of $R_s$ that, in synergy with the surmised regulation of Mg${}^{2+}$ concentration, contributes to a fine tuning of the synaptic activity. As shown by the CV computed at peak (see Fig. 3) this factor can produce a variability of mean response up to $\sim$14 %.

Conclusions

In conclusions, we propose a model of glutamatergic synaptic activity that realistically considers the possible role of synaptic morphology expressed in terms of resistance. This model explains the possible cooperation between the AMPA and NMDA receptors. The AMPA–NMDA co-operation and its regulatory systems can play an important role in the transfer of information by glutamatergic synapses, in the formation of the neural code contributing to phenomena like LTP and LTD. From our results it is evident that these phenomena cannot be only attributed to the variation of the number of receptors on the PSD and that a non negligible role is played also by transient or permanent variations of the biophysical properties of the synaptic structures.