Locating and navigation mechanism based on place-cell and grid-cell models

Abstract

Extensive experiments on rats have shown that environmental cues play an important role in goal locating and navigation. Major studies about locating and navigation are carried out based only on place cells. Nevertheless, it is known that navigation may also rely on grid cells. Therefore, we model locating and navigation based on both, thus developing a novel grid-cell model, from which firing fields of grid cells can be obtained. We found a continuous-time dynamic system to describe learning and direction selection. In our simulation experiment, according to the results from physiology experiments, we successfully rebuild place fields of place cells and firing fields of grid cells. We analyzed the factors affecting the locating accuracy. Results show that the learning rate, firing threshold and cell number can influence the outcomes from various tasks. We used our system model to perform a goal navigation task and showed that paths that are changed for every run in one experiment converged to a stable one after several runs.

Introduction

Hippocampus is a key organization for learning and memory. Correlated with hippocampus, goal locating and navigation is a basic function of animals. Some principal cells distributed in hippocampus are identified as place cells (PCs). Place cells fire with a higher frequency in some particular locations than other places (O’Keefe and Dostrovsky 1971; O’Keefe and Nadel 1978). These particular locations within an environment are named place fields (PFs). Many models have been founded for place cells, using such tools as Gaussian function in (O’Keefe and Burgess 1996; Hartley et al. 2000; Foster et al. 2000), neuronal plasticity in (Arleo et al. 2004; Sheynikhovich et al. 2005; Krichmar et al. 2005), independent component analysis in (Franzius et al. 2007), and circuit-level model in (Jayet Bray et al. 2010). These studies most focus on fire description and place field (PF) formation. However, there is little discussion over the locating accuracy of place cells which remains an important issue in animal navigation (Etienne and Jeffery 2004; Jeffery et al. 2003; Hines and Whishaw 2005; Harvey et al. 2009).

Grid cells are another type of important cells for navigation task in entorhinal cortex, which has been reported in previous studies (Hafting et al. 2005; Moser and Moser 2008; Giocomo et al. 2011; Stensola et al. 2012; Brandon et al. 2014). They fire with a higher frequency like place cells in specific locations in an environment, but differ from place cells in that grid cell firing fields (FFs) are organized into a hexagonal grid. In this study, a new model developed from Gaussian functions is employed to simulate grid cell FF formation.

Some experiments were performed on goal navigation task by rats in (Etienne and Jeffery 2004; Jeffery et al. 2003; Hines and Whishaw 2005; Chen et al. 2013). Consequently, some models were proposed based on place cells in (Arleo et al. 2004; Sheynikhovich et al. 2005; Krichmar et al. 2005; Arleo and Gerstner 2000; Kulvicius et al. 2008). It is commonly believed that place cells may be driven by grid cells (McNaughton et al. 2006; Solstad et al. 2006a, b; Molter and Yamaguchi 2008; Si and Treves 2009). But little is known about the interactive mechanism of place cells and grid cells. Recently, some studies demonstrate that grid cells may also depend on place cells in a reverse direction (O’Keefe and Burgess 2005; Kropff and Treves 2008; Sreenivasan and Fiete 2011). In the study by Bonnevie et al. (2013), experimental data suggest that the feedback from place cells to grid cells is more prominent than that of grid cells on place cells. Meanwhile, the study addresses that grid cells may also play an important role on navigation. However, most of the previous model studies on navigation were mainly based on place-cell models, and only few on grid-cell models, not to mention those on both of them. Thus, natural questions are how place cells interact with grid cells, and what their interactive roles are on goal navigation?

Another interesting question is how the rats learn environmental cues. Studies show that one of the main functions of hippocampal neurons, like place cells and grid cells, is the learning of spatial location information from an environment (Huxter et al. 2003; Nakazawa et al. 2004; Moser et al. 2014). Meanwhile, a phenomenon called remapping has been discussed in the literature (Muller and Kubie 1987; Wilson and McNaughton 1993; Shapiro et al. 1997; Tanila et al. 1997; Knierim et al. 1998). Accordingly, the centre and shape of a place cell will change, when a rat switches to a new environment. Therefore, the focus of the current study is on how to learn the environmental information.

Models and methods

Experiment environment and neural networks

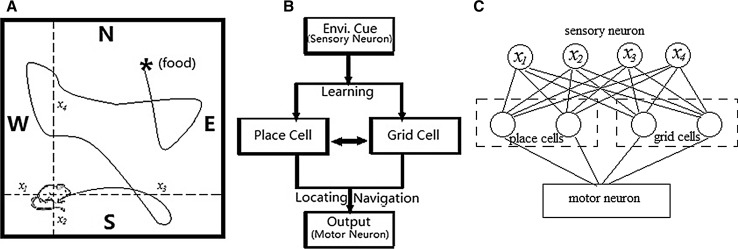
We set a square space with side length L (see Fig. 1a). A rat is placed randomly in a position of the environment, setting a task of finding food in the experiment. In this environment, the rat perceives environmental cues by using its visual system, then learns and integrates the sensory information by its neural network made of place cells and grid cells, and finally performs locating and navigation in the task (Fig. 1b). Place cells in the model mainly undertake the function of locating, while grid cells are concerned more on the integration of the navigation path. Especially, it is known from the literature (McNaughton et al. 2006; Molter and Yamaguchi 2008; O’Keefe and Burgess 2005; Bonnevie et al. 2013) that the connection is mutual between hippocampus place cells and cortex grid cells. Therefore, we design an interactive mechanism of these two kinds of neurons. The locating function of place cells is the premise of navigation, while path integration by grid cells will in turn affect the next locating of place cells. Directions are chosen in navigation for the next step by motor neurons.

Fig. 1.

a Experimental environment and design. A rat is randomly placed in a square environment with the task of finding the goal marked by “asterisks”. The rat running in the square can only estimate the distances to borders W, S, E and N. These distances are sensory inputs to its neural system. b Locating and navigation neural network structure. System receives the sensory inputs to neurons by learning environmental cues. Locating and navigation are determined by the interaction between place cells and grid cells. Results will be output to motor neurons, which are used to complete the goal searching task. c A simply feedforward fully-connected neural network

Sensory model

In the experiment, the environment is a square place without any references, where the rat can only get visual information from four walls W, E, S and N. We choose the distances from the rat’s current location to all four walls as sensory inputs, using the same processing method in many earlier studies (O’Keefe and Burgess 1996; Ollington and Vamplew 2004). Note that the real location of the rat at time t is X(t) = (x₁(t), x₂(t), x₃(t), x₄(t)), where x_i(t) is the real distance from wall i, i = 1, 2, 3, 4 corresponding to W, S, E and N (Fig. 1a). Obviously, x₁(t) + x₃(t) = x₂(t) + x₄(t) = L. However, sensory neurons of the rat have no accurate perception of its own locations. The perception input model is given by the following formula:

$$\left\{\begin{array}{c}\widehat{X}(t)=\left({\widehat{x}}_1(t),{\widehat{x}}_2(t),{\widehat{x}}_3(t),{\widehat{x}}_4(t)\right)\hfill \\ {\widehat{x}}_i(t)=x_i(t)(1+\mathit{\alpha }\mathit{\eta }),i=1,2,3,4.\hfill \end{array}\right.$$ 1

where α signifies the error rate of the visual perception, which is related to the individual rats. η is a random number from a uniform distribution within the interval [−1, 1]. Namely, η ~ U[−1, 1].

Place-cell and grid-cell models

We use a simple feedforward neural network to describe the system model. Place cells receive the input $\widehat{X}(t)$ from the sensory neurons. It is a fully-connected network where every sensory neuron is connected to every place cell with weights $W^P\left(t\right)={(w_{ij}^P(t))}_{4\times N_P}$, where i = 1, 2, 3, 4, j = 1, 2, …, N_P and N_P is the total number of place cells, and $w_{ij}^P(t)$ is the connection weight from the ith sensory neuron to the jth place cell. Similar to place cells, grid cells have weights $W^G(t)={(w_{ij}^G(t))}_{4\times N_G}$, where i = 1, 2, 3, 4, j = 1, 2, …, N_G and N_G is the total number of grid cells.

Weights are initialized by the following functions:

$$w_{ij}^P\left(0\right)={\left(1+exp\left(\frac{\mathit{\gamma }-E\left(\mathit{\gamma }\right)}{2{\mathit{\sigma }}^2}\right)\right)}^{-1}$$ 2

$$w_{ij}^G\left(0\right)=sin\left(L/{\left(1+exp\left(\frac{\mathit{\gamma }-E\left(\mathit{\gamma }\right)}{2{\mathit{\sigma }}^2}\right)\right)}^{-1}\right)$$ 3

where γ is a random number with $\mathrm{\gamma }\sim \text{U}\left[0,1\right]$.

Then, we choose the model in (Hartley et al. 2000; Kulvicius et al. 2008) to describe the place cells,

$$r_j^P\left(t\right)=exp\left(-\frac{\frac{1}{n}∥\frac{\widehat{X}\left(t\right)}{L}-W_j^P\left(t\right)∥}{2{\mathit{\sigma }}_j^2}\right)$$ 4

where $r_j^P(t)$ is the firing rate of the jth place cell, n is the number of sensory inputs, $W_j^P\left(t\right)$ is the jth row of $W^P\left(t\right)$, σ_j is a random number from a normal distribution, and the norm is the Euclidean distance. Results show that σ_j affects the width of PFs. Therefore, the random number σ_j ~ N(0.03, 0.005) can be used to simulate the diversity of cells.

A new model developed from the above equation is employed to represent grid cells, as

$$\begin{array}{cc}\hfill r_j^G\left(t\right)& =exp\left(-\frac{\frac{1}{n}∥sin\left(\frac{\widehat{X}\left(t\right)}{m}\right)-W_j^G\left(t\right)∥}{2{\mathit{\sigma }}_j^2}\right)\hfill \\ \hfill & +exp\left(-\frac{\frac{1}{n}∥-sin\left(\frac{\widehat{X}\left(t\right)}{m}\right)-W_j^G\left(t\right)∥}{2{\mathit{\sigma }}_j^2}\right)\hfill \\ \hfill \end{array}$$ 5

where the parameters are similar to that of place cells.

Learning, locating and navigation

According to a learning rule with a winner-takes-all mechanism, the cell with the maximal firing rate wins the learning chance (Kulvicius et al. 2008). Obviously, the model has the low learning efficiency because we can only change one cell’s weights at every step. Therefore, we modified the competition learning strategy as follows:

$$\left\{\begin{array}{c}\frac{\text{d}{W}_{J1}^P\left(t\right)}{\text{d}t}={\mathit{\mu }}_1\left(\frac{\widehat{X}\left(t\right)}{L}-W_{J1}^P\left(t\right)\right)\hfill \\ \frac{\text{d}{W}_{J2}^G\left(t\right)}{\text{d}t}={\mathit{\mu }}_2\left(sin\left(\frac{\widehat{X}\left(t\right)}{m}\right)-W_{J2}^G\left(t\right)\right)\hfill \\ J1=\left\{j|r_j^P\left(t\right)>R_{\text{thr}}\right\}\hfill \\ J2=\left\{j|r_j^G\left(t\right)>R_{\text{thr}}\right\}\hfill \end{array}\right.$$ 6

where μ_i is the learning rate, R_thr is the responding threshold and J1 (J2) is the responding set. In our model, all the cells responding to the current position can win a chance to modify their weights from sensory neurons.

From the former model, we get all place cells’ firing rates $r^P\left(t\right)$. For place cells, place fields can be obtained by analyzing the positions where they respond to. Meanwhile, the centre of PFs is

$$C_j^P=\frac{{\int }_0^T{r}_j^P\left(t\right)\widehat{X}\left(t\right)dt}{{\int }_0^T{r}_j^P\left(t\right)dt}$$ 7

Now, we build a place-cell locating model as follows:

$$P\left(t\right)=\frac{{\sum }_j{s}_j^P\left(t\right)C_j^P}{{\sum }_j{s}_j^P\left(t\right)}$$ 8

$$s_j^P\left(t\right)=\left\{\begin{array}{cc}1\hfill & r_j^P\left(t\right)>R_{\text{thr}}\hfill \\ 0\hfill & r_j^P\left(t\right)\le R_{\text{thr}}\hfill \end{array}\right.$$ 9

where $s_j^P\left(\text{t}\right)$ is the responding function.

We elaborate the navigation process in two aspects, namely goal-orientation-selection and Q value selection. Goal-orientation-selection focuses on the prediction of the goal position, which depends on the perception and estimation of the rat. Note that the goal prediction at t of the rat is

$${\widehat{X}}_{goal}(t)=\left({\widehat{x}}_1^{goal}(t),{\widehat{x}}_2^{goal}(t),{\widehat{x}}_3^{goal}(t),{\widehat{x}}_4^{goal}(t)\right)$$

Then, the goal orientation preference is defined as follows:

$${\widehat{\mathit{\theta }}}_{goal}\left(t\right)=arg\left(({\widehat{x}}_1^{goal}\left(t\right)-x_1\left(t\right))+\left({\widehat{x}}_2^{goal}\left(t\right)-x_2\left(t\right)\right)i\right)$$

Simultaneously, Q-values are selected based on the past path integration. The model is designed by programming.

$$\underset{0\le \mathit{\theta }\le 2\mathit{\pi }}{\text{max}}Q\left(\mathit{\theta },t\right)=\frac{{\sum }_j{s}_j^G\left(t\right){\mathit{\phi }}_j\left(\mathit{\theta }\right)}{{\sum }_j{s}_j^G\left(t\right)}$$

$$\left\{\begin{array}{c}{s}_j^G\left(t\right)=\left\{\begin{array}{cc}1\hfill & r_j^G\left(t\right)>R_{\text{thr}}\hfill \\ 0\hfill & r_j^G\left(t\right)\le R_{\text{thr}}\hfill \end{array}\right.\hfill \\ \frac{d{\mathit{\phi }}_j}{d\mathit{\theta }}={\mathit{\alpha }}_{\mathit{\phi }}{s}_j^G\left(t\right)\left({\mathit{\phi }}_j-\mathit{\beta }{Q}_{max}\right)\hfill \end{array}\right.$$ 10

where Q_max is the maximum Q-value in the previous step. The optimal solution of this programming, ${\widehat{\mathit{\theta }}}_Q\left(t\right)$, is used as Q-value selection preference.

Further, we define the final direction preference by

$$\left\{\begin{array}{c}\widehat{\mathit{\theta }}\left(t\right)=\mathit{\rho }{\widehat{\mathit{\theta }}}_{goal}\left(t\right)+\left(1-\mathit{\rho }\right){\widehat{\mathit{\theta }}}_Q\left(t\right)+\mathit{\zeta }\frac{\mathit{\pi }}{4}\hfill \\ \mathrm{\Delta }\mathit{\rho }=\mathit{\delta }S\mathit{\rho }\left(1-\mathit{\rho }\right)\hfill \end{array}\right.$$ 11

where $\mathrm{\zeta }\sim \text{U}\left[-0.1,0.1\right]$ is noise, S refers to runs that the rat gets the food, and $\mathrm{\delta }$ is the rate factor.

We suppose that the angle turning right or left cannot be more than $\mathrm{\pi }/2$. The final direction at time t is modified as follows:

$${\widehat{\mathit{\theta }}}_f\left(t\right)=\left\{\begin{array}{cc}\widehat{\mathit{\theta }}\left(t-\mathrm{\Delta }t\right)+\frac{\mathit{\pi }}{2},\hfill & \widehat{\mathit{\theta }}\left(t\right)-\widehat{\mathit{\theta }}\left(t-\mathrm{\Delta }t\right)>\frac{\mathit{\pi }}{2}\\ \widehat{\mathit{\theta }}\left(t\right),\hfill & \left|\widehat{\mathit{\theta }}\left(t\right)-\widehat{\mathit{\theta }}\left(t-\mathrm{\Delta }t\right)\right|\le \frac{\mathit{\pi }}{2}\\ \widehat{\mathit{\theta }}\left(t-\mathrm{\Delta }t\right)-\frac{\mathit{\pi }}{2},\hfill & \widehat{\mathit{\theta }}\left(t\right)-\widehat{\mathit{\theta }}\left(t-\mathrm{\Delta }t\right)<-\frac{\mathit{\pi }}{2}\end{array}\right.$$ 12

where $\mathrm{\Delta }t$ is the time step. Thus, the position of the rat is changed according to the following equations:

$$\mathrm{\Delta }{x}_1=\left(R+2\mathit{\eta }\right)cos\left({\widehat{\mathit{\theta }}}_f\left(t\right)\right)$$ 13

$$\mathrm{\Delta }{x}_2=\left(R+2\mathit{\eta }\right)sin\left({\widehat{\mathit{\theta }}}_f\left(t\right)\right)$$ 14

where R is the distance of one step.

Parameter values in the model are:

$$\begin{array}{cc}\hfill L& =100,\mathit{\alpha }=0.1,{\mathit{\alpha }}_{\mathit{\phi }}=0.1,\mathit{\beta }=0.7,N_P=2000,\hfill \\ \hfill N_G& =1000,\mathit{\sigma }=0.2,m=5,n=4,{\mathit{\mu }}_1=0.5,\hfill \\ \hfill {\mathit{\mu }}_2& =0.003,\mathit{\delta }=0.05,R=5.\hfill \\ \hfill \end{array}$$

Results

Place fields and firing fields

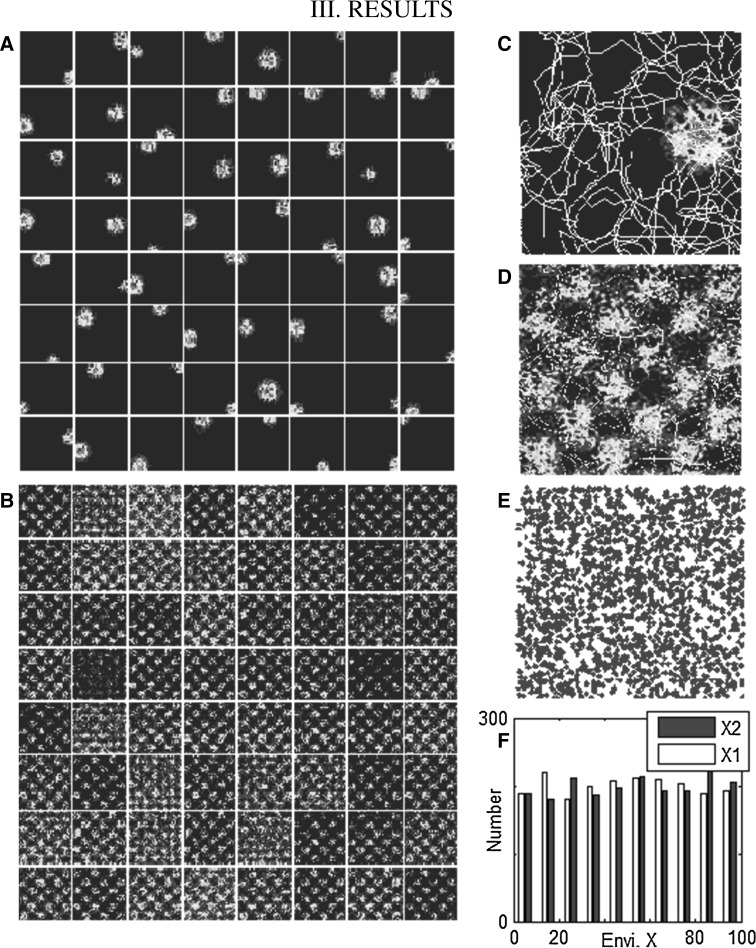
We choose a square’s left bottom corner as the origin of coordinates, E direction as the positive direction of abscissa axis, and N direction as the positive direction of vertical axis. In the simulated experiment, we discretize the time steps for computational convenience. The rat freely explores the new experimental environment for 50,000 time steps (Fig. 1a) to learn and familiarize itself with environmental cues. After exploring, according to the discharge data, the PFs can be obtained (Fig. 2). Results show that place cells can only display the high frequency discharge response to a certain position of the environment (Fig. 2a, c) and that the corresponding grid cells make the high frequency response to some position in the environment. Moreover, these positions can form hexagons on the geometry (Fig. 2b, d). These hexagon firing fields are in accordance with other experimental results in (Moser and Moser 2008; Giocomo et al. 2011; Stensola et al. 2012).

Fig. 2.

PF/FF formation and distribution of place cells and grid cells. a 64 place fields are chosen from 2000 place cells. They are scattered uniformly in the square with diverse sizes according to physiological experiment data. Red represents high frequency response to the position, where blue is for resting. b 64 firing fields are chosen from 1000 grid cells. These places responding to some cells are organized as hexagons. c The PF of a place cell is enlarged for better visualization. A line in the square is the path that the rat has explored. d The FF of a grid cells is enlarged for better visualization. e The distribution of place cells’ PF centers. We compute the centers of all place cells and plot them into the environment. f Frequency analysis results with coordinates of place field centers. (Color figure online)

The PF centers of place cells are located everywhere in the environment (Fig. 2e), which indicates that the distribution of centers is in accordance with the uniform distribution features (Fig. 2f). Such a distribution allows the rat to have higher identifiability of the environment in the navigation task. Due to the individual differences among place cells, the PF sizes are not consistent, highly similar to the actual experiment results in (O’Keefe and Dostrovsky 1971; O’Keefe and Nadel 1978).

Analysis of locating accuracy

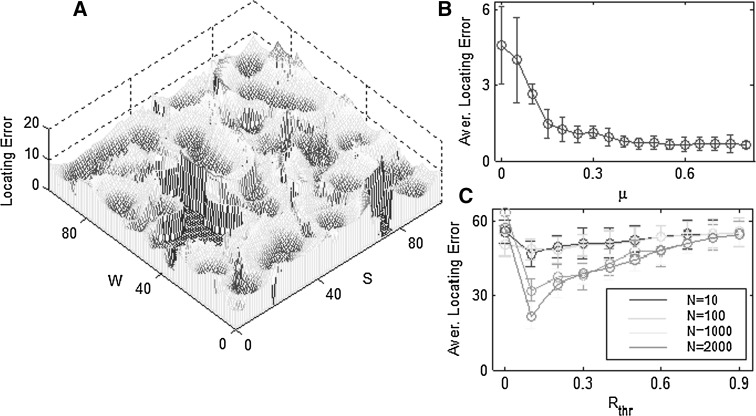
We are concerned with the errors of the locating system on the rat, among which the sum of squared errors between the locating and the actual locations of the nervous system, and their means are the assessment standards (Fig. 3). A simulation experiment was carried out for a total of 100 times. Results show that the distribution of locating accuracy in different positions is random in the whole environment (Fig. 3a), for the rat passes by all the positions unevenly when it explores and learns environmental cues. Therefore, locating of some positions makes errors, which explains the reason why rats in the experiment box are always more familiar with the places they have been to, than the sites they have not been to before.

Fig. 3.

Analysis of the locating accuracy. a Locating errors are defined between the real position and the locating position. They are distributed in the square. The errors in some positions are zero because the rat didn’t go through these places in its random exploration. b Average locating errors of all the explored positions are obtained from 100 experiments with standard deviations. c Average locating errors versus the firing threshold and the number of cells

The learning rate μ represents the learning ability of the rat in the environment. The higher the learning rate is, the greater the locating ability is and the more accurate location the rat has (Fig. 3b). In particular, μ = 0 means that the locating error becomes larger when entering into a new environment without learning. Hence, learning is a way for the rat to familiarize itself with the environmental cues, and increasing the learning rate above 0.5 is a point of saturation.

The effect of different thresholds and the number of place cells on the locating accuracy are now discussed (Fig. 3c). Firing threshold refers to the critical firing rate which responds to any position. Big locating errors appear at both ends of the threshold, which results in the smallest or the largest threshold values. The smallest threshold leads to many place cells being involved in locating, including those almost resting place cells, while relatively low firing rate cells lead to errors. Especially, when the threshold is zero, all the place cells take part in locating. Conversely, the largest threshold results in few place cells to access the learning environmental cues, for which errors are amplified. The optimal threshold value is 0.1 and it is opted in our studies. Simultaneously, it is shown that the locating accuracy is improved due to the larger quantity of cells.

Compared with the threshold given in our study, the winner-takes-all mechanism is employed to illustrate the learning in (Kulvicius et al. 2008). In this mechanism, only one cell with the highest firing rate gets the opportunity to learn while cells with firing rate bigger than the threshold get opportunities to learn in our work. We found that a large number of place cells under sufficient learning contribute to more accurate locating, because a small number of neurons cannot cover all the positions with their PFs. A small number of neurons responding to the uncovered positions turn out to be not enough, and even useless. The direct effect is that the positions are dislocated or cannot be located. Specific comparative results are shown in Table 1.

Table 1.

Comparative results

	Ave. steps	Ave. runs	Stability
Results of our work	16	10	Strong
Results of Ref. (Kulvicius et al. 2008)	22	13	Weak

Navigation

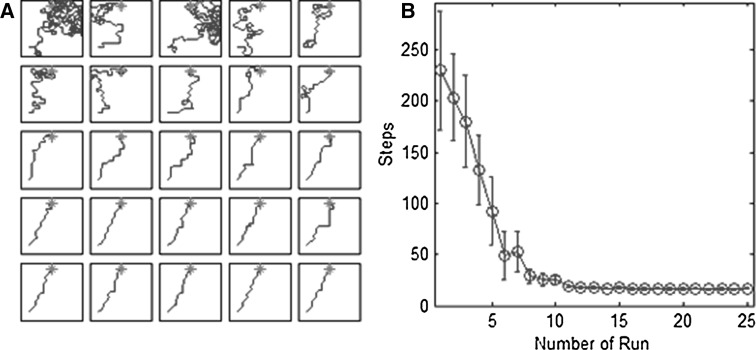
The navigation task for the rat is presented (Fig. 4a). The environment is a very big square space. Namely, we suppose that the rat cannot see or smell the food directly. The goal can only be seen or smelt when the distance between the goal and the rat is <5. Confronted with a new environment, the rat begins to tentatively and randomly explore the environment. The foraging path presents great randomness, while many steps are taken to learn environmental cues. Once the rat finds the goal, it will be located intangibly. The more runs rats have, the more precisely the goal is located. After about ten runs, the rat selects a better direction and path towards the goal immediately.

Fig. 4.

Results of navigation. a The paths of the first 25 runs in one experiment are arranged. The first row is 1–5 runs, while the second row is 6–10. The others are similar to them. It has the higher randomness in the earlier runs than the latter runs. b Average steps needed to reach the goal from 100 runs with SDs. It becomes stable after about 10 runs

The number of runs in an experiment depends on the moment when an optimal path is found. Data were obtained from 100 experiments. With the increase of the number of learning times, the total steps it needs fall rapidly (Fig. 4b). Steps needed to a stable state converged to 16 after about 10 runs, which means that the goal position is located and memorized precisely. In the navigation task, the goal can only be found when the distance between the goal and the rat is <5. The task will be failed and the rat will abandon searching the goal when the steps exceed 1000 because of the sluggishness of the rat.

It is about 22 steps after 13 runs in (Kulvicius et al. 2008) while only 16 steps after 10 runs in our work (Table 1). After learning, the convergent navigation path in our results has stronger stability than the one in (Kulvicius et al. 2008). The path and steps needed to get the goal are fluctuant after sufficient runs while ours are not.

Conclusions

In 2014, John O’Keefe, May-Britt Moser and Edvard Moser won the Nobel prize in medicine for their discovery of place cells and grid cells. It is commonly accepted that the two kinds of neurons take an important part in locating and navigation. In other words, they may reveal the answers to the following two questions: where we are now and where we will go? Previous model studies (Arleo et al. 2004; Sheynikhovich et al. 2005; Krichmar et al. 2005; Arleo and Gerstner 2000; Kulvicius et al. 2008) focus on the possible navigation mechanism based on place cells or grid cells. None of the models goes with these two kinds of cells, or with their interaction in navigation tasks, which motivated our present study. For the first time, to our knowledge, we have implemented a place-cell and grid-cell model, and applied it for goal navigation learning. Moreover, we proposed a locating and navigation mechanism which leads to a better performance than models based on a single place cell (Kulvicius et al. 2008).

The basic models of place cells and grid cells are founded. We model place cell feedforward network based on radial basis functions. O’Keefe and Burgess (Kulvicius et al. 2008) used the thresholded sum of the Gaussian tuning-curves of the rat’s distance from each box wall to describe the place cell, which seems similar to ours. Another work where the firing rate of a place cell is modeled as the thresholded sum of boundary vector cells is the product of distance function and head direction function (Kulvicius et al. 2008). Compared with them, our model has a simpler form. Moreover, we can keep the width or shape diversity of PFs (Fig. 2a) by a σ_j obeying normal distribution, while they depend on the distance to the wall: the larger the distance is, the broader the field is. Namely, the width of PFs in environment centre is bigger than that in edge, which has not appeared in physiological experiment. We use trigonometric function to develop grid cell model. The periodicity of trigonometric function results in hexagon firing fields. It is more convenient in simulation than the function which is constructed from a sum of three two-dimensional sinusoidal gratings (Kulvicius et al. 2008). The advantages of our place cell model are also presented in grid cell model because the grid cell model is improved from place cells.

The locating accuracy is related to the relative path explored. Some positions cannot be accurately located due to the lack of exploration learning. Specifically speaking, no accurate location is reflected when getting lost in an actual task and choosing directions at random. Therefore, it is concluded that locating errors are relatively big without learning or with low learning rates, that an increase of the learning rate can reduce the locating errors, and that the locating error remains unchanged when the learning rate is above a certain threshold. The firing threshold, as an indicator, is used to distinguish whether neurons can respond to events. The effect of firing thresholds on the locating errors turns out to be in a “V” shape. Threshold values at both ends, large or small, will enlarge the locating errors. An optimal threshold is obtained minimizing the average error. Another effective way of reducing the average locating error is to increase the number of place cells. When the number of neurons in the model decreases, the error rate becomes relatively high, while the increase of the number of neurons can obviously decrease the errors. Correspondingly, the brain can process a large number of cells. All these methods can be used to reduce the locating errors, which brings fewer average steps needed to get the food and higher rate of convergence of optimal path.

Simulation results show that after learning environmental cues in several times, a rat can successfully complete the navigation task, searching from an inefficient initial path to an optimal one. In our model, the navigation mechanism involves two key issues: locating and directing. These two are fundamental and supportive to each other, with place cells mainly undertaking the locating function, and grid cells mainly selecting directions and estimating distances. Finally, their combination finishes the navigation task.