Structural Asymmetry of the Human Cerebral Cortex: Regional and Between-Subject Variability of Surface Area, Cortical Thickness, and Local Gyrification

Abstract

Structural asymmetry varies across individuals, brain regions, and metrics of cortical organization. The current study investigated regional differences in asymmetry of cortical surface area, thickness, and local gyrification, and the extent of between-subject variability in these metrics, in a sample of healthy young adults (N = 200). Between-subject variability in cortical structure may provide a means to assess the extent of biological flexibility or constraint of brain regions, and we explored the potential influence of this variability on the phenotypic expression of structural asymmetry. The findings demonstrate that structural asymmetries are nearly ubiquitous across the cortex, with differing regional organization for the three cortical metrics. This implies that there are multiple, only partially overlapping, maps of structural asymmetry. The results further indicate that the degree of asymmetry of a brain region can be predicted by the extent of the region’s between-subject variability. These findings provide evidence that reduced biological constraint promotes the expression of strong structural asymmetry.

1. Introduction

Asymmetry of function is a hallmark feature of brain organization in the human cortex. It is sometimes claimed that structural cerebral asymmetries are small and of minor significance compared to strong and prominent functional asymmetries (e.g., Wey et al., 2014). If so, then one would need to argue that functional asymmetries arise primarily from differing patterns of brain activity that are subserved by similar anatomical substrates (e.g., differing functional connectivity networks – see Wey et al., 2014). While this is not entirely implausible, function tends to parallel form in many areas of biology. Hence it is worth looking closely at a variety of neurostructural measures before concluding that structural bases of hemisphere asymmetries are lacking. Asymmetries can be found at multiple spatial scales (cytoarchitecture, cortical morphometrics, structural networks within and across hemispheres). In the current investigation, we examine asymmetries of cortical surface area, thickness, and local gyrification in a relatively large sample of healthy young adults. We find that structural asymmetries vary from region to region but are ubiquitous across all measures of cortical organization, suggesting that these structural features can provide a platform for the emergence of functional hemisphere differences.

Individual variability is an important component of biological systems. Hence, some significant variability in structural asymmetry is to be expected across different brain regions, as well as across individuals within the same region. Regional differences in asymmetry of surface area (Kang et al., 2012; Koelkebeck et al., 2014; Van Essen, Glasser, Dierker, Harwell, & Coalson, 2012) and cortical thickness (Koelkebeck et al., 2014; Plessen et al., 2014; Zhou et al., 2013) have been reported, and a few prior studies have reported between-subject variability in regional cortical volume (Kennedy et al., 1998) or thickness (Mueller et al., 2013). However, there has been no consideration of the relationship between these two indices of variation. In other words, are brain regions with high between-subject variability more or less likely to be strongly asymmetrical at the population level? Answering this question may provide insight into why some regions are more asymmetrical than others, as discussed further below. In the current investigation we explore both regional and individual variation in the morphometry of left and right cortex, and investigate whether the degree of asymmetry of a given region may be predicted by the extent of its phenotypic variation.

1.1 Prior Research on Macrostructural Asymmetries

In the modern era, consideration of structural asymmetries was initiated by Geschwind & Levistsky’s (1968) discovery, using post-mortem data, of prominent leftward asymmetry of the planum temporale. With the advent of MRI scans, these findings were replicated by identifying sulcal landmarks to delineate specific regions, and then manually tracing serial sections to estimate the surface area of the region. Using these methods, planum temporale asymmetries were replicated many times, and some additional perisylvian regions were shown to be asymmetrical (e.g., leftward asymmetry of Heschl’s gyrus, rightward asymmetry of the planum parietale) (Chiarello, Kacinik, Manowitz, Otto, & Leonard, 2004; Foundas, Leonard, & Hanna-Pladdy, 2002; Shapleske, Rossell, Woodruff, & David, 1999). However, the need to individually identify anatomical landmarks and manually trace each region on serial MRI sections precluded the analysis of asymmetries across the entire brain and tended to limit sample size.

Automated methods are now available to measure asymmetries across the entire cortex, enabling substantially larger samples to be examined. Further, surface based methods permit estimation of multiple aspects of cortical structure (surface area, thickness, gyrification) (Dale, Fischl, & Sereno, 1999; Fischl, Sereno, & Dale, 1999; Schaer et al., 2008). It is widely acknowledged that cortical surface area (tangential extent), thickness (radial extent), and gyrification (surface area folding) can vary independently of each other (Wallace et al., 2013), and differ in their genetic bases (Panizzon et al., 2009; Winkler et al., 2010), network structure (Sanabria-Diaz et al., 2010) and developmental trajectories (Hogstrom, Westlye, Walhovd, & Fjell, 2013; Raznahan et al., 2011). Understanding the structural basis of cerebral asymmetry will require exploration of asymmetries for each metric, as well as how the various indices of asymmetry relate to each other.

Two general approaches have been used to examine asymmetries across the entire cortex.¹ In one approach, point-to-point comparisons across left and right hemispheres are made which requires complex matching algorithms to determine corresponding points despite hemisphere differences in cortical surface anatomy (Luders et al., 2006; Plessen et al., 2014; Van Essen et al., 2012). After correction for multiple comparisons, a whole-brain asymmetry map is then constructed. Here measurement precision is optimized, but quantitative values for asymmetry of specific regions are not provided. A second approach uses sulcal boundaries to independently demarcate regions within each hemisphere, and then left/right asymmetries are computed for each a priori identified region (Koelkebeck et al., 2014). This second approach is similar to traditional anatomical methods, but eliminates the need for human identification of anatomical regions and manual measurements. The FreeSurfer analysis suite (Dale et al., 1999; Fischl et al., 1999; Fischl, Sereno, Tootell, & Dale, 1999) provides a standardized method for parcellating the cortex, simplifying quantitative comparisons across studies with reference to common anatomical atlases (Desikan et al., 2006; Destrieux, Fischl, Dale, & Halgren, 2010). However, the sulcal boundaries used to parcellate the cortex may not represent the optimal means to reveal regions with differing asymmetries, as values are summed or averaged across all vertices/voxels within each region. Nevertheless, although early cytoarchitectural work emphasized the lack of correspondence between cytoarchitectural and sulcal boundaries (Amunts et al., 1999), more recent findings indicate that, for many brain regions, sulci boundaries provide reasonable indications of cytoarchitectural transitions (Fischl et al., 2008; Weiner & Ziles, 2015).

Van Essen et al. (2012) examined surface area asymmetries on a point-to-point basis from a variety of published data sets (various age groups) and noted statistically significant asymmetries across approximately 2/3 of the cortex. Leftward asymmetries included posterior perisylvian regions, ventromedial and anterior temporal areas, insula, mid-to-posterior cingulate, medial and lateral parietal, and some lateral frontal regions. Prominent rightward asymmetries were observed near the angular gyrus and dorsomedial prefrontal cortex with additional rightward asymmetries in lateral temporal, occipital, and orbitomedial prefrontal cortex.

Three additional studies employed varying methods to investigate point-to-point cortical thickness asymmetries across the entire adult brain. Luders et al. (2006) examined 60 young adults and observed thicker left than right cortex in the ACC, anterior temporal and prefrontal cortex, precentral and supramarginal gyri. Rightward thickness asymmetries were observed in the IFG, lateral posterior ITG, precuneus and lingual gyrus. Two other investigations examined age-related changes in cortical thickness asymmetry from childhood to late middle age (Plessen et al., 2014; Zhou et al., 2013). Both studies found region-specific changes in asymmetry with age, however the presentation of the data does not allow regional comparisons of their young adult participants to those studied by Luders et al., (2006) or the current investigation.

Several previous studies have reported automated parcellation-level asymmetries within specific regions of interest (e.g., surface area of language areas - Chiarello, Vazquez, Felton, & Leonard, 2013; thickness and surface area of auditory cortex Meyer et al., 2014). Only one prior study has investigated surface area and cortical thickness asymmetries across the entire adult brain using an automated parcellation approach (Koelkebeck et al., 2014). In this study MRI scans from 101 Japanese individuals (mean age 33.3 yrs) were parcellated into 33 brain regions using the Desikan et al. (2006) atlas. In this study leftward surface area asymmetries were found in the pars opercularis, Heschl’s gyrus, temporal pole, and entorhinal cortex, and lateral occipital cortex, postcentral gyrus, SFG, caudal MFG, and rostral ACC. Rightward area asymmetries were observed in the IFG, several medial regions, MTG, inferior parietal and frontal pole. For cortical thickness, leftward asymmetries were found through most regions of the cingulate cortex, and rightward asymmetries were obtained in the IFG, several temporal regions (temporal pole, STS, MTG, Heschl’s gyrus), as well as entorhinal and lateral occipital regions. Negative correlations were obtained between surface area and thickness asymmetries in many regions. This study demonstrated that surface area and cortical thickness yield differing, and often opposing, patterns of asymmetries, implying that that more than one neurobiological mechanism may underlie the lateral organization of the brain. Unfortunately, the parcellation scheme employed by Koelkebeck et al. (2014) did not yield a separate measure for the planum temporale, nor for gyral vs sulcal cortex that are known to differ anatomically (Deng et al., 2014; Fischl & Dale, 2000; Nie et al., 2012).

Prior studies document surface area and cortical thickness asymmetries throughout the adult cortex, although variations in methods and subject populations make comparisons across studies difficult. Only one investigation explored two metrics of cortical structure in the same group of participants (Koelkebeck et al., 2014), permitting cross-metric correlation of asymmetry. Furthermore, gyrification asymmetries have not been thoroughly explored. Although gyrification increases as cortical surface area expands, both phylogenetically and ontogenetically (Zilles, Palomero-Gallager, & Amunts, 2013), there is evidence that groups can differ in regional gyrification, despite having similar surface area in the same regions (Wallace et al., 2013; McDowell et al., in press). Hence, it is important to independently investigate surface area and gyrification asymmetries. The current study investigates surface area, thickness, and gyrification asymmetries in the same sample of healthy young adults using a regional parcellation approach.

1.2 Prior Research on Regional Differences in Variability of Cortical Morphometry

Individual differences in cortical morphometry are sometimes dismissed as “noise” – perhaps reflecting measurement error or insignificant variability around the population mean. However, there is increasing recognition that such variation is meaningful and important for understanding the neural bases of individual differences in function, behavior, and risk (Kanai & Rees, 2011; Zilles & Amunts, 2013). In addition to promoting better understanding of individual differences, the extent to which the anatomy of a given brain region varies across persons may provide a metric of biological flexibility and constraint during lifelong brain development. Three prior studies have investigated regional differences in cortical structure variability (Hill et al., 2010; Kennedy et al., 1998; Mueller et al., 2013).

In an early investigation, individual variability of cortical volume was determined from a sample of 20 young adults (Kennedy et al., 1998). The cortex was manually divided into 48 parcellation units, which generally corresponded to major gyri. The coefficient of variability (CV) was reported for each parcellation [CV range: 11.1 (insula) to 49.0 (occipital pole)], but regional differences in this variability were not discussed. However, the authors determined that overall brain volume or measurement error (inter-rater reliability) were very small contributors to the variation of parcellation volume. These findings support the claim that the extent of between-subject variability varies substantially from region to region. However, there are several factors that limit the generalizability of the findings. First, the sample size was very small, making it unlikely that the variability estimates index the true range of population variance. Second, because cortical volume is the product of thickness and surface area, it is unclear how much each component contributes to the volumetric variance. Since cortical thickness and surface area have differing genetic bases and developmental trajectories (Hogstrom et al., 2013; Panizzon et al., 2009; Winkler et al., 2010), it is reasonable to expect that they may also differ in the extent and regional distribution of between-subject variability. Third, the parcellation scheme employed in this study is not widely used, making comparisons across studies difficult.

Hill et al. (2010) reported variability of sulcal depth (one measure of gyrification) in 10 newborn infants and compared this to published data on 12 adults (Van Essen, 2005). The pattern of sulcal depth variability was similar in both age groups, and was greatest in lateral parietal, temporal, and prefrontal regions. A more recent study examined cortical thickness and sulcal depth variation as part of an investigation of individual variability in functional connectivity (Mueller et al., 2013). Vertex-level analyses of thickness and sulcal depth variability were conducted in a sample of 23 middle-aged adults. Although formal comparisons were not done, the regional distribution of variability for these two measures of cortical structure appeared quite different (see Mueller et al., 2013, Figure 4). Medial frontal and parietal regions as well as lateral temporal cortex had high between-subject variability for cortical thickness, whereas sulcal depth variability was high for lateral prefrontal and temporal-occipital regions. Interestingly, sulcal depth variability correlated positively with variability in resting state functional connectivity, while thickness variability did not. The authors suggest that higher variability in later maturing association cortex may reflect increased exposure to varying environmental experiences.

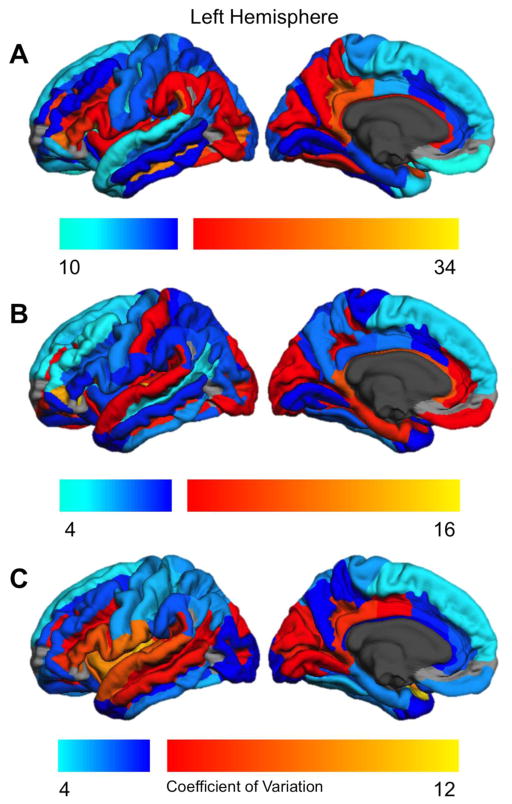
Figure 4.

Regional coefficient of variation for the left hemisphere. Cool colors indicate coefficients below the median value; warm colors indicate coefficients above the median value. Regions not examined due to low concordance indices (Destrieux et al., 2010) are indicated in gray.

These prior studies indicate that the extent of individual variability in brain structure is not uniform across the cortex, and also hint that variability within a given region may differ depending on what aspect of cortical organization is being measured. However, strong conclusions about the extent of individual variability must be tempered given the very small sample sizes used. In addition, the relationship between variation in cortical surface area, thickness, and gyrification has not been adequately addressed. Finally, whether or not this variability is associated with asymmetry is unknown. We now explore why this association may be meaningful for our understanding of the biological basis of cerebral asymmetry.

1.3 Potential Associations Between Individual Variability and Structural Asymmetry

Current research indicates that while cortical structural asymmetry is present at birth, it changes across the lifespan (Nie et al., 2013; Plessen et al., 2014). These changes no doubt reflect gene X environment interactions as, in the proper environment, genetic variation can either be expressed or suppressed (e.g., Oleksiak & Crawford, 2012). In addition, experiences and learning can sculpt brain structure and the nature of these experiences will differ across individuals. One question to be explored in the current investigation is whether there is any necessary relationship between the degree of structural asymmetry and the extent of individual variability in cortical organization. That is, are brain regions with greater individual variability more or less likely to be strongly asymmetrical? This is an interesting question because the extent of individual variability may be an index of biological constraint: highly constrained brain regions will be more resistant to change and tend to limit the extent of phenotypic variation (Olek & Crawford, 2012; Meiklejohn & Hartl, 2002). To the degree that this is true, we can then examine whether structural asymmetry is associated with high or low biological constraint. There are several possible outcomes.

One possibility is a positive association between individual variability and asymmetry the most variable brain regions also have the largest asymmetry. This outcome would suggest that in regions with less constraint, the hemispheres would be more free to develop independently resulting in hemisphere differences in connectivity, pruning, etc. In more highly constrained brain regions, the hemispheres would be less likely to vary independently thereby reducing asymmetry. A second possibility is a negative association between variability among individuals and asymmetry – the least variable regions evidence the greatest asymmetry. This could be the case if structural asymmetry is a strongly canalized trait, one that is resistant to change (i.e., buffered) regardless of variation in the environment or genotype (Siegel & Bergman, 2002; Waddington, 1957). Under this scenario, brain regions with less constraint (higher variability) would tend to be less asymmetrical. This is because with less constraint, genetic and environmental variation would be more able to influence brain organization and “deflect” it away from a developmental pathway favoring asymmetry, and towards more symmetrical organization. A final possibility is that there is no necessary relationship between asymmetry and between-subject variability. In this case, regions would have greater or lesser asymmetry for reasons unrelated to the degree of biological constraint. Of course, this third possibility represents the null hypothesis, precluding any strong interpretation. By examining the relationship between variability and asymmetry, then, we may be able to shed light on factors that promote or resist the phenotypic expression of strong cerebral asymmetry.

1.4 Outline of the Current Study

This study had several objectives. First, we wished to identify the extent of regional asymmetries across the entire cortex for three different indices of cortical organization: surface area, thickness, and local gyrification. No prior study has explored all three measures in a relatively large sample of healthy young adults. We employed a readily available parcellation scheme (Destrieux et al., 2010) that will enable future comparisons across large-scale databases such as BIL&GIN (Mayozer, et al., 2015). This approach can reveal whether structural asymmetry is a general feature of the human cerebral cortex, or whether it is specific to relatively few regions (e.g., those recognized as having strong functional asymmetries). In addition, we examined whether association areas are more structurally asymmetrical than unimodal cortex and whether key nodes of the left functional language network are similarly lateralized. Second, because each cortical metric represents a different organizational feature of the cortex, we investigated the relationship of these asymmetries to each other within the predefined cortical parcellations. Uncorrelated asymmetries may indicate that the neurobiological factors underlying asymmetry within a given region are independent. Third, we also sought to identify the extent of between-subject variability across brain regions using the same three measures of cortical structure with a large enough sample size to obtain robust estimates of variation. We also examined whether the current data would substantiate prior claims that high variability regions predominate in association rather than unimodal cortex (Hill, et al., 2010; Mueller, et al., 2014). Finally, we investigated the relationship between degree of asymmetry and the extent of between-subject variability in order to examine the role of biological constraint on the expression of regional structural asymmetry.

2. Method

2.1 Participants

Two hundred university student volunteers (100 male) participated, receiving $100 compensation (mean age = 21.6 years; range 18–34). They were recruited as part of the Biological Substrates for Language project (Chiarello et al., 2009; Leonard et al., 2008). In order to recruit a sample that represented the typical range of laterality, participants were free to enroll regardless of handedness. Subjects with a history of brain injury or disease or conditions incompatible with an MRI scan were excluded. A neuroradiologist reviewed all scans for pathology, and four additional participants were excluded from the final sample due to abnormal findings on the MRI. All participants were native English speakers with normal or corrected-to-normal vision. Handedness was determined via scores on the 5-item Bryden (1977, 1982) hand preference questionnaire that yields an index ranging from +1.00 (extreme right handedness) to −1.00 (extreme left-handedness). Mean handedness score for our sample was +.71 (median = +.90), and 26 of the 200 participants (12 female) had left or no hand preference.

2.2 Brain Imaging Procedure

Two MRI scans were obtained for each participant on a 1.5-T GE Signa scanner (3-D SPGR, 1.2 mm thick sagittal images, TR 11 ms, TE 2.2 ms, flip angle 25°, field of view 24 cm, acquisition time 4.36 min). Cortical reconstruction and volumetric segmentation was performed using the FreeSurfer v 4.5 analysis suite (Dale et al., 1999; Fischl et al., 1999a,b) that is documented and freely available for download online (http://surfer.nmr.mgh.harvard.edu/). Briefly, processing includes motion correction and coregistration of T1 weighted images, removal of non-brain tissue, automated Talairach transformation, segmentation of deep grey and subcortical white matter volumetric structures, intensity normalization, tessellation of gray and white matter boundaries, automated topology correction, and surface deformation after intensity gradients optimally identify boundaries based on greatest intensity shifts. Manual inspection of the gray/white segmentation for all 400 hemispheres was performed.

A variety of surface based data representations were created using both intensity and continuity information from the entire three-dimensional MR volume. During processing, surface images are produced and mapped onto an averaged surface for each hemisphere. These surfaces are used to parcellate the cerebral cortex into units based on gyral and sulcal structure independently for the left and right hemispheres, using the atlas of Destrieux et al. (2010). These parcellations utilize standard anatomical conventions and generally correspond to accepted anatomical/functional units. We examined 68 cortical parcellations that had acceptable concordances with manual measurements (Destrieux et al., 2010)². The individual surfaces are nonlinearly warped back into individual subject space prior to analyses (Destrieux et al., 2010).

Cortical surface area (pial area), and thickness values were automatically extracted for left and right hemispheres by the FreeSurfer software. Surface area within each parcellation is calculated by adding the surface area of all faces of the triangulated mesh. Regional measures for thickness and local gyrification (see below) are obtained by averaging the value the vertices within each parcellation. Procedures for the measurement of cortical thickness have been validated against histological analysis (Rosas et al., 2002) and manual measurements (Kuperberg et al., 2003; Salat et al., 2004). Freesurfer morphometric procedures have been demonstrated to show good test-retest reliability across scanner manufacturers and across field strengths (Han et al., 2006; Reuter et al., 2012).

The extent to which the cortex is folded can be measured in several ways, with common approaches examining either the depth of (selected) sulci (Mueller et al., 2013) or a relative gyrification index (Zilles, Armstrong, Schleicher, & Kretschmann, 1988; Schaer et al., 2008) that compares the total cortical surface area to the extent of cortex on the exposed outer surface (larger numbers indicate greater extent of buried sulcal cortex). We utilized the latter approach. Local gyrification will increase with both the number and depth of sulci and as such is a measure of cortical complexity, whereas sulcal depth is singular dimension of folding (Schaer et al., 2008). A 3D local gyrification index (LGI) was computed using the procedures outlined by Schaer et al. (2008). This calculation divides the amount of pial surface by the amount of cortex on a closely fitting outer contour of the brain (hull surface). Computation starts at a given vertex of the tessellated surface and calculates within a given sphere of designated size (25 mm radius) the amount of surface area on the outer hull compared to the total amount of pial surface area. Larger LGI values indicate greater cortical folding within the radius. LGI for each cortical parcellation is estimated by averaging across all vertices within that parcellation.

2.3 Statistical Analyses

Asymmetries for each parcellation were calculated by subtracting the right measure from the left and dividing by the average, so that leftward asymmetries yielded positive coefficients. Note that asymmetry coefficients (ACs) are relative indices, allowing us to compare asymmetries across different anatomical measures. Univariate t-tests were used to assess whether regional asymmetries were significantly different from zero. Reported p-values were FDR corrected at p < .05 (Benjamini & Hochberg, 1995) to adjust for multiple comparisons. We also examined the correlation of the AC across metrics within each parcellation (i.e., surface area/thickness, surface area/LGI, thickness/LGI). FDR-corrected Pearson correlations were computed across each participant’s AC for each pair of metrics.

The coefficient of variation (standard deviation/mean) was used to estimate the extent of between subject variability since it can be readily compared between measures with very different means (Bedeian & Mossholder, 2000). The coefficient of variation (CV) is appropriate only for ratio-scale variables that have a naturally occurring fixed zero-point (Bedeian & Mossholder, 2000). For this reason, CV was computed separately for left and right hemisphere cortical measures, but not for the asymmetry coefficient. Pearson correlations examined the strength of association of CV between the 3 cortical measures, and these coefficients were statistically compared via the method of Lee & Preacher (2013).

To examine the correlation of degree of asymmetry and variability across regions, within each parcellation we first obtained the absolute value of each participant’s asymmetry. These unsigned asymmetry values were then averaged across participants within the parcellation, and that value was paired with the CV for the region. The Pearson correlation was then computed across the 68 brain regions.

3. Results

3.1 Regional Asymmetries in Cortical Surface Area, Thickness, and Local Gyrification

Figure 1 displays the t-values that examined the significance of regional asymmetries for cortical surface area (A), thickness (B), and local gyrification (C). Mean asymmetry coefficient and relevant statistical data for each parcellation are given in Supplementary Table 1. Abbreviations used for the brain regions are defined in the Appendix. We first describe the asymmetry findings for each cortical metric and then note some preliminary generalizations.

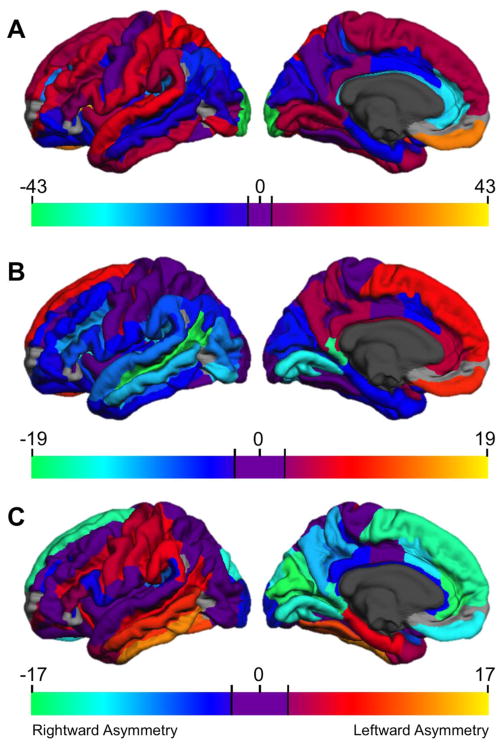
Figure 1.

Statistical map of univariate t-values testing the significance of regional asymmetries. Positive values (warm colors) indicate leftward asymmetry, negative values (cool colors) indicate rightward asymmetries. Areas with nonsignificant asymmetries are shown in purple. Regions not examined due to low concordance indices (Destrieux et al., 2010) are indicated in gray.

For surface area (Figure 1A) leftward asymmetries were observed for much of the dorsolateral prefrontal cortex (including most of the IFG/S) extending to dorsomedial prefrontal, anterior insula, superior temporal (including HG and PT), inferior temporal and inferomedial temporo-occipital (including ITG/S, lingual gyrus/sulcus and calcarine sulcus), anterior dorsolateral parietal (including SPG, SMG, and postcentral gyri), and posterior cingulate. Rightward surface area asymmetries were found in much of the orbitofrontal cortex, anterior to midposterior cingulate, MTG and STS extending posteriorly to angular gyrus and IPS, and posteromedial occipital and parahippocampal regions. Thus, greater left than right surface area was observed for perisylvian language regions, although adjacent language-relevant cortex (MTG, angular gyrus) had greater right surface area.

As a check on the reproducibility of our findings, we were able to compare the current surface area asymmetry data to that reported by Kang et al. (2012). They examined a sample of 138 right-handed young adults (69 female) and reported the mean LH and RH values for each of the Destrieux et al. (2010) parcellations. Using their published means, we computed hemisphere asymmetries for each parcellation as per the current study. The correlation of asymmetries across the two investigations was very strong, r = .914, p < .00001, indicating that the methods employed in the current study are robust and reproducible.³

Cortical thickness asymmetries were smaller and somewhat less numerous than surface area asymmetries. Much of the medial frontal and parietal cortex was thicker in the left, than the right hemisphere, as was the central sulcus. Rightward asymmetries included virtually all of the temporal lobe, inferior parietal (including SMG and AG), lateral and medial occipital (including IOG/S, MOG, calcarine sulcus, cuneus), and several lateral and orbito-frontal regions (including IFG/S, MFG, and much of the orbitofrontal cortex).

Leftward local gyrification asymmetries were observed in middle and inferior temporal cortex (STS, ITG/S, MTG, fusiform, parahippocampal gyri), and lateral paracentral regions (pre- and postcentral gyri, central sulcus) extending posteriorly to include the supramarginal gyrus, and anteriorly to include IFS and pars triangularis. Rightward asymmetries included medial frontal (SFG, anterior/midanterior cingulate), parietal (precuneus, posterior cingulate, POS, subparietal sulcus), and occipital (SOG, lingual gyrus, cuneus, calcarine sulcus, occipital pole) regions, as well as the planum temporale and pars opercularis.

Inspection of these data permits several generalizations. First, structural cortical asymmetries are ubiquitous. Of the 68 regions we examined, 64 had significant asymmetries for surface area, 48 for thickness, and 44 for gyrification. Every parcellation was asymmetrical for at least one cortical measure. Clearly left/right asymmetries are the rule, rather than the exception, when one examines various indices of cortical morphometry. However, regional surface area asymmetries are most prominent in size and frequency, with a larger range of asymmetries (AC range −.386 to + .320) than either thickness (−.140 to + .094) or LGI (−.073 to +.045).

Second, there is no necessary relationship across the 3 metrics in the presence or direction of asymmetry. Only 6 regions had significant asymmetries in the same direction across the 3 measures. The central sulcus was consistently leftward asymmetrical. Five other regions were consistently rightward asymmetrical: the posterior ramus of the lateral sulcus, the midanterior cingulate gyrus/sulcus, and 3 adjacent medial to posterior occipital regions (cuneus, SOG, POS). In general, however, statements about the direction of asymmetry of a given region must take into account the particular metric of cortical organization. For example, the well-known leftward asymmetry of the planum temporale reflects greater left, than right, surface area (Shapleske et al., 1999). We replicated this asymmetry for surface area (AC = +.176), but also found that the right planum was significantly thicker than the left (AC = −.041), and also had greater local gyrification (AC = −.014).

3.2 Asymmetry Correlations Between Cortical Indices

Although, as noted above, asymmetries differed across the 3 cortical measures, this need not preclude associations within at least some regions. To investigate this, within each parcellation we examined correlations of asymmetry scores between each pair of cortical indices. Figure 2 displays the significant correlations (see Supplementary Table 2 for statistics by region), and indicates that for relatively few regions were asymmetries correlated across cortical measures.

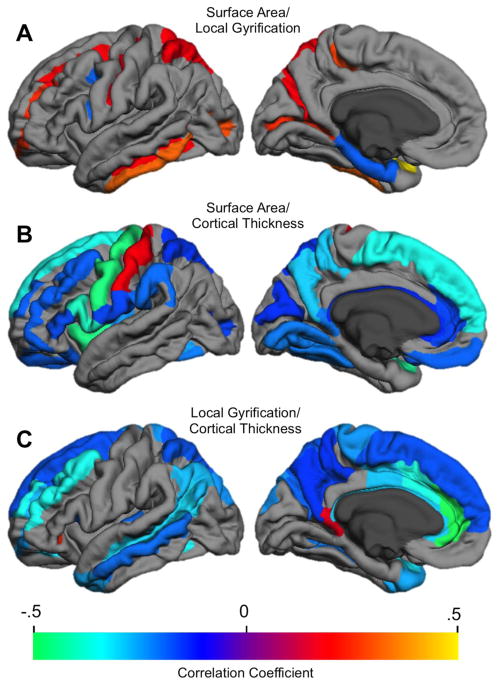
Figure 2.

Correlation of asymmetries across each cortical metric (only FDR-corrected statistically significant correlations are shown). A. Surface area X local gyrification asymmetry correlation. B. Surface area X Thickness asymmetry correlation. C. Thickness by local gyrification asymmetry correlation.

Although asymmetries for surface area and local gyrification were not correlated across much of the cortex, when associations were present they were usually positive (Figure 2A). These positive asymmetry associations predominated in sulci within dorsolateral frontal (SFS, MFS, central) and posterior medial (parieto-occipital, calcarine, marginal cingulate sulci) cortex, as well as ITG/S and superior parietal gyrus.

When area and thickness asymmetries were associated, they were generally negatively correlated (Figure 2B). These opposing asymmetries occurred primarily in gyral, rather than sulcal, cortex and included all major frontal lobe gyri, lateral (SMG and SPG) and medial (precuneus, posterior cingulate) parietal, insula, and inferomedial temporal occipital (cuneus, fusiform, lingual gyri) regions. We did not replicate the few regions that Koelkebeck et al. (2014) found to be positively correlated, but we did replicate the major regions they found to be negatively correlated. It is interesting to note that the area/thickness and area/LGI asymmetry association maps are in a near complementary relationship: most regions with significant area/thickness asymmetry correlations did not evidence asymmetry correlations between area and LGI, and vice versa.

Similarly, thickness and local gyrification asymmetries, when correlated, were nearly always negatively related (Figure 2C). These opposing asymmetries predominated in dorsolateral and medial frontal (MFG/S, SFG/S, anterior and middle cingulate) and parietal (AG, SPG, precuneus, subparietal sulcus) regions, midlateral temporal (MTG/S, temporal pole), and Heschl’s gyrus. These regions partly overlapped with those showing negative correlations of surface area and thickness asymmetries.

3.3 Between-subject Variability and Relationship to Asymmetry

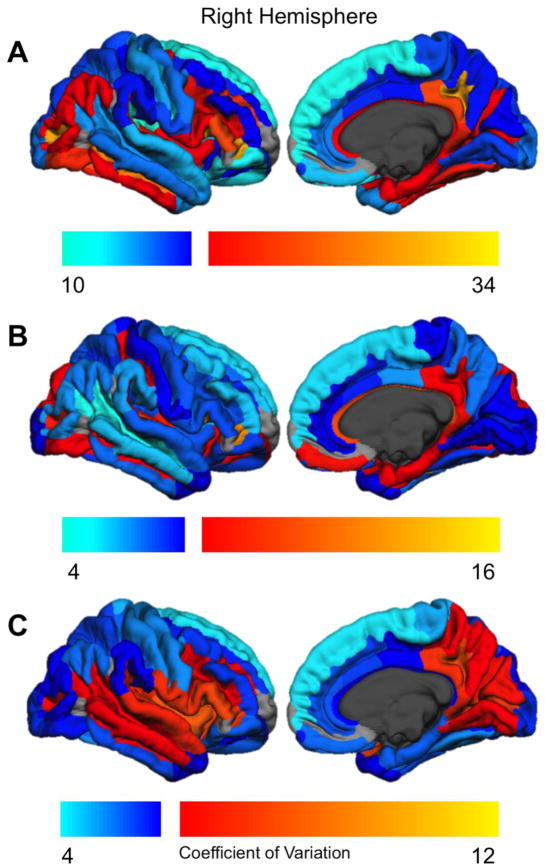
Figure 3 displays the coefficient of variation for surface area (3A), thickness (3B), and local gyrification (3C) for the right hemisphere; Figure 4 shows the same data for the left hemisphere. The coefficients of variation for each parcellation are given in Supplementary Table 3. As indicated, there are substantial regional differences in between-subject variability. There was approximately a 3-fold difference in variability between the least and most variable regions for each metric (surface area CV range 10.58–33.92; thickness 4.54–15.35, LGI 4.05–11.91). However, in general, regions with high variability in the left hemisphere also were highly variable in the right hemisphere. The CV correlations across hemispheres were substantial: surface area r = .905, thickness r = .904, local gyrification r = .928 (p < .0001). Across both hemispheres, CV was larger for surface area than for either thickness, t(134) = 23.78, p < .0001, or LGI t(134) = −5.84, p < .0001.

Figure 3.

Regional coefficient of variation for the right hemisphere. Cool colors indicate coefficients below the median value; warm colors indicate coefficients above the median value. Regions not examined due to low concordance indices (Destrieux et al., 2010) are indicated in gray.

For surface area (Figures 3A, 4A), regions with relatively high variability included anterior inferior frontal and inferior temporal cortex, medial parietal (subparietal sulcus, posterior cingulate) and lateral occipital regions, and the superior temporal plane (including HG). Areas with the lowest surface area variability included paracentral cortex, lateral superior and middle temporal regions, and the SFG.

For cortical thickness (Figures 3B, 4B), high variability regions included the PT and HG (and adjacent transverse temporal sulcus), inferior temporal occipital and orbitofrontal sulci, and the anterior lateral fissure. The following regions had relatively low variability in cortical thickness: middle and superior frontal (SFG/S, MFG, IFS), central sulcus and precentral gyrus/sulcus, ITG, STS, SMG, AG, pars opercularis, anterior insula and precuneus.

High variability local gyrification areas (Figures 3C, 4C) included the entire insula and surrounding sulci, adjacent IFG and anterior lateral fissure, HG and lateral STG, and medial parietal occipital areas. Areas with relatively low gyrification variability included paracentral cortex, SFG, inferior temporal (fusiform, PHG, ITG), lateral parietal (AG, SPG), and anterior cingulate cortex.

We note that there is not a clear distinction in the amount of variability between unimodal vs association areas. One the one hand, primary somatomotor cortex (pre- and postcentral gyri, central sulcus) had relatively low variability across all 3 cortical metrics. However, primary auditory (HG) cortex had very high variability for all measures, and primary visual cortex (calcarine sulcus, cuneus) had intermediate values for CV. Similarly, association cortex included both regions with high (pars triangularis, anterior lateral fissure) and low-to-intermediate (SFG, MTG, SMG) between-subject variability (see Supplementary Table 3).

Table 1 provides the correlations of CV between each measure of cortical structure, by hemisphere. All correlations were positive suggesting that highly variable regions for a given cortical metric tend to also be highly variable for the other metrics. As indicated, individual variability was most strongly correlated for surface area and thickness, for both hemispheres regions with high surface area variability also tended to have high variability in cortical thickness (see Figures 3A/3B, 4A/4B). These correlations were significantly greater than the correlations of thickness and LGI variability, (LH: Z = 2.40, p < .02; RH: Z = 2.46, p < .02), and the surface area/LGI correlations (LH: Z = 2.04, p < .05; RH: Z = 1.85, p = .06).

Table 1.

Pearson Correlation of the Coefficient of Variation Across Measures of Cortical Structure, By Hemisphere. Each correlation coefficient was computed over the 68 regional parcellations.

	Surface Area/Thickness	Surface Area/Local Gyrification	Thickness/Local Gyrification
Left hemisphere	.512***	.226	.182
Right Hemisphere	.585***	.361**	.295*

^***p < .0001

^**p < .01

^*p < .05

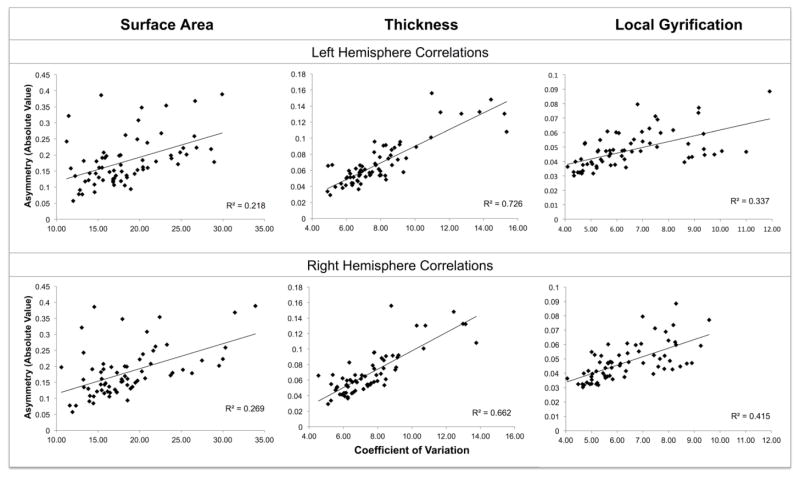
Scatterplots for the correlations between variability and asymmetry are given in Figure 5. As is evident, there are strong positive correlations between the degree (absolute value) of asymmetry and the extent of between-subject variability, for all 3 measures of cortical structure: regions with high variability evidence larger asymmetries than regions with low variability. This was found both for left hemisphere variability (Surface Area r = .467, Thickness r = .852, LGI: r = .581) and right hemisphere variability (Surface Area r = .518, Thickness r = .814, LGI r = .645), all p’s < .0001. The asymmetry/variability correlation was significantly larger for thickness than for either surface area (LH: Z = −4.32, p < .0001; RH: Z = −3.22, p < .01) or LGI (LH: Z = 3.42, p < .001; RH: Z = 2.12, p < .05). No relation between variability and asymmetry was found when CV was correlated with signed asymmetries (r’s between −.014 and −.236, all nonsignificant). Hence, there is a regular relationship across brain regions between variability and the magnitude (but not direction) of structural asymmetry.

Figure 5.

Scatterplots of the correlations between the absolute value of asymmetry and the coefficient of variation. Each correlation coefficient was computed over the 68 regional parcellations.

4. Discussion

Structural asymmetry is the norm, rather than the exception, in the human cerebral cortex. In a relatively large sample of healthy young adults, we documented significant structural asymmetry across most regions of the cortex whether surface area, thickness, or local gyrification was measured. Contrary to the claim that structural asymmetries are few and insignificant (Wey et al., 2014), asymmetrical organization predominates in the healthy adult brain. The same structural indices of cortical organization demonstrated regional differences in between-subject variability. Importantly, the extent of between-subject variation predicted the degree of asymmetry of a region. If such variability is an indicator of biological constraint, then this finding implies that asymmetries will be most prominent in regions that have the greatest structural plasticity. Before interpreting our results, we briefly review what is known about the neurobiological bases of variations in surface area, thickness, and gyrification, in order to better interpret differential asymmetries for these measures. We then discuss specific findings in detail, consider the limitations of the current study, and offer suggestions for future investigations.

4.1 Neurobiological Bases of Cortical Structure Indices

Although the specific neurobiological interpretation of each cortical metric is still unsettled, several proposals have empirical support. For example, across many, but not all, regions there is an inverse relationship between neuronal density and cortical thickness (la Fougère et al., 2011) – thicker areas have reduced neural density, most likely due to increased number of dendrites and synapses per neuron (Wagstyl, Ronan, Goodyer, & Fletcher, 2015). In addition, cortical thinning that occurs in later childhood and adolescence is generally associated with white matter expansion and increased axonal organization in the same regions (Alemán-Gómez et al., 2013; Vandekar et al., 2015). This suggests that in many regions cortical thickness is associated with variations in cortical connectivity. Variations in surface area are influenced by the number and spacing of cortical columns (Rakic, 1995). Cortical columns are not added after birth, yet surface area expands dramatically during childhood (Hill et al., 2010). Hence, surface area variations will be strongly influenced by columnar spacing and expansion of neuropil between columns. Supporting this interpretation Buxthoeveden et al. (2001) demonstrated that minicolumns in the human left planum temporale were wider and separated by increased neuropil space relative to the right hemisphere. There may also be a white matter contribution to expansion of surface area, when this is associated with cortical thinning. According to the “balloon” model, expansion of underlying white matter results in stretching and thinning of the overlying cortex, increasing surface area and decreasing thickness (Hogstrom et al., 2013; Seldon, 2005; Vandekar et al., 2005).

Gyrification has been attributed to both gray and white matter processes. One theory holds that differential tangential surface expansion (faster growth of one region relative to an adjacent one) causes the cortex to fold (Xu et al., 2010; Ronan et al., 2014). Alternatively, mechanical tension produced by growth of axons may pull together strongly interconnected regions, producing cortical folds and thereby reducing wiring length (Van Essen, 1997). Another white matter theory posits that developing connections in some cortical regions “push” outward in a tangential direction to form gyri (H. Chen et al., 2013). A recent review notes that gyrification is likely caused by the interaction of cell generation processes and evolving fiber tract connectivity (Zilles et al., 2013). Variations in local gyrification may also reflect the extent to which local vs distant connections predominate in a region (Deng et al., 2014). Although major sulci are present at birth, gyrification continues to increase until at least 2 years of age, and is developmentally distinct from expansion of surface area (G. Li et al., 2014). Hence, some dissociations between surface area and gyrification are to be expected. Because the neural bases may vary across cortical regions, this suggests that no single interpretation of the cellular basis of variations in surface area, thickness, or gyrification will suffice. However, examination of how asymmetries vary across multiple cortical measures may provide hints about underlying neurobiological factors.

4.2 Regional Asymmetries in Cortical Surface Area, Thickness, and Local Gyrification

Above we noted the strong quantitative consistency of our surface area asymmetry results with those found by Kang et al. (2012) who also employed the same parcellation methods. Although precise comparisons with other prior asymmetry studies are not possible due to differences in methods and parcellation approaches, our findings broadly replicate several previous reports. With respect to surface area, we replicated the Van Essen et al. (2011) findings of leftward asymmetry of posterior perisylvian and lateral prefrontal regions, anterior insula, temporal pole, posterior cingulate, SMG, SPG, lingual gyrus/collateral sulcus, and rightward asymmetry of angular gyrus, MTG, STS, MOG. Likewise, our findings comport with the leftward surface area asymmetry of SFG, MFG, HG, pars opercularis, temporal pole, and postcentral gyrus obtained by Koelkebeck et al. (2014), as well as their rightward asymmetry of AG, pericalcarine cortex, and MTG. With respect to cortical thickness, our asymmetry findings replicate virtually all of the significant asymmetries reported by Koelkebeck et al. (2014) (leftward: ACC; rightward: IFG, HG, temporal pole, MTG, STS, lateral occipital cortex). However, relative to Koelkebeck et al. (2014), the current study also observed additional areas of significant asymmetry for both surface area and thickness, perhaps attributable to our larger sample size as well as the larger number of discrete areas we examined. Our findings also replicate several of Luders et al. (2006) cortical thickness asymmetries (leftward: ACC, dorsomedial and orbitofrontal; rightward: IFG, ITG, lingual gyrus), although we obtained opposite asymmetries from that report in some areas (anterior temporal, precuneus, SMG).

As noted above, surface area asymmetries were more frequently observed than cortical thickness asymmetries, similar to the findings of Koelkebeck et al. (2014). Although these authors did not offer an explanation of the more widespread surface area asymmetries, the current study suggests one important factor. As discussed further below, regional structural asymmetry is positively correlated with the degree of between-subject variability, and the coefficient of variation is significantly greater for surface area than for thickness. Hence, the increased variability of surface area could account, at least in part, for the more extensive asymmetries observed for this cortical metric.

For many regions a significant leftward surface area asymmetry was associated with a significant rightward cortical thickness asymmetry. This pattern was observed throughout most of the perisylvian cortex, as well as additional temporal, occipital, and lateral frontal regions. This suggests that core regions of the left hemisphere language network are characterized by greater surface area but thinner cortex. This structural pattern could be produced by greater expansion of underlying white matter in the left hemisphere that thins and “stretches” the overlying cortex (Hogstrom et al., 2013; Seldon, 2005).

We also observed a number of regions with rightward asymmetries of both surface area and cortical thickness. The pattern was found in lateral posterior regions adjacent to perisylvian cortex (MTG, AG, STS) extending to lateral occipital regions, orbitofrontal cortex, and several medial regions. Asymmetries in these regions could be due to more extensive proliferation of right hemisphere gray matter due to greater neuropil within and between cortical columns (Buxthoeveden et al., 2001; Wagstyl et al., 2015).

To our knowledge, there have been no previous reports of adult gyrification asymmetries across the entire cortex. Because gyrification tends to increase with surface area, we might expect the direction of significant asymmetries to be the same across these measures. This was indeed observed across many regions, consistent with tangential expansion as the underlying mechanism for gyrification (Xu et al., 2010; Ronan et al., 2014). However, we also observed several areas in which the direction of LGI and surface area asymmetries reversed. In these regions one could not attribute the hemisphere difference in gyrification to a difference in surface area. Perhaps in these regions increased gyrification reflects greater local connectivity independent of processes of surface area expansion or pruning (Deng et al., 2014).

The structural findings support the view that there are multiple maps of cortical asymmetry, and that generalizations cannot be made independent of the specific measure. For example, one question is whether association cortex is more asymmetrical than unimodal cortex. On the one hand, somatomotor cortex evidences either slight or no asymmetry for all three measures. On the other hand, primary auditory cortex has very strong leftward asymmetry for surface area, but a slight rightward asymmetry for thickness, and no asymmetry for LGI. Unimodal visual cortex presents another pattern: only slight asymmetries for surface area and thickness, but very strong rightward gyrification asymmetry. Similarly, a given region of association cortex (AG) can have a strong (rightward) surface area asymmetry, slight (rightward) thickness asymmetry, and no gyrification asymmetry, while for another (SFG) small leftward asymmetries were observed for surface area and thickness, with a larger (rightward) LGI asymmetry. In general, however, there is no clear support for the view that asymmetries are larger for association, than for unimodal, cortex.

The functional significance of the asymmetries we document here cannot be determined as we lack such data for the current sample. However, the fact that regional asymmetries vary depending on the particular measure of cortical structure implies that attempts to link structural to functional asymmetries based on single metric can be misleading, and may have contributed to conflicting results on the relation between structural and functional asymmetry (Chiarello et al., 2004; Eckert, Leonard, Possing, & Binder, 2006). Rather, functional asymmetry may be the product of conjoint asymmetries across multiple areas and scales of structural organization.

4.3 Regional Asymmetry Correlations Between Cortical Indices

An additional focus of the current investigation was to explore the extent to which participants’ asymmetries were associated across the 3 cortical metrics, on a region-by-region basis. Prior research indicates that when such associations are examined across the entire cortex (combined over hemispheres), surface area is generally positively correlated with gyrification and negatively correlated or uncorrelated with cortical thickness; similarly, thickness and gyrification are reported to be uncorrelated or negatively associated (Hogstrom et al., 2012; Klein et al., 2014; Winkler et al., 2010). Our examination of asymmetry correlations largely followed these trends (see Figure 2): generally positive associations of surface area and LGI asymmetry, and mostly negative correlations of cortical thickness with surface area or LGI. Yet these associations were only observed for selected regions of the cortex for many regions asymmetries were uncorrelated. This suggests that the mechanisms producing each type of asymmetry need not be intrinsically related. This result is reminiscent of findings that various types of functional and behavioral asymmetries do not highly correlate (Hellige, 1993).

However, it is important to examine the asymmetry correlations that we did observe. One unexpected finding was the very different regional patterns of correlation between surface area and LGI asymmetries on the one hand, and area and thickness asymmetries on the other hand (compare figures 2A and 2B). The former positive correlations tended to predominate in sulcal cortex, while the latter negative correlations were mainly observed in gyral cortex. Gyral and sulcal cortex have been found to differ in several respects. There are denser axonal connections to gyri than to sulci (H. Chen et al., 2013; Nie et al., 2012), and structural and functional connectivity data suggest that gyral regions connect rather distantly to other gyri while sulcal regions primarily connect locally to adjacent gyri (Deng et al., 2014). In addition, sulcal cortex is thinner than gyral cortex and differs in its developmental trajectory during childhood (Fischl & Dale, 2000; Vandekar et al., 2015). The positive correlation of area and LGI asymmetries (Figure 2A) indicates that the hemisphere with greater surface area also has greater gyrification, a pattern consistent with expansion of surface area; since this was observed more frequently in sulcal than in gyral cortex it may reflect hemisphere differences in regions with more local connections. The negative correlations of area and thickness (Figure 2B) indicate that the hemisphere with increased surface area has thinner cortex, which suggests expansion of underlying white matter as a mechanism (Seldon, 2005; Hogstrom et al., 2013). As this pattern was primarily seen in gyral cortex, this could reflect greater connectivity across more distant cortical regions in the hemisphere with larger surface area and thinner cortex. This interpretation is admittedly speculative, but it suggests avenues for further research in the structural bases of hemisphere asymmetry. Nevertheless, the current data emphasize the importance of differentiating between gyral and sulcal cortex in subsequent investigations of structural asymmetries and their intercorrelations. The only prior study to explore correlations of surface area and thickness asymmetries used a parcellation scheme that does not clearly separate gyral and sulcal cortex⁴ (Koelkebeck et al., 2014) and so the current findings, while intriguing, await replication.

We also observed negative correlations between LGI and cortical thickness, for both gyral and sulcal cortex (Figure 2C). In these regions, the hemisphere with greater gyrification also had thinner cortex. This pattern may be consistent with tension theories of cortical folding (Van Essen, 1997) if increased connectivity also involves increased intracortical myelination. The frequent association of cortical thinning with white matter expansion/organization suggests intracortical myelination as a potential contributing mechanism (Sowell et al., 2004; Vandekar et al., 2015). However, firmer interpretations of the LGI/thickness association will require asymmetry investigations that measure these cortical metrics along with white matter structure.

To summarize, although asymmetry correlations between cortical metrics are obtained in only some regions, the nature of the correlations suggests that different neurobiological mechanisms may underlie these associations. It is unlikely that a single explanation can account for the diverse pattern of asymmetry correlations observed.

4.4 Regional Differences in Between-subject Variability of Cortical Structure

Individual differences in cortical structure can be attributed to differing genetics, varying life experiences, and gene X environment interactions. There is little reason to think that these factors will produce similar ranges of individual variability across the entire cortex. A unique feature of the current investigation was examination of regional differences in the extent of between-subject variability for three different cortical metrics in a relatively large sample. Prior studies used very small sample sizes, which may not permit robust estimates of between-subject variation (Kennedy et al., 1998; Mueller, et al., 2013). However, we can broadly compare our findings to Mueller et al.’s (2013) report of vertex-level cortical thickness and sulcal depth variation. Although both studies observed low variability in infero-temporal cortex, in general we did not replicate their thickness findings (compare current Figures 3B, 4B to their Figure 4B). Our findings for local gyrification also substantially depart from Mueller et al. (compare current Figures 3C, 4C to their Figure 4A). However, it is important to note that the LGI measure reflects both the depth of sulci as well as their frequency within local regions (Schaer et al., 2008). In addition to the differences in methods and sample sizes, participants in the Mueller et al. (2013) study were middle-aged adults. Given the adult lifespan changes in cortical morphometry (Hogstrom et al., 2013; Zhou et al., 2013), the relative lack of correspondence may not be surprising.

As Figures 3 and 4 indicate, there are both differences between the measures in the extent of variability, as well as some regions of overlap. However, we cannot conclude that unimodal cortex has less variability than association cortex. Somatomotor cortex does evidence low variability across the board, but auditory and visual regions do not. Similarly, dorsomedial prefrontal cortex and some lateral parietal association regions have relatively low between-subject variation. In general, variability was greater for surface area than for either thickness or gyrification, but for all metrics there was a 3-fold difference in the coefficient of variation between the least and most variable regions.

Although regional distribution of variability differed across metrics, the correlations of CV across each metric were always positive (see Table 1). This suggests that the extent of phenotypic variation within a cortical region may be similarly manifest across several neurobiological indices. The CV correlation between surface area and thickness was much stronger than was the correlation with either variable and LGI. This is surprising given that surface area and thickness dissociate developmentally (Raznahan et al., 2011), genetically (Panizzon et al., 2009; Winkler, et al., 2010), and in network organization (Sanabria-Diaz et al., 2010). Further, when these metrics are related they are often negatively associated. Nevertheless, our findings indicate that whatever factors promote/restrict variability in surface area also promote/restrict variability in thickness. Because the genetic correlation between thickness and surface area is very low (Panizzon et al., 2009; Winkler et al., 2010), one intriguing possibility is that some regions are more open to environmental sculpting of neuropil in both tangential and radial dimensions. However, regardless of the ultimate interpretation, it is reasonable to interpret the extent of between-subject variability as one index of the degree of biological constraint. We can now consider the question of whether regional differences in such constraint are related to the extent of hemispheric asymmetry.

4.5 Relationship of Regional Variability and Asymmetry

One striking aspect of our findings was the positive association, for all 3 cortical metrics, of variability and the degree of asymmetry. This finding suggests that cortical regions with the most between-subject variability also have the greatest structural asymmetry, regardless of direction. To the extent that such variability indexes the extent of biological constraint, the results indicate that highly asymmetrical regions are the least constrained, and hence are more open to the expression of genetic and experiential variation. We suggest that in regions with high between-subject variability, the left and right hemispheres are more able to take somewhat different developmental paths, perhaps via differences in the pruning or enhancement of cortical circuits and connectivity. Our findings are not consistent with the alternate view that structural asymmetry is strongly canalized trait that is buffered from change (Siegel & Bergman, 2002; Waddington, 1957).

The variability/asymmetry association is also consistent with findings from developmental research. Although some structural asymmetries arise in fetal life (Habas et al., 2012), asymmetries continue to develop during childhood and adolescence (G. Li et al., 2014; Nie et al., 2013) and are modulated throughout the adult lifespan (Plessen et al., 2014; Zhou et al., 2013). These developmental trajectories of structural asymmetry also vary from region to region, and it will be interesting to investigate in future studies whether regions with more or less variability differ in the timing and extent of developmental change.

Investigations of the genetics of structural asymmetry have generally found little left/right hemisphere difference in genetic determinants, leading to the conclusion that the degree of surface area and thickness asymmetry is not under close genetic control (Eyler et al., 2014; Chen et al., 2012, 2013). Such findings suggest that the variability/asymmetry association observed in the current study may be a reflection of more experiential sources of variation. It has been reported that cortical thickness has somewhat lower heritability estimates than does surface area (Eyler et al., 2012; Panizzon et al., 2009; but see also Winkler et al., 2010). If this is the case, it could help interpret our finding that the variability/asymmetry correlation was stronger for thickness than for surface area or local gyrification. If variations in cortical thickness have greater experience-based plasticity than do surface area variations, then its stronger association with asymmetry would implicate greater experiential effects on thickness asymmetry. This is a speculative interpretation. However, cortical thickness has been shown to vary with learning and differences in experience in other domains (e.g., Kang et al., 2013; Li, Legault, & Litcofsky, 2014; Wenger et al., 2012), whereas surface area has been shown to correlate with more stable indices of general cognitive ability (Colom et al., 2013; Vuoksimma et al., 2014).

In our view, there are two important implications of the finding that the degree of structural asymmetry is predicted by the extent of between-subject variability. First, the current data demonstrate that regional differences in variability have predictive value. This should not be the case if such variability were indeed a reflection of “noise” or of random fluctuations around the population mean. The degree to which a brain region is variable across individuals may be an important expression of biological constraint, and it will be important to investigate whether this can help account for other regional differences in brain structure and function. Second, our findings imply that regional differences in structural asymmetry are related to the extent of biological constraint operating within the region. In other words, enhanced asymmetry may be one outcome of structural plasticity. Heschl’s gyrus may be a case in point here. This region demonstrated high variability across all 3 cortical metrics in the current study, and other research has documented strong individual variability within this region using various anatomical methods (e.g., Warrier et al., 2009; Marie et al., 2015). Heschl’s gyrus anatomical asymmetry is related to functional asymmetry of auditory processing (Tzourio-Mazoyer et al., 2015; Warrier et al., 2009), and anatomical variation of this region is associated with experiential differences in bilingual language exposure (Ressel et al., 2012), and musical training (Hyde et al., 2009). Concurrent examination of anatomical variability, functional and structural asymmetry, and experience-dependent plasticity is likely to be a fruitful area of inquiry. The current study contributes to this effort by demonstrating a substantial link between structural variation/biological constraint and anatomical asymmetry.

4.6 Limitations and Future Directions

We acknowledge several limitations of the current research. The absence of white matter data is a significant limitation. Our interpretations of regional and between-subject variations in cortical organization often appealed to explanations based on variations in white matter. Although these explanations were based on much prior research, simultaneous examination of cortical and white matter structure in the same individuals will be needed confirm or reject many suggestions made in the current report. In addition, it is important to recognize that our conclusions about regional differences in asymmetry and variability are based on a priori defined brain areas, rather than vertex-based approaches that do not pre-specify boundaries. Because values for each metric are summed or averaged within parcellations, some important regional differences may be obscured. There are some off-setting advantages, however, in increased statistical power (many fewer comparisons are made) and in the ease of quantitative comparison of results across studies that use the same readily available parcellation scheme (c.f. section 3.1).

Our study was also limited to data collected at a single time point. Since each of the three cortical measures varies across the life span, we cannot determine how generalizable our results are to different age groups. We also report sample-wide findings without considering the influence of variables such as sex, handedness, or intellectual ability. It will be important to address such influences in subsequent studies. The current study also lacks data on functional brain activity, and it remains to be seen whether there are associations between structural and functional variability (Mueller et al., 2014) or whether structural variability modulates the relationship between structural and functional lateralization.

We further note that the coefficient of variation is not a pure index of between-subject variability, as measurement error can also contribute to apparent structural differences between individuals. We sought to minimize this influence by removing parcellations with low anatomical concordance values (Destrieux et al., 2010) from our analyses, but this will not eliminate all measurement error. However, it is worth pointing out that brain regions that are difficult to measure reliably are often difficult precisely because there are large differences across individuals in the sulcal and gyral anatomy of the region. Hence, the coefficient of variability, when applied across a large sample of individuals, may provide a reasonable estimate of the true individual variability of a brain region.

In addition to the factors mentioned above, it will be important for future studies to further examine potential asymmetry differences between gyral and sulcal cortex, and to consider the potential neurobiological bases of structural features such as surface area, cortical thickness and gyrification. Although the interpretation of these features is currently an active area of inquiry, a complete understanding of the why and the how of hemispheric asymmetry will depend on careful analysis of the potential cellular bases of macroscopic asymmetries.

4.7 Conclusions

The current investigation examined regional differences in structural asymmetries and in between-subject variability using 3 different cortical metrics in a large sample of healthy young adults. The study of regional asymmetry and variability is still relatively young, but several conclusions follow from our findings. First, the structure of the human cerebral cortex is largely asymmetrical. Surface area, cortical thickness, and local gyrification all evidenced significant asymmetries across most regions of the cortex. However, the size and direction of asymmetry varies over regions, over the metrics of cortical structure, and across individuals. Such variability is to be expected for a complex biological system such as the human brain. Second, the differing regional organization of the three cortical metrics implies that there are multiple, only partially overlapping, maps of structural asymmetry. We suggest that functional asymmetries are likely to emerge from the conjoint contributions of multiple brain regions and levels of cortical structural organization. Hence a single explanation cannot account for the diverse patterns of structural asymmetry described here. There are likely to be several underlying mechanisms producing structural asymmetries (e.g., pruning and elaboration of neuropil, white matter expansion, local vs long range connectivity) that can vary across brain regions. Third, the results suggest that between-subject variability in cortical structure may provide a means to assess the extent of biological flexibility or constraint of brain regions. Finally, our findings imply that reduced biological constraint promotes the phenotypic expression of strong structural asymmetry, and that regional differences in biological constraint contribute to regional variations in asymmetry. Not only is variability not noise, but it may play an important role in understanding the biological basis of hemispheric asymmetry.

Highlights.

• Asymmetries in cortical surface area, thickness, and gyrification are ubiquitous

• Asymmetry varies over regions, across cortical metrics, and across individuals

• There are multiple, partially overlapping maps of structural asymmetry

• Between-subject variability in cortical structure can index biological constraint

• Reduced constraint promotes regional expression of strong structural asymmetry

Appendix

Abbreviations used for Brain Regions:

ACC

Anterior cingulate cortex

AG

Angular gyrus

HG

Heschl’s gyrus

IFG

Inferior frontal gyrus (pars triangularis + pars opercularis)

IFS

Inferior frontal sulcus

IOG

Inferior occipital gyrus

IOS

Inferior occipital sulcus

IPS

Intraparietal sulcus

ITG

Inferior temporal gyrus

ITS

Inferior temporal sulcus

MFG

Middle frontal gyrus

MFS

Middle frontal sulcus

MOG

Middle occipital gyrus

MTG

Middle temporal gyrus

MTS

Middle temporal sulcus

PHG

Parahippocampal gyrus

POS

Parieto-occipital sulcus

Pars T

Pars triangularus

PT

Planum temporale

SFG

Superior frontal gyrus

SFS

Superior frontal sulcus

SMG

Supramarginal gyrus

SOG

Superior occipital gyrus

SPG

Superior parietal gyrus

STG

Superior temporal gyrus

STS

Superior temporal sulcus