Measuring B₁ distributions by B₁ phase encoding

Abstract

Purpose

We propose a method to acquire B₁ distribution plots by encoding in B₁ instead of image space. Using this method, B₁ data is acquired in a different way from traditional spatial B₁ mapping, and allows for quick measurement of high dynamic range B₁ data.

Methods

To encode in B₁, we acquire multiple projections of a slice, each along the same direction, but using a different phase sensitivity to B₁. Using a convex optimization formulation, we reconstruct histograms of the B₁ distribution estimates of the slice.

Results

We verify in vivo B₁ distribution measurements by comparing measured distributions to distributions calculated from reference spatial B₁ maps using the Earth Mover’s Distance (EMD). Phantom measurements using a surface coil show that for increased spatial B₁ variations, measured B₁ distributions using the proposed method more accurately estimate the distribution than a low-resolution spatial B₁ map, resulting in a 37% EMD decrease while using fewer measurements.

Conclusion

We propose and validate the performance of a method to acquire B₁ distribution information directly without acquiring a spatial B₁ map. The method may provide faster estimates of a B₁ field for applications that do not require spatial B₁ localization, such as the transmit gain calibration of the scanner, particularly for high dynamic B₁ ranges.

Introduction

In magnetic resonance imaging (MRI), mapping the transmit radiofrequency (B₁) field is important for a variety of applications, including calibrating the transmit gain of the scanner, measuring coil performance, and parallel transmit pulse design [1, 2]. To visualize B₁ field variations in a volume, a spatial B₁ map is often acquired and displayed as two-dimensional (2D) images. There exist a variety of methods for spatial B₁ mapping, categorized as either signal magnitude-based [3–10] or signal phase-based [11–16] methods.

We propose a method to acquire B₁ distribution plots that estimate the histogram of B₁ values in a volume, rather than acquiring spatial B₁ maps. B₁ distribution plots may offer benefits over traditional spatial B₁ mapping methods when spatial localization of the B₁ field is not necessary, and knowledge of the distribution of B₁ in the volume suffices (e.g., for the scanner transmit gain calibration). Distribution measurements may be useful for nonproton imaging, where rapid measurement of the B₁ field is important [17–19], or for volumes with very rapid spatial B₁ variations that may experience unwanted intra-voxel signal averaging with spatial mapping techniques.

We propose a B₁ distribution measurement method that uses an existing signal phase-based B₁ mapping method, BEAR [15]. When acquiring a spatial B₁ map, BEAR is insensitive to T₁, T₂, repetition time (TR) and off-resonance frequency variations, and allows for direct mapping between signal phase and B₁. Another important property of BEAR is the easily tunable, approximately linear, phase sensitivity to B₁ variations. The proposed method acquires a series of BEAR projection measurements using different phase sensitivities to B₁, so that the result is an acquisition which has phase-encoding as a function of B₁, rather than as a function of image space. We describe the theory behind the acquisition and reconstruction of the proposed technique, and validate the method in vivo at 3T and with a phantom at 1.5T.

Theory

Phase sensitivity tuning

This study uses the BEAR method [15, 20], a phase-based B₁ mapping method, to encode B₁ variations into an MR signal. Figure 1a shows the BEAR sequence diagram with two adiabatic full passage HSn pulses [21] that have different relative peak magnitudes, and different magnitude and frequency sweep shapes, which are determined by the parameters n₁ and n₂. These two HSn pulses create a twice-refocused spin-echo whose phase is proportional to B₁. The particular choice of n₂ given n₁ is determined by minimizing any residual phase error over the HSn pulse bandwidth and a B₁ range of choice [20].

Fig. 1.

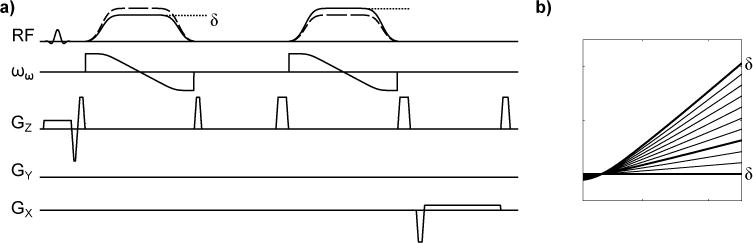
a. The BEAR sequence using HSn pulses is used to acquire B₁ projections with different values of δ, n₁ and n₂. A second projection is acquired for each set of parameters with the order of the adiabatic pulses reversed (dashed lines), and the phase difference between the two acquisitions is used to map to B₁, thereby removing any unwanted external phase sources that are present in both acquisitions. b. The phase sensitivity as a function of B₁ is plotted for different values of δ optimized for 3T, with δ=0.80,0.94,1 bolded.

Figure 1b shows the phase sensitivity to B₁, which can be varied by varying the magnitude ratio between the HSn pulses, δ. In this study, we denote changes in phase sensitivity by specifying the parameter δ, however, in practice n₂ also slightly varies because the sequence is re-optimized for each δ to better minimize any residual phase error [20]. The phase relationship to B₁ is approximately linear above the adiabatic threshold of the sequence. We refer to the slope of a first-degree polynomial fit of the phase relationship to B₁ simply as the sensitivity, α. Table 1 summarizes δ, n₂, and α for this study.

Table 1.

HSn n₂ values for n₁ = 4 for varying δ and main-field strengths. The linear approximation of the sensitivity, α, is also given for each δ. For 1.5T, B_1,nom = 0.086 G and the measured B₁ was expected to vary ±20%. For 3T, B_1;nom = 0.12 G and the measured B₁ was expected to vary ±40%.

δ		0.80	0.82	0.84	0.86	0.88	0.90	0.92	0.94	0.96	0.98	1
1.5T	n2	4.226	4.203	4.178	4.155	4.133	4.111	4.088	4.065	4.044	4.022	4
	α (rad/G)	90.4	81.6	72.6	63.7	54.7	45.7	36.6	27.5	18.4	9.20	0
3T	n2	4.335	4.300	4.265	4.230	4.195	4.155	4.129	4.095	4.055	4.031	4
	α (rad/G)	98.6	88.9	79.1	69.2	59.4	49.3	39.7	29.7	19.6	9.92	0

B₁ distribution plots

Figure 2a shows a comparison of a typical 2D B₁ map to an example B₁ distribution plot. A distribution plot essentially shows the distribution of B₁ values seen in a volume or slice, as shown in Figure 2a. When compared to a spatial B₁ map of the same imaging region, distribution plots consist of histograms of the B₁ values seen along one axis/several axes of choice. For example, in Figure 2a, the B₁ values seen over each horizontal line in the 2D B₁ map are represented by a B₁ histogram in the B₁ distribution plot, and are displayed as a horizontal line at the same original vertical location as in the 2D map. Thus, in Figure 2a, the B₁ distributions represent the B₁ values seen along the x-axis of the 2D map.

Fig. 2.

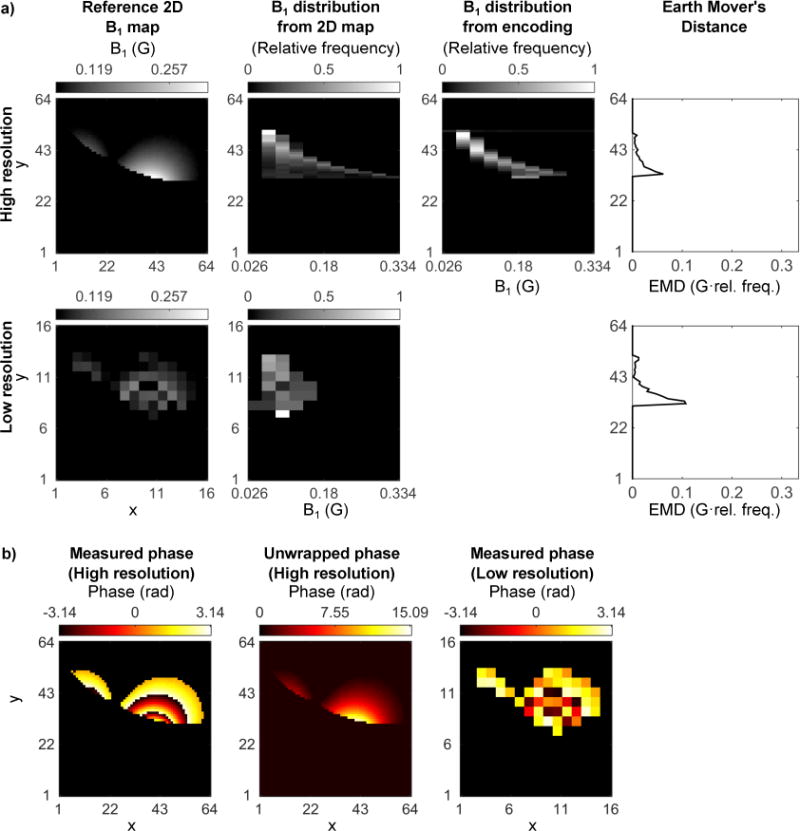
a. The relationship between a typical 2D B₁ map and a B₁ distribution plot is shown. Given the sequence in Figure 1a, let y represent the readout direction, which is resolved spatially for both image encoding and B₁ encoding. Each y location in the 2D B₁ map gives a 1D B₁ map, which can then be represented as a 1D B₁ distribution. The B₁ distribution plot displays the B₁ distribution for each y location as in the original 2D map. b. Acquisition and reconstruction strategy for the B₁ distribution plots. i. Shows an existing spatial B₁ variation in an object, and ii. shows three examples (δ=0.80,0.94,1) of the phase from the two acquired projections of Figure 1 (dashed gray and solid black lines). iii. Taking the inverse Fourier transform and phase difference converts each projection from k-space to image-space, which is used in Equation 4 to estimate iv., the B₁ distribution in the imaging region.

Figure 2b illustrates the theory for acquiring an MR signal with phase-encoding as a function of B₁ rather than spatial position. Given unknown B₁ values in a slice (represented by the 2D map of Figure 2b.i), we acquire multiple projection measurements, each along the same direction but using a different phase sensitivity. In the example illustrated in Figure 2b, the projection direction is always along the x-axis, whereas y is in the readout direction of the sequence. Two projections are acquired for each phase sensitivity, the second with the order of the HSn pulses reversed, so that unwanted phase sources can be removed by taking the phase difference between the two acquisitions. Figure 2b.ii shows example phases of acquired k-space MR signals for δ = [0.8, 0.94, 1]. 1D inverse Fourier transforms along k_y, and phase differences are calculated for each δ, which result in the final acquired projections that exhibit B₁ phase-encoding (Figure 2b.iii). These are used to calculate the B₁ distribution plot (Figure 2b.iv). The B₁ distribution plots displayed in this study are normalized so that each histogram sums to one for each y location.

An estimate of the B₁ distribution is calculated using the acquired projections and the known phase sensitivity to B₁ for each projection. A B₁ distribution for the slice seen at one y position can be binned into a histogram with K bins, with each bin representing a particular B₁ range, B_1,k. The fraction of spins in the slice with B₁ ∈ B_1,k is c_k. Given J total projection measurements, each with a known phase sensitivity to B₁, ϕ_j(B₁), then the j^th acquired projection is:

$${\mathrm{p}}_{\mathrm{j}}={\displaystyle \sum _{k=1}^K{\mathrm{c}}_{\mathrm{k}}{\mathrm{e}}^{i{\varphi }_{j,k}}}$$ (1)

where ϕ_j,k=ϕ_j(B_1,k). This can be simplified into matrix form as:

$$\left[\begin{array}{c}{\mathrm{p}}_1\\ {\mathrm{p}}_2\\ ⋮\\ {\mathrm{p}}_J\end{array}\right]=\left[\begin{array}{cccc}{\mathrm{e}}^{i{\varphi }_{1,1}}& {\mathrm{e}}^{i{\varphi }_{1,2}}& \cdots & {\mathrm{e}}^{i{\varphi }_{1,K}}\\ {\mathrm{e}}^{i{\varphi }_{2,1}}& {\mathrm{e}}^{i{\varphi }_{2,2}}& \cdots & {\mathrm{e}}^{i{\varphi }_{2,K}}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathrm{e}}^{i{\varphi }_{J,1}}& {\mathrm{e}}^{i{\varphi }_{J,2}}& \cdots & {\mathrm{e}}^{i{\varphi }_{J,K}}\end{array}\right]\left[\begin{array}{c}{\mathrm{c}}_1\\ {\mathrm{c}}_2\\ ⋮\\ {\mathrm{c}}_K\end{array}\right]$$ (2)

or equivalently:

$$\mathbf{p}=\mathbf{\Phi }\mathbf{c}$$ (3)

where p and c are vectors that contain the measured projections and unknown B₁ distribution fractions, respectively, and Φ is a phase matrix calculated from the known phase sensitivities and chosen B₁ histogram bin centers.

While the phase-based BEAR method is independent of T₁ and T₂, the actual B₁ distribution frequencies are based on signal magnitude, and will therefore be affected by T₁, T₂ and the excitation B₁. Note that the maxima and minima B₁ values can still be measured independently of these factors. The B₁ dependence on the magnetization can be approximated in Equation 2 by adding a magnitude term into Φ that represents the effective tip angle at the B₁ bin centers, however, in practice we have found this addition to provide no appreciable improvement on the results of this study. It may be possible to model T₁ and T₂ effects if there is prior knowledge of these parameters for the imaging region. For this study, we assume a homogenous sample that does not have magnitude weighting from T₁ and T₂, and use the basic representation shown in Equation 3.

The form of Φ in Equation 2 is similar to a typical discrete Fourier transform matrix, often used for spatial imaging in MRI. However, here c relates to the ratio of spins with respect to B₁ bins, rather than to spatial position.

With the measured projections, p, and known phase sensitivities, Φ, Equation 3 has only one unknown: the B₁ distribution vector c. A simple inversion of Φ can be used to solve for c: c=Φ⁻¹p, however, in practice the performance of this method is improved by introducing constraints in the form of a convex optimization problem. c can be found by minimizing the difference between p and $\mathbf{\Phi }\mathbf{c}:\underset{\mathbf{c}}{min}f(\mathbf{p}-\mathbf{\Phi }\mathbf{c})$, where f() is a chosen cost function. To improve the performance of the optimization, we create a scalarized multi-objective problem by introducing smoothing via finite second derivative matrices λ₁D₁ and λ₂D₂, which smooth along the B₁ and readout dimensions respectively, as is expected of typical B₁ distributions. For a more robust performance against noise, we also add constraints limiting the size of c and ensuring that c is nonnegative real. The final problem is formulated as:

$$\begin{array}{c}\underset{\mathbf{c}}{\text{minimize}}{\displaystyle \sum \mathrm{h}(\mathbf{p}-\mathbf{\Phi }\mathbf{c})}+{\lambda }_1{\displaystyle \sum \mathrm{h}({\mathbf{D}}_1\mathbf{c})}+{\lambda }_2{\displaystyle \sum \mathrm{h}({\mathbf{D}}_2\mathbf{c})}+{\lambda }_3{\mathbf{1}}^T\mathbf{c}\\ \text{subject to}\mathbf{c}\ge 0\end{array}$$ (4)

where h() is the Huber loss function with h(x)=x² for x≤1 and h(x)=2|x|−1 for x≥1, and is used to reduce sensitivity to outliers, and 1 is a vector of ones.

Methods

Parameter selection

The HSn parameters were chosen as in reference [20], with 773 Hz pulse bandwidth. For imaging, K = 11 B₁ bins and J = 11 sensitivities, uniformly distributed in the range of δ = [0.8, 1], were used. The δ range of the HSn pulses was chosen to maximize the range of phase sensitivities, while remaining insensitive to the adiabatic threshold of the sequence, ~0.051/δ G. The expected B₁ range over which n₂ was optimized was (1±0.2)0.086 G for 1.5T and (1±0.4)0.12 G for 3T. The chosen δs and resulting n₂s and αs are shown in Table 1.

The range of sensitivities used is analogous to the amount of k_y excursion in traditional Fourier imaging, while the number of B₁ bins is analogous to the number of phase encodes. Following this analogy and examining Equation 2, the field of view in B₁ is approximately 2π/Δα_max, where Δα_max is the maximum sensitivity difference between successive δ values, and the resolution in B₁ is approximately 2π/(α_max−α_min), where α_max and α_min are the maximum and minimum phase sensitivities. For the parameters chosen here, this results in a B₁ resolution of 0.069/0.064 G and field of view of 0.68/0.63 G for 1.5/3T respectively. Increasing the number of B₁ bins may improve the resolution of the measurements, at the cost of increased scan time. In practice, using the optimization formulation of Equation 4, we can improve on the expected B₁ resolution. We use a B₁ range of 0.136 G and 11 bins, giving a B₁ resolution of 0.012 G, which we have found to produce good results despite pushing the method beyond the theoretical expectations with the Fourier imaging comparison.

Projection acquisition

In vivo scans used a 3T General Electric (GE) Discovery MR750 scanner with a transmit body coil and receive head coil. B₁ distribution plots were acquired with 11 B₁ bins and a readout size of 128. Additionally, 128×128 2D B₁ maps were acquired for reference with a field of view of 24 cm. All scans used a single-slice acquisition protocol with a 40° excitation tip angle, 44 ms echo time, and TR = 500 ms. The distribution scans acquired 22 measurements, two for each δ, giving a total theoretical scan time of 11 s, while the 2D maps had a total scan time of about 2 min. The implementation of the method was such that δ was manually changed for each scan, resulting in a slight pause between successive scans and an effective scan time longer than 11 s for the distribution plots. For all scans, the adiabatic pulses were non-selective and a single signal acquisition was used.

Phantom scans used a 1.5T GE Signa Excite scanner with a transmit/receive surface coil. Imaging used a slice oblique to the orientation of the surface coil to test the performance of the method for a B₁ field that has increased spatial variations. A wire was placed along the surface of the phantom to simulate increased B₁ variations in the presence of a guidewire. The B₁ distribution plots used 11 B₁ bins and a readout size of 64. 2D B₁ maps were acquired at two different matrix sizes: 64×64 and 16×16, with a field of view of 8 cm. TR = 200 ms and the total theoretical scan time was 4.4 seconds for the distribution plots, and less than a minute for the 2D maps. All remaining scanning parameters were the same as for the in vivo scans at 3T.

B₁ distribution reconstruction

The projection for δ = 1 did not have B₁ encoding and was used to create a mask in y by excluding pixels with signal less than 3% of the maximum. Φ was calculated using B₁ bin centers uniformly spaced between [0.017, 0.153] G, with ϕ_j,k=ϕ_j(B_1,k). Although the phase relationship to B₁ can be approximated by α, in practice, we used Bloch simulations to determine ϕ_j(B_1,k). For the optimization, each regularization parameter λ was successively selected by searching over a parameter space, and the optimal value was chosen located near the L-curve corner when plotting the λ regularization against the Huber penalty result. The proposed method was solved using the CVX package [22, 23].

To evaluate the accuracy of the measured B₁ distributions, we created B₁ histograms from the 2D B₁ maps over the same projection direction. To compare distributions calculated from 2D maps and those created using the proposed method, the Earth Mover’s Distance (EMD) [24] metric was calculated for each y location, which estimates the work needed to transform one distribution into the other. A smaller EMD value indicates greater similarity between distributions.

Results

For each set of data in Figures 3 and 4, the columns show, from left to right: acquired 2D B₁ maps for reference, B₁ distribution plots calculated from the 2D maps, B₁ distribution plots using the method proposed here, and the EMD calculated between the two distributions for each y location.

Fig. 3.

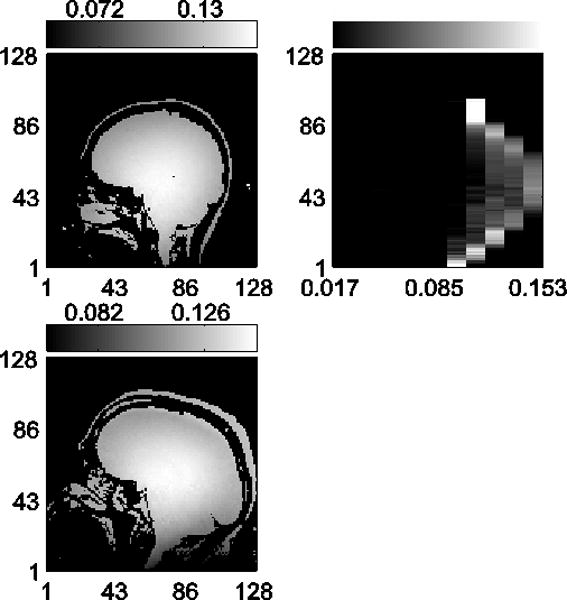
In vivo data results for B₁ distribution measurements at 3T. Shown are two representative datasets with (left to right): 2D B₁ maps acquired for reference, B₁ distributions calculated from the reference 2D maps, B₁ distributions using the encoding method proposed here, and EMD calculated between the two distributions. The mean EMD are 0.0022 G*(Relative frequency) and 0.0034 G*(Relative frequency) for top and bottom, respectively.

Fig. 4.

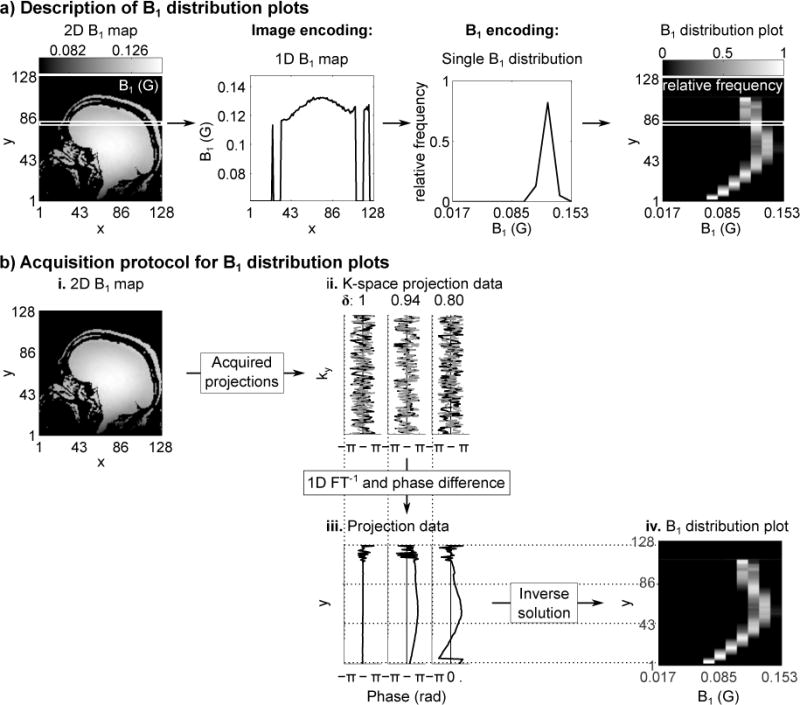
Phantom B₁ distribution results using a transmit and receive surface coil at 1.5T. Imaging used a wire along the surface of the phantom, placed perpendicular to the imaging plane and between the phantom and surface coil, to simulate increased B₁ variations in the presence of a guidewire. a. Shown are the 2D B₁ maps acquired at two different resolutions at an oblique slice to the surface coil to show large B₁ variation, as well as the B₁ distributions calculated from the 2D maps. The distribution using the encoding method proposed here is also shown, which uses fewer measurements than the lower resolution image, but has a mean EMD of 0.0136 G*(Relative frequency) whereas the average EMD for the low-resolution case, calculated by piecewise constant interpolation of the low-resolution image, is 0.0202 G*(Relative frequency).

b. Phase images of the acquired 2D maps are shown for both high- and low-resolution images. Due to the large B₁ range present in the imaging slice, phase wrapping occurs. This phase can be easily unwrapped for the high-resolution image, but not for the low-resolution image, causing increased errors in the B₁ approximation for the low-resolution image.

In vivo results at 3T are shown in Figure 3. The B₁ distributions using the proposed method closely match the distributions from the 2D maps, and exhibit low average EMD values of [0.0022, 0.0034] G*(Relative frequency) over a 0.136 G B₁ range and with 0.012 G B₁ bins.

The phantom results obtained at 1.5T were examined to assess the performance of the proposed method when there are increased spatial B₁ variations and are shown in Figure 4a. A B₁ distribution is calculated from the 64×64 resolution 2D B₁ map. The B₁ distribution using the 16×16 2D B₁ map varies from the 64×64 resolution distribution, due to intra-voxel averaging of the phase. Additionally, because of the high B₁ range, phase unwrapping must be employed, as can be seen in Figure 4b. For the low-resolution image, without prior knowledge of the B₁ range, phase unwrapping is not easily achieved due to increased intra-voxel averaging. This results in increased inaccuracies in the resulting low-resolution B₁ map. To compare the high- and low-resolution distributions, the EMD is calculated by piecewise constant interpolation of the low-resolution image, and is 0.0202 G*(Relative frequency). Alternatively, the B₁ distribution plot that uses the proposed method more closely matches the B₁ distribution of the 64×64 2D map with EMD = 0.0136 G*(Relative frequency), even though it uses fewer measurements than the 16×16 2D map (11 measurements for the measured distribution, 16 measurements for the 2D map). This indicates that the proposed method provides a good approximation of the B₁ distribution for the slice using a small number of measurements.

Discussion

We have demonstrated a new method that estimates the B₁ distribution in a slice without acquiring 2D image data. By encoding the MR signal as a function of B₁, we were able to acquire B₁ distribution measurements that correlated well with distributions calculated from 2D B₁ maps. Most of the errors are concentrated along the B₁ distribution, suggesting the errors are most likely due to misplaced counts in consecutive bins, with only small errors in the underlying B₁.

The convex optimization formulation was shown to be accurate for both the in vivo and phantom measurements in this study, but additional constraints may improve the performance of the method. The optimization formulation is a general approach, allowing for more B₁ bins than number of encodings, and also for nonuniform binning.

The B₁ distribution measurements represent relative B₁ frequency based on signal magnitude, rather than volume. While the phase-based BEAR method is independent of T₁ and T₂, the actual distribution frequencies will be affected by the signal magnitude, and therefore by anything that affects the signal magnitude, e.g., T₁, T₂, the excitation B₁, proton density and the receive coil sensitivity. Nevertheless, the method can measure the extrema of the B₁ distribution. Furthermore, the signal magnitude dependence on flip angle, due to variations in the excitation B₁, can be approximated in Equation 2 by adding a magnitude term into Φ that represents the effective tip angle at the B₁ bin centers. It may be possible to minimize T₁ and T₂ effects on the signal magnitude by imaging with a longer TR and minimized TE, respectively; however, the effects of proton density and receive coil sensitivity on the signal magnitude cannot be removed. We have demonstrated in this study that the B₁ distribution itself can be accurately measured even using the basic optimization formulation presented here.

The proposed method will in general require fewer measurements than acquiring a full spatial B₁ map. For example, the B₁ distributions measured in this study required 11 B₁ encoding measurements, versus 128 phase encodes for the 2D map. Note, however, that the time needed for spatial B₁ mapping may be decreased by using efficient acquisition strategies, such as echo-planar imaging. This is not the case for the proposed method, because the nature of the B₁ encoding requires an individual excitation for each acquired projection with a different phase sensitivity.

With 11 B₁ encodings we found the method measured B₁ distributions accurately for in vivo measurements at 3T compared to distributions calculated from 2D B₁ maps. We interpolated δ linearly in the range of [0.8, 1], however any number of encodings, δ range, and nonlinear interpolation can be used. Ideally, the δ range would be chosen to approximate the same phase encoding in Equation 2 as a typical discrete Fourier transform. For example, the phase of a discrete Fourier transform is 2πnk/N, where n and k vary from [0, N-1] and represent the indices over the signal’s spatial and frequency components. The maximum phase is therefore 2π(N−1)²/N, corresponding to 57.1 rad for N = 11. Using the HSn pulses described here, there is a maximum phase change of 12.3 rad for ±20% variation in B₁ at 1.5T, and 13.4 rad for ±40% variation in B₁ at 3T. Even though this is less than the theoretical amount of phase variation that would be needed for the discrete Fourier transform to reach the same resolution, by including regularization in the optimization problem we have found the method to perform well. Future implementations could increase the phase sensitivity by increasing n or decreasing δ.

The proposed method was able to measure increased spatial B₁ variations in a phantom at 1.5T with the presence of a wire. The B₁ distributions using the proposed method had better approximations of the B₁ distribution from 2D maps when compared to a low-resolution spatial map of the same slice. This is due to intra-voxel phase averaging for the low-resolution image. This results in increased B₁ errors because a larger voxel encompasses a larger B₁ range and will therefore have more dephasing, and also because phase unwrapping was difficult to employ for the low-resolution phase image. Phase wrapping occurs due to the very large B₁ range seen in the slice, even though a relatively low sensitivity (δ = 0.9) was used to acquire the images. To reduce phase wrapping, a lower sensitivity may be used, but would come at the cost of decreased B₁-to-noise ratio.

For very low B₁ values below the sequence adiabatic threshold, the phase dependence on B₁ will be nonlinear and the measurements will be expected to have increased noise due to low phase sensitivity. It is possible to decrease the adiabatic threshold by using higher n or δ, at the cost of potentially increased errors within the bandwidth of the pulses, or lower phase sensitivity to B₁. An analysis of the effect of decreased B₁ values below the adiabatic threshold conducted in the original BEAR paper [15] illustrated that the largest effect on the acquired signal comes from the decrease in the magnitude of the signal below the adiabatic threshold. For the HSn pulses used in this study, a decrease of 50% in the expected refocused magnitude occurs for B₁ ~ 56% of the adiabatic threshold. Finally, we assume that the MR system will be able to generate signal at B₁ values in the ranges above the adiabatic thresholds described here. If a system is unable to generate such peak RF values, this method will suffer. Note however, that when assuming linearity of the RF system, as is typically done for B₁ mapping, measuring B₁ in a range that is higher than will be used for subsequent scans is still useful for calibration of the transmit system.

The BEAR method’s reliable formation of a twice-refocused spin-echo signal makes it especially useful for this application, since it will not experience unwanted phase cancellation over the projected volume due to off-resonance effects, and it allows for robust refocusing independent of B₁ variations. Other phase-based B₁ mapping methods that allow for a spin-echo acquisition could also be used in a similar manner to acquire B₁ distribution measurements. Magnitude-based methods may also be used, although care must be taken to mitigate relaxation effects.

Compared to 2D B₁ mapping methods, the proposed B₁ distribution method may be useful to acquire faster estimates of the B₁ distribution in a volume, or to estimate a distribution where B₁ is varying rapidly spatially, such as near a conducting guidewire. In this study we acquired B₁ distributions over a slice, however, it is possible to apply this method over a 3D volume to get B₁ distributions for the entire volume, which may be useful for the transmit gain calibration of the scanner. This method may be particularly useful for acquiring a quick preliminary scan to determine the RF scaling and B₁ range required for any subsequent spatial mapping methods; for example, in setting the RF amplitude of any subsequent adiabatic pulses.

Conclusion

We demonstrated a new method for acquiring B₁ distributions in a slice without acquiring full spatial image data, by encoding the signal in B₁. We validated the performance of the method in vivo, and in a phantom study with increased spatial variations in B₁. The optimization formulation used in this study was a basic formulation that was shown to produce accurate distribution estimates, however, improvements in the problem formulation, especially with respect to T₁, T₂, and B₁ dependence, may lead to improved performance. This method could be useful for acquiring fast estimates of the B₁ distribution in a volume, particularly where there is a high dynamic B₁ range within the imaging region. This distribution information could also be useful for the transmit gain calibration of the scanner.