Spatial Moran models, II: cancer initiation in spatially structured tissue

Abstract

We study the accumulation and spread of advantageous mutations in a spatial stochastic model of cancer initiation on a lattice. The parameters of this general model can be tuned to study a variety of cancer types and genetic progression pathways. This investigation contributes to an understanding of how the selective advantage of cancer cells together with the rates of mutations driving cancer, impact the process and timing of carcinogenesis. These results can be used to give insights into tumor heterogeneity and the “cancer field effect,” the observation that a malignancy is often surrounded by cells that have undergone premalignant transformation.

1 Introduction

Cancer initiation is often driven by the accumulation of a series of oncogenic mutations in a healthy tissue. These mutations can confer fitness advantages (e.g., by boosting cellular reproduction rates or leading to avoidance of apoptosis signals) and thus enable the spatial expansion of premalignant clones within the tissue. There has been a substantial amount of previous effort devoted to the study of temporal dynamics of mutation accumulation in the setting of homogeneously mixed (non-spatially structured) populations. Much work in this area uses multi-type Moran models to model the turnover of cells in a fixed-size compartment (see, e.g., the books by Nowak (2006), Wodarz and Komarova (2014) and references therein). We refer the reader to Part I of this work by Durrett and Moseley (2014) for a discussion of multi-type Moran models.

Most human tumors arise from epithelial tissue, see Chapter 2 in Weinberg (2013). Epithelial tissue covers the exterior and interior surfaces of the body and is made up of closely packed cells arranged in one or more structured layers. To model the process of carcinogenesis within epithelial tissue, we consider a stochastic spatial model on a two or three dimensional lattice. In population genetics the stepping stone model of Kimura and Weiss (1964) has been used to understand the impact of that type of spatial structure on genetic diversity, see e.g., Chapter 5 of Durrett (2008). In the current work, we will use a related model to obtain a quantitative understanding of the effects of spatial population structure on the dynamics of mutation accumulation and clonal expansion processes that lead to cancer initiation.

Williams and Bjerknes (1972) introduced a model of tumor growth on the d-dimensional lattice. There are two cell types: 0 (healthy) and 1 (tumor), with fitnesses 1 and λ > 1. Each site in the lattice is inhabited by a single cell. Each cell gives birth at a rate equal to its fitness to an offspring that replaces the cell at one of its 2d nearest neighbors chosen at random. Bramson and Griffeath (1980b, 1981) proved the first rigorous results about the asymptotic behavior of this model, which they called the biased voter model (BVM). In particular they proved a “shape theorem” for the asymptotic behavior of the process which is stated in (2) and will be an important part of our analysis.

Here, we will study the spatial Moran model, which generalizes the biased voter model by having more types and incorporating mutation. On the d-dimensional lattice the state of the process at time t is η_t : ℤ^d → {0, 1, 2, …} with η_t (x) = i indicating that position x is occupied by a cell with i mutations, which we will refer to as a ‘type i’ cell. Type 0 cells are considered to be healthy cells, while type i cells have fitness (1 + s)ⁱ. Thus fitness effects are “additive”, i.e., there are no epistatic interactions between mutations. Each cell reproduces at rate equal to its fitness and then replaces one of its 2d nearest neighbors cells at random with its progeny, which inherits the parental fitness. Type i cells also mutate to type i + 1 cells at rate u_i+1. Throughout the rest of the manuscript we will assume that u_i = 0 for i ≥ 2, i.e., there are only type 0, 1, or 2 cells present.

To investigate cancer initiation, we will consider the spatial Moran model on the lattice with periodic boundary conditions (ℤ mod L)^d and N = L^d sites. Komarova (2007) studied the one-dimensional version of this model and investigated τ₂ the time of the first mutation to type 2. She concentrated on the case in which mutations were almost neutral (or deletrious) and showed that adaptation in the spatial model was much slower than in the homogeneously mixing case. For more, see Komarova (2013). In Part I of this paper, Durrett and Moseley (2014) generalized her work to study the waiting time τ₂ in dimensions two and three for (almost) neutral mutations. They found that the slow down due to spatial structure was much less drastic than in the one-dimensional case.

In the present paper, we will focus on the case in which new mutations are not neutral but instead have a selective advantage s > 0 over the previous ones. Martens and Hallatschek (2011) have used simulation and heuristic arguments to study a discrete time version of the spatial Moran model in one dimension and on a hexagonal lattice in two dimensions when the fitness advantage s was small. The authors studied the dynamics of mutation accumulation, and found that the speed of adaptation of the population saturates once the domain size exceeds a characteristic length, given in (11) below. In a follow-up work by Martens et al. (2011), this model was utilized to study the process of carcinogenesis in crypt-structured tissue (e.g., in the colon). Simulations of this model showed that in the presence of clonal interference, spatial structure increases the waiting time for cancer initiation.

In Sect. 2 we discuss the behavior of the biased voter model starting from a single type 1. We state the Bramson-Griffeath shape theorem, and give a new result that describes the asymptotic behavior of the propagation speed as s → 0. In Sect. 3 we show that, under some assumptions that are far from optimal, the waiting time σ₁ for the first the “successful” type 1 mutation is asymptotically exponential with mean 1/Nu₁s. Intuitively a successful mutation is one that starts a family that does not die, but on a finite set it must be instead defined as one that lasts for a long time. Details of the definition are given in Sect. 3.

In Sect. 4, we introduce a simplified continuum spatial stochastic model that approximates the macroscopic growth of successful clones with a deterministic description inspired by the Bramson-Griffeath shape theorem. Under this simplified model, we can then analytically investigate the asymptotic behavior of σ₂, the time of the first successful type 2 mutation, which we regard as the timing of cancer initiation. In Sect. 5 we study the time until type 1’s take over the system, i.e., rise to frequency > 1 − ε where ε is small. In Sect. 6 we state our main results, regarding the asymptotic behavior of σ₂. Technical details of the proofs are presented in the appendices.

Throughout the paper we will use the following notation for the asymptotic behavior of positive functions.

f (t) ~ g(t)	if f (t) / g(t) → 1 as t → ∞
f (t) = o(g(t)) or ≪ g(t)	if f (t) / g(t) → 0 as t → ∞
f (t) ≫ g(t)	if f (t) / g(t) → ∞ as t → ∞
f (t) = O(g(t))	if f (t) ≤ Cg(t) for all t
f (t) = Θ(g(t))	if cg(t) ≤ | f (t)| ≤ Cg(t) for all t

To extend the last notion to random variables, we say that X_n = Θ(a_n) if X_n/a_n is tight and no subsequence X_n(k)/a_n(k) converges to 0.

Throughout the paper we are interested in the asymptotic regime of s → 0. Unless otherwise specified all asymptotic notation will refer to the limit s → 0. In addition we will assume that N, u₁, u₂ are positive functions of s so that as s → 0, N(s) → ∞ and u_i (s) → 0 for i = 1, 2. The limit results will depend on the relationship between these parameters. For ease of notation we will suppress the s dependence in these parameters for the remainder of the paper.

2 Growth starting from a single type 1 mutant

Suppose now that each site in ℤ^d is occupied either a type 0 cell or a type 1 cell. These cells divide at rates 1 and λ = 1 + s respectively. The cell division rules are the same as those described above for the spatial Moran model η_t, however there is no longer the possibility of mutation. Denote the lattice sites occupied by type 1 cells at time t by ξ_t. This process is also known as the biased voter model (BVM).

Note that on each boundary edge connecting a 1 with a 0, there is a competition with the interactions along this edge, with the 0 changing to 1 at rate λ = 1 + s and the 1 changing to 0 at rate 1. From this observation it follows that while ξ_t ≠ ∅, the size of the set, |ξ_t|, is a time change of an asymmetric simple random walk which makes jumps at rate equal to 1 + λ times the number of boundary edges: |∂ξ_t| = |{x ∈ ξ_t, y ∉ ξ_t : |x − y| = 1}|, and when it jumps it goes up with probability p = λ/(λ + 1) and down with probability 1 − p. Thus |ξ_t| is a sum of i.i.d. ±1 valued random variables, i.e., a time-change of a random walk.

Elementary results about discrete time asymmetric simple random walk imply that if we let T_k = inf{t : |ξ_t| = k} and use a subscript of 1 to indicate starting from one type 1 individual

$$P_1(T_0=\infty )=1-\frac{1-p}{p}=1-\frac{1}{\lambda }=\frac{\lambda -1}{\lambda }=\frac{s}{1+s}.$$

Maruyama (1970, 1974) as well as Lieberman et al. (2005) have shown that the fixation probability is not changed by considering a spatial model. Our limit theorems will be proved under the assumption that s → 0 so we will use the approximation

$$P_1(T_0=\infty )~s.$$ (1)

Let ${\xi }_t^0$ be the set of sites occupied by individuals of type 1 at time t when initially there is a single 1 at the origin at time 0. Bramson and Griffeath (1980b, 1981) showed that when ${\xi }_t^0$ does not die out, it grows linearly and has an asymptotic shape D. That is, for any ε > 0, there is a t_ε (which depends on the outcome ω) so that on {T₀ = ∞} we have

$$(1-\epsilon )tD\cap {\mathbb{Z}}^d\subset {\xi }_t\subset (1+\epsilon )tD\text{ for }t\ge t_{\epsilon }(\omega ).$$ (2)

D is convex and has the same symmetries as those of ℤ^d that leave the origin fixed, e.g., rotation by 90 degrees around an axis, or reflection through a hyperplane through the origin perpendicular to an axis.

Let e₁ be the first unit vector and define the growth rate c_d(s) so that the intersection of D with the x axis is [−c_d(s)e₁, c_d (s)e₁]. It is easy to compute c₁(s). If ξ_t ≠ ∅ then ξ_t = [l_t, r_t]. The right edge r_t increases by 1 at rate λ and decreases by 1 at rate 1, so r_t/t → λ − 1 = s, i.e., c₁ (s) = s. The proof of Bramson and Griffeath implies that c_d (s) ≥ b_ds where b_d is a positive constant. By using techniques of Durrett and Zähle (2007), we can prove:.

Theorem 1

As s → 0 we have

$$c_d(s)~\{\begin{array}{cc}s\hfill & d=1\hfill \\ \sqrt{(\pi /4)s/\text{log}(1/s)}\hfill & d=2\hfill \\ \sqrt{{\beta }_{d}s}/d\hfill & d\ge 3,\hfill \end{array}$$

where β_d is the probability that two d dimensional simple random walks started at 0 and e₁ = (1, 0, … 0) never hit.

The proof of this result is found in Appendix G. Even though this is an asymptotic result, it is reasonably accurate for the values relevant to this study. Foo et al. (2014) computed the speed by simulation. See Figure 3 in their paper. The smallest value they considered was s = 0.025 for which they found the speed to be 0.0715 ± 0.0043 (95 % confidence interval). Using our formula gives 0.0729.

Fig. 3.

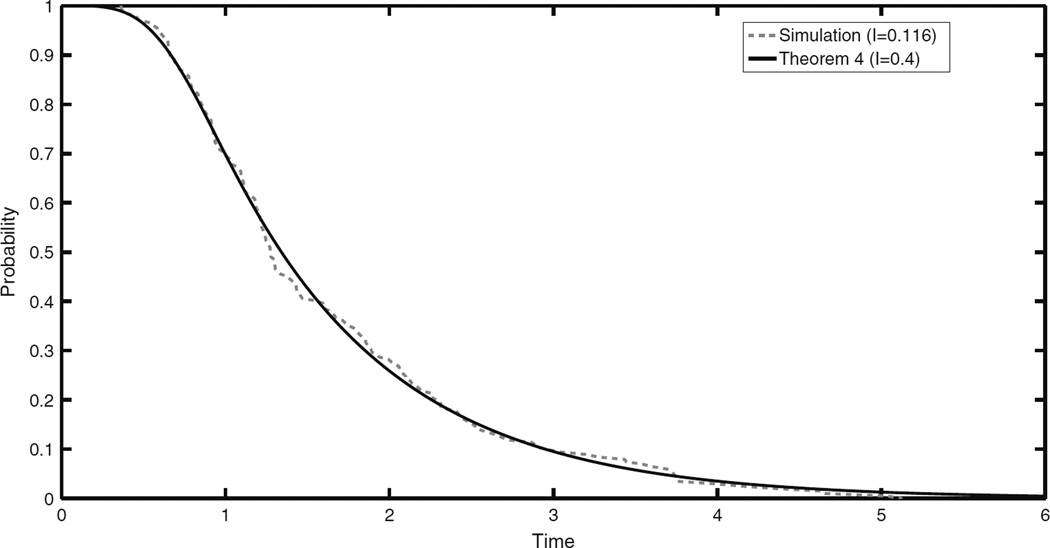
Comparison of empirical complementary CDF of Nu₁sσ₂ based on 200 replications and prediction of Theorem 4, when N = 10^5.5, u₁ = 8 × 10⁻⁸, u₂ = 8 × 10⁻⁶, and s = 0.01

The proof of the Bramson-Griffeath result and of Theorem 1 are based on duality between the biased voter model and a system of branching coalescing random walks (BCRW) ζ_t explained in Appendix A. Particles in ζ_t jump to each nearest neighbor at rate 1, give birth onto each nearest neighbor at rate s. When two particles occupy the same site they immediately coalesce into one particle. If we let ${\zeta }_t^B$ denote the BCRW starting from particles on B then the duality relation states that

$$P({\xi }_t^A\cap B\ne \varnothing )=P({\zeta }_t^B\cap A\ne \varnothing ).$$

In the special case B = {x} this says that the probability $x\in {\xi }_t^A$ is equal to the probability ${\zeta }_t^x\cap A\ne \varnothing$. Therefore, we are able to study the speed of the spread of the biased voter model by looking at the speed of the spread of the BCRW. An upper bound on the speed of the BCRW is obtained by ignoring coalescence events and using standard results to study the speed of the branching random walk. The lower bound on the speed is more difficult and requires the use of a block construction argument, a type of renormalization argument that the reader can find described in Durrett’s (1995) St. Flour Notes.

3 Time to the first successful type 1 mutant

Consider the biased voter model on ℤ^d starting from a single 1 at the origin. We say that the type 1 family it starts is successful if it never dies out and unsuccessful otherwise. On the finite set (ℤ mod L)^d it is not clear how one appropriately defines a successful family. Let

$$\ell (s)=\{\begin{array}{cc}{s}^{-2}\hfill & d=1,\hfill \\ s^{-1}\text{ log}(1/s)\hfill & d=2,\hfill \\ s^{-1}\hfill & d\ge 3.\hfill \end{array}$$ (3)

Our notion of successful is based on the following Lemma whose proof is provided in Appendix B.

Lemma 1

For δ > 0 there exists M such that the probability an unsuccessful type 1 family on ℤ^d will last for time ≥ Mℓ(s) or will escape from a cube of radius Mℓ(s)^1/2 is ≤ δs.

Now consider the biased voter model η_t on the torus, and note that there will be a Poisson process of type 1 mutations that occur at the space-time points Λ = {(x_i, t_i)}_i≥1. We wish to develop a test that tells us with reasonable certainty (to be made precise shortly) whether one of these mutations would be successful were it to live on ℤ^d. The result in Lemma 1 essentially states that on ℤ^d, unsuccessful mutant families do not escape the specified space-time box with high probability. We therefore use this as a criterion for defining unsuccessful mutant families on the finite set (ℤ mod L)^d.

Let M_s be a positive function with M_s → ∞ as s → 0 and M_sℓ(s)^1/2 < L. Denote the sites occupied by the descendants of the jth mutation t time units after t_j by ${\xi }_t^{(j)}$, the extinction time of the clone by T (j), the interval of time that the clone exists by I_j = [t_j, t_j + T(j)] and say this family is successful if $\{{\xi }_t^{(j)};t\in I_j\}\times I_j$ is not contained in

$${[x_j-M_s\ell {(s)}^{1/2},x_j+M_s\ell {(s)}^{1/2}]}^d\times [t_j,t_j+M_s\ell (s)],$$ (4)

i.e., the descendants of the mutant escape from a large space-time box centered at the space-time point of the initial mutant. The subset of Λ for which the mutations have this property is denoted by 𝒮 for successful. It is immediate from Lemma 1 that

$$P((x_j,t_j)\in 𝒮|T(j)<\infty )=o(s).$$ (5)

Thus if s is small, the arrival time of the first successful type 1 will with high probability be σ₁ = inf{t_j, j ≥ 1; (t_j, x_j) ∈ 𝒮}.

Since mutations to type 1 occur at rate Nu₁ and are successful with a probability that ~ s, it is natural to guess that as s → 0,

$${\sigma }_1·(N{u}_{1}s)\Rightarrow W\text{ where }W\text{ is a rate }1\text{ exponential random variable}.$$

To prove this result, we have to show that we can ignore interference between the growth of different mutations, and hence they are almost independent. To do that, we need the following two assumptions as s → 0:

• –(A0) u₁ℓ(s)^(d+2)/2 → 0
• –(A0’) N/(ℓ(s))^d/2 → ∞.

The second one is natural since it says that the boxes we use in our definition of success are much smaller than the torus. The first one, which says that the average number of mutations per box tends to 0, is probably not needed for the result to hold. It is a very conservative way of guaranteeing that the fates of different mutations are independent. However, we do not know how to prove the result without it.

Theorem 2

Under assumptions (A0) and (A0′),

$$P({\sigma }_1>t/(N{u}_{1}s))\to e^{-t}\mathit{\text{ as }}s\to 0.$$

The assumptions (A0) and (A0′) will be in force throughout the remainder of the paper. so first question to be addressed is:

Are assumptions (A0) and (A0′) reasonable for cancer?

In a study of glioblastoma and colorectal cancer, Bozic et al. (2010) concluded that the average selective advantage of somatic mutations was surprisingly small, 0.004. Here we adopt a slightly larger value, 0.01, as the typical selective advantage. In this case

$$\ell (s)=\text{log}(1/s)/s=460.5\text{ and }{\text{log}}_{10}(\ell (s))=2.663.$$ (6)

To identify the order of magnitude of N, we note that cells have a diameter of roughly 10 microns, or 10⁻³ cm, so there are 10⁶ in 1 cm², and 10⁸ in (10 cm)². The point mutation rate has been estimated, see Jones (2008), to be 5 × 10⁻¹⁰ per nucleotide per cell division. To compute the u_i this number needs to be multiplied by the number of nucleotides that when mutated lead to cancer. In some cases there are a small number of nonsynonymous mutations that achieve the desired effect, while in other cases there may be hundreds of possible mutations that knock out the gene and there may be a number of genes which can be hit to damage a metabolic pathway. Bozic et al. (2010) estimate that in their applications the number of possible mutations is 34,000. Thus mutation rates can range from 10⁻⁹ to 10⁻⁵, or can be larger after the mechanisms that govern DNA replication are damaged.

Since, as the previous remarks indicate, there are a wide variety of possible values for the number of cells and the mutation rates, we let

$$N={10}^a,\hspace{1em}{u}_1={10}^{-b},\hspace{1em}{u}_2={10}^{-c}.$$ (7)

To determine if the technical conditions (A0) and (A0′) hold for given parameter values, we need a nonasymptotic version of x ≫ y. If we use x > 10y, then in d = 2 we need

$$b>6.362\text{ for }(\mathrm{A}0)\text{ and }a>3.663\text{ for }(\mathrm{A}0’)$$ (8)

The assumption that the number of cells is larger than 10^3.663 is harmless. Requiring u₁ ≤ 10^−6.362 will rule out some applications, but we believe that Theorem 2 will hold under weaker assumptions than (A0).

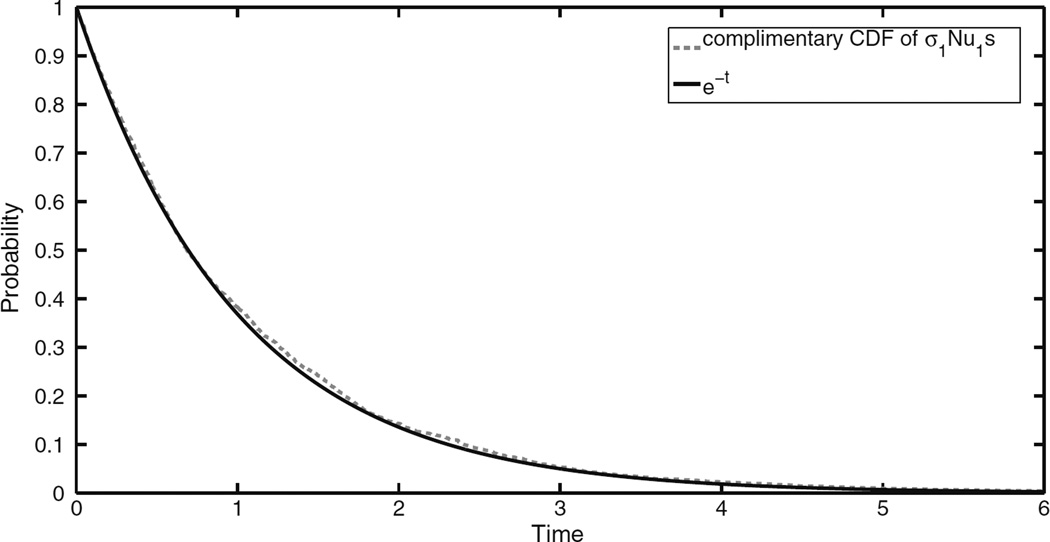
In order to test the rate of convergence in Theorem 2 we simulated the spatial Moran model until the first successful type-1 cell was created. By repeating this simulation 1000 times we were able to get an empirical estimate of the complimentary CDF of Nu₁sσ₁ which we then compared to the function e^−t in Fig. 1. In that figure we can see an excellent agreement between the limit theorem and the behavior of Nu₁sσ₁.

Fig. 1.

Comparison of empirical complementary CDF of Nu₁sσ₁ based on 1000 replications and e^−t, when N = 10^5.5, u₁ = 8 × 10⁻⁸ and s = 0.01

4 Simplified model

The analysis of the time to the first successful type 2 mutation, σ₂, is more complicated than that of σ₁, so to avoid getting bogged down in technicalities, we will introduce a simplified model on the real torus 𝒯 = (ℝ mod L)^d in which successful mutations initiate expanding clones that are growing balls (in the usual ℓ₂ norm) whose radius at time t is c_d(s)t, where c_d(s) is the constant in Theorem 1. Chatterjee and Durrett (2011) took the same approach in their study of Aldous’ gossip processes, in which information can spread by long range jumps on the torus in addition to a nearest neighbor process that is first passage percolation.

The state of our model at any time t is described by χ_t ⊂ 𝒯, which is the space occupied by successful type 1 families in 𝒯 at time t. The set χ_t will be a union of balls, see (9). As we will explain below, we will also introduce other simplifications. To have a completely rigorous proof, we would have to prove estimates to show that these approximations are justified. However, our goal here is to compute the limit distribution of σ₂, so we adopt a compromise. We will state precisely the facts we are using without proof.

Assumption I

Mutations to type 1 are generated by space-time Poisson process Π₁ with intensity ${\lambda }_1(x,t)=1_{\{x\in {\chi }_t^c\}}{u}_{1}s$. Let B_x,r = {y : |y − x| ≤ r}, where | · | is the ℓ₂ norm. If Π₁ ∩ (𝒯 × [0, t]) = {(x₁, t₁), …, (x_k, t_k)} then

$${\chi }_t=\underset{i=1}{\overset{k}{\cup }}{B}_{x_i,(t-t_i)c_d(s)}.$$ (9)

Explanation

The Bramson-Griffeath shape theorem allows us to approximate the growth of the successful mutants by tD. To simplify, without much loss of precision, we replace D by the ball of radius c_d (s). We take the union of the balls in (9) because the biased voter model with mutation is additive. That is, if we start the biased voter model with no 1’s and there are mutations at x_i at times t₁ < t₂ < … t_k < t then

$${\hat{\xi }}_t=\underset{i=1}{\overset{k}{\cup }}{\xi }_t^{x_i,t_i}$$ (10)

where ${\xi }_t^{x_i,t_i}$ is the biased voter model without mutation starting with x_i occupied at time t_i.

Assumption II

We do not consider the effect of unsuccessful type 1 and unsuccessful type 2 mutations on the growth of the successful type 1’s.

Explanation

By additivity, (10), unsuccessful type 1 mutations do not interfere with the growing balls generated by a successful type 1 families. An unsuccessful type 2 mutation can only effect the growth of a successful type 1 family, if it lands near the boundary. We do not believe that these events have a significant effect, but proving this seems difficult.

Assumption III

Mutations to type 2 are generated by space-time Poisson process Π₂ with intensity

$${\lambda }_2(x,t)=1_{\{x\in {\chi }_t\}}{u}_{2}s+1_{\{x\in {\chi }_t^c\}}{u}_1{u}_{2}sI(s)$$

where $I(s)=E({\int }_0^{T_0}|{\overline{\xi }}_t^0|dt|T_0<\infty )$ is the expected space-time volume of the biased voter model starting from a single type 1 at the origin and conditioned to die out.

Explanation

The first term gives the mutations to type 2 in successful type 1 families. In formulating the second, we do not include the dynamics of the unsuccessful type 1 families in the model, but only flip a coin to see if they give rise to a successful type 2 mutation. Estimates will show that for the parameters we consider, the first successful type 2 mutation does not come from an unsuccessful type 1 family.

5 Takeover by 1’s

Consider now the special case of our simplified model in which we start with no individuals of type 1. We are interested first in finding the time at which the 1’s take over the space, i.e., rise to a frequency > 1−ε, where ε > 0 is small. By assumption II we can ignore the influence of unsuccessful type 2 mutations. Later results will show that there will be no successful type 2 mutations over the time scale of interest here. By Theorem 2, the time until the first successful type 1 mutation will be Θ(1/L^du₁s). Since successful mutations spread at rate c_d (s), the time for a successful mutation to spread to cover the torus will be Θ(L/c_d). Comparing the two formulas, we see that if

$$L\ll L_c={\left(\frac{c_d}{s{u}_1}\right)}^{1/(d+1)}$$ (11)

then we will have sequential fixation: successful mutations will fix faster than they arise. When (11) holds, the times between successive mutations are almost the same as the waiting time for the first successful type 1 mutation starting from all 0’s, so by Theorem 2 they will be exponential with mean 1/Nu₁s. The observations above are due to Martens and Hallatschek (2011).

Let γ_d be the volume of a ball of radius 1 in d dimensions,

$${\gamma }_1=2,\hspace{1em}{\gamma }_2=\pi ,\hspace{1em}{\gamma }_3=4\pi /3.$$ (12)

Ignoring the small volume in space covered by unsuccessful type 1 mutations, a site x will be type 1 at time t if there is a successful type 1 mutation in the space-time cone {(y, r) : |y − x| < c_d (t − r)}. Such mutations are approximately a Poisson process with rate u₁s so

$$P(x\in {\xi }_t)\approx 1-\text{exp }(-u_{1}s{\int }_0^t{\gamma }_d{(c_{d}r)}^{d}dr)\approx 1-\text{exp}(-u_{1}s\frac{{\gamma }_d{c}_d^d{t}^{d+1}}{d+1})$$ (13)

This quantity will go from a small density ε to 1 − ε at times of order

$${(1/su{c}_d^d)}^{1/(d+1)}=L_c/c_d.$$

6 Main results

Next we state the two main results in the paper regarding behavior of σ₂, the waiting time until cancer initiation (i.e., the arrival of the first successful type 2 mutant). Throughout this section, we are taking the limit as s, u₁, u₂ → 0, N → ∞, and proving our results for the simplified model. The limit depends on the value of

$$\Gamma ={(N{u}_{1}s)}^{d+1}{(c_d^d{u}_{2}s)}^{-1}.$$ (14)

Intuitively, Γ^1/(d+1) is the number of successful type 1 mutations needed (after the first one) to produce the first successful type 2. To be precise if Γ → 0, as it does in the first result, we only need one successful type 1 mutation.

6.1 Γ → 0

In this case, the first successful mutation to type 2 occurs in the first successful type 1 family and before it reaches fixation. The next result comes from Stephen Moseley’s 2011 Ph.D. thesis at Cornell.

Theorem 3

If we assume,

$$(A1)\hspace{1em}{\left(\frac{c_d}{u_{2}s}\right)}^{d/(d+1)}\ll N\ll \frac{{(c_d^d{u}_{2}s)}^{1/d+1}}{u_{1}s}\hspace{1em}(A2)$$

and (A3) u₂ ≪ 1/ℓ(s) then P(σ₂ > t/Nu₁s) → exp(−t) as s → 0.

Here ℓ(s) is the quantity defined in (3). To connect with the title of the subsection note that (A2) is the condition Γ → 0. The proof is given in Sect. E.

What do the conditions mean?

Since the conditions of Theorem 3 are somewhat complicated, we will now explain them intuitively. To see the reason for (A1), we note that $t_2={(c_d^d{u}_{2}s)}^{-1/(d+1)}$ units of time after a successful type 1 mutation, the space-time volume covered by its descendents

$${\int }_0^{t_2}{(c_{d}r)}^{d}dr=\Theta (1/u_{2}s).$$

At that time the radius of the set of 1’s is

$$c_d{t}_2={(c_d/u_{2}s)}^{1/(d+1)}.$$

For this ball to fit inside our torus, we need to have

$${(c_d/u_{2}s)}^{d/(d+1)}\ll L^d=N.$$ (15)

To explain (A2), note that if we let σ₁ be the time of the first successful 1 mutation then by Theorem 2

$$P({\sigma }_1>t/N{u}_{1}s)\approx e^{-t},$$ (16)

so for the result in Theorem 3 to hold we must have σ₂ − σ₁ ≪ σ₁, which requires

$$t_2={(c_d^d{u}_{2}s)}^{-1/(d+1)}\ll 1/N{u}_{1}s.$$ (17)

Rewriting things in terms of N,

$$N\ll \frac{{(c_d^d{u}_{2}s)}^{1/(d+1)}}{u_{1}s},$$ (18)

which is the condition (A2). Dividing (18) by 1/Nu₁s we have

$$\frac{t_2}{1/N{u}_{1}s}=N{u}_{1}s{(c_d^d{u}_{2}s)}^{-1/(d+1)}={\Gamma }^{1/(d+1)}.$$

Finally, (A3) is needed to rule out the possibility that the successful mutation to type 2 occurs among the descendants of an unsuccessful type 1 mutation. Lemma 5 will show that if ${\xi }_t^0$ is the set of 1’s in a supercritical biased voter model on ℤ^d with λ = 1 + s and T₀ is the time at which the process dies out then

$$E({\int }_0^{T_0}|{\xi }_t^0|dt|T_0<\infty )\le C\ell (s)$$

where ℓ(s) was defined in (3). Mutations to type 2 that land on an unsuccessful type 1 family will succeed with a probability between s and 2s, since when they grow outside the unsuccessful type 1 family they will be competing with type 0’s. Since the expected number of type 1 mutations before time t/Nu₁s is O(1/s), the expected number of successful mutations to type 2 that occur in these families is O(u₂ℓ(s)) → 0 by (A3).

When do conditions (A1) and (A3) hold?

To begin the study of our special case s = 0.01 and d = 2, we note that

$$c_2={((\pi /4)s/\text{log}(1/s))}^{1/2}=0.04129\hspace{1em}{\text{log}}_{10}(c_2)=-1.384$$

Condition (A1) says (c_d/u₂s)^d/(d+1) ≪ N. If we again replace x ≪ y by 10x < y, then the condition is

$${(0.04129·{10}^{c+2})}^{2/3}<{10}^{a-1},$$

which after taking logarithms and simplifying can be written as

$$3a/2>c+2.116.$$ (19)

If a = 6 the right-hand side is 9, so this is satsified for u₂ = 10⁻⁶. If c = 8 the right-hand side is 12. Thus this condition which guarantees that initiation occurs before the pre-cancerous region is larger than the size of the tissue is reasonable.

Condition (A3), u₂ ≪ 1/ℓ(s), that guarantees the successful type 2 mutation will not arise from an unsuccessful type 1 family is now simply, see (6),

$$c>2.663\text{ or }{u}_2<2.17\times {10}^{-3}$$ (20)

which should be satisfied in most cases

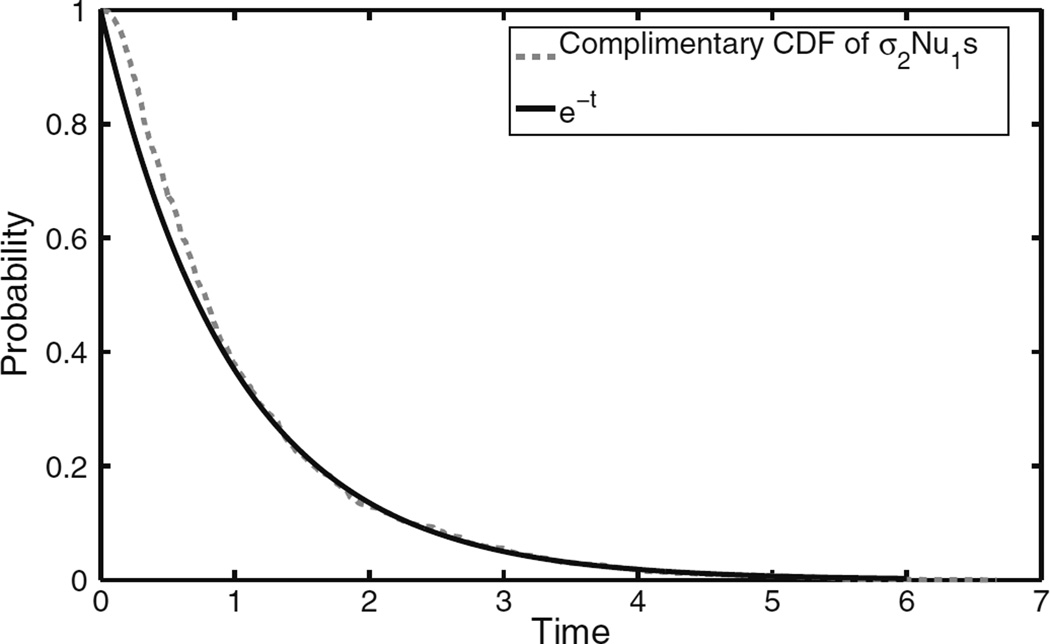
In Fig. 2 we compare the curve e^−t with the empirical complimentary CDF of Nu₁σ₂ (based on 1000 simulations of spatial Moran model). In this plot we see a rather good agreement between the limit of Theorem 3 and the behavior Nu₁σ₂, except for small times. This comes from the fact that we ignore σ₂ − σ₁, which can be a serious error if σ₁ is small. A similar discrepancy was observed in the homogeneously mixing case by Durrett and Schmidt (2008), see their Figure 2.

Fig. 2.

Comparison of empirical complementary CDF of Nu₁sσ₂ based on 1000 replications and e^−t, when N = 10^5.5, u₁ = 8 × 10⁻⁸, u₂ = 4.5 × 10⁻⁴, and s = 0.01

6.2 Γ → I ∈ (0, ∞)

Theorem 4

If we assume (A1), (A3), and Γ → I ∈ (0, ∞) then

$$P({\sigma }_2>t/N{u}_{1}s)\to \text{exp }(-{\int }_0^{t}1-\text{exp }[-\frac{{\gamma }_d}{I}\times \frac{y^{d+1}}{d+1}\left]dy\right)$$ (21)

as s → 0. The proof is given in Appendix F. Note that if I = 0, the exponential inside the integral vanishes and the limit is e^−t. Since (A2) is the condition Γ → 0, Theorems 3 and 4 can be combined into one.

When t ≪ I ^1/d+1 the integrand in (21) is ≈ 0, while if t ≫ I^1/(d+1) the integrand is equal to 1, and probability decays exponentially. Thus we expect Θ(Γ^1/(d+1)) successful type 1 mutations will occur before σ₂.

Why is Theorem 4 true?

The number of unsuccessful mutations by time t/Nu₁s is of order 1/s, so as in the discussion of the previous theorem, (A3) implies that we can ignore the possibility that the successful type 2 comes from a type 1 family that dies out. To explain the form of the limit, let t′ = t/(Nu₁s) to simplify notation. Extending Theorem 2, we will show in Appendix F that while 1’s cover a small fraction of the space successful type 1 mutations happen are a rate Nu₁s Poisson process on [0, t/Nu₁s]. When one occurs at time r, it will cover a space-time volume at time t′ of size

$$\upsilon (r)={\gamma }_d{c}_d^d{(t\prime -r)}^{d+1}/(d+1),$$

and hence produce a Poisson number of successful type 2 mutations with mean u₂sυ(r). A useful result, which can be found in Parzen (1999) or on page 421 of Komarova (2007), implies

$$P({\sigma }_2>t\prime )=\text{exp }(-{\int }_0^{t\prime }N{u}_{1}s·[1-\text{exp}(-u_{2}s\upsilon (r))]dr).$$ (22)

Intuitively, this formula follows from thinning the Poisson process of successful type 1 mutations. If we only accept successful type 1 mutations that give rise to at least one successful type 2 mutation by time t′, then the number of accepted points is Poisson with a mean equal to the integral in the formula. Since we have σ₂ > t′ if and only if no points are accepted, we have (22). The theorem follows easily from (22) by changing variables y = Nu₁s(t′ − r) and using the definition of Γ in (14) to conclude

$$u_{2}s{\gamma }_d{c}_d^d{(N{u}_{1}s)}^{-(d+1)}={\gamma }_d/\Gamma .$$

The reader may have noticed that our calculations assume that the production of successful type 2’s by different type 1 families are independent. We will prove this by showing that at times ≤ C/Nu₁s type 1’s cover a small fraction of the space and that with high probability the space time cones that successful type 1 mutations generate are disjoint.

In Fig. 3 we compare the predictions of Theorem 4 with the results from a simulation. We see a good agreement between the prediction and the simulation, but we have to use a larger value of the limit variable I (0.4) than our value of Γ (0.11). It should be observed however that the shape of the empirical complementray CDF is very close to the theoretical prediction of Theorem 4.

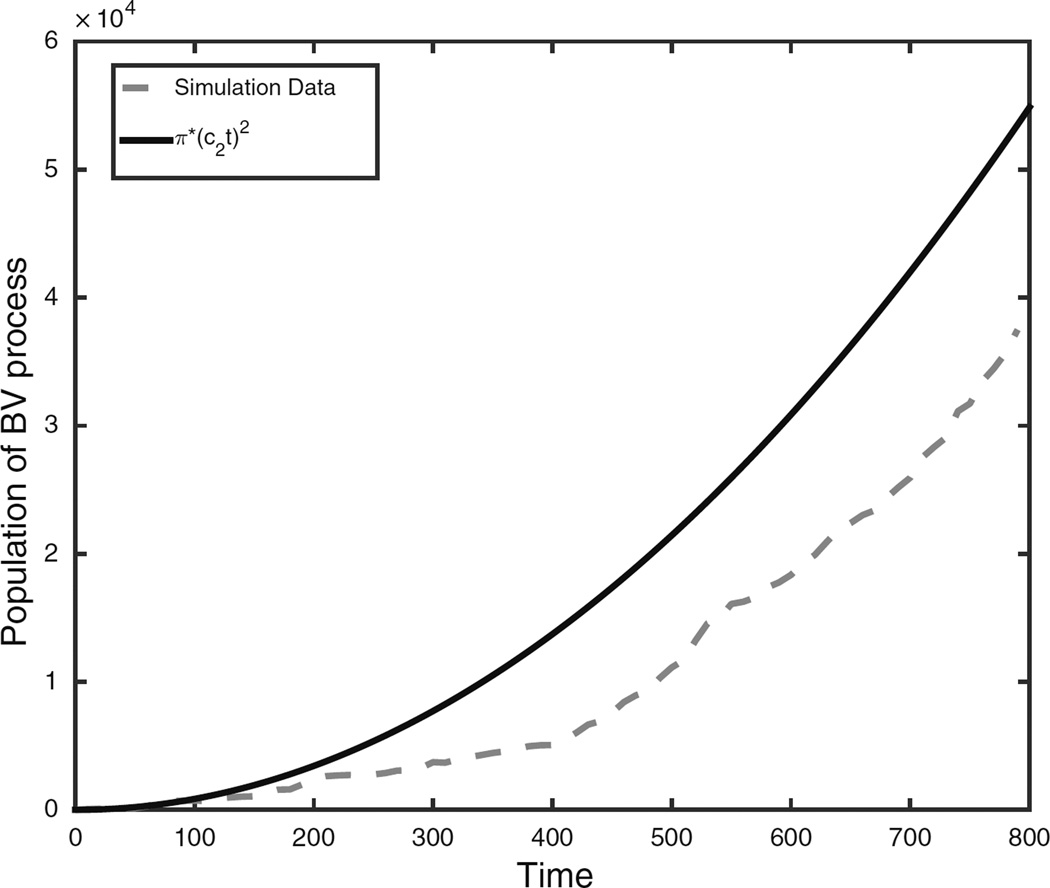
Due to the discrepancy between the predictions of Theorem 4 and our simulations we performed additional simulations. In particular, we wanted to understand why σ₂ was on average larger than Theorem 4 predicted. In Fig. 4 we see that on a short time scale the theoretical predicted population size π(c₂t)² over estimates the simulated population size. However, we can see from the plot that the simulated population size is starting to catch up to the theoretical prediction. We believe that this discrepancy is an artifact of the small simulation size, and that if run for long enough the population size of the biased voter model will behave like π(c₂t)². Note that at the end of the simulation there are 40,000 cells while even small tumors will have millions of cells, so the theoretical result should be accurate for the biological application, a regime that is difficult to study by simulation.

Fig. 4.

Population size versus time in biased voter model with s = 0.01 compared with the theoretical predicted population as a function of time

7 Conclusions

In this work, we have studied various aspects of the spatial Moran model with mutation. The parameters of this general model can be tuned to study a variety of cancer types. Thus, these analyses develop theoretical tools to study the differences in spatial cancer initiation dynamics (e.g. premalignant field size and geometry) and initiation timing between cancers of different tissues, or cancers arising from different genetic pathways within the same tissue. Theorem 1 gives an approximate formula for the rate of spread of mutant clones as a function of the selection advantage s, assuming s is small. This provides insight into how an increased cellular division rate due to a genetic alteration influences the spreading rate of the subsequent premalignant clone.

Our other main results concern the time σ_i until the first successful type i mutation when i = 1, 2. These quantities are of interest because the associated mutations may bring more aggressive growth or resistance to therapy. Theorem 2 shows that the time until the first successful type 1 mutation is asymptotically exponential with rate Nu₁s. This result is intuitive: type 1 mutations arise at rate Nu₁ and are successful with probability s but we can only prove this assumption under conditions that are far from optimal.

Theorems 3 and 4 show that the asymptotic behavior of σ₂ is determined by the value of the composite parameter

$$\Gamma ={(N{u}_{1}s)}^{d+1}{(c_d^d{u}_{2}s)}^{-1}$$

Intuitively Γ^1/d+1 is the number of additional type 1 mutations (after the first one) needed to give rise to a successful type 2. To avoid technicalities, we prove our results for a simplified version of the spatial Moran model, but the agreement between our results and the simulation of the spatial Moran model show that our simplifications are a good approximation.

The spatial Moran model omits many important features of cancer growth, such as interactions between the tumor and its microenvironment, e.g., hypoxia, acidity associated with anerobic glycolysis, angiogeneis, etc. However, the results described here have been used to study the spatial structure of tumor heterogeneity and to give insights into the “cancer field effect,” in which secondary tumors arise from premalignant lesions surrounding primary tumors. See Foo et al. (2014) for details. Our results may also be used to develop quantitative measures of spatial heterogeneity during the premalignant phase of cancer initiation; such measures can be used to develop sampling guidelines for monitoring premalignant conditions. Finally, our analyses can be used to study the potential effect of preventative measures that may alter certain factors such as mutation rate or the selective advantage of each genetic hit, and to determine the impact of such measures on the risk of cancers arising during the human lifetime.

Appendix A: Construction and duality

To make the paper self-contained and to recall some facts that may not be widely known, we will now construct the two type biased voter model and explain its duality with coalescing branching random walk.

To construct the biased voter model, we follow the approach in Griffeath (1978). Associated with each order pair (x, y) of nearest neighbors, we have two Poisson processes, $T_n^{x,y,\upsilon }$, n ≥ 1 and $T_n^{x,y,b}$, n ≥ 1 with rates 1/2d and (λ − 1)/2d; υ is for voter and b is for birth. Here, all of the Poisson processes are independent, and together constitute the graphical representation. At each time t = T^x,y,υ we draw an arrow (y, t) → (x, t) and put a δ at (x, t), while at each time t = T^x,y,b we draw an arrow (y, t) → (x, t). We think of arrows as little tubes that allow fluid to flow in the direction indicated, while the δ’s are dams that stop the passage of the fluid. The δ’s occur just before the arrows so they don’t block the fluid that flows through them.

Given an initial set A of sites that are occupied by 1’s, the set of sites that are occupied by 1’s at time t is the set ${\xi }_t^A$ of points that are wet if fluid is injected at points of A at time 0. By checking cases, one can see that the effect of an arrow-δ from y to x is as follows:

Before		After
x	y	x	y
0	0	0	0
0	1	1	1
1	0	0	0
1	1	1	1

The first case should be clear. In the second the arrow spreads the fluid from y to x. In the third the δ at x stops the fluid, but there is nothing from y to replace it, while in the fourth case there is. Thus the arrow-δ produces a voter model step: x imitates y.

If we remove the δ, then only the third line changes and the overall result is a birth from y to x, with the two particles coalescing to one if x is already occupied:

Before		After
x	y	x	y
0	0	0	0
0	1	1	1
1	0	1	0
1	1	1	1

The graphical representation has the useful property that it constructs the biased voter model for all initial conditions on the same probability space. As Harris (1976) noted, this implies that the constructed processes are additive:

$${\xi }_t^{A\cup B}={\xi }_t^A\cup {\xi }_t^B.$$ (23)

since a space-time point can be reached from A ∪ B at time 0 if and only if it can be reached from A or from B. A consequence of additivity is that $A\to {\xi }_t^A$ is increasing, a property that is called “attractive.”

An important reason for constructing a process from a graphical representation is that it allows us to construct a dual process. Let ${\zeta }_r^{x,t}$ be the set of points at time t − r that can be reached by a path starting from x at time t that goes down the graphical representation and crosses the arrows in the direction OPPOSITE their orientation. If we recall that the δ’s occur just before the arrows on the way up then we see that the effect of an arrow-δ from y to x on the dual process is

Before		After
x	y	x	y
0	0	0	0
0	1	0	1
1	0	0	1
1	1	0	1

In words this is a coalescing random walk. If there is a particle at x (corresponding to a 1) it jumps to y. If there is also a particle at y the two coalesce to 1. It is easy to see that an arrow without a δ has the same effect in the dual as it did in the forward process except that now the birth is from x to y.

Given a set of sites B, let ${\zeta }_s^{B,t}={\cup }_{x\in B}{\zeta }_s^{x,t}$. It is immediate from the definitions that

$$\{{\xi }_t^A\cap B\ne \varnothing \}=\{{\zeta }_t^{B,t}\cap A\ne \varnothing \},$$

i.e., the two events are equal. To get rid of the superscript t from the dual process, we note that if t < t′ then the distribution of ${\zeta }_r^{B,t\prime }$ for r ≤ t is the same as ${\zeta }_r^{B,t}$ for r ≤ t. Invoking Kolmogorov’s extension theorem there is process ${\zeta }_r^B$ defined for all time r ≥ 0 that has the same distribution as ${\zeta }_r^{B,t}$ for r ≤ t. This process satisfies

$$P({\xi }_t^A\cap B\ne \varnothing )=P({\zeta }_t^B\cap A\ne \varnothing ).$$ (24)

In what follows, we will be interested in the biased voter model with mutation 0 → 1 at rate u₁. Mutation can be incorporated into the graphical representation by adding independent Poisson processes $T_n^{x,\mu }$, n ≥ 1 with rate u₁. If we let ${\hat{\xi }}_t^A$ be the biased voter model with mutation starting with A occupied at time t, and suppose that there are mutations at x_i at times t₁ < t₂ < ⋯ t_k < t then

$${\hat{\xi }}_t^A={\xi }_t^A\cup {\xi }_t^{x_1,t_1}\cdots \cup {\xi }_t^{x_k,t_k}$$

where ${\xi }_t^{x_i,t_i}$ is the biased voter model without mutation starting with x_i occupied at time t_i.

In our proofs, it will be useful to be able to quantify the notion that two processes, ${\xi }_t^A$ and ${\xi }_t^B$ or ${\xi }_t^{x_1,t_1}$ and ${\xi }_t^{x_2,t_2}$ are independent when they don’t hit each other. To do this we use a coupling due to Griffeath (1978). We define the first process on a graphical representation, and the second on an independent graphical representation with the caveat that events in the second process that involve an edge (x, y) where x or y is occupied in the first process must use the first graphical representation, so that the pair of processes has the same joint distribution as if they were both defined on the same graphical representation.

Appendix B: Proof of Lemma 1

In this section we find a space-time box that the sub-critical biased voter model does not escape with high probability. To prove this in d ≥ 2 we will use a result of Merle (2008), who studied the likelihood of the voter model to wander far from its starting point. The result extends easily to the subcritical biased voter model because it is dominated by the voter model.

Merle’s (2008) results are based on the work Bramson et al. (2001), who studied the ordinary voter model with kernel p(x, y). That is, voter at x changes opinions at rate 1, and imitates the one at y with probability p(x, y) where p(x, y) = p(0, y − x) is irreducible and symmetric with p(0, 0) = 0 and ∑_x p(0, x)_xixj = σ²δ(i, j). Here δ(i, j) = 1 if i = j and 0 otherwise. To get a limit, they scale space so that the voters live on ${\mathbb{Z}}^d/\sqrt{n}$, run time at rate n and denote the resulting voter model by ${\xi }_t^n$. Let m_n = n/ log n in d = 2 and n in d ≥ 3, and define a measure valued process by

$$X_t^n=\frac{1}{m_n}\sum _{y\in {\xi }_t^n}{\delta }_y.$$

We write $X_t^{n,0}$ when the initial state is ${\xi }_0^n=\{0\}$. Let D be the space of functions from [0, ∞) into the space of finite measures on ℝ^d that are right-continuous and have left limits in the weak topology. Of particular interest is Theorem 4 from Bramson et al. (2001):

Theorem 5

Assume d ≥ 2 and let N₀ be the excursion measure of super-Brownian motion on ℝ^d with branching rate 2β_d and diffusion coefficient σ². Let α > 0 and let F be a bounded continuous function on D with F(ω) = 0 if ω_t = 0 for t ≥ α. Then

$$\underset{n\to \infty }{\text{lim}}{m}_{n}EF(X_{·}^{n,0})={\mathbf{N}}_0(F).$$

The excursion measure is defined by starting the super process from εδ₀, multiplying the probability measure by 1/ε and letting ε → 0. See Section 3 of Bramson et al. (2001) and references in that paper for more details. This is the super-process analogue of starting Brownian motion at ε, killing it when it hits 0, considering the limit of (1/ε) times the probability measure, which defines Ito’s excursion measure. See Chapter XII of Revuz and Yor (1991) for a thorough treatment. In most cases the killed Brownian motion B̄_t dies out quickly but when ε < 1

$$(1/\epsilon )P_{\epsilon }(\underset{t}{\text{max}}{\overline{B}}_t>1)=1.$$

Theorem 5 tells us that a rescaled version of the voter model behaves like the excursion measure of a super Brownian motion. Since the super Brownian motion has compact support it makes sense that the voter model should not be able to run much farther than the spatial scaling used in Theorem 5. This result is made precise in Merle (2008) which we then extend to establish Lemma 1.

Proof

We will first establish the result for the voter model. In particular, define T₀ to be the extinction time of the voter model started from a single site on ℤ^d, and p(t) = P(T₀ > t). Recall from Bramson and Griffeath (1980a) the large t asymptotics

$$p(t)~\{\begin{array}{cc}\frac{1}{{\beta }_{d}t},\hfill & d\ge 3\hfill \\ \frac{1}{\pi }\frac{\text{log }t}{t},\hfill & d=2.\hfill \end{array}$$ (25)

Based on these asymptotics it is easy to verify that

$$p(M\ell (s))~s/M,$$

which establishes the claim with regards to survival time. In order to establish the claim with regard to escape from the large box we use Claim 1 of Merle 2008 (p828):

Claim

There exists a positive K₀ and K₂ such that for any α > 1 and any A ≥ 1

$$P(\underset{t\le 2\alpha }{\text{sup}}\underset{x\in {\xi }_t^0}{\text{sup}}|x|>A\sqrt{\alpha })\le K_{0}p(\alpha )\text{ exp}(-K_{2}A)$$

where ${\xi }_t^0$ is a voter model started with a single seed at the origin. Now consider

$$P(\underset{t>0}{\text{sup}}\underset{x\in {\xi }_t^0}{\text{sup}}|x|>M\sqrt{\ell (s)})\le P(\underset{t\le 2\sqrt{M}\ell (s)}{\text{sup}}\underset{x\in {\xi }_t^0}{\text{sup}}|x|>M\sqrt{\ell (s)})+p(2\sqrt{M}\ell (s))\le p(2\sqrt{M}\ell (s))(K_0{e}^{-K_2\sqrt{M}}+1).$$

The result then follows for the subcritical biased voter model by comparison.

Appendix C: Proof of Theorem 2

Proof

If each new mutant was placed on its own graphical representation then the number of successful type 1 mutations by time t/Nu₁s would converge to a Poisson with mean t. Recalling the definition of successful mutation given in (4), we divide space-time

$${ℬ}_{L,t}={(\mathbb{Z}\text{ mod }L)}^d\times [0,t/(N{u}_{1}s)]$$

into boxes with time length T = M_sℓ(s) and spatial side length R = M_sℓ(s)^1/2 where M_s → ∞ sufficiently slowly such that, see (A0) and (A0’),

$$u_1{R}^{d}T=u_1\ell {(s)}^{(d+2)/2}{M}_s^{d+1}\to 0$$

$$K_s=L/R=L/(\ell {(s)}^{1/2}{M}_s)\text{ is an integer and }{K}_s\to \infty .$$

For m ∈ ℤ^d with 0 ≤ m_i < K_s for 1 ≤ i ≤ d, and integers n ≥ 0 let B_m,n be the box with spatial side length R, time length T and lower left corner at Rm, Tn. Let B̄_m,n be the space time cube consisting of the 5^d+1 boxes closest to B_m,n. If we have mutation in B_m,n and another not in B̄_m,n then the success of these two mutations are independent events.

The expected number of successful mutations that occur in a box B_m,n in ℬ_L,t, along with another mutation (successful or not) in B̄_m,n is

$${\left(\frac{L}{R}\right)}^d·\frac{t/N{u}_{1}s}{T}·(R^{d}T{u}_{1}s)(5^d{R}^{d}T{u}_1)=t{5}^d{R}^{d}T{u}_1=t{5}^d{M}_s^{d+1}\ell {(s)}^{d+2/2}\to 0$$

This shows that with high probability all the successful type 1 mutants act as if they are independent. Form this we see that the probability of no successful mutants in ℬ_L,t → e^−t, which gives the desired result.

To prepare for later developments note that if we know that the fraction of the boxes occupied by successful type 1 mutations is small, the successful type 1 mutations will be a Poisson process.

Appendix D: Upper bounds on the subcritical BVM

In this lengthy section we bound the size of type 1 families that later die out. These results are needed for the proofs of Theorems 3 and 4 but the reader can skip them and still understand those proofs. The first step is to determine the effect on the process of conditioning it to die out.

Our first result relates unsuccessful type 1 clones to a subcritical biased voter process.

Lemma 2

Let ${\xi }_t^0$ be the set of 1’s in a supercritical biased voter model with λ = 1+s on ℤ^d starting from ${\xi }_0^0=\{0\}$. Let T₀ be the time at which the process dies out. Let ${\overline{\xi }}_t^0$ be the biased voter model with ${\overline{\xi }}_0^0=\{0\}$ and the roles of 1 and 0 interchanged, i.e., 1’s give birth at rate 1, and 0’s give birth at rate λ. Then

$$(\{|{\xi }_t^0|,t\le T_0\}|T_0<\infty )={}_d\{|{\overline{\xi }}_t^0|,t\le T_0\}$$

Proof

If ${\xi }_t^0=A$ with |A| = k and |∂ A| = ℓ then $|{\xi }_t^0|$ grows to size k + 1 at rate λℓ, and shrinks to size k − 1 at rate ℓ, so the transition probability of the embedded discrete time chain is

$$p(k,k+1)=\frac{\lambda }{1+\lambda }\hspace{1em}p(k,k-1)=\frac{1}{1+\lambda }$$ (26)

If we let φ(x) = λ^−x then it is easy to check that

$$\phi (k)=p(k,k+1)\phi (k+1)+p(k,k-1)\phi (k-1)$$

hence if a < x < b then

$$P_x(T_a<T_b)=\frac{\phi (b)-\phi (x)}{\phi (b)-\phi (a)}\hspace{1em}{P}_x(T_b<T_a)=\frac{\phi (x)-\phi (a)}{\phi (b)-\phi (a)}$$ (27)

Let a = 0, x = 1, and b → ∞ in the first formula

$$P_k(T_0<\infty )={\lambda }^{-k}.$$ (28)

If we condition a random walk with positive drift to hit 0 then the conditioned process has transition probability

$$\overline{p}(k,k+1)=\frac{p(k,k+1)\phi (k+1)}{\phi (k)}=\frac{1}{1+\lambda }\hspace{1em}\overline{p}(k,k-1)=\frac{\lambda }{1+\lambda }$$ (29)

In words, the result is a random walk with the probabilities of up and down interchanged. Conditioning ξ_t to hit 0 does not change the exponential holding times, and desired result follows.

Next we need to relate the behavior of the subcritical biased voter process, ${\overline{\xi }}_t^0$ to the behavior of the unbiased voter process (i.e., s = 0) denoted by ${\hat{\xi }}_t^0$.

Lemma 3

Let P_s be the law of the subcritical biased voter process ${\overline{\xi }}_t^0$ and let P₀ be the law of an unbiased voter process run at a sped up rate, so that the rate of events is (2+s)/2d on each edge between a type 0 and type 1. The Radon-Nikodym derivative between these two measures until n steps is given by:

$$\frac{d{P}_s}{d{P}_0}={\left(\frac{2}{2+s}\right)}^{n_{+}-n_{-}}{\left(\frac{4+4s}{4+4s+s^2}\right)}^{n_{-}},$$ (30)

where n₊ and n₋ are the number of jumps up and down respectively, and n₋+n₊ = n.

Proof

Under P₀, the law of the voter model dictates that a type 1 next to a type 0 forces it to flip at rate (1 + s/2)/2d and a type 0 next to a type 1 also forces it to flip at rate (1 + s/2)/2d. Under P_s, the law of the subcritical voter model dictates that a type 1 next to a type 0 forces it to flip at rate 1/2d and a type 0 next to a type 1 forces it to flip at rate (1 + s)/2d. Thus when we look at the Radon-Nikodym derivative it will only depend on the embedded chain.

$$\frac{d{P}_s}{d{P}_0}={\left(\frac{2}{2+s}\right)}^{n_{+}}{\left(\frac{2+2s}{2+s}\right)}^{n_{-}}$$ (31)

where n₊ is the number of up jumps and n₋ is the number of down jumps. Rewriting this gives the statement of the Lemma.

For what follows it will be useful to establish a bound on the Radon-Nikodym derivative in the previous lemma.

Lemma 4

If |ξ̄₀| = O(1/s) as s → 0 then d P_s/d P₀ = O(1) as s → 0.

Proof

For ease of notation define n₀ = |ξ̄₀|. Since 0 is an absorbing state for the stochastic process |ξ̄_t| we know that n₊ − n₋ ≥ −(n₀ + 1). Rearranging the result in Lemma 3 and then applying the inequality n₋ ≤ n₊ + (n₀ + 1) we get that

$$\frac{d{P}_s}{d{P}_0}={(1+\frac{s}{2+s})}^{n_{-}}{(1-\frac{s}{2+s})}^{n_{+}}\le {\left[\right(1-\frac{s}{2+s}\left)\right(1+\frac{s}{2+s}\left)\right]}^{n_{+}}{(1+\frac{s}{2+s})}^{n_0+1}\le {(1+\frac{s}{2+s})}^{n_0+1}=\text{exp }[(n_0+1)\text{log}(1+s/(2+s))]\le \text{exp }[s(n_0+1)/(2+s)]=O(1).$$

and we have proved the desired result.

Lemma 4 will allow us to derive results for the subcritical biased voter model from those for the ordinary voter model. The size of the voter model, when $|{\xi }_t^0|>0$, is a time change of symmetric simple random walk, with jumps happening at two times the size of the boundary $|\partial {\xi }_t^0|$, which is the number of nearest neighbor pairs with $x\in {\xi }_t^0$ and $y\notin {\xi }_t^0$. The one dimensional case is easy because when ${\xi }_t^0\ne \varnothing$ the boundary $|\partial {\xi }_t^0|=2$. The key to the study of the process in d ≥ 2 is the observation that there are constants β_d so that

$$|\partial {\xi }_t^0|{~}_p\{\begin{array}{cc}2d{\beta }_d|{\xi }_t^0|\hfill & d\ge 3,\hfill \\ 4{\beta }_2|{\xi }_t^0|/\text{ log}(|{\xi }_t^0|)\hfill & d=2.\hfill \end{array}$$ (32)

where $|\partial {\xi }_t^0|{~}_{p}f(|{\xi }_t^0|)$ means that when $|{\xi }_t^0|$ is large, $|\partial {\xi }_t^0|/f(|{\xi }_t^0|)$ is close to 1 with high probability.

The intuition behind this result is that the voter model is dual to a collection of coalescing random walks, so in d ≥ 3 neighbors of points in ${\xi }_t^0$ will be unoccupied with probability ≈ β_d, the probability two simple random walks started at 0 and e₁ = (1, 0, … 0) never hit. In dimension d = 2, the recurrence of random walks implies that when $|{\xi }_t^0|=k$ is large, most neighbors of points in ${\xi }_t^0$ will be occupied, but due to the fat tail of the recurrence time sites will be vacant with probability ~ β₂/ log k, where β₂ = π.

Let $V_{n,s}^{\prime }(x)$ be the fraction of sites adjacent to x in state 0 at time s (with the prime indicating that we multiply this by log n in d = 2, see page 196). A key step in the proof in Cox et al. (2000) is to show, see (I1) on page 202, that for nice test functions ϕ

$$E\left[{({\int }_0^T{X}_s^n(\{V_{n,s}^{\prime }-{\beta }_d\}{\varphi }^2)ds)}^2\right]\to 0$$ (33)

where $X_s^n(f)$ denote the integral of the function f against the measure $X_s^n$. The result in (33) shows that when we integrate in time and average in space (multiplying by a test function to localize the average) then (32) is true.

If one wants to give a rigorous proof of the estimates in this section, then small values of k, can be treated with the inequalities

$$C{k}^{(d-1)/d}\le |\partial {\xi }_t^0|\le 2dk,$$

and one can control large values of k using (33) and estimates such as (J1) and (J2) on page 208 of Cox et al. (2000). In order to avoid getting bogged down in technicalities we will suppose that

Assumption 1

Let k be a non-negative integer. If |ξ ¯_t| = k then |∂ξ ¯_t| = ∂(k) where

$$\partial (k)=\{\begin{array}{cc}2d{\beta }_{d}k\hfill & d\ge 3\hfill \\ 4{\beta }_{2}k/\text{ log }k\hfill & d=2.\hfill \end{array}$$ (34)

Using Lemma 2 and Assumption 1, we can approximate the space-time volume of unsuccessful type 1 mutants. To this end we generalize the subcritical biased voter model defined in Lemma 2 to have arbitrary initial starting state and denote this process by ξ̄_t. Furthermore, we denote the expectation operator conditioned on |ξ̄₀| = k by E_k, i.e. E_k [·] ≐ E[·|ξ̄₀| = k]. Then we can prove the following upper bound on the space-time volume of unsuccessful type 1 mutants. Here and in other proofs in this section we will sometimes suppose in addition to λ > 1 that λ ≤ 2 in order to get rid of λ’s from the formulas.

Lemma 5

There is a positive constant C that depends only on d such that

$$E_1({\int }_0^{T_0}|{\overline{\xi }}_t|dt)\le C\ell (s)$$

where ℓ(s) was defined in (3)

Proof

Let S̄_n be the simple random walk that jumps according to p̄ defined in (29) and note that |ξ̄_t | is a continuous time version of S̄_n that jumps approximately at rate q(k) = (1 + λ)∂(k) when in state k and makes jumps according to p̄. Let $T_k^{+}=\text{min}\{n\ge 1:S_n=k\}$. By considering the expected number of visits to k and the amount of time spent there on each one we have

$$E_1({\int }_0^{T_0}|{\overline{\xi }}_t|dt)=\sum _{k=1}^{\infty }\frac{{\overline{P}}_1(T_k<T_0)}{{\overline{P}}_k(T_k^{+}=\infty )}·\frac{k}{q(k)}$$ (35)

If P̄ is the law of the conditioned chain with transition probability (29), and P is the law of the process with transition probability chain following (26) then by symmetry and (27),

$${\overline{P}}_1(T_k<T_0)=P_{k-1}(T_0<T_k)=\frac{{\lambda }^{-k}-{\lambda }^{-(k-1)}}{{\lambda }^{-k}-1}=\frac{\lambda -1}{{\lambda }^k-1}.$$ (36)

Using symmetry and (27) again,

$${\overline{P}}_k(T_k^{+}=\infty )=\frac{\lambda }{1+\lambda }{\overline{P}}_{k-1}(T_0<T_k)=\frac{\lambda }{1+\lambda }{P}_1(T_k<T_0)=\frac{\lambda }{1+\lambda }·\frac{{\lambda }^{-1}-1}{{\lambda }^{-k}-1}=\frac{\lambda -1}{(1+\lambda )(1-{\lambda }^{-k})},$$ (37)

so we have

$$\frac{{\overline{P}}_1(T_k<T_0)}{{\overline{P}}_k(T_k^{+}=\infty )}=\left(\frac{\lambda -1}{{\lambda }^k-1}\right)\left(\frac{1+\lambda }{\lambda -1}\right){\lambda }^{-k}({\lambda }^k-1)={\lambda }^{-k}(1+\lambda )$$

and (35) becomes

$$E({\int }_0^{T_0}|{\overline{\xi }}_t|dt)=(1+\lambda )\sum _{k=1}^{\infty }{\lambda }^{-k}·\frac{k}{q(k)}.$$ (38)

In one dimension q(k) = 2(1 + λ), so doing some algebra and using the formula for the mean of the geometric distribution, two times the quantity in (38) is

$$\sum _{k=1}^{\infty }k{\lambda }^{-k}=\frac{1/\lambda }{(1-1/\lambda )}\sum _{k=1}^{\infty }k{\lambda }^{-(k-1)}(1-1/\lambda )=\frac{1/\lambda }{{(1-1/\lambda )}^2}\le C{s}^{-2}.$$ (39)

Since q(k) ~ 2d(1 + λ)β_dk, in d ≥ 3, so the quantity in (38) is

$$\frac{1}{2d{\beta }_d}\sum _{k=1}^{\infty }{\lambda }^{-k}=\frac{1}{2d{\beta }_d}\times \frac{1/\lambda }{1-1/\lambda }\le C{s}^{-1}.$$ (40)

In d = 2 we have q(k) ~ 4(1 + λ)β₂k/ log k so the quantity in (38) is

$$\frac{1}{4{\beta }_2}\sum _{k=1}^{\infty }{\lambda }^{-k}\text{ log }k\le C{s}^{-1}\text{ log}(1/s).$$ (41)

To see the last inequality note that for k ≤ 1/s², log k ≤ 2 log(1/s) and as s → 0 we can ignore the contribution from k > 1/s².

Appendix E: Proof of Theorem 3

Proof

Let A_t be the event that the first successful type 2 mutant comes from an unsuccessful type 1 family that arises before time t/Nu₁s. The expected number of such families is t/s. Using Lemma 5 to bound the space time volume covered by an unsuccessful mutation and ignoring the possibility that they overlap, we have

$$P(A_t)\le u_{2}s·\frac{t}{s}·C\ell (s)\to 0$$ (42)

by assumption (A3).

In view of Theorem 2, it suffices to show that P(σ₂ − σ₁ > ε/Nu₁s) → 0 for any ε > 0. Since the expected number of successful type 1 mutations in a time interval of length ε/Nu₁s is ≤ ε, this tells us that the possibility of a second successful type 1 mutation can also be ignored.

Under the simplified model, the total space-time volume occupied by descendants of the successful type 1 mutation up to time σ₁ + t is

$$g(t)=\frac{{\gamma }_d{c}_d^d{t}^{d+1}}{d+1},$$

assuming that at this time the diameter is < L. Let B(t) be the event that there is no successful type 2 mutation by time σ₁ + t, and let

$$t_2={(u_{2}s{\gamma }_d{c}_d^d/(d+1))}^{-1/(d+1)}.$$

be chosen so that g(t₂) = 1/u₂s. Using the Poisson approximation

$$P(B(M{t}_2))~\text{exp }(-u_{2}sg(M{t}_2))\to \text{exp }(-M^{d+1}).$$

This shows that if M is large, σ₂ − σ₁ ≤ Mt₂ with high probability. Now the diameter of the ball covered by the descendants of the successful type 1 at time σ₁ + Mt₂ is

$$O(c_d{t}_2)=O\left({(c_d/u_{2}s)}^{1/(d+1)}\right)\ll L$$

by assumption (A1), so our computation of the volume is legitimate. Finally, the time

$$t_2=O\left({(c_d^d{u}_{2}s)}^{-1/(d+1)}\right)\ll 1/N{u}_{1}s$$

by assumption (A2). This shows that the time difference σ₂ − σ₁ = o(1/Nu₁s) and completes the proof.

Appendix F: Proof of Theorem 4

Proof

The number of unsuccessful mutations by time t/Nu₁s is of order 1/s, so as in the discussion of the previous theorem, (A3) implies that we can ignore the possibility that the successful type 2 comes from a type 1 family that dies out.

We next show that the probability of overlap between successful type 1 clones by time t/(Nu₁s) is negligible. By time t/(Nu₁s) the maximum possible radius of a successful type 1 clone is r = (c_dt)/(Nu₁s). Let X and Y be two independent random variables distributed uniformly over the torus (ℤ mod L)^d, and note that it suffices to establish that

$$P(|X-Y|\le 2r)\ll 1$$

where | · | is the Euclidean norm. By rotating the torus we can suppose that X = 0.

$$P(|Y|\le 2r)\le P({\Vert Y_1\Vert }_{\infty }\le 2r)={(2r/L)}^d.$$

Then we use assumption (A1) to establish the desired result

$$r/L={\left(\frac{1}{N}\right)}^{1/d}\left(\frac{c_d}{N{u}_{1}s}\right)=\frac{c_d}{N^{(d+1)/d}{u}_{1}s}\ll 1.$$

Since we have shown that the fraction of the torus occupied by successful type 1 families is small, it follows from the proof of Theorem 2 that if we run time at rate 1/Nu₁s then type 1 mutations are a rate 1 Poisson process.

Denote the number of successful type 1 mutations to arrive by time t by M(t), and their arrival times by T₁, …,. Since we can know that overlaps occur with negligible probability we compute that

$$P({\sigma }_2>t)=E\text{ exp }(-u_{2}s\sum _{j=1}^{M(t)}{V}_j(t)),$$

where

$$V_j(t)=\frac{{\gamma }_d{c}_d^d(s){(t-T_j)}^{d+1}}{d+1}.$$

We define

$$\varphi (t)=\frac{1}{t}{\int }_0^t\text{exp}(-\frac{u_{2}s{\gamma }_d{c}_d^d(s)}{d+1}{(t-x)}^{d+1})dx,$$

so that P(σ₂ > t|M(t)) = (ϕ(t))^M(t). Next consider t′ = t/Nu₁s, then

$$\varphi (t\prime )=\frac{N{u}_{1}s}{t}{\int }_0^{t/N{u}_{1}s}\text{exp}(-\frac{u_{2}s{\gamma }_d{c}_d^d(s)}{d+1}{(t/N{u}_{1}s-x)}^{d+1})dx=\frac{1}{t}{\int }_0^t\text{exp}(-\frac{u_{2}s{\gamma }_d{c}_d^d(s)}{(d+1){(N{u}_{1}s)}^{d+1}}{(t-x)}^{d+1})dx\to \frac{1}{t}{\int }_0^t\text{exp }[-\frac{{\gamma }_d}{(d+1)I}{y}^{d+1}]dy\doteq \hat{\varphi }(t).$$

The limit in the previous display comes from the fact that 1/Γ → 1/I as s → 0.

Note that M(t′) is a Poisson random variable with mean t, so

$$P({\sigma }_2>t\prime )=\text{exp }[t(\varphi (t\prime )-1)]\to \text{exp }\left[t\right(\hat{\varphi }(t)-1\left)\right]$$

as s → 0.

Appendix G: Proof of Theorem 1

Convergence to Branching Brownian Motion

This part of the proof is from Durrett and Zähle (1997). To make it easier to compare with their computation, we use their time scale which is 2d times as fast as the one used in this paper. When we are done we have to divide the speeds computed here by 2d. Let ζ_t be the coalescing random walk in which:

1. Particles jump at rate 2d to a randomly chosen neighboring site.

2. Particles give birth at rate s to a particle sent to a randomly chosen neighboring site.

3. If a particle lands on an occupied site (due to jump or a birth) then the two coalesce to 1.

If we let ${\zeta }_t^B$ be the system starting with ${\zeta }_0^B=B$ and let ${\xi }_t^A$ be the biased voter model starting from ${\xi }_0^A=A$ then the two systems satisfy the duality equation (24):

$$P({\xi }_t^A\cap B\ne \varnothing )=P({\zeta }_t^B\cap A\ne \varnothing ).$$

In d ≥ 3 random walks are transient, so there is positive probability β_d that an offspring will never coalesce with its parent. Durrett and Zähle (1997) show that in this case if time is run at rate 1/s, and space is scaled by $1/\sqrt{s}$, the coalescing random walk converges to a branching Brownian motion χ_t in which

1. Particles perform independent Brownian motions run at rate 2

2. and give birth to new particles at rate β_d.

In order to achieve weak convergence they have to remove the particles that coalesce with their parents, because these result in temporary increases of the population that last (on the sped up time scale) for times of order s. To do this, they ignore the new born particles for time $\tau (s)=\sqrt{s}$ before we assign them mass 1.

In d = 2 random walks are recurrent but the probability an offspring does not coalesce with its parent for time >t is

$$~\pi /(\text{log }t)$$ (43)

see e.g., Lemma 3.1 of Zähle, Cox and Durrett (2005). To compensate for the fact that most particles coalesce with their parents, they run time at rate h(s) = (1/s) log(1/s) and scale space by $\sqrt{h(s)}$. Furthermore we ignore the new born particles for time $\tau (s)=1/\sqrt{\text{log}(1/s)}$ (on the sped up time scale) before we assign them mass 1. Note that on the sped-up time scale we create new particles at rate sh(s) = log(1/s), and we assign mass to only the fraction of those that survive for τ(s) units of time, which from (43) is ~ π/ log(1/s). Therefore we assign mass to new particles at O(1) rate. Based on this the rescaled coalescing random walk converges to a branching Brownian motion χ_t in which

1. Particles perform independent Brownian motions run at rate 2

2. Give birth to new particles at rate π.

At this point if one ignores the detail of interchanging two limits Theorem 2 is obvious. If particles are born at rate

$$\rho =\{\begin{array}{cc}{\beta }_d\hfill & d\ge 3\hfill \\ \pi \hfill & d=2\hfill \end{array}$$

and perform Brownian motions with covariance matrix σ² I then the mean measure at time t for the process started with a single particle at 0 at time 0 is

$$e^{wt}\frac{1}{{(2\pi t)}^{d/2}}{e}^{-|x{|}^2/2{\sigma }^{2}t}$$ (44)

Ignoring the polynomial this is 1 when

$$|x|=t\sqrt{2{\sigma }^{2}w}$$

Taking into account that time is run at rate 1/s in d ≥ 3 and at rate (1/s) log(1/s) in d = 2, the desired result follows.

The lower bound on the speed follows from a block construction. The argument is almost the same as in Durrett and Zähle (2007), but we have to change some details to get a sharp result. Let I = [−1, 1]^d, let e₁ be the first unit vector, let $\upsilon <\sqrt{4\rho }$, and for each m let I_m = 2m(Lυ)e₁ + I. Let χ̂_t be a modification of the branching Brownian motion in which particles are killed when they land outside [−4Lυ, 4Lυ]^d. Calculations on page 1760 of Durrett and Zähle (2007) show that for any ε > 0, we can pick L large and then K large enough so that if there are at least K particles in I₀ in ζ̂₀ then with probability ≥ 1−ε we have |ζ̂(L²) ∩ I₁| ≥ K and |ζ̂(L²) ∩ I₋₁| ≥ K. Picking L large makes the mean of |ζ̂(L²) ∩ I₁| large because of (44). Then picking K large controls the probability of deviations from the mean.

For integers m ≥ 0 and n with m + n even let θ(m, n) = 1 if |χ̂(nL²) ∩ I_m| ≥ K. The result in the previous paragraph implies that χ dominates 1-dependent oriented percolation with density 1 − ε. Let r_n = sup{m : θ(m, n) = 1}. A result in Durrett (1984), see (2) on page 1030, implies that if δ > 0 and ε < ε(δ) then on the set where the oriented percolation does not die out, lim inf_n→∞ r_n/n ≥ 1−δ. This implies that for the rescaled process the edge speed is ≥ (1 − δ)υ, which gives the lower bound.

The upper bound is proved by comparing the dual process on its original time scale with the branching process. Suppose first that d ≥ 3. If we ignore newborn particles that will coalesce with their parents then we have a branching process in which particles are born at rate w = β_ds. We ignore coalescence events other than mother-daughter so we can project onto the x-axis to get a one-dimensional branching process Z_t at time t. The number of particles to the right of ct at time t is

$$E{Z}_t(ct,\infty )=e^{wt}P(S_t\ge ct)$$ (45)

where S_t is a random walks that takes steps that are ±1 with equal probability at rate 2. The steps have moment generating function

$$\varphi (\theta )=\frac{e^{\theta }+e^{-\theta }}{2}$$

so the continuous time walk has

$${\psi }_t(\theta )=E\text{ exp}(\theta S_t)=\sum _{n=0}^{\infty }{e}^{-2t}\frac{{[2t]}^n}{n!}\varphi {(\theta )}^n=\text{exp }(2t(\varphi (\theta )-1)).$$

As θ → 0, ϕ(θ) − 1 ~ θ²/2, so if δ > 0 and 0 < θ < θ₀(δ)

$$\varphi (\theta )-1\le \frac{{\theta }^2}{2-\delta }.$$

Using Markov’s inequality,

$$P(S_t\ge (a+b)t)\le e^{-{\theta }_a(a+b)t}{\psi }_t({\theta }_a)\le \text{exp }(-t[{\theta }_a(a+b)-\frac{2{\theta }_a^2}{2-\delta }\left]\right)$$

Changing notation θ = a/2, the right-hand side is

$$=\text{exp }(-t[\frac{a(a+b)}{2}-\frac{a^2}{2(2-\delta )}\left]\right)=\text{exp }(-t[\frac{ab}{2}+\frac{a^2(1-\delta )}{2(2-\delta )}\left]\right)$$

If we let $a=\sqrt{2w(2-\delta )/(1-2\delta )}$, which is just a little larger than $\sqrt{4w}$ then the above is

$$\le \text{exp }(-t[\frac{1-\delta }{1-2\delta }w+\frac{ab}{2}\left]\right)$$

Using (45)

$$P(Z_t((a+b)t,\infty ))>0)\le \text{exp }(-t[\frac{\delta w}{1-2\delta }+\frac{ab}{2}]).$$

To bound the spread of the biased voter model, let Λ = ℤ^d − [−at, at]^d, By duality

$$P({\xi }_t^0\cap {[-\mathit{\text{at}},\mathit{\text{at}}]}^d\ne \varnothing )=P(0\in {\zeta }_t^{\mathrm{\Lambda }})\le \sum _{x\in \mathrm{\Lambda }}P(0\in {\zeta }_t^x)\le \sum _{k=\mathit{\text{at}}}^{\infty }{c}_d{k}^{d-1}P(Z_t(k,\infty )>0)\le e^{-ct}.$$

To prove the result in d = 2 we will compare the dual process with a branching random walk, where if multiple offspring land on one site they are all retained. Modifying the construction of Durrett and Zähle (2007) we ignore new born particles for time 1/s, and add them to the dual only if they have not collided with their parents. Let Z_t denote the number of particles in the modified branching random walk by time t and let m(t) = E[Z_t]. From the result (43) we know that the fraction of newly created particles that are eventually added to the process is ~ π/ log(1/s). Thus for t > 1/s we have

$$m(t)\le \text{exp }\left(\frac{\pi s}{\text{log}(1/s)}t\right).$$

If we set w = πs/ log(1/s) and repeat the calculation for the case d ≥ 3, we obtain the desired result in d = 2.