Sparse Reconstruction Techniques in MRI: Methods, Applications, and Challenges to Clinical Adoption

Abstract

The family of sparse reconstruction techniques, including the recently introduced compressed sensing framework, has been extensively explored to reduce scan times in Magnetic Resonance Imaging (MRI). While there are many different methods that fall under the general umbrella of sparse reconstructions, they all rely on the idea that a priori information about the sparsity of MR images can be employed to reconstruct full images from undersampled data. This review describes the basic ideas behind sparse reconstruction techniques, how they could be applied to improve MR imaging, and the open challenges to their general adoption in a clinical setting. The fundamental principles underlying different classes of sparse reconstructions techniques are examined, and the requirements that each make on the undersampled data outlined. Applications that could potentially benefit from the accelerations that sparse reconstructions could provide are described, and clinical studies using sparse reconstructions reviewed. Lastly, technical and clinical challenges to widespread implementation of sparse reconstruction techniques, including optimization, reconstruction times, artifact appearance, and comparison with current gold-standards, are discussed.

Introduction

Magnetic Resonance Imaging (MRI) scans are often long, and it can be challenging and sometimes impossible for patients to comply with long requisite periods of stillness or breath-hold commands for imaging certain organs. Moreover, rapid motion or contrast changes are difficult to capture with MRI, and any anatomic, physiologic, or contrast media concentration changes that occur during data collection can lead to errors in the resulting images. There are many clinical applications where information from MRI could be useful, but this information cannot be captured accurately with standard MR imaging techniques.

Significant research effort has been directed towards finding ways to accelerate MR imaging. Techniques including the family of parallel imaging reconstruction methods^1–4 have been successful in reducing clinical MRI scan times by factors of two or four, or even higher in some applications^5–8. These acceleration techniques have also been used to improve image quality or reduce artifacts while maintaining scan time^9,10. However, the scan time reduction with parallel imaging is limited, and other ways of reconstructing images from undersampled data have been explored, including sparse reconstruction methods such as compressed sensing^11–28.

While compressed sensing has recently received a lot of attention for its potential to accelerate MRI data collection, compressed sensing is just one type of reconstruction which exploits image sparsity to reduce scan time and/or improve image quality. Other sparse reconstruction techniques include partially separable techniques^29–45, k-t methods^46–54 and model based reconstructions^55–74. At the heart of these sparse reconstructions is the idea that MR images are compressible, or contain redundant information. If the data can be undersampled in such a way that the essential components are still captured, data collection time can be dramatically reduced while maintaining image quality. Because these techniques rely on image sparsity, and not hardware as in parallel imaging, the potential for scan time reduction exceeds that of parallel imaging. Indeed, some groups have shown that sparse reconstruction techniques could be used to generate images that have been accelerated by factors of 225³⁰ or more⁷⁵. Such high acceleration rates and resulting increased spatial and/or temporal resolution could make possible applications that have traditionally been impossible with MRI. However, while the promise of extremely rapid imaging has driven significant research into sparse reconstruction techniques, many of these methods have fallen short of entering routine clinical practice. When employed for imaging, conservative acceleration rates are often used due to the observation that sparse imaging techniques such as compressed sensing may generate unpredictable artifacts that are highly dependent on the object, potentially interfering with image interpretation. Reconstructions of dynamic datasets which take information from multiple timeframes into account, and which thus have a long “temporal footprint,” may lead to images with inaccurate temporal behavior, also compromising clinical utility. Lengthy reconstruction times and many tunable parameters complicate optimization and assessment for clinical efficacy. Such technical and clinical challenges make clinical adoption of these methods difficult and can only be solved through combined input from MR physicists/engineers and physicians.

This review describes the basic concepts behind sparse reconstruction techniques, how these technologies could be applied to improve MR imaging, and the challenges to widespread implementation of sparse reconstruction techniques from both a technical and clinical perspective.

MRI Data Collection and Acceleration

MRI data are collected in a space that is mathematically related to the image, called k-space. Once the k-space data have been collected, they can then be transformed into an image using the mathematical function that relates the two spaces, the Fourier Transform (as shown in Figure 1a). Collecting a complete set of k-space points can be time-consuming, and there are many situations in which it is desirable to accelerate the data collection process by simply collecting less data, or undersampling the k-space data. However, while undersampling k-space can reduce scan time, it often leads to artifacts in the image.

Figure 1.

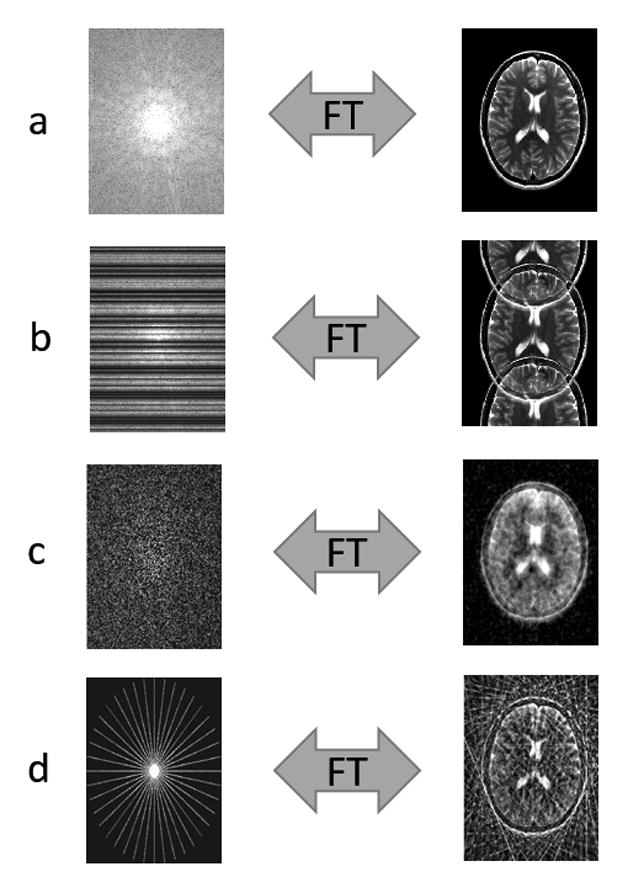
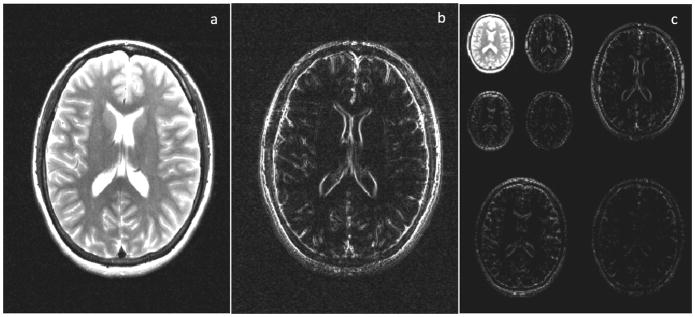
(a) Fully sampled k-space is converted to an image via the Fourier Transform. (b) Cartesian undersampling by factor of 2, where every other line of k-space is missing. The resulting image is corrupted by aliasing or fold-over artifacts. (c) Random Cartesian undersampling. If k-space points are skipped in such random fashion, the resulting aliasing artifacts no longer appear as distinct replicas of the image (as in (b)), but instead as blurring or noise-like artifacts. This type of sampling is typically not realizable in 2D. (d) Radial undersampling by factor of 9. The resulting image contains streak artifacts due to the undersampling, but the bulk of the image is recognizable since the center of k-space is well sampled.

Artifacts caused by undersampling can take on many forms depending on the sampling scheme. If the data are undersampled such that only every other line of the full k-space were collected, the total scan time is cut in half. However, skipping lines results in aliasing, or fold-over, artifacts in the image (Figure 1b). Other sampling patterns, such as the random undersampling shown in 1c or the radial undersampling in 1d, will result in different types of artifacts. In most cases, the image must be “reconstructed” to eliminate these aliasing artifacts before it can be used clinically. There are several techniques that can be used to reconstruct full images from incomplete data, including the sparse reconstruction techniques that are the topic of this review.

Sparse Reconstruction Techniques

Sparse reconstruction (including methods which fall under the terms constrained reconstructions, compressive sampling, and compressed sensing) is a set of techniques which uses image properties that are known a priori to reconstruct MR images from highly undersampled k-space data. While there are many different types of sparse reconstruction methods, they all share the same overarching goal: To generate an image that is consistent with the data collected which also exhibits specific image properties, determined by the user.

Sparse reconstructions are based upon the combination of three main concepts:

1. Image Sparsity

2. “Noise-like” or benign aliasing artifacts

3. The use of a specialized reconstruction for image recovery

In a “sparse” image, most of the information in the image is contained in small number of image pixels. One example of a sparse MR image is an angiogram, where a few image pixels are bright (with high signal intensity values), and the rest are dark (with low values, ideally zero). Figure 2a shows a sparse MR image, in this case a single partition subtraction image from a 3D abdominal and pelvic contrast-enhanced MR angiogram. If undersampled k-space data are collected, the resulting accelerated image will contain aliasing artifacts and may no longer be sparse; this is the case in Figure 2b. However, if it is known a priori that the fully-sampled image should be sparse, and that the lack of sparsity in the accelerated image is due to aliasing, it may be possible to use a sparse reconstruction to recover the unaliased, sparse image from the undersampled data.

Figure 2.

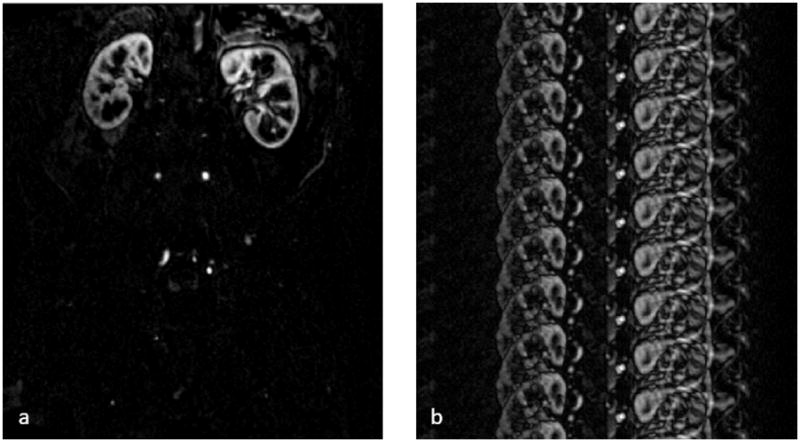
(a) An example of a sparse MR image, specifically a single partition subtraction image from a 3D abdominal and pelvic contrast enhanced MR angiogram, where few of the image pixels contain signal (and are bright), but most of the image pixels are near zero. (b) When the k-space data are undersampled, the resulting image is no longer sparse due to the presence of aliasing artifacts. If it is known a priori that the image should be sparse, a sparse reconstruction can be used to recover the original image.

Most MR images are not intrinsically sparse, but as long as the image is sparse in some representation, or domain, a sparse reconstruction can still be used. A sparsifying transform, often denoted by the symbol Ψ, is a reversible user-selected mathematical operation that can be applied to an image to increase sparsity. For instance, the image in Figure 3a, which is not sparse, can be made sparser by applying a spatial finite differences transform, resulting in Figure 3b. The spatial finite differences transform involves calculating the difference between intensity values of neighboring pixels, thereby highlighting edges in the image. Figure 3c shows the sparse image that results from applying a wavelet transform to the image in Figure 3a.

Figure 3.

(a) An axial brain image. (b) Horizontal finite differences transform of the image shown in (a). This transform shows the differences between neighboring pixels, and thus highlights edges in the image. Many images are sparse, i.e. contain more pixels with near-zero values, after such a spatial finite differences transform. (c) Wavelet transform of the image shown in (a), where the transformed images are again sparse compared to the untransformed image (a).

In addition to exhibiting spatial sparsity, some dynamic MR images are temporally sparse, or sparse “through time.” An example of such a dynamic dataset is a time series of images showing cardiac motion, as shown in Figure 4a. In this example, only a small subset of image pixels varies through the image series. Such images can be made sparse by subtracting one time frame from the next, as depicted in Figure 4b. The resulting temporal difference image is sparser than the original because only pixels near the heart, where motion occurs, are non-zero. Figure 4c shows how the Fourier transform in the temporal direction can also be used to sparsify dynamic images.

Figure 4.

(a) A time series of dynamic cardiac images is shown, where the x-y plane shows the images, and the t axis depicts the time dimension (left). Three different images of the heart show the motion that occurs through time (right). (b) When one frame from the dynamic dataset is subtracted from another, the result is a sparser image because many tissues are stationary from frame to frame. Only pixels near the heart change, and these are reflected in the temporal difference image. (c) The 3D space-time data can be examined along one slice of the x-t plane (left), designated by the white dotted line. The areas with significant motion can be clearly seen in the “x-t space” image (middle). If a Fourier transform is applied to the x-t space in the time direction, the result is the image representation in the spatiotemporal domain (x-f space, right). Static areas of the image will only have a single bright pixel in the x-f space (orange arrow), and only pixels with significant motion will contribute many non-zero pixels (purple arrow), making x-f space sparse in many dynamic applications.

The second requirement for sparse reconstruction techniques is that the true image signal is distinguishable from the aliasing artifacts that arise from undersampling. While sparsity in the image domain is a key feature for sparse reconstructions, it is important to recall that MRI data are collected in k-space. The selection of an appropriate k-space sampling pattern, which determines the appearance of the aliasing artifacts, is also essential to the ability of the sparse reconstruction to generate an acceptable image. Many sparse reconstruction methods rely on using a data sampling pattern that results in incoherent, or “noise-like” aliasing artifacts. With a regular, evenly spaced undersampling pattern where every other line is skipped, the fold-over artifacts are clearly visible and indistinguishable from the true signal (see Figure 1b). However, if k-space is randomly undersampled, the aliasing artifacts look more like noise, and the actual image can be readily distinguished from the artifacts (Figure 1c).

Random undersampling in k-space provides the noise-like aliasing necessary for many sparse reconstruction algorithms. However, the data collection path through k-space must be smooth, and thus for 2D imaging applications, truly random Cartesian undersampling is not realizable. When encoding MRI data for 3D or dynamic 2D datasets, random or pseudo-random sampling can be achieved by appropriately collecting phase encoding lines^4,13,76,77. In place of random undersampling in 2D, non-Cartesian trajectories including radial^14,78,79, spiral^64,80,81,, and rosette paths⁸², among others⁸³, can be employed. These non-Cartesian paths offer a smooth movement through k-space that can be implemented in practice while also providing noise-like artifacts when undersampled (see Figure 1d for an example of radial undersampling). 3D non-Cartesian trajectories have also been explored, including radial⁸⁴ or cone-shaped paths⁸⁵. Some of these sampling trajectories, including 3D radial, lead to such diffuse noise-like artifacts when undersampled at modest levels that it is not necessary to resolve the artifacts, and a specialized reconstruction scheme is not needed⁸⁴. Because the selection of the appropriate trajectory is so important, trajectory optimization for sparse reconstructions is itself an area of research^86,87

All sparse reconstruction methods make use of sparsity and specialized sampling patterns, but the information used to recover unaliased images varies greatly from method to method. The large number and variety of sparse reconstruction techniques makes it impossible to describe each of them here. However, it is possible to roughly group some of the methods based on their underlying assumptions of the data. It is important to note that there is some overlap between these techniques, and other techniques may not fall into any of these categories. However, the basic ideas of sparse reconstructions can be generally understood by looking at techniques in these four groups:

• Methods which separate spatial characteristics from temporal dynamics (such as RIGR²⁹ or HYPR³⁰)

• Methods which separate aliased pixels in the spatiotemporal domain (such as UNFOLD⁴⁸ or k-t BLAST⁵⁰)

• Compressed sensing techniques (including L1 SPIRiT¹³ and k-t SPARSE-SENSE¹⁵)

• Model-based reconstruction methods (including dictionary-based techniques such as Magnetic Resonance Fingerprinting⁶⁴ and patch-based methods)

Each of these groups of reconstruction methods will be briefly described below.

Separable Methods

Some of the first sparse reconstruction techniques to be employed used the concept of “partial separability,” or the idea that spatial information could be separated from temporal changes in a dynamic series of images. In such methods, aliased or low resolution images which capture rapid temporal dynamics are used together with one or more static high spatial resolution images to generate a dynamic series of images with a high spatial resolution showing the desired contrast changes or motion. Some methods use temporal redundancy only, including MR fluoroscopy³² as well as view-sharing and keyhole imaging^33–36. Other more sophisticated methods use both temporal and spatial redundancy to improve the reconstruction. Methods in this group include the early sparse reconstruction technique RIGR²⁹ as well as HYPR³⁰ and its variants^37–44. While these methods do not explicitly enforce sparsity, they do rely on the assumption that few image pixels actually change from frame to frame, and that this change is slow and smooth. In HYPR (shown schematically in Figure 5), it is assumed that the signal intensity changes primarily in the blood vessels during the arrival of the contrast bolus in a contrast-enhanced MR Angiography exam. Following the injection of contrast agent, radial data are collected in such a way that they can be highly undersampled to generate low spatial resolution images with a high temporal resolution (Figure 5, top), or reconstructed together to make one high-resolution static image that does not show contrast dynamics. The high-resolution static image is known as the composite image and it shows the locations of all of the blood vessels (Figure 5, center). While the undersampled dynamic timeframes show many areas of “bright” signal due to the undersampling artifacts, only the pixels that are also bright in the composite image are actually blood vessels and should be bright in each of the single timeframes. The HYPR reconstruction uses the undersampled dynamic images to weight the composite image to give it the correct contrast for each timeframe. In this way, a high-resolution dynamic time series can be recovered (Figure 5, bottom). More detailed descriptions of these types of techniques can be found elsewhere^31,75.

Figure 5.

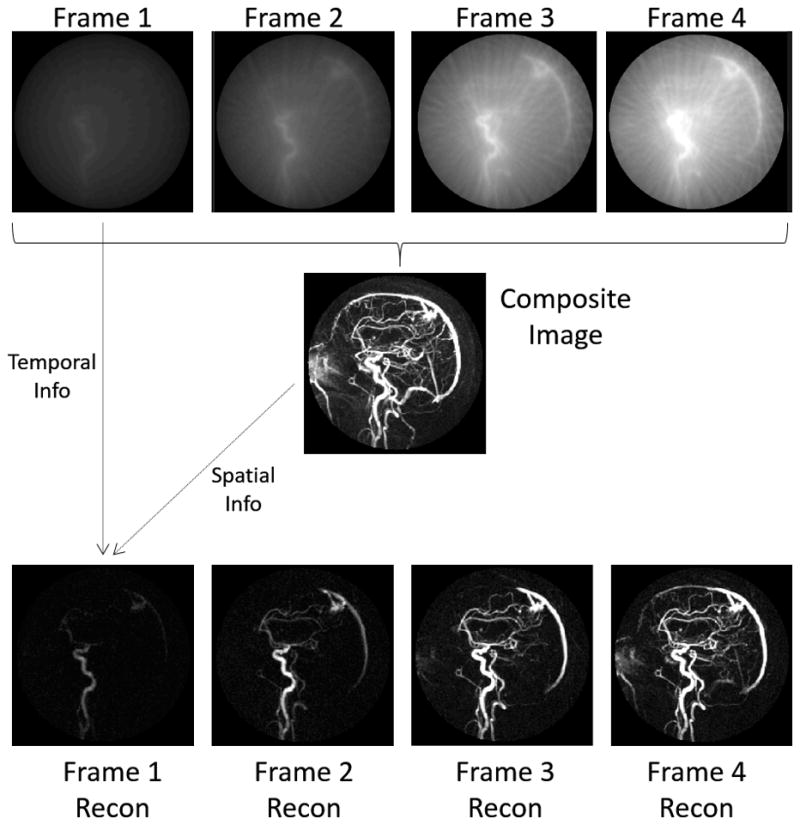
(top) By sampling data using an undersampled radial scheme, dynamic images of low spatial resolution but high temporal resolution can be collected. These images show the enhancement in different regions over time, but are not usable because of their low resolution. (middle) By gathering all acquired radial projections from each timeframe, a high spatial resolution composite image can be created. This single static image displays all enhanced vessels at a high resolution, but does not show the order in which they enhance. HYPR works by combining spatial information from the high-resolution composite image with temporal information from the low-resolution dynamic images. This reconstruction yields a time series of high spatial and high temporal resolution images (bottom row) that shows dynamic enhancement of the vessels.

These partially separable techniques can only be used to accelerate dynamic time series, and they function best when the changes from timeframe to timeframe are small. The application that is most frequently accelerated with such techniques is contrast-enhanced MR Angiography, and acceleration rates of over 800⁷⁵ have been reported using separable methods due to the high degree of sparsity in the image series. It may also be possible to accelerate myocardial perfusion^37,38, pulmonary perfusion⁴⁰, and ultra-short TE spectroscopy³⁹ using the ideas of partial separability.

Another group of techniques known as low-rank completion methods uses the idea that the background of the image can be separated mathematically from dynamic portions^58,88–91. If only a few dynamic components are required to represent signal changes, the signal is sparse in this representation. Although included in the separable methods section, these techniques are typically combined with explicit sparsity constraints in compressed sensing-type reconstructions. Additionally, some such methods can be thought of as model-based techniques if the sparse components make up a dictionary. Such hybrid techniques serve to highlight the complex nature of sparse reconstructions and lack of clear boundaries separating the different groups of methods.

k-t Methods

Like partially separable techniques, k-t methods^46–54 take advantage of the sparsity of a dynamic time series. However, unlike those methods described above, k-t techniques use spatial and temporal sparsity (or joint spatiotemporal sparsity) together instead of separating them. While a detailed review of k-t methods can be found elsewhere⁵¹, this section describes the basic concepts.

In many types of dynamic images, only certain areas of the images contain motion, while other portions remain static. For example, in a cardiac cine image series, it can be assumed that organs other than the heart do not move substantially during the imaging process. This can be seen by looking at an x-t plot of the dynamic images, or the cross-section which shows changes in the images through time (Figure 4c). In the so-called x-f space, which is calculated by applying the Fourier transform through time, only portions of the image that move will lead to signal spread (indicated with the purple arrow); pixels with no motion will be confined to a single pixel (indicated with the orange arrow). This property makes the x-f space sparse in imaging applications were few pixels change over time. If the accelerated k-space data are undersampled in an interleaved fashion, the aliasing in the images appears as distinct and often non-overlapping replicas in the x-f space. k-t methods, which include techniques such as UNFOLD⁴⁸ and k-t BLAST/SENSE⁵⁰, rely on the separation of these replicas in the x-f space for reconstruction.

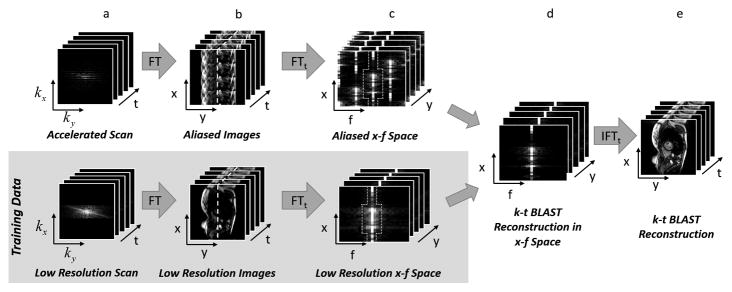
UNFOLD uses a low-resolution training dataset to determine what the signal should look like in the full x-f space, and then filters the accelerated x-f space to remove the aliasing artifacts. k-t BLAST⁵⁰ instead takes the approach of resolving the copies by determining an unmixing matrix using the low-resolution time series, which can provide a more nuanced reconstruction of signals in the x-f space. Figure 6 illustrates the basic idea of k-t BLAST. Aliasing from interleaved undersampling can be seen in the accelerated data in x-f space (Figure 6c, top), but with knowledge of the structure of the true x-f profile (dotted line in Figure 6c, bottom), a set of unaliased images can be generated (Figure 6e). k-t SENSE is a form of k-t BLAST in which parallel imaging is incorporated to help resolve aliased pixels, enabling higher acceleration factors to be employed. Other k-t variants exist, including those that involve parallel imaging in a different way or use sparsifying transforms other than the temporal Fourier transform^52–54.

Figure 6.

A schematic of the k-t BLAST reconstruction technique. Both undersampled data with high spatial and temporal resolution (a, top) and fully-sampled low resolution data (a, bottom) are collected. The undersampled accelerated data are used to generate the image, and the low resolution data serve as training data for the k-t BLAST reconstruction. After using Fourier transform to convert the datasets into the image domain (b), the aliasing in the undersampled data can be seen (b, top). By applying a Fourier transform in time, the data are converted to the x-f domain (c). If the undersampled data are collected using the k-t interleaved sampling pattern, the duplicates seen in the x-f domain will be offset in the undersampled data (c, top). However, the low resolution training data do not show aliasing in the x-f domain because they are fully-sampled (c, bottom). A knowledge of the structure of the x-f training data (indicated by the dashed shape in x-f space) can be used to remove aliasing in the high resolution aliased x-f space (d). The final images are generated by applying an inverse Fourier transform to the reconstructed high resolution x-f data (e).

The various k-t methods provide the ability to accelerate dynamic acquisitions. However, they only work for dynamic time series and perform best when motion is smooth and limited to a subsection of the image. These methods have been applied to cardiac functional and perfusion imaging^49,50,53,54 and fMRI⁴⁸ but have the potential to be used in any case which meets these requirements. Additionally, k-t methods are often combined with other types of sparse reconstruction techniques, such as the compressed sensing-based k-t FOCUSS⁴⁷ and k-t SPARSE²⁸.

Compressed Sensing

Although sparsity has been exploited to accelerate MR imaging for many years, sparse reconstructions regained popularity after the introduction of compressed sensing (also known as compressive sampling)^11,12. The basic idea of compressed sensing is that if MRI data are collected such that the undersampling artifacts appear as noise (incoherent aliasing) and the images are sparse, the full image can be recovered using an appropriate non-linear reconstruction method. These nonlinear reconstruction techniques enforce two conditions:

1. Sparsity of the image in the transform domain

2. Consistency of the reconstruction with the acquired data

The first condition enables aliasing artifacts to be separated from actual signals in the image by requiring that the reconstructed image is sparse (or sparse in the transform domain). The second condition ensures that the reconstruction does not replace actual acquired data with arbitrary data in the interest of making the final solution sparse. Thus these two requirements balance the desire for a sparse image, and an image that is consistent with the data collected.

This problem can be formulated mathematically using the following minimization:

$$\text{minimize}{\Vert F_{u}m-y\Vert }_2^2+\lambda {\Vert \mathrm{\Psi }m\Vert }_1$$ (1)

where Ψ is a sparsifying transform chosen by the user to convert the image m into a sparse domain, y are the actual undersampled k-space data acquired, and F_u is the Fourier transform for the data collection trajectory that was employed. The first term ensures that the reconstructed image m is consistent with the k-space data that have been collected, y. This term calculates the least-squares difference, denoted as ||•||₂, between the k-space of the reconstructed image and the k-space that was acquired. The second term ensures that the reconstructed image m is sparse in the selected transform domain. This term uses the L1 norm, ||•||₁, which calculates the degree of sparsity in the image by summing the absolute value of the pixels in the image (or the image after the sparsifying transform). Thus, described in words, this equation seeks to find an image m which is both sparse (or transform sparse) and also consistent with the data that has been collected The so-called regularization parameter, λ, controls the relative importance of the two terms in the reconstruction. Selecting a small value of λ will lead to a solution that is closer to the collected data and relies less on the sparsity term, whereas a large value of λ will lead to a final image that may deviate from the collected data in the interest of providing a sparse solution.

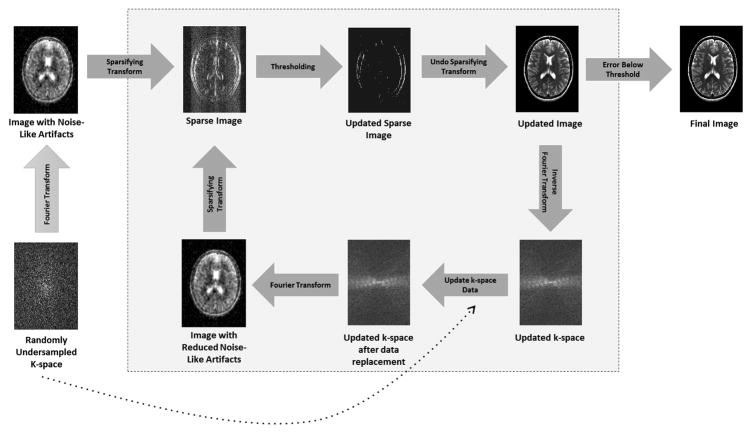
A schematic example of a basic compressed sensing algorithm is shown in Figure 7. The gray box shows how the algorithm iterates between enforcing sparsity (top row) and ensuring data consistency (bottom row). Note that there are much more elegant and efficient techniques which can be used to solve these minimization problems, for instance projections onto convex sets or iterative soft thresholding.

Figure 7.

A schematic of a simplified compressed sensing reconstruction. Randomly undersampled k-space data are collected (bottom left), leading to an image which exhibits noise-like aliasing artifacts (top left). A sparse representation of this undersampled image can be obtained by applying a sparsifying transform such as finite differences, which highlights edges. Because the artifacts look like noise, it is possible to retain most of the significant pixels in the sparse image while removing some noise-like artifacts by thresholding this image. After thresholding, only true edges remain, although some may have been lost in the thresholding process. An updated image is generated by “undoing” the sparsifying transform, and this updated image with reduced aliasing artifacts is converted back to k-space. This k-space may contain data that is different from the collected k-space data after the thresholding step. Therefore, to ensure data consistency, the original k-space data are reinserted into the k-space of the updated image. This updated k-space is then converted into an image, which is now both consistent with the original data and contains reduced aliasing artifacts, and the loop begins again. When the error between the previous iteration of the updated image and the current iteration reaches the stopping criteria set by the user, the iteration loop is broken and the final image is output.

Unlike the methods described in the previous sections, compressed sensing can be used to accelerate static images by using only spatial transforms, or temporal transforms can be included when reconstructing accelerated dynamic data. Parallel imaging is often incorporated into these techniques to further increase the data reduction factor and improve image quality^13,15,18. Because motion, including cardiac and respiratory motion, can reduce the efficacy of compressed sensing reconstructions, a number of groups have incorporated navigator information^19–21, image registration^22–24, or even an additional motion dimension^25,26, directly into the reconstruction.

An example of a static compressed sensing reconstruction is L1 SPIRiT¹³ which uses the parallel imaging method SPIRiT⁴ combined with a spatial wavelet transform to sparsify the images. L1 SPIRiT is an iterative reconstruction that is typically used with 3D Cartesian datasets collected using a pseudo-random Poisson disk sampling pattern. This technique has the potential to accelerate clinical MRI scans by a factor of 8 in applications such as pediatric body imaging^13,27.

k-t SPARSE-SENSE¹⁵ is a compressed sensing method which takes advantage of sparsity in the spatiotemporal domain by using a temporal total variation transform. This technique has been used for high frame rate dynamic cardiac imaging, angiography, and free-breathing liver imaging with acceleration factors up to 8. GRASP¹⁴ (Golden-Angle Radial Sparse Parallel) is a version of k-t SPARSE-SENSE which works with radial data collected in a continuous fashion for dynamic 3D imaging. GRASP has been demonstrated in dynamic contrast-enhanced free-breathing liver, pediatric body, breast, and neck imaging with acceleration factors up to 28.7.

While L1 SPIRiT and k-t SPARSE-SENSE/GRASP have been used as examples of compressed sensing techniques in this section, there are many more compressed sensing type reconstruction algorithms that have been presented in the literature and reviewed elsewhere^92,93.

Model-Based Methods

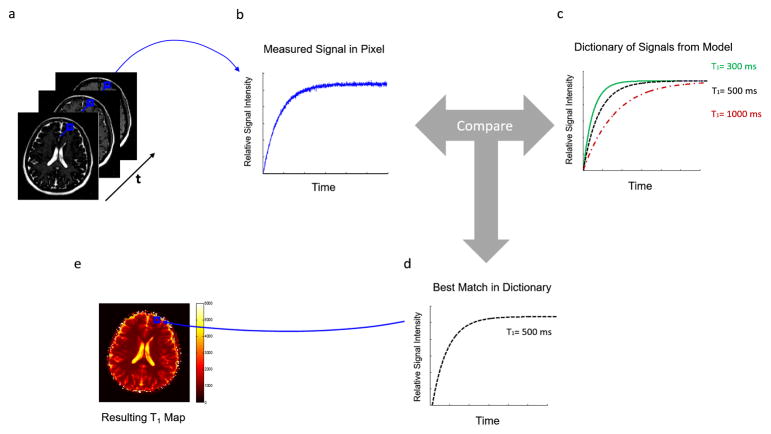
Model-based methods are another type of sparse reconstruction technique which make the assumption that the final image or time series can be described using a set of parameters that is much smaller than the total number of image pixels, which would indicate that the data are redundant and can tolerate high degrees of undersampling. For instance, in the case of T₁ relaxation parameter mapping, a time course made up of several T₁ weighted images is usually collected and used to determine the T₁ value for each pixel by performing a mathematical fit (Figure 8a and 8b). However, although many T₁ weighted images are collected to yield an accurate value of T₁, only two unknowns actually must be determined for each pixel, the proton density and T₁. Thus, a dictionary of possible time courses for the T₁ weighted images can be determined mathematically; these are the only possible time courses that can be found in the images (excluding noise), as the physics of T₁ relaxation are well understood (Figure 8c). If the images in the time course are randomly undersampled, this dictionary can be used to recover the T₁ maps despite the aliasing that results from the accelerated scan (Figure 8d and 8e).

Figure 8.

(a) From a set of rapidly collected undersampled T₁-weighted images, one pixel is selected and examined through time (b). With a knowledge of the underlying physics, a model can be used to calculate all possible signal timecourses for different values of T₁. In this case, the dictionary consists of signals which could arise from T₁ values of 300ms, 500ms, or 1000ms. The actually measured signal is then compared to the signals in the dictionary to find the closest match (d), in this case, the curve for T₁=500ms. (e) The value of 500ms is then assigned as the T₁ value for this pixel. The process is repeated for every pixel of interest to produce a T₁ map.

There are different ways of using a model to perform a sparse reconstruction. For instance, some sparse reconstruction techniques employ the dictionary of possible elements as a sparsifying transform in a compressed sensing reconstruction^55,59–63. MR Fingerprinting⁶⁴ is a dictionary-based approach in which highly undersampled pixel time courses are matched to a dictionary of possible time courses to derive T₁ and T₂ maps. While MR Fingerprinting does not rely on the image time series itself to be sparse, this method uses the idea that a sparse set of dictionary elements, in this case a single element, can be used to represent the time course of each pixel. Yet other techniques employ a signal model directly in the reconstruction to constrain the resulting images or time courses to follow a specific mathematical form^94–98. Such a parametric approach does not require the user to explicitly calculate all of the possible elements to form a dictionary, which may allow improved results as any values of the model parameters can result from the reconstruction (and not just those found in the dictionary). Although the example of T₁ mapping has been used here, any other physical property can be treated in the same manner if a well-defined mathematical relationship exists between the signal time course and the property to be measured, such as T₂ ⁶⁵, proton density⁵⁶, fat fraction^95–98, or susceptibility mapping⁹⁴. Additionally, there are methods which use the images themselves to determine an appropriate signal model; here an explicit knowledge of the mathematical model is not required^59,61,66.

In addition to using mathematical models to depict signal time courses, some sparse reconstruction techniques use spatial “patches” to model the information in MR images^67–74. Such methods assume that each block of pixels in an image can only be described by the elements in a dictionary of possible blocks. These possible blocks are determined either empirically or using a priori information such as a set of similar images. These techniques can use 2D^70,71 or 3D blocks ^72,73, and can even be combined with time course modeling methods for further sparsification^58,69.

Clinical Applications of Sparse Reconstruction Techniques

A sparse reconstruction technique is often directed towards accelerating a particular application, such as dynamic cardiac or abdominal imaging, MR angiography, or high-resolution brain imaging. The performance of the technique is then demonstrated in a small set of proof-of-concept reconstructions using in vivo data, typically collected from healthy volunteers and sometimes a small number of patients. However, the impact of the various sparse reconstruction techniques in clinical practice with regard to diagnostic accuracy has been less extensively studied⁹³. The following section describes some applications where sparse reconstructions hold clinical promise. The literature reviewed is representative, but by no means exhaustive.

Vascular and Flow Imaging

MR angiograms are relatively sparse in the image domain and can be further sparsified in both the image domain and in the time domain. Therefore, MR angiography (MRA) is a natural application for sparse reconstructions. Both contrast enhanced⁹⁹ and non-contrast enhanced MRA¹⁰⁰ have been examined in a variety of applications, including intracranial vasculature^101,102, carotids^103,104, coronaries¹⁹, and pulmonary veins¹⁰⁵. Reducing the acquisition time enables the dynamic visualization of the flow of blood sequentially into arteries and then veins via repeated rapid imaging. This may allow the characterization of pathologies such as abnormal blood flow dynamics and arteriovenous malformations¹⁰⁶.

The challenge of collecting angiograms in regions where the degree of physiological motion encountered requires high temporal resolution imaging to capture the anatomy or the contrast bolus during peak enhancement has also driven the development of fast imaging methods. Pulmonary angiography, thoracic angiography, and coronary angiography are important representative techniques in which respiratory and cardiac motion pose major difficulties, necessitating ultrafast imaging^{19,85,105,107–109}. Abdominal MR angiography poses the twin challenges of rapid contrast dynamics and a need for very large field of view coverage. Thus significant efforts to use sparse reconstruction techniques for acceleration in the abdomen are underway, both in adults and children¹¹⁰.

The use of sparse reconstructions has also been explored for improving 4D flow or phase contrast imaging¹¹¹, to evaluate valvular insufficiency, improve accuracy in delineating shunt pathology, assess anomalous flow in pulmonary veins, and visualize hemodynamics in congenital heart disease^112–116. Sparse reconstructions have been used to obtain single breath-hold characterization of portal flow¹¹⁷ and can yield improved vessel conspicuity while retaining accuracy of quantification of portal flow¹¹⁸. While the carotid vasculature does not pose the same motion problems as thoracic and abdominal regions, the very high resolutions needed for vessel wall imaging in these regions necessitate extremely long acquisitions (8–10 minutes are not unusual). Early exploration of sparse reconstructions in this setting in volunteers and two patients shows greater than 8-fold acceleration of the exam with improved flow quantification¹¹⁹.

Cardiac Imaging

Cardiac examinations are some of the longest MRI protocols and are dependent on patient compliance and the patient’s ability to hold his or her breath. Technologies for accelerating cardiac imaging using sparse reconstructions are being explored for free-breathing cine imaging^23,120–124 and for breath-held functional assessment of measurements such as left ventricular volume, ejection fraction, and mass^125–127. The largest study included 21 patients and showed that single accurate breath-hold functional measurements are feasible in patients with a variety of cardiac pathologies¹²⁶. Multiple groups are exploring the application of sparse reconstruction techniques to first pass perfusion imaging^15,128–132 in pathologies such as atrial fibrillation, where it was previously impossible to obtain diagnostic exams¹³³. Such advances could contribute to a highly efficient and rapid throughput approach that could greatly simplify cardiac MR¹³⁴. However, questions remain regarding image quality compared to traditional exams¹³⁴ and whether CS-based methods suffer from worsened spatiotemporal blurring compared to parallel imaging-based acceleration^135,136. Acceleration of late gadolinium enhancement (LGE) exams with sparse reconstructions for faster/free breathing acquisitions or greater anatomical coverage has also been explored^136–138. An early study of 3D isotropic LGE imaging on 28 patients indicates that accelerated scans may be used to visualize left ventricular scar with a high spatial resolution, and potentially pulmonary vein and left atrial scar post ablation for atrial fibrillation¹³⁷.

Abdominal and Pelvic Imaging

Abdominal imaging requires large fields-of-view for organs such as the liver, or entire abdominal/pelvic cavity for imaging the bowel for applications such as enterography, while retaining sufficient resolution for visualization and characterization of pathology. Children have particular difficulty in providing the long breath-holds required; these patients are scared and often sedated or anesthetized. Thus application to pediatric abdominal imaging is one of the first areas where early application of sparse reconstructions such as compressed sensing has been particularly promising, for improved delineation of key structures in the abdomen with significantly shortened acquisition times^{14,20,79,139,140}.

Abdominal perfusion imaging in kidneys and liver is particularly challenging for quantitative analysis due to the need for dynamic imaging of large fields-of-view at a high resolution. Ultrafast imaging techniques, including the family of sparse reconstruction techniques discussed here, are potentially enabling technologies for robust abdominal perfusion analysis with improved 3D coverage. Application of compressed sensing acquisitions has been reported for quantitative renal and hepatic perfusion imaging^141,142 with volumetric coverage and high spatial resolution. Similarly for MR enterography in Crohn Disease, a free-breathing accelerated acquisition could be used to enable perfusion measurements in addition to qualitative imaging of terminal ileitis, opening the door for quantitative analysis¹⁴³. Accelerated DCE imaging of the prostate with quantitative perfusion characterization has also been explored¹⁴⁴.

Fat and water imaging plays an important role in the abdomen and multiple groups have accelerated these acquisitions using sparse reconstructions^96–98,145. Faster imaging to reduce breath-hold lengths could lead to improved image quality, and acceleration for this purpose has been demonstrated^146,147 and used for measurement of hepatic steatosis in diabetic patients without compromising accuracy of measurement¹⁴⁷. Quantitative measurement of relaxation times in the upper abdominal organs with Magnetic Resonance Fingerprinting has also been explored, and early work indicates that colorectal cancer hepatic metastases can be differentiated from surrounding parenchyma¹⁴⁸.

MR Spectroscopic Imaging (MRSI) has potential in characterizing tumors in the prostate, but long acquisitions are required, which can be clinically prohibitive. Recent advances have shown that sparse reconstructions can be used to significantly reduce these acquisition times while providing quantitative information on multiple relevant metabolites. It remains to be seen whether such advances can make the technique more feasible for routine clinical application¹⁴⁹.

Neuroimaging

As in other anatomical regions, sparse reconstructions could be used in neuroimaging to enable exams that have traditionally been too long for practical use. For example, arterial spin labeling (ASL), a non-contrast method for measuring perfusion, can be made significantly faster and yet more accurate using sparse reconstructions¹⁵⁰. Similarly, accelerated dynamic contrast-enhanced imaging has been achieved for accurate characterization of brain perfusion parameters¹⁵¹. Accelerated scans have been used for qualitative and quantitative analysis of pituitary adenomas¹⁵². As with prostate, spectroscopic imaging can be shortened and made more feasible¹⁵³ for assessment of pathologies such as obstructive sleep apnea¹⁵⁴, which have been shown to be associated with biochemical alterations of multiple metabolites. Applications of quantitative relaxometry technologies such as MR Fingerprinting indicate that subtle but measurable region-specific aging-related changes may occur¹⁵⁵, leading to the possibility of using relaxation time changes to assess diffuse pathologies and potentially focal lesions.

Functional MRI (fMRI) is a challenging application requiring rapid imaging and quantitative characterization of very small signal changes. Sparse reconstruction approaches have been used to accelerate fMRI exams while still providing high quality activation maps in areas of low SNR¹⁵⁶ and improved sensitivity to functional activation⁸¹. Sparse imaging has also been employed to reduce susceptibility artifacts in fMRI and improve imaging efficiency, making use of the fact that hemodynamic signal changes in fMRI are typically small from frame to frame¹⁵⁷.

A major area of development within neuroimaging is diffusion tensor imaging (DTI). For applications such as high angular resolution diffusion imaging (HARDI), a very large number of high spatial resolution images must be obtained, which result in long acquisition times. Acceleration with sparse reconstruction techniques is being actively explored improve these q-space or HARDI acquisitions^158–161. In addition to tractography and basic neuroanatomical research, these technologies have application in accelerating fiber tracking around tumors for surgical planning¹⁶².

Lung Imaging

The high temporal resolution acquisitions enabled through modern reconstruction techniques are starting to make pulmonary MRI a feasible alternative to CT, and a number of groups are exploring the utility of sparse reconstruction techniques for imaging lung structure and function. Enabling the use of MRI for rapid and high-resolution structural assessment of the lungs, for instance in children with cystic fibrosis, could reduce the large burden of radiation associated with repeated CT scans. In a review exploring MR imaging for lung cancer screening, it has been suggested that compressed sensing may provide some of the acceleration needed for MR to image small tumors in the lungs¹⁶³. Another developing area of clinical interest has been imaging of the lungs and lung function using hyperpolarized ³He imaging¹⁶⁴. Acceleration enables accurate calculation of ventilation, with initial application in imaging ventilation changes in asthma¹⁶⁵. The same group has previously explored hyperpolarized ³He for chronic obstructive pulmonary disease (COPD)¹⁶⁶ and application to this pathology is also likely feasible. Alternatively, an ultrashort echo time (UTE) approach has been used with compressed sensing for imaging COPD patients, where UTE MR signal intensity correlates to CT density and can be related to pulmonary function metrics such as FEV1/FRC¹⁶⁷.

Musculoskeletal Imaging

While imaging of joints such as the knee is not intrinsically complicated by motion, many patients, especially children, have difficulty laying still for the entire exam. Early clinical implementations of sparse reconstructions for clinical use thus included imaging the knee for the pediatric population¹⁴⁰. Sparse reconstructions may make it possible to image areas such as the cartilage in the hip, which can be as thin as 1–2 mm, at higher spatial resolution in a given scan time. An area of particular interest in musculoskeletal radiology is the development of technologies that enable imaging near metal. Multispectral imaging approaches for imaging around metal can be accelerated using sparse reconstruction techniques, without loss of image quality, in clinically relevant settings such as patients with implanted spinal fixation hardware¹⁶⁸. Spectroscopic imaging of areas such as the calf¹⁶⁹ may also be feasible with the increases in imaging speed afforded by sparse reconstruction techniques.

High field sodium imaging of cartilage holds promise because it could help quantify glycosaminoglycan content, which in turn could relate to the degree of cartilage degradation in early osteoarthritis. It has been shown that sparse reconstructions can be used for faster and yet accurate quantitative sodium imaging of knee cartilage at 7T, opening the door for sodium imaging-based quantitative assessment of osteoarthritis¹⁷⁰. Quantification of T_1ρ similarly holds promise for characterization of osteoarthritis, and acceleration of T_1ρ mapping in the knee has been demonstrated in early feasibility studies^171,172. Accelerated dynamic functional metabolic imaging of phosphocreatine kinetics after calf muscle exercise has also been shown for 3D ³¹P spectroscopic imaging at 7T¹⁷³. Such technology could be used to study exercise physiology and also pathology related to altered bioenergetics in skeletal muscle. Accelerated fat fraction with incorporation of effects of R2* has been demonstrated for improving accuracy in fat fraction mapping in musculature of patients with Becker muscular dystrophy, with implications for clinical trials where such quantification is needed^174,175.

Technical Challenges

While sparse reconstruction techniques show promise in many MR applications, the selection and optimization of an acceleration technique for a given application is both technically and clinically challenging. Before a method can replace the current clinical standard-of-care technique, significant testing must be performed. In the best cases, this testing is difficult and time-consuming, and in the worst case, nearly impossible to perform due to the need for repeat patient scans. Moreover, the results of comparisons between sparse reconstruction techniques and more commonly-employed acceleration methods can yield different results depending on the specific application, reconstruction techniques that are examined, and method of comparison. Some groups have reported advantages when replacing conventional imaging methods with sparse reconstruction techniques^{25,109,114,162,176,177}, while others have seen that standard clinical techniques continue to outperform these novel methods^135,178. These conflicting reports stem from the challenges that basic scientists and clinicians alike face when employing sparse reconstruction methods. The following sections examine some of these challenges associated with both testing sparse reconstructions in a research setting as well as using sparse reconstructions in a clinical setting.

A major obstacle faced by researchers is that it is difficult to compare the quality of various reconstruction approaches, as the true test of a reconstruction is the diagnostic value of the resulting images. However, it is clearly not feasible for radiologist to assess the results of every reconstruction technique under development, and thus proxy metrics are often used. In some studies, authors calculate an “image error” metric by comparing the results of their image reconstruction to gold-standard images where all the data can be collected^86,175,179. However, the ability of the reconstruction technique to enable visualization of specific pathology and anatomy are far more important to a radiologist than a mathematical match to what might also be a flawed gold-standard. Thus, while the use of these metrics simplifies the comparison of techniques in a research setting, these analyses may lead to methods that do not translate well to clinical practice. Overall image quality or feature conspicuity as rated by a radiologist may be preferable^140,168,180 but even these are proxies for a true comparison of diagnostic accuracy in a clinical setting.

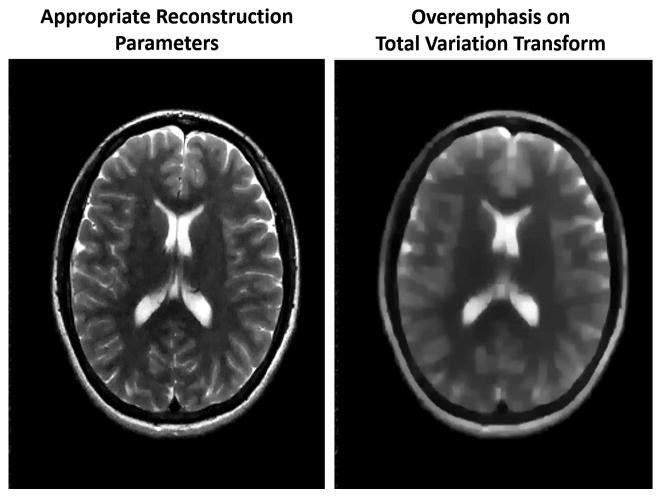
A second challenge is that the performance of each method depends strongly on the parameters used in the reconstruction. For instance, in compressed sensing reconstructions, a number of different sparsifying transforms beyond finite differences and wavelets have been proposed, including but not limited to singular value decomposition ¹⁸¹, principal component analysis^53,151, Haar¹⁸² and temporal Fourier transforms¹⁸². To complicate matters, some proposed compressed sensing implementations use more than one sparsifying transform^151,182. Once the number and type of sparsifying transforms have been selected, it is often necessary to determine an appropriate value for the regularization parameter associated with each transform. The results of the sparse reconstruction depend highly on the choice of the regularization parameter(s). Figure 9 demonstrates how an improperly tuned regularization value can lead to an image that has lost many essential features, as the sparsifying transform has been overemphasized. The optimal value of the tunable parameter(s) can be drastically different between methods, and while it may be possible to determine suitable parameters for an application through extensive testing¹⁸³, these parameters will apply only for that application¹⁸⁴. Some groups have attempted to move to techniques which do not require an adjustable regularization parameter^185,186, but the relative performance of these methods has not been assessed.

Figure 9.

(left) An image generated using a sparse reconstruction with properly tuned parameters. The image appears clear and with no obvious aliasing artifacts remaining. (right) An image generated with the same data and sparse reconstruction but with a larger regularization term. The overemphasis on the sparsifying transform, in this case total variation, leads to a blurry reconstruction.

In addition to the regularization parameter, the performance of many sparse reconstruction methods is highly dependent on the way that the MRI data are sampled and the degree of undersampling. Often retrospective undersampling is employed for testing, as only one dataset must be collected and simply downsampled with different sampling patterns. However, the behavior of the magnetization may be different when collecting accelerated data than it was when collecting fully-sampled data due to the underlying physics⁸⁷. Thus, the sampling pattern and acceleration rate that are found to be optimal with retrospectively undersampled data may not be the same for prospectively undersampled data. However, to collect prospectively undersampled data with different sampling patterns and acceleration factors, many more actual experiments must be performed, which is both expensive and time-consuming.

Another challenge is that most sparse reconstruction methods use complicated algorithms which can be difficult to implement. While researchers are able to develop and expand upon their own techniques, they may not be able to properly implement the techniques of others, even after the methods have been published. This makes unbiased comparisons of different sparse reconstruction techniques nearly impossible. However, there have been several attempts to help make fair and appropriate comparisons, which typically fall under the term “reproducible research”. For instance, there has been a push in the scientific community to deposit reconstruction code in code repositories, such as “MRI Unbound” ¹⁸⁷ or the fat-water toolbox that is available online as part of the ISMRM Workshop “Fat-Water Separation: Insights, Applications & Progress in MRI”¹⁸⁸. Code in these repositories can then be downloaded by others for comparison purposes. Another option for algorithm comparison is a so-called “reconstruction contest,” in which a research society provides a dataset that is available for download. Multiple research groups can use their own techniques to reconstruct the images, which are then uploaded back to the society and then compared either quantitatively to a gold-standard image, qualitatively by radiologists, or both, to determine the “best” reconstruction method. For instance, in such a contest sponsored by ISBI 2012, 20 different reconstruction algorithms were tested using HARDI data and the results compared in terms of image quality and quantitative accuracy¹⁸⁹. In this contest, none of the methods was found to significantly outperform the others in all experimental conditions, further highlighting the challenge in selecting just one for clinical adoption.

Because many sparse reconstruction techniques are computationally intensive, the generation of images using these techniques can take a significant amount of time. Reconstruction times on the order of hours or even days have been reported^14,42,72,151. Such long reconstruction times make it difficult to test the relative performance of different methods or determine optimal parameters. Many groups have moved to using dedicated image reconstruction platforms which employ hardware and code optimized for rapid computations¹⁹⁰. The use of specialized hardware and implementations including Graphics Processing Units (GPUs)^27,191, distributed computing¹⁹², and/or multicore processors¹⁹³ has been shown to enable 50-fold reductions in computation time, making clinical application of these sparse reconstruction techniques feasible¹⁹¹.

Challenges to Clinical Application

In addition to the technical challenges associated with sparse reconstruction techniques, there remain significant clinical barriers to widespread testing, let alone adoption, of these methods. Ultimately, the success of a technique such as sparse image reconstruction depends on its acceptance by the radiology community, as these physicians are the end users of the technology. Full validation of new imaging methods must demonstrate diagnostic accuracy, or equivalent accuracy at a reduced scan time. Unfortunately, such validation is a lengthy and challenging process as it must show that the new imaging technology not only produces images of higher quality based on quantitative metrics, but also impacts clinical care in a meaningful way.

A major barrier to clinical adoption is that the imaging community has relatively little experience with the artifacts that can arise from these sparse reconstruction techniques. For example, the artifact profile with compressed sensing has been described to include significant image blurring and a “global ringing” similar in appearance to motion ghosting, and these can have deleterious effects even at a two-fold acceleration¹⁸⁰. Furthermore, since many of these technologies take advantage of image information collected over a wider time window than a single frame of the imaging time series, it is possible that “temporal” artifacts are produced; in other words, each individual image may be acceptable, but the temporal fidelity with which events are observed in the imaged anatomy may be compromised. While the presence of artifacts in any accelerated image is an expected phenomenon, the unfamiliar and unpredictable nature of these artifacts means that radiologists or technologists may not be able to troubleshoot or even recognize them. This problem can be compared to the use of iterative reconstruction methods for reducing the radiation dose in Computed Tomography. The images generated with these new approaches look different than those reconstructed with more traditional filtered back projection approaches, and in many cases while they have less noise, the iterative reconstruction techniques may in fact obscure pathology¹⁹⁴. Due to the large number of parameters in an MRI pulse sequence and contrasts which can be created, this challenge is compounded in MRI.

Another important problem with sparse reconstruction techniques is that of long image reconstruction times; while this creates technical challenges as described above, it can also hinder the use of such technologies clinically. Even if data are collected in real-time, the reconstructed images may not be clinically helpful if they are only available for review hours later. If the reconstruction is not successful due to an incorrect sampling pattern or overly ambitious acceleration rate, the patient would need to return for a second scan. Some patients may be too sick or lack proper transportation to return for repeat imaging, and the cost of repeat scanning may be prohibitive. If there are acutely important findings in the images, the reconstruction time could effectively delay or even preclude treatment. Such practical considerations may make it difficult to replace current clinical standard exams with the computationally intensive techniques, no matter how enticing their potential benefits are.

Another complication is that testing sparse reconstruction techniques against a clinical gold standard can be problematic. Ideally head-to-head comparisons in non-contrived clinical settings are needed. Some exams, especially dynamic contrast-enhanced series, may be difficult or even impossible to repeat. Even if repeated, it may be challenging to replicate the scan on two different dates or time points. Thus testing of diagnostic utility against an accepted standard may not always be possible. Indeed, such testing in a clinical environment has been performed only with small groups of patients at advanced research hospitals due to the demanding nature of these studies^113,139,180. True blinded comparisons are further complicated by the fact that the scans to be tested appear clearly different than the clinical standard in terms of SNR, imaging features (i.e. edges, contrast), and artifact profile.

Finally, in some applications, even promising sparse reconstructions may not deliver higher acceleration rates or improved image quality over existing (and emerging) techniques. Multislice^195,196, 3D CAIPIRINHA^197,198, and non-Cartesian parallel imaging techniques¹⁹⁹ enable rapid imaging in many of the clinical applications discussed above, often at acceleration factors which are similar to those used in sparse reconstruction methods. Only a demonstrated dramatic increase in diagnostic efficacy can motivate the decision to use a time-consuming and complex sparse reconstruction technique instead of either the current gold-standard methods or another simpler emerging technology.

Conclusion

Sparse reconstructions, including but not limited to the family of compressed sensing techniques, have the potential to significantly accelerate MRI scans. In this review, the fundamental ideas behind sparse reconstruction methods have been introduced. While many different types of sparse reconstruction techniques have been proposed, all rely on image sparsity, noise-like or benign aliasing artifacts, and the use of a specialized reconstruction. This review also describes the principles of four basic categories of sparse reconstruction techniques, namely separable methods, k-t methods, compressed sensing, and model-based methods. Each of these techniques places different requirements on the collected data and exploits different aspects of the underlying images, and thus some techniques may be better suited to the acceleration of a specific imaging application than others.

While decreasing imaging time for standard exams may be possible using sparse reconstructions, the true benefit of these techniques will be realized if new applications can be enabled through faster imaging. Additionally, it may be possible to better scan patient populations that have traditionally been challenging to image with MRI, including children or patients who cannot hold their breath, thus expanding the role of MR in diagnostic imaging. Despite this great potential, sparse reconstruction techniques have not been widely adopted in the clinic. In order to make such adoption possible, it is essential for researchers and clinicians to work closely together to design, optimize, validate and compare these sparse reconstruction techniques and competing methods. The few studies which have explored the use of sparse reconstructions in a clinical setting typically recommend factors of 2 to 4 for static imaging, and up to 8 to 12 for dynamic imaging. At these data reduction factors, it will be important to demonstrate the benefit of moving to the more complex and time-consuming sparse reconstruction technique instead of relying solely on parallel imaging, which is well-accepted clinically and broadly used. Thus far, the majority of the work on sparse reconstruction algorithms has been performed by integrated teams of researchers and physicians in academic settings. More general acceptance and routine utilization will require the reconstructions to be rapid and predictable, such that technologists or radiologists can understand and troubleshoot any residual artifacts and either re-reconstruct the data or recollect images while the patient is still on the table.