Development of Real-Time Magnetic Resonance Imaging of Mouse Hearts at 9.4 Tesla – Simulations and First Application

Abstract

A novel method for real-time magnetic resonance imaging for the assessment of cardiac function in mice at 9.4 T is proposed. The technique combines a highly undersampled radial gradient echo acquisition with an image reconstruction utilizing both parallel imaging and compressed sensing.

Simulations on an in silico phantom were performed to determine the achievable acceleration factor and to optimize regularization parameters. Several parameters characterizing the quality of the reconstructed images (such as spatial and temporal image sharpness or compartment areas) were calculated for this purpose. Subsequently, double-gated segmented cine data as well as non-gated undersampled real-time data using only six projections per timeframe (temporal resolution ~ 10 ms) were acquired in a mid-ventricular slice of four normal mouse hearts in vivo. The highly accelerated data sets were then subjected to the introduced reconstruction technique and results were validated against the fully sampled references.

Functional parameters obtained from real-time and fully sampled data agreed well with a comparable accuracy for left-ventricular volumes and a slightly larger scatter for mass.

This study introduces and validates a real-time cine-MRI technique, which significantly reduces scan time in preclinical cardiac functional imaging and has the potential to investigate mouse models with abnormal heart rhythm.

I. Introduction

Magnetic Resonance Imaging (MRI) is a well-established tomographic modality in non-invasive clinical and preclinical diagnosis. One important application in cardiology is the accurate measurement of ventricular volumes and mass in order to non-invasively characterize global cardiac function in small animal models of human cardiac disease. Conventional, multi-frame (‘cinematic’), gradient echo-based sequences are typically applied throughout the cardiac cycle with prospective (e.g. [1–3]) or retrospective [4–7] synchronization to the heartbeat, acquiring at least one line of k-space for each timeframe per RR-interval. Thus, the imaging process captures the average cardiac function over N_PE × NA cardiac cycles, with N_PE the total number of phase encoding steps / radial projections and NA the number of averages, respectively. This approach is time-consuming and renders the investigation of animal models with irregular heartbeat extremely difficult. The application of acceleration techniques, such as parallel imaging [8, 9] or compressed sensing (CS, [10]), have yielded scan-time-reductions in the assessment of left-ventricular function in mice and rats of 3 or 4 for parallel imaging [11–13], and 3 to 15 for CS [14, 15], without compromising the accuracy of cardiac functional indices. Fast, non-Cartesian imaging sequences, combined with parallel imaging [16], nonlinear inverse reconstruction [17] or k-t-SPARSE-SENSE [18] enabled the acquisition of real-time (RT) imaging of the human heart with a temporal resolution of 22–43 ms. The application of RT imaging to the mouse is particularly hampered by the 8–10 times higher heart rates combined with its miniature size, which requires temporal resolutions of ~10 ms or better and sufficient spatial resolution to be diagnostically meaningful. Here, we combine a CS approach with an improved radial GRAPPA technique [16] to reconstruct highly undersampled radial MR data with the objective to acquire murine cardiac images in real time. The paper reports on a proof-of-concept study to guide developmental efforts and to demonstrate technical feasibility. Simulations were performed prior to the MR experiment with the aim to define an optimal acquisition strategy. Cardiac functional indices obtained from the real time acquisition agreed well with those measured with a conventional prospectively gated Cartesian multi-frame sequence. This approach may further speed up and simplify the investigation of mouse models of human cardiovascular disease.

II. Methods

A. In Silico Phantom

In order to define the optimal acquisition strategy, an in silico phantom based on real murine in vivo data was first designed, consisting of a simplified representation of an axial cross-section across a mouse thorax (referred to as “body”). The body contained compartments mimicking liver, skeletal muscle, blood and left-ventricle, respectively (Fig. 1) with corresponding, experimentally determined signal intensities. While “body” and “liver” were assumed to remain static, volumes of the left ventricle and blood-vessel were simulated to oscillate (albeit phase-shifted by 45°) with a periodicity of 120 ms (corresponding to a heart rate of 500 bpm). The motion pattern was based on a second order Fourier series, obtained from fitting a time-volume curve of a mid-ventricular murine cine-series (see Table 1 for details). The dynamics of the left-ventricle yielded an ejection fraction of ~66% in agreement with the literature [1, 2]. Gaussian noise was added to the radial k-space data, yielding a maximum signal-to-noise ratio (SNR) in image space of about 10 for the left ventricle. The in silico images were multiplied with experimentally determined coil-sensitivity profiles for a four-channel cardiac array and Fourier-transformed into Cartesian k-space, from which radial projections were calculated using cubic spline interpolation.

Fig. 1.

In silico phantom: Top left images show the phantom with the artificial coil sensitivities superimposed. The large image on the right depicts a sum of squares of all four single coil images. The temporal series on the bottom demonstrates the dynamics of the phantom, again in a sum of squares representation.

TABLE I.

Parameters for artificial “mouse” images.

	Signal Intensity	Dynamics(Volume)
Body	69	static
Liver	100	static
Blood vessel	105	0.70 + 0.28 · cos(2π · i · Δt − 0.25 − π) + 0.034 · cos(4π · i · Δt + 0.55 − π)
Myocardium	37	Epicardium: static Endocardium: 0.70 − 0.28 · cos(2π · i · Δt − 0.25) − 0.034 · cos(4π · i · Δt + 0.55)
Cavity	156	0.70 + 0.28 · cos(2π · i · Δt − 0.25) + 0.034 · cos(4π · i · Δt + 0.55)

i: Number of frame in cardiac cycle; $\mathrm{\Delta }\mathrm{t}=\frac{T{R}^{\mathit{\text{Seq}}}·HR}{60s}$ with heart rate HR and repetition time of sequence TR^Seq

B. Simulation of Real-Time Imaging sequence

A radial sequence with refocused read-out gradient as shown in Figure 2 of ref [19] with a target grid size of 128 × 128 was simulated in Matlab (Mathworks, The Mathworks Inc, Natick, US) on an Intel Core i7 CPU @ 3.6 GHz. The prescribed matrix size required, 200 radial projections to fulfill the Nyquist sampling criterion. In order to realize a temporal resolution of < 20 ms, highly undersampled frames consisting of n_proj = 4, 6 or 8 projections with a TR = 1.60 ms (based on experimentally realizable parameters) were reconstructed. Two acquisition schemes were investigated: (i) in the linearly segmented (LS) case, the projections were equi-angularly distributed with an increment between adjacent projections of Δφ = 180°/n_proj. The projections of successive frames were rotated by an angle Δϑ = 180° / total number of projections (128/120) ≈ 1.41° / 1.50° with respect to each other to increase the total k-space coverage throughout the cycle. (ii) For Golden Angle (GA) acquisitions, the increment between consecutive projections was set to $111.25°\approx 2\pi /(\sqrt{5}+1)$, guaranteeing optimal profile distribution for any arbitrary number of projections used in reconstruction [20]. Each simulated cine series covered approximately two cardiac cycles, with acceleration factors of 19 – 50.

Fig. 2.

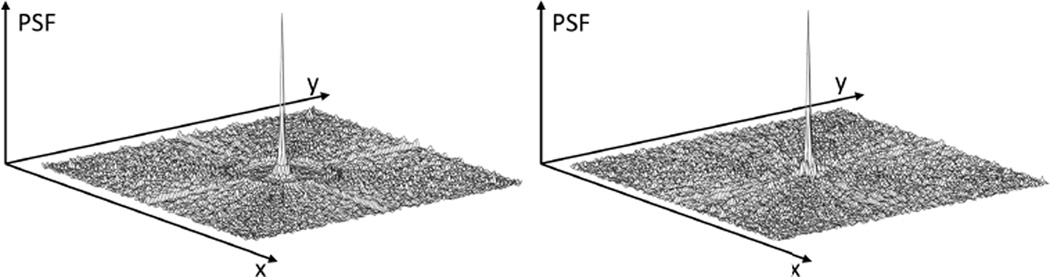
Point spread functions following GRAPPA-operator gridding using six acquired projections per timeframe and RGRAPPA = 4 (left: linear segmented, right: golden angle). Note: the sidelobes exhibit very low energy levels, suggesting high incoherence.

C. Image Reconstruction

The highly undersampled frames were individually subjected to a hybrid reconstruction consisting of parallel imaging and compressed sensing.

1. Parallel Imaging (GRAPPA)

In a first step, through-time radial GRAPPA [16] was applied in order to double (R_GRAPPA = 2), triple (R_GRAPPA = 3) or quadruple (R_GRAPPA = 4) the initial number of projections per time frame. Additional calibration data, required for this step, and consisting of 128 × R_GRAPPA · n_Proj × n_Rep (linear segmented) and 128 × 288 × n_Rep (Golden Angle) data points for each rotation angle Δϑ were generated as described above. The last dimension (n_Rep) of this dataset specifies the number of repetitions needed for fitting the radial GRAPPA kernels (segment size 4 × 1 in the read and projection directions), and was fixed to n_Rep = 80 [16]. For Golden Angle acquisitions, the projections were sorted prior to the application of radial GRAPPA in order to optimize the performance of the reconstruction [21]. Note, in contrast to the linear case, “real time data” can be obtained by building an arbitrary subset of consecutive projections out of the calibration data.

2. Compressed Sensing

The intermediate dataset resulting from the GRAPPA reconstruction (i.e. n_Proj × R_GRAPPA projections per frame) still features non-Cartesian coordinates. In order to avoid the time-consuming non-uniform transform of non-Cartesian k-space data to image space and back for each iteration of the subsequent CS-optimization, the data were assigned to a Cartesian grid first. GRAPPA operator gridding [22] was applied, which exploits the variation of the coil sensitivities to perform small shifts in k-space. Figure 2 shows the point spread functions following GRAPPA-operator gridding using six acquired projections per timeframe and RGRAPPA = 4. Since the sidelobes exhibit very low energy levels, high incoherence can be assumed. The following CS optimization was used to determine fully sampled data:

$${\text{min}}_{\mathbf{I}}{\Vert \mathbf{\Psi }\mathbf{S}\mathbf{I}\Vert }_1+\frac{\mu }{2}{\Vert \mathbf{k}-\mathbf{R}\mathbf{I}\Vert }_2^2$$ (1)

where I represents the image-series to be reconstructed, k the undersampled k-space after applying radial GRAPPA. R stands for a partial discrete Fourier transform and S holds the information of the coil sensitivities. The application of S corresponds to a coil combination operation [23] resulting in one single complex valued image. A fully sampled temporal average was obtained from the calibration data to determine S. Ψ is the temporal total variation (TV) operator, calculating the discrete gradient of the image series in the temporal domain, thereby sparsifying the dataset [24].

The problem in Equ. (1) was reformulated such that a fast iterative shrinkage-thresholding algorithm for linear inverse problems (FISTA, [25]) could be applied for solving. In a first step, a new optimization variable J ≔ Ψ S I was introduced:

$${\text{min}}_{\mathbf{I},\mathbf{J}}{\Vert \mathbf{J}\Vert }_1+\frac{\mu }{2}{\Vert \mathbf{k}-\mathbf{R}\mathbf{I}\Vert }_2^2\text{ subject to }\mathbf{\Psi }\mathbf{S}\mathbf{I}=\mathbf{J}$$ (2)

A penalty technique with sufficiently large penalty parameter α > 0 as described e.g. in [26] was then applied to obtain an unconstrained problem

$${\text{min}}_{\mathbf{I},\mathbf{J}}{\Vert \mathbf{J}\Vert }_1+\frac{\mu }{2}{\Vert \mathbf{k}-\mathbf{R}\mathbf{I}\Vert }_2^2+\frac{\alpha }{2}{\Vert \mathbf{\Psi }\mathbf{S}\mathbf{I}-\mathbf{J}\Vert }_2^2,$$ (3)

which is suitable for an optimization using our FISTA-TV.

Before describing the algorithm, the following functions need to be defined:

• The second and third summand in Equ. (3) are substituted with :

  $$f_2(I,J)≔\frac{\mu }{2}{\Vert \mathbf{k}-\mathbf{R}\mathbf{I}\Vert }_2^2+\frac{\alpha }{2}{\Vert \mathbf{\Psi }\mathbf{S}\mathbf{I}-\mathbf{J}\Vert }_2^2.$$
• 𝕊_τ (x) represents the thresholding function

  $${𝕊}_{\tau }(x)≔\{\begin{array}{ccc}\hfill x-\tau \hfill & \hfill \mathit{\text{if}}\hfill & \hfill x>\tau \hfill \\ \hfill 0\hfill & \hfill \mathit{\text{if}}\hfill & \hfill |x|\le \tau \hfill \\ \hfill x+\tau \hfill & \hfill \mathit{\text{if}}\hfill & \hfill x<\tau \hfill \end{array}$$
• s stands for the steepest descent functions with steplength 1/L:

  $$s_{f_2}^I(I,J)≔I-\frac{1}{L(f_2)}{\nabla }_I{f}_2(I,J);$$

  $$s_{f_2}^J(I,J)≔J-\frac{1}{L(f_2)}{\nabla }_J{f}_2(I,J),$$

where L(f₂) is the Lipschitz constant of the function ∇ f₂.

The FISTA-TV algorithm works as follows:

Require: R, k, Ψ, S, I0, J0, μ, α

Calculate L (f2):

$L={\lambda }_{\mathit{\text{max}}}\left(\begin{array}{cc}\hfill \mu ·R^{T}R+\alpha ·S^T{\mathrm{\Psi }}^T\mathrm{\Psi }S\hfill & \hfill -\alpha S^T{\mathrm{\Psi }}^T\hfill \\ \hfill -\alpha \mathrm{\Psi }S\hfill & \hfill \alpha ·Id\hfill \end{array}\right)$

where λmax (A) is the largest eigenvalue of the matrix A.

Set Î0 = I0; Ĵ0 = J0; t0 = 1

while 0 ≤ k ≤ K − 1 do

$I_{k+1}=s_{f_2}^I({Î}_k,{Ĵ}_k)$

$J_{k+1}={𝕊}_{1/L}(s_{f_2}^J({Î}_k,{Ĵ}_k))$

$t_{k+1}=(1+\sqrt{1+4t_k^2})/2$

${Î}_{k+1}=I_k+\frac{t_k-1}{t_{k+1}}(I_k-I_{k+1})$

${Ĵ}_{k+1}=J_k+\frac{t_k-1}{t_{k+1}}(J_k-J_{k+1})$

end while

In addition to the hybrid reconstruction technique (GRAPPA and CS), the datasets described above were reconstructed using FISTA-TV only (i.e. R_GRAPPA = 1).

D. Image Quality

In order to automatically assess the image quality and the ability to accurately resolve cardiac motion for the various simulated reconstructions, several metrics were defined (see Fig. 3 for details). Fully sampled reference datasets consisting of 200 projections per frame (indicated with “Full” in the following) were created for this purpose, featuring timeframes identical to those of the real-time sequence (“effective repetition times” of 30–80 µs). The following quality parameters were quantified:

1. Mean artifact level: $\overline{AF}=\sqrt{\frac{{\sum }_{i=1}^{NV}{(I_{\mathit{\text{Full}}}^i-I_{\mathit{\text{Acc}}}^i)}^2}{{\sum }_{i=1}^{NV}{(I_{\mathit{\text{Full}}}^i)}^2}}$, with $I_{\mathit{\text{Full}}/\mathit{\text{Acc}}}^i$ the image space magnitude of the fully-sampled / accelerated frame at pixel i, and NV the number of voxels in an area exceeding the “cardiac” region by ~50% (see red rim in Fig. 3).

2. Spatial image sharpness: The numerical gradient at the endocardial border ${\overline{NG}}^{i,j}=\frac{\partial I^{i,j}}{\partial z^j}$ was determined for both fully sampled and accelerated data sets (${\overline{NG}}_{\mathit{\text{Full}}/\mathit{\text{Acc}}}$). i represents the timeframe (total number: tf), j is the interface between myocardial tissue and blood on the profile in Fig. 3b (green line, total number of interfaces = 16). z^j points in direction of the profile. The overall loss in spatial sharpness.S̄ was then calculated as a relative error: $\overline{S}=\frac{1}{16·tf}{\sum }_i^{tf}{\sum }_j^{16}\frac{{\overline{NG}}_{\mathit{\text{Full}}}^{i,j}-{\overline{NG}}_{\mathit{\text{Acc}}}^{i,j}}{{\overline{NG}}_{\mathit{\text{Full}}}^{i,j}}$

3. Temporal image sharpness: The numerical gradient along the temporal domain ${\overline{NTG}}^{k,l}=\frac{\partial I^{k,l}}{\partial t}$ was calculated for the four points k indicated by the red crosses in Fig. 3b both in the fully sampled and the accelerated data sets (${\overline{NTG}}_{\mathit{\text{Full}}/\mathit{\text{Acc}}}$). l represents the timeframe when the four pixels change from blood to myocardium and vice versa (total number = 2). The overall loss in temporal sharpness $\overline{TS}$ was calculated: $\overline{TS}=\frac{1}{4·2}{\sum }_k^4\sum _l^2\frac{{\overline{NTG}}_{\mathit{\text{Full}}}^{k,l}-{\overline{NTG}}_{\mathit{\text{Acc}}}^{k,l}}{{\overline{NTG}}_{\mathit{\text{Full}}}^{k,l}}$

4. Deviation $\overline{\mathrm{\Delta }A}$ from the ‘true’ ventricular cavity area: $\overline{\mathrm{\Delta }A}=\frac{1}{tf}{\sum }_{i=1}^{tf}\frac{|A_{\mathit{\text{Full}}}^i-A_{\mathit{\text{Acc}}}^i|}{A_{\mathit{\text{Full}}}^i}$, with A_Full/Acc the area obtained in the fully-sampled / accelerated frame. tf again is the total number of timeframes, such that $\overline{\mathrm{\Delta }A}$ represents the temporal average of the deviation. A region growing algorithm was used [27] to determine the areas automatically, free from measurement errors induced by a human operator (Fig. 3c).

Fig. 3.

Image quality analysis: a) Reconstruction of a noisy phantom. The mean artifact level is determined within the area marked by a red frame. b) The spatial image sharpness is measured at the blood pool / myocardium interface and averaged for 16 locations (green lines). The temporal sharpness is measured and averaged for the four red crosses. c) The ventricular volume was assessed by an automatic segmentation algorithm. Each of the determined quality parameters are compared between the fully sampled reference reconstructions and their accelerated counterparts.

E. Optimizing the regularization of FISTA-TV

The choice of the two regularization parameters α and μ within the optimization problem [3] has significant impact on the reconstruction performance of FISTA-TV and, therefore, on the image quality of the resulting cine series. In order to determine optimal values for α and μ, the CS reconstruction of each simulation was performed for a range of different combinations of α and μ. Both values were incremented from 10¹ to 10⁶ in 26 steps leading to a matrix (26 × 26) of different reconstructions. $\overline{AF}$, S̄, $\overline{TS}$ and $\overline{\mathrm{\Delta }A}$ were determined for each pair. A normalized combination of the four measures was built in order to find a joint minimum error and therefore an optimal choice of α and μ.

F. Experimental Setup

In vivo experiments were carried out on a horizontal 9.4T MR system comprising of a VNMRS DDR2 console (Agilent, Santa Clara, US), a 1000 mT/m shielded gradient system (id 6 cm) and a four-channel cardiac array (operated in combination with an actively decoupled, quadrature-driven volume resonator (id 42 mm) – both Rapid Biomedical, Germany). A fast, radial gradient echo sequence allowing both for linear (matrix sizes: 128 × 128 for segment size 4 and 8; 128 × 120 for segment size 6) and GA sampling (matrix size 128 × 288) was implemented [19] and used for real time imaging (i.e. without cardiac or respiratory gating). Slice refocusing and read de- / re-phasing gradients were applied either with maximum amplitude at shortest duration (resulting TE/TR = 0.8 / 1.6 ms), or balanced (i.e. TE/TR = 0.99 / 1.98 ms)

Other imaging parameters were: FOV = 30 × 30 mm, mid-ventricular slice (thickness 1 mm) in short-axis orientation, 250 µs Gaussian excitation pulse with the flip angle varied from 5° to 30° in 5° steps, 50 repetitions. Calibration data (80 repetitions) were additionally acquired and the undersampled datasets were subjected to the reconstruction algorithm using R_GRAPPA = 4 as described above. A fully-sampled, double-gated reference cine data set [2] was acquired in the same session (with a matrix size 128 × 128, TE / TR = 1.79 / 4.6 ms, FOV = 30 × 30 mm, slice thickness 1 mm, 1 average) for validation purposes.

Four healthy female C57Bl6/J mice (26.7 ± 1.8 g) were subjected to MR Imaging. Anesthesia was induced in an anesthetic chamber using 4% isoflurane in 100% oxygen. Mice were positioned prone on the animal cradle and maintained at 1.5–2% isoflurane at 2 l/min oxygen flow throughout the experiments. Temperature was maintained at ~37°C using the integrated heating system of the animal cradle. Cardiac and respiratory signals were continuously monitored using an in-house developed ECG and respiratory gating device [28]. All experiments were approved by the institutional ethical review committee and conform with the UK Home Office Guidance on the Operation of the Animal (Scientific Procedures) Act, 1986 (HMSO).

G. In vivo Image Reconstruction and Analysis

All in vivo RT data were processed offline, using purpose written Matlab scripts (Mathworks, The Mathworks Inc, Natick, US). Radial trajectories were corrected using the method described in [29]. A series of 320 / 288 frames was created for linear / GA samplings and exported into tiff-format, respectively. An averaged sharpness was assessed at the interface between myocardial tissue and blood pool in order to determine the optimal flip angle for image segmentation. The spatial gradient, depicted by a green line in Figure 3b was calculated at eight locations and averaged in the temporal domain. The resulting values were plotted and visually compared for all flip angles / radial acquisitions. Subsequently, left-ventricular functional parameters (i.e. slice volume / mass in end-systole / end-diastole) were assessed for one data set of each sampling scheme, as well as for the prospectively gated fully sampled reference data. This analysis was performed manually in Amira 5.3 (FEI, Hillsboro, Oregon, US) by an operator blinded to mouse id / acquisition scheme.

III. Results

A. Simulations

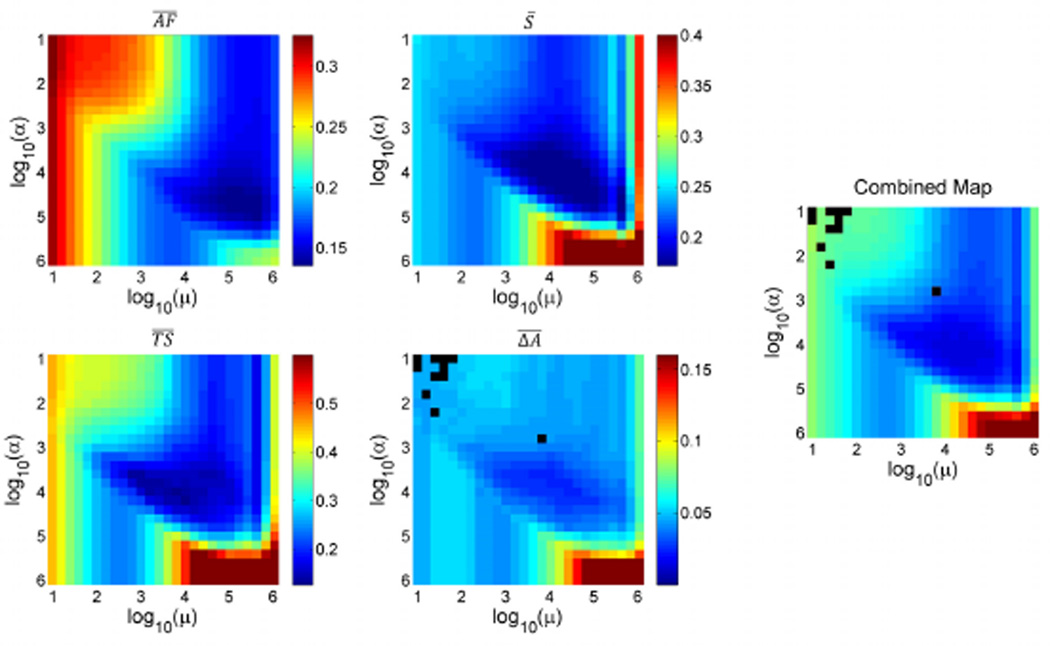
Figure 4 illustrates the optimization of the regularization parameters for the example of a Golden Angle simulation, using 8 projections per timeframe and GRAPPA acceleration of 4. Each of the observed image quality parameters $\overline{Af}$, S̄, $\overline{TS}$ and $\overline{\mathrm{\Delta }A}$ are color-coded in a map for α and μ running from 10¹ to 10⁶. For $\overline{\mathrm{\Delta }A}$, a few combinations of α and μ led to reconstruction results where the automatic segmentation did not converge. Those are encoded with black pixels. In general, all maps show a region of minimum errors in approximately the same locations. In the periphery of the maps, however, the trends clearly differ, especially between the mean artefact level $\overline{AF}$ and remaining parameters. Furthermore, the weighted combination of all maps (right panel in Fig. 4) shows a common region where the error is minimized for all indices. This allowed then for determining a joint pair (α^opt, μ^opt) of optimized parameters by averaging the locations of the determined minima in the combined maps throughout all settings: α^opt = 6.31 · 10³, μ^opt = 1.58 · 10⁴.

Fig. 4.

Determination of optimized regularization parameters. The graphs illustrate the results for a Golden Angle simulation, using 8 projections and GRAPPA acceleration of 4. The combined map allows determining a pair of regularization parameters α,μ which fulfil a best compromise for all errors investigated. As the location of the valley within the combined map was very similar throughout all simulations, a joint pair of parameters was determined for all settings, thereby making the further usage of the reconstruction method more comfortable.

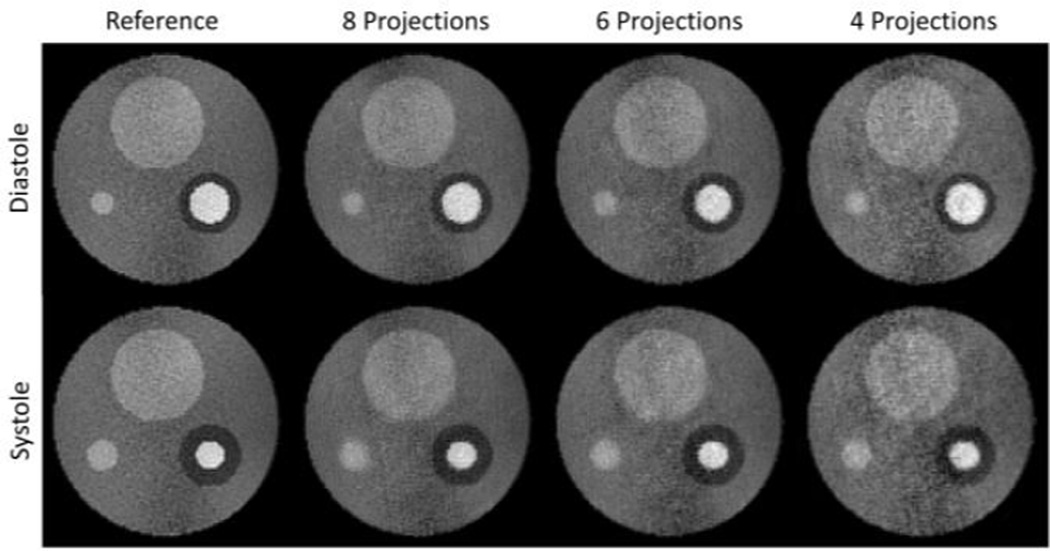
Figure 5 depicts the diastolic and the systolic frame for fully sampled reference series and various accelerated simulations. Despite the high undersampling factor, the images are virtually artifact-free. The corridor in the center of the phantom, which shows increased noise level in the reference, becomes more accentuated with decreasing number of projections.

Fig. 5.

End-diastolic and end-systolic frame for the reference dataset and several representative simulations of accelerated acquisitions (RGRAPPA = 4, linear segmented).

Table II lists the results of the image quality assessment across all simulations performed. In general, R_GRAPPA = 4 led to the smallest errors with respect to the fully sampled reference for all investigated measures. In a comparison throughout groups of different acceleration factors and sampling strategies (linear/Golden Angle), the simulation using 8 Golden Angle projections per timeframe resulted in the smallest deviations in total. Importantly, while results from simulations with higher acceleration factors predominantly suffer from increased temporal blurring ($\overline{TS}$), this did not detrimentally impact the results of the automated segmentation of the cavities ($\overline{\mathrm{\Delta }A}$).

TABLE II.

Overview of normalized, mean quality parameters obtained from the artificial “mouse” images.

		LS Simulation				GA Simulation
	GRAPPA	$\overline{AF}$	S̄	$\overline{TS}$	$\overline{\mathrm{\Delta }A}$	$\overline{AF}$	S̄	$\overline{TS}$	$\overline{\mathrm{\Delta }A}$
4 Projections	1	0.32	0.38	0.78	0.09	0.28	0.30	0.58	0.08
	2	0.30	0.31	0.63	0.07	0.21	0.32	0.69	0.06
	3	0.24	0.35	0.65	0.05	0.19	0.24	0.50	0.05
	4	0.21	0.29	0.51	0.04	0.19	0.24	0.60	0.05
6 Projections	1	0.28	0.35	0.35	0.09	0.22	0.31	0.39	0.07
	2	0.22	0.30	0.27	0.05	0.19	0.24	0.44	0.04
	3	0.20	0.23	0.36	0.03	0.17	0.21	0.23	0.04
	4	0.17	0.21	0.39	0.03	0.16	0.18	0.28	0.03
8 Projections	1	0.28	0.26	0.47	0.10	0.22	0.24	0.20	0.07
	2	0.20	0.24	0.38	0.05	0.18	0.20	0.15	0.03
	3	0.17	0.20	0.38	0.03	0.16	0.16	0.14	0.03
	4	0.16	0.16	0.31	0.01	0.15	0.17	0.14	0.03

AF – artifact level; S – spatial sharpness; TS – segmentation.

B. In Vivo

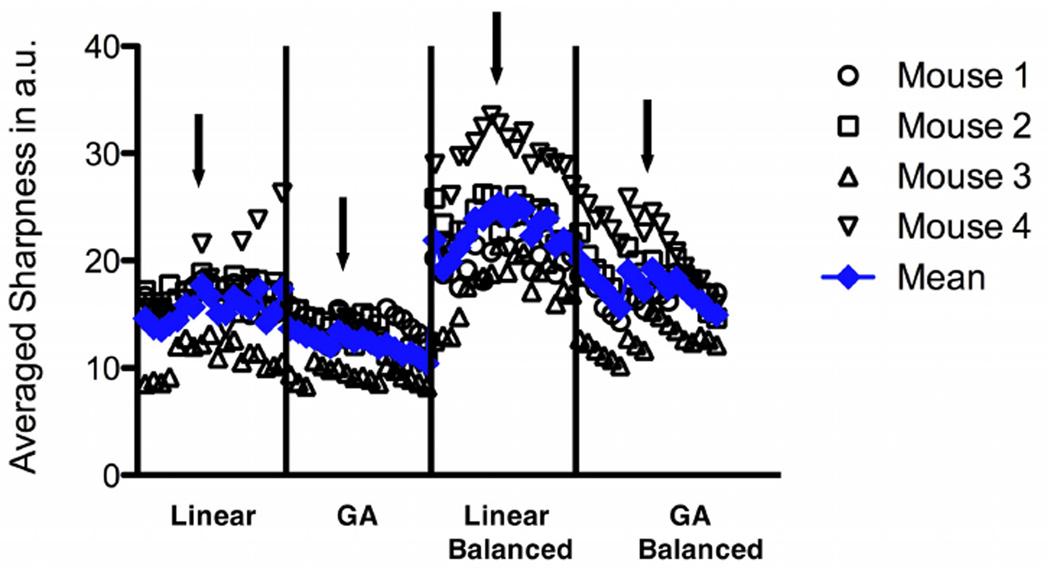
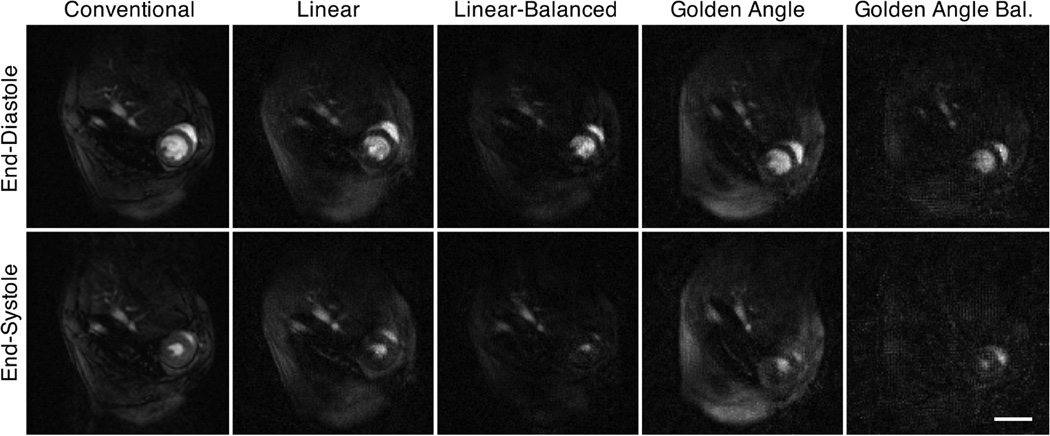
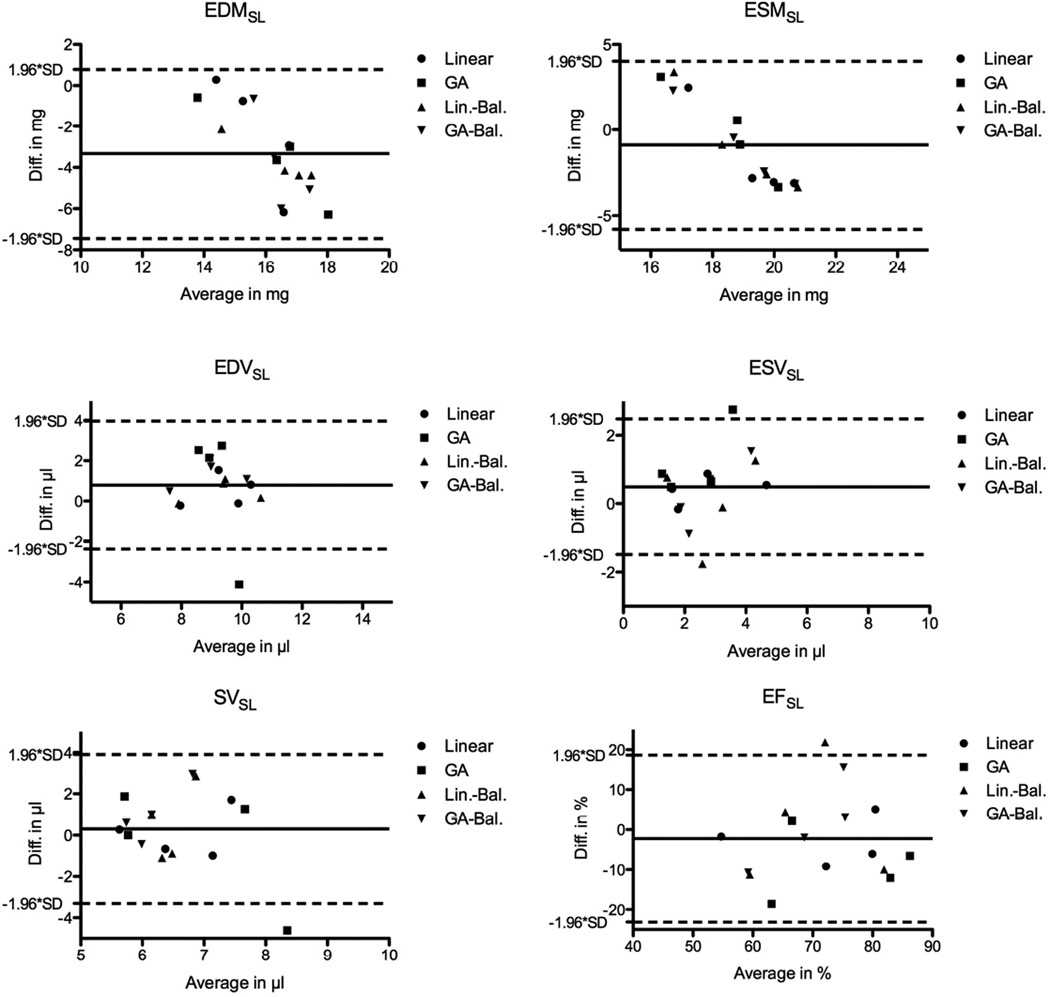
Figure 6 shows the averaged sharpness individually (for each mouse) and the smoothed average for all in vivo RT data (i.e. sampling schemes and flip angle). Local maxima can be identified for each sampling scheme (arrows) corresponding to 6 projections and flip angles of 10° for the sequence with maximum gradient amplitude / shortest duration, and 15° for the balanced sequence, respectively. These data sets, which provided a temporal resolution of < 12 ms per frame, were selected for quantitative analysis. Representative end-diastolic (top row) and end-systolic (bottom row) frames are shown in Figure 7 for conventional (left column) and RT acquisitions, respectively. While the left-ventricular wall and cavity were well resolved in all cases, the linear sampling schemes showed better image quality compared to the GA acquisitions. The left-ventricular functional parameters obtained by blinded analysis in a mid-ventricular slice are listed in Table III, and show generally good agreement between RT and fully sampled data. The spread of LV mass as measured in the RT data was larger than for the conventional data, while it was comparable for the volumes. Bland-Altman analysis (Figure 8) revealed only a significant bias for EDM_SL, whereas it was close to 0 for all other indices. Note that the solid / dashed lines in Fig. 8 show the bias / confidence interval for all RT acquisitions combined, while the encoding of the various acquisition schemes with different symbols is only for illustration purposes. Heart and respiratory rates during radial and conventional acquisitions were comparable (464 ± 63 bpm / 60 ± 16 breaths per min vs. 490 ± 50 bpm / 67 ± 19 breaths per min – radial vs. conventional, respectively).

Fig. 6.

Individual (open black symbols) mean (filled blue symbols) averaged sharpness for the different acquisition schemes / flip-angles. The arrows indicate the maximum for each acquisition scheme, which were subjected to segmentation.

Fig. 7.

Mid-ventricular slice through the same mouse thorax showing the heart in short-axis orientation, acquired with a prospectively-gated Cartesian multi-frame sequence (left column) and with the radial real-time sequence. Top row: end-diastole; bottom row: end-systole. Scale bar – 5 mm.

TABLE III.

*	Fully-Sampled	LS	GA	LS-Balanced	GA-Balanced
EDMSL in mg	14.5 ± 0.8	16.9 ± 2.5	17.9 ± 2.9	18.3 ± 1.8	18.3 ± 1.8
EDVSL in µl	9.6 ± 1.2	9.1 ± 1.0	8.8 ± 2.2	9.1 ± 1.1	8.3 ± 1.0
ESMSL in mg	18.5 ± 0.5	20.1 ± 2.8	18.6 ± 2.9	19.3 ± 3.2	29.4 ± 2.9
ESVSL in µl	2.9 ± 1.5	2.5 ± 1.3	1.7 ± 0.8	2.9 ± 1.2	2.6 ± 0.6
SVSL in µl	6.7 ± 1.1	6.6 ± 0.9	7.1 ± 2.6	6.2 ± 0.8	5.7 ± 0.4
EFSL in %	70 ± 13	73 ± 12	79 ± 12	69 ± 12	68.9 ± 3.9

^*The index ‘SL’ stands for ‘Slice’.

Fig. 8.

Bland-Altman plots for slice-selective, left-ventricular functional and mass parameters. The solid line indicates the bias, while the dashed lined depicts the confidence intervals. Each of the radial acquisitions was compared to the fully sampled prospectively gated Cartesian reference data set.

IV. Discussion

The aim of this study was to develop and validate real time functional imaging in mouse hearts by applying both compressed sensing and parallel imaging to highly undersampled radial acquisitions. To the best of our knowledge, only one conference publication has reported on real-time cine MRI in mice so far [30], which, however, did not exploit the high tissue-blood contrast of radial gradient echo sequences.

To investigate whether or not the introduced method enables the high acceleration factors required for real time imaging, simulations based on in silico phantoms were performed prior to implementation on the MR scanner. Especially the low deviations for the automated segmentation indicated that the assessment of cardiac volumes with only 6 projections per timeframe is possible. Temporal smoothing turned out to represent the most prominent difference with respect to a fully sampled cine series, which originated from the TV model in the temporal domain within the FISTA reconstruction.

All simulations were performed using variable regularization parameters within FISTA-TV to determine a set of values, which are optimal for overall image quality. Since the errors were minimal for a larger area within the investigated range, global regularization parameters were determined for all reconstructions performed in this study. Optimizing those values individually for each undersampling factor / sampling strategy proved to be of only marginal advantage.

The results of the simulations were confirmed by the subsequent in vivo study. The balanced gradient approach of the implemented radial sequence provided better image quality (as assessed with the averaged sharpness) than the one with maximum gradient strength at shortest duration. Using six projections per time frame resulted in a temporal resolution of 11.8 ms / 9.6 ms for the two pulse sequence types. All volumetric parameters (EDV_SL, ESV_SL, SV_SL) showed only a small bias at moderate variances between RT and fully sampled data (Fig. 8). The assessment of EDM_SL and ESM_SL yielded a greater bias between RT and reference data with a trend of overestimation for higher values in the RT group. Given the small sample size (i.e. n = 4), the results from the RT acquisition were pooled and then subjected to the Bland-Altman analysis. Visual inspection of the individual plots, which depict the various RT acquisitions in different symbols, justifies this approach as the scatter of the data is similar for each RT acquisition scheme. The standard deviation (SD) of the EF is rather high, primarily driven by one mouse, which had a comparably low EF. This would suggest that the high variability in EF, both for fully sampled and accelerated reconstruction did not originate from image quality issues. Nevertheless, this has to be assessed and validated in a follow-up study of a larger cohort.

The evaluation of potential noise enhancement of the introduced technique is challenging, mainly due to the reconstruction behavior of CS. CS represents a non-linear and nonstationary transform, which “fits” the undersampled data to a defined model. Therefore, systematic errors usually occur instead of an increase of the random error in the case of a failed reconstruction. Moreover, in the case of relaxed data consistency, CS may also suppress the random error. According to the discussion in reference [31], the noise enhancement of the through-time GRAPPA method is significantly smaller compared to many other dynamic parallel imaging methods at high acceleration factors. This is mainly due to the fact that the central part of k-space featuring the majority of the energy is fully sampled for the radial acquisitions. The results of both the simulations and the in vivo study accordingly do not suffer from intensive noise enhancement. Nevertheless, a drop in SNR is inevitable for the high acceleration factors used (see Fig. 7).

The sparse model used in this proof-of-concept study was rather simple and might be refined in future applications. While only a discrete gradient in the temporal domain was applied, the spatial domain was not sparsified by any transform. Potential candidates are Total Variation and/or Wavelet Transforms as reported in already a number of different publications [10, 32–34]. Specifically, a TV constraint approach would provide additional denoising of the data. In recent papers, Low-Rank models have been applied to accelerate cardiac imaging [35], which may also be of great interest for real time imaging.

Furthermore, additional improvements of the parallel imaging step may be possible. The through-time radial GRAPPA method was used for this study as described in [16], but the spacing between source and target points in the GRAPPA kernels of the peripheral k-spaces are quite large for the highly undersampled radial acquisitions. It has to be investigated whether or not it is favorable to restrict the radial GRAPPA step to the central part of k-space and instead to employ higher acceleration factors for CS. Finally, the number of calibration kernels n_Rep was fixed to 80. Given the fast heart and respiratory rates observable in small animals, a higher number of calibration kernels may lead to a more accurate estimation of the coil weights, particularly in noisy parts of the k-space. This, however, would in return increase the total scan time.

Besides our approach, a number of other combinations of parallel imaging and compressed sensing have been published [24, 33, 36, 37]. While these studies report on a simultaneous application of the two theories within a joint iterative reconstruction, our approach can be regarded as an extension to the through time radial GRAPPA method presented earlier [16]. Therefore, the structure of our reconstruction method is modular and basically consists of two separated steps, which allow for easier adjustment of single components, e.g. a straightforward exchange of the CS algorithm. Separate calibration data (coil sensitivities) were used for both the radial GRAPPA reconstruction and repeatedly within the CS reconstruction: the GRAPPA reconstructed multi-coil data were combined for the thresholding step but treated individually to enforce the data consistency in each iteration. An integrated solution of the combination of parallel imaging and compressed sensing may be more effective for example with respect to the convergence behavior. A direct comparison between the different approaches and the extension to small animals would be interesting and will be subject to a future study.

Conventional imaging (pro- or retrospectively gated) as routinely applied in preclinical MR-labs requires many cardiac cycles to obtain the full data set, resulting in an averaged cardiac function over the imaging time per slice. Conversely, the proposed technique does not rely on averaging, but can assess cardiac function “instantaneously”. The prospectively-gated, Cartesian cine-data acquired as a reference in our study had a temporal resolution of 4.6 ms and thus more than twice the frame-rate of the real-time acquisitions. However, a literature review showed a wide range of temporal resolutions reported (anything from 4–20ms). Particularly, retrospectively gated data are commonly reconstructed with 10 frames per cardiac cycle (see for example [38]). Furthermore, time-volume analysis of the entire left ventricle showed that both diastole and systole have periods of 15–20ms, during which very little changes in left-ventricular volumes are observed (Fig. 6 of reference [12]). This is in line with early reports claiming that a temporal resolution of ~10 ms suffices to least determine end-diastole and end-systole with physiologically acceptable accuracy [1]. Nevertheless, higher frame rates will result in an improved resolution of cardiac motion, may positively affect image quality and therefore benefit segmentation. The lack of sharpness of the end-systolic endocardial border in Fig. 7 reinforces the importance of this. Improved temporal resolution may potentially be achieved in the future using a sliding-window reconstruction, particularly of the Golden Angle acquisition, novel CS reconstruction approaches and / or a combination of parallel imaging and compressed sensing reconstructions mentioned above.

Post-processing of measured data was performed offline and lasted approximately 2.5 min for one mid-ventricular slice (Fig. 7, 32 timeframes) using the PC described above (27 min for 320 frames). This implicates that results cannot be analyzed immediately after completion of a scan, which may resemble a problem if adjustments or corrections of scan parameters have to be made during an imaging session. In this particular case however, the long reconstruction time did not resemble a problem, as the assessment of cardiac functional parameters was performed offline after the in vivo experiments. Notably, the reconstruction time can be drastically reduced using parallel or GPU computing as demonstrated clinically.

In this paper, only one mid-ventricular slice was scanned to demonstrate feasibility of the new technique as proof-of-concept. Ultimately, a characterization with full ventricular coverage is needed to allow for a comprehensive validation of left-ventricular parameter measurements and a comparison with literature. Furthermore, animal models of cardiovascular disease have to be included in the validation process to establish whether or not the accuracy in normal mice presented extrapolates to pathological cases. The technique should particularly be suitable for mouse models of ventricular arrhythmias [39]. All this will be addressed in future studies.

V. Conclusion

The initial results presented here demonstrate the feasibility of real-time cardiac acquisitions in mice at 9.4T. The proposed technique applies a highly undersampled radial acquisition and a combination of through-time radial GRAPPA with compressed sensing for image reconstruction, yielding a temporal resolution of 10–12 ms. Our method significantly reduces the scan time and promises to enable the investigation of small animal models with ventricular arrhythmias for the first time. While this study aimed to show proof-of-concept, future efforts need to focus on improving temporal resolution and to provide a comprehensive validation of left-ventricular function measurements to make this technique applicable for routine phenotyping.