Spatial Mapping of Translational Diffusion Coefficients Using Diffusion Tensor Imaging: A Mathematical Description

Abstract

In this article, we discuss the theoretical background for diffusion weighted imaging and diffusion tensor imaging. Molecular diffusion is a random process involving thermal Brownian motion. In biological tissues, the underlying microstructures restrict the diffusion of water molecules, making diffusion directionally dependent. Water diffusion in tissue is mathematically characterized by the diffusion tensor, the elements of which contain information about the magnitude and direction of diffusion and is a function of the coordinate system. Thus, it is possible to generate contrast in tissue based primarily on diffusion effects. Expressing diffusion in terms of the measured diffusion coefficient (eigenvalue) in any one direction can lead to errors. Nowhere is this more evident than in white matter, due to the preferential orientation of myelin fibers. The directional dependency is removed by diagonalization of the diffusion tensor, which then yields a set of three eigenvalues and eigenvectors, representing the magnitude and direction of the three orthogonal axes of the diffusion ellipsoid, respectively. For example, the eigenvalue corresponding to the eigenvector along the long axis of the fiber corresponds qualitatively to diffusion with least restriction. Determination of the principal values of the diffusion tensor and various anisotropic indices provides structural information. We review the use of diffusion measurements using the modified Stejskal–Tanner diffusion equation. The anisotropy is analyzed by decomposing the diffusion tensor based on symmetrical properties describing the geometry of diffusion tensor. We further describe diffusion tensor properties in visualizing fiber tract organization of the human brain.

INTRODUCTION

Diffusion of individual molecules in a homogeneous environment such as water is characterized by Brownian motion, based on random motion initiated by thermal energy (1). Nuclear magnetic resonance has successfully been used to observe translational Brownian motion among molecules, in terms of a variation in the echo amplitude in an observed signal. Although diffusion can be an undesired result in conventional T1-and T2-weighted magnetic resonance imaging (MRI), one can obtain images in which the diffusion of water molecules can be the dominant source of contrast. In conventional spin–echo imaging methods, the effect of diffusion on the signal amplitude is negligible due to its dependence on echo time (T_E) as T_E³ (2–4). However, signal sensitivity to diffusion alone can be accentuated with modifications to spin–echo techniques, as described in a classic paper by Stejskal and Tanner (5). This method is known as diffusion weighted imaging (DWI), and has since been used extensively in clinical settings and serves as a gold standard in the early detection of acute stroke (6–8). Further, it has also been used to detect and characterize clinically relevant lesions in multiple sclerosis patients (9–11). Diffusion of water molecules is greatly influenced by the structural environment of the tissue (12, 13). For example, the tubular shape of axonal pathway greatly facilitates motion of water molecules parallel to the long axes of tubes but hinders motion along the direction perpendicular to the tube. Thus, the tracts based on diffusion of water molecules follow a path parallel to axonal pathways. The resulting anisotropy in the measured diffusion of water molecules reflects fiber tract orientation with respect to a quantifiable coordinate system. In this coordinate system, the diffusion coefficient corresponding to the largest eigenvalue is projected along the direction of least restriction. Therefore, the diffusion-sensitive imaging technique provides an indirect means of noninvasively evaluating axonal pathways (14–16).

As Brownian motion leads to movement of water molecules in multiple directions simultaneously, it forms a complex projection on Cartesian axes. The relationship between the properties of the driving force that generates diffusion of water molecules and the complex pattern of their movement in the tissue can be described by a tensor, also called diffusion tensor. The diffusion tensor is used to represent diffusion in a graphical form. Its elements contain information about the magnitude and direction of diffusion and are a function of the coordinate system in which it is described. The experimental measurement yields elements of a diffusion tensor with respect to a measurement frame, which is called a “laboratory axis frame” (LAF). Measured quantities, in this case, rely on a specific orientation of molecules with the laboratory axes system. To describe molecular motion that is independent of the frame of reference, the results must be transformed to a frame fixed with respect to the fiber, called the principal axis frame (PAF). The transformation from LAF to PAF is achieved using a set of Euler angle rotations as described in Appendix A. In PAF system, the off-diagonal terms do not exist and the tensor is reduced only to its diagonal elements, which are independent of any coordinate system of measurement. The diagonalization procedure transforms the LAF into PAF, and the transformation matrix provides projections of original elements of diffusion tensor onto an orthogonal PAF. The result of diagonalization provides two sets of information: 1) eigenvectors that contain all of the spatial information of diffusion and 2) a transformation matrix with eigenvalues, which contains complete information about the magnitude of diffusion, anisotropy, and skewness, independent of the reference frame in which measurements were made (17). The diagonalization scheme is developed using two different approaches. In the first, all six elements of diffusion tensor are used. In the second, cylindrical symmetry is assumed, reducing the number of required elements to four (18–21).

MRI SIGNAL IN THE PRESENCE OF DIFFUSION

In MRI, signal attenuation in an image pixel is due to combined effects of diffusion and other macroscopic processes such as flow and relaxation. The effect of each of these processes can be calculated by solving the Bloch equation (2). Spin dephasing due to relaxation effects are inherent to the tissue and arise solely from spin–spin interactions. Flow-related effects arise from the bulk transport of magnetization and result in spin dephasing when flow takes place during the active magnetic field gradients. On a microscopic scale, spatial variation in the concentration of spins occurs because of Brownian motion. In a system of freely diffusing molecules, in a homogeneous medium, where diffusion is isotropic, the continuity equation for molecular transport is given by (22):

$$\frac{\partial \rho (\overrightarrow{r},t)}{\partial t}=-D{\nabla }^2\rho (\overrightarrow{r},t).$$ (1)

In eq. 1, ∇² is the three-dimensional (3D) Laplacian operator and D is the diffusion coefficient. Here, the density or concentration of particles, ρ is the probability of finding a particle in a certain spatial location. The above equation is commonly referred to as the “diffusion equation,” as the differential form of equation gives the probability of finding a particle or a molecule at a time t at a position $\overrightarrow{r}$ from its initial location ${\overrightarrow{r}}_0$. With the initial condition that the concentration of particles follows Dirac's delta function, $\rho (\overrightarrow{r},0)=\delta (\overrightarrow{r}-{\overrightarrow{r}}_0)$, the solution of eq. 1 is a Gaussian distribution of the form

$$\rho (\overrightarrow{r},{\overrightarrow{r}}_0,t)=\frac{1}{\sqrt{{\left(4\pi Dt\right)}^3}}\exp \left\{-\frac{{(\overrightarrow{r}-{\overrightarrow{r}}_0)}^2}{4Dt}\right\}$$ (2)

The above equation is the fundamental solution of the diffusion equation describing free or unrestricted diffusion for isotropic diffusion defined by coefficient D. It allows the calculation of the mean square value of molecular displacement during the observation time, t.

$$\langle {\overrightarrow{r}}^2\left(t\right)\rangle ={\int }_{-\infty }^{\infty }\rho (\overrightarrow{r},t){\overrightarrow{r}}^{2}d\overrightarrow{r}=6Dt$$ (3a)

The symbol < > in Eq.(3a) describes an average value. The above relation is referred to as Einstein's equation of diffusion, where diffusion, D, relates the random spatial variation (displacement: ξ) of spins to the density (density: ρ) on a MRI time scale as (22):

$$\xi =\sqrt{\langle {\overrightarrow{r}}^2\left(t\right)\rangle }=\sqrt{\langle x^2\left(t\right)+y^2\left(t\right)+z^2\left(t\right)\rangle }=\sqrt{2NDt}$$ (3b)

Here, t is the measurement time and N is the dimensionality of space in which diffusion is measured. Diffusion theory provides an estimate of the root mean square (RMS) displacement of a freely diffusing molecule over time τ in one direction to be $\sqrt{2D\tau }$. The diffusing mass flows in the direction of decreasing concentration, which is indicated by minus sign in eq. 1. In a typical imaging setup where N = 1, with a measurement time of 20–60 ms, the mean displacement of water molecules (D ~ 2.95 × 10⁻³ mm²/s) is on the order of 11–19 μm, which is further reduced by a factor of two in tissue. For example, in cerebral gray matter (D ~ 0.74 × 10⁻³ mm²/s), the mean displacement of water molecules is 5–10 μm (23). With a mean cellular dimension of the order of 20–30 μm, such a displacement among spins within each pixel does not significantly alter phase to reduce overall tissue proton signal in conventional imaging techniques. Therefore, use of strong magnetic field gradients is essential to increase the effects of diffusion on the signal.

DIFFUSION TENSOR

In an anisotropic medium, diffusion in eq. 1 takes the following tensorial form:

$$\frac{\partial \rho }{\partial t}=-\sum _{\alpha ,\beta }^{1,2,3}{D}_{\alpha ,\beta }\cdot \frac{{\partial }^2\rho }{\partial x_{\alpha }\partial x_{\beta }},$$ (4)

where D is expressed as a tensor, whose elements provide orientational information in biological tissue. Due to the symmetric nature of diffusion in 3D space, the diffusion coefficient is limited to elements of a symmetric tensor. It has a total of six degrees of freedom and should be completely constructed with a 3 × 3 symmetric matrix. The signal attenuation due to flow, diffusion, and relaxation is obtained by solving the Bloch equation by including these effects. The time dependence of transverse magnetization, m, during the application of a gradient, g, is defined as (2, 3):

$$\frac{\partial m_{x,y}(r,t)}{\partial t}=-\frac{m_{x,y}(r,t)}{T_2}-i({\omega }_0+\gamma g\cdot r)m_{x,y}(r,t)+D{\nabla }^2{m}_{x,y}(r,t),$$ (5)

where ω₀ is the Larmor angular frequency, γ is the gyromagnetic ratio, g is the amplitude of the gradient, T₂ is the transverse spin–spin relaxation time, and ∇ is the Laplacian operator. The spin motion is represented in the displacement r, which can be expanded using static (r₀) and first-order velocity (ν) terms as r ≈ r₀ + νt.

In a rotating frame where the effects of Larmor frequency can be ignored, the above equation takes the form

$$\frac{\partial m_{x,y}}{\partial t}=-\frac{m_{x,y}}{T_2}-i\gamma g{r}_0{m}_{x,y}-i\gamma g\cdot \upsilon t{m}_{x,y}+D{\nabla }^2{m}_{x,y}.$$ (6)

The transverse magnetization, m_xy including flow with velocity ν, relaxation and diffusion is a solution to above eq. 6 and is given by (24–26):

$$m_{xy}(r,\mathrm{TE})=m_0{e}^{-\frac{\left(\mathrm{TE}\right)}{T_2}}{e}^{-\frac{1}{4}i\gamma gv{\left(\mathrm{TE}\right)}^2}{e}^{-\frac{1}{12}{\gamma }^2{g}^{2}D{\left(\mathrm{TE}\right)}^3}$$ (7)

where TE is the time between the center of excitation radio frequency (RF) pulse and the center of k-space where signal is maximum. As can be seen from eq. 7, the flow and diffusion terms depend on TE as TE² and TE³, respectively (2–4). Carr and Purcell extended the idea by using multiple refocusing pulses in which diffusion effects were made independent of refocusing RF pulse spacing (26). Consequently, diffusion effects can be made negligible under a constant gradient and by increasing the number of echoes.

The aforementioned method of imaging was not very useful for studying isolated diffusion effects, because T2 effects contaminate the signal during the T_E period. Hence, decoupling of diffusion from relaxation effects improves data quality. Stejskal and Tanner used pulsed gradients to analyze the signal dependence of diffusion effects and proposed decoupling of diffusion effects from T2 effects. With a pulsed gradient, the solution for transverse magnetization m_xy is given by (3, 5):

$$m_{xy}(r,\mathrm{TE})=m_0{e}^{-\frac{\left(\mathrm{TE}\right)}{T_2}}{e}^{-\frac{1}{4}i\gamma gv{\left(\mathrm{TE}\right)}^2}{e}^{-{\gamma }^2{g}^2{\delta }^2(\Delta -\frac{\delta }{3})D}$$ (8)

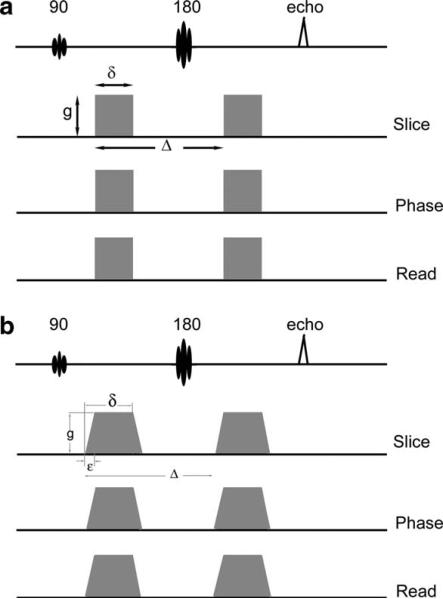
where Δ is the separation between gradient leading edges, δ is the duration of the gradient, and g is the amplitude as described in Fig. 1(a).

Figure 1.

A. Stejskal–Tanner diffusion prep uses gradients of equal amplitude and duration placed on either side of 180 RF pulse. The gradients are high enough to be sensitive to microscopic motion. B. Typical trapezoidal gradients used in a diffusion-weighted imaging experiment. Due to finite rise time, gradient maximum plateau is reached in a time, ε. Equation 15 refers to elements of modified b-matrix.

To conveniently express parameters related to diffusion in terms of measurable quantities using a simple bipolar gradient waveform, the b-factor is defined as:

$$b={\gamma }^2{g}^2{\delta }^2\left[\Delta -\frac{\delta }{3}\right].$$ (9)

The quantity b with units of s/m² serves as a measure of diffusion sensitivity that summarizes the influence of gradients on diffusion-weighted images (27, 28). In a tissue, movement of water molecules are restricted by cellular boundaries and the magnitude of diffusion is less when molecules are not restricted. The measured diffusion is called apparent diffusion coefficient (ADC). In the absence of noise, due to round-off errors, the choice of b-factor does not matter when calculating ADC. It is important to note that the signal loss due to intravoxel dephasing is caused by both diffusion and perfusion of water molecules. Dephasing from perfusion is generally completed at relatively low values of the b-factor. This is largely due to bulk coherent flow (29–31). Thus, signal loss from diffusion can be separated from perfusion or flow by working at sufficiently large values of b. However, if the b-factor is too large, this signal may drop below the system noise level due to high signal attenuation. If it is too low, then diffusion induced signal attenuation is comparable to variance of the DW data resulting in underestimation of ADC. For example, diffusion induced signal is attenuated by a factor of e^−bD_adc. Therefore, if the product bD_adc = 0.85, then the signal drops by a factor e^−1.0 (= 37%); with bD_adc = 0.85, it drops by a factor of 43% of the T2-weighted signal. Due to the wide range of D_adc in white matter, it is difficult to precisely define optimum b-values. Past experience in brain diffusion imaging has shown that an optimum b-factor is chosen so that the product (bD) is nearly 0.85, which corresponds to a drop of 43% of T2-weighted signal. For example, this corresponds to a b-factor of 1,200–1,000 s/mm² for a D_av = 0.7–0.85 × 10⁻³mm²/s. Most clinical studies have used a fixed value of 1,000 s/mm².

In treating effects of gradient pulses on diffusion, bulk flow and relaxation effects can be combined to rewrite the transverse magnetization as a function of gradients. Using eq. 8 and the definition of b, the signal amplitude within each pixel in an image is proportional to the transverse magnetization integrated within the excited volume and can be written as;

$$\begin{array}{cc}\hfill S(g,\mathrm{TE})=& \int m_{xy}(r,\mathrm{TE})d^{3}r\hfill \\ \hfill =& e^{-b\cdot D}\int \left[m_0{e}^{-\frac{\mathrm{TE}}{T_2}}{e}^{-\frac{1}{4}i\gamma g\upsilon {\mathrm{TE}}^2}\right]d^{3}r.\hfill \end{array}$$ (10)

For the case of random spin motion in an isotropic and homogeneous medium, combining eqs. (8–10), on a logarithmic scale the diffusion coefficient can be expressed as;

$$\ln \left[\frac{{S(g,\mathrm{TE})\mid }_{b\ne 0}}{{S\left(\mathrm{TE}\right)\mid }_{b=0}}\right]=-b\cdot D$$ (11)

where S(TE)|_b=0 represents the signal at the location r, in the presence of only the imaging gradients and RF pulses, and S (g, TE)|_b represents the signal during the presence of pulsed diffusion magnetic field gradients and imaging gradients. Typically, gradient amplitudes are altered such that a fixed b-factor is obtained along at least three orthogonal directions to obtain average diffusion.

A fundamental description of diffusion assumes that the probability distribution function of water in any brain voxel is Gaussian for each of three orthogonal planes. Signal decay is represented by a monoexponential function. As the motion of water molecule becomes complex within cells and membranes, the diffusion probability distribution deviates from a Gaussian form. This deviation can be quantified and defined as excess kurtosis. Under this condition, the deviation from Gaussianity is expressed through a modified relationship that includes both mono- and nonmonoexponential decay functions (32–34), expressed as;

$$\ln \left[\frac{{S(g,\mathrm{TE})\mid }_{b\ne 0}}{{S\left(\mathrm{TE}\right)\mid }_{b=0}}\right]\approx -b\cdot D+\frac{1}{6}{(b\cdot D)}^2\cdot K$$ (12)

In eq. 12, the higher order terms in b are neglected. The term K, a dimensionless parameter, is called the kurtosis coefficient. It tells us if the diffusion is more sharply or less sharply peaked than a Gaussian diffusion. Gaussian diffusion corresponds to K = 0. It is possible to directly estimate the diffusion kurtosis by acquiring three DWI measurements for different b-values (including b = 0 unweighted image). The method is known as diffusion kurtosis imaging (32–34). Due to the positive contribution of the second term, there is a limited range of b-factors. Jensen et al. (33) have found that to obtain the diffusional kurtosis with a reasonable degree of precision, b values somewhat larger than those usually used in DWI are necessary, so that the departure from linearity is clearly apparent. In the brain, maximum b-values of about 2,000 s/mm² are sufficient. For low b-values, as are used in most diffusion tensor imaging (DTI) studies, it suffices to treat diffusion assuming Gaussianity.

DIFFUSION OF WATER IN NONISOTROPIC MEDIUM

In tissues, diffusion is largely anisotropic. This directional anisotropy may be exploited by sensitizing gradients along a preferential direction to obtain information about diffusion along that direction. During the measurement process, components transverse to the preferred direction will be undetected and this result may affect the measured quantity. In such cases, the anisotropic diffusion assumes the tensorial form given by (28);

$$\begin{array}{cc}\hfill & \ln \left[\frac{S(g,\mathrm{TE})}{S\left(\mathrm{TE}\right)}\right]=-\sum _{i,j}^{x,y,z}{b}_{i,j}\cdot D_{i,j}.\hfill \\ \hfill & =-(b_{xx}{D}_{xx}+b_{yy}{D}_{yy}+b_{zz}{D}_{zz}+2b_{xy}{D}_{xy}+2b_{yz}{D}_{yz}+2b_{xz}{D}_{xz})\hfill \end{array}$$ (13)

The diagonal elements of diffusion tensor (i.e., D_xx, D_yy, and D_zz) correspond to the diffusion coefficients estimated with gradients applied along the x, y, and z directions of the axes frame fixed with the scanner, also called the LAF. The off-diagonal elements (i.e., D_xy, D_yx, D_yz, D_zy, D_xz, D_zx) represent the correlation between diffusion along the respective paired axes of the LAF. The correlation between x and y is the same as the correlation between y and x. Therefore, the matrix is symmetric, that is, D_xy = D_yx, D_xz = D_zx, and D_yz = D_zy. Also, the quantity b_ij represents the elements of the b-matrix of row i and column j, and is related to ijth direction (i = x, y, and z; j = x, y, and z) (35–38). The exact expression depends on gradient shapes used in the measurement. Using rectangular bipolar pulse gradients of the form described by Stejskal and Tanner, the gradient-time integral is expressed as (5):

$$b_{i,j}={\gamma }^2{g}_i\cdot g_j\left[{\delta }^2\left(\Delta -\frac{\delta }{3}\right)\right].$$ (14)

In practice, however, gradient waveforms are never rectangular but with a finite rise and fall time to reach the maximum amplitude. In symmetric trapezoidal gradient waveform as described in Fig. 1(b), with a rise and fall time of ε, b_ij takes the following form (21, 23):

$$b_{i,j}={\gamma }^2{g}_i\cdot g_j\left[{\delta }^2\left(\Delta -\frac{\delta }{3}\right)+\frac{{\epsilon }^3}{30}-\frac{\delta {\epsilon }^2}{6}\right].$$ (15)

One can use different forms of gradients to produce a similar effect to accentuate diffusion related signal change (39–41). Table 1 describes various gradient schemes and corresponding effective b-values used in this measurement.

Table 1.

Expression for Estimating b-Values Based on Different Gradient Structures

Gradient Waveform	b-Value Expression
Constant gradient: Hahn single echo	$\frac{{\gamma }^2{g}^2{T}_{{\mathrm{E}}^3}}{12}$
Constant gradient—Carr–Purcell multiple n-echoes	$\frac{{\gamma }^2{g}^2{T}_{{\mathrm{E}}^3}}{12n^2}$
Sinusoidal	$\frac{3{\gamma }^2{g}^2{\delta }^3}{{\pi }^2}$
Pulse gradient—Stejskal–Tanner	${\gamma }^2{g}^2{\delta }^2[\Delta -\frac{\delta }{3}]$
Pulse gradient—trapezoidal	${\gamma }^2{g}^2[{\delta }^2(\Delta -\frac{\delta }{3})+\frac{{ϵ}^3}{30}-\frac{\delta {ϵ}^2}{6}]$

Here, g = gradient amplitude, T_E = echo time, γ = gyromagnetic ratio, Δ = time interval between leading edges of pulse gradient g, δ = width of gradient g, and ε = rise and fall time of trapezoidal gradient of amplitude.

Equation 13 suggests that, for anisotropic diffusion, diffusion is directionally dependent and the calculation of the b-matrix is considerably more complex. The directional dependency in eq. 13 can be resolved by measuring the diffusion coefficient by sensitizing diffusion gradient in each direction. For example, using orthogonal x, y, and z gradients, one can estimate diffusion coefficients along the x, y, and z directions. Measured values represent the diagonal elements of the diffusion tensor.

The measured diffusion tensor matrix elements are diagonal if the direction of diffusion is collinear with the coordinate system. However, in reality, this is never the case. For example, if the diffusion direction is rotated with the coordinate system in which measurements are made, the resulting diffusion matrix will have elements that are diagonal and off-diagonal. The off-diagonal elements of D^lab provide the correlation of random motions between x, y, and z directions. The result reflects the dependency on the coordinate system in which measurements are performed. It is best to always define the tensor elements in a frame of reference fixed, for example, with the fiber tracts. A simplified method involves measurement of diffusion along each direction in a frame fixed with respect to the laboratory (or scanner) (x,y,z). This is possible by sensitizing diffusion gradients along each of these axes separately and measuring the diffusion coefficient along that direction. The measurement reflects the diffusion coefficients representing elements of the diffusion (D^lab) tensor in the laboratory frame where gradient values and directions are known. To estimate the diffusion along the local fiber tract, a frame is fixed with respect to fiber called PAF and is represented by (x′,y′,z′). The elements of diffusion tensor in the PAF are called D^PAF. These elements of D^PAF are related to the experimentally measured elements of D^lab through a series of rotations that transform the elements from one frame of reference to the other. In the fiber PAF frame, elements of the diffusion tensor are diagonal.

GEOMETRIC REPRESENTATION OF THE DIFFUSION TENSOR

An interesting and useful geometric representation can be formed based on the anisotropic nature of the diffusion tensor. The surface of the tensor ellipsoid describes the basic structural arrangement of the surroundings in which water is diffusing. For example, the shape of diffusion tensor ellipsoid can be described in terms of eigenvalues and eigenvectors. The Gaussian probability distribution function in eq. 2 can be generalized to the case of anisotropic diffusion by introducing the second-order diffusion tensor D in the eq. 1 to yield

$$\rho \{\overrightarrow{r}\mid \tau \}=\frac{1}{\sqrt{{\left(4\pi D\tau \right)}^3}}\exp \left\{-\left(\frac{1}{2}\right)r^T{\left(2D\tau \right)}^{-1}r\right\}$$ (16)

Here, $\rho \{\overrightarrow{r}\mid \tau \}$ is the probability that a particle initially at r = 0 is found at a location r (x,y,z) at a later time τ, “T” is the transpose of r-vector. When the exponent is chosen to be constant, the surfaces of $\rho \{\overrightarrow{r}\mid \tau \}$ are concentric spheres. When one chooses r^T (2Dτ)⁻¹ r = 1, we get

$$r^2=x^2+y^2+z^2=2D\tau .$$ (17)

The radius of the diffusion sphere, $\sqrt{2D\tau }$, is also the standard deviation of probability function $\rho \{\overrightarrow{r}\mid \tau \}$, σ, which is the mean displacement eq. 2 obtained by Einstein's formula.

There is one-to-one correspondence between the symmetric tensor D_ij and quadric surfaces of the form (42)

$$r^T{\left(2D\tau \right)}^{-1}r=1$$ (18)

The principal axes of this surface are clearly the same as the principal axes of the tensor D_{i′ j′}. In the PAF system corresponding to the coordinates (x′,y′,z′), eq. 18 takes the form (12)

$$D_{x^{\prime }{x}^{\prime }}{\left(x^{\prime }\right)}^2+D_{y^{\prime }{y}^{\prime }}{\left(y^{\prime }\right)}^2+D_{z^{\prime }{z}^{\prime }}{\left(z^{\prime }\right)}^2=\frac{{\left(x^{\prime }\right)}^2}{{\left(\sqrt{2{\lambda }_1\tau }\right)}^2}+\frac{{\left(y^{\prime }\right)}^2}{{\left(\sqrt{2{\lambda }_2\tau }\right)}^2}+\frac{{\left(z^{\prime }\right)}^2}{{\left(\sqrt{2{\lambda }_3\tau }\right)}^2}=1$$ (19)

The principal eigenvalues (λ₁,λ₂,λ₃) are defined such that λ₃ ≥ λ₂ ≥ λ₃. If λ₁,λ₂,λ₃ are all positive, then the surface (eq. 16) is an ellipsoid, called a tensor ellipsoid, with semiaxes of length $\sqrt{2{\lambda }_1\tau }$, $\sqrt{2{\lambda }_2\tau }$, and $\sqrt{2{\lambda }_3\tau }$. The magnitude of diffusion in different directions, represented by corresponding eigenvalues, are scaled such that the quantity $\sqrt{2\lambda \tau }$ represents the RMS displacement $\sqrt{r^2}$ along the principal axes (x′,y′,z′) during a measurement time τ, and eq. 19 is dimensionless.

The eigenvalues and eigenvectors describe the shape of the tensor ellipsoid. To illustrate geometric measures, using the definition of diffusion tensor as described in Appendix B, the inverse transformation from an eigensystem onto a tensor is given by:

$$D={\left[\begin{array}{ccc}\hfill {\widehat{e}}_1\hfill & \hfill {\widehat{e}}_2\hfill & \hfill {\widehat{e}}_3\hfill \end{array}\right]}^{-1}\cdot \mathrm{diag}\left[\begin{array}{ccc}\hfill {\lambda }_1\hfill & \hfill {\lambda }_2\hfill & \hfill {\lambda }_3\hfill \end{array}\right]\cdot \left[\begin{array}{ccc}\hfill {\widehat{e}}_1\hfill & \hfill {\widehat{e}}_2\hfill & \hfill {\widehat{e}}_3\hfill \end{array}\right],$$ (20)

where, [ê_i] are considered normalized eigenvectors corresponding to [λ_i]. In our case, eigenvectors [ê₁ê₂ê₃] represent PAF [x′,y′,z′]. In the case of a symmetric tensor, the above equation simplifies to

$$D=\begin{array}{ccc}\hfill {\lambda }_1\hfill & \hfill {\widehat{e}}_1\hfill & \hfill {{\widehat{e}}_1}^T\hfill \end{array}+\begin{array}{ccc}\hfill {\lambda }_2\hfill & \hfill {\widehat{e}}_2\hfill & \hfill {{\widehat{e}}_2}^2\hfill \end{array}+\begin{array}{ccc}\hfill {\lambda }_3\hfill & \hfill {\widehat{e}}_3\hfill & \hfill {{\widehat{e}}_3}^T\hfill \end{array}$$ (21)

Here, eigenvectors (ê₁ê₂ê₃) form an orthonormal basis. The combination of eigenvalues in the PAF provides not only the estimation of various anisotropies but also the shape of the diffusion ellipsoid. The diffusion ellipsoid is divided into three basic shapes:

1. Linear case (λ₃ ≥ λ₂ ≈ λ₁), where diffusion is mainly in the direction of the eigenvector of the largest eigenvalue:

   $$D\approx {\lambda }_3{D}_1=\begin{array}{ccc}\hfill {\lambda }_3\hfill & \hfill {\widehat{e}}_3\hfill & \hfill {{\widehat{e}}_3}^T\hfill \end{array},$$ (22a)
2. Planar case (λ₃ ≈ λ₂ ≥ λ₁), where diffusion is mainly in the plane spanned by the two eigenvectors corresponding to the two largest eigenvalues:

   $$D\approx 2{\lambda }_3{D}_{\mathrm{p}}={\lambda }_3(\begin{array}{cc}\hfill {\widehat{e}}_3\hfill & \hfill {{\widehat{e}}_3}^T\hfill \end{array}+\begin{array}{cc}\hfill {\widehat{e}}_2\hfill & \hfill {{\widehat{e}}_2}^T\hfill \end{array}),$$ (22b)
3. Spherical case (λ₃ ≈ λ₂ ≈ λ₁), where diffusion is isotropic in all directions:

   $$D\approx 3{\lambda }_3{D}_{\mathrm{s}}={\lambda }_3(\begin{array}{cc}\hfill {\widehat{e}}_3\hfill & \hfill {{\widehat{e}}_3}^T\hfill \end{array}+\begin{array}{cc}\hfill {\widehat{e}}_2\hfill & \hfill {{\widehat{e}}_2}^T\hfill \end{array}+\begin{array}{cc}\hfill {\widehat{e}}_1\hfill & \hfill {{\widehat{e}}_1}^T\hfill \end{array}).$$ (22c)

A general diffusion tensor can be written as a combination of these three cases.

Expanding the diffusion tensor D using these three cases gives:

$$\begin{array}{c}\hfill D=\begin{array}{ccc}\hfill {\lambda }_1\hfill & \hfill {\widehat{e}}_1\hfill & \hfill {{\widehat{e}}_1}^T\hfill \end{array}+\begin{array}{ccc}\hfill {\lambda }_2\hfill & \hfill {\widehat{e}}_2\hfill & \hfill {{\widehat{e}}_2}^T\hfill \end{array}+\begin{array}{ccc}\hfill {\lambda }_3\hfill & \hfill {\widehat{e}}_3\hfill & \hfill {{\widehat{e}}_3}^T\hfill \end{array}\hfill \\ \hfill =({\lambda }_3-{\lambda }_2)\begin{array}{cc}\hfill {\widehat{e}}_3\hfill & \hfill {{\widehat{e}}_3}^T\hfill \end{array}+({\lambda }_2-{\lambda }_1)(\begin{array}{cc}\hfill {\widehat{e}}_3\hfill & \hfill {{\widehat{e}}_3}^T\hfill \end{array}+\begin{array}{cc}\hfill {\widehat{e}}_2\hfill & \hfill {{\widehat{e}}_2}^T\hfill \end{array})\hfill \\ \hfill +{\lambda }_1(\begin{array}{cc}\hfill {\widehat{e}}_3\hfill & \hfill {{\widehat{e}}_3}^T\hfill \end{array}+\begin{array}{cc}\hfill {\widehat{e}}_2\hfill & \hfill {{\widehat{e}}_2}^T\hfill \end{array}+\begin{array}{cc}\hfill {\widehat{e}}_1\hfill & \hfill {{\widehat{e}}_1}^T\hfill \end{array}),\hfill \end{array}$$ (23)

where (λ₃ – λ₂), (λ₂ – λ₁) and λ₁ are the coordinates of D in the tensor basis (D_l D_p D_s) The above definition can be applied to any measurement of diffusion to see how close the diffusion tensor is to the cases of line, plane or sphere. These parameters are represented by the components of the matrix representing the principal axes frame (39, 42).

$$\frac{1}{3\stackrel{‒}{\lambda }}\left[\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill {\lambda }_2\hfill \\ \hfill {\lambda }_3\hfill \end{array}\right]=C_{\mathrm{lin}}\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right]+C_{\mathrm{pla}}\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 1∕2\hfill \\ \hfill 1∕2\hfill \end{array}\right]+C_{\mathrm{sph}}\left[\begin{array}{c}\hfill 1∕3\hfill \\ \hfill 1∕3\hfill \\ \hfill 1∕3\hfill \end{array}\right],$$ (24a)

where

$$\overline{\lambda }=\frac{({\lambda }_1+{\lambda }_2+{\lambda }_3)}{3};C_{\mathrm{lin}}=\frac{({\lambda }_3-{\lambda }_2)}{({\lambda }_1+{\lambda }_2+{\lambda }_3)};C_{\mathrm{pla}}=\frac{2({\lambda }_2-{\lambda }_1)}{({\lambda }_1+{\lambda }_2+{\lambda }_3)};C_{\mathrm{sp}}=\frac{3{\lambda }_1}{({\lambda }_1+{\lambda }_2+{\lambda }_3)}.$$

The coefficients C_lin, C_plan, and C_sph represent linear, planar, and spherical shapes, respectively. For planar and spherical shapes, scaling factors of 2 and 3 have been used, respectively, so that each coefficient independently lies in the range (0–1) and C_lin + C_plan + C_sph = 1. In Fig. 2, a mathematical object shape based on the set of three eigenvectors corresponding to eigenvalues λ₁, λ₂, and λ₃ is described. The normalization is performed using the trace. However, another useful measure in this context is to normalize the sum of the measurements to 1 using the magnitude of the largest eigenvalue of the diffusion tensor. The corresponding shapes are; $C_{\mathrm{lin}}=\frac{({\lambda }_3-{\lambda }_2)}{{\lambda }_3}$; $C_{\mathrm{pla}}=\frac{({\lambda }_2-{\lambda }_1)}{{\lambda }_3}$; and $C_{\mathrm{sp}}=\frac{{\lambda }_1}{{\lambda }_3}$.

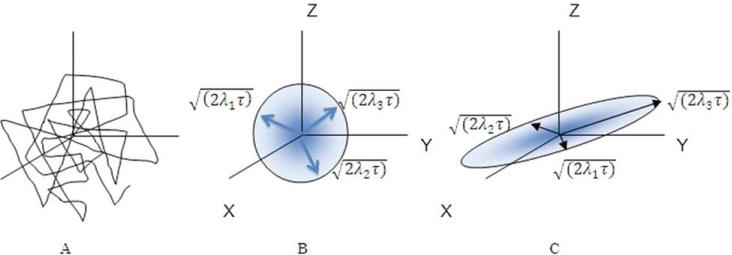
Figure 2.

Diffusion paths of molecules experiencing Brownian motion (A). (B) and (C) show isoprobability surfaces corresponding to eq. 22 and 24. The surfaces represent the locations in space where the probability of finding water molecule at time t. For spherical diffusion (B), the motion is isotropic with equal likelihood of diffusion in all direction with eigenvalues equal in magnitude in all directions λ₃ = λ₁ = λ₂). However, with anisotropy in diffusion, the anisotropy is described by three orthogonal Gaussian distributions with magnitude (eigenvalues) resulting in ellipsoidal diffusion. (C) shows a configuration where eigenvalues differ from each other. The actual magnitude of displacement in each of the orthogonal direction is proportional to the square root of the product of the eigenvalue and the time of diffusion.

This model-based approach to measuring diffusion is called DTI. The parallel diffusivity measure (diffusion parallel to the long axis) is equal to the largest eigenvalue. The perpendicular diffusivity measure, also called radial diffusivity, is equal to the average of the two smaller eigenvalues. In DTI of the brain, these measures can be interpreted as diffusivity parallel and perpendicular to the fiber tract.

DIFFUSION SAMPLING SCHEME

The original description considers diffusion to be scalar and isotropic with no preference for direction. However, in biological tissue, cell boundaries, membranes, and myelin fibers, which form the underlying micro-structure of biological tissue, restrict Brownian diffusion of water molecules. The average diffusion length over time is shorter in a restricted space compared to a restriction-free space. Therefore, the experimentally observed diffusion coefficient in tissue is defined with ADC. The complete determination of diffusion characteristics of tissues under these conditions requires the determination of the full diffusion tensor of the ADC.

To estimate components of the PAF diffusion tensor, a total of six independent elements of the tensor in the laboratory frame are needed, in which the diagonal elements are measured by applying gradients along three orthogonal axes in the laboratory frame. Introducing g^k = g·r^k as the gradient vector along the direction k and a product of magnitude of gradient and the unit vector along the direction k, eq. 13 can be written as (28, 40, 41):

$$\ln \left[\frac{S(g^k,\mathrm{TE})}{S\left(\mathrm{TE}\right)}\right]=S_k=-\sum _{i,j}^{x,y,z}{b}_{ij}{r}_i^{k\left(T\right)}{D}_{ij}{r}_j^k,$$ (25)

where r^k(T) is the transpose of vector r^k. The left hand side represents the natural logarithm of the ratio of signal with a gradient sensitized along the kth direction and signal without any gradients. We will represent this quantity by S_k. Six directions are chosen, in which three represent orthogonal directions and the other three represent directions obtained from a combination of any two orthogonal directions. In all, six unit vectors representing six noncollinear directions, namely;

$$r^1=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right],r^2=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right],r^3=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right],r^4=\frac{1}{\sqrt{2}}\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right],r^5=\frac{1}{\sqrt{2}}\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \end{array}\right],r^6=\frac{1}{\sqrt{2}}\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right]$$ (26)

are used. Of these six measurements, three measurements are along the orthogonal directions (r¹,r²,r³) and provide the ADC along those directions. However, off-diagonal terms are determined by solving a system of linear equations that contain diffusion coefficients obtained by applying gradients along the r⁴, r⁵, and r⁶ directions.

From eq. 25, it can be seen that each element b_i,j of the b-matrix is a weighting factor of corresponding diffusion tensor component D_i,j, and the product of these two terms is linearly changing with measured logarithmic MR signal ratio (23). Using b_ij for a symmetric trapezoidal gradient waveform as described in eq. 15 and simplifying for an isotropic medium with a constant diffusivity D₀ (21),

$$\ln \left[\frac{S(g^k,\mathrm{TE})}{S\left(\mathrm{TE}\right)}\right]=S_k=-{\gamma }^2\mid g^2\mid \left[{\delta }^2\left(\Delta -\frac{\delta }{3}\right)+\frac{{\epsilon }^3}{30}-\frac{\delta {\epsilon }^2}{6}\right]D_0=-b{D}_0$$ (27)

Typically, in any DWI, both imaging and diffusion gradients are applied. Therefore, calculation of b_ij of the b-matrix requires knowledge of timing and amplitude of all gradients applied in a pulse sequence. With imaging gradients also present, the b-factor in eq. 21 consists of three terms:

$$b=b^{\mathrm{diff}}+b^{\mathrm{img}}+b^{\mathrm{ct}}.$$ (28)

The first term, b^diff, is exactly as defined in eq. 15. The second term b^img, is generated by imaging gradients (G) and is related to pulse sequence parameters (field-of-view (FOV), matrix, slice thickness, orientation) with negligible effect on diffusion. The third term, b^ct, also called the “cross-term,” is related to the product of a diffusion gradient and one imaging gradient (g·G). One method to eliminate the cross-term is to use diffusion gradients with opposite signs, corresponding to measuring diffusion in both the forward and the backward direction. The geometric average of these two images results in the elimination of the cross-term. This method was first described by Neeman et al. (43, 44). The basic idea can be described as:

$$b^{+}=g_{\mathrm{diff}}^2{\tau }_{\mathrm{diff}}+G_{\mathrm{img}}^2{\tau }_{\mathrm{img}}+g_{\mathrm{diff}}{G}_{\mathrm{imag}}{\tau }_{\mathrm{ct}},$$ (29)

where τ is function of timing parameters for diffusion, imaging, and cross-term gradients involved. If the polarity of only the diffusion gradients is reversed, only the cross-term changes sign:

$$b^{-}=g_{\mathrm{diff}}^2{\tau }_{\mathrm{diff}}+G_{\mathrm{img}}^2{\tau }_{\mathrm{img}}-g_{\mathrm{diff}}{G}_{\mathrm{imag}}{\tau }_{\mathrm{ct}}.$$ (30)

The expression for signal in these two cases is:

$$S(+)=S\left(0\right)\cdot e^{-(g_{\mathrm{diff}}^2{\tau }_{\mathrm{diff}}+G_{\mathrm{img}}^2{\tau }_{\mathrm{img}}+g_{\mathrm{diff}}{G}_{\mathrm{imag}}{\tau }_{\mathrm{ct}})D_0}$$ (31a)

$$S(-)=S\left(0\right)\cdot e^{-(g_{\mathrm{diff}}^2{\tau }_{\mathrm{diff}}+G_{\mathrm{img}}^2{\tau }_{\mathrm{img}}-g_{\mathrm{diff}}{G}_{\mathrm{imag}}{\tau }_{\mathrm{ct}})D_0}$$ (31b)

The geometric average of two images obtained with b⁺ and b⁻ results in an image that does not contain the cross-term attenuation contribution.

$$S=\sqrt{S(+)S(-)}=S\left(0\right)e^{-(g_{\mathrm{diff}}^2{\tau }_{\mathrm{diff}}+G_{\mathrm{img}}^2{\tau }_{\mathrm{img}})D_0}$$ (32)

Likewise, the square root of the ratio between the two images will contain only the cross-term effects and is given by;

$$\sqrt{\frac{S(+)}{S(-)}}=e^{-b_{\mathrm{ct}}{D}_0}$$ (33)

Although the positive–negative approach has advantages, it is not routinely practiced because it requires two scans in each direction doubling scan time. For most imaging applications, the influence of imaging gradients alone on diffusion is ignored. In general, the diagonal elements of the b-matrix include effects of both diffusion and imaging gradients, and effects of off-diagonal elements of the b-matrix are ignored (21). To understand and estimate the effect of imaging gradients in calculating elements of the b-matrix accurately, Mattiello et al. (45) have performed a series of experiments in a water phantom, to evaluate whether the isotropic property of water would indeed provide only diagonal elements of diffusion tensor, resulting in a constant scalar value, whereas the off-diagonal values are near zero. The authors found that contributions from readout- and phase-encode gradient pulse trains have negligible effect on the echo, but the contributions from other imaging gradients applied not necessarily in readout- or phase-encode directions cause significant change in echo amplitude (45). The percentage error in the b-matrix element produces the same percentage error in the corresponding element of the estimated diffusion tensor but of opposite sign (46, 47). Other potential sources of errors in the calculated diffusion tensor elements are eddy currents induced from the magnitudes and directions of gradient pulses, causing nonuniformity of the errors in the diagonal elements of the diffusion tensor, fast switching of gradients, causing mechanical vibration due to higher vibrational frequencies in gradient coils.

A simplified approach uses a fixed gradient waveform, where b-factors of the three orthogonal acquisitions are equal (i.e., b_xx = b_yy = b_zz = b) and off-diagonal elements of the b-matrix are ignored (i.e., b_ij ≈ 0 for i ≠ j). On substitution in eq. 25 using gradient vectors defined in eq. 26, signal expression in each directions is calculated as (48);

$$S_1=-b{D}_{xx}$$ (34a)

$$S_2=-b{D}_{yy}$$ (34b)

$$S_3=-b{D}_{zz}$$ (34c)

$$S_4=-\frac{b}{2}[D_{xx}+D_{yy}+2D_{xy}]$$ (34d)

$$S_5=-\frac{b}{2}[D_{yy}+D_{zz}+2D_{yz}]$$ (34e)

$$S_6=-\frac{b}{2}[D_{xx}+D_{zz}+2D_{xz}]$$ (34f)

Although the above approach is simple to use, there are some obvious drawbacks that need to be addressed. Due to the anisotropic nature of diffusion in tissues, sampling of diffusion will be directionally dependent. First, the above scheme uses gradients in specific directions, and therefore, is not sampled isotropically. Sampling of diffusion in any one direction, therefore, may be influenced by diffusion along other directions. Bias in the measurement direction may be overcome by sampling isotropically with the same diffusion weighting along each sampled direction. Second, using a gradient in a single direction such as xx, yy, and zz, pulsing will generate stronger eddy currents, because physical direction is not being shared by two gradients. Any spatial distortion will be more evident because the level of eddy current generation along xx, yy, and zz directions will be significantly greater than along the xy, yz, and zx directions, where the sensitization direction is being shared between two physical gradients.

These drawbacks are avoided with a balanced gradient approach in which gradients are used simultaneously in multiple directions, as described by Conturo et al. (27) and Basser and Pierpaoli (28). The scheme that we chose in our work is one in which the gradient directions are sampled isotropically and all DWIs have the same diffusion weighting. By sharing the sensitization direction with all six projections, the b-value can be maintained and eddy currents minimized. This will subsequently minimize spatial distortions in the final result. In our study, the gradient direction scheme is similar to one used by Basser and Pierpaoli (28), in which the unit vectors represent the following six independent directions.

$$r^1=\frac{1}{\sqrt{2}}\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right],r^2=\frac{1}{\sqrt{2}}\left[\begin{array}{c}\hfill -1\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right],r^3=\frac{1}{\sqrt{2}}\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \end{array}\right],r^4=\frac{1}{\sqrt{2}}\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill -1\hfill \end{array}\right],r^5=\frac{1}{\sqrt{2}}\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right],r^6=\frac{1}{\sqrt{2}}\left[\begin{array}{c}\hfill -1\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right]$$ (35)

Substituting these gradient vectors in eq. 25, six independent equations are given by:

$$S_1=-\frac{b}{2}[D_{xx}+D_{zz}+2D_{xz}]$$ (36a)

$$S_2=-\frac{b}{2}[D_{xx}+D_{zz}-2D_{xz}]$$ (36b)

$$S_3=-\frac{b}{2}[D_{yy}+D_{zz}+2D_{yz}]$$ (36c)

$$S_4=-\frac{b}{2}[D_{yy}+D_{zz}+2D_{yz}]$$ (36d)

$$S_5=-\frac{b}{2}[D_{xx}+D_{yy}+2D_{xy}]$$ (36e)

$$S_6=-\frac{b}{2}[D_{xx}+D_{yy}-2D_{xy}]$$ (36f)

These simultaneous equations are solved for diffusion tensor elements:

$$D_{xx}=\frac{[(S_3+S_4)-(S_1+S_2)-(S_5+S_6)]}{2b}$$ (37a)

$$D_{yy}=\frac{[(S_1+S_2)-(S_3+S_4)-(S_5+S_6)]}{2b}$$ (37b)

$$D_{zz}=\frac{[(S_5+S_6)-(S_1+S_2)-(S_3+S_4)]}{2b}$$ (37c)

$$D_{xy}=\frac{\left[(S_6-S_5)\right]}{2b}$$ (37d)

$$D_{yz}=\frac{\left[(S_4-S_3)\right]}{2b}$$ (37c)

$$D_{xz}=\frac{\left[(S_2-S_1)\right]}{2b}$$ (37f)

The denominator in eq. 33 with a factor of 2 differs from eq. 6 of Basser and Pierpaoli (28). The difference is due to the factor of 2 used in the definition of b_ij by Basser and Pierpaoli.

SCALAR ROTATIONALLY INVARIANT MEASURES FROM DIFFUSION TENSOR

The diagonal and off-diagonal terms constitute a diffusion tensor. In tissue, the diffusion tensor as defined in eq. 18 can be mathematically represented by a symmetric second-rank Cartesian tensor in LAF. These elements are defined as:

$$D_{i,j}=\left[\begin{array}{ccc}\hfill D_{x,x}\hfill & \hfill D_{x,y}\hfill & \hfill D_{x,z}\hfill \\ \hfill D_{x,y}\hfill & \hfill D_{y,y}\hfill & \hfill D_{y,z}\hfill \\ \hfill D_{x,z}\hfill & \hfill D_{y,z}\hfill & \hfill D_{z,z}\hfill \end{array}\right]$$ (38)

The diffusion tensor can be decomposed into symmetric (isotropic) and asymmetric (anisotropic) parts as follows:

$$\langle D_{i,j}\rangle =\stackrel{‒}{D}I+(D-\stackrel{‒}{D}I).$$ (39)

Here, D̄ defines an isotropic diffusion tensor, (D – D̄) is a diffusion deviation tensor whose elements represent deviation from isotropy, the symbol < > is the average of diffusion tensor, and I is the identity matrix. In terms of corresponding eigenvalues, eq. 39 in PAF becomes;

$$=\overline{\lambda }\mid \begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\mid +\mid \begin{array}{ccc}\hfill ({\lambda }_1-\overline{\lambda })\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill ({\lambda }_2-\overline{\lambda })\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill ({\lambda }_3-\overline{\lambda })\hfill \end{array}\mid$$ (40)

Eigenvalues and eigenvectors are useful in defining morphologic features of the diffusion tensor. However, diffusion anisotropy is intrinsically related to eigenvalues, which is based on shape of the diffusion tensor, not related to eigenvectors, which define the orientation. The best way to compare between tissue structures is to define a set of several rotationally invariant indices derived strictly from the eigenvalues of the tensor that do not contain eigenvectors. These are algebraic combinations of eigenvalues normalized such that a value of 0 represents perfectly isotropic diffusion, and a value of 1 represents completely anisotropic diffusion where diffusion is parallel to the infinitely long, thin fiber. By imposing these limits, tensors based on different morphologies can be compared and distinguished using scalar indices. For example, there are three main groups resulting from algebraic combination of eigenvalues normalized between (0) and (1): relative anisotropy (RA), fractional anisotropy (FA), and volume ratio (VR). RA measures the ratio of anisotropic and isotropic parts of the diffusion tensor. The exact expression for RA is given by the ratio of RMS difference between the calculated principal diagonal values and the average diffusion value and mean diffusion value (10, 18). It is zero with complete isotropy (λ₁ = λ₂ = λ₃) and is equal to 1 with complete anisotropy (λ₁ = λ₂ = 0, λ₃ > 0)(42, 49–52)

$$\mathrm{RA}=\frac{1}{\sqrt{6}}\frac{\sqrt{{\sum }_{i=x,y,z}{(D_{ii}-\overline{D})}^2+2(D_{xy}^2+D_{yz}^2+D_{zx}^2)}}{\overline{D}},$$ (41)

where $\overline{D}=\frac{1}{3}{\sum }_{i=x,y,z}{D}_{ii}$.

In the principal axes frame, off-diagonal terms are zero and the diagonal terms represent eigenvalues, in which case eq. 41 reduces to

$$\mathrm{RA}=\sqrt{\frac{1}{6}}\cdot \frac{\sqrt{{({\lambda }_1-\overline{\lambda })}^2+{({\lambda }_2-\overline{\lambda })}^2+{({\lambda }_3-\overline{\lambda })}^2}}{\overline{\lambda }}.$$ (42)

The second and more commonly used anisotropy measure, FA, is a measure of the fraction of total magnitude of D that varies from a value of 0 (complete isotropy) to 1 (complete anisotropy). It is defined as (50–53):

$$\mathrm{FA}=\sqrt{\frac{3}{2}}\cdot \sqrt{\frac{{({\lambda }_1-\overline{\lambda })}^2+{({\lambda }_2-\overline{\lambda })}^2+{({\lambda }_3-\overline{\lambda })}^2}{({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2)}}.$$ (43)

Interestingly, FA also measures the deviation of the tensor from a sphere (1–C_sph), which is also the sum of linear and planar measures. The relationship between FA and RA is defined analytically as;

$$\mathrm{FA}=\sqrt{\frac{3{\left(\mathrm{RA}\right)}^2}{2{\left(\mathrm{RA}\right)}^2+1}}\text{and}\mathrm{RA}=\sqrt{\frac{{\left(\mathrm{FA}\right)}^2}{3-2{\left(\mathrm{FA}\right)}^2}}.$$ (44)

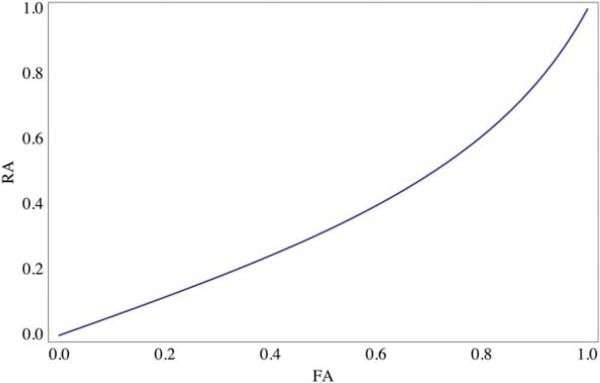
The scaling method used in defining RA and FA is based on its value being 0 for complete isotropy and 1 for complete anisotropy (diffusion strictly along a single direction). This approach is not important as long as one clearly states the anisotropy index when reporting anisotropy values. The analytical relationship between RA and FA as shown in eq. 44 is plotted in Fig. 3.

Figure 3.

Analytical relationship between RA and FA.

Pierpaoli et al. (54) and Le Bihan et al. (55) have suggested a third scalar invariant that is the ratio of the volumes of a diffusion ellipsoid and a diffusion sphere. This ratio is defined as VR:

$$\mathrm{VR}=\frac{\text{Ellipsoid volume}}{\text{Spherical volume}}=\frac{\frac{4\pi }{3}{D}_{x^{\prime }{x}^{\prime }}{D}_{y^{\prime }{y}^{\prime }}{D}_{z^{\prime }{z}^{\prime }}}{\frac{4\pi }{3}{\left(\stackrel{‒}{D}\right)}^3}=\frac{\left({\lambda }_1{\lambda }_2{\lambda }_3\right)}{{\overline{\lambda }}^3}=27\frac{{\lambda }_1{\lambda }_2{\lambda }_3}{{({\lambda }_1+{\lambda }_2+{\lambda }_3)}^3}$$ (45a)

which has a normalized value between 1 (complete isotropy) and 0 (complete anisotropy). Some authors prefer to use the volume fraction,VF, which has normalized values between 0 (complete isotropy) and 1 (complete anisotropy) (55).

$$\mathrm{VF}=(1-\mathrm{VR})=\frac{{\overline{\lambda }}^3-\left({\lambda }_1{\lambda }_2{\lambda }_3\right)}{{\overline{\lambda }}^3}.$$ (45b)

Additionally, various authors have also used other indices to represent the degree of anisotropy in the morphological features of a diffusion tensor (56–58).

VISUALIZATION OF DIFFUSION TENSORS IN HUMAN BRAIN IMAGING

A practical application of DTI was demonstrated in human brain imaging. DTI was performed on 10 normal healthy volunteers who consented with an Institutional Review Board's approval. Data was acquired using Siemens Magnetom (Sonata 1.5 T) equipped with echo-planar capability. A circularly polarized head coil was used for image acquisition. All images were acquired in an axial plane with the head positioned firmly inside the circularly polarized head coil. To maintain rigid position of head, a tape over the forehead was used to secure the position inside the coil throughout scanning. A standard echo-planar version of spin–echo pulse sequence was used with b = 0 and b = 1,000 s/m². A single loop with a repetition time included gradient sensitization along six noncollinear directions: (x,y,z) = [(1,0,1), (−1,0,1), (0,1,1), (0,1,–1), (1,1,0), (−1,1,0)]. A b-value requested by the user was then used to scale the gradient amplitudes (x,y,z) appropriately to coincide with the final b-value. Diffusion sensitive gradient pulses were trapezoidal pulses whose magnitudes were determined based on the Stejskal–Tanner scheme in which the time interval between leading edges of gradient pulses (Δ) is 32.5 ms and the width of gradient pulse (δ) is 5.40 ms. Using appropriate gradient amplitudes across x, y, and z directions, a b-value of 1,000 s/mm² was achieved. Other MR parameters included T_R (ms)/T_E (ms) = 4,600/105, 5 mm thick slices, 30% interslice gap, 104 lines with echo factor = 0.84, matrix = 104 × 128 interpolated to 256 × 256, FOV = 180 × 220 mm² with an in-plane resolution of 1.7 × 1.7 mm². A single chemically selective Gaussian RF pulse was used for fat saturation and the readout pixel bandwidth = 1,346 Hz.

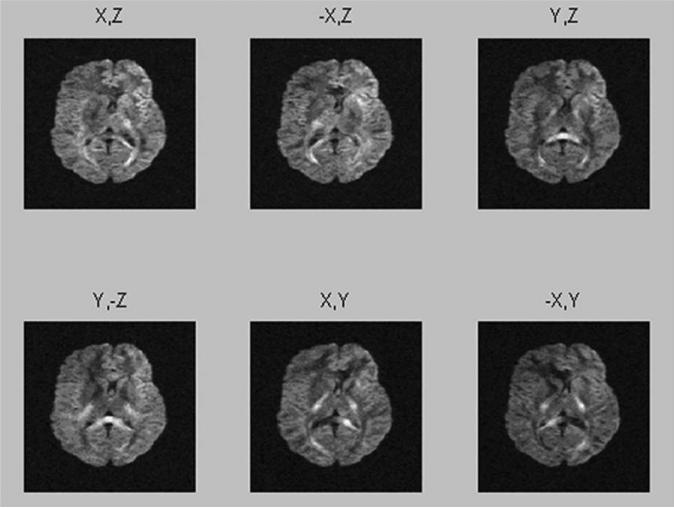
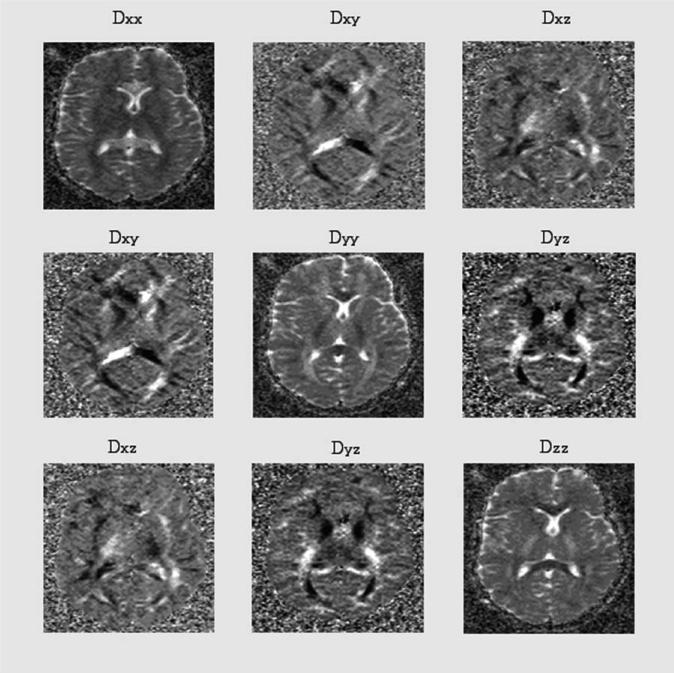
Figure 4 shows the set of source images obtained with a combination of gradients, resulting in six noncol-linear directions based on eqs. 35 and 36. A total of six averages per measurement direction were performed to improve the signal/noise ratio and to avoid potential negative eigenvalues in the measurements.

Figure 4.

Source images obtained using a combination of gradients resulting in 6 noncollinear directions based on eq. 31a. Six averages per each measurement direction were acquired to improve S/N and to avoid potential negative eigenvalue in the measurement. Imaging parameters are; T_E = 105 ms, T_R = 4,600 ms, 5 mm slices with 30% interslice gap, 104 lines with echo factor 50.84, matrix = 104 × 128 interpolated to 256 × 256, field-of-view × 180 × 220 mm² with an in-plane resolution = 1.7 × 1.7 mm². A single chemically selective Gaussian RF pulse was used for fat saturation with a read-out bandwidth per pixel of 1,346 Hz.

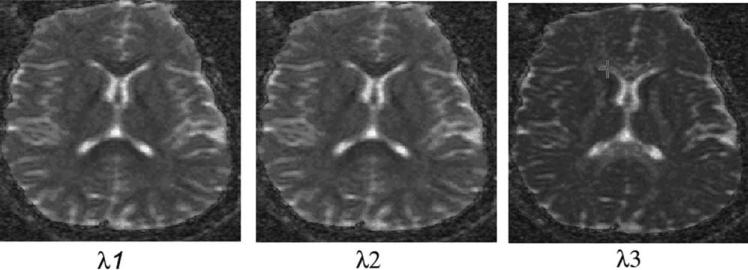
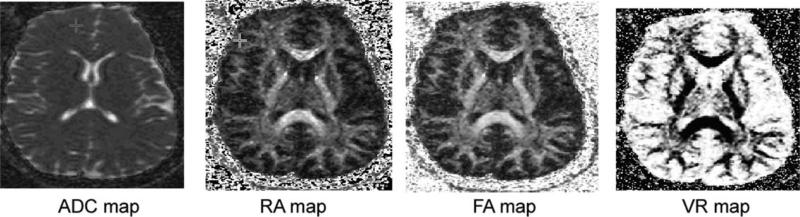
Figure 5 represents a symmetric diffusion tensor obtained with six non-zero component images. The diagonal elements are similar except for intensity differences in the white matter near genu and splenium. Each image represents a calculated ADC image based on eq. 37. The symmetry of the off-diagonal elements are due to the fact D_i,j = D_j,i. The off-diagonal elements are based on combination of gradient directions in the LAF. In addition, the gray scale level of the off-diagonal images differs strongly from that of the diagonal ones. Figure 6 shows the eigenvalue image based on diagonalization scheme described in the text. Figure 7 shows corresponding calculated maps based on eqs. 42, 43, and 45a. For comparison, a corresponding ADC map is also included.

Figure 5.

The symmetric diffusion tensor with six non-zero components. Each image is a calculated apparent diffusion coefficient image along the direction in the laboratory frame. These images are calculated pixel-by-pixel by solving eq. 32.

Figure 6.

The eigenmap along the three mutually orthogonal directions of principal axes frame fixed with local fiber direction.

Figure 7.

The calculated anisotropy maps of RA, FA, and VR. For comparison, ADC map is included at the same slice level.

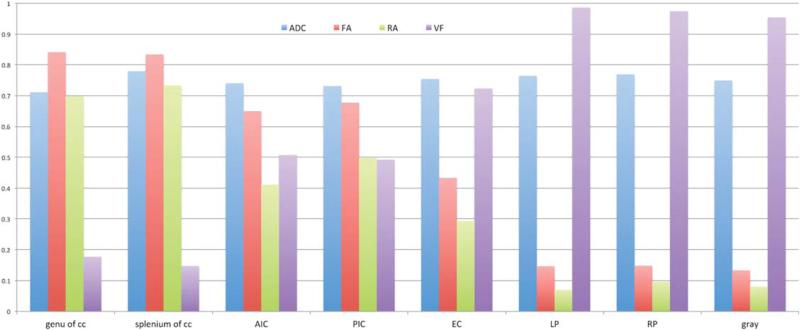
Among all parameters derived from DTI, FA is the most commonly reported parameter. The measure of FA is based on relative asymmetry between eigenvalues. The CSF in ventricular system has an FA value near zero, whereas moving from gray matter to the genu (Fig. 8) shows a steady increase in FA, indicating an organization of fiber structures in a regular and parallel fashion. Any decrease in FA from an expected range in these areas shows compromised white matter integrity. Figure 8 shows a bar graph of anisotropy indices compared with ADC values obtained at eight different ROIs that covered tissues with both white and gray matter. This result is based on an average value obtained among 10 subjects.

Figure 8.

Bar graph shows calculated ADC, normalized values of FA, RA, and VF = (1 – VR). We have chosen VF (instead of VR) such that FA, RA, and VF are normalized between zero (isotropic) and one (anisotropic). The measurements are based on ROIs selected around corpus callosum and putamen to include white and gray matter region. Across the range of ROIs, there is relatively a little difference in ADC values when compared with anisotropy values. (cc: corpus callosum, AIC: anterior internal capsule, PIC: posterior internal capsule, EC: external capsule, LP: left putamen, RP: right putamen). ADC is measured in units of ×10⁻³ mm²/s. Larger change in FA, RA compared to ADC make them a sensitive marker for evaluating anisotropy in tissues.

Overall, the elements of the diffusion tensor matrix in the PAF contain information about the magnitude of water diffusion that is independent of measurement coordinate axes. The relationship between PAF and LAF is provided through the use of Euler rotation angles. Scaled invariants and anisotropy measures are derived based on tensor elements in the PAF. Noisy DWI will alter the elements of diffusion tensor, causing in some instances negative eigenvalues. Such negative eigenvalues are meaningless, as negative diffusion does not exist; the observed tensor must be positive, which is the case only when the diagonal elements are larger than the off-diagonal elements of the tensor. To avoid numerically setting negative eigenvalues to be zero, the non-negative eigenvalue requirement can be fulfilled with higher signal/noise ratios or increased voxel size. Multiple averages may also be used to improve signal/noise ratios.

Among rotationally invariant quantities, FA maps are routinely used for comparison between various tissues. FA maps provide gray–white matter contrast, and are a widely utilized index of anisotropy in the literature (59–62). Our measurements on normal healthy volunteers showed relative differences in ADC and FA in eight different regions of interest (ROI). The measurements of FA in the putamen and CSF were found to be the lowest but non-zero. This result is obvious due to the nature of the environment of the CSF and putamen, where diffusion is less restrictive. The non-zero apparent asymmetry may be due to acquired noise, contaminating eigenvalue computation intrinsic to the putamen. The splenium of corpus callosum showed, by far, the strongest apparent asymmetry in diffusion. Our technique of measurement yielded a wide range of apparent anisotropy within the various portions of the corpus callosum. The work by Chepuri et al. (63) suggests multiple possible explanations, including tighter packing of axons or less permeable myelin sheaths. Further investigation is warranted in a larger study population.

TRACTOGRAPHY

One of the applications of DTI is to noninvasively map out anatomic white matter connectivity. Several methods have defined connectivity between different regions of the brain. While diffusion weighting information uses sampling along three orthogonal directions, DTI uses a minimum of six directions to assess connectivity in anisotropic regions of tissue. More robust methods use more than six directions to minimize sampling bias. The resulting images are known as “fiber-tractography,” and can be used to display structures that are parallel to native fiber orientations.

There are two main approaches to tractography: deterministic or “tract propagation” approaches, and probabilistic or “energy minimization” approaches (64, 65). Deterministic tractography computes fiber tracks based on the assumption of a single value for the dominant fiber orientation, whereas probabilistic tractography explicitly characterizes the distribution of fiber orientation to provide a probabilistic treatment of the different fiber track possibilities. The deterministic approach, however, has difficulty tracing reliably in areas with low diffusion anisotropy, and as such, generally may not produce reliable tracks in areas with low diffusion anisotropy. As a result, the tracts reconstructed by deterministic tractography tend to be the major pathways in the brain such as the commissural projection and association pathways (66). Additionally, the assumption of a single dominant fiber direction per voxel fails to accurately represent voxels with multiple fiber populations, as is the case in voxels with crossing or closely adjacent fibers. Probabilistic tractography, conversely, allows for reconstruction of more minor pathways, by accounting for the possibility of multiple fiber populations per voxel.

Deterministic approaches, also known as “principal eigenvector streamline approaches,” involve three basic steps: 1) estimation of local fiber orientation for a given voxel; 2) propagation of a line from this voxel based on estimated fiber orientation; and 3) termination, which is typically based either on low anisotropy or sharp bends in fiber orientation (64).

1. Fiber orientation is first estimated, using either the diffusion tensor or the principal eigenvector of the diffusion tensor. The latter is more straightforward (64), involving spectral decomposition of the diffusion tensor D=UVU⁻¹, where U is a 3 × 3 matrix whose ith column is the ith eigenvector, and V is a 3 × 3 diagonal matrix such that V_ii = λ_i for all i = 1, 2, 3. However, use of the principal eigenvector alone is reliable only in the case of oblate tensors (λ₃ ≠ λ₁ ≈ λ₂). It is less accurate in cases of low anisotropy, in which the diffusion ellipsoid approaches a sphere. In this case, the principal eigenvector is determined by noise rather than by the longest axis of the ellipsoid.

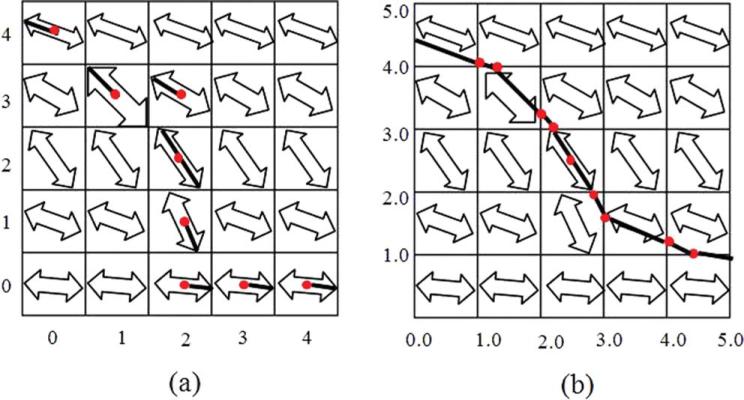
2. The fiber assignment by continuous tracking algorithm, proposed by Mori et al. (67), provides the basis for many deterministic fiber-tracking algorithms. Tracking is initiated from the center of a voxel, and is propagated along the direction given by the diffusion tensor or principal eigenvector of the diffusion tensor for the given voxel. As the direction of the principal eigenvector does not have polarity, the line is propagated in two opposite directions. When the track leaves the voxel and enters another, it assumes the direction of the next voxel. Because of the nonpolarity of the principal eigenvector of the next voxel, there are two possible choices for propagating the next line: an acute and obtuse angle from the original eigenvector. The line is always propagated by choosing the obtuse angle, except in the case of a 90° angle, in which case the line is terminated. A continuous rather than discrete vector field is utilized (Fig. 9), so that tracking is not limited to the 26 angle directions that would only be available if a discrete vector field were used (64).

3. One criteria for termination is based on the occur-rence of sharp bends in fiber orientation. Specifically, we calculate

   $$R=\sum _i^s\sum _j^s\frac{\mathrm{abs}\left(v_{{\lambda }_{1}i}\cdot v_{{\lambda }_{1}j}\right)}{s(s-1)},$$ (46)

   the summation of the inner product of the nearby data points, where νλ₁ is the unit vector representing the longest eigenvector, and s is the number of data points. Smaller values of R correspond to sharper bends in fiber orientation, with a common termination criterion being R < 0.8 (67). An alternative termination criterion involves termination when FA falls below 0.15–0.3, as gray matter typically has an FA of 0.05–0.15 (64) (Fig. 10). Smoothing is then induced using any of a variety of interpolation methods.

Figure 9.

Deterministic tracking in (A) discrete versus (B) continuous voxel coordinates. A continuous rather than discrete vector field is utilized in order not to constrain tracking to a limited number of angle directions.

Figure 10.

Deterministic tractography performed using an FA termination threshold of 0.20 and minimum fiber length of 10 mm. Color green refers to association fibers along A–P direction, red refers to commissural fibers along L–R direction and blue refers to projection fibers along S–I direction. A-P, anterior-posterior; L-R, left-right; S-I, superior-inferior.

Streamline approaches generally suffer from several limitations, including sensitivity to noise and the interpolation scheme chosen. Although the “fibers” tracked by any tracking algorithm are generally considered representative of actual nerve axons, they are more accurately understood as estimates of the principal direction of diffusion, which may differ from actual axonal architecture in cases when fibers cross, diverge, or display tight curvature. Noise generated by differences between the estimated vector direction and actual fiber orientation also accumulates with increased track propagation, so that longer tracks are noisier than shorter tracks. Other limitations include partial volume effects, in which voxels falling between multiple unrelated fibers may have an estimated fiber angle, which is a weighted average of the unrelated fiber angles, and failure to model branching fibers, as only one line propagates from each seed voxel (64). There are several approaches that have been proposed to handle these limitations, including smoothing via B-splines, bootstrapping the diffusion weighted images to generate tensor fields (64), and front propagation methods, described below.

A central problem in deterministic tractography is that the diffusion tensor is a reliable indicator of the principal direction of diffusion only if oblate tensors (λ₃ ≠ λ₂ ≈ λ₁) are present. The diffusion tensor fails to account for situations in which the fiber orientation is undetermined, which is the case in prolate or isotropic cases. Tracking based on the diffusion tensor model also fails in brain regions with multiple fiber orientations, such as crossing or kissing fibers, due to the assumption of a single dominant fiber orientation per voxel. This presents a large practical problem, as brain histology in primates shows that much of white matter is composed of multiple fiber directions (68). Assuming a single dominant fiber orientation in the case of crossing fibers has two possible implications in tractography. First, the voxel may appear isotropic due to the summation of several fiber directions, leading to early termination of the track due to a falsely low anisotropy levels (false negatives). Second, crossing fibers may lead to inference of erroneous directions: either the tracking may be shifted systematically from the true path, or the tracking may switch from the true path to an unrelated crossing tract (false positives) (64, 69). One effective model-free approach for addressing crossing fibers is to increase directional information through more sensitized scanning techniques, including high angular resolution diffusion imaging (70, 71), diffusion spectrum imaging (72), q-ball imaging (73), and high b-value imaging (74). However, scan time is long for these techniques compared with the time available for clinical scans. Therefore, current research on crossing fibers commonly focuses on approaches that utilize DTI data acquired in short, clinically practical scan times (69, 75). Many approaches to crossing-fiber regions using conventional DTI acquisitions have been proposed, including cylindrically constrained two-component models (68, 76), direct deconvolution using a discrete diffusion tensor basis functions (77), and utilization of compressed sensing optimization criteria for estimating mixture fractions (75), and research is ongoing.

Many issues in deterministic tractography relating to false positives, however, may be resolved through tract editing based on a priori anatomical knowledge. After tractography is performed, tracks can be required to pass through multiple ROIs drawn using Boolean operators. This may include “AND” operators, which allow for the elimination of false paths due to the low probability of a false path intersecting all of the same regions as the true path, and “NOT” operators, which allow specification of regions through which the path is known not to pass based on biological knowledge.

FAST MARCHING TRACTOGRAPHY

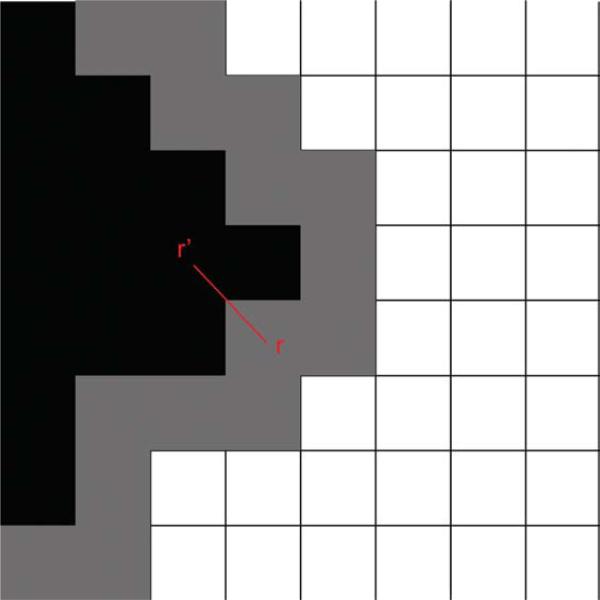
Front propagation methods attempt to identify connectivity pathways through the brain by propagating a 3D surface (or front), rather than a line, from the seed voxel, using the principal eigenvector of the tensor (78, 79). Fast marching tractography (FMT) provides an illustrative example of a front propagation method, which accounts for multiple fibers through the fast marching method (Fig. 11). The four main steps of FMT are detailed below, following the proposed description by Parker et al. (78).

Figure 11.

Front propagation in the fast marching algorithm. Black voxels represent voxels passed by the front, with front voxels located at the border of the evolving wave. Gray voxels represent narrow band voxels, and white voxels represent outside voxels not yet crossed by the front. In each propagation step from r′ → r, one voxel of the narrow band, selected such that the vector (r – r′) is most closely aligned with the direction n(r), is included into the set of front voxels.

1. A 3D front is first evolved from the seed voxel using the principal eigenvector of the tensor, at a rate governed by a defined speed function. For example, the front propagation speed at position r can be defined based on voxel similarity, as (78)

   $$F_1\left(r\right)=\frac{1}{1-\min \{\left(\mid {\epsilon }_1\left(r\right)\cdot n\left(r\right)\mid \right),\left(\mid {\epsilon }_1\left(r^{\prime }\right)\cdot n\left(r\right)\mid \right),\left(\mid {\epsilon }_1\left(r\right)\cdot {\epsilon }_1\left(r^{\prime }\right)\mid \right)\}},$$ (47)

   where n(r) is the direction of the normal to the front at the point where front expansion is considered, ε₁ is the principal eigenvector; r is the position of any voxel potentially crossed by the front; and r′ is the position of a voxel neighboring r that has already been crossed by the front such that (r – r′) is most closely aligned with n(r). This ensures that front evolution will be fastest along white matter tracts. Another possible speed function is based on embedded connectivity information, given by (69)

   $$F_2\left(r\right)=\min \{F_2\left(r^{\prime }\right),\mid {\epsilon }_1\left(r^{\prime }\right)\cdot n\left(r\right)\mid \},$$ (48)

   so that dependence on F₂(r) provides “memory” of previous front locations.
2. Level set and fast marching methods are then used to generate minimum cost paths from all possible voxels to the seed point. Specifically, given a cost function G(x₁,x₂,. . .,x_n) and seed pointA ∈ R³, the minimum cost path χ(τ):[0, ∞)→R³ from A to r ∈ R³ minimizes

   $${\int }_{A=\chi \left(0\right)}^{\Xi =\chi \left(L\right)}G\left(\chi \left(\tau \right)\right)d\tau ,$$

   where L is the total length of χ and τ is the position on χ. By the fast marching algorithm, the minimum cost in traveling from A to r is the time of arrival, T(r). Therefore, the minimum cost path satisfies

   $$T\left(r\right)=\underset{\chi }{\min }{\int }_{A=\chi \left(0\right)}^{\Xi =\chi \left(L\right)}G\left(\chi \left(\tau \right)\right)d\tau ,$$

   which can be found by gradient descent through T (78).
3. A connectivity metric φ, estimating the likelihood that a given pathway represents a true anatomical connection, is then computed for each pathway. A natural choice for φ is

   $$\phi =\min \left\{F\left(\chi \left(\tau \right)\right)\right\},$$

   where F is the speed function defined above. An alternative metric measures how faithful the path is to the underlying ε₁ field, by using the inner product of the path tangent w and the ε₁ direction (78):

   $${\phi }_2=\min \left\{\mid w\left(\chi \left(\tau \right)\right)\cdot {\epsilon }_1\chi \left(\tau \right))\mid \right\}.$$

4. Lastly, by thresholding φ, the most probable subset of pathways is selected.

PROBABILISTIC METHODS

Probabilistic tractography was developed to overcome a critical limitation in deterministic tractography, namely that deterministic tractography fails to account for the variability in estimating fiber orientation. Probabilistic methods differ from deterministic methods in the use of the probability density functions (PDFs) of fiber orientation to explicitly characterize the distribution of fiber orientations, in order to estimate the probability of connection between regions. Methods may assume a Gaussian or Watson distribution, or the distribution may otherwise be estimated using Bayesian or bootstrap methods. Parametric assumptions center a Gaussian (80, 81) or Watson (82) distribution on a point estimate of the dominant fiber orientation, such as the principal eigenvector of a diffusion tensor. However, calibrations are inefficient in the case of noisy data, such as in the case of interexperimental variation or intersubject variation (83). Bayesian methods estimate a posterior distribution on the dominant fiber orientation given a prior distribution and likelihood function, whereas bootstrap methods estimate the true distribution of samples by permuting the data samples with replacement. The Bayesian approach is useful in allowing the placement of prior constraints on parameters when such constraints make sense, such as requiring that the eigenvalues have positive values. Both Bayesian and bootstrap approaches have been developed to account for multifiber populations per voxel (69, 84–86).

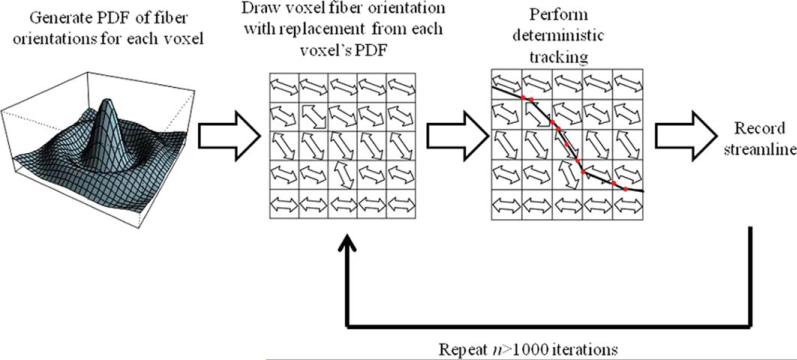
There are four main classes of probabilistic tractography methods: 1) front propagation methods (described above); 2) Monte Carlo streamline approaches; 3) random walk and simulated diffusion approaches; and 4) global connection probability models (83). Front propagation methods may use either a deterministic approach as described above (see Fast Marching Tractography), or a probabilistic approach, in which the point estimate for fiber orientation direction is replaced with a random sample from the fiber orientation PDF. Monte Carlo streamline approaches simulate the range of possible pathways according to the probability distribution of fiber orientations in order to quantify the confidence of each estimate (Fig. 12).

Figure 12.

Schematic of Monte Carlo streamline methods. First, the PDF of fiber orientations for each given voxel is estimated using either parametric assumptions, Bayesian, or bootstrap methods. Next, a fiber orientation is drawn with replacement from the fiber orientation PDF. Deterministic tracking is then performed using the sampled fiber orientation, and the streamline is recorded. The process is repeated for n > 1,000 iterations.

In Monte Carlo streamline approaches, fiber orientation PDFs are first generated for each voxel according to the methods described above. Next, deterministic tracking is run on data for n iterations (where n is some large number typically greater than 1,000), each iteration using fiber orientations drawn with replacement, with a draw probability based on the given voxel's fiber orientation PDF. Each streamline is then recorded (66, 81, 83). Another class of methods includes the random walk and simulated diffusion approach, in which a particle performs a random walk through the set of voxels. At each step, the particle jumps to another site within the image volume, using a constant jump size and jump direction defined by a transition probability matrix. Out of n random walks starting in region A, the proportion of random walks ending in region B is calculated to yield an estimate of the neuronal connectivity between regions A and B (87, 88). For example, one set of transition probabilities from voxel m to voxel n is given by Koch et al. (88) as

$$\mathrm{Pr}(m\to n)=\frac{{[d(r_{mn},m)+d(r_{mn},n)]}^a}{\sum _{n=1}^8{[d(r_{m{n}^{\prime }},m)+d(r_{m{n}^{\prime }},n^{\prime })]}^a},$$ (49)

where a is a tuning parameter set empirically and d(r_mn, m) is the diffusion coefficient in voxel m along the line connecting the centers of voxels m and n.

Global connection probability models (89–91) assess all proposed pathways simultaneously, rather than successively and independently defining connections using local, voxel-wise fiber orientations. Based on a predictive model of some characteristic of the proposed tract, the predicted values for the tract characteristic are compared to the observed values, with the highest probability route of connection minimizing the difference between the two. For example, the dominant orientation of diffusion for a given voxel is one tract characteristic that may be used for this purpose (83). Several optimization methods for identifying the route that minimizes differences between the observed and predicted data, including simulated annealing and maximum likelihood, have been proposed (83, 89). These optimization routines are often subject to a constraint on curvature (90, 91), based on the assumption that fiber tracts generally do not exhibit high curvature (83, 89–91).

APPLICATIONS

DTI enables in vivo assessment of white matter pathology by measuring FA, a measure of fiber tract coherence derived from water diffusion properties. DTI also permits visualization of the 3D structure of major axonal projection, commissural and association pathways of the white matter. In addition, DTI can be used to identify subtle pathologies in white and gray matter. This has been proven to be useful especially in multiple sclerosis, where normal-appearing white matter on conventional imaging techniques reveals underlying diffuse white matter changes with DTI (92, 93). A recent study suggests decreased apparent anisotropy of white matter in children with developmental delays and autism (94–97). Another potential application of DTI is in evaluating stroke patients in which the diffusion of water during the temporal evolution of stroke is related to the histopathological response of white and gray matter to ischemic injury (6–8, 98, 99). Overall, DTI may prove to be a useful tool for in vivo detection of subtle brain abnormalities present in early stage diseases, before detection is possible by conventional MRI techniques.

Biography

Anil Shetty received his Ph.D. in liquid crystal physics using NMR spectroscopy from Kent State University. He joined the University of Pennsylvania for post-doctoral work under NIH fellowship to study MR imaging. His research dealt with designs of receiver probes for sodium and proton chemical shift imaging using horizontal bore animal imaging system. Fol lowing fellowship, he joined Siemens Medical System R & D division in Iselin, NJ. Later, he joined William Beaumont Hospital, Michigan as a clinical scientist before moving to Texas. He is currently working as an associate professor in the department of OBGYN of Baylor College of Medicine. His primary area of research involves fetal MR imaging using techniques such as MR spectroscopy and DTI tractography. He has co-authored a book, Netter's Atlas of Neuroscience, for Elsevier.

Sharon Chiang received her B.A. degree in statistics from Rice University, Houston, Texas, in 2009, along with a B.A. in mathematical economic analysis. She is currently an M.D. student at Baylor College of Medicine and a Ph.D. student in the Department of Statistics at Rice University. Her research interests include statistical clustering methods, Bayesian modeling, and methods in neural signal processing including electro-physiological and neuroimaging data.

Mirjana Maletic-Savatic, MD, PhD, is a child neurologist and a neuroscientist. She graduated from the School of Medicine, University of Belgrade, Serbia, in 1996. She continued her education in the USA, first as a postdoctoral fellow at the Cold Spring Harbor Laboratory, and then pursuing Child Neurology specialty training at Stony Brook University, New York. Since 2008, she joined the Jan and Dan Duncan Neurological Research Institute at Texas Children's Hospital and Baylor College of Medicine. Dr. Savatic's research interests include neurogenesis, neuroinflammation, and their metabolomic biomarkers that may be utilized for mechanistic studies and cell tracking. Her major interest is in translation of basis neuroscience research to clinical practice, and she utilizes different modalities of the MRI to bridge those two areas of science. She has received numerous prizes, such as the Runner-up Breakthrough Publication of the Year, Science (1999), Phillip R. Dodge Young Investigator Award (2007), Brain Neuroimmunology Imaging Award from the DANA Foundation (2008), The McKnight Neuroscience of Brain Disorders Award (2009), and the Simmons Foundation Award (2010). She has been selected as the Best Doctors in America since 2007.

Gregor Kasprian, MD, is a radiologist at the Medical University of Vienna, Austria and currently working as postdoctoral research fellow at the Baylor College of Medicine, Houston, Texas. His main scientific interest is in the field of fetal brain imaging, where he and his group could successfully introduce advanced MR imaging techniques. His work in the field of Diffusion tensor MR imaging of the fetal brain and of peripheral nerves has been recently acknowledged with young investigator awards by the Radiological Society of Northern America, the European Society of Radiology and the American Society of Neuroradiology. He is founding member of the international working group of perinatal neurology and reviewer for several top journals in the field of neuro-science and radiology. After having partly finished the residency in adult neurology he is clinically working as neuroradiologist.

Dr. Vannucci is Professor of Statistics at Rice University, Houston, TX. She is also an adjunct faculty member of the UT M.D. Anderson Cancer Center, TX, and the Rice Director of the Interinstitutional Graduate Program in Biostatistics. She received the Laurea (B.S.) degree in Mathematics in 1992 and the Ph.D. degree in Statistics in 1996, both from the University of Florence, Italy. Prior to joining Rice in 2007, Dr. Vannucci was Research Fellow at the University of Kent at Canterbury, UK, during 1996-1998. In 1998 she joined the Department of Statistics at Texas A&M University, TX, as Assistant Professor, became Associate Professor in 2003 and Full Professor in 2005. She was the recipient of an NSF CAREER award in 2001 and won the Mitchell prize from the International Society for Bayesian Analysis in 2003. She is an elected Fellow of the American Statistical Association (ASA), since 2006, the Institute of Mathematical Statistics (IMS), since 2009, and the American Association for the Advancement of Science (AAAS), since 2012, and an elected Member of the International Statistical Institute (ISI), since 2007.

Wesley Lee is a Professor in Obstetrics and Gynecology at Baylor College of Medicine and works at the Texas Children's Pavilion for Women in Houston, Texas. He serves as Section Chief for Women's and Fetal Imaging and Co-Director of the Fetal Center. His medical degree was from Oregon Health Sciences University in Portland, with OBGYN residency training at Park land Memorial Hospital in Dallas. Additional training included a maternal-fetal medicine fellowship at Baylor College of Medicine in Houston. He is an Associate Investigator with the Perinatology Research Branch of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) and was also a Scientific Advisor to the World Health Organization. Other activities have included Chair, Clinical Standards Committee at the International Society of Ultrasound in Obstetrics and Gynecology, Deputy Editor of the Journal of Ultrasound in Medicine, and co-editor of a textbook, Sonography in Obstetrics & Gynecology, Principles and Practice, 7th edition, McGraw-Hill, 2011.

APPENDIX A

DIFFUSION TENSOR

The experimental measurement of ADCs is made with respect to laboratory frame of reference where gradient magnitudes are known. The diffusion measured along the axes in the LAF are not the eigenvalues. Upon transforming to the principal axes frame fixed with local fiber, the axes are along the diffusion ellipsoid axes and the ADC measured along these directions is an eigenvalue.

Measured components of diffusion tensor (D^lab) are expressed as elements of 3 × 3 matrix in the LAF (39, 40).

$$\left[\begin{array}{ccc}\hfill D_{xx}\hfill & \hfill D_{xy}\hfill & \hfill D_{xz}\hfill \\ \hfill D_{xy}\hfill & \hfill D_{yy}\hfill & \hfill D_{yz}\hfill \\ \hfill D_{xz}\hfill & \hfill D_{yz}\hfill & \hfill D_{zz}\hfill \end{array}\right]$$ (A1)

The eigenvalues of the tensor are assumed to represent the size and shape of the tensor whereas; the eigenvectors represent the orientation of the tensor. For example, the eigenvector corresponding to the largest eigenvalue represents the longest fiber axis.

However, to express the motional aspects at the molecular or local myelin fiber level, one defines another frame of reference that is fixed with respect to local fiber orientation in which the long axis of the fiber is fixed along one of the axes of this frame. This frame is called the PAF (x′,y′,z′). The elements of diffusion tensor in this PAF are:

$$\left[\begin{array}{ccc}\hfill D_{xx}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill D_{yy}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill D_{zz}\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill {\lambda }_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\lambda }_2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda }_3\hfill \end{array}\right]$$ (A2)

Here, the goal is to define components of D measured in (x,y,z) LAF system in terms of elements of the diffusion tensor in (x′,y′,z′) PAF system. This is same as describing the orientation of final rotated coordinate system (x,y,z) relative to fixed coordinate system (x′,y′,z′). Transformation of coordinates is described by three sets of angles called Euler angles. The transformation matrix provides projections of original elements of diffusion tensor in LAF system on to an orthogonal PAF system. Corresponding transformation is defined by;

$$D_{i,j}^{\mathrm{lab}}=\sum _{m,n}^{x^{\prime },y^{\prime },z^{\prime }}{\alpha }_{i,m}\cdot {\alpha }_{j,n}{D}_{m,n}^{\mathrm{PAF}}$$ (A3)

where α_i;mare the direction cosines in terms of the three Euler angles (φ, θ, ψ) represent the elements of the rotation matrix. These angles define the relative orientation between LAF and PAF by three successive rotations of the LAF coordinate system that align with the PAF coordinate system. Therefore, the rotation operator R is defined by the product of three Euler angle rotations acting on LAF to project it on to PAF system. Here again, LAF coordinate system in which measurements are made and the PAF frame fixed with tissue fiber, which coincides with the self directions of diffusivity. The diffusion tensor defined in the PAF has only the diagonal elements with nondiagonal elements = 0.

The rotation matrix of cumulative rotations is defined as

$$R=R_{z^{″}}\left(\psi \right)R_{y^{″}}\left(\theta \right)R_z\left(\varphi \right),$$ (A4)

where ψ, φ ∈ [0,2π) and θ ∈ [0,π). The corresponding matrix elements representing projections are written as

$$\begin{array}{c}\hfill x^{\prime }\hfill \\ \hfill y^{\prime }\hfill \\ \hfill z^{\prime }\hfill \end{array}\begin{array}{c}\hfill \begin{array}{ccc}\hfill x\hfill & \hfill y\hfill & \hfill z\hfill \end{array}\hfill \\ \hfill \left(\begin{array}{ccc}\hfill {\alpha }_{x,x^{\prime }}\hfill & \hfill {\alpha }_{y,x^{\prime }}\hfill & \hfill {\alpha }_{z,x^{\prime }}\hfill \\ \hfill {\alpha }_{x,y^{\prime }}\hfill & \hfill {\alpha }_{y,y^{\prime }}\hfill & \hfill {\alpha }_{z,y^{\prime }}\hfill \\ \hfill {\alpha }_{x,z^{\prime }}\hfill & \hfill {\alpha }_{y,z^{\prime }}\hfill & \hfill {\alpha }_{z,z^{\prime }}\hfill \end{array}\right)\hfill \end{array}$$ (A5)

where

$$\left[\begin{array}{ccc}\hfill {\alpha }_{x,x^{\prime }}\hfill & \hfill {\alpha }_{y,x^{\prime }}\hfill & \hfill {\alpha }_{z,x^{\prime }}\hfill \\ \hfill {\alpha }_{x,y^{\prime }}\hfill & \hfill {\alpha }_{y,y^{\prime }}\hfill & \hfill {\alpha }_{z,y^{\prime }}\hfill \\ \hfill {\alpha }_{x,z^{\prime }}\hfill & \hfill {\alpha }_{y,z^{\prime }}\hfill & \hfill {\alpha }_{z,z^{\prime }}\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill \cos \psi \hfill & \hfill \sin \psi \hfill & \hfill 0\hfill \\ \hfill -\sin \psi \hfill & \hfill \cos \psi \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\cdot \left[\begin{array}{ccc}\hfill \cos \theta \hfill & \hfill 0\hfill & \hfill -\sin \theta \hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill \sin \theta \hfill & \hfill 0\hfill & \hfill \cos \theta \hfill \end{array}\right]\cdot \left[\begin{array}{ccc}\hfill \cos \phi \hfill & \hfill \sin \phi \hfill & \hfill 0\hfill \\ \hfill -\sin \phi \hfill & \hfill \cos \phi \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$ (A6)

Upon simplification (39)

$${\alpha }_{x{x}^{\prime }}=\cos \phi \cdot \cos \theta \cdot \cos \psi -\sin \phi \cdot \sin \psi$$ (A7a)

$${\alpha }_{y{x}^{\prime }}=\sin \phi \cdot \cos \theta \cdot \cos \psi +\cos \phi \cdot \sin \psi$$ (47b)

$${\alpha }_{z{x}^{\prime }}=-\sin \theta \cdot \cos \psi$$ (47c)

$${\alpha }_{x{y}^{\prime }}=-\cos \phi \cdot \cos \theta \cdot \sin \psi -\sin \phi \cdot \cos \psi$$ (47d)

$${\alpha }_{y{y}^{\prime }}=-\sin \phi \cdot \cos \theta \cdot \sin \psi +\cos \phi \cdot \cos \psi$$ (47e)

$${\alpha }_{z{y}^{\prime }}=\sin \theta \cdot \sin \psi$$ (47f)

$${\alpha }_{x{z}^{\prime }}=\sin \theta \cdot \cos \phi$$ (47g)

$${\alpha }_{y{z}^{\prime }}=\sin \theta \cdot \sin \phi$$ (47h)

$${\alpha }_{z{z}^{\prime }}=\cos \theta$$ (47i)

A generalized expression may be obtained for estimating diffusion coefficient in any arbitrary direction in terms of principal values as

$$D_{xx}=D_{x^{\prime }{x}^{\prime }}{\cos }^2\theta {\cos }^2\phi +D_{y^{\prime }{y}^{\prime }}{\sin }^2\phi +D_{z^{\prime }{z}^{\prime }}{\sin }^2\theta {\cos }^2\phi$$ (48a)

$$D_{yy}=D_{x^{\prime }{x}^{\prime }}{\cos }^2\theta {\sin }^2\phi +D_{y^{\prime }{y}^{\prime }}{\cos }^2\theta +D_{z^{\prime }{z}^{\prime }}{\sin }^2\theta {\sin }^2\phi$$ (48b)

$$D_{zz}=D_{x^{\prime }{x}^{\prime }}{\sin }^2\theta +D_{z^{\prime }{z}^{\prime }}{\cos }^2\theta$$ (A8c)

$$D_{xy}=\frac{\sin 2\phi }{2}[D_{x^{\prime }{x}^{\prime }}{\cos }^2\theta -D_{y^{\prime }{y}^{\prime }}+D_{z^{\prime }{z}^{\prime }}{\sin }^2\theta ]$$ (A8d)

$$D_{xz}=\frac{\sin 2\theta }{2}\cos \phi [D_{z^{\prime }{z}^{\prime }}-D_{x^{\prime }{x}^{\prime }}]$$ (A8e)

$$D_{yz}=\frac{\sin 2\theta }{2}\sin \phi [D_{z^{\prime }{z}^{\prime }}-D_{x^{\prime }{x}^{\prime }}]$$ (A8f)

Although axial symmetry is a good approximation of parallel fiber tissue architecture, it is generally not applicable to all anisotropic media. The advantage of cylindrical symmetry is that the process of diagonalization reduces the number of estimated parameters to four in determining the diffusion tensor. However, a generalized approach should include all elements of the diffusion tensor.

A.1. Axially Symmetric Diffusion Tensor

A useful assumption is that fiber tracts are cylindrically symmetric. Under this condition one has

$$D_{\perp }=D_{x^{\prime }{x}^{\prime }}=D_{y^{\prime }{y}^{\prime }}$$

and

$$D_{\parallel }=D_{z^{\prime }{z}^{\prime }}$$ (A9)

With this approximation one can reduce the tensor to have only diagonal elements:

$$\left[\begin{array}{ccc}\hfill D_{\perp }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill D_{\perp }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill D_{\parallel }\hfill \end{array}\right]$$ (A10)

Upon substitution of direction cosine angles;

$$D_{xx}={\sin }^2\phi \cdot D_{\perp }+{\cos }^2\phi \cdot \left({\cos }^2\theta \cdot D_{\perp }+{\sin }^2\theta \cdot D_{\parallel }\right)$$ (A11a)

$$D_{yy}={\cos }^2\phi \cdot D_{\perp }+{\sin }^2\phi \cdot \left({\cos }^2\theta \cdot D_{\perp }+{\sin }^2\theta \cdot D_{\parallel }\right)$$ (A11b)

$$D_{zz}={\sin }^2\theta \cdot D_{\perp }+{\cos }^2\theta \cdot D_{\parallel }$$ (A11c)

$$D_{xy}=\left(\sin \phi \cdot \cos \phi \cdot {\sin }^2\theta \right)\cdot \left(D_{\parallel }-D_{\perp }\right)$$ (A11d)

$$D_{yz}=\left(\sin \phi \cdot \cos \theta \cdot \sin \theta \right)\cdot \left(D_{\parallel }-D_{\perp }\right)$$ (A11e)

$$D_{xz}=\left(\cos \phi \cdot \cos \theta \cdot \sin \theta \right)\cdot \left(D_{\parallel }-D_{\perp }\right)$$ (A11f)

It is further simplified following notational terms (27).

$$\stackrel{‒}{D}=\frac{1}{3}(D_{x^{\prime }{x}^{\prime }}+D_{y^{\prime }{y}^{\prime }}+D_{z^{\prime }{z}^{\prime }})$$ (A12)

$$\eta =D_{z^{\prime }{z}^{\prime }}-\frac{(D_{x^{\prime }{x}^{\prime }}+D_{y^{\prime }{y}^{\prime }})}{2}$$ (A13)

$$\delta =D_{z^{\prime }{z}^{\prime }}-\stackrel{‒}{D}=\frac{2}{3}\eta$$ (A14)

Upon substitution,

$$D_{xx}=\eta \cdot {\cos }^2\phi \cdot {\sin }^2\theta +D_{\perp }$$ (A15a)

$$D_{yy}=\eta \cdot {\sin }^2\phi \cdot {\sin }^2\theta +D_{\perp }$$ (A15b)

$$D_{zz}=\eta \cdot {\cos }^2\theta +D_{\perp }=\overline{D}+\frac{\delta }{2}\left(3{\cos }^2\theta -1\right)$$ (A15c)

$$D_{xy}=\eta \cdot \left(\sin \phi \cdot \cos \phi \cdot {\sin }^2\theta \right)$$ (A15d)

$$D_{yz}=\eta \cdot \left(\sin \phi \cdot \cos \theta \cdot \sin \theta \right)$$ (A15e)

$$D_{zx}=\eta \cdot \left(\cos \phi \cdot \cos \theta \cdot \sin \theta \right)$$ (A15f)

The angle θ can be defined as the angle between the long axis of the fiber and the z axis of the LAF and angle φ is the angle between x axis and the projection of fiber on to x–y plane;

$$\phi ={\tan }^{-1}\left[\frac{D_{yz}}{D_{xz}}\right]$$ (A16)

and

$$\theta ={\tan }^{-1}\left(\frac{1}{\sin \phi }\right)\left[\frac{D_{xy}}{D_{xz}}\right]$$ (A17)

On substituting for sin φ,

$$\theta ={\tan }^{-1}\left(\frac{D_{xy}\sqrt{D_{xz}^2+D_{yz}^2}}{D_{xz}{D}_{yz}}\right)$$ (A18)

One defines, using axial symmetry in fibers, an anisotropy index of fiber as

$$A_{\mathrm{f}}=\frac{(D_{\parallel }-D_{\perp })}{(D_{\parallel }+2D_{\perp })}$$ (A19)

Alternatively, one can determine principal diffusivities based on measured elements of diffusion tensor. Upon substitution, one finds

$$D_{\perp }=\frac{D_{xx}+D_{yy}\pm \sqrt{{(D_{xx}-D_{yy})}^2+4D_{xy}^2}}{2}$$ (A20)

and

$$D_{\parallel }=D_{xx}+D_{yy}+D_{zz}-2D_{\perp }$$ (A21)

Again using eqs. A.12 and A.13

$$\begin{array}{c}\hfill \theta =\pm {\cos }^{-1}\left(\sqrt{\frac{D_{zz}-D_{\perp }}{\eta }}\right)\hfill \\ \hfill \phi =\pm {\cos }^{-1}\sqrt{\frac{D_{zz}-D_{\perp }}{D_{\perp }{\cos }^2\theta +D_{\parallel }{\sin }^2\theta -D_{\perp }}}\hfill \end{array}$$ (A22)

Above equation shows the required number of diffusion coefficients is reduced to four elements of the diffusion tensor, namely D_xx, D_yy, D_zz, and D_xy to determine the principal diffusion tensor.

B.1. Nonaxially Symmetric Diffusion Tensor

In this case, D_x′x′ ≠ D_y′y′ ≠ D_z′z′. Although axial symmetry is a good approximation in the case of parallel fiber tissue, in general it is not applicable to all anisotropic media. Advantage of cylindrical symmetry is that it reduces the number of estimated parameters to four in describing diffusion tensor. However, in a truly anisotropic medium the expression relating each of these components in principal axes to components measured in laboratory axes gets more complicated. The diagonalization of the experimentally observed diffusion tensor always provides the values for the principal axes components, which can be used to deduce anisotropy. A simplified picture is presented in which only z direction in laboratory frame is fixed.

Using ν′ and δ, one finds ADC along z axis as

$$D_{zz}=\stackrel{‒}{D}+\frac{\delta }{2}\left(3{\cos }^2\theta -1-{\eta }^{\prime }{\sin }^2\theta \cos 2\phi \right).$$ (A23)

Here,

$${\eta }^{\prime }=\frac{D_{y^{\prime }{y}^{\prime }}-D_{x^{\prime }{x}^{\prime }}}{D_{z^{\prime }{z}^{\prime }}-\stackrel{‒}{D}}=\frac{D_{y^{\prime }{y}^{\prime }}-D_{x^{\prime }{x}^{\prime }}}{\delta }$$ (A24)

The above relationship simplifies to eq. A.15c when an axial symmetry is considered.

APPENDIX B

ROTATIONALLY INVARIANT QUANTITIES OF A DIFFUSION TENSOR

The inherent diffusivity measure of molecules is possible when measurements are represented along the principal coordinate system. However, both laboratory coordinate system and principal coordinate system seldom coincide. It is possible to define certain invariant scalar combinations from the diffusion tensor elements (41). In a second rank tensor T_ik, the eigenvalues are scalars and independent of the choice of coordinate system. For example, the characteristic equation for a tensor T_ik is obtained by diagonalizing the tensor. Second rank tensors can be represented by a matrix and also be decomposed into eigenvalues and eigenvectors. The eigenvector and corresponding eigenvalue of a tensor have the property that inner product of the original tensor and the eigenvector results in a vector, that is, a scalar multiple of the original eigenvector:

$$Tx={\lambda }_{l}xx\ne 0$$ (B1)

The solutions λ_l are the eigenvectors of tensor T_ik. The above equation can be rewritten as (T–λ_lI)x=0, where I represents the identity matrix. It also implies that the matrix T – λ_lI is singular and its determinant is zero and solutions are the eigenvalues of the secular equation:

$$\mid T_{i,k}-\lambda I\mid =0$$ (B2)

$$\mid \begin{array}{ccc}\hfill T_{11}-\lambda \hfill & \hfill T_{12}\hfill & \hfill T_{13}\hfill \\ \hfill T_{21}\hfill & \hfill T_{22}-\lambda \hfill & \hfill T_{23}\hfill \\ \hfill T_{31}\hfill & \hfill T_{32}\hfill & \hfill T_{33}-\lambda \hfill \end{array}\mid =0$$ (B3)

or

$${\lambda }^3-{\lambda }^2{I}_1+\lambda I_2-I_3=0,$$ (B4)

where quantities

$$\begin{array}{c}\hfill I_1=T_{11}+T_{22}+T_{33}\hfill \\ \hfill I_2=\mid \begin{array}{cc}\hfill T_{22}\hfill & \hfill T_{32}\hfill \\ \hfill T_{23}\hfill & \hfill T_{33}\hfill \end{array}\mid +\mid \begin{array}{cc}\hfill T_{11}\hfill & \hfill T_{21}\hfill \\ \hfill T_{12}\hfill & \hfill T_{22}\hfill \end{array}\mid +\mid \begin{array}{cc}\hfill T_{11}\hfill & \hfill T_{31}\hfill \\ \hfill T_{13}\hfill & \hfill T_{33}\hfill \end{array}\mid ,\hfill \\ \hfill I_3\mid \begin{array}{ccc}\hfill T_{11}\hfill & \hfill T_{12}\hfill & \hfill T_{13}\hfill \\ \hfill T_{21}\hfill & \hfill T_{22}\hfill & \hfill T_{23}\hfill \\ \hfill T_{31}\hfill & \hfill T_{32}\hfill & \hfill T_{33}\hfill \end{array}\mid \hfill \end{array}$$ (B5)

are invariants of the tensor T_ik. In our study, the elements D_ij, measured in a laboratory frame are transformed to elements of D_i′j′ in the PAF. The relationship between diffusion tensor invariants and D_ij and D_i′j′ are

$$\begin{array}{c}\hfill I_1\left(\mathrm{LAB}\right)=D_{xx}+D_{yy}+D_{zz}\hfill \\ \hfill I_1\left(\mathrm{PAF}\right)=D_{x^{\prime }{x}^{\prime }}+D_{y^{\prime }{y}^{\prime }}+D_{z^{\prime }{z}^{\prime }}={\lambda }_1+{\lambda }_2+{\lambda }_3\hfill \end{array}$$ (B6)

The most widely known of these invariant quantities is the trace, I₁, which is given by the sum of the three diagonal elements of diffusion tensor in either measurement coordinate system. When scaled properly, it provides average diffusion, which is a useful parameter that represents averaged motion when diffusion along each axis is different. It is defined as D_av = I₁/3.

The other two invariants can be defined based on geometric properties of tensor ellipsoid, namely;

$$\begin{array}{c}\hfill I_2\left(\mathrm{LAB}\right)=D_{xx}{D}_{yy}+D_{yy}{D}_{zz}\hfill \\ \hfill +D_{zz}{D}_{xx}-2(D_{xy}+D_{yz}+D_{zx})\hfill \\ \hfill I_2\left(\mathrm{PAF}\right)=D_{x^{\prime }{x}^{\prime }}{D}_{y^{\prime }{y}^{\prime }}+D_{y^{\prime }{y}^{\prime }}{D}_{z^{\prime }{z}^{\prime }}\hfill \\ \hfill +D_{z^{\prime }{z}^{\prime }}{D}_{x^{\prime }{x}^{\prime }}={\lambda }_1{\lambda }_2+{\lambda }_2{\lambda }_3+{\lambda }_3{\lambda }_1\hfill \end{array}$$ (B7)

$$\begin{array}{c}\hfill I_3\left(\mathrm{LAB}\right)=D_{xx}(D_{yy}{D}_{zz}-D_{zy}{D}_{yz})\hfill \\ \hfill -D_{xy}(D_{yx}{D}_{zz}-D_{zx}{D}_{yz})+D_{xz}(D_{yx}{D}_{zy}-D_{zx}{D}_{yy}\hfill \\ \hfill I_3\left(\mathrm{PAF}\right)=D_{x^{\prime }{x}^{\prime }}{D}_{y^{\prime }{y}^{\prime }}{D}_{z^{\prime }{z}^{\prime }}={\lambda }_1{\lambda }_2{\lambda }_3.\hfill \end{array}$$ (B8)