SUMMARY
Community water fluoridation is an important public health measure to prevent dental caries, but it continues to be somewhat controversial. The Iowa Fluoride Study (IFS) is a longitudinal study on a cohort of Iowa children that began in 1991. The main purposes of this study (http://www.dentistry.uiowa.edu/preventive-fluoride-study) were to quantify fluoride exposures from both dietary and non-dietary sources and to associate longitudinal fluoride exposures with dental fluorosis (spots on teeth) and dental caries (cavities). We analyze a subset of the IFS data by a marginal regression model with a zero-inflated version of the Conway-Maxwell-Poisson distribution for count data exhibiting excessive zeros and a wide range of dispersion patterns. In general, we introduce two estimation methods for fitting a ZICMP marginal regression model. Finite sample behaviors of the estimators and the resulting confidence intervals are studied using extensive simulation studies. We apply our methodologies to the dental caries data. Our novel modeling incorporating zero inflation, clustering and overdispersion sheds some new light on the effect of community water fluoridation and other factors. We also include a second application of our methodology to a genomic (next generation sequencing) dataset that exhibits underdispersion.
Keywords: Bootstrap, Caries Data, Generalized Estimating Equation, Generalized Linear Model, Expectation-Solution Algorithm, Iowa Fluoride Study, Genomics
1. Introduction
There has been growing interest in analyzing various types of count data encountered in practice leading to improved and specialized statistical methods. Some count datasets, in particular, have more zero values than expected from a certain common count distribution such as Poisson or negative binomial. This phenomenon, called zero-inflation, takes place in diverse fields such as engineering, dentistry, health surveys, transport and so on. To this end, zero-inflated versions of these distributions and related inferential procedures have been derived (Bohning, 1998; McLachlan, 1997; Yau, Wang and Lee, 2003).
A Poisson distribution is well known for modeling count data. It is a relatively simple distribution that belongs to an exponential family which makes it convenient for analysis within the generalized linear models (GLM) framework. However, a Poisson distribution may not be the best choice in certain cases when the data is under- or over- dispersed, which violates the property that the variance and the mean are equal. The negative binomial is a popular choice to model data overdispersion, however, that is not the case for underdispersion. The Conway-Maxwell-Poisson (CMP) distribution introduced by Conway and Maxwell (1962) is a great tool to overcome this difficulty, since it can model a wide range of dispersion. In addition, it belongs to an exponential family as well.
Often in practice not all the data values are independent. Instead they arise as independent groups called clusters. The goal of the present paper is to develop a marginal regression model framework for analyzing count data with a zero-inflated CMP model (ZICMP, hereafter) where the data values are clustered. The motivation behind this work comes for our attempt to analyze a dataset of caries experience scores (CES) for each tooth of a collection of nine year old children from the Iowa Fluoride Study (IFS), which we return to in Section 3. The response variable for this case study exhibits zero inflation and overdispersion; in addition, each child represents a cluster since the CES values for all teeth belonging to a particular child are likely to be correlated due to shared genetic and environmental factors.
Currently, SAS version 13.1 has a procedure, PROC COUNTREG which allows us to perform a regression analysis based on the ZICMP distribution and the COMPoissonReg package in R performs a CMP regression analysis based on a GLM framework (Sellers and Shmueli, 2010). In addition, a recent paper by Barriga and Louzada (2014) introduces Bayesian inference with a ZICMP distribution. However, all these procedures and papers are only applicable to independent data. In this paper, we explore two different statistical approaches for fitting marginal regression models to clustered count data using a ZICMP distribution: a maximum pseudo-likelihood (MPL) method with an adjusted variance estimator for cluster dependency, and a modified generalized estimating equation based method we call the modified expectation-solution (MES) algorithm along with a cluster bootstrap based variance estimator.
The rest of the paper is organized as follows: In Section 2, we provide a brief introduction to a CMP distribution and its zero inflated version and review some important properties; we introduce the parameters estimation procedures for a ZICMP model based on the two different regression methods mentioned above. In Section 3, we apply both the MPL and MES methods to analyze the dental caries data. Our novel modeling of the dental data incorporating zero inflation, clustering, and overdispersion sheds some new light on the effect of community water fluoridation and other factors. In addition, we also include a second real data example to illustrate the case of underdispersion; this involves the modeling of read counts of a given gene under four different genotypes in a next generation sequencing (NGS) experiment with maze hybrids (Paschold et. al, 2014). Section 4 presents two simulation studies. In the first simulation, we investigate the sampling properties of both the MPL and MES methods in a setting similar to the dental data along with a comparison with a zero-inflated Poisson (ZIP) regression model that is readily available in an existing R-package. In the second simulation, we compare the MPL and MES algorithms in a different setting motivated by a data on airfreight breakage, where we also examine the effect of increasing the number of clusters. Finally, our paper ends with a Conclusion section. Some technical details and additional results are placed in the Web appendices.
2. Material and Method
The probability mass function (pmf) of a CMP distribution is given by
| (1) |
where . Here λ > 0 is a shape parameter and v ≥ 0 is a dispersion parameter. If v is 1, a CMP distribution is exactly a Poisson distribution which means there is equidispersion. It turns out that v > 1 represents underdispersion and v < 1 represents overdispersion. Note that this distribution belongs to an exponential family since p(y) = exp{ylog(λ) − vlog(y!)}Z−1(λ, v). The limiting cases of a CMP distribution also include a Bernoulli distribution (v = ∞), or a geometric distribution (v = 0 and λ < 1) Thus, a CMP distribution has great flexibility to include various types of count distributions. Another important feature of the CMP distribution is about the expectation function of Y. In general, means behave independently from the dispersion parameters; in other words, the dispersion parameters do not affect the means. However, Equation (2) shows that the mean of Y in the CMP distribution is not only a function of the shape parameter λ, but also of the dispersion parameter v:
| (2) |
A zero-inflated model consists of two components: the zero-degenerated distribution δ0 and a particular count distribution W. The zero-degenerated part controls excessive zeros in the form of a binary distribution and a count distribution, the CMP distribution in this case, controls counts including the expected number of zeros. Thus, the ZICMP marginal model has probability mass function described by
| (3) |
where p ∈ [0,1]is a parameter of the distribution representing the mixing proportion of the degenerate at zero part. Our data consists of clustered responses {yij}, where yij denotes the jth observation in the ith cluster with 1 ≤ j ≤ ni, and 1 ≤ i ≤ N. Note that ni is the size of the ith cluster and N is the total number of independent clusters in our dataset. In general, the y in a given cluster are correlated. We assume that the dispersion parameter v is the same for all subjects; the other two ZICMP parameters corresponding to yij will be denoted by pij and λij.
The expectation-maximization (EM) algorithm is widely used for estimating parameters in a zero-inflated model. However, the EM algorithm, by itself, is not a valid tool for clustered data. In three sub-section parts, we will explain the mechanism of the two methods mentioned in the Introduction section, accounting for not only zero-inflation but also dependency.
2.1. MES algorithm based on a modified Newton-Raphson method
Instead of using an EM algorithm, Hall and Zhang (2004) suggested applying the ES (Expectation-Solution) algorithm (Hall and Zhang, 2004; Rosen, Jiang and Tanner, 2000) when the data are clustered. The ES algorithm combines elements of both the GEE (Liang and Zeger, 1986) and the EM algorithms, so that one can account for dependency (clustering) in the data. However, the ES algorithm as prescribed by Rosen, Jiang and Tanner (2000) has a major limitation in that it is only applicable to an exponential dispersion family which has a form of , where θij is the canonical parameter, wij is a constant, and ϕ is a dispersion parameter. Unfortunately, the CMP distribution does not belong to the exponential dispersion family. Since the Z function can not be factored into a function of λij( = log(θij)) and a function of v, it cannot be re-expressed in the exponential dispersion family form. As a consequence of this, the expectation of Y is not only related to λ but also to v making a regression formulation complicated.
Therefore, we propose the following modification of the standard ES algorithm to deal with the CMP family; we call it the MES algorithm. Note that given a specified value of v, the CMP distribution indexed by λ belongs to an exponential dispersion family with h = (y!)−ν, k = logZ(λ, v), w = 1 and ϕ = 1 So, instead of using the ES algorithm for estimating all parameters, we applied the ES algorithm for only regression coefficients other than v. For estimating v, a log-likelihood function is applied instead of GEE. The parameters of interest based on this algorithm consist of θ = {β, γ, v, ρ, δ}: a dispersion parameter, v, both β and γ as coefficients of the count and zero-inflation parts from the GLM framework of log(λ(β)) = Xββ and logit(p(γ)) = Xγγ and correlation coefficients, ρ and δ from correlation matrices corresponding to the count and zero-inflation parts in GEE formulation. Xβ and Xγ are covariates in the CMP distribution and zero-degenerated distribution, respectively. The covariates are determined depending on researchers’ interests.
An MES algorithm starts with the complete log-pseudo-likelihood of ZICMP model given by
| (4) |
where uij are latent (i.e., unobserved) binary indicators of the degenerate at zero part. (We call it a pseudo-likelihood because it is a product over likelihoods of individual terms as if they were independent.) Subsequently, it alternates between two main steps: the expectation (E) step and the solution (S) step. The E-step is to calculate the expectation of the expressions in each side of Equation (4) by replacing uij with E(uij) leading to
where
| (5) |
Let denote this value at the hth iteration. In the solution step, given E(u) ( = uh), estimates of β, γ, and v are obtained by solving there own linearized estimating equations leading to the following updating schemes:
| (6) |
where
| (7) |
and
| (8) |
See Web Appendix A.1 and A.2 for the details of the estimating functions Ψ1 and Ψ2 Note that the estimating functions for γ and β are of the GEE form (as in a standard ES algorithm) whereas that for the v is from a complete data pseudo-likelihood. As explained in the beginning of Section 2, the CMP distribution does not fall under an exponential dispersion family for changing v, and consequently we cannot apply the GEE methodology to estimate v. Also note that a step-size parameter κ is introduced in the updating scheme as compared with the classical Newton-Raphson method so that the algorithm converges slowly and steadily. The iterative algorithm stops when the maximum componentwise difference of the estimates between two successive iterations falls below a threshold ε. Depending on the datasets, it may be possible to use other versions of the updating scheme to get more stable updates. As for example, we could replace the sequential updates and the Ψ functions by their Cesàro sums.
The working variance-covariance matrices for the zero-inflation and the count parts are specified as and , respectively. Here Ai = Ai(pi(γ)) = Var(ui) = Diag(pi(1 − pi)), Di = Di((E(yi|β, v)) = Diag(Var(yi)), and R(δ) and R(ρ) are working correlation matrices.
For estimating the correlation coefficients, δ and ρ, the GEE formulations are used. The corresponding estimating equations are given by
| (9) |
| (10) |
where
the weight matrices Wγi and Wβi are both taken to be the identity matrices in this article. Furthermore, we assume a compound symmetry structure for both R(δ) and R(ρ) leading to a simple expression for the common correlations (see Web Appendix B.1 and B.2).
Note that all the estimated parameters are updated iteratively as explained before. We are sometimes suppressing the index h for notational simplicity.
2.2. The Maximum Pseudo-Likelihood (MPL)
Estimators from the MPL method are obtained by maximizing the observed log-pseudo-likelihood function
| (11) |
with respect to β, γ associated with covariates, Xβ and Xγ, and the dispersion parameter v. The above log-pseudo-likelihood is constructed under the independence assumption; so, an adjusted variance method is used to account for the dependency within clusters. The adjusted variance proposed in this article is based on the log-pseudo-likelihood-based sandwich variance and is illustrated in Subsection 2.3 in detail.
2.3. Variance estimation
We investigate two different variance estimation methods: a sandwich-variance based on the large sample approximation and one using a nonparametric bootstrap at the cluster level.
Large sample sandwich variances are calculated both for the MPL estimators and the estimators obtained from the MES algorithm. The typical sandwich covariance matrix is of the form B−1M(BT)−1. The matrices B and M for the MPL method for independent data are given by
| (12) |
| (13) |
where ℓ is the observed log-pseudo-likelihood function in Equation (11) pβ and pγ are the numbers of covariates used for the count part and the zero part, respectively (see Web Appendix C.1 for details). However, Equation (13) does not account for dependence within a cluster; so an adjusted sandwich covariance matrix is applied in the complete log-pseudo-likelihood function. The adjusted sandwich covariance matrix (Adj_SW) for the MPL estimators is obtained in the form of using the independence of the clusters where
| (14) |
The sandwich covariance matrix for θ̂MES = (β̂T, γ̂T, v̂)T obtained from the MES algorithm is in the form of , where the matrix BMES is obtained by adding two different matrices, B1 and B2; the expressions for these matrices and MMES are given in Web Appendix C.2. We note that it is not possible to estimate BMES based on the model assumptions since we do not specify the joint likelihood of the clustered observations. Therefore, using a bootstrap based standard error (15) is a natural option in this case. Of course, the same bootstrap resampling that is described in the next paragraph could be used for obtaining the standard errors for the MPL estimators as well.
We employ a cluster bootstrap technique (Field and Welsh, 2007) to perform the resampling since the clusters are independent and the primary sampling units. This way, the intra-cluster correlation will be preserved for the resampled data. Thus, each bootstrap sample is generated by resampling at the cluster level with replacement. Mathematically, let be a random sample of indices drawn with replacement from {1, ⋯, N}, for 1 ≤ b ≤ B. Then the bth bootstrap dataset is given by , where . The bootstrap standard errors based on B bootstrap resamples are calculated as
| (15) |
where is the vector of estimates obtained by either the MPL method or the MES algorithm from the bth bootstrap sample and is the mean of the B bootstrap estimates.
3. Real Data Applications
In this section, we introduce two different count datasets that include both zero inflation and clustering characteristics. The first dataset is obtained from the Iowa Fluoride Study (Levy et al., 2003) that serves as an example of the overdispersion phenomenon; the second illustrative dataset is taken from an NGS assay on maze hybrids and provides an example of underdispersion in count data.
3.1 An application for the Iowa Fluoride Study (IFS)
We apply our marginal regression model to analyze a dataset on dental caries from the Iowa Fluoride Study (Levy et al., 2003). As mentioned before, this dataset possesses the characteristics of zero-inflation, overdispersion and clustered counts. IFS was a longitudinal study of Iowa children who were recruited at age 5 (http://www.dentistry.uiowa.edu/preventive-fluoride-study). For this illustration, we looked at the data at the first follow-up when they were about nine years of age.
The response is the caries experience score (CES) that is obtained by summing the scores of individual dental surface scores for each tooth (scored 0, 1 or 2 depending on the caries severity). Eight potential risk/protective factors (covariates) are available:
| Gender | Gender of the child; Male is coded as 1. |
| DentalExamAge | Age in years at the time of the dental examination. |
| AUCmhF5_9yrs | Daily Fluoride intake (mg) from water, other beverages and selected foods, ingested dentifrice and fluoride supplements. Computed using AUC trapezoidal method using all available data within the time span 5 to 9 years. |
| AUCSodaOz5_9yrs | Daily soda pop intake (oz.) computed using AUC trapezoidal method using all available data within the time span 5 to 9 years. |
| ToothBrushingFeq.Per_DayAvg | Average of all tooth brushing frequencies reported for the period 5 to 9 years. |
| DentalVisitPast6monthAvg | Proportion of times a dental visit was indicated with each individual point assessing the previous 6 months. |
| FluorideTreatmentPast6monthAvg | Average proportion of times a professional dental fluoride treatment was received with each individual point assessing the previous 6 months. |
| HomeFluorideppmAvg | Average home tap water fluoride level for all returned questionnaires for the period 5 to 9 years. |
Altogether, 464 children are included in our analysis.
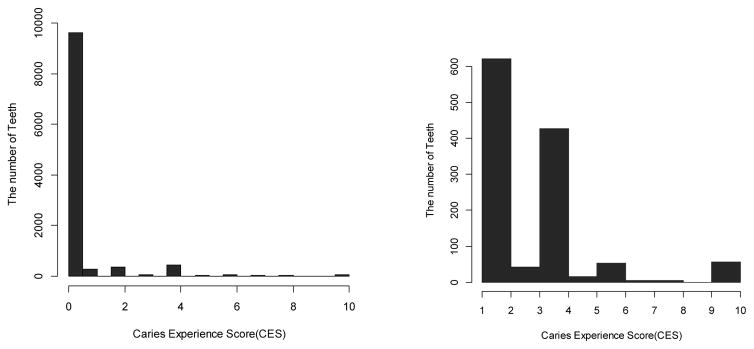
We treat the outcomes (i.e., CES) on teeth belonging to the same child to be clustered. It is likely that they will be correlated due to shared genetic and environmental factors. The cluster size varies between 16 and 24. Overall, there are 10,838 observations on the CES. A preliminary inspection of the CES values reveals that zero-inflation is a concern for this dataset (Figure 1).
Figure 1.
Summary plots of the data of the nine-year-old children from the Iowa Fluoride Study: Frequency histogram of caries experience scores (CES) summarized over all teeth and children in our sample (left panel), and the frequency histogram of CES excluding zero counts summarized over all teeth and children in our sample (right panel).
We fit a clustered ZICMP model to these data where the parameters are estimated using both the MPL and MES methods. The ZIP estimates obtained from the R package ‘pscl’ are used as the starting values in the MES algorithm. The standard errors of the MPL estimators are calculated by using the adjusted sandwich variance method mentioned before. For the standard errors of MES estimators, the bootstrap scheme (outlined in Section 2) is used with bootstrap size B = 500. Finally, p-values for each of the potential risk/protective factors are calculated using a large sample Wald test.
Before we describe the significance of the risk/protective factors, we want to note that v̂ turned out to be about 0.6 for both the MPL and MES methodologies (Table 1), indicating that the data are somewhat overdispersed. Because v̂ < 1, it is important to test whether this apparent overdispersive pattern is statistically significant. The observed absolute Z-statistic corresponding to the MES estimator, is larger than z0.025 ≈ 1.96, indicating statistical significance at the commonly applied 5% level. A similar conclusion is reached from v̂MPL as well. Therefore, the ZICMP model is recommended over the simpler ZIP model for analyzing this dataset. Furthermore, we also compare the ZICMP model with the ZIP model with adjusted sandwich variance accounting for the cluster dependence (Table 1).
TABLE 1.
Results for the data of the nine-year-old children from the Iowa Fluoride Study. We used the Maximum Pseudo Likelihood (MPL) estimators with adjusted sandwich standard error (Adj_SW) and the Modified Expectation-Solution (MES) estimators with a B = 500 size bootstrap standard error (BS). Results from a standard zero-inflated Poisson analysis with a Hessian-based standard error from the pscl package (SE (pscl)) are also shown for comparison.
| ZICMP (MPL) | ||||||
|---|---|---|---|---|---|---|
| Counts | SE (Adj_SW) | P-value | Zero-inflation | SE (Adj_SW) | P-value | |
| Intercept | 1.2571 | 0.4708 | 0.008** | 2.1507 | 0.7839 | 0.006** |
| Gender(Male=1) | −0.0154 | 0.0545 | 0.777 | 0.1363 | 0.1235 | 0.270 |
| DentalExamAge | −0.0360 | 0.0394 | 0.361 | −0.0791 | 0.0795 | 0.320 |
| AUCmhF5_9yrs | 0.0137 | 0.1087 | 0.900 | 0.7741 | 0.2127 | <0.0001** |
| AUCSodaOz5_9yrs | −0.0120 | 0.0116 | 0.302 | −0.0721 | 0.0241 | 0.003** |
| ToothBrushingFeq.Per_DayAvg | −0.1476 | 0.0612 | 0.016* | 0.5607 | 0.1249 | <0.0001** |
| Dental VisitPat6moth Avg | 0.1161 | 0.1522 | 0.446 | −0.5297 | 0.2785 | 0.057 |
| FluorideTreatmentPast6monthAvg | 0.1010 | 0.1264 | 0.424 | −0.0186 | 0.1951 | 0.924 |
| HomeFluorideppm.Avg | −0.1551 | 0.0801 | 0.053 | −0.3179 | 0.1710 | 0.063 |
| v | 0.6027 | 0.1060 | ||||
|
| ||||||
| ZICMP (MES) | ||||||
| Counts | SE (BS) | P-value | Zero-inflation | SE (BS) | P-value | |
| Intercept | 0.9273 | 0.6253 | 0.138 | 2.2401 | 0.8463 | 0.008** |
| Gender(Male=1) | −0.0134 | 0.0548 | 0.807 | 0.1408 | 0.1266 | 0.266 |
| DentalExamAge | −0.0081 | 0.0591 | 0.891 | −0.0884 | 0.0902 | 0.327 |
| AUCmhF5_9yrs | 0.0135 | 0.1136 | 0.905 | 0.7041 | 0.2293 | 0.002** |
| AUCSodaOz5_9yrs | −0.0098 | 0.0119 | 0.409 | −0.0704 | 0.0245 | 0.004** |
| ToothBrushingFeq.Per_DayAvg | −0.1225 | 0.0649 | 0.059 | 0.5664 | 0.1371 | <0.0001** |
| Dental VisitPat6moth Avg | −0.0604 | 0.1745 | 0.729 | −0.4932 | 0.3537 | 0.163 |
| FluorideTreatmentPast6monthAvg | 0.0765 | 0.1228 | 0.533 | −0.0643 | 0.2138 | 0.7636 |
| HomeFluorideppm.Avg | −0.1580 | 0.0854 | 0.064 | −0.2877 | 0.1892 | 0.1283 |
| v | 0.5975 | 0.1362 | ||||
|
| ||||||
| ZIP | ||||||
| Counts | SE (pscl, adj_sw) | P-value(pscl, adj_sw) | Zero-inflation | SE (pscl, adj_sw) | P-value(pscl, adj_sw) | |
| Intercept | 0.5737 | 0.2994, 0.4886 | 0.055, 0.2403 | 2.1560 | 0.4469, 0.7578 | <0.0001**, 0.0044** |
| Gender(Male=1) | −0.0174 | 0.0369, 0.0690 | 0.639, 0.8017 | 0.1540 | 0.0648, 0.1224 | 0.018*, 0.2084 |
| DentalExamAge | 0.0771 | 0.0296, 0.0480 | 0.009**, 0.1080 | −0.0814 | 0.0451, 0.0773 | 0.071, 0.2928 |
| AUCmhF5_9yrs | −0.0185 | 0.0688, 0.1355 | 0.788, 0.8911 | 0.4701 | 0.1129, 0.1963 | <0.0001**, 0.0166* |
| AUCSodaOz5_9yrs | −0.0055 | 0.0075, 0.0146 | 0.466, 0.7073 | −0.0560 | 0.0129, 0.0235 | <0.0001**, 0.0114* |
| ToothBrushingFeq.Per_DayAvg | −0.0745 | 0.0418, 0.0708 | 0.075, 0.2926 | 0.6070 | 0.0697, 0.1221 | <0.0001**, < 0.0001** |
| Dental VisitPat6moth Avg | 0.0962 | 0.1045, 0.1791 | 0.358, 0.5912 | −0.2886 | 0.1678, 0.2862 | 0.085, 0.3133 |
| FluorideTreatmentPast6monthAvg | 0.0029 | 0.0677, 0.1397 | 0.967, 0.9837 | −0.2490 | 0.1135, 0.2055 | 0.028*, 0.2256 |
| HomeFluorideppm.Avg | −0.1863 | 0.0477, 0.0961 | <0.0001**, 0.0525 | −0.1573 | 0.0768, 0.1503 | 0.041*, 0.2952 |
0.01 < p-value < 0.05,
p-value < 0.01
Based on our fitted ZICMP model and the corresponding p-values (Table 1), it turns out that AUCmhF5_9yrs, AUCSodaOz5_9yrs, and ToothBrushingFeq.Per_DayAvg have statistically significant effects (p-values are all less than 0.01) on the excessive zero part for 9-year-old children data for both the MPL and MES methodologies. According to the signs of the coefficients of these model terms, frequent tooth brushing and greater daily fluoride intake are protective against the development of caries, whereas soda pop intake is a risk factor for the same. HomeFluorideppm.Avg is the one which is a moderately significant factor for both the count part and the excessive zero part (just above 5% level) with the MPL method; however, the message is mixed. The result for the count part makes clinical sense and indicates that the presence of fluoride in tap water might reduce the severity of caries. Also noteworthy is that the data from the same mouth exhibited low correlation (ρ̂ ≈ 0.27, for the count part and δ̂ ≈ 0.11, for the excessive zero part).
The standard ZIP model, which operates under the independence assumption, yields a different set of significant factors for both count and excessive zero parts. In addition to the three significant factors based on our marginal ZICMP model, Gender(Male=1), FluorideTreatmentPast6monthAvg, and HomeFluorideppm.Avg have significant effects in the count part (p-values < 0.01). Thus, overall, the significance results from the simpler ZIP model appear to be a bit too optimistic. This may be due, in part, to the fact that the ZIP analysis did not account for (positive) correlations within the cluster members and over-dispersion of the data. This leads to the consequence that the variance of the covariate effects are underestimated, leading to an inflated Z-statistic (and low p-value). On the other hand, the ZIP model with the adjusted sandwich variance obtained using a similar formula as (14) identifies the same set of significant factors as the ZICMP model (perhaps with the exception of ToothBrushingFeq.Per_DayAvg, which is borderline significant under the MES method). This consequence is natural because the ZIP with the adjusted sandwich variance reflects the dependency of data. However, dispersion characteristics cannot be captured by a ZIP model even with the adjusted sandwich variance and may lead to biased inference. Indeed we verify this to be the case in a simulation study in the next section.
It is perhaps worth mentioning that the CES values were all less than or equal to 10 because there were five surfaces for each tooth. Thus, use of a truncated ZICMP, say, may be more appropriate. However, we have calculated the probability of a response y exceeding 10 under the fitted model and found it to be too small to make a practical difference in this analysis.
3.2 An application to maze hybrids data
We also apply our marginal ZICMP methods to a next generation sequencing (NGS) dataset to demonstrate a case of zero inflated, clustered count data, with underdispersion. This dataset emerges from a maze hybrids experiment (Paschold et. al, 2014). A complete analysis of this dataset from a biological standpoint is not intended here which consists of 39,656 gene IDs with four different genotypes (B73, B73 × Mo17, Mo17 × B73 and Mo17), four different tissues of each experimental unit (in this case, a certain genotype of a maze) and four biological replications. Since four tissues are harvested from the same root, there could exist some correlation among tissues belonging to the corresponding root. Therefore, this data is clustered. Out of all gene IDs, “GRMZM2G042361” is selected for an providing an illustrative example of zero-inflation with underdispersion. For this specific gene ID, we have 64 observations (read counts) including 37 zeros, 23 ones, 3 twos and 1 three.
Both the MPL and MES methods are applied to fit a marginal ZICMP model to the data. Since differences in total numbers of read counts over genes exist across biological sample units or different lanes, we need to account for this additional characteristic of NGS data in our model. Hence, we include the total read counts as an offset term into our regression model for a normalization across the biological samples. Therefore, our count part link function is modified as logλ = genotype + log(offset). The number of clusters is not deemed to be large enough for us to use the normal based confidence interval calculations. Instead, we report the point estimates along with a first order bootstrap confidence interval using the cluster bootstrap scheme described in the previous section with B = 100.
The dispersion estimates v̂ ≈ 2 for both methods (Table 2) and indicate that the expression data for GRMZM2G042361 is significantly underdispersed since the bootstrap confidence intervals do not include the value 1. All the coefficients for genotype effects are similar in both the MPL and MES methods. Only the Mo17 genotype has a significant effect on this specific gene ID for the count part since the corresponding bootstrap confidence interval excludes zero for both MPL and MES confidence intervals. Note that, for a full scale analysis of this dataset, additional considerations such as multiple hypotheses corrections need to be taken into account.
TABLE 2.
Results for the GRMZM2G042361 gene from the maze hybrids data. Parameter estimates are reported along with cluster bootstrap based (nonasymptotic) confidence intervals (BS_CI).
| MPL | ||||
|---|---|---|---|---|
| Count part | BS_CI | Zero part | BS_CI | |
| Intercept | −16.6529 | (−16.70, −15.93) | −11.2535 | (−24.46, −2.04) |
| B73 × Mo17 | 0.5264 | (−0.29, 0.71) | −1.9622 | (−18.75, 6.86) |
| Mo17 | 1.4999 | (0.66, 3.24) | −3.9165 | (−10.27, 15.54) |
| Mo17 × B73 | 0.6317 | (−1.22, 2.97) | −4.9595 | (−14.67, 13.64) |
| v | 2.1020 | (1.86, 4.93) | ||
|
| ||||
| MES | ||||
| Count part | BS_CI | Zero part | BS_CI | |
| Intercept | −16.6490 | (−16.69, −15.93) | −11.2748 | (−24.46, −2.04) |
| B73 × Mo17 | 0.5150 | (−0.28, 0.71) | −1.9740 | (−18.75, 6.85) |
| Mo17 | 1.5027 | (0.65, 3.23) | −3.8774 | (−10.26, 15.53) |
| Mo17 × B73 | 0.6273 | (−1.22, 2.96) | −4.9362 | (−14.67, 13.63) |
| v | 2.1056 | (1.86, 4.93) | ||
4. Simulation Studies
We perform two different sets of simulations to study the finite sample performance of our methodology. The first simulation study is guided by the dental data analyzed in the previous section. Here we study the bias and variance of our MPL and MES estimators as well as the performance of the adjusted sandwich based variance estimator and the bootstrap based variance estimator, respectively. Performances of the estimators based on ZIP model and both variance estimators are also included for comparison. The second simulation study is guided by a dataset on airfreight breakage which has only one covariate; however, the covariate is a subject level (rather than cluster level) covariate. In addition, we are able to study the effect of increasing the number of clusters on the performance of these estimators.
4.1 Simulation guided by the dental data
The CES dataset of the nine-year-old children from the Iowa Fluoride Study (Levy et al., 2003) is described in detail in the previous section, which is also used for application of our marginal ZICMP model. The present large simulation study is guided by that dataset. We generate the clustered CES scores using a correlated ZICMP regression model with four cluster level covariates for both parts of the model. These covariates were the significant factors (based on results from Section 3) for the zero part: AUCmhF5_9yrs, AUCSodaOz5_9yrs and ToothBrushingFeq.Per_DayAvg except HomeFluorideppmAvg which was borderline significant for both the count and the zero parts based on the MPL analysis. Noisy versions of these covariate vectors resampled from the original dataset were used to generate the CES scores using the subject specific parameters through the links explained in Section 2. We use parameter values β = (1.00,0.01, −0.01, −0.13, −0.16) for the count part, γ = (2.00, 0.70, −0.07, 0.56, −0.30) for the zero part and v = 0.6. These are close to both MPL and MES estimates obtained for the dental data in Section 3.
In order to keep the computational burden in check, the total number of clusters, N, is taken to be 200 and a constant cluster size of ni = 15 is used for all the clusters. That is, Xi,β = Xi,γ is a 15 × 5 matrix including an intercept term for each of the count and zero parts. Following Kong et al. (2014), correlated Bernoulli variables to generate the zero values are, simulated using the Cholesky decomposition of a compound symmetric correlation matrix with a common correlation coefficient δ̃, whereas the correlated count (CMP) data are generated by the inverse CDF transformation technique starting with a multivariate normal distribution with zero mean and a compound symmetric correlation matrix with a common correlation ρ̃. We consider both low (ρ̃ = δ̃ = 0.2) and high (ρ̃ = δ̃ = 0.8) intra-cluster correlation cases.
For each setting, we create 100 datasets, calculate the MPL and MES estimates for each dataset, and obtain the empirical bias and standard error for each parameter estimator. The adjusted sandwich variance estimates are calculated for the MPL method and the variance estimates for the MES estimators are obtained through the bootstrap scheme (Field and Welsh, 2007) based on 100 bootstrap resamples as detailed in Section 2. ZIP estimates with their asymptotic variance and the adjusted sandwich variance estimates are also obtained for each Monte Carlo dataset by applying the pscl R package and using an analogous adjusted sandwich variance formula as (14), respectively.
Estimators obtained from the ZIP model have larger biases than both the MPL and MES estimators of the ZICMP model (Table 3). This is more notable in high intra-cluster correlation case. The bias for the high intra-correlation case is larger for almost all estimators compared to the low intra-cluster case in both the ZICMP and ZIP models, as expected.
TABLE 3.
Empirical bias and variance of our estimators in a simulation study guided by the dental data of nine-year-old children from the Iowa Fluoride Study. The number of clusters is 200; the size of each cluster is 15. Each entry is based on 100 Monte Carlo iterations. The performances of ZIP estimators are also added.
| MPL | ||||||||
|---|---|---|---|---|---|---|---|---|
| Low intraclass correlation | High intraclass correlation | |||||||
| True | Bias | SE | SE (Adj_SW) | Bias | SE | SE (Adj_SW) | ||
| Count part | Intercept | 1.00 | 0.0645 | 0.2040 | 0.2835 | 0.3191 | 0.5564 | 0.5916 |
| AUCmhF5_9yrs | 0.01 | −0.0006 | 0.1388 | 0.1274 | 0.0462 | 0.3889 | 0.2966 | |
| AUCSodaOz5_9yrs | −0.01 | −0.0011 | 0.0201 | 0.0167 | −0.0076 | 0.0558 | 0.0430 | |
| ToothBrushingFeq.Per_DayAvg | −0.13 | −0.0117 | 0.0920 | 0.0879 | −0.0290 | 0.2439 | 0.2086 | |
| HomeFluorideppm.Avg | −0.16 | 0.0080 | 0.1000 | 0.0999 | −0.0631 | 0.3174 | 0.2453 | |
| v | 0.60 | 0.0427 | 0.1030 | 0.1277 | 0.1892 | 0.2052 | 0.2461 | |
| Low intraclass correlation | High intraclass correlation | |||||||
| True | Bias | SE | SE (Adj_SW) | Bias | SE | SE (Adj_SW) | ||
| Zero part | Intercept | 2.00 | 0.0533 | 0.4238 | 0.4117 | 0.0274 | 0.7473 | 0.8477 |
| AUCmhF5_9yrs | 0.70 | 0.0044 | 0.3068 | 0.3156 | 0.0356 | 0.5244 | 0.6381 | |
| AUCSodaOz5_9yrs | −0.07 | 0.0091 | 0.0489 | 0.0433 | 0.0129 | 0.0879 | 0.0902 | |
| ToothBrushingFeq.Per_DayAvg | 0.56 | −0.0417 | 0.2324 | 0.2235 | −0.0157 | 0.4599 | 0.4592 | |
| HomeFluorideppm.Avg | −0.30 | −0.0006 | 0.2491 | 0.2317 | 0.0328 | 0.5282 | 0.4942 | |
|
| ||||||||
| MES | ||||||||
| Low intraclass correlation | High intraclass correlation | |||||||
| True | Bias | SE | SE (BS) | Bias | SE | SE (BS) | ||
| Count part | Intercept | 1.00 | −0.0045 | 0.0687 | 0.1016 | −0.0068 | 0.1481 | 0.1593 |
| AUCmhF5_9yrs | 0.01 | −0.0025 | 0.0487 | 0.0820 | 0.0133 | 0.1235 | 0.1282 | |
| AUCSodaOz5_9yrs | −0.01 | −0.0003 | 0.0074 | 0.0099 | −0.0019 | 0.0177 | 0.0182 | |
| ToothBrushingFeq.Per_DayAvg | −0.13 | −0.0006 | 0.0353 | 0.0531 | −0.0033 | 0.0717 | 0.0862 | |
| HomeFluorideppm.Avg | −0.16 | 0.0032 | 0.0359 | 0.0558 | −0.0154 | 0.0934 | 0.0982 | |
| v | 0.60 | −0.0069 | 0.0539 | 0.0686 | −0.0034 | 0.0640 | 0.0430 | |
| Low intraclass correlation | High intraclass correlation | |||||||
| True | Bias | SE | SE (BS) | Bias | SE | SE (BS) | ||
| Zero part | Intercept | 2.00 | 0.0240 | 0.1537 | 0.1623 | 0.0115 | 0.3154 | 0.3664 |
| AUCmhF5_9yrs | 0.70 | −0.0046 | 0.1061 | 0.1182 | 0.0048 | 0.2075 | 0.2734 | |
| AUCSodaOz5_9yrs | −0.07 | 0.0027 | 0.0161 | 0.0158 | 0.0072 | 0.0335 | 0.0358 | |
| ToothBrushingFeq.Per_DayAvg | 0.56 | −0.0140 | 0.0820 | 0.0816 | −0.0052 | 0.1786 | 0.1913 | |
| HomeFluorideppm.Avg | −0.30 | −0.0026 | 0.0767 | 0.0877 | 0.0176 | 0.1798 | 0.2022 | |
|
| ||||||||
| ZIP | ||||||||
| Low intraclass correlation | High intraclass correlation | |||||||
| True | Bias | SE | SE (pscl, Adj_SW) | Bias | SE | SE (pscl, Adj_SW) | ||
| Count part | Intercept | 1.00 | 0.7203 | 0.2361 | 0.1665, 0.2038 | 0.7002 | 0.5395 | 0.1922, 0.4104 |
| AUCmhF5_9yrs | 0.01 | −0.0063 | 0.1782 | 0.1374, 0.1646 | 0.0721 | 0.4532 | 0.1597, 0.3348 | |
| AUCSodaOz5_9yrs | −0.01 | −0.0044 | 0.0272 | 0.0182, 0.0215 | −0.0102 | 0.0654 | 0.0231, 0.0484 | |
| ToothBrushingFeq.Per_DayAvg | −0.13 | −0.0566 | 0.1253 | 0.0919, 0.1123 | −0.0620 | 0.2790 | 0.1067, 0.2312 | |
| HomeFluorideppm.Avg | −0.16 | −0.0418 | 0.1372 | 0.1038, 0.1265 | −0.1092 | 0.3700 | 0.1249, 0.2710 | |
| Low intraclass correlation | High intraclass correlation | |||||||
| True | Bias | SE | SE (pscl, Adj_SW) | Bias | SE | SE (pscl, Adj_SW) | ||
| Zero part | Intercept | 2.00 | 0.0596 | 0.4234 | 0.3117, 0.4086 | 0.0372 | 0.7874 | 0.3220, 0.8389 |
| AUCmhF5_9yrs | 0.70 | −0.0069 | 0.3026 | 0.2446, 0.3122 | 0.0335 | 0.5423 | 0.2532, 0.6292 | |
| AUCSodaOz5_9yrs | −0.07 | 0.0114 | 0.0490 | 0.0333, 0.0429 | 0.0135 | 0.0880 | 0.0354, 0.0882 | |
| ToothBrushingFeq.Per_DayAvg | 0.56 | −0.0258 | 0.2333 | 0.1671, 0.2219 | −0.0047 | 0.4678 | 0.1733, 0.4534 | |
| HomeFluorideppm.Avg | −0.30 | 0.0174 | 0.2469 | 0.1801, 0.2288 | 0.0388 | 0.5456 | 0.1957, 0.4911 | |
SE: Monte Carlo; SE (BS): bootstrap estimated standard error, SE (Adj_SW): square root of adjusted sandwich variance estimate, SE (pscl): standard errors obtained from the Hessian matrix.
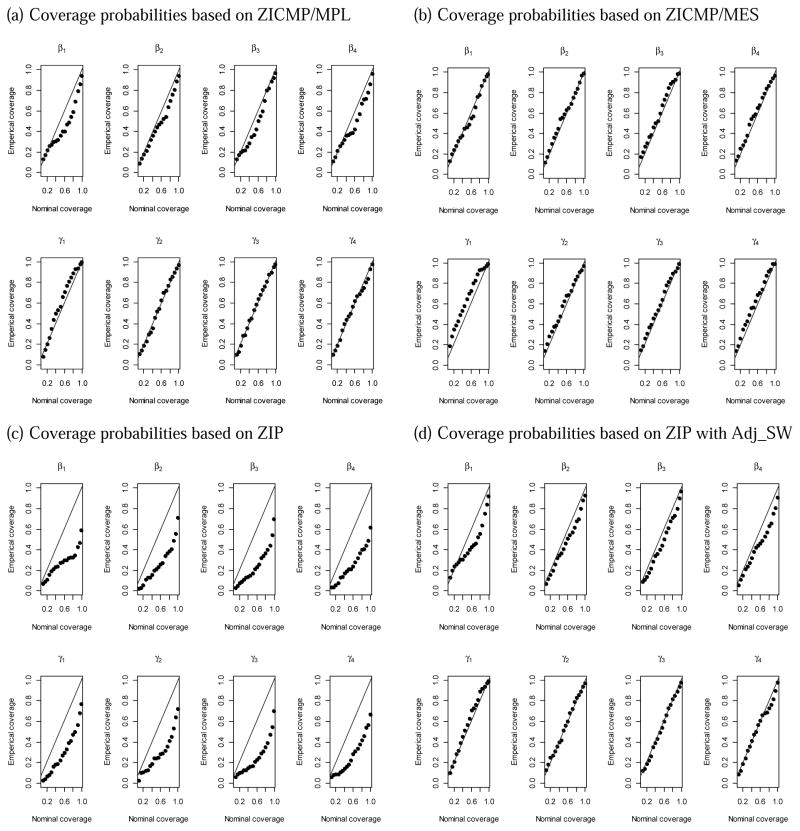
The estimators based on the simpler ZIP model are accompanied by Hessian-based standard errors, SE (pscl), obtained by the ‘zeroinfl’ function in pscl R package. For the low correlation case, these are not too different from the true standard errors for both count and zero parts. However, in the high intra-cluster correlation case, ZIP standard errors (SE (pscl)) are considerably smaller than the true ones. This implies that the Hessian-based standard errors are deflated which leads to a more liberal interpretation of p-values. This happens because the ZIP estimators do not account for the dependency of data in a cluster. This issue turns out to be more apparent for the high intra-cluster correlation case. On the other hand, the adjusted sandwich variance estimators tend to be closer to the true standard errors (SE). Thus, the inference from a ZIP model along with an adjusted sandwich variance has an ability to account for the clustering characteristic of data but still lacks the ability to handle data dispersion (under or over). This aspect may causes prominently larger bias, especially in the count part, which may lead to incorrect inference as shown by the probability-probability (p-p) plots (Figure 2 and Web Figure 1).
Figure 2.
Empirical coverage of the confidence intervals in a simulation study guided by the dental data of nine-year-old children from the Iowa Fluoride Study. The p-p plots are for N = 200 and n = 15 when intra-cluster correlation is high. Three sets of plots are provided for the regression parameters corresponding to the four covariates: ZICMP/MPL (upper left panel), ZICMP/MES (upper right panel), ZIP (bottom left panel) and ZIP with Adj_SW (bottom right panel).
While the MES estimators yield smaller biases and true standard errors (SE) than MPL estimates (Table 3), they need to use the bootstrap-based standard errors for variance estimates which consumes a considerable amount of computational efforts.
In order to study the performance of the resulting inferences of the effects of covariates/factors, we created the p-p plots where we plot the targeted nominal coverage of a confidence interval in the horizontal axis and the corresponding true coverage, as measured by the Monte Carlo simulation, in the vertical axis. Thus, a diagonal p-p plot would indicate that the asymptotic normal approximation to various estimators is accurate so we can have proper inferences using them. Overall, we noticed that all the p-p plots obtained from both the MPL and MES methods are relatively close to the solid reference lines (see Figures 2 and Web Figure 1) even for the high correlation case. However, none of the p-p plots based on the ZIP model with standard variance estimates is very linear even in the low correlation case. As mentioned earlier, the situation improves when we use the adjusted sandwich variance with the ZIP model. Nevertheless, the p-p plots for most of the regression parameters still exhibit varying extent of under coverage. Thus, the ZIP model may not be a satisfactory method for analyzing zero-inflated clustered data with overdispersion.
4.2 Simulation guided by the airfreight breakage data
In this simulation, we investigate the performance of our ZICMP marginal model with a subject (observation) level covariate by building a simulation plan around the airfreight breakage data (Kutner, Nachtsheim and Neter, 2003, page 35, Exercise 1.21) which consists of 10 observations and one scalar covariate. A CMP model for this data was fit by Sellers and Shmueli (2010), which yielded parameter estimates of β = (1.38, 1.3)T and v = 5.7818. Going forward, we use the same parameter values for generating the count part of our data, with covariates Xβ resampled from the set of scalar covariates in the original dataset (to match the desired number of observations). The zero-inflated part is generated by a regression model as described in Section 2, with the same set of covariates, i.e., Xγ = Xβ but with the regression parameters γ = (2, −3)T. For generating clustered ZICMP data, we need to generate correlated zeros, as well as, correlated counts. These are generated as explained in the Section 4.1
In this simulation, we consider three different combinations of number of clusters and the cluster size, namely, N = 30 with n = 20, N = 50 with n = 30, and N = 75 with n = 15. For each condition, we generate data with low (ρ̃ = δ̃ = 0.2) or high (ρ̃ = δ̃ = 0.8) correlations within each cluster. Both MPL and MES methods are applied to each of the 100 simulated dataset and the results are averaged to compute the empirical bias and variances of our estimators. We also used the bootstrap to compute variance estimates for both estimators in addition to the adjusted sandwich variance estimate for the MPL estimator. In order to keep the computational resources in check, we have used a modest number of bootstrap resamples ( = 100) which is still deemed to be sufficient for our purpose. As mentioned earlier, in order to calculate bootstrap variance, we resample 100 times at the cluster level with replacement so that the correlation structures are preserved within a cluster. Finally, bootstrap variance estimates are given by the empirical variances of the parameter estimates obtained for the 100 bootstrap resamples. The results for N = 50 are provided in Table 4; results for the other two cases are placed in the Web Tables 1 and 2.
TABLE 4.
Empirical bias and variance of our ZICMP estimators in a simulation study guided by the airfreight breakage data. The number of clusters is 50; the size of each cluster is 30. Each entry is based on 100 Monte Carlo iterations.
| MPL | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Low intraclass correlation | High intraclass correlation | ||||||||
| True | Bias | SE | SE (BS) | SE (Adj_SW) | Bias | SE | SE (BS) | SE (Adj_SW) | |
| β0 | 13.8 | 0.2484 | 0.8425 | 0.8341 | 0.8144 | 0.9945 | 2.1666 | 2.2882 | 2.2576 |
| β1 | 1.3 | 0.0260 | 0.0847 | 0.0816 | 0.0797 | 0.0965 | 0.2088 | 0.2173 | 0.2139 |
| γ0 | 2 | 0.0130 | 0.1703 | 0.1727 | 0.2089 | 0.0691 | 0.3803 | 0.3469 | 0.4054 |
| γ1 | −3 | −0.0384 | 0.1538 | 0.1622 | 0.1918 | −0.0726 | 0.3309 | 0.3358 | 0.3788 |
| v | 5.7818 | 0.1040 | 0.3490 | 0.3467 | 0.3384 | 0.4152 | 0.9048 | 0.9540 | 0.9403 |
|
| |||||||||
| MES | |||||||||
| Low intraclass correlation | High intraclass correlation | ||||||||
| True | Bias | SE | SE (BS) | Bias | SE | SE (BS) | |||
| β0 | 13.8 | 0.2498 | 0.8430 | 0.8419 | 0.9978 | 2.1712 | 2.1816 | ||
| β1 | 1.3 | 0.0254 | 0.0848 | 0.0838 | 0.0952 | 0.2069 | 0.3223 | ||
| γ0 | 2 | 0.0151 | 0.1704 | 0.1702 | 0.0732 | 0.3910 | 0.4453 | ||
| γ1 | −3 | −0.0381 | 0.1534 | 0.1626 | −0.0763 | 0.3356 | 0.3394 | ||
| v | 5.7818 | 0.1040 | 0.3491 | 0.3493 | 0.3937 | 0.9372 | 0.9446 | ||
SE: Monte Carlo based empirical standard error; SE (BS): bootstrap estimated standard error, SE (Adj_SW): square root of adjusted sandwich variance estimate.
Web Table 1 results show that, in the case of N = 30, the estimators obtained from both MPL and MES methods have comparable performances in terms of bias and standard errors for both low and high intra-cluster correlation cases. For the low intra-cluster correlation case, bootstrap standard errors of both MPL and MES estimators match the true standard errors fairly well. However, in the high correlation case, the accuracy of the bootstrap standard errors worsens in both the MPL and the MES methods. Similarly, the adjusted sandwich standard errors based on the MPL method are fairly close to the true standard errors in the low intra-cluster correlation case, but not in the high correlation case. The bias terms for both MPL and MES methods are similar to each other and the bias tends to be larger in the high intra-cluster correlation case, as expected.
When the number of clusters increases to 50 (Table 4), the variance results were again comparable for the two sets of estimators in the case of both low and high intra-cluster correlations. In addition, the bootstrap based standard errors for both sets of estimators are very close to the true standard errors in both low and high intra-cluster correlation cases. Moreover, the adjusted sandwich standard errors based on the MPL method are quite comparable to the bootstrap standard errors in both low and high correlation cases, even though the bootstrap estimates are slightly closer to the true standard errors.
When the number of clusters N further increases to 75 in Web Table 2, the performance improves across the board. From the results based on all the three scenarios, both the MPL method and MES algorithm have similar performances with respect to bias and standard errors. Note, however, that the MPL method is generally easier to implement and comes with a closed form sandwich variance estimate. The standard errors obtained using the bootstrap method appear to be reasonably close to the true SE as obtained by the Monte Carlo method; the estimates obtained from the adjusted sandwich formula for the MPL estimator can be adequate when the number of clusters is large.
We would like to point out that the biases for the intercept terms from the count parts based on these two simulations (Table 3 and Table 4) appear to be large compared to those for the other terms. In fact, the true values of the intercept parameters are relatively large compared to the other regression coefficients and consequently the relative biases of the intercept terms are comparable to those for the other terms.
5. Discussions
The CMP model has received a great deal of attention in recent years in many fields of application. In particular, the article by Shmueli et al. (2005) advocating the use of CMP distributions has already been cited 165 times according to Google Scholar (accessed September 5, 2015). While Sellers and Shmueli (2010) developed regression modeling for CMP distributed data, in this paper we provide two significant extensions of the CMP methodology for making frequentist inference, thereby making this applicable to a greater variety of problems. Our version of the methodology can handle excessive zeros (zero-inflation) in the data and also when the data are clustered so that not all observations are independent. In particular, we have analyzed a dataset from the Iowa Fluoride Study using our model and show that more reliable inference can be obtained using it than the ZIP regression.
In this paper, we have introduced two methods to fit a ZICMP marginal model with clustered data that has over or under dispersion. In our simulations, the MES method produced slightly more efficient estimators through the use of a working variance-covariance matrix like the GEE. However, the corresponding variance estimates are computationally more expensive. The MPL method, on the other hand, affords a close form variance estimator. Like any other numerical optimization/estimating equation based methods, these methods may have convergence issues for certain datasets and changing the initial values and the optimization method (e.g., use a different method rather than the default in the R function ‘optim’) or the updating scheme (e.g., acceleration constant, Cesàro updating) may help the situation.
We also demonstrated that a cluster bootstrap method is capable of producing reasonable variance estimates for both sets of estimators through two different simulations. With respect to this, it is important for the reader to note that certain R packages that are directly able to calculate the sandwich variances may not work as well as using bootstrap to estimate the variances. We also obtain a theoretical form of the asymptotic variance covariance matrix of the MES estimators that explains the variability in the estimation of the indicators of the zero part. However, it is not possible to obtain an empirical analogue of this for general clustered data, since we do not know the exact joint likelihood of the cluster-correlated observations. On the other hand, we can obtain a valid sandwich variance estimators for the MPL method even for clustered data by utilizing the independence of the cluster sums of the corresponding estimating functions.
The two real data examples demonstrate the scope of applications of our methodology to diverse fields and it is our hope that with time more applications to these models for clustered count data with zero inflation and wide range of dispersion will be discovered.
Supplementary Material
Acknowledgments
We thank the co-editor and reviewers for their constructive comments. This research was supported by National Institutes of Health grants 1R03DE020839-01A1, 1R03DE022538-01, R01-DE09551, R01-DE12101, M01-RR00059.
Footnotes
The Web Appendices referenced in Sections 2 and 4 plus the R-code for the dental data analysis are available with this paper at the Biometrics website on Wiley Online Library.
References
- Barriga GDC, Louzada F. The zero-inflated Conway-Maxwell-Poisson distribution: Bayesian inference, regression modeling and influence diagnostic. Statistical Methodology. 2014;21:23–34. [Google Scholar]
- Böhning D. Zero-inflated Poisson models and C.A.MAN: a tutorial collection of evidence. Biometrical Journal. 1998;40:833–843. [Google Scholar]
- Conway RW, Maxwell WL. A queuing model with state dependent service rates. Journal of Industrial Engineering. 1962;12:132–136. [Google Scholar]
- Field CA, Welsh AH. Bootstrapping clustered data. Journal of Royal Statistical Society Ser B. 2007;69:369–390. [Google Scholar]
- Hall DB, Zhang Z. Marginal models for zero-inflated clustered data. Statistical Modelling. 2004;4:161–180. [Google Scholar]
- Jackman S. Technical Report. Stanford, CA: Political Science Computational Laboratory, Stanford University; 2006. Package ‘pscl’. http://cran.r-project.org/web/packages/pscl/pscl.pdf. [Google Scholar]
- Kong M, Xu S, Levy SM, Datta S. GEE type inference for clustered zero-inflated negative binomial regression with application to dental caries. Computational Statistics and Data Analysis. 2015;85:54–66. doi: 10.1016/j.csda.2014.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutner MH, Nachtsheim CJ, Neter J. Applied Linear Regression Models. 4. McGraw-Hill; New York: 2003. [Google Scholar]
- Lambert D. Zero-inflated Poisson regression, with an application to defects in manufacturing. Technometrics. 1992:1–14. [Google Scholar]
- Levy SM, Warren JJ, Broffitt BA, Hillis SL, Kanellis MJ. Fluoride, beverages and dental caries in the primary dentition. Caries Research. 2003;37:157–165. doi: 10.1159/000070438. [DOI] [PubMed] [Google Scholar]
- Liang KY, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- McLachlan GJ. On the EM algorithm for overdispersed count data. Statistical Methods in Medical Research. 1997;6:76–98. doi: 10.1177/096228029700600106. [DOI] [PubMed] [Google Scholar]
- Paschold A, Larson NB, Marcon C, Schnable JC, Yeh CT, Lanz C, Nettleton D, Piepho HP, Schnable PS, Hochholdinger F. Nonsyntenic genes drive highly dynamic complementation of gene expression in mazie hybrids. The Plant Cell. 2014;26:3939–3948. doi: 10.1105/tpc.114.130948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosen O, Jiang W, Tanner MA. Mixtures of marginal models. Biometrika. 2000;87:391–404. [Google Scholar]
- SAS (13.1) http://support.sas.com/documentation/cdl/en/etsug/66840/HTML/default/viewer.htm#etsug_countreg_details15.htm.
- Satten GA, Datta S. The S-U algorithm for missing data problems. Computational Statistics. 2000;15:243–277. [Google Scholar]
- Sellers KF, Lotze T. 2010 http://cran.r-project.org/web/packages/COMPoissonReg/COMPoissonReg.pdf.
- Sellers KF, Shmueli G. A flexible regression model for count data. The Annals of Applied Statistics. 2010;4:943–961. [Google Scholar]
- Shmueli G, Minka TP, Kadane JB, Borle S, Boatwright P. A useful distribution for fitting discrete data: revival of the Conway–Maxwell–Poisson distribution. Applied Statistics. 2005;54:127–142. [Google Scholar]
- Yau KKW, Wang K, Lee AH. Zero-inflated negative binomial mixed regression modeling of over-dispersed count data with extra zeros. Biometrical Journal. 2003;45:437–452. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.