Significance
The 3D opening of the interendothelial slit in human spleen creates a physical fitness test for red blood cells (RBCs) and clears them from circulation if their geometry and deformability are altered. We present a unique computational framework for the development of prognostic markers for diseases that alter RBC physical characteristics and identify quantitative limits for splenic slit clearance. Our work shows how the splenic slit determines distributions of size and shape of healthy RBCs. Our work lays the groundwork for systematic reconstruction of RBC navigation in the human spleen with consequences for a variety of acute and chronic medical conditions associated with hereditary alterations of RBCs, infectious diseases, and cancers.
Keywords: erythrocytes, microcirculation, spleen clearance, malaria, spherocytosis
Abstract
Red blood cells (RBCs) can be cleared from circulation when alterations in their size, shape, and deformability are detected. This function is modulated by the spleen-specific structure of the interendothelial slit (IES). Here, we present a unique physiological framework for development of prognostic markers in RBC diseases by quantifying biophysical limits for RBCs to pass through the IES, using computational simulations based on dissipative particle dynamics. The results show that the spleen selects RBCs for continued circulation based on their geometry, consistent with prior in vivo observations. A companion analysis provides critical bounds relating surface area and volume for healthy RBCs beyond which the RBCs fail the “physical fitness test” to pass through the IES, supporting independent experiments. Our results suggest that the spleen plays an important role in determining distributions of size and shape of healthy RBCs. Because mechanical retention of infected RBC impacts malaria pathogenesis, we studied key biophysical parameters for RBCs infected with Plasmodium falciparum as they cross the IES. In agreement with experimental results, surface area loss of an infected RBC is found to be a more important determinant of splenic retention than its membrane stiffness. The simulations provide insights into the effects of pressure gradient across the IES on RBC retention. By providing quantitative biophysical limits for RBCs to pass through the IES, the narrowest circulatory bottleneck in the spleen, our results offer a broad approach for developing quantitative markers for diseases such as hereditary spherocytosis, thalassemia, and malaria.
The spleen, about 10–12 cm in length with a mass of 100–200 g and located in the left superior abdomen, is the largest lymphatic organ in the human body (1, 2). The spleen plays a key role in the human immune system by protecting the body from pathogenic microorganisms reaching the bloodstream, through innate phagocytosis or adaptive responses operated by lymphocytes and antibodies. The spleen also serves as a filter that can remove red blood cells (RBCs) from circulation because of either physiological senescence or pathological alterations.
RBCs can be recognized as altered when changes in their shape, size, or surface are detected or their deformability is impaired as a consequence of such changes. Archetypical surface alterations are externalization of phosphatidyl-serine on the outer leaflet of the phospholipid bilayer of the RBC membrane or fixation of antibody on surface antigens, as occurs in transfusion mismatch. Sensing of these alterations by macrophages can occur all over the body with strong predominance in the spleen and liver (3). By contrast, recognition of altered size, shape, and deformability is considered a spleen-specific function. Surface area loss and reduced deformability also occur during aging of healthy RBCs (4). The archetypical disease where mechanical retention of RBCs in the spleen is the central pathogenic process is hereditary spherocytosis (HS). HS is a genetic disorder resulting in dysfunctional membrane proteins that play a role in transforming the shape of the RBC from a normal discocyte to a sphere. HS occurs at a frequency of 1 in 5,000 births in the Caucasian population and is the most common origin of hereditary intravascular and extravascular hemolysis. In HS, defects in band 3, ankyrin and spectrin membrane proteins connecting the RBC membrane to the spectrin network can lead to the vesiculation of unsupported lipid bilayer. Such vesiculation causes a gradual reduction in cell surface area by as much as 20% compared with that of a healthy RBC (5). This reduction, in turn, can significantly increase the retention rates of RBCs in the spleen because of their increased sphericity (6). Severe reduction in RBC deformability attributable to spherocytosis results in the flow of RBCs to be obstructed as they pass through the spleen (7, 8). Consequently, the RBCs are phagocytosed causing hemolytic anemia and splenomegaly (i.e., enlarged spleen). The fact that surgical removal of the spleen (splenectomy) alleviates anemia to a large extent in patients with severe HS lends support to the argument that recognition of altered deformability of RBCs is a specific function of the spleen. Increased in vitro mechanical retention of RBCs collected in splenectomized subjects further supports this inference (9). RBC deformability is impaired in several other conditions including thalassemia (10), burns (11), and Plasmodium falciparum malaria (12). During its 48-h life cycle, the P. falciparum-infected RBC progressively increases in stiffness. During the so-called “ring” stage (i.e., within 24 h of host cell invasion by the parasite), the infected RBCs (iRBCs) undergo ∼9.6% surface area loss (13) and reduced deformability arising from up to a fourfold increase in membrane shear modulus (14). Innate mechanical retention of a proportion of normally circulating ring-iRBCs has been observed ex vivo in a human spleen perfusion system (15) and in vitro (13, 16). The mechanical retention of iRBCs in the spleen is predicted to markedly impact the initial evolution of infection (17, 18) and is exploited in the search for new antimalarial drugs (19). Studies of iRBCs and human spleen have further validated the notion that mechanical retention of RBCs is modulated by the spleen-specific 3D structure of the IES in the red pulp (15).
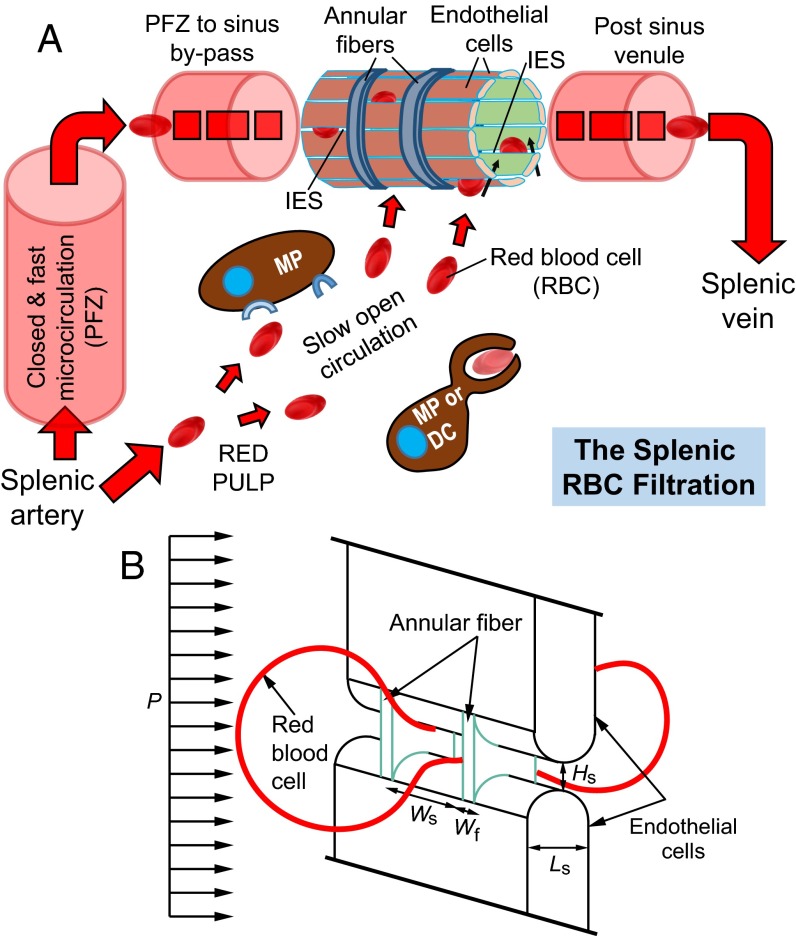
The spleen is the largest filter of RBCs in the body where the smallest openings for RBC passage are located (1). Splenic parenchyma is made of white pulp nodules and sheaths—that contain mainly T and B lymphocytes—interspersed into the red pulp, a spongy tissue that accounts for 75% of the splenic volume. The red pulp comprises splenic sinusoids, which are blood vessels juxtaposed with the connective tissue of splenic cords. About 10% of blood entering the spleen is directed into so-called open circulation, where RBCs are forced to go from the cords into venous sinuses (Fig. 1A). The sinuses consist of a lining of endothelial cells that are positioned in parallel and connected by stress fibers to annular fibers, which are made up of extracellular matrix components. Fig. 1B illustrates the squeezing of healthy RBCs through the narrow slits when crossing the sinus wall through the cords to the sinus lumen. The splenic IES is narrower and shorter than capillaries and forces RBCs to adopt a dumbbell shape as they pass through (20). This peculiar, dynamic 3D process has been observed in vivo only in rodents (21), the spleen of which can be transilluminated, unlike the human spleen. Detailed studies of the mechanisms involved in healthy and diseased RBC clearance by the human spleen have been hampered by two factors (16). (i) The human spleen displays anatomical and physiological features not observed in murine models. (ii) Because of the risk of potentially life-threatening intraperitoneal bleeding following any invasive exploration, the human spleen is not readily amenable to in vivo investigation by recourse to such techniques as spleen biopsy or needle aspiration. As a result, there is a critical need for studies that explore the biomechanical filtering unit of the human spleen through detailed computational simulations and modeling. Simulations using a boundary integral method have been carried out recently to study how RBCs pass through spleen-like slits and the effects of RBC flow rate and cytosol viscosity (22). However, our current knowledge of the biomechanics of the spleen is far from complete.
Fig. 1.
(A) Illustration of the splenic RBC filtration function (adapted from ref. 18). Blood flow is from lower left to upper right and may follow two parallel paths. The closed and fast circulation goes from the splenic artery to central arterioles and their branches and then through the perifollicular zone (PFZ), PFZ-to-sinus bypasses, sinus lumens, and post-sinus venules that converge in the splenic vein, which consists of 80–90% of the splenic blood flow. The open and slow circulation through the red pulp involves (i) a microcirculatory structure without endothelial cells where cord macrophages (MPs) and reticular cells screen the slowly traversing blood cells and (ii) narrow and short IES in the sinus wall that RBCs must cross to go back to the general circulation. Less deformable RBCs retained mechanically by the IES and abnormal RBCs identified can be removed through phagocytosis by macrophages (MPs) or dendritic cells (DCs). (B) Computational model geometry setup of an RBC passing through an IES with a height of Hs, width of Ws, and length of Ls, which is divided by annular fibers with a fiber width of Wf. This process is driven by the hydrodynamic pressure gradient P.
Studies of blood samples collected from healthy human subjects demonstrated (23) that the volume and the surface area of healthy RBCs have a linear relationship to each other. To rationalize this observation using simple geometric considerations, it has been proposed (23) that for an RBC to squeeze through an infinitely long tube of the smallest constant diameter (an idealized representation of a capillary in microcirculation), it should assume an optimal “cigar” shape. This postulate leads to the requirement that the surface area and volume are mutually dependent parameters. Based on this theory, the smallest diameter of the capillary that 95% of healthy human RBCs can traverse was estimated to be about 3.7 µm (23). For a small number of HS patients who had undergone splenectomy, the minimum capillary diameter for RBC traversal shifted significantly to greater values (23), and many RBCs that could not pass through the restriction of a cylindrical tube of 3.7 µm in diameter were present in blood samples. This finding [albeit considered inconclusive by the authors of that study (23) because of the limited number of reliable data points] led to the inference that the spleen might play a significant role in defining the distributions of the size and shapes of healthy RBCs in circulation. No physical mechanisms have been proposed to date to rationalize this hypothesis. As a result, the specific role of the spleen in defining the size and shape distributions of RBCs in circulation has also remained an open topic for the past several decades. Basic research into the biophysical function of the human spleen as well as into the mechanics of how cells undergo splenic clearance in health and disease inevitably calls for a better understanding of the answers to the following questions. How do variations in mechanical and physical properties due to age, disease, or genetic mutation affect the ability of an RBC to pass the “physical fitness test” in the human spleen? What pressure differences exist across the sinus slit in the human spleen, and how does this pressure gradient influence the clearance of healthy and diseased RBCs? Does the spleen play a role in defining and determining the distributions in size and shape of RBCs? If so, what are the quantitative descriptions of critical conditions for this effect? By applying the latest computational simulation tools, what new insights could be gained about the ability of an RBC to navigate through the IES as a function of different geometrical parameters as well as those altered by different disease states?
We have developed computational models that benefit from ex vivo experiments of passage and trapping of healthy RBCs and P. falciparum-invaded iRBCs in the human spleen (16) as well as from similar experiments performed on a synthetic spleen (20). In addition, ultrastructural characterization of the human spleen in the transmission electron microscope (TEM) in the latter study has provided high-resolution information of the spleen geometry, which is helpful in framing our theoretical analyses and spleen simulations.
We use the dissipative particle dynamics (DPD) computational simulation technique (24) to consider a wide range of fluid–structure interactions as RBCs pass through the IES in human spleen, by including detailed molecular-level models of RBC membranes in splenic passage (25). In addition, we also develop an analytical model that provides the overall trends and bounds for comparison with computations and experiments so as to determine how the spleen influences the size and shape distributions of RBCs.
Results and Discussion
Computational Framework.
We use the DPD-based RBC model (25, 26) for simulations. The details can be found in Methods and SI Text.
Fig. 1A is a schematic illustration of a venous sinus located in the cords in the red pulp of the human spleen. The sinuses comprise aligned endothelial cells that are connected by stress fibers to annular fibers. From such geometrical considerations and from detailed structural studies of the sinus wall in the TEM (20), we constructed the computational model for RBC traversal through the IES (Fig. 1B). The average height of the slits, Hs ∼ 0.65 µm with a range from 0.25 to 1.2 µm and an SD of 0.5 µm, and average length (the thickness of the slit wall) Ls ∼ 1.89 µm with a range from 0.9 to 3.2 µm and an SD of 0.9 µm. The width of the slit Ws ∼ 2–3 µm and the stress fiber width Wf ∼ 1 µm (27). Unless otherwise noted, we use the following reference geometry of the IES for all simulations in this study: height Hs = 1.2 µm, width Ws = 4.0 µm, and length Ls = 1.89 µm. The stress fiber width is Wf = 1 µm. These geometrical parameters were chosen from the upper bound value for slit height from TEM ultrastructural characterization experiments (20) for two reasons. First, because of the observation angle, the IES dimensions measured experimentally might have been underestimated. Second, the actual IES opening shape is not a rectangle with sharp corners. The opening is likely closer to an elongated ellipse, and the cross-section observed in the experiment might not exceed the maximum dimension in the height direction. Note that the effective stiffness of endothelial cells is ∼100 times higher than that of RBCs (28); the slit walls were thus modeled as rigid side walls of circular cylinders, comprising endothelial cells, and thin slabs, representing annular stress fibers (Fig. 1B).
Analytical Framework.
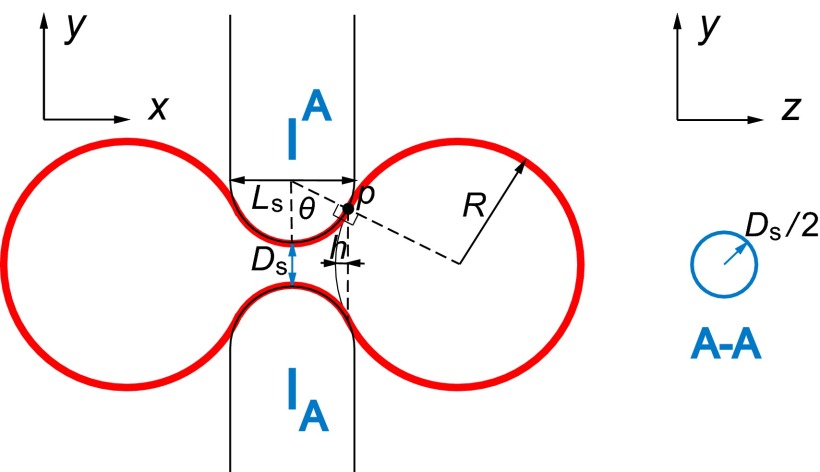
A simplified axisymmetric model amenable to theoretical analysis is first considered here (Fig. 2) to elucidate the effects of geometric constraints on RBC–IES interactions, which are further taken up for much more detailed investigation in our computational simulations that relax many of these geometric constraints.
Fig. 2.
Schematic illustration of the limiting geometry considered in the theoretical framework. The red solid line represents the RBC. At point p, the RBC surface is tangential to the surfaces of the endothelial cells. The cross-section A-A is shown on the right, where the solid line circle represents the slit cross-section. We approximate the real rectangular slit with the circular slit with the same cross-sectional area.
We assume that the slit cross-section in the y-z plane is circular (Fig. 2) instead of rectangular (Fig. 1B), but with the same cross-sectional area such that
| [1] |
The 3D slit geometry (Fig. 1B) is therefore approximated by the surface of a torus (Fig. 2). The deformed RBC at the critical condition consists of three parts: two spherical balls connected by a central connecting part (torus). The area and volume of the RBC are given, respectively, as
| [2] |
and
| [3] |
where
| [4] |
is shown in Fig. 2, which is the height of spherical cap cut by the y-z plane intersecting point p,
| [5] |
is the y coordinate of the centroid of the upper one-half cross-section of the torus part,
| [6] |
is one-half of the cross-section area of the torus part in the x-y plane, and
| [7] |
is an angle of the torus part as shown in Fig. 2. The area and volume of the middle part are calculated based on Pappus’s centroid theorem. Given the radius of the slit opening, Ds, and the thickness of the sinus wall, Ls, the axisymmetric theory thus provides the maximum volume at which the RBC with fixed surface area will be able to cross the slit of a given geometry. If Eq. 3 is rewritten as and its inverse function is given by , Eq. 4 and Eq. 7 can be expressed as and . The relationship between the surface area A and the volume V is given by
| [8] |
Comparison with Experiments.
The bounds predicted by the foregoing analysis can be compared with experimental observations in the literature (23) as well as with our computational simulations. These comparisons benefit from further insights gained through ex vivo experiments performed on isolated perfused human spleen (16) as well as on a synthetic spleen comprising a microsphere filtration system (20). The latter work suggests that the geometric characteristics obtained from spleen experiments could be recapitulated using micrometer-sized metal spheres. The microsphere filtration device was designed based on the observed slit shape and dimensions, with a 5-mm-thick layer of mixture of spheres, 5 to 15 µm in diameter. The pressure difference in the experiments where the RBC suspension was pushed through the device was held at 63.2 cm H2O, giving an average pressure gradient of 1 Pa/µm inside the filter (20). These experiments reveal that RBCs with abnormal properties were selectively retained by the microsphere filter with retention rates similar to those observed ex vivo in the isolated perfused human spleen (16). The experiments also guide the choice of critical pressure gradient required for the RBC to pass splenic slits.
These experimental results (16, 20) directly verify the mechanical sensing of RBCs by the human spleen. The results further suggest that the microsphere filter provides a mechanically equivalent system to the human spleen, by recourse to which controlled experiments could be performed to quantify the mechanics of the spleen in a manner that is not possible in the human spleen. Such experiments reveal that retention of abnormal RBCs is based mainly on their mechanical properties even without any ligand–receptor interactions between RBCs and splenic structures (20).
Volume–Area Relationship of Healthy RBC Population for IES Clearance.
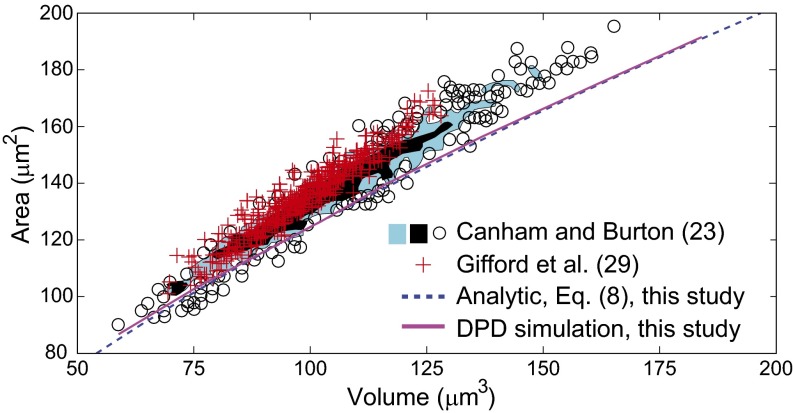
The size distribution of RBCs present in healthy human subjects is quite broad, with cell surface area varying from 80 to 180 µm2 and volume varying from 60 to 160 µm3, as shown in Fig. 3. A pressure gradient of 1.0 Pa/µm has been estimated from microsphere experiments and companion isolated perfused human spleen studies (6, 13, 20) to be sufficient for RBCs of all sizes found in blood to pass through the IES. To compare our analysis with the experimental data, we performed DPD simulations of the passage of healthy RBCs of different size through the IES at a fixed pressure gradient of 1.0 Pa/µm. For each RBC surface area, we found the critical RBC volume below which cells can fully clear the IES, whereas the IES crossing of cells with larger volume is obstructed.
Fig. 3.
Predicted relationship between healthy RBC cell volume versus surface area for a pressure gradient of 1 Pa/µm. Solid curve, prediction by DPD simulations; dashed curve, prediction by the analytical theory, Eq. 8. The scatter circle points representing individual cells and shaded areas representing two different densities (blue and black regions representing less than and greater than three cells per 1 µm5, respectively) denote the experimental measurements of Canham and Burton (23). The red data points are from the experiments of Gifford et al. (29). Healthy RBCs with volumes and areas to the left of these curves would cross the splenic slits, whereas of RBCs located to the right of the curves would be retained at the IES.
The simulation results are summarized by the solid line shown in Fig. 3, indicating the maximum RBC volume as a function of RBC surface area. Here, RBCs with surface area and volume located on the plot to the right of this solid line would fail to pass through the interendothelial slits, and therefore these RBCs would not be present in blood circulation. The predictions of our analytical model, Eq. 8, are also indicated in Fig. 3 by the dashed line. The critical conditions predicted by the analysis for the RBC volume–area relationship for IES clearance match computational simulations. The results also confirm that all RBCs present in the blood of healthy subjects are able to pass through the human spleen. The theoretical and simulation results shown by the solid and dashed lines also bound the experimental data points for the healthy RBC volume versus surface area (23). The simulation results are also consistent with more recent data (29) obtained with a high-throughput device consisting of thousands of parallel microchannels to measure the RBC surface area and volume. These findings suggest that the spleen plays an important role in defining the size of the RBCs in human circulation. Less than 3% RBCs measured in ref. 23 are found slightly below our predicted limit (the solid or dashed line). These RBCs are relatively small in volume and surface area; they are likely to be older and stiffer cells (30). These outlier RBCs could be pushed through the IES because of local pressure variation (higher pressure) or IES size variation (larger IES size) in the spleen. Alternatively, these senescent cells may reflect a small component that just reached the physical limits triggering retention but has not yet been directed to the filtering beds of the spleen.
Splenic Slit Clearance of RBCs Parasitized by P. falciparum.
We first simulate the crossing of the IES in human spleen of ring-stage iRBCs, which we model with average properties of ring-stage populations, with a cell volume of 94 µm3 and a surface area of 122 µm2 (13). The membrane shear modulus of 15.5 pN/µm was chosen from three independent experiments involving membrane flickering and microfluidics (31–33). We applied a fixed pressure gradient in each simulation to force the iRBC to cross the slit opening. By decreasing the pressure gradient in successive simulations, the critical condition for obstruction of ring-stage iRBCs in the IES was identified. The RBC model used in our DPD simulations has been extensively calibrated with systematic experiments on parasitized iRBCs in microfluidic devices (32, 33).
We begin with a DPD simulation of an iRBC with a fixed surface area of 122 µm2. In order for this iRBC to completely squeeze through the IES, the critical pressure gradient required was 1.42 Pa/µm. We then allowed for up to a 7% increase of the RBC surface area during IES crossing to account for the fact that the surface area of the RBC membrane changes during large deformation of the cell. With this increased surface area, the critical pressure gradient required for traversing the IES was reduced to 0.64 Pa/µm. Typical values of membrane area increase reported in the literature are about 2–4% (34), depending on the type of deformation and stress state. Precise values of area change during the RBC traversal through the spleen are not known, and hence the two cases considered here represent, to some degree, extreme conditions.
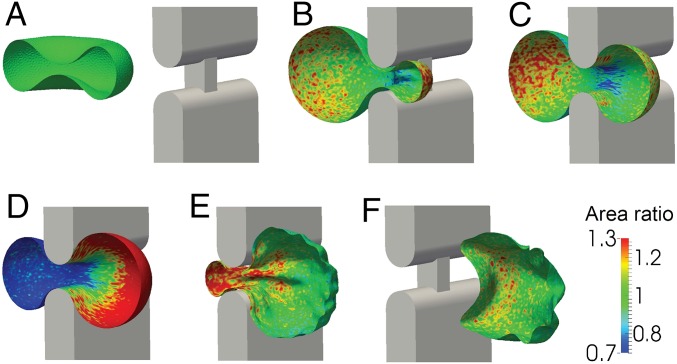
Fig. 4 comprises a sequence of six images showing a ring-stage iRBC as it clears a splenic slit under a critical pressure gradient 0.64 Pa/µm (also see Movie S1). The color contours show the fractional local surface area change of the composite layer comprising the membrane and the spectrin network cytoskeleton. Movie S1 also reveals that there can be considerable time delay for the iRBC to traverse the slit upon application of critical pressure gradient. If the pressure gradient is increased, the RBC traversal time is reduced. If we assume that the increase in typical membrane area for the cell of about 2–4%, the critical pressure gradient in the spleen would be predicted, from our DPD simulations, to be between 1.42 and 0.64 Pa/µm. This value is close to 1.0 Pa/µm, derived from the microsphere filtration experiments, which were also compared with those from isolated perfused spleen experiments (13, 20). Under this pressure gradient of 1.0 Pa/µm, the retention rate in the spleen of ring-stage iRBCs was about 50%, which implies that this pressure gradient was the critical value for an average ring-stage iRBC to pass through the splenic slit.
Fig. 4.
DPD simulation of a sequence of six steps (A–F) as an iRBC parasitized by P. falciparum passes through a slit in the human spleen at a constant pressure gradient of 0.64 Pa/µm. During this large deformation process, the iRBC is allowed to have a change up to 7% in total surface area from its undeformed value of 122 µm2. Only one-half of the RBC is shown for clarity and visualization. The color contours show local values of the ratio of the deformed to undeformed surface area of the RBC membrane. Here, area expansion occurs for values >1.0, whereas compression occurs for values <1.0.
Effects of Cell Surface Area and Stiffness.
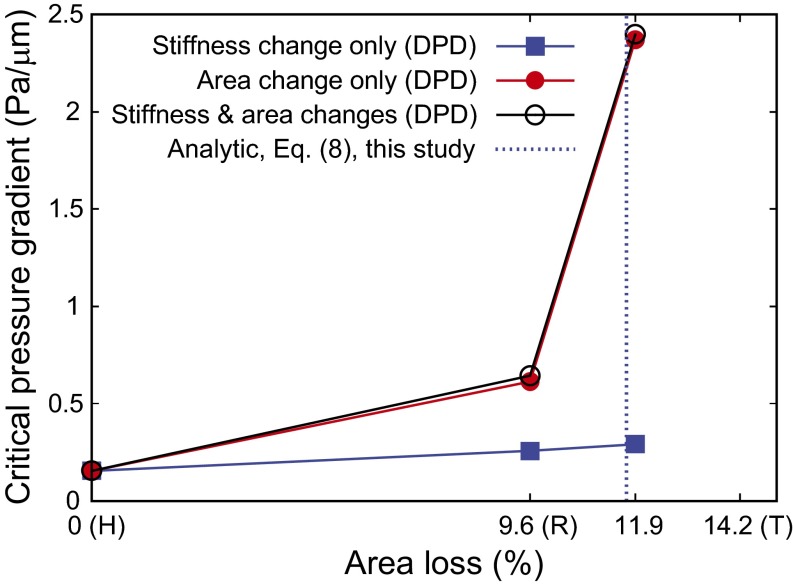
We now consider healthy, ring-, and trophozoite-stage RBCs invaded by P. falciparum merozoites; the surface area of the RBCs in these three cases, respectively, was taken to be 135, 122.04, and 115.83 µm2 (13), and the respective values of the membrane shear modulus were 5.5, 15.5, and 28.9 pN/µm (31). The cell volume was taken to be 94 µm3 for all three cases. For ring and trophozoite cells, with intracellular parasite maturation over 6–24 and 24–36 h, respectively, we performed three simulations: (i) only stiffness change was considered, (ii) only surface area change was considered, and (iii) both stiffness change and surface area change were considered. By changing the magnitude of the pressure gradient, we identified the critical, minimum pressure gradient necessary for the cells to pass through the slit, as shown in Fig. 5.
Fig. 5.
The critical minimum pressure gradient for P. falciparum-infected RBCs in different stages to pass through the IES, as predicted by DPD. The blue dashed line is the limiting condition predicted by theory, Eq. 8, for critical area loss at fixed cell volume. Beyond this limiting geometry, an infinitely high pressure gradient is required for the RBCs to clear the splenic slit. The surface area loss for healthy (H), ring (R), and trophozoite (T) RBCs are taken to be 0%, 9.6%, and 14.2%, respectively, from the experiments of Safeukui et al. (13).
The simulation results show that the surface area loss arising from RBC parasitization plays a much more important role than the ensuing stiffness increase. There is a significant increase in the critical pressure gradient from the ring to trophozoite stage. For trophozoite, no RBC passed the IES opening even for very high values of applied pressure gradient, if an area loss of 14.2% is considered. Therefore, we used area loss of 11.9% for trophozoite, which is the midpoint between the ring and trophozoite stages and can be considered as young trophozoite (35).
The blue vertical dashed line in Fig. 5 shows the theoretical prediction, Eq. 8, of the maximum area loss allowed for RBCs (at the fixed cell volume) to pass the circular opening with the same surface area as that considered in the DPD simulations. In physical terms, our theory indicates that cells with larger surface area loss than this critical value (at a fixed volume) will require an infinitely large pressure gradient for RBC passage; this prediction is consistent with the results of the computational simulations.
Effects of Cell Volume.
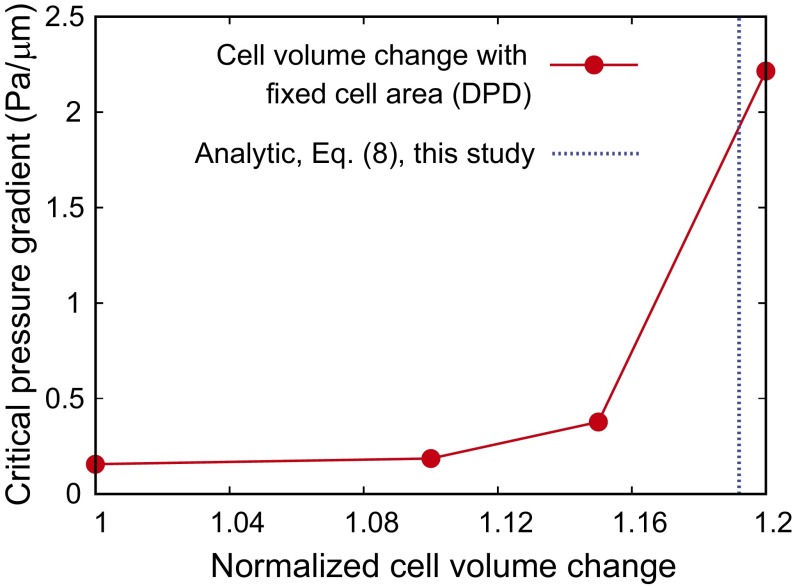
Finally, we investigate how the cell volume influences the critical pressure gradient for RBCs to pass through the splenic slit. For these studies, we focus on the ring-stage iRBCs with a surface area of 122 µm2 and a membrane shear modulus of 15.5 pN/µm. Fig. 6 shows the effect of the cell volume, for a fixed cell surface area, on the critical minimum pressure gradient for passage through the IES. The critical pressure gradient steeply increases as the change in the RBC volume approaches 20%. Cells with larger volumes were not able to clear the slit in our DPD simulations.
Fig. 6.
Dependence of the critical pressure gradient on the cell volume for fixed cell surface area. Blue dashed lines are the limiting geometries predicted by the theory Eq. 8.
The blue dashed vertical line in Fig. 6 shows the maximum volume increase predicted by our theory for the RBC to clear the circular opening, with the same cell surface area as that considered in the DPD simulations. The theory predicts a maximum value of 19% volume increase (113 µm3) for a standard healthy cell (95 µm3), beyond which the minimum pressure gradient necessary to clear the slit becomes too large. The simulation results (red solid line) are seen to be in agreement with this axisymmetric theory. Hence, the analytical theory could serve as a rough guide for defining the critical RBC geometry in the limiting case.
Conclusions
We have developed computational simulations, coupled with a theoretical analysis, of the mechanics of RBC clearance by the spleen. We have generated a unique quantitative framework for RBCs crossing a narrow slit in the spleen, a process that cannot be dynamically observed in humans. Shape deformation during this most stringent biomechanical challenge on RBCs in circulation (20) appeared very different from the bullet-shaped deformation of RBCs in narrow capillaries (36). Our analyses and simulations provide limiting conditions of surface area and volume beyond which healthy RBCs can cross the spleen; these predictions are in agreement with the distributions of size and shape of healthy RBCs observed in circulation (Fig. 3). These results are also consistent with independent experimental results obtained by challenging human spleens with human RBCs modified either artificially (6) or by infection with the intraerythrocytic parasite P. falciparum (13). The present computations do not fully account for the interactions between the lipid bilayer and the cytoskeleton, which will inevitably require a more computationally expensive, two-component model. The computations also do not consider the effects of intrinsic stiffness of the membrane–cytoskeleton complex and viscosity of the cytoplasm on RBC passage through the splenic slits. However, as previously observed experimentally (6) and predicted here (Fig. 3), the surface to volume ratio is by far the most important parameter of RBC deformability.
Taken together, these results provide a robustly validated quantitative framework on how the human spleen plays its biomechanical filtering role that contributes to the quality assurance of circulating RBCs. This framework opens unique pathways for the use of quantitative morphological features of circulating RBC—now rapidly obtained by imaging flow cytometry (6, 37)—as markers of hyposplenism in patients with suspected inherited or acquired splenic dysfunction, a condition associated with severe infectious, circulatory, and proliferative complications (38). In addition to splenectomized patients (38), hyposplenism affects a majority of children with sickle-cell disease (39) and patients suffering from an array of acute or chronic medical conditions (40), such as celiac disease, inflammatory bowel diseases, cirrhosis, and viral or bacterial infections. More precise estimates of splenic function would guide patient management for an optimal adaptation of antimicrobial prophylaxis (41) and prevention of thrombotic events (42). Several conditions, such as malaria, thalassemia, or severe hematological diseases (leukemia and lymphomas), induce enlargement of the spleen with subsequent propensity to filter not only abnormal cells but also healthy RBCs (43), thus causing anemia. Our approach forms the first step of a potential systematic reconstruction of the navigation of RBCs in the human spleen across narrow slits but also upstream and downstream from this unique circulatory bottleneck.
Methods
RBC Model.
The details of the DPD based RBC model can be found in SI Text, RBC Model.
Ex Vivo and Synthetic Spleen Studies and Structural Characterization.
Clinical interventions associated with left splenopancreatectomy for benign tumors of the pancreas (16) have led to ex vivo experiments in isolated human spleen perfused with healthy RBCs, iRBCs invaded by P. falciparum, as well as chemically treated RBCs with controlled surface area loss (6, 13, 16, 20). Geometric characteristics of RBC interactions and trapping from ex vivo human spleen have also been replicated using a “synthetic spleen” made of metal spheres (20). These studies showed that the retention of abnormal RBCs was influenced predominantly by their mechanical properties and that these effects could occur in the absence of ligand–receptor interactions between RBCs and the relevant splenic structures. Additional discussions are included in SI Text, Ex Vivo and Synthetic Spleen Studies and Structural Characterization.
DPD Method.
The DPD method invokes a coarse-grained molecular dynamics approach, further details of which are described in SI Text, DPD Model and Scaling of Physical Units.
Simulation Setup.
The simulation setup is illustrated in Fig. 1B. More details and input parameters can be found in SI Text, Simulation Setup.
SI Text
RBC Model.
The DPD model (25, 26) mimics the structure of the RBC membrane, which comprises a lipid bilayer and an attached cytoskeleton consisting primarily of spectrin proteins arranged in a network and linked by short actin filaments at junction complexes. There are about 25,000 junction complexes per healthy human RBC. In the computational model, the RBC is represented by a collection of particles. Each particle directly corresponds to a junction complex in the RBC membrane. The particles are connected with links, with each representing a spectrin link in the RBC cytoskeleton. The mechanical properties of the links are described using the worm-like chain model, reflecting the entropic-chain behavior of the spectrin. In addition, viscous components are added to represent the behavior of the RBC membrane. The links form a triangular tessellation of the model surface. For adjacent triangles, bending resistance of the lipid bilayer is added. Two additional constraints are present in the model. The surface area is held constant, taking into account low compressibility of the lipid bilayer. The volume of RBCs is controlled by the osmotic effects and is practically constant even for quite severe deformation. This constraint is reflected by the constant volume in the simulations. Specific details of the RBC model and parameters can be found in refs. 25 and 26.
Ex Vivo and Synthetic Spleen Studies and Structural Characterization.
Clinical interventions associated with left splenopancreatectomy for benign tumors of the pancreas (16) have led to ex vivo experiments in isolated human spleen perfused with healthy RBCs, iRBCs invaded by P. falciparum malaria parasites, as well as chemically treated RBCs with controlled surface area loss (6, 13, 16, 20). These studies have also yielded the retention rate of iRBCs by the spleen under different pathological states post-P. falciparum invasion. When healthy RBCs were treated with lysophosphatidylcholine (1–18 μmol/L) in PBS at 1% hematocrit to induce 18% average surface area loss and more than 27% reduction in surface area-to-volume ratio, they were rapidly and entirely retained within the spleen (6). By monitoring surface area loss in P. falciparum-infected RBCs using ImageStream imaging cytometer (Ideas v4.0; Amnis) with at least 10,000 images collected for each sample, the surface area loss and the resultant increase in sphericity were found to be linked to ring-stage iRBC retention, thereby contributing to splenic entrapment of a subpopulation of ring-stage iRBCs (13). Detailed analysis of the structure of the sinus wall in the spleen has also been performed (20), whereby the dimensions of interendothelial slits were determined from observations in the transmission electron microscope.
Geometric characteristics of RBC interactions and trapping from ex vivo human spleen have also been replicated using a “synthetic spleen” made of micrometer-sized metal spheres (20). The microsphere filtration device was designed based on the observed slit shape and dimensions of the human spleen, with a 5-mm-thick layer of a mixture of metal spheres, 5 to 15 µm in diameter. Experiments showed that RBCs with abnormal properties were selectively retained by the microsphere filter with retention rates similar to those observed in the isolated perfused human spleen (16). For the specific questions examined in this study, the experiments (20) also showed that the retention of abnormal RBCs was influenced predominantly by their mechanical properties and that these effects could occur in the absence of ligand–receptor interactions between the surfaces of the RBC external surface and the relevant splenic structures.
DPD Model and Scaling of Physical Units.
Each particle in DPD represents a cluster of atoms or molecules (24). The DPD particles interact through pairwise forces: conservative, random, and dissipative. Every particle in the RBC membrane becomes a DPD particle in simulations. The RBC is immersed into and filled with the DPD fluid. The RBC particles interact with the fluid particles through the DPD forces, and the motion of the RBC membrane is fully coupled with the motion of the fluid. Specific details of the DPD method implementation can be found in ref. 26.
When setting up the DPD model, reduced units are implemented for the mass, length, and energy. In the following, the scaling relationships between model units and physical units are developed (26).
If represents the length scale in the physical system in SI units and represents the length scale of the DPD model, then the same initial diameter () of the RBC can be expressed in both the DPD system and the physical system as
| [S1] |
where and m is meter. The variables with upper index “P” (e.g., ) are values (numbers without units) of the quantities (e.g., ) in the physical system with SI units, whereas the variables with upper index “M” (e.g., ) are values (numbers without units) of the quantities (e.g., ) in the DPD system. We can choose the length scale of the DPD system, and usually specific values of and depend on the size of the DPD system.
Because , where denotes the dimension of a quantity, is the shear modulus, is the Boltzmann constant, and is the temperature, we should have
| [S2] |
Plugging Eq. S1 into Eq. S2, we get
| [S3] |
Similarly for the force N, because , we have
| [S4] |
For time scaling, because , where is a characteristic viscosity, we have
| [S5] |
where second is the time scale in the physical system with SI units, and is the time scale in the DPD system. Plugging Eq. S4 into Eq. S5, we get the time scale of the DPD system as
| [S6] |
where s denotes second.
Specifically, in our simulations, the RBC diameter, the membrane Young’s modulus and the interior fluid viscosity are = 25.806, = 4.704, and = 1.8, respectively, corresponding to , = 5.5 , and = 0.006 in the physical system with SI units. Consequently, the DPD time scale is 0.8639 ms.
Simulation Setup.
The simulation setup is illustrated in Fig. 1B. The endothelial cells are modeled by two slabs with cylindrical edges, and the annular fibers are modeled as slabs perpendicular to the endothelial cells. The bounce-back boundary condition (26) is enforced between the RBC membrane and the surfaces of the endothelial cells and the annular fibers. We considered 23,867 junction complexes in the RBC DPD model. The initial shear modulus for a healthy cell is 5.5 pN/µm (31), and the bending stiffness is 2 × 10−19 J. The total cell surface area and cell volume are conserved during simulations.
Supplementary Material
Acknowledgments
I.V.P. thanks Maria Grazia Giuffreda [Swiss National Supercomputer Center (CSCS)] for her support. This work is supported by National Institutes of Health (NIH) Grants U01HL114476 and R01HL121386, a Swiss Platform for Advanced Scientific Computing grant, CSCS Grant s583, National Science Foundation XSEDE Project TG-MCB130124, and the new DOE Collaboratory on Mathematics for Mesoscopic Modeling of Materials (CM4). I.V.P, Z.P., M.D., and S.S. acknowledge partial support from the Singapore-MIT Alliance for Research and Technology (SMART) Center. Simulations were carried out at CSCS under Projects s583 and u4, Kraken and Darter at the National Institute for Computational Sciences (NICS) under Project TG-MCB130124, and also at the Argonne Leadership Computing Facility (ALCF) through the Innovative and Novel Computational Impact on Theory and Experiment (INCITE) program at Argonne National Laboratory (ANL).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1606751113/-/DCSupplemental.
References
- 1.Mebius RE, Kraal G. Structure and function of the spleen. Nat Rev Immunol. 2005;5(8):606–616. doi: 10.1038/nri1669. [DOI] [PubMed] [Google Scholar]
- 2.Petroianu A. The Spleen. Bentham Science Publishers; Hilversum, The Netherlands: 2011. [Google Scholar]
- 3.Jandl JH, Greenberg MS, Yonemoto RH, Castle WB. Clinical determination of the sites of red cell sequestration in hemolytic anemias. J Clin Invest. 1956;35(8):842–867. doi: 10.1172/JCI103338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Waugh RE, et al. Rheologic properties of senescent erythrocytes: Loss of surface area and volume with red blood cell age. Blood. 1992;79(5):1351–1358. [PubMed] [Google Scholar]
- 5.Suresh S. Mechanical response of human red blood cells in health and disease: Some structure-property-function relationships. J Mater Res. 2006;21(8):1871–1877. [Google Scholar]
- 6.Safeukui I, et al. Quantitative assessment of sensing and sequestration of spherocytic erythrocytes by the human spleen. Blood. 2012;120(2):424–430. doi: 10.1182/blood-2012-01-404103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kumar V, Abbas AK, Aster JC. Robbins Basic Pathology. 9th Ed Elsvier, Saunders; Philadelphia: 2012. [Google Scholar]
- 8.Perrotta S, Gallagher PG, Mohandas N. Hereditary spherocytosis. Lancet. 2008;372(9647):1411–1426. doi: 10.1016/S0140-6736(08)61588-3. [DOI] [PubMed] [Google Scholar]
- 9.Prendki V, et al. Reduced deformability of circulating erythrocytes: A marker of hyposplenism. Am J Hematol. 2012;87(10):E81–E82. doi: 10.1002/ajh.23297. [DOI] [PubMed] [Google Scholar]
- 10.Dondorp AM, et al. Red cell deformability, splenic function and anaemia in thalassaemia. Br J Haematol. 1999;105(2):505–508. doi: 10.1111/j.1365-2141.1999.01367.x. [DOI] [PubMed] [Google Scholar]
- 11.Zaets SB, et al. Burn-induced red blood cell deformability and shape changes are modulated by sex hormones. Am J Surg. 2003;186(5):540–546. doi: 10.1016/j.amjsurg.2003.07.022. [DOI] [PubMed] [Google Scholar]
- 12.Cranston HA, et al. Plasmodium falciparum maturation abolishes physiologic red cell deformability. Science. 1984;223(4634):400–403. doi: 10.1126/science.6362007. [DOI] [PubMed] [Google Scholar]
- 13.Safeukui I, et al. Surface area loss and increased sphericity account for the splenic entrapment of subpopulations of Plasmodium falciparum ring-infected erythrocytes. PLoS One. 2013;8(3):e60150. doi: 10.1371/journal.pone.0060150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mills JP, et al. Effect of plasmodial RESA protein on deformability of human red blood cells harboring Plasmodium falciparum. Proc Natl Acad Sci USA. 2007;104(22):9213–9217. doi: 10.1073/pnas.0703433104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Safeukui I, et al. Retention of Plasmodium falciparum ring-infected erythrocytes in the slow, open microcirculation of the human spleen. Blood. 2008;112(6):2520–2528. doi: 10.1182/blood-2008-03-146779. [DOI] [PubMed] [Google Scholar]
- 16.Buffet PA, et al. Ex vivo perfusion of human spleens maintains clearing and processing functions. Blood. 2006;107(9):3745–3752. doi: 10.1182/blood-2005-10-4094. [DOI] [PubMed] [Google Scholar]
- 17.Buffet PA, Safeukui I, Milon G, Mercereau-Puijalon O, David PH. Retention of erythrocytes in the spleen: A double-edged process in human malaria. Curr Opin Hematol. 2009;16(3):157–164. doi: 10.1097/MOH.0b013e32832a1d4b. [DOI] [PubMed] [Google Scholar]
- 18.Buffet PA, et al. The pathogenesis of Plasmodium falciparum malaria in humans: Insights from splenic physiology. Blood. 2011;117(2):381–392. doi: 10.1182/blood-2010-04-202911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Duez J, et al. Mechanical clearance of red blood cells by the human spleen: Potential therapeutic applications of a biomimetic RBC filtration method. Transfus Clin Biol. 2015;22(3):151–157. doi: 10.1016/j.tracli.2015.05.004. [DOI] [PubMed] [Google Scholar]
- 20.Deplaine G, et al. The sensing of poorly deformable red blood cells by the human spleen can be mimicked in vitro. Blood. 2011;117(8):e88–e95. doi: 10.1182/blood-2010-10-312801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Groom AC, Schmidt EE, MacDonald IC. Microcirculatory pathways and blood flow in spleen: New insights from washout kinetics, corrosion casts, and quantitative intravital videomicroscopy. Scanning Microsc. 1991;5(1):159–173. [PubMed] [Google Scholar]
- 22.Freund JB. The flow of red blood cells through a narrow spleen-like slit. Phys Fluids. 2013;25(11):110807. [Google Scholar]
- 23.Canham PB, Burton AC. Distribution of size and shape in populations of normal human red cells. Circ Res. 1968;22(3):405–422. doi: 10.1161/01.res.22.3.405. [DOI] [PubMed] [Google Scholar]
- 24.Hoogerbrugge PJ, Koelman J. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys Lett. 1992;19(3):155–160. [Google Scholar]
- 25.Pivkin IV, Karniadakis GE. Accurate coarse-grained modeling of red blood cells. Phys Rev Lett. 2008;101(11):118105. doi: 10.1103/PhysRevLett.101.118105. [DOI] [PubMed] [Google Scholar]
- 26.Peng Z, et al. Lipid bilayer and cytoskeletal interactions in a red blood cell. Proc Natl Acad Sci USA. 2013;110(33):13356–13361. doi: 10.1073/pnas.1311827110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen LT, Weiss L. The role of the sinus wall in the passage of erythrocytes through the spleen. Blood. 1973;41(4):529–537. [PubMed] [Google Scholar]
- 28.Hochmuth RM. Micropipette aspiration of living cells. J Biomech. 2000;33(1):15–22. doi: 10.1016/s0021-9290(99)00175-x. [DOI] [PubMed] [Google Scholar]
- 29.Gifford SC, et al. Parallel microchannel-based measurements of individual erythrocyte areas and volumes. Biophys J. 2003;84(1):623–633. doi: 10.1016/S0006-3495(03)74882-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sens P, Gov N. Force balance and membrane shedding at the red-blood-cell surface. Phys Rev Lett. 2007;98(1):018102. doi: 10.1103/PhysRevLett.98.018102. [DOI] [PubMed] [Google Scholar]
- 31.Park Y, et al. Refractive index maps and membrane dynamics of human red blood cells parasitized by Plasmodium falciparum. Proc Natl Acad Sci USA. 2008;105(37):13730–13735. doi: 10.1073/pnas.0806100105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bow H, et al. A microfabricated deformability-based flow cytometer with application to malaria. Lab Chip. 2011;11(6):1065–1073. doi: 10.1039/c0lc00472c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Quinn DJ, et al. Combined simulation and experimental study of large deformation of red blood cells in microfluidic systems. Ann Biomed Eng. 2011;39(3):1041–1050. doi: 10.1007/s10439-010-0232-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Evans EA, Waugh R, Melnik L. Elastic area compressibility modulus of red cell membrane. Biophys J. 1976;16(6):585–595. doi: 10.1016/S0006-3495(76)85713-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dondorp AM, et al. Direct in vivo assessment of microcirculatory dysfunction in severe falciparum malaria. J Infect Dis. 2008;197(1):79–84. doi: 10.1086/523762. [DOI] [PubMed] [Google Scholar]
- 36.Guest MM, Bond TP, Cooper RG, Derrick JR. Red blood cells - Change in shape in capillaries. Science. 1963;142(3597):1319–1321. doi: 10.1126/science.142.3597.1319. [DOI] [PubMed] [Google Scholar]
- 37.Jauréguiberry S, et al. French Artesunate Working Group Postartesunate delayed hemolysis is a predictable event related to the lifesaving effect of artemisinins. Blood. 2014;124(2):167–175. doi: 10.1182/blood-2014-02-555953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kristinsson SY, Gridley G, Hoover RN, Check D, Landgren O. Long-term risks after splenectomy among 8,149 cancer-free American veterans: A cohort study with up to 27 years follow-up. Haematologica. 2014;99(2):392–398. doi: 10.3324/haematol.2013.092460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rogers ZR, et al. BABY HUG Biomarkers of splenic function in infants with sickle cell anemia: Baseline data from the BABY HUG Trial. Blood. 2011;117(9):2614–2617. doi: 10.1182/blood-2010-04-278747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Di Sabatino A, Carsetti R, Corazza GR. Post-splenectomy and hyposplenic states. Lancet. 2011;378(9785):86–97. doi: 10.1016/S0140-6736(10)61493-6. [DOI] [PubMed] [Google Scholar]
- 41.Lammers AJJ, et al. Hyposplenism: Comparison of different methods for determining splenic function. Am J Hematol. 2012;87(5):484–489. doi: 10.1002/ajh.23154. [DOI] [PubMed] [Google Scholar]
- 42.Crary SE, Buchanan GR. Vascular complications after splenectomy for hematologic disorders. Blood. 2009;114(14):2861–2868. doi: 10.1182/blood-2009-04-210112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Looareesuwan S, et al. Dynamic alteration in splenic function during acute falciparum malaria. N Engl J Med. 1987;317(11):675–679. doi: 10.1056/NEJM198709103171105. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.